Abstract
Conjunctive queries play a key role in retrieving data from a database. In a database, a query containing many conditions in its predicate, connected by an “and/&/∧” operator, is called a conjunctive query. Retrieving the outcome of a conjunctive query from thousands of records is a heavy computational task. Private data access to an outsourced database is required to keep the database secure from adversaries; thus, private conjunctive queries (PCQs) are indispensable. Cheon, Kim, and Kim (CKK) proposed a PCQ protocol using search-and-compute circuits in which they used somewhat homomorphic encryption (SwHE) for their protocol security. As their protocol is far from being able to be used practically, we propose a practical batch private conjunctive query (BPCQ) protocol by applying a batch technique for processing conjunctive queries over an outsourced database, in which both database and queries are encoded in binary format. As a main technique in our protocol, we develop a new data-packing method to pack many data into a single polynomial with the batch technique. We further enhance the performances of the binary-encoded BPCQ protocol by replacing the binary encoding with N-ary encoding. Finally, we compare the performance to assess the results obtained by the binary-encoded BPCQ protocol and the N-ary-encoded BPCQ protocol.
1. Introduction
In this digital age, data are produced every day at a gigantic rate because of the use of various types of software by hospitals, clinics, research organizations, banks, insurance companies, e-commerce companies, and many others. These organizations do not want their data to be vulnerable to malicious persons, but they do want their data to be available online. They therefore either allow access to the data using queries from anywhere in the world or apply some functions to the data for retrieving statistics on the data. Simultaneously, they need to protect their own sensitive data along with their customers. Therefore, they should store data on some trusted online servers. Practically, it is hard to find trusted online servers. Nowadays, we can achieve data privacy using some techniques such as steganography and cryptography. Steganography is the art of hiding data in multimedia files such as images, audio clips, and video clips. Steganography provides privacy of embedded data, but it compromises the data size. Furthermore, protecting data by some cryptographic techniques is another solution to data privacy. However, conventional encryption does not support computation over the encrypted data. If we use conventional encryption schemes to encrypt the data before storing them to the cloud, encrypted data need to be decrypted. To perform addition and multiplication over encrypted data, homomorphism [1] is a solution to computation over the encrypted data. Using the homomorphism property, Rivest et al. [1] introduced the concept of homomorphic encryption, in which they showed multiplicative homomorphism using the RSA algorithm [2]. The homomorphic encryption (HE) ensures computation over the encrypted data without distorting their originality, i.e., any operation performed over cipher text produces the same result after decryption if that operation is performed over the corresponding plain text. For example, considering messages and , we can calculate the function from and without having prior knowledge of the actual messages and , where E denotes an encryption function. Before Gentry’s invention [3], computation over encrypted data was limited to either a few additions or a multiplication [4,5,6,7]. According to the computation capability of the homomorphic encryption scheme, homomorphic encryption can be classified into three categories: partial homomorphic encryption (PHE) [1,5,6,7,8], somewhat homomorphic encryption (SwHE) [3,9,10], and fully homomorphic encryption (FHE) [3,11,12,13,14].
1.1. Motivation
In 2009, Gentry [3] introduced a fully homomorphic encryption scheme, which can be constructed from SwHE by applying a bootstrapping technique to the SwHE. Bootstrapping is an intermediate procedure of refreshing homomorphically operated ciphertexts, which is a costly computation. Therefore, the performance of this FHE cannot be used practically due to its inefficiency in processing the encrypted data [15] and producing large ciphertexts. Later, Brakerski and Vaikuntanathan [10] proposed a ring-learning-with-errors-based (RLWE) SwHE scheme, which allows many additions and a few multiplications over the encrypted data. Actually, the scheme uses an degree polynomial to pack n data using a packing method. Because of packing many data into a single polynomial, it reduces the ciphertext size after encryption and thus reduces the time of the computation over those packed ciphertexts. The security of the SwHE depends on the hardness of the LWE problems [16] on an ideal lattice, which is thought to be secure against cryptanalysis using a quantum computer. Therefore, RLWE-based SwHE is considered a post-quantum encryption. Given this advantageous nature of RLWE-based SwHE, it is used in many applications in the cloud such as statistics computation [17,18], genomic computations [19,20], private equality tests [21,22], private database queries [23,24,25], and private inequality tests [26,27]. In these applications, data-encoding methods, also called packing methods, play an important role in the efficiency. Therefore, RLWE-based SwHE with tailored packing methods can be used for constructing more efficient and quantum-secure applications such as private database queries, genomic computation, and so on.
We use database queries to directly access data from a local database and remotely from an outsourced database in the cloud. For example, we suppose a patient table in a hospital database. A query to access data from the table can be represented as select * from patient. Whenever we want to access more specific data from the patient table in the database, we need to add one or more conditional statements to the query. When we add two or more conditions to the predicate of a query using the and/&/∧ operator, the query is called a conjunctive query. For instance, a conjunctive query, select * from patient, where diseases=‘cholera’ and patient_age≥12, can select the patients from the patient table who are suffering from cholera and are 12 years of age and over. If this hospital database is a private outsourced database, it is indispensable for database users to choose private conjunctive queries rather than plain conjunctive queries to maintain the privacy both of the database and the users’ queries In this paper, we focus on the private conjunctive query (PCQ), which has two or more equality conditions in the predicate of the queries.
From the above example, the PCQ plays a significant role in securely accessing data from an outsourced private database in reply to private queries by the users. To ensure the privacy both of the database and queries and to support encrypted computations, the RLWE-based SwHE [10] provides a suitable solution. To effectively use RLWE-based SwHE in different applications, several data packing methods [17,18,19,20] have been proposed. In this respect, we considered developing a new packing method to efficiently solve PCQ problems.
1.2. Problem Statements
A conventional solution for evaluating a private conjunctive query with k equality conditions in the predicate requires evaluating k sub-queries. The expected outcome can be determined by taking the intersection of the individual results obtained from the sub-queries. For example, consider a database containing a table of record along with k attributes and the corresponding value of each attribute is denoted by with . Then, a conjunctive query like select count(id) from record where contains k equality conditions in its predicate. Here, we first evaluate k sub-queries by counting “id” for and then compute the intersection for the conjunctive query. If we outsource this computation to the cloud without keeping any security, it will disclose information regarding the database records to the cloud. In 2016, Cheon et al. [28] proposed a PCQ protocol using search-and-compute circuits in which they used SwHE for guaranteeing their protocol security. Supplementarily, they admitted that they need to improve the performance of their PCQ protocol for practical use. Therefore, an efficient protocol must be designed to solve this PCQ problem in the cloud. As such, Saha and Koshiba [24] proposed an efficient protocol for processing PCQ in the cloud. They used a fixed-length binary data-packing method for encoding multi-dimensional data together with a concatenation technique. Their packing method is polynomial-based, where every binary datum is encoded as the coefficient of x with different exponents for a polynomial . Therefore, the degree of the polynomial increases with the increase in the length of the binary data to be packed. The efficiency of the proposed protocol depends on the degree of the polynomial. Moreover, the computational cost increases with the increase in the lattice dimension in RLWE-based SwHE [10]. For this reason, the efficiency of the protocol could be improved using encoding that is different from binary encoding.
1.3. System Model
A basic system model for processing three-party PCQ in the cloud is shown in Figure 1. In this model, we suppose that Charlie is a database owner and Alice is a client who wants to retrieve data from Charlie’s database. Here, Charlie wants to answer Alice’s query Q by revealing as little information as possible about the database D. Alice also wants to retrieve the required data without losing much information on the query. To process a PCQ in this scenario, a third party like Bob in the cloud can perform their task with the help of homomorphic encryption. For ensuring privacy, we consider securing the data in the database and the value of each attribute existing in the predicate of the query. In the model, Alice generates both a public key and its secret key and sends the public key to Charlie. Alice encrypts the query Q using the public key after parsing the values and sends the encrypted values to the cloud. Charlie sends their encrypted database to the cloud. Now, Bob homomorphically computes to decide the conjunctive equalities between and where ⊙ defines some homomorphic operations. Then, Bob sends the result back to Alice for decryption. Alice decrypts by using her secret key and decides the conjunctive equalities between Q and D.
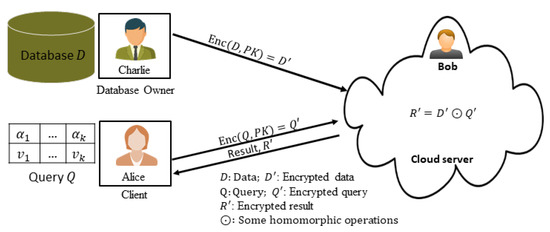
Figure 1.
Basic three-party system model to solve the private database queries (PCQ) problem in the cloud.
1.4. Key Technique
For solving the PCQ problem stated in Section 1.2, we use a special method called the concatenation technique with fixed-length data instead of the traditional technique for comparing values in the predicate of a query with the data in the database. As shown in Figure 1, the PCQ problem can be solved by involving a third party like Bob in the cloud, where a database owner and a query owner are different entities. Let us consider the conjunctive query containing k equality conditions in its predicate (select count(id) from patientRecord where and and ⋯ and , where ). If we use the traditional approach to decide the k equalities, we need to send k equality queries to the cloud, which return some IDs. The expected outcome can be calculated by taking the intersection of those IDs. In this case, information regarding the database will be revealed to Alice. However, our goal is to process PCQ with revealing as little information to Alice as possible. To solve this problem, Alice can encode values from the predicate of the query as fixed-length data and pack those encoded values sequentially as the coefficients of x with different exponents in a single polynomial and send the packed data to the cloud after encryption. Similarly, Charlie can pack the values of k attributes of the database in the same order and send them to the cloud. Next, Bob blindly matches them using the Hamming distance and returns the encrypted distances to Alice. In the end, Alice decrypts those encrypted distances and counts the Hamming distances of being zero to decide the conjunctive equalities. Moreover, the table consists of numerous records. To process the PCQ with k conditions, the concatenation approach needs to perform the equality comparison many times. We can solve this problem using a batch equality technique as mentioned in [29]. The strengths of the above technique are listed below.
- The set intersection operation can be omitted to avoid information leakage to Alice.
- The multiplication depth of the equality test can be reduced through batching.
- The number of homomorphic multiplications required for conjunctive equality tests can be decreased using the batch technique.
1.5. Previous Works
Here, we review recent works on private conjunctive queries using different cryptographic schemes. In 2013, Boneh et al. [30] proposed a new method to address private conjunctive queries in the database. However, their method requires set intersection operations, which reveal some information to the user. In 2014, Pappas et al. [31] constructed a technique called blind seer to support quite a rich query set over a private database management system (DBMS) using Yao’s garbled circuits [32] and oblivious transfer in the semi-honest model. Then, Fisch et al. [33] improved the security of blind seer by making the system secure against malicious clients. However, both require a communication of non-constant rounds for searching data where they essentially use Yao’s garbled circuits [32]. Cheon et al. [28] reported a method of conjunctive query processing. They guaranteed the privacy of the values in the predicate. However, the performance of their protocol was impractical. Kim et al. [34] proposed another method of evaluating private database queries. They reduced the communication cost of accessing records, which was required by previous methods. However, they required a multiplicative depth of to process each l-bit data and did not provide the individual query performance. None of these methods addressed conjunctive queries with low multiplication depth, which led to efficient execution of the method. In 2019, Saha et al. [23] introduced a private conjunctive query protocol that works with the query, including k conditions in the predicate of that query. Here, they calculated the conjunctive query by sending k sub-queries separately to the cloud to determine the record IDs satisfying each query and then performed intersection of those IDs to generate the desired output of the user’s query. Here, information leakage is caused by revealing many of the record IDs of the data owner to the user before the intersection operation. After this, Kim et al. [35] introduced another private database query protocol in which 0.119 s were required to process each record. They generated random databases that consisted of 16 keyword attributes with entries with maximum sizes of 48 or 64 bits. The testing platform was a server with 3.7 GHz Intel® XeonTM Platinum 8170 and 192 GB RAM. In terms of efficiency, the protocol is not suitable for practical use because it requires about 20 min to access data from a database of 10,000 records.
1.6. Our Contributions
In this paper, we affirmatively resolve the problems mentioned in Section 1.2 and produced the following results.
- We propose an efficient batch private conjunctive query (BPCQ) protocol with the binary encoding, which we call the BPCQ2 protocol. Here, we use RLWE-based SwHE for providing security for the binary-encoded values appearing in the predicate of a query and the data in the database.
- As a main technique in our protocol, we develop a data-packing method with a concatenation technique to encode the binary fixed-length multi-dimensional data appearing in the query and the database to evaluate the PCQ in a few multiplications. Because of using this concatenation technique, our methods presented in this paper overcome the weakness stated in Section 1.5 for conjunctive query processing.
Compared to a preliminary version [24] of this paper, we include the following new results.
- We propose another efficient protocol for PCQ processing using an N-ary fixed-length encoding (), which we call the BPCQN protocol.
- Theoretically, we are able to reduce the lattice dimension by a factor of in the BPCQN protocol because of using N-ary fixed-length encoding rather than the binary fixed-length data encoding used in the BPCQ2 protocol.
- The developed data-packing method is modified to show how the Euclidean distance computation is used to decide conjunctive equality for the N-ary-encoded BPCQN protocol.
- Through comparative analysis, we demonstrate that the BPCQN protocol works at least four times faster than the BPCQ2 protocol because of using N-ary data encoding.
1.7. Notations
denotes the ring of integers. For a prime number q, the ring of integers modulo q is denoted by . In addition, defines an n-dimensional integer vector space. denotes the ring of polynomials over the integer coefficients. Let , where and are a cyclotomic polynomial such that . For a vector , the maximum norm is defined as . Let denote the inner product between two vectors and . The function defines the encryption of a message m using the public key to produce the ciphertext . The ciphertexts and denote the homomorphic addition and multiplication, respectively, of ciphertexts and . indicates that s is chosen from the Gaussian distribution . The distribution indicates the n-dimensional discrete Gaussian distribution for some standard deviations .
We consider that a database is an array (or table). We call a collection of values appearing in each row of the table a record. We call a collection of records a block. Let p, , and denote the total number of blocks, the block size, and the total number of records, respectively. In the sequel, k denotes the number of conditions appearing in the predicate of a conjunctive query. is the ith value in the predicate, where is the length of and is the ith value in the dth record of the th block. denotes the exponent of x.
1.8. Outline of This Paper
This paper is structured as follows. Section 2 describes the security tool used for the security of our protocols. Section 3 discusses the binary encoding-based BPCQ protocol for processing the private conjunctive queries to the cloud. As a main technique in our protocol, Section 4 outlines the data representation procedure for conjunctive query processing; reviews an existing data-packing method, which does not make the BPCQ protocol efficient; and discusses how our tailored packing method creates an efficient BPCQ protocol. Section 5 highlights the technique used to improve the performance of the BPCQ protocol with N-ary encoding, which is used to pack the data. Section 6 outlines the homomorphic evaluation procedure of our protocols using the security tool (see Section 2) along with our packing methods mentioned in Section 4. We evaluate the performance of the BPCQ protocol both theoretically and practically in Section 7. We compare the performance of the binary-encoded BPCQ protocol with the N-ary-encoded BPCQ protocol in Section 8. Finally, Section 9 concludes this paper.
2. Security Tool
We discuss the cryptographic technique that will be used to maintain the privacy of the proposed protocols. In 2011, Brakerski and Vaikunthanathan [10] proposed an SwHE scheme and proved its correctness. Here, we review the asymmetric variant [17] of their SwHE scheme. To solve the problem indicated in Section 1.2, we use this secure scheme as an important ingredient.
2.1. Asymmetric SwHE Scheme
We consider some parameters for the SwHE scheme in [17] as follows.
- is a cyclotomic polynomial, where .
- n denotes the lattice dimension of the ring , where . Here, the value of n is a power of 2, that is, , where .
- q: modulus q is an odd prime such that defines the ring , which denotes a ciphertext space.
- t is an integer , which defines the message space of the scheme as , the ring of integer polynomials modulo , and t.
- is a standard deviation, where . It is also used to represent a discrete Gaussian error distribution with an n-dimensional integer vector .
Now, we discuss the algorithms used for key generation, encryption, homomorphic evaluation, and decryption in the SwHE scheme in [17] as follows.
2.1.1. Key Generation
The key generation algorithm first selects a ring element according to . Then, it samples a uniformly random element and an error according to and sets . Finally, it outputs a secret key and its public key .
2.1.2. Encryption
If we have a message and a public key , the encryption algorithm samples , where . Then, the encryption algorithm outputs a ciphertext , which is defined as
Here, the plaintext is in because .
2.1.3. Homomorphic Evaluations
Generally, the homomorphic operation is performed between two ciphertexts and . The homomorphic addition (⊞) between and can be defined as
We can also define the homomorphic subtraction that is analogous to the above component-wise addition. For a symbolic variable z, the homomorphic multiplication (⊠) between the above two ciphertexts, and , can be defined as
where .
2.1.4. Decryption
The decryption algorithm decrypts a new or homomorphically-operated ciphertext as follows,
where . This means the algorithm uses the secret key vector , such that . For example, the decryption of a fresh ciphertext generated by (1) can be written as
in the ring as . The decryption algorithm recovers the desired plaintext from a fresh ciphertext if the value does not wrap around mod q and all errors are sufficiently small. Here, the decryption algorithm recovers the plaintext m using the mod t operation from . If the wrap-around does not occur in the encrypted results after the homomorphic operations, the decryption algorithm outputs the following for two ciphertexts and :
Next, we discuss the security and correctness of the mentioned encryption scheme.
2.2. Security of RLWE-Based SwHE Scheme
For the given parameters , we demonstrate the security of the SwHE scheme using the polynomial RLWE assumption (RLWE) as mentioned by Lauter et al. [17]. The assumption holds if any polynomial number of samples of the form is true, where is uniformly random and . As the s are uniformly random in , s () are also uniform in . For this reason, distinguishing from a uniformly random pair is a hard problem. Besides, the RLWE assumption is reducible to the worst-case hardness of problems on ideal lattices that is thought to be secure against attacks using the quantum computer [16].
2.3. Correctness of RLWE-Based SwHE Scheme
The correctness of the SwHE scheme depends on how the decryption can recover the original result from the ciphertext after some homomorphic operations. We can write the decryption process as
Section 1.1 in [10] describes the above process. Here, ciphertexts and come from and , respectively, after encryption. The above decryption process will not lose any information about the plaintext if the following lemma holds as mentioned in [36]:
Lemma 1.
(Condition for successful decryption.) For a ciphertext , the decryption recovers the correct result if does not wrap around mod q, namely, if the condition is satisfied, where for an element . Specifically, for a fresh ciphertext , the ∞-norm is given by . For a homomorphically-operated ciphertext, the ∞-norm can be computed using Equation (4).
3. Our Protocol
When solving our problem stated in Section 1.2, we needed to construct a secure protocol. In this section, we briefly describe the protocol scenario for PCQs and the traditional technique for solving the PCQ problem. Then, we provide an overview of the proposed concatenation technique for solving the PCQ problem, a batch technique for boosting performance, and a batch private conjunctive query protocol.
3.1. Protocol Scenario
In this section, we describe how to use our protocol for private conjunctive query processing in a real-world scenario as shown in Figure 2. As depicted in Figure 3, consider that a hospital (Charlie) maintains a database of their admitted patients in the patientRecord table, where Charlie has low computation capacity. A government health research institute (Alice) wants to determine the number of male patients admitted to that hospital in the last year who suffered from tuberculosis (TB), which is a conjunctive equality query request to Charlie from Alice. The corresponding SQL statement of this request is select count(id) from patientRecord where sex=“M” and dis=“TB” and year=2019. Here, Alice has a little computation ability, which includes key generation, encryption, and decryption. Charlie must not disclose their patients’ information to Alice. Therefore, they want to outsource the computation to a third party like the cloud (Bob) without disclosing the query and corresponding data to Bob.
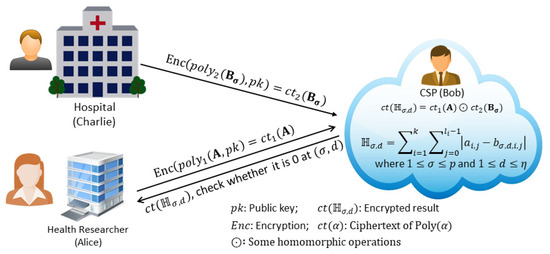
Figure 2.
Real-world scenario of private conjunctive query protocol.
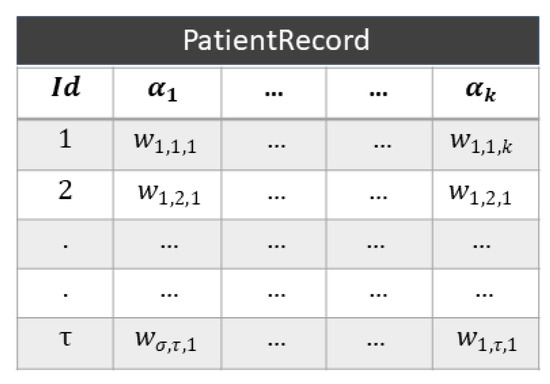
Figure 3.
Sample of a patient record table.
3.2. Traditional Technique for Solving the PCQ Problem
As mentioned in the problem scenario in Section 1.2 and the real-world scenario in Section 3.1, the PCQ problem can be solved by involving a third party like Bob in the cloud, where the database owner and the query owner are different entities. Note that we need to solve this problem with leaking as little information to Alice about the database as possible. Here, the query includes k () equality conditions connected by conjunction operators. If we use the traditional method for solving this conjunctive query problem, which contains three equality conditions in its predicate, Alice needs to send three equality requests separately to Bob, which returns some distances for each record after processing the equality blindly using the Hamming distance. Now, Alice finds the record IDs that contain Hamming distances of zero. Then, Alice finds the number of male patients by counting the number of IDs appearing in the intersection of those IDs, as shown in Figure 4.
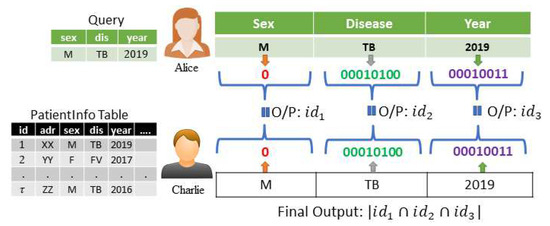
Figure 4.
Traditional technique to solve the PCQ problem when .
3.3. Proposed Concatenation Technique for Solving PCQ Problem
If we use the traditional method to solve many equality conditions, more IDs that Alice should not have will be revealed to her. Ase k conditions are conjunctive, every value in each condition can be encoded as a fixed-length record. Then, Alice can concatenate k values sequentially, and sends the concatenated values as a single query to the cloud after encryption, as shown in Figure 5. Moreover, Charlie sends the corresponding k values from each record of the table of the database to the cloud after encryption using the same approach as Alice. Then, Bob blindly performs the matching blindly using the Hamming distance and returns the distances. In the end, Alice decrypts the result and counts the Hamming distances that are zero to obtain her desired result.
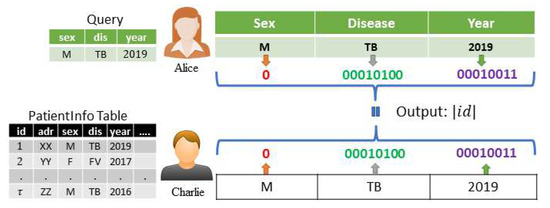
Figure 5.
Concatenation technique to solve the PCQ problem when .
For the protocol scenario mentioned in Section 3.1, Alice owns a conjunctive query that has k equality conditions connected by the “and” operator appearing in its predicate. For example, select count(id) from patientRecord where and and ⋯ and , where . For the security of this conjunctive query, we take care about only security of the value () appearing in the predicate of the query. Now, we form a set from the values of k attributes , which exist in the predicate of the query. Here, we consider a binary vector of length with . In the hospital database, Charlie owns records in their patient record table, which consists of attributes. For evaluating the conjunctive query, we need only the k attributes from attributes and their values in each record. From k values, we form a record . Here, each value is represented as a binary vector , such that with and . To determine the conjunctive equality of V and , we generate a large binary vector from the set V as by concatenating k binary vectors sequentially in the set V. Similarly, we generate another large binary vector from the set as . Here, . We calculate the conjunctive equality between two sets V and using the following equation,
where the Hamming distance between two binary vectors and is denoted by . In Equation (6), if for any , ; otherwise, . Then, count the number of zeros for some positions to determine the total number of records matched with the given query. If the values in the query and database are encrypted here using the encryption algorithm of RLWE-based SwHE, Alice can securely verify her conjunctive equality query with the help of Bob and using the homomorphism property of the RLWE-based SwHE.
Here, the computation will be inefficient if we calculate the Hamming distance for all records one by one instead of processing many records at a time. Therefore, a technique is needed to improve the performance of the required protocol for conjunctive query processing. A database consists of some tables, and each table contains numerous records. To process the PCQ with k conditions, the concatenation approach needs to perform the equality comparison many times. Therefore, the problem requires determining many equalities. We can solve this problem using the batch equality technique, as mentioned in [29].
3.4. Batch Technique for Boosting Performance
The method of running a single instruction on multiple data is called batching. We can enhance the performance of the required PCQ protocol using this batch technique within the lattice dimension n, which is called the batch private conjunctive query (BPCQ) protocol.
3.4.1. Batching for Traditional Methods
The performance of our techniques can be enhanced using the batch technique since we use RLWE-based SwHE for the homomorphic computation in which the performance mostly depends on the ring size, i.e., the lattice dimension n. Using the batch technique, each value of the attribute should be compared with values of the corresponding attribute in the table of a database. If the length of each record is l, the total length of the records will be . In addition, n should be at least to process all records at a time for batch computation. We know that any high lattice dimension requires large amounts of memory, which may cause a sudden failure in the computation. Instead of , say data can be processed within the lattice dimension, i.e., . Then, records of each attribute j can be divided into blocks. Here, records from a column of a table comprise a block.
3.4.2. Batching for Concatenation Method
Suppose that the length of each and corresponding values in the database is , i.e., the records are variable in length, as k values will be compared with the corresponding k values of each record from the table of a database to decide the conjunctive equality. equality tests require processing the query over records. We use RLWE-based SwHE for the homomorphic calculation in the cloud in our protocol, in which the performance depends on the lattice dimension n, as mentioned in Section 3.4.1. Consider that the total length of k values in the query is . If we want to support batch processing of the PCQ problem, similar to the private batch equality test (PriBET) protocol as mentioned in [29], we need to compare many records from the database with our conjunctive query of length L. We already assumed that we have records in the table. If we want to process all records at a time, n should be equal to . Running the batch computation may create a large lattice dimension, which requires large memory in the system in the cloud. This massive memory requirement can surpass a regular machine’s capacity in the cloud. To reduce the usage of memory, a block of data is processed at a time instead of all records, where all records of a table are split into blocks. For the given records, let denote the total number of records accessed within the lattice dimension n such that . In addition, we split the total records into p blocks such that . Here, individual access of the -record of the table requires -round communication between Charlie and Bob. Conversely, the required BPCQ protocol will be able to access records at a time, which reduces the rounds of communication between Charlie and Bob. Theoretically, we can decrease the communication complexity from to because of using the batch technique when sending records to the cloud. Now, we can encode the records of each block as the coefficients of x with different exponents in a single polynomial to support the batch computation.
3.5. Batch Private Conjunctive Query Protocol
In this section, we discuss the required protocol for private conjunctive queries with the batch technique, which we name the batch private conjunctive query (BPCQ) protocol. Here, we consider the same scenario as mentioned in Section 3.1 to discuss the BPCQ protocol. In the given scenario, consider the same query vector owned by Alice, where , as mentioned in Section 3.3. Charlie owns a patient record table, which contains records. For and , each record of the patient record table with k elements is represented by , where . To support batch computation in the protocol, we create a block as containing records, where . Then, we form another batch binary vector from all records for each block as where . The length of (resp., ) is L (resp., ). Here, multiple Hamming distance helps Bob to decide conjunctive equality between two vectors and , which can be expressed as
where and . In the above equation, the Hamming distance between two binary vectors and is denoted by . Here, the dth sub-vector of the vector is . If in Equation (7) for some (), ; otherwise, . As such, one can verify their conjunctive equality query and count the number of zeros for some () to determine the total number of records satisfying the given conjunctive query. With the help of the above technique, the required BPCQ protocol is described by the following steps:
| Inputs:, where and for and . Output: BPCQ protocol:
|
3.6. Security of the Protocol
We demonstrate the security of our BPCQ protocol using the following theorem along with its proof, as mentioned in [23].
Theorem 2.
The BPCQ protocol is secure respecting the assumption that Bob is a semi-honest party, i.e., no probabilistic polynomial time (PPT) algorithm can obtain any information about the values existing in the predicate of a conjunctive query and the data in the database on the basis of exploiting an IND-CPA-secure RLWE-based SwHE applied to the protocol.
Proof.
In our BPCQ protocol, Bob in the cloud is a semi-honest (also known as honest-but-curious) party, i.e., he always follows the protocol but tries to gain information from the protocol. In the semi-honest model, the BPCQ protocol is IND-CPA-secure if it attains indistinguishability against chosen-plaintext attack (CPA) by any PPT adversary. As the BPCQ protocol uses the RLWE-based SwHE scheme mentioned in Section 2, it generates a ciphertext pair for every message according to Equation (1). In a CPA attack, any adversary has access to the encryption algorithm and can choose the messages.
For each value with appearing in the predicate of a query, a challenger generates the ciphertext pair using the encryption algorithm of the RLWE-based SwHE scheme and sends them to the PPT adversary. The PPT adversaries randomly choose the query values and send them to the challenger for encryption. For input , the challenger outputs the ciphertext pair and sends the pair to the adversary. According to the RLWE assumption mentioned in Section 2.2,
where denotes computational distinguishable between and . Therefore, the adversary cannot distinguish the two ciphertext pairs and according to the RLWE assumption. In this situation, we affirm, in the semi-honest adversary model, that the BPCQ protocol is IND-CPA-secure under the RLWE assumption, which completes the proof. □
4. Data Representation and Its Packing Method
In this section, we discuss the data representation procedure and the required packing methods for conjunctive query processing.
4.1. Data Representation for Conjunctive Query Processing
Depending on the dimension, data can be classified into two types: one-dimensional data and multi-dimensional data, as shown in Figure 6. All the values of an attribute appearing in the single column of a table in the database define one-dimensional data. For instance, one-dimensional data can be presented by a data set denoting the sex of the hospital’s patients for a particular disease in 2014 as shown in Figure 6a. In contrast, all the values of several attributes appearing in the multiple columns of a table defines multi-dimensional data. For instance, multi-dimensional data compose a data set defining the sex of the patients with various diseases over several years, as shown in Figure 6b. However, we do not require one-dimensional data for evaluating our conjunctive query with the help of the batch technique. For evaluating the BPCQ protocol, we require a tailored packing method to efficiently process the multi-dimensional data, in which data security is ensured by the RLWE-based SwHE.
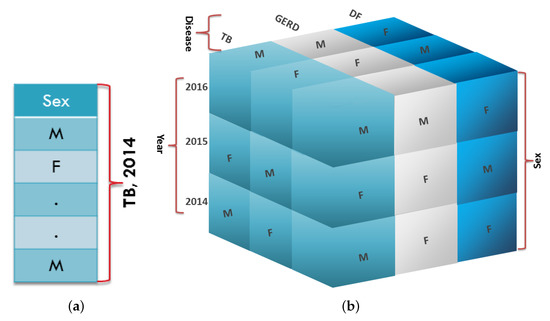
Figure 6.
(a) One-dimensional data and (b) multi-dimensional data.
4.2. Packing Methods
The data packing method is the technique of binding the many bits in a single polynomial as the coefficient of x with any exponent. From the existing literatures [17,18,36], a packing method can help make efficient protocols using the RLWE-based SwHE scheme. Now, we discuss the earlier packing methods used for secure computation with RLWE-based SwHE and their weaknesses, our tailored packing method, and the inner product property of the tailored packing method in the next subsections.
4.3. Existing Packing Method
Several packing methods [17,18,36] can be used in different applications along with RLWE-based SwHE for secure computation in the cloud. Lauter et al. [17] applied a packing method to sum 100 128-bit integers. They encoded every integer in a single polynomial of degree n by embedding every bit as the coefficient of x with different exponents. For instance, if we want to encode an n-bit integer, we need to make an n-bit binary vector , which can be represented by a polynomial using their packing method as follows,
Lauter et al. [17] used the above packing method to encode every integer and encrypt them as using the RLWE-based SwHE. Then, they sent those encrypted vectors to the cloud to perform the required addition homomorphically. The homomorphic evaluation of many arithmetic requires many additions and multiplications. The addition of two vectors such as and is easily computed using the above packing method. However, the homomorphic multiplication of and will increase the degree of the polynomial if we use the above packing method to encode these two vectors. If we want to keep the degree of the polynomial within n and perform () multiplications, we need to reduce the degree of the polynomial to .
To overcome the weakness of reducing the degree of polynomial and performing many multiplications within the degree of n, Yasuda et al. [36] proposed another packing method within the polynomial degree of n, which helps privacy-preserving computation of the Hamming distance and Euclidean distance. For their packing method, they took two vectors and of length n and define the packing as
For the above pair of packing methods, the second method is new, whereas the first method is the same as the packing method in [17]. However, the above packing methods are helpful for packing one-dimensional data. For processing our conjunctive query, we needed to design a packing method suitable for packing multi-dimensional data. Besides, we needed to introduce batching over the batch technique for the efficient computation of multiple Hamming distances in Equation (7). To increase the efficiency of calculation, our goal was to calculate multiple Hamming distances in a few multiplications. For this reason, a new packing method was needed to encode the multi-dimensional data within a single polynomial of degree n.
4.4. Our Packing Method
To decide the conjunctive equality between the query values and the data in the database using the multiple Hamming distance, we needed to encode the multi-dimensional data shown in Figure 6b. Here, we aimed to calculate this multiple Hamming distance with a few multiplications using the batch technique. To measure the Hamming distance between the query vector and each record of the th block, let us form an integer vector from the set V of length L, where . Then, we form another integer block vector , where and . Here, the vector is formed from each record of the th block. The multiple Hamming distance means the distances between the vector and each sub-vector in . The multiple Hamming distance in Equation (7) can be obtained by the inner product . To measure this securely with RLWE-based SwHE in Section 2, we constructed a different packing method than the packing methods in Equation (8). To produce the inner product within degree n, we encoded the vectors and using such polynomials so that the inner product does not wrap around a coefficient of x with any exponent. By modifying the packing in [36], the desired packing methods to encode and can be formed in the same ring with and as follows,
where . Now, we can obtain the desired inner product after multiplying the above two polynomials, which later helps the multiple Hamming distance calculation between and . Here, each Hamming distance appears as a coefficient of x with different exponents after multiplying the polynomials and , which produces multiple inner products, as described in the next subsection.
4.5. Obtaining the Multiple Inner Products
From the work in [36], the Hamming distance between two vectors can be calculated by the inner product of those two vectors. To obtain multiple inner products, consider the above two vectors and again. For , multiplication of the polynomials and in Equation (9) can be presented as
where . In the above equation, is a binary vector and defines the dth sub-vector of the binary vector , where . ToHD defines the terms of higher degree with and the ToLD defines the terms of lower degrees with . Equation (10) shows that a single multiplication produces inner products of and . To complete the private computation in the cloud using RLWE-based SwHE, we can encrypt the polynomials in Equation (9) with as
where defines the packed ciphertext of . To obtain multiple inner products over packed ciphertexts, the following proposition needs to be true:
Proposition 1.
Suppose is an integer vector, where and . Let be another integer vector where and . For , the vector includes η sub-vectors, where the length of each sub-vector is L. These vectors and are encoded as polynomials and , respectively, by Equation (9). From Equation (11), if we represent the ciphertexts of and as and , respectively, the decryption of the result obtained from will output a polynomial in including coefficients of under the condition of Lemma 1.
Proof.
and are constructed from the vectors and , respectively, using the packing method in Equation (9). By applying RLWE-based SwHE to the polynomials and , the ciphertexts and are produced, respectively, by Equation (11). By the correctness in Equation (5) and Lemma 1, the homomorphic multiplication of and corresponds to the multiplication of the polynomials and in the ring . From the multiple inner products in Equation (10), the multiplication of the polynomials and outputs inner products as the coefficients of , which equals for . Consequently, the homomorphic multiplication of the packed ciphertexts and simultaneously computes the multiple inner products for and . For this reason, Proposition 1 holds under the correctness in Equation (5) and Lemma 1. □
5. Improving the Batch Private Conjunctive Query Protocol
In this section, we briefly discuss another encoding technique used to improve the performance of our BPCQ protocol mentioned in Section 3.5. Next, we demonstrate the improved protocol using the encoding technique, the required packing methods, and the multiple inner products obtained from the packing methods.
5.1. Binary vs. Nary Encoding
Binary encoding refers to the technique of converting an l-bit integer into binary over . We already used binary data encoding for the BPCQ protocol, which is mentioned in Section 3.5. As mentioned in Section 4, the packing method allows encoding many data in a single polynomial of degree n. We know from the works in [21,22] that the computational cost of an RLWE-based protocol increases with the increase in the lattice dimension n. Therefore, if we can exploit the lattice dimension, we can reduce the computational cost of the BPCQ protocol. In contrast, the N-ary () encoding refers to the technique of converting data into N-ary-encoded numbers. Yasuda et al. [18] employed N-ary encoding for their efficient statistical computation in the cloud. In this paper, we consider exploiting the N-ary fixed-length data encoding [22] rather than the naive N-ary encoding to improve the performance of the BPCQ protocol. In N-ary fixed-length encoding, the most significant digit is zero if the length of the encoded number is less than estimated length of an N-ary-encoded number. Furthermore, data are encoded over , in which denotes the length of the N-ary-encoded number. If we encode an l-bit integer Z into an -digits N-ary-encoded number, then
From the above equation, we achieve a lattice reduction factor of when processing the BPCQ protocol using N-ary encoding rather than binary encoding.
5.2. Private Conjunctive Query Protocol Using N-ary Encoding
From RLWE-based homomorphic encryption, the computational cost mostly depends on the lattice dimension required for the computation. If we can reduce the lattice dimension by keeping the message space and security at an acceptable level, we can reduce the cost of the homomorphic computation. Saha and Koshiba [22] noted a lattice reduction factor of by employing N-ary fixed-length encoding. They used the encoding in their PriBET protocol to improve the protocol’s efficiency. To use the same encoding in our BPCQ protocol, we modified our multiple Hamming distance computation and packing method as follows.
Let us consider the same l-bit integers and (see Section 3.5), which appear in the query and database, respectively. By applying N-ary encoding to and , they can be represented by vectors and , respectively. We want to measure the distance between two N-ary-encoded vectors and . To apply the batch technique, we make two large batch vectors, such as a query vector of length and record vector where with . As the Hamming distance only works for binary data, we need a different distance measurement technique than the multiple Hamming distance in Equation (7) to measure the conjunctive equality between query vector and record vector . Here, we can use the square Euclidean distance (SED) technique to measure the distance between and as follows,
where and . In the above equation, denotes the Euclidean distance between two N-ary-encoded vectors and . Here, is the dth sub-vector of . For some positions d in the block in Equation (12), if , ; otherwise, . Then, count the number of zeros for some positions d in the th block to decide the total number of records satisfying the given query, which, in turn, helps to evaluate the conjunctive equality query.
In particular, consider the same integer vectors from the set V of length and in which length of each element of the vectors is . In addition, we make the following subtle change in the packing methods in Equation (9),
where and . Let us name the binary encoding-based BPCQ protocol in Section 3.5 the BPCQ2 protocol. We needed to make some changes to the BPCQ2 protocol to comply with N-ary encoding. That means Bob computes using Equation (12) and sends the encrypted result to Alice to determine the batch equalities. Here, we name the BPCQ protocol with N-ary encoding the BPCQN protocol.
| Inputs:, , where and for and . Output: BPCQN protocol:
|
Remark 1.
We can prove the security of the above protocol in a similar fashion to that mentioned in Theorem2. This means the above protocol is secure with respect to the assumption that Bob is semi-honest, i.e., they follow the protocol always. However, Bob tries to acquire as much information as possible from the protocol.
5.3. Obtaining Multiple Inner Products
Here, we take the same vectors and . To obtain the required multiple inner products, we exploit the multiplication of the polynomials and , which can be presented as
where . Here, is the dth sub-vector of record vector , where and . The length of both vectors and is . ToHD means and ToLD means . The result in Equation (14) shows that one multiplication produces inner products . Saha and Koshiba [22] showed that the inner product helps to calculate the square Euclidean distances. The following proposition must be satisfied to calculate multiple Euclidean distances using the inner product.
Proposition 2.
Let be an N-ary-encoded integer vector, where and . Let be another N-ary-encoded integer vector of length , where . For , the vector contains η sub-vectors, where . Now, encode the vectors and as polynomials and , respectively, using Equation (13). If the ciphertexts of and can be represented as and , respectively, by Equation (11), the decryption of the homomorphic multiplication will produce a polynomial in with coefficients of with respect to Lemma 1.
Proof.
We pack the vectors and to form polynomials and , respectively, using the packing method in Equation (13). In addition, the ciphertexts and are generated from and , respectively, by Equation (11). By the correctness in Equation (5) and Lemma 1, the homomorphic multiplication of and corresponds to the polynomial multiplication of and in the ring . From the inner product in Equation (10), the polynomial multiplication of and produces the inner products as the coefficients of , which equals for . The homomorphic multiplication of and concurrently produces multiple inner products for and . For this reason, Proposition 2 holds under the correctness in Equation (5) and Lemma 1. □
6. Homomorphic Evaluation of Private Conjunctive Query Protocols
In the following subsections, we demonstrate the process of homomorphic evaluation of the batch private conjunctive query (BPCQ) protocols (see Section 3 and Section 5.2 for details) in the cloud.
6.1. Homomorphic Evaluation of the BPCQ2 Protocol
We performed the homomorphic evaluation of our BPCQ2 protocol using the RLWE-based SwHE scheme in Section 2, the packing method in Equation (13), and the multiple inner products in Equation (10), along with Proposition 1. For and , Bob needs to determine the values of the Hamming distance as mentioned in Equation (7).
6.1.1. Evaluation Over Packed Ciphertext
In the BPCQ2 protocol, Bob needs to determine the Hamming distance between two integer vectors and (see Section 4.4 for details) in an encrypted manner. To provide security for the protocol, we use the RLWE-based SwHE in which the encryption and decryption algorithms work on polynomials rather than integer vectors. For this reason, Alice (resp., Charlie) encodes the integer vector (resp., ) as (resp., ) using the packing methods in Equation (9). They also encrypt and ) using Equation (11) to produce packed ciphertext vectors and , respectively, and send these packed ciphertexts to Bob in the cloud. The Hamming distance can be calculated by the inner products. Now, Bob can determine multiple Hamming distances in an encrypted manner using the multiple inner products property in Equation (10), which produces the output . With the help of the homomorphic property of RLWE-based SwHE, Bob calculates over the packed ciphertexts as
where is obtained by only three homomorphic multiplications along with two homomorphic additions for packed ciphertexts. In the above equation, (resp., ) defines the integer vector of length (resp., L) in which every element of the vector is 1 such as . According to the multiple inner products property, contains the desired Hamming distances as the coefficients of . Then, Bob transmits to Alice to recover the actual Hamming distances that are zeros to decide the equality between vector and the sub-vectors of . According to Proposition 1 and the BPCQ2 protocol, Alice engages the decryption algorithm to decrypt using her secret key in the ring and obtains all as the coefficients of from the plaintext of . Then, Alice counts the number of for some and . As such, Alice determines the total number of records that satisfies the conjunctive conditions in the given query of the BPCQ2 protocol.
6.1.2. Solving Additional Information Leakage Problem of the BPCQN Protocol
As Alice obtains the packed ciphertext from Bob for decryption in the BPCQ2 protocol and checks every coefficient to find , she may learn more information than her required information from the protocol. According to Proposition 1, Alice must only check the coefficients of . To solve this problem, we use a random polynomial in which every coefficient is random except when the coefficient of is zero. In the BPCQ2 protocol, Bob adds to . This random polynomial in the ring R can be defined as
We know that includes three ciphertext components as . Here, Bob adds the random polynomial to , which produces another ciphertext such that . Using this randomization, Bob hides all coefficients of the polynomial from Alice except some coefficients with . As such, the mentioned information leakage problem is solved in the BPCQ2 protocol.
6.2. Homomorphic Evaluation of the BPCQN Protocol
In this subsection, we discuss the homomorphic evaluation of the BPCQN protocol mentioned in Section 5.2. We evaluate the BPCQN protocol with the help of the RLWE-based SwHE scheme in Section 2, the packing methods in Equation (13), multiple inner products property in Equation (14), and Proposition 2. For this protocol, we need to determine , as mentioned in Equation (12), which defines the Euclidean distance between the vector and each sub-vector of . We know that the encryption and decryption algorithms of RLWE-based SwHE scheme work on polynomials. In our protocol, Alice encodes the vector as the polynomial using the packing methods in packing methods in Equation (13). Using Equation (11), she encrypts the polynomial as and and transmits them to Bob in the cloud. Similarly, Charlie encodes as the polynomial using the same packing methods and transmits and to Bob after encryption using Equation (11). We know that the Euclidean distance can be computed by three homomorphic multiplications and two homomorphic additions. Similar to the BPCQ2 protocol, we homomorphically evaluate as
where (resp., ) defines the integer vector of length (resp., ), which forms as . The ciphertext contains the desired Euclidean distances . Now, Bob sends to Alice for decryption. Similar to the BPCQ2 protocol, Alice decrypts in the ring with her secret key and extracts as a coefficient of from the plaintext of by Proposition 2. As such, Alice estimates the total number of records satisfying the conjunctive conditions in the given query.
Similar to the BPCQ2 protocol, the BPCQN protocol also suffers from the information leakage problem because of revealing the whole polynomial to Alice, as Alice only need to verify the coefficients of to decide the conjunctive equalities. We can solve this information leakage problem by using an analogous technique applied to the BPCQ2 protocol as indicated in Section 6.1.2. We use the following random polynomial in the ring R as
Owing to the single homomorphic multiplication in the Euclidean distance computation by Bob, the ciphertext is composed of three components: , , and . To prevent information leakage, Bob adds to the ciphertext such that . In this case, the resulting ciphertext contains all the conjunctive equality information between the vector and each sub-vector of as the coefficients of , and conceals all other coefficients using the mentioned randomization. With this technique, the information leakage from the decryption of the polynomial is suppressed excluding the coefficients of .
Remark 2.
Here, the coefficients of (resp., ) are leaked to Alice during checking the zero values despite addressing the information leakage problems in the BPCQ2 (resp., BPCQN) protocol. However, it does not reveal any information regarding actual values in the database along with record indexes.
7. Performance Analysis
In this section, we briefly discuss the security weaknesses of the proposed protocols and their possible countermeasures. Then, we compare the performance of our BPCQ2 protocol with that of Cheon et al.’s protocol [28] (in short, CKK protocol) when processing the private conjunctive query. Here, the BPCQ2 protocol scenario is different from that of the CKK protocol [28], though both protocols process private conjunctive query. First, we discuss the theoretical evaluation of the protocol along with its correctness and the experimental settings of the used parameters in the protocol. Then, we analyze the security of the BPCQ2 protocol using an experimental evaluation to show its practical performance using RLWE-based SwHE.
7.1. Security Weaknesses and Countermeasures
Here, we describe the probable weaknesses related to security that may arise in our proposed protocols and their possible countermeasures.
7.1.1. Security Weaknesses
In this paper, we propose the BPCQ2 and BPCQN protocols, and we use RLWE-based SwHE in the semi-honest model. Here, we ensure the security of the values appearing in the predicate of the queries and the data in the database. Both of our protocols are CPA-secure, i.e., secure against attacks using quantum computers. We consider following two weaknesses for our protocols.
- When Charlie encrypts and sends Bob all the encrypted data with an insecure channel, Alice can eavesdrop. Alice provides Charlie with a public key and has a private key for it, so if Alice obtains Charlie’s encrypted data, Alice can obtain all the database’s information. This will compromise the basic security of the cryptographic protocol.
- Our protocols are unable to prevent real-world attacks by malicious adversaries because we followed the semi-honest model for protocol security.
7.1.2. Countermeasures Against the Weaknesses
To mitigate against eavesdropping attacks during data transmission between Charlie and Bob, we can use a standard encryption that was used in an earlier work [37]. In our protocols, Charlie encrypts his database using the public key provided by Alice. Then, Charlie re-encrypts the encrypted data using the secret key shared by Charlie and Bob. Now, Alice will not be able to eavesdrop during the data transmission from Charlie to Bob. Here, encryption will ensure data secrecy during transmission through an insecure channel. To resolve the next problem, we can convert our protocol from the semi-honest model to malicious model. If we want to convert the protocols from the semi-honest model to the malicious model, existing works [38,39] support the conversion, but the efficiency of our protocols will be decreased by this conversion. We used the semi-honest model to ensure the efficiency of the designed protocols.
7.2. Theoretical Evaluation
In this subsection, we theoretically compare the CKK [28] protocol with our BPCQ2 protocol in terms of the multiplication depth of the equality computation. We determine the conjunctive equality using the Hamming distance in Equation (7). As indicated in Equation (15), three polynomial multiplications are required for the homomorphic evaluation of this Hamming distance. As shown in Table 1, the CKK protocol needs a multiplication depth of for their equality circuit for comparing two l-bit integers. Conversely, due to using our tailored packing method, our method requires a multiplication depth of for the conjunctive equality circuit, which compares two l-bit integers. The communication complexity of the BPCQ2 protocol is . Now, we discuss the correctness of the homomorphic evaluation of the BPCQ2 protocol.

Table 1.
Theoretical performance comparison between BPCQ2 method and Cheon et al.’s method [28].
7.3. Correctness
The ciphertext in Equation (15) generates a correct result if it satisfies the condition according to Lemma 1. In case of any fresh ciphertext , U defines the upper bound for the ∞ norm , where (see Theorem 3.3 in [17]). Now, we define the ∞-norm size of with the inequality as (see [36] for details). We achieve the correctness of ciphertext if .
7.4. Experimental Settings
In the experiment using the BPCQ2 protocol, the database settings for Charlie were the same as in the CKK protocol, but our protocol scenario is different from theirs. The conjunctive query of the BPCQ2 protocol contains equality as a comparison operator, which is the same as the CKK protocol for conjunctive query processing. Table 2 shows the parameter settings used for the experiment with the BPCQ2 protocol. We used and to represent the number of equality conditions in the query. The data size and block size were set to and , respectively. For successful decryption, we set appropriate values of to help attain a certain security level. According to the BPCQ2 protocol mentioned in Section 4.4, we need to have . As a result, we set . For all experiments, we chose . Furthermore, we set and chose for the ciphertext space . For this reason, we set . In the next subsection, we analyze the security of the BPCQ2 protocol.

Table 2.
Parameter settings in the experiment using the BPCQ2 protocol.
7.5. Security Analysis
In this subsection, we analyze the security to determine the security level provided by our protocols. The NIST [40] declares the strength of many security algorithms by showing their achieved security levels and corresponding validity periods. Usually, the strength of a cryptographic algorithm depends on the data owner or the organization using that algorithm. For instance, the U.S. federal government accepts a security algorithm with a security level of 112 bits [41]. After the introduction of post-quantum cryptographic algorithms, NIST noted that a security algorithm with 112 bit security is acceptable up to 2030. They stated that any security algorithm will require at least the 128 bit security level after 2030. For RLWE-based SwHE, we considered defending our protocols against two attacks: distinguishing attack [42] and decoding attack [43]. We chose our parameter settings according to the settings in [43] to achieve a security level of greater than 128 bits. We also considered the security of our protocols in defending against distinguishing and decoding attacks with the advantage . To attain the 80 bit security level, Chen and Nguyen [44] estimated that lattice-based cryptographic schemes require the root Hermite factor where . As mentioned in [17], the running time is defined as
7.6. Experimental Evaluation of the BPCQ2 Protocol
The practical performance of our BPCQ2 protocol is compared with that of the CKK protocol in Figure 7 and Figure 8 with six different settings. In our implementation of the BPCQ2 protocol, the required code was written in C programming language using the Pari library (version 2.7.5) in [45]. Then, we ran the code on a single machine (3.6 GHz Intel core-i7 CPU and 8 GB RAM) in the Linux environment. We then analyzed and compared the performance between our BPCQ2 protocol and the CKK protocol [28] for three different data sets of 100, 1000, and 10,000 records. In addition, the same indexing is used for Figure 7 and Figure 8 as in the first column of Table 2 to show the relationship between parameter settings and the corresponding performance. Figure 7 shows that the workability of the BPCQ2 protocol is faster than that of the CKK protocol [28] for conjunctive query processing. Our developed system worked noticeably faster than the CKK propocol because of using a low multiplicative-depth equality circuit along with the batch technique. Our developed system required less RAM than that of CKK protocol [28]. In addition, our BPCQ2 protocol attained thef bit security level, whereas CKK protocol [28] attained a security level of 80 bits, as shown in Figure 8.
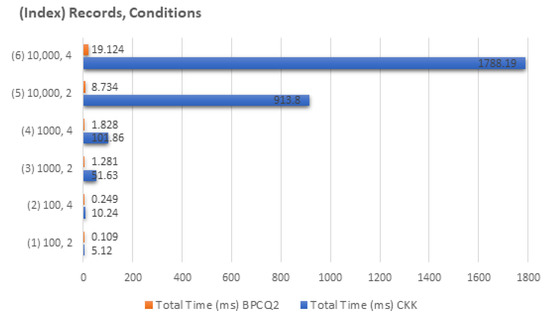
Figure 7.
Performance comparison between the CKK protocol and BPCQ2 protocol in terms of computational time.
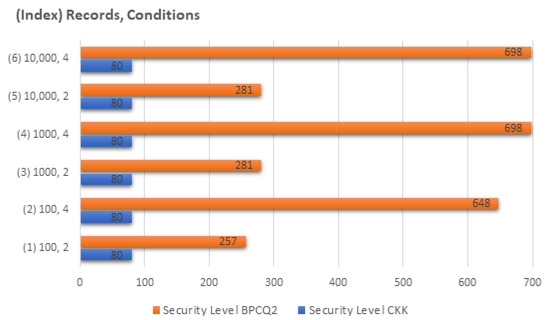
Figure 8.
Comparison of the security level between the CKK and BPCQ2 protocols.
8. Comparative Performance Analysis with the Latest Research Methods
Herein, we describe the comparative performance analysis between the BPCQ2 and BPCQN protocols along with their parameter settings.
8.1. Correctness
The correctness of the BPCQN protocol is similar to that mentioned in Section 7.3. The ciphertext in Equation (15) generates a correct result if it satisfies the condition according to Lemma 1. In addition, we achieve the correctness of ciphertext if the following relation holds,
due to using N-ary encoding in the BPCQ protocol instead of binary encoding.
8.2. Parameter Settings
The parameter settings used for comparing the BPCQ2 and BPCQN protocols are shown in Table 3. We considered the same scenario mentioned in Section 3, which used three conjunctive equality conditions of 19 bits. We set for all three comparative experiments for the two protocols. We set the value of t to 2048 (resp., 65,536) for the BPCQ2 (resp., BPCQN) protocol. We set the value of N as 2 (resp., 256) for binary (resp., N-ary) encoding since we attained a lattice reduction factor of , which is obvious from the value of n in Table 3.

Table 3.
Parameter settings between BPCQ2 and BPCQN protocols.
8.3. Performance Comparison
As shown in Figure 9 and Figure 10, we performed a comparative analysis of the BPCQ2 and BPCQN protocols using experiments with the same machine mentioned in Section 7.6. To process a conjunctive query with three conditions upon 1000 (resp., 2000) records, the BPCQ2 protocol required 3.953 s (resp., 4.562 s) whereas the BPCQN protocol required 0.251 s (resp., 0.937 s). The BPCQ2 protocol required 7.437 s, whereas BPCQN protocol required 0.938 s to determine the conjunctive equality among 4000 records. With our settings, the BPCQ2 protocol achieved a security level of 3419 bits and the BPCQN protocol achieved a security level of more than 306 bits. The BPCQN protocol required at about 0.304 ms, on average, to process each record of the database, whereas the BPCQ2 protocol required 2.279 ms. Here, the security of the BPCQ2 protocol is higher than that of the BPCQN protocol; however, the security level of BPCQN exceeds the minimum 128-bit security level mentioned in Section 7.5. Therefore, from these findings, it is evident that BPCQN protocol performs at least four times faster than the BPCQ2 protocol.
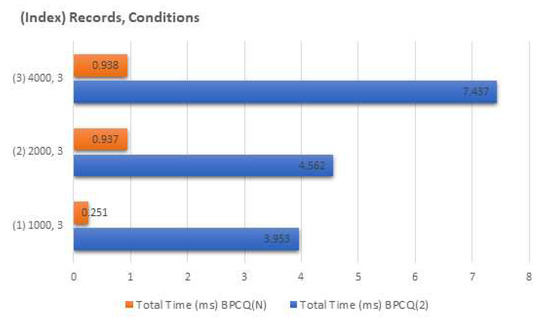
Figure 9.
Performance comparison between BPCQ2 and BPCQN protocols in terms of computational time.
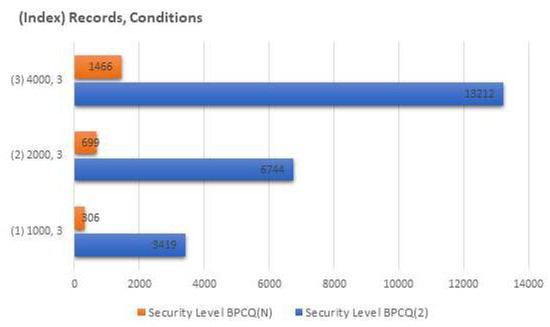
Figure 10.
Comparison of security level between BPCQ2 and BPCQN protocols.
9. Conclusions
In this paper, we proposed a BPCQ protocol using RLWE-based SwHE for answering private conjunctive queries to a private database outsourced in the cloud. To ensure the efficiency of the protocol, we also proposed a data-packing method to pack many binary-encoded data within a single polynomial. We call this protocol the BPCQ2 protocol. We demonstrated an implementation of our protocol using C programming with the Pari library. We evaluated our protocol using random data and measured its performance. From the performance of BPCQ2 protocol, our protocol works 50 times faster than that of Cheon et al. [28]. Here, we assessed our technique in a different setting than theirs. We further improved the efficiency of the BPCQ protocol using the N-ary data encoding, which we call the BPCQN protocol. We were able to reduce the lattice dimension by a factor of because of using N-ary encoding rather than binary data encoding. We also compared the performance of the BPCQ2 and BPCQN protocols using the same settings, which verified the performance improvement provided by the BPCQN protocol when applying N-ary encoding to the BPCQ protocol. We think that our packing method along with N-ary encoding is expandable to processing many new queries. In the future, we will investigate private disjunctive and threshold queries, which are used for obtaining data from a private outsourced database in the cloud.
Author Contributions
Conceptualization, T.K.S.; Funding acquisition, T.K.; Investigation, T.K.S.; Methodology, T.K.S.; Project administration, T.K.; Writing—original draft, T.K.S.; Writing—review and editing, T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by KAKENHI grant number JP16H0175.
Acknowledgments
The authors would like to thank all the anonymous reviewers for their comments and suggestions, which helped us to improve the presentation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rivest, R.L.; Adleman, L.; Dertouzos, M.L. On Data Banks and Privacy Homomorphisms. Found. Secur. Comput. 1978, 4, 169–180. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Gentry, C. Fully Homomorphic Encryption using Ideal Lattices. In Proceedings of the Forty-First Annual ACM Symposium Theory Computimg (STOC), Bethesda, MD, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Cohen, J.D.; Fischer, M.J. A Robust and Verifiable Cryptographically Secure Election Scheme. In Proceedings of the 26th Annual Symposium on Foundations of Computer Science, Portland, OR, USA, 21–23 October 1985; pp. 372–382. [Google Scholar]
- ElGamal, T. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms. In Proceedings of the Crypto 1984, Santa Barbara, CA, USA, 19–22 August 1984; Volume 196, pp. 10–18. [Google Scholar]
- Goldwasser, S.; Micali, S. Probabilistic Encryption & How to Play Mental Poker Keeping Secret All Partial Information. In Proceedings of the Fourteenth Annual ACM Symposium Theory Computing, San Francisco, CA, USA; 1982; pp. 365–377. [Google Scholar]
- Paillier, P. Public-key Cryptosystems Based on Composite Degree Residuosity Classes. In Proceedings of the International Conference Theory Application of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; Volume 1592, pp. 223–238. [Google Scholar]
- Benaloh, J. Dense Probabilistic Encryption. In Proceedings of the Workshop on Selected Areas of Cryptography, Kingston, ON, Canada, 5–6 May 1994; pp. 120–128. [Google Scholar]
- Boneh, D.; Goh, E.J.; Nissim, K. Evaluating 2-DNF Formulas on Ciphertexts. In Proceedings of the 2nd TCC, Cambridge, MA, USA, 10–12 February 2005; Volume 3378, pp. 325–341. [Google Scholar]
- Brakerski, Z.; Vaikuntanathan, V. Fully Homomorphic Encryption from ring-LWE and Security for Key Dependent Messages. In Proceedings of the 31st Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Volume 6841, pp. 505–524. [Google Scholar] [CrossRef]
- Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. Faster Fully Homomorphic Encryption: Bootstrapping in Less than 0.1 Seconds. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 4–8 December 2016; Volume 10031, pp. 3–33. [Google Scholar] [CrossRef]
- Ducas, L.; Micciancio, D. FHEW: Bootstrapping Homomorphic Encryption in Less Than a Second. In Proceedings of the Eurocrypt 2015, Sofia, Bulgaria, 26–30 April 2015; Volume 9056, pp. 617–640. [Google Scholar]
- Van Dijk, M.; Gentry, C.; Halevi, S.; Vaikuntanathan, V. Fully Homomorphic Encryption Over the Integers. In Proceedings of the Eurocrypt 2010, Nice, France, 30 May–3 June 2010; Volume 6110, pp. 24–43. [Google Scholar]
- Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. (Leveled) Fully Homomorphic Encryption Without Bootstrapping. ACM Trans. Comput. Theory 2014, 6, 1–36. [Google Scholar] [CrossRef]
- Hu, Y. Improving the Efficiency of Homomorphic Encryption Schemes. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2013. [Google Scholar]
- Lyubashevsky, V.; Peikert, C.; Regev, O. On Ideal Lattices and Learning with Errors over Rings. In Proceedings of the Eurocrypt 2010, Nice, France, 30 May–3 June 2010; Volume 6110, pp. 1–23. [Google Scholar] [CrossRef]
- Naehrig, M.; Lauter, K.; Vaikuntanathan, V. Can Homomorphic Encryption be Practical? In Proceedings of the 3rd ACM Workshop Cloud Computing Security Workshop, Chicago, IL, USA, 21 October 2011; pp. 113–124. [Google Scholar]
- Yasuda, M.; Shimoyama, T.; Kogure, J.; Yokoyama, K.; Koshiba, T. Secure Statistical Analysis Using RLWE-based Homomorphic Encryption. In Proceedings of the ACISP 2015, Brisbane, QLD, Australia, 29 June–1 July 2015; Volume 9144, pp. 471–487. [Google Scholar] [CrossRef]
- Saha, T.K.; Koshiba, T. An Enhancement of Privacy-preserving Wildcards Pattern Matching. In Proceedings of the International Symposium on Foundations and Practice of Security—FPS 2016, Québec City, QB, Canada, 24–26 October 2016; Volume 10128, pp. 145–160. [Google Scholar]
- Yasuda, M.; Shimoyama, T.; Kogure, J.; Yokoyama, K.; Koshiba, T. Secure Pattern Matching Using Somewhat Homomorphic Encryption. In Proceedings of the 2013 ACM Workshop on Cloud Computing Security Workshop, Berlin, Germany, 8 November 2013; pp. 65–76. [Google Scholar]
- Saha, T.K.; Koshiba, T. Outsourcing Private Equality Tests to the Cloud. J. Inf. Secur. Appl. 2018, 43, 83–98. [Google Scholar] [CrossRef]
- Saha, T.K.; Koshiba, T. Privacy-preserving Equality Test towards Big Data. In Proceedings of the International Symposium on Foundations and Practice of Security—FPS 2017, Nancy, France, 23–25 October 2017; Volume 10723, pp. 95–110. [Google Scholar] [CrossRef]
- Saha, T.K.; Rathee, M.; Koshiba, T. Efficient Private Database Queries Using Ring-LWE Somewhat Homomorphic Encryption. J. Inf. Secur. Appl. 2019, 49, 102406. [Google Scholar] [CrossRef]
- Saha, T.K.; Koshiba, T. Private Conjunctive Query over Encrypted Data. In Proceedings of the Africacrypt 2017, Dakar, Senegal, 24–26 May 2017; Volume 10239, pp. 149–164. [Google Scholar] [CrossRef]
- Saha, T.K.; Mayank; Koshiba, T. Efficient Protocols for Private Database Queries. In Proceedings of the 31st Annual IFIP WG 11.3 Conference on DBSec 2017, Philadelphia, PA, USA, 19–21 July 2017; Volume 10359, pp. 337–348. [Google Scholar]
- Saha, T.K.; Koshiba, T. An Efficient Privacy-preserving Comparison Protocol. In Proceedings of the NBiS 2017, Toronto, ON, Canada, 24–26 August 2017; Volume 7, pp. 553–565. [Google Scholar]
- Wang, L.; Saha, T.K.; Aono, Y.; Koshiba, T.; Moriai, S. Enhanced Secure Comparison Schemes Using Homomorphic Encryption. In Proceedings of the Advances in Networked-Based Information Systems—NBiS 2020, Victoria, BC, Canada, 31 August–2 September 2020; Volume 1264, pp. 211–224. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, M.; Kim, M. Optimized Search-and-compute Circuits and Their Application to Query Evaluation on Encrypted Data. IEEE Trans. Inf. Forensics Secur. 2016, 11, 188–199. [Google Scholar] [CrossRef]
- Saha, T.K.; Koshiba, T. Private Equality Test Using Ring-LWE Somewhat Homomorphic Encryption. In Proceedings of the 2016 3rd Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), Nadi, Fiji, 5–6 December 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Boneh, D.; Gentry, C.; Halevi, S.; Wang, F.; Wu, D.J. Private Database Queries Using Somewhat Homomorphic Encryption. In Proceedings of the ACNS 2013, Banff, AB, Canada, 25–28 June 2013; Volume 7954, pp. 102–118. [Google Scholar]
- Pappas, V.; Krell, F.; Vo, B.; Kolesnikov, V.; Malkin, T.; Choi, S.G.; George, W.; Keromytis, A.; Bellovin, S. Blind Seer: A Scalable Private DBMS. In Proceedings of the IEEE Symposium on Security and Privacy, San Jose, CA, USA, 18–21 May 2014; pp. 359–374. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for Secure Computations. In Proceedings of the 23rd Annual Symposium Foundations Computing Science, Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Fisch, B.A.; Vo, B.; Krell, F.; Kumarasubramanian, A.; Kolesnikov, V.; Malkin, T.; Bellovin, S.M. Malicious-client Security in Blind Seer: A Scalable Private DBMS. In Proceedings of the 36th IEEE Symposium on Security and Privacy (S&P), San Jose, CA, USA, 18–20 May 2015; pp. 395–410. [Google Scholar]
- Kim, M.; Lee, H.T.; Ling, S.; Wang, H. On the Efficiency of FHE-based Private Queries. IACR Cryptol. ePrint Arch. 2015, 2015, 1176. [Google Scholar] [CrossRef]
- Kim, M.; Lee, H.T.; Ling, S.; Ren, S.Q.; Tan, B.H.M.; Wang, H. Search Condition-hiding Query Evaluation on Encrypted Databases. IEEE Access 2019, 7, 161283–161295. [Google Scholar] [CrossRef]
- Yasuda, M.; Shimoyama, T.; Kogure, J.; Yokoyama, K.; Koshiba, T. Practical Packing Method in Somewhat Homomorphic Encryption. In DPM/SETOP-2013; Garcia-Alfaro, J., Lioudakis, G., Cuppens-Boulahia, N., Foley, S., Fitzgerald, W.M., Eds.; Springer: Heidelberg, Germany, 2014; Volume 8247, pp. 34–50. [Google Scholar] [CrossRef]
- Kandah, F.; Singh, Y.; Zhang, W. Mitigating Eavesdropping Attack Using Secure Key Management Scheme in Wireless Mesh Networks. J. Commun. 2012, 7, 596–605. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. How to Play Any Mental Game. In Proceedings of the 19th annual ACM Symposium Theory Computing, New York, NY, USA, 25–27 May 1987; Aho, A., Ed.; ACM Press: New York, NY, USA, 1987; pp. 218–229. [Google Scholar]
- Ishai, Y.; Prabhakaran, M.; Sahai, A. Founding Cryptography on Oblivious Transfer–Efficiently. In Proceedings of the CRYPTO 2008, Santa Barbara, CA, USA, 17–21 August 2008; Volume 5157, pp. 572–591. [Google Scholar]
- Barker, E. NIST Special Publication 800-57—Part 1 Revision 4; Recommendation for Key Management—Part 1: General, Dept. Commerce; National Institute of Standard and Technology: Gaithersburg, MD, USA, 2016. [CrossRef]
- Barker, E.; Roginsky, A. Transitioning the Use of Cryptographic Algorithms and Key Lengths; Technical Report; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2018.
- Micciancio, D.; Regev, O. Post-Quantum Cryptography; Springer: Heidelberg, Germany, 2009; pp. 147–191. ISBN 978-3-540-88701-0. [Google Scholar]
- Lindner, R.; Peikert, C. Better Key Sizes (and Attacks) for LWE-based Encryption. In Proceedings of the CT-RSA 2011, San Francisco, CA, USA, 14–18 February 2011; Volume 6558, pp. 319–339. [Google Scholar]
- Chen, Y.; Nguyen, P.Q. BKZ 2.0: Better Lattice Security Estimates. In Proceedings of the ASIACRYPT 2011, Seoul, Korea, 4–8 December 2011; Volume 7073, pp. 1–20. [Google Scholar]
- PARI Group. PARI/GP Version 2.7.5. Bordeaux, 2014. Available online: https://pari.math.u-bordeaux.fr/archives/pari-announce-15/msg00004.html (accessed on 24 August 2018).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).