Statically Aggregate Verifiable Random Functions and Application to E-Lottery

Abstract

Cohen, Goldwasser, and Vaikuntanathan (TCC’15) introduced the concept of aggregate pseudo-random functions (PRFs), which allow efficiently computing the aggregate of PRF values over exponential-sized sets. In this paper, we explore the aggregation augmentation on verifiable random function (VRFs), introduced by Micali, Rabin and Vadhan (FOCS’99), as well as its application to e-lottery schemes. We introduce the notion of static aggregate verifiable random functions (Agg-VRFs), which perform aggregation for VRFs in a static setting. Our contributions can be summarized as follows: (1) we define static aggregate VRFs, which allow the efficient aggregation of VRF values and the corresponding proofs over super-polynomially large sets; (2) we present a static Agg-VRF construction over bit-fixing sets with respect to product aggregation based on the q-decisional Diffie–Hellman exponent assumption; (3) we test the performance of our static Agg-VRFs instantiation in comparison to a standard (non-aggregate) VRF in terms of costing time for the aggregation and verification processes, which shows that Agg-VRFs lower considerably the timing of verification of big sets; and (4) by employing Agg-VRFs, we propose an improved e-lottery scheme based on the framework of Chow et al.’s VRF-based e-lottery proposal (ICCSA’05). We evaluate the performance of Chow et al.’s e-lottery scheme and our improved scheme, and the latter shows a significant improvement in the efficiency of generating the winning number and the player verification.

1. Introduction

Verifiable random functions (VRFs), initially introduced by Micali, Rabin, and Vadhan [1], can be seen as the public key equivalent of pseudorandom functions (PRFs) that, besides the pseudorandomness property (i.e., the function looks random at any input x), also provide the property of verifiability. More precisely, VRFs are defined by a pair of public and secret keys $\left(\mathsf{pk},\mathsf{sk}\right)$ in such a way that they provide not only the efficient computation of the pseudorandom function $f_{\mathsf{sk}}\left(x\right)=y$ for any input x but also a non-interactive publicly verifiable proof ${\pi }_{\mathsf{sk}}\left(x\right)$ that, given access to $\mathsf{pk}$, allows the efficient verification of the statement $f_{\mathsf{sk}}\left(x\right)=y$ for all inputs x. VRFs have been shown to be very useful in multiple application scenarios including key distribution centres [2], non-interactive lottery systems used in micropayments [3], domain name security extensions (DNSSEC) [4,5,6], e-lottery schemes [7], and proof-of-stake blockchain protocols such as Ouroboros Praos [8,9].

Cohen, Goldwasser, and Vaikuntanathan [10] were the first to investigate how to answer aggregate queries for PRFs over exponential-sized sets and introduced a type of augmented PRFs, called aggregate pseudo-random functions, which significantly enriched the existing family of (augmented) PRFs including constrained PRFs [11], key-homomorphic PRFs [12], and distributed PRFs [2]. Inspired by the idea of aggregated PRFs [10], in this paper, we explore the aggregation of VRFs and introduce a new cryptographic primitive, static aggregate verifiable random functions (static Agg-VRFs), which allow not only the efficient aggregation operation both on function values and proofs but also the verification on the correctness of the aggregated results.

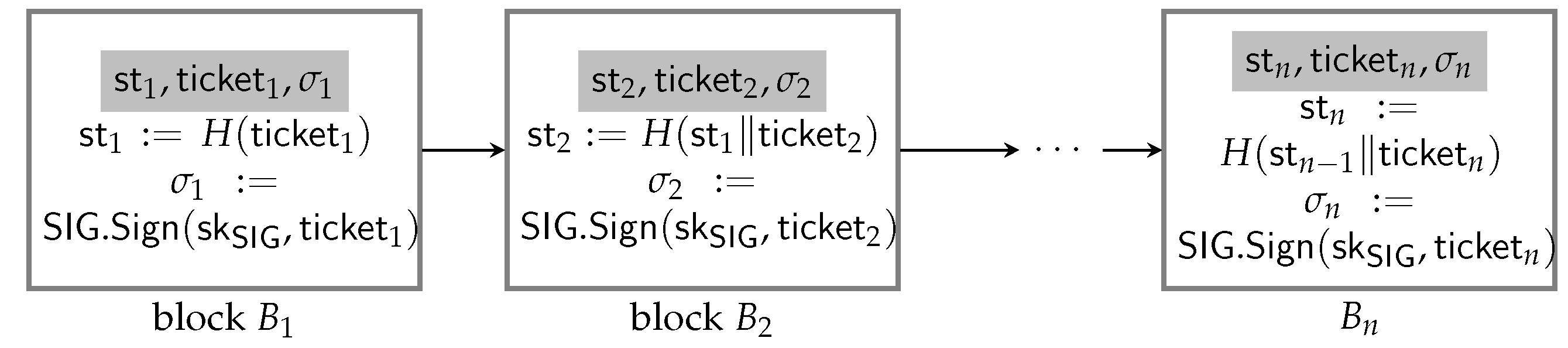
Aggregate VRFs allow the efficient aggregation of a large number of function values, as well as the efficient verification of the correctness of the aggregated function result by employing the corresponding aggregated proof. Let us give an example to illustrate this property. Consider a cloud-assisted computing setting where a VRF can be employed in the client–server model, i.e., Alice is given access to a random function where the function description (or the secret key) is stored by a server (seen as the random value provider). Whenever Alice requests an arbitrary bit-string x, the server simply computes the function value $y=f\left(x\right)$ together with the corresponding proof $\pi$ and returns the tuple $(x,y,\pi )$ to Alice. Alice may also request the aggregation (such as the product) of the function values over a large number of points (e.g., $x_1,x_2,\dots ,x_n$, which may match some pattern, such as having same bits on some bit locations). In this case, aggregate VRFs allow the server to compute the product of $f\left(x_1\right),\dots ,f\left(x_n\right)$ efficiently, instead of firstly evaluating $f\left(x_1\right),\dots ,f\left(x_n\right)$ and then calculating their product. On receiving either the function value y of an individual input or the aggregated function value $y^{\mathsf{agg}}$ over multiple inputs, Alice needs to verify the correctness of the returned value. VRFs allow the verification of the correctness of y using $\pi$, while, to verify the correctness of $y^{\mathsf{agg}}$, there is a trivial way, namely firstly verifying $(x_i,y_i,{\pi }_i)$ for $i=1,\dots ,n$ using the verification algorithm of VRFs and then checking if $y^{\mathsf{agg}}={\prod }_{i=1}^n{y}_i$, but the running time of which depends on the number n. Via aggregate VRFs, the verification of $y^{\mathsf{agg}}$ can be achieved much more efficiently by using the aggregated proof ${\pi }^{\mathsf{agg}}$ that is generated by the server and returned to Alice along with $y^{\mathsf{agg}}$.

A representative application of aggregate VRFs is in e-lottery schemes. More precisely, aggregate VRFs can be employed in VRF-based e-lottery schemes [7], where a random number generation mechanism is required to determine not only a winning number but also the public verifiability of the winning result, which guarantees that the dealer cannot cheat in the random number generation process. In this paper, we provide an e-lottery scheme, which has significant gain in the efficiency of generating the winning numbers and verifying the winning results. In a nutshell, VRF-based e-lottery schemes [7] proceed as follows: Initially, the dealer generates a secret/public key pair $(\mathsf{sk},\mathsf{pk})$ of VRFs and publishes the public key $\mathsf{pk}$, together with a parameter $\mathcal{T}$ associated with the time (this is the input parameter controlling the time complexity of the delaying function $D(·)$) during which the dealer must release the winning ticket value. To purchase the ticket, a player chooses his bet number $\mathsf{s}$ and obtains a ticket ${\mathsf{ticket}}_i$ (please refer to Section 4.2 for the generation of ticket ${\mathsf{ticket}}_i$ on a bet number x in detail) from the dealer. The dealer links the ticket to a blockchain, which could be created as ${\mathsf{chain}}_1:=H\left({\mathsf{ticket}}_1\right)$, ${\mathsf{chain}}_i:=H({\mathsf{chain}}_{i-1}\left|\right|{\mathsf{ticket}}_i)$ for $i>1$, and publishes ${\mathsf{chain}}_j$ where j is the number of tickets sold so far. To generate the random winning number, the dealer first computes a VRF as $(w_0,{\pi }_0)=(f_{\mathsf{sk}}\left(d\right),{\pi }_{\mathsf{sk}}\left(d\right))$ on $d=D\left(h\right)$, where h is the final value of the blockchain (i.e., suppose there are n tickets sold, then $h:=H\left({\mathsf{chain}}_n\right)$). Assume that the numbers used in the lottery game are $\{1,2,\dots ,N_{\mathsf{max}}\}$. If $w_0>N_{\mathsf{max}}$, then the dealer iteratively applies the VRF on $w_{i-1}\parallel d$ to obtain $(w_i,{\pi }_i)=(f_{\mathsf{sk}}(w_{i-1}\parallel d),{\pi }_{\mathsf{sk}}(w_{i-1}\parallel d))$. Suppose that, within $\mathcal{T}$ units of time after the closing of the lottery session, until applying the VRF for t times, the dealer obtains $(w_t,{\pi }_t)$ such that $w_t\le N_{\mathsf{max}}$. Afterwards, the dealer publishes $(w_t,{\pi }_t)$ as the winning number and the corresponding proof as well as all the intermediate tuples $(w_0,{\pi }_0),\dots ,(w_{t-1},{\pi }_{t-1})$. If $\mathsf{s}=w_t$, a player wins. To verify the validity of a winning number $w_t$, each player verifies the validity of $(w_i,{\pi }_i)$ for $i=0,\dots ,t$.

Chow et al.’s e-lottery scheme [7] seems to be very promising when considering an ideal case that after a small number t of times that the VRF is applied, a function value $w_t$ such that $w_t\le N_{\mathsf{max}}$ can be obtained successfully. Otherwise, it means that the dealer needs to calculate the VRF more times, while the player needs to verify the correctness of more tuples in order to verify the winning result; the latter leads to large computational overhead and requires storage of all intermediate tuples of VRF function values and corresponding proofs, both from the dealer and the player.

Observe that both the evaluation and verification of multiple pairs of VRF function value/proof are time consuming. By using our aggregate VRF instantiation, we improve the e-lottery by devising the dealer to evaluate aggregate VRF twice at most so as to obtain a random winning number together with corresponding proof, thus rendering the verification for only such a single pair. This reduces the amount of data written to the dealer’s storage space and also decreases the computational cost for the verification process of each player.

Our Contribution. We introduce the notion of static aggregate verifiable random functions (static Agg-VRFs). Briefly, a static Agg-VRF is a family of keyed functions each associated with a pair of keys, such that, given the secret key, one can compute the aggregation function for both the function values and the proofs of the VRFs over super-polynomially large sets in polynomial time, while, given the public key, the correctness of the aggregate function values could be checked by the corresponding aggregated proof. It is very important that the sizes of the aggregated function values and proofs should be independent of the size of the set over which the aggregation is performed. The security requirement of a static Agg-VRF states that access to an aggregate oracle provides no advantage to the ability of a polynomial time adversary to distinguish the function value from a random value, even when the adversary could query an aggregation of the function values over a specific set (of possibly super-polynomial size) of his choice.

In this paper, the aggregate operation we consider is the product of all the VRF values and proofs over inputs belonging to a super-polynomially large set. We show how to compute the product aggregation over a super-polynomial size set in polynomial time, since it is impossible to directly compute the product on a super-polynomial number of values. More specifically, we show how to achieve a static Agg-VRF under the Hohenberger and Waters’ VRF scheme [13] for the product aggregation with respect to a bit-fixing set. We stress that after revisiting the JN-VRF scheme [14] proposed by Jager and Niehuesbased (currently the most efficient VRFs with full adaptive security in the standard model), we find that, even though JN-VRF almost enjoys the same framework of HW-VRF (since an admissible hash function $H_{\mathsf{AHF}}$ is applied on inputs x before evaluating the function value and the corresponding proof, which impacts negatively the nice pattern of all inputs in a bit-fixing set), it is impossible to perform productive aggregation of a super-polynomial number of values $f_{sk}\left(H_{\mathsf{AHF}}\left(x\right)\right)$ efficiently over bit-fixing sets.

We implemented and evaluated the performance of our proposed static aggregate VRF in comparison to a standard (non-aggregate) VRF for inputs with different lengths i.e., 56, 128, 256, 512, and 1024 bits, in terms of the costing time for aggregating the function values, aggregating the proofs as well as the cost of verification for the aggregation. In all cases, our aggregate VRFs present significant computational advantage and are more efficient than standard VRFs. Furthermore, by employing aggregate VRFs for bit-fixing sets, we propose an improved e-lottery scheme based on the framework of Chow et al.’s VRF-based e-lottery proposal [7], by mainly modifying the winning result generation phase and the player verification phase. We implemented and tested the performance of both Chow et al.’s and our improved e-lottery schemes. Our improved scheme shows a significant improvement in efficiency in comparison to Chow et al.’s scheme.

Core Technique. We present a construction of static aggregate VRFs, which performs the product aggregation over a bit-fixing set, following Hohenberger and Waters’ [13] VRF scheme. A bit-fixing set consists of bit-strings which match a particular bit pattern. It can be defined by a pattern string $v\in {\{0,1,\perp \}}^{poly\left(\lambda \right)}$ as $S_v=\{x\in {\{0,1\}}^{poly\left(\lambda \right)}:\forall i,x_i=v_i\mathrm{or}{v}_i=\perp \}$. The evaluation of the VRF on input $x=x_1\parallel x_2\parallel \dots \parallel x_{\ell }$ is defined as $y=e{(g,h)}^{u_0{\prod }_{i=1}^{\ell }{u}_i^{x_i}}$, where $g,h,U_0=g^{u_0},\dots ,U_{\ell }=g^{u_{\ell }}$ are public keys and $u_0,\dots ,u_{\ell }$ are kept secret. The corresponding proofs of the VRF are given using a step ladder approach, namely, for $j=1$ to ℓ, ${\pi }_j=g^{{\prod }_{i=1}^j{u}_i^{x_i}}$ and ${\pi }_{\ell +1}=g^{u_0{\prod }_{i=1}^{\ell }{u}_i^{x_i}}$.

Let $\mathrm{Fixed}\left(v\right)=\{i\in \left[\ell \right]:v_i\in \{0,1\}\}$ and $\left|\mathrm{Fixed}\right(v\left)\right|=\tau$. To aggregate the VRF, let ${\pi }_0^{\mathsf{agg}}=g^{2^{\ell -\tau }}$, for $i=1,\dots ,\ell$; we compute

$${\pi }_i^{\mathsf{agg}}=\left\{\begin{array}{cc}{\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{u_i^{v_i}}\hfill & \mathrm{if}i\in \mathrm{Fixed}\left(v\right)\hfill \\ {\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{(u_i+1)/2}\hfill & \mathrm{if}i\notin \mathrm{Fixed}\left(v\right)\hfill \end{array}\right.$$

(1)

and ${\pi }_{\ell +1}^{\mathsf{agg}}={\left({\pi }_{\ell }^{\mathsf{agg}}\right)}^{u_0}$. The aggregated function value is computed as

$$y^{\mathsf{agg}}=e{(g,h)}^{u_0{\prod }_{i\in \mathrm{Fixed}\left(v\right)}{u}_i^{v_i}{\prod }_{i\in \left[\ell \right]\setminus \mathrm{Fixed}\left(v\right)}(u_i+1)}.$$

(2)

The aggregation verification algorithm checks the following equations: for $i=1,\dots ,\ell$

$$e(g,{\pi }_i^{\mathsf{agg}})=\left\{\begin{array}{cc}e({\pi }_{i-1}^{\mathsf{agg}},g)\hfill & \mathrm{if}i\in \mathrm{Fixed}\left(v\right)\mathrm{and}{v}_i=0\hfill \\ e({\pi }_{i-1}^{\mathsf{agg}},U_i)\hfill & \mathrm{if}i\in \mathrm{Fixed}\left(v\right)\mathrm{and}{v}_i=1\hfill \\ e{({\pi }_{i-1}^{\mathsf{agg}},g·U_i)}^{1/2}\hfill & \mathrm{if}i\notin \mathrm{Fixed}\left(v\right)\hfill \end{array}\right.$$

(3)

and $e({\pi }_{\ell +1}^{\mathsf{agg}},g)=e({\pi }_{\ell }^{\mathsf{agg}},U_0)$ and $e({\pi }_{\ell +1}^{\mathsf{agg}},h)=y^{\mathsf{agg}}$.

Improved Efficiency. We provide some highlights on the achieved efficiency.

Efficiency of Aggregate VRF. The construction of our static aggregate VRF for a bit-fixing (BF) set achieves high performance in the verification process, since it takes only $\mathcal{O}\left(\ell \right)$ bilinear pairing operations, even when verifying an exponentially large set of function values, where ℓ denotes the input length. The experimental results show that, even for 1024 bits of inputs, the aggregation of $2^{1004}$ pairs of function values/proofs can be computed very efficiently in 6881 ms. Moreover, the time required to verify their aggregated function values/proofs of $2^{1004}$ pairs only increases $50\%$, comparing with the verification time for each single function value/proof pair of standard VRF. Section 3.2 and Section 3.3 present a detailed efficiency discussion and our experimental tests and comparisons.

Efficiency of Improved E-Lottery Scheme. We test the performance of Chow et al.’s e-lottery scheme [7] and our improved (aggregate VRF based) counterpart and make a comparison. In our improved e-lottery scheme, the computation of the aggregate function value/proof pair and the verification are performed via a single step of Aggregation and AggVerify algorithms, respectively, while Chow et al.’s e-lottery scheme is processed by t steps. We perform some experiments on Chow et al.’s scheme to see how big/small the t is so as to reach the point where the dealer obtains $(w_t,{\pi }_t)$ such that $w_t\le N_{\mathsf{max}}$, thus figuring out the computation-time for the corresponding multiple function evaluation and verification. In the experiments, we ran 10 times Chow et al.’s scheme and we obtained the median of all the runs. We reached $t\approx 2$ and it took ≈100 s for each run of the winner generation and ≈5 s for player verification. In our improved version, the generation of the winner ticket costs less than 90 s, and the time for verification decreases to ≈2.5 s, which shows a significant improvement in efficiency.

Related work. We summarize relevant current state-of-the-art.

Verifiable Random Functions. Hohenberger and Waters’ VRF scheme [13] is the first that shows all the desired properties for a VRF (we say that a VRF scheme has all the desired properties if it allows an exponential-sized input space, achieves full adaptive security, and is based on a non-interactive assumption). Formerly, there have been several VRF proposals [15,16,17], all of which have some limitations: they only allow a polynomial-sized input space, they do not achieve fully adaptive security, or they are based on an interactive assumption. Thus far, there are also many constructions of VRFs with all the desired properties based on the decisional Diffie–Hellman assumption (DDH) or the decision linear assumption (DLIN) presenting different security losses [18,19,20,21,22]. Kohl [22] provided a detailed summary and comparison of all existing efficient constructions of VRFs in terms of the underlying assumption, sizes of verification key and the corresponding proof, and the associated security loss. Recently, Jager and Niehues [14] provided the most efficient VRF scheme with adaptive security in the standard model, relying on the computational admissible hash functions.

Aggregate Pseudorandom Functions. Cohen et al. [10] introduced the notion of aggregate PRFs, which is a family of functions indexed by a secret key with the functionality that, given the secret key, anyone is able to aggregate the values of the function over super-polynomially many PRF values with only a polynomial-time computation. They also proposed constructions of aggregate PRFs under various cryptographic hardness assumptions (one-way functions and sub-exponential hardness of the Decisional Diffie–Hellman assumption) for different types of aggregation operators such as sums and products and for several set systems including intervals, bit-fixing sets, and sets that can be recognized by polynomial-size decision trees and read-once Boolean formulas. In this paper, we explore how to aggregate VRFs, which involves efficient aggregations both on the function evaluations and on the corresponding proofs, while providing verifiability for the correctness of aggregated function value via corresponding proof.

E-lottery Schemes/Protocols. In 2005, Chow et al. [7] proposed an e-lottery scheme using a verifiable random function (VRF) and a delay function. To reduce the complexity in the (purchaser) verification phase, Liu et al. [23] improved Chow et al.’s scheme by proposing a multi-level hash chain to replace the original linear hash chain, as well as a hash-function-based delay function, which is more suitable for e-lottery networks with mobile portable terminals. Based on the secure one-way hash function and the factorization problem in RSA, Lee and Chang [24] presented an electronic t-out-of-n lottery on the Internet, which allows lottery players to simultaneously select t out of n numbers in a ticket without iterative selection. Given that the previous schemes [7,23,24] offer single participant lottery purchases on the Internet, Chen et al. [25] proposed an e-lottery purchase protocol that supports the joint purchase from multi-participants that enables them to safely and fairly participate in a mobile environment. Aiming to provide an online lottery protocol that does not rely on a trusted third party, Grumbach and Riemann [26] proposed a novel distributed e-lottery protocol based on the centralized e-lottery of Chow et al. [7] and incorporated the aforementioned multi-level hash chain verification phase of Liu et al. [23]. Considering that the existing works on e-lottery focus either on providing new functionalities (such as decentralization or threshold) or improving the hash chain or delay function, the building block of VRFs has received little attention. In this paper, we explore how to improve the efficiency of Chow et al.’s [7] e-lottery scheme by using aggregate VRFs.

2. Preliminaries

2.1. Verifiable Random Functions

Let $F:\mathcal{K}\times \mathcal{X}\to \mathcal{Y}\times \mathcal{P}$ be an efficient function, where the key space $\mathcal{K}$, domain $\mathcal{X}$, range $\mathcal{Y}$, and proof space $\mathcal{P}$ are dependent on the security parameter $\lambda$. Consider $(\mathsf{Setup},\mathsf{Eval},\mathsf{Verify})$ as the following algorithms:

• $\mathsf{Setup}\left(1^{\lambda }\right)\to (sk,pk)$ takes as input a security parameter $\lambda$ and outputs a key pair $(pk,sk)$. We say that $sk$ is the secret key and $pk$ is the verification key.
• $\mathsf{Eval}(sk,x)\to (y,\pi )$ takes as input the secret key $sk$ and $x\in \mathcal{X}$ and outputs a function value $y\in \mathcal{Y}$ and a proof $\pi \in \mathcal{P}$. We write ${\mathsf{Fun}}_{sk}\left(x\right)$ to denote the function value y and ${\mathsf{Prove}}_{sk}\left(x\right)$ to denote the proof of correctness computed by Eval on input $(sk,x)$.
• $\mathsf{Verify}(pk,x,y,\pi )\to \{0,1\}$ takes as input the verification key $pk$, $x\in \mathcal{X}$, $y\in \mathcal{Y}$, and the proof $\pi \in \mathcal{P}$ and outputs a bit.

Definition 1.

We say that $(\mathsf{Setup},\mathsf{Eval},\mathsf{Verify})$ is a verifiable random function (VRF) if all the following properties hold.

1. 

Provability: For all $(pk,sk)\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$ and inputs $x\in \mathcal{X}$ it holds: if $(y,\pi )\leftarrow \mathsf{Eval}(sk,x)$, then $\mathsf{Verify}(pk,x,y,\pi )=1$.

2. 

Uniqueness: For all $pk$ (not necessarily generated by $\mathsf{Setup}$) and inputs $x\in \mathcal{X}$, there does not exist a tuple $(y_0,y_1,{\pi }_0,{\pi }_1)$ such that: $\left(1\right)y_0\ne y_1$, $\left(2\right)\mathsf{Verify}(pk,x,y_0,{\pi }_0)=\mathsf{Verify}(pk,x,y_1,{\pi }_1)=1$.

3. 

Pseudorandomness: For all p.p.t. attackers $D=(D_1,D_2)$, there exists a negligible function $\mu \left(\lambda \right)$ such that:

$$\begin{array}{cc}\hfill \mathrm{Pr}[& (pk,sk)\leftarrow \mathsf{Setup}\left(1^{\lambda }\right);(x^{*},\mathsf{st})\leftarrow D_1^{\mathsf{Eval}(sk,·)}\left(pk\right);y_0={\mathsf{Fun}}_{sk}\left(x^{*}\right);y_1\leftarrow \mathcal{Y};\hfill \\ \hfill & b\leftarrow \{0,1\};b^{\prime }\leftarrow D_2^{\mathsf{Eval}(sk,·)}(y_b,\mathsf{st}):b^{\prime }=b\wedge x^{*}\notin L^{\mathsf{Eval}}]\le \frac{1}{2}+\mu \left(\lambda \right),\hfill \end{array}$$

where $L^{\mathsf{Eval}}$ denotes the set of all inputs that D queries to its oracle $\mathsf{Eval}$.

Here, we note that $\mathsf{Eval}$ and $\mathsf{Fun}$ denote two different functions. The former denotes the function that outputs both function value y and proof $\pi$, while the latter denotes the function that only outputs function value y.

2.2. Bilinear Maps and the HW-VRF Scheme

Bilinear Groups. Let $\mathbb{G}$ and ${\mathbb{G}}_T$ be algebraic groups. A bilinear map is an efficient mapping $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$ which is both: (bilinear) for all $g\in \mathbb{G}$ and $a,b\leftarrow {\mathbb{Z}}_p$, $e(g^a,g^b)=e{(g,g)}^{ab}$; and (non-degenerate) if g generates $\mathbb{G}$, then $e(g,g)\ne 1$.

Assumption A1

(q-Decisional Diffie–Hellman Exponent (q-DDHE)). Let $\mathbb{G},{\mathbb{G}}_T$ be groups of prime order $p\in \mathsf{\Theta }\left(2^{\lambda }\right)$. For all p.p.t. adversaries $\mathcal{A}$, there exists a negligible function μ such that:

$$\begin{array}{cc}\hfill \mathrm{Pr}[g,h& \leftarrow \mathbb{G};a\leftarrow {\mathbb{Z}}_p;y_0=e{(g,h)}^{a^q};y_1\leftarrow {\mathbb{G}}_T;b\leftarrow \{0,1\};\hfill \\ \hfill & b^{\prime }\leftarrow \mathcal{A}(g,h,g^a,\cdots ,g^{a^{q-1}},g^{a^{q+1}},\cdots ,g^{a^{2q}},y_b):b=b^{\prime }]\le \frac{1}{2}+\mu \left(\lambda \right).\hfill \end{array}$$

HW-VRF Scheme Here, we describe one of the elegant constructions of VRFs proposed by Hohenberger and Waters [13] (that is abbreviated as HW-VRF scheme). The latter is employed as a basis for our aggregate VRF scheme. HW-VRF is the first fully-secure VRF from the Naor-Reingold PRF [27] with exponential-size input space whose security is based on the so-called q-type complexity assumption, namely q-DDHE assumption, and is built as follows.

• Setup$(1^{\lambda },1^{\ell })$: The setup algorithm takes as input the security parameter $\lambda$ as well as the input length ℓ. It firstly runs $\mathcal{G}\left(1^{\lambda }\right)$ to obtain the description of the groups $\mathbb{G}$, ${\mathbb{G}}_T$ and of a bilinear map $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$. The description of $\mathbb{G}$ contains the generators $g,h\in \mathbb{G}$. Let ${\{0,1\}}^{\ell }$ be the input space. It next selects random values $u_0$, $u_1,\dots ,u_{\ell }\in {\mathbb{Z}}_p$ and sets $U_0=g^{u_0}$, $U_1=g^{u_1},\dots ,U_{\ell }=g^{u_{\ell }}$. It then sets the keys as: $pk=(g,h,U_0,U_1,\dots ,U_{\ell }),sk=(u_0,u_1,\dots ,u_{\ell })$.
• Fun$(sk,x)$: For $x\in {\{0,1\}}^{\ell }$, the function ${\mathsf{Fun}}_{sk}$ evaluates $x=x_1\parallel x_2\parallel \dots \parallel x_{\ell }$ as:

  $$y={\mathsf{Fun}}_{sk}\left(x\right)=e{(g,h)}^{u_0{\prod }_{i=1}^{\ell }{u}_i^{x_i}}.$$
• Prove$(sk,x)$. This algorithm outputs a proof $\pi$, which is comprised as follows. Let ${\pi }_{\ell +1}=g^{u_0{\prod }_{i=1}^{\ell }{u}_i^{x_i}}$, for $j=1$ to ℓ it computes: ${\pi }_j=g^{{\prod }_{i=1}^j{u}_i^{x_i}}$. Set $\pi =({\pi }_1,\dots ,{\pi }_{\ell },{\pi }_{\ell +1})$.
• Verify$(pk,x,y,\pi )$. Let $\pi =({\pi }_1,\dots ,{\pi }_{\ell },{\pi }_{\ell +1})$. To verify that y was computed correctly, proceed in a step-by-step manner by checking that

  $$e({\pi }_1,g)=\left\{\begin{array}{cc}e(g,g),\hfill & \mathrm{if}{x}_1=0;\hfill \\ e(U_1,g),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

  then for $i=2,\dots ,\ell$ it checks, if the following equations are satisfied:

  $$e({\pi }_i,g)=\left\{\begin{array}{cc}e({\pi }_{i-1},g),\hfill & \mathrm{if}{x}_i=0;\hfill \\ e({\pi }_{i-1},U_i),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$
  Finally, it checks that $e({\pi }_{\ell +1},g)=e({\pi }_{\ell },U_0)$ and $e({\pi }_{\ell +1},h)=y$. It outputs 1, if and only if all checks verify. Otherwise, it outputs 0.

3. Static Aggregate VRFs

In a (static) aggregate PRF [10] (here, we call the aggregate PRF proposed by Cohen, Goldwasser, and Vaikuntanathan [10] as a static aggregate PRF since their aggregation algorithm needs the secret key of the PRF to be taken as input), there is an additional aggregation algorithm which given the secret key can (efficiently) compute the aggregated result of all the function values over a set of all the inputs in polynomial time, even if the input set is of super-polynomial size. Note that in an aggregate VRF, similarly to an aggregate PRF, an additional aggregation algorithm is brought into the ordinary VRF [1]. Thus, aggregate VRFs can be regarded as an extension of ordinary VRFs. The static aggregate VRF differs from a static aggregate PRF [10] in that given the secret key the aggregation operation is performed not only on the function values but also on the corresponding proofs. Moreover, the resulted aggregate function value can be publicly verified by using aggregate proof (together with the public key and the input subset), which proves that the aggregate function value is a correct result on the aggregation of all function values over the input subset.

Cohen, Goldwasser, and Vaikuntanathan [10] were the first to consider the notion of aggregate PRFs over the super-polynomial large but efficiently recognizable set classes. In their model, they treat the efficiently recognizable set ensemble as a family of predicates, i.e., for any set S there exists a polynomial-size boolean circuit $C:{\{0,1\}}^{*}\to \{0,1\}$ such that $x\in S$ if and only if $C\left(x\right)=1$. Boneh and Waters [11] also employed such a predicate to define the concept of constrained PRFs with respect to a constrained set. In this paper, we employ the concept and formalization of the efficiently recognizable set in the definition of static aggregate VRFs.

Recall that a verifiable random function (VRF) [1] is a function $F:\mathcal{K}\times \mathcal{X}\to \mathcal{Y}\times \mathcal{P}$ defined over a secret key space $\mathcal{K}$, a domain $\mathcal{X}$, a range $\mathcal{Y}$, and a proof space $\mathcal{P}$ (and these sets may be parameterized by the security parameter $\lambda$). Let $\mathsf{Fun}:\mathcal{K}\times \mathcal{X}\to \mathcal{Y}$ denote the mapping of random function evaluations on arbitrary inputs and $\mathsf{Prove}:\mathcal{K}\times \mathcal{X}\to \mathcal{P}$ denote the mapping of proof evaluations on inputs, each of which can be computed by a deterministic polynomial time algorithm.

Let ${\Psi }_{\lambda }:{({\mathcal{Y}}_{\lambda },{\mathcal{P}}_{\lambda })}^{*}\to ({\mathcal{Y}}_{\lambda },{\mathcal{P}}_{\lambda })$ be the aggregation function that takes as inputs multiple pairs of values from the range ${\mathcal{Y}}_{\lambda }$ and the proof space ${\mathcal{P}}_{\lambda }$ of the function family, and aggregates them to output an aggregated function value in the range ${\mathcal{Y}}_{\lambda }$ and the corresponding aggregated proof in the proof space ${\mathcal{P}}_{\lambda }$.

Definition 2

(Static Aggregate VRF). Let $\mathcal{F}={\left\{{\mathcal{F}}_{\lambda }\right\}}_{\lambda \in \mathbb{N}}$ be a VRF function family where each function $F\in {\mathcal{F}}_{\lambda }:\mathcal{K}\times \mathcal{X}\to \mathcal{Y}\times \mathcal{P}$ computable in polynomial time is defined over a key space $\mathcal{K}$, a domain $\mathcal{X}$, a range $\mathcal{Y}$ and a proof space $\mathcal{P}$. Let $\mathcal{S}$ be an efficiently recognizable ensemble of sets ${\left\{{\mathcal{S}}_{\lambda }\right\}}_{\lambda }$ where for any $S\in \mathcal{S}$, $S\subset \mathcal{X}$, and ${\Psi }_{\lambda }:{({\mathcal{Y}}_{\lambda },{\mathcal{P}}_{\lambda })}^{*}\to ({\mathcal{Y}}_{\lambda },{\mathcal{P}}_{\lambda })$ be an aggregation function. We say that $\mathcal{F}$ is an $(\mathcal{S},\Psi )$-static aggregate verifiable random function family (abbreviated $(\mathcal{S},\Psi )$-sAgg-VRFs) if it satisfies:

• Efficient aggregation:There exists an efficient (computable in polynomial time) algorithm ${\mathsf{Aggregate}}_{F,\mathcal{S},\Psi }(sk,S)\to (y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})$ which on input the secret key $sk$ of a VRF and a set $S\in \mathcal{S}$, outputs aggregated results $(y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})\in \mathcal{Y}\times \mathcal{P}$ such that for any $S\in \mathcal{S}$, ${\mathsf{Aggregate}}_{F_{sk},\mathcal{S},\Psi }(sk,S)=\Psi (F_{sk}\left(x_1\right),\dots ,F_{sk}\left(x_{\left|S\right|}\right))$ where $F_{sk}\left(x_i\right)=(y_i={\mathsf{Fun}}_{sk}\left(x_i\right),{\pi }_i={\mathsf{Prove}}_{sk}\left(x_i\right))$ for $i=1,\dots ,\left|S\right|$;
• Verification for aggregation:There exists an efficient (computable in polynomial time) algorithm $\mathsf{AggVerify}(pk,S,y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})\to \{0,1\}$ which on input the aggregated function value $y_{\mathsf{agg}}$ and the proof ${\pi }_{\mathsf{agg}}$ for an ensemble $S\in \mathcal{S}$ of the domain, verifies if it holds that $y_{\mathsf{agg}}=\Psi ({\mathsf{Fun}}_{sk}\left(x_1\right),\dots ,{\mathsf{Fun}}_{sk}\left(x_{\left|S\right|}\right))$ using the aggregated proof ${\pi }_{\mathsf{agg}}$.
• Correctness of aggregated values:For all $(pk,sk)\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, set $S\in \mathcal{S}$ and the aggregate function $\Psi \in {\Psi }_{\lambda }$, let $(y,\pi )\leftarrow \mathsf{Eval}(sk,x)$ and $(y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})\leftarrow {\mathsf{Aggregate}}_{F,\mathcal{S},\Psi }(sk,S)$, then $\mathsf{AggVerify}(pk,S,y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})=1$.
• Pseudorandomness:For all p.p.t. attackers $D=(D_1,D_2)$, there exists a negligible function $\mu \left(\lambda \right)$ s.t.:

  $$\begin{array}{cc}\hfill \mathrm{Pr}[& (pk,sk)\leftarrow \mathsf{Setup}\left(1^{\lambda }\right);(x^{*},\mathsf{st})\leftarrow D_1^{\mathsf{Eval}(sk,·),{\mathsf{Aggregate}}_{F,\mathcal{S},\Psi }(sk,·)}\left(pk\right);b\leftarrow \{0,1\};\hfill \\ \hfill & y_0={\mathsf{Fun}}_{sk}\left(x^{*}\right);y_1\leftarrow \mathcal{Y};b^{\prime }\leftarrow D_2^{\mathsf{Eval}(sk,·),{\mathsf{Aggregate}}_{F,\mathcal{S},\Psi }(sk,·)}(y_b,\mathsf{st}):\hfill \\ \hfill & b^{\prime }=b\wedge C_{S_i}\left(x^{*}\right)=0\mathit{for}\mathit{all}{S}_i\in L^{\mathsf{Agg}}\wedge x^{*}\notin L^{\mathsf{Eval}}]\le \frac{1}{2}+\mu \left(\lambda \right),\hfill \end{array}$$

  where $L^{\mathsf{Eval}}$ is the set of all inputs that D queries to its oracle $\mathsf{Eval}$, $L^{\mathsf{Agg}}$ consists of all the sets $S_i$ that D queries to its oracle $\mathsf{Aggregate}$, and $C_{S_i}$ is the polynomial-size boolean circuit that is able to recognize the ensemble $S_i$.
• Compactness:There exists a polynomial $poly(·)$ such that for every $\lambda \in \mathbb{N}$, $x\in \mathcal{X}$, set $S\in \mathcal{S}$ and the aggregate function $\Psi \in {\Psi }_{\lambda }$, it holds with overwhelming probability over $(pk,sk)\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, $(y,\pi )\leftarrow \mathsf{Eval}(sk,x)$ and ${\mathsf{Aggregate}}_{F,\mathcal{S},\Psi }(sk,S)\to (y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})$ that the resulting aggregated value $y_{\mathsf{agg}}$ and aggregated proof ${\pi }_{\mathsf{agg}}$ has size $|y_{\mathsf{agg}}|,|{\pi }_{\mathsf{agg}}|\le poly(\lambda ,\left|x\right|)$. In particular, the size of $y_{\mathsf{agg}}$ and ${\pi }_{\mathsf{agg}}$ are independent of the size of the set S.

We stress that the set S over which the aggregation is performed can be super-polynomially large. Clearly, given exponential numbers of values $F_{sk}(·)$, it is impossible to perform aggregation on them but yet, we show how to efficiently compute the aggregation function on an exponentially large set with respect to a concrete VRF given the secret key.

Some explanations on the notion of static aggregate VRFs. Firstly, the algorithm ${\mathsf{Aggregate}}_{F,\mathcal{S},\Psi }$ achieves an efficient aggregation on function values/proofs over super-polynomially large sets S in polynomial time. We stress that our aim is to work on super-polynomially large sets, since, for any constant size of sets, the (productive) aggregation can be computed trivially, given the function value/proof pairs on all inputs in such a set. Secondly, the verification algorithm $\mathsf{AggVerify}$ is employed to efficiently verify the correctness of the aggregated function values $y_{\mathsf{agg}}$. Given ${\left\{(x_i,y_i,{\pi }_i)\right\}}_{i=1}^{\mid S\mid }$ and the aggregated function value $y_{\mathsf{agg}}$, there is a trivial way to verify the correctness of $y_{\mathsf{agg}}$, by verifying the correctness of each tuple $(x_i,y_i,{\pi }_i)$ for $i=1,\dots ,\mid S\mid$ and then checking if $y_{\mathsf{agg}}={\prod }_{i=1}^{\mid S\mid }{y}_i$, which is not computable in polynomial time if S is a super-polynomially large set. Therefore, our main concern is to achieve efficient verification on $y_{\mathsf{agg}}$ via the corresponding proof ${\pi }_{\mathsf{agg}}$, the size of which is independent of the size of S. Thirdly, the condition $\mathsf{AggVerify}(pk,S,y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})=1$ is interpreted as that value $y_{\mathsf{agg}}$ is a correct result on the aggregation of ${\left\{{\mathsf{Fun}}_{sk}\left(x_i\right)\right\}}_{i=1}^{\mid S\mid }$, i.e., $y_{\mathsf{agg}}=\Psi ({\mathsf{Fun}}_{sk}\left(x_1\right),\dots ,{\mathsf{Fun}}_{sk}\left(x_{\mid S\mid }\right))$, by using the corresponding proof ${\pi }_{\mathsf{agg}}$. We note that the verification for the aggregation does not violate the uniqueness of the underlying basic VRF. Indeed, there probably exist different sets $S_1$ and $S_2$ that result in a same $y_{\mathsf{agg}}$, but the uniqueness for any input point $x\in S_1$ ($x\in S_2$) always holds. Looking ahead, in our instantiation of aggregate VRFs, to find two sets $S_1\ne S_2$ such that ${\prod }_{x_i\in S_1}{\mathsf{Fun}}_{sk}\left(x_i\right)={\prod }_{x_i\in S_2}{\mathsf{Fun}}_{sk}\left(x_i\right)$ is computationally hard, without knowledge of $sk$. Lastly, the condition $\mathsf{AggVerify}(pk,S,y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})=1$ does not imply $\mathsf{Verify}(pk,x_i,y_i,{\pi }_i)=1$ for all $i=1,\dots ,\mid S\mid$, since by maintaining a correct pair $(y_{\mathsf{agg}},{\pi }_{\mathsf{agg}})$, we always can alter any two tuples as $(x_i,y_i·r,{\pi }_i)$ and $(x_j,y_j·r^{-1},{\pi }_j)$ for any random $r\in \mathbb{G}$, which means $\mathsf{Verify}(x_i,y_i·r,{\pi }_i)=\mathsf{Verify}(x_j,y_j·r^{-1},{\pi }_j)=0$.

3.1. A Static Aggregate VRF for Bit-Fixing Sets

We now propose a static aggregate VRF, whose aggregation function is to compute products over bit-fixing sets. In a nutshell, a bit-fixing set consists of bit-strings, which match a particular bit pattern. We naturally represent such sets by a string in ${\{0,1,\perp \}}^{poly\left(\lambda \right)}$ with 0 and 1 indicating a fixed bit location and ⊥ indicating a free bit location. To do so, we define for a pattern string $v\in {\{0,1,\perp \}}^{poly\left(\lambda \right)}$ the bit-fixing set as $S_v=\{x\in {\{0,1\}}^{poly\left(\lambda \right)}:\forall i,x_i=v_i\mathrm{or}{v}_i=\perp \}$.

We show based on an elegant construction of VRFs proposed by Hohenberger and Waters [13] (abbreviated as HW-VRF scheme) how to compute the productive aggregation function over a bit-fixing set in polynomial time; thus, yielding a static aggregate VRF. Please refer to Section 2.2 for detailed description of HW-VRF scheme. The aggregation algorithm for bit-fixing sets takes as input the VRF secret key $sk$ and a string $v\in {\{0,1,\perp \}}^{\ell }$. Let $\mathrm{Fixed}\left(v\right)=\{i\in \left[\ell \right]:v_i\in \{0,1\}\}$ and $\left|\mathrm{Fixed}\right(v\left)\right|=\tau$. The aggregation algorithm and the verification algorithm for an aggregated function value and the corresponding proof works as follows:

• Aggregate$(sk,v)$:
  Let ${\pi }_0^{\mathsf{agg}}:=g^{2^{\ell -\tau }}$. We define the aggregated proof as ${\pi }^{\mathsf{agg}}=({\pi }_1^{\mathsf{agg}},\dots ,{\pi }_{\ell }^{\mathsf{agg}},{\pi }_{\ell +1}^{\mathsf{agg}}),$ where for $i=1,\dots ,\ell$,

  $${\pi }_i^{\mathsf{agg}}=\left\{\begin{array}{cc}{\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{u_i^{v_i}}\hfill & \mathrm{if}i\in \mathrm{Fixed}\left(v\right)\hfill \\ {\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{(u_i+1)/2}\hfill & \mathrm{if}i\notin \mathrm{Fixed}\left(v\right).\hfill \end{array}\right.$$

  and ${\pi }_{\ell +1}^{\mathsf{agg}}={\left({\pi }_{\ell }^{\mathsf{agg}}\right)}^{u_0}$. The aggregated function value is defined as:

  $$y^{\mathsf{agg}}=e{(g,h)}^{u_0·\left({\prod }_{i\in \mathrm{Fixed}\left(v\right)}{u}_i^{v_i}\right)·\left({\prod }_{i\in \left[\ell \right]\setminus \mathrm{Fixed}\left(v\right)}(u_i+1)\right)}.$$
• AggVerify$(pk,v,y^{\mathsf{agg}},{\pi }^{\mathsf{agg}})$:
  Parse ${\pi }^{\mathsf{agg}}=({\pi }_1^{\mathsf{agg}},\dots ,{\pi }_{\ell }^{\mathsf{agg}},{\pi }_{\ell +1}^{\mathsf{agg}})$. Let ${\pi }_0^{\mathsf{agg}}=g^{2^{\ell -\tau }}$. The aggregation verification algorithm checks if the following equations are satisfied: for $i=1,\dots ,\ell$

  $$e(g,{\pi }_i^{\mathsf{agg}})=\left\{\begin{array}{cc}e({\pi }_{i-1}^{\mathsf{agg}},g)\hfill & \mathrm{if}i\in \mathrm{Fixed}\left(v\right)\mathrm{and}{v}_i=0\hfill \\ e({\pi }_{i-1}^{\mathsf{agg}},U_i)\hfill & \mathrm{if}i\in \mathrm{Fixed}\left(v\right)\mathrm{and}{v}_i=1\hfill \\ e{({\pi }_{i-1}^{\mathsf{agg}},g·U_i)}^{1/2}\hfill & \mathrm{if}i\notin \mathrm{Fixed}\left(v\right).\hfill \end{array}\right.$$

  and $e({\pi }_{\ell +1}^{\mathsf{agg}},g)=e({\pi }_{\ell }^{\mathsf{agg}},U_0)$ and $e({\pi }_{\ell +1}^{\mathsf{agg}},h)=y^{\mathsf{agg}}$. Output 1 if and only if all checks verify. Otherwise, output 0.

Letting ${\mathcal{S}}^{\mathrm{BF}}={\left\{{\mathcal{S}}_{\ell \left(\lambda \right)}^{\mathrm{BF}}\right\}}_{\lambda \in \mathbb{N}}$ where ${\mathcal{S}}_{\ell \left(\lambda \right)}^{\mathrm{BF}}={\{0,1,\perp \}}^{\ell }$ is the bit-fixing sets on ${\{0,1\}}^{\ell }$, we now prove the following theorem:

Theorem 1.

Let $ϵ>0$ be a constant. Choose the security parameter $\lambda =\mathsf{\Omega }\left({\ell }^{1/ϵ}\right)$, and assume the $(2^{{\lambda }^{ϵ}},2^{-{\lambda }^{ϵ}})$-hardness of q-DDHE over the group $\mathbb{G}$ and ${\mathbb{G}}_T$. Then, the collection of verifiable random functions F defined above is a secure aggregate VRF with respect to the subsets ${\mathcal{S}}^{\mathrm{BF}}$ and the product aggregation function over $\mathbb{G}$ and ${\mathbb{G}}_T$.

The compactness follows straightforward, since the aggregated function value $y^{\mathsf{agg}}\in {\mathbb{G}}_T$ and the aggregated proof ${\pi }^{\mathsf{agg}}=({\pi }_1^{\mathsf{agg}},\dots ,{\pi }_{\ell +1}^{\mathsf{agg}})\in {\mathbb{G}}^{\ell +1}$, the sizes of which are independent of the size of the bit-fixing set $S_v$, i.e., $2^{\ell -\tau }$.

The proof for pseudorandomness is similar to that of HW-VRF scheme in [13] since our static aggregate VRF is built on the ground of HW-VRF and the only phase we need to deal with in the proof is to simulate the responses of the aggregation queries. Here, we provide the simulation routine that the q-DDHE solver executes to act as a challenger in the pseudorandomness game of the aggregated VRFs. The detailed analysis of the game sequence is similar to the related descriptions in [13].

Proof of Theorem 1.

Let $Q\left(\lambda \right)$ be a polynomial upper bound on the number of queries made by a p.p.t. distinguisher D to the oracles $\mathsf{Eval}$ and $\mathsf{Aggregate}$. We use D to create an adversary $\mathcal{B}$ such that, if D wins in the pseudorandomness game for aggregate VRFs with probability $\frac{1}{2}+\frac{3ϵ}{64Q(\ell +1)}$, then $\mathcal{B}$ breaks the q-DDHE assumption with probability $\frac{1}{2}+\frac{3ϵ}{64Q(\ell +1)}$, where $q=4Q(\ell +1)$, and ℓ is the input length of the static Agg-VRFs.

Given $(\mathbb{G},p,g,h,g^a,\cdots ,g^{a^{q-1}},g^{a^{q+1}},\cdots ,g^{a^{2q}},y)$, to distinguish $y=e{(g,h)}^{a^q}$ from $y\leftarrow {\mathbb{G}}_T$, $\mathcal{B}$, proceed as follows:

$\mathsf{Setup}$. Set $m=4Q$ and choose an integer $k\stackrel{\$}{\leftarrow }[0,\ell ]$. It then picks random integers $r_1,\cdots ,r_{\ell },r^{\prime }$ from the interval $[0,m-1]$ and random elements $s_1\cdots ,s_{\ell },s^{\prime }\in {\mathbb{Z}}_p$, which are all kept internal by $\mathcal{B}$.

For $x\in {\{0,1\}}^{\ell }$, let $x_i$ denote the ith bit of x. Define the following functions:

$$\begin{array}{cc}\hfill & C\left(x\right)=m(1+k)+r^{\prime }+\sum _{i=1}^{\ell }{x}_i{r}_i,\widehat{C}(x,i)=\sum _{j=1}^i{x}_j{r}_j,J\left(x\right)=s^{\prime }\prod _{i=1}^{\ell }{s}_i^{x_i},\widehat{J}(x,i)=\prod _{j=1}^i{s}_j^{x_j}\hfill \end{array}$$

$\mathcal{B}$ sets $U_0={\left(g^{a^{m(1+k)+r^{\prime }}}\right)}^{s^{\prime }}$ and $U_i={\left(g^{a^{r_i}}\right)}^{s_i}$ for $i=1,\dots ,\ell$. It sets the public key as $(\mathbb{G},p,g,h,U_0,\cdots ,U_{\ell })$, and the secret key implicitly includes the values $u_0=a^{m(1+k)+r^{\prime }}{s}^{\prime }$ and ${\{u_i=a^{r_i}{s}_i\}}_{i\in [1,\ell ]}$.

Oracle Queries to $\mathsf{Eval}(sk,·)$. The distinguisher D will make queries of VRF evaluations and proofs. On receiving an input x, $\mathcal{B}$ first checks if $C\left(x\right)=q$ and aborts if this is true. Otherwise, it defines the function value as $F\left(x\right)=e({\left(g^{a^{C\left(x\right)}}\right)}^{J\left(x\right)},h)$, and the corresponding proof as $\pi =({\pi }_0,{\pi }_1,\dots ,{\pi }_{\ell })$ where ${\pi }_0={\left(g^{a^{C\left(x\right)}}\right)}^{J\left(x\right)}$, ${\pi }_i={\left(g^{a^{\widehat{C}(x,i)}}\right)}^{\widehat{J}(x,i)}$ for $i=1,\dots ,\ell$. Note that for any $x\in {\{0,1\}}^{\ell }$ it holds:

• The maximum value of $C\left(x\right)$ is $m(1+\ell )+(1+\ell )(m-1)=(2m-1)(1+\ell )<2m(1+\ell )=2q$.
• The maximum value of $\widehat{C}(x,i)$ is $\ell (m-1)<m(1+\ell )=q$ for $i\in \left[\ell \right]$.

As a result, if $C\left(x\right)\ne q$, $\mathcal{B}$ could answer all the $\mathsf{Eval}$ queries.

Oracle Queries to ${\mathsf{Aggregate}}_{F_{sk},\mathcal{S},\Psi }(·)$. The distinguisher D will also make queries for aggregate values. On receiving a pattern string $v\in {\{0,1,\perp \}}^{\ell }$, $\mathcal{B}$ uses the above secret key to compute the aggregated proof and the aggregate function value. More precisely, $\mathcal{B}$ answers the query ${\mathsf{Aggregate}}_{F_{sk},\mathcal{S},\Psi }\left(S_v\right)$ as follows: Let ${\pi }_0^{\mathsf{agg}}:=g^{2^{\ell -\tau }}$. Since the aggregated proof is defined as ${\pi }^{\mathsf{agg}}=({\pi }_1^{\mathsf{agg}},\dots ,{\pi }_{\ell }^{\mathsf{agg}},{\pi }_{\ell +1}^{\mathsf{agg}}),$ where, for $i=1,\dots ,\ell$,

$${\pi }_i^{\mathsf{agg}}=\left\{\begin{array}{cc}{\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{u_i^{v_i}}\hfill & \mathrm{if}i\in \mathrm{Fixed}\left(v\right)\hfill \\ {\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{(u_i+1)/2}\hfill & \mathrm{if}i\notin \mathrm{Fixed}\left(v\right).\hfill \end{array}\right.$$

and ${\pi }_{\ell +1}^{\mathsf{agg}}={\left({\pi }_{\ell }^{\mathsf{agg}}\right)}^{u_0}$, $\mathcal{B}$ will compute concretely:

$${\pi }_1^{\mathsf{agg}}=\left\{\begin{array}{cc}{\left(g^{a^{v_1{r}_1}{s}_1^{v_1}}\right)}^{2^{\ell -\tau }}\hfill & \mathrm{if}1\in \mathrm{Fixed}\left(v\right)\hfill \\ g^{2^{\ell -\tau -1}(1+a^{r_1}{s}_1)}\hfill & \mathrm{if}1\notin \mathrm{Fixed}\left(v\right)\hfill \end{array}\right.$$

and, for $j=2,\cdots ,\ell$, ${\pi }_j^{\mathsf{agg}}=g^{2^{\ell -\tau -{\overline{\tau }}_j}\left({\prod }_{i\in \left[j\right]\cap \mathrm{Fixed}\left(v\right)}{\left(a^{r_i}{s}_i\right)}^{v_i}\right)\left({\prod }_{i\in \mathrm{Flex}\left(v_j\right)}(1+a^{r_i}{s}_i)\right)}$ where $\mathrm{Flex}\left(v_j\right):=\{i\in \left[\ell \right]:i\le j\wedge v_i=\perp \}$ and ${\overline{\tau }}_j:=\left|\mathrm{Flex}\left(v_j\right)\right|$. The above value could be computed by $\mathcal{B}$ through its knowledge of $r_i,s_i$. The value of

$${\pi }_{\ell +1}^{\mathsf{agg}}=g^{\left({\displaystyle \prod _{i\in \left[\ell \right]\cap \mathrm{Fixed}\left(v\right)}}{\left(a^{r_i}{s}_i\right)}^{v_i}\right)·\left({\displaystyle \prod _{i\in \left[\ell \right]\setminus \mathrm{Fixed}\left(v\right)}}(1+a^{r_i}{s}_i)\right)·a^{m(1+k)+r^{\prime }}·s^{\prime }}$$

can be handled similarly using $m,k,r^{\prime },s^{\prime }$. While the aggregated function value is defined as $y^{\mathsf{agg}}=e({\pi }_{\ell +1}^{\mathsf{agg}},h)$.

Challenge.D will send a challenge input $x^{*}$ with the condition that $x^{*}$ is never queried to its $\mathsf{Eval}$ oracle. If $C\left(x^{*}\right)=q$, $\mathcal{B}$ returns the value y. When D responds with a bit $b^{\prime }$, $\mathcal{B}$ outputs $b^{\prime }$ as its guess to its own q-DDHE challenger. If $C\left(x^{*}\right)\ne q$, $\mathcal{B}$ outputs a random bit as its guess. This ends our description of q-DDHE adversary $\mathcal{B}$. □

Remark 1.

Discussion on the impossibility of productive aggregation on JN-VRF for bit-fixing sets. Recently, based on q-DDH-assumption, Jager and Niehues [14] proposed the currently most efficient VRFs (that is abbreviated as JN-VRF scheme) with full adaptive security in the standard model. JN-VRF almost enjoys the same framework of HW-VRF, and the only difference is that in the former an admissible hash function $H_{\mathsf{AHF}}$ is applied on inputs x before evaluating the function value and corresponding proof, while the latter is not. We stress that hash function $H_{\mathsf{AHF}}:{\{0,1\}}^{\ell }\to {\{0,1\}}^n$ on inputs x destroys the nice pattern of all inputs in a bit-fixing set, which implies that, for any $x\in S_v$, i.e., for all $i\in \left[\ell \right]$, $x_i=v_i\vee v_i=\perp$, there does not exist a bit-string $v^{\prime }{\{0,1,\perp \}}^n$ such that $H_{\mathsf{AHF}}\left(x\right)=h_1\parallel \dots \parallel h_n\notin S_{v^{\prime }}$, where $S_{v^{\prime }}=\{h_j\in {\{0,1\}}^n:\forall j,h_j=v_j^{\prime }\mathrm{or}{v}_j^{\prime }=\perp \}$. Otherwise, it is possible to find the collisions of $H_{\mathsf{AHF}}$. Therefore, given exponential numbers of values $F_{sk}\left(H_{\mathsf{AHF}}\left(x\right)\right)$, it is impossible to perform productive aggregation over them efficiently by using the same technique as in the last subsection.

3.2. Efficiency Analysis

Analysis of Costs. The instantiation in Section 3.1 is very compact since the aggregated function value consists of a single element in ${\mathbb{G}}_T$, while the aggregated proof is composed of $\ell +1$ elements in $\mathbb{G}$, which are independent of the size of a set S. The Aggregate algorithm simply requires at most ℓ multiplications plus one exponentiation to compute $y^{\mathsf{agg}}$ and $\ell +2$ exponentiations to evaluate ${\pi }^{\mathsf{agg}}$, which needs much less computation compared to computing $2^{\ell -\tau }$ multiplications to obtain $y^{\mathsf{agg}}$ and $2^{\ell -\tau }·(\ell +1)$ multiplications to obtain ${\pi }^{\mathsf{agg}}$ on all $2^{\ell -\tau }$ number of inputs in S. The AggVerify algorithm simply requires at most $(2\ell +3)$ pairing operations, while $2^{\ell -\tau }·(2\ell +3)$ pairings are needed for verifying $2^{\ell -\tau }$ number of function values/proofs on all inputs in S.

We summarize the cost for the Aggregate and AggVerify algorithms in

Table 1. The computation operations for the static aggregate VRF scheme with respect to bit-fixing sets.

Scheme	Assump.	Input Length	Cost for Aggregating Function Value	Cost for Aggregating Proof	Cost on Verification for Aggregation
HW-VRF [13]	q-DDHE	ℓ	$2^{\ell -\tau }$ MUL on ${\mathbb{G}}_T$	$2^{\ell -\tau }·(\ell +1)$ MUL on $\mathbb{G}$	$2^{\ell -\tau }·(\ell +1)$ bilinear pairings
Our static Agg-VRFs for bit-fixing sets	q-DDHE	ℓ	ℓ MUL on ${\mathbb{Z}}_p$ & one EXP	$(2\ell +3)$ EXP	$(2\ell +3)$ bilinear pairings

, where MUL is the shortened form of the multiplication operation, EXP is the abbreviation for the exponentiation operation, and ADD denotes the addition operation.

3.3. Implementation and Experimental Results

Choice of elliptic curves and pairings. In our implementation, we use Type A curves as described in [28], which can be defined as follows. Let q be a prime satisfying $q=3mod4$ and let p be some odd dividing $q+1$. Let E be the elliptic curve defined by the equation $y^2=x^3+x$ over ${\mathbb{F}}_q$; then, $E\left({\mathbb{F}}_q\right)$ is supersingular, $\#E\left({\mathbb{F}}_q\right)=q+1$, $\#E\left({\mathbb{F}}_{q^2}\right)={(q+1)}^2$, and $\mathbb{G}=E\left({\mathbb{F}}_q\right)\left[p\right]$ is a cyclic group of order p with embedding degree $k=2$. Given map $\Psi (x,y)=(-x,iy)$, where i is the square root of $-1$, $\Psi$ maps points of $E\left({\mathbb{F}}_q\right)$ to points of $E\left({\mathbb{F}}_{q^2}\right)\backslash E\left({\mathbb{F}}_q\right)$, and if f denotes the Tate pairing on the curve $E\left({\mathbb{F}}_{q^2}\right)$, then defining $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{F}}_{q^2}$ by $e(P,Q)=f(P,\Psi (Q\left)\right)$ gives a bilinear nondegenerate map. For more details about the choice of parameters, please refer to [28]. In our case, we use the standard parameters proposed by Lynn [28] (https://crypto.stanford.edu/pbc/), where q has 126 bits and $p=730750818665451621361119245571504901405976559617$. To generate random elements, we use libsodium (https://libsodium.gitbook.io/). Our implementation uses the programming language “C” and the GNU Multiple Precision Arithmetic for arithmetic with big numbers. We use the GCC version 10.0.1 with the following compilation flags: “-O3 -m64 -fPIC -pthread -MMD -MP -MF”.

Implementing HW-VRF. In our implementation, we use the bilinear map as pairing implemented by Lynn [28] for the BLS signature scheme. We notice that, when computing the function value ${\mathsf{Fun}}_{sk}\left(x\right)=e{(g,h)}^{u_0{\prod }_{i=1}^{\ell }{u}_i^{x_i}}$, we usually compute first the bilinear $e(g,h)$, and then do the exponentiation. However, it is expensive to do the exponentiation of an element in ${\mathbb{G}}_T$. To improve the efficiency of computing ${\mathsf{Fun}}_{sk}\left(x\right)$, we use the following mathematical trick: $e{(g,h)}^{ab}=e(g^a,h^b)$, which implies that we calculate ${\mathsf{Fun}}_{sk}\left(x\right)$ as $e(g^{u_0},h^{{\mathsf{\Pi }}_{i=1}^{\ell }{u}_i^{x_i}})$. Since the computation of $g^a$ (or $h^b$) corresponds to the scalar multiplication of a point P (or Q) by a scalar a (or b), using this trick, we avoid the exponentiation on an element in ${\mathbb{G}}_T$ by requiring cost of two scalar multiplications of a point of the curve.

Implementing our static Agg-VRFs. Since p is fixed, when calculating the aggregated proof as ${\pi }_i^{\mathsf{agg}}:={\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{(u_i+1)/2}$, we can precompute the inversion of 2 and thus only need to compute ${\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{(u_i+1)\mathsf{inv}\left(2\right)}$ by the scalar multiplication of a point on curve with scalar $(u_i+1)\star \mathsf{inv}\left(2\right)$. We use a similar approach when computing $e{({\pi }_{i-1}^{\mathsf{agg}},g·U_i)}^{1/2}$; in this case, we always perform $e({\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{\mathsf{inv}\left(2\right)},g·U_i)$. Again, ${\left({\pi }_{i-1}^{\mathsf{agg}}\right)}^{\mathsf{inv}\left(2\right)}$ corresponds to the scalar multiplication of a point with scalar $\mathsf{inv}\left(2\right)$, while $g·U_i$ corresponds to the additive operation on two points on the elliptic curve.

Comparison. We tested the performance of our static Agg-VRFs in comparison to a standard (non-aggregate) VRF, for five different input lengths, i.e., 56, 128, 256, 512, and 1024 bits. In all cases, we set the size of the fixed-bit equal to 20. Thus, naturally, we wanted to compare the efficiency of our aggregated VRF versus the evaluation and corresponding verification of $2^{36}$, $2^{108}$, $2^{236}$, $2^{492}$, and $2^{1004}$ VRF values. To perform our comparisons, we recorded the verification time for 100 pairs of function values and their corresponding proofs, if the verification is performed one-by-one (i.e., without using the aggregation) versus the corresponding performance of employing our proposed static aggregate VRF. Obviously, it holds $100\ll 2^{36}$, $100\ll 2^{108}$, $100\ll 2^{236}$, $100\ll 2^{492}$, and $100\ll 2^{1004}$. In fact, it is fine to choose any number that is smaller than $2^{36}$. We choose 100 to have sensible running time for the performance of the standard (non-aggregate) VRF. By taking the 56 bits input length with 20 fixed bits as an example, the bit-fixing set should contain $2^{36}$ elements; then, we should consider the verification time for $2^{36}$ pairs of function values-proofs, which is drastically larger than the running time when we evaluate the verification for only 100 pairs. Thus, showing that our aggregate VRF is much more efficient than the evaluation and corresponding verification of 100 VRF values obviously implies that it is more efficient than the evaluation and corresponding verification of $2^{36}$, $2^{108}$, $2^{236}$, $2^{492}$, and $2^{1004}$ VRF values, correspondingly.

Table 2. Running time (milliseconds) of the aggregate VRFs and standard (non-aggregate) VRF.

	HW-VRFs [13]			Aggregate VRFs
Input Length (bits)	Verify (ms)	Blocks Num.	Total Verification (ms)	Fixed-Bit Size	Aggregate (ms)	Our AggVerify (ms)
56	89	100	949	20	41	122
128	197	100	22371	20	196	298
256	472	100	52199	20	602	579
512	842	100	95233	20	1924	1212
1024	1556	100	164129	20	6881	2459

shows the result of our experiments. The column “Verify” corresponds to the required time for verifying a single pair of function value/proof. We tested how much time it costs to aggregate all the function values and their proofs for inputs belonging to the bit-fixing set. Furthermore, we evaluated the verification time to check the aggregated function value/proof. The column “Total Verification” corresponds to the total required time for verifying 100 pairs of function values/proofs via the standard VRFs (i.e., verification one-by-one), while the column “AggVerify” represents the costing time for verifying the aggregated value/proof via aggregate VRF (i.e., aggregated verification algorithm). The experimental results show that, even for 1024 bits of inputs, the aggregation of $2^{1004}$ pairs of function values/proofs can be computed very efficiently in 6881 ms. Moreover, the time required to verify their aggregated function values/proofs of $2^{1004}$ pairs only increases $50\%$ compared to the verification time for each single function value/proof pair of HW-VRFs.

We stress that our implementation is hardware independent. The only requirement is to have a compiler that is able to translate C code to the specific architecture. To give an estimation of what would happen if a different frequency in a computer architecture is used to run our code for HW-VRFs as well as our aggregate VRFs, we considered the original run using 56, 128, 256, 512, and 1024 bits, respectively. Then, we computed the difference between the frequencies and multiply for this result, as shown in

Table 3. Table of estimation of time for different frequencies.

Size	Frequency (GHz)	Time (ms) for AggVerify	Time (ms) for Verify of HW-VRFs [13]
56	$1.6$	122	89
	$2.1$	85	62
	$3.0$	70	51
128	$1.6$	298	197
	$2.1$	208	138
	$3.0$	172	114
256	$1.6$	579	472
	$2.1$	405	330
	$3.0$	335	274
512	$1.6$	1212	842
	$2.1$	848	589
	$3.0$	702	488
1024	$1.6$	2459	1556
	$2.1$	1696	1089
	$3.0$	1426	902

. For different frequencies (GHz), the verification time for the aggregated function values/proofs increases 30–50%, compared to that for each single function value/proof pair of the HW-VRFs, as shown in Table 3.

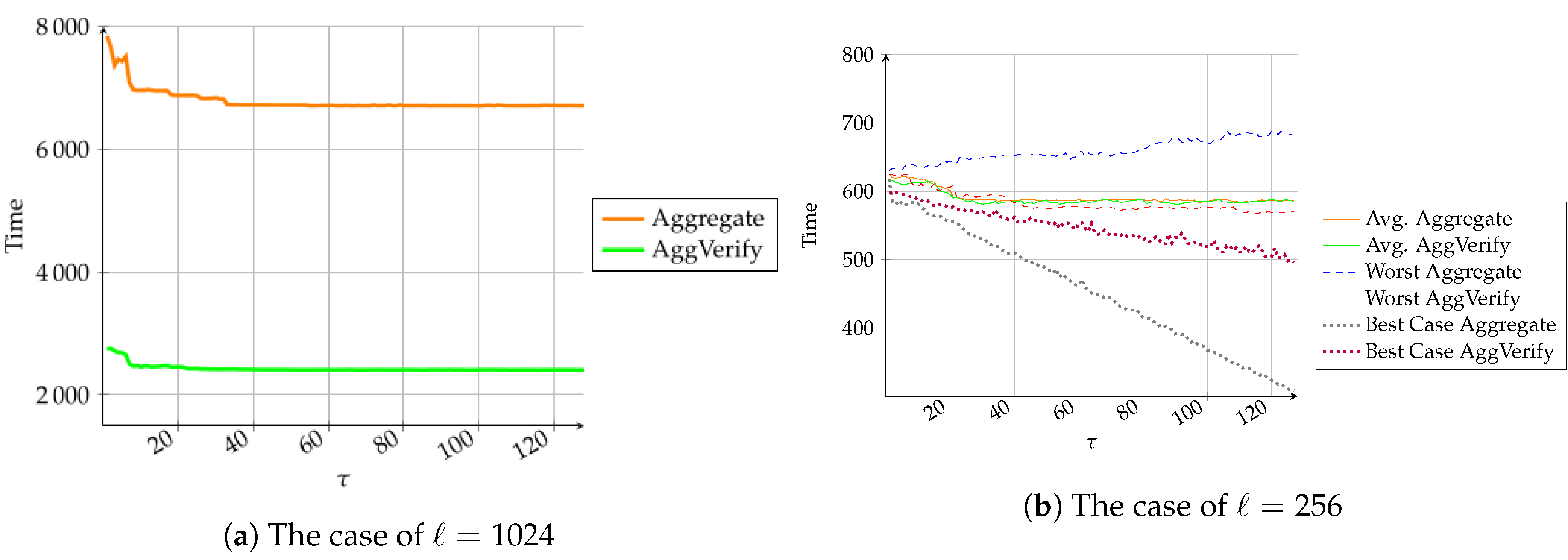
Moreover, we performed experiments for the cases where the input lengths ℓ are equal to 256 (depicted in Figure 1b) and 1024 (in Figure 1a), respectively, by choosing different numbers $\tau$ of the fixed bits to see the variation of the costing time on the aggregation and verification processes. When $\ell =256$, we ran experiments for three cases, i.e., worst-case where all $\tau$ fixed bits are 1, best-case where all $\tau$ fixed bits are 0, and average-case where $\tau$ fixed bits are chosen at random from $\{0,1\}$. In the worst-case, the Aggregate algorithm requires 256 multiplications plus 1 exponentiation to compute $y^{\mathsf{agg}}$ and 258 exponentiation to evaluate ${\pi }^{\mathsf{agg}}$, while the AggVerify algorithm requires 515 pairing operations, as shown in Figure 1b with square dot dashed line, which cost almost the same amount of time with different $\tau$. In the best-case, the Aggregate algorithm requires $(256-\tau )$ multiplications plus 1 exponentiation to compute $y^{\mathsf{agg}}$ and $(258-\tau )$ exponentiation to evaluate ${\pi }^{\mathsf{agg}}$, while the AggVerify algorithm requires $(516-\tau )$ pairing operations, as shown in Figure 1b with round dot dashed line, where the running time decreases with the increase of $\tau$. The average-case, as shown with solid lines in Figure 1b, lies between the range of the best-case and the worst-case. When $\ell =1024$, we show the time cost on the aggregation and verification algorithms in average-case, i.e., for randomly chosen $\tau$ fixed bits.

4. Application to the E-Lottery Scheme

4.1. Discussion on the Practical Instantiation of Chow et al.’s E-Lottery

Chow et al. [7] proposed an e-lottery scheme based on VRFs, where a random number generation mechanism is required to determine not only a winning number (chosen from a predefined domain) but also the public verifiability of the winning result, which guarantees that the dealer cannot cheat in the random number generation process. Let the numbers used in the lottery game be $\{1,2,\dots ,N_{\mathsf{max}}\}$. To generate the winning number, Chow et al. [7] employed a VRF that maps a bit-string of k length into a bit-string of l length. More precisely, the dealer firstly computes $(w_0,{\pi }_0):=(\mathsf{VRF}.\mathsf{Fun}({\mathsf{sk}}_{\mathsf{VRF}},d),\mathsf{VRF}.\mathsf{Prove}({\mathsf{sk}}_{\mathsf{VRF}},d))$, where d is the ‘hash value’ of all tickets sold so far. If $w_0>N_{\mathsf{max}}$, then the dealer iteratively calculates $(w_i,{\pi }_i):=(\mathsf{VRF}.\mathsf{Fun}({\mathsf{sk}}_{\mathsf{VRF}},w_{i-1}\parallel d),\mathsf{VRF}.\mathsf{Prove}({\mathsf{sk}}_{\mathsf{VRF}},w_{i-1}\parallel d))$ for $i=1,2,\dots$, until obtaining $(w_t,{\pi }_t)$ such that $w_t\le N_{\mathsf{max}}$. Afterwards, the dealer publishes the final $(w_t,{\pi }_t)$ and the intermediate tuples $(w_i,{\pi }_i)$ for $i=0,1,\dots ,t-1$ of VRF function values and their corresponding proofs.

To instantiate such an e-lottery scheme, a practical and concrete VRF scheme is needed. To the best of our knowledge, so far, most of the efficient instantiations of VRFs are based on bilinear maps (e.g., [13,14,18,19,22]), where the input spaces of VRFs are defined over binary strings and the function values on inputs are elements in a group ${\mathbb{G}}_T$, i.e., $w_i\in {\mathbb{G}}_T$, while the verification needs to compute some pairings.

Chow et al.’s construction [7] seems to be very promising when considering an ideal case that after a small number t of times that the VRF is applied, a function value $w_t$ such that $w_t\le N_{\mathsf{max}}$ can be obtained successfully. Nevertheless, what if t is a large number? Then, it implies that the dealer needs to calculate the VRF more times, while the player needs to verify the correctness of more tuples in order to verify the winning result, which also requires more consumption on pairing-computations from both the dealer and the player.

In the following section, we show how we modify Chow et al.’s e-lottery scheme [7] by employing our aggregate VRF, in order to reduce the computational overhead for the verification process of each player.

4.2. An E-Lottery Scheme Based on Aggregate VRFs

Observing that the intermediate tuple $(w_i,{\pi }_i)$ is a VRF function value/proof on an input $w_{i-1}\parallel d$, which has the same last $\mid d\mid$ bits and consists of a bit-fixing set. Thus, we compress all the intermediate tuples into a single function value $w^{\mathsf{agg}}=e{(g,h)}^{u_0·\left({\prod }_{i=\ell -\left|d\right|+1}^{\ell }{u}_i^{d_i}\right)·\left({\prod }_{i=1}^{\ell -\left|d\right|}(u_i+1)\right)}$ and corresponding proof ${\pi }^{\mathsf{agg}}$. If the exponent of $w^{\mathsf{agg}}$ is less than $N_{max}$, $w^{agg}$ can be set as the winning number. Otherwise, the dealer can output a value $w^{\prime agg}=e{(g,h)}^{u_0·\left({\prod }_{i=\ell -\left|d\right|+1}^{\ell }{u}_i^{d_i}\right)·\left({\prod }_{i=1,i\notin \{j_1,\dots ,j_k\}}^{\ell -\left|d\right|}(u_i+1)\right)}$ for indices $j_1,\dots ,j_k\in [1,\ell -|d\left|\right]$ as a winning number whose exponent is less than $N_{max}$. Thus, the player only needs to verify the correctness of a single aggregated function value/proof via the efficient aggregation verification algorithm. This approach reduces not only the amount of data written to the dealer’s storage space but also the computational cost for the verification process of each player. Our improved e-lottery scheme shares the same framework as Chow et al.’s scheme [7], with some modifications in the winning result generation phase and the player verification phase. The concrete description of our improved e-lottery scheme is as follows.

Let $H:{\{0,1\}}^{*}\to {\{0,1\}}^{{\ell }_H}$ be a collision-resistant hash function and $D:{\{0,1\}}^{{\ell }_H}\to {\{0,1\}}^{{\ell }_D}$ a verifiable delay function (VDF). Please refer to Appendix A for a detailed description of the VDF that we use. Let VRF be a function with input space ${\{0,1\}}^{\ell }$, where $\ell >{\ell }_D$, the function value space ${\mathbb{G}}_T$ and the proof space ${\mathbb{G}}^{\ell +1}$. Suppose any element in group ${\mathbb{G}}_T$ is represented as a bit-string with length ${\ell }_{\mathsf{bt}}$.

Setup:

Dealer side:

• Generate a public/secret key pair of VRF as $({\mathsf{pk}}_{\mathsf{VRF}},{\mathsf{sk}}_{\mathsf{VRF}})\leftarrow \mathrm{VRF}.\mathrm{Setup}\left(1^{\lambda }\right)$ and key pair of a signature scheme as $({\mathsf{pk}}_{\mathsf{SIG}},{\mathsf{sk}}_{\mathsf{SIG}})\leftarrow \mathrm{SIG}.\mathrm{Setup}\left(1^{\lambda }\right)$.
• Choose an arbitrary integer $N_{max}\in {\mathbb{Z}}_p^{*}$. The numbers used in the lottery game are $\{1,2,\dots ,N_{max}\}$.
• Publish a collision-resistant hash function, public key of VRF ${\mathsf{pk}}_{\mathsf{VRF}}$, public key of signature scheme ${\mathsf{pk}}_{\mathsf{SIG}}$, the delaying function $D(·)$, and the amount of time $\mathcal{T}$ in which the dealer must release the generated winning ticket value.

Ticket Purchase:

Player side:

• The player chooses $x\in {\mathbb{Z}}_p^{*}$ as bet number and randomly samples $r\leftarrow {\mathbb{Z}}_p^{*}$. r is kept secret.
• The player obtains a sequence number s of the ticket from the dealer.
• Compute $H(x\parallel s\parallel r)$, and send ${\mathsf{ticket}}_i=s\parallel (x\oplus r)\parallel H(x\parallel s\parallel r)$ to the dealer.

Dealer side:

• The dealer generates a signature for ticket ${\mathsf{ticket}}_i$ as ${\sigma }_i\leftarrow \mathsf{SIG}.\mathsf{Sign}({\mathsf{sk}}_{\mathsf{SIG}},{\mathsf{ticket}}_i)$ and returns ${\sigma }_i$ to the player to acknowledge the recipient of player’s purchase request.
• The dealer creates the state of ${\mathsf{ticket}}_1$ as ${\mathsf{st}}_1:=H\left({\mathsf{ticket}}_1\right)$, and ${\mathsf{st}}_i:=H({\mathsf{st}}_{i-1}\parallel {\mathsf{ticket}}_i)$ for $i=2,3,\dots$.
• The dealer generates blocks which contain: (1) the current state ${\mathsf{st}}_i\in {\{0,1\}}^{{\ell }_H}$; (2) ticket ${\mathsf{ticket}}_i$; and (3) signature ${\sigma }_i$ for ticket ${\mathsf{ticket}}_i$ under ${\mathsf{sk}}_{\mathsf{SIG}}$, e.g., with the following block structure:

  $$B_i=({\mathsf{st}}_i,{\mathsf{ticket}}_i,{\sigma }_i):=({\mathsf{st}}_i:=H({\mathsf{st}}_{i-1}\parallel {\mathsf{ticket}}_i),{\mathsf{ticket}}_i,{\sigma }_i).$$
• The dealer links all blocks to a blockchain, which is a sequence of blocks $B_1,B_2,\dots$.
• The dealer publishes a blockchain $\mathcal{C}=B_1,B_2,\dots ,B_n$ where n is the number of tickets sold so far. The length of a chain $\mathsf{len}\left(\mathcal{C}\right)=n$ is its number of blocks. The structure of a blockchain $\mathcal{C}$ is depicted in Figure 2:

Winning Result Generation:

Dealer side:

• Let the final state of the blockchain $\mathcal{C}$ be ${\mathsf{st}}_n$; the dealer computes $d:=D\left({\mathsf{st}}_n\right)$ by the delaying function and publishes d.
• Pad $d\in {\{0,1\}}^{{\ell }_D}$ with ⊥ as $\tilde{d}:={\perp }^{\ell -{\ell }_D}\parallel d$. Let $\tilde{d}={\perp }^{\ell -{\ell }_D}\parallel d_1\parallel \cdots \parallel d_{{\ell }_D}$. Define a set $S_{\tilde{d}}:=\{\xi \in {\{0,1\}}^{\ell }:\forall i\in \left[\ell \right],{\xi }_i={\tilde{d}}_i\mathrm{or}{\tilde{d}}_i=\perp \}$.
• The dealer calculates the productive aggregation of all $|S_{\tilde{d}}|=2^{\ell -{\ell }_D}$ numbers of function values and their corresponding proofs by using the efficient aggregation algorithm as $(y^{\mathsf{agg}},{\pi }^{\mathsf{agg}}):=\mathrm{Aggregate}({\mathsf{sk}}_{\mathsf{VRF}},\tilde{d})$. More precisely, since ${\mathsf{sk}}_{\mathsf{VRF}}=(u_0,u_1,\dots ,u_{\ell })$, which is defined by HW-VRFs scheme in Section 2.2, we have $y^{\mathsf{agg}}=e{(g,h)}^{u_0·\left({\prod }_{i=\ell -{\ell }_D+1}^{\ell }{u}_i^{d_i}\right)·\left({\prod }_{i=1}^{\ell -{\ell }_D}(u_i+1)\right)}$.
• Let $\mathsf{EXP}\left(y^{\mathsf{agg}}\right):=u_0·\left({\prod }_{i=\ell -{\ell }_D+1}^{\ell }{u}_i^{d_i}\right)·\left({\prod }_{i=1}^{\ell -{\ell }_D}(u_i+1)\right)$. The dealer checks if $\mathsf{EXP}\left(y^{\mathsf{agg}}\right)(\mathrm{mod}p-1)\le N_{max}$. If it is true, then set $y_{\mathsf{win}}:=y^{\mathsf{agg}}$ as the winning result.
• Otherwise, the dealer chooses a random index $\zeta \in [1,\ell -{\ell }_D]$ and then uses $\zeta$ to define a new wildcard ${\tilde{d}}^{\prime }\leftarrow {\perp }^{\zeta -1}\parallel 0\parallel {\perp }^{\ell -{\ell }_D-\zeta }\parallel d_1\parallel \cdots \parallel d_{{\ell }_D}$. The dealer computes $\mathsf{EXP}\left({\tilde{d}}^{\prime }\right):=u_0·\left({\prod }_{i=\ell -{\ell }_D+1}^{\ell }{u}_i^{d_i}\right)·\left({\prod }_{i=1,i\ne \zeta }^{\ell -{\ell }_D}(u_i+1)\right)$, and checks if $\mathsf{EXP}\left({\tilde{d}}^{\prime }\right)(\mathrm{mod}p-1)\le N_{max}$. Once finding a $\zeta \in [1,\ell -{\ell }_D]$ s.t. $\mathsf{EXP}\left({\tilde{d}}^{\prime }\right)(\mathrm{mod}p-1)\le N_{max}$, the dealer sets $y_{\mathsf{win}}:=e{(g,h)}^{\mathsf{EXP}\left({\tilde{d}}^{\prime }\right)}$ as the winning result and computes the corresponding proof by using the efficient aggregation algorithm $\mathrm{Aggregate}({\mathsf{sk}}_{\mathsf{VRF}},{\tilde{d}}^{\prime })$.
• The dealer publishes the winning result and its proof $(y_{\mathsf{win}},{\pi }_{\mathsf{win}})$ together with corresponding ${\tilde{d}}^{\prime }$ within $\Delta$ units of time after the closing of the lottery session.

Prize Claiming:

• The player checks if $e{(g,h)}^x=y_{\mathsf{win}}$. If it is true, the player wins.
• The player submits $(s,r)$ to the dealer.
• The dealer checks whether there exists a ticket ${\mathsf{ticket}}_i$ in the blockchain $\mathcal{C}$ such that ${\mathsf{ticket}}_i=s\parallel (x\oplus r)\parallel H(x\parallel s\parallel r)$.
• If it is true, the dealer checks whether the tuple $(s,r)$ has already been published (i.e., the prize has been claimed by someone already).
• If the prize is not yet claimed, the dealer pays the player and publishes $(s,r)$.

Player Verification:

Player side:

• The player checks whether his/her ticket(s) is/are included in the blockchain $\mathcal{C}$ and checks whether the final state ${\mathsf{st}}_n$ of the blockchain $\mathcal{C}$ is correct.
• The player verifies the correctness of d by using the verification algorithm of VDF.
• The player parses ${\tilde{d}}^{\prime }={\perp }^{\zeta -1}\parallel 0\parallel {\perp }^{\ell -{\ell }_D-\zeta }\parallel d_1\parallel \cdots \parallel d_{{\ell }_D}$ and checks if $d=d_1\parallel \cdots \parallel d_{{\ell }_D}$.
• The player verifies the correctness of $y_{\mathsf{win}}$ by using the verification algorithm $b\leftarrow \mathrm{AggVerify}({\mathsf{pk}}_{\mathsf{VRF}},{\tilde{d}}^{\prime },y_{\mathsf{win}},{\pi }_{\mathsf{win}})$.
• For each winning ticket published, the players verify the validity of $s\parallel (x\oplus r)\parallel H(x\parallel s\parallel r)$.

4.3. Implementation and Comparison on Chow et al.’s/Improved E-Lottery

To implement Chow et al.’s e-lottery scheme, we use the instantiation of HW-VRF presented in Section 2.2, while using our aggregate VRF scheme in Section 3.1 to implement the improved counterpart. When implementing the winning result generation phase and the player verification phase, we reuse part of the code for our implementation in Section 3.3. For the required delay functions, we use an instantiation of VDFs proposed by Pietrzak [29] (see Appendix A for details), which is defined as $D\left(x\right):=x^{2^{\mathcal{T}}}\left(\mathrm{mod}N\right)$, where $N=p_1{q}_1$ is a product of two large, distinct primes $p_1$ and $q_1$, x is a random element in ${\mathbb{Z}}_N^{*}$, and $\mathcal{T}$ is the timing parameter. For the signature scheme, we used EdDSA [30] provided in the libsodium (https://libsodium.gitbook.io/doc/) library.

Parameters. In our concept implementation, we consider Pietrzak’s VDF scheme [29] with the following parameters, where the statistical soundness security parameter of a proof is ${\lambda }_{\mathsf{Sound}}=100$, the time parameter is $\mathcal{T}=2^{40}$, the bit-lengths of two safe primes $p_1$ and $q_1$ are ${\lambda }_{\mathsf{QR}}/2=256$ bit safe primes $p_1,q_1$, and the bit-length of an RSA modulus $N=p_1{q}_1$ is ${\lambda }_{\mathsf{RSA}}=512$. (Here, we set ${\lambda }_{\mathsf{RSA}}=512$ as a toy example of implementation, which can be easily scaled to 1024 or 2048, if we adjust the corresponding parameters of the hash function as well as the inputs/outputs spaces of the VRFs.) Then, the VDF defines a function $D:{\{0,1\}}^{256}\to {\{0,1\}}^{512}$. We use SHA-256 as a hash function $H:{\{0,1\}}^{*}\to {\{0,1\}}^{256}$. The inputs/outputs of the VRFs are set equal to 1024 binary strings. We randomly choose an integer $N_{max}\in {\mathbb{Z}}_p$ s.t. $1\le N_{max}<p-1$, and the numbers used in the lottery game are $\{1,2,\dots ,N_{max}\}$. For every outcome $w\in {\mathbb{G}}_T$ of VRFs evaluation, to check if w can be set as a winning number, the dealer actually checks if the discrete log of w under the base generator $e(g,h)$ lies in the set $\{1,2,\dots ,N_{max}\}$. In fact, as explained in the implementation of HW-VRF and the aggregate VRF in Section 3.3, to obtain the function value ${\mathsf{Fun}}_{sk}\left(x\right)=e{(g,h)}^{u_0{\prod }_{i=1}^{\ell }{u}_i^{x_i}}$, the exponent $u_0{\prod }_{i=1}^{\ell }{u}_i^{x_i}$ is computed beforehand, which makes it handy to decide if w can be set as a winning number or not.

Results.

Table 4. Running time (seconds) of the e-lottery schemes.

Lottery Scheme	Winning Number Generation	Player Verification
Scheme in [7]	96.12992 s	4.384418 s
Our Scheme	90.13322 s	2.782610 s

shows the implementation results for both Chow et al.’s and our improved e-lottery schemes, particularly regarding the costing time for the winning number generation and the player verification. We employ a small blockchain scenario, where we have 1000 blocks, that is, there are 1000 random tickets in the system. The running time in Table 4 is for the experimental scenario that in Chow et al.’s e-lottery scheme the VRF is applied only twice and a function value is obtained, whose exponent $\mathsf{EXP}\left(w_1\right)(\mathrm{mod}p-1)\le N_{\mathsf{max}}$, while in our scheme the exponent of $y^{\mathsf{agg}}$ is beyond $N_{max}$, i.e., $\mathsf{EXP}\left(y^{\mathsf{agg}}\right)(\mathrm{mod}p-1)>N_{max}$, so that extra time is taken to search for another $y^{\prime \mathsf{agg}}$ whose exponent is below $N_{max}$. We consider such a case, because it optimally shows the efficiency gain of our e-lottery scheme over Chow et al.’s, since in this case the fewest iterative applications of VRFs are involved in Chow et al.’s scheme, while the extra step of recomputing $y^{\prime \mathsf{agg}}$ occurs in ours. The experimental results show that our scheme takes less time to generate the winning ticket than Chow et al.’s, and the player verification phase takes almost half less time as that of Chow et al.’s.

5. Conclusions

Inspired by the idea of aggregated PRFs [10], in this paper, we investigate how we may efficiently aggregate VRF values and their corresponding proofs. We introduce the notion of static aggregate VRFs. We show how to achieve static aggregate VRFs under the Hohenberger and Waters’ VRF scheme [13] for the product aggregation with respect to a bit-fixing set, based on the q-decisional Diffie–Hellman exponent assumption. Furthermore, we apply our aggregate VRFs to improve the prior VRF-based e-lottery scheme in the efficiency of generating the winner number and player verification phases. We test the performances of our static aggregate VRFs and improved e-lottery scheme, which show significant computation advantage and efficiency gains compared to the original counterparts.

As future work, it would be interesting to explore if it is possible to realize static aggregate VRFs for much more expressive sets, such as sets that can be recognized by polynomial-size decision trees, read-once Boolean formulas, or polynomial-size boolean circuits. Furthermore, it would be interesting to consider a public dynamic aggregate VRF, which allows taking any two fresh (aggregate) function values and proofs and combine them into a new aggregate function value and proof, without requiring the exponential number of inputs (from an exponentially large set) to be known in advance, as required in static aggregation.