Abstract
A concept for creating a large class of lightweight stream ciphers as Key Stream Generators KSGs is presented. The resulting class-size exceeds 2323 possible different KSGs. If one unknown cipher from the KSG-class is randomly picked-up and stored irreversibly within a VLSI device, the device becomes physically hard-to-clone. The selected cipher is only usable by the device itself, therefore cloning it requires an invasive attack on that particular device. Being an unknown selection out of 2323 possible KSGs, the resulting cipher is seen as a Secret Unknown Cipher (SUC). The SUC concept was presented a decade ago as a digital alternative to the inconsistent traditional analog Physically Unclonable Functions (PUFs). This work presents one possible practical self-creation technique for such PUFs as hard-to-clone unknown KSGs usable to re-identify VLSI devices. The proposed sample cipher-structure is based on non-linear merging of randomly selected 16 Nonlinear Feedback Shift Registers (NLFSRs). The created KSGs exhibit linear complexities exceeding 281 and a period exceeding 2161. The worst-case device cloning time complexity approaches 2162. A simple lightweight identification protocol for physically identifying such SUC structures in FPGA-devices is presented. The required self-reconfiguring FPGAs for embedding such SUCs are not yet available, however, expected to emerge in the near future. The security analysis and hardware complexities of the resulting clone-resistant structures are evaluated and shown to offer scalable security levels to cope even with the post-quantum cryptography.
1. Introduction
Physical Unclonable Functions (PUFs) [1,2] were increasingly proposed as central building blocks in cryptographic protocols and security architectures. Their main usage is in secure physical device identification/authentication [3,4], memoryless key storage [5] and intellectual property protection [6]. Most traditional PUFs as analog systems, exhibit noisy and inconsistent long-term response limiting their entropy and usability. To remedy such drawbacks, fuzzy extractors [7,8] were proposed to filter out noise and attain consistent long-term response. Fuzzy extractors as error correcting mechanisms require helper redundant data and complex decoding algorithms. Such error correction mechanisms are expensive and require large gate count [7,8]. SRAM based intrinsic PUFs are the most used in practical VLSI applications and were recently exposed to efficient attacks to reveal the intrinsic state of memory [9]. Promising modeling attacks were also proposed to clone strong PUFs [10]. In [11], side channel attack was used to analyze PUFs architecture and fuzzy extractor implementations by deploying power analysis. Recent trends combine both side channel and modeling attacks [12] to facilitate machine learning in modeling attacks.
Traditional PUFs with perfect consistency are equivalent to unknown digital hash functions. Clone-resistant units based on pseudo-random functions were proposed to overcome PUFs drawbacks, mainly their inconsistency and the vulnerability of some PUFs to modelling attacks. They were coined as Secret Unknown Cipher (SUC) [13]. SUC is defined as a randomly, internally and irreversibly self-created cipher inside a non-volatile self-reconfiguring FPGA device fabric where the user has no access or influence on its creation process. Even the VLSI manufacturer should not be able to back-trace the creation process to disclose the created cipher. Creating such SUCs is a very challenging task, it requires designing huge families of secure ciphers with hard to predict random components. In [14], a SUC creation process based on random block ciphers was proposed, it is deploying random optimal S-Boxes as source of randomness of the SUC design in addition to the secret key. In [15], a Random Stream Cipher (RSC) based on single cycle T-Functions (Triangular Functions) class has been proposed to construct a low-cost class of SUCs. The proposed RSC-SUC makes use of the DSP blocks embedded in modern SoC FPGAs to implement single cycle T-Functions as keystream generators.
All proposed designs in [14,15] are possible variations to create SUCs using low hardware resources as LUTs or Math-blocks. In this paper, we propose a new alternative SUC design template based on combining well-selected NLFSRs having low complexity feedback functions. Locating the NLFSRs within the FPGA fabric area is expected to be reachable as each NLFSR can be implemented in a small free area of the FPGA and provide its single output bit to the combining function by one-bit routing. This may allow a zero-cost SUC implementation in best-cases with a low-vulnerability to side channel attacks.
The contributions of this work can be summarized as follows: firstly, a huge-class of low-complexity KSGs is created. Any selected KSG/cipher, even when randomly selected, exhibits the same designed security level. The cardinality of the cipher-class exceeds 2323 for a sample set of NLFSRs with a state size of 223 bits. Secondly, the resulting ciphers are optimized to be embedded at low-cost in future VLSI-devices to convert them into clone-resistant devices with long-term consistency. Finally, a simple generic-lightweight identification/authentication protocol is shown for VLSI-devices when using such SUC-based structures.
The remainder of this paper is organized as follows: Section 2 describes the state of the art of digital clone-resistant units. It also discusses Kerckhoffs’s principles vs. SUC concept. Section 3 presents a detailed description of the proposed keystream generator architecture. In Section 4, the security analysis of the proposed family of new stream ciphers is investigated. Section 5 describes a concept for deploying this family to create SUCs and provide unique, robust and clone-resistant physical identities within SoC units. Section 6 evaluates the hardware complexity of the proposed SUC, and Section 7 concludes the results and provides some future perspectives.
2. Proposed Digital Clone-Resistant Physical VLSI Structure
2.1. The Concept of Secret Unknown Ciphers SUCs
To make the presentation self-contained, the concept of creating secret unknown ciphers was reproduced with more details summarizing early publications.
Definition 1.
A Secret Unknown Cipher (SUC) is a randomly and internally self-created unpredictable cipher inside a chip, where the user has no influence on its created ciphering functions. The resulting cipher is permanent, non-removable and tamper-proof. Even the device manufacturer should not be able to back trace the creation process, nor predict or reveal the resulting cipher.
The best devices for embedding such ciphers are the non-volatile and self-reconfiguring System on Chip (SoC) FPGA devices. Such technology does not exist yet, however, it is expected to emerge in the near future as smart SoC FPGAs, such as those produced by Microsemi (Microchip) as programmable non-volatile devices.
Each generated SUC can be defined as an invertible Pseudo Random Function (PRF) in encryption mode as:
And in decryption mode as:
In the case that the SUC is designed as a block cipher, i.e. n = m. The optimum form is the involutive SUC mappings, where SUC = SUC−1, that is:
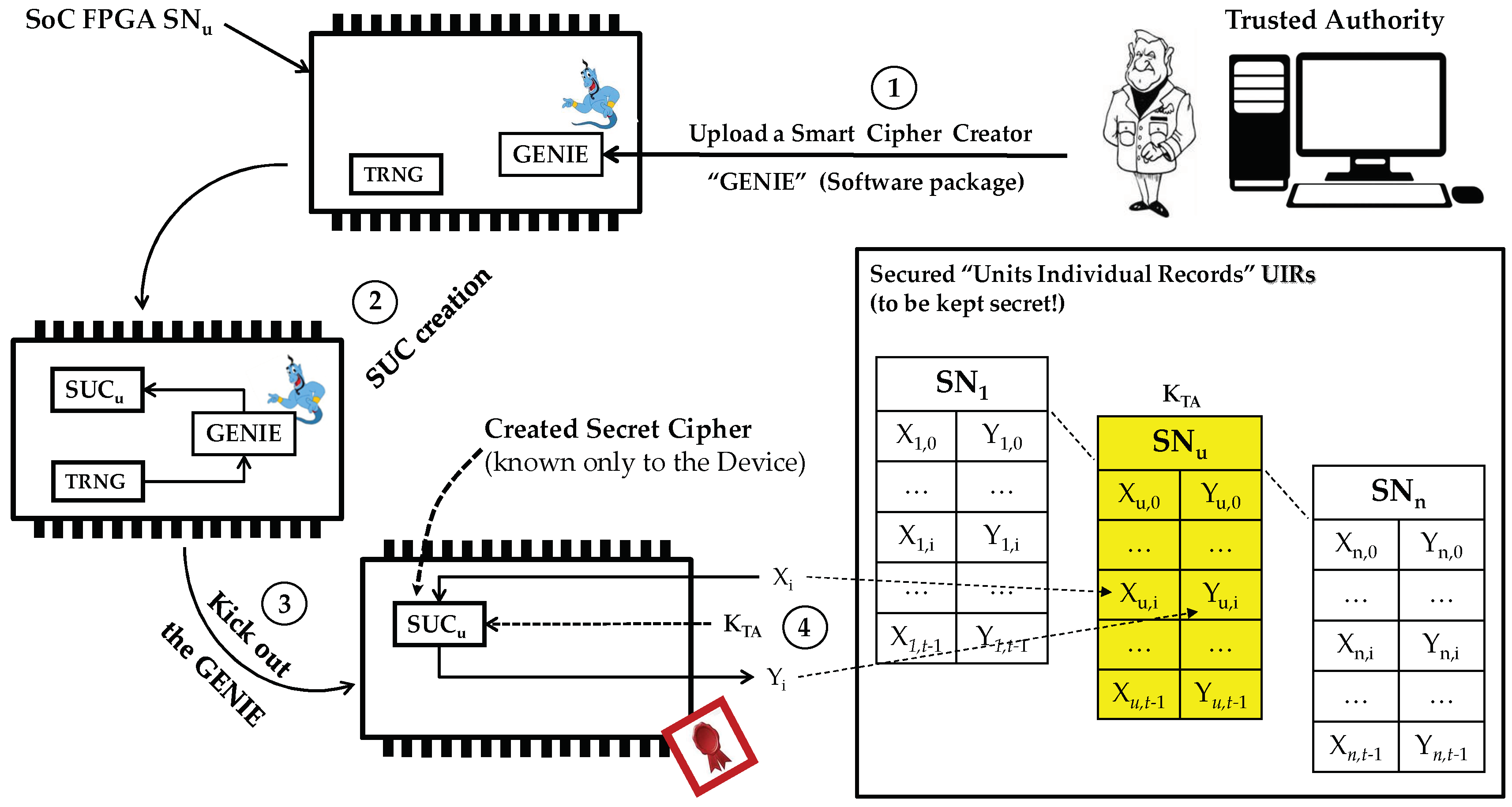
Figure 1 describes the conceptual scenario for embedding a SUC in a System on Chip (SoC) FPGA device. The device (SoC FPGA) personalization process proceeds as follows:
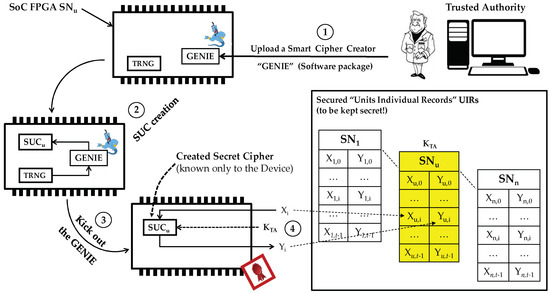
Figure 1.
The concept for creating SUCs in SoC FPGAs environment.
- The Trusted Authority (TA) uploads a software package as a smart cipher designer called “GENIE”. “The GENIE concept is taken from 1001-night miracles as a powerful, honest and obedient creature which can realize any wishes after getting out of Aladdin’s lamp”.
- The GENIE is then ordered to create a non-predictable cipher (SUC) with the help of the True Random Number Generator (TRNG) located within the SoC to assure randomized, unpredictable and unknown results. The GENIE stores the created SUC permanently at unknown location/s within the FPGA fabric and makes it usable for encrypting and decrypting data.
- The GENIE is then kicked-out (that is, deleted as a program and ordered to leave the device forever). The end result is a usable cipher which nobody knows. Notice that the created ciphers are basically different, even when having an unknown individual structure and unknown locations for each individual device.
- In this enrollment step, the TA (or any other TA’) challenges each SUCu by a set of t-cleartext patterns to generate the corresponding t-ciphertext set where . Then, the TA stores the X/Y pairs on the corresponding area in its Units Individual Records (UIR) labeled by the serial number of the device . The Xi/Yi pairs are to be used later by the TA/TA’ to identify and authenticate devices. Notice that multiple TA’s can operate completely independently for their own individual application by using the same SUC.
The concept is comparable to the conventional PUF, with the advantage that a SUC-based technique is a collision-free one-to-one mapping. A SUC as a bijective cipher exhibits higher entropy compared with a conventional PUF, which is equivalent to a collision-prone hash function. Invertibility is an advantageous property that was deployed in [16] to build a strict chain of trust for a secured vehicular software update protocol which is much more complex in traditional PUFs.
Notice that if the cardinality of the created cipher-class = |KSG| is huge, that is:
|KSG| → ∞, then a randomly selected KSGi is deemed to be unpredictable.
And the probability of creating two equal KSGs approaches zero.
2.2. SUC Generic Use Protocol as Provable Physical Identity
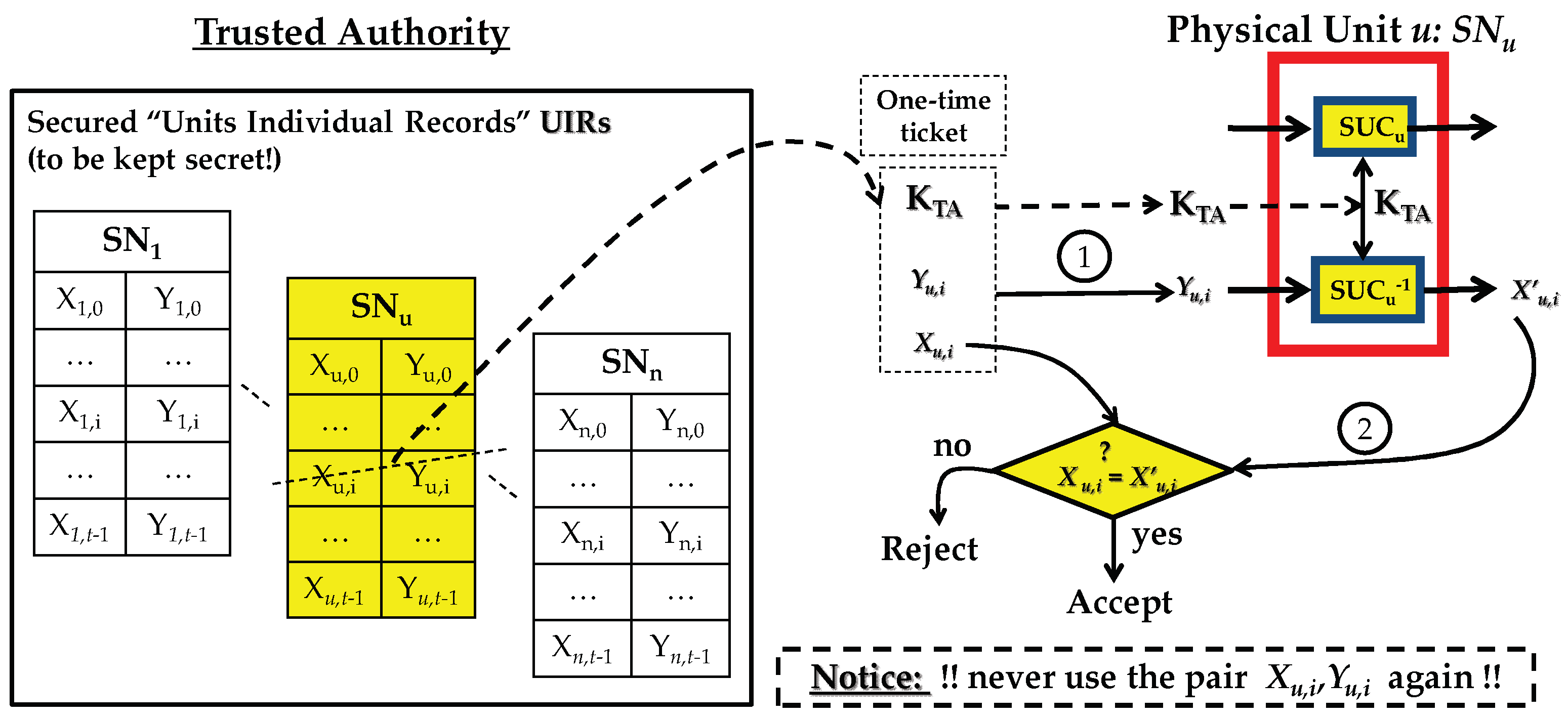
At the end of the personalization process (4) in Figure 1, TA stores the X/Y pairs securely for each unit as Units Individual Records (UIR).
Figure 2 shows how to make use of UIR to identify a physical unit u having label (SNu) in a two-path protocol:
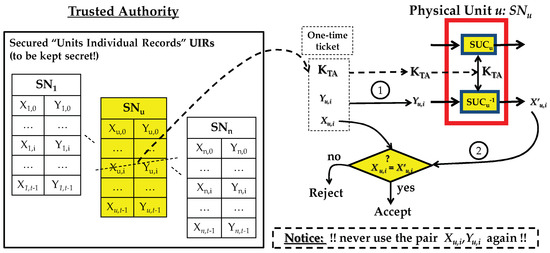
Figure 2.
A generic simple authentication protocol for a Secret Unknown Cipher SUC.
- Path-1: TA randomly selects one of the pairs and challenges unit u with by asking for Xu,i.
- Path-2: Unit u deploys its to decrypt as and sends to TA. The TA then checks if , if true, then unit u is deemed as authentic. The used pair is marked as consumed or deleted, and should never be used again.
The SUC invertibility property as a cipher proved to be very efficient in generic identification and authentication protocols as in [13] allowing novel applications such as e-coin systems [17]. Particularly, in [13], two generic identification/authentication protocols were presented, exhibiting a very efficient X/Y pairs management which eliminates the need to store a large number of pairs. The device requires a very small memory of only t-bit to detect and manage t-consumed X/Y pairs. Further refinements were shown to avoid the need of deleting the used pairs during communication with a unit as in [13]. All such efficient management strategies are not possible in the conventional PUFs environment, which does not make them attractive for a large class of applications.
2.3. Kerckhoffs’s Principle (Shannon’s Maxim) and the SUC Concept
In [18], Kerckhoffs stated that the cipher should be secure, even if everything is known about the cipher, except the user’s key. This should apply to any cryptosystem.
The SUC concept is assuming that the VLSI technology would offer the possibility of creating unknown secrets and even unknown ciphers. Therefore, we claim that:
“The only perfect secret is the one which nobody knows”
The resulting system is actually quite new. Cryptographers never had practical means to create unknown operational ciphers before. However, PUFs as mappings equivalent to hard-wired unknown hash functions, were usable as unclonable physical entities. VLSI technology is offering new horizons by allowing self-creation of hardwired one-way functions. These functions may become technologically physical one-way functions, in such a way that an invasive attack on a VLSI structure to reach the secret, would lead to destructing the secret itself. The 3-D VLSI architectures may soon offer such capabilities when flash technology is integrated in 3-D VLSI structures. The fact that a SUC and its key are only reachable by invasive attacks, is a frustrating fact facing attackers.
SUC concept do not contradicts with Kerckhoffs’s principles. Let us consider the two cases; the case of published GENIE and the case of unpublished GENIE:
- 1.
- The Case of Published GENIE: In worst case, the GENIE is assumed to be published. That is, the whole cipher design rules are known to the opponent. If the cipher class size = |SUC| is huge, that is:as the cipher is selected randomly, and each cipher is selected randomly equally. If the SUC has a key size equal to k, then the total SUC cloning entropy CE is:|SUC| = N and N is huge, that is N → ∞CE = Log2 N + kAs both the cipher and its key are unknown. Also, it is assumed that if the cipher designer is using state-of-the-art crypto knowledge, then the minimum value is CEmin = k, in the case that the attacker finds the cipher due to the design weakness of the GENIE. Assuming that the GENIE designer is a good up to date cryptographer, then the cloning entropy approaches:CEmax = Log2 N + k
- 2.
- The Case of Unpublished GENIE: To let SUC concept works, TA is not actually required to publish the GENIE. In that case, the minimum CE is:where N0 is some unknown upper bound of the cipher class cardinality under consideration. The security analysis of the proposed family of KSG/stream ciphers is investigated by considering that the cipher design is publicly known. i.e. the NLFSRs’s feedback functions are known.CEmin = Log2 N0 + k
Cryptanalyzing SUCs in real fields would require two steps:
- Revealing the secret cipher components: An adversary is forced to reveal the randomly selected functions that are used in constructing the SUC.
- Breaking the resulting stream cipher: After revealing the SUC’s secret parameters, this SUC could be considered as a publicly known cipher, and an adversary should apply known cryptanalytical attack to break this SUC.
Since each SUC is assumed to be generated randomly, attacking each SUC requires to repeat the same attack procedure with the same attack complexity. This is a major advantage over attacking any published stream cipher with just a randomly generated secret key. For the latest case, the attack complexity is based only on breaking the publicly known stream cipher. Another SUC security advantage, is that unknown cipher structures and parameters as number of stages and configurations may be distributed at unknown locations making SUCs highly resistant to side channel attacks.
2.4. State of the Art in Designing SUC Creating GENIEs
The most challenging and difficult task in creating SUCs to convert devices into clone-resistant units, is the design of a low-cost and fast GENIE. The GENIE should be capable to create a high-quality cipher with acceptable complexity within a short processing time. The main objective of this work is to design such a GENIE with good performance profile for the targeted unknown cipher-classes.
In [14], a template based SUC GENIE-realization is presented, where a block cipher with random components is designed as pre-casted SUC template. Optimal 4-bit S-Boxes are used as a source of randomness. The GENIE selects few S-Boxes from the sets of all optimal 4-bit S-Boxes. Each resulting SUC from this class has the same security level. Furthermore, in [15], Mars et al. proposed the first attempt towards a digital clone-resistant function prototype based on Random Stream Cipher (RSC) deploying a class of T-Functions (Triangular Functions) as key stream generators. SUC designs ensure that it is secure against known mathematical cryptanalysis as in [14,15]. Each randomly created SUC should exhibit the same security level. Since each device embeds a unique SUC, an adversary needs to break each unit individually. That is, the same attack complexity is required for each unit. Hence, break-one-break-all do not work against SUCs. Moreover, SUC can be implemented with zero cost if unconsumed FPGA resources are deployed for that purpose. Most industrial applications do not make full usage of the whole FPGA resources. Therefore, one of the main targets of the designed GENIEs is to make use of unconsumed resources and hence create SUCs possibly at zero-cost.
3. Designing a GENIE for Creating Unknown Keystream Generators
A short review on the state of the art in designing stream ciphers is given, in order to introduce the adopted GENIE design-strategy for creating the target system of this work.
3.1. Selected State of the Art on Key Stream Generators
In 2005, the European project ECRYPT launched a competition to design new stream ciphers that might be suitable for widespread adoption. This project is called eSTREAM (ECRYPT Stream Cipher Project) [19] and it received 35 submissions. When it came to its end in 2008, four of the proposals in the final portfolio were suited to fast software encryption: HC-128, Rabbit, Salsa20/12 and Sosemanuk, while other four stream ciphers offered particularly efficient hardware implementation: Grain v1, MICKEY 2.0, Trivium and F-FCSR-H which were excluded later because of recent cryptanalytic results. A number of NLFSR-based stream ciphers have been proposed to the eSTREAM project, such as Achterbahn [20]. Achterbahn was one of the challenging new designs based on combining several NLFSRs with a nonlinear combining function, which performs nonlinear operations on sequences with distinct minimal polynomials. In [21], the authors highlighted some problems in the design principle of Achterbahn addressing the small length of the NLFSRs and the weakness of the combining function. The complexity of the attack presented in [20] depends exponentially on the number of shift registers and their size, and to the number of shift registers outputs that would cancel the nonlinear part of the combining function if they are equal to zero. The proposed family of stream ciphers design overcomes the previous cryptanalytical attacks.
3.2. Creating SUCs Based on Random Keystream Generators
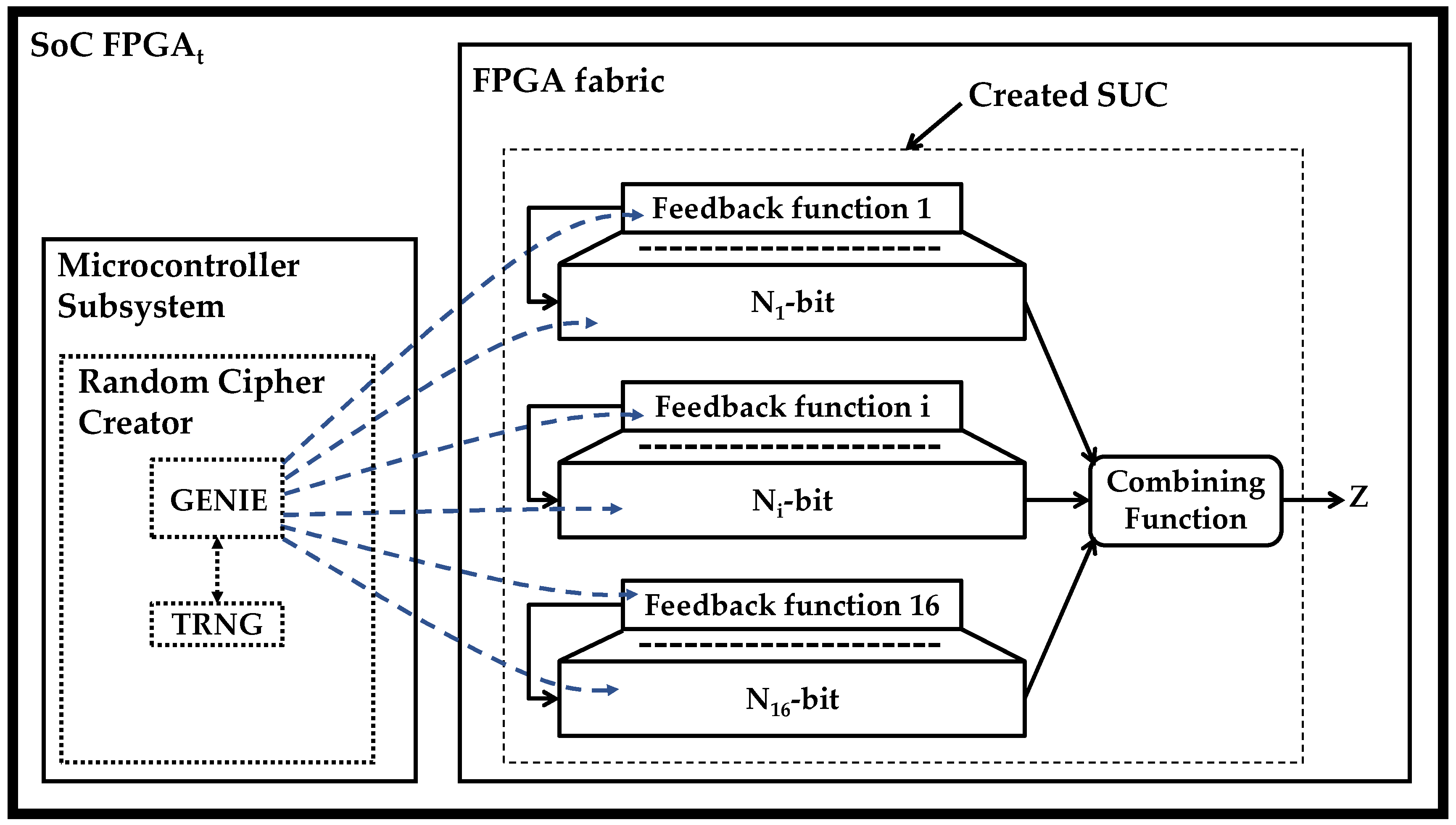
Figure 3 describes a methodology for creating a class of SUCs based on combining NLFSRs. In this sample design, the SUC-design template deploys 16 NLFSRs, where their outputs are combined with a selected combining function. Each NLFSR is providing one bit per cycle to the combining function. This allows to distribute NLFSRs over the whole FPGA where only one connection is required to connect one NLFSR to the combining function. This constitutes an advantage over SUC based on block cipher designs.
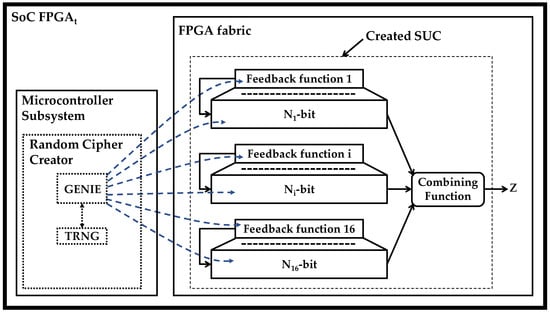
Figure 3.
Creating KSG core as SUC based on combining NLFSRs.
The GENIE runs once in the microcontroller subsystem during the personalization process. For each selected NLFSR length, the GENIE has a set of feedback functions. Referring to Figure 3, the personalization of a SoC FPGAt proceeds as follows:
- The GENIE triggers the TRNG and gets random numbers
- The GENIE selects randomly, for each NLFSR, a feedback function from a pre-defined set and loads it to the corresponding area in the FPGA fabric. Also, the GENIE generates a random initial state for each NLFSR.
- Furthermore, the combining function can also be selected randomly by fulfilling some conditions to ensure that the GENIE is going to generate SUCs with an acceptable minimum-security level.
This process results in a creation of random and unpredictable cipher/KSG.
3.3. Description of the Created Random Keystream Generator
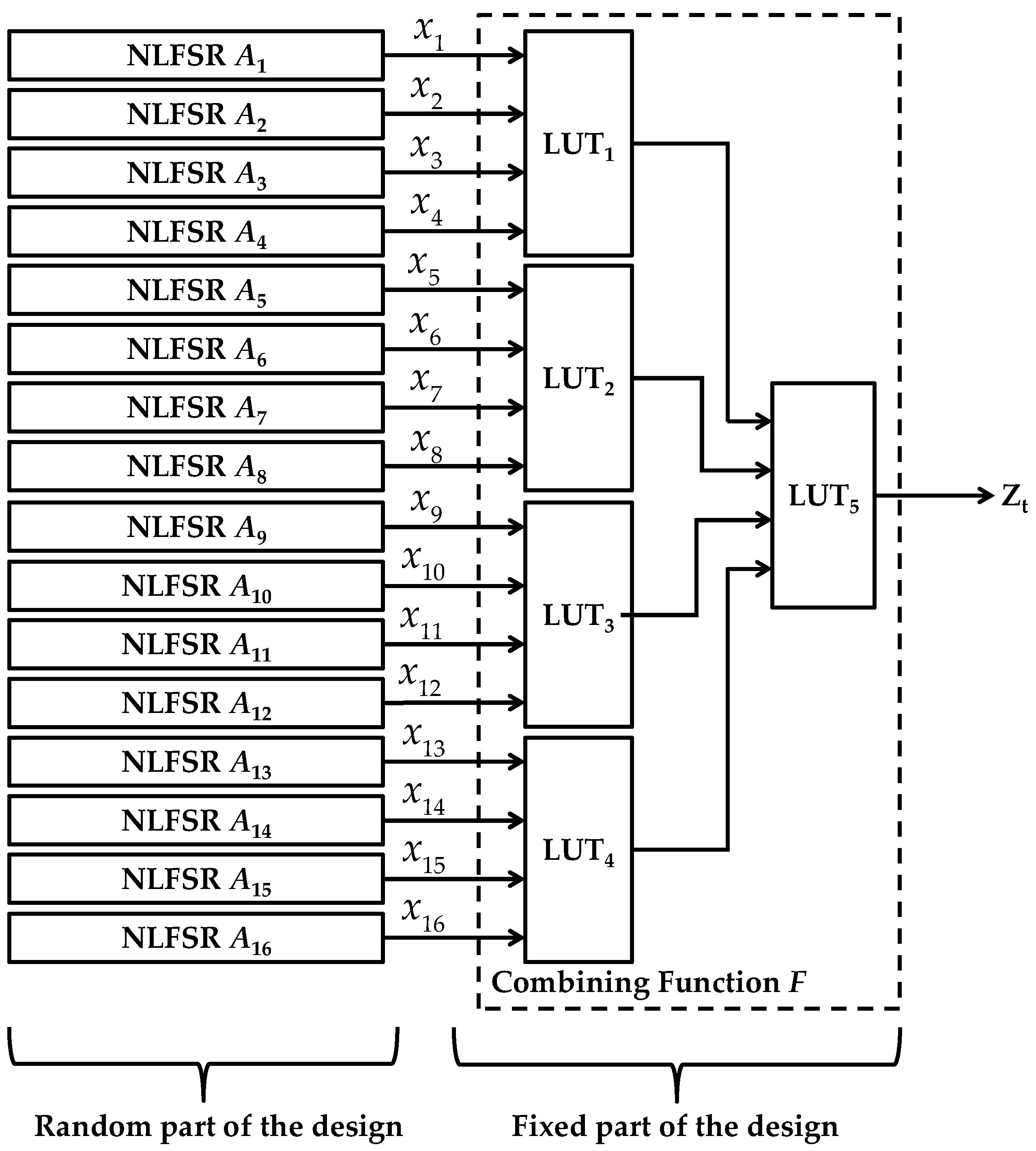
The basic components of the KSG are 16 Non-Linear Feedback Shift Registers (NLFSRs) of lengths 6 to 17 and 19, 21, 22 and 23, combined by a balanced Boolean function F with algebraic degree 4, correlation immunity 8 and algebraic immunity 4. Each NLFSR produces binary sequences of a maximum period of , where N is the length of the shift register. For each NLFSR, a feedback function is selected internally and randomly by the GENIE from a set of selected nonlinear feedback functions (see Table A1). The outputs of the 16 NLFSRs provide the 16 inputs to the combining function F, which outputs the running key . Figure 4 describes the proposed stream cipher design template.
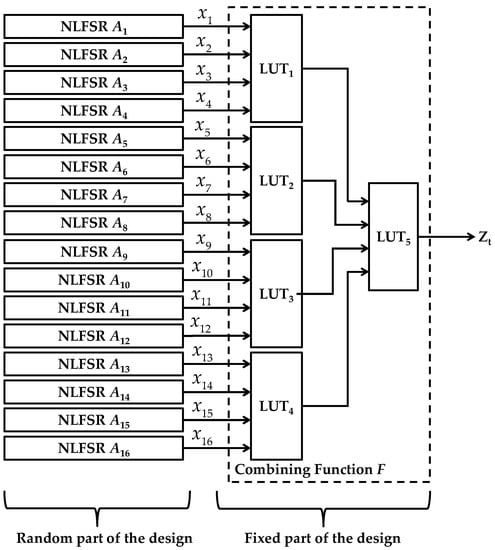
Figure 4.
Description of the created keystream generator.
The 5 4-bits Look Up Tables (4-LUTs) implement the Boolean combining function F. The total number of all NLFSRs state bits is 223 bits. This design is hardware optimized to the target FPGA environment, where the basic logic unit is a 4-LUT. The key-loading algorithm that determines the initial internal states of the NLFSRs having a key size K (K ≥ 80 bits) and an initial vector (IV) will not be investigated in this paper, since it is not required for the proposed SUC usage, i.e. the key can be the initial NLFSRs states. A key scheduling algorithm can be added to the SUC design template; however, additional overhead should be considered.
The resulting KSG sequence period is: lcm (26 − 1, 27 − 1, …, 223 − 1) ≈ 2161 which is considered as adequate.
3.3.1. Selected Sets of Non-Linear Feedback Shift Registers
The principal components of KSG are the 16 NLFSRs with lengths from 6 to 17 and 19, 21, 23 and 24. Each N-bit NLFSR has a set of feedback functions ensuring a maximum period of 2N − 1 for each one. This section describes in details the NLFSRs design methodology.
Definition 2.
A feedback Shift Register generates pure cycle-loops if and only if its feedback function has the form:
where g is any Boolean function that does not depend on.
Definition 3.
A (binary) de Bruijn sequence is a sequence of period 2N, in which each N-bit tuple occurs exactly once in one period of the sequence [xxx].
The linear complexities of order N de Bruijn sequences are bounded by and [22].
Definition 4.
A modified de Bruijn sequence is a sequence of period, in which each N-bit tuple occurs exactly once in one period of the sequence.
In [23], for each NLFSR with where , a set of feedback functions ensuring a maximum period of was presented. All feedback functions have the form of Equation (4). The search covered three types of feedback functions with algebraic degree two:
where .
Any set of N-bit Fibonacci NLFSRs with the period can be partitioned into 4 subsets [23]: basic, reverse of basic, complement of basic, and reverse complement of basic. In [23], only NLFSRs with basic form were listed. The forms of the reverse, complement and reverse complement of the basic form (Equation (4)) are described as follows:
- Reverse form:
- Complement form:
- Reverse complement form:
Thus, for each listed feedback function in [23], three feedback functions generating the reverse, complement or reverse complement sequence can be deduced.
For NLFSRs with , denotes the set of Boolean functions g listed in [23] (by removing the XORed ) together with their reverse, complement and reverse complement form. We coin those functions as Random Feedback Functions (). The set with only the functions having basic form (by removing the XORed ) are listed in Table A1.
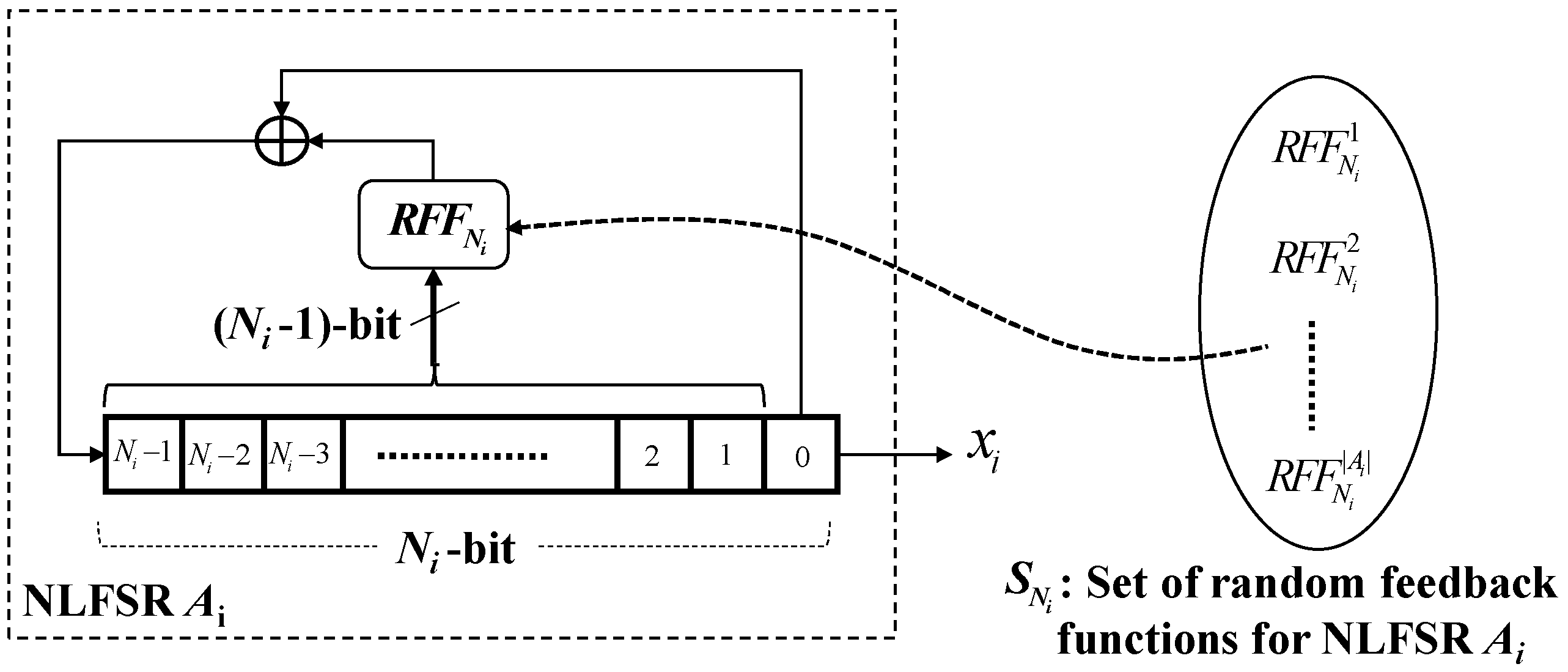
Figure 5 describes the general structure of the used NLFSRs. For each NLFSR of length , the feedback function contains a Random Feedback Function (). Its general form is defined as follows:
where: for each NLFSR of length , a set of random feedback functions is selected such that each of its allows the NLFSR to attain a maximum period of . where:
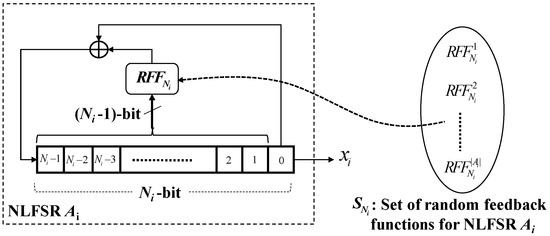
Figure 5.
General structure of the selected NLFSRs sets.
During the personalization process, one of the feedback functions is to be selected randomly from a predefined set for each NLFSR .
Each selected NLFSR in Figure 4 has a form of the general structure in Figure 5, and generates a nonlinear sequence of period which is a nonlinear modified de Bruijn sequence. The linear complexity of an NLFSR is bounded by:
The number of NLFSRs and their lengths are selected to satisfy the following basic security requirements:
- Berlekamp-Massey (B-M) Algorithm attack: In order to ensure that the attack complexity of B-M Algorithm is over 280; in terms of time complexity. Where the attack complexity is defined as L2, where L is the B-M linear complexity of the total key stream sequence which should exceed 240.
- Correlation immunity: If an adversary succeeds to recover the randomly selected feedback functions, a correlation attack may be launched. As the designed correlation immunity of the combining function is 8, the total size of the shortest 9 (8+1) NLFSRs should be larger than 80. In that case the correlation attack complexity would become 280, which is considered as sufficiently secure for contemporary non-post-quantum cryptography.
Following the two above constraints, optimal NLFSRs designs are always attained.
In the appendix, Table A1 shows the 16 sets of the possible predefined random feedback functions having the basic form. The reverse, complement and reverse complement forms can be deduced easily. In the format of the , indexes of the variables of each product-term of a feedback function are separated by commas. A round bracket around the indexes denotes that those indexes belong to the same product-term. For example, 1,2,(2,4) represent the :
3.3.2. Cardinality of the Designed KSG Class
The proposed KSGs can be used to create a family of SUCs. In general, this design randomness is based on deploying all possible feedback functions ensuring that any N-bit NLFSR generates a sequence of period .
In this design, the NLFSRs selected for the proposed structure can be made random, since for each N-bit NLFSR there exist a number of possible feedback functions ensuring a maximum period of . Hence, randomly selecting one of the feedback functions for each NLFSR will ensure the same security level of the resulting random KSG as will be shown later.
Table 1 presents the number of possible selections of the NLFSRs for each deployed NLFSR having length .

Table 1.
Number of selectable NLFSRs for each Ni.
Theorem 1.
Letbe the lengths of the NLFSRs of the KSG, wheresuch as.
Let denotes the number of usable NLFSRs in the class Ai. The cardinality of all possible creatable KSGs is then:
In the sample case above, . As refers to the size of the total initial states of the deployed NLFSRs which is randomly selected. In that case, the key entropy is . This results with a total KSGs cardinality of: .
3.3.3. Keystream Boolean Combining Function F
The Algebraic Normal Form (ANF) of the proposed Boolean combining function F is as follows:
Referring to Figure 4, the function F consists of two parts:
- The linear part, which contains the monomials of degree one to , which can be realized with two 4-LUTs,
- The non-linear part containing monomials of degree two and three, related to the terms to which can also be realized with another two 4-LUTs. The outputs of all four 4-LUTs are combined using one 4-LUT to generate the keystream .
Definition 5.
The Boolean combining function F can be described as follows:
A secure combining Boolean function should have the following properties: balanced, high algebraic degree, high correlation immunity and high nonlinearity.
In the following, we present the analysis results of the Boolean combining function F.
a. Balancing the Construction of F
If the function F is not balanced, then the whole system would be vulnerable to cryptanalytic attacks. A Boolean combining function is balanced if and only if the numbers of ‘1’s and ‘0’s in its truth table are equal. Since the LFSRs/NLFSRs are supposed to be randomly i.i.d. (independently identically distributed), the resulting combining function are then balanced satisfying the pseudo-randomness requirement.
b. Algebraic degree of F
The algebraic degree of F is the degree of ANF of the Boolean combining function. Since the ANF of the Boolean combining function has degree 4, the algebraic degree of F is 4.
c. Correlation immunity of F
Before we introduce the correlation immunity, an introduction to Walsh Transformation is needed.
Definition 6.
Letbe n-tuples over {0,1}, and the dot product of x andis defined as:
The Walsh Transformation on a n-variable Boolean function is defined as:
The Correlation immunity can be calculated based on the Walsh Transformation as follows: if for all , where is the weight of , and the Walsh Transformation , then the integer t is called the correlation immunity.
The correlation immunity of the designed Boolean combining function F is 8.
d. Nonlinearity of F
The nonlinearity is the distance from the combining function F to the set of affine functions having n-variables (An):
The nonlinearity of the designed combining function F is then found to be: NL(F) = 26624.
e. Algebraic immunity of F
For , define , any function is called the annihilator of F. The algebraic immunity of F is the minimum degree of all the nonzero annihilators of F and of all those of . In [24], it was proved that the algebraic immunity is less than, or equal to for any n-variable Boolean function F. The simulation showed that the algebraic immunity of the Boolean combining function F is 4.
In summary, the designed Boolean combining function F is balanced with algebraic degree = 4, correlation immunity = 8, nonlinearity = 26,624 and algebraic immunity = 4.
4. Security Analysis
The security analysis of the resulting stream ciphers/KSGs is evaluated considering the following attacks: Brute force attack, correlation attack, algebraic attack and parity check attack.
4.1. Brute Force Attack
4.1.1. Exhaustive Search Attack on the NLFSRs Initial States as Secret Key Seeds
The first brute force attack is an exhaustive search of all the internal states in NLFSRs and all possible NLFSRs selections. The Adversary should enumerate all possible states, then generate the corresponding sequence in each possible NLFSR selection and compare it with a known portion of the keystream. If the generated sequence and the keystream match, then the internal states of the NLFSR are found and the cipher is broken with a relatively high probability.
The complexity of the attack is:
As he total length of the NLFSRs is 223 bits and the cardinality of the KSG is about 2100, the resulting complexity is of the order of 2323. We conclude that the complexity of a brute force attack to guess all possible internal states is beyond the possible state of the art computational power. Therefore, the cipher is secure against such attacks.
4.1.2. Stream Ciphers Linear Complexity and Berlekamp-Massey Algorithm
In order to analyze the complexity of the B-M algorithm on the proposed cipher, it is necessary to compute the lower bound of the total linear complexity of the output bitstream. The time complexity of the B-M algorithm attack is the square of the total linear complexity. If the lengths of the t-shift registers are pairwise relatively prime, then the linear complexity of the keystream z is known to be bounded as:
If the lengths of the primitive NLFSRs are not pairwise relatively prime, then the above bound does not hold. In this case, F(L1,…,Lt) provides only an upper bound for L(ζ). However, in the following corollary cases, it is still possible to derive a reasonable lower bound for the linear complexity of ζ.
Lemma 1.
[25] Let σ1,…,σt be nonzero output sequences of primitive binary NLFSRs of lengths N1,…,Nt, respectively, having the corresponding linear complexities L1,…,Lt. Let F(x1,…,xt) be a Boolean function of algebraic degree d ≥ 1. A lower bound for the linear complexity of the sequence ζ = F(σ1,…,σt) is reached if the following two conditions are fulfilled:
- 1.
- The algebraic normal form (ANF) of F(x1,…,xt) contains a monomialof degree d for which the corresponding shift register lengthsare pairwise relatively prime.
- 2.
- For all monomials of degree d, which have the form, the following holds:.
If both conditions are true, then:
The Boolean combining function F has the algebraic degree 4, its ANF contains the following monomial with degree d = 4:.
- The monomial satisfies condition 1 in the previous lemma: The lengths of the corresponding shift registers contributing in a monomial having d = 4 are which are pairwise relatively prime.
- The other monomials in the ANF of the Boolean combining function are of degree less than the degree 4 of the monomial . therefore, condition 2 holds.
We conclude that the linear complexity of the keystream is:
B-M algorithm requires a time complexity of 2162 and a 282 = 2L disclosed KSG bits to break a created KSG.
4.2. Correlation Attacks
The correlation attack was firstly proposed by T. Siegenthaler in 1984 [26], then improved by W. Meier and O. Staffelbach in 1989 as fast correlation attack [27]. The main idea of the correlation attack is to focus on the Boolean combining function of the KSG, and find the correlation between the combination of several LFSRs/NLFSRs and the output keystream. This requires having previous knowledge about the used NLFSRs, i.e. an adversary should reveal the randomly selected feedback functions before applying this attack. Since, there are more than 2100 possible combinations of feedback functions and about 2223 initial states, trying to reveal the feedback functions is not feasible.
Considering that an adversary knows the used feedback functions, in this case, the adversary can apply correlation attack to recover the NLFSRs initial states. Applying the classical fast-correlation attack and assuming that the Boolean combining function has a correlation immunity n, the adversary needs at least shift registers at the same time. Knowing that the correlation immunity of the Boolean combining function F is 8; results with the total length of the shortest 9 NLFSRs as:
Thus, if an adversary discloses the used feedback functions of a SUC, the time complexity of the correlation attack is at least 290. However, this attack cannot be practically realized, since for each SUC the random feedback functions are unpredictable and are securely located inside the chip’s hardwired structure.
4.3. Algebraic Attacks
Algebraic attack [28] is another important attack against stream ciphers. It is targeting to find a well-chosen multivariate polynomial G(s), such that G.F is of substantially lower degree, where F(s) is the combining Boolean function and s is the current state. To examine the degree of the linear polynomial equations system, an assertion for the degree of the algebraic equations from [29] will be used. It is described in the following fact:
Fact 1.
[29].For, the kth entry in the monomial spectrum of the shift registers, with, containsdifferent monomials having in general a degree of.
According to [29], different monomials are required to express the bits of the sequence by the initial state of each register. So, we need:
different monomials in order to express the bits of the sequence from the highest degree term. Excluding the complexity of the remaining different monomials, the minimum complexity for solving the system of equations is:
where is the exponent of the fast matrix multiplication [29]. The complexity of solving the system of equations is at least as in (22), this ensures that the proposed algorithm is secure against algebraic attack.
4.4. Parity Check Attack
The parity check attack was firstly proposed in [21], which can successfully break the Achterbahn stream cipher. It starts attacking the weakness of the Achterbahn Boolean combining function; when two terms are equal to 0, then the whole nonlinear part would be 0, therefore the Boolean combining function is purely linear. After the linearization of the Boolean combining function, a parity check is applied in order to retrieve possible inner states of some certain registers. A parity check attack is very sensitive to the number of terms in the combining function after linearization.
In the following, the security analysis of the proposed algorithm against parity check attack is investigated. The ANF of the Boolean combining function F is known to the attacker as:
It has a linear part and a nonlinear part. When we examine the common terms of the nonlinear part, if , then the Boolean combining function would degenerate into a pure linear Boolean combining function, that is:
The upper bound of the linear complexity in that case is then relatively low:
So, an LFSR with length L can be built, and parity check can be applied on the sequence output of the sequence from the linear Boolean combining function.
The periods of the 8 participating NLFSRs in (24) are as follows:
where denotes the period of NLFSR Ai.
Let:
Since the period of the first register is , this expression does not contain any term of .
Similarly, let:
Therefore, contains only terms of . Thus, it satisfies:
In terms of the l(i) output bits, the following should hold:
This is the basic parity check on l(t) that can be used to attack the KSG, it is the XOR between 256 bits from the sequence, within the time interval:
It is the complexity required for the parity check attack, but the degeneration happens under the condition and the complexity to satisfy this condition should be considered. Consider the register first, which is the condition for further parity check attack. For every bit used in parity check, totally 256 bits, they should all satisfy the condition in Equation (29), i.e., . The number of all the possible internal states in register is 214. Since the output should be independent and identically distributed, the expected number of cases that satisfy this condition in Equation (29) is:
At this stage, the attack cannot continue, since the possibility of finding a case satisfying the condition is too small. Similar results can be derived for .
4.5. Side Channel Attacks
In this section, we provide a discussion about the vulnerability of the proposed family of stream ciphers to side channel attacks. In [30], the stream ciphers candidates of the eSTREAM phase-3 in respect to side channel analysis were discussed. For SUC concept, it is assumed that the ciphers are generated randomly and internally inside the SoC FPGA, as depicted in Figure 3. For the purpose of authentication use-case in the next section, a resynchronization process of the initial vector or any additional key is not required. In the following, we present a discussion on the security of the SUC-based stream cipher design against side channel attacks:
- Timing analysis: It exploits dependencies between the execution time of an algorithm and the secret key bits. The proposed stream cipher design template does not include conditional branches, and hence any randomly generated stream cipher inside the FPGA will provide the response time for any key. Therefore, timing attacks are not feasible.
- Power analysis: Two major categories are discussed; Simple power analysis (SPA) uses a single measurement to reveal a secret key by searching for key dependent patterns in the power trace, while Differential Power Analysis (DPA) uses many power measurements that are evaluated by statistical analysis to reveal the secret key. In [31], a power analysis of stream ciphers which requires frequent resynchronization is investigated. Since, in SUC case, the internal state is selected randomly and unpredictably just once during the personalization of the SoC FPGA, there is no initial vector or key to manipulate from outside to allow such attacks.
5. Generic Use-Case of the Created Random KSG Structures for Authentication
Secret Unknown Cipher (SUC) is a digital clone-resistant unit that can be deployed as a security anchor in wide spectrum of applications such as automotive security [16]. Recently, all published generic protocols deploying SUC [13] so far are designed to be used for SUC based on block ciphers. In the following, a generic simple identification/authentication protocol of a physical device incorporating keystream-generator-based SUCs is demonstrated:
5.1. Protocol’s Enrollment Phase
During the enrollment process, the Trusted Authority (TA) challenges a unit A to generate a set of t k-bit responses set . Each response set represents t k-bit vector from the KSG after k-cycles for each vector. The initial register states are fixed and unknown as a part of the unknown KSG unit’s structure.
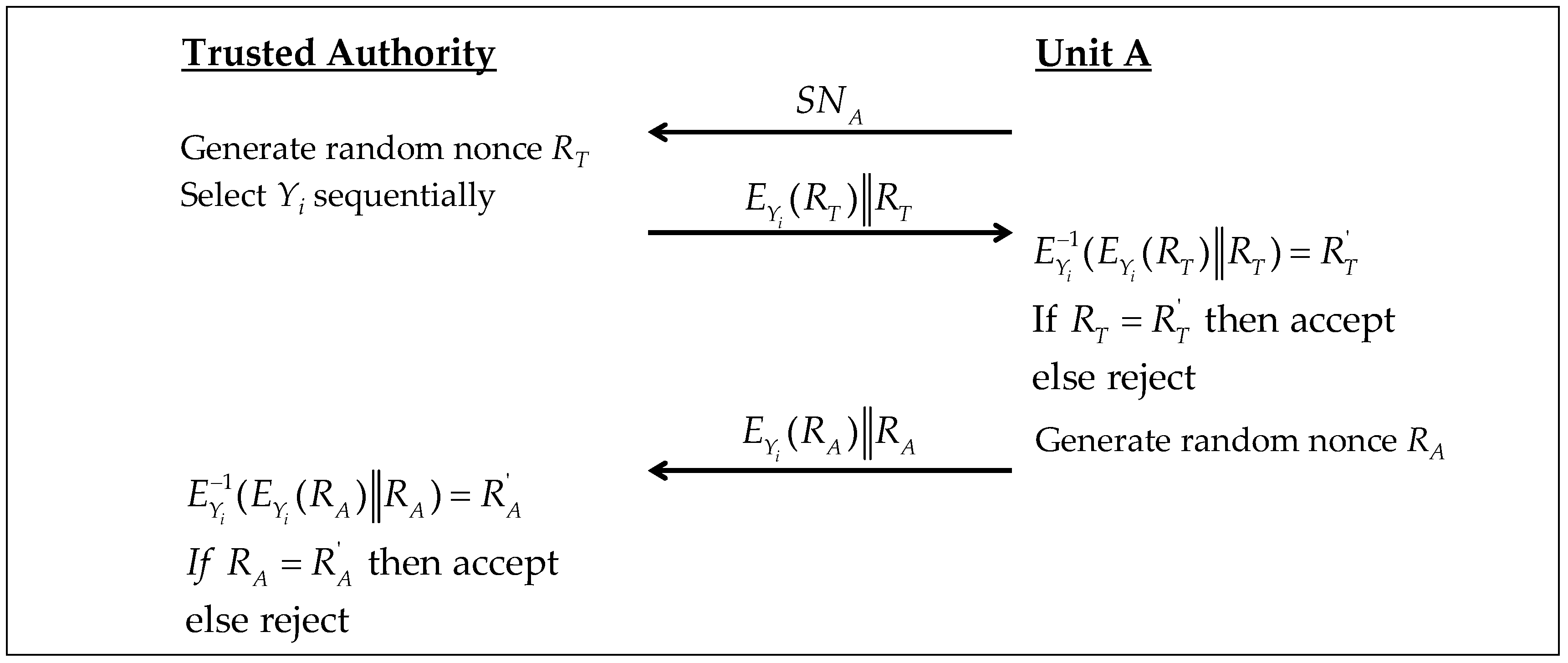
5.2. Identification Protocol
Figure 6 describes a possible simple 3-path identification protocol, it proceeds as follows:
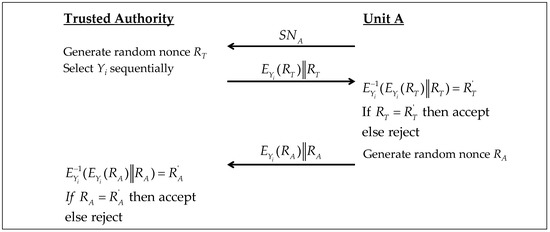
Figure 6.
Identification protocol of SUC based on random stream cipher.
- Unit A sends its serial number to the TA that checks for its existence in the TA unit’s identification records (UIR). If , then TA accepts and continues otherwise it rejects and aborts the communication.
- The TA selects the next unused and generates a random nonce . Then, encrypts with a standard cipher by using as a key and sends it concatenated to as . Unit A generates the next response and decrypts the received message as . If , unit A rejects TA and keeps its state . this retains system synchronization. Otherwise, and TA is authentic.
- Unit A generates a random nonce , encrypts it by the same and sends it concatenated to as a response back to TA. TA decrypts the received message as . If , then unit A is deemed as authentic. Yi should never be used again.
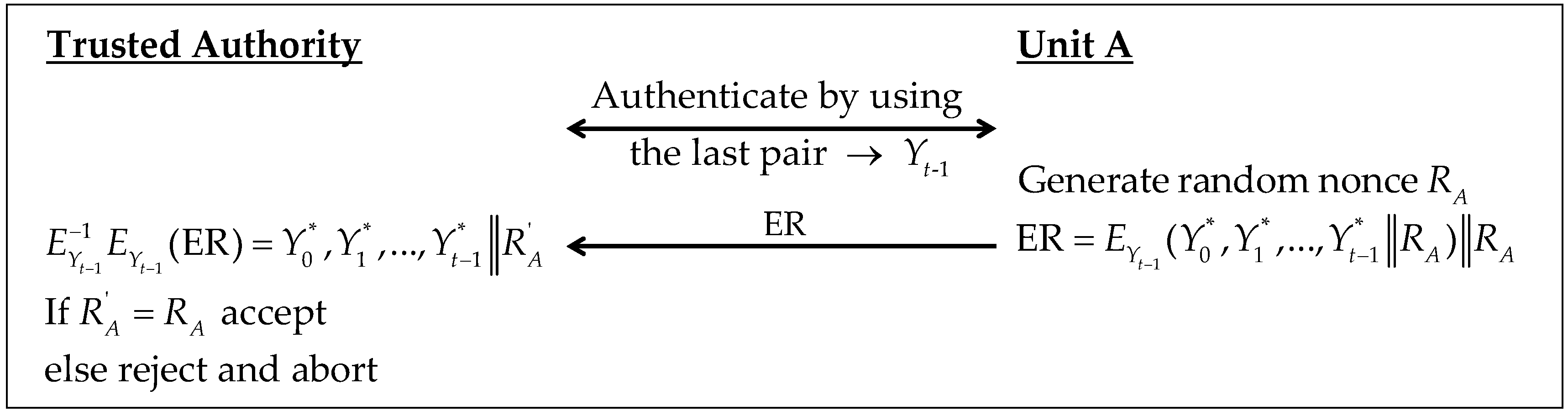
5.3. UIR Update Protocol
If all stored pairs are about to be consumed, the unit’s records need to be updated. Figure 7 describes a simple two-path update protocol. It proceeds as follows:
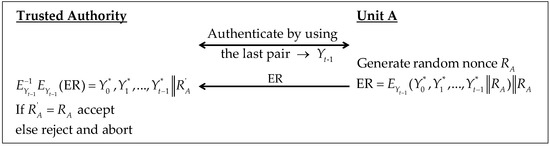
Figure 7.
Update protocol of SUC based on random stream cipher.
- The TA and unit A authenticate each other by using the final response as in the identification protocol above.
- Unit A generates a random nonce RA and a new t-responses set vectors . Then, it sends the encrypted responses (ER) to TA. TA decrypts ER by using as . If , the new response set is accepted.
6. Hardware Complexity
Mass production requires lightweight authentication mechanisms for economic reasons. SUC as clone-resistant identity gains special interest as it may be implemented with zero-cost in some cases. Most FPGA applications do not consume the total resources offered by the deployed FPGA. In such cases, and if the created SUC requires very low FPGA resources, it may end up with a zero-cost SUCs.
The KSG described in Figure 4 is modeled in VHDL and synthesized to check its hardware complexity and performance in Microsemi FPGA technology. Libero SoC with its integrated tools is used to implement a sample prototype. Mentor Graphics Modelsim ME design tool was used for simulation and Synplify pro ME for synthesis. Table 2 describes the consumed resources for different SmartFusion®2 SoC FPGAs. The KSG required 37 LUTs and 223 DFFs, this can be considered as zero cost in many real application cases. The practical realization mechanisms of the proposed family of new stream ciphers is out of the scope of this work. A concept for creating SUCs practically in real SoC FPGAs is a very challenging task. A sample realization procedure is proposed to be published in [14].

Table 2.
Hardware complexity of the KSG in SmartFusion®2 SoC FPGAs.
To make a usable comparison with the state-of-the-art stream ciphers, the hardware complexity of the proposed family of stream ciphers is compared with all profile-2 eSTREAM finalists: Grain v1 [32], MICKEY2 [33] and Trivium [34].
To compute the required gate counts for a hardware design, estimations for each logical/arithmetic in terms of NAND2 gates is necessary. Trivium inventors presented a detailed hardware complexity estimates as gate counts in [34]. For Grain [32], 8 GEs (Gate Equivalents) were assumed for each DFF, while 12 GEs were assumed Trivium in [34]. Table 3 shows our adopted GEs for each function to estimate the required area for the proposed created stream ciphers (KSGs).

Table 3.
The gate count used for different functions.
For our created KSGs, each NLFSR has a set of feedback functions, therefore, different hardware complexities would result for each created KSG. Complexities may range from a best-case to a worst-case hardware complexity. In a sample hardware compilation, the best case complexity was 223 DFFs, 63 XOR and 29 AND gates. Whereas, the worst-case hardware complexity had additional 32 XOR gates compared to the best-case.
Table 4 presents the hardware complexity and power consumption for our KSGs in comparison to the eSTREAM portfolio-2 finalists. The complexity and power evaluations for eSTREAM portfolio-2 finalists are taken from [35].

Table 4.
The gate count used for different functions.
7. Conclusions
In this paper, a new large class of Key Stream Generators KSGs as stream ciphers is presented. The class was created by a random/unpredictable selection of a set of maximum-period NLFSRs with different lengths. It was shown that any internal random selection of one Secret Unknown Cipher (SUC)/KSG from this class, may serve to convert future VLSI-devices (in a post-fabrication process) into clone-resistant entities. The security level of the proposed cipher class was evaluated against many attacks. The security levels are shown to be scalable to cope even with the post-quantum security requirements (i.e. attack complexity exceeds 2160). The resulting randomized KSG-structures exhibit moderate implementation complexities. A sample prototype case showed that one SUC structure consumes relatively minor percentage of the FPGA resources; (0.61% of the LUTs, 3.71% of DFFs) for the smallest Microsemi SmartFusion®2 SoC FPGA M2S005 devices. A simple use-case generic lightweight identification/authentication protocol deploying such physical KSGs is also presented. Future work is in progress to fine-tune and optimize such KSGs as SUC structures for emerging VLSI technologies.
Author Contributions
Conceptualization, A.M. and W.A.; methodology, A.M.; software, A.M.; validation, A.M. and W.A.; formal analysis, A.M.; investigation, A.M.; resources, W.A.; data curation, A.M.; writing—original draft preparation, A.M.; writing—review and editing, A.M. and W.A.; visualization, A.M.; supervision, W.A.; project administration, W.A.; funding acquisition, W.A.
Funding
This research was supported by Volkswagen AG and Microsemi, a Microchip Company, San Jose USA as well as the German Federal Foreign Office funding by DAAD combined scholarship and support program (STIBET).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SoC | System on Chip |
| SUC | Secret Unknown Cipher |
| PUF | Physical(ly) Unclonable Function |
| KSG | Key Stream Generator |
| NLFSR | Nonlinear Feedback Shift Register |
| ANF | Algebraic Normal Form |
| RFF | Random Feedback Function |
| RSC | Random Stream Cipher |
| UIR | Users Individual Records |
| TA | Trusted Authority |
Appendix A

Table A1.
Sets of selected random feedback functions for each NLFSR length.
Table A1.
Sets of selected random feedback functions for each NLFSR length.
| NLFSR | Length Ni | Set of Random Feedback Functions |
|---|---|---|
| A1 | 6 | 1,2,(1,2); 1,2,(2,4); 1,3,(1,5); 1,4,(1,4); 2,3,(1,3); 2,3,(1,5); 2,3,(2,3); 2,3,(2,4); 1,(1,2),(4,5); 1,(1,3),(3,5); 1,(2,3),(2,5); 2,(1,3),(2,4); 2,(1,3),(3,4); 2,(1,3),(3,5); 2,(1,5),(2,4); 2,(1,5),(4,5); 2,(2,3),(3,5); 2,(3,4),(3,5); 3,(1,4),(2,3); 3,(1,4),(2,4); 3,(1,4),(3,4); |
| A2 | 7 | 1,2,(2,6); 1,4,(1,3); 1,5,(1,5); 1,5,(3,5); 1,5,(4,6); 2,4,(1,2); 2,4,(2,5); 1,(1,2),(5,6); 1,(1,5),(3,4); 1,(1,6),(4,5); 1,(2,3),(3,5); 1,(2,5),(3,5); 1,(2,5),(4,5); 1,(3,4),(4,5); 2,(1,2),(4,6); 2,(1,4),(3,4); 2,(1,5),(2,6); 2,(1,6),(2,4); 2,(1,6),(3,6); 2,(1,6),(5,6); 2,(2,4),(3,5); 2,(2,5),(4,6); 2,(2,6),(4,6); 2,(3,6),(5,6); 3,(1,2),(2,3); 3,(1,3),(1,6); 3,(1,4),(3,6); 3,(1,5),(3,5); 3,(1,6),(3,4); 3,(2,3),(4,5); 3,(2,5),(3,5); 1,2,3,4,(1,6); 1,2,3,4,(2,3); 1,2,3,4,(2,6); 1,2,3,6,(1,3); 1,2,3,6,(1,5); 1,2,3,6,(2,6); 1,2,4,5,(1,2); 1,2,4,5,(1,5); 1,2,4,5,(2,6) |
| A3 | 8 | 1,5,(1,5); 1,6,(1,2); 1,6,(1,7); 1,6,(2,4); 1,6,(4,5); 1,6,(5,6); 2,5,(2,4); 2,5,(3,7); 2,5,(4,5); 3,4,(2,4); 3,4,(2,7); 3,4,(3,4); 3,4,(4,6); 3,4,(4,7); 3,4,(6,7); 1,(1,4),(2,4); 1,(1,6),(2,5); 1,(2,3),(2,4); 1,(2,4),(6,7); 1,(3,4),(4,7); 2,(1,3),(4,6); 2,(1,3),(5,7); 2,(1,5),(6,7); 2,(1,7),(2,3); 2,(3,7),(6,7); 3,(1,2),(2,4); 3,(1,4),(2,4); 3,(1,6),(3,6); 3,(1,6),(4,6); 3,(1,6),(4,7); 3,(2,3),(5,6); 3,(2,4),(6,7); 3,(2,6),(3,7); 1,2,3,5,(2,6); 1,2,3,6,(3,5); 1,2,3,6,(5,7); 1,2,4,5,(2,4); 1,2,4,7,(1,5); 1,2,5,7,(2,4); 1,3,4,7,(1,4); 1,3,4,7,(1,6); 1,3,4,7,(3,7) |
| A4 | 9 | 1,6,(4,6); 1,6,(4,8); 2,4,(4,5); 3,4,(3,7); 1,(1,5),(2,5); 1,(1,6),(6,7); 1,(1,8),(2,7); 1,(1,8),(5,6); 1,(2,3),(3,8); 1,(2,8),(3,7); 1,(3,4),(3,5); 1,(3,7),(5,8); 2,(1,5),(4,6); 2,(1,6),(2,7); 2,(1,8),(3,4); 2,(2,7),(4,6); 2,(4,7),(5,6); 3,(1,2),(4,7); 3,(1,6),(1,7); 3,(1,7),(4,8); 3,(2,3),(4,7); 4,(1,3),(2,8); 4,(1,6),(3,6); 4,(2,3),(5,8); 4,(2,5),(2,8); 4,(2,7),(3,8); 4,(2,8),(6,7); 4,(3,5),(3,7); 1,2,3,4,(3,7); 1,2,3,7,(4,6); 1,2,4,7,(1,6); 1,2,5,6,(1,6); 1,2,5,6,(2,6); 1,2,5,8,(2,6); 1,2,6,7,(3,6); 1,3,4,5,(3,7); 1,3,5,7,(5,6); 1,3,5,8,(3,5); 1,4,6,7,(1,7); 2,3,4,7,(2,8) |
| A5 | 10 | 1,2,(8,9); 1,4,(3,7); 1,8,(6,7); 2,5,(1,5); 4,5,(2,6); 4,5,(4,8); 4,5,(4,9); 1,(1,2),(3,4); 1,(2,4),(2,5); 1,(2,8),(7,9); 1,(3,8),(4,7); 1,(4,8),(6,7); 2,(1,3),(4,7); 2,(1,4),(3,7); 2,(1,5),(3,5); 2,(1,5),(4,9); 2,(1,6),(1,7); 2,(1,7),(4,6); 2,(1,9),(5,9); 2,(3,5),(3,7); 2,(3,9),(8,9); 3,(1,2),(2,8); 3,(1,3),(7,9); 3,(1,6),(3,8); 3,(1,6),(6,9); 3,(2,3),(2,6); 3,(2,7),(8,9); 3,(2,8),(7,9); 3,(6,7),(8,9); 4,(1,3),(1,7); 4,(1,3),(7,8); 4,(1,3),(7,9); 4,(1,5),(1,9); 4,(1,5),(7,9); 4,(7,8),(7,9); 1,2,4,8,(1,5); 1,2,4,8,(2,4); 1,2,5,8,(5,9); 1,3,4,7,(3,6); 1,3,6,7,(1,6); 1,4,5,9,(1,9); 1,4,5,9,(4,9); 1,4,5,9,(5,9); 1,5,6,7,(2,8); 2,3,4,6,(3,6); 2,4,5,8,(2,4); 2,4,6,7,(1,6) |
| A6 | 11 | 1,9,(1,4); 2,5,(1,9); 2,8,(6,9); 1,(1,7),(2,8); 1,(1,9),(2,7); 1,(2,3),(4,5); 1,(2,5),(3,4); 1,(2,7),(3,10); 1,(3,7),(3,8); 1,(3,7),(7,8); 2,(4,5),(6,10); 2,(4,6),(9,10); 2,(7,9),(8,10); 3,(1,6),(8,9); 3,(1,9),(5,10); 3,(2,7),(5,7); 3,(3,5),(6,9); 3,(3,6),(5,8); 3,(3,7),(7,10); 4,(1,2),(9,10); 4,(2,3),(2,10); 4,(3,7),(4,8); 5,(1,4),(6,9); 5,(2,8),(6,8); 5,(4,7),(6,7); 1,2,3,5,(4,6); 1,2,4,5,(4,6); 1,2,4,7,(2,3); 1,2,4,7,(4,9); 1,2,4,7,(8,9); 1,2,4,10,(1,9); 1,2,4,10,(3,9); 1,2,7,8,(1,9); 1,2,7,8,(9,10); 1,3,4,10,(6,10); 1,3,6,8,(6,8); 1,3,6,10,(7,9); 1,3,7,9,(1,8); 1,4,5,8,(5,7); 1,4,7,10,(1,9); 1,5,6,8,(5,9); 1,5,7,9,(2,8); 1,6,8,9,(2,6); 2,3,7,8,(4,10); 2,3,7,8,(6,10); 2,3,7,8,(7,10); 2,4,5,9,(5,9); 3,4,5,6,(2,10); 3,4,6,7,(2,3); 3,5,6,7,(4,8) |
| A7 | 12 | 3,8,(3,9); 4,7,(1,7); 4,7,(4,7); 1,(2,3),(3,4); 1,(2,5),(3,10); 1,(2,8),(6,10); 1,(7,8),(8,10); 1,(8,11),(9,10); 2,(1,3),(3,6); 2,(1,7),(2,8); 2,(1,10),(1,11); 2,(2,3),(7,9); 2,(3,9),(3,11); 2,(3,9),(5,9); 2,(5,11),(8,11); 2,(7,9),(7,11); 3,(1,8),(7,10); 3,(5,11),(6,10); 1,2,3,5,(5,9); 1,2,5,9,(7,11); 1,2,6,11,(2,6); 1,3,6,7,(4,10); 1,3,6,9,(1,9); 1,3,6,9,(4,10); 1,3,7,10,(4,5); 1,4,8,10,(2,5); 1,5,6,8,(4,6); 1,5,6,8,(6,10); 1,5,6,11,(7,8); 1,5,7,9,(1,11); 1,5,9,10,(6,7); 2,3,4,10,(3,8); 2,3,6,8,(3,6); 2,3,6,10,(2,6); 2,3,6,10,(4,10); 2,5,6,10,(2,10) |
| A8 | 13 | 1,11,(5,9); 4,8,(9,10); 1,(1,7),(3,7); 1,(2,3),(6,11); 1,(2,5),(5,11); 1,(2,6),(6,8); 1,(2,9),(4,5); 2,(1,6),(9,12); 2,(7,10),(10,12); 3,(1,9),(2,11); 3,(4,6),(9,11); 3,(8,9),(9,10); 4,(1,3),(4,6); 4,(1,3),(10,12); 4,(2,9),(8,10); 5,(1,5),(4,9); 5,(1,12),(7,11); 5,(2,9),(4,5); 5,(3,6),(4,9); 5,(3,12),(9,11); 6,(1,5),(2,12); 1,2,4,5,(1,7); 1,2,10,11,(6,12); 1,3,4,6,(6,10); 1,4,5,10,(4,8); 1,5,6,7,(5,9); 1,5,7,9,(8,9); 1,5,7,11,(8,10); 1,7,10,11,(2,6); 1,8,9,10,(8,9); 2,3,8,11,(1,10); 2,5,6,11,(8,11); 2,6,7,10,(8,12); 3,4,5,12,(4,5); 3,5,6,10,(8,11); 3,5,7,10,(2,10) |
| A9 | 14 | 1,2,(7,12); 1,(2,13),(4,12); 1,(5,12),(9,12); 2,(1,5),(3,11); 3,(1,6),(4,12); 3,(2,4),(6,12); 3,(2,12),(6,13); 3,(5,10),(7,12); 5,(2,4),(6,13); 6,(1,13),(5,9); 6,(5,9),(12,13); 1,2,3,5,(1,3); 1,2,4,7,(1,3); 1,4,5,8,(2,8); 1,4,5,13,(1,6); 1,4,7,11,(1,11); 1,6,10,12,(3,7); 1,6,10,12,(7,9); 1,7,9,12,(3,13); 2,3,5,7,(1,5); 2,3,10,12,(9,10); 2,5,6,12,(6,10); 2,7,9,11,(11,12); 4,5,6,8,(1,4); 4,6,7,10,(5,13) |
| A10 | 15 | 5,9,(2,11); 2,(6,8),(12,14); 4,(2,11),(7,10); 4,(5,6),(5,14); 4,(6,10),(9,10); 4,(7,8),(12,14); 6,(8,11),(12,13); 7,(2,11),(10,13); 7,(3,12),(3,13); 1,3,7,11,(9,10); 1,4,5,12,(3,4); 1,4,6,11,(2,14); 1,4,9,10,(7,10); 1,5,11,13,(5,11); 2,3,9,10,(6,10); 2,3,9,13,(3,7); 2,4,10,14,(4,10); 3,4,5,10,(3,7); 3,5,7,8,(3,13); 4,5,7,10,(1,14); 4,8,12,14,(5,6); 4,9,11,14,(1,13); 5,6,11,14,(5,8); 5,6,12,13,(5,9) |
| A11 | 16 | 2,13,(2,3); 3,(1,5),(5,7; 3,(2,13),(7,14); 5,(4,8),(6,12); 5,(4,12),(7,8); 7,(2,6),(10,13); 7,(8,14),(11,12); 1,2,3,9,(6,14); 1,5,13,14,(14,15); 1,11,12,13,(5,15); 2,5,10,14,(6,14); 2,6,11,12,(14,15); 2,7,8,10,(3,6); 2,7,8,13,(3,15); 4,8,9,10,(8,12) |
| A12 | 17 | 1,(7,10),(9,15); 3,(6,9),(13,14); 5,(4,7),(6,13); 6,(2,9),(7,12); 7,(1,8),(9,14); 8,(10,12),(11,16); 1,3,9,12,(7,13); 1,3,12,14,(2,10); 1,5,9,11,(1,13); 1,7,11,13,(6,14); 2,4,9,12,(6,16); 3,6,7,10,(9,15); 3,8,11,12,(3,11); 4,6,10,16,(3,11); 5,6,9,14,(6,14) |
| A13 | 19 | 7,10,(6,18); 9,12,(1,13); 2,(6,8),(8,10); 4,(5,16),(7,14); 6,(4,8),(17,18); 1,4,5,8,(5,15); 1,4,8,17,(1,13); 3,7,9,16,(3,17); 5,6,12,14,(2,18) |
| A14 | 21 | 1,15,17,19,(13,15); 2,7,12,17,(4,10); 3,5,9,13,(15,17); 4,8,9,11,(3,11) |
| A15 | 22 | 1,(4,10),(11,18); 5,(4,12),(7,14); 1,6,8,12,(10,17); 1,10,16,18,(3,21); 5,6,11,15,(9,21) |
| A16 | 23 | 3,(13,19),(18,19); 2,6,10,14,(5,13); 3,11,16,18,(4,19) |
References
- Wael, A.; Ayoub, M. Physical and Mechatronic Security, Technologies and Future Trends for Vehicular Environment. In Proceedings of the VDI-Fachtagung Automotive Security, VDI Berichte, Nürtingen, Germany, 27 September 2017; Volume 2310, pp. 73–95. [Google Scholar]
- Maes, R.; Verbauwhede, I. Physically Unclonable Functions: A Study on the State of the Art and Future Research Directions. In Towards Hardware-Intrinsic Security; Springer: Berlin, Germany, 2010; pp. 3–37. ISBN 978-3-642-14451-6, 978-3-642-14452-3. [Google Scholar]
- Sadeghi, A.-R.; Visconti, I.; Wachsmann, C. Enhancing RFID Security and Privacy by Physically Unclonable Functions. In Towards Hardware-Intrinsic Security; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Tuyls, P.; Batina, L. RFID-tags for anti-counterfeiting. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Jose, CA, USA, 13–17 February 2006; pp. 115–131. [Google Scholar]
- Škoric, B.; Tuyls, P.; Ophey, W. Robust key extraction from physical uncloneable functions. In Proceedings of the Applied Cryptography and Network Security, New York, NY, USA, 7–10 June 2005; Volume 3531, pp. 407–422. [Google Scholar]
- Guajardo, J.; Kumar, S.S.; Schrijen, G.-J.; Tuyls, P. FPGA Intrinsic PUFs and Their Use for IP Protection. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2007, Vienna, Austria, 10–13 September 2007; Volume 4727, pp. 63–80. [Google Scholar]
- Bösch, C.; Guajardo, J.; Sadeghi, A.-R.; Shokrollahi, J.; Tuyls, P. Efficient Helper Data Key Extractor on FPGAs. Cryptogr. Hardw. Embed. Syst. 2008, 5154, 181–197. [Google Scholar]
- Dodis, Y.; Ostrovsky, R.; Reyzin, L.; Smith, A. Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, St. Petersburg, Russia, 28 May–1 June 2006. [Google Scholar]
- Nedospasov, D.; Seifert, J.-P.; Helfmeier, C.; Boit, C. Invasive PUF Analysis. In Proceedings of the Fault Diagnosis and Tolerance in Cryptography (FDTC), Washington, DC, USA, 20 August 2013; pp. 30–38. [Google Scholar]
- Rührmair, U.; Sölter, J.; Sehnke, F.; Xu, X.; Mahmoud, A.; Stoyanova, V.; Dror, G.; Schmidhuber, J.; Burleson, W.; Devadas, S. PUF modeling attacks on simulated and silicon data. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1876–1891. [Google Scholar] [CrossRef]
- Merli, D.; Schuster, D.; Stumpf, F.; Sigl, G. Side-Channel Analysis of PUFs and Fuzzy Extractors. In Proceedings of the International Conference on Trust and Trustworthy Computing, Pittsburgh, PA, USA, 22–24 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 33–47. [Google Scholar]
- Mahmoud, A.; Rührmair, U.; Majzoobi, M.; Koushanfar, F. Combined Modeling and Side Channel Attacks on Strong PUFs. IACR Cryptol. ePrint Arch. 2013, 2013, 632. [Google Scholar]
- Adi, W.; Mars, A.; Mulhem, S. Generic identification protocols by deploying Secret Unknown Ciphers (SUCs). In Proceedings of the 2017 IEEE International Conference on Consumer Electronics—Taiwan (ICCE-TW), Taipei, Taiwan, 12–14 June 2017; pp. 255–256. [Google Scholar]
- Mars, A.; Adi, W. Converting NV-FPGAs into Physically Clone-Resistant Units by Digital Mutations. 2019; submitted for publication. [Google Scholar]
- Mars, A.; Adi, W.; Mulhem, S.; Hamadaqa, E. Random stream cipher as a PUF-like identity in FPGA environment. In Proceedings of the Seventh International Conference on Emerging Security Technologies (EST), Canterbury, UK, 6–8 September 2017; pp. 209–214. [Google Scholar]
- Mars, A.; Adi, W. Clone-Resistant Entities for Vehicular Security. In Proceedings of the IEEE 13th International Conference on Innovations in Information Technology (IIT), Al Ain, UAE, 18–19 November 2018. [Google Scholar]
- Mars, A.; Adi, W. New Concept for Physically-Secured E-Coins Circulations. In Proceedings of the 2018 NASA/ESA Conference on Adaptive Hardware and Systems, Edinburgh, UK, 6–9 August 2018. [Google Scholar]
- Kerckhoffs, A. LA CRYPTOGRAPHIE MILITAIRE. Available online: http://www.petitcolas.net/kerckhoffs/la_cryptographie_militaire_i.htm (accessed on 2 April 2019).
- eSTREAM, the ECRYPT Stream Cipher Project. Available online: http://www.ecrypt.eu.org/stream/ (accessed on 2 April 2019).
- Gammel, B.M.; Göttfert, R.; Kniffler, O. The Achterbahn stream cipher. eSTREAM 2005. submitted. [Google Scholar]
- Johansson, T.; Meier, W.; Müller, F. Cryptanalysis of Achterbahn. In Proceedings of the International Workshop on Fast Software Encryption, Graz, Austria, 15–17 March 2006; Springer: Berlin/Heidelberg, Germany; Volume 4047, pp. 1–14. [Google Scholar]
- Chan, A.H.; Games, R.A.; Key, E.L. On the complexities of de Bruijn sequences. J. Comb. Theory Ser. A 1982, 33, 233–246. [Google Scholar] [CrossRef]
- Dubrova, E. A List of Maximum Period NLFSRs. IACR Cryptol. ePrint Arch. 2012, 2012, 166. [Google Scholar]
- Courtois, N.T.; Meier, W. Algebraic Attacks on Stream Ciphers with Linear Feedback. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003. [Google Scholar]
- Gammel, B.M.; Göttfert, R.; Kniffler, O. Status of Achterbahn and Tweaks. In Proceedings of the SASC 2006-Stream Ciphers Revisited, Leuven, Belgium, 2–3 February 2006. [Google Scholar]
- Siegenthaler, T. Correlation-immunity of nonlinear combining functions for cryptographic applications (Corresp.). IEEE Trans. Inf. Theory 1984, 30, 776–780. [Google Scholar] [CrossRef]
- Meier, W.; Staffelbach, O. Fast correlation attacks on certain stream ciphers. J. Cryptol. 1989, 1, 159–176. [Google Scholar] [CrossRef]
- Courtois, N.T. Fast Algebraic Attacks on Stream Ciphers with Linear Feedback. In Proceedings of the CRYPTO 2003: Advances in Cryptology, Santa Barbara, CA, USA, 17–21 August 2003; Volume 2729, pp. 176–194. [Google Scholar]
- Gammel, B.; Göttfert, R.; Kniffler, O. Achterbahn-128/80: Design and analysis. In Proceedings of the ECRYPT Workshop SASC 2007—The State of the Art of Stream Ciphers, Bochum, Germany, 31 January–1 February 2007. [Google Scholar]
- Gierlichs, B.; Batina, L.; Clavier, C.; Eisenbarth, T.; Gouget, A.; Handschuh, H.; Kasper, T.; Lemke-Rust, K.; Mangard, S.; Moradi, A.; et al. Susceptibility of eSTREAM Candidates towards Side Channel Analysis. In Proceedings of the ECRYPT Workshop SASC 2008–The State of the Art of Stream Ciphers, Lausanne, Switzerland, 13 February 2008. [Google Scholar]
- Lano, J.; Mentens, N.; Preneel, B.; Verbauwhede, I. Power analysis of synchronous stream ciphers with resynchronization mechanism. In Proceedings of the ECRYPT Workshop SASC 2004–The State of the Art of Stream Ciphers, Brugge, Belgium, 14–15 October 2004; pp. 327–333. [Google Scholar]
- Hell, M.; Johansson, T.; Meier, W. Grain-A Stream Cipher for Constrained Environments. Int. J. Wirel. Mob. Comput. 2007, 2, 86–93. [Google Scholar] [CrossRef]
- Babbage, S. The stream cipher MICKEY 2.0. In New Stream Cipher Designs; Springer: Berlin, Germany, 2006. [Google Scholar]
- De Cannìere, C.; Preneel, B. TRIVIUM Specifications. eSTREAM: the ECRYPT Stream Cipher Project. 2006. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.59.9030 (accessed on 6 April 2019).
- Good, T.; Benaissa, M. Hardware performance of eStream phase-III stream cipher candidates. In Proceedings of the ECRYPT Workshop SASC 2008–The State of the Art of Stream Ciphers, Lausanne, Switzerland, 13 February 2008; pp. 163–173. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).