Abstract
The AKS algorithm is an important breakthrough in showing that primality testing of an integer can be done in polynomial time. In this paper, we study the optimization of its runtime. Namely, given a finite cardinality set of alphabets of a deterministic polynomial runtime Turing machine and the number of strings of an arbitrary input integer whose primality is to be tested as the system parameters, we consider the randomized AKS primality testing function as the objective function. Under randomization of the system parameters, we have shown that there are definite signatures of the local and global instabilities in the AKS algorithm. We observe that instabilities occur at the extreme limits of the parameters. It is worth mentioning that Fermat’s little theorem and Chinese remaindering help with the determination of the underlying stability domains. On the other hand, in the realm of the randomization theory, our study offers fluctuation theory structures of the AKS primality testing of an integer through its maximum number of irreducible factors. Finally, our optimization theory analysis anticipates a class of real-world applications for future research and developments, including optimal online security, system optimization and its performance improvements, (de)randomization techniques, and beyond, e.g., polynomial time primality testing, identity testing, machine learning, scientific computing, coding theory, and other stimulating optimization problems in a random environment.
1. Introduction
The Agrawal‒Kayal‒Saxena (AKS) algorithm plays an important role in determining the primality of an integer [1]. In the realm of modern computer science, it finds significance in cryptography, viz. the block ciphers, banking system, and associated online security [2,3]. Namely, from the perspective of the formal theory of computation, an apt design of protocols is achieved via a suitable algorithm to efficiently perform a given computational task [4,5]. The AKS primality testing finds further importance, as well. For example, see [6] concerning its elementary description, correctness, and asymptotic analysis towards the primality testing of an integer. From the inception of the AKS algorithm, the prime factoring problem, presumed to be an -type problem, has become a -type problem in the realm of the randomization theory. Here, stands for the class of algorithms running in polynomial time and that of for nondeterministic polynomial runtime problems [7]. In the light of computational complexity [8], it is known that the above and type problems are polynomial time verifiable and solvable classes, respectively. Before the discovery of the AKS algorithm, there were numerous questions about testing of an integer on a particular machine that executes the algorithm in the shortest time.
Time is considered in a discrete dynamical sense, i.e., the number of steps required to achieve the final state of an algorithm. On the other hand, there have been various attempts to determine the equivalence between - and -type complexity classes [9]. Indeed, the complexity classification finds discrete mathematical perspectives in connection with satisfiability problems, Boolean constraint circuits, and weighed optimization problems [10]. Furthermore, the AKS algorithm finds an important role in computer science via the randomization hypothesis [11]. There are various consequences of primality testing in counting problems, complexity theory, and cryptography [12,13,14]. In the realm of probabilistic models, the underlying goal of testing the primality of an integer is achieved via Fermat’s little theorem and the Chinese remainder theorem; see [15] for aspects of the mathematical background such as the modular equivalence, encryption, decryption, cryptographic protocol, digital signature and designing of safety measures, and related security issues towards safe multi-party computation. The AKS algorithm is an important breakthrough in showing that primality testing can be done in polynomial time. Hence, optimizing runtime for the implementation of this algorithm is an important problem. As per the above consideration, it is worth mentioning that the mathematics involved appears to be interesting, see Section 2 for an overview. The respective results are discussed qualitatively and quantitatively in Section 3 and Section 4.
The aim of this paper is to study the case of the corresponding ring of integers when it is prolonged to the field of real numbers. The AKS algorithm is used for testing the integer primality that follows via the fundamentals of number theory on the optimization of AKS primality testing in the light of an absolute deterministic polynomial runtime randomized algorithm that can help with the determination of the prime factors of an arbitrary integer. Given the algorithm, we optimize the AKS primality testing of an arbitrary integer by determining its stability structures. In particular, in order to test the optimize the AKS algorithm, we concentrate on the case when the corresponding ring of integers is prolonged to the field of real numbers. Under the randomization hypothesis of Agrawal and Biswas [11], it is worth emphasizing that the aforementioned AKS algorithm [1] brings the primality testing of an arbitrary integer into the category of -type problems [8]. The AKS primality testing receives distinct roles in both (i) pure mathematics, e.g., probabilistic algorithms [11] and (ii) its applications to modern cryptography—see [15] for an introduction to information security, commitments, and Oblivious transfer functions. Generically, the role of the AKS algorithm in testing the primality of an integer follows the fundamentals of number theory [16], which is particularly rooted in the domain of the algorithmic number theory [17].
We focus on the optimization of AKS primality testing in the light of an absolute deterministic polynomial runtime randomized algorithm that can help one to know whether a given integer is prime or not. In other words, we concentrate on the determination of the prime factors of an arbitrary integer. In particular, for the case of large integers, the realization of such a goal is obtained on a specific Turing machine, whereby the cardinality of the set of its alphabets plays a vital role in computing the corresponding primality; see [18] concerning the fundamentals of the computable functions, (un)decidability, and unsolvable problems. In this case, we concentrate on a given integer whose primality is to be tested on a definite machine of finite cardinality. In order to optimize the AKS primality testing, we apply the notion of the fluctuation theory [19] by randomizing the system parameters, viz. (i) the input integer whose primality is to be tested as a string and (ii) the cardinality of the set of alphabets of the machine.
We find optimal domains of the AKS primality testing of an arbitrary integer with the inverse of the number of steps required to execute the algorithm as the order of the uncertainty. As the input integer tends to a large value, the determination of its primality becomes accurate. Our proposal generically enables one to address the issue of the stability of the AKS primality testing algorithm. This is realized by considering the maximum value of the cardinality of the group of alphabets as the objective function. Note that such a function arises as a map from the space constituted by the input integer and the size of the group of residues from the set of all numbers that are introspective [1] to the polynomials in a set of the field of real numbers. Namely, when both the input integer and machine parameter are allowed to vary, the fluctuation theory analysis [19] offers an apt platform to optimize the AKS primality testing function as a real-valued map from the space of algorithm parameters to the field of real numbers. Following the notion of the intrinsic geometry and embedding theory [20], we determine the critical points, stability domains, and its correlation with a chosen machine performing the AKS algorithm. We give its global stability structures in the proximity of the critical points of the AKS primality testing function. In this setup, we compute fluctuation vectors in order to determine an intrinsic length of the AKS primality testing of the input integer string and machine parameters.
Following the above notion, we determine the regions where the ASK algorithm remains stable or unstable. Considering the fact that it is among the best primality testing methods of an arbitrary integer, we examine how the AKS algorithm behaves under variations of the input integer and the machine parameters that are used in its primality testing. Next, we tested its stability at the asymptotic limits. The qualitative discussion also shows that instabilities arise only in extreme regions, namely, near the initiation or halting stages of the algorithm. This supports the claim of AKS [1] that the AKS algorithm becomes almost exact for large integers. Indeed, there are various models that could be interesting to investigate further in the light of primality testing and optimization theory. See Section 2 for an overview.
At this juncture, the framework of randomization theory turns outs to be promising because of its probabilistic nature. We have considered the optimal Cunningham factorization of an arbitrary integer in the light of randomization theory [21]. To that end, we provide a brief account of previously known primality testing algorithms such as Fermat’s little theorem, the Miller‒Rabin algorithm, the Solovay‒Strassen models, and others in the Appendix A. Following the assessment of the AKS primality testing and the above models, a natural research direction would be to compare the stability domains of the AKS testing with the above models. Bearing in mind that the AKS algorithm is the most efficient primality test of an integer to date, we focus on examining its optimality properties under fluctuations of the system parameters.
Following the above models and related fundamentals, we summarize the highlights of our analysis as follows. Our contribution is to classify the parameter space regions of the ASK primality testing algorithm, where it remains optimal. Namely, we focus on the optimization of the AKS primality testing of an arbitrary integer. Therefore, we examine the behavior of the peaks concerning the AKS primality testing on an input integer. This is realized by executing a qualitative analysis of the fluctuation quantities in the space of parameters in their specified ranges. For this, we use the asymptotic properties of the AKS algorithm. Interestingly, we observe that the qualitative behavior of the fluctuations remains the same when the input ranges are increased by 10 times. Following the AKS scaling structures, we anticipate that the asymptotic behavior of peaks holds with the incorporation of fluctuations in the model parameters. This offers enlightening insight in the areas of stability analysis, fluctuation theory, randomization theories, integer primality testing and identity testing.
The rest of the paper is organized as follows. In Section 2, we give a brief evolution of the AKS algorithm and its relation to Fermat’s little theorem, AKS primality testing, and the randomization hypothesis in the light of ring theories and their localizations. In Section 3, we examine the stability structures of the AKS primality testing by randomizing the input integer string and cardinality of the set of alphabets of the machine executing the algorithm. In Section 4, we provide a qualitative discussion of the results and their implications towards the optimization of the AKS algorithm. Finally, in Section 5, we conclude the paper with prospective directions for future research and developments.
2. Randomized AKS Primality Testing
In this section, we offer a brief review of the AKS algorithm in light of Fermat’s little theorem and Chinese remainder theorem in the light of randomization theory [21], also see [22] for basics of the subject matter under the consideration. From the perspective of the versus problem [7], we illustrate how the AKS primality testing falls in the domain of -type problems. Concerning the geometric and algebraic perspectives, see [20] for embedding, submersion and convexity theory, and [23] for the related commutative algebra background such as modules, fields, and rings.
First of all, in order to determine whether a given input number is prime or not, an efficient primality testing algorithm requires guaranteeing its polynomial runtime complexity [1]. See the Appendix A.1 for a brief evolution of primality testing algorithms. In contrast to the probabilistic primality testing, the AKS primality testing [1] of an integer is based on a cyclotomic generalization of the Fermat’s little theorem over a finite ring. This offers both a deterministic and polynomial time complexity of a reduced order. In particular, as highlighted in the Appendix A.2, the AKS algorithm essentially overcomes the exponential runtime complexity of Fermat’s little theorem by comparing the coefficients of a polynomial with modular operation in terms of another polynomial of the form . This settles a long-standing problem in primality testing: whether it falls in the domain of -type or -type problems.
Following the above breakthrough, the deterministic characteristic of the AKS primality testing algorithm is brought down to the table by the value of , which is bounded in polynomial runtime of its order , as in the Algorithm 1 below. The associated details are relegated to the Appendix A.2. At this point, it is worth mentioning that the AKS primality testing [1] satisfies all four requirements for an efficient prime testing algorithm in comparison to the previously mentioned algorithms. As a matter of fact, it possesses a reduced polynomial time complexity compared to the associated primality testing algorithms as in Appendix A.1. There, whereby we have summarized the associated concepts such as the computational complexity and its role in the analytic number theory [24] and others such as the Miller‒Rabin test [25] and Solovay‒Strassen primality testing [26] of an integer in the light of the algorithmic number theory.
This accounts for the wide usage of the AKS primality testing algorithm in the realm of applied cryptography and related subject matters. Indeed, there have been various reductions in the time complexity of the cyclotomic AKS primality testing of an integer.
In this paper, we offer the undermining experimental, mathematical, and computational perspectives. Namely, we focus on the optimization of the AKS algorithm in order to determine the regions of its input parameters that yield the optimal primality testing of an arbitrary integer. In short, the AKS primality testing [1] of an integer can be summarized as per the below Algorithm 1.
| Algorithm 1: The AKS algorithm (the AKS primality testing [1] of an integer) | |
| 1- | An integer is said to be a composite number if there exists a pair such that for some and . |
| 2- | Given a triple with , find the smallest such that holds. Then, the order of modulo must satisfy the inequality . |
| 3- | For an integer with its factor , is said to be composite if . |
| 4- | The input integer returns a prime if we have . |
| 5- | For , an integer is said to be composite, if the Equation (A3) as in Appendix A.2 is not satisfied over , where . Here, denotes the Euler totient function, which counts the relatively prime numbers less than . |
| 6- | Otherwise the input integer is a prime. |
It is worth mentioning that the AKS algorithm [1] arises via the randomization of Fermat’s little theorem; see the Appendix A.2 for an overview. From Algorithm 1, we observe that if the input integer returns the algorithm in steps 1 and 3, it is a composite number. On the other hand, the input integer turns out to be a prime if the algorithm returns in steps 4 and 6. In determining the primality of an integer via the AKS algorithm, steps 2 and 5 emerge as the key ingredients. Notice that step 2 plays an equally important role in testing the primality of an integer as it determines a suitable such that steps 2 and 3 are not satisfied whenever is a prime. The above primality testing of an integer is examined locally by introducing the notion of a modular function in a given quotient ring with the maximum value of as as above in step 5. The proof of the AKS algorithm as depicted above in Algorithm 1 involves the introspective properties of a modular function; see [1] for the concerning details in the light of the algebraic closure, addition, multiplication, and quotient ring in a given basis of cyclotomic polynomials over a finite field.
In general, there are various higher-dimensional extensions of such a ring that consist of finitely many local rings of the form , where . On the other hand, the randomization depicted in Algorithm 1 designates an extension from the integral valued inputs to their real counterparts [11]. However, the converse problem, termed de-randomization [1], is anticipated to yield the inverse procedure as a restriction map; see [20] in connection with the embedding and submersion theories over real and complex spaces. It is worth stressing that such a map carried out in number of steps accompanies an effective error . Thus, for a sufficiently large , it follows that the randomization error concerning the primality testing of an integer turns out to be negligible or less than the precision of the machine.
In the light of the versus problem [7], the primality testing of an integer that was believed to be an -type problem for several decades is now reduced to a -type problem via the AKS algorithm [1]. Furthermore, in the realm of algorithmic number theory and computer science, Cook [7] finds that the SAT problem is complete; see also [27] for parameterized and exact computations in the light of sub-exponential runtime Turing reductions. This leads to a -type solvable problem, whenever there exist various algorithms that positively answer the equivalence between the complexity classes of and type problems [7]. In light of the primality testing of an arbitrary integer, we anticipate that in terms of the computational capacity of an algorithm, whatever is achievable on a modern computer is equally achievable on a Turing machine; see [18] for an original account of the computable numbers. In the next section, we offer an intrinsic stability analysis of the AKS algorithm towards the primality testing of an arbitrary integer on a given Turing machine.
With the aforementioned motivations, in this paper, we study the case of the corresponding ring of integers when it is prolonged to the field of real numbers. Herewith, the AKS algorithm is used in testing the integer primality that follows via the fundamentals of number theory. In the light of an absolute deterministic polynomial runtime randomized algorithm, our analysis relies on the optimization of AKS primality testing that can help on the determination of the prime factors of an arbitrary integer. In particular, we have obtained the algorithm that optimizes the AKS primality testing of an arbitrary integer by determining its stability structures. From the fluctuation theory perspective, an essential rudiment of related works on prime factoring is addressed in Appendix A.1. Following the above insightful background, we focus on the AKS algorithm and its applications in the realm of fluctuation theory. The concerned stability analysis is considered in Section 3.
In Section 4, upon the multivariable analysis that is performed on an arbitrary randomized set of input parameters, we purpose in this paper to study the signatures of quantities concerning the runtime stability. This includes the eigenvalues of the fluctuation matrix that have algorithmic significance towards the global stability of the randomized AKS primality testing of an integer. Namely, Section 4 vividly portrays the same via plotted 3-D graphs of the mathematical findings with reported features. In this regard, we acknowledge the implication of asymptotic analysis, time complexities and runtime complications in such cases as interesting research. We suggest considering the former among future research directions. Pertinently, it is worth mentioning that a study of the randomized AKS algorithm at higher dimensions may equally be discussed; however, due to limited time constraints, we anticipate examining such investigations and their feasibility structures in future research and developments.
3. Fluctuation Theory Perspective
In this section, we explore the stability of the AKS primality testing algorithm for an arbitrary input integer by a deterministic Turing machine having a finite cardinality set of its alphabets. It is known that the AKS primality testing arises as an exponential execution of the algorithm [1]. We consider the maximum number of irreducible factors of an input integer as the objective function. In the setup of a randomized algorithm, we examine the corresponding local and global stability structures by determining the signatures of the heat capacities and determinant of the fluctuation matrix at its critical points. This enables us to classify the domains where we have the optimized AKS primality testing of an integer.
3.1. Stability Analysis
In the above setup, we concentrate to determine an optimized AKS primality testing algorithm with the objective function as the number of the prime factors of an arbitrary integer on a given machine. Namely, by varying the input integer whose primality is to be tested on a certain Turing machine of finite cardinality , we examine the efficiency of the AKS algorithm via the randomization hypothesis of Agrawal and Biswas (see [11]). In light of the versus problem, the AKS algorithm [1] arises as the maximum number of possible factors of an arbitrary integer determined by a deterministic polynomial runtime Turing machine having cardinality of the set of its alphabets. Thus, the AKS primality testing of an integer on the Turing machine can be viewed as a finite integral valued map from to as per the assignment .
In the limit of randomized input parameters , it follows [1] that the asymptotic AKS primality testing function is simplified as
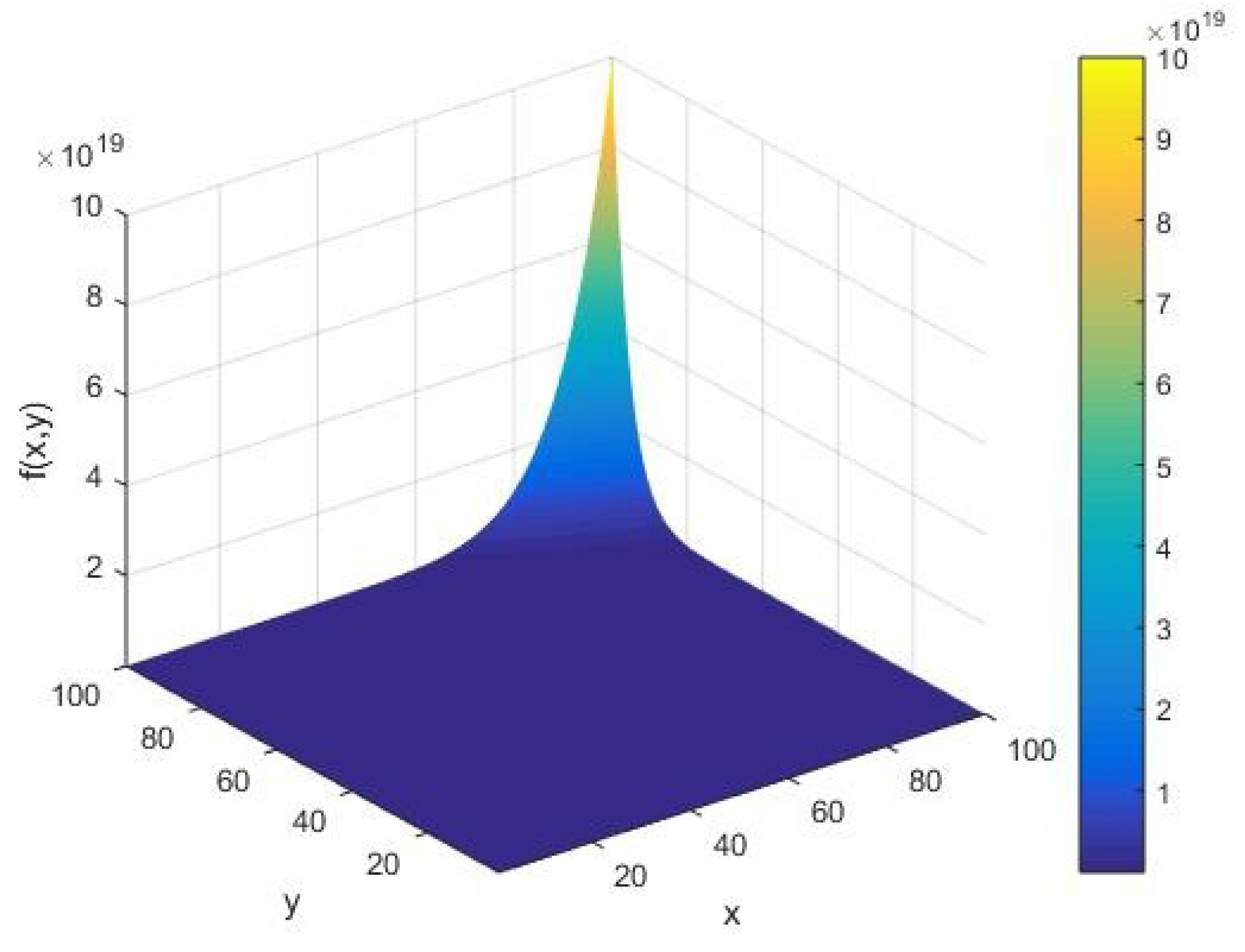
where signifies the efficiency of the algorithm. In a domain of varying , the qualitative behavior of the AKS function is shown in Figure 1. In order to optimize the AKS primality testing algorithm, we consider the randomized setting [11], whereby and vary over the set of real numbers . We consider the AKS primality testing function as a real valued map that assigns a given pair of real numbers to a real number . We perform an optimization analysis of the randomized AKS primality testing function to determine its stability domains. Namely, in the setup of fluctuation theory [19,20,21], we offer a stability analysis of an arbitrary polynomial factoring towards the primality testing of an integer by a machine of the cardinality of the set of its alphabets. By differentiating as in Equation (1) with respect to , we find the following flow component
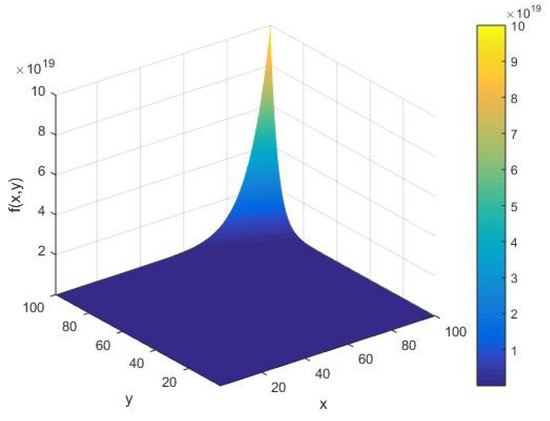
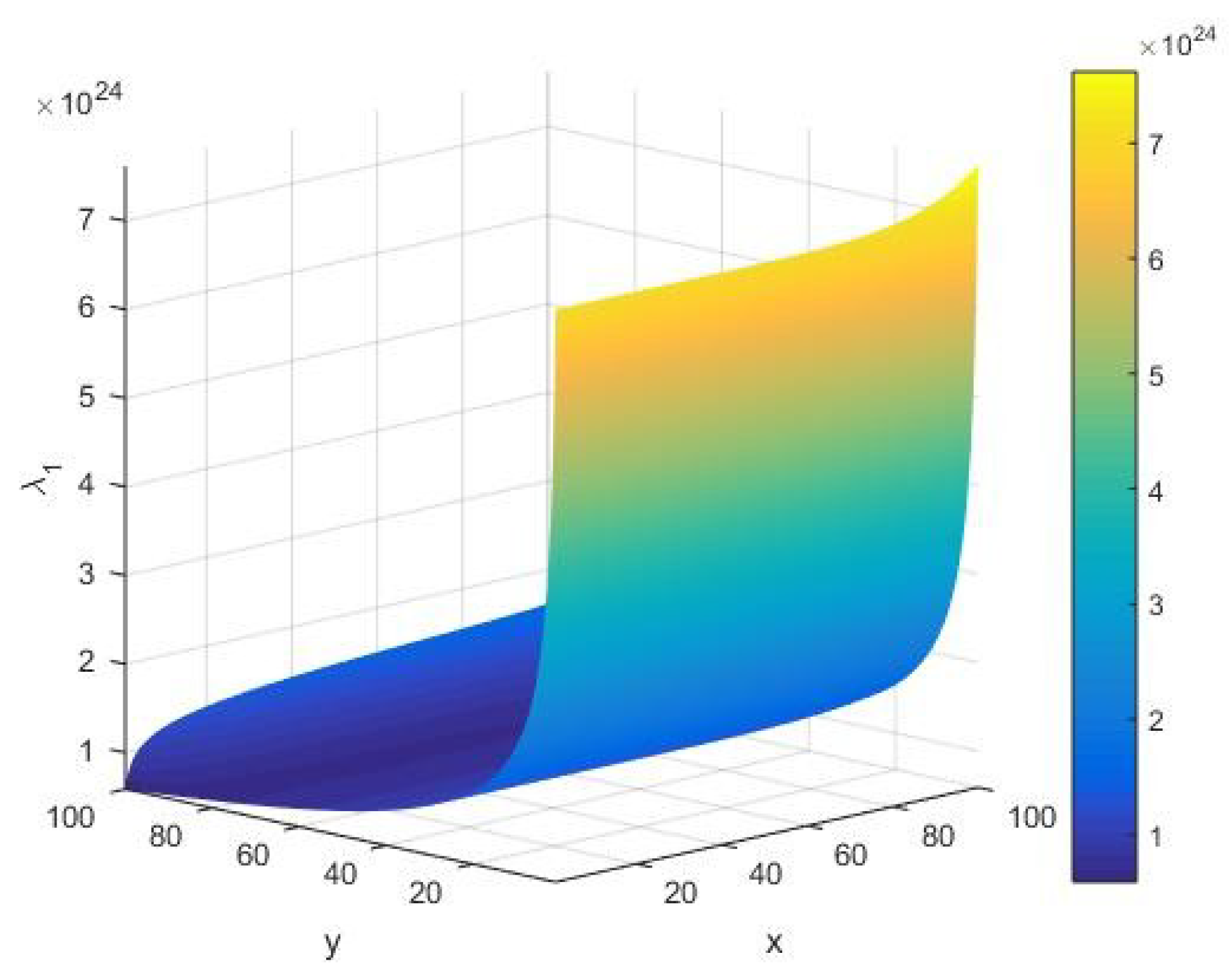
Figure 1.
The AKS primality testing function as a function of the input integer and cardinality of the set of alphabets of the machine executing the AKS algorithm plotted in the range .
Similarly, under variations of the cardinality of the set of alphabets of a Turing machine , the corresponding rate of the AKS primality testing function of the integer satisfies
The critical points of are computed as the zeros of the flow equations and . In this case, the limiting critical points of arise as the pairs and . In order to discuss the nature of the critical points of , we need to calculate the heat capacities and the local correlation factor . The local stability of the AKS primality testing computation is determined by the signature of one of the capacities . Under variations of the input integer , the heat capacity as the pure fluctuation component is given by
Similarly, under variations of the cardinality , the pure fluctuation component reads as
Moreover, it is not difficult to see that the mixed correlation component simplifies as
Herewith, at the critical point , we see that both the pure fluctuation components vanish identically while the correlation factor diverges. Namely, we have the following limiting behavior and . On the other hand, at the critical point , we find that all the pure and mixed correlation components become ill-defined, i.e., we have an undefined triple . It is worth mentioning that the pure correlation components and signify the heat capacity of the input integer whose primality is to be tested on a machine of the cardinality of the set of its alphabets. Physically, can be viewed as factors for investigating the overheating of a given computation state of the machine while testing the primality of an integer , whereby we may design an apt cooling system of a Turing machine.
In order to examine the global stability of the AKS algorithm, given the objective function as in Equation (1), we define its fluctuation matrix as a symmetric matrix
where signify the heat capacities of the system as defined in Equations (4) and (5) respectively. The cross-component denotes the local correlation of the system, see Equation (6). Substituting the values of from Equations (4)–(6), we have the following Hessian matrix:
In order to achieve a stable domain of the AKS algorithm in testing the primality of a given input integer , the randomized as the objective function of the optimization problem must yield a positive definite Hessian determinant:
By substituting the values of the heat capacities from Equations (4) and (5) and the correlation factor from Equation (6), it follows that the above determinant simplifies as
To determine the signature of , we need to factorize the quadratic polynomial as a function of . It follows that the corresponding quadratic equation leads to the following roots:
In Equation (11), let and be the respective positive and negative roots in as follows:
Thus, the overall stability of the AKS algorithm depends on the range of the input integer and the cardinality of the set of alphabets of the machine. In particular, when lies between and , as above in Equations (12) and (13), there is a globally stable AKS algorithm with a positive Hessian determinant for . In the other case, for a negative corresponding to damped oscillations as the algorithm proceeds, it follows that must either be larger than the root as in Equation (12) above or less than the root as above in Equation (13), viz. we have the optimal solution whenever satisfies the inequality for . Therefore, we can achieve an optimal AKS primality testing algorithm for different values of input parameters . Namely, our analysis shows that the AKS algorithm renders the optimal prime testing of an arbitrary integer on a suitable Turing machine of the cardinality of the set of its alphabets.
3.2. Limiting Stability Analysis
In this subsection, we provide limiting behaviors of the local and global stability components as the model parameters approach the specific critical points and of . In doing so, we examine specific values of the local heat capacities and correlation . Furthermore, we see that the global stability component tends to infinity when the point approaches the root of the flow Equations (2) and (3). On the other hand, it follows that becomes ill-defined when it is evaluated at the critical point . Thus, for any physical model, we deem such an outcome algorithmically undesirable as the cardinality of the set of alphabets is assumed to be a finite positive number.
In order to examine the limiting behavior, we randomize the roots and to their corresponding values and with and . Physically, could represent the possible size of the hard disk of a given machine and the step size, which could be the least value of the randomized integer whose primality is to be tested by the AKS algorithm [1]. For the randomized root , from Equation (4) we find that the input integer heat capacity simplifies as
From Equation (5), we see that the limiting local capacity corresponding to the cardinality of the set of alphabets of the machine vanishes identically, namely, as we approach the critical point we have . Furthermore, from Equation (6), we find that the cross-correlation solely depends on the efficiency of the chosen machine executing the algorithm. Namely, the correlation satisfies
On the other hand, at the critical point , we see that the determinant of the Hessian matrix takes a negative value for all positive and . From Equation (10) it follows that we have
Thus, in the randomized limit, it follows that the system remains stable for a negative value of . Furthermore, from Equation (16), we find a definite signature of global instabilities in the limit of . Similarly, in the limit of large , the stability components corresponding to the randomized root of the flow Equations (2) and (3) lead to a positive value of the heat capacities . In particular, for a given machine being used for the primality testing of an integer , it turns out that the AKS algorithm yields the following local heat capacities:
For a positive value of the determinant , the system remains stable as long as either of the heat capacities remains positive, that is, we have either or . Furthermore, at the limit of , we find that the heat capacity for . However, the other heat capacity becomes ill-defined by entailing fluctuations of large negative amplitudes. This follows from the fact that the logarithm of a small number approaching zero is a large negative number. On the other hand, we find that the corresponding correlation reads as
In this case, there exists a positive correlation whenever the randomized root satisfies the inequality . From Equation (19), we see that the correlation largely modulates as per the first term. This is because the second term takes a small negative value in comparison to the first term whenever , viz. the sample parameters and satisfy the constraint . Therefore, we find that the AKS algorithm becomes highly correlated in the limit of . Qualitatively, as a function of , we observe that the correlation , as in Equation (19), displays identical behavior under different values of .
The global stability is determined by the signature of the determinant of the Hessian matrix as in Equation (10). At the critical point , the value of the pre-factor of the determinant depends on two competing terms and . Namely, the factor takes a small positive value in the limit of and . Furthermore, the factor can take both the positive and negative values depending upon the values of and . For example, for and , it follows that takes an approximate value of . Thus, from Equation (10), we find a positive signature of the determinant . In such cases, the AKS algorithm remains stable while testing the primality of an integer.
3.3. Eigenvalues and Eigenvectors of
For a given AKS primality testing function with the fluctuation matrix as in Equation (8), the corresponding global (in)stability can be examined via the relative signature of the eigenvalues of . Namely, given the heat capacities as in Equations (4) and (5) and the system correlation factor as in Equation (6), we evaluate the eigenvalues and associated eigenvectors of as a function of for the AKS primality testing function as in Equation (1) of an arbitrary integer on a machine of the cardinality of the set of its alphabets.
3.3.1. Evaluation of Eigenvalues
As per the aforementioned representation of the Hessian matrix as in Equation (7), there exists an eigenvalue if we have a non-null vector satisfying the following eigenvalue equation:
Algebraically, for a given triple , the characteristic equation arises as a condition of the vanishing determinant of the matrix for all nonzero . In other words, we have
It follows that the eigenvalue of satisfies the quadratic equation
From Equation (22), we find the following eigenvalues:
To study the linear transformation properties of the fluctuation vector for a given eigenvalue as above in Equation (23), we consider two invariants of as the trace and determinant . In this setup, it follows that the eigenvalues can be expressed as
We find a unique real eigenvalue of whenever the above linear class operators satisfy the equality . The qualitative description of the global stability component and eigenvalues is relegated to the next section.
3.3.2. Evaluation of Eigenvectors
Next we compute the corresponding fluctuation vectors underlying the AKS primality testing function as in Equation (1). Namely, the fluctuation vectors are defined as the eigenvectors of the fluctuation matrix as in Equation (20). In this case, there are two eigenvalues, whereby we have two corresponding eigenvectors. For a given pair of eigenvalues , the eigenvectors are evaluated by the eigenvalue equation, viz. Equation (20). For , the eigenvector is obtained as the following two-dimensional vector:
For the fluctuation matrix as in Equation (7), the corresponding eigenvalue equation reads as
In other words, we have the following pair of simultaneous linear equations:
In order to solve the above pair of linear equations as in Equations (27) and (28), we may choose . Thus, from Equation (28), it follows that we have
With these values of and , the eigenvector corresponding to the eigenvalue is given by
Therefore, the corresponding norm of the fluctuation vector is given by
In this case, the normalized eigenvector associated to reads as
where is given as above in Equation (23) with the choice of the positive signature. By following the aforementioned methodology, the fluctuation vector corresponding to the eigenvalue of can be obtained in a similar manner. Namely, by defining the eigenvector
with the choice of , we obtain the first component of as
For with the above , the eigenvector has the following norm:
Finally, it follows that the normalized eigenvector reduces as
where reads as above in Equation (23) with the choice of the negative signature. The above pair of normalized eigenvectors as depicted in Equations (32) and (36) gives the direction of fluctuations under the randomized AKS primality testing of an arbitrary integer on a particular machine of the cardinality of the set of its alphabets. The corresponding norms , as in Equations (31) and (34), respectively, signify the intrinsic errors in determining the primality of the integer on the machine . In this concern, the total error is defined as the maximum of the norms of eigenvectors of the fluctuation matrix , viz. we have as the effective uncertainty in testing the primality of an arbitrary integer string on .
4. Discussion of the Results
In this section, we provide the qualitative description of the results concerning the optimized primality testing of an arbitrary integer via the AKS algorithm [1]. For an illustration, we take an efficient AKS algorithm with a varying input integer whose primality is to be tested on a machine of the cardinality of the set of its alphabets. Henceforth, without loss of generality, we may choose a randomized AKS algorithm with its pre-factor . For the purpose of qualitative discussion, we set the parameters as below.
We depict the qualitative behavior of the randomized AKS primality testing function , associated flow components, heat capacities , local correlation , and the determinant of its fluctuation matrix under fluctuations of the system parameters . The positivity of and determines the underlying stability domains of the AKS primality testing of an integer with the maximum number of its prime factors obtained by a given machine of the cardinality of the set of its alphabets as the objective function.
For a given AKS primality testing function , as in Equation (1) as the objective function, we perform our analysis by increasing the input integer x whose primality is to be tested on a machine of the cardinality of the set of its alphabets. Namely, from Figure 1, we see that the objective function has an amplitude of the order . In due course of execution of the algorithm, we observe that behaves smoothly for all values of the system parameters , except at their extreme values, where it blows up. Furthermore, we find that there are no fluctuations in for small values of . In this case, it follows that increases as we augment the algorithm parameters of the AKS primality testing of an integer.
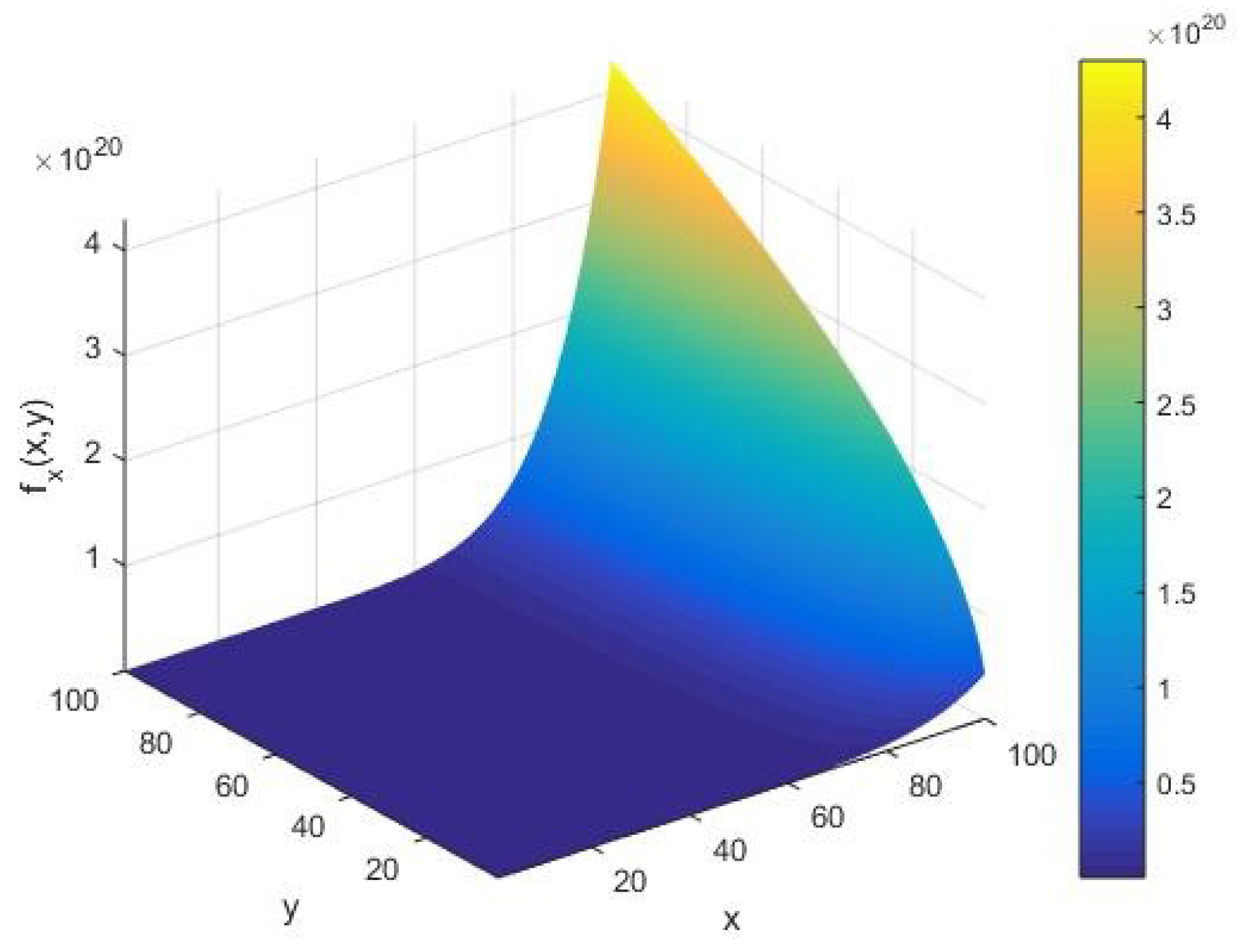
We assess the qualitative behavior of the input integer rate of the AKS primality testing function under variations in the input parameters . From Figure 2, we find that the rate concerning the input integer takes an amplitude on the order of as and vary. Moreover, for a large input , we see that forms an increasing arc with respect to the cardinality of the set of alphabets of the machine executing the AKS algorithm.
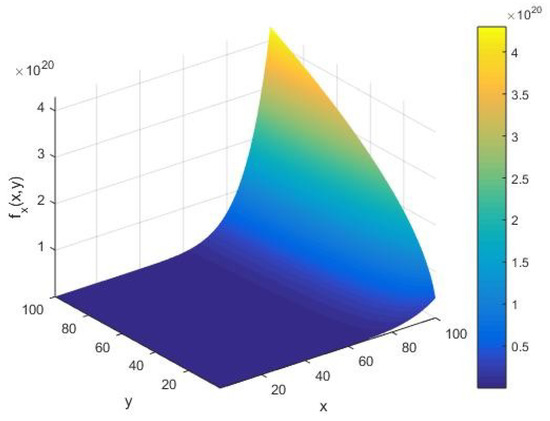
Figure 2.
The input integer rate as a function of the input integer and cardinality of the set of alphabets of the machine executing the AKS algorithm plotted in the range .
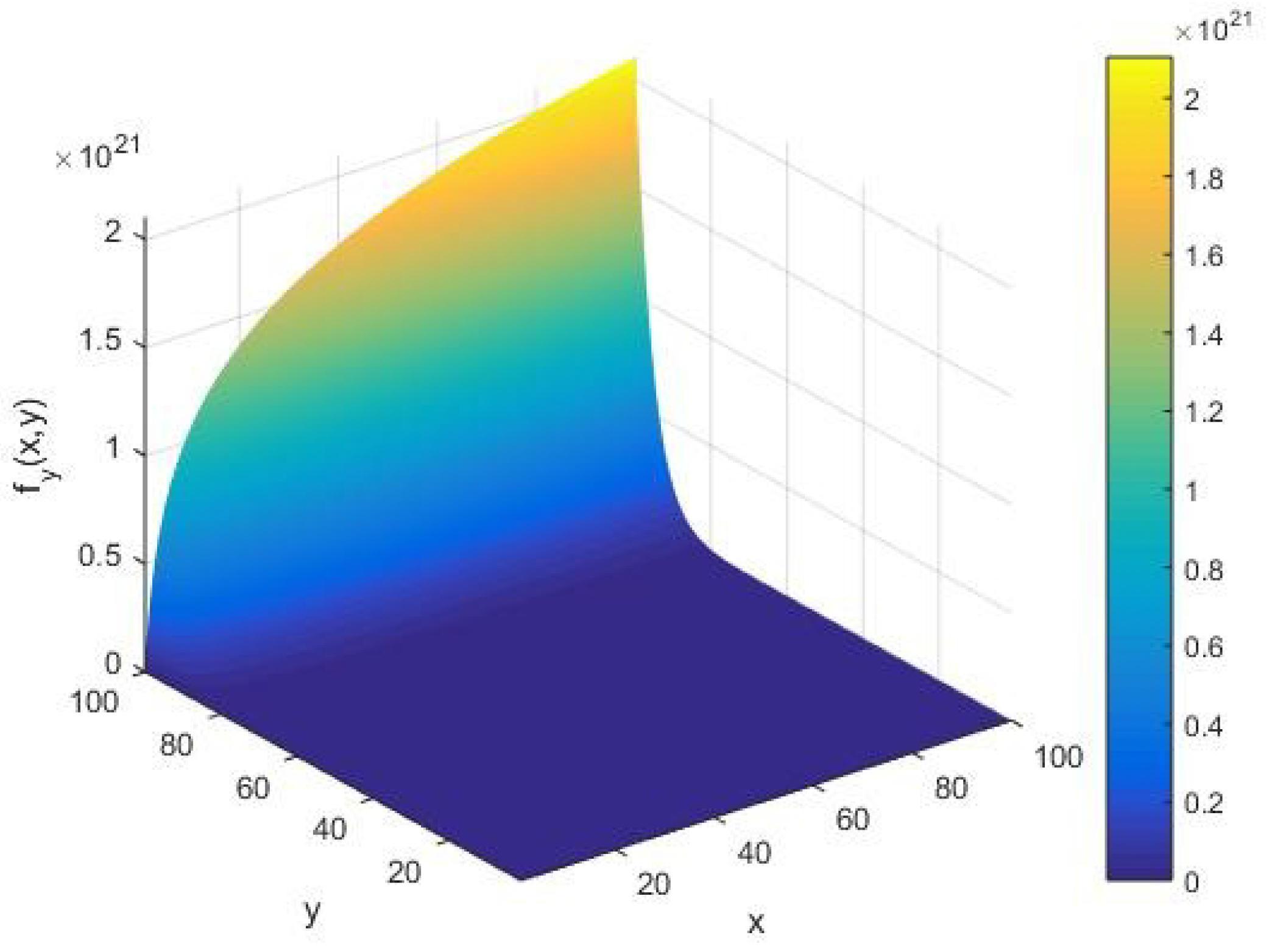
We assess the qualitative behavior of the AKS primality testing rate with respect to the cardinality of the set of alphabets of the machine as in Figure 3. This is realized by varying the first partial derivative of the AKS function with respect to the input parameters , as represented in Equation (3). In this case, we find that there is an increasing arc with respect to the input integer in the limit of a large cardinality of the set of alphabets of the machine. In particular, from Figure 3, we notice that the appearance of arc shifts along the -axis for the rate in contrast to the input integer rate when they vary with respect to the parameters of the algorithm.
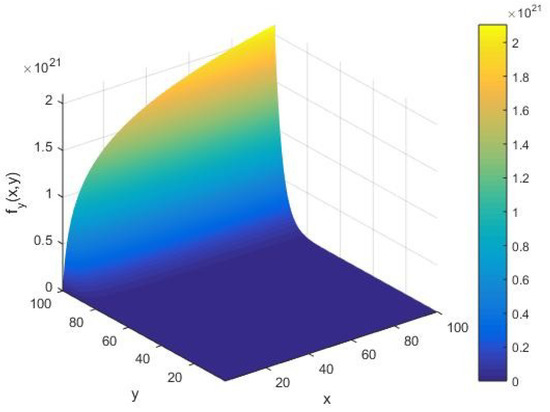
Figure 3.
The rate as a function of the input integer and cardinality of the set of alphabets of the machine executing the AKS algorithm plotted in the range .
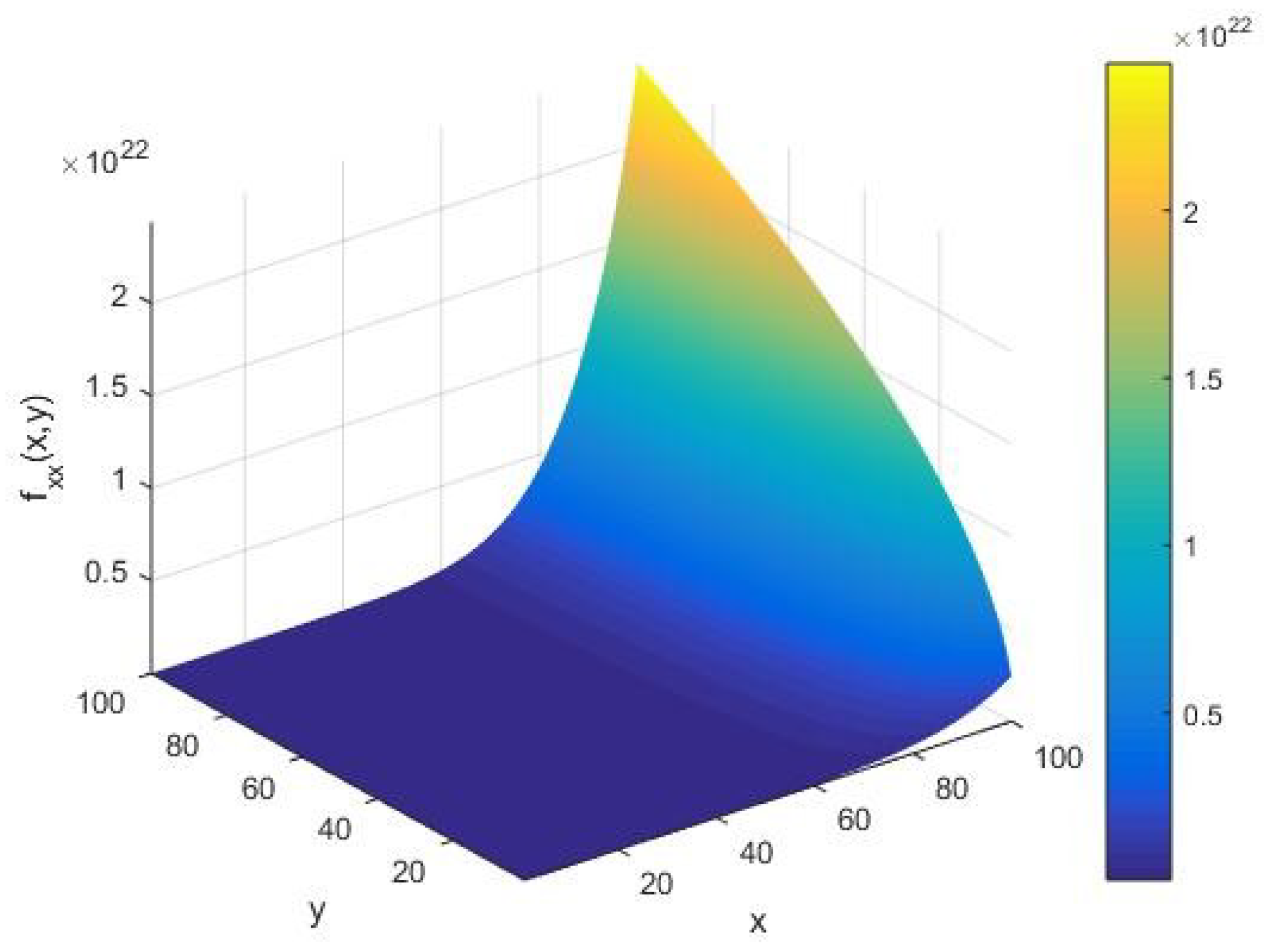
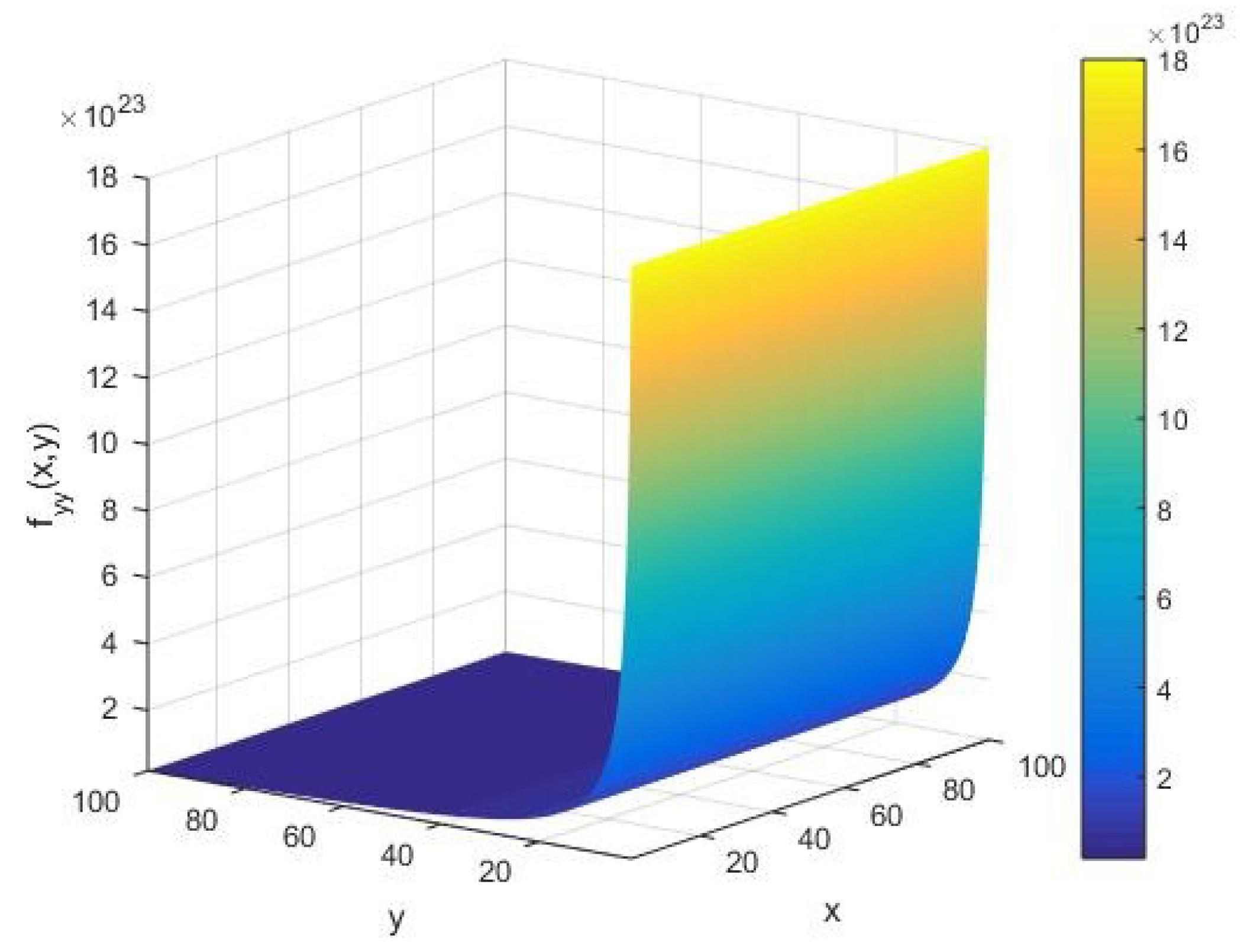
From Figure 4, we find that the local input integer capacity takes the amplitude of the order as vary in the interval (1, 100). For a given input integer , from Figure 4, we see that the input string capacity increases in an arc with respect to the cardinality of the set of alphabets of the machine executing the AKS primality testing algorithm. Furthermore, as increases, we observe that remains constant up to a certain value of ; however, it starts showing a sharply increasing amplitude of the order of at an extreme value of . This implies that the primality testing of an arbitrary integer in its randomized limit possesses a nonzero input string heat capacity for all values of the cardinality of the machine executing the algorithm.
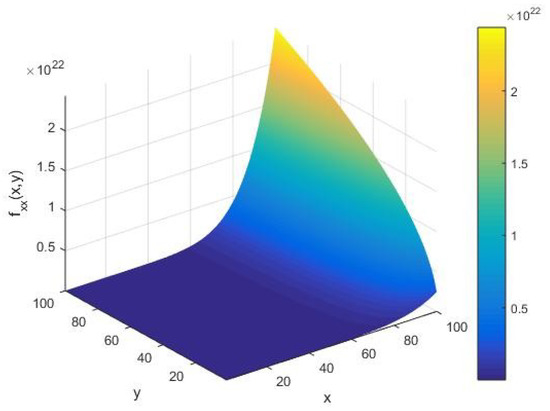
Figure 4.
The input integer capacity as a function of the input integer x and cardinality y of the set of alphabets of the machine executing the AKS algorithm plotted in the range (1, 100).
From Figure 5, we see that the runtime heat capacity has a large amplitude of fluctuations on the order of at an initial stage of the execution. However, as the algorithm proceeds, we find a vanishingly small value of the machine heat capacity , that is, the primality testing of an integer is approximately granted for all values of as in Figure 5. Subsequently, for an arbitrary input integer , we observe that is a well-behaved function of , with an amplitude on the order of in the limit of small .
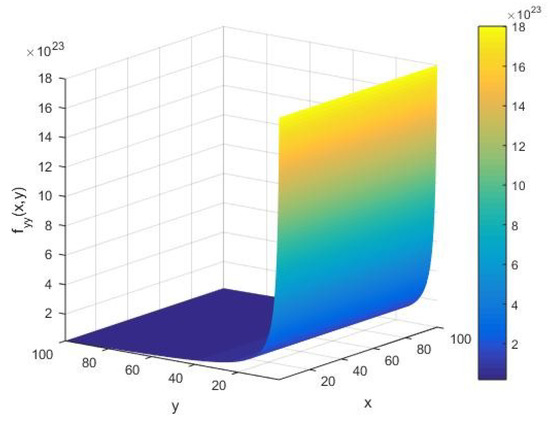
Figure 5.
The local runtime capacity as a function of the input integer x and cardinality y of the set of alphabets of the machine executing the AKS algorithm plotted in the interval (1, 100).
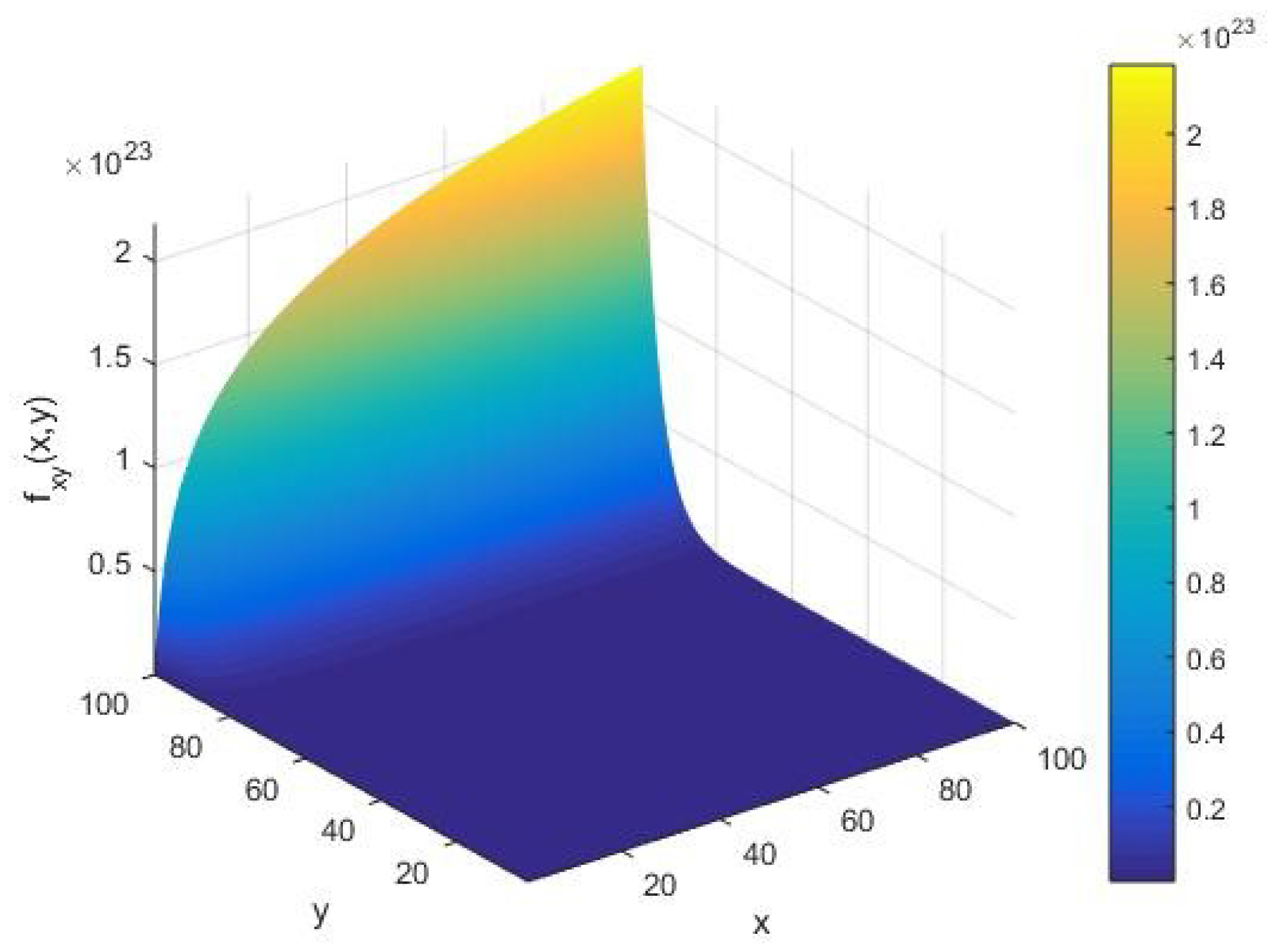
In Figure 6, we show the qualitative behavior of the local correlation underlying the AKS primality testing function under variations of the input integer and cardinality of the set of alphabets of the machine. In this case, apart from the amplitude of fluctuations, we see that possesses an identical character to the execution rate as far as variations in the input integer and execution of the algorithm are concerned. In the limit of a large , we find that modulates with the amplitude on the order of in an increasing arc upon an increase of the input integer whose primality is to be tested. In the course of executing the AKS primality testing algorithm, the above arc shifts along the -axis in contrast to the rate under variations of the system parameters .
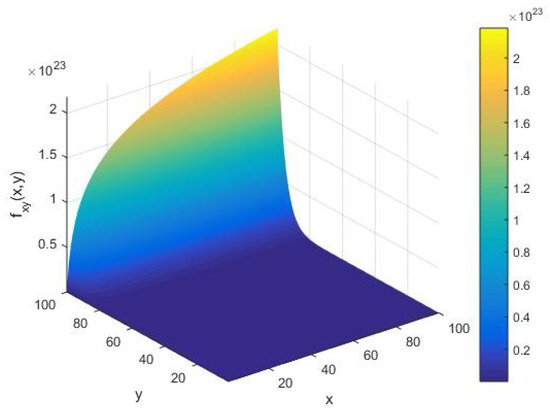
Figure 6.
The correlation as a function of the input integer x and the cardinality y of the set of alphabets of the machine executing the AKS algorithm plotted in the range .
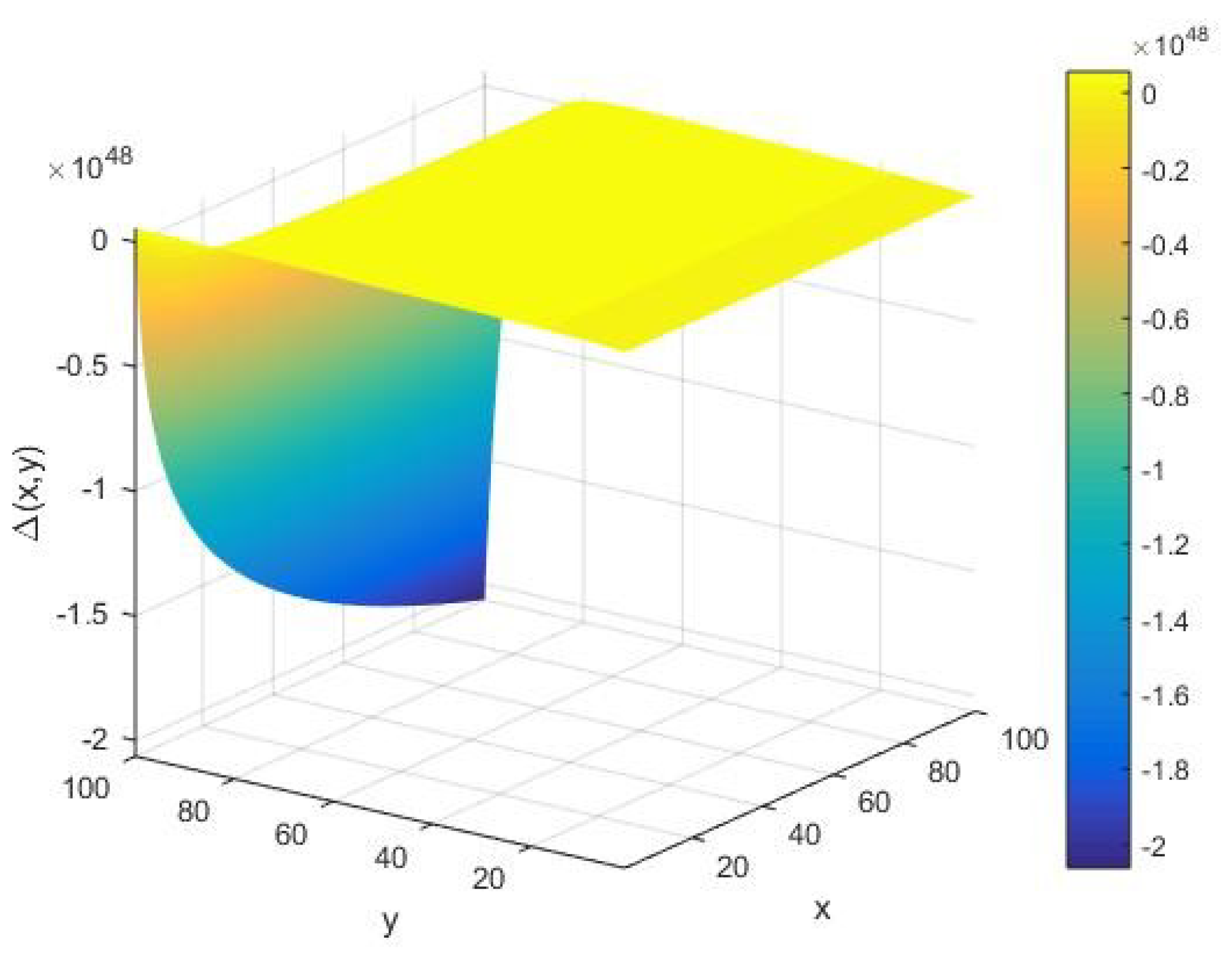
In Figure 7, we provide a qualitative depiction of the global stabilities underlying the AKS primality testing algorithm of an arbitrary integer on a Turing machine of the cardinality of its set of alphabets as the positivity of the determinant as in Equation (7) for . For a given input integer , we see that takes a large negative value with its amplitude of the order in the limit of large cardinality . On the other hand, for relatively smaller values of the system parameters , we find that has vanishingly small fluctuations. This implies that the AKS primality testing could be globally unstable under certain values of . In addition, we find that the above qualitative behavior of remains the same for large values of , e.g., . In this case, the corresponding fluctuations in however grows to a large amplitude of the order .
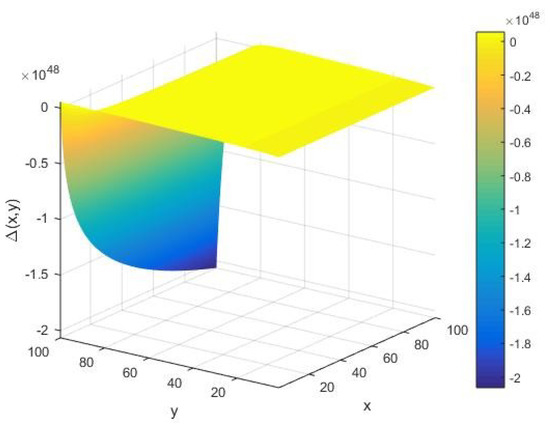
Figure 7.
The determinant of the Hessian matrix as a function of the input integer x and cardinality y of the set of alphabets of the machine executing the AKS algorithm plotted in the interval .
Figure 8 displays the corresponding qualitative behavior of the discriminant defining the eigenvalues as in Equation (23) of the fluctuation matrix of the AKS primality testing function . For all values of the system parameters , we see that the discriminant always remains positive with the amplitude of the order . Furthermore, in an intermediate range of , we find that it has a vanishingly small value. This implies that both the eigenvalues and of the Hessian matrix of take an approximately identical value.
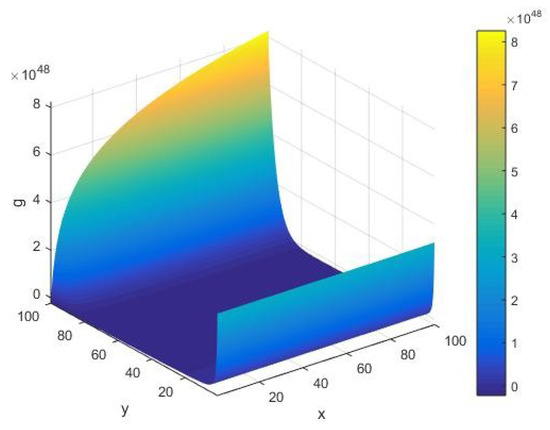
Figure 8.
The discriminant as a function of the input integer and cardinality of the set of alphabets of the machine executing the AKS algorithm plotted in the interval .
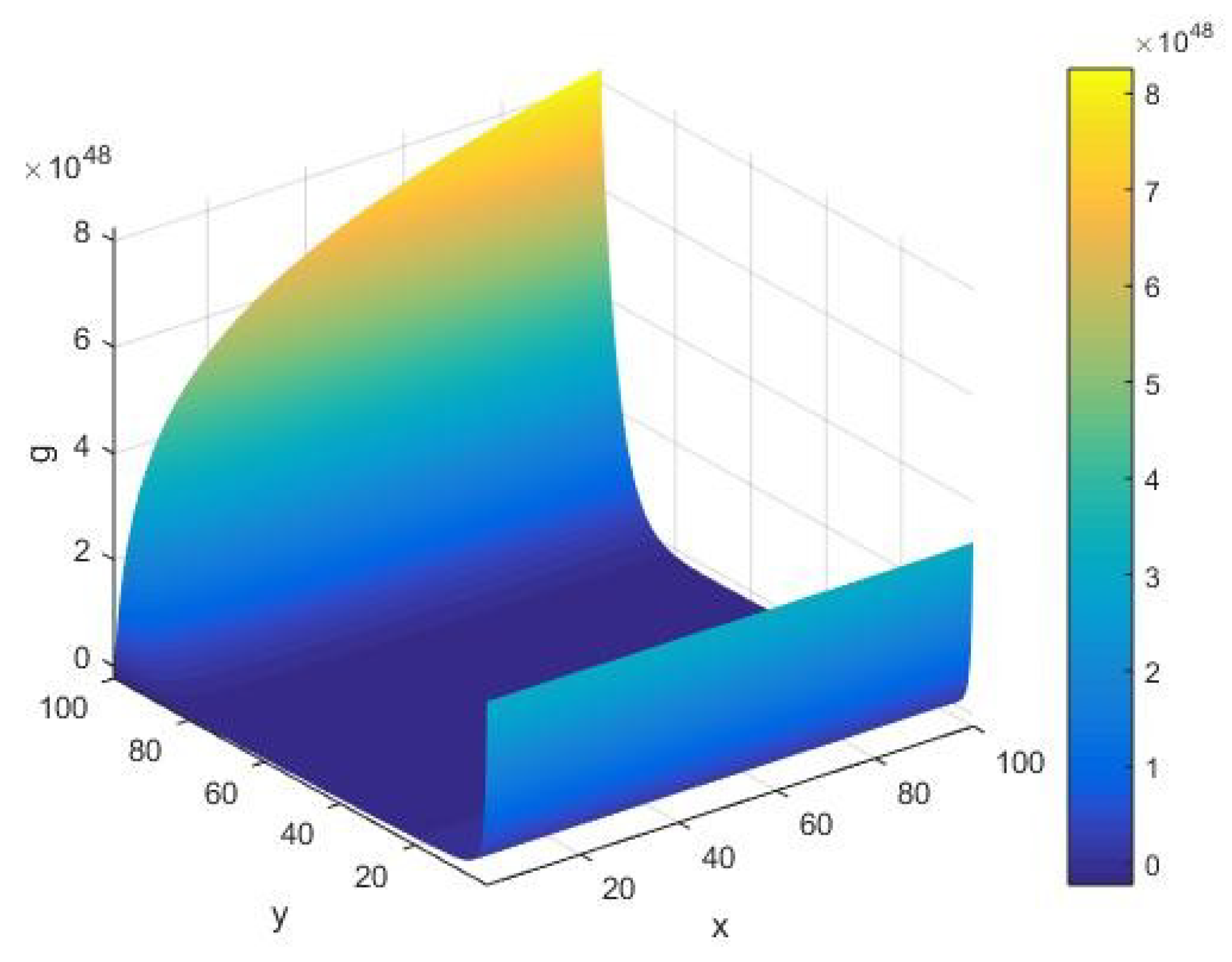
From Figure 9, we see that the eigenvalue , as a global stability component, always remains positive for various values of system parameters . It is observed that grows to large amplitudes of the order at an initial execution of the algorithm. Furthermore, in the limit of small , it follows that the amplitude of fluctuations in takes a relatively higher numerical value than its corresponding value at a large . A smaller value of shows that the AKS primality testing algorithm of an integer gets stabilized upon its execution with increasing values of .
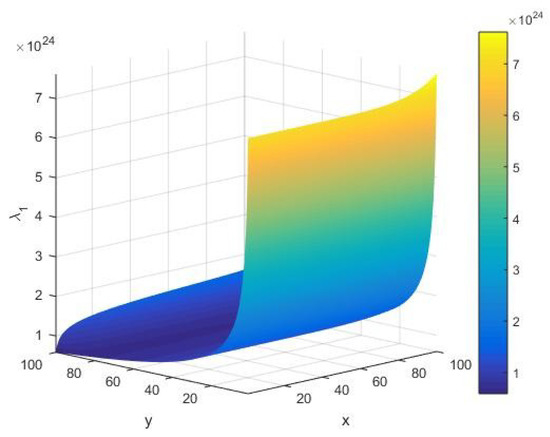
Figure 9.
The eigenvalue of the Hessian matrix as a function of the input integer and cardinality of the set of alphabets of the machine executing the AKS algorithm plotted in the range .
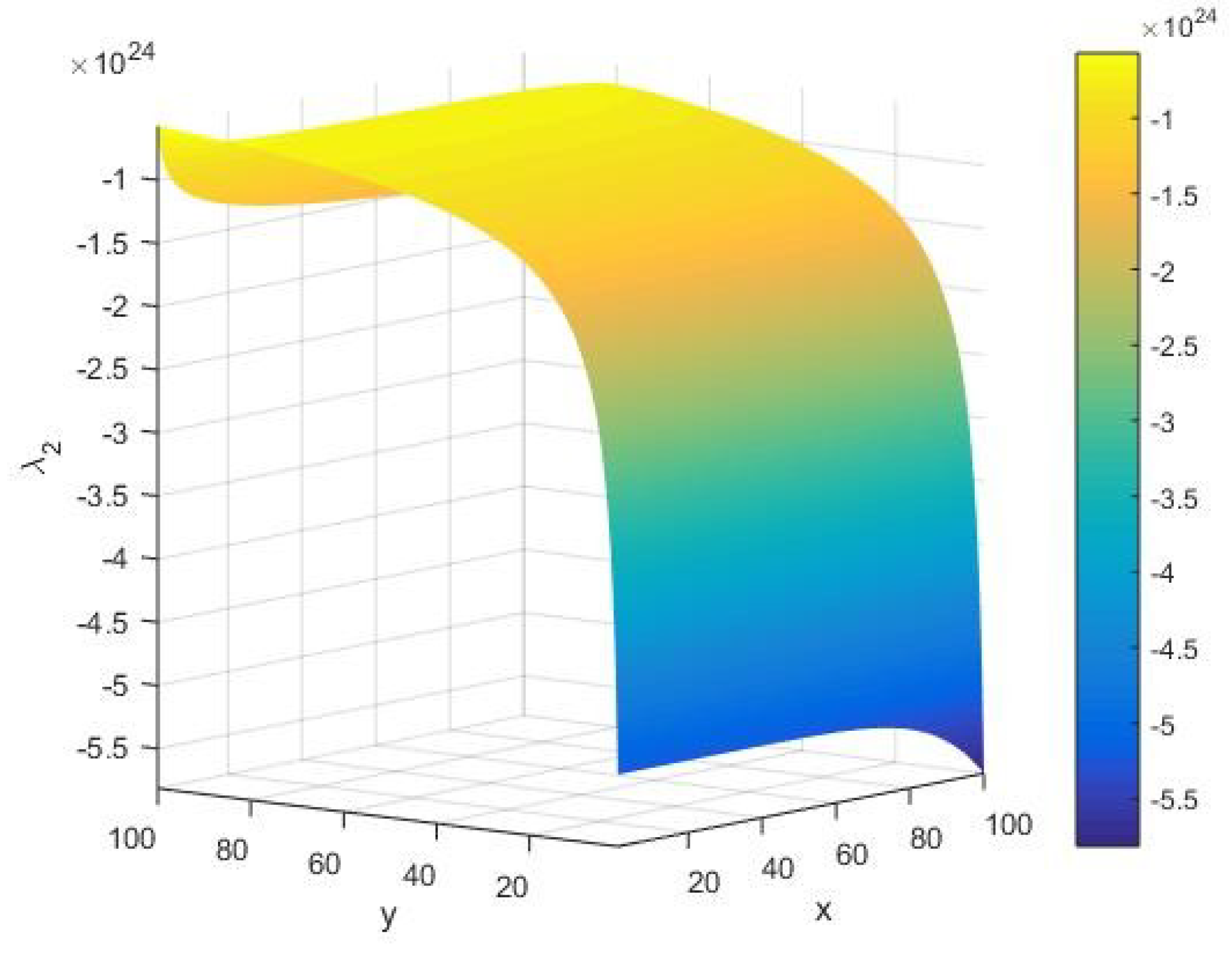
In Figure 10, we display the qualitative behavior of the eigenvalue as the other global stability component under variations of the system parameters . In this case, we find that always takes a large negative value of the amplitude of the order . Namely, in the limit of large and small , we find the signature of possible instabilities in execution of the AKS primality testing algorithm of an integer on a given Turing machine. On the other hand, it is noted that stability rises in the limit of increasing values of . However, towards its extreme values, we see that the stability of the AKS primality testing algorithm increases for an arbitrary input integer and .
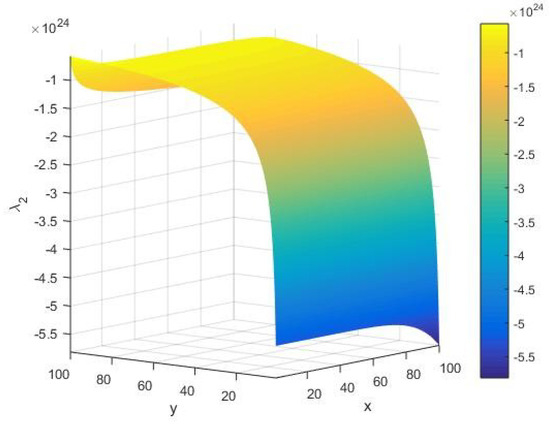
Figure 10.
The eigenvalue of the Hessian matrix as a function of the input integer and cardinality of the set of alphabets of the machine executing the AKS algorithm plotted in the range .
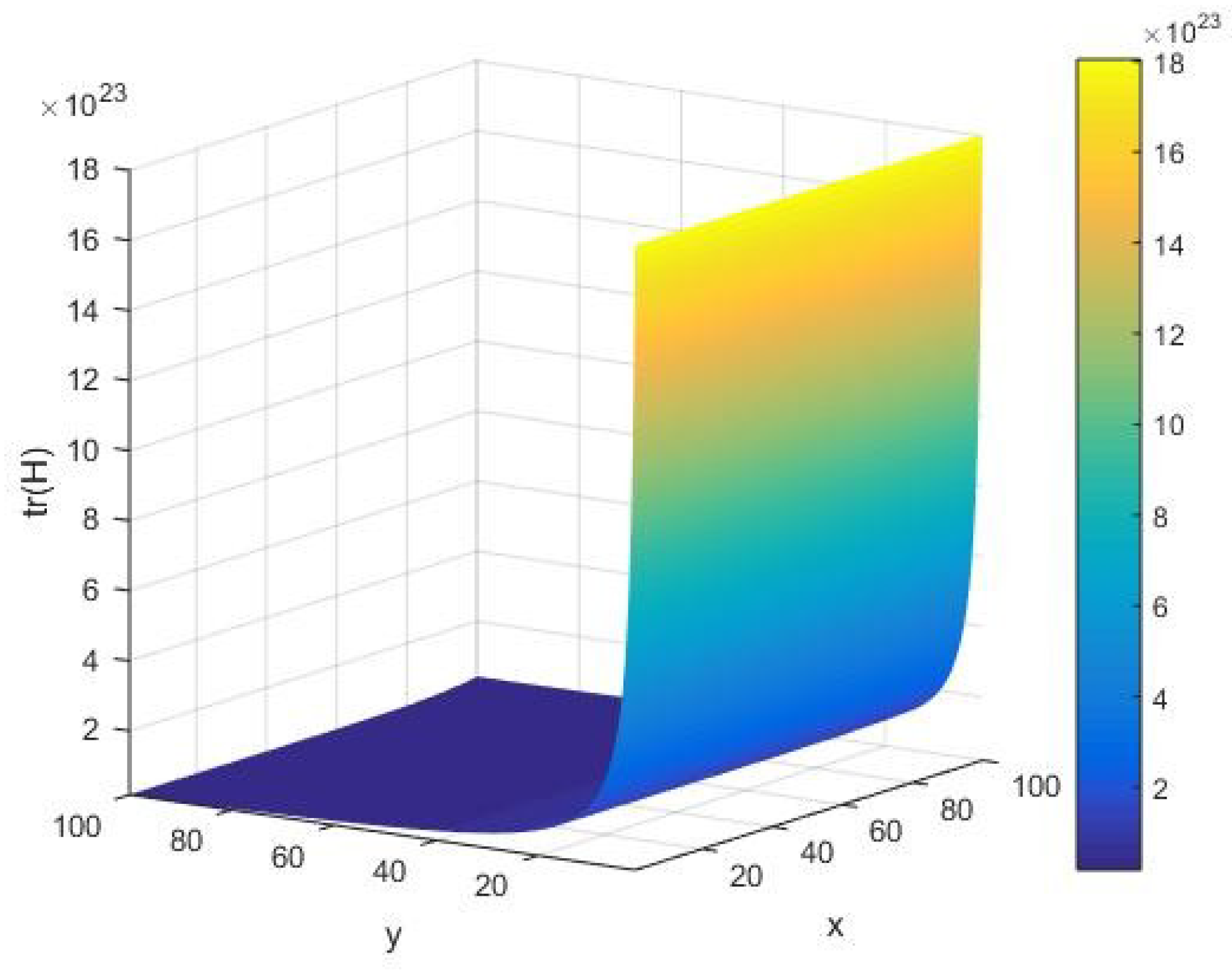
In Figure 11, we offer a qualitative description of the trace of the fluctuation matrix as in Equation (7) under variations of the system parameters . In this case, it follows that has a nonzero value of the amplitude of the order at an initial execution of the algorithm. However, as the algorithm runs, we find that it attains a vanishingly small value in the limit of large The AKS primality testing of an integer is approximately granted, viz. we can determine whether it is prime or not. Furthermore, for a given input integer , it is observed that is a well-behaved decreasing function of . It is worth mentioning that equally has large amplitude of the order of in the limit of a large .
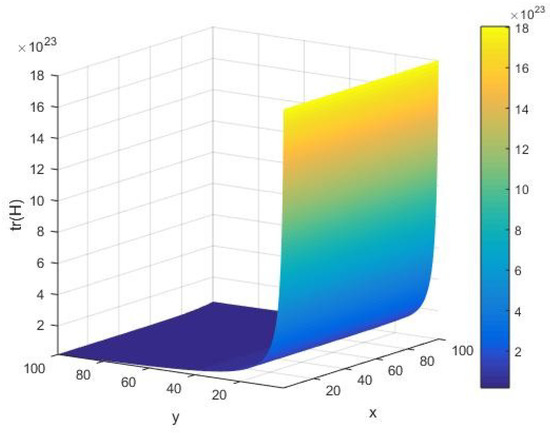
Figure 11.
The trace of the Hessian matrix as a function of the input integer and cardinality y of the set of alphabets of the machine executing the AKS algorithm plotted in the interval .
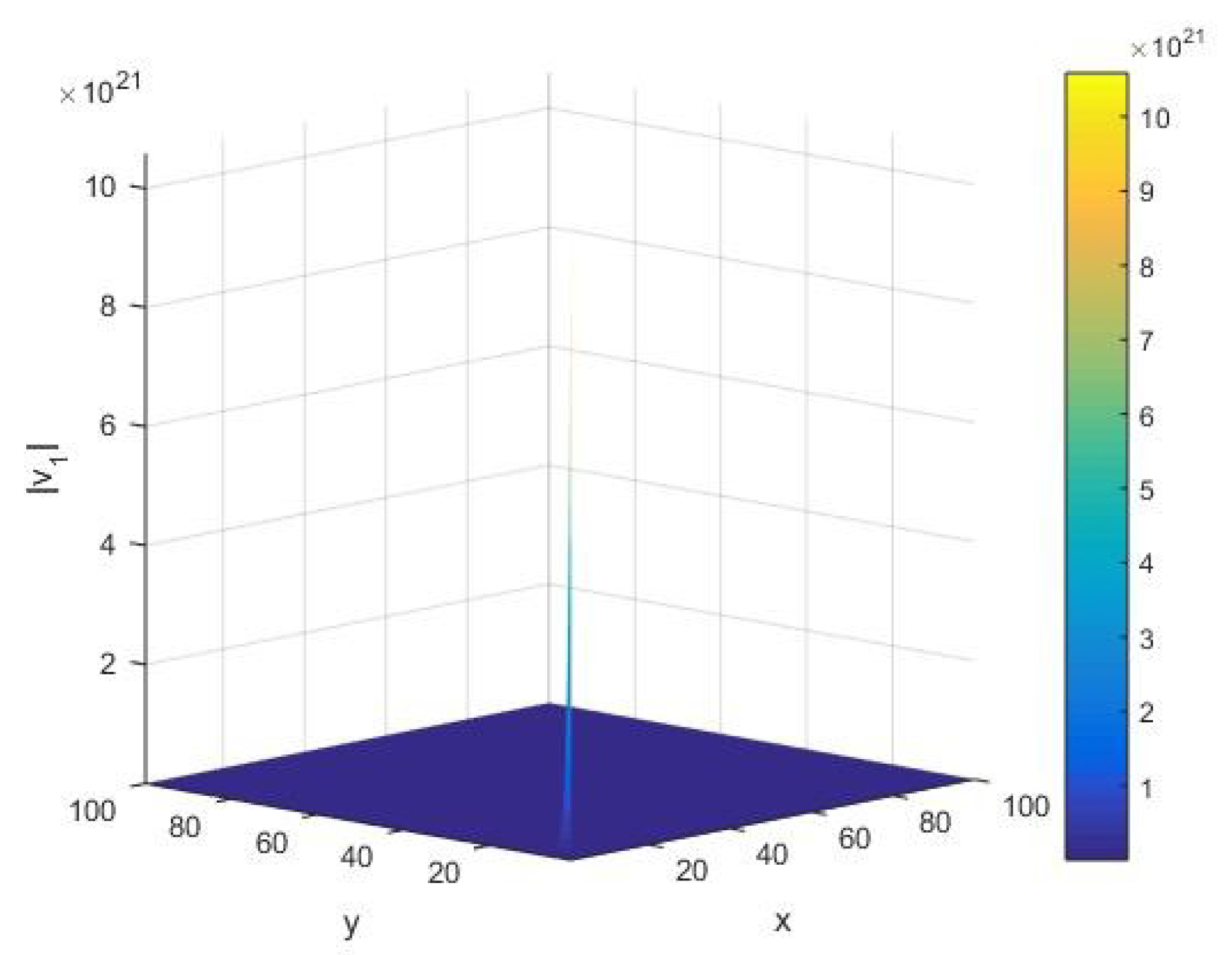
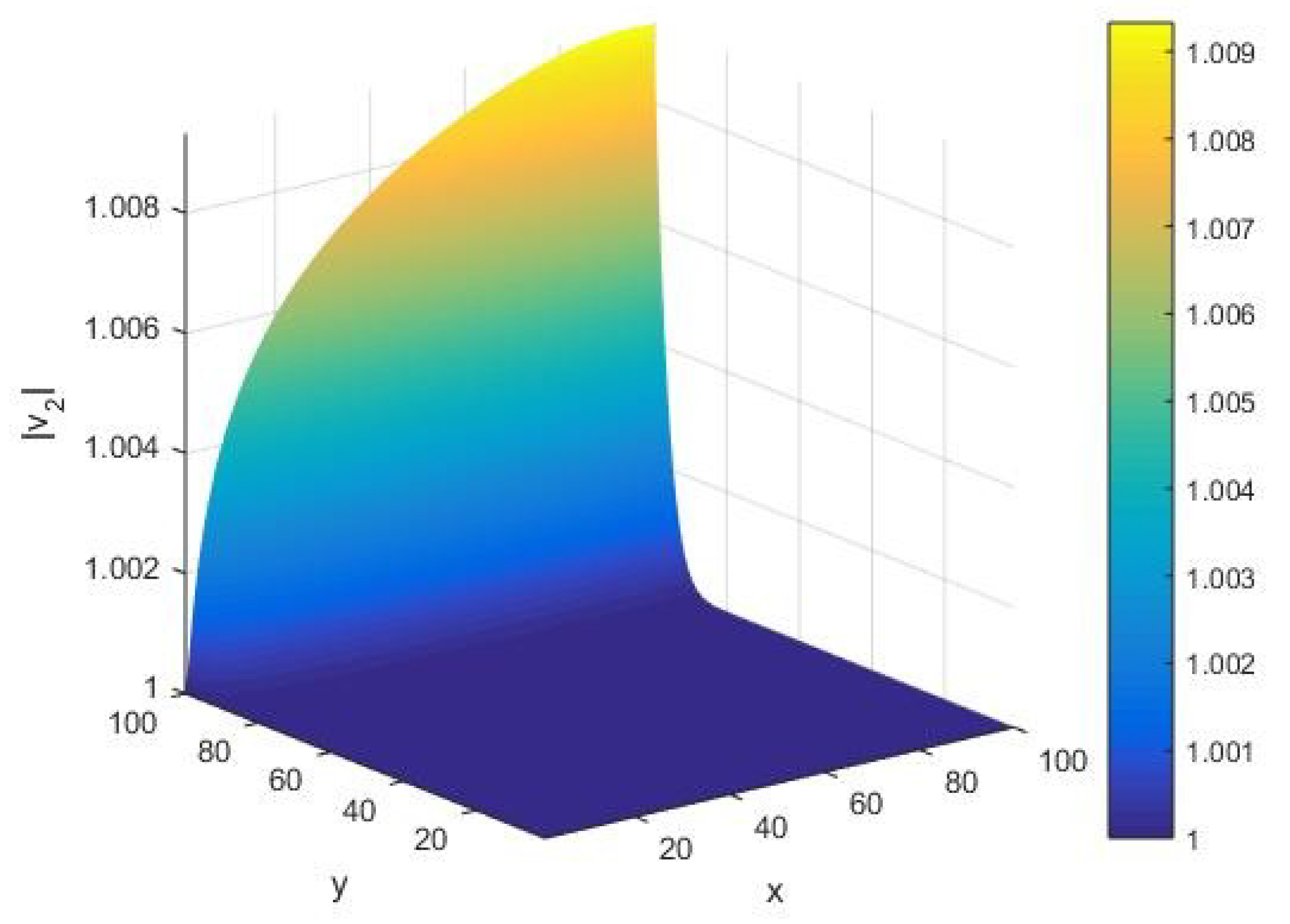
From Figure 12, we see the qualitative behavior of the norm of the fluctuation vector corresponding to the eigenvalue of under variations of the input integer and cardinality of the set of alphabets of the machine. In this case, in the limit of small values of the system parameters , we find that there exists a large peak of the order of . Furthermore, we notice that the AKS primality testing exists smoothly, without variations in the norm of the fluctuation vector for various values of system parameters governing the algorithm.
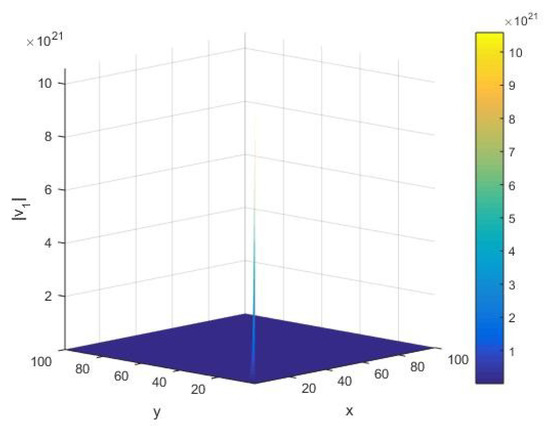
Figure 12.
The norm corresponding to the eigenvalue of the Hessian matrix H as a function of the input integer x and cardinality y of the set of alphabets of the machine executing the AKS algorithm plotted in the interval .
Under variations of the input integer and cardinality y of the set of alphabets of a Turing machine, in Figure 13, we offer the corresponding qualitative behavior of the norm of the fluctuation vector concerning execution of the AKS algorithm. Note that our calculation is performed in their randomized limits. Given a Turing machine with the set of its alphabets of a large cardinality , we find that the norm increases on an arc for increasing values of the input integer . On the other hand, for , we observe that the norm takes a unit value for all input integers whose primality is to be tested by the machine with its set of alphabets of the cardinality . Furthermore, we note that the appearance of an arc in shifts along the x-axis when the input integer is varied with respect to a given machine with the set of its alphabets of the cardinality executing the algorithm.
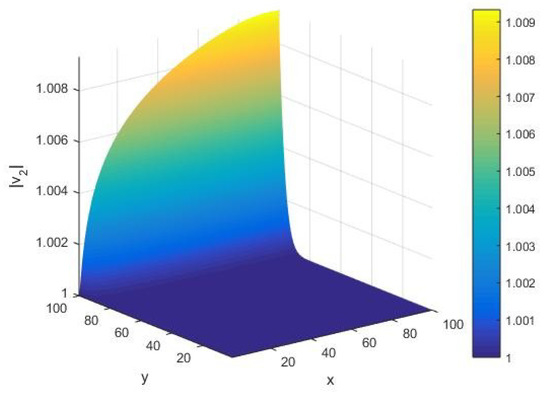
Figure 13.
The norm corresponding to the eigenvalue of the Hessian matrix H as a function of the input integer x and cardinality y of the set of alphabets of the machine executing the AKS algorithm plotted in the interval .
5. Summary and Conclusions
In this paper, we study the AKS primality testing of an integer from the perspective of optimization theory. Namely, by concentrating on the randomization hypothesis, we optimize the AKS algorithm under fluctuations of the input integer and cardinality of the set of alphabets of the machine. We examine the (in)stability domains of the AKS algorithm under variations of input integers in testing their primality. This yields a deterministic finite time polynomial type optimized solution for testing the primality of an arbitrary integer. From the viewpoint of the randomization theory [11], our analysis leads to an optimal system with a pair of system parameters as the input integer and cardinality of the set of alphabets of the machine executing the algorithm. In order to do so, we choose the input integer in a given representation, e.g., a definite sequence of in the binary representation, whereby allowing the positions of the numbers and to vary. As far as the AKS primality testing of an integer is concerned [1], there have been various research articles, books, and monographs in computer science, number theory, complexity theories, and others; see [27] for the complexity and satisfiability theories. Fermat’s little and Chinese remainder theorems play an important role in extending the primality testing of integers from their modular representations to real counterparts.
In particular, we optimize the AKS primality testing algorithm of an arbitrary integer on a Turing machine by determining its stability structures. By invoking the rule of multivariable analysis, we offer the corresponding quantitative and qualitative depictions. Considering the maximum number of irreducible factors of a given integer, as determined by the deterministic polynomial time Turing machine as the AKS objective function, our investigation is realized by randomizing the cardinality of the set of alphabets of the machine and the input integer whose primality is to be tested. As the input integer becomes large, the number of its prime factors also probabilistically grows, whereby we offer an asymptotic stability analysis of the randomized AKS primality testing of an arbitrary integer. Furthermore, this is realized via multidimensional illustrations of the fluctuation components concerning the local and global execution stability of the AKS algorithm. Here, the local heat capacities with respect to the system parameters are defined as the pure second-order derivatives of the AKS primality testing function, whereas the associated correlation between them is taken as its mixed derivative. At the critical point corresponding to a unit input integer, we find that both the heat capacities vanish identically; however, the correlation turns out to be ill-defined. Moreover, we observe that both the heat capacities and the local correlation become ill-defined at the critical point corresponding to the set of alphabets of a large cardinality of the machine, performing a computation of the primality testing of an integer.
On the other hand, given the AKS primality testing function of an integer, the global stability regions are determined by the positivity of the determinant of its fluctuation matrix with a positive fluctuation capacity. We find both stable and unstable regions depending on the value of the input integer and the cardinality of the set of alphabets of the machine. Furthermore, we provide a limiting analysis of the stability components at the roots of the flow components. Indeed, our consideration follows from the randomization hypothesis [11] of an algorithm as well. Our analysis does not stop here, but continues further in the realm of local linear algebra. We investigate the behavior of randomized fluctuation vectors as the basis vectors of the fluctuation matrix. The corresponding fluctuations in their norms provide execution stability characteristics of the AKS primality testing algorithm. In addition, we offer the qualitative behavior of the AKS primality testing function as the objective function, with its flow rates, correlation, and the local and global stability regions revealed through the positivity of the heat capacities and that of the determinant of the fluctuation matrix, respectively. Our analysis confirms that the AKS primality testing falls in the realm of -type problems. By taking up the randomization theory of Agrawal and Biswas [11], this paper gives the parameter space optimization of the AKS algorithm. Namely, we offer the optimization theory perspective of the AKS algorithm under variations of its parameters, viz. the number of alphabets of the input string and the cardinality of the set of alphabets of a machine performing the primality testing. Following this optimization theory initiative of the AKS algorithm, the associated execution time analysis and issues pertaining to the asymptote time complexity, potential extensions towards higher dimensions and comparisons with other primality testing and identity testing models are relegated to separate research publications.
From the perspective of stability theories, it is worth emphasizing that the optimization characteristics of the AKS primality testing are well determined for an arbitrary integer. This enables us to classify the local and global (in)stability domains of the AKS primality testing. Following the above classification, our proposal shows that the determinant has a large amplitude of fluctuations around one of its critical points (see Figure 7). Depending on the signature of the Hessian determinant of the AKS primality testing function as the objective function, we see that there are both concave and convex type domains of the AKS algorithm. Indeed, apart from the field of real numbers, an extension of our analysis is anticipated to be realized by localizing a finite ring of integers to different algebraic sets, e.g., the field of complex numbers, hyper-complex numbers, quaternions, octonions, and higher spin representations in the light of Clifford algebra and octonions [28]. Interesting perspectives are expected to arise via an extension of the input parameters to the set of rational numbers, algebraic sets, and varieties [20,21,22,23]. Industrial applications are sought via complexity classifications of the classical P, NP, coNP, PSPACE, NC, #P type classes and some modern ones such as PO and NPO, arising from the approximations of certain optimization problems [10,29,30] towards the complexity classifications of algorithms and their generalizations. Finally, we anticipate that the corresponding (de)randomization maps [1,11,20,21,22] could play an equally important role in understanding the notion of parametric fluctuations of the AKS algorithm in testing the primality of an arbitrary integer. We leave such investigations open for future research and developments.
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “conceptualization, B.N.T.; methodology, B.N.T., J.K.K. and J.M.A.; software, B.N.T., J.K.K. and J.M.A.; validation, B.N.T., J.K.K. and J.M.A.; formal analysis, B.N.T., J.K.K. and J.M.A.; investigation, B.N.T., J.K.K., J.M.A. and N.M.; resources, B.N.T., J.K.K., J.M.A. and N.M.; data curation, B.N.T., J.K.K. and J.M.A.; writing—original draft preparation, B.N.T., J.K.K. and J.M.A.; writing—review and editing, B.N.T., J.K.K., J.M.A. and N.M.; visualization, B.N.T., J.K.K., J.M.A. and N.M.; supervision, B.N.T. and N.M.; project administration, B.N.T. and N.M.; funding acquisition, B.N.T., J.K.K., J.M.A. and N.M.”.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the Ministries of Education and Science of the Republic of Macedonia and the Istituto Nazionale di Fisica Nucleare, Ministero dell’Istruzione, dell’Università e della Ricerca, Italy for providing a stimulating environment for the realization of this research.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Below, we briefly depict the evolution of the AKS algorithm and its relationships to Fermat’s little theorem and Chinese remaindering. In doing so, we provide a brief account of the evolution of the AKS algorithm of an arbitrary integer. In particular, we give an explicit presentation of the AKS primality testing algorithm and its relation to the randomization hypothesis in light of the ring theories and their localizations as the following.
Appendix A.1. A Brief Account of the Evolution of Primality Testing
Below, among the known facts for primality testing, we review essentials from the theory of numbers, viz. Fermat little theorem, Chinese remainder theorem, Sieve of Eratosthenes, Miller-Rabin test, etc. Scientifically, this provides essential rudiment of related works and insightful background that makes repeated references in the known literature on prime factoring as developed in Section 3. First of all, recall that in order to determine whether the given input number is a prime or not, an efficient primality testing algorithm requires having a polynomial runtime [1]. In general, this is required to possess the unconditional and deterministic properties of the algorithm. It is worth remembering that the Sieve of Eratosthenes [21,22] was the first prime testing algorithm, which may be referred to as an antiquity test of the primality of an integer. Despite it being able to categorize a given input as prime or not, it fell short of having an exponential runtime with its complexity for an input string of size ; see [24] for an overview of the computational complexity and associated concepts in the realm of the analytic number theory.
Fermat’s little theorem [21,22] was an immediate precursor of the former test. The Fermat test played a significant role in the prime determination of a given integral valued input. Despite the fact that it correctly determined the nature of a given input (whether it was a prime or not), it presented some technical difficulties. Namely, it occasionally classified some composite numbers as the primes, as well. Such integers include numbers such as the pseudo-primes, Carmichael primes, Mersenne’s primes, and Cunningham numbers; see [21,22] for details. Thus, Fermat’s test is extended towards the probabilistic primality testing algorithms.
With the above motivations, the Miller‒Rabin test [25], which is founded on the principle of Fermat’s little theorem, unconditionally and probabilistically certifies the prime characterization of a given input, that is, it enables us to know whether a given integer is prime or not. In terms of the runtime complexity, its overall time complexity is of a polynomial type of the order for a given input of size . Here, the factor quantifies the number of bases that are used in the algorithm; see [25] for the randomized Miller‒Rabin test and related notions.
In the course of improving the prime testing algorithms, the Solovay‒Strassen primality [26] encompasses an exciting working principle. This was jointly built as a consequence of Euler’s Criterion and Fermat’s little theorem [21,22]. However, this test presents the probability of failure as , where is the total number of different bases that are used in the primality testing algorithm. Furthermore, the probability of failure makes the overall accuracy of the algorithm similar to that of Fermat testing. In addition, it is worth mentioning that the concerned accuracy in the prime characterization is less than that of the Miller‒Rabin test [25,26]. The time complexity is of the order of , which is closer to that of the Miller‒Rabin test. It is important to note that both the above tests are probabilistic in nature as they rely on the choice of a random base ; see [25,26] for an introduction to the Miller‒Rabin and Solovay‒Strassen primality testing of an integer.
Appendix A.2. The AKS Algorithm: An Overview
The deterministic characteristics of AKS primality testing are bounded as a polynomial runtime algorithm. Namely, in order to define the AKS primality testing of an integer [1], we begin by recalling Fermat’s little theorem [21,22], which may be viewed as the modular equivalence:
It is worth mentioning that the AKS algorithm locally extends as a primality testing of a given polynomial, whether it vanishes identically or not in a ring of local polynomials [1]. In this setup, the AKS algorithm [1] results as the following (generalized Fermat’s little theorem):
It is worth mentioning that the above modular congruence as in Equation (A2) can be verified as a -type problem, whenever is polynomial to the digits of the given input integer . The above localization statement [11] of Fermat little’s theorem emerges from the identity
Thus, the primality testing of an integer can be realized as a modular identity by choosing an integer such that Equation (A3) holds. This follows via the binomial expansion of over . Namely, the coefficients in the binomial expansion of the polynomial
vanish identically over for all . Notice further that the above congruence, as depicted in Equation (A2), can be viewed as a particular equality in the polynomial ring . By evaluating a quotient ring of , one finds an upper bound to the degree of the polynomials . Thus, the AKS primality testing algorithm evaluates the vanishing of in the quotient ring . This results in an explicit dependence of the computational complexity of the algorithm on the size of . Namely, for a given pair of polynomials , the modular equivalence in Equation (A2) can be expressed as the validation of the identity . Consequently, by setting and , it follows that all the primes obeying the congruence relation satisfy the aforementioned equivalence (A3), whenever is a prime.
By localizing as in Equation (A3), for a given integer , we may concentrate on modular valued polynomials ; see [1,11] for associated details. In light of the standard modular equivalence [21,22], the above statement concerning the vanishing of does not hold globally as in the case of the standard Fermat’s little theorem, as depicted above in Equation (A1). This is because lies in the ring , which is strictly allowed to fluctuate over . With a suitable extension as , the localized version of Fermat’s little theorem arises as per the modular equivalence
This justifies the AKS primality testing algorithm of an integer, as stated above in Equation (A2). From the above-localized version of Fermat’s little theorem, we observe that the primality testing of an integer reduces as a convenient way of obtaining the roots of the modular polynomial . Whenever Equation (A5) holds, the input integer results as a prime. Hereby, we can obtain a definite value of and a set of the values of with the properties mentioned in Algorithm 1 in Section 2, such that is a prime whenever the congruence (A2) holds.
Finally, it is worth mentioning that, unlike in the case of the standard Fermat’s little theorem in Equation (A1), when varies over the set of integers, i.e., we have elements forming the ring , we may concentrate on a randomized version of the AKS identity as in Equation (A2) for the primality testing of an arbitrary integer . This can be performed via an extension of the Chinese remaindering in a local ring consisting of a set of finite degree polynomials ; see [1,11] for an extended introduction of the primality and identity testing algorithms.
References
- Agrawal, M.; Kayal, N.; Saxena, N. PRIMES is in P. Ann. Math. 2004, 160, 781–793. [Google Scholar] [CrossRef]
- Savu, L. Cryptography role in information security. In Proceedings of the 5th WSEAS International Conference on Communications and Information Technology (CIT11), Corfu Island, Greece, 14–17 July 2011; pp. 36–41. [Google Scholar]
- Knudsen, L.R.; Matthew, J.B.R. The Block Cipher Companion; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Van Sinderen, M.; Pires, L.F.; Vissers, C.A. Protocol design and implementation using formal methods. Comput. J. 1992, 35, 478–491. [Google Scholar] [CrossRef][Green Version]
- Sharp, R. Principles of Protocol Design; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Clark, K. An Algorithm that Decides PRIMES in Polynomial Time. Available online: https://sites.math.washington.edu/~morrow/336_11/papers/kevin.pdf (accessed on 20 April 2019).
- Cook, S. The P versus NP problem. In The Millennium Prize Problems; Carlson, J., Carlson, J.A., Jaffe, A., Wiles, A., Eds.; Clay Mathematics Institute: Cambridge, MA, USA; American Mathematical Society: Providence, RI, USA, 2006; pp. 87–104. [Google Scholar]
- Fortnow, L.; Homer, S. A Short History of Computational Complexity; Computer Science: Technical Reports, 2003-10-02; Boston University Computer Science Department: Boston, MA, USA, 2003. [Google Scholar]
- Sudan, M. The P vs. NP problem. Available online: http://madhu.seas.harvard.edu/papers/2010/pnp.pdf (accessed on 20 April 2019).
- Creignou, N.; Khanna, S.; Sudan, M. Complexity Classifications of Boolean Constraint Satisfaction Problems; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Agrawal, M.; Biswas, S. Primality and identity testing via Chinese remaindering. J. ACM (JACM) 2003, 50, 429–443. [Google Scholar] [CrossRef]
- Sudan, M. Algebra and Computation, Lecture 12. Available online: http://people.csail.mit.edu/madhu/ST12/scribe/lect12.pdf (accessed on 20 April 2019).
- Kopparty, S. Primality Testing, Lecture 14, Algorithmic Number Theory. Available online: http://www.math.rutgers.edu/~sk1233/courses/ANT-F14/lec14.pdf (accessed on 20 April 2019).
- Hansen, P.B. Primality Testing. Available online: http://surface.syr.edu/eecs_techreports/169/ (accessed on 20 April 2019).
- Smart, N.P. Cryptography: An Introduction, 3rd ed.; Mcgraw-Hill: New York, NY, USA, 2003; pp. 1–22. [Google Scholar]
- Hardy, G.H.; Wright, E.M. Introduction to the Theory of Numbers, 6th ed.; Oxford University Press: Oxford, UK, 2008; pp. 63–72. [Google Scholar]
- Sudan, M. Primality Testing, Lecture 12, Algebra and Computation. Available online: http://people.csail.mit.edu/madhu/ST12/scribe/lect12.pdf (accessed on 20 April 2019).
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1937, 2, 230–265. [Google Scholar] [CrossRef]
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605–659. [Google Scholar] [CrossRef]
- Tiwari, B.N. Geometric perspective of entropy function: Embedding, spectrum and convexity. arXiv 2011, arXiv:1108.4654. [Google Scholar]
- Tiwari, B.N.; Adeegbe, J.M.; Kibindé, J.K. Randomized Cunningham Numbers in Cryptography: Randomization theory, Cryptanalysis, RSA cryptosystem, Primality testing, Cunningham numbers, Optimization theory; LAP LAMBERT Academic Publishing: Riga, Latvia, 2018. [Google Scholar]
- Rosen, K.H. Discrete Mathematics and Its Applications, 7th ed.; McGraw-Hill Pub: New York, NY, USA, 1998; pp. 237–310. [Google Scholar]
- Atiyah, M.F.; MacDonald, I.G. Introduction to Commutative Algebra; Addison-Wesley Series in Mathematics; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Borwein, J.; Borwein, P.B. Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity; Wiley: New York, NY, USA, 1987; p. 6. [Google Scholar]
- Conrad, K. The Miller–Rabin Test. Available online: http://www.math.uconn.edu/~kconrad/blurbs/ugradnumthy/millerrabin.pdf (accessed on 20 April 2019).
- Conrad, K. The Solovay–Strassen Test. Available online: http://www.math.uconn.edu/~kconrad/blurbs/ugradnumthy/solovaystrassen.pdf (accessed on 20 April 2019).
- Impagliazzo, R.; Paturi, R. Exact Complexity and Satisfiability. In Parameterized and Exact Computation, Proceedings of the International Symposium on Parameterized and Exact Computation, IPEC 2013, Sophia Antipolis, France, 4–6 September 2013; Gutin, G., Szeider, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2013; Volume 8246, pp. 1–3. [Google Scholar]
- Baez, J.C. The Octonions. Bull. Amer. Math. Soc. 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Creignou, N.; Schmidt, J.; Thomas, M. Complexity Classifications for Propositional Abduction in Post’s Framework. J. Logic Comput. 2012, 22, 1145–1170. [Google Scholar] [CrossRef]
- Wang, X.Z.; Wang, R.; Xu, C. Discovering the relationship between generalization and uncertainty by incorporating complexity of classification. IEEE Trans. Cybern. 2018, 48, 703–715. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).