CMCC: Misuse Resistant Authenticated Encryption with Minimal Ciphertext Expansion

Abstract

In some wireless environments, minimizing the size of messages is paramount due to the resulting significant energy savings. We present CMCC (CBC-MAC-CTR-CBC), an authenticated encryption scheme with associated data (AEAD) that is also nonce misuse resistant. The main focus for this work is minimizing ciphertext expansion, especially for short messages including plaintext lengths less than the underlying block cipher length (e.g., 16 bytes). For many existing AEAD schemes, a successful forgery leads directly to a loss of confidentiality. For CMCC, changes to the ciphertext randomize the resulting plaintext, thus forgeries do not necessarily result in a loss of confidentiality which allows us to reduce the length of the authentication tag. For protocols that send short messages, our scheme is similar to Synthetic Initialization Vector (SIV) mode for computational overhead but has much smaller expansion. We prove both a misuse resistant authenticated encryption (MRAE) security bound and an authenticated encryption (AE) security bound for CMCC. We also present a variation of CMCC, CWM (CMCC With MAC), which provides a further strengthening of the security bounds.

1. Introduction

The current paradigm of providing confidentiality and integrity protection for distributed applications through the use of encryption combined with MAC’s (Message Authentication Codes) is reasonably efficient for many environments. In particular, for network message sizes that range from several hundred bytes or more, having MAC’s that utilize 8–20 bytes is not unduly inefficient. For resource constrained environments, where message lengths are often less than one-hundred bytes, existing MAC’s impose a more significant overhead. Since it requires more energy to send longer messages, it is important to reduce message sizes in protocols used by wireless devices. This need becomes even more critical for low bandwidth networks.

In this paper we present a new authenticated encryption mode, CMCC. CMCC utilizes a pseudorandom function (PRF) (e.g., AES but other choices are possible). Our construction uses multiple invocations of the PRF so that any modifications to ciphertext result in a randomized plaintext.

CBC-MAC-CTR-CBC (CMCC) mode is a general purpose authenticated encryption mode [1]. We apply CBC (Cipher Block Chaining) encryption in the first round, use a MAC followed by a CTR (Counter) mode in the 2nd round, and CBC encryption again in the 3rd round (see Algorithms 1, 2, and Figure 1). We prove that CMCC is misuse resistant [2]: encryptions using the same message number, plaintext, and associated data are identifiable to the adversary as such, but security is preserved if the same message number is reused where either the plaintext or associated data is distinct. Since changes to the ciphertext randomize the resulting plaintext, with high probability, we achieve authentication by appending a string consisting of $\tau$ bits set to zero to the plaintext prior to encryption. Relative to SIV [2], CMCC has smaller ciphertext expansion.

Figure 1. CMCC Stateless Encryption: $L_4={\overline{L}}_2$.

CMCCv1.0 was originally submitted to the Caesar competition on authenticated encryption. Barwell [3] pointed out a vulnerability in the padding mechanism of CMCCv1.0 which was fixed in CMCCv1.1. This paper presents the CMCC v1.1 algorithm and proves security in the MRAE and AE security models.

We obtain MRAE and AE security with competitive security bounds using only a small number of bytes of ciphertext expansion, for a full range of message sizes.

We will make use of variable length input pseudorandom functions $f_i.$ In order to better understand the intuition behind our scheme, consider the case where the plaintext is the concatenation of the strings $P_1$ and $P_2$ where each string’s length equals the pseudorandom function output size (e.g., 16 bytes in the case of AES). Consider the scheme:

$$\begin{array}{c}\hfill X=f_3(W,P_1)\oplus P_2\\ \hfill X_2=f_2(W,X)\oplus P_1\\ \hfill X_1=f_1(W,X_2)\oplus X\end{array}$$

where the ciphertext is $X_1,X_2,$ and W is an unpredictable pseudorandom value. For maximum security, W is unique, with high probability, for each message encrypted under a given key $K.$ Then if the adversary flips some bits in $X_1,$ the corresponding bits in X are flipped during decryption, and this produces random changes to $P_1$ during decryption (see 2nd equation). The first equation is then applied which results in random changes to $P_2.$ A similar argument applies if we flip one or more bits in $X_2.$ Since changes to any bits in the ciphertext result in random changes to the plaintext, we will see that the authentication tag can be a string of zero bits appended to the plaintext, and that the corresponding term in the security bound, due to this ciphertext expansion, is smaller than in comparable schemes.

1.1. Definitions for Authenticated Encryption (AE)

We give motivation for our definition of authenticated encryption.

Consider OCB [4] or a counter mode variant (e.g., GCM [5]) with a 4 byte authentication tag (NIST guidance on GCM is that at most $2^{11}$ messages, given a maximal packet size of 1024 bytes, should be decrypted given a 4 byte tag). Then for the AE security game (see Section 2.2 for definition), submit the message (plaintext) with all 1’s and also the message with all 0’s. The adversary obtains a ciphertext response corresponding to one of the plaintexts. Then randomly flip bits in this ciphertext for each new ciphertext query and attach a random authentication tag. Then the probability of winning is $q(2^{-32})$. The reason is that this bound is the probability that one of the submitted ciphertexts is valid. If it’s valid then we get the plaintext back which shows us the bits that we flipped. And if the flipped bits are zero, then the original message had all 1’s and vice versa. Now compare this to CMCC with a 4 byte zero bit authentication string. Then our AE security bound is approximately $q(q-1)(2^{-65})$ for a 12 byte message. Thus CMCC has stronger AE security given a short authentication tag. If we run the same attack against CMCC as in the preceding paragraph, then the probability of a valid ciphertext is approximately the same. But the corresponding plaintext would be randomized with high probability and thus would give us no information about the challenge plaintext.

The MRAE–AE definition in [2] does not distinguish between the security levels in the two cases above, but the PRI (Pseudo Random Injection) definition in [2] does distinguish them.

This distinction becomes more important given short authentication tags; in particular, classifying a forgery as a a complete loss of security is not always appropriate. Depending on the application, a single forgery may not be enough to disrupt the application (e.g., VoIP), and depending on the encryption scheme, it may be detectable during higher layer protocol checks. Our security definition should be general enough to handle the case of a valid ciphertext query where changes to the ciphertext randomize the resulting plaintext so that the upper layer protocol checks detect and reject the message. (None of our security bounds include any factor related to upper layer protocol checks.)

Our definition gives the Adversary encryption and decryption oracles (real world) vs. a random injection function and its inverse and asks the Adversary to distinguish between the two (see Section 2). This definition is the same as the PRI definition in [2].

1.2. Applications

For CMCC, we can shorten our MAC tag since the adversary cannot make a predictable change to the encrypted message, as in many counter-mode based schemes. (These other schemes depend on the MAC to detect such a change). A change to a CMCC encrypted message is highly likely to cause the message to be rejected due to a failure to satisfy application protocol checks. Another possibility (e.g., Voice over IP (VoIP)) is that the randomized message will have a minimal effect. With only a small probability can the adversary achieve a successful integrity attack. Since network transmission and reception incurs significant energy utilization, it follows that we can expect to achieve significant energy savings. For wireless sensor networks, energy utilization is proportional to packet length, and the cryptographic computational processing impact on energy use is minor.

If we consider VoIP, a 20 byte payload is common. The transport and network layer headers (IP, UDP, and RTP) bring another 40 bytes, but compression [6,7] is used to reduce these fields down to 2–4 bytes. The link layer headers add another 6 bytes. Thus the total packet size is 30 bytes, assuming the UDP checksum of 2 bytes is included. In this case, by omitting the recommended 10 byte authentication tag and using CMCC with 2 bytes of expansion, we obtain a 1/5 savings in message size and corresponding savings in energy utilization. Furthermore if the encryption boundary is just after the CID field (which is used to identify the full headers), then the UDP checksum is encrypted and acts as an additional 2 byte authentication tag. Even if the adversary was lucky enough to obtain the correct checksum, the resulting Voice payload would be noise, with high probability.

Wireless sensor networks also use short packets [8] to maximize resource utilization; these packets are often in the range of 10–30 bytes. For the adversary, large numbers of queries are likely to be either impossible or highly anomalous in these constrained low bandwidth networks.

1.3. Our Contributions

Our contributions are as follows:

• We give a new family of private key encryption schemes with minimal ciphertext expansion. We obtain AE security with a competitive security bound using only a small number of bytes of ciphertext expansion, for a full range of message sizes. When message numbers are not reused for CMCC, we obtain a security bound which is dominated by $q(q-1)2^{-\tau -1}(1/\beta +2^{-\tau })+2e(q-1)/\beta$ where $\beta =min\{\alpha ,2^B\},$ B is the block cipher block length in bits, and $\alpha =2^{8m}$ where $Len$ is the byte length of the minimal length plaintext query response, $m=\lfloor Len/2\rfloor$ and $\tau$ is the bit length of the authentication tag.
• CMCC is a general purpose misuse resistant authenticated encryption mode. We define security for misuse resistant authenticated encryption and prove a MRAE security bound for CMCC. CMCC has less ciphertext expansion than SIV [2]. In particular, the ciphertext expansion $\tau$ due to the SIV IV contributes a $q(q-1)/2^{\tau }$ term to the SIV security bound, whereas the CMCC ciphertext expansion due to the authentication tag adds a $q(q-1)/2^{2\tau }$ term to the CMCC AE bound, and a $q/2^{\tau }$ term to the CMCC MRAE security bound.
• We present a variant of CMCC, CMCC with MAC, or CWM. CWM replaces the authentication tag consisting of zero bits in CMCC with an authentication tag consisting of a MAC computed over the plaintext in order to obtain a stronger security bound. When message numbers are not reused for CWM, we obtain a security bound which is dominated by $q^2/2^{3\tau }+q^2/(2^{2\tau }\beta )+q/(2^{\tau -1}\beta )$ and if message numbers can be reused then we obtain a bound dominated by $q^2/2^{2\tau +1}+q^3/2^{3\tau +2}+q^2/(2^{2\tau }\beta )+q/(2^{\tau }\beta )+q^2/\beta .$

1.4. Related Work

There was originally work in the IETF IPsec Working Group on a confidentiality-only mode; the original version of ESP provided confidentiality without integrity protection [9]. However, Bellovin [10] showed that CBC and stream-cipher like constructions were vulnerable to attacks that could be prevented with a MAC.

Given a message with redundancy, the idea that authenticity can be obtained by enciphering it with a strong pseudorandom permutation goes back to [11]. The authors formally prove a bound on adversary advantage against authenticity which requires that the probability that an arbitrary string decodes to a valid message is low. In [12], the authors show that public redundancy is not always sufficient and that private (keyed) redundancy leads to stronger authentication properties. Struik [13] presented application requirements and constraints, independently of this work at roughly the same time this work was started.

In [14], Desai gives CCA-secure symmetric encryption algorithms that don’t use a MAC and don’t provide explicit integrity protection outside of the CCA-security. The most efficient one is UFE which utilizes variable length pseudorandom functions. Its ciphertext expansion is $\left|r\right|$ bits where r is a uniform random value; security can be compromised if the same r is used for multiple messages. Since r is uniform random, collisions are likely after $2^{\left|r\right|/2}$ messages. The UFE security bound is $q(q+1)/2^{\left|r\right|}.$ If the adversary can make $2^{20}$ queries, then Theorem 2 gives a security bound around $2^{-57}$ for CMCC with a 6 byte authentication string, given a 14 byte message. UFE would require a 13 byte ciphertext expansion to assure the same security level.

Rogaway and Shrimpton introduced misuse resistant authenticated encryption (MRAE) in the seminal paper [2], where they present the MRAE schemes SIV and PTE. SIV includes a MRAE scheme where the expansion includes the block cipher block size (e.g., 16 byte) IV plus the nonce. Thus CMCC is a MRAE scheme with smaller expansion (which is important for short messages), and comparable security for applications that require less than a 16 byte MAC. The SIV ciphertext expansion adds a $q(q-1)/2^{\tau }$ term to the SIV security bound, while the CMCC ciphertext expansion adds a $q(q-1)/2^{2\tau }$ term to the CMCC AE bound, and a $q/2^{\tau }$ term to the CMCC MRAE security bound. SIV has roughly the same number of block cipher invocations as CMCC (see Table 1). Our security definition is the same as the PRI security definition [2].

Table 1. Number of Block Cipher Calls For CMCC, SIV, and CWM for Varying Message Sizes (CMCC, CWM message sizes include message tag).

Message Length	No. CMCC Prf Calls	No. SIV Prf Calls	No. CWM Prf Calls
1–16 bytes	5	4	6
17–32 bytes	5	6	7
33–48 bytes	9	8	12
49–64 bytes	9	10	13
65–80 bytes	13	12	18
81–96 bytes	13	14	19

CMCC uses the same authentication construction as PTE. However, the TES (Tweakable Enciphering Scheme) that [2] recommends for PTE is not capable of encrypting messages with less than the block size of the underlying block cipher.

Collisions in the IV [2] (or random message number in [14]) will result in loss of privacy for the affected messages. Thus security is increased if the IV is long (e.g., 16 bytes for SIV). In other words, decreasing ciphertext expansion results in less security. Security for our scheme is aided by message length, so privacy is stronger when ciphertext expansion is minimal, given short message lengths. The parameter X in our scheme is similar to the $\sigma$ parameter in [14] and to the IV in [2]. These last two parameters create ciphertext expansion whereas X does not. Our scheme is targeted at environments where minimizing ciphertext expansion is a requirement.

Other fully nonce-misuse resistant schemes include AEZ [15], HS1-SIV [16], Julius [17], MRO [18], HBS [19], BTM [20], and GCM-SIV [21] with the first three being Caesar Authenticated Encryption competitors along with CMCC. Of the above schemes, similarly to CMCC AEZ addresses smaller length messages and minimal ciphertext expansion. The ciphertext expansion, or stretch, is a user controlled parameter that is an input to the encryption function. The AEZ paper does not give a security bound when message length plus stretch is less than 16 bytes. For some message/stretch sizes between 16 and 32 bytes, the CMCC security bounds are stronger. AEZ also makes use of a nonstandard 4 round AES function.

Processing performance for CMCC is similar to SIV, whereas the above schemes are more efficient (for processing but not energy usage) than SIV.

Bock [22] surveys Internet facing https servers and proxies to detect nonce reuse for AES-GCM in TLS. Their study uncovered nonce reuse thus showing the value of nonce-misuse resistance.

Shrimpton and Terashima [23] use a 3 round unbalanced Feistel network approach to obtain schemes TCT1 and TCT2 where the latter has BBB (Beyond Birthday Bound) security for longer messages (messages of length $\ge 2n$ where the underlying blockcipher has length $n.$ Both schemes are STPRP’s (Strong Tweakable PRP’s, e.g., the adversary may reuse tweaks.)

There is recent work to address leakage from unverified plaintexts which is likely to occur when handling large ciphertexts including RUP (Release of Unverified Plaintexts) by Andreeva et al. [24]. Security against RUP was one of the desired security properties listed for the Caesar competition [25]. RUP security is one of the properties of the APE AEAD algorithm [26,27].

Further work with respect to AEAD security definitions include SAE (Barwell et al.) [28], and RAE (Robust Authenticated Encryption) (Hoang et al.) [15]. RIV (Abed et al.) [29] is a scheme based on SIV that is provably secure when releasing unverified plaintexts. Badertscher [30] studies RAE within the constructive cryptography framework of Maurer and Renner [31,32]. Boldyreva [33] models the case where the adversary may receive one of a finite set of decryption failure errors. Earlier work including [34,35] motivates the need for RUP security based on limited memory to hold the decrypted ciphertext or real time requirements for processing encrypted data. Zhang et al. [36] consider the RUP and nonce-misuse security of OCB and propose extensions.

Additional work in the area of small domain encryption includes [37].

1.5. Organization

In Section 2, we give cryptographic definitions. In Section 3, we present CMCC which is an authenticated encryption scheme with minimal ciphertext expansion. Section 4 gives theorems and proofs for the CMCC misuse resistant authenticated encryption (MRAE) and authenticated encryption (AE) security bounds. We also present CWM in this section. In Section 5, we briefly discuss CMCC performance. In Section 6 we draw conclusions.

2. Definitions

2.1. Pseudorandomness

All strings are binary strings (if S is a string, then $S\in {\{0,1\}}^{\ast }$). The concatenation of two strings S and T is denoted by $S\left|\right|T,$ or $S,T$ where there is no danger of confusion. For a string $S,$ $\left|S\right|$ is its length (in bits). If $1\le i\le j\le \left|S\right|,$ then $S[i\dots j]$ is the substring from the $ith$ to the $jth$ characters, inclusive.

We write $w\leftarrow W$ to denote selecting an element w from the set W using the uniform distribution. We write $x\leftarrow f()$ to denote assigning the output of the function f, or algorithm f, to $x.$ $S^C$ denotes the complement of set $S.$

Throughout the paper, the adversary is an algorithm which we denote as $\mathcal{A}.$

We follow [38] as explained in [39] for the definition of a pseudo-random function: Let $l_1$ and $l_2$ be positive integers, and let $\mathcal{F}={\{h_L\}}_{L\in K}$ be a family of keyed functions where each function $h_L$ maps ${\{0,1\}}^{l_1}$ into ${\{0,1\}}^{l_2}.$ Let $H_{l_1,l_2}$ denote the set of functions from ${\{0,1\}}^{l_1}$ to ${\{0,1\}}^{l_2}.$

Given an adversary $\mathcal{A}$ which has oracle access to a function in $H_{l_1,l_2}$ or $\mathcal{F}.$ The adversary will output a bit and attempt to distinguish between a function uniformly randomly selected from $\mathcal{F}$ and a function uniformly randomly selected from $H_{l_1,l_2}.$ We define the PRF-advantage of $\mathcal{A}$ to be

$$Ad{v}_{\mathcal{F}}^{prf}(\mathcal{A})=|Pr[L\leftarrow K:{\mathcal{A}}^{h_L}()=1]-Pr[f\leftarrow H_{l_1,l_2}:{\mathcal{A}}^f()=1]|$$

$$Ad{v}_{\mathcal{F}}^{prf}(q,t)=\underset{\mathcal{A}}{max}\{Ad{v}_{\mathcal{F}}^{prf}(\mathcal{A})\}$$

where the maximum is over adversaries that submit at most q queries and run in time $t.$

Intuitively, $\mathcal{F}$ is pseudo-random if it is hard to distinguish a random function selected from $\mathcal{F}$ from a random function selected from $H_{l_1,l_2}.$

We also define $Ad{v}_{\mathcal{F}}^{prp}(q,t)$ in the same manner where the comparison is with a random permutation and $\mathcal{F}$ is a family of keyed permutations.

2.2. Authenticated Encryption (AE) and Misuse Resistant Authenticated Encryption (MRAE)

Given plaintext (message) set $\mathcal{P},$ associated data set $\mathcal{AD},$ ciphertext set $\mathcal{C},$ key set $\mathcal{K},$ header string set $\mathcal{H},$ and message number set $\mathcal{N}$. An authenticated encryption scheme (AE) is a tuple $\Pi =(\mathcal{K},\mathcal{E},\mathcal{D})$ such that $\mathcal{E}:\mathcal{K}\times \mathcal{H}\times \mathcal{N}\times \mathcal{AD}\times \mathcal{P}\to \mathcal{C},$ $\mathcal{D}:\mathcal{K}\times \mathcal{H}\times \mathcal{N}\times \mathcal{AD}\times \mathcal{C}\to \mathcal{P}\cup \{\perp \},$ and $\mathcal{D}(K,H,N,A,\mathcal{E}(K,H,N,A,P))=P$ for all $H\in \mathcal{H},N\in \mathcal{N},A\in \mathcal{AD},$ $P\in \mathcal{P}.$ If there is no $P\in \mathcal{P}$ such that $C=\mathcal{E}(K,H,N,A,P),$ then $\mathcal{D}(K,H,N,A,C)=\perp .$ We write $D_K$ and $E_K$ in place of $\mathcal{D}(K,\dots )$ and $\mathcal{E}(K,\dots ).$

For our security definition, we define the ideal world object as a random injective function. The expansion function is $e:\mathcal{H}\times \mathcal{N}\times \mathcal{AD}\times \mathcal{P}\to \mathbb{N}.$ The expansion function depends only on the length of its arguments. Let $In{j}_e^{\mathcal{H},\mathcal{N},\mathcal{AD}}(\mathcal{P},\mathcal{C})$ be the set of injective functions f from $\mathcal{H}\times \mathcal{N}\times \mathcal{AD}\times \mathcal{P}$ into $\mathcal{C}$ such that $|f(H,N,A,P)|=\left|P\right|+e(|H|,|N|,|A|,|P|).$

Let $\Pi =(\mathcal{K},\mathcal{E},\mathcal{D})$ be an AE with message space $\mathcal{P}$, associated data set $\mathcal{AD},$ header string set $\mathcal{H},$ message number set $\mathcal{N},$ and expansion $e.$ The AE-advantage of adversary $\mathcal{A}$ against $\Pi$ is

$$\begin{array}{c}{\mathbf{Adv}}_{\Pi }^{AE}(\mathcal{A})=Pr[K\leftarrow \mathcal{K}:{\mathcal{A}}^{{\mathcal{E}}_K(.,.,.){\mathcal{D}}_K(.,.,.)}\Rightarrow 1]-\\ Pr[f\leftarrow In{j}_e^{\mathcal{H},\mathcal{N},\mathcal{AD}}(\mathcal{P},\mathcal{C}):{\mathcal{A}}^{f(.,.,.),f^{-1}(.,.,.)}\Rightarrow 1]\end{array}$$

where encryption oracle queries use unique message numbers. $f^{-1}(H,N,A,C)=P$ if $f(H,N,A,P)=C$ and returns ⊥ if no such tuple $(H,N,A,P)$ exists. We define MRAE-advantage and $Ad{v}_{\Pi }^{MRAE}(\mathcal{A})$ analogously except encryption oracle queries are allowed to repeat message numbers. We also define $Ad{v}_{\Pi }^{AE}(q,t,\mu )=maxAd{v}_{\Pi }^{AE}(\mathcal{A})$ over all adversaries $\mathcal{A}$ that ask at most q queries totaling $\mu$ blocks in time $t.$ We define $Ad{v}_{\Pi }^{MRAE}(q,t,\mu )=maxAd{v}_{\Pi }^{MRAE}(\mathcal{A})$ over all adversaries $\mathcal{A}$ that ask at most q queries totaling $\mu$ blocks in time t for the MRAE environment where message numbers may be repeated in encryption oracle queries. We will also consider the case where the game is restricted if the adversary submits a decryption oracle query which returns $\perp ;$ in this case, the adversary will not be allowed to make additional oracle queries prior to its output. We define $Ad{v}_{\mathcal{E}}^{priv}(\mathcal{A})=|Pr[L\leftarrow K:{\mathcal{A}}^{E_L}()=1]-Pr[{\mathcal{A}}^{\$}=1]|$ for encryption scheme $\mathcal{E}$ with expansion $\tau$ where $ returns a random string with $\tau$ bits plus the input string’s bitlength. We also define $Ad{v}_{\mathcal{E}}^{priv}(q,t,\mu )=maxAd{v}_{\mathcal{E}}^{priv}(\mathcal{A})$ over all adversaries $\mathcal{A}$ that ask q queries totaling $\mu$ blocks in time $t.$ $CT{R}_K(N,P)$ denotes Counter Mode encryption with key $K,$ nonce $N,$ and plaintext $P.$

$Tim{e}_{CTR}(\mu )$ is the sum of the worst case times to select key $K,$ compute $CT{R}_K(IV,P)$ on plaintext P inputs of total length $\mu$, and to compute $CT{R}_K(IV,C)$ on ciphertext C inputs of total length $\mu .$

3. CMCC

We now present CBC-MAC-Counter-CBC (CMCC) mode. CMCC is a general purpose authenticated encryption mode which is misuse resistant and optimized for energy constrained environments.

3.1. Overview

We initially utilize CBC mode and obtain the value $X.$ Here we utilize $E_{\overline{K}}$ to create the CBC IV W from the message number $M.$ This prevents the adversary from being able to manipulate M and $P_1$ in a way that allows collisions in X values to be created. Then we apply a MAC algorithm to $W,X$ and use the result as the IV for counter mode encryption to encrypt $P_1$ and obtain $X_2.$ Note that if the message has length less than or equal to 32 bytes, then the output of the MAC function is xor’d with $P_1$ to obtain $X_2$ and additional counter blocks are not needed. Finally we create the other half of the ciphertext, $X_1$ using CBC mode applied to $X_2$ and exclusive-or with $X.$

Algorithms 1, 2, and Figure 1 describe CMCC.

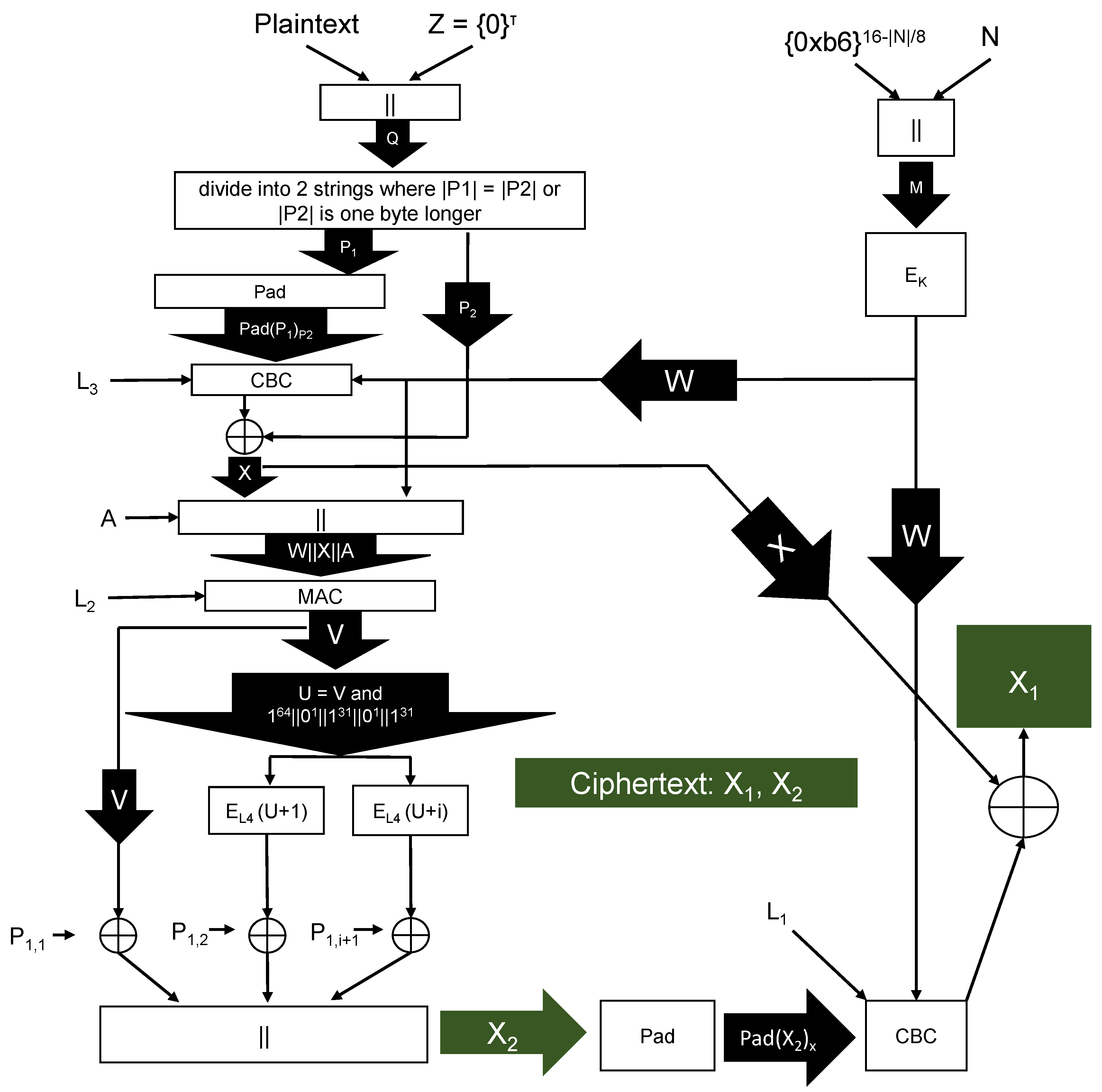
Algorithm 1 CMCC Encryption: Encryption inputs are plaintext $P,$ key $K=\overline{K},L_3,L_2,{\overline{L}}_2,L_1,$ public message number $N,$ and associated data $A.$ $CBC(IV,P,Key)$ is CBC encryption with initialization vector $IV,$ plaintext $P,$ and key $Key.$ A choice for $MAC(P,Key)$ is the CMAC MAC algorithm [40] with plaintext P and key $Key.$ $pad()$ is the padding algorithm defined in Section 3.3. $E_{\overline{K}}$ is the block cipher with key $\overline{K}.$ $\left|P\right|,$ the bitlength of P, is a multiple of 8, as is $\tau .$ U is obtained from V by zeroing bits 31 and 63 to enable faster addition (prevent carries) [41]. $U+j$ is integer addition, $1\le j\le i$. When xor’ing two strings of different length, the longer string is first truncated to the length of the shorter string.

CMCC Encrypt($P,$$\overline{K},L_3,L_2,{\overline{L}}_2,L_1,$$N,$A)   1: $M\leftarrow {(10110110)}^{16-\left|N\right|/8}\left|\right|N$   2: $Z\leftarrow 0^{\tau }$   3: $W\leftarrow E_{\overline{K}}(M)$   4: $Q\leftarrow P\left|\right|Z$   5: $L\leftarrow \left|Q\right|/8$   6: if$L=0mod2$then   7:      $P_1\leftarrow MS{B}_{L/2}(Q)$   8:      $P_2\leftarrow LS{B}_{L/2}(Q)$   9: else 10:      $P_1\leftarrow MS{B}_{(L-1)/2}(Q)$ 11:      $P_2\leftarrow LS{B}_{(L+1)/2}(Q)$ 12: end if 13: $X\leftarrow CBC(W,pad{(P_1)}_{P_2},L_3)\oplus P_2$ 14: $Y\leftarrow X\left|\right|A$ 15: $V\leftarrow MAC(W||Y,L_2)$ 16: $i\leftarrow \lfloor \left|P_1\right|/B\rfloor$ 17: $P_1={\overline{P}}_{1,1}\left|\right|\dots \left|\right|{\overline{P}}_{1,i}\left|\right|{\overline{P}}_{1,i+1}$ where $|{\overline{P}}_{1,1}|=\dots =|{\overline{P}}_{1,i}|=B$ and $|{\overline{P}}_{1,i+1}|=|P_1|modB.$ 18: $U\leftarrow Vand(1^{64}|\left|0^1\right|\left|1^{31}\right|\left|0^1\right||1^{31})$ 19: $X_2\leftarrow V\oplus {\overline{P}}_{1,1}\left|\right|E_{{\overline{L}}_2}(U+1)\oplus {\overline{P}}_{1,2}\left|\right|\dots \left|\right|E_{{\overline{L}}_2}(U+i)\oplus {\overline{P}}_{1,i+1}$ 20: $X_1\leftarrow CBC(W,pad{(X_2)}_X,L_1)\oplus X$

Algorithm 2 CMCC Decryption: Decryption inputs are ciphertext $X_1{X}_2,$ key $K=\overline{K},L_3,L_2,{\overline{L}}_2,L_1,$ public message number $N,$ and associated data $A.$

CMCC Decrypt($X_1,X_2,$$\overline{K},L_3,L_2,{\overline{L}}_2,L_1,$$N,$A)   1: $M\leftarrow {(10110110)}^{16-\left|N\right|/8}\left|\right|N$   2: $Z\leftarrow 0^{\tau }$   3: $W\leftarrow E_{\overline{K}}(M)$   4: $X\leftarrow CBC(W,pad{(X_2)}_{X_1},L_1)\oplus X_1$   5: $Y\leftarrow X\left|\right|A$   6: $V\leftarrow MAC(W||Y,L_2)$   7: $i\leftarrow \lfloor \left|X_2\right|/B\rfloor$   8: $X_2={\overline{X}}_{2,1}\left|\right|\dots \left|\right|{\overline{X}}_{2,i}\left|\right|{\overline{X}}_{2,i+1}$ where $|{\overline{X}}_{2,1}|=\dots =|{\overline{X}}_{2,i}|=B$ and $|{\overline{X}}_{2,i+1}|=|X_2|modB.$   9: $U\leftarrow Vand(1^{64}|\left|0^1\right|\left|1^{31}\right|\left|0^1\right||1^{31})$ 10: $P_1\leftarrow V\oplus {\overline{X}}_{2,1}\left|\right|E_{{\overline{L}}_2}(U+1)\oplus {\overline{X}}_{2,2}\left|\right|\dots \left|\right|E_{{\overline{L}}_2}(U+i)\oplus {\overline{X}}_{2,i+1}$ 11: $P_2\leftarrow CBC(W,pad{(P_1)}_X,L_3)\oplus X$ 12: $Q=P_1\left|\right|P_2,$ 13: $U=LS{B}_{\tau /8}(Q)$ 14: if$(U!=Z)$then 15:      return ⊥ 16: else 17:      $Q=\tilde{P}\left|\right|Z$ 18:   return Plaintext $\tilde{P}$ 19: end if

3.2. Notation

We use ⊕ to denote bitwise xor. When we xor two strings with different lengths, the longer string is first truncated to the length of the shorter string. $b^j$ is the bit b repeated j times. $S^j$ denotes the bit string S repeated j times. Thus ${(0110)}^2=01100110.$ $AandB$ is the logical AND operation on two equal length strings A and B. The notation $R_{128}=0^{120}10000111$ denotes the bit string with 120 zero bits, followed by the bits 1,0,0,0,0,1,1, and 1. $x<<n$ denotes the left shift operator (filling vacated bits with zero bits), after shifting the string x by n bits to the left. B denotes the block length of the underlying block cipher (128 bits for AES). $E_k$ denotes encryption using the block cipher and input key $k.$

$LS{B}_j(x)$ and $MS{B}_j(x)$ denote the j least significant bytes and j most significant bytes of byte string x respectively.

3.3. Padding (Definition of Pad Function)

We will apply the padding scheme from the AES-CMAC algorithm to our mode when CBC encryption is performed. One difference is that we will sometimes need to pad by a full block length ($B/8$ bytes). (If $S_1$ is a multiple of B and $S_2$ is one byte longer, than we pad $S_1$ with $B/8$ bytes. If both strings are the same length which is a multiple of B then we do not add any padding bytes.)

• Given the CBC encryption key $K,$ and byte strings $S_1$ and $S_2,$ where $|S_1|\le |S_2|.$ We define $pad{(S_1)}_{S_2}$ as follows:
• $pad\_length$ is the number of bits (which is a multiple of 8) needed to bring $S_1$ up to the length of $S_2$ and then bring $S_1$ up to a multiple of the block size. More formally,

  $$pad\_length=|S_2|-|S_1|+B-(|S_2|modB)$$

  where mod values are taken between 1 and $B.$
• We define $L=E_K(0^B).$ If the most significant bit of L is zero, then define $K1=L<<1,$ otherwise, we define $K1=(L<<1)\oplus R_{128}.$ If the most significant bit of $K1$ is zero, then define $K2=K1<<1.$ Otherwise, we define $K2=(K1<<1)\oplus R_{128}.$
  If $pad\_length=0,$ then $|S_1|$ is a multiple of $B;$ let L be the last block of $S_1:$ $S_1=F\left|\right|L.$ Then $pad{(S_1)}_{S_2}=F\left|\right|(L\oplus K1).$
  If $8\le pad\_length\le B,$ then we append the following string to $S_1:{10}^{pad\_length-1}:$ $\overline{S_1}=S_1\left|\right|{10}^{pad\_length-1}.$ Let $\overline{S_1}=F\left|\right|L$ where L has B bits. Then $pad{(S_1)}_{S_2}=F\left|\right|(L\oplus K2).$

4. Proof of Security

We first give some examples illustrating attacks against CMCC. We will then prove a MRAE security bound for CMCC (see Theorem 1). A key point is that ciphertext queries that do not return invalid can be used to create new plaintexts that satisfy a relation (see examples below) that is less likely to be satisfied given a random injection. Of course the MRAE security bound is also an AE security bound for CMCC, but we prove a smaller AE security bound in Theorem 2.

To give more insight into the best attacks and security properties of CMCC, we utilize the following examples.

Example 1.

Without the encoding step (for the zero bit authentication tag), CMCC is not MRAE secure (the adversary advantage is large in the MRAE security game). To illustrate this fact, the adversary submits a plaintext query followed by a ciphertext query using the same message number M and value $X_2.$ Both queries are twice the block length of the underlying block cipher. The adversary can compute $X_1\oplus {\overline{X}}_1=X\oplus \overline{X}.$ The adversary then creates two new plaintexts by modifying both $P_2$ and ${\overline{P}}_2$ so that the two corresponding ciphertexts have equal X values. Note that the two plaintexts have distinct $P_1$ values ($P_{11}$ and $P_{12}$). The adversary submits both plaintexts along with the message number M and receives the two ciphertexts whose $X_2$ values xor to $P_{11}\oplus P_{12}.$ This relation is only satisfied with probability $1/\alpha$ for a random injection and thus the adversary advantage is large.

Example 2.

Given a collision of X values for two plaintext queries in the MRAE security game (message numbers may be reused). Then the adversary can modify the respective $P_2$ values to create two new plaintexts such that the corresponding ciphertexts have equal X values. Then the adversary can win with high probability as in the preceding example. This attack works even if the zero bit authentication tag is being used. Thus $q(q-1)/2\alpha$ will be part of the security bound for CMCC MRAE security.

Lemma 1.

([2]—Theorems 2 and 7) SIV has MRAE security bound

$$Ad{v}_{SIV}^{MRAE}(q,t,\mu )\le Ad{v}_{CMAC}^{prf}(q,\acute{t})+Ad{v}_{CTR}^{priv}(q,\acute{t},\mu )+5q/2^B+q^2/2^{B+9}$$

where $\acute{t}=t+c\mu +Tim{e}_{CTR}(\mu )$ and c is a constant.

Lemma 2.

Consider the following generalization of the SIV [2] algorithm, SIV-G: We include a distinguished string T as part of the header $H.$ We replace the plaintext P in the PRF calculation with $f(P,T)$ where f is an injective function (thus $f(P,T)=f(\overline{P},\overline{T})$ implies $P=\overline{P}$ and $T=\overline{T}.$) See Algorithms 3 and 4. The security bound for SIV-G is unchanged from SIV: SIV-G has MRAE security bound

$$Ad{v}_{SIV-G}^{MRAE}(q,t,\mu )\le Ad{v}_{CMAC}^{prf}(q,\acute{t})+Ad{v}_{CTR}^{priv}(q,\acute{t},\mu )+5q/2^B+q^2/2^{B+9}.$$

where $\acute{t}=t+c\mu +Tim{e}_{CTR}(\mu )$ and c is a constant.

Algorithm 3 SIV-G Encryption: Encryption inputs are header $H=T,$ nonce $N,$ associated data $A,$ and plaintext $P.$

SIV-G Encrypt$E_{L_2,{\overline{L}}_2}(H,N,A,P)$ 1: $X\leftarrow f(P,T)$ 2: $IV\leftarrow CMA{C}_{L_2}(N|\left|X\right||A)$ 3: $C\leftarrow CT{R}_{{\overline{L}}_2}(IV,P)$ 4: return$Y=IV\left|\right|C$

Algorithm 4 SIV-G Decryption: Decryption inputs are header $H=T,$ nonce $N,$ associated data $A,$ and Y.

SIV-G Decrypt$D_{L_2,{\overline{L}}_2}(H,N,A,Y)$   1: if$\left|Y\right|<B$then   2:   return⊥   3: else   4:   $IV\leftarrow Y[1\dots B]$   5:   $C\leftarrow [B+1\dots |Y|]$   6:   $P\leftarrow CT{R}_{{\overline{L}}_2}(IV,C)$   7:   $X\leftarrow f(P,T)$   8:   $I{V}_2\leftarrow CMA{C}_{L_2}(N|\left|X\right||A)$   9:   if $IV=I{V}_2$ then 10:   return P 11:   else 12:   return⊥ 13:   end if 14: end if

Theorem 1.

Let $b_i=$ number of bytes in ith query response, $1\le i\le q$. Let $\mu ={\sum }_{i=1}^q\lceil b_i/32\rceil .$ B is the cipher block length. Let $\beta =min\{\alpha ,2^B\}.$ Let the CMCC MAC function be CMAC [40]. Let s be the maximum number of CMAC blocks in a query; $c_1$ is a constant. CMCC is a misuse resistant authenticated encryption scheme with MRAE-advantage bounded by

$$\begin{array}{c}q(q-1)/\beta +1-{(1-1/\beta -2^{-\tau })}^x+(5s^2+1)q^2/2^B+\\ Ad{v}_E^{prp}(sq+1,t+c_{1}sq+Tim{e}_{CTR}(\mu ))+Ad{v}_E^{prp}(sq,t)+sq(sq-1)/2^{B+1}+\mu (\mu -1)/2^{B+1}+\\ Ad{v}_{CTR}^{priv}(q,\acute{t},\mu )+5q/2^B+q^2/2^{B+9}+3q(q-1)/2^{B+1}+Ad{v}_E^{prp}(q,t)\end{array}$$

given that the adversary is restricted to q queries and t time, E is the underlying block cipher for CMAC (e.g., AES), $\alpha =2^{8m}$ where $Len$ is the byte length of the minimal length plaintext query response, $m=\lfloor Len/2\rfloor ,$ assuming up to x invalid ciphertexts do not result in session termination, and τ is the number of bits in the authentication tag. We also assume $q-1\le 2^{\tau }.$

Remark 1.

Intuitively, there are two types of relations that distinguish CMCC from a random injection:

• For messages where $\left|\alpha \right|$ is shorter than the block length, and $M=\overline{M},$ we have the relation $X_2\oplus {\overline{X}}_2=P_1\oplus {\overline{P}}_1$ with higher probability equal to $1/\alpha +(\alpha -1)/{\alpha }^2$ for CMCC versus $1/\alpha$ for the random injection. The reason is that we may have a collision of X values with probability $1/\alpha$ and if that does not occur, the resulting V values may still be equal in the first ${log}_2(\alpha )$ bits.
• If $M=\overline{M},$ $X_2={\overline{X}}_2,$ and $P_1={\overline{P}}_1,$ then $X_1\oplus {\overline{X}}_1=P_2\oplus {\overline{P}}_2.$ The latter occurs with probability $1/\beta$ for CMCC but it occurs with probability $1/{\beta }^2$ for a random injection.

Proof. 

Case I: All plaintexts have length $\le 2\ast B+8-\tau$ bits: We use a games based proof to establish the bound claim for the theorem. Game $G_0$ is depicted in Algorithm 5. Game $G_0$ gives the adversary the CMCC encryption and decryption oracles and the adversary’s probability of success is equal to the adversary’s MRAE-advantage against CMCC.

Algorithm 5 CMCC MRAE proof Game G0.

Initialize: Select the CMCC key, using the uniform random distribution. Let Z be the bit string with $\tau$ zero bits. $ba{d}_4=ba{d}_5=false.$ Let $set\_of\_used\_X=\varnothing .$ Encrypt(P, A, N): See Algorithm 1 for definition. Decrypt(C, A, N): See Algorithm 2 for definition. Output: Return the adversary’s output.

Game $G_1$ is the same as game $G_0$ except we replace the CMAC MAC function with a random function. Now consider an adversary ${\mathcal{A}}^{\mathcal{E},\mathcal{D}}$ where $\mathcal{E}$ and $\mathcal{D}$ are either the game $G_0$ encrypt and decrypt oracles or the game $G_1$ encrypt and decrypt oracles. When $\mathcal{A}$ submits P, $A,$ $N,$ then $X_1,$ $X_2$ is returned and we give the distinguisher D$X_2\oplus P_1=F(P,A,N)$ where F is either CMAC or a random function. When $\mathcal{A}$ submits $X_1$, $X_2,$ $A,$ N then P is returned and we give the distinguisher D$X_2\oplus P_1=F(P,A,N).$ When $\mathcal{A}$ outputs $b,$ D also outputs b ($b\in \{0,1\}).$ Then ${\mathcal{A}}^{\prime }s$ probability of success is bounded by the probability bound for any adversary to distinguish CMAC from a random function which is $(5s^2+1)q^2/2^B+Ad{v}_E^{prp}(sq+1,t+c_{1}sq+Tim{e}_{CTR}(\mu ))$ [42] where E is the underlying block cipher, e.g., AES, and s is the maximum number of blocks in any query.

Thus

$$|Pr[{\mathcal{A}}^{G_1}\Rightarrow 1]-Pr[{\mathcal{A}}^{G_0}\Rightarrow 1]|\le (5s^2+1)q^2/2^B+Ad{v}_E^{prp}(sq+1,t+c_{1}sq+Tim{e}_{CTR}(\mu ))$$

Game $G_2$ is the same as game $G_1$ except the block ciphers used in CBC encryption for computing $X_1$ and X are replaced with random functions. Consider the game F (see Algorithm 6) where prf game adversary $\mathcal{B}$ has oracle access to functions $f_1$ and $f_2$ and distinguishes between the following:

• $f_1=E_{L_3}$, $f_2=E_{L_1}$, and
• $f_1=g_1\in H_{128,128}$, $f_2=g_2\in H_{128,128}$ ($g_1$ and $g_2$ are random functions.)

$f_1=E_{L_3}$ if and only if $f_2=E_{L_1}.$ $\mathcal{B}$ will run ${\mathcal{A}}^{G_i}$ as a subroutine, $i=1,2.$ If $f_1=E_{L_3},$ then $\mathcal{A}$ is in game $G_1,$ and if $f_1=g_1$ then $\mathcal{A}$ is in game $G_2.$

Algorithm 6 Game F with PRF Adversary $\mathcal{B}$.

Initialize:$\mathcal{B}$ selects keys $\overline{K},$ ${\overline{L}}_2,$ $L_2$ using the uniform distribution. $\mathcal{B}$ has oracle access to $f_1$ and $f_2.$ Response to ${\mathcal{A}}^{\prime }s$ encrypt query: $\mathcal{B}$ computes and returns $X_1,X_2$ to $\mathcal{A}.$ Response to ${\mathcal{A}}^{\prime }s$ decrypt query: $\mathcal{B}$ computes and returns $P_1,P_2$ to $\mathcal{A}.$ Output: Return $\mathcal{A}$’s output.

Each encryption query from $\mathcal{A}$ results in ${\mathcal{B}}^{\prime }s$ query of $W\oplus pad{(P_1)}_{P_2}$ to $f_1.$ $\mathcal{A}$ will output a bit indicating whether it is in game $G_1$ or game $G_2.$ $\mathcal{B}$ outputs the same bit for the prf game. Thus ${\mathcal{A}}^{\prime }s$ probability of success is bounded by ${\mathcal{B}}^{\prime }s$ probability of success. Let q be the number of queries to $f_1.$ Then $Adv(\mathcal{A},q,t)\le Ad{v}_E^{prf}(q,t)$ where E is the block cipher.

Thus we obtain

$$|Pr[{\mathcal{A}}^{G_2}\Rightarrow 1]-Pr[{\mathcal{A}}^{G_1}\Rightarrow 1]|\le Ad{v}_E^{prf}(q,t)\le Ad{v}_E^{prp}(q,t)+q(q-1)/2^{B+1}$$

Game $G_3$ is the same as game $G_2$ except:

• Initialize is modified: Initially we set $QD(N,A)=\varnothing$ for all $N,A.$ $QD(N,A)$ is a subset of the plaintexts.
• The line: if $(U!=Z)$ return ⊥; otherwise $Q=\tilde{P}\left|\right|Z$ and return Plaintext $\tilde{P},A,N$ is replaced with:
  $\overline{Q}$ is a random string of length $\left|Q\right|$ such that the prefix of $\overline{Q}$ of length $\left|Q\right|-\tau$ is in $QD{(N,A)}^C,$ $\overline{U}=LS{B}_{\tau /8}(\overline{Q}).$ If ($\overline{U}!=Z$) return $\perp ,$ else $\overline{Q}=\tilde{P}\left|\right|Z,$ return $\tilde{P},A,N.$
• If the adversary submits the encryption query $P,A,N,$ then we set $QD(N,A)=QD(N,A)\cup \{P\}.$

Then the advantage of $\mathcal{A}$ in distinguishing $G_3$ and $G_2$ is bounded by the probability of obtaining a valid response from the decryption oracle. Consider the adversary’s optimal strategy for obtaining a valid ciphertext response in game $G_2;$ given the ciphertext query ${\overline{X}}_1,{\overline{X}}_2,\overline{N}.$ Clearly if no encryption queries have been submitted (so no query responses have been received) then the probability of a valid response is $2^{-\tau }.$ Suppose we have submitted one previous encryption query: $P_1,P_2,N,A$ returning $X_1,X_2.$

case a: $\overline{N}=N$ and ${\overline{X}}_2\ne X_2$.

Then the probability of a valid response is independent of this previous query since we evaluate the random function at a new domain point. Thus $\overline{X}$ is uniform random, and the value $P_2$ will be uniform random, so the probability of a valid response is $2^{-\tau }.$

case b: $\overline{N}\ne N$ and ${\overline{X}}_2=X_2$.

The argument as in case a applies; the probability of a valid response is $2^{-\tau }.$

case c: $\overline{N}\ne N$ and ${\overline{X}}_2\ne X_2$.

The adversary may select ${\overline{X}}_1=X_1$. Then $X=\overline{X}$ due to $\overline{W}\oplus \overline{X_2}=W\oplus X_2$ with probability $2^{-B}.$ The input to the random function for computing $P_2$ will also be the same with probability $2^{-B};$ otherwise, the probability of a valid response will be $2^{-\tau }.$ Thus the probability of a valid response is $2^{-\tau }+2^{-B}(2^{-B}+2^{-\tau }).$

case d: $\overline{N}=N$ and ${\overline{X}}_2=X_2$.

We have $Pr[{\overline{P}}_1=P_1]=1/\beta$ and in that case if the last $\tau$ bits of ${\overline{X}}_1$ equal the last $\tau$ bits of $X_1$ then the query is valid. We have ${\overline{P}}_1\ne P_1$ with probability $(\beta -1)/\beta .$ In this case, $P_2$ is uniform random so the probability that the query is valid is $2^{-\tau }.$ Thus the probability of a valid query is $1/\beta +((\beta -1)/\beta )2^{-\tau }.$

Case d maximizes the probability of a valid response. There are two strategies for additional queries: multiple encryption queries followed by decryption queries or a single encryption query followed by decryption queries. Multiple encryption queries are likely to result in distinct $X_2$ values; in any case, two responses with equal N and $X_2$ values allows the Adversary to distinguish CMCC from a PRI with high probability without any decryption queries (see Games $G_4$ and $G_5$.) Thus the optimal strategy for multiple queries using the case d strategy is a single encryption query followed by decryption queries.

For cases a and b, multiple encryption queries followed by ciphertext queries does not increase the probability of a valid decryption query beyond $2^{-\tau }.$ Thus these strategies are suboptimal in the multiple queries case as well.

For case c, multiple encryption queries followed by multiple decryption queries does increase the probability of a valid decryption query. The success probability is dominated by $q^2(2^{-B-\tau })$ which is less than the optimal case d strategy.

Thus the optimal adversary strategy is a single plaintext query followed by successive ciphertext queries that match the N and $X_2$ values from the plaintext query.

The bound for Adversary success, assuming at most $x,1\le x\le q,$ invalid ciphertext queries prior to session termination, is

$$|Pr[{\mathcal{A}}^{G_3}\Rightarrow 1]-Pr[{\mathcal{A}}^{G_2}\Rightarrow 1]|\le 1-{(1-1/\beta -2^{-\tau })}^x.$$

Game $G_4$ is the same as game $G_3$ except the line

$X=CBC(W,pad{(P_1)}_{P_2},L_3)\oplus P_2,$

is replaced with

$X=CBC(W,pad{(P_1)}_{P_2},L_3)\oplus P_2;$ if $X\in set\_of\_used\_X,$ $ba{d}_5=true$ and reselect $X:$ $X\leftarrow set\_of\_used\_X^C.$ If $X\notin set\_of\_used\_X,$ $set\_of\_used\_X=set\_of\_used\_X\cup \{X\}.$ Then

$$|Pr[{\mathcal{A}}^{G_4}\Rightarrow 1]-Pr[{\mathcal{A}}^{G_3}\Rightarrow 1]|\le q(q-1)/2\beta +q(q-1)/2^B.$$

Game $G_5$ is depicted in Algorithm 7. Then game $G_5$ and game $G_4$ are indistinguishable except that collisions are possible in the strings $S_2$ where C includes $S_1\left|\right|S_2.$ When such a collision occurs, the games are distinguishable; the bound on collisions is $q(q-1)/2\beta .$ It is possible in game $G_4$ that a ciphertext query that is not invalid will return a plaintext and another encrypt query with a different plaintext returns the same ciphertext. This last sequence is not possible in game $G_5.$ However, the bound from Game $G_3$ allows us to assume that no valid ciphertext queries occur. Thus

$$|Pr[{\mathcal{A}}^{G_5}\Rightarrow 1]-Pr[{\mathcal{A}}^{G_4}\Rightarrow 1]|\le q(q-1)/2\beta +q(q-1)/2^{B+1}.$$

Thus the bound claimed in the theorem statement holds.

Algorithm 7 CMCC MRAE proof Game $G_5$.

Initialize: Select a random injection $f\in In{j}_e^{\mathcal{N},\mathcal{A}}(\mathcal{P},\mathcal{C})$. Let Z be the bit string with $\tau$ zero bits. $e(N,A,P)=\tau$ for all N, A, and $P.$ Encrypt(P, A, N): Return $f(N,A,P).$ Decrypt(C, A, N): $f^{-1}(N,A,C)=P$ if $f(N,A,P)=C$ and return ⊥ if no such triple $(N,A,P)$ exists. Output: Return the adversary’s output.

case ii: Some plaintexts have length greater than or equal to $2\ast B+16-\tau$ bits:

We note that this case is a suboptimal strategy for the adversary. Game $G_1$ is unchanged and for game $G_2$ the term $Ad{v}_E^{prp}(q,t)+q(q-1)/2^{B+1}$ from above is generalized to $Ad{v}_E^{prp}(sq,t)+sq(sq-1)/2^{B+1}.$ The game $G_3$ bound holds. For $CBC(W,pad{(X_2)}_X)$ in game $G_3,$ if the every input to each random function invocation is a previously unseen input (fresh input), then the output is random (the function is a random function). This bound on failure here is $\mu (\mu -1)/2^{B+1}+q(q-1)/2^{B+1}.$

Lemma 2 applies if all of the X values from the queries are distinct. For the function f in the Lemma, we use $P=2ndblockof{P}_1,\cdots ,lastblockof{P}_1,$ $T=P_2\left|\right|1stblockof{P}_1,$ and $f(P,T)=X=CBC(W,pad{(P_1)}_{P_2},L_3)\oplus P_2$. The probability that the X values from the queries is not distinct is bounded by $q(q-1)/2\beta +q(q-1)/2^B.$ The $X_1$ values and first block of $X_2$ are random strings when these failure events do not occur and thus the CMCC adversary’s advantage is the same as the SIV-G advantage. Thus the CMCC adversary’s advantage in distinguishing between games $G_3$ and $G_5$ is bounded by the sum of the two terms above plus the SIV-G security bound. ☐

We now prove a security bound for the CMCC AEAD algorithm; here message numbers are not allowed to be repeated in encryption (plaintext) queries. In the following, games $H_0,H_1,H_2,$ and $H_3$ are identical to games $G_0,G_1,G_2,$ and $G_5$ respectively, except the $H_i$ games are in the AE security game where encryption queries may not reuse message numbers from previous encryption queries.

Lemma 3.

Let $q-1\le 2^{\tau }.$ Given the adversary strategy in game $H_2$ (in the AE game) where the adversary submits a plaintext query $P_1,P_2,N$ and obtains the response $X_1,X_2.$ The adversary then submits a succession of ciphertext queries of the form ${\overline{X}}_1,X_2,N$ where the last τ bits of ${\overline{X}}_1$ are equal to the last τ bits of $X_1.$ Given the relation

$$\begin{array}{c}\hfill {\widehat{X}}_1\oplus {\overline{X}}_1={\widehat{P}}_2\oplus {\overline{P}}_2\end{array}$$

(1)

Then

$$\begin{array}{c}Pr[2distinctqueries{\widehat{P}}_1,{\widehat{P}}_2,N,{\widehat{X}}_1,X_{2}and{\overline{P}}_1,{\overline{P}}_2,N,{\overline{X}}_1,X_{2}satisfy(1)]\le \\ (q-1)\sum _{i=0}^{q-2}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right){\lambda }_1/2^{i\tau }<{\lambda }_{1}e(q-1)<2e(q-1)/\beta \end{array}$$

where ${\lambda }_1=1/\beta +(\beta -1)/{\beta }^2.$

Proof. 

We use induction over the number of queries. If $q=2,$ we have $Pr[(1)holds]={\lambda }_1=(q-1){\sum }_{i=0}^{q-2}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right){\lambda }_1/2^{i\tau }<{\lambda }_{1}e.$ Suppose the lemma is valid for $k=q-1.$ We now prove the $k=q$ case. We have

$$\begin{array}{c}Pr[(1)in{H}_{2}withqqueries]=Pr[(1)in{H}_{2}withfirstq-1queries]+\\ Pr[not(1)in{H}_{2}withfirstq-1queries\cap (1)in{H}_{2}withqthquery]\le \\ Pr[(1)in{H}_{2}withfirstq-1queries]+Pr[(1)in{H}_{2}withqthquery]\le \\ (q-2)\sum _{i=0}^{q-3}\left(\genfrac{}{}{0pt}{}{q-3}{i}\right){\lambda }_1/2^{i\tau }+{\lambda }_1+(1-{\lambda }_1)\left(\sum _{i=0}^{q-2}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right)2^{-i\tau }{(1-2^{-\tau })}^{q-2-i}i{\lambda }_1\right)<\\ (q-2)\sum _{i=0}^{q-3}\left(\genfrac{}{}{0pt}{}{q-3}{i}\right){\lambda }_1/2^{i\tau }+{\lambda }_1+\sum _{i=0}^{q-2}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right)i{\lambda }_1/2^{i\tau }=\\ \sum _{i=0}^{q-3}\left(\left(\genfrac{}{}{0pt}{}{q-3}{i}\right)(q-2){\lambda }_1/2^{i\tau }+\left(\genfrac{}{}{0pt}{}{q-2}{i}\right)i{\lambda }_1/2^{i\tau }\right)+{\lambda }_1+(q-2){\lambda }_1/2^{(q-2)\tau }=\\ \sum _{i=0}^{q-3}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right)(q-2){\lambda }_1/2^{i\tau }+(q-2){\lambda }_1/2^{(q-2)\tau }+{\lambda }_1=\\ {\lambda }_1+(q-2)\sum _{i=0}^{q-2}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right){\lambda }_1/2^{i\tau }<\\ (q-1)\sum _{i=0}^{q-2}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right){\lambda }_1/2^{i\tau }.\end{array}$$

Also,

$$\sum _{i=0}^{q-2}\left(\genfrac{}{}{0pt}{}{q-2}{i}\right)1/2^{i\tau }<\sum _{i=0}^{q-2}1/i!<e$$

which completes the proof. ☐

Lemma 4.

Let $q-1\le 2^{\tau }.$ Given the adversary strategy in game $H_3$ above where the adversary submits a plaintext query $P_1,P_2,N$ and obtains the response $X_1,X_2.$ The adversary then submits a succession of ciphertext queries of the form ${\overline{X}}_1,X_2,N$ where the last τ bits of ${\overline{X}}_1$ are equal to the last τ bits of $X_1.$ Then

$$\begin{array}{c}Pr[2distinctqueries{\widehat{P}}_1,{\widehat{P}}_2,N,{\widehat{X}}_1,X_{2}and{\overline{P}}_1,{\overline{P}}_2,N,{\overline{X}}_1,X_{2}satisfy(1)]\ge \\ (q-1)2^{-\tau }/\beta \end{array}$$

Proof. 

The probability that (1) is satisfied is bounded below by

$$\begin{array}{c}1-{(1-2^{-\tau }/\beta )}^{q-1}=\\ 1-\sum _{i=0}^{q-1}\left(\genfrac{}{}{0pt}{}{q-1}{i}\right){(-2^{-\tau }/\beta )}^i\ge 1-(1-(q-1)2^{-\tau }/\beta )=(q-1)2^{-\tau }/\beta \end{array}$$

 ☐

Theorem 2.

Let $b_i=$ number of bytes in ith query response, $1\le i\le q$. Let $\mu ={\sum }_{i=1}^q\lceil b_i/32\rceil .$ B is the cipher block length. Let $\beta =min\{\alpha ,2^B\}.$ Let the CMCC MAC function be CMAC [40]. Let s be the maximum number of CMAC blocks in a query; $c_1$ is a constant. $L=ma{x}_{1\le i\le q}\{b_i\}.$ CMCC encryption (stateless version) is an authenticated encryption with associated data (AEAD) scheme with AE-advantage bounded by

$$\begin{array}{c}q(q-1)2^{-\tau -1}(1/\beta +2^{-\tau })+2e(q-1)(1/\beta +(L-1)/2^{B+\tau }+2^{-B})+\\ (5s^2+1)q^2/2^B+Ad{v}_E^{prp}(sq+1,t+c_{1}sq+Tim{e}_{CTR}(\mu ))+Ad{v}_E^{prp}(sq,t)+sq(sq-1)/2^{B+1}+\\ \mu (\mu -1)/2^{B+1}+Ad{v}_{CTR}^{priv}(q,\acute{t},\mu )+5q/2^B+q^2/2^{B+9}\end{array}$$

given that the adversary is restricted to q queries and t time, E is the underlying block cipher for CMAC (e.g., AES), $\alpha =2^{8m}$ where $Len$ is the byte length of the minimal length plaintext query response, $m=\lfloor Len/2\rfloor ,$ and $\tau >0$ is the number of bits in the authentication tag. We also assume $q-1\le 2^{\tau }.$

Proof. 

case 1: All plaintexts have length $\le 2\ast B+8-\tau$ bits:

For the transition from game $H_2$ to game $H_3$ we have two mechanisms for the adversary to distinguish between the two: $X_2\oplus {\overline{X}}_2=P_1\oplus {\overline{P}}_1,$ and $X_1\oplus {\overline{X}}_1=P_2\oplus {\overline{P}}_2$ (1) for two distinct queries $X_2,X_1,N,P_1,P_2$ and ${\overline{X}}_2,{\overline{X}}_1,\overline{N},{\overline{P}}_1,{\overline{P}}_2.$ (If neither of the Equation (1) or Equation (2) hold in game $H_2$, then every invocation of the random functions is on a fresh point and thus is indistinguishable from game $H_3.$)

We first consider distinguishing between $H_2$ and $H_3$ via (1):

case a: Here the adversary uses the strategy from Lemma 3: the adversary submits a single plaintext query with message number N and receives a response with $X_1$ and $X_2,$ followed by ciphertext queries with $\overline{N}=N,$ and ${\overline{X}}_2=X_2,$ where the last $\tau$ bits for ${\overline{X}}_1$ are equal to the last $\tau$ bits of $X_1$ from the plaintext query. Then we have

$$\begin{array}{c}|Pr[{\mathcal{A}}^{H_2}\Rightarrow 1]-Pr[{\mathcal{A}}^{H_3}\Rightarrow 1]|\le \\ 2e(q-1)/\beta -(q-1)2^{-\tau }/\beta \le 2e(q-1)/\beta \end{array}$$

where we have applied both Lemma 3 and Lemma 4 from above.

case b: Games $H_2$ and $H_3$ can also be distinguished if a collision occurs on $W\oplus pad{(P_1)}_{P_2}$ and $W\oplus pad{(X_2)}_X$ between 2 distinct plaintext queries in game $H_2$ which gives a slightly higher probability for the relation $X_1\oplus {\overline{X}}_1=P_2\oplus {\overline{P}}_2$ in $H_2$ versus $H_3.$ This probability is bounded by $q(q+1)2^{-2B-1}.$ We can ignore the corresponding case where one or both queries are ciphertext queries since the probability would be less. Furthermore, this strategy is sub-optimal compared to the case a strategy above.

case c: Neither of the above two cases: then at least one of the CBC random function replacements get evaluated on a point distinct from the point in any other query. Thus the probability of (1) is the same in both $H_2$ and $H_3.$

We now check the adversary’s optimal strategy to distinguish between $H_2$ and $H_3$ based on

$$\begin{array}{c}\hfill X_2\oplus {\overline{X}}_2=P_1\oplus {\overline{P}}_1\end{array}$$

(2)

case d: Given two previous valid ciphertext queries with identical $X_2,$ $N,$ and last $\tau$ bits of $X_1$ values, the adversary may leverage the technique from the examples above to create a new encryption query that will have the same N value and which will match one of the previous query’s X value. Then this query response can be used to distinguish between $H_2$ and $H_3.$ The adversary advantage is bounded by $q(q-1)2^{-\tau -1}(1/\beta +2^{-\tau }).$

case e: Given a combination of zero or more plaintext queries and one or more ciphertext queries, with at least two total queries. If we have a match on the last $\tau$ bits of $X_1$ values for some queries as well as a collision on $W\oplus pad{(X_2)}_X$ then the adversary can follow the approach in case d above and distinguish between $H_2$ and $H_3$ based on (2) above. Note that the $X_2$ and N values are distinct across the queries. The probability of such a collision between two queries is at best $2^{-B}$ and therefore this strategy is suboptimal.

case f: The new query (either ${\overline{X}}_1,{\overline{X}}_2,\overline{N}$ or ${\overline{P}}_1,{\overline{P}}_2,\overline{N}$) is such that $\overline{N}$ is distinct from the N in previous queries. Then $X_2\oplus {\overline{X}}_2=P_1\oplus {\overline{P}}_1$ occurs with the same probability in both $H_3$ and $H_2$ since $\overline{N}$ results in a previously unseen point for the domain of the CMAC random function replacement.

case g: The new ciphertext query is such that ${\overline{X}}_2$ and $\overline{N}$ match the corresponding values in a set of previous queries: Then the corresponding X values are distinct. So $X_2\oplus {\overline{X}}_2=P_1\oplus {\overline{P}}_1$ occurs with the same probability in both $H_3$ and $H_2.$ (Here we assume that the last $\tau$ bits of the $X_1$ values are distinct, or alternatively, that all of the previous queries are plaintext queries, to distinguish this case from case d above.)

case h: The new ciphertext query is such that ${\overline{X}}_2$ is distinct from and $\overline{N}$ matches the corresponding values in a set of previous queries:

Note that only one of the previous queries is a plaintext query whereas the others must be valid ciphertext queries. Then we have a similar scenario as for case a above, and we can apply Lemma 3 with the collision bound $2^{-\tau +1}/\beta$ in place of $1/\beta +(\beta -1)/{\beta }^2.$ Since the latter value is larger, this strategy is suboptimal.

case i: None of the above cases. Then the inputs to the $CBC(W,pad{(X_2)}_X)$ random function replacement are distinct across all queries. Thus the probability of $X_1\oplus {\overline{X}}_1=X\oplus \overline{X}$ is $1/\beta$ for any two queries. Also, the above cases are exhaustive for $(X,N)=(\overline{X},\overline{N})$. Thus the probability of (2) is the same in both $H_2$ and $H_3.$

case 2: At least some plaintexts have length $\ge 2\ast B+16-\tau$ bits:

The case with longer plaintexts/ciphertexts is similar to the Theorem 1 case ii above. The term $2e(q-1)/\beta$ is generalized to $2e(q-1)(1/\beta +(L-1)/2^{B+\tau }+2^{-B}).$ ☐

4.1. CMCC with MAC (CWM)

In this section, we present a variant, CMCC with MAC (CWM). Algorithms 8 and 9 specify CWM. For the proof of CWM AE security, the main distinction with CMCC above is that we no longer restrict $q-1\le \tau .$ By requiring the MAC computation, CWM achieves a stronger security bound at the cost of additional processing, when compared with CMCC.

Algorithm 8 CWM Encryption: Encryption inputs are plaintext $P,$ key $K=\overline{K},\tilde{K},L_3,L_2,{\overline{L}}_2,L_1,$ public message number $N,$ and associated data $A.$ $CBC(IV,P,Key)$ is CBC encryption with initialization vector $IV,$ plaintext $P,$ and key $Key.$ One choice for $MAC(P,Key)$ is the CMAC MAC algorithm [40] with plaintext P and key $Key.$ $pad()$ is the padding algorithm defined in Section 3.3. $E_{\overline{K}}$ is the block cipher with key $\overline{K}.$ $\left|P\right|,$ the bitlength of P, is a multiple of 8, as is $\tau .$ U is obtained from V by zeroing bits 31 and 63 to enable faster addition (prevent carries) [41]. $U+j$ is integer addition, $1\le j\le i$. When xor’ing two strings of different length, the longer string is first truncated to the length of the shorter string.

CWM Encrypt($P,$$\overline{K},\tilde{K},L_3,L_2,{\overline{L}}_2,L_1,$$N,$A)   1: $M\leftarrow {(10110110)}^{16-\left|N\right|/8}\left|\right|N$   2: $Z\leftarrow MAC(P,\tilde{K})$   3: $W\leftarrow E_{\overline{K}}(M)$   4: $Q\leftarrow P\left|\right|Z$   5: $L\leftarrow \left|Q\right|/8$   6: if$L=0mod2$then   7:      $P_1\leftarrow MS{B}_{L/2}(Q)$   8:      $P_2\leftarrow LS{B}_{L/2}(Q)$   9: else 10:      $P_1\leftarrow MS{B}_{(L-1)/2}(Q)$ 11:      $P_2\leftarrow LS{B}_{(L+1)/2}(Q)$ 12: end if 13: $X\leftarrow CBC(W,pad{(P_1)}_{P_2},L_3)\oplus P_2$ 14: $Y\leftarrow X\left|\right|A$ 15: $V\leftarrow MAC(W||Y,L_2)$ 16: $i\leftarrow \lfloor \left|P_1\right|/B\rfloor$ 17: $P_1={\overline{P}}_{1,1}\left|\right|\dots \left|\right|{\overline{P}}_{1,i}\left|\right|{\overline{P}}_{1,i+1}$ where $|{\overline{P}}_{1,1}|=\dots =|{\overline{P}}_{1,i}|=B$ and $|{\overline{P}}_{1,i+1}|=|P_1|modB.$ 18: $U\leftarrow Vand(1^{64}|\left|0^1\right|\left|1^{31}\right|\left|0^1\right||1^{31})$ 19: $X_2\leftarrow V\oplus {\overline{P}}_{1,1}\left|\right|E_{{\overline{L}}_2}(U+1)\oplus {\overline{P}}_{1,2}\left|\right|\dots \left|\right|E_{{\overline{L}}_2}(U+i)\oplus {\overline{P}}_{1,i+1}$ 20: $X_1\leftarrow CBC(W,pad{(X_2)}_X,L_1)\oplus X$

Algorithm 9 CWM Decryption: Decryption inputs are ciphertext $X_1{X}_2,$ key $K=\overline{K},\tilde{K},L_3,L_2,{\overline{L}}_2,L_1,$ public message number $N,$ and associated data $A.$

CWM Decrypt($X_1,X_2,$$\overline{K},\tilde{K},L_3,L_2,{\overline{L}}_2,L_1,$$N,$A)   1: $M\leftarrow {(10110110)}^{16-\left|N\right|/8}\left|\right|N$   2: $W\leftarrow E_{\overline{K}}(M)$   3: $X\leftarrow CBC(W,pad{(X_2)}_{X_1},L_1)\oplus X_1$   4: $Y\leftarrow X\left|\right|A$   5: $V\leftarrow MAC(W||Y,L_2)$   6: $i\leftarrow \lfloor \left|X_2\right|/B\rfloor$   7: $X_2={\overline{X}}_{2,1}\left|\right|\dots \left|\right|{\overline{X}}_{2,i}\left|\right|{\overline{X}}_{2,i+1}$ where $|{\overline{X}}_{2,1}|=\dots =|{\overline{X}}_{2,i}|=B$ and $|{\overline{X}}_{2,i+1}|=|X_2|modB.$   8: $U\leftarrow Vand(1^{64}|\left|0^1\right|\left|1^{31}\right|\left|0^1\right||1^{31})$   9: $P_1\leftarrow V\oplus {\overline{X}}_{2,1}\left|\right|E_{{\overline{L}}_2}(U+1)\oplus {\overline{X}}_{2,2}\left|\right|\dots \left|\right|E_{{\overline{L}}_2}(U+i)\oplus {\overline{X}}_{2,i+1}$ 10: $P_2\leftarrow CBC(W,pad{(P_1)}_X,L_3)\oplus X$ 11: $Q=P_1\left|\right|P_2,$ 12: $U=LS{B}_{\tau /8}(Q)$ 13: $Q=\tilde{P}\left|\right|U$ 14: if$(U!=MAC(\tilde{P},\tilde{K})$then 15:   return⊥ 16: else 17:   return Plaintext $\tilde{P}$ 18: end if

We give the MRAE security bound and the AE security bound for CWM in the next two theorems.

Theorem 3.

Let $b_i=$ number of bytes in $ith$ query response, $1\le i\le q$. Let $\mu ={\sum }_{i=1}^q\lceil b_i/32\rceil .$ B is the cipher block length. Let $\beta =min\{\alpha ,2^B\}.$ Let the CMCC MAC function be CMAC [40]. Let s be the maximum number of CMAC blocks in a query; $c_1$ is a constant. $L=ma{x}_{1\le i\le q}\{b_i\}.$ CWM encryption (stateless version) is a misuse resistant authenticated encryption scheme with MRAE-advantage bounded by

$$\begin{array}{c}q(q-1)/\beta +q/(2^{\tau }\beta )+(q-1)(q-2)/(2^{2\tau }\beta )+\\ (L-1)((q-1)/(2^{B+\tau -1})+(q-1)(q-2)/2^{B+2\tau })+(q-1)(q-2)/2^{2\tau +1}+q(q-1)(q-2)/2^{3\tau +2}+\\ (5s^2+1)q^2/2^B+Ad{v}_E^{prp}(sq+1,t+c_{1}sq+Tim{e}_{CTR}(\mu ))+Ad{v}_E^{prp}(sq,t)+sq(sq-1)/2^{B+1}+\\ \mu (\mu -1)/2^{B+1}+Ad{v}_{CTR}^{priv}(q,\acute{t},\mu )+5q/2^B+q^2/2^{B+9}+3q^2/2^{B+1}+Ad{v}_E^{prp}(q,t)\end{array}$$

given that the adversary is restricted to q queries and t time, E is the underlying block cipher for CMAC (e.g., AES), $\alpha =2^{8m}$ where $Len$ is the byte length of the minimal length plaintext query response, $m=\lfloor Len/2\rfloor ,$ assuming up to x invalid ciphertexts do not result in session termination, and τ is the number of bits in the authentication tag.

Proof. 

The proof is similar to the proof of Theorem 1 above with the main difference being the bound for the strategy in Lemma 3. Also, we use the game structure from Theorem 2, except we are in the MRAE security model. Consider the strategy from Lemma 3 for the case where plaintexts have short length ($\le 2B+1-\tau$). Then we have (in game $H_2$):

$$\begin{array}{c}Pr[(1)]=Pr[(1)with1stquery]+Pr[(1)without1stquery]=\\ (q-1)(1/(2^{\tau }\beta )+(\beta -1)/(2^{\tau }{\beta }^2))+\left(\genfrac{}{}{0pt}{}{q-1}{2}\right)(1/(2^{2\tau }\beta )+(\beta -1)/({\beta }^2{2}^{2\tau }))<\\ q/(2^{\tau }\beta )+(q-1)(q-2)/(2^{2\tau }\beta )\end{array}$$

This term generalizes to

$$\begin{array}{c}\hfill q/(2^{\tau }\beta )+(q-1)(q-2)/(2^{2\tau }\beta )+(L-1)((q-1)/(2^{B+\tau -1})+(q-1)(q-2)/2^{B+2\tau })\end{array}$$

for the arbitrary length messages case.

Also, we have that

$$Pr[(2)]=(q-1)(q-2)/2^{2\tau +1}+q(q-1)(q-2)/2^{3\tau +2}$$

(Here we ignore the strategy consisting of a plaintext query followed by ciphertext queries, all with the same nonce value, where the $X_1$ and $X_2$ values are randomly chosen. This strategy would add some of the same terms to the security bound as the current strategy adds above for (1). But since the final result is smaller, we ignore this strategy). We have

$$Pr[{\mathcal{A}}^{H_2}\Rightarrow 1]\le Pr[(1)]+Pr[(2)].$$

Thus

$$|Pr[{\mathcal{A}}^{H_2}\Rightarrow 1]-Pr[{\mathcal{A}}^{H_3}\Rightarrow 1]|\le Pr[(1)]+Pr[(2)]$$

 ☐

Theorem 4.

Let $b_i=$ number of bytes in $ith$ query response, $1\le i\le q$. Let $\mu ={\sum }_{i=1}^q\lceil b_i/32\rceil .$ B is the cipher block length. Let $\beta =min\{\alpha ,2^B\}.$ Let the CMCC MAC function be CMAC [40]. Let s be the maximum number of CMAC blocks in a query; $c_1$ is a constant. $L=ma{x}_{1\le i\le q}\{b_i\}.$ CWM encryption (stateless version) is an authenticated encryption with associated data (AEAD) scheme with AE-advantage bounded by

$$\begin{array}{c}q(q-1)2^{-3\tau -1}+(q-1)/(2^{\tau -1}\beta )+(q-1)(q-2)/(2^{2\tau }\beta )+\\ (L-1)((q-1)/(2^{B+\tau -1})+(q-1)(q-2)/2^{B+2\tau })+(5s^2+1)q^2/2^B+\\ Ad{v}_E^{prp}(sq+1,t+c_{1}sq+Tim{e}_{CTR}(\mu ))+Ad{v}_E^{prp}(sq,t)+sq(sq-1)/2^{B+1}+\\ \mu (\mu -1)/2^{B+1}+Ad{v}_{CTR}^{priv}(q,\acute{t},\mu )+5q/2^B+q^2/2^{B+9}+2q^2/2^{B+1}+Ad{v}_E^{prp}(q,t)\end{array}$$

given that the adversary is restricted to q queries and t time, E is the underlying block cipher for CMAC (e.g., AES), $\alpha =2^{8m}$ where $Len$ is the byte length of the minimal length plaintext query response, $m=\lfloor Len/2\rfloor ,$ and $\tau >0$ is the number of bits in the authentication tag.

Proof. 

We use the game structure from Theorem 2. The proof is similar to the proof of Theorem 2 above with the main difference being the bound for the strategy in Lemma 3 and the bound for the other potentially optimal strategy from case 1d in the proof of Theorem 2. The bound for the case 1d strategy is

$$q(q-1)2^{-3\tau -1}$$

which replaces

$$q(q-1)2^{-2\tau -1}$$

in Theorem 2 above.

For the strategy in Lemma 3, we have

$$\begin{array}{c}\hfill (q-1)/(2^{\tau -1}\beta )+(q-1)(q-2)/(2^{2\tau }\beta )+(L-1)((q-1)/(2^{B+\tau -1})+(q-1)(q-2)/2^{B+2\tau })\end{array}$$

which replaces the term $2e(q-1)(1/\beta +(L-1)/2^{B+\tau }+2^{-B}).$ ☐

4.2. Security Bound Summary and Security Comparison

Table 2 summarizes the dominant terms from the security bounds for CMCC and CWM for short messages (less than $2B+16$ bits), for both AE and MRAE security. We also include the GCM and SIV authenticated encryption algorithms for comparison.

Table 2. Dominant Terms for Security Bounds for GCM, SIV, CMCC and CWM (smaller message lengths).

Algorithm/Misuse Resistant?	Ciphertext Expansion	Security Bound (Confidentiality)
GCM/No	$\tau$	$q/2^{\tau }+\dots$
SIV/Yes	$\left|IV\right|$	$q(q-1)/2^{\left|IV\right|+1}+\dots$
CMCC (MRAE)/Yes	$\tau$	$q/2^{\tau }+q/\beta +q(q-1)/\beta$
CMCC (AE)/No	$\tau$	$q(q-1)2^{-\tau -1}(1/\beta +2^{-\tau })+2e(q-1)/\beta$
CWM (MRAE)/Yes	$\tau$	$q^2/2^{2\tau +1}+q^3/2^{3\tau +2}+q^2/(2^{2\tau }\beta )+q/(2^{\tau }\beta )+q(q-1)/\beta$
CWM (AE)/No	$\tau$	$q^2/2^{3\tau }+q^2/(2^{2\tau }\beta )+q/(2^{\tau -1}\beta )$

We compare the security of SIV, CMCC MRAE, CMCC AE, CWM MRAE, and CWM AE for a 16 byte plaintext with a 4 byte authentication tag (SIV’s IV length is 16 bytes so a 4 byte IV length, although possible, is not currently an option for SIV). Respectively, we obtain approximate security bounds of $q^2/2^{32},$ $q/2^{32},$ $q^2/2^{64},$ $q^2/2^{65},$ and $q^2/2^{96}.$

5. Performance

Table 1 compares the number of block cipher calls for the CMCC, SIV, and CWM algorithms, for varying message sizes. CMCC requires $3\lceil Length/32\rceil +2+\lceil (Length/32)-1\rceil$ block cipher calls, where $Length$ is the message length (including tag).

Table 3 compares the processing performance of GCM, OCB, HS1-SIV v2, and CMCC for two AMD machines and two message sizes (64 and 1536 bytes). These numbers (cycles per byte) were obtained as part of the Supercop performance testing for the Caesar competition. The results are the median for many test runs of encrypting messages with the two sizes. Decryption results are omitted since they are very similar to the encrypt numbers.

Table 3. Machine 1: AMD64 Zen 800f12 AMD EPYC 7601, 64 × 2200 MHz and Machine 2: AMD64; Zen (800f11); 2017 AMD Ryzen 7 1700; 8 × 3000 MHz (cycles per byte).

Algorithm	Machine 1: 1536 Bytes	Machine 1: 64 Bytes	Machine 2: 1536 Bytes	Machine 2: 64 Bytes
OCB	0.56	5.84	0.84	7.97
GCM	1.13	8.94	1.80	24.84
HS1-SIV2	1.96	13.75	2.58	17.34
CMCC	7.63	20.62	9.00	27.19

Much of the cycles per byte disparity between CMCC and HS1-SIV v2 for 64 byte messages can be explained by the block cipher for CMCC vs. stream cipher for HS1-SIV v2. There is not much difference in processing for CMCC between a 64 byte plaintext (with a tag added on) and a 96 byte message (including the tag). The number of block cipher operations is the same. A more favorable comparison for CMCC would be a 60 byte plaintext plus a 4 byte authentication tag for a total size of 64 bytes.That reduces the number of block operations from 13 to 9.

Scope and Limitations

CMCC (and CWM) are targeted for energy constrained environments where devices may only have a single CPU and primarily send short messages. Cycles per byte performance cannot be improved substantially given the use of AES underneath and the assumption of no parallelism (single CPU).

Also, the benefits of parallelism are less when messages are short as the supercop measurements above show.

However, given parallelism and longer messages, we would expect the number of cycles per byte to drop by about half if we replaced each round per the generalized PRF structure described in Section 1 with the HS1 SIV v2 algorithm from Krovetz. This hypothesis is supported by the supercop results above.

In other words, given parallelism and longer messages we expect CMCC cycles per byte to drop to about 1.5 times as much as HS1 SIV v2, when replacing each CMCC round with HS1-SIV v2. This follows since each CMCC round operates on half of the total bytes.

We now consider energy usage due to ciphertext expansion. In [43], the authors measure energy utilization for a variety of cryptographic algorithms due to CPU utilization and networking for the Berkeley/Crossbow motes platform, specifically on the Mica2dot sensor platform. Their measurements show that 59.2 $\mathsf{\mu }$J (microJoules) are needed to transmit one byte. Only 1.6 $\mathsf{\mu }$J are needed per byte for AES encryption including key setup. Given the CWM security bound of $q^2/2^{96}$ for a 4 byte authentication tag for a 12 byte plaintext, SIV requires a 12 byte IV for comparable security. Thus the energy usage is roughly 1.5 times as much for SIV vs. CWM, to encrypt and send the message.

6. Conclusions

We have presented CMCC, a scheme providing provably secure misuse resistant authenticated encryption, and it leverages existing modes such as CBC, Counter, and CMAC. The main focus for this work is minimizing ciphertext expansion, especially for short messages including plaintext lengths less than the underlying block cipher length (e.g., 16 bytes). Depending on the environment, we obtain security with only 2–6 bytes of ciphertext expansion. Since changes to the ciphertext randomize the plaintext, we can leverage the protocol checks in higher layer protocols as additional authentication bits allowing us to reduce the length of the authentication tag. Our CWM variation provides a further strengthening of the security bounds for the short messages scenario at the cost of an additional MAC operation over the plaintext.

CMCC can achieve significant energy savings when applied to protocols that send short messages due to its small ciphertext expansion.