Deterministic Authenticated Encryption Scheme for Memory Constrained Devices

Abstract

A technique of authenticated encryption for memory constrained devices called sp-AELM was proposed by Agrawal et al. at ACISP 2015. The sp-ALEM construction utilizes a sponge-based primitive to support online encryption and decryption functionalities. Online encryption in the construction is achieved in the standard manner by processing plaintext blocks as they arrive to produce ciphertext blocks. However, decryption is achieved by storing only one intermediate state and releasing it to the user upon correct verification. This intermediate state allows a legitimate user to generate the plaintext herself. However, the scheme is nonce-respecting, i.e., the scheme is insecure if the nonce is repeated. Implementation of a nonce is non-trivial in practice, and reuse of a nonce in an AE scheme is often devastating. In this paper, we propose a new AE scheme called dAELM, which stands for deterministic authenticated encryption (DAE) scheme for low memory devices. DAE is used in domains such as the key wrap, where the available message entropy omits the overhead of a nonce. For limiting memory usage, our idea is to use a session key to encrypt a message and share the session key with the user depending upon the verification of a tag. We provide the security proof of the proposed construction in the ideal cipher model.

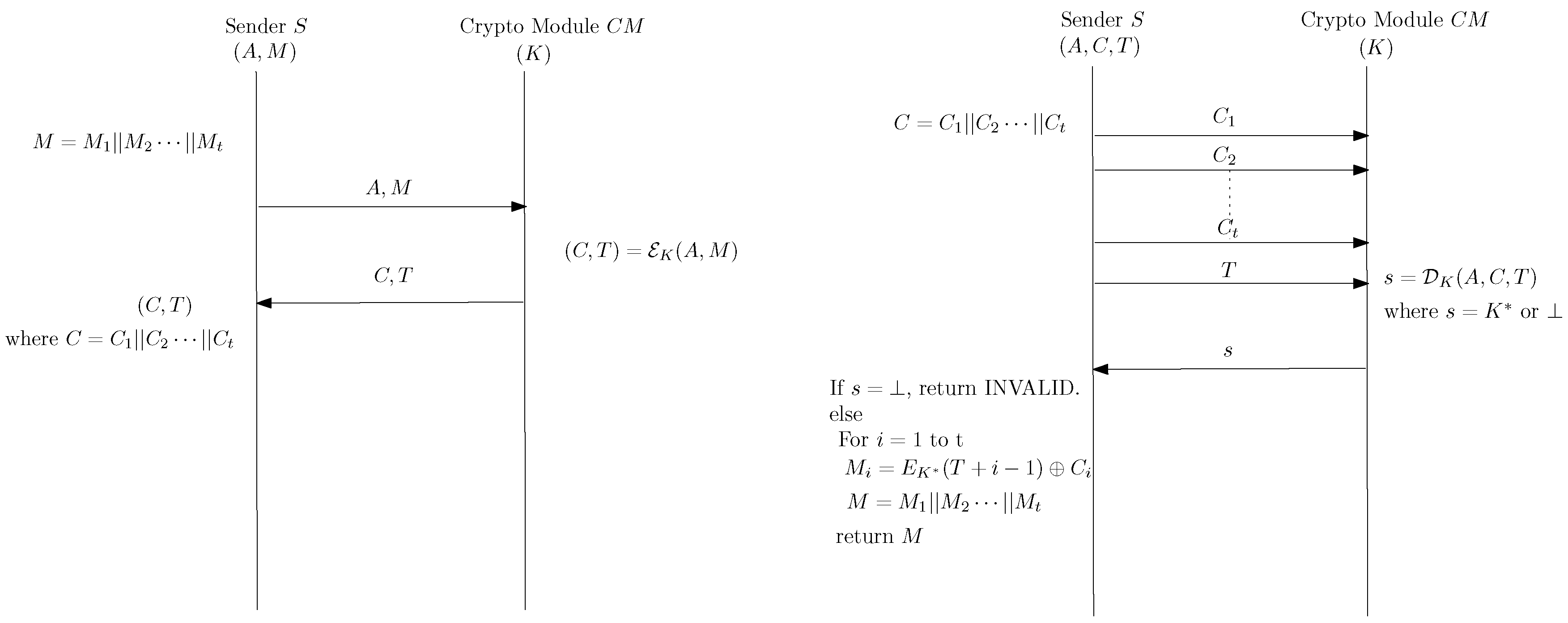
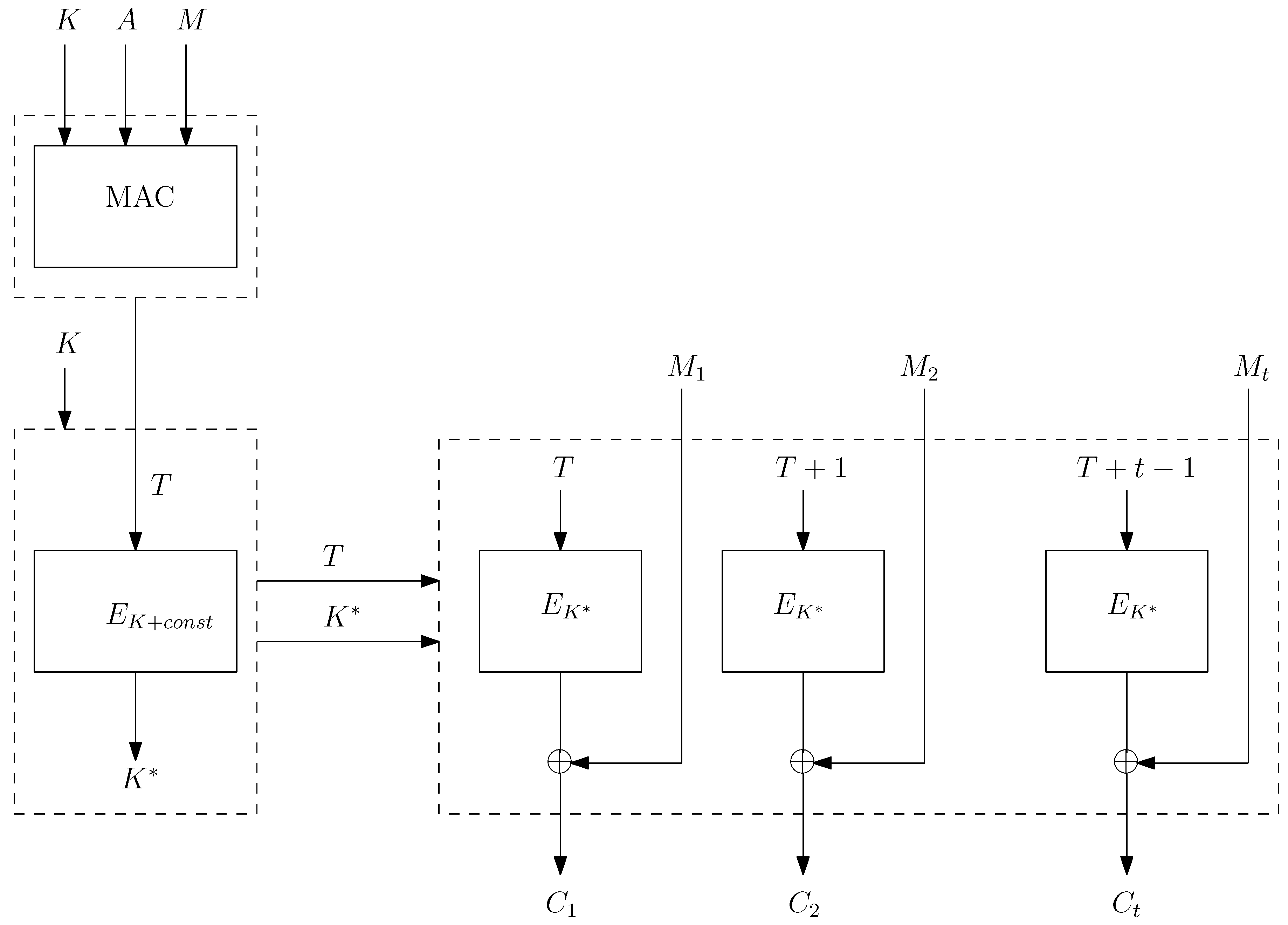
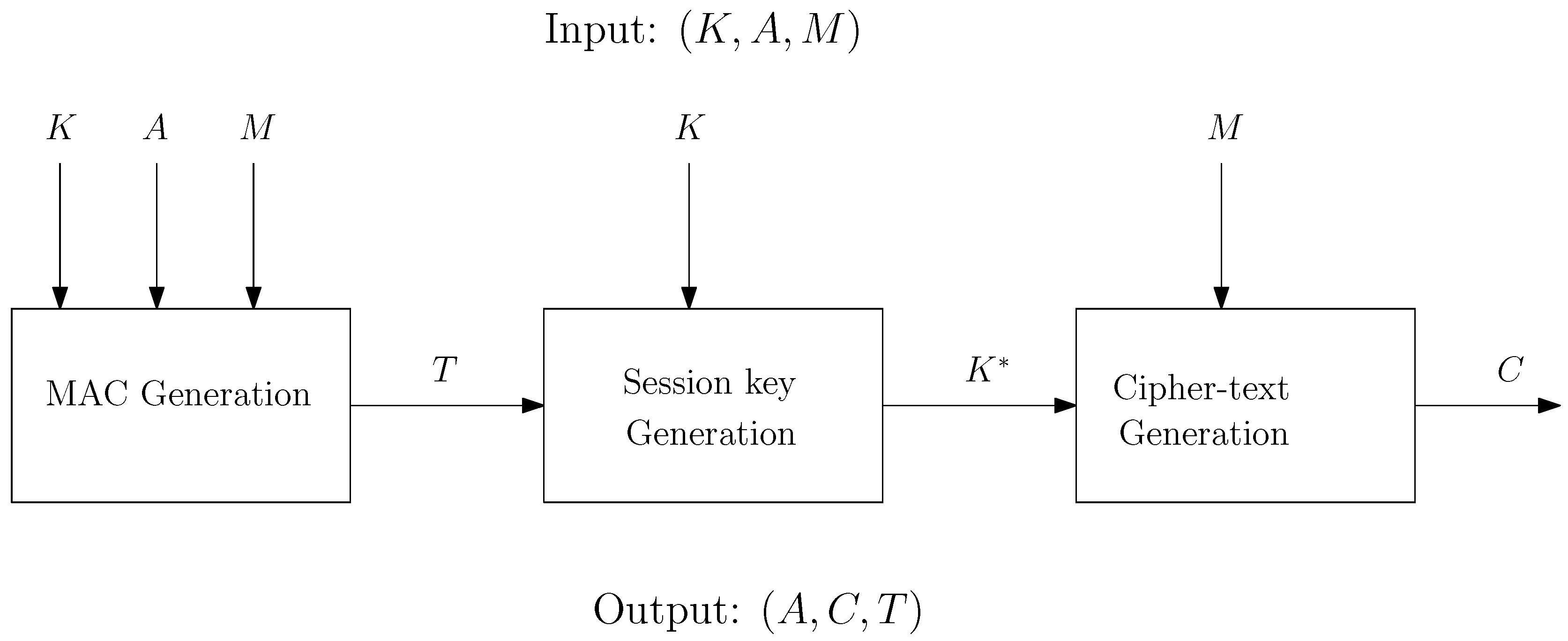
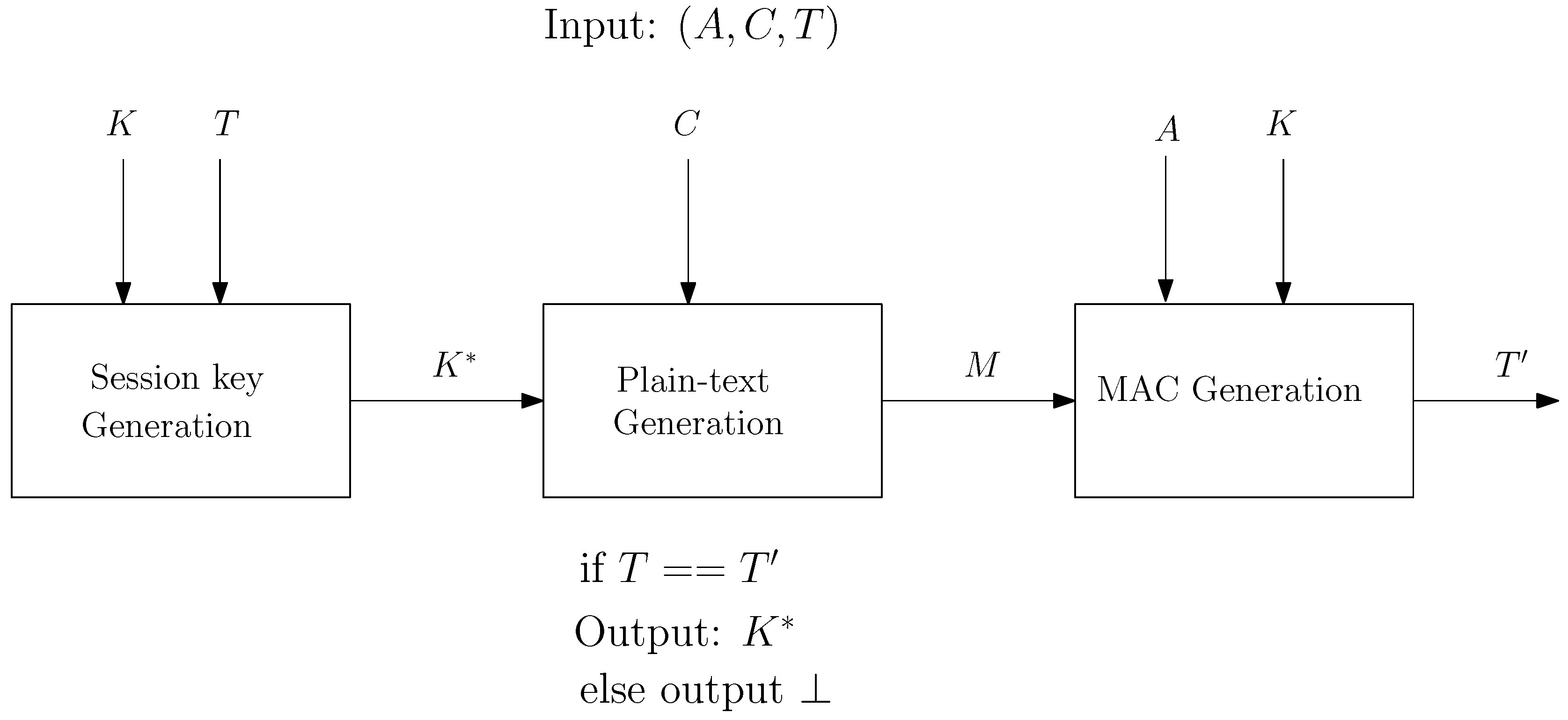
1. Introduction

Authenticated Encryption $\left(AE\right)$ is a symmetric encryption scheme that aims to provide authenticity as well as confidentiality using a single construction. The ongoing CAESAR( Competition for Authenticated Encryption: Security, Applicability, and Robustness) competition [1] has led to a spur in research and analysis of AE schemes. The idea of $AE$ was first introduced by Bellare and Namprempre in 2000 [2]. Thereafter, several notions of authenticated encryption have emerged over a series of works [3,4,5,6,7], which include misuse-resistant $AE$ [8] and $AE$ for memory constrained devices [9,10].

Due to the ongoing Internet of Things (IoT) revolution, the area of designing lightweight AE schemes has gained momentum. Various lightweight schemes have been proposed in recent past. Some of them include Hummingbird-2 [11], ALE [12], ASCON [13], NORX [14], Ketje [15], PFX [16], IAR-CTR, and IAR-CFB [17]. Due to the limited storage capabilities of these IoT devices, it has become necessary to design a $AE$ scheme which can process long messages even with these memory constraints. Encryption of the message on the fly (i.e., as they arrive) is not an issue in most of the block-cipher-based AE schemes. However, decrypting the ciphertext with limited memory poses a challenge. This is because the sender cannot return decrypted data without first verifying its authenticity, and verifying the authenticity requires the data to be seen in a first pass followed by the actual decryption in the second pass. To avoid the user supplying different data during the authentication and the decryption passes, the device needs to store the data, which may not be feasible for the devices with restricted memory space.

2. Related Work

A few methods for supporting authenticated encryption in a memory constrained scenario have been proposed. However, all of them have restrictions. The first method to support online decryption was proposed by Fouque et al. [9], who designed a generic construction called “decrypt-then-mask” (DTM). In this method, a pseudorandom number generator is used to mask the plaintext blocks during decryption, and this masked data is released to the receiver. Once the tag gets verified, the cryptographic module returns the PRNG seed used for masking plaintext block to the receiver who can run the same PRNG at her end and unmask the received data. A drawback of this construction is that the decryption device using DTM must implement a pseudorandom number generator, which may not fit on a constrained device. To overcome this problem, a sponge-based construction called sp-AELM was proposed in [10]. The main idea behind this construction is to store an intermediate state while performing decryption, instead of storing the complete plaintext. Depending on the ciphertext-tag pair passing the validation test, either the saved intermediate state or an invalid symbol is returned to the user. If the verification was correct, then the receiver can recover the plaintext from this intermediate state along with the already available ciphertext. A schematic representation of sp-AELM is shown in Figure 1. The intermediate state ($a_0,b_0$) as shown in Figure 1 is stored and released upon correct verification. For more details of the construction, one can refer to [10]. However, the main drawback of this scheme is that it is nonce-respecting, and no security guarantees are available in the case of nonce being repeated.

In [18], Hoang et al. introduced a new notion called OAE2, which supports both online encryption and online decryption. It processes plaintext and ciphertext by partitioning them into a sequence of segments. The size of these segment is decided by the user, and different segments can have different lengths. On an input message M that gets segmented by a user to $(M_1,M_2,\dots ,M_n)$, OAE2 encrypts each segment as soon as it arrives, carrying forward only a constant size state. Thus, input message M produces a segmented ciphertext $(C_1,C_2,\dots ,C_n)$, where $|C_i|\ge |M_i|(1\le i\le n)$ to support expedient verification of what has come so far. Each $C_i$ must result in an immediate recovery of $M_i$ without waiting for the availability of $C_{i+1}$. However, OAE2 is not secure when the nonce repeats. In practice, it is difficult to ensure that nonce never repeats during the operation of a device. Even when it is feasible to generate a unique nonce for each encryption, it is usually through an expensive operation. In other words, implementation of a nonce is non-trivial in practice. Moreover, repeating a nonce in an AE scheme is often devastating [18].

With the increasing usage of low-cost RFID devices, sensors, and trusted platform modules (TPMs), the need for an AE scheme which can support both the encryption and the decryption functions in a resource-constrained environment is increasing day by day. As already mentioned, existing AE schemes which are suitable for low memory devices are vulnerable to attacks in nonce-repeating scenarios. To overcome this limitation, we propose a new deterministic authenticated encryption (DAE) scheme, which we call dAELM.

The concept of the DAE scheme was introduced by Rogaway and Shrimpton in [8]. In a DAE scheme, the encryption algorithm deterministically produces a ciphertext for a given key, associated data, and a message. The DAE construction in [8] was termed “SIV,” which stands for synthetic $IV$. This construction combines a conventional $IV$-based encryption scheme and a pseudorandom function that takes a vector of strings as input. The scheme [8] first applies a $PRF$ to associated data and a message to produce an $IV$ and uses the resultant $IV$ for the encryption scheme. The $SIV$ construction is proven to be secure, assuming all of its components are secure. However, the SIV construction is not designed for resource-constrained environments; in particular, it may not be suitable for a scenario where the cryptomodule does not have enough space to store the complete message M during decryption. This memory requirement is because the decryption procedure cannot return the plaintext before successful verification of the tag. In this work, we design an efficient and provably secure DAE scheme that is suitable for memory-constrained cryptomodules.

Our scheme resembles the SIV construction and exploits the existing entropy in messages to omit the overhead for nonces. It also saves bandwidth by eliminating the need to send nonces or random values over the communication channel.

The important feature that makes our construction differ from SIV is the use of the cryptographic module. In dAELM, we assume encryption and decryption takes place inside a cryptographic module which has a secret key embedded on it and has a very limited memory space. The reason behind using the cryptographic module is to increase the security of the key. We don’t want the key to being accessible outside the cryptographic module.

The remainder of the paper is organized as follows. Section 3 provides definitions that we use in defining the security of the proposed scheme. Section 4 provides a specification of the proposed scheme dAELM. Section 5 presents the security proof of the scheme. Section 6 compares dAELM with other existing schemes. Section 7 shows the software implementation results of our scheme, followed by a discussion in Section 8. Finally, we conclude in Section 9.

3. Preliminaries

Definition 1 (DAE).

A deterministic AE scheme [8] is a tuple $\mathsf{\Pi }=(\mathcal{K},\mathcal{E},\mathcal{D})$, where $\mathcal{K}$ is a non-empty set of strings and the encryption algorithm $\mathcal{E}$ and decryption algorithm $\mathcal{D}$ are deterministic. $\mathcal{E}:\mathcal{K}\times \mathcal{A}\times \mathcal{M}\to \mathcal{C}$ and $\mathcal{D}:\mathcal{K}\times \mathcal{A}\times \mathcal{C}\to \mathcal{M}\cup \perp$ with associated non-empty key space $\mathcal{K}$, associated-data space $\mathcal{A}$, and message/ciphertext space $\mathcal{M},\mathcal{C}\subseteq {\{0,1\}}^{*}$. For each $K\in \mathcal{K}$, $A\in \mathcal{A}$ and $M\in \mathcal{M}$, ${\mathcal{E}}_K^A\left(M\right)$ or ${\mathcal{E}}_K(A,M)$ maps $(A,M)$ to an output C such that $\left|C\right|=\left|M\right|+\tau$ for a fixed τ. ${\mathcal{D}}_K^A\left(C\right)$ or ${\mathcal{D}}_K(A,C)$ outputs corresponding message M iff C is valid, and $\perp$ otherwise. We assume correctness; i.e., for all $(K,A,M)\in \mathcal{K}\times \mathcal{A}\times \mathcal{M}$, it holds that ${\mathcal{D}}_K^A\left({\mathcal{E}}_K^A\left(M\right)\right)=M$.

Definition 2 (Deterministic Privacy (detPriv)).

We adapt the same notion of privacy as in [8], namely in terms of indistinguishability of the output from a random string. Let $\mathsf{\Pi }=(\mathcal{K},\mathcal{E},\mathcal{D})$ be a DAE scheme with a fixed associated data space $\mathcal{A}$ and message space $\mathcal{M}$. Let A be an computationally bounded adversary having access to encryption oracle $\mathcal{E}$ and an ideal primitive π and its inverse ${\pi }^{-1}$. We then define detPriv advantage of adversary A in attacking Π as

$$Ad{v}_{\mathsf{\Pi }}^{detPriv}\left(A\right)=\left|Pr[K\stackrel{\$}{\leftarrow }\mathcal{K}:A^{{\mathcal{E}}_K(·,·),\pi ,{\pi }^{-1}}=1]-Pr[A^{\$(·,·),\pi ,{\pi }^{-1}}=1]\right|$$

where $ is an oracle which on input $(A,M)\in \mathcal{A}\times \mathcal{M}$ outputs a random string of length $|{\mathcal{E}}_K(·,·)|$. We assume that adversary A does not allow repeated queries on the same inputs.

Definition 3 (Deterministic Authenticity (detAuth)).

Let $\mathsf{\Pi }=(\mathcal{K},\mathcal{E},\mathcal{D})$ be a DAE scheme with message space $\mathcal{M}$ and associated data space $\mathcal{A}$. Consider an adversary A with access to encryption and decryption oracles ${\mathcal{E}}_K$ and ${\mathcal{D}}_K$ respectively, and an ideal primitive π and its inverse ${\pi }^{-1}$. We then define A’s detAuth advantage in attacking Π as

$$Ad{v}_{\mathsf{\Pi }}^{detAuth}\left(A\right)=Pr[K\stackrel{\$}{\leftarrow }\mathcal{K}:A^{{\mathcal{E}}_K(·,·),{\mathcal{D}}_K(·,·),\pi ,{\pi }^{-1}}suceedsinforgery].$$

Definition 4 (PRF Advantage).

Let $f:\mathcal{K}\times \mathcal{X}\to \mathcal{Y}$ be a function with a non-empty key space $\mathcal{K}$ and A a computationally bounded adversary with access to an oracle, where $K\stackrel{\$}{\leftarrow }\mathcal{K}$ and $g\stackrel{\$}{\leftarrow }Func(\mathcal{X},\mathcal{Y})$. Thus, the PRF advantage of an adversary A on f is defined as

$$Ad{v}_f^{prf}\left(A\right)=\left|Pr[K\stackrel{\$}{\leftarrow }\mathcal{K}:A^{F(K,·)}=1]\right|-\left|Pr[g\stackrel{\$}{\leftarrow }Func(\mathcal{X},\mathcal{Y}):A^{g(·)}=1]\right|.$$

Definition 5 (rka-ind-advantage).

Let Φ be a set of mappings from ${\{0,1\}}^n$ to ${\{0,1\}}^n$. Let A be an adversary whose queries have the form $(\varphi ,X)$, where $X\in {\{0,1\}}^n$, $\varphi \in \mathsf{\Phi }$ and $\mathsf{\Phi }\in \{{\varphi }_{ident},{\varphi }_{const}\}$. The rka-ind-advantage of A in a Φ-restricted-related key attack on $\pi :{\{0,1\}}^n\times {\{0,1\}}^n\to {\{0,1\}}^n$ is given by

$$\begin{array}{ccc}Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi }}^{rka-ind}\left(A\right)\hfill & =& \left|Pr[K\stackrel{\$}{\leftarrow }{\{0,1\}}^n,A^{\pi (RK(·,K),·),\pi ,{\pi }^{-1}}=1]-\right.\hfill \\ \hfill & & Pr[g\stackrel{\$}{\leftarrow }Maps({\{0,1\}}^{2n},{\{0,1\}}^n),K\stackrel{\$}{\leftarrow }{\{0,1\}}^n,\hfill \\ \hfill & & \left.A^{g(RK(·,K),·),\pi ,{\pi }^{-1}}=1]\right|\hfill \end{array}$$

where, on query $(\varphi ,X)$, the oracle $\mathcal{O}\left(RK\right(·,K),·)$ returns the value of $\mathcal{O}\left(\varphi \right(K),X)$ to adversary A.

4. Specifications of dAELM

In this work, we propose a new deterministic authenticated encryption scheme dAELM for memory constrained devices. In the next subsection, we will explain the operational environment for our scheme followed by the description of dEALM in Section 4.2.

4.1. An Operational Scenario for the Proposed Scheme

Our scenario assumes three entities—namely the sender, the receiver, and the cryptographic module—are interacting in the protocol. We assume that the encryption and decryption functionality is carried out inside the cryptographic module, which has limited storage capability and a built-in secret key. The purpose of using the cryptographic module is to provide a secure practical setup to prevent the leakage of the secret key from the device. The sender encrypts a message M, generates the ciphertext and tag pair $(C,T)$, and sends the pair to the receiver. The receiver, having access to a similar cryptographic module, passes this $(C,T)$ pair to the module for decryption. This cryptographic module decrypts ciphertext C to produce M, and without storing this M, he passes it directly to the $MAC$ function for the calculation of tag $T^{\prime }$ ($MAC$ computation is done in parallel with decryption operation). If at the end computed tag $T^{\prime }$ gets verified with the received tag, (i.e., $T=T^{\prime }$) then cryptographic module reveals the session key $K^{\prime }$ to the receiver. After that, the receiver can decrypt C using $K^{\prime }$ to obtain the original M. The flow diagram for encryption and decryption are shown in Figure 2.

4.2. Description

This section defines the generic construction. The schematic structure of the proposed scheme is shown in Figure 3. Let $\mathcal{K}$ be a non-empty key space, and let $\mathcal{A}\subseteq {\{0,1\}}^{*}$ denote the associated data space.

Encryption of dAELM takes three inputs key $K\in \mathcal{K}$, associated data $A\in \mathcal{A}$, and plaintext M, where associated data is optional and produces ciphertext tag pair $(C,T)$ as output. Encryption works by first calculating MAC T over associated data A and plaintext M using key K. Further, T is encrypted using key $K+const$ to produce session key $K^{*}$. and plaintext M is then encrypted as C in a counter mode using T as a counter and $K^{*}$ as key. Finally, $(C,T)$ pair is produced as an output. For the decryption, first the session key $K^{*}$ is generated using K and T, and ciphertext is then decrypted using the $K^{*}$ to obtain plaintext M. Afterward, a tag is generated and compared with the received tag. If both tags are matched, then $K^{*}$ is returned, otherwise invalid. Now using $K^{*},T$, and C, original message M can be easily produced. Algorithms for encryption and decryption of dAELM constructions are shown in Algorithms 1 and 2 respectively, and the block diagrams representing encryption and decryption are shown in Figure 4 and Figure 5, respectively.

Algorithm 1: Encryption ${\mathcal{E}}_K(A,M)$

Algorithm 2: Decryption ${\mathcal{D}}_K$$(A,C,T)$

The underlying assumption for the dAELM construction is that it works for the block-cipher-based MAC only and works sequentially. In other words, we will consider only those MAC who processes message block-wise instead of processing as a whole.

5. Security Results for the New Construction dAELM

In this section, we provide the security bounds for the privacy and authenticity of the dAELM construction. We gave the security proof in the ideal cipher model. For writing this proof, we have made an assumption that the underlying MAC in the proposed scheme works in a sequential manner, i.e., as soon as it receives a message block, MAC computation starts. We used a code-based game playing framework introduced by Bellare and Rogaway in [19] to write the proof. Theorem 1 states the privacy, and Theorem 2 states the authenticity of the proposed construction in the following sections.

5.1. Privacy

Theorem 1.

Let $\mathsf{\Pi }=(\mathcal{K},\mathcal{E},\mathcal{D})$ be the proposed DAE scheme with an ideal primitive π, that operates on n bits. The adversary A is given access to π and ${\pi }^{-1}$. Then the privacy advantage of adversary A is given by

$$\begin{array}{ccc}\hfill {Adv}_{\mathsf{\Pi }}^{detPriv}\left(A\right)& =& Pr[K\stackrel{\$}{\leftarrow }\mathcal{K}:A^{{\mathcal{E}}_K,\pi ,{\pi }^{-1}}=1]-Pr[K\stackrel{\$}{\leftarrow }\mathcal{K}:A^{\$\left(\right),\pi ,{\pi }^{-1}}=1]\hfill \\ \hfill {Adv}_{\mathsf{\Pi }}^{detPriv}\left(A\right)& \le & Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi },\pi }^{rka-ind}\left({\mathcal{B}}_A\right)+{\displaystyle \frac{\sigma (\sigma -1)}{2^{n+1}}}+Ad{v}^{prf}\left(D_A\right)\hfill \end{array}$$

where $ is defined in Definition 2 in Section 3, and σ is the maximum number of block calls to π and ${\pi }^{-1}$ by encryption $\mathcal{E}$ and decryption $\mathcal{D}$. $Ad{v}^{prf}\left(D_A\right)$ is the prf advantage and $Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi },\pi }^{rka-ind}\left({\mathcal{B}}_A\right)$ is the related key advantage defined in Definitions 4 and 5 respectively in Section 3.

Proof. 

For the proof of privacy, we use code-based game-playing framework introduced by Bellare and Rogaway in [19]. We present a set of games from $G0$ to $G5$ (shown in the appendix in Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5). Starting from Game $G0$ and modifying it one step at a time, we construct a chain of games $G0⟶G1⟶\dots ⟶G5$. Here, Game $G0$ represents the actual construction, and Game $G5$ represents a completely random output. A description of each game is given the following:

$\mathbf{G}\mathbf{0}$: In this game, the encryption oracle perfectly simulates the proposed algorithm, and $\pi ,{\pi }^{-1}$ oracle simulates the ideal permutation and its inverse. As we will consider block-cipher-based MAC only, here we represent it by ${MAC}^{\pi (K,·)}\left(M\right)$, where $\pi (K,·)$ represents internal block-cipher calls on an input message M.

$$Pr[A^{{\mathcal{E}}_k,\pi ,{\pi }^{-1}}=1]=Pr[A^{G0}=1].$$

$\mathbf{G}\mathbf{1}$: Game $G1$ is the same as $G0$ except in $G1$ the block cipher calls during MAC computation and session key generation has been replaced by subroutine g, which generates a random output for a given input. Adversary A cannot make a direct call to the subroutine g.

Let us assume that an adversary A distinguishes these two games. We build an adversary $\mathcal{B}$ against the subroutine g who uses adversary A. The process is as shown in appendix in Figure A6. □

Adversary ${\mathcal{B}}_A$: In this game, the challenger chooses the key K, and the adversary ${\mathcal{B}}_A$ is provided with the oracles $\mathcal{O}\left(RK\right(*,K),·)$, which are simply a related key oracle and $\pi$ oracle. For each $(A,M)$, query adversary $\mathcal{B}$ internally calls oracle $\mathcal{O}$ and replies to adversary A with answer $(C,T)$.

Finally, A receives the $(C,T)$ pair for his queries either with the related key oracle or a random oracle. This game perfectly simulates the game $G0$ if $\mathcal{B}$ uses the related key oracle. Therefore, we have

$$Pr[G0]=Pr[{\mathcal{B}}_A^{\pi \left(RK\right(*,K),·),\pi }=1].$$

If adversary $\mathcal{B}$ uses a random oracle, then this game perfectly simulates game $G1$.

$$Pr[G1]=Pr[{\mathcal{B}}_A^{g(·,·),\pi }=1].$$

Lemma 1.

For any $rka-ind$ adversary A with q queries, there exists an adversary ${\mathcal{B}}_A$ such that

$$|Pr[A^{G1}=1]-Pr[A^{G0}=1]|\le Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi },\pi }^{rka-ind}\left({\mathcal{B}}_A\right)$$

where $G0$ and $G1$ are shown in Figure A1, and ${\mathcal{B}}_A$ is defined in Figure A6. ${\mathcal{B}}_A$ can make only two queries: $({\varphi }_{ident},·)$ and $({\varphi }_{const},·)$. $\mathsf{\Phi }=\{{\varphi }_{ident},{\varphi }_{const}\}$, where ${\varphi }_{ident}\left(x\right)=x$ and ${\varphi }_{const}\left(x\right)=x\oplus const$.

$\mathbf{G}{\mathbf{1}}^{\prime }$: Game $G{1}^{\prime }$ and $G1$ are exactly the same. Therefore,

$$Pr[A^{G{1}^{\prime }}=1]=Pr[A^{G1}=1].$$

$\mathbf{G}\mathbf{2}$: Game $G{1}^{\prime }$ and $G2$ differ only when a bad event occurs, otherwise, in absence of a bad event, both games are the same.

$$\mid Pr[A^{G{1}^{\prime }}=1]-Pr[A^{G2}=1]\mid \le Pr[bad].$$

A bad event occurs when an input to $\pi$ and ${\pi }^{-1}$ collide with the elements in set $I_{\pi }$. Therefore, the probability of a bad event will be equal to the probability of collision in $\pi$ and ${\pi }^{-1}$. Hence, the probability difference between $G1$ and $G2$ is

$$\mid Pr[A^{G{1}^{\prime }}=1]-Pr[A^{G2}=1]\mid \le \frac{\sigma (\sigma -1)}{2^{n+1}}.$$

$\mathbf{G}{\mathbf{2}}^{\prime }$: Games $G{2}^{\prime }$ and $G2$ are exactly the same. Therefore,

$$Pr[A^{G{2}^{\prime }}=1]=Pr[A^{G2}=1].$$

$\mathbf{G}\mathbf{3}$: Game $G{2}^{\prime }$ and $G3$ are identical. In Game $G3$, the $\mathcal{E}$ oracle itself simulates the behavior of $\pi$, so it becomes independent of $\pi$. Hence, Games $G2$ and $G3$ are the same from an adversarial point of view.

$$Pr[A^{G3}=1]=Pr[A^{G{2}^{\prime }}=1].$$

$\mathbf{G}\mathbf{4}$: Games $G3$ and $G4$ are the same except on Line 3.

Let us assume that an adversary A distinguishes these two games. We build an adversary D against the MAC oracle who uses adversary A. The process is as shown in appendix in Figure A7.

Adversary $D_A$: In this game, the challenger chooses the key K, and the adversary $D_A$ is provided with the oracles $\mathcal{O}(·)$, which is either a $MA{C}^{g(K,·)}(·)$ or $\$(·)$ oracle. For each $(A,M)$, query adversary D internally calls oracle $\mathcal{O}$ and replies to adversary A with answer $(C,T)$.

Finally, A receives the $(C,T)$ pair for his queries either with MAC oracle or random oracle. This game perfectly simulates Game $G3$ if D uses the MAC oracle. Therefore, we have

$$Pr[G3]=Pr[D_A^{MA{C}^{g(K,·)}(·),\pi ,{\pi }^{-1}}=1].$$

If adversary D uses a random oracle, then this game perfectly simulates Game $G4$.

$$Pr[G4]=Pr[D_A^{\$(·),\pi ,{\pi }^{-1}}=1].$$

Lemma 2.

For any $prf$ adversary A, there exists an adversary $D_A$ such that

$$|Pr[A^{G3}=1]-Pr[A^{G4}=1]|\le Ad{v}^{prf}\left(D_A\right).$$

$\mathbf{G}\mathbf{5}$: In Game $G4$, each ciphertext block is generated randomly and the concatenated ciphertext is returned to an adversary. Similarly, a tag is also generated randomly. However, in Game $G5$, ciphertext and tag of the desired length is selected as a random string and returned to an adversary. This move from $G4$ to $G5$ does not make any difference, as in both games output is generated as a completely random value. Therefore,

$$Pr[A^{G5}=1]=Pr[A^{G4}=1].$$

Finally, by using the fundamental lemma of the game-based framework,

$$\begin{array}{ccc}{Adv}_{\mathsf{\Pi }}^{detPriv}\left(A\right)\hfill & =& Pr[K\stackrel{\$}{\leftarrow }\mathcal{K}:A^{{\mathcal{E}}_K,\pi ,{\pi }^{-1}}=1]-Pr[K\stackrel{\$}{\leftarrow }\mathcal{K}:A^{{\$}_{pad}\left(\right),\pi ,{\pi }^{-1}}=1]\hfill \\ \hfill & =& |Pr[A^{G0}=1]-Pr[A^{G5}=1]|\hfill \\ \hfill & =& \mid (Pr[A^{G0}=1]-Pr[A^{G1}=1])\mid +\mid (Pr[A^{G1}=1]-Pr[A^{G{1}^{\prime }}=1])\mid \hfill \\ \hfill & & +\mid (Pr[A^{G{1}^{\prime }}=1]-Pr[A^{G2}=1])\mid +\mid (Pr[A^{G2}=1]-Pr[A^{G{2}^{\prime }}=1])\mid \hfill \\ \hfill & & +\mid (Pr[A^{G{2}^{\prime }}=1]-Pr[A^{G3}=1])\mid +\mid (Pr[A^{G3}=1]-Pr[A^{G4}=1])\mid \hfill \\ \hfill & & +\mid (Pr[A^{G4}=1]-Pr[A^{G5}=1])\mid \hfill \\ \hfill & \le & Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi },\pi }^{rka-ind}\left({\mathcal{B}}_A\right)+0+{\displaystyle \frac{\sigma (\sigma -1)}{2^{n+1}}}+0+0+Ad{v}^{prf}\left(D_A\right)+0.\hfill \end{array}$$

5.2. Authenticity

In this section, we analyze the security of the authenticity of the tag produced in our scheme. The forgery of an AE scheme is defined as the ability of an adversary A to generate a valid $(A,M,C,T)$ tuple, without directly querying it to the encryption oracle. The adversary is allowed to make a limited number of queries to encryption, decryption, and the $\pi$ and ${\pi }^{-1}$ oracles. For an AE scheme, we say the adversary A is successful in forging if it outputs an $(A,C,T)$ tuple, where ${\mathcal{D}}_K(A,C,T)\ne INVALID$ and adversary A has not asked fora query ${\mathcal{E}}_K(A,M)$ that resulted in response $(C,T)$.

Let $Ex{p}_{\mathsf{\Pi }}^{Auth}\left(A\right)$ be the forging experiment for a given $AE$ scheme $\mathsf{\Pi }=(\mathcal{K},\mathcal{E},\mathcal{D})$. Then the forging experiment is defined as follows:

• Adversary A can query encryption oracle $\mathcal{E}$ and decryption oracle $\mathcal{D}$ at most $q_{enc}and{q}_{dec}$ times, respectively.
• All the query responses of encryption oracle $\mathcal{E}$ are stored in a set, say, R. This set contains an $(A,C,T)$ tuple, which has been returned by an encryption query.
• If adversary A is able to generate a new $(A,C,T)$ pair ∉R that produces valid message M, then he wins and output is 1; otherwise, output is 0, after trying $q_{dec}$ number of queries.

We say the adversary wins, i.e., he succeeds in creating a forgery if $Ex{p}_{\mathsf{\Pi }}^{Auth}\left(A\right)=1$. Therefore, the advantage of an adversary in forging the scheme is defined as

$$Ad{v}_{AE}^{detAuth}\left(A\right)=Pr[Ex{p}_{\mathsf{\Pi }}^{Auth}\left(A\right)=1].$$

Suppose an adversary makes a $q_{enc}$ number of encryption queries and stores a result in set R that consists of tuple $(A_i,C_i,T_i)$, where $1\le i\le q_{enc}$. Now his goal is to generate a new tuple $(A^{\prime },C^{\prime },T^{\prime })\notin R$, which generates a valid $M^{\prime }$ on verification.

Theorem 2.

Let $\mathsf{\Pi }=(\mathcal{K},\mathcal{E},\mathcal{D})$ be the proposed authenticated encryption scheme with an ideal primitive (π) that operate on n bits. The adversary A is given access to encryption oracle $\mathcal{E}$, decryption oracle $\mathcal{D}$, and the π and ${\pi }^{-1}$ oracles. Then $\mathsf{\Pi }=(\mathcal{K},\mathcal{E},\mathcal{D})$ is forgeable with the probability

$$\begin{array}{ccc}Pr[Ex{p}_{\mathsf{\Pi }}^{detAuth}\left(A\right)=1]\hfill & \le & Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi },\pi }^{rka-ind}\left({\mathcal{B}}_A\right)+{\displaystyle \frac{\sigma (\sigma -1)}{2^{n+1}}}+Ad{v}^{prf}\left(D_A\right)\hfill \\ \hfill & & +\frac{q_{dec}^2}{2^n}+\frac{2}{2^n}.\hfill \end{array}$$

where σ is a maximum number of blocks to $\pi ,{\pi }^{-1}$ by encryption oracle $\mathcal{E}$, and decryption oracle $\mathcal{D}$ and $q_{dec}$ is the number of queries to the decryption oracle. $Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi },\pi }^{rka-ind}\left({\mathcal{B}}_A\right)$ is the related key advantage, and $Ad{v}^{prf}\left(D_A\right)$ is the prf advantage.

Proof. 

To give authenticity proof, we first use the same sequence of games ($G0$–$G4$) as in privacy proof with an additional decryption oracle. This sequence of games transforms the MAC into a pseudorandom function, and the block cipher calls into ideal permutation by considering their respective advantages. Here, we are directly using the advantages of games from the above privacy proof. After these transformations, we do further analysis. □

There are two possible cases to consider:

• An adversary generates a forgery pair $(A^{\prime },C^{\prime },T^{\prime })$ which produces a valid $M^{\prime }$ such that $(\ast ,\ast ,T^{\prime })\in R$; i.e., he chooses a new ($A,C$) pair, which corresponds to the same tag $T_i(=T^{\prime })$ that has been previously used for some other $(A_i,C_i)$, where $1\le i\le q_{enc}$. T and $T^{\prime }$ will correspond to the same session key $K^{*}$ for a given key K. This same $K^{*}$ will result in the same output for further block cipher calls. This can be divided into cases.

  (a)

  $C^{\prime }=C_i$: In this case, necessarily $A^{\prime }\ne A_i$. As all block cipher outputs are the same, XORing them with $C(=C_i)$ will produce the same $M(=M_i)$. For a successful forgery, we need at least one parameter to be different in the $(A^{\prime },C^{\prime },T^{\prime })$ tuple. Since $C^{\prime }=C_i$ and $T^{\prime }=T_i$, $A^{\prime }$ should be different from $A_i$. Therefore, the probability of happening this case will be same as the birthday bound on the MAC output.

  (b)

  $C^{\prime }\ne C_i$: In this case, for $T_i(=T^{\prime })$, $C^{\prime }\ne C_i$ will result in $M^{\prime }\ne M_i$. Therefore, the probability of this case will again become the same as the birthday bound on the MAC output.

  Therefore, the overall probability of this case will be given by $\frac{q_{dec}^2}{2^n}$.
• An adversary generates a forgery pair $(A^{\prime },C^{\prime },T^{\prime })$, where $T^{\prime }$ is new, i.e. $(\ast ,\ast ,T^{\prime })\notin R$. This case is further possible in two scenarios:

  (a)

  An adversary is able to guess the key K correctly; i.e. he has access to the system and can generate any number of valid queries. The probability of this case will be equivalent to guessing the key, which is $\frac{1}{2^n}$.

  (b)

  Suppose adversary guesses the tag $T^{\prime }$ correctly for a given key K and $(A^{\prime },M^{\prime })$ pair. Then, for further calculations of ciphertext, he also needs to guess the session key $K^{\prime }$. Then only he can generate the forgery. Therefore, the probability of happening this case will be the product of the probability of guessing the tag $T^{\prime }$ and session key $K^{\prime }$ that is equal to $\frac{1}{2^{2n}}$.

  Therefore, the overall probability of this case will be $\frac{1}{2^n}$.

Hence, the overall advantage of authenticity is given as

$$\begin{array}{ccc}{Adv}_{\mathsf{\Pi }}^{detAuth}\left(A\right)\hfill & =& |Pr[A^{G0}=1]-Pr[A^{G4}=1]|+{\displaystyle \frac{q_{dec}^2}{2^n}}+{\displaystyle \frac{2}{2^n}}\hfill \\ \hfill & =& \mid (Pr[A^{G0}=1]-Pr[A^{G1}=1])\mid +\mid (Pr[A^{G1}=1]-Pr[A^{G{1}^{\prime }}=1])\mid \hfill \\ \hfill & & +\mid (Pr[A^{G{1}^{\prime }}=1]-Pr[A^{G2}=1])\mid +\mid (Pr[A^{G2}=1]-Pr[A^{G{2}^{\prime }}=1])\mid \hfill \\ \hfill & & +\mid (Pr[A^{G{2}^{\prime }}=1]-Pr[A^{G3}=1])\mid +\mid (Pr[A^{G3}=1]-Pr[A^{G4}=1])\mid \hfill \\ \hfill & & +\frac{q_{dec}^2}{2^n}+\frac{2}{2^n}.\hfill \end{array}$$

$$\begin{array}{ccc}{Adv}_{\mathsf{\Pi }}^{detAuth}\left(A\right)\hfill & \le & Ad{v}_{\pi \left(RK\right(·,K),·),\mathsf{\Phi },\pi }^{rka-ind}\left({\mathcal{B}}_A\right)+0+\frac{\sigma (\sigma -1)}{2^{n+1}}+0+0+Ad{v}^{prf}\left(D_A\right)\hfill \\ \hfill & & +\frac{q_{dec}^2}{2^n}+\frac{2}{2^n}.\hfill \end{array}$$

6. Comparison

In

Table 1. Results of a comparison of dEALM with sp-AELM, OAE2, and SIV, where $\tau$ represents the tag length.

Parameters	sp-AELM [10]	OAE2 [18]	SIV [8]	dAELM [This Paper]
Type of AE	Randomized	Randomized	Deterministic	Deterministic
Online Encryption	Yes	Yes	No	No
Online Decryption	No	Yes	No	No
Low memory support	Yes	Yes	No	Yes
Misuse-resistant	No	No	Yes	yes
Segmentation	Fixed size block	Variable size segment	Fixed size block	Fixed size block
Ciphertext expansion	$\tau$ bits	$\tau$ bits per segment	$\tau$ bits	$\tau$ bits

, we present a comparison of the newly proposed scheme dAELM with existing schemes sp-AELM [10], OAE2 [18], and SIV [8]. Among these four schemes, sp-AELM and OAE2 are randomized schemes requiring nonces to produce the randomness. The remaining two schemes, the SIV and the dAELM are deterministic. They use the available message entropy to omit the overhead of a nonce. Schemes sp-AELM and OAE2 support online encryption, whereas SIV and dAELM do not provide online encryption features due to their misuse-resistant behavior. As mentioned in [18], misuse-resistant AE schemes cannot be online since every bit of the ciphertext must depend on every bit of plaintext in a misuse-resistant scheme. This ensures that one cannot output the first bit of a ciphertext before reading the last bit of the plaintext. Among the four schemes, only OAE2 supports online decryption at the cost of generating a tag for every individual segment of the plaintext. All these schemes provide low memory support, except SIV. Further, sp-AELM and OAE2 are vulnerable to a nonce-repeating attack, while this is not the case with SIV and dAELM.

OAE2 operates by dividing the plaintext into variable size segments of user-determined lengths, whereas sp-AELM, SIV, and dAELM process the plaintext into fixed size blocks of fixed lengths. In sp-AELM, SIV, and dAELM, the ciphertext length is a sum of plaintext and tag length ($\tau bits$), whereas in the OAE2 scheme the tag is generated for each segment.

7. Software Implementation

We implemented the proposed scheme dAELM in ATmega128 microcontroller and compared the performance against an existing SIV scheme. ATmega128 microcontroller is an 8-bit AVR RISC-based microcontroller, which combines 128 KB of programmable flash memory, 4 KB SRAM, and a 4 KB EEPROM. The device supports throughput of 16 MIPS at 16 MHz and operates at 4.5–5.5 volts. We used the C language for programming ATmega 128. For the implementation of dAELM and SIV, we used the AES-128 as an underlying block cipher and HMACSHA1 as an underlying MAC function. We executed the experiments for the messages of various length and analyzed how much memory is taken by the program performing encryption and decryption.

Pseudocode of decryption is shown in Algorithms 3 and 4. Three additional functions are used for computing the HMACSHA1 tag without describing the details due to its wide compatibility. HMACSHA1.INIT() initializes an HMACSHA1 structure to use the hash function and the key. HMACSHA1.UPDATE() is repeatedly called with chunks of the messages to be authenticated. HMACSHA1.FINAL() completes the HMACSHA1 operation after the last message is processed and returns the message authentication code. For the decryption process, instead of storing the entire decrypted message after decrypting the entire ciphertext, it decrypts the four blocks (each of 128 bit), and HMACSHA1.UPDATE() takes them as an input repeatedly.

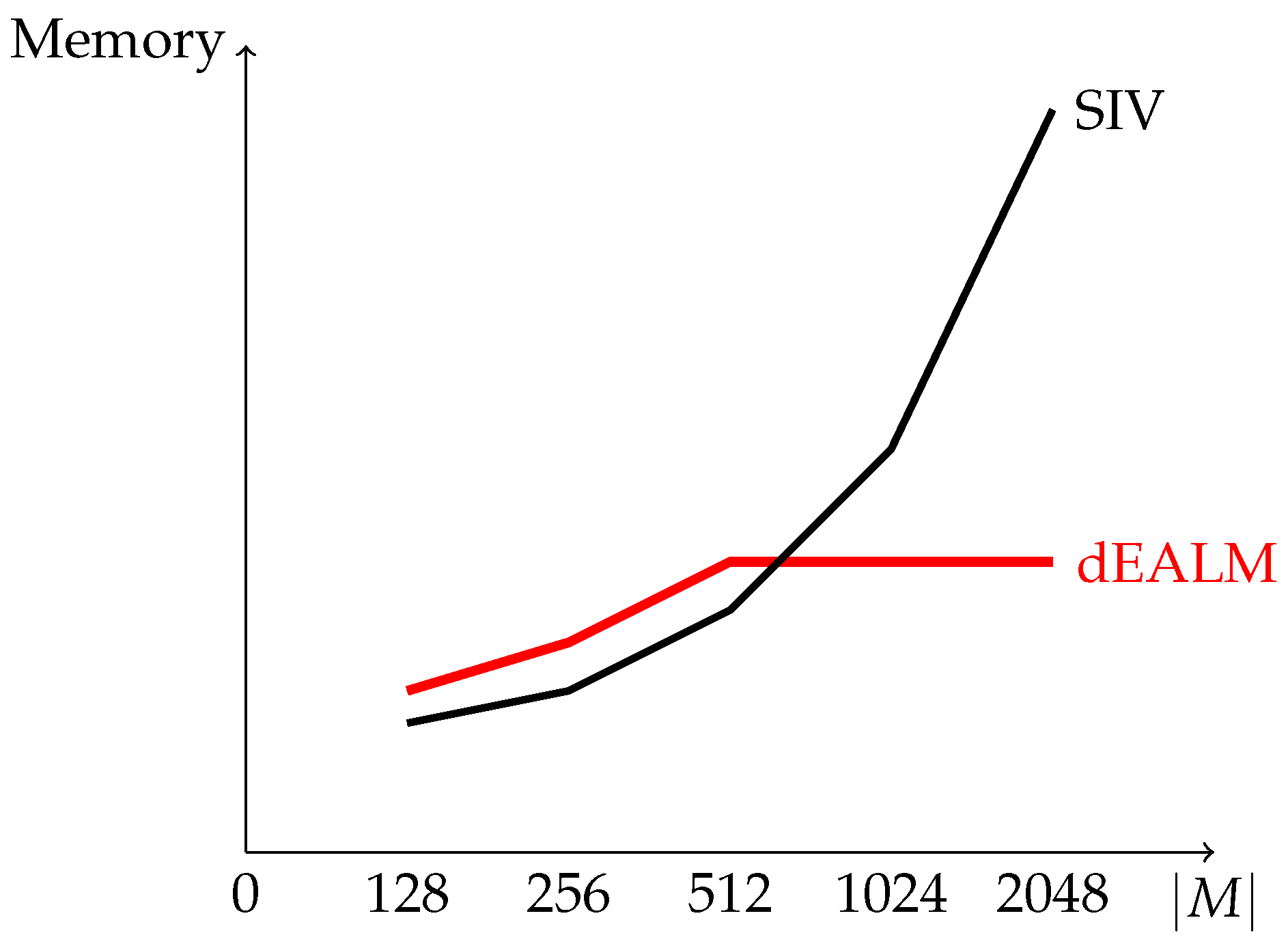
Figure 6 shows the memory usage during the decryption process for the various messages lengths. For the messages of length less than 512 bits, memory required by the decryption process for dAELM is a bit more than SIV due to one extra AES call for session key generation. This difference in memory usage of only 512 bits is because of the consideration of HMAC-SHA1 in our implementation, which process a message in 512 bit blocks. After 512 bits, memory usage becomes constant for dAELM, regardless of message length, whereas in SIV, the memory usage depends on the length of a message.

Algorithm 3: Decryption ${\mathcal{D}}_K(A,C,T)$

Algorithm 4:$AES\_CTR\_DEC\_4BLOCKS(K,C,CTR)$

$C=C_1\left|\right|C_2\left|\right|C_3\left|\right|C_4$ where $|C_i|=128$ for $i=1,2,3,4$  $M_1=C_1\oplus AE{S}_K\left(CTR\right)$  $M_2=C_2\oplus AE{S}_K(CTR+1)$  $M_3=C_3\oplus AE{S}_K(CTR+2)$  $M_4=C_4\oplus AE{S}_K(CTR+3)$  $M=M_1\left|\right|M_2\left|\right|M_3\left|\right|M_4$  Return M

In general, the memory required by dAELM is $\left|K\right|+|K^{*}|+|A|+|B|$, where $\left|K\right|$ and $|K^{*}|$ is a length of a key and a session key, respectively, $\left|A\right|$ is the length of an associated data, and $\left|B\right|$ is the block size of the message processed in the MAC. For example, $\left|B\right|$ is 512 bits in the case of HMAC-SHA1. However, the memory required by SIV is $\left|K\right|+\left|A\right|+\left|M\right|$, where $\left|K\right|,\left|A\right|$, and $\left|M\right|$ represent the length of a key, associated data, and a message, respectively. In other words, memory usage for dAELM depends on the block size of MAC, which is constant, whereas, for SIV, it depends on the message length. If we consider a MAC with a small block size, then dAELM will perform better than SIV, even for short messages.

8. Discussion

In this work, our proposed $AE$ scheme targets the devices, which have a limited amount of memory and are incapable of processing the large message. These memory-constrained devices include, in tiny IoT devices, cryptomodules such as TPMs (trusted platform modules), which are used in laptops, tablets, smartphones, set-top-boxs, ATM machines, etc. A cryptomodule is basically a secure cryptoprocessor used for carrying out the specific cryptographic operations and storing secret keys. These cryptomodules usually have a storage capacity of only a few bytes, which may not be sufficient to process long messages. For example, ATMELAT97SC3204 is a TPM that has only 1732 bytes of storage for the user-defined data. Similarly, these small IoT devices also have a limited amount of storage. Under these memory constraints, it becomes impossible to process a large data in one go. Hence, our proposed scheme provides a solution for all those memory-constrained devices to process a long message.

9. Conclusions

In this work, we presented a new DAE scheme (dAELM) that is suitable for memory-constrained scenarios. Our proposed construction is based on the SIV mode and does not require nonce as an input. We also provide the security bounds for both the privacy and the authenticity of the construction.