1. Introduction
SIMON and SPECK are two families of block ciphers that were designed by the NSA [
1]. These lightweight ciphers have widely attracted the attention of researchers [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14]. In [
2], some linear characteristics for the SIMON family of block ciphers were presented. The authors of [
3] provided differential attacks of up to slightly more than half of the number of rounds for SIMON and SPECK families of block ciphers. A technique for the automatic search for differential trails in ARX ciphers was used to improve the previous attacks on SIMON and SPECK block cipher families in [
4]. In [
5], significantly improved differential attacks against all 10 variants of SPECK were presented. Two variants of the SIMON family of ciphers were investigated in [
6], and a 14-round linear approximation for SIMON-32, as well as a 17-round linear approximation for SIMON-48 were presented. In [
7], using quadratic constraints or constraints from H-representation of a specific convex hull, a method for constructing a mixed-integer (non)linear programming model for SIMON was provided. The authors of [
8] studied the security of a version of SIMON, using some kind of truncated differentials, and an attack of up to 26 rounds was presented. In [
9], improved linear attacks on all reduced versions of SIMON were presented with dynamic key guessing. The authors of [
10] showed that overlooking linear hulls, formed by a single round, may lead to the wrong estimations of linear correlations. In [
11], a partial linear mask table was used to speed up the search progress to attack reduced round SPECK. In [
12], firstly, the properties of the linear approximation of the bitwise AND with dependent input bits were investigated, and then, using MILP, improved linear characteristics for several versions of SIMON were obtained. The authors of [
13], reducing the sufficient bit conditions corresponding to the differential propagations, and avoiding the guess for some subkey bits or equivalent key bits involved in the conditions, extended differential attacks on SIMON by 2–4 more rounds. In [
14], an algorithm to find a differential path in ARXstructures was proposed, and based on this, previous differential attacks on various versions of SPECK were improved. All of the mentioned papers investigated SIMON and/or SPECK from linear and/or differential aspects and examined the resistance of these ciphers against linear and differential cryptanalysis.
Some authors have studied the properties of the components of these ciphers from theoretical aspects [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24]. In [
15,
16], linear and differential properties of SIMON-like ciphers were investigated, from the mathematical viewpoint, and an efficient formula for computing linear and differential probabilities of SIMON was presented. In [
18], after a theoretical examination, the authors studied how rotational cryptanalysis is affected when constants are injected. In [
17], after some mathematical investigations, the resistance of SIMON-like ciphers against differential cryptanalysis was analyzed, and upper bounds for the differential probabilities of differential characteristics for some certain instances were provided. In [
19,
20], upon some theoretical studies, upper bounds for differential probabilities and squared correlations for SIMON-like ciphers were provided, and provably optimal differential trails for various versions of SIMON were presented. In [
21,
22,
23,
24], linear properties of addition mod
were investigated, from the mathematical viewpoint.
In this note, based on the previous studies, nonlinear components of SIMON and SPECK families of ciphers are examined. The method of the research of this paper is somewhat similar to [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24]: we study the linear and differential properties of the components of SIMON and SPECK families of block ciphers, from the mathematical viewpoint.
The only nonlinear component of SIMON family of block ciphers is the quadratic mapping:
for
. The mapping
f is equivalent to
below, through a permutation of coordinates and EA-equivalence:
Based on the previous research on the linear and differential properties of SIMON [
15,
16,
18,
19,
20], a simple explicit formula for differential probabilities and squared correlations of
is given. Besides, a full description of DDT and LAT of
is provided, in this paper.
The only nonlinear operation in the SPECK family of block ciphers is addition mod
, with
. Based on the previous studies on the linear and differential properties of this operation [
21,
22,
23,
24], a closed formula for differential probabilities and squared correlations of modular addition mod
, along with straightforward algorithms for finding the output masks with the maximum squared correlation, given the input masks and the output differences with the maximum differential probability, given the input differences, are presented.
By the aid of the main contribution of the current paper, i.e., the full description of DDT and LAT of , which in turn leads to the full determination of DDT and LAT of the core quadratic mapping of SIMON, as well as the straightforward algorithms for finding the optimum output differences, given the two input differences and the optimum output masks, given the two input masks for the operation of modular addition mod , the process of finding good linear and differential characteristics for the lightweight ciphers SIMON and SPECK could be sped up, and the complexity of linear and differential attacks against these ciphers could be reduced.
Section 2 gives the preliminary notations and definitions.
Section 3 is devoted to the examination of the linear and differential properties of SIMON.
Section 4 discusses the linear and differential properties of SPECK, and
Section 5 is the conclusion.
2. Preliminary Notations and Definitions
In the sequel i, j, m, n, t, r, and s are natural numbers. The n-dimensional space over , the finite field with two elements, is denoted by . Left rotation by t times on x is denoted by . The operations of AND, OR, and XOR are denoted by ⊙, ∨, and ⊕, respectively. The Hamming weight of a binary number or vector x is represented by and the complement of x by . The standard dot product in is denoted by ·. The all one and the all zero vectors are represented by and , respectively.
Let
. Define:
The matrix or table
,
, is called the Difference Distribution Table (DDT) of
f. The normalized DDT of
f is defined as:
Not that for every
, we have:
If we have for some , then x is called an admissible output difference for a in this paper.
The Walsh coefficient of
f on
a and
b is defined as:
The matrix or table
,
, is called the Linear Approximation Table (LAT) of
f. The normalized LAT of
f is defined as:
Not that for every
, we have:
If we have for some , then x is called an admissible input mask for b, in the current paper.
Let
. Put
with
,
: the indices are calculated mod
n. In this paper, this representation is called the pseudo-octal representation of
a. It is obvious that every binary number
a has a unique pseudo-octal representation; but a sequence of octal symbols is not necessarily the pseudo-octal representation of a binary number. If a sequence of octal symbols is the pseudo-octal representation of a binary number, then it is called admissible in this paper. For an
to be admissible, the consecutive appearance of octal symbols should be as follows:
For example, 110010 has the pseudo-octal representation 641253. This representation is used in
Section 3.
Another representation for binary numbers that is used in
Section 3, is as follows: any binary number could be represented by consecutive gaps and blocks. A gap is a series of zeroes, and a block is a series of ones. Any number, except the all one and all zero vectors, up to a rotation, consists of some
m many gaps and blocks
, with
,
. For example, the number 0011010110, rotated two times to the left, is of the form
.
3. Linear and Differential Properties of SIMON
Linear and differential properties of the core quadratic mapping of the SIMON family of block ciphers were studied in [
15,
16,
17,
18,
19,
20]. The mapping:
is equivalent to the core quadratic mapping of SIMON, through a permutation of coordinates and EA-equivalence [
15,
16]. In this section, based on the previous examinations, the simple closed formula for differential probabilities and squared correlations of
is given. Besides, a full description of DDT and LAT of
is provided. Firstly, a theorem from [
15,
16] is recalled:
Theorem 1. The differential probability of ϕ on α and β is:where: Theorem 2. Let consist of gaps and blocks of the form , , according to the notations presented in Section 1. Then, for any admissible output difference , we have:where ; i.e., s is the number of gaps of length greater than one. Proof. Firstly, note that
, where:
According to
Table 1 and (
1), the theorem is proven via case-by-case analysis. The blocks of length one and the blocks of length greater than one should be treated separately. Furthermore, the gaps before and after this block should be analyzed separately, according to their lengths: again, the gaps of length one and the gaps of length greater than one should be verified separately. All the cases could also be examined by programming. For instance, consider the pattern
with the pseudo-octal representation
. Either the pattern is of the form
or
in pseudo-octal representation, in which the symbols 2, 3, 6, and 4 each add one to the absolute value of the exponent of differential probability, according to
Table 1; or the leftmost block in the pattern is of length greater than one. For the sake of simplicity, suppose that the pattern is of the form
, which corresponds to
, where 4, 6, 3, 6, and 3 each have a contribution of one. Therefore, for the presented pattern, the differential probability equals the weight, plus the number of blocks, minus the number of gaps of length one. ☐
In spite of the fact that the core mapping of SIMON does not inherit all the visual properties of
, but regarding the equivalence between the core quadratic mapping of SIMON and
, Theorem 5 in [
19] and Lemma 2 in [
17] are direct results of Theorem 2.
Before stating the next theorem, some notations are explained. In the following theorems,
denotes an arbitrary
t-bit number, or equivalently, the set off all
t-bit numbers, and
stands for the set of
t-bit words with a half-rate. For example:
Theorem 3. Let consist of gaps and blocks of the form , . Then, all the admissible output differences for α could be represented by gaps and blocks of the following forms. Note that, rotating α by a suitable number, we could start from the first block: Proof. Regarding
Table 1, for x to be admissible,
(in which the symbols are in pseudo-octal representation) should follow the next patterns:
For example, for the symbol 5, only for 0, 1, 6, and 7, both:
are 0. Since
and for any admissible
, we have
, so there are exactly
admissible output differences. Thus, it only suffices to show that all the presented output differences are admissible. Again, according to
Table 1, it is straightforward to prove that every presented output difference is admissible: the case-by-case analysis or programming could be applied to prove the theorem. For instance, consider the input pattern
with pseudo-octal representation
. The output admissible patterns could be of the following forms:
considering
Table 1. Note that the number of these patterns is
. Therefore, the theorem is proven in this case. ☐
As an example, let
and
. Since
and
has one gap of length greater than one, so for any admissible
, we have:
by Theorem 2. Rotating
two times to the right gives 00001011. Now, by Theorem 3, the admissible output differences are of the form
; i.e.,
The actual differences are the above numbers, rotated two times to the left.
Theorem 4. Let consist of gaps and blocks of the form , . Then, for any admissible input mask , we have:where ; i.e., t is the number of blocks of odd length. Furthermore, all the admissible input masks consist of gaps and blocks of the form:where denotes all the -bit patterns with: Proof. The theorem could be proven either directly, using Theorem 5 in [
15,
16], or considering the comments in Appendix A (A.2) in [
15]. In fact,
is equal to:
Now, if
is even, the contribution of this block in the absolute value of the exponent is only its length, and if
is odd, the contribution is equal to its length, plus one. Therefore, the presented formula is correct. For the admissible input masks, note that similar to the case of differential probability, since we have
, for any admissible
, and
, so there are exactly
admissible input masks. Again, either by Theorem 5 in [
15,
16] or considering the comments of Appendix A (A.2) in [
15], the admissibility of the presented input masks is proven. ☐
Regarding the equivalence between the core quadratic mapping of SIMON and
, Theorem 5 in [
20] is a direct result of Theorem 4.
Let
and
. Since
and
has one block of odd length, so for any admissible
, we have:
by Theorem 4. Rotating
, two times to the left, gives 10110000. Now, by Theorem 4, the admissible output masks are of the form
; i.e.,
The actual masks are the above numbers, rotated two times to the right.
Remark 1. It is worth noting that, Theorems 3 and 4 characterize the set of all admissible input masks (output differences) for a given output mask (input difference) for the mapping ϕ; this in turn culminates in complete determination of the corresponding input masks (output differences) for the core quadratic mapping of SIMON. Note that, using the previous methods and without the proposed characterization, given any input difference or output mask, we should search for desired admissible output differences or input masks and then verify whether they are admissible or not; but, with the aid of the provided characterization, we simply search within the set of all admissible masks or differences. Further, we could even save a table for the sparse masks or differences (the ones with a low Hamming weight) to speed the search process. This way, the complexity of finding optimal linear and differential characteristics could be reduced, significantly.
Defining as the number of such that for any admissible and as the number of such that for any admissible , we have the following propositions.
Proof. The least absolute value for the exponent is two, which corresponds to n numbers of Hamming weight one. There are n numbers with only one block of length two, whose absolute value for the exponent equals three, and n numbers with only one pattern of 101, whose absolute value for the exponent is also equal to three. The n numbers with weight have the absolute value for the exponent equal to n, as well as the n numbers with weight . ☐
The proof of the next preposition is straightforward.
Table 2 presents
and
for
.
Remark 2. On the one hand, the discussions of this section, combined with other techniques and using suitable data structures, could improve linear and differential attacks on the SIMON family of block ciphers, as stated in Remark 1. On the other hand, these studies show why this family of ciphers is resistant to (classical?) linear and differential cryptanalysis: in fact, regarding Table 2, we see that the number of input differences and output masks with large differential probability or large squared correlation is small, compared to . 4. Linear and Differential Properties of SPECK
In this section, based on the previous studies on linear and differential properties of the operation of addition mod , the explicit formula for differential probabilities and linear biases of modular addition mod , along with straightforward algorithms for finding the output masks with maximum squared correlation, given the input masks and the output differences with the maximum differential probability, given the input differences, are presented.
Let
,
, and
be the two input masks and the output mask for the operation of addition mod
, respectively. We wish to find
, where
. Put:
The sequence
could be represented as a series of blocks
,
, for some
m, where each
is an e-block (a block of symbols 3, 5, and 6), an o-block (a block of symbols 1, 2, and 4), a 0-block, or a 7-block. The number of symbols in a block
is denoted by
, in the current paper. The following theorem, whose proof is illustrated in
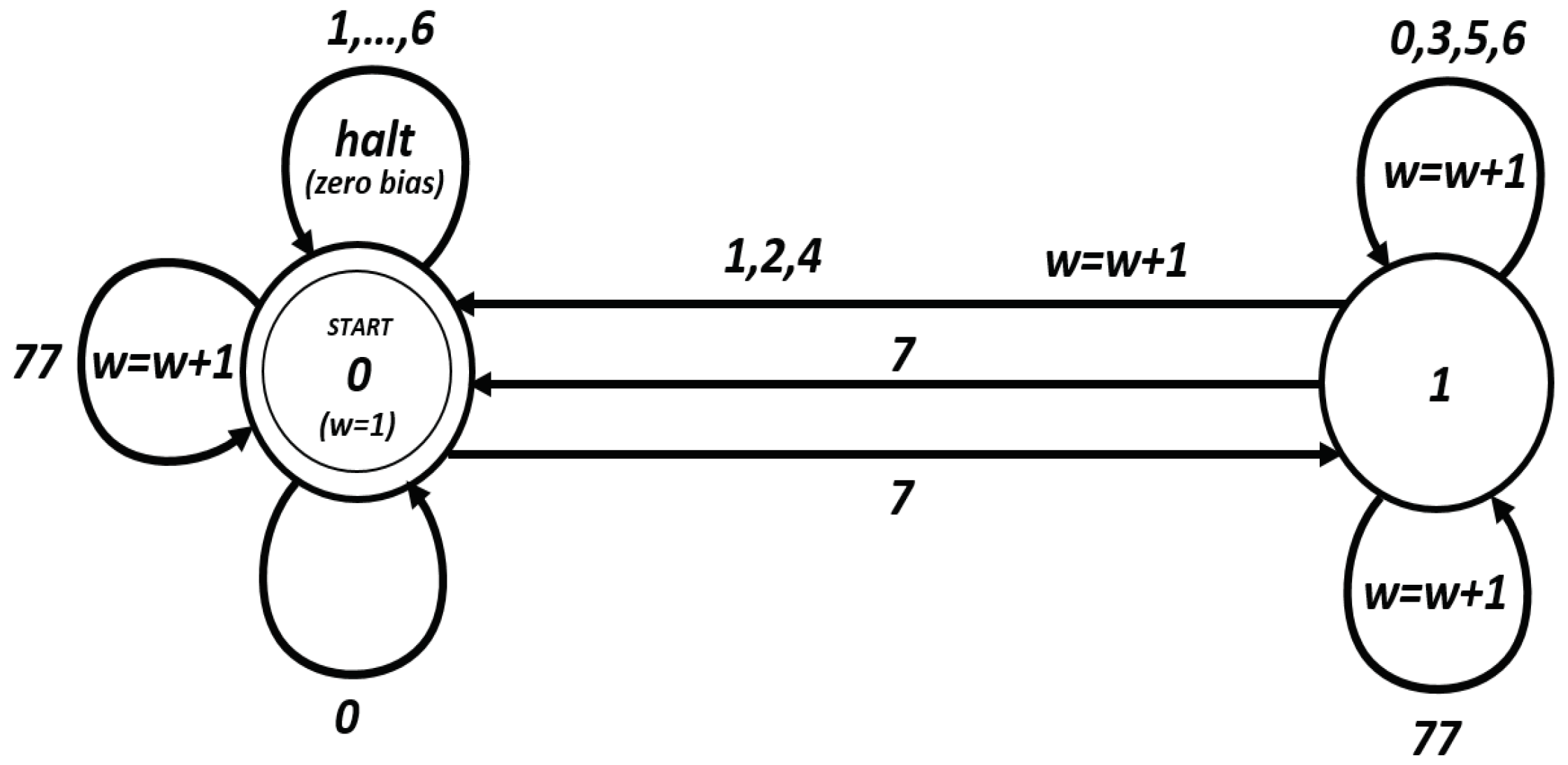
Figure 1, is proven in [
24]. Start from the START state and traverse the diagram in
Figure 1. If we are in State 0 and we see a symbol in
, then the correlation is zero. Otherwise, the absolute exponent for the bias is the number of times we see
. Note that if this bias equals
, then the squared correlation is equal to
.
Theorem 5. With the notations as above, we have:where:and , and for , Here, stands for the set of all e-blocks, stands for the set of all o-blocks, denotes the set of all 7-blocks, and represents the set of all 0-blocks.
We have if and only if there exists such that and , and , otherwise. Note that, in any case, the absolute value for the exponent of any nonzero linear bias is greater than or equal to .
Suppose that
, and
, are the two input masks. Put:
Clearly,
consists of 0-blocks, 3-blocks, and
-blocks, i.e., blocks of Symbols 1 and 2. Now, regarding the diagram in
Figure 1, we have the following straightforward algorithm for finding output masks with maximum correlation:
“Firstly, put for every symbol in every 0-block, and , otherwise. Therefore, we have 0-blocks, 7-blocks, and e-blocks. Now, starting from the first block, for each series of consecutive 0-blocks and 7-blocks, put for the last symbol in each 7-block of odd length, to make it of even length. For the last 7-block in this series of blocks, if it is of even length, make it of odd length by setting , for the last symbol in this 7-block. For each e-block, make the last symbol an o-block of length one by setting for its corresponding symbol. Note that, if the first block which is always a 7-block is of length one, it could not be rendered an even block; so, if there is a series of 0-blocks and 7-blocks after this 7-block, then the first appearing 7-block should be made of odd length.”
As an example, Let
,
Then, an optimum output mask is .
Let
,
, and
be the two input differences and the output difference, respectively. We want to find:
Here, + stands for addition mod
. Put:
The sequence
could be represented as a series of blocks
,
, for some
m, where each
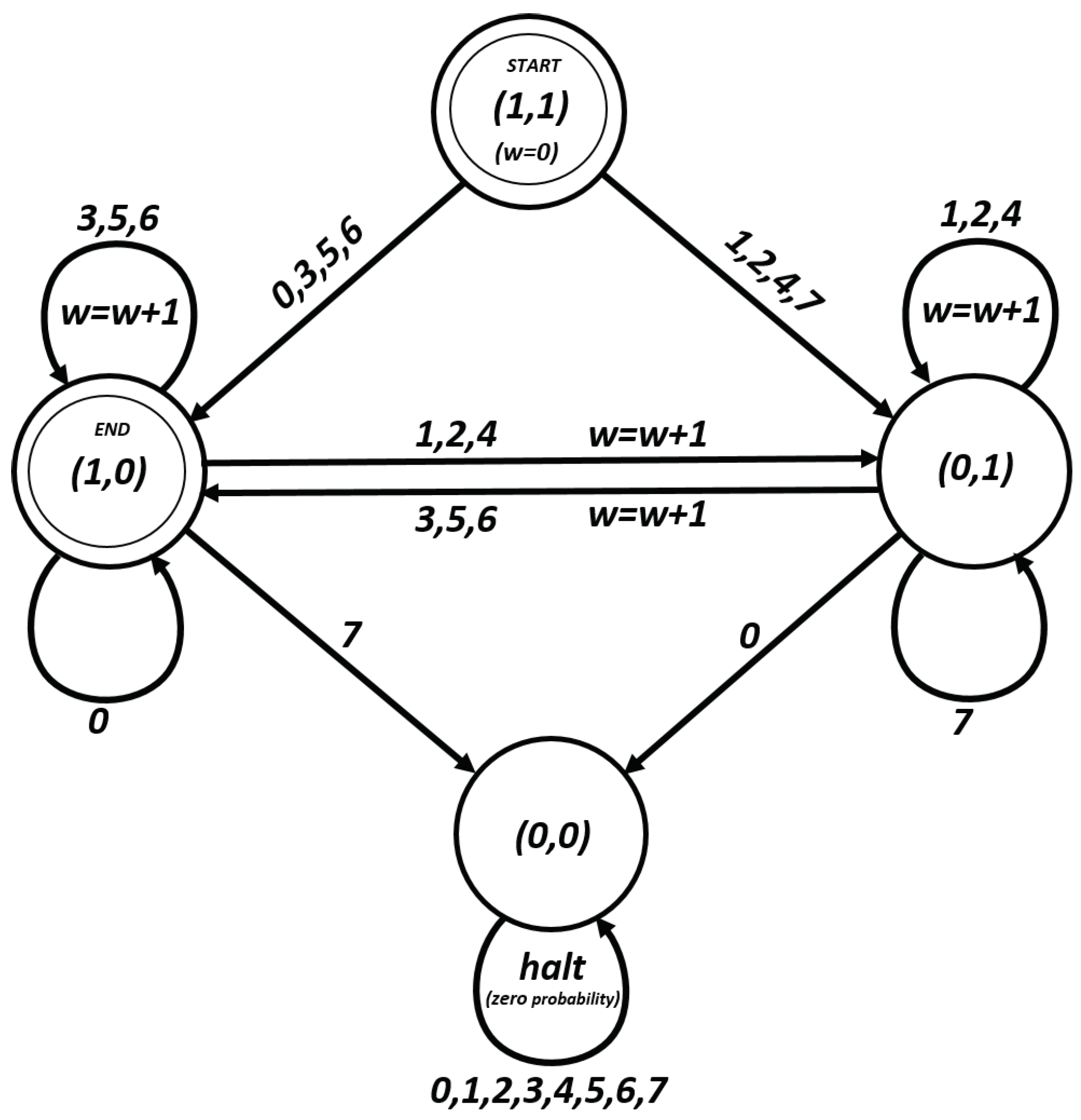
is an e-block, an o-block, a 0-block, or a 7-block. The next theorem is proven considering
Figure 2. This picture is due to [
18].
Theorem 6. With the notations as before, we have:where:and if and only if there exists an , such that and , or and , or when ; and , otherwise. The correctness of the following algorithm is justified considering
Figure 2: note that the differential probability is zero if we end at states (1,0) or (0,0). The absolute value for the exponent is equal to the number of times we see
.
Suppose that
and
are the two input differences. Put:
Obviously,
consists of 0-blocks, 3-blocks, and
-blocks. Now, regarding the diagram in
Figure 2, we have the following straightforward algorithm for finding output differences with maximum differential probability:
“If is a 0-block and is a -block, for some t, then make this -block an e-block, by setting for all the symbols in this block. If is a 0-block and is a 3-block, then make an o-block of length one, by setting for the last symbol in this 0-block. If is a 3-block and is a -block, then make this -block an o-block by setting for all the symbols in this block. If is a 3-block and is a 0-block, then make an e-block of length one, by setting for the last symbol in this 3-block. If is an o-block and is a 0-block, then make an e-block of length one by setting for the last symbol in this o-block. If is an e-block and is a 3-block, then make an o-block of length one by setting for the last symbol in this 0-block. Finally, if the last block is an o-block or a 3-block, make an e-block of length one by setting for the last symbol in the o-block or setting for the last symbol in the 3-block.”
As an example, Let
,
Then, an optimum output difference is .
Remark 3. Similar to the case of SIMON, the presented algorithms characterize optimum output masks (output differences) for given input masks (input differences) for the operation of addition mod . Without the proposed algorithms, given any input differences or masks, we should search for desired admissible output differences or masks; but, with the aid of the proposed algorithms, we simply search within the set of optimum masks or differences. In the case of sparse masks or differences (the ones with a low Hamming weight), even a table could be saved to speed the search process. This way, the complexity of finding linear and differential characteristics could be reduced, significantly.
Remark 4. On the one hand, the studies of this section, combined with other methods and using suitable data structures, could reduce the complexity of linear and differential attacks on the SPECK family of block ciphers and speed up the search for finding the optimal differences or masks. On the other hand, they somehow show why this family of ciphers is resistant to (classic?) linear and differential cryptanalysis: Theorems 5 and 6 show that, whatever the two input masks and differences are, the absolute value in the exponent of nonzero differential probabilities and squared correlations could not be smaller than some lower bounds.