An Attack Bound for Small Multiplicative Inverse of φ(N) mod e with a Composed Prime Sum p + q Using Sublattice Based Techniques

Abstract

In this paper, we gave an attack on RSA (Rivest–Shamir–Adleman) Cryptosystem when $\phi (N)$ has small multiplicative inverse modulo e and the prime sum $p+q$ is of the form $p+q=2^n{k}_0+k_1$, where n is a given positive integer and $k_0$ and $k_1$ are two suitably small unknown integers using sublattice reduction techniques and Coppersmith’s methods for finding small roots of modular polynomial equations. When we compare this method with an approach using lattice based techniques, this procedure slightly improves the bound and reduces the lattice dimension. Employing the previous tools, we provide a new attack bound for the deciphering exponent when the prime sum $p+q=2^n{k}_0+k_1$ and performed an analysis with Boneh and Durfee’s deciphering exponent bound for appropriately small $k_0$ and $k_1$.

1. Introduction

RSA Cryptosystem [1] is the first public key cryptosystem invented by Ronald Rivest, Adi Shamir and Leonard Adleman in 1977. The primary parameters in RSA are the modulus $N=pq$, which is the product of two large distinct primes, a public exponent e such that $gcd(e,\phi (N))=1$ and a private exponent d, the multiplicative inverse of e modulo $\phi (N)$. In this system the encryption and decryption are based on the fact that for any message m in $Z_N$, $m^{ed}=mmodN$. The security of this system depends on the difficulty of finding factors of a composite positive integer, which is a product of two large primes. In 1990, M. J. Wiener [2] was the first one to describe a cryptanalytic attack on the use of short RSA deciphering exponent d. This attack is based on continued fraction algorithm which finds the fraction $\frac{t}{d}$, where $t=\frac{ed-1}{\phi (n)}$ in a polynomial time when d is less than $N^{0.25}$ for $N=pq$ and $q<p<2q.$ Using lattice reduction approach based on the Coppersmith techniques [3] for finding small solutions of modular bivariate integer polynomial equations, D. Boneh and G. Durfee [4] improved the wiener result from $N^{0.25}$ to $N^{0.292}$ in 2000 and J. Blömer and A. May [5] has given an RSA attack for d less than $N^{0.29}$ in 2001, which requires lattices of dimension smaller than the approach by Boneh and Durfee. In 2006, E. Jochemsz and A. May [6], described a strategy for finding small modular and integer roots of multivariate polynomial using lattice-based Coppersmith techniques and by implementing this strategy they gave a new attack on an RSA variant called common prime RSA.

In the paper [7], first we described an attack on RSA when $\phi (N)$ has small multiplicative inverse k of modulo e, the public encryption exponent by using lattice and sublattice based techniques. Let $N=pq,q<p<2q,p-q=N^{\beta }$ and $e=N^{\alpha }>p+q$. As $(e,\phi (N))=1,$ there exist unique $r,s$ such that $(p-1)r\equiv 1(mode)\mathrm{and}(q-1)s\equiv 1(mode).$ For $k=rs(mode)$, $k\phi (N)\equiv 1(mode)$ and define $g(x,y)=x(y+B)-1$ where $B=N+1-⎡2\sqrt{N}⎤$. Then the pair $(x_0,y_0)=(k,-((p+q)-⎡2\sqrt{N}⎤))$ is a solution for the modular polynomial equation $g(x,y)\equiv 0(mode)$. Now applying the lattice based techniques given by Boneh-Durfee in [4] using $x,y$ shifts and using only x shifts to the above modular polynomial equation, we get the attack bounds for $\delta$, $\left|k\right|\le N^{\delta }$ are $\delta <\frac{3\alpha +\beta -2\sqrt{\beta (3\alpha +\beta )}}{3}$ and $\delta <\frac{\alpha -\beta }{2}$, respectively. Also, we improved the bound for $\delta$ up to $\alpha -\sqrt{\alpha \beta }$ by implementing the sublattice based techniques given by Boneh and Durfee in [4] under the condition $\delta >\alpha -\beta (1+\alpha )$ and improved the bound for $\delta$ up to $\delta <\frac{2\alpha -6\beta +2\sqrt{{\alpha }^2-\alpha \beta +4{\beta }^2}}{5}$ by implementing the sublattice based techniques with lower dimension given by J. Blömer and A. May in [5]; this bound is slightly less than the above bound but this method requires lattices of smaller dimension than the above method. All these attack bounds are depending on the prime difference $p-q=N^{\beta }$ and $\alpha -\sqrt{\alpha \beta }$ is the maximum upper bound for $\delta$.

Later in paper [7], we described that, for $\beta \approx 0.5$, the maximum bound for $\delta$ may be improved if the prime sum $p+q$ is in the form of the composed sum $p+q=2^n{k}_0+k_1$ where n is a given positive integer and $k_0$ and $k_1$ are two suitably small unknown integers. Define the polynomial congruence $f(x,y,z)\equiv 0(mode)$ for

$$f(x,y,z)=\left\{\begin{array}{c}(N+1)x+xy+(2^n)xz-1\mathrm{if}|k_0|\le |k_1|\hfill \\ 2^{n^{\prime }}x(N+1)+xy+2^{n^{\prime }}xz-2^{n^{\prime }}\mathrm{if}|k_1|\le |k_0|\hfill \end{array}\right.$$

where $2^{n^{\prime }}$ is an inverse of $2^{n}mode.$ By using lattice based techniques to the above polynomial congruence, the attack bound for $\delta$ is such that $\delta <\frac{1}{2}\alpha -\frac{1}{2}{\gamma }_1+\frac{1}{16}{\gamma }_2-\frac{1}{16}\sqrt{48(\alpha -{\gamma }_1){\gamma }_2+33{\gamma }_2^2}$ where $N^{{\gamma }_1}$, $N^{{\gamma }_2}$ are the upper bounds for $max\left\{\right|k_0|,|k_1\left|\right\}$, $min\left\{\right|k_0|,|k_1\left|\right\}$ respectively.

Now, in this paper, we slightly improved the above bound by using the sub-lattice based techniques given by J. Blömer, A. May in [5] to the above polynomial congruence and this method requires lattice of smaller dimension than the above method. The new bound on $\delta$ is $\frac{1}{2}\alpha -\frac{1}{2}{\gamma }_1-\frac{1}{6}\sqrt{6(\alpha -{\gamma }_1){\gamma }_2+3{\gamma }_2^2}$ and showed that this is a little bit greater than the former bound graphically. Note that this new attack bound is also an attack bound for the deciphering exponent d.

2. Preliminaries

In this section we state basic results on lattices, lattice basis reduction, Coppersmith’s method and Howgrave-Graham theorem that are based on lattice reduction techniques.

Definition 1.

Let ${\mathit{b}}_1,{\mathit{b}}_2,\dots ,{\mathit{b}}_n\in {\mathbb{R}}^m$ be a set of linearly independent vectors. The lattice L generated by ${\mathit{b}}_1,{\mathit{b}}_2,\dots ,{\mathit{b}}_n$ is the set of linear combinations of ${\mathit{b}}_1,{\mathit{b}}_2,\dots ,{\mathit{b}}_n$ with coefficients in $\mathbb{Z}$.

A basis for L is any set of independent vectors that generates L. The dimension of L is the number of vectors in a basis for L.

Definition 2.

Let L be a lattice of dimension n and let ${\mathit{b}}_1,{\mathit{b}}_2,...,{\mathit{b}}_n$ be a basis for L. The fundamental domain for L corresponding to this basis is the set [8]

$$\mathcal{F}({\mathit{b}}_1,{\mathit{b}}_2,...,{\mathit{b}}_n)=\{t_1{\mathit{b}}_1+t_2{\mathit{b}}_2+...+t_n{\mathit{b}}_n:0\le t_i<1\}.$$

Definition 3.

Let L be a lattice of dimension n and let $\mathcal{F}$ be a fundamental domain for L. Then the n-dimensional volume of $\mathcal{F}$ is called the determinant of L. It is denoted by $det(L)$ [8].

Remark 1.

If L is a full rank lattice, which means $n=m$ then the determinant of L is equal to the absolute value of the determinant of the $n\times n$ matrix whose rows are the basis vectors ${\mathit{b}}_1,{\mathit{b}}_2,...,{\mathit{b}}_n$.

In 1982, A. K. Lenstra, H. W. Lenstra, Jr. and L. Lovasz [9] invented the LLL lattice based reduction algorithm to reduce a basis and to solve the shortest vector problem. The general result on the size of individual LLL-reduced basis vectors is given in the following Theorem.

Theorem 1.

Let L be a lattice and ${\mathit{b}}_1,{\mathit{b}}_2,...,{\mathit{b}}_n$ be an LLL-reduction basis of L. Then

$$\parallel {\mathit{b}}_1\parallel \le \parallel {\mathit{b}}_2\parallel \le ...\parallel {\mathit{b}}_i\parallel \le 2^{\frac{n(n-1)}{4(n+1-i)}}det{(L)}^{\frac{1}{n+1-i}}$$

for all $1\le i\le n$ [10].

An important application of lattice reduction found by Coppersmith in 1996 [3] is finding small roots of low-degree polynomial equations. This includes modular univariate polynomial equations and bivariate integer equations. In 1997 Howgrave-Graham [11] reformulated Coppersmith’s techniques and proposed a result which shows that if the coefficients of $h(x,y)$ are sufficiently small, then the equality $h(x_0,y_0)=0$ holds not only modulo N, but also over integers. The generalization of Howgrave-Graham result in terms of the Euclidean norm of a polynomial $h(x_1,x_2,...,x_n)=\sum a_{i_1...i_n}{x}_1^{i_1}...x_n^{i_n}$ is defined by the Euclidean norm of its coefficient vector i.e., $\left|\right|h(x_1,x_2,...,x_n)\left|\right|=\sqrt{\sum a_{i_1...i_n}^2}$ given as follows:

Theorem 2.

(Howgrave-Graham): Let $h(x_1,x_2,...,x_n)\in \mathbb{Z}[x_1,x_2,...,x_n]$ be an integer polynomial that consists of at most ω monomials. Suppose that

• $h\left(x_1^{(0)},x_2^{(0)},...,x_n^{(0)}\right)\equiv 0mod{e}^m$ for some m where $|x_1^{(0)}|<X_1,|x_2^{(0)}|<X_2\dots \left|x_n^{(0)}\right|<X_n$, and
• $\left|\right|h(x_1{X}_1,x_2{X}_2,...,x_n{X}_n)\left|\right|<\frac{e^m}{\sqrt{\omega }}.$

Then $h(x_1,x_2,...,x_n)=0$ holds over the integers.

Definition 4.

The resultant of two polynomials $f(x_1,x_2,\dots ,x_n)$ and $g(x_1,x_2,\dots ,x_n)$ with respect to the variable $x_i$ for some $1\le i\le n$, is defined as the determinant of Sylvester matrix of $f(x_1,x_2,\dots ,x_n)$ and $g(x_1,x_2,\dots ,x_n)$ when considered as polynomials in the single indeterminate $x_i$, for some $1\le i\le n$.

Remark 2.

The resultant of two polynomials is non-zero if and only if the polynomials are algebraically independent.

Remark 3.

If $\left(x_1^{(0)},x_2^{(0)},\dots ,x_n^{(0)}\right)$ is a common solution of algebraically independent polynomials $f_1,f_2,\dots ,f_m$ for $m\ge n$, then these polynomials yield $g_1,g_2,\dots ,g_{n-1}$ resultants in $n-1$ variables and continuing so on the resultants yield a polynomial $t(x_i)$ in one variable with $x_i=x_i^{(0)}$ for some i is a solution of $t(x_i).$ Note the polynomials considered to compute resultants are always assumed to be algebraically independent.

3. An Attack Bound Using Sublattice Reduction Techniques

In this section, an attack bound for a small multiplicative inverse k of $\phi (N)$ modulo e when the prime sum $p+q$ is of the form $p+q=2^n{k}_0+k_1$, where n is a given positive integer and $k_0$ and $k_1$ are two suitably small unknown integers using sublattice reduction techniques is described.

In a previous paper [7], we proposed an attack on RSA when $\phi (N)$ has small multiplicative inverse modulo e and the prime sum $p+q$ is of the form $p+q=2^n{k}_0+k_1$, where n is a given positive integer and $k_0$ and $k_1$ are two suitably small unknown integers using lattice reduction techniques.

For $2^{n^{\prime }}$ is an inverse of $2^{n}mode$, define $f(x,y,z)$ = $\left\{\begin{array}{c}(N+1)x+xy+(2^n)xz-1\mathrm{if}|k_0|\le |k_1|\hfill \\ 2^{n^{\prime }}x(N+1)+xy+2^{n^{\prime }}xz-2^{n^{\prime }}\mathrm{if}|k_1|\le |k_0|.\hfill \end{array}\right.$

If $|k_0|\le |k_1|$, then $(k,-k_1,-k_0)$ is a solution and if $|k_1|\le |k_0|$ then $(k,-k_0,-k_1)$ is a solution for the modular polynomial equation $f(x,y,z)\equiv 0(mode)$.

Now define the set $M_k=\bigcup _{0\le j\le t}\left\{x^{i_1}{y}^{i_2}{z}^{i_3+j}\right|x^{i_1}{y}^{i_2}{z}^{i_3}$ is a monomial of $f^m$ and $\frac{x^{i_1}{y}^{i_2}{z}^{i_3}}{l^k}$ is a monomial of $f^{m-k}\}$, where l is a leading monomial of f and define the shift polynomials as

$$g_{k,i_1,i_2,i_3}(x,y,z)=\frac{x^{i_1}{y}^{i_2}{z}^{i_3}}{l^k}{(f^{\prime }(x,y,z))}^k{e}^{m-k},\mathrm{for}k=0,...,m,x^{i_1}{y}^{i_2}{z}^{i_3}\in M_k\backslash M_{k+1}$$

and $f^{\prime }=a_l^{-1}fmode$ for the coefficient $a_l$ of l. For $0\le k\le m$, divide the above shift polynomials according to $t=0$ and $t\ge 1$. Then for $t=0$, the shift polynomials $g(x,y,z)$ are

$$g(x,y,z)=\{\begin{array}{c}{z}^{i_3}{(f(x,y,z))}^k{e}^{m-k},\mathrm{for}{i}_1=i_2=k,i_3=0\hfill \\ x^{i_1-k}{z}^{i_3}{(f(x,y,z))}^k{e}^{m-k},\mathrm{for}k\le m-1,i_1=k+1,...,m,i_2=k,i_3=0,...,(i_1-i_2).\hfill \end{array}$$

and for $t\ge 1$, the shift polynomials $h(x,y,z)$ are

$$h(x,y,z)=\{\begin{array}{c}{z}^{i_3}{(f(x,y,z))}^k{e}^{m-k},\mathrm{for}{i}_1=i_2=k,i_3=1,...,t\hfill \\ x^{i_1-k}{z}^{i_3}{(f(x,y,z))}^k{e}^{m-k},\mathrm{for}k\le m-1,i_1=k+1,...,m,i_2=k,i_3=(i_1-i_2)+1,...,(i_1-i_2)+t.\hfill \end{array}$$

Let L be the lattice spanned by the coefficient vectors $g(xX,yY,zZ)$ and $h(xX,yY,zZ)$ shifts with dimension $(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)+\left(\frac{1}{2}(m^2+m)t+(m+1)t\right)$ [7]. Let M be the matrix of L with each row is the coefficients of the shift polynomial

$$g-\mathrm{shifts}\left\{\begin{array}{c}{e}^m,x{e}^m,xz{e}^m,x^2{e}^m,x^{2}z{e}^m,x^2{z}^2{e}^m,...,x^m{e}^m,x^{m}z{e}^m,...,x^m{z}^m{e}^m,\hfill \\ f{e}^{m-1},xf{e}^{m-1},xzf{e}^{m-1},...,x^{m-1}f{e}^{m-1},x^{m-1}zf{e}^{m-1},...,x^{m-1}{z}^{m-1}f{e}^{m-1},\hfill \\ ⋮\hfill \\ f^{m-1}e,x{f}^{m-1}e,xz{f}^{m-1}e,\hfill \\ f^m,\hfill \end{array}\right.$$

$$h-\mathrm{shifts}\left\{\begin{array}{c}z{e}^m,...z^t{e}^m,x{z}^2{e}^m,...,x{z}^{1+t}{e}^m,...,x^m{z}^{m+1}{e}^m,...,x^m{z}^{m+t}{e}^m,\hfill \\ zf{e}^{m-1},...z^{t}f{e}^{m-1},x{z}^{2}f{e}^{m-1},...,x{z}^{1+t}f{e}^{m-1},...,x^{m-1}{z}^{m}f{e}^{m-1},...,x^{m-1}{z}^{(m-1)+t}f{e}^{m-1},\hfill \\ ⋮\hfill \\ z{f}^{m-1}e,...,z^t{f}^{m-1}e,x{z}^2{f}^{m-1}e,...,x{z}^{1+t}{f}^{m-1}e,\hfill \\ z{f}^m,...,z^t{f}^m\hfill \end{array}\right.$$

and each column is the coefficients of each variable (in shift polynomials)

$$(\mathrm{first}(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)\mathrm{columns})\left\{\begin{array}{c}1,x,xz,x^2,x^{2}z,x^2{z}^2,...,x^m,x^{m}z,...,x^m{z}^m,\hfill \\ xy,x^{2}y,x^{2}yz,x^{3}y,x^{3}yz,x^{3}y{z}^2,...,x^{m}y,x^{m}yz,...,x^{m}y{z}^{m-1},\hfill \\ ⋮\hfill \\ x^{m-1}{y}^{m-1},x^m{y}^{m-1},x^m{y}^{m-1}z,\hfill \\ x^m{y}^m,\hfill \end{array}\right.$$

$$(\mathrm{remaining}\left(\frac{1}{2}(m^2+m)t+(m+1)t\right)\mathrm{columns})\left\{\begin{array}{c}z,...,z^t,x{z}^2,...,x{z}^{1+t},...,x^m{z}^{m+1},...,x^m{z}^{m+t},\hfill \\ xyz,...,xy{z}^t,x^{2}y{z}^2,...,x^{2}y{z}^{1+t},...,x^{m}y{z}^m,...,x^{m}y{z}^{(m-1)+t},\hfill \\ ⋮\hfill \\ x^{m-1}{y}^{m-1}z,...,x^{m-1}{y}^{m-1}{z}^t,x^m{y}^{m-1}{z}^2,...,x^m{y}^{m-1}{z}^{1+t},\hfill \\ x^m{y}^{m}z,...,x^m{y}^m{z}^t.\hfill \end{array}\right.$$

As $xy$ is the leading monomial in $f(x,y,z)$ with coefficient 1, the diagonal elements in the matrix M are

$$g-\mathrm{shifts}\left\{\begin{array}{c}{e}^m,X{e}^m,XZ{e}^m,X^2{e}^m,X^{2}Z{e}^m,X^2{Z}^2{e}^m,...,X^m{e}^m,X^{m}Z{e}^m,...,X^m{Z}^m{e}^m,\hfill \\ XY{e}^{m-1},X^{2}Y{e}^{m-1},X^{2}YZ{e}^{m-1},...,X^{m}Y{e}^{m-1},X^{m}YZ{e}^{m-1},...,X^{m}Y{Z}^{m-1}{e}^{m-1},\hfill \\ ⋮\hfill \\ X^{m-1}{Y}^{m-1}e,X^m{Y}^{m-1}e,X^m{Y}^{m-1}Ze,\hfill \\ X^m{Y}^m,\hfill \end{array}\right.$$

$$h-\mathrm{shifts}\left\{\begin{array}{c}Z{e}^m,...,Z^t{e}^m,X{Z}^2{e}^m,...,X{Z}^{1+t}{e}^m,...,X^m{Z}^{m+1}{e}^m,...,X^m{Z}^{m+t}{e}^m,\hfill \\ XYZ{e}^{m-1},...,XY{Z}^t{e}^{m-1},X^{2}Y{Z}^2{e}^{m-1},...,X^{2}Y{Z}^{1+t}{e}^{m-1},...,X^{m}Y{Z}^m{e}^{m-1},...,X^{m}Y{Z}^{(m-1)+t}{e}^{m-1},\hfill \\ ⋮\hfill \\ X^{m-1}{Y}^{m-1}Ze,...,X^{m-1}{Y}^{m-1}{Z}^{t}e,X^m{Y}^{m-1}{Z}^{2}e,...,X^m{Y}^{m-1}{Z}^{1+t}e,\hfill \\ X^m{Y}^{m}Z,...,X^m{Y}^m{Z}^t.\hfill \end{array}\right.$$

Note that the matrix M is lower triangular matrix. Therefore, the determinant is

$$det(L)=e^{n(e)}{X}^{n(X)}{Y}^{n(Y)}{Z}^{n(Z)}$$

where $n(e)$, $n(X)$, $n(Y)$ and $n(Z)$ are the number of e’s, X’s, Y’s and Z’s in all diagonal elements respectively, and

$$\begin{array}{cc}\hfill n(e)& =(((1/8)m^4+(3/4)m^3+(11/8)m^2+(3/4)m)+((1/6)(2m^3+3m^2+m)t+(1/2)(m^2+m)t))\hfill \\ \hfill n(X)& =(((1/8)m^4+(3/4)m^3+(11/8)m^2+(3/4)m)+((1/6)(2m^3+3m^2+m)t+(1/2)(m^2+m)t))\hfill \\ \hfill n(Y)& =(((1/24)m^4+(1/4)m^3+(11/24)m^2+(1/4)m)+((1/6)(m^3-m)t+(1/2)(m^2+m)t))\hfill \\ \hfill n(Z)& =(((1/24)m^4+(1/4)m^3+(11/24)m^2+(1/4)m)+\hfill \\ & ((1/4)(m^2+m)t^2+(1/2)(m+1)t^2+(1/12)(2m^3+9m^2+7m)t+(1/2)(m+1)t))\hfill \end{array}$$

Let $N^{\delta }$, $N^{{\gamma }_1}$ and $N^{{\gamma }_2}$ be the upper bounds for X, $max\{k_0,k_1\}$ and $min\{k_0,k_1\}$ respectively, then the bound for $\delta$ in which the generalized Howgrave-Graham result holds given in the following theorem.

Theorem 3.

[7] Let $N=pq$ be an RSA modulus with $q<p<2q$. Let $e=N^{\alpha },X=N^{\delta },Y=N^{{\gamma }_1},$ $Z=N^{{\gamma }_2}$ and k be the multiplicative inverse of $\phi (N)$ modulo e. Suppose the prime sum $p+q$ is of the form $p+q=2^n{k}_0+k_1$, for a known positive integer n and for $\left|k\right|\le X,max\left\{\right|k_0|,|k_1\left|\right\}\le Y$ and $min\left\{\right|k_0|,|k_1\left|\right\}\le Z$ one can factor N in polynomial time if

$$\delta <\frac{1}{2}\alpha -\frac{1}{2}{\gamma }_1+\frac{1}{16}{\gamma }_2-\frac{1}{16}\sqrt{48(\alpha -{\gamma }_1){\gamma }_2+33{\gamma }_2^2}.$$

(1)

To improve this bound in a lower dimension than the above dimension, first we construct a sublattice $S_L$ of L and after that we apply the sublattice based techniques to the lattice $S_L$ given by J. Blömer, A. May in [5], and are described in the following sections.

3.1. Construction of a Sublattice ${\mathit{S}}_L$ of L

The construction of a sublattice $S_L$ of L in order to improve the bound for $\delta$ is given in the following.

• First remove following rows in M corresponding to g-shifts
  $e^m,x{e}^m,xz{e}^m,...,x^{m-1}{e}^m,...,x^{m-1}{z}^{m-1}{e}^m$,
  $f{e}^{m-1},xf{e}^{m-1},xzf{e}^{m-1},...,x^{m-2}f{e}^{m-1},...,x^{m-2}{z}^{m-2}f{e}^{m-1}$,
  ⋮
  $f^{m-2}{e}^2,x{f}^{m-2}{e}^2,xz{f}^{m-2}{e}^2$,
  $f^{m-1}e$.
  Therefore the remaining rows in M corresponding to g-shifts are
  $x^m{e}^m,x^{m}z{e}^m,...,x^m{z}^m{e}^m$,
  $x^{m-1}f{e}^{m-1},...,x^{m-1}{z}^{m-1}f{e}^{m-1}$,
  ⋮
  $x{f}^{m-1}e,xz{f}^{m-1}e$,
  $f^m,$
  and its corresponding g-shifts can be written as

  $$g_s(x,y,z)=x^{l_1}{z}^{l_2}{(f(x,y,z))}^k{e}^{m-k}\mathrm{for}k=0,...,m,l_1=m-k,l_2=0,...,l_1.$$

• Now remove some rows in M corresponding to h-shifts are
  $z{e}^m,...,z^t{e}^m,...,x^{m-1}{z}^m{e}^m,...,x^{m-1}{z}^{(m-1)+t}{e}^m$,
  $zf{e}^{m-1},...,z^{t}f{e}^{m-1},...,x^{m-2}{z}^{m-1}f{e}^{m-1},...,x^{m-2}{z}^{(m-2)+t}f{e}^{m-1},$
  ⋮
  $z{f}^{m-2}{e}^2,...,z^t{f}^{m-2}{e}^2,x{z}^2{f}^{m-2}{e}^2,...,x{z}^{1+t}{f}^{m-2}{e}^2,$
  $z{f}^{m-1}e,...,z^t{f}^{m-1}e.$
  Therefore the remaining rows in M corresponding to h-shifts are
  $x^m{z}^{m+1}{e}^m,...,x^m{z}^{m+t}{e}^m,$
  $x^{m-1}{z}^{m}f{e}^{m-1},...,x^{m-1}{z}^{(m-1)+t}f{e}^{m-1},$
  ⋮
  $x{z}^2{f}^{m-1}e,...,x{z}^{t+1}{f}^{m-1}e,$
  $z{f}^m,...,z^t{f}^m$, and its corresponding h-shifts can be written as

  $$h_s(x,y,z)=x^{l_1}{z}^{l_2}{(f(x,y,z))}^k{e}^{m-k}\mathrm{for}k=0,...,m,l_1=m-k,l_2=l_1+1,...,l_1+t.$$

Now, let $S_L$ be the sub-lattice of L spanned by the coefficients of the vectors $g_s(xX,yY,zZ)$ and $h_s(xX,yY,zZ)$ shifts and $M_s$ be the matrix of the lattice $S_L$.

Note that the matrix $M_s$ is not square. So apply the sublattice based techniques to the basis of $S_L$ or the rows of $M_s$ to get a square matrix. Using that square matrix, the attack bound can be found and is given in the following section.

3.2. Applying Sub-Lattice Based Techniques to Get an Attack Bound

In [5], J. Blomer, A. May proposed a method to find an attack bound for low deciphering exponent in a smaller dimension than the approach by Boneh and Durfee’s attack in [4]. Apply their method based on sublattice reduction techniques to our lattice $S_L$ to get an attack bound and is described in the following.

In order to apply the Howgrave-Graham’s theorem [11] by using Theorem 1, we need three short vectors in $S_L$ as our polynomial consists of three variables. However, note that $M_s$ is not a square matrix. So, first construct a square matrix $M_{sl}$ by removing some columns in $M_s$, which are small linear combination of non-removing columns in $M_s$. Then the short vector in $M_{sl}$ lead to short reconstruction vector in $S_L$.

Construction of a square sub-matrix ${\mathit{M}}_{\mathit{sl}}$ of ${\mathit{M}}_{\mathit{s}}$.

Columns in M and $M_s$ are same and each column in M is nothing but the coefficients of a variable, which is a leading monomial of the polynomial g or h-shifts. The first $(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)$ and remaining $\left(\frac{1}{2}(m^2+m)t+(m+1)t\right)$ columns are corresponding to the leading monomial of the polynomials g and h-shifts respectively. Therefore,

• the first $(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)$ columns are the coefficients of the each variable $x^{i_1}{y}^{i_2}{z}^{i_3}$ for $i_1=i_2=k,i_3=0$ and $i_1=k+1,...,m,i_2=k,i_3=0,...,(i_1-i_2)$ and remaining $\left(\frac{1}{2}(m^2+m)t+(m+1)t\right)$ columns are the coefficients of the each variable $x^{i_1}{y}^{i_2}{z}^{i_3}$ for $i_1=i_2=k,i_3=1,...,t$ and $i_1=k+1,...,m,i_2=k,i_3=(i_1-i_2)+1,...,(i_1-i_2)+t$. So the variable $x^{i_1}{y}^{i_2}{z}^{i_3}$ corresponds a column in first $(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)$ columns if $i_1\ge i_2+i_3$ and corresponds a column in remaining $\left(\frac{1}{2}(m^2+m)t+(m+1)t\right)$ columns if $i_1<i_2+i_3$.
• As $1,x,xy,xz$ are the monomials of f, the set of all monomials of $f^m$ for $m\ge 0$ is $\{x^{i_1}{y}^{i_2}{z}^{i_3};i_1=0,...,m,i_2=0,...,i_1,i_3=0,...,i_1-i_2\}$. Therefore, the coefficient of the variable $x^{i_1}{y}^{i_2}{z}^{i_3}$ in $f^m$ is non-zero if and only if $i_3\le i_1-i_2$, i.e., $i_1\ge i_2+i_3$.

Remove columns in $M_s$ corresponding to the coefficients of the variable $x^a{y}^b{z}^c$ for all $0\le a\le m-1$ and note that every such column is $\left(\frac{m-(a-b)}{(m-a)!b!}\right)·\frac{1}{X^{m-a}{Y}^{m-a}}$ multiple of a non-removed column, corresponding to the coefficients of $x^m{y}^{m-(a-b)}{z}^c$ and is proved in the following theorem.

Theorem 4.

Each column in $M_s$ corresponding to the coefficients of the variable $x^a{y}^b{z}^c$, a leading monomial of the polynomial g or h-shifts, for all $0\le a\le m-1$ is $\left(\frac{m-(a-b)}{(m-a)!b!}\right)·\frac{1}{X^{m-a}{Y}^{m-a}}$ multiple of a non-removed column, represents the coefficients of the variable $x^m{y}^{m-(a-b)}{z}^c$.

Proof. 

First assume that $|k_0|\le |k_1|$, then $f(x,y,z)=(N+1)x+xy+2^{n}xz-1$.

For $n=0,...,m,k_1=m-n,k_2=0,...,k_1$, the $g_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ corresponds first $(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)$ rows in $M_s$ and for $n=0,...,m,k_1=m-n,k_2=k_1+1,...,k_1+t$, the $h_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ corresponds remaining rows in $M_s$. We prove this theorem in two cases.

Case(i): Any column in first $(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)$ columns of $M_s$. i.e., a column corresponding coefficients of a variable $x^a{y}^b{z}^c$ with $a\ge b+c$, from the above analysis in (1).

Given that $0\le a\le m-1$. From the above analysis in (1) and (2), the coefficient of $x^a{y}^b{z}^c$ is non-zero in $g_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ if and only if $a\ge k_1,b\le m-k_1,c\ge k_2$ and $a-k_1\ge b+(c-k_2)$. As $k_1\ge k_2$, $k_2\ge 0$ and $a-k_1\ge b+(c-k_2)$, $max\{0,k_1-(a-(b+c))\}\le k_2\le min\{k_1,c\}$ and also as $a-k_1<b+(c-k_2)$ for $k_1>a-b$, $k_1$ is such that $0\le k_1\le a-b.$

Therefore, the coefficient of $x^a{y}^b{z}^c$ is non-zero in $g_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ if and only if $a\ge k_1,b\le m-k_1,c\ge k_2$ and $k_1=0,...,a-b,k_2=max\{0,k_1-(a-(b+c))\},...,min\{k_1,c\}$.

Similarly we can prove that, the coefficient of $x^a{y}^b{z}^c$ is non-zero in $h_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ if and only if $a\ge k_1,b\le m-k_1,c\ge k_2$ and $k_1=0,...,c,k_2=k_1+1,...,min\{c,k_1+t\}$ using the inequalities $k_1+1\le k_2\le k_1+t$, $a\ge b+c$ and analysis in (1) and (2), and say $min\{c,k_1+t\}=l_t$

The formula for finding a coefficient of a variable $x^{l_1}{y}^{l_2}{z}^{l_3}={(1)}^{n-l_1}{x}^{l_1-(l_2+l_3)}{(xz)}^{l_3}{(xy)}^{l_2}$ for $l_1\le n-1$ in $f^n$ is

$$\frac{n!}{(n-l_1)!(l_1-(l_2+l_3))!l_2!l_3!)}{(-1)}^{n-l_1}{(N+1)}^{l_1-(l_2+l_3)}{(2^n)}^{l_3}$$

and coefficient of $x^a{y}^b{z}^c$ in $x^{k_1}{y}^{k_2}{f}^n{e}^{k_1}$ is nothing but a coefficient of $x^{a-k_1}{y}^b{z}^{c-k_2}$ in $f^n$.

Note that a column corresponding to a variable $x^m{y}^{m-a}{z}^c$ is in the non-removing columns in $M_s$ and coefficient of $x^m{y}^{m-a}{z}^c$ is zero for $k_1>a-b$ in $g_s$-shifts, $k_1>c$ in $h_s$-shifts. The columns corresponding to a variable $x^a{y}^b{z}^c$ and a variable $x^m{y}^{m-a}{z}^c$ only with non-zero terms is depicted in Table 1.

Table 1. A column in first $(\frac{1}{6}{m}^3+m^2+\frac{11}{6}m+1)$ columns of $M_s$ and a column corresponding to coefficients of a variable $x^m{y}^{m-a}{z}^c$ only with non-zero terms.

Rows Corresponding to g and h Shifts	Column Corresponding to ${\mathit{x}}^{\mathit{a}}{\mathit{y}}^{\mathit{b}}{\mathit{z}}^{\mathit{c}}$	Column Corresponding to ${\mathit{x}}^{\mathit{m}}{\mathit{y}}^{\mathit{m}-\mathit{a}}{\mathit{z}}^{\mathit{c}}$
$x^{a-b}{z}^c{f}^{m-(a-b)}{e}^{a-b}$	$\frac{(m-(a-b))!}{(m-a)!b!}{(-1)}^{m-a}{X}^a{Y}^b{Z}^c{e}^{a-b}$	$X^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b}$
$x^{a-b-1}{z}^{c-1}{f}^{m-(a-b-1)}{e}^{a-b-1}$	$\frac{(m-(a-b)+1)!}{(m-a)!b!}{(-1)}^{m-a}{2}^n{X}^a{Y}^b{Z}^c{e}^{a-b-1}$	$\frac{(m-(a-b)+1)!}{(m-(a-b))!}{2}^n{X}^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b-1}$
$x^{a-b-1}{z}^c{f}^{m-(a-b-1)}{e}^{a-b-1}$	$\frac{(m-(a-b)+1)!}{(m-a)!b!}{(-1)}^{m-a}(N+1)X^a{Y}^b{Z}^c{e}^{a-b-1}$	$\frac{(m-(a-b)+1)!}{(m-(a-b))!}(N+1)X^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b-1}$
⋮	⋮	⋮
$x^{a-b-(c-1)}z{f}^{m-((a-b)-(c-1))}{e}^{a-b-(c-1)}$	$\frac{(m-(a-b)+(c-1))!}{(m-a)!b!(c-1)!}{(-1)}^{m-a}{(2^n)}^{c-1}{X}^a{Y}^b{Z}^c{e}^{a-b-(c-1)}$	$\frac{(m-(a-b)+(c-1))!}{(m-(a-b))!(c-1)!}{(2^n)}^{c-1}{X}^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b-(c-1)}$
⋮	⋮	⋮
$x^{a-b-(c-1)}{z}^c{f}^{m-((a-b)-(c-1))}{e}^{a-b-(c-1)}$	$\frac{(m-(a-b)+(c-1))!}{(m-a)!b!(c-1)!}{(-1)}^{m-a}{(N+1)}^{c-1}{X}^a{Y}^b{Z}^c{e}^{a-b-(c-1)}$	$\frac{(m-(a-b)+(c-1))!}{(m-(a-b))!(c-1)!}{(N+1)}^{c-1}{X}^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b-(c-1)}$
$x^{a-b-c}{f}^{m-(a-b)+c}{e}^{a-(b+c)}$	$\frac{(m-(a-b)+c)!}{(m-a)!b!c!}{(-1)}^{m-a}{(2^n)}^c{X}^a{Y}^b{Z}^c{e}^{a-b-c}$	$\frac{(m-(a-b)+c)!}{(m-(a-b))!c!}{(2^n)}^c{X}^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b-c}$
⋮	⋮	⋮
$x^{a-b-c}{z}^c{f}^{m-(a-b)+c}{e}^{a-(b+c)}$	$\frac{(m-(a-b)+c)!}{(m-a)!b!c!}{(-1)}^{m-a}{(N+1)}^c{X}^a{Y}^b{Z}^c{e}^{a-b-c}$	$\frac{(m-(a-b)+c)!}{(m-(a-b))!c!}{(N+1)}^c{X}^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b-c}$
⋮	⋮	⋮
$f^m$	$\frac{m!}{(m-a)!b!c!(a-(b+c))!}{(-1)}^{m-a}{(N+1)}^{(a-(b+c))}{(2^n)}^c{X}^a{Y}^b{Z}^c$	$\frac{m!}{(m-(a-b))!c!(a-(b+c))!}{(N+1)}^{a-(b+c)}{(2^n)}^c{X}^m{Y}^{m-(a-b)}{Z}^c$
$x^{c-1}{z}^c{f}^{m-(c-1)}{e}^{c-1}$	$\frac{(m-(c-1))!}{(m-a)!b!(a-(b+c)+1)!}{(-1)}^{m-a}{(N+1)}^{a-(b+c)+1}{X}^a{Y}^b{Z}^c{e}^{c-1}$	$\frac{(m-(c-1))!}{(m-(a-b))!(a-(b+c)+1)!}{(N+1)}^{a-(b+c)+1}{X}^m{Y}^{m-(a-b)}{Z}^c{e}^{c-1}$
⋮	⋮	⋮
$x{z}^2{f}^{m-1}e$	$\frac{(m-1)!}{(m-a)!b!(c-2)!(a-(b+c)+1)!}{(-1)}^{m-a}{(N+1)}^{a-(b+c)+1}{(2^n)}^{c-2}{X}^a{Y}^b{Z}^{c}e$	$\frac{(m-1)!}{(m-(a-b))!(c-2)!(a-(b+c)+1)!}{(N+1)}^{a-(b+c)+1}{(2^n)}^{c-2}{X}^m{Y}^{m-(a-b)}{Z}^{c}e$
⋮	⋮	⋮
$x{z}^{l_t}{f}^{m-1}e$	$\frac{(m-1)!}{(m-a)!b!(c-l_t)!(a-(b+c)+l_t-1)!}{(-1)}^{m-a}{(N+1)}^{a-(b+c)+l_t-1}{(2^n)}^{c-l_t}{X}^a{Y}^b{Z}^{c}e$	$\frac{(m-1)!}{(m-(a-b)!(c-l_t)!(a-(b+c)+l_t-1)!}{(N+1)}^{a-(b+c)+l_t-1}{(2^n)}^{c-l_t}{X}^m{Y}^{m-(a-b)}{Z}^{c}e$
$z{f}^m$	$\frac{m!}{(m-a)!b!(c-1)!(a-(b+c)+1)!}{(-1)}^{m-a}{(N+1)}^{a-(b+c)+1}{(2^n)}^{c-1}{X}^a{Y}^b{Z}^c$	$\frac{m!}{(m-(a-b))!(c-1)!(a-(b+c)+1)!}{(N+1)}^{a-(b+c)+1}{(2^n)}^{c-1}{X}^m{Y}^{m-(a-b)}{Z}^c$
⋮	⋮	⋮
$z^{l_t}{f}^m$	$\frac{m!}{(m-a)!b!(c-l_t)!(a-(b+c)+l_t)!}{(-1)}^{m-a}{(N+1)}^{a-(b+c)+l_t}{(2^n)}^{c-l_t}{X}^a{Y}^b{Z}^c$	$\frac{m!}{(m-(a-b))!(c-l_t)!(a-(b+c)+l_t)!}{(-1)}^{m-a}{(N+1)}^{a-(b+c)+l_t}{(2^n)}^{c-l_t}{X}^m{Y}^{m-(a-b)}{Z}^c$

Therefore, from Table 1 the result holds in this case.

Case(ii): Any column in remaining $\left(\frac{1}{2}(m^2+m)t+(m+1)t\right)$ columns of $M_s$, i.e., a column corresponding coefficients of a variable $x^a{y}^b{z}^c$ with $a<b+c$, from the above analysis in (1).

The coefficient of $x^a{y}^b{z}^c$ is non-zero in $g_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ if and only if $a\ge k_1,b\le m-k_1,c\ge k_2$, $a-k_1\ge b+(c-k_2)$ and note for $a<b+c$, $a-k_1<b+(c-k_2)$ as $k_1\ge k_2$ in $g_s$-shifts. So the coefficient of $x^a{y}^b{z}^c$ is zero in all rows corresponding to $g_s$-shifts.

The coefficient of $x^a{y}^b{z}^c$ is non-zero in $h_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ if and only if $a\ge k_1,b\le m-k_1,c\ge k_2$ and $a-k_1\ge b+(c-k_2)$. For $k_1>a-b,$$a-k_1<b+(c-k_2)$ and from the inequalities $k_1+1\le k_2\le k_1+t$, $a-k_1\ge b+(c-k_2)$, we have the coefficient of $x^a{y}^b{z}^c$ is non-zero in $h_s$-shifts $x^{k_1}{z}^{k_2}{f}^n{e}^{k_1}$ if and only if $a\ge k_1,b\le m-k_1,c\ge k_2$ and $k_1=0,...,a-b$, $k_2=max\{k_1+1,k_1+(b+c)-a\},...,min\{c,k_1+t\}$. Take $l_t=min\{c,k_1+t\}$.

Note that coefficient of $x^m{y}^{m-a}{z}^c$ is zero in all $g_s$-shifts as $a>c$ and for $k_1>a-b$ in $h_s$-shifts. The columns corresponding to a variable $x^a{y}^b{z}^c$ and a variable $x^m{y}^{m-a}{z}^c$ only with non-zero terms is depicted in Table 2. Therefore, from Table 2 the result holds in this case.

Table 2. A column in the last $\left(\frac{1}{2}(m^2+m)t+(m+1)t\right)$ columns of $M_s$ and a column corresponding to coefficients of a variable $x^m{y}^{m-a}{z}^c$ only with non-zero terms.

Rows Corresponding to g and h Shifts	Column Corresponding to ${\mathit{x}}^{\mathit{a}}{\mathit{y}}^{\mathit{b}}{\mathit{z}}^{\mathit{c}}$	Column Corresponding to ${\mathit{x}}^{\mathit{m}}{\mathit{y}}^{\mathit{m}-\mathit{a}}{\mathit{z}}^{\mathit{c}}$
$x^{a-b}{z}^c{f}^{m-(a-b)}{e}^{a-b}$	$\frac{(m-(a-b))!}{(m-a)!b!}{(-1)}^{m-a}{X}^a{Y}^b{Z}^c{e}^{a-b}$	$X^m{Y}^{m-(a-b)}{Z}^c{e}^{a-b}$
⋮	⋮	⋮
$x^2{z}^{(b+c)-a+2}{f}^{m-2}{e}^2$	$\frac{(m-2)!}{(m-a)!b!((a-b)-2)!}{(-1)}^{m-a}{(2^n)}^{(a-b)-2}{X}^a{Y}^b{Z}^c{e}^2$	$\frac{(m-2)!}{(m-(a-b))!((a-b)-2)!}{(2^n)}^{(a-b)-2}{X}^m{Y}^{m-(a-b)}{Z}^c{e}^2$
⋮	⋮	⋮
$x^2{z}^{l_t}{f}^{m-2}{e}^2$	$\frac{(m-2)!}{(m-a)!b!(c-l_t)!(l_t-((b+c)-a+2))!}{(-1)}^{m-a}{(N+1)}^{l_t-((b+c)-a+2)}{(2^n)}^{c-l_t}{X}^a{Y}^b{Z}^c{e}^2$	$\frac{(m-2)!}{(m-(a-b))!(c-l_t)!(l_t-((b+c)-a+2))!}{(N+1)}^{l_t-((b+c)-a+2)}{(2^n)}^{c-l_t}{X}^m{Y}^{m-(a-b)}{Z}^c{e}^2$
$x{z}^{b+c-a+1}{f}^{m-1}e$	$\frac{(m-1)!}{(m-a)!b!((a-b)-1)!}{(-1)}^{m-a}{(2^n)}^{(a-b)-1}{X}^a{Y}^b{Z}^{c}e$	$\frac{(m-1)!}{(m-(a-b))!((a-b)-1)!}{(2^n)}^{(a-b)-1}{X}^m{Y}^{m-(a-b)}{Z}^{c}e$
⋮	⋮	⋮
$x{z}^{l_t}{f}^{m-1}e$	$\frac{(m-1)!}{(m-a)!b!(c-l_t)!((l_t-(b+c-a+1))!}{(-1)}^{m-a}{(N+1)}^{(l_t-(b+c-a+1)}{(2^n)}^{c-l_t}{X}^a{Y}^b{Z}^{c}e$	$\frac{(m-1)!}{(m-(a-b))!(c-l_t)!((l_t-(b+c-a+1))!}{(N+1)}^{(l_t-(b+c-a+1)}{(2^n)}^{c-l_t}{X}^m{Y}^{m-(a-b)}{Z}^{c}e$
$z^{b+c-a}{f}^m$	$\frac{m!}{(m-a)!b!(a-b)!}{(-1)}^{m-a}{(2^n)}^{a-b}{X}^a{Y}^b{Z}^c$	$\frac{m!}{(m-(a-b))!(a-b)!}{(2^n)}^{a-b}{X}^m{Y}^{m-(a-b)}{Z}^c$
⋮	⋮	⋮
$z^{l_t}{f}^m$	$\frac{m!}{(m-a)!b!(c-l_t)!(l_t-((b+c)-a))!}{(-1)}^{m-a}{(N+1)}^{l_t-((b+c)-a)}{(2^n)}^{c-l_t}{X}^a{Y}^b{Z}^c$	$\frac{m!}{(m-(a-b))!(c-l_t)!(l_t-((b+c)-a))!}{(-1)}^{m-a}{(N+1)}^{l_t-((b+c)-a)}{(2^n)}^{c-l_t}{X}^m{Y}^{m-(a-b)}{Z}^c$

Now apply the above analysis to the polynomial $f(x,y,z)=2^{n^{\prime }}x(N+1)+xy+2^{n^{\prime }}xz-2^{n^{\prime }}$ for $|k_1|\le |k_0|$, then this result is obtained.  □

From the above theorem, all columns corresponding to a variable $x^a{y}^b{z}^c$ for all $0\le a\le m-1$ are depending on a non-removed column, corresponding to a variable $x^m{y}^{m-(a-b)}{z}^c$ in $M_s$. Let $M_{sl}$ be a matrix formed by removing all above columns from the matrix $M_s$ and $S_l$ be a lattice spanned by rows of $M_{sl}$. Then the short vector in $S_l$ lead to short reconstruction vector in $S_L$, i.e., if $u={\displaystyle \sum _{b\in B}}{c}_{b}b$ is a short vector in $S_l$ then this lead to a short vector $\overline{u}={\displaystyle \sum _{b\in \overline{B}}}{c}_{b}b$ (same coefficients $c_b$) in $S_L$ where B and $\overline{B}$ are the basis for $S_l$ and $S_L$ respectively.

As we removed all depending columns in $M_s$ to form a matrix $M_{sl}$, apply the lattice based techniques to $S_l$ instead of $S_L$ to get an attack bound and this lattice reduction techniques gives a required short vectors in $S_L$ for a given bound. The matrix $M_{sl}$ is lower triangular with rows same as in $M_s$ and each column corresponding to coefficients of one of the variables (leading monomials of $g_s$ and $h_s$-shifts)

$$g_s-\mathrm{shift}\left\{\begin{array}{c}{x}^m,x^{m}z,...,x^m{z}^m,\hfill \\ x^{m}y,...,x^{m}y{z}^{m-1},\hfill \\ ⋮\hfill \\ x^m{y}^{m-1},x^m{y}^{m-1}z,\hfill \\ x^m{y}^m,\hfill \end{array}\right.$$

$$h_s-\mathrm{shift}\left\{\begin{array}{c}{x}^m{z}^{m+1},...,x^m{z}^{m+t},\hfill \\ x^{m}y{z}^m,...,x^{m}y{z}^{(m-1)+t},\hfill \\ ⋮\hfill \\ x^m{y}^{m-1}{z}^2,...,x^m{y}^{m-1}{z}^{1+t},\hfill \\ x^m{y}^{m}z,..,x^m{y}^m{z}^t.\hfill \end{array}\right.$$

Therefore $S_l$ is a lattice spanned by coefficient vectors of the shift polynomials $g_{sl}(xX,yY,zZ)$ and $h_{sl}(xX,yY,zZ)$ where

$$g_{sl}(x,y,z)=x^{l_1}{z}^{l_2}{(f(x,y,z)-\mathrm{constant}\mathrm{term}\mathrm{of}f)}^n{e}^{l_1}\mathrm{for}n=0,...,m,l_1=m-n,l_2=0,...,l_1\mathrm{and}$$

$$h_{sl}(x,y,z)=x^{l_1}{z}^{l_2}{(f(x,y,z)-\mathrm{constant}\mathrm{term}\mathrm{of}f)}^n{e}^{l_1}\mathrm{for}n=0,...,m,l_1=m-n,l_2=l_1+1,...,l_1+t.$$

Since $S_l$ is full-rank lattice, $det{S}_l=det{M}_{sl}=e^{n(e)}{X}^{n(X)}{Y}^{n(Y)}{Z}^{n(Z)}$ where $n(e),n(X),n(Y),n(Z)$ are denotes the number of $e^{\prime }s,X^{\prime }s,Y^{\prime }s,Z^{\prime }s$ in all the diagonal elements of $M_{sl}$ respectively. As $x^n{y}^n$ is a leading monomial of $f^n$ with coefficient 1, we have

$$\begin{array}{cc}\hfill n(e)& =\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=0}^{l_1}{l}_1+\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=l_1+1}^{l_1+t}{l}_1\hfill \\ & =(1/3)m^3+m^2+(1/2)(m^2+m)t+(2/3)m,\hfill \\ \hfill n(X)& =\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=0}^{l_1}n+l_1+\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=l_1+1}^{l_1+t}n+l_1\hfill \\ & =(1/2)m^3+(3/2)m^2+(m^2+m)t+m,\hfill \\ \hfill n(Y)& =\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=0}^{l_1}n+\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=l_1+1}^{l_1+t}n\hfill \\ & =(1/6)m^3+(1/2)m^2+(1/2)(m^2+m)t+(1/3)m,\hfill \\ \hfill n(Z)& =\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=0}^{l_1}{l}_2+\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=l_1+1}^{l_1+t}{l}_2\hfill \\ & =(1/6)m^3+(1/2)(m+1)t^2+(1/2)m^2+(1/2)(m^2+2m+1)t+(1/3)m\hfill \\ \hfill \mathrm{and}dim(S_l)& =\omega =\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=0}^{l_1}1+\sum _{n=0}^m\sum _{l_1=m-n}\sum _{l_2=l_1+1}^{l_1+t}1\hfill \\ & =(1/2)m^2+(m+1)t+(3/2)m+1.\hfill \end{array}$$

Take $t=\tau m$, then for sufficiently large m, the exponents $n(e),n(X),n(Y),n(Z)$ and the dimension $\omega$ reduce to

$$\begin{array}{cc}\hfill \omega & =\left(\frac{1}{2}+\tau \right)m^2+o(m^2),\hfill \\ \hfill n(e)& =\left(\frac{1}{3}+\frac{1}{2}\tau \right)m^3+o(m^3),\hfill \\ \hfill n(X)& =\left(\frac{1}{2}+\tau \right)m^3+o(m^3),\hfill \\ \hfill n(Y)& =\left(\frac{1}{6}+\frac{1}{2}\tau \right)m^3+(m^3),\hfill \\ \hfill n(Z)& =\left(\frac{1}{6}+\frac{1}{2}\tau +\frac{1}{2}{\tau }^2\right)m^3+o(m^3).\hfill \end{array}$$

Applying the LLL algorithm to the basis vectors of the lattice $S_l$, i.e., coefficient vectors of the shift polynomials, we get a LLL-reduced basis say $\{v_1,v_2,...,v_{\omega }\}$ and from the Theorem 1 we have

$$\left|\right|v_1\left|\right|\le \left|\right|v_2\left|\right|\le \left|\right|v_3\left|\right|\le 2^{\frac{\omega (\omega -1)}{4(\omega -2)}}det{(S_l)}^{\frac{1}{\omega -2}}.$$

In order to apply the generalization of Howgrave-Graham result in Theorem 2, we need the following inequality

$$2^{\frac{\omega (\omega -1)}{4(\omega -2)}}det{(S_l)}^{\frac{1}{\omega -2}}<\frac{e^m}{\sqrt{\omega }}.$$

from this, we deduce

$$det(S_l)<\frac{1}{{\left(2^{\frac{\omega (\omega -1)}{4(\omega -2)}}\sqrt{\omega }\right)}^{\omega -2}}{e}^{m(\omega -2)}<\frac{1}{{\left(2^{\frac{\omega (\omega -1)}{4(\omega -2)}}\sqrt{\omega }\right)}^{\omega -2}}{e}^{m\omega }.$$

As the dimension $\omega$ is not depending on the public encryption exponent e, $\frac{1}{{\left(2^{\frac{\omega (\omega -1)}{4(\omega -2)}}\sqrt{\omega }\right)}^{\omega -2}}$ is a fixed constant, so we need the inequality $det(S_l)<e^{m\omega },$ i.e., $e^{n(e)}{X}^{n(X)}{Y}^{n(Y)}{Z}^{n(Z)}<e^{m\omega }.$

Substitute all values and taking logarithms, neglecting the lower order terms and after simplifying by $m^3$ we get

$$(-1-3\tau )\alpha +(3+6\tau )\delta +(1+3\tau ){\gamma }_1+(1+3\tau +3{\tau }^2){\gamma }_2<0.$$

The left hand side inequality is minimized at $\tau =\frac{\alpha -(2\delta +{\gamma }_1+{\gamma }_2)}{2{\gamma }_2}$ and putting this value in the above inequality we get

$$\delta <\frac{1}{2}\alpha -\frac{1}{2}{\gamma }_1-\frac{1}{6}\sqrt{6(\alpha -{\gamma }_1){\gamma }_2+3{\gamma }_2^2}.$$

From the first three short vectors $v_1,v_2$ and $v_3$ in LLL reduced basis of a basis B in $S_l$ we consider three polynomials $g_1(x,y,z),g_2(x,y,z)$ and $g_3(x,y,z)$ over $\mathbb{Z}$ such that $g_1(x_0,y_0,z_0)=g_2(x_0,y_0,z_0)=g_3(x_0,y_0,z_0)=0$. These short vectors $v_1,v_2$ and $v_3$ lead to a short vector $\overline{v_1},\overline{v_2}$ and $\overline{v_3}$ respectively and $\overline{g_1}(x,y,z),\overline{g_2}(x,y,z)$ and $\overline{g_3}(x,y,z)$ its corresponding polynomials. Apply the same analysis in paper [7] to the above polynomials to get the factors p and q of RSA modulus N.

Theorem 5.

Let $N=pq$ be an RSA modulus with $q<p<2q$. Let $e=N^{\alpha },X=N^{\delta },Y=N^{{\gamma }_1},$ $Z=N^{{\gamma }_2}$ and k be the multiplicative inverse of $\phi (N)$ modulo e. Suppose the prime sum $p+q$ is of the form $p+q=2^n{k}_0+k_1$, for a known positive integer n and for $\left|k\right|\le X,max\left\{\right|k_0|,|k_1\left|\right\}\le Y$ and $min\left\{\right|k_0|,|k_1\left|\right\}\le Z$ one can factor N in polynomial time if

$$\delta <\frac{1}{2}\alpha -\frac{1}{2}{\gamma }_1-\frac{1}{6}\sqrt{6(\alpha -{\gamma }_1){\gamma }_2+3{\gamma }_2^2}.$$

(2)

Proof. 

Follows from the above argument and the LLL lattice basis reduction algorithm operates in polynomial time [9].  □

Note that for any given primes p and q with $q<p<2q$, we can always find a positive integer n such that $p+q=2^n{k}_0+k_1$ where $0\le |k_0|,|k_1|\le \approx 0.25$. A typical example is $2^n\approx \frac{3}{\sqrt{2}}{N}^{0.25}$ as $p+q<\frac{3}{\sqrt{2}}{N}^{0.5}$ [12]. So take ${\gamma }_1$ and ${\gamma }_2$ in the range (0, 0.25).

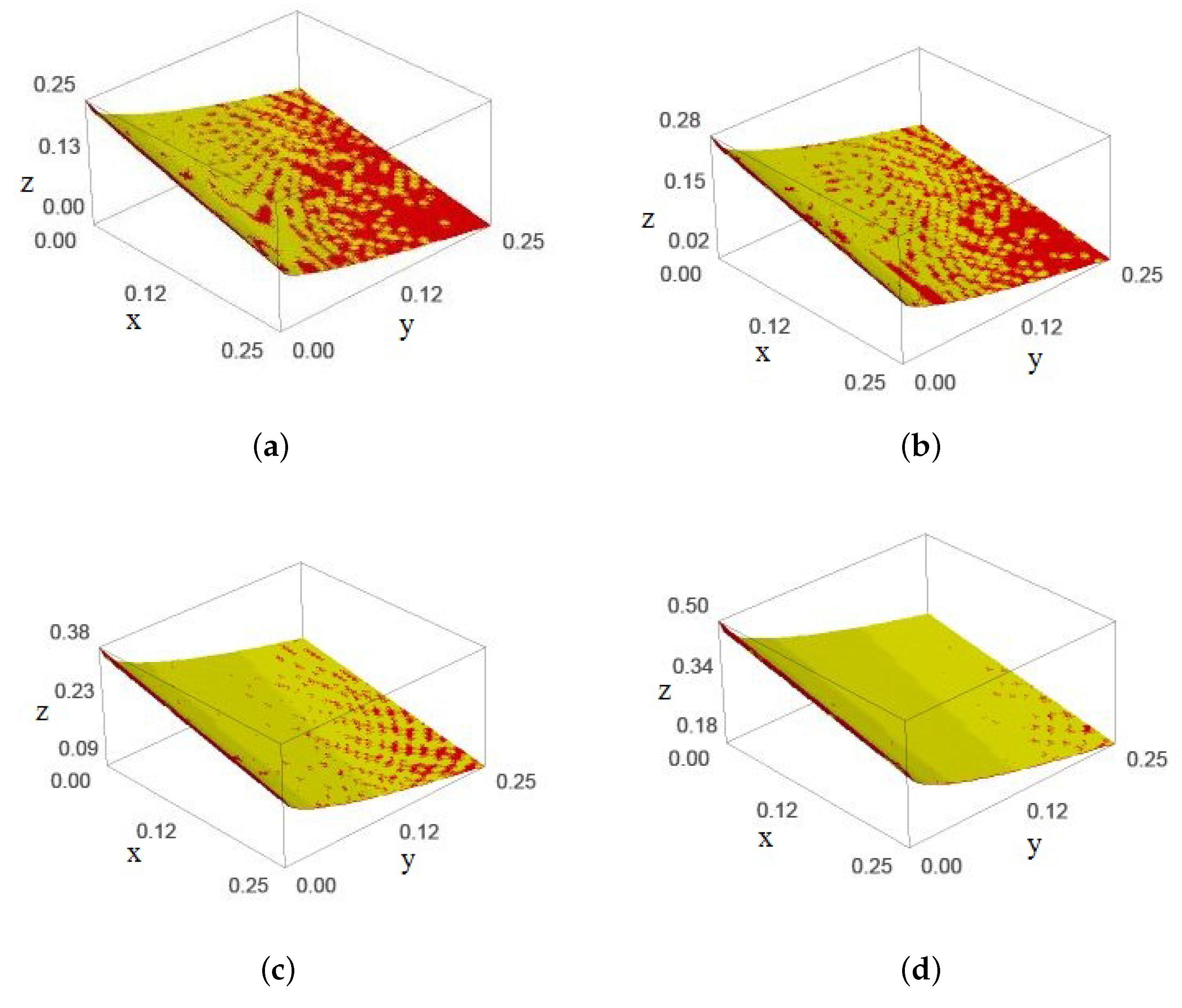
Let ${\delta }_L$ and ${\delta }_{sl}$ be the bounds for $\delta$ in inequalities (1) and (2) respectively. Then note that ${\delta }_{sl}$ is slightly larger than ${\delta }_L$ and is depicted in Figure 1 for $\alpha =\mathrm{0.51.0.55.0.750}$ and 1.

Figure 1. The region of ${\delta }_{sl}$ and ${\delta }_L$ for $\alpha =0.501,0.55,0.75,1$; (a) $\alpha =0.501$; (b) $\alpha =0.55$; (c) $\alpha =0.75$; (d) $\alpha =0.1$.

In the Figure 1, $x,y$, z-axis represents ${\gamma }_1,$${\gamma }_2$, bound for $\delta$ respectively and yellow, red regions represents ${\delta }_{sl}$, ${\delta }_L$ receptively. From this figure, it is noted that the yellow region is slightly above the red region, i.e., ${\delta }_{sl}$ is slightly grater than ${\delta }_L$ and this improvement increases when the values of $\alpha$ increases.

As the dimension of L is $(1/6)m^3+(1/2)m^2(t+2)+(1/6)m(9t+11)+(t+1)$ for $t=\left(\frac{\alpha -(2\delta +{\gamma }_1+{\gamma }_2)}{3{\gamma }_2}\right)m$ [7] and $S_l$ is $(1/2)m^2+(m+1)t+(3/2)m+1$ for $t=\left(\frac{\alpha -(2\delta +{\gamma }_1+{\gamma }_2)}{2{\gamma }_2}\right)m$, note the dimension of $S_l$ is $(1/6)m^3+(1/3)t(m^2-1)+(1/2)m^2+(1/3)m$, for $t=\left(\frac{\alpha -(2\delta +{\gamma }_1+{\gamma }_2)}{2{\gamma }_2}\right)$ smaller than the dimension of L.

3.3. A New Attack Bound for Deciphering Exponent d with a Composed Prime Sum

In this section, we apply the same analysis for getting bound for d which we have earlier obtained resultant bound for k.

From the relation $ed\equiv 1(mod\phi (N))$, we get

$$t(N+1-(2^n{k}_0+k_1))+1\equiv 0(mode)$$

(3)

for $t=\frac{ed-1}{\phi (N)}$ and the prime sum $p+q=2^n{k}_0+k_1$.

Now define

$$f^{\prime }(x,y,z)=\left\{\begin{array}{c}(N+1)x+xy+(2^n)xz+1\mathrm{if}|k_0|\le |k_1|\hfill \\ 2^{n^{\prime }}x(N+1)+xy+2^{n^{\prime }}xz+2^{n^{\prime }}\mathrm{if}|k_1|\le |k_0|.\hfill \end{array}\right.$$

From Equation (3), note that if $|k_0|\le |k_1|$ then $(t,-k_1,-k_0)$ is a solution and if $|k_1|\le |k_0|$ then $(t,-k_0,-k_1)$ is a solution for the modular polynomial equation $f^{\prime }(x,y,z)\equiv 0(mode)$.

As the polynomials $f(x,y,z)$, $f^{\prime }(x,y,z)$ differ by signs only, we can implement the above argument for $f(x,y,z)$ to $f^{\prime }(x,y,z)$ and obtained new bound on d for $t<d=N^{{\delta }^{\prime }}$, $max|k_0|,|k_1|\le N^{{\gamma }_1}$, $min|k_0|,|k_1|\le N^{{\gamma }_2}$ and for $e=N^{\alpha }$ is

$${\delta }^{\prime }<\frac{1}{2}\alpha -\frac{1}{2}{\gamma }_1-\frac{1}{6}\sqrt{6(\alpha -{\gamma }_1){\gamma }_2+3{\gamma }_2^2}.$$

(4)

For $\alpha =1$, the Boneh and Durfee’s bound for $d=N^{\delta }$ is $N^{0.292}$. The new bound on d may overcome this bound for $\alpha =1$ and for some values of ${\gamma }_1$ and ${\gamma }_2$ and that values are depicted in Table 3.

Table 3. For $\alpha =1$, the values of bound on ${\delta }^{\prime }$ in terms of ${\gamma }_1$ and ${\gamma }_2$.

${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	${\mathit{\delta }}^{\prime }$ New Bound
0.40	0.005–0	0.2929–0.3
0.35	0.0094–0	0.2929–0.325
0.25	0.052–0	0.2929–0.375
0.15	0.1152–0	0.2929–0.425
0.01	0.009–0	0.4563–0.495

4. Conclusions

In this paper, another attack bound for k, a small multiplicative inverse of $\phi (N)$ modulo e is given when the prime sum $p+q$ is of the form $p+q=2^n{k}_0+k_1$ where n is a given positive integer and $k_0$ and $k_1$ are two suitably small unknown integers using sublattice reduction techniques and Coppersmith’s methods for finding small roots of modular polynomial equations. This attack bound is slightly larger than the bound, in the approach using lattice based techniques and requires lattice of smaller dimension than the approach given by using lattice based techniques. Also, we gave a new attack bound for the deciphering exponent d with above composed prime sum and compare it to Boneh and Durfee’s bound.