Robust Secure Authentication and Data Storage with Perfect Secrecy
Abstract
:1. Introduction
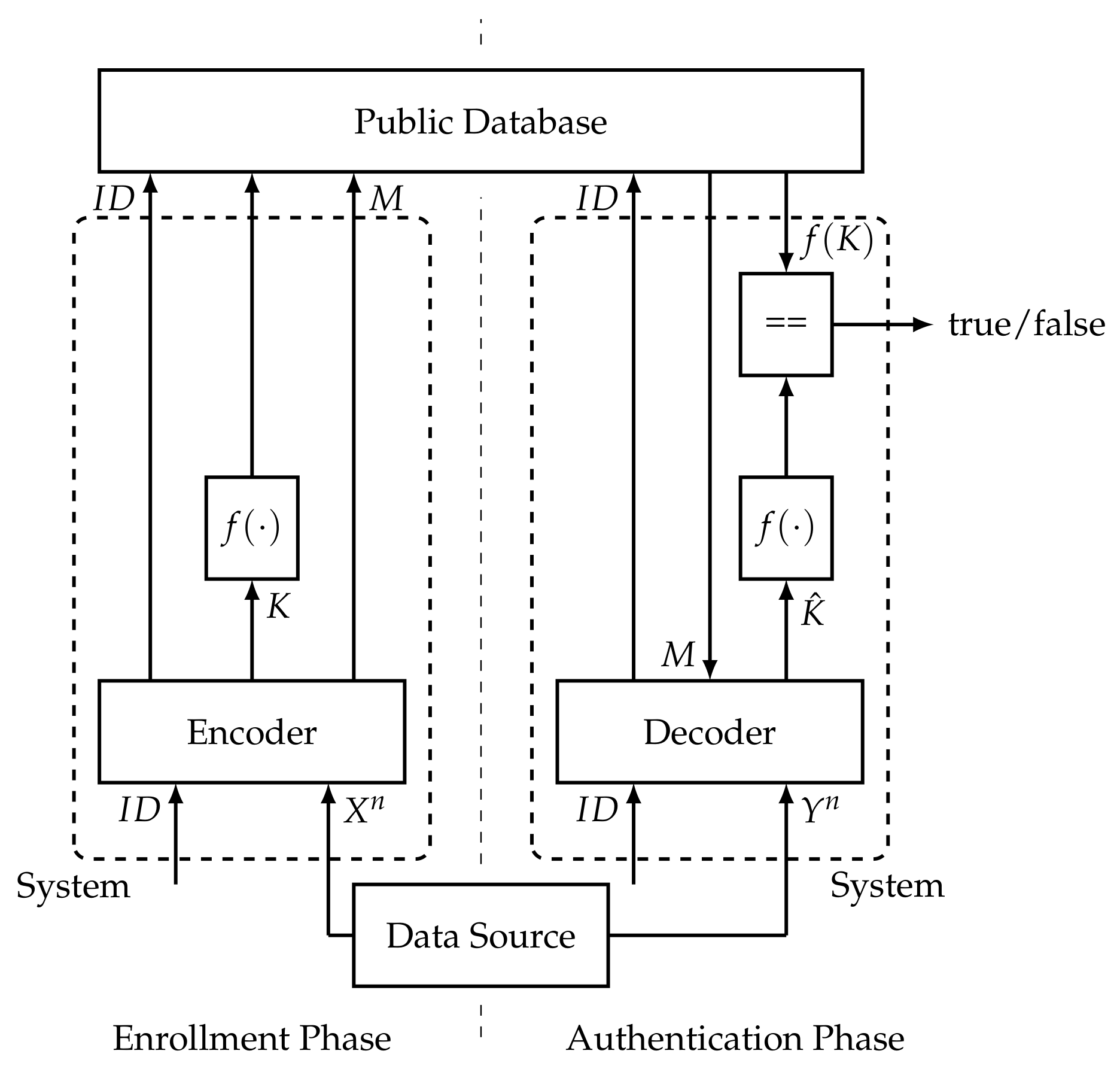
2. Authentication Model
3. Various Definitions of Achievability
4. Capacity Regions for the Authentication Model
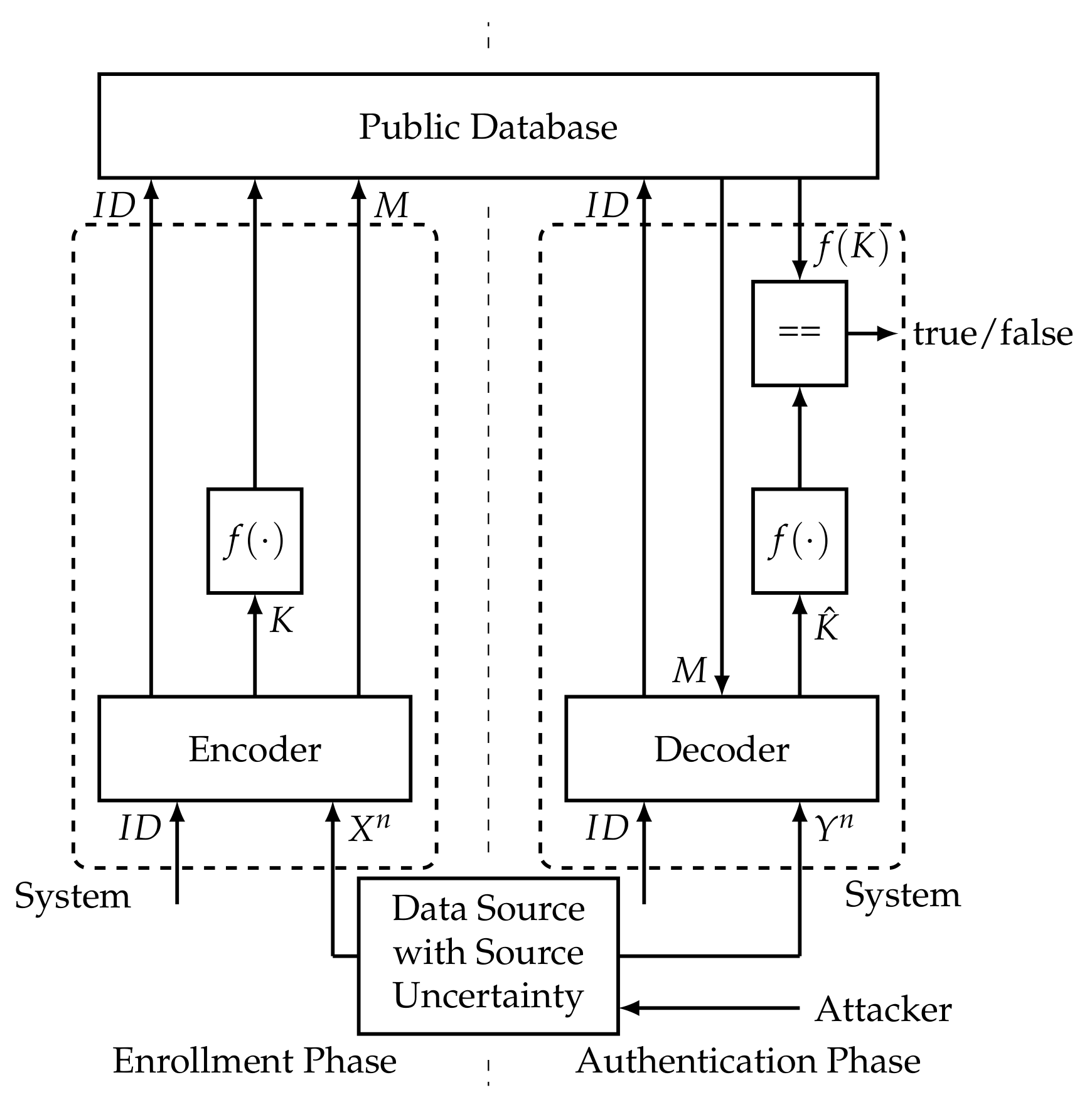
5. Compound Authentication Model
6. Achievability for the Compound Model
7. Capacity Regions for the Compound Authentication Model
- We consider a partition of the set of all sets in subsets. Thus, we denote the sets by , , indicating to which subset they belong. We denote the set of indices m corresponding to by . For each , we have
- Each consists of sequences of the same type.
- It holds thatfor and all .
- For each , one can define pairs of mappings that are compound -codes, , for the channels , for all in the following way. Define an (arbitrary) bijective mapping and an appropriate mapping . Then, is such a code. This meansfor all and for all codewords in . This is possible for all .
- We define and as follows. The system gets a sequence . It checks if , , for an (We can choose small enough and n large enough such that the are disjoint). If this is true for , the channel is used n times to generate from . For , the system looks in for . If the system chooses for m the index of the subset containing . If it chooses an arbitrary . In addition, if , it chooses an arbitrary . For , the system looks in for . If , it considers the compound -code corresponding to the subset containing . Ifwe consider the following deterministic mapping . Here,The preimage of any under is a subset of of sizeThe rest of the is mapped on . Ifthe system chooses . In this case, we also define where is injective. If , k is chosen at random according to a uniform distribution on the alphabet. The same holds if is mapped on or if .
- We define as follows. The system gets a sequence and m. It decodes using the code corresponding to . Then, is used on the result. The result is if it differs from . Otherwise, an arbitrary is chosen.
- We define the following events:According to ([3], Lemma 2.10), we can choose small enough such that implies and . We haveHere, follows as for the system uses to generate from . Thus,Now, we useand getNow, we define the RV withWe haveas for allAs and imply for an , we knowandfor . Thus, we haveWe know forUsing , we haveThus, using Inequality (9), we havefor n large enough. Now, consider , . We getasfor . We realize that, for andwhere the last step follows asThus, we getThe last term is constant for all of the same type. Thus,is constant for . Asfor , we havefor . Now, we getWe haveand getorrespectively, if, for the source state s, it holds that for the corresponding to the smallest . Here,Thus, for n large enough,and Inequality (5) is fulfilled for small enough constants and n large enough.
- We defineand the RV . We haveNow, consider . It holds thatWe knowfor . Thus,for all . This meansas is constant for all . We also knowfor , as k is chosen according to a uniform distribution on in this case. Thus,This means Equations (6) and (7) are fulfilled.
- For the secret-key rate, we have
- Finally, we analyse the privacy-leakage rate. We havewhere we use for the second equality (see ([3], Problem 3.1)). Now, we usefor and n large enough. We also use for and getThus,We now usewhere ,Thus, is arbitrarily small for large n.
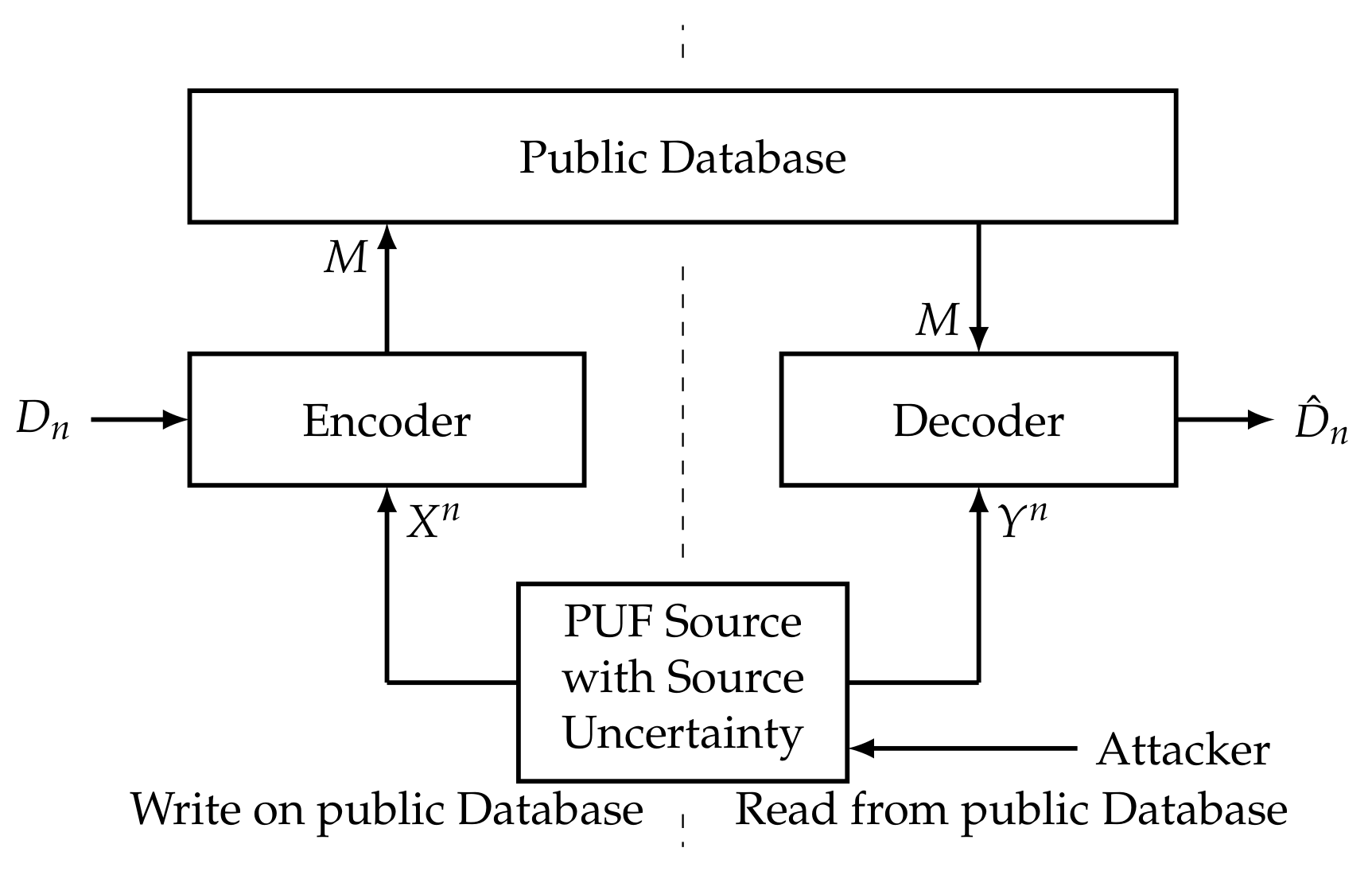
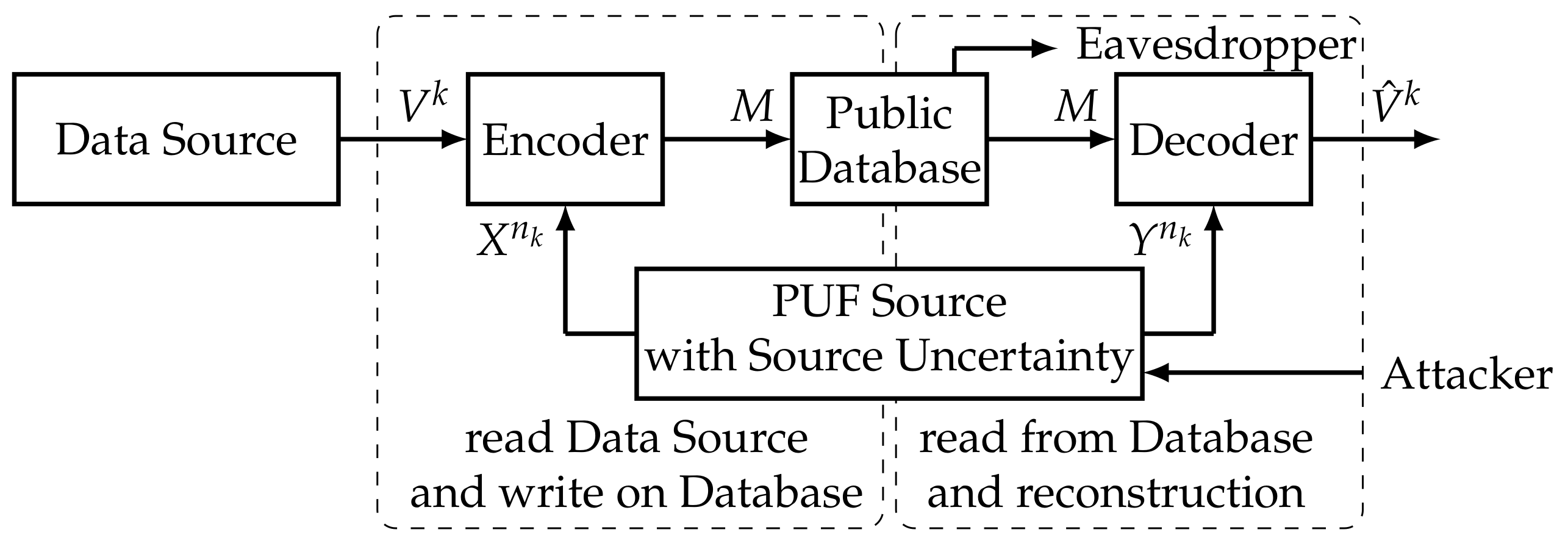
8. Secure Storage
9. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Theorem 4
Appendix B. Equivalence of Rate Regions
Appendix C. Modifying Markov Chains
- We havefor all . Here, follows from . Thus, we see that Equivalence (A10) is true.
- We have for all from . Summing both sides over all , we get Implication (A11).
- We havefor all , where follows from and from Implication (A11). This means Implication (A12) is true.
- We havefor all , where follows from and ( and ( follow as C is independent of . Thus, we have Implication (A13).
References
- Schaefer, R.F.; Boche, H.; Khisti, A.; Poor, H.V. Information Theoretic Security and Privacy of Information Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J. Physical-Layer Security: From Information Theory to Security Engineering; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ahlswede, R.; Csiszár, I. Common randomness in information theory and cryptography. Part I: Secret sharing. IEEE Trans. Inf. Theory 1993, 39, 1121–1132. [Google Scholar] [CrossRef]
- Ignatenko, T.; Willems, F.M. Biometric security from an information theoretical perspective. Found. Trends Commun. Inf. Theory 2012, 7, 135–316. [Google Scholar] [CrossRef]
- Grigorescu, A.; Boche, H.; Schaefer, R.F. Robust PUF based authentication. In Proceedings of the IEEE International Workshop on Information Forensics and Security (WIFS), Rome, Italy, 16–19 November 2015; pp. 1–6. [Google Scholar]
- Lai, L.; Ho, S.-W.; Poor, H.V. Privacy-security tradeoffs in biometric security systems. In Proceedings of the 46th Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, 23–26 September 2008; pp. 268–273. [Google Scholar]
- Boche, H.; Wyrembelski, R.F. Secret key generation using compound sources-optimal key-rates and communication costs. In Proceedings of the 2013 9th International ITG Conference on Systems, Communication and Coding (SCC), München, Germany, 21–24 January 2013. [Google Scholar]
- Grigorescu, A.; Boche, H.; Schaefer, R.F. Robust Biometric Authentication from an Information Theoretic Perspective. Entropy 2017, 19, 480. [Google Scholar] [CrossRef]
- Baur, S.; Boche, H. Robust authentication and data storage with perfect secrecy. In Proceedings of the 2017 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Atlanta, GA, USA, 1–4 May 2017; pp. 553–558. [Google Scholar]
- Baur, S.; Boche, H. Robust Secure Storage of Data Sources with Perfect Secrecy. In Proceedings of the IEEE Workshop on Information Forensics and Security, Rennes, France, 4–7 December 2017. [Google Scholar]
- Baur, S.; Boche, H. Storage of general data sources on a public database with security and privacy constraints. In Proceedings of the 2017 IEEE Conference on Communications and Network Security (CNS), Las Vegas, NV, USA, 9–11 October 2017; pp. 555–559. [Google Scholar]
- Willems, F.; Ignatenko, T. Authentication based on secret-key generation. In Proceedings of the 2012 IEEE International Symposium on Information Theory Proceedings (ISIT), Cambridge, MA, USA, 1–6 July 2012; pp. 1792–1796. [Google Scholar]
- Gallager, R. Information Theory and Reliable Communication; Springer: Berlin, Germany, 1968. [Google Scholar]
- Wolfowitz, J. Coding Theorems of Information Theory; Springer: Berlin, Germany, 1978. [Google Scholar]
- Blackwell, D.; Breiman, L.; Thomasian, A.J. The capacity of a class of channels. Ann. Math. Stat. 1959, 30, 1229–1241. [Google Scholar] [CrossRef]
- Tavangaran, N.; Baur, S.; Grigorescu, A.; Boche, H. Compound biometric authentication systems with strong secrecy. In Proceedings of the 2017 11th International ITG Conference on Systems, Communication and Coding (SCC), Hamburg, Germany, 6–9 February 2017. [Google Scholar]
- Han, T.S. Information-Spectrum Methods in Information Theory; Springer Science & Business Media: New York, NY, USA, 2013; Volume 50. [Google Scholar]
- Boche, H.; Cai, N. Common Random Secret Key Generation on Arbitrarily Varying Source. In Proceedings of the 23rd International Symposium on Mathematical Theory of Networks and Systems (MTNS2018), Hong Kong, China, 16–20 July 2018. in press. [Google Scholar]
- Schaefer, R.F.; Boche, H.; Poor, H.V. Secure Communication Under Channel Uncertainty and Adversarial Attacks. Proc. IEEE 2015, 103, 1796–1813. [Google Scholar] [CrossRef]
- Wiese, M.; Nötzel, J.; Boche, H. A Channel Under Simultaneous Jamming and Eavesdropping Attack—Correlated Random Coding Capacities Under Strong Secrecy Criteria. IEEE Trans. Inf. Theory 2016, 62, 3844–3862. [Google Scholar] [CrossRef]
- Nötzel, J.; Wiese, M.; Boche, H. The Arbitrarily Varying Wiretap Channel—Secret Randomness, Stability, and Super-Activation. IEEE Trans. Inf. Theory 2016, 62, 3504–3531. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baur, S.; Boche, H. Robust Secure Authentication and Data Storage with Perfect Secrecy. Cryptography 2018, 2, 8. https://doi.org/10.3390/cryptography2020008
Baur S, Boche H. Robust Secure Authentication and Data Storage with Perfect Secrecy. Cryptography. 2018; 2(2):8. https://doi.org/10.3390/cryptography2020008
Chicago/Turabian StyleBaur, Sebastian, and Holger Boche. 2018. "Robust Secure Authentication and Data Storage with Perfect Secrecy" Cryptography 2, no. 2: 8. https://doi.org/10.3390/cryptography2020008



