Evaluating the Efficiency of Physical and Cryptographic Security Solutions for Quantum Immune IoT

Abstract

The threat of quantum-computer-assisted cryptanalysis is forcing the security community to develop new types of security protocols. These solutions must be secure against classical and post-quantum cryptanalysis techniques as well as feasible for all kinds of devices, including energy-restricted Internet of Things (IoT) devices. The quantum immunity can be implemented in the cryptographic layer, e.g., by using recent lattice-based key exchange algorithms NewHope or Frodo, or in the physical layer of wireless communication, by utilizing eavesdropping-resistant secrecy coding techniques. In this study, we explore and compare the feasibility and energy efficiency of selected cryptographic layer and physical layer approaches by applying an evaluation approach that is based on simulation and modeling. In particular, we consider NewHope and Frodo key exchange algorithms as well as novel physical layer secrecy coding approach that is based on polar codes. The results reveal that our proposed physical layer implementation is very competitive with respect to the cryptographic solutions, particularly in short-range wireless communication. We also observed that the total energy consumption is unequally divided between transmitting and receiving devices in all the studied approaches. This may be an advantage when designing security architectures for energy-restricted devices.

1. Introduction

Quantum computers will revolutionize the cryptanalysis field as they can easily solve [1,2,3] foundational problems that modern cryptographic algorithms have relied on. Quantum computers can be used to break asymmetric cryptography and, thus, make it possible to eavesdrop and tamper most communication that is protected with modern security protocols. This threat of quantum computers forces us to replace the vulnerable algorithms used for securing communication and data in billions of devices. Hence, the security field is currently searching for authentication and confidentiality solutions that provide immunity against quantum computers and that are feasible for all kinds of devices including energy-restricted and Internet of Things (IoT) devices. Standards for quantum immune cryptography are currently being developed through an open competition [4].

Quantum immune cryptographic algorithms for encryption, key exchange, authentication and digital signing are based on problems that are assumed to be resistant to quantum computing as well as classical cryptanalysis. Recent lattice-based proposals for key exchange, such as NewHope [5] and Frodo [6], have also been considered computationally feasible. However, in addition to cryptography, there are other security alternatives providing quantum immunity, including the quantum-key distribution for optics (see, e.g., [7,8]) and secrecy coding for wireless communications, which is our focus in this article.

Physical layer security is a new research field [9,10] that utilizes the physical properties of radio communication channels to make eavesdropping very difficult. Physical layer security can be generally divided into two categories: secrecy coding methods that secretly convey information using the properties of the wireless medium, and extraction methods that seek to build secret information by adopting the inherent randomness of wireless channels. Roughly speaking, in secrecy coding methods, it is possible to communicate secretly if one can devise a way to ensure that the wireless channel between the legitimate transmitter and receiver is better than the channel of any illegitimate receiver. For example, the transmitter can generate a special jamming signal that affects all but the the legitimate receiver [11]. Then, in theory, the channel between the legitimate parties has a higher capacity than an eavesdroppers’ channel, and the eavesdroppers get less information than the legitimate receiver. The information that the eavesdroppers do not get is a shared secret. Extraction methods, on the other hand, seek to use the unique space, time, and frequency characteristics of the wireless channel as the source of shared secret information between a transmitter and a receiver. Consequently, physical layer security methods could be used to exchange a shared secret and thus complement quantum immune security systems, e.g., by providing a (quantum immune) confidentiality property for the key exchange system.

The research related to the post-quantum security field has so far focused on the hardness and security level of algorithms. Feasibility of the proposals has been validated by analysing the computational complexity of the algorithms and by evaluating the implementations experimentally (see e.g., [5,6,12,13,14,15,16,17,18]). In this paper, we propose a simulation-based approach—based on the ABSOLUT tool [19]—for evaluating the energy efficiency of security algorithms. The simulation-based approach allows us to study easily the energy and power consumption of algorithms on different hardware platforms. With the ABSOLUT tool, we can more easily study how changes in algorithm or hardware design will affect energy consumption.

The contributions of this paper are concluded as follows:

• We present an implementation of a secrecy coding scheme from [20] that provides resistance against eavesdropping and, thus, quantum immunity.
• We evaluate the feasibility and usability of different quantum immune key exchange algorithms (physical and cryptographic) for common IoT hardware platforms Raspberry Pi2 and Raspberry Pi3.
• We analyse the energy efficiency of NewHope, Frodo, and the implemented physical layer security scheme. Our analysis illustrates the energy efficiency benefits for physical layer security research area.
• We study the suitability of simulation-based evaluation for security algorithms. The proposed approach is a quick and flexible method for design-time energy efficiency evaluation of a large amount of solutions on various platforms.
• Based on the observations, we provide guidelines for implementing energy-efficient security architectures and algorithms for quantum immune IoT.

The rest of the article is organised as follows: In Section 2, we describe the quantum threat and present two threat models, encompassing issues relevant both for physical and cryptographic security. Section 3 describes prominent solutions for quantum immune key exchange: lattice-based cryptosystems and physical layer secrecy coding. We also analyse these algorithms from the energy-efficiency perspective. Section 4 reviews related work on simulation-based energy efficiency analysis. In Section 5, we describe our evaluation approach to energy efficiency evaluations. In Section 6, we present the obtained results. Section 7 discusses our main observations on the evaluation approach as well as on the evaluated quantum immune security approaches. The section also provides guidelines for security protocol implementations. Conclusions as well as future research topics are presented in Section 8.

2. Security Threats in the Post-Quantum Era

This section provides background information on post-quantum security. It explores the security threats against communication security and particularly against key exchange that are enabled by the development of quantum computers. After providing an overview of the ‘quantum threat’, we contribute two threat models that encompass both physical layer and cryptographic security aspects.

Current quantum computers are energy inefficient as they operate at temperatures close to the absolute zero. However, for specific applications, quantum computers are more efficient than classical computers. A prominent application for quantum computers is cryptanalysis, i.e., the breaking of cryptographic protocols. In particular, the following algorithms for quantum computers are efficient and will have a major impact on security:

• Shor’s algorithm [1,2] will break asymmetric cryptography. The algorithm can be used to solve integer factorization and (elliptic curve) discrete logarithms, which have been used in many existing public keys cryptosystems, including Rivest–Shamir–Adleman (RSA), Digital Signature Algorithm (DSA), Diffie–Hellman (DH) key exchange, as well as Elliptic Curve Cryptography (ECC).
• Grover’s algorithm [3] will weaken symmetric cryptography. The algorithm will speed up brute force attacks against symmetric cryptography, such as Advanced Encryption Standards (AES) and Secure Hash Algorithm versions 2 and 3 (SHA-2, SHA-3).

At the moment, the quantum threat is theoretical as quantum computers that fulfill the requirements of Shor’s algorithm are not available. To break an RSA algorithm with a key size of 2048, a quantum computer of 10,000 qubits [21] or 4000 qubits with 100 million gates [22] is needed. To break a 160-bit ECC key, a quantum computer of around 1000 qubits is needed [23]. The first commercial special-purpose quantum computers have reached capacities of around 2000 qubits [24] but only with high error rates and thus do not qualify for Shor’s algorithm. Universal quantum computers—applicable for quantum breaking—have only recently reached a capacity of 16 qubits [25] that is far away from quantum breaking capabilities. Different opinions on the availability of quantum computers for Shor’s algorithm have been proposed. According to the most optimistic views, a million qubit system (corresponding to 1000 error corrected qubits) might be conceivable within 10 years [26]. Many believe that the construction of a quantum computer for Shor’s algorithm will take decades should it ever emerge at all. Nevertheless, the potential existence of even one quantum computer offers motivation to secure trillions of connections with solutions, which are not weak against quantum computers. Therefore, National Institute of Standards and Technology (NIST) is currently standardizing algorithms [4] and the first standards for post-quantum crypto are expected in 2022–2023.

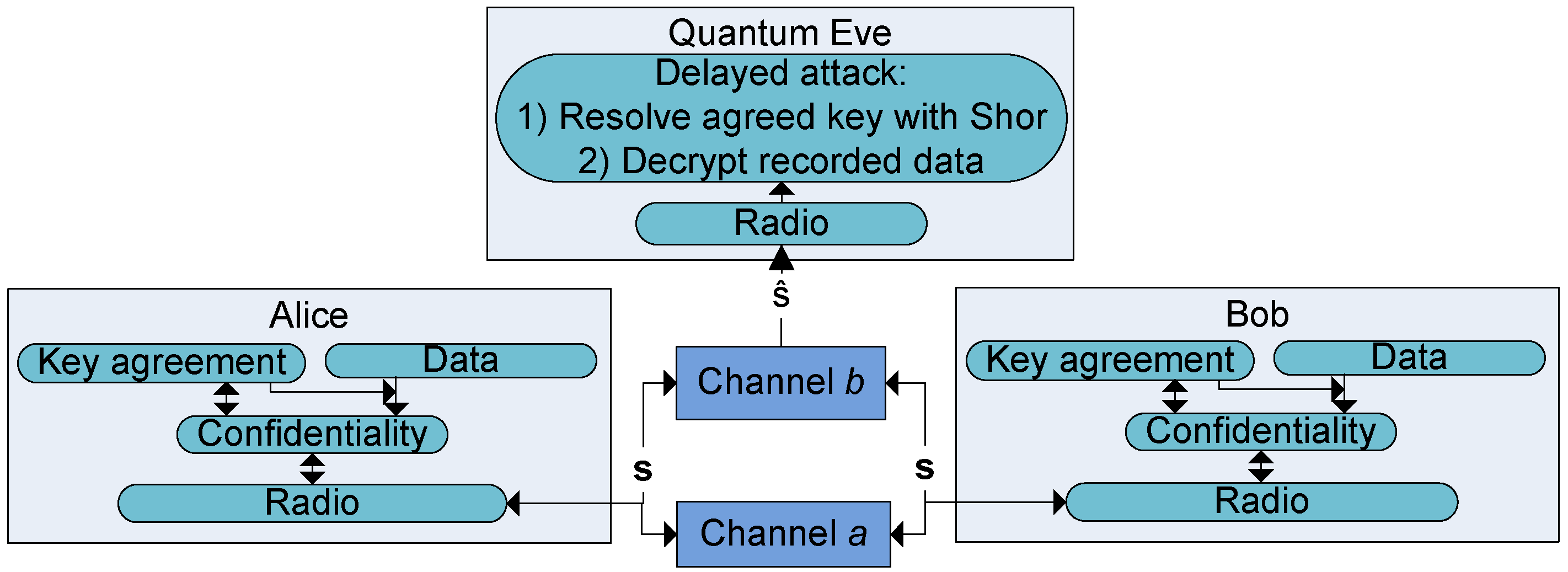
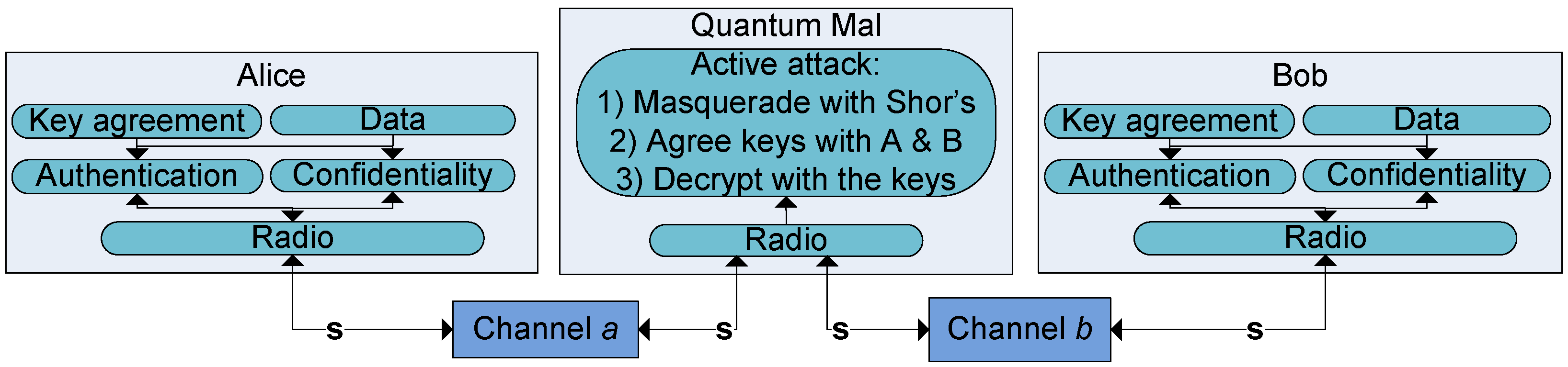
Figure 1 and Figure 2 illustrate two different threat models in post-quantum scenarios. The figures combine elements that are relevant both for the physical layer security as well as for cryptographic security. In both figures, we have Alice and Bob communicating via a wireless channel.

In the first figure, we have the passive eavesdropper Eve. To prevent eavesdropping, Alice and Bob are trying to agree on a secret session key that can be used to protect (with some symmetric cipher) the confidentiality of any subsequent application data. The key agreement must be confidential, but it can be based on a cryptographic or physical layer scheme. Note that Eve does not need to have run-time quantum breaking capabilities. If she is able to capture all the transmitted key exchange information and subsequent protected communication, she may, later when she has a quantum computer, resolve the session key using Shor’s algorithm and decrypt the recorded communication. Attackers’ abilities to capture transmissions have been considered as granted in classical (Dolev–Yao based [27]) threat models for cryptographic solutions. However, in the case of physical layer security, this assumption is sometimes considered too strong.

In the second scenario, we have the active man-in-the-middle attacker Mal. This threat model requires an additional authentication approach resistant against the man-in-the-middle attacker. This requirement can be fulfilled e.g., with cryptographic authentication (but not with secrecy coding in the physical layer that lacks strong authentication capabilities). When Mal is quantum capable, she will be able to break classical asymmetric algorithms at run-time using Shor’s algorithm. Hence, if the key agreement uses classical asymmetric algorithms for authentication, Mal is able to break the protection and masquerade as Bob to Alice and as Alice to Bob. However, as noted by Bos et al. [16], classical authentication methods also work in the pre-quantum era as Mal cannot break them in real time.

Consequently, the time when security solutions must be quantum immune is the quantum era (the time when quantum computers for Shor’s algorithm exist) minus N years, where N is the time that the protected information must be kept secret. In authentication N is zero because, to break an authentication scheme, the attacker must have quantum computer capabilities during the authentication procedure (and active attack). In confidentiality protection, on the other hand, the attacker can just store the ciphertext and then wait until the quantum computer emerges. This insight is relevant for quantum immune solutions that do not provide authentication. In the era where we are waiting quantum computers, it is safe to use classical authentication mechanisms as long as other parts of the security system are quantum immune (for instance, the key distribution is protected with physical layer confidentiality and the application data is protected using AES with long keys).

3. Quantum Immune Security Solutions

Quantum immune, or so called post-quantum, security solutions address both the passive and/or active threat models that we described in the previous section. Quantum immune security solutions apply algorithms that are unaffected by (known) cryptanalysis techniques based on quantum computers. Essentially, the hardness of these solutions is based on something else than integer factorization or discrete logarithm problems. In this section, we will present three alternative solutions—the lattice-based cryptographic algorithms NewHope and Frodo as well as the polar-coding-based physical layer security—and explore their feasibility to provide quantum immunity for energy and resource restricted IoT devices.

3.1. Quantum Immune Cryptography

Quantum immune cryptographic solutions address both passive and active adversaries, with quantum capabilities. Research on cryptographic algorithms that are resistant against quantum computers fall into six categories that are presented in

Table 1. Categories of quantum immune cryptography.

Approach	Description
Lattice-based	The strength of the lattice cryptography is based on difficulty of some lattice problems, e.g., the problems of finding the closest or shortest vector in the agreed lattice. Algorithms include NTRU/NTRUEncrypt for encryption, Bimodal Lattice Signature Scheme (BLISS) for signatures, and Learning with Errors (LWE) algorithms for key exchange. The approaches have been considered energy efficient [31].
Multivariate	Multivariate cryptography is based on the hardness of solving multivariate quadratic equations over a finite field. The problem has been proved to be non-deterministic polynomial-time (NP)-hard. The proposed algorithms include Tame Transformation Signatures (TTS), Rainbow, and Hidden Fields Equations (HFE). The multivariate approaches have been considered energy efficient [31].
Supersingular elliptic curve isogeny	Supersingular elliptic curve isogeny cryptography provides a variant of the Diffie–Hellman algorithm that uses supersingular elliptic curves. The approach can achieve compact key sizes [32] and is therefore suitable for devices with memory/bandwidth limitations (but with sufficient battery/processing capabilities).
Code-based	Code-based schemes, such as McEliece’s [33], encrypt messages into codewords with added errors in such a way that only the private key holder can recover the original message without errors. The schemes require transmission of large keying material.
Symmetric	To compensate for the threat of accelerated brute-force by Grover’s algorithm, the key sizes used in existing symmetric algorithms must be doubled. As a consequence, symmetric algorithms will become more expensive in the way of memory requirements, processing costs, and speed, as well as energy consumption. For example, some estimates [34] indicate that the doubling of the Advanced Encryption Standard (AES) key size from 128 to 256 bits increases costs by 20%.
Hash-based	To address the threat of Grover’s algorithm, the output sizes of hash functions must be enlarged. Increasing the outputs from 254 to 512 bits has a negligible impact on the energy consumption of the CPUs [35]. There will, however, be some extra costs from increased transmissions.

. We focus on the lattice-based cryptography [28,29] that is a prominent candidate for IoT, as it provides good performance in addition to immunity against classical and quantum cryptanalysis. Lattice-based constructs have also been used to achieve fully homomorphic encryption [30].

A lattice is a set of points in an n-dimensional space with a periodic structure. The security of lattice-based cryptography depends on the assumption that particular lattice problems cannot be solved efficiently with classical or quantum computers. A foundational problem in lattice-based cryptography was the Shortest Vector Problem [28], i.e., finding a non-zero lattice vector with minimal Euclidean length. Recent key exchange protocols have applied lattice-based algorithm variations: Learning with Errors (LWE) and Ring Learning with Errors (R-LWE) problems [36]. Prominent implementations derived from these problems include:

• NewHope [5] is a recent implementation of a key exchange protocol based on the R-LWE problem. An early version of the protocol was described by Ding, Xie and Lin [37] and improved by Peikert [38]. Bos et al. [16] implemented the first version of the protocol. NewHope optimized the implementation with new parameters and a better error distribution. The optimized NewHope implementation outperforms the classical Elliptic Curve Diffie–Hellman key exchange (having around a 20% faster Transmission Layer Security (TLS) handshake) [39]. The algorithm has been integrated into the Google Chrome browser [40]. Recent variations of the protocol include HILA5 [41] that optimizes error-correction functions. It is based on NewHope, but is slightly more versatile as it can also be used for encryption as well as key exchange. It has almost the same performance characteristics as NewHope.
• Frodo [6] is based on the LWE problem that uses generic lattices. Frodo avoids the ring structure (of ideal lattices) that may contain some vulnerabilities. Instead, it uses generic lattices with some efficiency side effects. More specifically, the latency of TLS handshake increases 1.3× in Frodo [39] when compared with classical Elliptic Curve Diffie–Hellman or 1.5× when compared with NewHope. [39] Frodo utilizes different optimization techniques: communication bandwidth optimization, dynamic generation of public parameters, and carefully chosen error distribution.

The hardness of lattice-based security is actively studied by the research community. All the attack vectors and vulnerabilities may not be known as the field is still relatively young. Efficient algorithms and implementations are still needed to demonstrate the secrecy and feasibility of lattice-based security approaches.

3.2. Efficiency of NewHope and Frodo Key Exchange Algorithms

The energy efficiency of cryptography depends mainly on the computational complexity of algorithms. Particularly, the energy costs depend on the use of different processors (CPUs, GPUs or crypto accelerators). However, also the use of memory (RAM, disk) as well as communication methods (transmissions and receiving through radio, fixed lines, or internal busses) affect the costs.

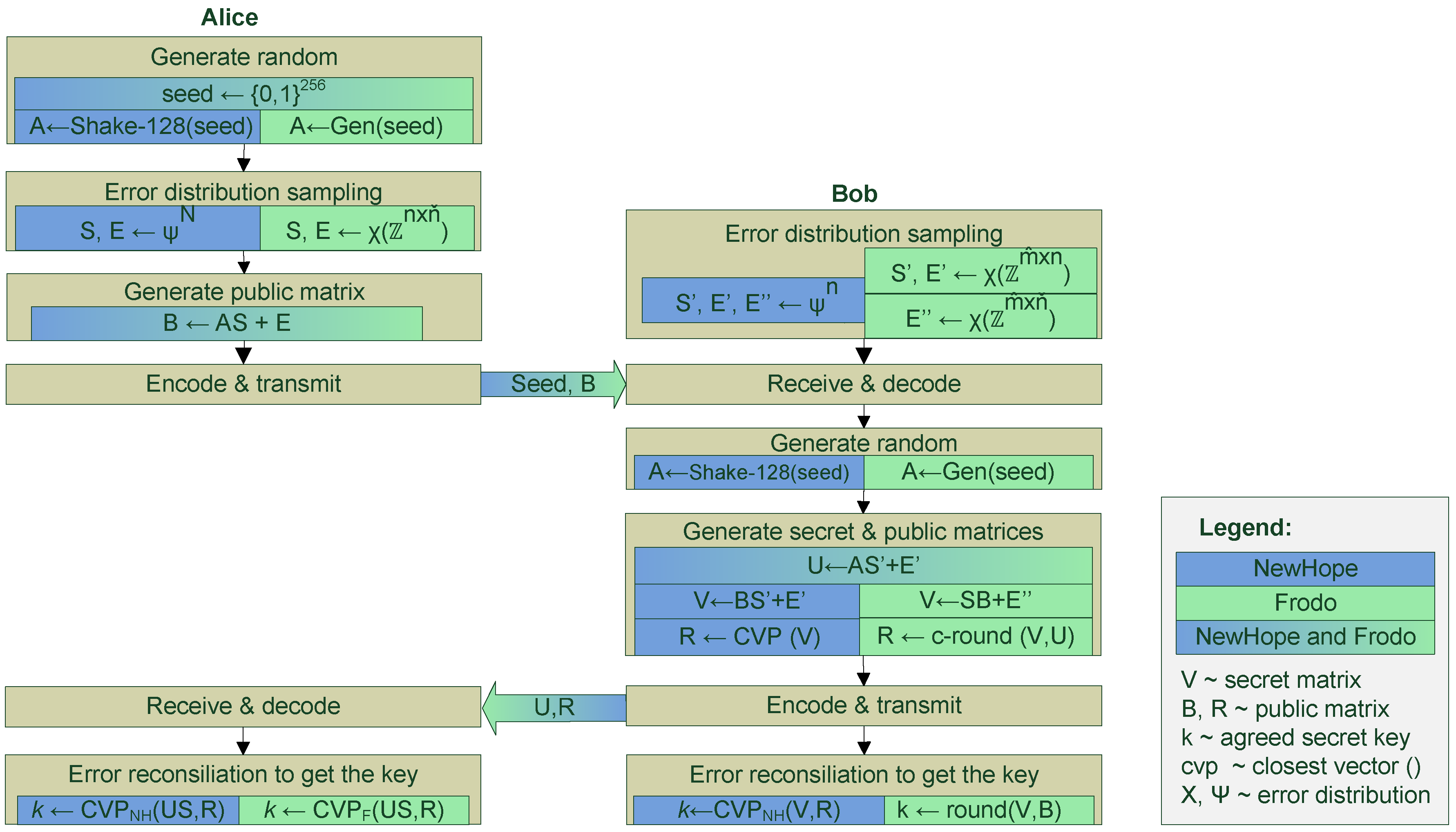
Figure 3 illustrates and compares computations executed by NewHope and Frodo. Other Ring- LWE algorithms, such as HILA5, are similar and follow the same procedures as NewHope, but may have some variations on the parameter selection. The main phases of the algorithms are:

• Random number generation—The procedure itself is not costly from the energy efficiency perspective. However, good entropy sources may not be available for IoT devices.
• Error distribution sampling—NewHope samples errors from the binomial distribution while Frodo presents four optimal discrete distributions. For NewHope, sampling is done once for both sides. For Frodo, the sampling is done once for Alice and twice for Bob. The sampling costs for optimized NewHope is around 5% of the total computation for both Alice and Bob [5].
• Generation of public and private matrices with errors—Alice and Bob use these matrices to agree on and generate a shared key. These phases include polynomial multiplications that are simple to implement also for memory and processor restricted embedded devices. However, algorithms require a large amount of computations that consumes energy. This is computationally the most expensive part as e.g., 15% of NewHope processing for Alice and Bob goes here [5]. Hence, NewHope implementations apply Number Theoretic Transform (NTT) techniques like fast Fourier transformation to improve the performance [5,42]. Frodo does not have the benefits that the ring structure brings but tries to minimize the costs of generating public parameters.
• Encoding and transmitting/decoding and receiving of messages between Alice and Bob—In NewHope, the first pass contains 1824 bytes and the second pass 2048 bytes [5]. In Frodo, which uses ideal lattices that require longer parameters, the first pass contains 11,377 bytes and the second 11,296 bytes [6].
• Error reconciliation—determining the exact key from the agreed matrices with errors. This phase also takes considerable processing power. For instance, around 11% of Alice’s and 6% of Bob’s computing time in NewHope is spent on error reconciliation [5].

3.3. Quantum Immune Physical Layer Security

Physical layer security addresses the passive quantum threat model that was described in Section 2. Physical layer security methods can be generally divided into two different categories: secrecy coding methods that secretly convey information using the properties of the wireless medium, and extraction methods that seek to build secret information by adopting the inherent randomness of wireless channels.

When it comes to extraction methods, Alice and Bob can agree on the common key by measuring a physical quantity common to both of them in a process commonly referred to as key extraction [43]. Due to the physical properties of the quantity measured, for example, channel impulse response, Alice and Bob obtain highly correlated measurements. On the other hand, the measurements obtained by the eavesdropper Eve are weakly correlated because she is most likely in a different place than Bob. This hypothetical gap of the correlation of measurements between Alice and Bob and the correlation of Eve’s measurements opens the door for a key exchange mechanism with an information reconciliation and privacy amplification step to enable the calculation of a secret key that is almost independent of the adversary’s view [43]. Thus, the physical layer key extraction between the two parties, Alice and Bob, is based on two basic premises: the measurements of both Alice and Bob are highly correlated, whereas Eve’s measurements are weakly correlated. These assumptions become relevant if the confidentiality of the key agreement is based on the physical layer properties and on the location of the attacker.

In secrecy coding methods, the goal is to design a coding scheme—namely, an encoding algorithm and the decoding algorithm—that makes it possible to communicate both reliably and securely between Alice and Bob in the presence of an eavesdropper Eve. The reliability of the secrecy code is quantified by its average probability of error with uniformly distributed messages M. The information leaked to Eve is given by the mutual information between Alice’s message M and Eve’s observations $Z^n$ where n denotes the number of samples. A rate R is said to be achievable under the strong secrecy requirement if there exists a sequence of codes for which both the average probability of error and the information leaked to Eve vanish as n tends to infinity. The supremum $C_s$ of the achievable rates is known as the secrecy capacity of the channel. In other words, reliable and secure communication is possible only at coding rates below or at secrecy capacity.

The definition of secrecy capacity is an information theoretic one, that is, secrecy does not depend on assumptions about computational hardness, and as such secrecy coding is not vulnerable to future developments in computer power such as quantum computing. However, the definition of secrecy capacity is based on the premise that the channel between the legitimate parties, Alice and Bob, is statistically better than any of the eavesdropper channels. In practice, Alice may jam Eve by generating an artificial noise-like signal that affects all receivers except the one used by Bob [11]. However, the jamming signal is location and channel dependent.

This fact opens the theoretical possibility to attack physical layer security schemes as described in [44]. The basic idea of the attack is that if an attacker’s antennas surround Alice and Bob completely and those antennas are cooled to a few degrees Kelvin, the attacker is then able to recover radio signals from Alice and Bob by using the Huygens principle and the Green integral representation of the electromagnetic fields. In other words, an attacker is able to accurately estimate the radio signals at Alice’s and Bob’s locations at any given time, which renders the jamming signal useless. However, for the attacker to succeed, she still needs to have considerable computing resources at her disposal to compute maximum-likelihood (ML) estimates of the transmitted bits. Computing ML estimates may seem a prohibitive task at the moment, but, in the future, can be significantly sped up using quantum search algorithms (QSA).

3.4. Implementation of Secrecy Coding Scheme

It is shown in [45] that polar codes provide strong security for binary discrete channels, that is, channels with binary inputs and outputs. One takes advantage of the so-called bit-channel polarization phenomenon of polar codes. If we assume that Alice’s message consists of n bits, then polar encoding operation can be seen as transmitting those n bits through n different parallel bit-channels. It can be shown that, as n grows, the bit-channels start polarizing: they approach either a noiseless channel or a pure-noise channel. We say that the noiseless bit-channels are good while the noise-pure channels are bad. Given the channel polarization phenomenon, the general idea of the secure communication scheme is quite simple. One transmits random bits over the bit channels that are good for Eve, message bits over the bit channels that are good for Bob but bad for Eve, and zeros, or frozen bits, over the bit channels that are bad for both Bob and Eve.

We implemented a polar-based secrecy-coding scheme shown schematically in Figure 4. We propose using a concatenated secrecy-coding scheme, where the outer polar code is concatenated with the inner forward-error correcting code, the scheme that is proposed in [20]. The inner low-density parity check (LDPC) code provides reliability, and the outer polar code provides secrecy.

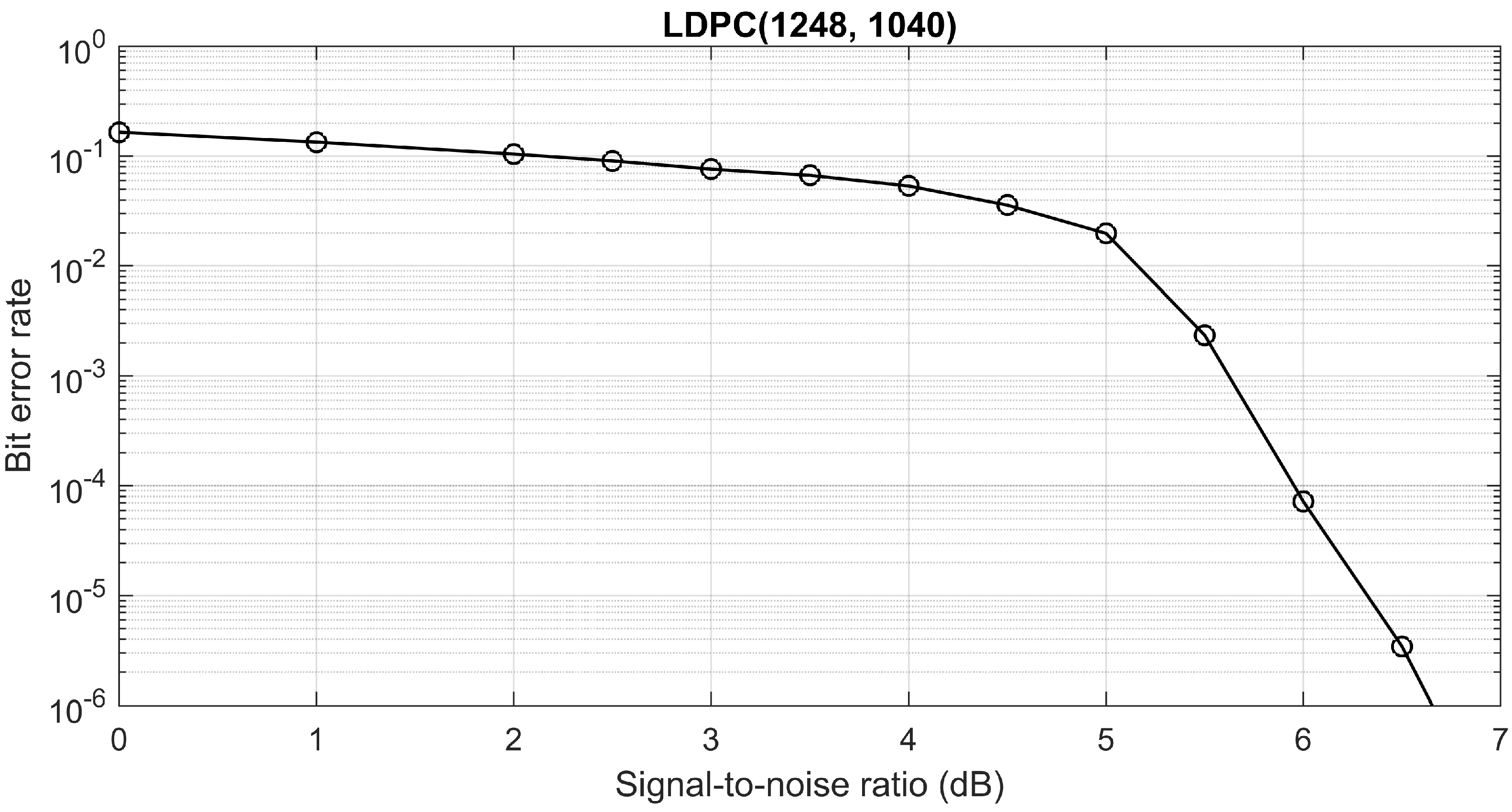
We use quadrature phase shift keying (QPSK) modulation with LDPC coding scheme from IEEE 802.16 standard with a code length of 1248 bits and a code rate 5/6, i.e., the payload is 1040 bits. We plot the bit error rate versus the signal-to-noise ratio that can be achieved with a given LDPC code in Figure 5. The rationale for selecting QPSK as modulation method is the fact that a communication channel between Alice and Bob, including QPSK modulator and demodulator, is equivalent to binary symmetric channel with a crossover probability $P_{Bob}$ [46]. Similarly, a communication channel between Alice and Eve is equivalent to another binary symmetric channel with a crossover probability $P_{Eve}$. These equivalence properties do not necessarily hold for high-order quadrature amplitude modulations (QAM) such as 16-QAM or 64-QAM.

Our design parameters for secrecy coding are as follows: We require Bob’s bit-error-rate to be at the most $P_{Bob}={10}^{-4}$ after LDPC decoding, which, in turn, implies that Bob’s signal-to-noise ratio should be at least 6 dB, cf. Figure 5. Furthermore, we would like Eve’s bit-error-rate to be at least $P_{Eve}={10}^{-1}$ after LDPC decoding, which, in turn, implies that Eve’s signal-to-noise ratio should be at most 2 dB, cf. Figure 5. The required difference in signal-to-noise ratios between Bob and Eve is commonly referred to as radio advantage. For the given parameters, the minimum required radio advantage is 4 dB. For the given values of Bob’s and Eve’s bit error rates, the secrecy capacity of a binary wiretap channel is

$$C_s=h\left(P_{Bob}\right)-h\left(P_{Eve}\right)\approx 0.457588\mathrm{bits}\mathrm{per}\mathrm{channel}\mathrm{use}.$$

(1)

The symbol $h\left(P\right)$ in (1) denotes the binary entropy function

$$h\left(P\right)=-P{log}_{2}P-\left(1-P\right){log}_2\left(1-P\right).$$

(2)

We have used the design method presented in [45] to determine which polar bit-channels should be used to convey a secret message under the assumption that we use 1024-bit long polar code, $P_{Bob}={10}^{-4}$, and $P_{Eve}={10}^{-1}$. Namely, we identified 479 bit-channels that are good for Eve, 361 bit-channels that are good for Bob but bad for Eve, and 184 bit-channels that are bad for both Bob and Eve. In other words, we use a polar code (361, 479, 184) where a single polar-encoded message consists of 361 message bits, 479 random bits, and 184 frozen (zero) bits. Thus, the code rate is 361/1024 = 0.352539 or approximately 77.0 per cent of the secrecy capacity. We use a conventional message-passing decoder and a successive-cancellation decoder for LDPC and polar decoding, respectively. The maximum number of iterations in the LDPC decoder is set to 50.

The transmitter (Alice) transmits artificially generated noise and thus creates the necessary radio advantage of Bob over Eve. Since this noise is generated by Alice’s transmitter, Alice can design it in such a way that only Eve’s channel is degraded. Thus, by selectively degrading Eve’s channel, secret communication between Alice and Bob can be guaranteed. The "selective" degradation of Eve’s channel is obtained with beamforming. Namely, Alice directs the main antenna beam towards Bob’s location and generates noise in every other direction. Alice also injects reference signals into the transmitted signals, so Bob can estimate the channel impulse response. We assume that Bob uses the least-squares (LS) method to estimate the impulse response of Alice–Bob channel [47].

3.5. Efficiency of Polar-LDPC Secrecy Coding Scheme

The energy-efficiency of secrecy coding schemes mainly depends on the additional amount of energy required to jam all eavesdroppers. Typically, the transmission power of a jamming signal is equal to the transmission power of the information-bearing signal [48], which means that an additional radio unit is required to transmit the jamming signal. As a result, the energy consumption of the transmitter employing secrecy-coding is doubled. It is thus reasonable to expect that secrecy-coding schemes will be energy-efficient in systems where transmission powers are relatively low, for example, short-range communication systems and local area networks.

Typical power consumptions of various WLAN cards and access points are presented in [49]. Since generating a jamming signal does not involve any processing for incoming or outgoing data packets, the power consumption of the network interface card is a valid figure of merit.

The computational complexity of the proposed secrecy coding scheme will be studied in Section 6.1.

4. Related Work on Efficiency Simulations

This subsection presents background information and related work on the simulation approaches for energy efficiency evaluation. The section compares and highlights the advantages of our approach, which will be described in the following section.

Simulation-based performance and/or power consumption evaluation approaches can be divided into two main categories: full system simulators and single component (e.g., processor, memory) simulators. The full system simulators can be further divided into virtual system approaches based on abstract models of both applications and execution platforms, virtual platform approaches, which simulate executable applications in functional platform models and virtual prototype approaches, which execute real applications in a detailed, low-level platform model. Both virtual platforms and virtual prototypes are instruction accurate, but virtual platforms are typically coarsely timed and fast to simulate, whereas virtual prototypes are highly accurate but require a lot of modeling effort and are slow to simulate. Virtual systems are not instruction accurate but facilitate low modeling effort and high enough precision for early evaluation and design space exploration.

Our ABSOLUT tool is a virtual system approach where both the security approach as well as different IoT platforms are modeled. It is suitable for cost-effective evaluation of post-quantum solutions as we want to study and compare a large amount of different algorithms and study their feasibility in IoT with a large amount of platforms. Porting all the algorithms to versatile platforms is not a feasible alternative. The simulation speed of ABSOLUT depends on the complexity of the modeled applications and platforms, but the typical range has been between 30 and 300 MOPS. The average simulation error in the case studies, verified with measurements in real hardware, has been 12%.

Gem5 [50] is an instruction accurate simulation system with configurable component models and speed/accuracy tradeoff capability. The nominal simulation speed varies between 300 KIPS and 3 MIPS. SimuBoost [51] is a method for the parallelization of full system simulation based on a virtual platform. Sniper [52] is a parallel multi-core simulator for the performance and power consumption of x86 architectures. It can achieve up to 2 MIPS simulation performance with at most 25% error. VirtualSoC [53] is a method for the full system simulation of a general purpose CPU and a many-core hardware accelerator using Quick Emulator (QEMU) and SystemC. Virtual system-based approaches have been proposed by [54,55]. COSSIM [56] is a framework for the full system simulation of networking and processing parts of cyber-physical systems (CPS). It is able to evaluate the performance, power-consumption and security aspects of CPS systems and proposes hardware acceleration with field-programmable gate arrays (FPGAs) to achieve rapid evaluation.

Quantum immune security approaches have typically been evaluated only by running them on real hardware platforms targeted for desktop or IoT devices. This has enabled development of solutions that are optimized for particular devices and processors. A simulation based approach has been used by one research group [57] who studied how the efficiency of application-specific integrated circuit (ASIC) plans for post-quantum crypto systems can be evaluated using the Bluespec SystemVerilog tool. They evaluated designs of two algorithms (NTRUEncrypt and TTS) and studied their performance in the respect of execution times. Our ABSOLUT simulator approach can be used to evaluate the same solutions of different platforms—from desktop to embedded—and it can be used to receive power consumption and energy efficiency information.

5. Evaluation Approach for Quantum Immune Security

This section describes our evaluation approach and implementations. Firstly, the simulator approach and implementation is described. Secondly, the test-bed set-up for the IoT scenario is described.

5.1. Simulation Approach

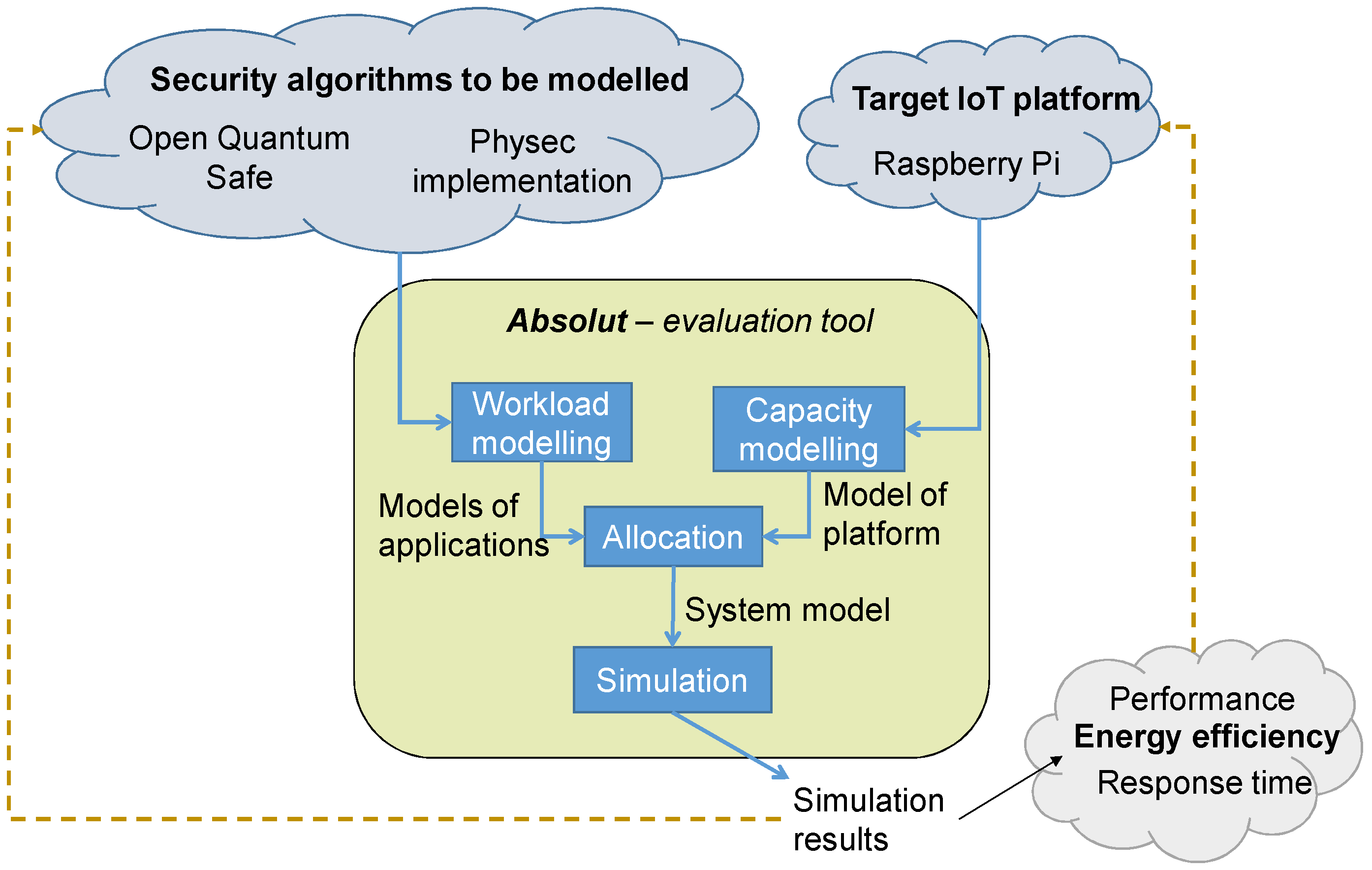
The ABSOLUT approach [19] is intended for the evaluation of computer system performance and power consumption in the early phases of design. ABSOLUT uses virtual system modeling, where abstract workload models of applications are simulated on top of performance capacity models of the computing platform (Figure 6). The workload models have basic block, function, process and application layers [19] and are implemented in SystemC [58]. The basic block layer of the workload models contains the abstract instructions read, write, and execute as well as requests for higher-level services, such as video decoding or direct memory access (DMA) transfer. Tools exist to enable the automatic generation of workload models from traces, measurements, source code or application binaries.

The platform models are also layered and semi-automatically generated from library components and text-based platform description and configuration files. The platform description defines which components are instantiated from the library and their connections, whereas the configuration file sets up parameters like the clock frequency. The model library includes capacity models of the processing unit, interconnect, memory, and hardware accelerator components implemented in transaction-level SystemC.

The processing unit models consume the abstract instructions from the workload models. They estimate the time needed to execute the instructions and calculate the resulting utilization and power consumption. They utilize other components of the system through transactions. High-level services are requested from an OS model and processed by the service provider, which typically is a HW accelerator or a workload model incorporated in the platform.

The modeling approach enables early evaluation, since mature hardware or software is not required for modeling and simulation. ABSOLUT is able to estimate the execution time of an application or a part of an application, the utilization of the modeled components in the execution platform, and the system-level power/energy consumption of the use case.

5.2. Implementations for IoT Key Exchange Scenario

To enable energy efficiency measurements, we implemented the physical layer secrecy coding approach and modeled it as well as crypto algorithms and IoT platforms for the simulator.

5.2.1. Modeled IoT Platform

The modeled platforms for simulation were Raspberry Pi2 and Pi3. Raspberry Pi2 contains a Broadcom BCM2836 chip, with a 900 MHz quad-core 32-bit ARM (Advanced RISC Machine CPU architecture designed by Arm Holdings) Cortex-A7 processor with 256 KB shared L2 cache, and 1 GB of RAM. Raspberry Pi3 contains a Broadcom BCM2837 chip with a 1.2 GHz 64-bit quad-core ARM Cortex-A53 processor, with 512 KB shared L2 cache, and 1 GB of RAM. Both have a separate graphical processing unit (GPU) that was not used in the simulations. All components required for modeling the execution platform for the use cases of this article could be instantiated from the ABSOLUT model library. Thus, the effort required for modeling the platform consisted of only making the connections between the components and setting the parameters of the models.

5.2.2. Modeled Cryptoalgorithms and Testbed

We studied the costs of key establishment in ARM platforms. To enable simulations, we created workload models for the NewHope and Frodo algorithms. The models were created using the workload model generators of the ABSOLUT toolset and the source codes from the Open Quantum Safe (OQS) project [59,60]. OQS is an open source effort to incorporate and adapt quantum-immune cryptographic software into a single library. Furthermore, the project integrates the key exchange algorithms to OpenSSL, which is an implementation of the Transmission Layer Security (TLS) protocol. The project has developed a C-language library (oqslib) of implementations for different key exchange algorithms. The supported key exchange algorithms include NewHope and Frodo (with recommended parameters). The library can be executed on the Intel and 64 bit ARM platform, but (14 November 2017 version) does not work e.g., on Raspberry Pi 3 devices with 32-bit Raspbian operating systems. However, the simulation models can be executed on a PC to evaluate the energy efficiency of the target system with a 64-bit OS.

The OQS library includes a test harness and a benchmarking functionality to evaluate and compare the performance of the implementations. Essentially, the test runs Alice’s and Bob’s algorithms for key exchange in a single machine where communication delays are not relevant, and measures the time and computation cycles used. We utilized the source codes from oqslib and test harness to generate NewHope and Frodo models for our simulator.

6. Results

In this section, the results are presented. First, we describe the computational cost results from the simulator. Then, we complement the simulated results of computational costs with an analysis that considers the costs of radio transmissions.

6.1. Simulation Results for Computational Costs

Simulations were performed by modeling the execution of the key exchange test runs for the selected cryptoalgorithms from the liboqs testharness as well as for the secrecy coding. To get comparable results, the number of transmitted secrecy coded bits must be equal to the level of bits that agrees with cryptographic algorithms. For NewHope, the security level corresponds to 229 bits (against classical cryptanalysis) and 206 (against quantum analysis), and for Frodo 156 and 142, correspondingly [6]. In our case, we can send the corresponding amount of bits in one physical layer frame that carries 361 secure bits. Physical layer test runs were executed by sending (from Alice to Bob) 1000 data frames, in order to get the average costs for the transmitted bits in one frame.

The simulated costs are presented in

Table 2. Costs of key exchange computation for Raspberry Pi 2—the simulation results.

	Frodo/Alice	Frodo/Bob	NH/Alice	NH/Bob	SC/Alice	SC/Bob
Execution time	20.4 s	12.6 s	14.0 s	7.2 s	7.2 ms	237.5 ms
CPU average power	190 mW	190 mW	190 mW	190 mW	190 mW	190 mW
Memory average power	143 mW	143 mW	143 mW	143 mW	151 mW	157 mW
System average power	1183 mW	1183 mW	1183 mW	1183 mW	1191 mW	1197 mW
Energy	24.1 J	14.9 J	16.6 J	8.5 J	8.6 mJ	284.2 mJ

and

Table 3. Costs of key exchange computation for Raspberry Pi 3—the simulation results.

	Frodo/Alice	Frodo/Bob	NH/Alice	NH/Bob	SC/Alice	SC/Bob
Execution time	13.6 s	8.4 s	9.3 s	4.8 s	5.2 ms	170.3 ms
CPU average power	252 mW	252 mW	252 mW	252 mW	252 mW	252 mW
Memory average power	143 mW	143 mW	143 mW	143 mW	154 mW	162 mW
System average power	1715 mW	1715 mW	1715 mW	1715 mW	1726 mW	1734 mW
Energy	23.3 J	14.4 J	15.9 J	8.1 J	9 mJ	295 mJ

. The results indicate that the energy costs of computations in secrecy coding (SC) are very small (from 3.6% to 0.04%) when compared to the costs of computation in Frodo and NewHope (NH).

For the secrecy coding, the decoding is significantly (around 33 times) more expensive than encoding. In decoding, the average memory consumption is also more intense. This can be caused by the less optimised code causing more cache misses and/or by the more memory intensive algorithm.

For the cryptographic algorithms, the power consumption is effectively constant in the simulation. This is because the execution of the test was limited to a single thread, and it fully utilises the CPU it is running on for the duration of the test. Thus, the variation in power consumption during the execution is limited to two factors. First, various instructions such as arithmetic, logical, load/store and vector instructions utilising the execution units of the CPU differently. However, this variation is minimal compared to the difference between the idle and active states of the CPU). Second, various parts of the code having different usage patterns for the components in the memory hierarchy. Apart from the approach where radio receiving is essential, bus and memory utilization is negligible. Furthermore, the applications were run on the ARM CPU cores of the Raspberry Pi platforms and did not use hardware acceleration.

6.2. Analysis of Transmission Costs

We have analysed the radio transmission costs of the presented quantum immune cryptographic schemes and secrecy coding. Our figure of merit is the estimate of the total energy consumption of the transmitters and receivers, which is calculated by estimating the transmission times and multiplying them by the average power consumption of a pre-selected network interface card. Namely, we use the average power consumption of a Cisco Linksys Dual-Band WirelessN Express-Card WEC600N2 card as listed in [49]: the average power consumption of the transmitter is 2640 mW and the average power consumption of the receiver is 1980 mW.

We assume that both legitimate devices, Alice and Bob, use radios compliant with the IEEE 802.11n standard in mixed mode. Furthermore, we assume that both radios use orthogonal frequency division multiplexing (OFDM) with 52 data subcarries and four pilot subcarriers, where the channel bandwidth is 20 MHz. Data bits are assembled into frames consisting of a 9-symbol preamble and a payload of up to 4096 OFDM symbols. The signalling speed is equal to 250 ksymbols/s, which implies that one symbol duration is four microseconds. We assume QPSK modulation with a 3/4 coding rate.

The estimates of energy consumption used by radio transmission are presented in

Table 4. Estimated costs of radio transmission in key exchange.

	Frodo/Alice	Frodo/Bob	NH/Alice	NH/Bob	SC/Alice	SC/Bob
Transmitted bits	91,016	90,368	14,592	16,384	1248	—
Transmitted symbols	885	878	150	167	21	—
Transmission time	3.5 ms	3.5 ms	0.60 ms	0.66 ms	0.084 ms	—
Transmission average power	2640 mW	2640 mW	2640 mW	2640 mW	5280 mW	—
Transmission Energy	9.34 mJ	9.27 mJ	1.58 mJ	1.76 mJ	0.44 mJ	—
Received bits	90,368	91,016	16,384	14,592	—	1248
Received symbols	878	885	167	150	—	21
Reception time	3.5 ms	3.5 ms	0.66 ms	0.60 ms	—	0.084 ms
Reception average power	1980 mW	1980 mW	1980 mW	1980 mW	—	1980 mW
Reception Energy	6.95 mJ	7.01 mJ	1.32 mJ	1.18 mJ	—	0.17 mJ
Total Energy	16.29 mJ	16.28 mJ	2.90 mJ	2.95 mJ	0.44 mJ	0.17 mJ

. The number of transmitted symbols is calculated by dividing the corresponding number of transmitted bits by the number of available data subcarriers (52) and the number of bits per modulation symbol (2) and accounting for nine extra preamble symbols. The average power consumption of a transmitter employing the secrecy-coding scheme is doubled to account for the additional energy consumption due to a need to generate a jamming signal.

The energy consumption of radio units is not affected by transmission latency between Alice and Bob as long as there is no need to retransmit any messages. In other words, the maximum allowed transmission latency should not exceed channel coherence time. Channel coherence time is a statistical measure of the time duration over which the channel is essentially invariant, and it is approximately equal to the inverse of maximum Doppler frequency. For example, if we consider a carrier frequency of 2.4 GHz, a vehicular speed of 125 kph, we get a coherence time of about 3.6 ms. As shown in Table 4, transmission times for secrecy coding schemes are much shorter than 3.6 ms.

7. Discussion

This section discusses our results and presents the lessons learned. We address the implications of the observations for IoT security architectures and implementations. We also compare our work to existing energy efficiency simulation approaches and to existing benchmarking results in order to study the advantages and disadvantages of our approaches.

7.1. Guidelines for Quantum Immune Security

The simulation results indicate that physical layer security is, from the energy efficiency perspective, a viable alternative for the cryptographic algorithms. From the security level perspective, the strength of physical layer secrecy coding is still an open debate (like the security level of cryptographic alternatives is as well). Both cryptographic and physical approaches may contain hidden vulnerabilities. Therefore, multi-layered approaches with both physical and cryptographic protection are an option for systems needing stronger assurance. The results indicate that such complementing approaches are feasible at least from the energy efficiency perspective.

When using physical layer security for key exchange, we need an additional authentication algorithm as secrecy coding is unauthentic. The authentication property may be implemented with a protocol based on cryptography. In the post-quantum era, this algorithm must be quantum immune against the active attacker. However, the design of the authentication protocol may be simplified as the confidentiality (eavesdropping-resistance) property is provided by the physical layer.

Future developments may also introduce authentication capabilities into the physical layer. For instance, quantum location verification [61] is a promising approach in this direction.

Architectural implications from our results come from the observation that the costs are divided asymmetrically between the agreeing parties. In IoT, a battery restricted “thing” should be given the less consuming role. In the case of cryptographic protocols, the “thing” should play Bob’s role while Alice plays the (cloud) server’s role. In the case of physical layer secrecy coding, the “thing” should play the physical layer transmitter’s role, while the access point end must play the receiver’s role.

The security protocol and algorithm design should support this requirement: the “thing”—whether it is the initiator or responder of the communication—should be given a lighter role. Many security protocols (such as TLS, Datagram TLS, and Secure Shell (SSH)) apply a client–server architecture where the client initiates the connections. They do not explicitly support such role selection. However, they support algorithm selection; thus, to enable role selection, two alternatives could be defined: an algorithm where a more consuming role is played by the connection initiator (client) and an algorithm where the more consuming role is played by the responder (server). Nevertheless, such algorithm selection is not possible in all cases, for instance, in the more optimized TLS v1.3 [62] the keying material may be delivered already in the first handshake message. In these cases, an application layer handshake is needed to trigger the IoT thing to act as Bob, i.e., as a TLS server.

In the physical layer security approach, the key should be generated by the “thing” as transmission is more energy efficient. However, many resource-restricted devices may not have hardware capabilities for generating good random numbers that are required for good cryptographic keys. In addition, the resource-restricted devices may not typically have additional antennas that are needed for beamforming. Recall that, in secrecy coding schemes, the transmitter typically has many antennas for efficient beamforming and sending artificial noise. Consequently, in these cases, the “thing” must become a receiver that is the most optimal role from the resource efficiency perspective. Fortunately, this limitation does not make physical layer solutions infeasible, as the efficiency advantage on the receiver-side is still large when compared with cryptographic schemes.

The physical layer secrecy coding protects only wireless communication that occurs between a device and access point, base station or another device. It cannot provide protection against threats, where the adversary is elsewhere within the end-to-end communication path, e.g., between an access point and a cloud server. For end-to-end security, cryptographic approaches are more flexible as they do not require the assurance that every physical link is quantum immune.

7.2. On the Advantages of Simulation Based Evaluations

Previous benchmarking efforts for post-quantum security have focused on execution time and computational complexity. An important advantage of our work was that we gained a holistic overview of the energy consumption. Different operations (CPU, GPU, memory, disk, as well as transmissions and receiving on different channels) consume different amounts of energy, and this information is not available just by counting computing cycles or times. With the simulated approach, we can quickly find energy-consumption related problems in unoptimized implementations and algorithms.

Another advantage of the simulator is that we can easily study the algorithms on platforms that are not yet available. For instance, in this study, the OQS algorithms and testsuites were tested on Raspberry Pi platforms even though the OQS has not been ported and does not work on the standard 32-bit Raspbian OS.

The simulation approach has also its limitations. The simulation covers cryptographic as well as secrecy coding operations. It currently does not simulate the radio transmission and receiving operations in the physical layer. However, we addressed these shortcomings by complementing the simulation results with an analysis that utilizes known results on the energy efficiency of communication.

Related Benchmarks of Post-Quantum Security

The designers of the original NewHope and Frodo algorithms provided benchmarking results of their implementations. Optimized implementations of NewHope have also been proposed and their computational performance measured on Intel platforms. Alkim et al. [63] even evaluated their NewHope algorithm also in the ARM platform. However, the results have focused on computational complexity (where units have been cycle counts). On the Intel platform, the relative performance difference between NewHope and Frodo seems to be even larger than in our simulated Raspberry ARM platform [6]. The measured time in NewHope was 0.146 ms for Alice and 0.164 ms for Bob, while in Frodo the time was 1.26 ms for Alice and 1.34 ms for Bob.

Kuo et al. [64] presented an efficient hardware (FPGA) implementation of NewHope. In their implementation, the costs (or execution time) was 0.1709 ms for Alice and 0.1624 ms for Bob. Our results indicate that, on unoptimised IoT platforms, the time overhead can be significantly (even ten times) larger and that the division of costs between Alice and Bob can be more asymmetric.

8. Conclusions

Approaches for physical layer security provide an interesting research field producing solutions that complement security applications and protocols that have so far been based purely on cryptography. For instance, in the post-quantum era, physical layer security may have a role in replacing the public-key algorithms that have been shown as vulnerable against quantum computer assisted cryptoanalysis. In particular, the exchange of cryptographic keys for wireless communication might be based on eavesdropping-resistant secrecy coding.

We compared physical and cryptographic key exchange approaches by focusing on IoT scenarios and energy efficiency. Our simulation results indicate that our physical layer secrecy coding approach is very competitive in IoT scenarios with short range wireless communication. We also observed that the energy costs both in physical layer and crypto solutions are divided asymmetrically between Alice and Bob, transmitter and receiver. This has implications on the design of security solutions for power-restricted devices. IoT security architectures should support role assignments, where the heavier role is given for access points. This is, unfortunately, not always feasible. However, for scenarios where IoT devices have sufficient antenna and/or random number generation capabilities, role assignments can be used as an advantage.

The model-based simulation approach proved to be a flexible way to evaluate the energy efficiency of security solutions. It is useful both when designing new algorithms—as it enables evaluations on platforms for which there are no working ported implementations—and when designing platforms as the effects of design decisions can be studied cost-effectively.

In this study, we focused on a few prominent approaches. For instance, for the crypto part, we focused on the lattice-based approaches NewHope and Frodo, as they have recently gained a lot of attention. However, there exist other post-quantum security implementations targeted for IoT devices, including lattice-based crypto [12,13,14,15] and multivariate crypto [17,18]. Furthermore, the efficiency of the NIST candidate proposals for post-quantum cryptography needs to be addressed. Studying the energy efficiency of these other approaches is left for future work. Future work also includes studying the synergies between physical and cryptographic security approaches. More work is also needed to understand what other ways there are for these research fields to better complement each other. For instance, it is important to understand how to incorporate cryptographic authentication efficiently to physical layer security, or how physical layer security can provide an additional confidentiality layer or support authentication with location specific information.