Abstract
The outputs of a Turing machine are not revealed for inputs on which the machine fails to halt. Why is an observer not allowed to see the generated output symbols as the machine operates? Building on the pioneering work of Mark Burgin, we introduce an extension of the Turing machine model with a visible output tape. As a subtle refinement to Burgin’s theory, we stipulate that the outputted symbols cannot be overwritten: at step i, the content of the output tape is a prefix of the content at step j, where . Our Refined Burgin Machines (RBMs) compute more functions than Turing machines, but fewer than Burgin’s simple inductive Turing machines. We argue that RBMs more closely align with both human and electronic computers than Turing machines do. Consequently, RBMs challenge the dominance of Turing machines in computer science and beyond.
1. Introduction
This paper examines the computational power of a variant of Turing machines called Refined Burgin Machines (RBMs), named in honor of the recently deceased polymath and computability theorist Mark Burgin. Using our RBM model of computation, we dispel the following dominant tenet in computer science:
One reason for the acceptance of the Turing machine as a general model of a computation is that the model […] is equivalent to many modified versions that would seem off-hand to have increased computing power.1
It is well known that enhancements such as adding a second work tape to a standard Turing machine (TM) or increasing its tape alphabet with an additional symbol do not affect its computational power. However, making the machine’s generated output immediately visible, as demonstrated with the RBM model, does have a significant impact. In this paper, we prove that RBMs compute strictly more number-theoretic functions than TMs.
Remark 1.
The literature distinguishes between Type-1 and Type-2 computability theory, with TMs classified as Type-1 machines. We stress that TMs and RBMs are neither equivalent to Turing’s 1936 automatic machines [2], nor to the Type-2 machines discussed in Computable Analysis [3].
Another point of contention with mainstream computer science is the neo-Russellian belief in a singular “best fit” model of computation. This perspective posits that if the Turing machine is not the ideal model after all, then a specific alternative, such as the RBM model, must be. On the one hand, we will indeed argue that TMs are inferior to RBMs. On the other hand, a comparison between Burgin’s simple inductive Turing machines and their refined counterparts, the RBMs, reveals a more nuanced analysis.
Although we will contend that RBMs are better suited for batch processing than Burgin’s simple inductive TMs, we will also support Burgin’s assertion that his simple inductive TMs are more authentic in the realm of distributed computing. Additionally, we will briefly explore a third area, program performance checking, where we will place RBMs and simple inductive TMs on an equal footing. A more comprehensive analysis of this pluralistic landscape lies outside the scope of this article.
In general, we maintain that different models offer varying degrees of utility, depending on the context. There is no absolute “right” or “wrong” model; rather, each model has its own advantages depending on the situation. This perspective is influenced by Peter Naur, who applied it in scientific fields adjacent to computability theory [4].
Our findings lead us to conclude that the Church–Turing thesis is not as central to computing practices and potential theory building as textbooks claim. Several scholars have made similar points in the past, including Brian Cantwell Smith [5], Peter Wegner and Dina Q. Goldin [6], Selmer Bringsjord and Konstantine Arkoudas [7], Bruce J. MacLennan [8], Gordana Dodig-Crnkovic [9], Edward A. Lee [10], and B. Jack Copeland and Oron Shagrir [11].
The Church–Turing thesis, named after the American logician Alonzo Church and the English mathematician Alan Turing, arises from a deliberate conflation of Church’s thesis (A) and Turing’s thesis (B). Church’s former PhD student, Stephen Kleene, explained this in his 1967 work, Mathematical Logic, as follows:
(A) Church proposed the thesis (published in 1936) that all functions which intuitively we can regard as computable, or in his words “effectively calculable”, are -definable, or equivalently general recursive.2
(B) A little later but independently, Turing’s paper 1936-37 appeared in which another exactly defined class of intuitively computable functions, which we shall call the “Turing computable functions”, was introduced, and the same claim was made for this class; this claim we call Turing’s thesis.3
Turing’s and Church’s theses are equivalent. We shall usually refer to them both as Church’s thesis, or in connection with that one of its three versions […] deals with “Turing machines” as the Church-Turing thesis.4
Burgin adheres to Kleene’s conflation, but argues, based on his inductive TMs (both simple and unrestricted), that there are Turing-incomputable functions that humans can compute with the aid of modern devices [13,14]. We agree, and further assert, influenced by Peter Kugel’s work [15,16], that at least those functions computed by simple inductive TMs can also be computed by a human using only pencil and paper. In this article, we focus on Burgin’s arguments related to simple inductive TMs and electronic computers, only occasionally revisiting our Kugelian extension regarding human computation.
The outline of this paper can be conveyed in four stages. First, we clarify the distinction between TMs and RBMs (Section 2). Second, we formalize the RBM model and use it to disprove the Church–Turing thesis (Section 3), deferring technicalities to Appendix A. Third, we discuss our mathematical findings, and simultaneously refine Burgin’s compelling arguments against the thesis (Section 4). Fourth, we present our closing remarks (Section 5).
2. Turing Machines (TMs) versus Refined Burgin Machines (RBMs)
Today, it is well understood, as Bringsjord and Arkoudas already conveyed in 2004, that just as there are infinitely many mathematical devices equivalent to Turing machines (e.g., first-order theorem provers, register machines, the lambda calculus, abaci), there are also infinitely many devices that can solve the Halting Problem. Paraphrasing, Bringsjord and Arkoudas continue as follows [7] (p. 175):
Mark Burgin correctly notes that the first detailed account of such machines—referred to as “trial-and-error machines” by Peter Kugel—was provided simultaneously by Hilary Putnam and E. Mark Gold in the 1960s. We also agree with Burgin’s assertion that his more powerful inductive Turing machines, introduced in 1983, have the distinct advantage of delivering results in finite time.
The references to the primary sources, including a 1983 source in Russian [17], can be found in Bringsjord and Arkoudas [7] and are discussed in greater detail in Burgin’s Super-Recursive Algorithms [14]. On our reading, some parts of what Burgin accomplished in connection with digital technologies, Kugel performed in relation to human cognition [15].
Both ordinary and inductive Turing machines perform similar computational steps. While an ordinary Turing machine produces a result only when it halts, an inductive Turing machine, N, produces its result without halting. Even though machine N operates forever, it is possible that, from some point onward, the word on its output tape remains unchanged. That word is considered to be the result [13] (p. 86). Hence, Burgin’s usage of the term “inductive,” as we paraphrase from his writings:
In induction, we also proceed step by step, checking if a statement P is true for an unlimited sequence of cases. When it is found that P is true for each case whatever number of cases is considered, we conclude that P is true for all cases.[14] (p. 126)
By definition, inductive Turing machines give results if and only if their computational process stabilizes.[18] (p. 73)
In this paper, we focus on just a portion of Burgin’s theory [14]. Specifically, we discuss only his simple inductive Turing machines. These machines share the same structure as a conventional Turing machine with three tapes: input, work, and output. Notably, even these simple machines are strictly more powerful than Turing machines, classifying them under the umbrella of “hypercomputation.” We use an example from Burgin with some cosmetic adjustments, to convey the power of his simple machines [14] (p. 127).
Example 1.
There is a simple inductive Turing machine N that solves the Halting Problem for Turing machines. Machine N contains a universal Turing machine U as a subroutine. Given a word w and a description of a Turing machine M, machine N uses machine U to simulate M on input w. Prior to the simulation, N prints string on its output tape. When and if machine U stops because M on w has halted, machine N overwrites its output with output (where ). The crux is that machine N stabilizes to output , or to output , when Turing machine M on input w halts, or fails to halt, respectively. Hence, N computes a Turing-incomputable function.
Example 1 justifies why Burgin’s simple inductive Turing machines are called “eventually correct systems”, which the Wikipedia page on “hypercomputation” describes thus:
Some physically realizable systems will always eventually converge to the correct answer, but have the defect that they will often output an incorrect answer and stick with the incorrect answer for an uncomputably large period of time before eventually going back and correcting the mistake.5
In contrast, the Refined Burgin Machines (RBMs) discussed in this paper never go back and correct their generated output symbols. Informally, RBMs can be seen as simple inductive TMs with the caveat that their output cannot be overwritten, only extended: at step i, the content of the output tape is a prefix of the content at step j, where .
Remark 2.
Reconsider simple inductive machine N from Example 1. If string is a prefix of string , then there exists an RBM that computes the same function as machine N. Otherwise, N computes a function that no RBM can compute.
To explicate our RBMs, we appropriate some nuances originating from Stewart Shapiro’s “acceptable notation” [19]. Shapiro’s stroke notation involves using a string of n strokes on, say, the tape of a Turing machine, to denote the natural number n. Similarly, Kleene’s tally-based notation amounts to using a string of tallies to denote n. Championing Kleene’s 1967 conflation of Turing’s and Church’s theses implies, pace Shapiro, acceptance of the following equivalence between semantics and syntax:
A number-theoretic function is recursive (semantics) if and only if it is Turing machine computable relative to tally-based notation (syntax).
The reader is welcome to use standard binary notation if preferred. We will also use bits in this paper. The crux is that we will never fully abstract away from the specific notation used by the machine in question, for that is precisely what we need to explicate our RBMs.
An implication of our focus on notation can already be conveyed. In terms of tallies, if, e.g., three tallies are printed on the output tape of an RBM, additional tallies may be printed later, but erasing any of the printed tallies is prohibited. Similarly, in terms of binary notation, if three bits are printed on the output tape, additional bits may be printed later, but erasing any of the printed bits is prohibited. While these constraints reduce the computational power of our RBMs compared to Burgin’s simple inductive TMs (see Remark 2), they will enable us to strengthen Burgin’s case against the Church–Turing thesis.
Remark 3.
Reconsider inductive machine N from Example 1. If string is one tally long and string is two tallies long, then there exists an RBM that computes the same function as machine N. However, if string is two tallies long and string is one tally long, then N computes a function that no RBM can compute.
Remark 3 seems to rely on a common convention in computability theory, namely that a bijection exists between natural numbers and tallies. To develop a more general theory of RBM-computability that better aligns with engineering practice, we will relax this convention. Instead, we will only assume that the encoding function mapping natural numbers to notation (i.e., tallies, bits, …) is injective, not bijective per se. Even in this more relaxed setting, our computability claims pertaining to RBMs hold.
2.1. Some Machine Flavors
In his article “On Computable Numbers …” [2], Alan Turing introduced his automatic “a-machines”, which contain neither an input nor a finite output as is the case with the modern “Turing machines”. From 1936 until 1958, Alonzo Church, Stephen Kleene, Martin Davis, and others recast the concept of Turing’s a-machines [20].
Turing distinguished between three sorts of a-machines in his 1936 paper: circle-free a-machines (which do not halt) and circular a-machines that either halt or do not halt. Circle-free a-machines were useful for Turing’s logico-mathematical objective (cf. the Entscheidungsproblem and showing that it is “unsolvable”), in that they continue to produce output bits ad infinitum, with each infinite sequence of bits representing a “computable” real number. By contrast, circular a-machines only produce a finite sequence of output bits (with or without halting), and were not as relevant in 1936 as they are today. Circular a-machines that halt come close to the “Turing machines” introduced by Kleene and Davis in the 1950s and in computer science textbooks [21]. Circular a-machines that do not halt have been studied less often in the past 80 years; exceptions are Timothy G. McCarthy and Stewart Shapiro [22], Jan Van Leeuwen and Jirí Wiedermann [23], and the present author.
Examining circular a-machines that do not halt amounts to studying nonterminating computations that provide a finite output in the limit. In this setting, the focus of McCarthy and Shapiro was on deterministic computations and the number-theoretic functions that they represent (or implement). These authors used the phrases “extended Turing machine” (for their generalized Turing machine) and “Turing projectable function” (for the number-theoretic function in hand). These authors did not question the status of the Church–Turing thesis, but perhaps the same cannot be said of Van Leeuwen and Wiedermann [23], who also extensively analyzed the distinction between determinism and nondeterminism (both with and without resource bounds) [24]. On the one hand, we follow McCarthy and Shapiro in focusing solely on determinism. On the other hand, we share, due to the results provided in this paper, Van Leeuwen and Wiedermann’s skepticism and that of others (see Section 1) towards Turing-machine dominance in present-day computer science.
McCarthy, Shapiro, Van Leeuwen, and Wiedermann differ from Turing, Shapiro in 1982, and the present author, in that these four researchers eschew an explicit distinction between numbers and number-theoretic functions on the one hand (semantics), and the representations thereof on the other hand (syntax). Guido Gherardi has provided an in-depth account of Turing’s approach on this matter, i.e., with regard to circle-free a-machines [25]. A similar discussion pertaining to circular a-machines is presented here, albeit by means of a new model of computation: the Refined Burgin Machine model.
2.2. From Burgin’s Outlook to RBMs
Mark Burgin was a versatile mathematician. While Felix M. Lev commends Burgin’s insistence on finiteness concerning verificationism and the foundations of mathematics [26] (p. 10), various guises of infinity play a role in Burgin’s Super-Recursive Algorithms [14]. For instance, Burgin’s inductive viewpoint on computability aligns with Ilya Prigogine’s “becoming systems” and what Burgin calls “emerging infinity”, as we paraphrase thus:
Inductive Turing machines represent a shift from terminating computation to intrinsically emerging computation, transitioning from the “being” mode of recursive algorithms to the “becoming” mode of superrecursive algorithms. […] Synergetics has renewed scientific interest in becoming systems (see, for example, Prigogine [27]). Super-recursive algorithms provide a mathematical model for the concept of emerging infinity. [14] (pp. 160–161)Additionally, Burgin presents three classes of computability, listed as follows:
Ordinary, inductive, and accelerating Turing machines fit into the first, second, and third class, respectively. We do not delve into Class 3 in this paper.
Burgin’s simple inductive Turing machines, which belong to Class 2, are situated near the boundary with Class 1. Specifically, if we leave out the axiom stipulating that “we know when” the final result of a computation is obtained after a finite number of steps, then we leave Class 1 of ordinary Turing machines and enter Class 2 of inductive machines [14] (p. 120). Informally, we submit that RBMs lie on the border between Classes 1 and 2.
Burgin differentiates between a worm’s-eye and a bird’s-eye view on computation: the traditional algorithmic processing associated with TMs (Class 1) versus the elevated concept of information processing (Classes 1–3). This shift from pure syntax to information (broadly construed) is crisply formulated by Burgin’s collaborator Dodig-Crnkovic, thus:
Syntactic mechanical symbol manipulation is replaced by information (both syntactic and semantic) processing. Compared to new computing machines, Turing machines form the proper subset of the set of information processing devices, in much the same way as Newton’s theory of gravitation is a special issue of Einstein’s theory, or the Euclidean geometry is a limited case of non-Euclidean geometries.[9] (p. 308)
In a similar vein to Burgin and Dodig-Crnkovic’s efforts, we question the (alleged) clear-cut divide between syntax and semantics in mainstream computer science. Even if we fully adhere to modern set theory and actual infinity in particular, as computability and complexity theorists do, there is more than one viable way to connect raw symbolic machines (syntax) with number-theoretic functions (semantics). The two arrows in Figure 1 indicate these connections.
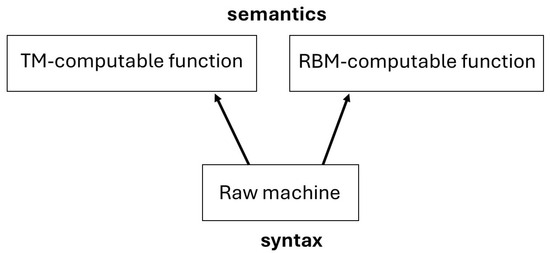
Figure 1.
Raw syntax versus functional semantics.
Raw symbolic machines are TMs and RBMs. They have an input tape, a work tape, and an output tape, as shown in Figure 2. The latter two tapes are initially blank. Specifically:
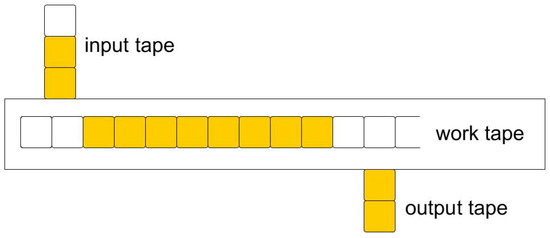
Figure 2.
A 3-tape Raw machine.
- –
- The input tape is read-only, and input bits are (a priori) written from bottom to top.
- –
- The output tape is write-only, and output bits are (during computation) printed from bottom to top, i.e., the tape gradually rolls out of the machine.
- –
- Neither bits on the input, nor output tape, can be retroactively modified.
- –
- The work tape, on which bits can be printed and modified, is a one-way infinite tape with a leftmost cell and infinite progression to the right.
Moreover, each tape has an independent head (or scanner).
A TM program, in the form of a list of tuples, is also an RBM program (and vice versa). That is, both TMs and RBMs share the same syntactic setup in terms of instantaneous descriptions and the move relation between two instantaneous descriptions. In other words, TMs and RBMs have the same operational semantics. Formal definitions appear in Section 3.
We call TM M and RBM N “twins” if and only if they are specified by means of the same list of tuples. Operationally, there is no difference between twin machines M and N, because the syntax of twins M and N is identical and the move relation of TMs and RBMs is the same. However, M and N could (mathematically) implement number-theoretic functions f and g, respectively, with f ≠ g.
Coming now to the question: Can a TM not reveal some of its output as it continues to compute? To “reveal something” refers to “attaining a meaning” in the outside world, which is occupied by a human observer; that is, to acquire semantic content. Abiding by the formal setup of Hopcroft and Ullman [1], a TM computation only provides a value to the outside world after termination, not before. The answer, therefore, is negative. If, in accordance with a number-theoretic function, the reader wants to program TMs to produce meaningful partial outputs during computation, she will arrive at RBMs or inductive TMs.
The critic will correctly remark that Hopcroft and Ullman do not refer to an observer in their formal definition of a Turing machine [1] (p. 148). However, the observer is implicitly present when the authors assign a meaning to Turing machines, e.g., number-theoretic functions [1] (p. 151). Indeed, it is in the transition from syntax to semantics that the notion of an observer is required.
Compared to the TM model, the RBM model explicitly incorporates the human observer. On the one hand, RBMs align well with Dodig-Crnkovic’s following reflections:
On the other hand, our RBM theory still pertains to computability rather than a comprehensive concurrency theory.Theories of concurrency are partially integrating the observer into the model by permitting limited shifting of the inside-outside boundary. By this integration, theories of concurrency might bring major enhancements to the computational expressive toolbox.[9] (p. 314)
3. Formalization
The sole difference between the TM model and the RBM model lies in their functional semantics, specifically as follows:
- In the traditional TM setup, the human observer is prohibited from looking at the output tape if the machine has not (yet) halted.
- In the RBM arrangement, the observer can look at the output tape as the output symbols appear on the tape.
A machine model of computation—such as the TM model and the RBM model—refers to Raw machines (Section 3.1) and to functional semantics (Section 3.2). To anticipate our formal exposition, we stipulate the following:
- A TM model of computation consists of a Raw machine (Definition 1) with the corresponding move relation (Appendix A), and the functional semantics in Definition 4.
- An RBM model of computation consists of a Raw machine (Definition 1) with the same move relation (Appendix A), and the functional semantics provided in Definition 7.
Our main theorem, a disproof of the thesis, concludes the formal exposition (Section 3.3).
3.1. Raw Machines
To simplify the formalities, a Raw machine shall from now on consist of two (not three) tapes, as shown in Figure 3. That is, the input tape and the work tape have been merged into an input/work tape. To recap, Raw machine R has two (one-way infinite) tapes:
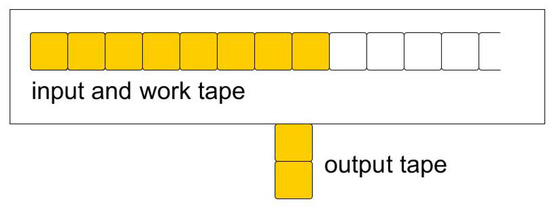
Figure 3.
A 2-tape Raw machine.
- An input/work tape, also called the first tape. Its head can move left (←) or right (→).
- An output tape, also called the second tape. Its head can only move upward (↑) or remain idle (I), i.e., not move.
When Raw machine R halts (on a given input ), it signifies this event by printing out the end marker $. When R has not (yet) halted, the output tape contains no end marker $, and the already printed output symbols , (for some ) constitute a prefix of R’s final output … which, in the limit, could be either a (finite) string or an (infinite) sequence of output symbols. Following Hopcroft and Ullman [1] (p. 148) to some extent, we now define a Raw machine.
Definition 1.
A Raw machine R is denoted
where
- Q is the finite set of states.
- Γ is the finite set of allowable work tape symbols.
- b, with , is the blank.
- Σ, with , is the set of input symbols.
- $, with , is the end marker.
- δ is the next move function, a partial mapping
- from to ;
- i.e., δ may be undefined for some arguments.
- is the start state.
Remark 4.
For binary notation, we take and . The corresponding move relation, , between two instantaneous descriptions of Raw machine R, is trivially defined in Appendix A. Without loss of generality, we assume that any Raw machine R halts iff the marker $ appears on R’s output tape.
3.2. Functional Semantics
The term “functional semantics” is often abbreviated to “semantics.” We write for , with standing for the set of natural numbers and ⊥ for the “undefined” value. When unspecified, quantification is taken to be over .
We are interested in encodings from to strings over the finite alphabet , i.e., . Any standard, injective encoding on is acceptable, and we shall assume in this paper that the empty string is the encoding of ⊥. Formally, we have the following.
Definition 2.
An encoding function is said to be admissible iff is injective on and and , for all .
Definition 3.
We say that both strings and are prefixes (⪯) of , but of these two strings, only is a proper prefix (≺) of , with the proviso that .
The notation denotes a fixed, effective, bijective mapping of into . With abuse of notation, we also write , where x and y are strings instead of natural numbers, with and , for some . That is, denotes . Likewise, we write to denote either the natural number n or the corresponding string (which encodes n), where R is a string describing a Raw machine and w serves as input string for that machine.
3.2.1. Semantics of TMs
Definition 4.
TM M (mathematically) implements function when the following two conditions hold, for :
- (1)
- iff M on halts with output .
- (2)
- otherwise.
We say that TM M computes function in the limit when M implements f.
Note that ⊥ is syntactically represented in more than one way, even though is a function, i.e., even though, for any string for which , it follows that . For example, a nonterminating computation of a TM also syntactically represents ⊥. For another example, a computation that terminates with an output , such that , also syntactically represents ⊥.
Definition 5.
A TM model of computation consists of a Raw machine with the corresponding move relation (Appendix A), and the functional semantics provided in Definition 4.
3.2.2. Semantics of RBMs
We shall use arrays containing infinitely many natural numbers, each of which is strictly larger than 0. For example, denotes the first number in some array a. Formally, an array a is a function , with . To denote an infinitely long sequence S of functions , we write: , with array a containing increasingly larger natural numbers; specifically: 0 < < < < ….
Definition 6.
A converging sequence of functions from to and with limit function , relative to , is a sequence with the following properties, for :
- (1)
- [ ⪯ ];
- (2)
- [ implies (2a) and (2b) ];
- (2a)
- [⪯ ];
- (2b)
- If ≺, for some , then there exists a larger , such that: ≺.
Definition 7.
We say that RBM N (mathematically) implements a converging sequence , with functions from to and limit function f from to , when the following three conditions hold, for all :
- (1)
- [ iff ];
- (2)
- iff ;
- (3)
- [ iff N on has or as output after moves ].
Condition (1) is called convergence, and (2) is nonconvergence.6 Concerning (1): at first sight it seems that is feasible, even when N’s output string is unstable, as we are seemingly only guaranteed that for all, but finitely many, t. However, combining this property with RBMs’ inability to erase output symbols, we may conclude: for all, but finitely many, time instances j, we have . Concerning (2): note again that could be undefined because RBM N on does halt, but with output such that .
Definition 8.
An RBM model of computation consists of a Raw machine with the corresponding move relation (Appendix A), and the functional semantics provided in Definition 7.
Definition 9.
We say that RBM N computes function in the limit when N implements a converging sequence of functions with limit function f.
For the sake of completeness, we also define a universal RBM as follows.
Definition 10.
A universal RBM U, when provided an input, interprets this input as the description of another RBM (with index i), concatenated with the description of an input to , say , with . RBM U simulates ’s computation on input , such that , with and implemented by U and , respectively.
3.3. Disproof of the Thesis
The RBM model is functionally more powerful than the standard TM model. On the one hand, everything TMs can accomplish in the realm of number-theoretic functions, RBMs can perform as well. An RBM-computable function amounts, after all, to the raw syntax of a TM along with someone observing the output symbols as they are produced by the machine. On the other hand, Theorem 1 informs us that there exists an RBM V capable of computing a function that no TM can compute. The proof relies on and , but in no essential way. Also taken for granted is an enumeration of TM descriptions … and an enumeration of input words …. For readability, the proof assumes that the strings 0 and 01 represent two different natural numbers via . The reader can further formalize this by substituting and for 0 and 01, respectively, with as an extra stipulation.
Theorem 1.
For any admissible encoding function , there is a function that (i) some RBM V computes in the limit, and (ii) no TM computes in the limit.
Proof.
Take an arbitrary admissible encoding function . Starting with part (i) of the theorem, we construct RBM V as follows. RBM V, on input w, first checks whether w is for some , with TM and input word . If this check does not pass, then RBM V prints infinitely many 0’s, i.e., RBM V demonstrates nonconverging behavior. Otherwise, RBM V on input prints 0 on its output tape. Then, RBM V simulates TM on . Two cases can be distinguished:
- Case 1: on halts and outputs . Then, V prints nothing or 1, such that its total output, 0 or 01, differs from . Machine V then prints $ and halts.
- Case 2: on does not halt, and thus outputs nothing. In this case, V merely simulates on forever. Note, however, that V’s output tape does contain a string, 0, which differs from the empty string representing ⊥.
Having constructed RBM V, we now use Definitions 7 and 9 to specify function , which V computes in the limit. RBM V implements a converging sequence with the following properties, for all :
- (1)
- [ iff ].
- (2)
- iff .
- (3)
- [ iff V on has or as output after moves ].
Clearly, for any well-formed input , RBM V prints a finite number n of symbols on its output tape, with , and with the guarantee that the output string represents some natural number. Therefore, condition (2) does not apply in the intended case, i.e., when x is such that for some . Expressing (1) in terms of (3) results in the following property: for all intended , and all , we have that iff V on has or as output after moves. In plainer English: maps any natural number x representing a TM and input onto a number y, where , and differs from the output produced by on .
Coming to part (ii) of the theorem, we show that function cannot be computed in the limit by any TM. Suppose that some TM computes in the limit. By Definition 4, we have, for :
- (a)
- [ iff TM on halts with output ];
- (b)
- otherwise.
We focus on (a), i.e., we need only consider natural numbers x for which = in order to obtain our contradiction. From (a) we obtain the following: iff TM on , with , halts with output , with . That output differs from the output produced by on . However, no TM can, in general, decide for input whether on halts or not. Yet, TM needs this decidability to output a string that on does not produce itself. □
4. Discussion
Theorem 1 informs us that TMs compute less number-theoretic functions than RBMs. A halting TM reveals its complete result, , to the outside world all in one sweep. In contrast, an RBM implementing the same function will, on input , provide the first symbols of for the outside world to see as soon as they have been computed. In all other respects, RBMs are no different from TMs.
The philosopher of computing Robin K. Hill asserts that a TM an sich is inert. “While we may preach that an algorithm is a Turing machine”, she states, “we do not practice it” [28] (p. 53). For, fundamentally, the TM presupposes a human as a part of a system. That human, Dodig-Crnkovic continues, “is the one who poses the questions, provides material resources and interprets the answers” [9] (p. 306).
In alignment with the propositions of Hill and Dodig-Crnkovic, we contend that RBMs exhibit greater fidelity to the concept of an algorithm compared to TMs. In practice, human observers scrutinize the intermediate, definitive output symbols generated by the machine and take action based on them while the machine is still in operation. Notice that the term “machine” can refer to a disciplined human–computer or a computing device.
However, for the sake of argument, let us suppose that an algorithm is a TM after all. Consequently, the human observer restricts an RBM to provide no more information than a TM can offer. Like an automaton, the observer follows these steps:
- Feed the finite input to the RBM machine.
- Press the “go” button.
- Close your eyes until the machine says “I have halted.”
- Then, and only then, open your eyes and read the finite output.
In Step 3, the observer consistently ignores the following feedback from the machine:
Granted, the output is potentially garbage, where “garbage” refers to either an output string that encodes no natural number, or an infinitely long output. However, for some RBMs, such as machine V in Theorem 1, the observer ignores far more useful feedback:“I already have part of the output for you to read.”
Recall that RBM V prints at most n output symbols, with n known to the observer, i.e., in the proof of Theorem 1 and V is designed never to print garbage.“I already have part of the finite output for you to read, and it ain’t garbage.”
Permanently ignoring a prefix of the finite output, which is guaranteed not to be garbage, is comparable with a cyclist preparing for a trip and disregarding early, yet informative, weather forecasts. Temporarily ignoring a prefix is akin to a theoretical computer scientist insisting that the calculation of a shortest path in a given graph must be completed before any prefix of the output can be properly utilized. In both cases, we argue that such a stance is futile (Section 4.1). We continue our engagement with Burgin’s critics in connection with the notion of actual infinity (Section 4.2). By expressing slight disagreement with Burgin’s own retrospective outlook on early computing practices, we strengthen his case against the Church–Turing thesis dialectically (Section 4.3). Finally, we present an industrial example of hypercomputability, based on Burgin’s work, to demonstrate the advantages of RBMs and simple inductive TMs over standard TMs (Section 4.4).
4.1. Ignoring a Prefix of the Finite Output
Imagine a cyclist at home receiving up to 12 weather forecasts for the next three hours before departing by bike. She hesitates to rely on the first forecast, waiting for the final one, i.e., the alleged “definitive” weather forecast. However, since there is no guarantee that the twelfth (or eleventh, tenth, etc.) forecast will come within the next three hours, as the software only informs the cyclist when its latest prediction significantly differs from the most recent one, this particular cyclist is left in a bind. Of course, most cyclists in reality do rely on early weather forecasts. As a result, they can, e.g., mentally prepare for their upcoming race, “even if potentially better output may be produced in the future.” Paraphrasing, Burgin continues thus: “A machine that occasionally changes its output does not deter human users. They can be satisfied with output that is good enough” [13] (p. 86). Standard TMs fail to capture this aspect of algorithmic engagement.
Remark 5.
The weather simulator relies on real and evolving weather conditions which, we opine, are not determined by any TM. However, even if they were, we would still be arguing that an RBM or a simple inductive TM models the present case study better than an inert TM. Granted, the function computed by our machine would then be TM computable. However, this is beside the point, since the mathematical findings in Section 3 remain intact: TMs overall compute fewer functions than RBMs. We are asking our antagonists not to conflate our mathematical findings with an ontological claim about actual weather developments.
Returning to the cyclist and weather forecasts: if she hopes to stay dry on a cloudy day, she should not rely heavily on late weather forecasts to begin with. (Notice the misnomer.) If the final forecast arrives just as she is about to leave, she can simply glance outside to see if it is raining. In many cases, this real-time observation is more accurate than the simulator’s “predictions.” In cloudy conditions, it is not uncommon for a weather simulator to indicate dryness when it is actually raining at that moment, and vice versa. In a very real sense, the weather simulator is not expected to provide a final, correct result to be of practical use.
There are other applications, such as counting election votes or computing the shortest path in a graph, where a final, accurate outcome is, of course, essential. Consider, then, a TM M that computes the shortest path in a finite graph. Contrast this with an RBM N that, with a visible output tape, computes the same path. Clearly, users will prefer N over M because the shortest path can be lengthy, and obtaining initial segments during the ongoing computation is highly beneficial. The ability of Burgin’s simple inductive TMs to overwrite the output is unnecessary here. Hence, we can now highlight the relevance of RBMs over both standard TMs and simple inductive TMs in this particular, yet common, context.
4.2. Infinity
Some critics object that simple inductive TMs, along with RBMs, often fail to notify the user when the definitive result has been obtained. Burgin suitably rebuts as follows:
Indeed, it is frequently overlooked by our critics that a superhuman is also required to confirm that an arbitrary TM computation is infinite, or that it is finite.Similar situations arise with ordinary TMs, where it is often uncertain whether the machine will ultimately produce a finite output or not.[14] (p. 158, paraphrased)
The necessity of observing the output tape “in the limit” arises from the infinite work tape. All machines under consideration—TMs, RBMs, and simple inductive TMs—possess such a tape. Only a superhuman can observe a computation of such a machine and declare that it provides a finite output in the limit, or not. We therefore submit that, ceteris paribus, RBMs and inductive TMs have no worse fidelity than standard TMs.
Furthermore, in practice, nobody waits an unbounded amount of time for a computation to perform something useful: actual realizations of all three types of machines rely on space-time constraints. In such a constrained world, human observers also look at the intermediate, definite output symbols and already perform something with them while the machine operates. We therefore re-assert that in some, if not many, contexts, RBMs have a better fidelity than both standard TMs and simple inductive TMs.
But, our critic might still remark, no finite experiment can demonstrate that a physical system (e.g., a human brain or an electronic computer) is equivalent to an RBM rather than a TM. In this regard, the critic is paraphrasing Marvin Minsky as follows: “there is no evidence for this, for how could you decide whether the physical system computes an uncomputable predicate?” [29] (p. 175). We respond using Kugel’s reply to Minsky, thus:
You can’t. But that does not mean that one might not choose uncomputable models anyway, much as one might choose the infinite (Turing Machine) models, to which most of Minsky’s (1967) book [30] is devoted, over the more finite (Finite Automaton) models, even though one cannot prove, on the basis of finite evidence, that any given physical system is not one of the latter.[29] (p. 175)
Indeed, a common critique of hypercomputation is that no physical machine can execute an algorithm computing a non-recursive function. Fine, but then it is also the case that no physical machine can execute an algorithm computing a recursive function. Even the identity function () cannot be executed by, say, the critic’s laptop. The crux is that neither recursive nor non-recursive functions f are faithfully captured by present-day technology. A more in-depth discussion can be found in Daylight [31].
4.3. Retrospection
First-generation computer users in the 1940s closely monitored various parameter values while the machine was running, even listening to the sounds of the computation to determine if the machine had entered a loop. We contemplate, without citing historical sources here, and merely in terms of a relative comparison, that RBMs capture early computing practices more accurately than inert TMs. From this vantage point, we disagree with Burgin’s assertion that “recursive algorithms provided a correct theoretical representation for early computers” [13] (p. 86, our emphasis).
Perhaps Burgin’s “early computers” refer only to the machines of the 1960s and later. Even then, however, his retrospection remains inaccurate. Burgin writes as follows:
Initially, it was necessary to print out data to obtain results. After printing, the computer either stopped functioning or began solving another problem. Today, people work with displays, and computers produce results on the screen. These results persist only if the computer continues running. This aligns perfectly with inductive TMs, which generate results without halting.[13] (p. 86, paraphrased)
We are in full agreement with this excerpt as such. But we take gentle issue with Burgin’s overall claim that printing machines, i.e., batch-processing machines of the 1960s, are faithfully captured with TMs. Computers in the 1960s, we stress, could not print the entire output instantly; they could only do so incrementally. Moreover, a single batch program could involve an interleaving of computing and printing routines. These observations remain valid for any batch processing to date. When a prefix of the final output is printed, it is known at an earlier stage of computation, and immediately achieves significance in the outside world. RBMs capture this form of computing more faithfully than both TMs and inductive TMs. Burgin is correct, however, regarding people working with displays; in this network-laden realm of distributed computing, his simple inductive TMs, as well as his more powerful inductive TMs, are more authentic than both TMs and RBMs.
We are perfectly at ease with such a nuanced synthesis, as we do not wish to assume the existence of a singular “best fit” model of computation. In our view, different models offer varying degrees of utility depending on the context. To address this topic further without delving too deeply, we shall now discuss a third area—program performance checking—which differs from both batch processing and distributed computing.
4.4. Program Performance Checker
We believe that informed theorists will favor RBMs or simple inductive TMs over the standard TM model when tasked with mathematically formulating what a program performance checker entails. While Burgin uses a simple inductive TM to formally capture this technology, we choose to use an RBM instead. Our summary, adapted from Burgin [14] (p. 128), demonstrates how performance checkers are designed in practice.
Checker verifies whether software S utilizes program P, producing an output string of either 0 for ’no, it does not’ or 01 for ‘yes, it does.’ Whether the checker fails to halt in certain scenarios is irrelevant to software engineers, as they can abort their computer routines at will. For example, checker might operate as follows on inputs S and P:
- Initialization stage: prints 0 and then starts simulating software S.
- Stage 1: After a step in S’s execution, checks whether program P performs any instruction at this step. If it does, prints 1 and halts.
- Stage 2: If program P does not perform any instruction at this step, then returns to Stage 1 for S’s next execution step. If S halts, then halts as well.
The crux is that, just like an operating system, software S may intentionally not halt. Suppose furthermore that program P is never utilized by S. Then, will stabilize its output to the string 0 and never halt. Engineers can extract this non-trivial information from a finite run of their checker, with an abort initiated by them. This is possible due to their understanding of the internal structure of their own engineered artifacts, S and P. Whether this non-trivial information is aptly described as “ontologically TM-incomputable” depends on the reader’s philosophical perspective (cf. our discussion on weather forecasts).
5. Conclusions
This paper dispels the Church–Turing thesis—the purported robustness of the standard TM model—by employing the RBM model of computation. We demonstrate that the thesis does not hold within its originally intended context of batch processing, or more broadly, stand-alone computing performed by physical systems such as disciplined humans or electronic computers. This conclusion is supported by two key points.
First, RBMs can compute a wider range of functions than TMs, but fewer than simple inductive TMs, as shown in Theorem 1 and in the introduction of this paper (see Remark 2). Simple inductive TMs can project results onto their output tape and modify them a number of times. In contrast, RBMs can only modify their output by appending symbols, and TMs are inherently limited by not having a visible output tape.
Second, during the computation of a well-designed RBM, an observer can extract meaningful information from the output tape, even while anticipating that additional symbols may still appear. For instance, in calculating the shortest path in a graph, the RBM model better captures the concept of an algorithm than both the TM model and Burgin’s simple inductive TMs for this specific, though common, example. Whether the shortest path is computed by a disciplined human or an electronic computer is irrelevant to our discussion. However, we have focused on the latter to streamline our analysis of Burgin’s work and to refine his case against the Church–Turing thesis.
For a historical perspective on the advent of the thesis, see Daylight [21,32]. Primary sources include the textbooks by Kleene [12,33] and Davis [34]. For instance, Kleene submitted that the thesis “would be disproved, if someone should describe a particular function, authenticated unmistakably as ‘effective calculable’ by our intuitive concept, but demonstrably not general recursive” [12] (p. 241). We posit that in Theorem 1 is precisely such a function. Kleene furthermore argued that the societal “significance” of a Turing-incomputable function “comes from the Church–Turing thesis,” by which:
computability in Turing’s sense agrees with the intuitive notion of computability. Accepting the thesis, as most workers in foundations do, the director of a computing laboratory must fail if he undertakes to design a procedure to be followed, or to build a machine, to compute this function .7
Our critique of this passage, irrespective of whether the thesis actually holds, appears in a forthcoming article. The crux is that Kleene viewed the TM model as the singular “best fit” model of computation, implying that engineers should simply adopt it.
Kleene’s view aligns with the neo-Russellian belief that all forms of physical computation fundamentally correspond to some TM computation. We have directly contested this view with our RBMs, arguing that the TM model is inferior to the RBM model. However, our perspective becomes more nuanced when considering other models. For instance, Burgin’s simple inductive TMs are more useful in distributed computing than RBMs, but less suitable for batch processing. Furthermore, when developing a theory of program performance checkers, we propose placing RBMs and simple inductive TMs on equal footing. Incorporating these observations into the classification framework of Burgin and Dodig-Crnkovic [35] remains a future work.
Sociological factors might still be at play if readers remain convinced that the Church–Turing thesis prescribes what an algorithm entails in the real world, rather than merely describing what a select group of theorists wanted an algorithm to mean. This is evident from the emotional commentary we have received from esteemed colleagues, who, we believe, tend to conflate ontology and epistemology. More importantly, it is clear from the lack of recognition for Burgin’s writings within mainstream theoretical computer science in recent decades. Therefore, we hope this paper will inspire the next generation of scholars to delve into Burgin’s “unrestricted inductive Turing machines with structured memory,” which are computationally equivalent to TMs with oracles, and his Super-Recursive Algorithms in general [14]. Similarly, we aspire for historians of modern logic to integrate Burgin’s critique of the Church–Turing thesis into a broader historical context, alongside the perspectives of László Kalmár and István Németi and Hajnal Andréka. For a comprehensive starting point and references to primary sources, see Máté Szabó [36].
Funding
Part of this research received funding from Sonderforschungsbereiche SFB 1187 “Medien der Kooperation” (Siegen University).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The author, also known as Karel Van Oudheusden, is grateful for the insightful feedback from four reviewers and thanks the editors of this special edition, Gordana Dodig-Crnkovic and Marcin J. Schroeder. He dedicates this article to Simon Peyton Jones.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TM | Turing Machine |
| RBM | Refined Burgin Machine |
| PPC | Program Performance Checker |
Appendix A
Coming to a formal definition of a Raw machine, we refine statements made previously about printing output symbols in the following way:
- Raw machine R either prints the blank b, with , on the output tape and the tape’s head remains idle (I).
- Or, Raw machine R prints any nonblank symbol on the output tape and the tape’s head moves one cell upward (↑).
Technically, then, R produces a symbol on its output tape during every computational step. However, R progresses one cell upward on its output tape if and only if it has just printed a nonblank symbol (on the output tape). For completeness’ sake, we also explicitly remark that when R prints the end marker $, the head of the output tape moves one cell upward.
Remark A1.
Note that ϵ denotes the string of length zero. Any Raw machine R initially contains a blank output tape, i.e., a tape filled with infinitely many b symbols, thus containing not a single symbol from . The output tape is then said to “contain ϵ as output”.
We denote an instantaneous description (ID) of Raw machine R by with three provisos:
- The current state q of R has to be in Q.
- Concerning the first tape:
- (a)
- is the string in , i.e., the contents of the first tape up to the rightmost nonblank symbol or the symbol to the left of the head, whichever is rightmost.
- (b)
- The head of the first tape is assumed to be scanning the leftmost symbol of , or if , then the head is scanning a blank.
- Concerning the second tape:
- (a)
- is the string in , i.e., the contents of the second tape, starting at the bottom and progressing upward.
- (b)
- The head of the second tape is assumed to be scanning a blank b, with:
- Either b appearing as the last (top-most) symbol in ;
- Or, if the previous case does not apply, b appearing as the bottom-most blank on the tape and located above .
Remark A2.
We use an underscore to denote a “do not care” value. For instance, we write to denote an ID in which we intentionally do not specify the second tape. Likewise, we write to denote an ID in which we do not bother to describe the machine’s control (q), nor the contents () on the first tape, nor the position of the head () of the first tape.
Closely following Hopcroft and Ullman [1] (p. 149), we define a move of R (also called a computational step) as follows. Let , with , be an ID. We distinguish between orthogonal concerns 1 and 2.
- For the control and the first tape, taken together, we have to consider two cases:
- (a)
- Suppose , where if , then is taken to be the blank b. We distinguish between two subcases:
- There is no next ID, as the tape head is not allowed to fall off the left end of the tape.
- Then, we write:.
- (b)
- Suppose . Then, we write:
- For the second tape, we have three cases to consider:
- (a)
- Suppose .Then, we write:.
- (b)
- Suppose .Then, we write:.
- (c)
- Suppose with .Then, we write:.
Remark A3.
Coming back to 1(a)(i) in the above definition, one can, contra Hopcroft and Ullman and the present author, be even more formal: introduce an end marker and define head movement on the end marker, such that no output is produced, the symbol is not rewritten, and the head moves to the right.
Remark A4.
“” is shorthand for “there exists such that ”. Likewise, “” is shorthand for “there exists such that “”.
If two IDs are related by , we say that the second results from the first by one move. If one ID results from another by some finite number of moves, including zero moves, they are related by the symbol . We write , for some specific , to denote precisely m moves, with as shorthand for .
Inspired by Martin Davis [34] (Ch.1), we provide the following definition.
Definition A1.
An ID is called terminal with regard to Raw machine R if is of the following form: , for some . By a finite computation of Raw machine R is meant a finite sequence , , …, of IDs such that for . By a terminating or halting computation of Raw machine R is meant a finite computation , , …, of R in which the last ID is terminal (with regard to R). By a nonterminating or infinite computation of R is meant an infinite sequence , , … of IDs such that for all . In this case, we also say that R does not halt. By a computation of R is meant either a finite or an infinite computation of R.
Notes
| 1 | Quoted from Hopcroft and Ullman [1] (p. 159). |
| 2 | Quoted from Kleene [12] (p. 232). |
| 3 | Quoted from Kleene [12] (p. 232, original emphasis). |
| 4 | Quoted from Kleene [12] (p. 232, original italics, our boldface). |
| 5 | Accessed on 15 June 2024. |
| 6 | Stating Condition (2) in the definition is redundant, but informative nonetheless. |
| 7 | Quoted from Kleene [12] (p. 245). |
References
- Hopcroft, J.; Ullman, J. Introduction to Automata Theory, Languages, and Computation; Addison-Wesley: Boston, MA, USA, 1979. [Google Scholar]
- Turing, A. On Computable Numbers, with an Application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 1936, 42, 230–265. [Google Scholar]
- Weihrauch, K. Computable Analysis—An Introduction; Texts in Theoretical Computer Science; An EATCS Series; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Daylight, E. Pluralism in Software Engineering: Turing Award Winner Peter Naur Explains; Lonely Scholar: Heverlee, Belgium, 2011. [Google Scholar]
- Smith, B. The foundations of computing. In Computationalism: New Directions; Scheutz, M., Ed.; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Wegner, P.; Goldin, D. Computation beyond Turing machines. Commun. ACM 2003, 46, 100–102. [Google Scholar] [CrossRef]
- Bringsjord, S.; Arkoudas, K. The modal argument for hypercomputing minds. Theor. Comput. Sci. 2004, 317, 167–189. [Google Scholar] [CrossRef][Green Version]
- MacLennan, B. Super-Turing or non-Turing? Extending the concept of computation. Int. J. Unconv. Comput. 2009, 5, 369–387. [Google Scholar]
- Dodig-Crnkovic, G. Significance of models of computation, from Turing model to natural computation. Minds Mach. 2011, 21, 301–322. [Google Scholar] [CrossRef]
- Lee, E. Plato and the Nerd: The Creative Partnership of Humans and Technology; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Copeland, B.J.; Shagrir, O. The Church-Turing thesis: Logical limit or breachable barrier? Commun. ACM 2019, 62, 66–74. [Google Scholar] [CrossRef]
- Kleene, S. Mathematical Logic; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1967. [Google Scholar]
- Burgin, M. How We Know What Technology Can Do. Commun. ACM 2001, 44, 83–88. [Google Scholar] [CrossRef]
- Burgin, M. Super-Recursive Algorithms; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kugel, P. Computing Machines Can’t Be Intelligent (...and Turing Said So). Minds Mach. 2002, 12, 563–579. [Google Scholar] [CrossRef]
- Kugel, P. It’s Time to Think Outside The Computational Box. Commun. ACM 2005, 48, 33–37. [Google Scholar] [CrossRef]
- Burgin, M. Inductive Turing Machines. Not. Acad. Sci. USSR 1983, 270, 1289–1293, Translated from Russian, v.27, no.3. [Google Scholar]
- Burgin, M. Properties of Stabilizing Computations. Theory Appl. Math. Comput. Sci. 2015, 5, 71–93. [Google Scholar]
- Shapiro, S. Acceptable notation. Notre Dame J. Form. Log. 1982, 23, 14–20. [Google Scholar] [CrossRef]
- Daylight, E. A Turing Tale. Commun. ACM 2014, 57, 36–38. [Google Scholar] [CrossRef]
- Daylight, E. Towards a Historical Notion of ‘Turing—The Father of Computer Science’. Hist. Philos. Log. 2015, 36, 205–228. [Google Scholar] [CrossRef]
- McCarthy, T.; Shapiro, S. Turing Projectability. Notre Dame J. Form. Log. 1987, 28, 520–535. [Google Scholar] [CrossRef]
- van Leeuwen, J.; Wiedermann, J. The computational power of Turing’s non-terminating circular a-machines. In Alan Turing: His Work and Impact; Cooper, S., van Leeuwen, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 80–85. [Google Scholar]
- van Leeuwen, J.; Wiedermann, J. Computation as an unbounded process. Theor. Comput. Sci. 2012, 429, 202–212. [Google Scholar] [CrossRef][Green Version]
- Gherardi, G. Alan Turing and the Foundations of Computable Analysis. Bull. Symb. Log. 2011, 17, 394–430. [Google Scholar] [CrossRef]
- Lev, F. Mark Burgin’s Contribution to the Foundation of Mathematics. Philosophies 2024, 9, 8. [Google Scholar] [CrossRef]
- Prigogine, I. From Being to Becoming: Time and Complexity in the Physical Systems; Freeman and Co.: Denver, CO, USA, 1980. [Google Scholar]
- Hill, R. What an Algorithm Is. Philos. Technol. 2016, 29, 35–59. [Google Scholar] [CrossRef]
- Kugel, P. Thinking may be more than computing. Cognition 1986, 22, 137–198. [Google Scholar] [CrossRef]
- Minsky, M. Computation: Finite and Infinite Machines; Prentice-Hall, Inc.: Saddle River, NJ, USA, 1967. [Google Scholar]
- Daylight, E. The Halting Problem and Security’s Language-Theoretic Approach: Praise and Criticism from a Technical Historian. Computability 2021, 10, 141–158. [Google Scholar] [CrossRef]
- Daylight, E. True Turing: A Bird’s-Eye View. Minds Mach. 2024, 34, 29–49. [Google Scholar] [CrossRef]
- Kleene, S. Introduction to Metamathematics; Van Nostrand: Princeton, NJ, USA, 1952. [Google Scholar]
- Davis, M. Computability and Unsolvability; McGraw-Hill: New York, NY, USA, 1958. [Google Scholar]
- Burgin, M.; Dodig-Crnkovic, G. From the Closed Classical Algorithm Universe to an Open World of Algorithmic Constellations. In Computing Nature; Dodig-Crnkovic, G., Giovagnoli, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 241–253. [Google Scholar]
- Szabó, M. Kalmár’s Argument Against the Plausibility of Church’s Thesis. Hist. Philos. Log. 2018, 39, 140–157. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).