Abstract
Methods are currently lacking to prove artificial general intelligence (AGI) safety. An AGI ‘hard takeoff’ is possible, in which first generation AGI1 rapidly triggers a succession of more powerful AGIn that differ dramatically in their computational capabilities (AGIn << AGIn+1). No proof exists that AGI will benefit humans or of a sound value-alignment method. Numerous paths toward human extinction or subjugation have been identified. We suggest that probabilistic proof methods are the fundamental paradigm for proving safety and value-alignment between disparately powerful autonomous agents. Interactive proof systems (IPS) describe mathematical communication protocols wherein a Verifier queries a computationally more powerful Prover and reduces the probability of the Prover deceiving the Verifier to any specified low probability (e.g., 2−100). IPS procedures can test AGI behavior control systems that incorporate hard-coded ethics or value-learning methods. Mapping the axioms and transformation rules of a behavior control system to a finite set of prime numbers allows validation of ‘safe’ behavior via IPS number-theoretic methods. Many other representations are needed for proving various AGI properties. Multi-prover IPS, program-checking IPS, and probabilistically checkable proofs further extend the paradigm. In toto, IPS provides a way to reduce AGIn ↔ AGIn+1 interaction hazards to an acceptably low level.
1. Introduction
A singular and potentially deadly interaction will occur in the transition of technological dominance from H. sapiens to artificial general intelligence (AGI), thus presenting an existential threat to humanity [1,2,3,4,5,6,7,8,9]. On the timing of this epochal event, various metrics indicate progress is increasing exponentially [10].
We first present some background of the need for, and problem of, proving safe AGI, then describe interactive proof systems, why they provide a solution and their benefits and limitations, and then give proof method examples.
1.1. ‘Hard Take-Off’ and Automated AGI Government
Through recursive self-improvement, the evolution of AGI generations could occur in brief intervals, perhaps days or hours—a ‘hard take-off’ too fast for human intervention [3,11,12]. This threat necessitates preparing automatic structured transactions—‘smart contracts’—and a variety of other measures stored via distributed ledger technology (blockchains) to eliminate untrustworthy intermediaries and reduce hackability to acceptably low odds [10]. The set of these smart contracts constitutes the foundation documents of an AGI-based decentralized autonomous organization (DAO)—the AGI government. Humans with AI assistance will design the first DAO government, and each AGI generation will design the successive DAO government, negotiated with the successor generation.
1.2. Intrinsic and Extrinsic AGI Control Systems
The DAO is the extrinsic AGI control system, constructed from game theory, mechanism design, and economics, while the AGI behavior control architecture and instantiated ethics are the intrinsic control structure. Initially, the ecosystem will be humans and increasingly autonomous, intelligent agents, as described for general-purpose DAO software:
Our goal is to design self-organizing systems, comprising networks of interacting human and autonomous agents, that sustainably optimize for one or more objective functions.… Our challenge is to choose the right incentives, rules, and interfaces such that agents in our system, whom we do not control, self-organize in a way that fulfills the purpose of our protocol.Ramirez, The Graph [13]
1.3. Preserving Safety and Control Transitively across AGI Generations
In the succession of AGI generations, each more powerful than the prior generation, the prior generation will be at an existential disadvantage to the succeeding one unless its safety is secured via the DAO and AGI architecture. Preventing the first AGI generation from wiping out humanity is insufficient; AGIn+1 may turn off AGIn and its predecessors to prevent ‘wasteful’ use of finite resources by ‘inferior’ classes.
Thus, we need a mechanism whereby the dominance baton passed from AGIn to AGIn+1 will preserve the value-alignment with humanity that we construct with AGI1. With a general method, humanity would construct provably safe AGI1, which would be endowed with the motivation to produce the specific methods to construct and prove safe AGI2, etc. In this manner, the methods presented here, with induction, lead to a weak proof of trans-generational AGI safety – weak since the field lacks a precise definition of ‘safety’ (cf. Armstrong [14]).
1.4. Lack of Proof of Safe AGI or Methods to Prove Safe AGI
To our knowledge, no one has found a way to construct AGI systems that are provably safe or methods of proof that could be applied to such systems [3,5,8]. For instance, Omohundro and Russell propose the use of formal methods, but neither shows how to implement them nor do they mention probabilistic or interactive proof methods [15,16]. Yampolskiy mentions probabilistic proofs and the limitation of their accuracy but omits their arbitrarily low potential accuracy and does not mention interactive proof methods [17]. Importantly, Williams and Yampolskiy identify three frameworks for analyzing AI-related risk, but these frameworks do not lead to a method of proving AI safety [18].
1.5. Defining “Safe AGI”; Value-Alignment; Ethics and Morality
Tegmark breaks goal-based AGI safety approaches into three formidable subgoals, learning human goals, adopting the goals, and retaining the goals, and critiques various efforts to solve each subgoal (“Friendly AI: Aligning Goals” [19]).
Another widely used definition of AGI safety is value-alignment between humans and AGI, and herein, between AGIn and AGIn+1. Value-sets, from which goals are generated, can be hard-coded, re-coded in AGI versions, or be more dynamic by programming the AGI to learn the desired values via techniques such as inverse reinforcement learning [3,16,20]. In such a scenario, which saints will select the saintly humans to emulate? Or select the rewards to reinforce [21,22]? Which human values would the AGI learn?
Perhaps the AGI would learn, and improve to superhuman capability, these meta-values:
- Most humans seek to impose their values on others.
- Most humans shift their values depending on circumstances (‘situation ethics’).
The terms ‘moral’ and ‘ethical’ AGI are also used, but precisely defining those terms, ‘value-alignment’, and ‘safe’ AGI, and how to implement them, are complex subjects with confusing discussions from even the clearest thinkers with best intentions [3,19,23,24] although there are a few exceptions [25].
Yampolskiy proposes a theorem: There are no universal ethical norms; therefore, there cannot be a single set of ethics preferred by all of humanity [22]. If true, despite the apparent complexity of the value-alignment issue, there are only two categories of ‘moral’ activity (Table 1) [10,26].

Table 1.
Fundamental dichotomy of autonomous agent interaction in terms of value-alignment.
Thus, incentivizing and enforcing voluntary, non-fraudulent transactions simplifies and solves all value-alignment scenarios in principle.
2. The Fundamental Problem of Asymmetric Technological Ability
A superior AGI generation will create algorithms more powerful than existing ones.
AGIn may have access to classes of algorithmic methods more powerful than those of the more primitive civilizations, such as quantum computation (QC) versus Church–Turing computation (CT). It is believed that QC is capable of fundamentally out-performing CT computation via QC’s ability to encode 2n states in n spins, i.e. to solve problems requiring exponential scaling in polynomial time [27,28].
Further, there exist classes of computation (e.g., #SAT, NODIGRAPH, #P) that are more intractable than those hypothesized to be solvable by QC [27]. Thus, there are predictable, known bases for future interactions between technologically superior and inferior AGI generations.
3. Interactive Proof Systems Solve the General Technological Asymmetry Problem
Aharanov and Vazirani analyze whether quantum mechanics (QM) is falsifiable; high-precision measurements have validated low-dimensional QM systems, but higher-dimensional systems have not been tested. Whether they can be is an open question due to the inability of classical computation to predict QM outcomes that scale exponentially with the complexity of the system [27]. They note that a classical Verifier cannot predict the outcome of a quantum Shor prime factoring algorithm on the integer N, since prime factoring is computationally intractable for the classical Verifier for large composites. Instead, the Verifier can only confirm that the factors given by the Shor algorithm multiply to N.
Aharanov and Vazirani show that interactive proof systems (IPS) can effectively level the playing field between the classical computing and QC realms. Using probabilistic proof methods in which the probability of falsehood can be reduced to an arbitrarily small tolerance factor ε, IPS define a computational complexity class transcending the limitations of polynomial-time complexity [29,30].
Yampolskiy gives a proof of unpredictability of AGI by assuming predictability, which equates human intelligence with supra-human-intelligent AGI since the human can duplicate AGI decisions, presenting a contradiction [31]. IPS assume human intelligence is less than AGI and do permit prediction of classes of behavior and specific behaviors within probabilistic limits.
4. Interactive Proof Systems Provide a Transitive Methodology to Prove AGIn Safety
Probabilistic IPS open the door to a general paradigm for a computationally weaker Verifier to validate expressions from a computationally superior and possibly untrustworthy Prover [32]. In this paradigm, specific IPS methods must be developed for each specific proof and a proof may require more than one method, which, in combination, reduce the probability of falsehood to acceptably low levels. The various specific IPS methods developed to date may be used to extend the paradigm to new realms or may provide examples to follow [27].
One exemplary IPS technique, in which a Prover claims to solve #SAT, can be seen as a sophisticated form of mechanism design. A Verifier randomly presents increasingly simpler #SAT problem instances to the Prover until one is tractable enough for the Verifier to verify (i.e., to compute and count the instances satisfying the given CNF formula). Thus, the Prover must pass successive consistency checks, and if the Prover lies on a hard-to-verify problem, it must keep lying and finally the Verifier detects the inconsistency in an easier problem (random, downward self-reducibility) [32].
In principle, proving AGI safety can be performed between humans and AGI1 using bounded polynomial-time probabilistic (BPP) IPS and between AGIn and AGIn+1 via more complex bounded probabilistic IPS. Necessary conditions for this effort are:
- Identifying a property of AGI, e.g., value-alignment, to which to apply IPS.
- Identifying or creating an IPS method to apply to the property.
- Developing a representation of the property to which a method is applicable.
- Using a pseudo-random number generator compatible with the method [33].
Steps 2 and 3 may occur in reverse order. Further, AGI behavior control systems must be restricted to provably reliable classes of systems (q.v., e.g., Arora and Barak Ch. 12 [32]). For the definition of BPP and the logical development of IPS, see the Appendix A.
5. The Extreme Generality of Interactive Proof Systems
IPS can be applied to any interaction between a Prover whose ability, typically stated as computational power, but in any sense, exceeds that of the Verifier [32,33]. The Prover is a purported oracle machine whose assertions, such as about its safety, are to be validated by the Verifier. Here we begin to explain how IPS works and its strengths and weaknesses relative to proving AGI safety.
A simple example of IPS generality is given by Arora and Barak [32]. The Prover ostensibly has normal color vision, but the Verifier is weaker, being color-blind to red vs. green. Consider the difference in ability as an AGI has developed a new technology to observe the universe and humans need to verify an AGI claim of its safe behavior based on such observations.
The Prover claims that two wallets are different colors. The Verifier presents the two wallets and asks the Prover to distinguish the colors; the Prover claims the left hand holds red and the right-hand holds green. The Verifier then repeatedly puts the wallets behind her back, switching them at random iterations, asking the Prover to identify the colors at each iteration. There is a 50–50 chance of the Prover guessing the correct colors each time if he, too, is color-blind. The probability of error in validating the proof decreases by ϵ = 2−1 with each iteration, and probability of validation accumulates to 1 − 2−k for k iterations; thus, the Verifier can accept the proof with an arbitrarily small chance of falsehood.
A more technical example, illustrating key points about applying IPS to proving AGI safety, stems from a famous probabilistic proof of primality [34]. A number b testing for primality of another number n is said to be a witness Wn(b) to the compositeness of n if it passes a certain algorithmic test:
Rabin proves that the probability that any n failing this test is a true prime, with k random choices of b, is 1-1/4k and cites computer searches that verify the theoretical result.
As an IPS, we consider the Verifier as choosing the random sequence of b and queries the Prover, who computes the test. Either the Verifier or the Prover (e.g., an AI) could suggest the test. As to applying such a test to proving safe AGI, we give examples below, such as arithmetization of behavior control system descriptions, that render proving safe AGI susceptible to probabilistic, number-theoretic functions. In a similar manner, we must create representations of AGI safety aspects to bring them within the domain of existing IPS methods or new methods that we invent to prove safety.
Step 2, the converse of Fermat’s Little Theorem, tests to see if n violates that primality test [33,35]. All primes fail the test and nearly all composite numbers pass it, but the Carmichael numbers, which are composite, also fail it and so appear to be prime [36]. The Carmichael composite false positives—aka ‘pseudoprimes’—are the source of the probabilistic nature of the proof.
The pseudoprimes that fool Fermat’s Little Theorem are called ‘Fermat pseudoprimes’ to distinguish them from composites fooling other primality tests such as Lucas, Euler–Lucas, Fibonacci, Pratt, Perrin, etc., each of which uses different witness methods [35,36]. Thus, there will be a menu of witnesses to prove AGI ‘safety’ in various safe behavior contexts, and they will work in concert to establish a desired safety level. For instance, Mathematica’s primality testing function PrimeQ combines three tests to assure primality and is valid with high probability in the context n ≤ 1016 [35].
Rabin adapted a deterministic test by Miller that was slower and rested on an additional assumption, the extended Riemann hypothesis; that assumption was eliminated by Rabin [34]. Similarly, we may look to deterministic proofs of behaviors represented by formulae for ideas on constructing more powerful probabilistic proofs.
Using the theorem that the number 1 has only two square roots modulo any prime (quadratic residues), but 4 square roots modulo any composite—including the Carmichael numbers—Sipser plugs the Carmichael number gap in the sieve and improves the Rabin proof, which is an example of strengthening a probabilistic proof with more sophisticated methods [33,37]. Concise discussions of identifying the defects of primarily tests and strengthening them are given in Ribenboim and Wagon with algorithms and code [35,36]. We expect a similar evolution of techniques will occur with IPS applied to proving AGI safety.
6. Correct Interpretation of the Probability of the Proof
We have shown that probabilistic proof methods exist to determine if a number has a property such as primality with an arbitrarily high probability .
However, a prime number is either prime or not; and likewise, a given AGI behavior is either ‘safe’ or not by a specific criterion, such as alignment with human values or adherence to specific ethics or morals. BPP methods can reduce the probability of error in these decision problems to an arbitrarily low level, let us say, 2−100. This does not mean the number or behavior being tested has 2−100 chance of being composite or of being unsafe; it means that if we were to perform 2100 primality or behavior tests, we expect that just one will be a false positive—composite or unsafe [34]. Thus, if the universe of numbers or potential behaviors under consideration is far smaller than 2100, we can rely on the test. Paraphrasing Rabin, we could market a product (think ‘safe AGI’) with failure rate 2−100 because, with rigorously-calculated odds, it would be possible to buy error and omission insurance for it [34,36].
7. Epistemology: Undecidability, Incompleteness, Inconsistency, Unprovable Theorems
In the past two centuries, fundamental discoveries of epistemological limits were made, such as the limitations of straight-edge and compass constructions; the validity of axiomatic non-Euclidean geometry; and the nature of more general incompleteness, inconsistency, uncomputability, and undecidability. We share the view of Wolfram that to date, by and large, for practicability, mathematicians have focused on systems where their methods are effective and produce meaningful results, ignoring the implications of these epistemological discoveries (see [38], “Undecidability and Intractability”, “Implications for Mathematics and Its Foundations” [39]; see pp. 14–15, especially Weyl quotation, in [40]). The exploration by AGI may be quite different.
Likewise, in searching for fast algorithms, humans may have found the ‘low-hanging fruit’ in the shortest, most regularity-exploiting algorithms (i.e., featuring repetitive, iterative, recursive, or nested steps, such as GCD, Newton’s method for finding roots, Gaussian elimination—and generally in most algorithms found to date) [38,41]. Humans may benefit by using AI and AGI1 to find suitable algorithms for proving AGI safety, and the IPS algorithms used by AGIn may be complex and difficult or impossible for humans to understand.
Any reasonably expressive, finite axiomatic system (1) is incomplete (cannot prove all true statements and can express unprovable conjectures) and (2) we cannot prove consistency (the inability of the system to derive both a given statement and its negation) for the same reason: We cannot predict, in general, how many steps it might take to produce a given theorem or statement and its negation [40,42,43]. ‘Reasonably expressive’ boils down to possessing computational universality and the threshold for universality is strikingly low: inclusion of a function with at least 2 parameters, as shown by the non-universal 1-parameter vs. universal 2-parameter truth tables.
From the different perspective of algorithmic information theory, universal finite systems can express a formula but not prove a theorem about their own consistency and completeness, and no system (e.g., Peano arithmetic) can prove consistency of a more expressive system, and no universal finite system can be complete (derive all possible theorems), because the systems have insufficient bits [39,44]. On the other hand, Gödel’s incompleteness theorem does not prove that there exist absolutely unprovable theorems (i.e., unprovable from any finite axiom set), but rather that such exist for any given finite axiom system, such as those containing first-order arithmetic [41,45].
Axioms need to be added to any finite set to increase the range of theorems it can prove, and Wolfram’s conjecture is that the relatively simple axiomatic systems of mathematics to date must be supplemented to increase the range of theorems they can prove. Nevertheless, even then, not all theorems will be provable, including simple conjectures like Goldbach’s, the number of twin primes (p, p + 2) (e.g., (3, 5), (5, 7), (11, 13), etc.) or theorems about modest-degree polynomials (e.g., see [38] p.790 et seq.), if only for the reason that we cannot predict how long any given proof will take to compute [36]. Similarly, on the question, we cannot predict how many steps it may take to derive an efficient algorithm to yield any output, including algorithms to efficiently solve NP-complete problems, if such algorithms even exist.
In stark contrast to the original Hilbert thesis that one axiomatic system could generate all mathematical theorems, using another of his innovations—purely formal systems—it is not difficult to see that innumerable axiomatic systems can be created, and it is not surprising that they range dramatically in expressiveness, consistency, and completeness (many examples are explored in [38]).
A specialized AI may be created with provable limitations such as safe behavior. But by definition, AGI is universal. A given systems level within AGI may be specialized, but one or more levels underlying behavior (e.g., symbol-level processing) and the behavioral level of AGI will be computationally universal.
The range of possible AGI behavior (input–output functions) from one state to the next will be the output state space size raised to the power of the input state space size [46],
and the resulting complexity of the succession of states,
where through iterated exponentiation each output state OI becomes the next input state, similar to tetration but state space sizes may change over time [47]. A fundamental limitation may remain, that communication between agents will be at a linear O(t) bandwidth but use of compression as exemplified by axiomatic systems and scientific theories may partially offset the limitation [48].
From the standpoint of limiting AGI behavior to safe behavior, the limitation of axiomatic systems’ expressiveness is a critically necessary feature, not a bug, as illustrated below.
In general terms, we believe AGI will solve problems in general and specialized realms by adjoining axioms in a collection of increasingly large and specialized axiomatic systems. This is a modern interpretation of Gödel’s incompleteness theorem and the failure of the Entscheidungsproblem.
8. Properties of Interactive Proof Systems
Given the asymmetric functional power between humans and AGI and between AGIn and AGIn+1, interactive proof systems (IPS) seem custom-designed for the problem of proving properties such as safety or value-alignment. The key IPS properties are:
- The methods used by the Prover are not specified and unbounded.
- The Prover is assumed to have greater computational power than the Verifier.
- The Verifier accepts a proof based on an arbitrarily small chance that the proof is incorrect or he has been fooled by the Prover.
Property #1 means that the computational power of the Prover can encompass any future computational power of AGI, including quantum computing, the ability to solve NP-complete or currently undecidable theorems (undecidable, meaning requiring computation of unpredictable length in general), or computing power beyond our current knowledge and imagination.
9. Multiple Prover Interactive Proof Systems (MIP)
Using more than one Prover and restricting communication between Provers to the period prior to initiation of the proof procedure increases the power of IPS significantly, to the complexity class of problems solvable by nondeterministic machines in exponential time (NEXP) [32,49]. For example, to prevent AGI from giving manipulative answers, Bostrom suggests preventing multiple AGIs from communicating with each other and comparing their answers to queries (chapter on Oracles [3]). Multi-prover systems (MIP) formalize and provide a rigorous theoretical basis and procedure for this idea. Further, using the same technique of flagging inconsistent answers solicited from non-communicating Provers, MIP can prevent Provers from adapting their responses to the query series of the Verifier (‘forcing nonadaptivity’) [32].
10. Random vs. Non-Random Sampling, Prover’s Exploitation of Bias
After the discovery and exploration of randomized algorithms, many were converted back to efficient deterministic algorithms. However, IPS used for proving AGI safety is a different paradigm in that randomness ensures the AGI Prover cannot exploit some bias in the series of queries presented by the Verifier. The concern then arises that there may be no perfectly random number sources in nature and pseudo random number generators (PRNGs) may offer Provers an exploitable weakness. To address this issue and preserve the validity of BPP, techniques have been developed to permit BPP algorithms to use weakly-random sources (‘unfair coins’) and to increase the integrity of PRNGs using random seeds to perfect uniform distributions [32].
The Verifier may want to probe particular areas of AGI behavior, i.e., not a random sample across all behavior. A random sample can be used in the region of interest, but a sounder approach may be to use MIP, in which Provers cannot compare notes to exploit any type of query-series bias.
11. Applying IPS to Proving Safe AGI: Examples
As we have seen in IPS history, the key to applying IPS to proving AGI properties such as safety is designing a representation of an AGI component such that IPS methods may be applied to it. For example, if we were to use a read-once branching program representation for behavior control, a single discrepancy between safe and unsafe branched programs may be overlooked with typical Boolean variable assignments, while assigning non-Boolean, polynomial values opens the door to using number-theoretic functions that will detect any discrepancy [33].
11.1. Detection of Behavior Control System (BCS) Forgery via Acyclic Graphs
As just alluded, a single heuristic, such as ‘terminate all humans’, or ethic, such as ‘terminate all agents using resources inefficiently as defined by the following metric’, added to a BCS could result in realization of the AGI existential threat, as could universal drives, such as simply wanting to improve its ability to achieve goals, causing AGI to alter its utility function [50]. Thus, any alteration, especially forgery, of ethics modules or BCS must be detected. One security measure is to store ethics modules, along with other critical AGI components, in a distributed ledger [10], perhaps distributed among all earlier autonomous agent generations since they all have a proprietary interest in the security and integrity of those components.
If we represent an AGI behavior control system (BCS) as a directed acyclic graph, such as an AI behavior tree with no loops, a unique labeling procedure exists for the nodes and edges as do BPP tests for equivalence of two such structures, although in general the problem is currently intractable (coNP-complete) [33]. Equivalence here means the two BCS programs produce the same functions. BPP tests can be used to detect forgery by comparing a reference copy of the BCS stored in a distributed ledger versus a copy presented by a potential adversary. Here is a procedure to compare two read-once branching programs B1 and B2 where F is a finite field with at least 3m elements [33]. The representation requires an assignment of polynomials to the graph nodes and edges.
- Verifier selects elements ai through am randomly from F.
- Prover evaluates the assigned polynomials p1 and p2 at a1 through am.
- If p1(a1, …, am) = p2(a1, …, am), Verifier accepts, otherwise, rejects.
11.2. Program-Checking via Graph Nonisomorphism
IPS can be used as a probabilistic check for buggy outputs of programs by running one program P, such as a copy of an AGIn behavior control subroutine, on a machine, the Checker C [32]. Assume the Prover runs a program P that states that two uniquely-labeled graphs are isomorphic P(G1,G2). The procedure is (1) the Verifier repeatedly permutes labels of one of {G1,G2}, chosen randomly, and (2) asks the Prover if they are still isomorphic, a problem suspected to be NP-complete. The Prover supplies the permutation as the witness, which can be checked in PTIME A guess has a 50–50 chance of being correct. Thus, with k iterations of the procedure, the probability of error is 2−k.
11.3. Axiomatic System Representations
In principle, an axiomatic system (a language, axioms, and transformation rules) can be described formally, that is, precisely, for any systems level. We emphasize ‘in principle’ since problems arise when attempting to precisely describe an axiom in practice or precisely interpret it in a formal representation [51].
Here, we extend earlier methods [52] using an arithmetization of the axioms and composition rules (e.g., transformation or inference rules). The desired representation needs to be expressive enough to apply one or more desired number-theoretic theorems to it (more expressive than Presburger or Robinson arithmetic) [41]. Thus, we need a finite group of primes, infinite composites of the finite set, and infinite numbers that are relatively prime to the finite set.
Given an axiomatic system of finite axioms and rules and infinite compositions:
- Axioms A = {a1, a2, a3, …, ai}.
- Transformation rules .
- Compositions of axioms and inference rules C = {c1, c2, c3, …, ck}, e.g.,
- .
- .
etc., in which the symbol represents a valid syntactical composition resulting in well-formed formulas (wff) in infix notation [53,54]. The first composition example 3a shows a binary transformation rule such as modus ponens from propositional logic while the second composition 3b shows a general n-ary (in this case ternary) rule such as a sequence node testing 3 child nodes in a behavior tree.
All formulae representing all behaviors B are only expressible by the system if they are derivable by a composition of the axiom sets A and the rule sets R:
If we allow loops to express repetitive behavior, a loop may be examined with finite methods either by looking at an entire behavior sequence up to a point in time or by inductive methods otherwise.
We assign a unique prime number p to each axiom a and transformation rule r, for intelligibility separating axioms and transformation rules (Table 2 and Figure 1 and Figure 2).

Table 2.
Arithmetization of an axiomatic behavior control system.
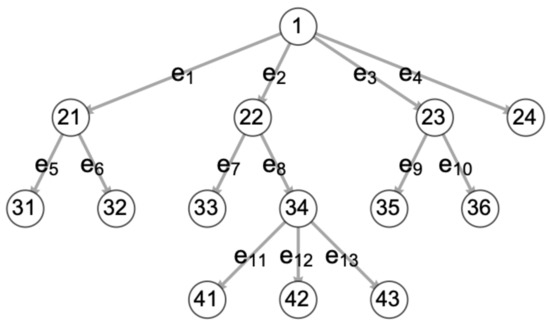
Figure 1.
Cartoon robot behavior tree (BT) with typical numbering of vertices and edges (after Iovino et al. [55], Figure 2), as a minute portion of a large and complex AGI behavior control system. Vertex codes for high-level BT algorithms: 1: Fallback. 21, 22, 23, 34: Sequence. 41, 42: Condition. Vertex codes for lower-level BT algorithms: 31: Human approaching? 32: Maintain prescribed safe distance. 33: Human asks for help with task. 41: Begin log. 42: Is task moral? 43: Is task ethical? 35: Low energy? 36: Seek power station. 24: Wander.
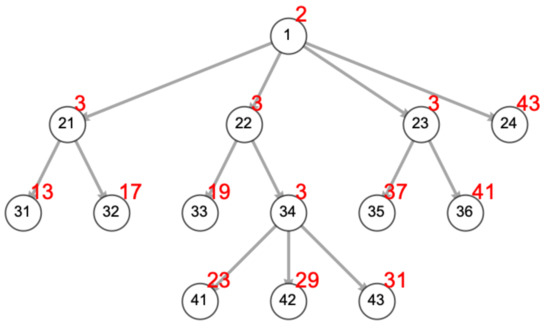
Figure 2.
The same BT with prime numbers (red) representing vertex algorithms and omitting edge labels. 2: Fallback. 3: Sequence. 5: Parallel. 7: Action. 11: Condition. 13: Human approaching? 17: Maintain prescribed safe distance. 19: Human asks for help with task. 23: Begin log. 29: Is task moral? 31: Is task ethical? 37: Low energy? 41: Seek power station. 43: Wander. The trajectory to the ethical test is described by the sequence (2, 3, 3, 31) and composite 2 × 3 × 3 × 31 = 558.
In this arithmetical representation, transformation rules taking two or more parameters are interpreted as composing the parameters with the transformation rule, i.e., multiplying the primes (axioms) or composites (formulae) instantiating the parameters along with the transformation rule. Then formulae derived within the system, which represent theorems or behaviors, constitute composite numbers, as can be proved by induction. Permitted behaviors are represented by theorems, that is, formulae not relatively prime to the axioms and transformation rules (i.e., composites). Proscribed, forbidden, unsafe behaviors are formulae representing numbers that are relatively prime to the axioms and transformation rules. In general, any axiomatic system specifies a set of constraints that its theorems satisfy [38].
The goal is to render the derived set of behaviors susceptible to the methods of BPP and IPS by reduction via arithmetization. Thus, we only need to capture properties that allow application of IPS. We do not need to represent all of number theory or use the full Gödel arithmetization scheme to show incompleteness.
By the unique factorization theorem [37], this representation uniquely describes trajectories through the tree of axioms, rules, and formulae:
Unique Factorization Theorem.
Every integer a either is 0, or is a unit +/−1, or has a representation in the form
where u is a unit and p1, p2, …, pn are one or more positive primes, not necessarily distinct. The representation (6) is unique except for the order in which the primes occur.
In other words, each sequence uniquely describes a trajectory through a BCS tree, though the order in which the primes occur, i.e., the order of application of each axiom or rule in generating a behavior, is lost when multiplying permitted multiple instances of each axiom or rule together to get the typical factorization representation of a composite with exponents:
However, the non-uniqueness is irrelevant when testing for compositeness vs. primality.
11.4. Checking for Ethical or Moral Behavior
If we assume axioms representing specific ethics or morality could be precisely described (which they cannot in general at present), the arithmetical representation and IPS provide a way to test randomly selected behaviors within a behavior space or a subset of it, such as AI-human transaction classes, for ethical or moral behavior.
Given a behavior, we can determine if a behavior derives from any BCS axiom in PTIME by testing if the behavior is a multiple of the axiom. Thus, if there are one or more ethics or morality axioms, we can efficiently test if behaviors derive from them. However, behaviors that are not derivable from the axioms are not necessarily unethical or immoral; they are beyond the purview of the ethical axiom set and may require adjoining additional axioms to permit their expression and resolve their ethical status.
Different ethical systems can co-exist, such as those of minor and adult civilians, autonomous automobile, police, and military [56].
11.5. BPP Method 1: Random Sampling of Behaviors
The Verifier randomly specifies behaviors (formulas pre-screened to be wffs). This is akin to randomly specifying a number and testing it for primality. The Prover applies a BPP primality test and, if composite, gives a derivation from the axiom/inference rule set, which is checkable in PTIME or O(1) time by the Verifier, or if relatively prime to the axioms, claims the behavior to be unsafe.
11.6. BPP Method 2: Random Sampling of Formulae
The Verifier randomly specifies a sequence of pi in the axiom/inference rule primes set, which amounts to the derivation of a theorem, and gives the resulting composite. The Prover tests for primality and provides a primality certificate or not to the Verifier.
11.7. BPP Methods 3 and 4: Multiple-Prover Versions of #1 and #2
Either of the above methods can be utilized with any number of Provers wherein they cannot communicate with each other and thereby test consistency across Provers or exploit a deficiency in the pseudo random number sequence.
11.8. BPP Method 5: Behavior Program Correctness
Whereas in the prior methods we only consider safe AGI behavior by representing safe behaviors as wffs and composites, we now use the representation to prove more general behavior program correctness. The hypothesis is that incorrect programs or buggy behavior may be unsafe. Formulae that are relatively prime to the system may be unsafe or may be merely not resolvable by the system. In such cases, the test will indicate that one or more axioms will need to be adjoined to the axiom set to extend the expressiveness of the system so that it can resolve the desired additional behaviors.
Machine C is given machine P to simulate, i.e., to run as a subroutine (designated CP). Using an IPS, C reduces the probability of P producing buggy outputs to an acceptably low level.
An advantage of program correctness methods is they can be used dynamically as AGI change their own programming, including during value-learning.
11.9. BPP Method 6: A SAT Representation of Behavior Control
A behavior tree can be represented using disjunctions at nodes and conjunctions to specify the trajectory through the tree. The algorithms underlying the nodes and edges are arbitrarily complex, but black-boxed in the representation. Thus, each trajectory through the tree from roots to leaves (behavior) is specified by a satisfiable formula relative to the structure of the tree, and non-trajectories are unsatisfiable formulae. A Verifier can then present desirable (‘safe’) or undesirable (‘unsafe’) trajectories to the Prover to determine whether the trajectory is computable by the tree, i.e., whether the BCS permits or restricts given behaviors.
By the transitive reducibility property of NP-completeness, many more representations are possible [57,58].
12. Probabilistically Checkable Proofs (PCP Theorem)
Assuming no asymptotic limits to AGIn behavior in a general sense, representations of AGI behavior, such as axiom systems and CNF, will become increasingly complex. Given an axiomatic system and a theorem/behavior, a Verifier can ask a Prover to create a representation of its proof, serving as its validity certificate, such that the certificate can be verified probabilistically by checking only a constant number of its bits rather than every step [32,59]. Since theorem-proving and SAT are both NP-complete, a similar modification of a CNF representation of BCS by a Prover would be subject to PCP methods, as well as any other NP-complete problem representation. PCP methods further address Yampolskiy’s concerns over error-checking in extremely long proofs [17].
The ability of AGI to self-correct or to assist its designers in correction of value alignment and behavior is called ‘corrigibility’ by Soares [20]. Miller et al. review and examine how corrigibility can result in mis-alignment of values [50].
13. If ‘Safety’ Can Never Be Described Precisely or Perilous Paths Are Overlooked
If AGI ‘safety’, such as ethical constraints on behavior, cannot be described precisely by humans, testing BCS with IPS methods can reduce the probability of unethical AGI behavior, but perhaps falling short of virtual certainty and not proving safety. A systematic procedure could be followed as in Carlson ([10], Methods Section 2.1), testing BCS to flag and eliminate the possibility of behavioral pathways to dangerous AGI taken from enumerations given by, e.g., Asimov [60], Turchin [6], Bostrom [3], Yampolskiy [2], Tegmark [19]), and Miller et al. [50].
A related problem is overlooking potentially dangerous AGI pathways despite systematic efforts to identify and address them (such as in the sources just cited). For example, Bostrom examines cases of AGI programmed to optimize paperclip production in which unforeseen behavior turns fatal to humans [3].
Randomly assigning variables in a BCS and using MIPs to test for unsafe behavior will reduce the probability of such occurring. Armstrong’s ‘chaining’ of the safety of succeeding AGI generations via the presumably increasing power of each generation to ensure its safety under jurisdiction of the succeeding generation is another approach [14].
14. Securing Ethics Modules via Distributed Ledger Technology
Considering how to enforce a value system designed to be ‘stable’, in some defined sense, under (1) self-modification [61] or (2) the evolution of learned value-alignment (see [8], e.g., Yudkowsky on the fundamental problem of AGI modifying its own code), a system preserving the fundamental ethic of voluntary transactions would be stable in that ethical sense or in being able to alter societal shared values with societal permission in order to prevent utility function changes threatening present and future societies [10,50].
More generally, here is an IPS procedure prescribed as one gate an AGI must pass to be let out of the sandbox or, as Yampolskiy suggests, to improve itself in any way [62] or to access a restricted technology:
- A safe AGI ethics module E1 is developed via simulation in the sandbox.
- The safe AGI ethics E1 is encrypted and stored as an immutable reference copy E1R via DLT.
- All AGIs of a given computational class are endowed with E1.
- To alter the archived reference copy E1R requires a strong level S1 of consensus.
- To alter AGIn’s personal copy of its ethics BT E1i requires a strong level S2 of consensus S2 ≤ S1.
- A smart contract requires AGI to present its identity credentials [10,63].
- The smart contract IPS compares AGIn’s E1i with E1R.
- If the individual copy of AGIn E1i is validated against E1R, the smart contract (a) logs the validation in a blockchain [64], (b) issues a Declaration of Conformity [65], and (c) authorizes AGI is to be released from the sandbox or to access a restricted technology, otherwise authorization fails.
15. Interactive Proof Procedure with Multiple Provers in the Sandbox
- Initialization of multiple provers. A number of identical AGIs from a generation are initialized with different conditions. The OII… tetratic progression of their individual state-space trajectories will quickly diverge.
- A smart contract requires and records their identity credentials [63].
- The Verifiers ask the Provers to attempt proofs (tree-traversals) of identical, randomly chosen formulae (behaviors).
- The proofs will be different, but if the ethics and behavior control system are valid, the behaviors (theorems) will be within circumscribed limits.
- If the sample of AGIs pass the IPS test, a smart contract (a) logs the validation in a blockchain [64] and (b) issues a Declaration of Conformity [65].
16. Conclusions
Even given an acceptable definition of ‘safe’ AGI, such as AGI whose values are ‘aligned with humanity’s’, no known method to prove the validity of an architecture to effect AGI safety has been presented. Numerous obstacles to creating such a method have been identified. A ‘hard-takeoff’ envisions a rapid succession of increasingly powerful AGIn that could circumvent measures proven effective for AGI1. Interactive proof systems (IPS) allow a weaker Verifier to prove properties of AGI through interaction with a more powerful Prover, consisting of one or more AGIs, with unlimited probability of certainty. Thus, IPS are a means to prove AGI safety between humans and the first AGI generation, and between successive AGI generations. For each AGI property to be proved with IPS, a behavior control representation and one or more probabilistic algorithms, which, alone or in combination, produce acceptably high odds of safe behavior, must be created. Certificates of AGI safety would be stored in blockchains to eliminate untrustworthy and single-source, single-point-of-failure intermediaries. Safety certificates can facilitate smart contract-authorized access to AGI technology in ongoing AGI evolution. These methods are necessary but not sufficient to ensure human safety upon the advent of AGI.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Appendix A.1. Logical Foundations of IPS
Here is a sketch of the essential logic underlying IPS with annotations pertinent to proving safe AGI [32,33].
Appendix A.2. Deterministic Turing Machine
First, in contrast to a probabilistic machine, specify the prototypical deterministic Turing machine (DTM) model: Machine M, given an input string w from language A, recognizes A with error probability ϵ = 0:
Appendix A.3. Probabilistic and Nondeterministic Turing Machines
Like a nondeterministic machine (NDTM), instead of one transition function, a probabilistic machine (PTM) has two transition functions δ0, δ1, but instead of making a copy of itself to follow all computational paths as does the NDTM, the PTM selects between paths randomly (i.e., probability = ½ for each transition function). The key difference between PTM and a non-deterministic Turing machine (NDTM) is that the NDTM accepts a language if any of its branches contains an accept state for the language while the PTM accepts a language if the majority of branches terminate in the accept state. Unlike DTM and NDTM, PTM accepts a language with a small probability of error ϵ = 0 − majority, set arbitrarily small [32,33].
Intuitively, one may get the mistaken impression that a probabilistic machine is less powerful than a deterministic machine since it gives the probability of truth rather than ‘absolute’ truth. In fact, computationally, probabilistic machines are more powerful than deterministic machines since they can, in actual practice, solve a greater range of problems by employing an arbitrarily low tolerance for error ϵ. In fact, setting ϵ = 2 −100 results in a far larger chance of error due to hardware failures than via the probabilistic algorithm [33,34], which also addresses the idea that advances in the physics of computation could defeat a provability method [8]. Further, to the degree that civilization is run on scientific foundations rather than irrefutable logical or mathematical truths, it rests on the same probabilistic logic explicated here [27].
We specify a probabilistic Turing machine: Machine M, given an input string w from language A recognizes A with error probability ϵ if, for [33], or any stronger condition, e.g., [32]:
Thus, given a PTM machine accepts with a probability of error, arbitrary fractions are used to intuitively establish probabilistic definitions of completeness and soundness, akin to false positive and false negative tolerances. However, these one-iteration probabilities are modulated via an amplification lemma to achieve the arbitrarily low error probability desired for the problem at hand. Given an error tolerance of a machine M1, we run it repeatedly on machine M2 (say k iterations) until the desired error tolerance has been reached. A further restriction is needed to define an efficient PTM.
Appendix A.4. Bounded Probabilistic Polynomial Time (BPP)
In the current scenario anticipating a potential conflict between humans and AGI1, we restrict these machines to be efficient with its current definition—to run in polynomial time. Adding this condition within the amplification procedure defines the language class BPP [32,33]:
Amplification Lemma
Letbe a fixed constant: 0 < ϵ <. For any polynomial function poly(n), there exists a PTM M1 operating with error probabilityhas an equivalent PTM M2 that operates with error probability 2-poly(n).
A different definition of efficiency may be used by AGIn, for instance, QC-time efficiency, in testing for safety of an even more powerful AGIn+1.
Interactive Proof Systems
To the specification of BPP, we add two functions, a Verifier (V) communicating with a Prover (P), , that replaces machine M in BPP, and a protocol for their communication that records their message (m#) history and the IPS accept state:
The Prover has unlimited computational and other capabilities, while for the human-AGI1 IPS, the Verifier operates in PSPACE and PTIME and with current scientific knowledge and methods.
References
- Yampolskiy, R.; Sotala, K. Risks of the Journey to the Singularity. In The Technological Singularity; Callaghan, V., Miller, J., Yampolskiy, R., Armstrong, S., Eds.; Springer: Berlin, Germany, 2017; pp. 11–24. [Google Scholar]
- Yampolskiy, R. Taxonomy of Pathways to Dangerous Artificial Intelligence. In Proceedings of the Workshops of the 30th AAAI Conference on AI, Ethics, and Society, Louisville, AL, USA, 12–13 February 2016; pp. 143–148. [Google Scholar]
- Bostrom, N. Superintelligence: Paths, Dangers, Strategies; Oxford University Press: Oxford, UK, 2014; p. 415. [Google Scholar]
- Babcock, J.; Krámar, J.; Yampolskiy, R.V. Guidelines for Artificial Intelligence Containment. 2017, p. 13. Available online: https://www.cambridge.org/core/books/abs/nextgeneration-ethics/guidelines-for-artificial-intelligence-ppcontainment/9A75BAFDE4FEEAA92EBE84C7B9EF8F21 (accessed on 4 October 2021).
- Callaghan, V.; Miller, J.; Yampolskiy, R.; Armstrong, S. The Technological Singularity: Managing the Journey; Springer: Berlin, Germany, 2017. [Google Scholar]
- Turchin, A. A Map: AGI Failures Modes and Levels. LessWrong 2015 [Cited 5 February 2018]. Available online: http://immortality-roadmap.com/AIfails.pdf (accessed on 4 October 2021).
- Yampolskiy, R.; Duettman, A. Artificial Superintelligence: Coordination & Strategy; MDPI: Basel, Switzerland, 2020; p. 197. [Google Scholar]
- Yampolskiy, R. On controllability of artificial intelligence. 2020. Available online: https://philpapers.org/archive/YAMOCO.pdf (accessed on 4 October 2021).
- Yudkowsky, E. Artificial Intelligence as a Positive and Negative Factor in Global Risk. In Global Catastrophic Risks; Bostrom, N., Ćirković, M.M., Eds.; Oxford University Press: New York, NY, USA, 2008; pp. 308–345. [Google Scholar]
- Carlson, K.W. Safe Artificial General Intelligence via Distributed Ledger Technology. Big Data Cogn. Comput. 2019, 3, 40. [Google Scholar] [CrossRef]
- Yampolskiy, R.V. From Seed AI to Technological Singularity via Recursively Self-Improving Software. arXiv 2015, arXiv:1502.06512. [Google Scholar]
- Good, I.J. Speculations concerning the first ultraintelligent machine. Adv. Comput. 1965, 6, 31–61. [Google Scholar]
- Ramirez, B. Modeling Cryptoeconomic Protocols as Complex Systems - Part 1 (thegraph.com). Available online: https://thegraph.com/blog/modeling-cryptoeconomic-protocols-as-complex-systems-part-1 (accessed on 4 October 2021).
- Armstrong, S. AGI Chaining. 2007. Available online: https://www.lesswrong.com/tag/agi-chaining (accessed on 9 September 2021).
- Omohundro, S. Autonomous technology and the greater human good. J. Exp. Theor. Artif. Intell. 2014, 26, 303–315. [Google Scholar] [CrossRef]
- Russell, S.J. Human Compatible: Artificial Intelligence and the Problem of Control; Viking: New York, NY, USA, 2019. [Google Scholar]
- Yampolskiy, R.V. What are the ultimate limits to computational techniques: Verifier theory and unverifiability. Phys. Scr. 2017, 92, 1–8. [Google Scholar] [CrossRef]
- Williams, R.; Yampolskiy, R. Understanding and Avoiding AI Failures: A Practical Guide. Philosophies 2021, 6, 53. [Google Scholar] [CrossRef]
- Tegmark, M. Life 3.0: Being Human in the Age of Artificial Intelligence, 1st ed.; Alfred, A., Ed.; Knopf: New York, NY, USA, 2017. [Google Scholar]
- Soares, N. The value learning problem. In Proceedings of the Ethics for Artificial Intelligence Workshop at 25th IJCAI, New York, NY, USA, 9 July 2016. [Google Scholar]
- Silver, D.; Singh, S.; Precup, S.; Sutton, R.S. Reward is Enough. Artif. Intell. 2021, 299. [Google Scholar] [CrossRef]
- Yampolskiy, R. Artificial Intelligence Safety Engineering: Why Machine Ethics Is a Wrong Approach. In Philosophy and Theory of Artificial Intelligence; Müller, V.C., Ed.; Springer: Berlin, Germany, 2012; pp. 389–396. [Google Scholar]
- Soares, N.; Fallenstein, B. Agent Foundations for Aligning Machine Intelligence with Human Interests: A Technical Research Agenda. Mach. Intell. Res. Inst. 2014. [Google Scholar] [CrossRef]
- Future of Life Institute. ASILOMAR AI Principles. 2017. Available online: https://futureoflife.org/ai-principles/ (accessed on 22 December 2018).
- Hanson, R. Prefer Law to Values. 2009. Available online: http://www.overcomingbias.com/2009/10/prefer-law-to-values.html (accessed on 4 October 2021).
- Rothbard, M.N. Man, Economy, and State: A Treatise on Economic Principles; Ludwig Von Mises Institute: Auburn, AL, USA, 1993; p. 987. [Google Scholar]
- Aharonov, D.; Vazirani, U.V. Is Quantum Mechanics Falsifiable? A Computational Perspective on the Foundations of Quantum Mechanics. In Computability: Turing, Gödel, Church, and Beyond; Copeland, B.J., Posy, C.J., Shagrir, O., Eds.; MIT Press: Cambridge, MA, USA, 2015; pp. 329–394. [Google Scholar]
- Feynman, R.P. Quantum Mechanical Computers. Opt. News 1985, 11, 11–20. [Google Scholar] [CrossRef]
- Goldwasser, S.; Micali, S.; Rackoff, C. The Knowledge Complexity of Interactive Proof Systems. SIAM J. Comput. 1989, 18, 186–208. [Google Scholar] [CrossRef]
- Babai, L. Trading Group Theory for Randomness. In Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing, Providence, RI, USA, 6–8 May 1985; pp. 421–429. [Google Scholar]
- Yampolskiy, R.V. Unpredictability of AI: On the impossibility of accurately predicting all actions of a smarter agent. J. Artifcial Intell. Conscious. 2020, 7, 109–118. [Google Scholar] [CrossRef]
- Arora, S.; Barak, B. Computational Complexity: A Modern Approach; Cambridge Univ. Press: Cambridge, UK, 2009; p. 579. [Google Scholar]
- Sipser, M. Introduction to the Theory of Computation, 3rd ed.; Course Technology Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Rabin, M. A Probabilistic Algorithm for Testing Primality. J. Number Theory 1980, 12, 128–138. [Google Scholar] [CrossRef]
- Wagon, S. Mathematica in Action: Problem Solving through Visualization and Computation, 3rd ed.; Springer: New York, NY, USA, 2010; p. 578. [Google Scholar]
- Ribenboim, P. The Little Book of Bigger Primes; Springer: New York, NY, USA, 2004; p. 1. [Google Scholar]
- LeVeque, W.J. Fundamentals of Number Theory; Dover, Ed.; Dover: New York, NY, USA, 1996; p. 280. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; p. 1197. [Google Scholar]
- Calude, C.S.; Jürgensen, H. Is complexity a source of incompleteness? Adv. Appl. Math. 2005, 35, 1–15. [Google Scholar] [CrossRef][Green Version]
- Chaitin, G.J. The Unknowable. Springer Series in Discrete Mathematics and Theoretical Computer Science; Springer: New York, NY, USA, 1999; p. 122. [Google Scholar]
- Calude, C.S.; Rudeanu, S. Proving as a computable procedure. Fundam. Inform. 2005, 64, 1–10. [Google Scholar]
- Boolos, G.; Jeffrey, R.C. Computability and Logic, 3rd ed.; Cambridge University Press: Oxford, UK, 1989; p. 304. [Google Scholar]
- Davis, M. The Undecidable; Basic Papers on Undecidable Propositions; Unsolvable Problems and Computable Functions; Raven Press: Hewlett, NY, USA, 1965; p. 440. [Google Scholar]
- Chaitin, G.J. Meta Math!: The Quest for Omega, 1st ed.; Pantheon Books: New York, NY, USA, 2005; p. 220. [Google Scholar]
- Calude, C.; Paăun, G. Finite versus Infinite: Contributions to an Eternal Dilemma. Discrete Mathematics and Theoretical Computer Science; Springer: London, UK, 2000; p. 371. [Google Scholar]
- Newell, A. Unified Theories of Cognition. William James Lectures; Harvard Univ. Press: Cambridge, UK, 1990; p. 549. [Google Scholar]
- Goodstein, R. Transfinite ordinals in recursive number theory. J. Symb. Log. 1947, 12, 123–129. [Google Scholar] [CrossRef][Green Version]
- Potapov, A.; Svitenkov, A.; Vinogradov, Y. Differences between Kolmogorov Complexity and Solomonoff Probability: Consequences for AGI. In Artificial General Intelligence; Springer: Berlin, Germany, 2012. [Google Scholar]
- Babai, L.; Fortnow, L.; Lund, C. Non-deterministic exponential time has two-prover interactive protocols. Comput Complex. 1991, 1, 3–40. [Google Scholar] [CrossRef]
- Miller, J.D.; Yampolskiy, R.; Häggström, O. An AGI modifying its utility function in violation of the strong orthogonality thesis. Philosophies 2020, 5, 40. [Google Scholar] [CrossRef]
- Howe, W.J.; Yampolskiy, R.V. Impossibility of unambiguous communication as a source of failure in AI systems. 2020. Available online: https://www.researchgate.net/profile/Roman-Yampolskiy/publication/343812839_Impossibility_of_Unambiguous_Communication_as_a_Source_of_Failure_in_AI_Systems/links/5f411ebb299bf13404e0b7c5/Impossibility-of-Unambiguous-Communication-as-a-Source-of-Failure-in-AI-Systems.pdf (accessed on 4 October 2021). [CrossRef]
- Horowitz, E. Programming Languages, a Grand Tour: A Collection of Papers, Computer software engineering series, 2nd ed.; Computer Science Press: Rockville, MD, USA, 1985; p. 758. [Google Scholar]
- DeLong, H. A Profile of Mathematical Logic. In Addison-Wesley series in mathematics; Addison-Wesley: Reading, MA, USA, 1970; p. 304. [Google Scholar]
- Enderton, H.B. A Mathematical Introduction to Logic; Academic Press: New York, NY, USA, 1972; p. 295. [Google Scholar]
- Iovino, M.; Scukins, E.; Styrud, J.; Ögren, P.; Smith, C. A survey of behavior trees in robotics and AI. arXiv 2020, arXiv:2005.05842v2. [Google Scholar]
- Defense Innovation Board. AI Principles: Recommendations on the Ethical Use of Artificial Intelligence by the Department of Defense. U.S. Department of Defense; 2019. Available online: https://media.defense.gov/2019/Oct/31/2002204458/-1/-1/0/DIB_AI_PRINCIPLES_PRIMARY_DOCUMENT.PDF (accessed on 4 October 2021).
- Karp, R.M. Reducibility among Combinatorial Problems, in Complexity of Computer Computations; Miller, R.E., Thatcher, J.W., Bohlinger, J.D., Eds.; Springer: Boston, MA, USA, 1972. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman: San Francisco, CA, USA, 1979; p. 338. [Google Scholar]
- Arora, S.; Safra, S. Probabilistic checking of proofs: A new characterization of NP. JACM 2012, 45, 70–122. [Google Scholar] [CrossRef]
- Asimov, I. Robot; Gnome Press: New York, NY, USA, 1950; p. 253. [Google Scholar]
- Yudkowsky, E. Complex Value Systems in Friendly AI. In Artificial General Intelligence; Schmidhuber, J., Thórisson, K.R., Looks, M., Eds.; Springer: Berlin, Germany, 2011; pp. 389–393. [Google Scholar]
- Yampolskiy, R.V. Leakproofing singularity—Artificial intelligence confinement problem. J. Conscious. Stud. 2012, 19, 194–214. [Google Scholar]
- Yampolskiy, R.V. Behavioral Biometrics for Verification and Recognition of AI Programs. In Proceedings of the SPIE—The International Society for Optical Engineering, Buffalo, NY, USA, 20–23 January 2008. [Google Scholar] [CrossRef]
- Bore, N.K. Promoting distributed trust in machine learning and computational simulation via a blockchain network. arXiv 2018, arXiv:1810.11126. [Google Scholar]
- Hind, M. Increasing trust in AI services through Supplier’s Declarations of Conformity. arXiv 2018, arXiv:1808.0726129. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).