1. Introduction
The conflict of a discrete and continuous model of the universe is deeply rooted in the beginning of natural philosophy. Ancient philosophers of atomism (Democritus et al.) believed in a world of interacting discrete particles as indivisible building blocks (atoms). These natural philosophers were criticized by Aristotle as an advocate of the continuum: In mathematics, a continuous line cannot be reduced to discrete points, like a chain of coupled pearls. Aristotle described change in nature by continuous dynamics. In the beginning of modern science, physicists assumed a mechanistic world of interacting atoms. However, mathematically, atoms were considered mass points with motions determined by continuous differential equations. Leibniz, as the inventor of differential calculus, tried to bridge the discrete and continuous world by his philosophical concept of monads, which were mathematically represented by infinitesimally small, but nevertheless non-zero quantities called differentials [
1] (Chapter 4).
Later on, scientific computing in physics and chemistry was mainly based on continuous functions. In practical cases, the solutions of their (real or complex) equations could often only be approximated by algorithms of numerical analysis in finitely many discrete steps (e.g., Newton’s method). Nevertheless, these procedures of numerical analysis depend on the continuous concept of real numbers. The discrete theory of computability is well-founded by the discrete concept of Turing machines (Church’s thesis).
With respect to modern quantum physics, physical reality seems to be reducible to discrete entities, like elementary particles. Quantum processes are computed by quantum algorithms—the universe as a quantum computer. Nevertheless, quantum field theories also use continuous functionals and spaces, real and complex numbers, to compute and predict events with great precision. Are analog and continuous concepts only useful inventions of the human mind, to solve problems in a discrete world with approximations? Natural constants are defined by fundamental proportions of physical quantities, which are highly confirmed by experiments. The fine-structure constant is an example of a dimensionless real number in physics. In mathematics, the real number, , is exactly defined by the relation of the circumference and diameter of a circle. However, as decimal expansion, there are only approximately finite values, which can be computed or measured by physical instruments in space and time.
If successful explanations and predictions of physical theories actually depend on real numbers as axiomatically defined infinite entities, then they could be interpreted as hints on a mathematical reality “behind” or “beyond” (better: Independent of) the observable and measurable finite world of physics. Is physical reality only a part in the universe of mathematical structures? It is the old Platonic belief in symmetries and structures as the mathematical ground of the world [
2], (Chapter 4).
In a modern sense of natural science, Ockham’s razor demands an economic use of theoretical assumptions for explanations of empirical events. Scientists should prefer explanations of empirical events that only need as few theoretical entities as possible. Ockham’s razor concerns the assumption of theoretical entities, like the Platonic belief in the existence of ideal mathematical entities (e.g., infinite sets, cardinal numbers and spaces). For a constructivist of modern mathematics, these entities are only justified as far as they can be introduced by algorithms and constructive procedures. Historically, in the Middle Ages, nominalism also criticized Platonism in the sense of Ockham’s razor. From Ockham’s point of view, the Platonic assumption of abstract mathematical structures is a waste of ontological entities. However, the existence of abstract mathematical universes beyond empirical physics cannot be excluded in principle. Modern string theories and supersymmetries are possible candidates who, until now, have nearly no empirical justification. Nevertheless, they are used to explain the quantum universe.
The foundational debate on the digital and analog, discrete and continuous has deep consequences for physics. In classical physics, the real numbers are assumed to correspond to continuous states of physical reality. For example, electromagnetic or gravitational fields are mathematically modeled by continuous manifolds. Fluid dynamics illustrate this paradigm with continuous differential equations.
However, in modern quantum physics, a “coarse grained” reality seems to be more appropriate. Quantum systems are characterized by discrete quantum states, which can be defined as quantum bits. Instead of classical information systems, following the digital concept of a Turing machine, quantum information systems with quantum algorithms and quantum bits open new avenues to digital physics. Information and information systems are no longer only fundamental categories of information theory, computer science, and logic, but they are also grounded in physics [
3] (Chapter 5).
The question arises whether it is possible to reduce the real world to a quantum computer as an extended concept of a universal quantum Turing machine. “It from bit” as proclaimed the physicist, John A. Wheeler [
4]. On the other side, fundamental symmetries of physics (e.g., Lorentz symmetry and electroweak symmetry) are continuous [
5] (Chapter 3). Einstein’s space-time is also continuous. Are they only abstractions (in the sense of Ockham) and approximations to a discrete reality?
Some authors proclaim a discrete cosmic beginning with an initial quantum system (e.g., quantum vacuum). The quantum vacuum is not completely empty, like the classical vacuum in classical mechanics. Because of Heisenberg’s uncertainty principle, there are virtual particles emerging and annihilating themselves. In this sense, it is discrete. In some models of the initial quantum universe with Planck length (quantum foam), even time is “granulated” (discrete). According to the standard theory of quantum cosmology, the initial quantum state has evolved in an expanding macroscopic universe with increasing complexity. In the macroscopic universe, the motions of celestical bodies can be approximately modeled by continuous curves in a Euclidean space of Newtonian physics. Actually, physical reality is discrete in the sense of elementary particle physics, and Newtonian physics with continuous mathematics only an (ingenious) human invention of approximation.
However, physical laws of quantum theory (e.g., Hilbert space) are also infused with real and complex numbers. Are these mathematical entities only convenient inventions of the human mind to manage our physical experience of observations and measurements? A mathematical constructivist and follower of Ockham’s razor would agree to this epistemic position. However, from an extreme Platonic point of view, we could also assume a much deeper layer than the discrete quantum world—the universe of mathematical structures themselves as primary reality with infinity and continuity.
2. Complexity of Quantum and Real Computing
In digital physics, the universe itself is assumed to be a gigantic information system with quantum bits as elementary states. David Deutsch et al. [
6] discussed quantum versions of Turing-computability and Church’s thesis. They are interesting for quantum computers, but still reduced to the digital paradigm. Obviously, modeling the “real” universe also needs real computing. Are continuous models only useful approximations of an actually discrete reality? In classical physics, solutions of continuous differential equations are approximated by numerical (discrete) procedures (e.g., Newton’s method). In quantum physics, a discrete structure of reality is assumed. Nevertheless, we use continuous mathematical tools (e.g., Schrödinger’s equation, functional analysis, etc.) in quantum physics. Therefore, from an epistemic point of view, continuous mathematical methods are only tools (inventions of the human mind) to explain and predict events in an actually discrete reality.
What do we know about the physical origin of information systems? As far as we can measure, the universe came into being 13.81 ± 0.04 billion years ago as a tiny initial quantum system, which expanded into cosmic dimensions according to the laws of quantum physics and general relativity. In a hot mixture of matter and radiation, the generation of nuclear particles was finished after 10−5 s. After the separation of matter and radiation in nearly 300,000 years, the universe became transparent. Gravitation began to form material structures of galaxies, Black Holes, and the first generations of stars. Chemical elements and molecular compounds were generated. Under appropriate planetary conditions, the evolution of life had developed. The evolution of quantum, molecular, and DNA-systems is nowadays a model of quantum, molecular, and DNA-computing.
In quantum computing, we consider the smallest units of matter and the limits of natural constants (e.g., Planck’s constant velocity of light) as technical constraints of a quantum computer. A technical computer is a physical machine with an efficiency that depends on the technology of circuits. Its increasing miniaturization has provided new generations of computers with an increasing capacity of storage and decreasing computational time. However, increasing diminution leads to the scaling of atoms, elementary particles, and smallest packages of energy (quantum), which obey physical laws different from classical physics.
Classical computing machines are replaced by quantum computers, which work according to the laws of quantum mechanics. Classical computing machines are, of course, technically realized by, e.g., transistors following quantum mechanics. However, from a logical point of view, classical computing machines are Turing machines (e.g., von Neumann machines) with classical states. Even a classical parallel computer (supercomputer) is only a Turing machine which connects Turing machines (e.g., von Neumann machines) in a parallel way. However, a quantum computer follows the laws of quantum mechanics with non-classical (quantum) states (superposition and entangled states). Therefore, R. Feynman demanded that the quantum world could only be simulated by quantum computers and not by classical computing machines.
Quantum computers would lead to remarkable breakthroughs of information and communication technology. Problems (e.g., the factorization problem), which classically are exponentially complex with practical unsolvability, would become polynomially solvable. In technology, quantum computers would obviously enable an immense increase of problem solving capacity. In complexity theory of computer science, high computational time of certain problems could perhaps be reduced from NP (nondeterministic polynomial time) to P (polynomial time). However, the question arises whether quantum computers can also realize non-algorithmic processes beyond Turing-computability.
A quantum computer works according to the laws of quantum physics. In quantum mechanics, the time-depending dynamics of quantum states are modeled by a deterministic Schrödinger equation. Therefore, the output of quantum states in a quantum computer is uniquely computable for given inputs of quantum states as long as their coherence is not disturbed. In that sense, quantum computer can be considered as a quantum Turing machine with respect to quantum states [
7] (Chapter 15).
However, are there logical-mathematical breakthroughs that undecidable and unsolvable problems become decidable and computable by quantum computers? The undecidability and unsolvability of problems depends on the logical-mathematical definition of a Turing machine. Therefore, even a quantum computer cannot solve more problems than a Turing machine according to algorithmic theory of computability. Problem solving with quantum computers will be accelerated with an immense computing velocity. However, algorithmically unsolvable and undecidable problems remain unsolvable even for quantum computers [
6].
Even analog and real computing do not change the fundamental logical-mathematical results of undecidability and unsolvability [
7] (Chapters 10–11), [
8] (Chapter 1). Real computing transfers the digital concepts of computability and decidability to the continuous world of real numbers. Blum, Cucker, Shub, and Smale [
9] introduced decision machines and search procedures over real and complex numbers. A universal machine (generalizing Turing’s universal machine in the digital world) can be defined over a mathematical ring and with that over real and complex numbers. On this basis, decidability and undecidability of several theoretical and practical mathematical problems (e.g., Mandelbrot set, Newton’s method) can rigorously be proved. Like in the digital world, we can introduce a complexity theory of real computing. Polynomial time reductions as well as the class of NP-problems are studied over a general mathematical ring and with that on real and complex numbers. Real computability can be extended in a polynomial hierarchy for unrestricted machines over a mathematical field.
Real and analog computing seem to be close to human mathematical thinking, with real numbers and continuous concepts. Human thinking uses the human brain, which has evolved during evolution with different degrees of complexity. In computational neuroscience, brains are modelled by neural networks. The biological hierarchy of more or less complex brains can be referred to a mathematical hierarchy of more or less complex neural networks. Mathematically, they are equivalent to computing machines with different degrees of complexity from finite automata to Turing machines [
7] (Chapter 12). Otherwise, the simulation of neural networks on digital computers would not be possible.
Concerning the cognitive capacities of automata, machines, and neural networks, computing machines can understand formal languages according to their degrees of computability from simple regular languages (finite automata) to Chomsky grammars of natural languages (Turing machines). Neural networks with synaptic weights of integers or rational numbers correspond to finite automata resp. Turing machines. Analog neural networks with real synaptic weights are real Turing machines. They correspond to real computing. Siegelmann et al. [
10] proved that they can operate on non-recursive languages beyond Chomsky grammars. However, they also have the logical-mathematical limitations of real and analog computing.
An example is the halting problem for a Turing machine, which is not decidable even for a quantum and analog computer. Another problem is the word problem of group theory, which demands a test of whether two arbitrary words of a symbolic group can be transformed into one another by given transformation rules. These and other problems are not only of academic interest. They are often basic for practical applications (e.g., whether expressions of different languages can be transformed into one another or not).
In the theory of computability, it is proved that there is no general algorithm that can decide everything. This is a simple consequence of Turing’s undecidability of the halting problem. Quantum and real computing will not change anything of these basic results. Even in a civilization with quantum computers, there will be no machine that can solve all problems algorithmically. Gödel’s and Turing’s logical-mathematical limitations will remain, although there will be a giant increase of computational capacities.
3. Is the Universe Digital?
The universe is mathematically modeled by equations of quantum and relativistic physics. They are philosophically interpreted as “natural laws” [
11]. The emergence of physical particles is mathematically considered as the solution of gauge equations describing the fundamental symmetries of the universe [
12]. If we, for example, try to solve the Schrödinger equation for five or less quarks, there are only two stable possibilities of coordination. They consist of either two up-quarks and one down-quark or two down-quarks and one up-quark. The former cluster is called “proton”, the last one “neutron”. In a next step, we can apply the Schrödinger equation to protons and neutrons as “atomic nuclei”. In this case, we get 257 stable possibilities with hydrogen, helium, et al. We can continue the application of the Schrödinger equation to molecules, crystal grids, and more complex objects. The names of “protons”, “neurons”, “atomic nuclei”, “hydrogen”, “molecules”, et al. are, of course, human inventions. The whole information of these objects is involved in the solutions of mathematical equations.
Mathematical equations can be classified in physics (e.g., general/special relativity, electromagnetism, classical mechanics, statistical mechanics, solid state physics, hydrodynamics, thermodynamics quantum field theory, nuclear physics, elementary particle physics, atomic physics), chemistry, biology, neurobiology, psychology, and sociology with the objects of protons, atoms, cells, organisms, populations, et al. as solutions.
Mathematical structures are systems of objects with (axiomatic) relations and equations. Examples are spaces, manifolds, algebras, rings, groups, fields, et al. Isomorphisms are mappings between structures, which conserve their relations. They satisfy the conditions of equivalence relations with reflexivity, symmetry, and transitivity. Therefore, mathematical structures can be classified in equivalence classes. Modern mathematics studies categories of structures with increasing abstraction in the tradition of Dedekind, Hilbert, and Bourbaki. Categories correspond to set-theoretical universes and transfinite cardinal numbers with increasing size. In recent foundational programs, mathematical structures and categories are represented and classified by types of formal systems [
7] (Chapter 9). Hilbert already tried to extend his axiomatization and classification of mathematical structures to physics (Corry 2004). Physical structures of space-time, fields, particles, crystals, grids, et al. are only special structures belonging to mathematical equivalence classes and categories.
The question arises whether the physical universe is finite with only finitely many mathematical structures or at least computable with computable functions and functionals. What about the natural constants, which determine fundamental forces of the universe? Mathematically, they are often real numbers with infinitely many decimal places, but practically, only finitely many decimal places are determined by our best measuring instruments and computers.
From a mathematical point of view, physical events are points of a four-dimensional structure of space-time. For example, in special relativity, the four-dimensional structure of space-time is definied by Minkowskian geometry, which is sometimes called block universe. The concept of a block universe can be generalized for the geometrical structure of general relativity. A block universe is a mathematical structure that never changes, which was never created, and which will be never destroyed. In a block universe, space-time is a four dimensional mathematical space with the three usual spatial dimension of length, width, and height, and the fourth dimension of time [
13].
Human intuition of space is restricted to three dimensions. In the three-dimensional space of length, width, and height, the orbit of the moon round the Earth can be illustrated by an (approximated) circle. In this geometrical representation, time-dependence can only be considered by the motion of the moon round the Earth. In order to illustrate the dimension of time, the four-dimensional space-time is reduced to the vertical time axis and two spatial coordinates. In this case, the circle is replaced by a spiral along the time axis. Actually, there is no change and motion of the moon, but only the unchangeable spiral in the space-time of a block universe.
In a three-dimensional illustration, space-time is distinguished in parallel layers of two-dimensional planes each of which represents the three-dimensional space at this moment with all simultaneous events. If an observer belongs to one of these layers, then this layer represents his present time. The layers above his present layer are his future, and below the layer, there is his past. Anyway, the distinction of future, present, and past is relative to an observer or, in the words of Einstein, a “subjective illusion”. From a physical point of view, there is no time-depending change, but only the mathematical structure of space-time with given unchangeable patterns (e.g., spiral of the moving moon).
The mathematical structure of four-dimensional space-time differs in special and general physics [
14]. In special relativity, space-time is not Euclidean like in classical physics, but Minkowskian, with respect to relativistic simultaneity. In general relativity, we have to consider a four-dimensional pseudo-Riemannian manifold of curved space-time. A curved (non-Euclidean) Riemannian manifold (e.g., the curved surface of a sphere) consists of infinitesimally small Euclidean planes. In an analogy to Euclidean geometry, Minkowskian geometry of special relativity is embedded as local space-time into the global general relativity of curved space-time.
If Einstein’s relativistic space-time is combined with quantum physics, the deterministic world is given up. In quantum field physics, we must consider possible worlds with different pasts, presents, and futures which are weighted by probabilities. The path of a quantum system (e.g., elementary particle) from one point to another cannot be determined by an orbit, like a ball in classical mechanics. We have to consider all possible paths with their weights, which are summed up in Feynman’s path integral. Therefore, the initial tiny quantum system of the early universe in the size of Planck’s constant could not develop in a classically well determined way. There are several possible paths of development according to the quantum laws. If we assume that all these possibilities are real in parallel, then we get the concept of a multiverse with quantum parallel universes [
15]. We cannot get observational data from these parallel worlds, because they are separated from our world by different ways of inflation, which blow up the universes in different ways. Nevertheless, they can be mathematically modeled by the laws of quantum physics.
In all these cases, there are given mathematical structures [
16]. The development of a quantum system is mathematically given by a pattern in quantum space-time (like the moving moon as a spiral in the Euclidean space-time). An organism, like our body, consists of a bundle of world lines representing the development of elementary particles, which are organized as atoms, molecules, cells, organs, et al. They converge during our growth as babies, develop during the period as adults in different ways (e.g., changing by diseases), but diverge again after our death [
17] (p. 409). Thus, the human body is a complex pattern of converging and diverging word lines in space-time. From a mathematical point of view, the pattern of our body is part of a given and unchangeable mathematical structure of space-time. It is a solution of a mathematical equation characterizing this mathematical structure. Only as living bodies do we have the “illusion” of change and development with birth and death. Thus, in terms of ancient natural philosophy, the unchangeable mathematical structure of the universe brings Parmenides’ world to the point.
Are these space-time structures continuous or discrete? In classical mechanics, fluids and materials are considered as dynamical systems, which are modeled by continuous differential equations. In electrodynamics, each point in magnetic and electric fields is characterized by real numbers of orientation, voltage, et al. Maxwell’s equations describe their continuous time-depending development. In quantum physics, classical electrodynamics is replaced by quantum field theory as the foundation of modern particle physics. The quantum wave function provides the probability of a particle in a certain area of space-time. Mathematically, the wave function is an abstract point in the Hilbert space, which is an (infinite) mathematical structure. In analogy to fields of photons (light) in quantum electrodynamics, we can also consider quantum field theories of all the other known elementary particles. There are electronic fields, quark fields, et al.
However, we still miss a complete “Theory of everything” unifying all fundamental forces and their interacting particles in relativistic and quantum physics. The main obstacle stone is the continuous and deterministic structure of relativistic physics contrary to the discrete and probabilistic character of quantum physics. The physical structure of a complete “Theory of everything” would be isomorphic to some mathematical structure, which would contain all information of the universe. In that sense, the universe would be completely founded in that mathematical structure. The physical universe would even be equal to this particular mathematical structure up to equivalence and isomorphism.
However, does mathematical infinity have a physical reality? Is the infinitesimally small in the continuum physically real? Fundamental equations of quantum physics (e.g., Schrödinger equation) are continuous differential equations. A quantum system is defined by a Hilbert space, which is an infinite mathematical object. Dirac’s delta function is a generalized function (distribution) on the real continuum that is zero everywhere except at zero, with an integral of one over the entire continuum. It is illustrated as a graph, which is an infinitely high, infinitely thin spike at the origin, with total area one under the spike. Physically, it is assumed to represent the density of an idealized point mass or point charge. There are natural constants, which are real numbers with infinitely many decimal places, but approximately measurable in finite steps. According to Emmy Noether, fundamental conservation laws of physics correspond to continuous symmetries of space-time. For example, the conservation of energy is equivalent to the translation symmetry of time, conservation of momentum to translation symmetry of space, conservation of angular momentum to rotational symmetry, et al. [
2] (Chapter 3.3), [
18] (Chapter 5).
Is the continuum with real numbers only a convenient approximation to compute the coarse molecular and atomic world of fluids, materials, and fields with elegant continuous procedures? Actually, the continuum is not only used in classical physics, but also in the quantum world. In quantum field theory, we use quantum fields with discrete computable solutions of crystal grids and emergent particles. Continuous space-time of the universe is assumed to become discrete in the Planck-scaling of elementary particles (quantum foam). Information flow in dynamical systems is measured by discretization in bit sequences (e.g., Poincaré cuts in [
7] (p. 313, Figure 30)), the complexity of which can be measured by their shortest algorithmic description as computer program [
7] (Chapter 13).
4. Is the Universe Computable?
Finite material structures in nature are isomorphic to equivalent finite mathematical structures (e.g., molecular crystals correspond to geometrical grids with group-theoretical symmetries), which can be uniquely encoded by natural numbers. Finite code numbers can be enumerated according to their size. Thus, in principle, all finite structures of the universe can be enumerated. Computable structures can be represented by Turing machines, which uniquely correspond to machine numbers as encoding numbers of a Turing program. Thus, all computable structures of the universe can also be enumerated.
In physics, infinite structures (e.g., space-time, fields, wave functions, Hilbert spaces) are practically handled by software programs (e.g., Wolfram’s MATHEMATICA), which can compute arbitrarily large numbers [
19]. Thus, infinite structures are approximated by finite structures, which can be processed by computers. However, do we actually need the continuum and infinity beyond Turing complexity in physics? Natural laws are mathematical equations. How far can they be represented in computers? The states in classical computers and quantum computers are discrete (bits resp. quantum bits). However, in order to model their dynamics, we need continuous mathematical concepts (e.g., Schrödinger equation as a continuous differential equation in quantum physics). Therefore, the epistemic question arises: Are these continuous concepts only convenient mathematical tools invented by the human mind to manage digital data or are they ontologically real.
In mathematical proof theory, we can determine degrees of constructivity and computation: How far can mathematical theorems be proved by constructive methods, like calculation in arithmetics? Since Euclid (Mid-4th century—Mid 3rd century BA), mathematicians have used axioms to deduce theorems. However, the “forward” procedure from axioms to theorems is not always obvious. How can we find appropriate axioms for a proof starting with a given theorem in a “backward” (reverse) procedure?
Pappos of Alexandria (290–350 AD) understood the “forward” procedure as “synthesis” (Greek for the Latin word “constructio” or English translation “construction”), because, in Euclid’s geometry, logical deductions from axioms to theorems are connected with geometric constructions of corresponding figures [
20]. The reverse search procedure of axioms for a given theorem was called “analysis”, which decomposes a theorem in its sufficient conditions and the corresponding geometric figures in their elementary building blocks (e.g., circle and straight line) [
21,
22].
In modern proof theory, reverse mathematics is a research program to determine the minimal axiomatic system required to prove theorems [
23]. In general, it is not possible to start from a theorem,
, to prove a whole axiomatic subsystem,
. A weak base theory,
, is required to supplement
:
If can prove , this proof is called a reversal. If proves and is a reversal, then and are said to be equivalent over .
Reverse mathematics enable us to determine the proof-theoretic strength resp. complexity of theorems by classifying them with respect to equivalent theorems and proofs. Many theorems of classical mathematics can be classified by subsystems of second-order arithmetic,
, with variables of natural numbers and variables of sets of natural numbers [
24,
25]. In short: In reverse mathematics [
26], we prove the equivalence of mathematical theorems (e.g., Bolzano-Weierstrass theorem in real analysis) with subclasses of arithmetic,
, of second order. Therefore, we could extend constructive reverse mathematics to physics and try to embed the equations of natural laws into subclasses of arithmetic
of second order. Are there constructive principles of
, which are equivalent to the equations of natural laws (e.g., Newton’s 2nd law of mechanics, Schrödinger’s equation)?
Most natural laws, which are mathematically formulated in real (or complex) analysis, can be reduced to the axiom of arithmetical comprehension in constructive analysis [
7] (Chapter 8). In general, no physical experiment is known that depends on the complete real continuum with non-computable real numbers. In this case, the universe would consist of constructive mathematical structures, which are classified in a hierarchy according to their degrees of constructivity. Only an extreme Platonism would believe that all mathematical structures are existent with the subclass of those structures that are isomorphic to physical structures of the universe. This ontological position cannot be excluded in principle. However, in the sense of Ockham’s razor, it makes highly abstract assumptions, which are not necessary for solving physical problems and which can be avoided by constructive concepts. Modern physical research with its huge amount of data (e.g., high energy and particle physics of accelerators) strongly depends on algorithms and software, which must detect correlations and patterns of data.
If quantum physics is assumed as a general theoretical framework, then nature with Planck’s length must be discrete. Nevertheless, quantum physicists use infinite and continuous concepts of real and complex numbers in their theories. The standard model of particle physics refers to 32 parameters with real constants. An example is the fine-structure constant, 1/ 137.0359 … Only finitely many decimal places are known with respect to contemporary capacities of measurement. From a strictly digital point of view, all infinitely many decimal places had to be input into a computer step by step for computing with real numbers, which is impossible. However, theoretical physicists compute with these parameters as “whole” quantities with algebraic representations, e.g., with , elementary charge, and Planck charge.
5. Computational Complexity of the Universe
In real computing (with real numbers), the physical question is still open whether real constants (e.g., the fine-structure constant, ) or Dirac’s function correspond to physically “real” entities. Otherwise, they are only approximate terms of a mathematical model. If there are non-computable real numbers (as natural constants of physical theories)), which:
- -
Definitely cannot be reduced to constructive procedures; and
- -
definitely influence physical experiments,
then, the unbelievable happens: Non-computable real numbers would not only be an invention of the human mind, but a physical reality. According to Hilbert’s classical criterion, the existence of a mathematical object is guaranteed by its consistency in an axiomatic system. However, in constructive mathematics, we need an effective procedure to construct an object and to prove the existential statement. Further on, in physics, the object must be measurable in an experiment or observation (at least approximately exact).
The discovery of non-computable objects in physics would be as surprising as the discovery of incommensurable relations in Antiquity. The Pythagoreans were not only horrified by the discovery of incommensurable mathematical relations [
27]. In Antiquity, Euclidean geometry was ontologically identified with really existing objects and relations. Therefore, incommensurability was historically understood as a loss of harmony and rational proportionality in the real world. However, incommensurable relations in Antiquity correspond to irrational numbers, which are computable like, e.g.,
. Non-computability in nature would be more dramatic. Turing introduced so-called “oracles” to denote concepts that are not known to be computable or not. They are the blind spots in the area of computability. In this case, there would be not only Black Holes in the universe (which are computable in quantum physics), but blind spots of computability or “computational oracles”.
Obviously, there are practical limits of computation depending on the technical limitations of computers. There are also limitations depending on certain methods of problem solving: For example, Poincaré’s many bodies problem is not solvable by standard solutions of integration. However, in principle, there is a mathematical solution with an infinite process of convergence. Further on, it is still an open question how far the highly nonlinear Navier-Stokes equations of turbulence are mathematically solvable. Until now, only special solutions under restricted constraints are provable [
28]. In this context, we focus on the physical meaning of real numbers. Can we restrict their meaning to the constructive procedure of measuring in finite steps or do we need the whole information of an infinite object mathematically defined by the axiomatic system of real numbers?
Since the beginning of modern physics, physicists and philosophers were fascinated by the mathematical simplicity and elegance of natural laws [
5] (Chapter 1). For example, the standard model is reduced to the symmetry group, SU(3) × SU(2) × U(1). Therefore, it is often argued that physics is finally founded in mathematical symmetries, which remind us of the old Platonic idea of regular bodies as building blocks of the universe [
2,
18,
29]. Natural laws formalize regularities and correlations of physical quantities. In a huge amount of observational data, laws provide a shorter description of the world.
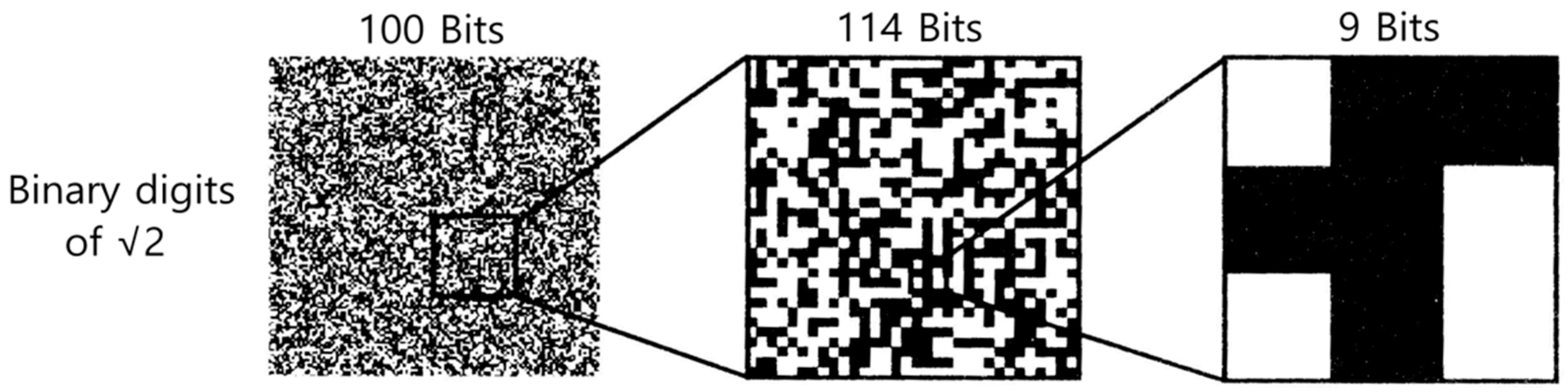
Algorithmic information of data is defined as the bit length of their shortest description [
30]. In this sense, natural laws are a shorter description of data patterns. In order to illustrate the relation of simple laws and complex data, we consider a mathematical example in
Figure 1 [
17] (p. 491): The left pattern is very complex and represents the decimal places of
as binary numbers of 0 and 1, which are illustrated by white and black squares. It is assumed (but still not rigorously proved) that the decimal places of
behave like random numbers with all kind of patterns. Nevertheless, there is a finite computer program to compute
, which only needs circa 100 bits. This computer program corresponds to a short (computable) law, which covers an unlimited huge amount of data. The description of the middle partial pattern in
Figure 1 is even more complex than the whole left pattern, because it needs 14 additional bits to locate the beginning bits of the partial pattern in the whole pattern. The right pattern only needs nine bits. There would be no advantage to locate this pattern by additional bits in the whole distribution.
These examples illustrate that general laws may be short and simple to describe the whole universe. However, special conditions and individual situations may be more complex, because we need additional information to locate them in the distribution of the whole. In relativistic and quantum physics, individual entities from atoms and molecules up to organisms are represented by more or less complex patterns of world lines in space-time. Thus, in the whole distribution of patterns, individual parts must be located, which needs additional information: Therefore, the description of individual life and persons may be more complex than the general laws of life and even the whole universe!
In order to predict future events, we do not only need laws, but also initial conditions. Sometimes, initial conditions seem to be randomly contrary to regular laws. However, from a universal point of view, initial conditions are not random. They must be located in the whole data pattern of the universe and need more information (bits). In this case, the algorithmic information of initial conditions and individual events is larger than the algorithmic length of the applied laws.
6. Conclusions
In natural philosophy, the traditional dispute on the discrete or the continuum has a long tradition since Antiquity [
31,
32,
33]. In modern quantum physics, the discrete structure of matter is explained by quantum systems with Planck length. In modern computer science, the discrete and the continuum are defined by digital and analog concepts. In digital physics, digital computing is related to discrete quantum systems. Thus, the question arises whether nature can be considered a huge quantum computer. Is nature computable? The article argues that we have to distinguish degrees of complexity and computability, which are well-defined in mathematics (e.g., reverse mathematics) and computer science (e.g., complexity theory).
Mathematical theories of nature are isomorphic to mathematical structures of different degrees and, by that, embedded in the categorical framework of mathematics. The ontological question is still open whether the categorical framework of mathematics is a creation of the human mind or has real existence independent of the human mind. In a naturalistic sense, one can argue that mathematical thinking is made possible by human brains, which have developed in the biological evolution on Earth. Following this line, mathematical concepts are only human inventions, like all human tools, which have been constructed to solve problems.
During history, humans invented different concepts to define and formulate the same mathematical structures: E.g., the Greeks used geometrical proportions to define “rational” and “irrational” numbers. In modern times, geometrical proportions were replaced by numeric representations as an expansion of decimal numbers and binary bits for computation by computers.
A well-known example is the definition of the number, , which is independent of its representation as a geometrical proportion of the circumference and diameter of a circle or as an expansion of decimal or binary numbers. In any way, even intelligent aliens on exoplanets may have some concept of this crucial number of our universe, but perhaps in a completely different and still unknown representation. The development of their mathematical thinking will depend on the special evolution of their “brains” on their planets. However, in the end, the truth of proofs and theorems is invariant and independent of brains and psychology. Humans and these aliens may have the intellectual capacity to understand the structure of their universe. However, these structures and laws have governed the cosmic expansion and biological evolution long before our brains emerged. Thus, they are independent of our mind and brain and made them possible.
In some cases, invariant mathematical structures represent physical reality. However, in most cases, mathematical structures do not represent physical realities. Nevertheless, these topological and algebraic structures have a rigorously defined existence. The distinguished character of mathematics is its universality. Therefore, the ontological question is still open whether continuous concepts of mathematics are only convenient abstractions of the human mind or rooted in a deeper layer of mathematical existence “below” the discrete nature of the quantum world. From an epistemic point of view, constructive models of nature are preferred, because they avoid a waste of ontological assumptions in the sense of Ockham’s razor. Anyway, the debate on the discrete and the continuum of nature illustrates that the ancient problems of natural philosophy are still alive and that modern physics continues natural philosophy with the new methods of mathematics, measuring, and computing.