Abstract
The concept of an operator is used in a variety of practical and theoretical areas. Operators, as both conceptual and physical entities, are found throughout the world as subsystems in nature, the human mind, and the manmade world. Operators, and what they operate, i.e., their substrates, targets, or operands, have a wide variety of forms, functions, and properties. Operators have explicit philosophical significance. On the one hand, they represent important ontological issues of reality. On the other hand, epistemological operators form the basic mechanism of cognition. At the same time, there is no unified theory of the nature and functions of operators. In this work, we elaborate a detailed analysis of operators, which range from the most abstract formal structures and symbols in mathematics and logic to real entities, human and machine, and are responsible for effecting changes at both the individual and collective human levels. Our goal is to find what is common in physical objects called operators and abstract mathematical structures, with the name operator providing foundations for building a unified but flexible theory of operators. The paper concludes with some reflections on functionalism and other philosophical aspects of the ‘operation’ of operators.
Keywords:
function; information; logic; mathematics; ontology; epistemology; nature; operator; science; society; system; theory 1. Introduction: Operators and Change
Human cognition is based on creation of concepts that reflect studied phenomena. However, in this process, many important concepts in philosophy and science have proven extremely resistant to systematic explanation and exact definition. Examples are change, consciousness, information and intelligence. At the same time, an improved understanding of these concepts is of increasing importance for building a more satisfactory theory of individual and collective behavior, ultimately aimed at an efficient support of responsible attitudes toward economic growth and sustainable environment. Some of the problems with the above concepts can be addressed using process methodology or the interactivist approach [1]. A theory of information that emphasizes both qualitative and quantitative properties of information and provides efficient means for solving problems of the contemporary Information Society has been recently created [2]. Conceptual understanding is additionally provided by the research focused on the inter- or trans-disciplinary aspects of these concepts [3], as well as on the combination of concepts from neuro-science and philosophy [4].
An additional general notion that has received little rigorous attention, and yet has implications throughout the whole reality is that of an operator. To our knowledge, no comparative study of operators and their substrates or operands in different areas, “from minds to machines”, has been made. Compartmentalized formalized concept definitions of operators are used in mathematics, logic, programming languages, and linguistics, while in everyday language, informal notions refer to familiar activities in the domains of machines, medicine, organizations and social activity.
However, the broad intermediate domain of non-mathematical real phenomena in which a causal impact is exerted by a person or entity that performs an operation and is, accordingly, an operator deserves a comprehensive unified theory. In this paper, we develop in some detail the notion of such “natural” operators. We position them as the proximal causes of the real change in a framework that includes the well-accepted symbolic operators of mathematics and physics and show the interrelationships abound in nature, mind and human organization and artifacts.
The major objective of this paper is, accordingly, to provide a comprehensive classification and discussion of natural operators and operations in several practical and theoretical areas of current interest, including a new kind of logic called Logic in Reality [5]. This logic is an extension of logic from its standard linguistic domain to real, complex processes and natural operators are themselves considered as active processes involved in effecting change at biological and cognitive levels of reality. Our grounding of their properties in physics, as well as our conceptualization of the self-operation of human beings and their organizations, further supports the utility and roles of natural operators in general and their usefulness for information technology in particular. We further propose that the natural-social operator split provides a key criterion for determining what entities may be considered autonomous, morally responsible agents and thus, contributing to a solution of the principal-agent problem (agency dilemma), which is urgent for political science, sociology and economics. We develop detailed consideration of the critical relations between the concepts of operators and those of self-organization in humans. This leads naturally to the point that if the hermeneutics of philosophy also depend on real, cognitive processes, operators ipso facto need to be considered in a philosophical role as well.
Operators definitely have explicit philosophical significance. On the one hand, they represent important ontological issues of reality reflecting its dynamical nature when some objects act on other objects. Our universe exists in interaction of its components and elements, while interaction can be decomposed of separate actions involving the structure of an operator. On the other hand, epistemological operators form the basic mechanism of cognition. Many cognitive processes, such as search, selection or recognition, are performed by physical operators, which can be natural or artificial and are represented by abstract operators decomposable into simpler operators. In this context, any scientist, measuring device or computer is a physical operator.
Contents of the Paper
The next Section 2 contains basic definitions of operators, specifying basic classes of operators and their properties and providing a conceptual framework for the other parts of this study.
Section 3 defines and analyzes natural operators, including information as a natural operator and the natural operators of logic in reality, explicating their relations to epistemology, causality, and the philosophy of mind. It is important to understand that information, as an operator, acts both in the mind, which is a repository and processor of information, and in machines, especially highly organized machines, such as computers.
In Section 4, we further study mind and knowing, defining the psyche as a natural operator with special attention to the complex set of operators that comprise different kinds of self-operation, such as self-organization, self-regulation and self-management. In the last sub-section of Section 4, we study knowledge as a natural operator.
Section 5 discusses the nature and role of operators in technology so that the differences, important for a complete theory, with natural operators are explicitly stated.
Section 6 discusses human operators and their intentionality paying critical attention to the on-going debate on the nature of agents vs. operators, suggesting possible new interpretations and approaches. Prospective work is suggested in both theoretical and practical directions in the areas of symbolic operators.
Our concluding Section 7 provides a brief discussion of operators from a perspective of the philosophy of science.
2. Basic Definitions and Classifications: Function and Type of Operators
The absence of a comprehensive discussion of operators has been due in part to the complexity of their differences in kind. The categorization we propose takes into account most if not all types of different operators, starting from a basic Definition 1, which identifies the most general concept of an operator. It allows us to categorize all existing operators by their essential characteristics.
Definition 1.
An operator is an object (system) that operates, i.e., performs operations on, some object, system or process.
Definition 2.
An operand is an object, system or process operated by an operator.
These definitions show that being an operator or an operand is a role and a characteristic of a system. One and the same system/object can be an operator in some situations and an operand in other situations, and an operator with respect to some systems and not an operator with respect to other systems. All operators are systems, but not all systems are operators since subsequent to their formation, some may exist in substantial isolation from their environment to all intents and purposes.
Definitions 1 and 2 express the fundamental dyadic relation between operators and their operands, which is actualized in the form of the operator triad:
This diagram demonstrates that an operation is a component of an operator. In addition to operations, operators have instructions and/or material tools for performing operations. This peculiarity was discovered by programmers. They found that when they want computers to execute some operation, it is necessary to create a symbolic operator, which provided computer realization of the given operation. As a result, for example, all logical operations were transformed into logical operators. For instance, AND operator is a Boolean operator that returns a value of TRUE if both its operands are TRUE, and FALSE otherwise. The difference between an operator and an operation or a function is that the operator acts, while the function/operation is realized or performed.
Symbolic and natural operators function in a variety of areas: linguistic operators operate on languages; topological operators operate in and on topological spaces; standard logical operators operate in standard logic; network operators operate in networks; program operators operate on data processed by computers and other information processing systems; bus and plane operators operate buses and planes respectively, and so on.
To put some order into this diversity of operators, we have developed the following framework of operator classifications. On the first level of this framework, operators are primarily classified by three basic parameters: form, operational medium and target.
The form-oriented classification:
Definition 3.
A symbolic operator is an operator that has a symbolic form.
Definition 4.
A material operator is an operator that has a material form.
Definition 5.
A mental operator is an operator that is a part (element) of mentality.
The medium-oriented classification:
Definition 6.
A social operator is an operator that works (functions) in society.
Definition 7.
A nature operator is an operator that works (functions) in nature.
Definition 8.
A technology operator is an operator that works (functions) in an artificial world created by people, which includes technology and has been created by technology.
The target-oriented classification:
Definition 9.
A socialized operator is an operator that works with/on social structures.
Definition 10.
A symbolized operator is an operator that works with/on symbols (symbolic structures).
Definition 11.
A naturalized operator is an operator that works/on with natural objects (systems).
Note that it is possible that an operator has different medium and target types. For instance, a social operator can and often does work with symbols, e.g., a writer, and thus, is a symbolized operator. Software systems are technology operators, which work with symbols and thus, are also symbolized operators. Besides, the same system, e.g., an individual, can work in society as well as in nature and machines. This means that this system acquires the roles of a social and nature operator.
At a second level of classification, the basic parameters are dynamics, origin (emergence), and function.
The dynamic classification:
Definition 12.
A system operator is a system that has both a static and dynamic structures or/and operates systems.
Definition 13.
A function operator is a function and/or an operator that operates functions.
Definition 14.
A process operator is a process and/or an operator that operates processes.
The existential classification:
Definition 15.
A natural operator is a natural object, i.e., an object that emerged in nature and functions as an operator.
Definition 16.
An artificial operator is an artificial object, i.e., an object that is created by people or other living beings and functions as an operator.
Definition 17.
A hybrid operator is partially natural and partially artificial.
The relation between a natural operator and a nature operator, Definition 7, is complex and requires further study.
The function-oriented classification:
Definition 18.
A cognitive operator is an operator the goal of which is knowledge acquisition.
Definition 19.
A search operator is an operator the goal of which is finding some object or information.
Definition 20.
A construction operator is an operator the goal of which is building some system.
Note that these categories are not independent. In fact, their key categorial feature is their Non-Separability, for which LIR provides a logical basis.
For a study of mental and machine operators, it is practical to take into account a number of important quantitative and qualitative properties of operators in addition to their basic classifications. The set of properties considered here is not intended to provide a complete scientific description of operators, but to serve to highlight general principles applicable to the entire category of operators.
For convenience, we have separated considered properties into three essentially philosophical categories, as follows:
- Intrinsic Properties
- -
- Complexity reflects how much resources are required
- -
- Power reflects what the operator can do
- -
- Capabilities reflect what means of actions are accessible (used) by the operator
- Relational Properties
- -
- Relation to the operated system (operand)
- -
- Attitude to the operated system (for human operators)
- -
- Conditions and Restrictions on operation of the operator
- Pragmatic Properties
- -
- Tentative (theoretical) costs of operation (individual human cost, moral cost and reputation cost)
- -
- Actual results (benefits, profit) from operation
- -
- Productivity reflects how well the operator functions
This overall approach establishes that operators are characterized by their single or multiple classificatory definitions and their properties. For example, human beings are material, natural, naturalized and socialized operators. When reference is made to one of these definitions in the text, it will be in the bold italicized font, as here. The indicated intrinsic, relational and pragmatic properties and its relevant disciplinary methodology further characterize operators. In the remainder of this paper, however, we have limited the discussion of the sets of properties to a few key examples.
3. Natural Operators
3.1. The Ubiquity of Natural Operators
The original concept of an operator, such as the differential operators d/dx, ∂/∂x, ∂/∂y, and ∂/∂z, Laplacian L, and Hamiltonian H, has been one of the most efficient and developed tools of theoretical physics. Even the basic arithmetic operations, such as + and −, are also operators as it has become clear with the advent of computer programming. Such symbolic, mostly mathematical, operators are natural operators that are studied by physics and describe physical concepts, reflecting their properties. For instance, mathematical operators are used as models of the term observable, which has become the standard concept in quantum mechanics as the counterpart of the term physical quantity or measurable quantity in classical physics. This term originated from the term observable quantity (beobachtbare Grösse) defined by Heisenberg in his groundbreaking work on matrix mechanics [6]. His goal was to specify physical quantities by means of an operational definition. As a result, in contemporary quantum mechanics, the observables of a physical system are represented by self-adjoint operators acting in the Hilbert space H associated with the system. In general, operators play a fundamental role in physics. For instance, the physics of quantum mechanics was reduced to the mathematics of operators on Hilbert spaces [7,8].
In general, an observable is a physical object or a property of such an object that some system (in a more restricted sense, people) can observe and/or measure. Thus, in the later development of quantum theory, several authors suggested the generalized representation of observables as positive operator measures [9,10,11]). This concept advanced the mathematical coherence and conceptual clarity at first of quantum mechanics and then of quantum field theory. From physics, mathematical operators were extended to quantum chemistry where they also have been successfully used to model different processes.
However, taking the Definition 15 of a natural operator (cf. Section 2), we see that the entire real world is full of operators. In essence, any physical or biological object or system that interacts with and impacts other physical and/or biological objects or systems is a natural operator. Indeed, all systems in nature interact with their environment, but our operator approach enables the characteristics of the interaction to appear more formally. Thus, a system A, which interacts with a system B, as a rule, has some impact on the system B—either the state of B is changed or functioning/behavior of B is changed or the whole system B is changed. Consequently, according to Definition 1, the system A is a natural operator, while according to Definition 2, the system B is a natural operand. The multitude of natural operators is studied by natural sciences. As a result, natural sciences could be called a study of operators!
3.2. Information as a Natural Operator
In the General Theory of Information [2] information is characterized by a system of principles and the General Transformation Principle 2, describes the essence of information in a broad sense as the potential (capacity) of things, both material and abstract, to cause changes (transform) other things. When this capacity (potential) is actualized, it becomes a nature or technology operator (cf. Definitions 7 and 8), which acts on different systems. Thus, it is reasonable to distinguish potentialized and actualized components of information, whose evolution follows the pattern of Logic in Reality, as discussed in Section 3.3.
It is necessary to stress that information, as an operator, acts both in the mind, which is a repository and processor of information, and in machines, especially highly organized machines, such as computers. Some of the further aspects of information that justify its designation as a natural operator emerge from theories that give a fundamental role to information in existence. For instance, Scarrott [12] asserts that every living organism, its vital organs and its cells are organized systems bonded by information, which operates organisms, organs and cells. In a similar way, Reading [13] writes, “one of the main impediments to understanding the concept of information is that the term is used to describe a number of disparate things, including a property of organized matter …” He considers energy and information as the two fundamental causal agents, i.e., natural operators, acting in the natural world.
Information plays an important role in evolution, as in the elegant theory of evolution developed by Csanyi [14] and Kampis [15]. Burgin and Simon [16] also demonstrated that information has been and is the currently prevailing force for evolution both in nature and society. Smith and Szathmary [17] discuss evolutionary progress in terms of radical improvements in the representation of biological information. All these processes are initiated and controlled by information as a natural operator. More recently, Deacon [18] has developed a theory of dynamic levels of complex processes that ties together both evolution and information by the concept of absence.
The issue of the ‘physicality’ of information is the subject of intensive on-going debate (information as a “physical essence”). Crutchfield [19] treats information as “the primary physical entity from which probabilities can be derived”. Landauer [20] stresses, information is inevitably physical. However, it is more reasonable not to claim that information itself is a physical essence but to suggest that people observe information only when it has a physical representation. Thus, all information in social organization and communities requires some physical form for its content to be transmitted.
Information exists in the form of portions of information. Informally, a portion of information is or can be considered (treated) as a separate entity. For instance, information in a word, in a sentence or in a book is a portion of information. Each such portion is an operator in its own right. Thus, we can conclude with Kaye [21]:
“Information is not merely a necessary adjunct to personal, social and organizational functioning, a body of facts and knowledge to be applied to solutions of problems or to support actions. Rather it is a central and defining characteristic of all life forms, manifested in genetic transfer, in stimulus response mechanisms, in the communication of signals and messages and, in the case of humans, in the intelligent acquisition of understanding and wisdom”.
In other words, natural information operators are pervasive in all complex systems.
We now come to another portrayal of natural operators, including informational ones, that emerges from the extension of formal logic to real systems made by Brenner [5]. According to this approach, the discussion of operators moves from the primarily theoretical domain toward the operational characteristics of the human mind.
One of the well-known examples of a natural operator is DNA, which stores genetic information in the linear sequence of nucleotides in DNA (deoxyribonucleic acid) and written as text in the alphabet of three base pair sequences (tri-nucleotides) called codons, while the genome is the entirety of an organism’s hereditary information [22]. Usually, the term genome means genetic information stored on a complete set of nuclear DNA. Sometimes this term is also applied to genetic information stored within DNA of organelles. To discern these cases biologists use such terms as the nuclear genome, mitochondrial genome and chloroplast genome. DNA of the human genome is arranged into 24 distinct chromosomes—physically separate molecules. Each chromosome contains many genes, the basic physical and functional units of heredity. Genes are specific sequences of bases that encode instructions on how to make proteins. Thus, genomes are examples of information as natural operators.
In his book “The Touchstone of Life” [23], Loewenstein persuasively demonstrates that information is the foundation of life. To do this, he gives his own definition of information, the conventional definition of Hartley-Shannon information theory being inapplicable. According to Loewenstein, information, in its connotation in physics, is a measure of order—a universal measure applicable to any structure or system. It quantifies the instructions that are needed to produce a certain organization. “The pivotal role of DNA for all living beings made it clear that life as a phenomenon is based on biological structures and information they contain. Information encoded in DNA molecules controls the creation of complex informational carriers such as protein molecules, cells, organs, and complete organisms.” As a result, genetic information plays the role of an operator for protein molecules, cells, organs, and complete organisms.
Another important example a natural operator is energy, which is information in a broad sense [2]. According to Smolin [24], the three-dimensional energetic world is the flow of information. In a similar way Stonier [25] asserts, structural and kinetic information is an intrinsic component of the universe, independently of whether any form of intelligence can perceive it or not. Reflecting this approach, Bekenstein [26] asserts that there is a growing trend in physics to define the physical world as being made of information itself. From this point of view, natural information operators are present in all natural systems. Even more radical point of view is expressed by Wheeler [27], who claims that every item of the physical world is information-theoretic in origin. In this view, all such information is composed of a multitude of information operators, e.g., information in an instruction is an information operator, a system or function operator (Definitions 12 or 13). Brenner [28], however, points out that views such as those of Wheeler and Bekenstein can lead to some misunderstandings about the correct ontological relation of priority between information and matter-energy. Usually it is supposed the latter being primitive in contrast to the former. However, the unified approach of the General Theory of Information explains that both phenomena are primitive but belong to the different spheres of reality [2]. Namely, matter-energy belongs to the ordinary physical world, while information dwells in the cognitive structural reality, whose instantiation in matter-energy, while real, is secondary to its functionality [29].
We know that the common usage of the word information does not imply such wide generalizations as the Ontological Principle 2 does. Thus, we need a more restricted theoretical meaning because an adequate theory, whether of information or of anything else, should correspond to our commonsense notions of its content. This brings us to the idea of proper information, which is formalized by the Ontological Principle 2a in the General Theory of Information [2].
3.3. The Natural Process Operators of Logic in Reality (LIR)
Logic is often defined as the theory of correct reasoning, where logic is understood as classical bivalent propositional and predicate logics or their modern multivalent, fuzzy, epistemic, temporal, modal, deontic or intuitionist versions [30]. Such logics are neither intended to describe nor have the capability of describing reality in nature or society. The applicability of logic and its symbolic operators and operations has been limited to language and mathematics. This is, however, based on a discretionary metalogical principle introduced by the scholastic followers of Aristotle and maintained by the linguistic turn of the 19th–20th centuries.
Writing (in French) in the middle of the last century, the Franco-Romanian philosopher Stéphane Lupasco (Bucharest, 1900–Paris, 1988) challenged the monolithic propositional, truth-functional character of logic and proposed an extension of logic to real process phenomena, based on the perceived dualities of matter-energy. In this new (old) way of “doing” logic, Lupasco essentially carried out a metalogical rejunction of logic with its original function as natural science [31]. Based on this work of Lupasco, Brenner [5] developed Logic in Reality (LIR), which is grounded in a particle/field view of the universe. At the same time, axioms and rules from LIR provide a framework for analyzing and explaining real world entities and processes, including information, at biological, cognitive and social levels of reality or complexity.
Details of LIR are provided in elsewhere (cf. [5,32]). Stated in a compressed form, the most important concepts of LIR are:
- (1)
- every real complex process is accompanied, logically and functionally, by its opposite or contradiction, but only in the sense that when one element is (predominantly) present or actualized, the other is (predominantly) absent or potentialized, alternately and reciprocally, without either ever going to zero (the Axioms of Conditional Contradiction and Asymptoticity);
- (2)
- the emergence of a new entity at a higher level of reality or complexity can take place at the point of equilibrium or maximum interaction or “counter-action” between the two (the Axiom of the Included Middle).
Together, these contradictional relations will be referred to as the Principle of Dynamic Opposition (PDO) of LIR . It can be roughly visualized in Figure 1 and Figure 2.
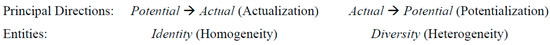
Figure 1.
Process change: LIR non-contradiction.
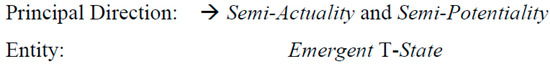
Figure 2.
Process change: LIR contradiction (counteraction).
These figures show the relationship between LIR and the fundamental triads (named sets) that represent processes of change [33]: processes can move in three directions, two toward non-contradiction as their LIR identity or diversity increases and one toward (maximum) non-linguistic contradiction, a T-state from which a new entity can emerge. All of these are considered aspects of the logic in reality. (In standard logic, of course, the contradiction at the point of semi-actuality and semi-potentiality simply invalidates a proposition.) Unlike the Hegelian triad of thesis, antithesis and synthesis, terms in which represent diachronic processes and form three fundamental triads, the LIR changes can be synchronic, with the initial elements and the emergent ones present at the same time, having different degrees of actuality and potentiality.
A major component of LIR is its categorial ontology in which the sole material category is Energy, and the most important formal category is Dynamic Opposition. From the LIR metaphysical standpoint, for real systems or phenomena or processes in which real dualities are instantiated, their terms are not separated or separable! Real complex phenomena display a contradictory relation to or interaction between themselves and their opposites or contradictions. On the other hand, there are many phenomena in which such interactions are not present, and they, and the simple changes in which they are involved can be described by classical, binary logic or its modern versions.
Therefore, LIR approaches in a new way the unavoidable cognitive problems that emerge from the classical philosophical dichotomies, such as appearance and reality, as well as the complementary concepts of space, time and causality, which are categories with separable categorial features, including, for example, final and effective causes. Non-Separability underlies a quantity of metaphysical and phenomenal dualities of reality, such as determinism and indeterminism (see below), subject and object, continuity and discreteness, internal and external, and simultaneity and succession. This is a ‘vital’ concept: to consider process elements that are contradictorially linked as separable is a form of a category error. The claim is that Non-Separability exists on the macroscopic and on the quantum levels, providing a principle of organization or structure in macroscopic phenomena that has been neglected in science and philosophy.
The function (Definition 13) and process (Definition 14) information operators in the General Theory of Information [2] provide the basis for a more formal characterization of the calculus developed by Lupasco and outlined in [5,32]. The connectives, that is, what is usually defined as the symbolic logical operators of implication, conjunction and disjunction, all correspond in LIR to real operators on real elements in the evolution of real dynamic processes. Accordingly, these operators are, also, subject to being actualized, potentialized or in a T-state. They operate not on theoretical states-of-affairs or propositions, considered as the abstract meaning of statements, but on events, processes and properties, where properties also have the character of processes.
The key concept is that the LIR operators themselves must be considered as processes, subject to the same logical rules, fundamental postulates and formalisms as other real and hence, natural processes. This answers a potential objection that the operations themselves would imply or lead to rigorous non-contradiction. Real processes are, accordingly, seen as constituted by series of series of series, etc., of alternating actualizations and potentializations. These series are not finite, however, in reality, processes do stop, and they are thus not infinite. Following Lupasco, we use the term transfinite for these series or chains, which are called ortho- or para-dialectics. The reader is referred to [5] for details of this applicable non-standard calculus.
One of the basic areas of application of these natural operators is, of course, language. However, the issues and relations addressed are much more complex than by standard linguistic operators. Ghils [34] has shown, for example, that the spatio-temporal dialectics in the linguistic theory of Roman Jakobson [35] is best described by the movement between actual and potential, using the corresponding operators as expressed by the Lupasco (LIR) calculus.
The natural operators of Logic in Reality are extremely complex, being both symbolic, material and mental, but also in part symbolized, naturalized and social, since implication, conjunction and disjunction obviously also function within social systems. As a final remark, the same picture applied to conjunction and disjunction as opposites provides the basis for a non-classical set theory, in which there is no absolute separation between sets and their members. According to de Morgan duality in classical logic, conjunction and disjunction are not independent, in the sense that a complementation operator takes any proposition to a similar one with the negative and operation inversed. This duality, however, still refers to a relation between abstract entities.
3.4. Operators and Causality
The discussion of the nature of operators allows us to explicate their relations to the notion of causality or cause and effect. It is easy to accept that all operators are efficient causes. However, are all causes operators? Further, what is the causal nature of the operator-operand interaction?
The key conceptions in standard theories are those of Prigogine [36] of dissipative systems far from equilibrium, continued by Salthe among many others. The thermodynamic view focuses upon a final causality that operates universally. A functional separation is maintained between cause and effect, reifying them as entities separate from the property-processes they are supposed to operate on. For example, the intervention I must completely change any causal relationships between X and its prior causes. Nevertheless, one comment of Woodward [37] suggests some underlying common intuition. He suggests that philosophers do tend to think of causes as properties or events, but that it is possible to move back and forth between such talk and a representation in terms of variables. When there is no well-defined notion of change or variation in value, almost any standard theory, e.g., of manipulability, will not see genuine cause, but some form of epiphenomenality.
By localizing the origin of action in the potential aspects of phenomenal processes, which in the LIR view are intrinsic properties of all operators, our approach cuts through the debate on whether causation by omission, absence and prevention are cases of causation or not. They are. This line of argument also applies to the artificial distinction between natural and causal change, as well as internal and external change. LIR thus supports and explicates Fair’s transference theory according to which, as discussed by Dowe [38] causation is a transfer of energy and/or momentum although causation by absence does not include any transfer of energy or momentum. Besides, in the context of the general theory of information, causation necessarily is a transfer of information [2].
Further detailed discussion of the subject of causality, (which has been called the “black hole” of philosophy), is beyond the scope of this paper. We believe that the major source of difficulties with standard views of the energetic aspects of cause, and the relation between cause and effect, have been due to the use of the conventional mutually exclusive categories of standard logic and category theory. In real complex situations, the reciprocal relations of feedback from operand to operator are of equivalent importance to the original relational property. Any human operator where the operation involves intentionality, operating as a cause, will be accompanied by a minority contradictorial tendency either not to operate or to cause the opposite effect. Logic in Reality permits a formalization of the parallel chains of causality [5]. Operation and cause are, accordingly, equivalent descriptions the choice of which will be defined by the specific focus of the subject of analysis.
4. Psyche as a Natural Operator
4.1. An Approach to a Theory of Mind
Most of the difficulties in the vast variety of theories of mind and knowledge have been in finding the essence of “what it is” to be an entity with conscious awareness and causal efficacy. The concept of natural operators as a description of the operation of the LIR principle of dynamic opposition provides access to a new epistemology in which the classical entities of knower, knowing and known (knowledge) are all seen as processes in dialectic or contradictorial interaction.
In this Section, we are concerned with both individual mental processes and their totality, exposing their nature as operators, and choosing the term psyche (the Greek word for mind and soul) following Jung who used it for this totality. There is a striking similarity between his foundational view of opposition as an inherent principle of human nature [39] and dynamic opposition in LIR. As Jung wrote,
“A psychological theory, if it is to be more than a technical makeshift, must base itself on the principle of opposition … There is no balance, no system of self-regulation, without opposition. The psyche is just such a self-regulating system.”
Jung described the forces at work in terms of energies in language that is easy to compare with the LIR grounding in energy, and the need for opposition is clear from his emphasis that “there is no energy unless there is a tension of opposites”.
We first note that members of all classifications of operators are instantiated in the psyche, providing a kind of rough measure of its existence as the most complex, natural object in the universe. To the suggestion that society, as an entity composed of multiple minds, is more complex, our answer is that many of the individual operations of society are less complex, involving fewer types of operators. Society as a collective entity or system (or ‘being’ in the sense of Minati and Pessa [40] instantiates emergent simplicity. In addition, the psyche is one of the basic concepts of depth psychology, comprising the forces in an individual that influence thought, behavior and the whole personality.
Freud [41] described the structure of the psyche as composed of three components:
- The Id, which represents the instinctual drives of an individual and functions mostly unconscious.
- The Super-Ego, which represents a person’s implicit knowledge about social environment, including internalization of social norms, morality and other standards, functioning mostly unconscious.
- The Ego, which represents a person’s conscience and serves to integrate the drives of the Id with the prohibitions of the Super-Ego.
In essence, Ego connects Id and Super-Ego, forming the following Fundamental Triad [33,42].
Thus, in this context, the psyche controls an individual’s functioning, behavior and personality. Consequently, psyche is a natural operator, with a compound structure built up from other simpler operators, forming a sophisticated hierarchy. Our intention is not to argue here for the validity of this descriptive system but simply to provide an interpretation in our “operator” language.
It is important to note, however, that the diagrams and discussions of the Fundamental Triad in this paper are univocal, without reference to bi-univocal relations, recursion and feedback involving operator and operand. The structure of such interactions is critical for any reasonable models of the mind, memory and complex social phenomena such as the economy. For discussions of these aspects, the reader is referred to Lupasco [43], Burgin [33,44] and Leydesdorff [45].
To further apply logical operations as dynamic processes, outlined in the previous sub-Section, to the human mental system, we start by looking at the dialectics of afferent and efferent systems in perception. Prior to excitation—a natural physical/biological operator—by internal or external stimuli, we assume that the afferent system is in a state of potentiality, maintained by the antagonistic actualization of the polarization or electrostatic equilibrium. Excitation results in a new actualization, potentializing the ionic equilibrium, the reception of an equivalent to heterogeneity of sensations. The new equilibrium state of perception appears, in its homogeneity, as something objective, exterior, an identity of which one can have ‘knowledge’, while sensations, although really belonging to the external world, appear interior to the senses and more subjective. The dialectics established in and by the afferent process is between the conscious mind of (or as) the ‘knower’, actualizing a series of energetic heterogeneities, and the ‘known’ displaced to the exterior in the potentiality of energetic homogeneity. This conception could be called ‘pan-energetics’, but it is not a pan-psychism, the mind appears as an aspect of the structuring and operation of energy.
The difference between actualizations that potentialize and potentializations that actualize is not continuous, and the pauses in the process, in the T-state, are what can be considered states of control. These constitute the dialectic of the psyche, which becomes what is generally called consciousness. There is thus in the LIR theory no ‘consciousness of’, no reification or objectification, only that which occupies the conscious mind, that which is potentiality itself, what is commonly called consciousness, with the capacity for causal change that justify its characterization as a natural operator. As a result, relations between the knower, knowing and known become explicitly processual. Our approach to a theory of mind is discussed further below in Section 6.2.
4.2. The LIR Theory of Knowledge
The LIR approach to knowledge purposefully includes it in reality. For instance, knowledge in a biological organism originates in, and can never be totally separated from, the set of processes that constitute its existence, including an organism’s systems of perception and action. All these processes instantiate both reciprocal degrees of actuality and potentiality and different tendencies toward identity and diversity. The objects subject to these systems relations are the knower and a knowable or a known, as well as the exterior and an interior reality. The essential hypothesis is that the knower does not and cannot know himself in the process of knowing insofar as he/she knows or is in a process of knowing. Using a Leibnizian argument, we can show that for knowledge to exist, the knowable and the known must be neither totally identical to nor totally different from the knower. This is similar to the fundamental Dynamic Knowledge Triad, an important case of the Fundamental Triad described by Burgin [33,44] where the structure (4) is the actual form and the structure (5) is a potential form of the structure (3). In LIR, knower, knowing and known all instantiate both actuality and potentiality.
We assume, following the fundamental postulate of LIR, that existence and non-existence and the knowable and known in which they manifest themselves are dualities with contradictory terms, for one to be (predominantly) actual, the other must be (predominantly) potential. Thus when we know or do something, we do not know (or pay attention to) our knowing of it. We can focus, by another cognitive act, on our knowing, which does not know itself as such, and so on.
The core of this theory is that we know only what is potential—what is conceptual and ‘ideal’, the inverse of that which is relegated to the unconscious and according to which we act. The actual is always impossible to know, due to the nature of knowing itself, a concept that corresponds to the general idea according to which one cannot act, contemplate, etc. and see oneself act, contemplate, etc. at the same time. The known is neither totally identical nor totally other than the knower. The dualities are contradictory as one of them is (mostly) actual, while the other must be (mostly) potential. Although the roles of these dualities are changing, the two are not both fully actual at once, but as one is primarily actualized, the other is primarily potentialized.
In the present theory, the known is an element or entity or process that is contrary and contradictory to the knower. Together, they constitute antagonistic dynamisms in which alternating actualization and potentialization converts known to knower and vice versa. A known becomes a knower since ‘knowledge’ is not the knowledge that a knower ‘has’ but is a process that is active in the knower. As a part of an individual’s total mental structure, this process, in a non-metaphorical sense, ‘knows’ or becomes a knower and accordingly, like knowing itself, is a natural operator as a consequence of the dialectics of contradiction.
We believe that the contribution of Lupasco, relating the terms used in philosophy since antiquity of knower and known to reality by focusing on knowing as a physical process is a major one that deserves more attention. The further discussion of the operator aspects of this process in the remainder of this paper, especially Section 6.3 on Intentionality and Section 7, should be read with this in mind. We can state already that our operators approach goes beyond any narrow functionalist conception of the mind.
5. Operators in Technology
5.1. Machines as Operators
Usually machines are not treated as operators. They are operands (in our terminology) controlled by human operators. Here we extend our understanding of operators and this allows us to better characterize the role of machines in our society. Now, for example, a new tendency has arisen when machines are considered as operators but only when they are able to perform complex operations, and at least for a time work independently of people and operate, e.g., control some other machine. For instance, a robot can be an operator of another machine but traditionally it is not treated as an operator. A robot that explores the surface of the moon or planets must be able to walk on rough terrain in a harsh environment, receive instructions from remote operators about where to go next, and reach those commanded goals autonomously.
At the same time, it is customary to say that computers operate data. So, according to Definition 1, computers are operators. It may be less habitual but still acceptable to say that programs operate computers, but to hear that data operate computers seems rather strange. However, any manufacturing machine, e.g., loom or lathe, operates material from which the product of this machine is produced. Thus, this machine is an operator according to Definition 1.
This is especially true for robots, which become more and more abound. Industrial robots are found in a variety of locations including the automobile and manufacturing industries. Robots cut and shape fabricated parts, assemble machinery and inspect manufactured parts and perform many other manufacturing tasks. Outside the manufacturing world robots can be found in hazardous duty service, CAD/CAM design and prototyping, maintenance jobs, fighting fires, medical applications, military and agricultural operations and so on.
Some machines produce nothing, e.g., a car or a plane. So, if we base our judgment on Definition 1, a car or plane is not an operator. However, a car, as well as a plane, bus, train or ship, operates on things and people by taking them from one place to another. Nevertheless, there is an essential difference between humans and machines in their role of operators. What is considered unique in humans functioning as operators is the intentional relation between themselves and the object, tool or machine, which they operate or use as agents. In productive operation, there is thus an intentional relation between operators and the objects they create. We will therefore look briefly at the issue of intentionality in machines. In Section 6.2, we consider intentionality in humans.
5.2. Intentionality in Machines?
Intentionality is an important property of human beings as operators, so, it is important to understand whether machines as operators also have intentionality. Some researchers tend to ascribe intentionality to such machines as computers, especially, when they have sophisticated software, e.g., softbots and other artificial intelligence programs. Other researchers completely deny a possibility for a machine to have intentionality. It is possible to suggest that such contrasting views are caused by a simplified understanding of intentionality, which exists now. Intentionality is considered as a binary property, which means that a system ether has intentionality or does not have —and nothing between these two possibilities.
To clarify the problem and eliminate this unnecessary restriction, we consider three kinds of intentionality:
- Inserted or programmed intentionality
- Induced, e.g., by persuasion, example or hypnosis, intentionality
- Inherent intentionality
Machines do not have inherent intentionality at all. For instance, a car goes only to the places directed by the driver. However, some machines, especially, those that can work autonomously, reach the first level of intentionality. There is a substantial debate in progress on whether machines can reach higher levels of intentionality. The debate is not addressed here although some evidence for the positive answer is given below.
In the new direction in programming called programming by example, there is reason to assume that programming by example actually induces some kind of intentionality in the corresponding computer. If robots will be able to learn from examples, then it would be reasonable to consider that they acquire induced intentionality. Again, there have been endless speculations as to if and how artificial intelligence embodied in thinking machines might acquire all the traits of a human being, including intentionality. However, contemporary computers have only inserted/programmed intentionality. We will return to machine-related questions in Section 6.2 on Intentionality and Section 6.3 on recursive processes (Self-Control and Self-Regulation).
6. Human Operators
6.1. Basic Concepts
In this Section, we study human operators, which epitomize almost all types of operators, especially, in the function-oriented classification. In fact, the idea that human beings are operators is so familiar that it rarely receives detailed discussions. It is a commonplace that “man as a “tool-making and tool-using” animal, but what is important from the standpoint of this paper is that humans, as biological systems, are natural operators in the sense of being evolving structures with causal power, natural and naturalized. At the same time, humans, as social units, are also social operators.
Obviously, the role of human operators is changing. Human operators are still required for the functioning and success of manufacturing systems, but advances in automation technology have caused fundamental changes in the way such systems operate. Functions of human operators have also evolved under the changing manufacturing environment. Human operators are currently performing more information processing, decision-making and control activities than ever before.
A brief historical remark: the classical view of man as a tool-maker, homo faber, indicated in Section 5, was developed by Bergson. Arendt proposed a subsequent social stage of man as animal laborans, man as worker [46]. Our conception of man as operator actually combines these two aspects and could be summarized by the term homo operator. This term was first used by Thomas Aquinas and more recent theologians with a rather negative connotation. (The term homo operans has also received a number of biological and theological definitions which will not be discussed here.) In our view, however, such a connotation is arbitrary. Ethical behavior or the lack of it supervenes on psychological and structural characteristics of an individual, some of which we discussed earlier, other than his or her functioning as an operator per se.
It is possible to consider all machines, from the simplest multiplier of force such as a lever or pulley to a computer, as operators. However, machines do nothing on their own but, like symbolic operators, have their origin in and are totally dependent on the mental and natural operators of human beings. The same remarks apply to recent man–machine hybrids. So, as Magnani [47] suggests, we exercise moral responsibility, giving them equivalent moral status. Such entities are, of course, paradigm examples of hybrid operators (Definition 17).
A simple model of a human operator is a person interacting with a machine in some kind of environment, for example, driving an automobile. The person and machine often are both modeled as information-processing devices, each with input component, central processor, and output component. The input component of a person consists of his/her sensors (e.g., eyes and ears) and the output component of a person consists of his/her effectors (e.g., hands and mouth). A computer and its ancillary devices has a similar operator structure. The environment can be characterized physically (e.g., vibration, noise, zero-gravity), cognitively (e.g., time pressure, uncertainty, risk), and/or organizationally (e.g., organizational structure, job design). This provides a convenient way for organizing some of the major concerns of human engineering: the selection and design of machine displays and controls; the layout and design of workplaces; design for maintainability; and the design of the work environment.
No matter how important it may be to match an individual operator to a machine, some of the most challenging and complex human problems arise in the design of large man-machine systems and in the integration of human operators into these systems. Examples of such large systems are a modern jet airliner, an automated post office, an industrial plant, a nuclear submarine, and a space vehicle launch and recovery system.
Summarizing from the list of properties, and in line with the ability of LIR to explicate their relation, we point to the junction and Non-Separability, in human beings, of the internal properties of our operations: intelligence, capacities, and skills, each of which has its own enormous literature, and what is operated upon, the external aspects as operands.
In the case of human beings, it is useful to differentiate between operation and intentional use, as well as between tool and machine. When spectators watch a movie in a theater, they use this movie but do not operate it. At the same time, operation can take place unintentionally. In such situations, it is possible to operate something but not to use it. For instance, when an individual destroys something, she does not use that thing.
There is also an essential difference between tools and machines. In philosophy, the concepts of machines and mechanisms refer to essences of things, while being a tool is a role of an object. For instance, a car is a machine whether it is used or not. It becomes a tool only when it is used for achieving some goal. There is also a discussion whether a human being is a machine in this sense or not when instrumentalized as a tool by and for another individual or a group, becoming an operand in the narrowest sense, that is, with the destruction of ethical reciprocity. As humans are created by nature as biological objects, it is more relevant to assume that they are not machines. This once more demonstrates the difference between tools and machines.
Tools in the form of physical machines are extensions of human physical and mental capacities. We nevertheless can only present a few key examples from the entire range of human activities, differentiated by attitude and complexity. One extreme is the (literally mindless!) repetitive operation of a machine epitomized by Charlie Chaplin in the film Modern Times. At the other extreme is the surgeon executing delicate operations that are now possible only through human-machine symbiosis.
René Thom, in his catastrophe theory, mathematically describes the process of using a tool or weapon. For instance, the form of an axe or projectile with a beveled edge, for example, is imagined by the maker as appropriate for causing a swallow-tail catastrophe (one of the seven basic types) in the skull of the animal or enemy. “The mental vision of the catastrophe to be provoked in the adversary creates a secondary field, that of the fabrication of the axe [48].”
In LIR terms, the actual mental image process and the potential external effect as potential are dialectically connected. In this context, Lupasco [49] discussed the operation of tools and machines, constructions of human beings and extensions of their capacities, in terms of a dialectic alternation between induction and deduction in science. He wrote that “after operating (sic) inductively, bringing to light theoretical phenomenological identities, it (physics) becomes deductive, in order to verify the effective actualization of these identities…” Physics constructs machines and creates applied science such that this actualization implies that the objects fabricated should be rather considered fabricated subjects, since it is the agent, the operator-subject, the extension of the subject that is doing the actualizing of that theoretical identity. Deduction is the verification operation of inductive science.
What is unique in humans functioning as operators is the intentional relation between themselves and the object, e.g., tool or machine, they operate and use. In productive operation, there is also the intentional relation between operators and products they create. We will therefore look further at the structure of the intentional process started in Section 5.1 in relation to machines.
6.2. Intentionality and Non-Symbolic Representational Theories of the Human Mind
The central problem for a philosophy of mind is to show how physical tokens in the form of the neuro-physiological processes occurring in the brain, can give rise to mental tokens that retain the properties of intentionality, “aboutness”, individuality and some level of causal powers or functionality. The weak point in some current views [50] is that physical and mental tokens are treated as identical (identity theories of mind (ITM)). The LIR principle of opposition at all levels of perception, mental processing and action gives the logical and scientific basis for saying that something is the same and different, here physical and mental tokens, in dynamic opposition at the same time. At this stage, we simply state as a postulate that no theory of mind, philosophical or metaphysical, that is based on separability between physical and mental entities can provide adequate explanations of mental phenomena. This is not necessary in LIR, since the latter are described in terms of the contradictorial but physical process relations between the appropriate elements or entities.
Above we defined the human mind in its capacity for knowing, the psyche, as a natural operator. As we focus in this sub-Section on the totality of the human individual, we need to discuss another major aspect of human existence, namely, intentionality. Further explanation of intentionality and mental causation is critical, since the strong intuition of the completeness of causal exclusion requires that every physical state have a complete, that is, a necessary and sufficient physical cause. We should emphasize out that the following discussion refers only to what has been defined in the previous section as inherent intentionality.
In Brentano’s conception, consciousness and mental phenomena are distinguished from physical by their intentionality. The characteristic property of the intentionality of mental states is their ‘aboutness’ or ‘object-directedness’, that is, consciousness of something. This involves critical issues regarding the object, the mental act of perception and the relation between them. A simple physicalist conception of, in particular, cause and the process involved in the perceptual acquisition of the object, is not sufficient to explain intentional relations. Our approach in terms of symbolic and natural operators provides a new perspective on the assumed presence and role of symbols in mental phenomena.
LIR demonstrates that there is something clearly missing or inadequate about the separation into mental and physical to begin with. The claim we make that offers a possible solution to the problem is that mental and physical phenomena are the same and different, and we will attempt to support this claim in the remainder of this Section.
LIR starts from the view that consciousness is an ensemble of dynamic processes, in which internal and external aspects cannot be totally separated from one another. Smith has criticized cognitive science for being reductionist specifically by its failure to preserve the properties of consciousness and intentionality, using the standard definition. “The phenomenological character of consciousness is not preserved, and Intentionality is not simply identical with the structure of a causal process…” [51]. LIR suggests the emergence of the phenomena of intentionality and qualia at the locus of the contradictorial interaction between the actualized subjective and potentialized objective parts of both incoming and outgoing stimuli.
In representationalist theories, internal entities of some sort stand for or correspond in some way to external processes and events. These mental representations explain or are explanatory devices for cognition in that they are, or correspond to intentional states, instances of intentionality considered as embodying the irreducible first-person properties that characterize consciousness, reasoning and qualia. The focus now shifts, therefore, to the representation of intentional states.
Without reproducing the entire debate, we note that in Fodor’s intentional realism, a cognitive process is a causal sequence of intentional states. However, such states are not physical properties in the usual sense. To naturalize the initial intentional state, to which causal efficacy is ascribed, it is first transformed into a representational one, and this subsequent representational reconstruction is naturalized. The former is characterized as a symbol, similar to a linguistic symbol, but its intentionality is given by the original intentionality of the mental state. In other words, intentionality is identified with the semantic properties, including the capacity of physical causality, of a mental representation. The language-of-thought hypothesis adds the concept that the system of mental symbols constructed above has a language-like structure, but the fundamental premise remains that a mental representation is a symbol, where a symbol is defined as something standing for something else, as noted.
The Fodorian construction implies that mental state and symbolic mental representation are identifiably separate entities, and in addition the second always exists in the relation between the state and the object. In other words, the idea that mental states could relate directly to objects without intermediaries is excluded. This depends on the idea that if a symbol makes a relation with something else possible, and is accordingly also an element, an intermediary one, all such relations must ipso facto be indirect. On the other hand, this is in contradiction with the accepted idea that some mental states are intuitive and accordingly in a direct relation with an intentional object.
Our preferred theory of intentionality is to involve non-symbolic mental representations, since in our view the above account of mental processes suffers from the need to introduce additional entities due to the lack of a principled categorial method of relating its critical concepts contradictorially. A mental phenomenon that is not something other than physical processes with emergent properties ‘displays’ its contradictorial origins in appearing to have symbolic and non-symbolic aspects, and being closer or farther from the center of attention at a particular time.
The difference of status between a representative content, in this picture, and a symbol can, first, be connected with the shift of attention that accompanies the movement from consciousness to consciousness of consciousness proposed above. Further, however, the underlying intuition is that representative content, although it is in a sense an intermediary in the intentional relation, is something other than a symbol because a symbol is an intended element as defined. The LIR conception of intentionality as a dynamic mental operator that avoids the reification of intentionality as a static posture of intent is still open, however, to the attack by anti-reductionists against all concepts of intentionality, namely, that they are unreliable. In the anti-reductionist, externalist theory of content, the thesis of intentionality need not be true. The reason given is that we do not know or are often wrong about the ‘content’ of intentional states. We will not argue these points here. In LIR, internal and external states are co-determining, and we do not require absolute truth for a workable phenomenological theory of intentionality.
In the LIR categorial ontology of mental process structures, intentionality thus appears as a kind of plan, composed of both actual and potential elements, more or less clear-cut or fuzzy (homogeneous or heterogeneous) in the contradictorial relation described above. Intentionality is thus best described, like knowledge, as a complex natural emergent operator, which emerges with respect to some primarily internal or external operand [52].
6.3. Self-Operation, Self-Operators, and Self-Organization
Self-operation is a phenomenon that refers to the ability of human operators and organizations of humans to operate on themselves, that is, recursively. The term self-operation actually includes a number of processes that also take place at lower levels of reality and thus, self-operation is abundant in nature, society and technology. Among the many kinds of self-operation studied by researchers and used for practical purposes are self-modification, self-organization, self-regulation, self-management, self-replication, self-production, self-control, and self-programming. All of these processes in the broadest sense refer to properties of a system to change both its internal environment (structure) and external behavior (functioning). In general, all of the natural and social operators that execute these operations are ipso facto self-operators. In this paper, we will limit our discussion to self-organization, self-control and self-regulation.
6.3.1. Self-Organization
We begin our discussion with the concept of self-organization in view of its importance for the understanding of all the reflexive processes, and because it illustrates the “operation” of the principles of Logic in Reality [5]. The concept of self-organization was born in the 1960’s in an attempt to establish a theory based on the standard logic of a system and its control.
The phenomenon of self-organization includes two sides (aspects): attributive, which is related to the inner structure of the system, and processual, which is related to the external behavior (functioning) of the system.
Definition 21.
Self-organization in a broad sense is the property of a system, which results in activity to better organize system’s internal environment (structure) and external behavior (functioning).
We thus include the above two aspects in our definition of self-organization: attributive and processual. In attributive self-organization, some systemic property is improved. In processual self-organization, some system functioning (behavior) becomes more organized.
There are two main approaches to self-organization in social systems. One of them is based on the model of a system composed of aggregated individuals where self-organization is generated by and results in the sum of the practices in the system induced by control, or self-control, in particular, and system logic. The second approach focuses on the practices of individuals deviating from the logic of a system, making the existing system fluctuate and transforming its structure. That is why, to exist, any organization has to self-organize itself.
As a result, self-organization is related to emergence of pattern or regular structures. Thus, the following definition is very often used:
Definition 22.
Self-organization is the process where a structure or pattern appears or grows in a system.
The problem in all discussions of self-organization as a kind of self-operation is to establish why some systems have the capacity to self-organize or to express self-organization and others do not. In fact, on close inspection, all systems to which self-organization is attributed depend for their capacity on some set of either initial conditions or on-going input of energy and information that transforms the term “self”- into a contradiction, correctly, a “self-contradiction”. This brings us to two extreme types of self-organization: independent and induced.
Definition 23.
Independent self-organization is a process where the organization (constraint, redundancy) of a system appears to spontaneously increase, i.e., without this increase being controlled by the environment or an encompassing or otherwise external system.
A 100% independent self-organization is, in fact, an ideal operation which is never realized in the process of system functioning. It must always be accompanied, dialectically and functionally, by non-self-organization or, more exactly, hetero-organization [53].
Definition 24.
Induced self-organization or hetero-organization is a process where the organization (constraint, redundancy) of a system increases under the influence, e.g., pressure, persuasion or advice, from the environment or from an encompassing or otherwise external system.
The problem to be resolved is then a proper definition of the interactions and differences between self- and hetero-organization. Indeed, an ordered structure capable of self-organization is nevertheless dependent on the input of external energy and information for it to form and persist [53]. It is not “spontaneously” generated within the system, even if it “spontaneously” forms. Once initiated, the process of self-organization does result in the creation of new entities. However, these require new (externally) available information for their further evolution. Hetero-organization refers, then, to a model for the delivery or introduction of this external information to the system.
The rigorous logical approach of LIR can be applied to the concept of self-organization. If one assumes a standard definition of a system, a self-organizing system is defined as distinguished by the formation of some states or entities arising from the reciprocal or collective interactions (encounters) between its components, quite independently of outside inputs. LIR theory, however, states that the critical terms of ‘self’ and ‘independent’ involve question-begging assumptions, given the critical LIR categorial feature of Non-Separability discussed above.
Brenner [5] suggested that the critical step in the organization process is not spontaneous, in the sense of uncaused by outside agents, which the use of the particle “self-” without qualification implies. New organizational structures are the effective consequences of the potentialities residing in the components and/or introduced during the original constitution of the natural system or artificial experiment. This view supplements the discussion of self-organization in society proposed by Fuchs [54], in which the emphasis is on a dialectical, emergent transition from simple elements defined by one or two parameters to more complex process-like entities instantiating quality or meaning. Fuchs also suggested the need for a new functional “logic of self-organization” in another recent paper. The advantage of LIR for a theory of organized systems is that it provides, at least, a partial answer to the question of why some systems self-organize, or display autopoiësis, and others do not. LIR simply takes the theory of self-organization and grounds it in (at least) one lower level of reality, without the need for invoking any non-causal spontaneous processes.
We propose, accordingly, that self-organization is not, in and of itself, a ‘self’-evident mode of system formation and change. All self-organizing systems also involve some degree of organization-by-external-agent, which is a case of hetero-organization and the two are dialectically related. Varela describes such a situation [55] when he states that coupled non-linear oscillators can give rise to kinds of self-organization that result in the emergence of neural structures from the component level. A local-global interdependence is necessary to understand the emergence. The components “attain relevance” through their relation with their global counterpart.
We further characterize self-organization, within the limitations discussed above as gradual or apparently spontaneous. Gradual self-organization is a basically a process of evolution where the effect of the environment is minimal, i.e., where the development of new, complex structures takes place primarily in and through the system itself, subject to control by the initial conditions. In many cases, it can be understood on the basis of the same variation and natural selection processes as other environmentally-driven evolutionary processes.
In processes of apparent spontaneous self-organization, fluctuations often operate as organizing forces when at the global level of a system, patterns emerge mostly from numerous interactions among the lower-level components of the system, for example, through the “order through fluctuations” mechanism discovered by Ilya Prigogine [36] in systems, which continuously export entropy in order to maintain their organization of dissipative structures.
As a definitive type of apparent self-organization, we may discuss self-organization in the restricted system sense [40,56].
Definition 25.
Restricted self-organization is the process where a structure or pattern appears in a system without a central authority or external element imposing it through planning and pressure, and is dependent on the prior potentialities of or initial conditions in or pertaining to the components of a system.
Therefore, many processes of restricted self-organization are in part induced by other systems involving hetero-organization of a collective of different systems.
Self-organizing processes in the restricted sense, such as herd behavior, groupthink and others, are abound in sociology, economics, behavioral finance and anthropology, as well as in economy, politics, industry, medicine, and technology. Biological science studies the creation of structures by social animals, such as many mammals and social insects (bees, ants, and termites), flocking behavior (such as the formation of flocks by birds, schools of fish, etc.).
In economy, we can see such self-organization processes as: growth, competition, extinction of companies; functioning of financial markets and stock markets. In politics, we have revolutions, “self-dynamics”, formation of public opinion and development of beliefs.
In social theory, the concept of self-organization was connected to self-referentiality and self-production by Luhmann [57], who treated the elements of a social system as self-producing communications when a communication produces further communications and hence a social system can reproduce itself as long as there is dynamic communication. At the same time, human beings are sensors in the environment of the social system. Based on these foundations Luhmann developed an evolutionary theory of society, using functional analysis and systems theory. These aspects of operators, however, will not be discussed further in this paper.
Various social structures, such as organizations and institutions, have the form of a network. Self-organization in such networks is triggered and fueled by an ideology or sociological force that is adhered to or shared by all participants in the network. Self-organization in human (social) and computer (technological) networks can give rise to a decentralized, distributed, self-healing systems, helping the actors in the network to protect their security by limiting influence of the entire system on individual actors. Self-organization emerges in the network as a distinctive synergistic behavior through combination of the behaviors of individual actors in the network.
The phenomenon of self-organization in the restricted sense also exists in many domains of nature, such as chemistry or biology. Examples of self-organization in the restricted sense in chemistry are molecular self-assembly, reaction-diffusion systems and oscillating chemical reactions, autocatalytic networks, liquid crystals, colloidal crystals, self-assembled monolayers, and microphase separation of block copolymers. Examples of self-organization in the restricted sense in biology are spontaneous folding of proteins and other biomacromolecules, formation of lipid bilayer membranes, pattern formation and morphogenesis, the coordination of human movement, the creation of structures by social animals discussed above.
The standard theoretical treatment of self-organization in the restricted sense is based both on microscopic, as well as macroscopic phenomenological approaches. Haken [56] formulated general principles of self-organization in the restricted sense or of self-organization as the reduction of complexity. They are based on general concepts, such as order parameters and the slaving principle. For instance, in large classes of systems their dynamics can be described by few order parameters.
In our view, however, the phenomenon of self-organization in the restricted sense, for which many more examples could be given in chemistry, biology and sociology are all dependent on the preexisting residual potentials present in the components of the system in its initial state. Since systems, accordingly, do not self-organize “by themselves”, the possibilities for changing the evolution of the systems are limited.
The consequences, particularly in the social field are significant. For example, there are two main approaches to self-organization in social systems. One of them is based on the model of a system composed of aggregated individuals where self-organization is generated by and results in the sum of the practices in the system induced by control, or self-control, in particular, and the logic of the system logic. The second approach focuses on the practices of individuals as agents deviating from the logic of a system, making the existing system fluctuate and transforming its structure. The original capacities of such individuals to make changes should not, accordingly, be considered as a part of the self-organization that is alleged to occur.
6.3.2. Self-Control
Proceeding from the general principles to self-operation and self-organization in human beings, we look at the process of self-control.
Definition 26.
Self-control in a broad sense is the property of a system to control itself, i.e., its internal processes and external behavior (functioning).
The concepts of self-regulation (see next sub-Section) and self-control are very close to one another. However, the concept of self-regulation is more popular in system theory and cybernetics, while the concept of self-control is more popular in psychology. For instance, emotional self-control: presupposes keeping disruptive emotions and impulses under control. An example of self-control is when one manipulates one’s own behavior by affecting states of deprivation or satiation. Psychological self-control means the ability to control one’s emotions, behavior and desires in order to reach some goal, as well as the capacity of efficient behavior oriented at the future.
In society, self-control of an individual is directly related to the pressure/influence the individual may face. Thus, it is possible to distinguish three situations: good pressure/influence, bad pressure/influence and no pressure/influence. An example of a good pressure/influence is when an individual is in a competitive, yet non-judgmental and non-prejudicial environment and wants to be like those around. This makes the individual motivated and inspired to gain self-control. On the other hand, when an individual is in a judgmental and prejudicial environment, the individual may become depressed and unmotivated, losing self-control. In the third case, when an individual is free and there is no competition, self-control is based on how an individual may feel.
Skinner [58] gives a survey of nine categories of self-control methods. They include physical restraint and physical aid, changing the stimulus, drugs, operant conditioning, punishment depriving and satiating, manipulating emotional conditions, using aversive stimulation, and doing something else.
Manz et al. [59] argue that self-control is at the core of the organizational control process, expanding, in such a way, the view of control is developed in which importance of self-control, as well as external control mechanisms are recognized. For example, many companies are trying to become learning organizations often using self-control rather than relying on rules and regulations. Thus we can see that the difference between self-regulation and self-control is that self-control demands intentionality, while self-regulation, as a rule, does not need it.
6.3.3. Self-Regulation
The next most general category within the framework of self-operation is self-regulation.
Definition 27.
Self-regulation in a broad sense is the property of a system to regulate its internal environment (state self-regulation) and external behavior or functioning (phase self-regulation) in order to maintain a stable, constant condition.
Any self-regulating system is an operator, specifically, a self-operator. Self-regulating systems exist on all levels: cells in an organism, human organism, and many social organizations are self-regulating systems.
All self-regulation mechanisms have three interdependent basic components for the system feature, e.g., a system parameter, being regulated, as follows: (1) the receptor system is the sensing component that monitors and reflects changes in the system and its environment and sends information about these changes to the control unit; (2) the control unit (or conceptor in the sense of Burgin and Gladun [60] processes information that comes from the receptor, formatting instructions (operational information) to the effector; (3) the effector system is the acting component that changes in the system state, e.g., a system parameter, and/or system behavior (functioning).
Information plays a crucial role in self-regulation, which is based on the feedback of the system. It is possible to understand self-regulation through the interplay of positive and negative feedback cycles when some variations tend to reinforce themselves, while others tend to reduce themselves. Both types of feedback are important to self-regulation: positive feedback because it increases parameters of the system (up to the point where resources become insufficient) and negative feedback because it stabilizes these parameters.
Let us take the human organism as an example of a self-regulating system. In it, most homeostatic regulation is controlled by the release of hormones into the bloodstream, while other regulatory processes rely on simple diffusion to maintain a balance. The process of self-regulation proceeds as follows. The receptor system, which may consists of several components or even of many autonomous units, is sensing different stimuli. When a relevant stimulus comes, the receptor sends information to the control unit, finds the state/phase of the organism and determines an appropriate response to the stimulus. In the human organism, the control unit (control center) is the brain. Then the control center sends signals to the effector system or to a part of this system, which can be muscles, organs or other structures that receive signals from the control center. After receiving the signal, a change occurs to correct the deviation by either enhancing it with positive feedback or depressing it with negative feedback
Neural networks, both natural and artificial usually work in the same way, having the same components: receptors, conceptors and effectors [60] organized to maintain state self-regulation aimed at homeostasis.
7. Conclusions
7.1. A Unified Theory of Operators and Logic in Reality
In this article, we have used two different but complementary strategies to arrive at a new coherent picture of operators in nature, mind and machines. First, we have defined and identified the natural operators that constitute and drive processes at the cognitive levels of reality. We have placed all operators in a comprehensive categorial framework, in which they are classified according to their form, media, target and function orientations and major general properties. The concept of natural operators at the level of the individual and collective human mind is given a new foundation. Second, we suggest that an applicable extension of logic, such as Logic in Reality (LIR), can make visible logical patterns in processes, in particular cognitive processes that have been previously considered irrational or disorganized, escaping any form of systematic or logical treatment. We show that the same structural logical principles are instantiated in the operators responsible in functioning of the human mind, the functioning of human society and the interaction between individual and group “minds”.
From one standpoint, we may consider our approach as a ‘Unified’ Theory of Operators, at least from the point of view of a complete classification of operators. However, we do not wish to imply that our theory is somehow monolithic and ‘closed’. Recent developments relevant to the problematic of unity have been well summarized by Jordi Cat in his article on the Unity of Science in the Stanford Encyclopedia of Philosophy [61]. Unification must not be created on the principle of ‘unity for the sake of unity”. Cat notes several positive, anti-reductionist trends in the philosophy of science, for example in moving from dependence on the concepts primarily taken from physics. One is struck, in fact, by the diversity of the sense, which can be given to the definition of unity! These definitions range from the possible single nature of the underlying ‘stuff’ of the universe, to the unification of the disciplines within science and with regard to these whether on is dealing with concepts or terms or the higher-level entity of theory and whether the relations are ones of reduction, explanation or logical inference. Cat suggests that the concept of unity can have a definite value at the practical level in science, to justify approaches and goals, and in philosophy to help choose what philosophical questions to pursue and what target areas to explore. The Unity of Science could suggest what science is to be referenced by philosophy as authoritative. He touches upon our point in the first paragraph by suggesting that “unities and unifications help us meet cognitive and practical demands upon our life…, contribute to our self-image and be seen as a source of aesthetic value, providing a grip on our intellectual imagination.” Our approach extends this view: the value of the Unity of Science, self-referentially, is itself a unity of a sort that neglects, intentionally or not, the value of diversity. We believe it is necessary to do so explicitly. Informational processes, in our theory and logic, are composites of unities (identities) and diversities and all share in part the properties of their opposites. We consider these remarks applicable to all theories of ‘unity’ whether of operators, science or knowledge.
7.2. Operators or Agents?
The debate regarding agency has taken on further dimensions for theories of mind with the advent of complex computational capabilities that seem to confer some kind of autonomy on machine operators, the artificial or machine operators that have been discussed briefly in this paper. The problem is that that there is no exact unambiguous definition of an agent. Traditional definition assumes that an agent is a system who/that acts on behalf of or/and represents another system or other systems, e.g., a businessman who buys or sells for another in exchange for a commission. A more modern understanding treats an agent either as a system who/that exerts some force or effect or as a system who/that acts or has the power or authority to act.
According to the traditional definition, any agent is an operator because to accomplish his/her/its mission, the agent has to operate. However, there are operators that are not agents because they are aimed at their own goals. This gives us two types of operators:
- Agent-operators who/that act/operate on behalf of or/and represent other systems.
- Free operators who/that are act/operate forming their goals and behavior by themselves.
Following our discussion of the requirements for moral responsibility that human operators have and the principle, inherent in LIR of required indeterminacy in entities resulting from the chain of potentializations in natural evolution, implies that no machine that is the result of human determination can be considered completely autonomous. All the functionality involved in machines apparently capable of autonomy is the consequence of utilization of symbolic operators and operations. However, to some extent, the same conclusion is true for people, autonomy of which is always more or less restricted. There are even situations when people in a definite state, e.g., one equivalent to zombies, act like machines directed/operated by others.
We thus propose, as one main conclusion of this study, that only natural human operators should be designated as agents. All others, that is, all symbolic and machine operators are consequently, non-agents and should be so designated. An interesting problem is to consider groups and association of agents in the context of the operator theory developed in this paper because, typically, agents form groups and other collective agents, whose behavior, as in the case of groups discussed above, may not be totally reducible to that of individual members.
Our next intention is to develop the concept of operators in both theoretical and practical directions. Our approach, which uses the tools of the General Theory of Information and Logic in Reality, can be also applied to the categorization of the various types of symbolic operators—mathematical, logical and linguistic—being derivable from natural operators. In particular, the issue of symbolic operators in Information Technology and Computer Science is addressed elsewhere.
7.3. Operators in Philosophy
Philosophical issues of our theory of operators arise in part due to changes in the foundations of knowledge, which both authors of this paper have discussed in different contexts. One focuses on the role and future of transdisciplinarity as a movement at the interface of science and philosophy. Another focuses on the impact on philosophy in general of the convergence in progress of the philosophy of information and information science.
In the preceding sections of this paper, we have provided definitions of operators primarily from the standpoints of mathematics, logic and science. The philosophical discussion was essentially limited to a classification of properties. Readers can see, we hope clearly, a thread of additional philosophical considerations running through this paper. In our analysis of both simple and complex operators, we take into account questions of causality, intentionality and meaning. Our discussion of the cognitive as well as physical role of operators thus raises further questions about their role in philosophy itself; it is demonstrated in the Introduction that operators are basic for ontology and epistemology. In addition, the role of natural and cognitive operators cannot be included in a structureless concept of functionalism. The identification of natural operators in the cognitive domain suggests that a recursive analysis of the implications of operators for what philosophy ‘is’ is required. A proper philosophical discussion of complex operators must accept their ontological existence as dynamic structures. This amounts to a second order naturalization of our theory of operators.
Issues in the areas of the naturalization of phenomenology and the naturalization of the philosophy of science will be familiar to readers of this Journal. Naturalization means, roughly, ‘bringing into science’ from a domain, philosophy, that can be defined as a set of disciplines—logic, ontology, metaphysics, epistemology—and their use via reasoning and analysis to arrive at a viewpoint about what it is for human beings to be alive and think. The primary domain of naturalization has been that of the Philosophy of Science. In other areas, we note the naturalization of epistemology of Quine [62] although his discussion seems limited to linguistic logical elements. Another recent example is the naturalization of metaphysics by Ladyman, Ross and their colleagues [63]. We also note the application by Petitot-Cocorda [64] of his catastrophe theory to the naturalization of phenomenology, as well as a major compendium on the subject [65].
This study reflects the convergence of science and philosophy, at least in the area of information considered by Wu Kun, who writes that it is impossible to separate information – information science - from its philosophy or metaphilosophy [66]. Our tentative conclusion is therefore that there is a philosophical dimension to the natural operators, which we have observed acting in cognitive processes and involving information, that is, in all cognitive processes. This convergence is obviously not intended to imply an ‘end’ to philosophy or its conflation with science. Philosophy will continue to explore issues that arise, in particular, in relation to language and knowledge in their aspects as unique cognitive products of the human condition, with a substantial abstract content. However, the question of relations of that condition to the rest of the world logically requires retaining the scientific properties of that world to insure the validity of the comparison. There is a set of new and unique relationships, which are developing between the classical disciplines of science and philosophy based on a new understanding of the science and philosophy of information. The overall movement is philosophization of science and scientification of philosophy, as Wu has described it. An example of such scientification and naturalization of philosophy is the article by Brenner [67] on the naturalization of the philosophy of Rafael Capurro, who is a scientist and philosopher of information.
The role of operators is especially important in epistemology where cognitive and epistemic operators model cognitive processes providing efficient means for exploration of knowledge and information [68,69,70,71].
In conclusion, it is useful to understand that our new logical conception and categorization of operators and their functioning provides sound foundation for a scientification of philosophy. On the one hand, this conceptual paper provides a further basis for discussion of key issues in information and the philosophy of science in the emerging Information Society, since it describes both the quantitative and qualitative properties of information as both a symbolic and natural operator itself. On the other, our discussion of natural operators in machines, humans, organizations and knowledge provides a new perspective for the potential discussion of new models of society and a further basis for differentiation between human and non-human agents and their respective ethical characteristics.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bickhard, M.H. The interactivist model. Synthese 2009, 166, 547–591. [Google Scholar] [CrossRef]
- Burgin, M. Theory of Information: Fundamentality, Diversity and Unification; World Scientific: New York, NY, USA; London, UK; Singapore, 2010. [Google Scholar]
- Nicolescu, B. Manifesto of Transdisciplinarity; State University of New York Press: Albany, NY, USA, 2002. [Google Scholar]
- Bennett, M.R.; Hacker, P.M.S. Philosophical Foundations of Neuroscience; Blackwell Publishing: Malden, MA, USA, 2003. [Google Scholar]
- Brenner, J.E. Logic in Reality; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Jordan, T.F. Linear Operators for Quantum Mechanics; John Wiley & Sons, Inc.: NewYork, NY, USA, 1969. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Davies, E.B.; Lewis, J.T. An Operational Approach to Quantum Probability. Commun. Math. Phys. 1970, 17, 239–260. [Google Scholar] [CrossRef]
- Kraus, K. States, Effects and Operations; Springer: Berlin, Germany, 1983. [Google Scholar]
- Ludwig, G. Versuch einer axiomatischen Grundlegung der Quanten mechanik und allgemeinerer physikalischer Theorien. Z. Phys. 1964, 181, 233–260. [Google Scholar] [CrossRef]
- Scarrott, G.G. The Nature of Information. Comput. J. 1989, 32, 262–266. [Google Scholar] [CrossRef]
- Reading, A. The Biological Nature of Meaningful Information. Biol. Theory 2006, 1, 243–249. [Google Scholar] [CrossRef]
- Csanyi, V. Evolutionary Systems and Society; Duke University Press: Durham, NC, USA; London, UK, 1989. [Google Scholar]
- Kampis, G.A. Causal Model of Evolution. 1991. Available online: http://www.jaist.ac.jp/~g-kampis/SEAL02/A_Causal_Model_of_Evolution.htm (accessed on 21 March 2017).
- Burgin, M.; Simon, I. Information, Energy, and Evolution. Preprintin Biology 2359, Cogprints. 2001. Available online: http://cogprints.ecs.soton.ac.uk (accessed on 21 March 2017).
- Smith, J.M.; Szathmary, E. The Origins of Life: From the Birth of Life to the Origin of Language I; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Deacon, T.W. Incomplete Nature. How Mind Evolved from Matter; W.W. Norton & Co.: London, UK; New York, NY, USA, 2012. [Google Scholar]
- Crutchfield, J.P. Information and its Metric. In Nonlinear Structures in Physical Systems—Pattern Formation, Chaos and Waves; Springer: New York, NY, USA, 1990. [Google Scholar]
- Landauer, R. Information is Inevitably Physical. In Feynman and Computation: Exploring the Limits of Computers; Westview Press: Oxford, UK, 2002; pp. 76–92. [Google Scholar]
- Kaye, D. The nature of information. Libr. Rev. 1995, 44, 37–48. [Google Scholar] [CrossRef]
- Sinden, R. DNA Structure and Function; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Loewenstein, W.R. The Touchstone of Life: Molecular Information, Cell Communication, and the Foundation of Life; OxfordUniversity Press: Oxford, UK; New York, NY, USA, 1999. [Google Scholar]
- Smolin, L. The Life of the Cosmos; Oxford University Press: Oxford, UK; New York, NY, USA, 1999. [Google Scholar]
- Stonier, T. Towards a new theory of information. J. Inf. Sci. 1991, 17, 257–263. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Information in the holographic universe. Sci. Am. 2003, 289, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.A. Information, Physics, Quantum: The Search for Links. In Complexity, Entropy, and the Physics of Information; Zurek, W., Ed.; Addison-Wesley: Redwood City, CA, USA, 1990; pp. 3–28. [Google Scholar]
- Brenner, J.E. The Philosophical Logic of Stéphane Lupasco. Log. Log. Philos. 2010, 19, 243–285. [Google Scholar]
- Burgin, M. Structural Reality; Nova Science Publishers: New York, NY, USA, 2012. [Google Scholar]
- Jacquette, D. Philosophy of Logic. In Handbook of the Philosophy of Science Series; Gabbay, D., Woods, J., Thagard, P., Eds.; North-Holland Press (Elsevier): Amsterdam, The Netherlands, 2007. [Google Scholar]
- Brenner, J.E. Stéphane Lupasco et la Rejonction Métalogique. In A la Confluence de deux Cultures: Lupasco Aujourd’hui, Proceedings of the International UNESCO Colloquium, Paris, France, 24 March 2010; Editions Oxus: Paris, France, 2010; pp. 250–285. [Google Scholar]
- Brenner, J.E. Processing Reality: A Logical Offering. Log. Philos. 2005, 14, 165–189. [Google Scholar]
- Burgin, M. Theory of Named Sets; Nova Science Publishers: New York, NY, USA, 2011. [Google Scholar]
- Ghils, P. Les Tensions du Langage; Peter Lang: Berne/Berlin, Germany, 1994. [Google Scholar]
- Jakobson, R. Language in Literature; Belknap Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Prigogine, I. From Being to Becoming: Time and Complexity in Physical Systems; Freeman & Co.: San Francisco, CA, USA, 1980. [Google Scholar]
- Woodward, J. Causation and Manipulability. In Stanford Encyclopedia of Philosophy (Fall 2001 Edition); Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2001; Available online: http://plato.stanford.edu/archives/fall2001/entries/causation-mani/ (accessed on 21 March 2017).
- Dowe, P. Causal Processes. In The Stanford Encyclopedia of Philosophy (Fall 2008 Edition); Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2008; Available online: http://plato.standford.edu/archives/fall2008/entries/causation-process/ (accessed on 21 March 2017).
- Jung, C.G. Two Essays on Analytical Psychology; Adler, G., Hull, R.F.C., Eds.; World Publishing (Meridian): New York, NY, USA; Cleveland, OH, USA, 1971; pp. 63–71. [Google Scholar]
- Minati, G.; Pessa, E. Collective Beings; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Freud, S. The Ego and the Id; The Hogarth Press Ltd.: London, UK, 1949. [Google Scholar]
- Burgin, M. Structural traits of psychoanalysis. Visnik Natl. Acad. Sci. Ukr. 1994, 2, 45–50. (In Ukrainian) [Google Scholar]
- Lupasco, S. L’énergie et la Matière Vivante; Éditions du Rocher: Monaco-Ville, Monaco, 1986. [Google Scholar]
- Burgin, M. Triad as a Fundamental Structure in Human Culture. Stud. Culturol. 1993, 2, 51–63. [Google Scholar]
- Leydesdorff, L. The Knowledge-Based Economy: Modeled, Measured, Simulated; Universal Publishers: Boca Raton, FL, USA, 2006. [Google Scholar]
- D’Entreves, M.P. Hannah Arendt. In The Stanford Encyclopedia of Philosophy (Fall 2008 Edition); Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2008; Available online: http://plato.stanford.edu/archives/fall2008/entries/arendt/ (accessed on 21 March 2017).
- Magnani, L. Morality in a Technological World: Knowledge as Duty; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Thom, R. Stabilité Structurelle et Morphogénèse; W.A. Benjamin, Inc.: Reading, MA, USA, 1972. [Google Scholar]
- Lupasco, S. Logique et Contradiction; Presses Universitaires de France: Paris, France, 1947. [Google Scholar]
- Esfeld, M.; Lam, V. Holism and Structural Realism. In Worldviews Science and Us: Studies of Analytical Metaphysics; Vanderbeeken, R., Weber, E., Eds.; World Scientific: Singapore, 2010. [Google Scholar]
- Smith, D.W. Intentionality Naturalized? In Naturalizing Phenomenology: Issues in Contemporary Phenomenology and Cognitive Science; Petitot, J., Varela, F.J., Pachoud, B., Roy, J.-M., Eds.; Stanford University Press: Stanford, CA, USA, 1999. [Google Scholar]
- Seibt, J. Forms of interaction in General Process Theory. Synthese 2009, 166, 479–512. [Google Scholar] [CrossRef]
- Wu, K. The Basic Theory of Philosophy of Information. In Proceedings of the 4th International Conference on the Foundations of Information Science, Beijing, China, 21–24 August 2010. [Google Scholar]
- Fuchs, C. The Dialectic of the Nature-Society System. Triple C 2006, 4, 1–39. [Google Scholar]
- Varela, F.J. The Specious Present. In Naturalizing Phenomenology: Issues in Contemporary Phenomenology and Cognitive Science; Petitot, J., Varela, F.J., Pachoud, B., Roy, J.-M., Eds.; Stanford University Press: Stanford, CA, USA, 1999. [Google Scholar]
- Haken, H. Advanced Synergetics: Instability Hierarchies of Self-Organizing Systems and Devices; Springer: New York, NY, USA, 1993. [Google Scholar]
- Luhmann, N. Social Systems; Stanford University Press: Stanford, CA, USA, 1995. [Google Scholar]
- Skinner, B.F. Science and Human Behavior; Simon & Schuster: New York, NY, USA, 1953. [Google Scholar]
- Manz, C.C.; Mossholder, K.W.; Luthanvs, F. Controlling Information Systems Development Projects: The View from the Client. Manag. Sci. 2002, 48, 484–498. [Google Scholar]
- Burgin, M.; Gladun, V. Mathematical Foundations of Semantic Networks Theory. Lect. Notes Comput. Sci. 1989, 364, 117–135. [Google Scholar]
- Cat, J. The Unity of Science. In Stanford Encyclopedia of Philosophy (Winter 2014 Edition); Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2014; Available online: http://plato.stanford.edu/archives/win2014/entries/scientific-unity/ (accessed on 21 March 2017).
- Van Quine, W.O. Epistemology Naturalized. In Ontological Relativity and Other Essays; Columbia University Press: New York, NY, USA, 1969; Chapter3. [Google Scholar]
- Ladyman, J.; Ross, D. Every Thing Must Go: Metaphysics Naturalized; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Petitot-Cocorda, J. Physique du Sens; CNRS Éditions: Paris, France, 1992. [Google Scholar]
- Petitot, J.; Varela, F.J.; Pachoud, B.; Roy, J.-M. (Eds.) Naturalizing Phenomenology: Issues in Contemporary Phenomenology and Cognitive Science; Stanford University Press: Stanford, CA, USA, 1999. [Google Scholar]
- Wu, K. The Interaction and Convergence of the Philosophy and Science of Information. Philosophies 2016, 1, 228–244. [Google Scholar] [CrossRef]
- Brenner, J.E. The ‘Naturalization’ of the Philosophy of Rafael Capurro. In A Festschrift in Honor of Rafael Capurro; Kelly, M., Bielby, J., Eds.; Springer: Wiesbaden, Germany, 2016; pp. 45–64. [Google Scholar]
- Burgin, M. Epistemic Information in Stratified M-Spaces. Information 2011, 2, 697–726. [Google Scholar] [CrossRef]
- Burgin, M. Weighted E-Spaces and Epistemic Information Operators. Information 2014, 5, 357–388. [Google Scholar] [CrossRef]
- Burgin, M. Theory of Knowledge: Structures and Processes; World Scientific: New York, NY, USA; London, UK; Singapore, 2016. [Google Scholar]
- Burgin, M.; Mikkilineni, R.; Mittal, S. Knowledge processing as structure transformation. Proceedings 2017, 1, 212. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).