Determining the Age of Terrace Formation Using Luminescence Dating—A Case of the Yellow River Terraces in the Baode Area, China
Abstract
1. Introduction
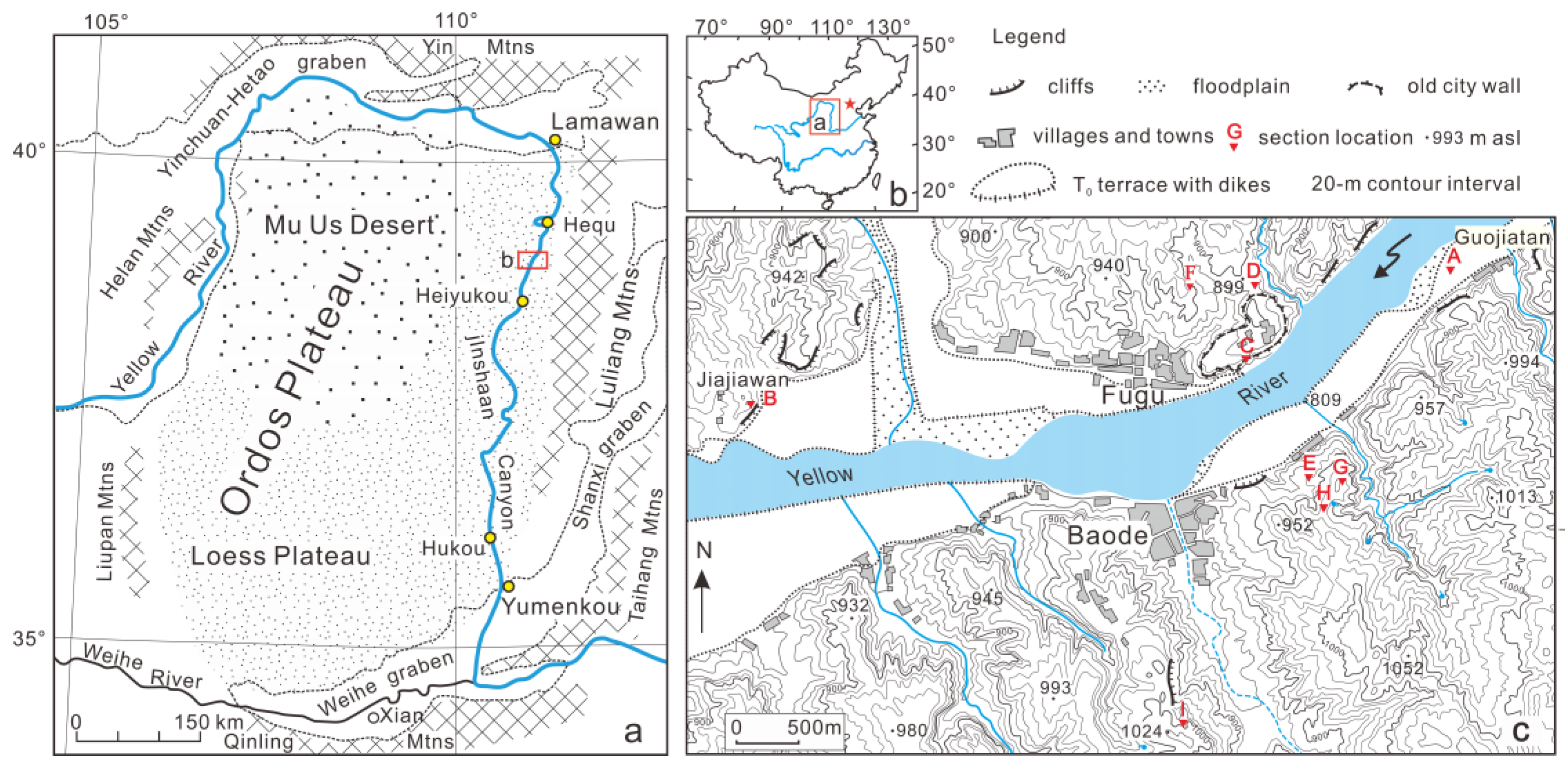
2. Geological and Geomorphologic Setting
3. Methodology
3.1. Field Work
3.2. Optical Dating
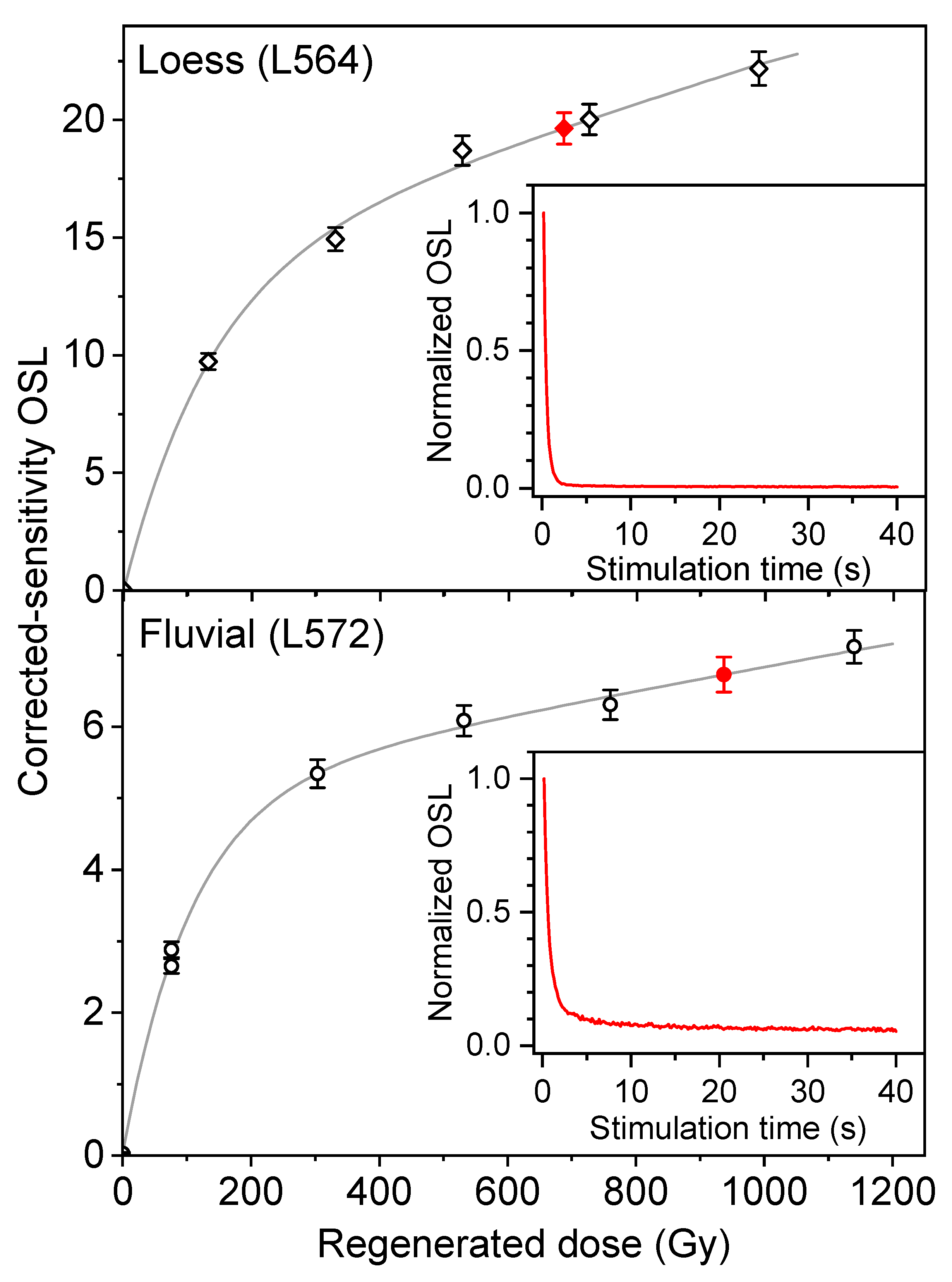
3.2.1. Equivalent Dose Measurements
3.2.2. Dose Rate Determination
4. Results
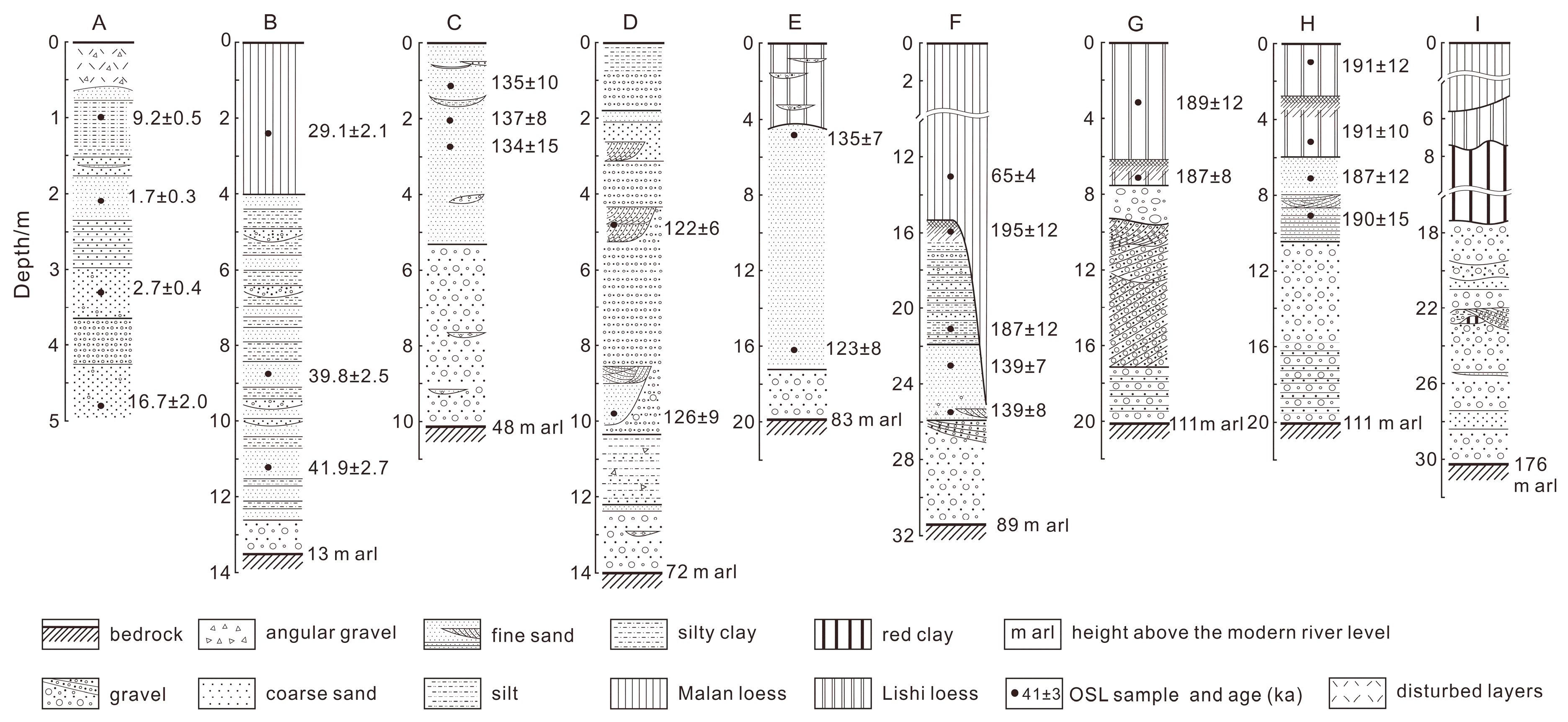
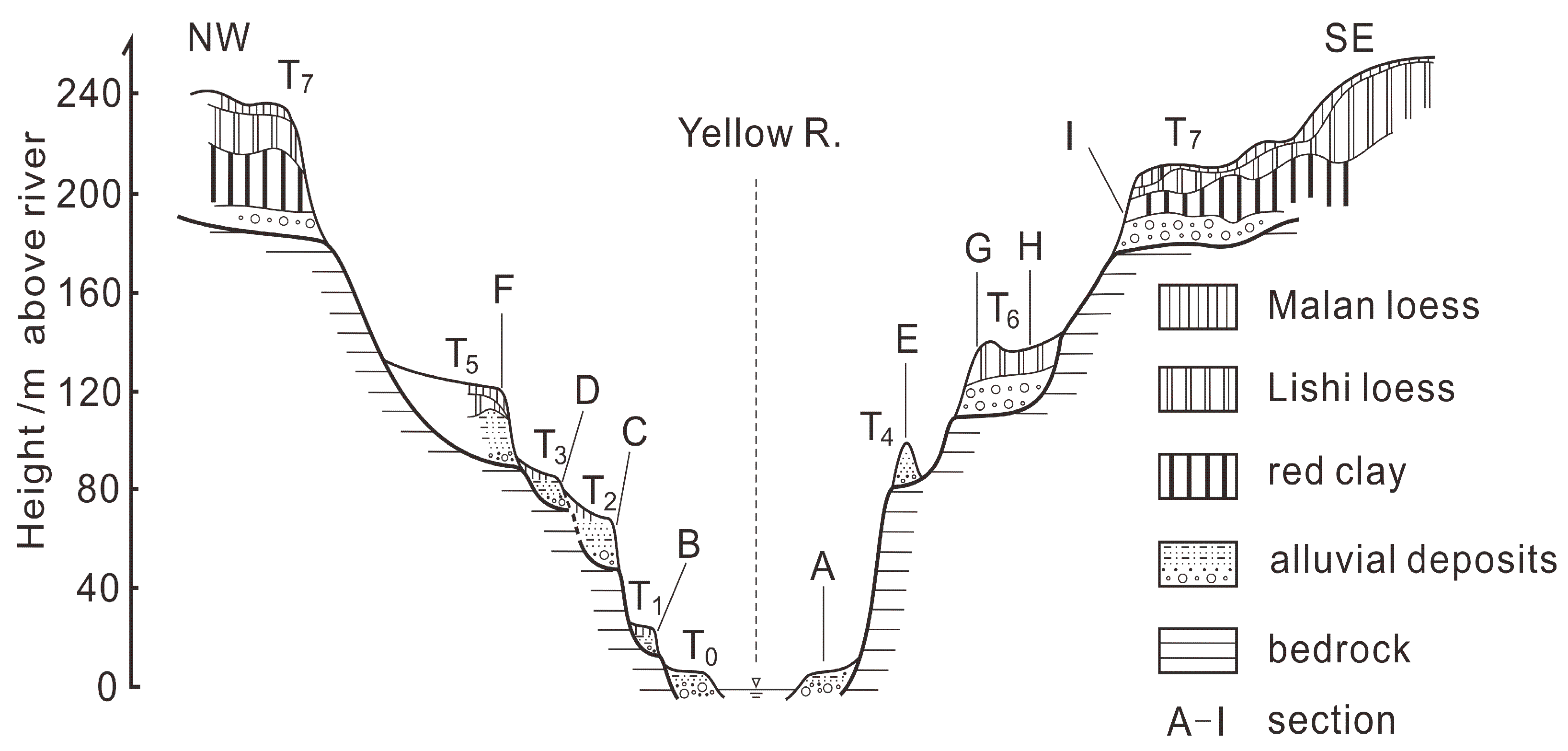
4.1. Terraces and Deposits
4.2. OSL Ages
5. Discussion
5.1. Reliability of OSL Ages
5.2. Terrace Ages and River Incision Rates
5.3. Implication for Dating Fluvial Terraces
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Merritts, D.J.; Vincent, K.R.; Wohl, E.E. Long river profiles, tectonism, and eustasy: A guide to interpreting fluvial terraces. J. Geoph. Res. 1994, 99, 14031–14050. [Google Scholar] [CrossRef]
- Lavé, J.; Avouac, J.P. Fluvial incision and tectonic uplift across the Himalayas of central Nepal. J. Geoph. Res. Solid Earth 2001, 106, 26561–26591. [Google Scholar] [CrossRef]
- Mishra, S.; White, M.J.; Beaumont, P.; Antoine, P.; Bridgland, D.R.; Limondin-Lozouet, N.; Santisteban, J.I.; Schreve, D.C.; Shaw, A.D.; Wenban-Smith, F.F.; et al. Fluvial deposits as an archive of early human activity. Quat. Sci. Rev. 2007, 26, 2996–3016. [Google Scholar] [CrossRef]
- Wegmann, K.W.; Pazzaglia, F.J. Late Quaternary fluvial terraces of the Romagna and Marche Apennines, Italy: Climatic, lithologic, and tectonic controls on terrace genesis in an active orogen. Quat. Sci. Rev. 2009, 28, 137–165. [Google Scholar] [CrossRef]
- Chauhan, P.R.; Bridgland, D.R.; Moncel, M.-H.; Antoine, P.; Bahain, J.-J.; Briant, R.; Cunha, P.; Despriée, J.; Limondin-Lozouet, N.; Locht, J.-L.; et al. Fluvial deposits as an archive of early human activity: Progress during the 20 years of the Fluvial Archives Group. Quat. Sci. Rev. 2017, 166, 114–119. [Google Scholar] [CrossRef]
- Aitken, M.J. An Introduction to Optical Dating: The Dating of Quaternary Sediments by the Use of Photon-stimulated Luminescence; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Rhodes, E.J. Optically stimulated luminescence dating of sediments over the past 200000 years. Annu Rev. Earth Planet. Sci. 2011, 39, 461–488. [Google Scholar] [CrossRef]
- Rittenour, T.M. Dates and rates of earth-surface processes revealed using Luminescence dating. Elements 2018, 14, 21–26. [Google Scholar] [CrossRef]
- Wallinga, J. Optically stimulated luminescence dating of fluvial deposits: A review. Boreas 2002, 31, 303–322. [Google Scholar] [CrossRef]
- Traher, I.M.; Mauz, B.; Chiverrell, R.C.; Lang, A. Luminescence dating of glaciofluvial deposits: A review. Earth Sci. Rev. 2009, 97, 133–146. [Google Scholar]
- Fuller, T.K.; Perg, L.A.; Willenbring, J.K.; Lepper, K. Field evidence for climate-driven changes in sediment supply leading to strath terrace formation. Geology 2009, 37, 467–470. [Google Scholar] [CrossRef]
- Gong, Z.J.; Li, S.H.; Li, B. The evolution of a terrace sequence along the Manas River in the northern foreland basin of Tian Shan, China, as inferred from optical dating. Geomorphology 2014, 213, 201–212. [Google Scholar] [CrossRef]
- Gong, Z.J.; Li, S.H.; Li, B. Late Quaternary faulting on the Manas and Hutubi reverse faults in the northern foreland basin of Tian Shan, China. Earth Planet. Sci. Lett. 2015, 424, 212–225. [Google Scholar] [CrossRef]
- Fu, X.; Cohen, T.J.; Fryirs, K. Single-grain OSL dating of fluvial terraces in the upper Hunter catchment, southeastern Australia. Quat. Geochronol. 2019, 49, 115–122. [Google Scholar] [CrossRef]
- Fu, X.; Li, S.-H.; Li, B.; Fu, B. A fluvial terrace record of late Quaternary folding rate of the Anjihai anticline in the northern piedmont of Tian Shan, China. Geomorphology 2017, 278, 91–104. [Google Scholar] [CrossRef]
- Hancock, G.S.; Anderson, R.S. Numerical modeling of fluvial strath-terrace formations in response to oscillating climate. Geol. Soc. Am. Bull. 2002, 114, 1131–1142. [Google Scholar]
- Foster, M.A.; Anderson, R.S.; Gray, H.J.; Mahan, S.A. Dating of river terraces along Lefthand Creek, western High Plains, Colorado, reveals punctuated incision. Geomorphology 2017, 295, 176–190. [Google Scholar] [CrossRef]
- Zhang, J.F.; Qiu, W.L.; Li, R.Q.; Zhou, L.P. The evolution of a terrace sequence along the Yellow River (HuangHe) in Hequ, Shanxi, China, as inferred from optical dating. Geomorphology 2009, 109, 54–65. [Google Scholar] [CrossRef]
- Guo, Y.J.; Zhang, J.F.; Qiu, W.L.; Hu, G.; Zhuang, M.G.; Zhou, L.P. Luminescence dating of the Yellow River terraces in the Hukou area, China. Quat. Geochronol. 2012, 10, 129–135. [Google Scholar] [CrossRef]
- Yan, Y.Y.; Zhang, J.F.; Hu, G.; Zhou, L.P. Luminescence chronology of the Yellow River terraces in the Heiyukou area, China, and its implication for the uplift rate of the Ordos Plateau. Geochronometria. in press.
- Cheng, S.P.; Deng, Q.D.; Zhou, S.W.; Yang, G.Z. Strath terraces of Jinshaan Canyon, Yellow River, and Quaternary tectonic movements of Ordos Plateau, North China. Terra Nova 2002, 14, 215–224. [Google Scholar] [CrossRef]
- Pan, B.T.; Hu, Z.B.; Wang, J.P.; Vandenberghe, J.; Hu, X.F. A magnetostratigraphic record of landscape development in the eastern Ordos Plateau, China: Transition from Late Miocene and Early Pliocene stacked sedimentation to Late Pliocene and Quaternary uplift and incision by the Yellow River. Geomorphology 2011, 125, 225–238. [Google Scholar] [CrossRef]
- Pan, B.T.; Hu, Z.B.; Wang, J.P.; Vandenberghe, J.; Hu, X.F.; Wen, Y.H.; Li, Q.; Cao, B. The approximate age of the planation surface and the incision of the Yellow River. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2012, 356, 54–61. [Google Scholar] [CrossRef]
- Hu, Z.; Pan, B.; Bridgland, D.R.; Vandenberghe, J.; Guo, L.; Fan, Y.; Westaway, R. The linking of the upper-middle and lower reaches of the Yellow River as a result of fluvial entrenchment. Quat. Sci. Rev. 2017, 166, 324–338. [Google Scholar] [CrossRef]
- Qiu, W.L.; Zhang, J.F.; Wang, X.Y.; Guo, Y.J.; Zhuang, M.G.; Fu, X.; Zhou, L.P. The evolution of the Shiwanghe River valley in response to the Yellow River incision in the Hukou area, Shaanxi, China. Geomorphology 2014, 215, 34–44. [Google Scholar] [CrossRef]
- Meng, Y.M.; Zhang, J.F.; Qiu, W.L.; Fu, X.; Guo, Y.J.; Zhou, L.P. Optical dating of the Yellow River terraces in the Mengjin area (China): First results. Quat. Geochronol. 2015, 30, 219–225. [Google Scholar] [CrossRef]
- Chen, X.B.; Zang, S.X.; Wei, R.Q. Is the stable Ordos block migrating as an entire block? Chin. J. Geophy 2011, 54, 1750–1757. [Google Scholar]
- Bao, X.W.; Xu, M.J.; Wang, L.S.; Mi, N.; Yu, D.Y.; Li, H. Lithospheric structure of the Ordos Block and its boundary areas inferred from Rayleigh wave dispersion. Tectonophysics 2011, 499, 132–141. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Mercier, J.L.; Vergely, P. Extension in the graben systems around the Ordos (China), and its contribution to the extrusion tectonics of south China with respect to Gobi-Mongolia. Tectonophysics 1998, 285, 41–75. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Liao, C.Z.; Shi, W.; Hu, B. Neotectonic evolution of the peripheral zones of the Ordos Basin and geodynamic setting. Geol. J. China Univ. 2006, 12, 285–297, (In Chinese with English abstract). [Google Scholar]
- Deng, G.D.; Cheng, S.P.; Min, W.; Yang, G.Z.; Reng, D.W. Discussion on Cenozoic tectonics and dynamics of Ordos block. J. Geom. 1999, 5, 13–21. (In Chinese) [Google Scholar]
- Lin, A.M.; Yang, Z.Y.; Sun, Z.M.; Yang, T.S. How and when did the Yellow River develop its square bend? Geology 2001, 29, 951–954. [Google Scholar] [CrossRef]
- Darby, B.J.; Ritts, B.D. Mesozoic contractional deformation in the middle of the Asian tectonic collage: The intraplate Western Ordos fold–thrust belt, China. Earth Planet. Sci. Lett. 2002, 205, 13–24. [Google Scholar] [CrossRef]
- Yang, M.H.; Liu, C.Y.; Zheng, M.L.; Lan, C.L.; Tang, X. Sequence framework of two different kinds of margins and their response to tectonic activity during the Middle-Late Triassic, Ordos Basin. Sci. China Ser. D 2007, 50, 203–216. [Google Scholar] [CrossRef]
- Yue, L.; Li, J.; Zheng, G.; Li, Z. Evolution of the Ordos Plateau and environmental effects. Sci. China Ser. D 2007, 50, 19–26. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Ma, Y.S.; Yang, N.; Shi, W.; Dong, S.W. Cenozoic extensional stress evolution in North China. J. Geodyn. 2003, 36, 591–613. [Google Scholar]
- Zhang, J.F.; Zhou, L.P.; Yue, S.Y. Dating fluvial sediments by optically stimulated luminescence: Selection of equivalent doses for age calculation. Quat. Sci. Rev. 2003, 22, 1123–1129. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhou, L.P. Optimization of the ‘double SAR’ procedure for polymineral fine grains. Radiat. Meas. 2007, 42, 1475–1482. [Google Scholar] [CrossRef]
- Murray, A.S.; Wintle, A.G. Luminescence dating of quartz using an improved single-aliquot regenerative-dose protocol. Radiat. Meas. 2000, 32, 57–73. [Google Scholar] [CrossRef]
- Wintle, A.G.; Murray, A.S. A review of quartz optically stimulated luminescence characteristics and their relevance in single-aliquot regeneration dating protocols. Radiat. Meas. 2006, 41, 369–391. [Google Scholar] [CrossRef]
- Duller, G.A.T. Assessing the error on equivalent dose estimates derived from single aliquot regenerative dose measurements. Anc. TL 2007, 25, 15–24. [Google Scholar]
- Bøtter-Jensen, L.; Bulur, E.; Duller, G.A.T.; Murray, A.S. Advances in luminescence instrument systems. Radiat. Meas. 2000, 32, 523–528. [Google Scholar] [CrossRef]
- Rees-Jones, J. Optical dating of young sediments using fine-grain quartz. Anc. TL 1995, 13, 9–14. [Google Scholar]
- Durcan, J.A.; King, G.E.; Duller, G.A.T. DRAC: Dose rate and age calculator for trapped charge dating. Quat. Geochronol. 2015, 28, 54–61. [Google Scholar] [CrossRef]
- Guerin, G.; Mercier, N.; Adamiec, G. Dose-rate conversion factors: Update. Anc. TL 2011, 29, 5–8. [Google Scholar]
- Brennan, B.J.; Lyons, R.G.; Phillips, S.W. Attenuation of alpha particle track dose for spherical grains. Int. J. Radiat. Appl. Instrum. Part D 1991, 18, 249–253. [Google Scholar] [CrossRef]
- Guerin, G.; Mercier, N.; Nathan, R.; Adamiec, C.; Lefrais, Y. On the use of the infinite matrix assumption and associated concepts: A critical review. Radiat. Meas. 2012, 47, 778–785. [Google Scholar] [CrossRef]
- Ding, Z.L.; Sun, J.M.; Liu, T.S.; Zhu, R.X.; Yang, S.L.; Guo, B. Wind-blown origin of the Pliocene red-clay formation in the central Loess Plateau, China. Earth Planet. Sci. Lett. 1998, 161, 135–143. [Google Scholar] [CrossRef]
- Zhu, Y.M.; Zhou, L.P.; Mo, D.W.; Kaakinen, A.; Zhang, Z.Q.; Fortelius, M. A new magnetostratigraphic framework for late Neogene Hipparion Red Clay in the eastern Loess Plateau of China. Palaeogeogr. Palaeocl. Palaeoecol. 2008, 268, 47–57. [Google Scholar] [CrossRef]
- Galbraith, R.F.; Roberts, R.G.; Laslett, G.M.; Yoshida, H.; Olley, J.M. Optical dating of single and multiple grains of quartz from Jinmium rock shelter, Northern Australia: Part I, experimental design and statistical models. Archaeometry 1999, 41, 339–364. [Google Scholar] [CrossRef]
- Dietze, M.; Kreutzer, S.; Burow, C.; Fuchs, M.C.; Fischer, M.; Schmidt, C. The abanico plot: Visualising chronometric data with individual standard errors. Quat. Geochronol. 2016, 31, 12–18. [Google Scholar] [CrossRef]
- Vermeesch, P. RadialPlotter: A Java application for fission track, luminescence and other radial plots. Radiat. Meas. 2009, 44, 409–410. [Google Scholar] [CrossRef]
- Galraith, R.F.; Green, P.F. Estimating the component ages in a finite mixture. Nucl. Tracks Radiat. Meas. 1990, 17, 197–206. [Google Scholar] [CrossRef]
- Arnold, L.J.; Bailey, R.M.; Tucker, G.E. Statistical treatment of fluvial dose distributions from southern Colorado arroyo deposits. Quat. Geochronol. 2007, 2, 162–167. [Google Scholar] [CrossRef]
- Hu, G.; Zhang, J.F.; Qiu, W.L.; Zhou, L.P. Residual OSL signals in modern fluvial sediments from the Yellow River (HuangHe) and the implications for dating young sediments. Quat. Geochronol. 2010, 5, 187–193. [Google Scholar] [CrossRef]
- Alexanderson, H. Residual OSL signals from modern Greenlandic river sediments. Geochronometria 2007, 26, 1–9. [Google Scholar] [CrossRef]
- Jain, M.; Murray, A.S.; Bøtter-Jensen, L. Optically stimulated luminescence dating: How significant is incomplete light exposure in fluvial environments. Quaternaire 2004, 15, 143–157. [Google Scholar] [CrossRef]
- Toth, O.; Sipos, G.; Kiss, T.; Bartyik, T. Variation of OSL residual doses in terms of coarse and fine grain modern sediments along the Hungarian section of the Danube. Geochronometria 2017, 44, 319–330. [Google Scholar] [CrossRef]
- Chamberlain, E.L.; Walling, J. Seeking enlightenment of fluvial sediment pathways by optically stimulated luminescence signal bleaching of river sediments and deltaic deposits. Earth Surf. Dynam. 2019, 7, 723–736. [Google Scholar] [CrossRef]
- Xu, J.X.; Yang, J.S.; Yan, Y.X. Erosion and sediment yields as influenced by coupled eolian and fluvial processes: The Yellow River, China. Geomorphology 2006, 73, 1–15. [Google Scholar] [CrossRef]
- Duller, G.A. Single-grain optical dating of Quaternary sediments: Why aliquot size matters in luminescence dating. Boreas 2008, 37, 589–612. [Google Scholar] [CrossRef]
- Thomsen, K.J.; Murray, A.S.; Jain, M. The dose dependency of the over- dispersion of quartz OSL single grain dose distributions. Radiat. Meas. 2012, 47, 732–739. [Google Scholar] [CrossRef]
- Reimann, T.; Lindhorst, S.; Thomsen, K.J.; Murray, A.S.; Frechen, M. OSL dating of mixed coastal sediment (Sylt, German Bight, North Sea). Quat. Geochronol. 2012, 11, 52–67. [Google Scholar] [CrossRef]
- Rui, X.; Li, B.; Guo, Y.J.; Zhang, J.F.; Yuan, B.Y.; Xie, F. Variability in the thermal stability of OSL signal of single-grain quartz from the Nihewan Basin, North China. Quat. Geochronol. 2019, 49, 25–30. [Google Scholar] [CrossRef]
- Jankowski, N.R.; Jacobs, Z. Beta dose variability and its spatial contextualisation in samples used for optical dating: An empirical approach to examining beta microdosimetry. Quat. Geochronol. 2018, 44, 23–37. [Google Scholar] [CrossRef]
- Zhang, J.F.; Qiu, W.L.; Wang, X.Q.; Hu, G.; Li, R.-Q.; Zhou, L.-P. Optical dating of a hyperconcentrated flow deposit on a Yellow River terrace in Hukou, Shaanxi, China. Quat. Geochronol. 2010, 5, 194–199. [Google Scholar] [CrossRef]
- Zhang, J.F.; Wang, X.Q.; Qiu, W.L.; Shelach, G.; Hu, G.; Fu, X.; Zhuang, M.G.; Zhou, L.P. The paleolithic site of Longwangchan in the middle Yellow River, China: Chronology, paleoenvironment and implications. J. Archaeol. Sci. 2011, 38, 1537–1550. [Google Scholar] [CrossRef]
- Sawakuchi, A.O.; Jain, M.; Mineli, T.D.; Nogueira, L.; Bertassoli, D.J.; Häggi, C.; Sawakuchi, H.O.; Pupim, F.N.; Grohmann, C.H.; Chiessi, C.M.; et al. Luminescence of quartz and feldspar fingerprints provenance and correlates with the source area denudation in the Amazon River basin. Earth Planet. Sci. Lett. 2018, 492, 152–162. [Google Scholar] [CrossRef]
- Murray, A.; Buylaert, J.P.; Henriksen, M.; Svendsen, J.I.; Mangerud, J. Testing the reliability of quartz OSL ages beyond the Eemian. Radiat. Meas. 2008, 43, 776–780. [Google Scholar] [CrossRef]
- Lai, Z.P. Chronology and the upper dating limit for loess samples from Luochuan section in the Chinese Loess Plateau using quartz OSL SAR protocol. J. Asian Earth Sci. 2010, 37, 176–185. [Google Scholar] [CrossRef]
- Lowick, S.E.; Buechi, M.W.; Gaar, D.; Graf, H.R.; Preusser, F. Luminescence dating of Middle Pleistocene proglacial deposits from northern Switzerland: Methodological aspects and statigraphical conclusions conclusions. Boreas 2015, 44, 459–482. [Google Scholar] [CrossRef]
- Zhang, J.F.; Huang, W.W.; Hu, Y.; Yang, S.X.; Zhou, L.P. Optical dating of flowstone and silty carbonate-rich sediments from Panxian Dadong Cave, Guizhou, southwestern China. Quat. Geochronol. 2015, 30, 479–486. [Google Scholar] [CrossRef]
- Timar-Gabor, A.; Buylaertm, J.P.; Guralnik, B.; Trandafir-Antohi, O.; Constantin, D.; Anechitei-Deacu, V.; Jain, M.; Murray, A.S.; Porat, N.; Hao, Q.; et al. On the importance of grain size in luminescence dating using quartz. Radiat. Meas. 2017, 106, 464–471. [Google Scholar] [CrossRef]
- Buechi, M.W.; Lowick, S.E.; Anselmetti, F.S. Luminescence dating of glaciolacustrine silt in overdeepened basin fills beyond the last interglacial. Quat. Geochronol. 2017, 37, 55–67. [Google Scholar] [CrossRef]
- Anechitei-Deacu, V.; Timar-Gabor, A.; Constantinm, D.; Trandafir-Antohim, O.; Del Valle, L.; Fornos, J.J.; Gomez-Pujol, L.; Wintle, A.G. Assessing the maximum limit of SAR-OSL dating using quartz of different grain sizes. Geochronometria 2018, 45, 146–159. [Google Scholar] [CrossRef]
- Weldon, R.J. Late Cenozoic Geology of Cajon Pass; Implications for Tectonics and Sedimentation Along the San Andreas Fault. Ph.D.’s Thesis, California Institute of Technology, Pasadena, CA, USA, 1986; p. 1986. [Google Scholar]
- Pazzaglia, F.J.; Brandon, M.T. A fluvial record of long-term steady-state uplift and erosion across the Cascadia forearc high, western Washington State. Am. J. Sci. 2001, 301, 385–431. [Google Scholar] [CrossRef]
- Maddy, D. Uplift-driven valley incision and river terrace formation in southern England. J. Quat. Sci. 1997, 12, 539–545. [Google Scholar] [CrossRef]
- Mady, D.; Bridgland, D.R.; Green, C.P. Crustal uplift in southern England: Evidence from the river terrace records. Geomorphology 2000, 33, 167–181. [Google Scholar] [CrossRef]
- Bull, W.B. Geomorphic Responses to Climate Change; Oxford Univ. Press: Oxford, UK, 1991. [Google Scholar]
- Wegmann, K.W.; Pazzaglia, F.J. Holocene strath terraces, climate change, and active tectonics: The Clearwater River basin, Olympic Peninsula, Washington State. Geol. Soc. Am. Bull. 2002, 114, 731–744. [Google Scholar] [CrossRef]
- Wilson, L.F.; Pazzaglia, F.J.; Anastasio, D.J. A fluvial record of active fault-propagation folding, Salsomaggiore anticline, northern Apennines, Italy. J. Geoph. Res. 2009. [Google Scholar] [CrossRef]
- Hedrick, K.; Owen, L.A.; Rockwell, T.K.; Meigs, A.; Costa, C.; Caffee, M.W.; Masana, E.; Ahumada, E. Timing and nature of alluvial fan and strath terrace formation in the Eastern Precordillera of Argentina. Quat. Sci. Rev. 2013, 80, 143–168. [Google Scholar] [CrossRef]
- Yildirim, C.; Schildgen, T.F.; Echtler, H.; Melnick, D.; Bookhagen, B.; Çiner, A.; Niedermann, S.; Merchel, S.; Martschini, M.; Steier, P.; et al. Tectonic implications of fluvial incision and pediment deformation at the northern margin of the Central Anatolia Plateau based on multiple cosmogenic nuclides. Tectonics 2013, 32, 1107–1120. [Google Scholar] [CrossRef]
- Gold, R.D.; Cowgill, E.; Wang, X.F.; Chen, X.H. Application of trishear fault-propagation folding to active reverse faults: Examples from the Dalong fault, Gansu Province, NW China. J. Struct. Geol. 2006, 28, 200–219. [Google Scholar] [CrossRef]
- Harkins, N.; Kirby, E.; Heimsath, A.; Robinson, R.; Reiser, U. Transient fluvial incision in the headwaters of the Yellow River, northeastern Tibet, China. J. Geoph. Res. 2007, 112, F03S04. [Google Scholar] [CrossRef]
- Craddock, W.H.; Kirby, E.; Harkins, N.W.; Zhang, H.P.; Shi, X.H.; Liu, J.H. Rapid fluvial incision along the Yellow River during headward basin integration. Nat. Geosci. 2010, 3, 209–213. [Google Scholar] [CrossRef]
- Bull, W.B. Tectonic Geomorphology of Mountains: A New Approach to Paleoseismology; Wiley-Blackwell: Oxford, UK, 2007. [Google Scholar]
- Burbank, D.W.; Leland, J.; Fielding, E.; Anderson, R.S.; Brozovic, N.; Reid, M.R.; Duncan, C. Bedrock incision, rock uplift and threshold hillslopes in the northwestern Himalayas. Nature 1996, 379, 505–510. [Google Scholar] [CrossRef]
- Mason, D.P.M.; Little, T.A.; Van Dissen, R.J. Rates of active faulting during the late Quaternary fluvial terrace formation at Saxton River, Awatere fault, New Zealand. Geol. Soc. Am. Bull. 2006, 118, 1431–1446. [Google Scholar] [CrossRef]
- Cowgill, E. Impact of riser reconstructions on estimation of secular variation in rates of strike-slip faulting: Revisiting the Cherchen River site along the Altyn Tagh Fault, NW China. Earth Planet. Sci. Lett. 2007, 254, 239–255. [Google Scholar] [CrossRef]
- Pan, B.T.; Wang, J.P.; Gao, H.S.; Guan, Q.Y.; Wang, Y.; Su, H.; Li, B.Y.; Li, J.J. Paleomagnetic dating of the topmost terrace in Kouma, Henan and its indication to the Yellow River’s running through Sanmen Gorges. Chin. Sci. Bull. 2005, 50, 657–664. [Google Scholar] [CrossRef]
- Pan, B.; Su, H.; Hu, Z.; Hu, X.; Gao, H.; Li, J.; Kirby, E. Evaluating the role of climate and tectonics during non-steady incision of the Yellow River: Evidence from a 1.24 Ma terrace record near Lanzhou, China. Quat. Sci. Rev. 2009, 28, 3281–3290. [Google Scholar] [CrossRef]
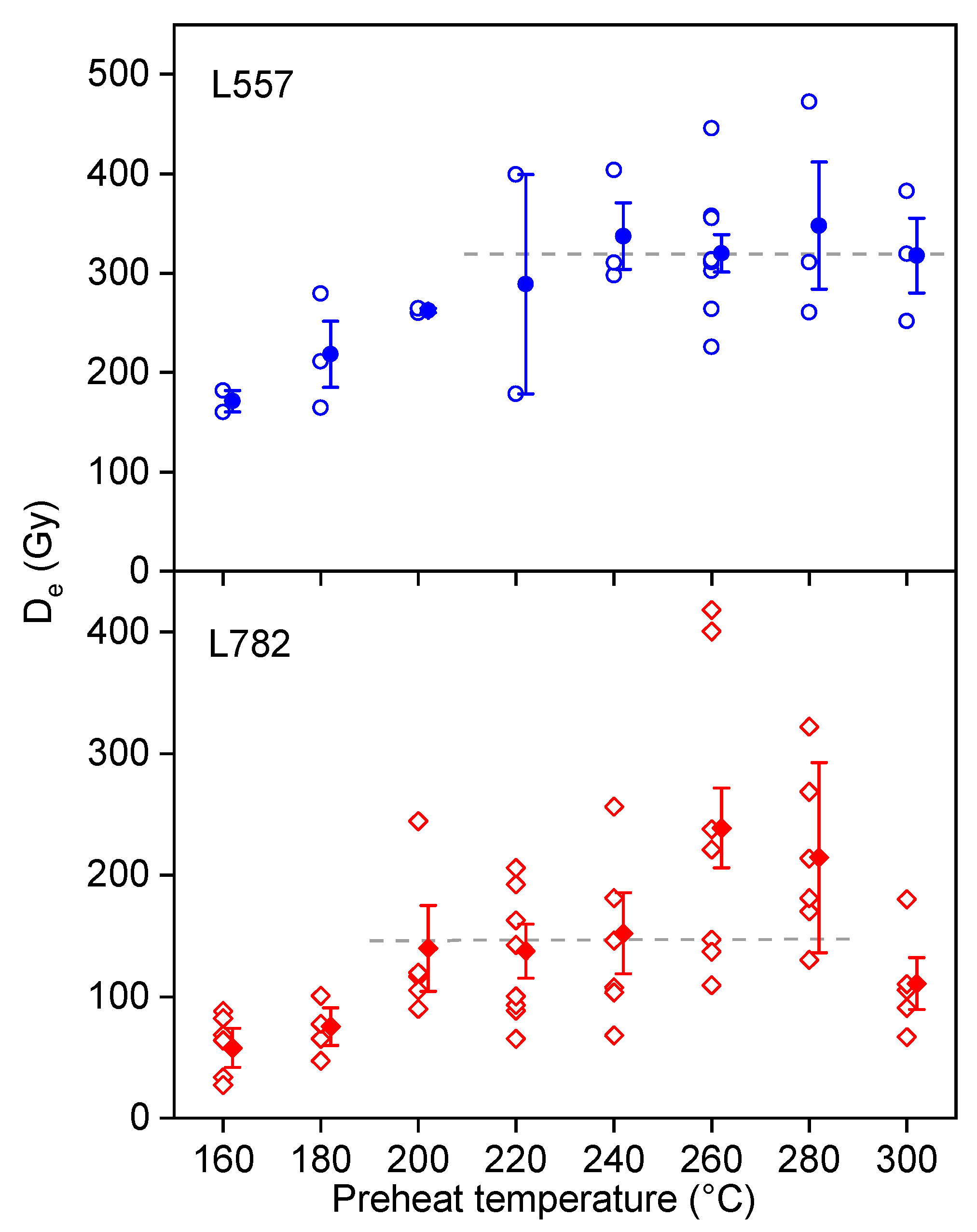
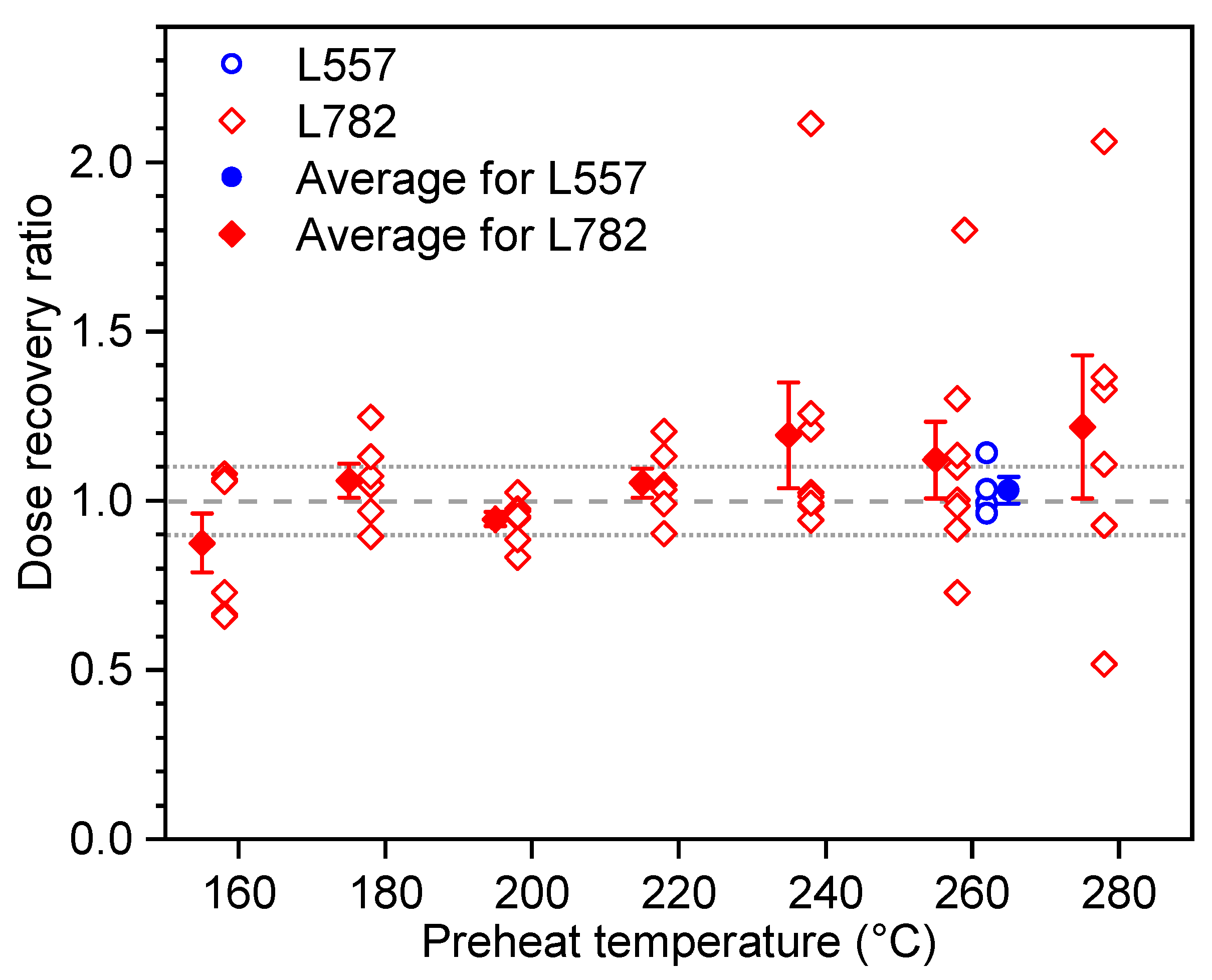
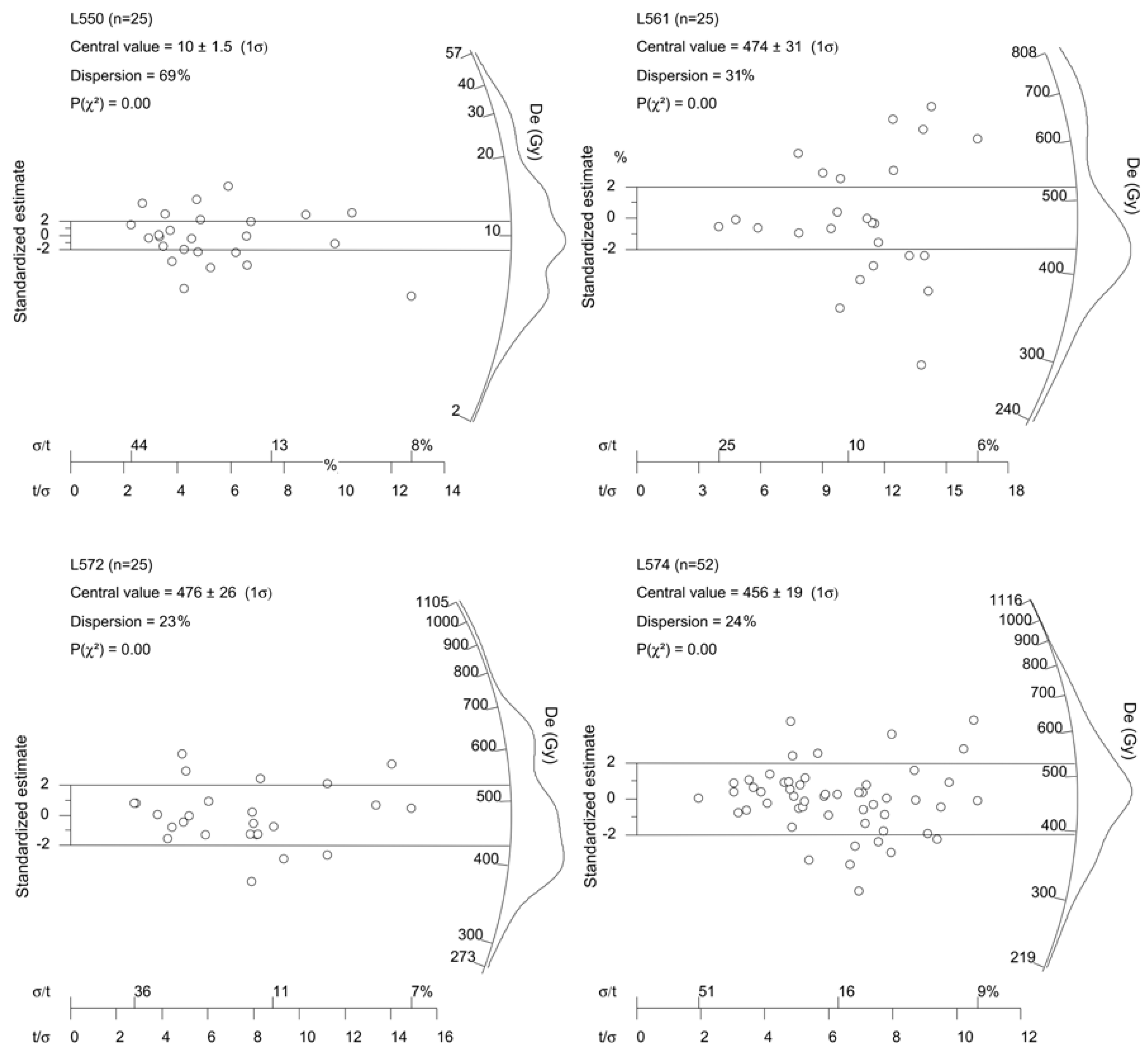
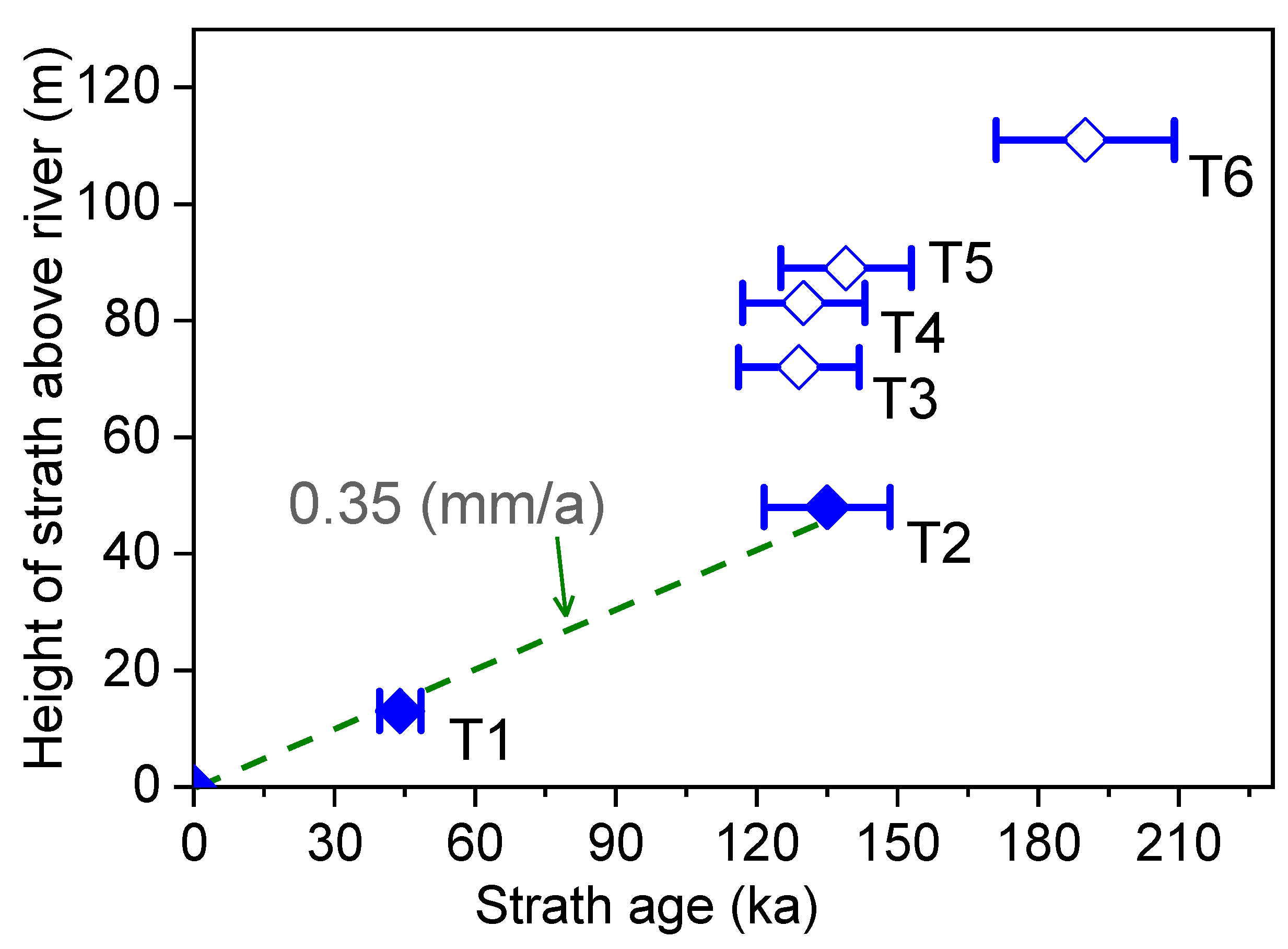

| Section No. | Lab Code | Field No. | Depth (m) | Sediment | Grain Size (µm) | K * (%) | K ** (%) | U ** (ppm) | Th ** (ppm) | Water Content # (%) | Dose rate (Gy/ka) | No. of Aliquots Measured | Arithmetic Mean De (Gy) | Central Age Modeling (CAM) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OD+ (%) | Mean De (Gy) | Age (ka) | ||||||||||||||
| Terrace T0 | ||||||||||||||||
| A | L552 | BD-OSL06 | 0.98 | Overbank silt | 4–11 | 1.8 | 1.87 ± 0.10 | 2.36 ± 0.10 | 9.81±0.24 | 10 | 3.30 ± 0.12 | 3 | 30.4 ± 1.1 | 30.5 ± 1.2 | 9.2 ± 0.5 | |
| L551 | BD-OSL05 | 2.05 | Channel sand | 90–125 | 1.72 | 1.63 ± 0.09 | 2.02 ± 0.09 | 10.10 ± 0.22 | 5 | 2.89 ± 0.08 | 21 | 6.7 ± 1.5 | 72 | 5.0 ± 0.8 | 1.7 ± 0.3 | |
| L550 | BD-OSL04 | 3.30 | Channel sand | 150–250 | 2.98 | 3.25 ± 0.11 | 0.68 ± 0.06 | 5.52 ± 0.17 | 5 | 3.69 ± 0.10 | 25 | 13.5 ± 2.4 | 69 | 10.0 ± 1.5 | 2.7 ± 0.4 | |
| L549 | BD-OSL03 | 4.77 | Channel sand | 150–250 | 2.35 | 2.32 ± 0.10 | 0.83 ± 0.07 | 5.63 ± 0.16 | 5 | 2.84 ± 0.09 | 21 | 53.7 ± 5.5 | 53 | 47.4 ± 5.6 | 16.7 ± 2.0 | |
| Terrace T1 | ||||||||||||||||
| B | L784 | BD06-OSL03 | 2.40 | Loess | 4–11 | 1.4 | 3.01 ± 0.37 | 11.41 ± 1.24 | 10 | 3.12 ± 0.15 | 4 | 91.3 ± 5.4 | 90.7 ± 4.8 | 29.1 ± 2.1 | ||
| L783 | BD06-OSL02 | 8.80 | Channel sand | 150–250 | 1.85 | 2.48 ± 0.33 | 9.13 ± 1.10 * | 5 | 2.95 ± 0.11 | 21 | 122.7 ± 7.2 | 22 | 117.6 ± 6.0 | 39.8 ± 2.5 | ||
| L782 | BD06-OSL01 | 11.20 | Channel sand | 150–250 | 1.65 | 2.01 ± 0.37 | 12.24 ± 1.24 * | 5 | 2.85 ± 0.11 | 21 | 125.2 ± 7.2 | 21 | 119.5 ± 6.3 | 41.9 ± 2.7 | ||
| Terrace T2 | ||||||||||||||||
| C | L567 | BD-OSL21 | 1.05 | Overbank silt | 90–125 | 1.72 | 1.68 ± 0.10 | 1.59 ± 0.07 | 8.75 ± 0.22 | 10 | 2.64 ± 0.09 | 16(2) | 378.9 ± 65.8 | 21 | 357 ± 24 | 135 ± 10 |
| L568 | BD-OSL22 | 2.00 | Overbank silt | 90–125 | 1.72 | 1.64 ± 0.10 | 1.90 ± 0.09 | 8.02 ± 0.20 | 10 | 2.60 ± 0.09 | 13 | 369.4 ± 17.6 | 12 | 355 ± 18 | 137 ± 8 | |
| L569 | BD-OSL23 | 2.70 | Overbank silt | 90–125 | 1.72 | 1.72 ± 0.10 | 1.80 ± 0.08 | 7.32 ± 0.20 | 10 | 2.59 ± 0.09 | 8 | 366.0 ± 41.8 | 29 | 346 ± 38 | 134 ± 15 | |
| Terrace T3 | ||||||||||||||||
| D | L571 | BD-OSL25 | 4.8 | Channel sand | 150–250 | 2.2 | 2.35 ± 0.09 | 1.09 ± 0.08 | 6.49 ± 0.18 | 5 | 2.98 ± 0.08 | 20 | 366.9 ± 14.5 | 13 | 365 ± 13 | 122 ± 6 |
| L570 | BD-OSL24 | 9.8 | Channel sand | 90–150 | 1.88 | 1.09 | 1.70 ± 0.10 | 8.62 ± 0.21 | 5 | 2.73 ± 0.09 | 22 | 361.8 ± 25.5 | 29 | 344 ± 23 | 126 ± 9 | |
| Terrace T4 | ||||||||||||||||
| E | L557 | BD-OSL11 | 4.80 | Channel sand | 125–150 | 1.8 | 1.80 ± 0.09 | 1.23 ± 0.07 | 5.83 ± 0.17 | 5 | 2.50 ± 0.08 | 23 | 357.3 ± 21.0 | 23 | 339 ± 15 | 135 ± 7 |
| L556 | BD-OSL10 | 16.2 | Channel sand | 150–250 | 2.2 | 2.10 ± 0.09 | 0.80 ± 0.07 | 5.03 ± 0.16 | 5 | 2.51 ± 0.08 | 23 | 321.1 ± 20.3 | 26 | 310 ± 18 | 123 ± 8 | |
| Terrace T5 | ||||||||||||||||
| F | L787 | BD06-OSL06 | 12.9 | Loess | 4–11 | 1.95 | 2.62 ± 0.40 | 13.19 ± 1.33 * | 10 | 3.55 ± 0.17 | 4 | 228.3 ± 3.2 | 228.9 ± 6.6 | 65 ± 4 | ||
| L786 | BD06-OSL05 | 16.00 | Overbank silty clay | 4–11 | 1.65 | 2.01 ± 0.35 | 10.89 ± 1.18 * | 10 | 2.93 ± 0.14 | 3 | 578.0 ± 20.4 | 570 ± 23 | 195 ± 12 | |||
| L785 | BD06-OSL04 | 22.20 | Overbank silty clay | 4–11 | 1.65 | 2.37 ± 0.35 | 10.72 ± 1.18 * | 10 | 2.99 ± 0.14 | 4 | 590.1 ± 53.6 | 559 ± 26 | 187 ± 12 | |||
| L573 | BD-OSL27 | 23.00 | Channel sand | 90–125 | 2.67 | 2.69 ± 0.10 | 1.00 ± 0.08 | 6.42 ± 0.18 | 5 | 3.27 ± 0.09 | 52 | 481.9 ± 20.6 | 24 | 456 ± 19 | 139 ± 7 | |
| L572 | BD-OSL26 | 25.7.00 | Channel sand | 90–125 | 2.35 | 2.45 ± 0.09 | 1.18 ± 0.08 | 11.50 ± 0.25 | 5 | 3.43 ± 0.08 | 25 | 509.3 ± 35.3 | 23 | 476 ± 26 | 139 ± 8 | |
| Terrace T6 | ||||||||||||||||
| G | L559 | BD-OSL13 | 3.10 | Loess | 4–11 | 1.72 | 1.78 ± 0.09 | 2.57 ± 0.09 | 9.67 ± 0.22 | 10 | 3.21 ± 0.12 | 5 | 612.8 ± 25.0 | 607 ± 32 | 189 ± 12 | |
| L558 | BD-OSL12 | 7.00 | Paleosol | 4–11 | 1.96 | 2.07 ± 0.09 | 2.07 ± 0.09 | 11.50 ± 0.25 | 15 | 3.26 ± 0.12 | 5 | 642.9 ± 38.0 | 609 ± 17 | 187 ± 8 | ||
| H | L564 | BD-OSL18 | 1.00 | Loess | 4–11 | 1.88 | 1.73 ± 0.10 | 1.88 ± 0.09 | 9.15 ± 0.22 | 10 | 3.00 ± 0.12 | 6 | 593.1 ± 37.1 | 571 ± 29 | 191 ± 12 | |
| L563 | BD-OSL17 | 5.15 | Paleosol | 4–11 | 2.04 | 2.23 ± 0.10 | 2.00 ± 0.08 | 9.60 ± 0.22 | 15 | 3.27 ± 0.12 | 6 | 605.1 ± 20.3 | 623 ± 24 | 191 ± 10 | ||
| L562 | BD-OSL16 | 7.10 | Channel sand | 150–250 | 2.2 | 2.32 ± 0.09 | 0.96 ± 0.07 | 5.64 ± 0.16 | 5 | 2.84 ± 0.08 | 21 | 547.0 ± 28.4 | 23 | 531 ± 29 | 187 ± 12 | |
| L561 | BD-OSL15 | 9.10 | Channel sand | 150–250 | 2.2 | 2.10 ± 0.09 | 0.80 ± 0.07 | 4.39 ± 0.15 | 5 | 2.50 ± 0.08 | 25 | 497.6 ± 32.2 | 31 | 474 ± 31 | 190 ± 15 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.-F.; Qiu, W.-L.; Hu, G.; Zhou, L.-P. Determining the Age of Terrace Formation Using Luminescence Dating—A Case of the Yellow River Terraces in the Baode Area, China. Methods Protoc. 2020, 3, 17. https://doi.org/10.3390/mps3010017
Zhang J-F, Qiu W-L, Hu G, Zhou L-P. Determining the Age of Terrace Formation Using Luminescence Dating—A Case of the Yellow River Terraces in the Baode Area, China. Methods and Protocols. 2020; 3(1):17. https://doi.org/10.3390/mps3010017
Chicago/Turabian StyleZhang, Jia-Fu, Wei-Li Qiu, Gang Hu, and Li-Ping Zhou. 2020. "Determining the Age of Terrace Formation Using Luminescence Dating—A Case of the Yellow River Terraces in the Baode Area, China" Methods and Protocols 3, no. 1: 17. https://doi.org/10.3390/mps3010017
APA StyleZhang, J.-F., Qiu, W.-L., Hu, G., & Zhou, L.-P. (2020). Determining the Age of Terrace Formation Using Luminescence Dating—A Case of the Yellow River Terraces in the Baode Area, China. Methods and Protocols, 3(1), 17. https://doi.org/10.3390/mps3010017





