1. Introduction
1.1. Overview
Luminescence dating, including optically stimulated luminescence (OSL) dating, is a valuable tool to archaeologists and geologists and remains arguably the best technique for the chronometric dating of archaeological or geological materials comprised of quartz and feldspar. In this manner, in archaeology, luminescence dating is widely applicable to pottery, minerogenic building materials and ceramic objects or sediments from archaeological contexts. While dating of recently excavated material can be routine (as in situ sampling can be done by a trained luminescence specialist aware of precisely what samples and measurements are required to achieve a luminescence age), working with more complex material, such as that recovered from museum contexts, can be more difficult. While working with recently recovered material suitable for OSL sampling is of course ideal, it is not always possible and in many cases OSL dating is not permitted, owing to strict archaeological laws which coincide with a lack of accessible laboratory facilities.
Archaeological materials housed in museums—most notably pottery vessels and ceramic objects—were often not collected with OSL dating in mind and in some cases were excavated and placed in collections well before OSL dating was even developed. As such, external dose rate () calculations can be incredibly difficult to reconstruct for museum material. Sometimes, for example if no external sediment from the original burial environment is forthcoming, it can be impossible to accurately reconstruct. However in some circumstances we can find museum material which is more favourable to OSL dating, for example, when original depositional sediment is attached to the vessels or is associated in some other way with the material. However, even then, the assumption of a uniform burial environment in archaeological luminescence dating is one that has often proved difficult for archaeologists to reconcile.
With the recent development of the
DosiVox radiation transport modelling software [
1], it has now become possible to reconstruct radiation transport throughout complex burial environments, where one must consider natural radiation from other archaeological materials, associated geological materials, and structural elements of the environment. Such modelling can vastly improve the accuracy of
determinations for both museum specimens, as well as for complex burial environments recently excavated.
In this paper, we outline the general process for building a DosiVox model of an archaeological site or other complex depositional environments. This model, along with the DosiVox software, allows us to calculate from first principles and certain basic assumptions, using all the information we have at our disposal (assuming direct measurement is not possible). Thus, for complex depositional environments where direct measurement is not possible, the model represents the best possible estimate of using tools available at the time of writing.
In
Section 1.2 we describe our approach to the measurement of
starting from first principles. In
Section 2 we begin by describing the application of the model to two complex sites from Early Dynastic Egypt where direct measurement of
is not possible. We then, continuing into
Section 3, compare the results to other possible methodologies for estimating
. In
Section 4.1 we describe how to construct a
DosiVox model based on known information about a site and in
Section 4.2 we describe our approach to running
DosiVox, including ensuring the quality of the simulations.
1.2. Theoretical Background
In our work, we start by observing that, owing to their very short attenuation depth, neither alpha nor beta radiation originating externally to the sample contribute to the equivalent dose. In other words, we assume is entirely composed of gamma radiation.
With that assumption, three key questions need to be answered when modelling :
what was the quantity (flux) of gamma radiation arriving at the target site (the location of the sample) per unit of time;
what fraction of that radiation was absorbed;
what dose of laboratory-delivered beta radiation would be equivalent to the absorbed dose of gamma radiation?
1.2.1. Grain Absorption and Equivalent Beta Dose
We begin by tackling the second and third questions, which we will find, in our case, to be less interesting than the first. To estimate the fraction of incident radiation that is absorbed by a grain of quartz, it would be possible to model the grains themselves using
DosiVox. However, given the extreme difference between the grain size and the gamma attenuation depth (roughly 1:2500) it is highly accurate to model the grains as thin targets, as is the usual practice [
2]. This means that we assume that grains are irradiated evenly. Thus, we omit grain models and use
DosiVox to calculate the average absorption in a uniform material of the right composition, as we will describe below.
In answer to the third question, we note first that the relationship between the luminescence caused by a dose of gamma radiation and the luminescence caused by the same dose of beta radiation remains impossible to determine from first principles. It would be possible to measure it experimentally by irradiating first with a gamma and then a beta source for the samples in question; however, it is in fact well established that the relationship between the two does not vary from one sample to another, and that it is accurate to assume that they are equal (Reference [
3]: 47).
Thus in answer to the second and third questions, it is both standard practice and accurate to assume that the dose is evenly absorbed and the equivalent beta dose is equal to the gamma dose.
1.2.2. Incident Dose
Answering the first question will be the primary focus of this work. In general, the radiation incident on the grains can be directly measured using in situ gamma spectrometry, estimated using the infinite matrix assumption (IMA, see below), or, as in this work, calculated using DosiVox. We begin by briefly discussing gamma spectrometry, then examine in more detail the advantages and pitfalls of the IMA, and then lay out the new possibilities when using a first-principles method like DosiVox.
Gamma Spectrometry
Gamma spectrometry is the direct measurement of the incident gamma flux at the site using a portable measuring device, that is, a gamma spectrometer (or a dosimeter, a gamma spectrometer may require an additional assumption about secular equilibrium). If it is possible to take a gamma spectrometer or dosimeter to the sample site and measure the incident dose directly, then that is undoubtedly the easiest method to pursue. However, there are reasons why this may not possible, for example:
A portable gamma spectrometer is unavailable or cannot be transported to the site.
The site has radically altered since antiquity; thus, the modern measurement of the gamma radiation intensity may not reflect what it was in the past.
The context of the sample has already been changed during the current excavation, for example as a result of the removal of stratigraphic layers above.
The artefact of interest was excavated in the past and its find spot either cannot be accessed or has been destroyed, for example, by backfilling.
Infinite Matrix Assumption Plus Geometric Model
Let us now turn to the case where direct in situ measurement of the incident gamma flux is not possible. A second method of determining the gamma flux begins by recovering samples of all materials within the gamma attenuation depth of the sample and determining the intensity of gamma radiation emitted by these materials. This may be through direct measurement using a lab-based gamma spectrometer, or by determining the radioisotopic concentrations within each sample using a form of mass spectrometery (e.g., ICP-MS). The gamma emissions of all commonly discovered radioisotopes are well-measured and readily available [
4]. Thus, if we know the radioisotopic content of any material or material mix we know the amount of radiation emitted by that material (per unit mass). Regardless of which method is used, the amount of radiation emitted by each material can be determined.
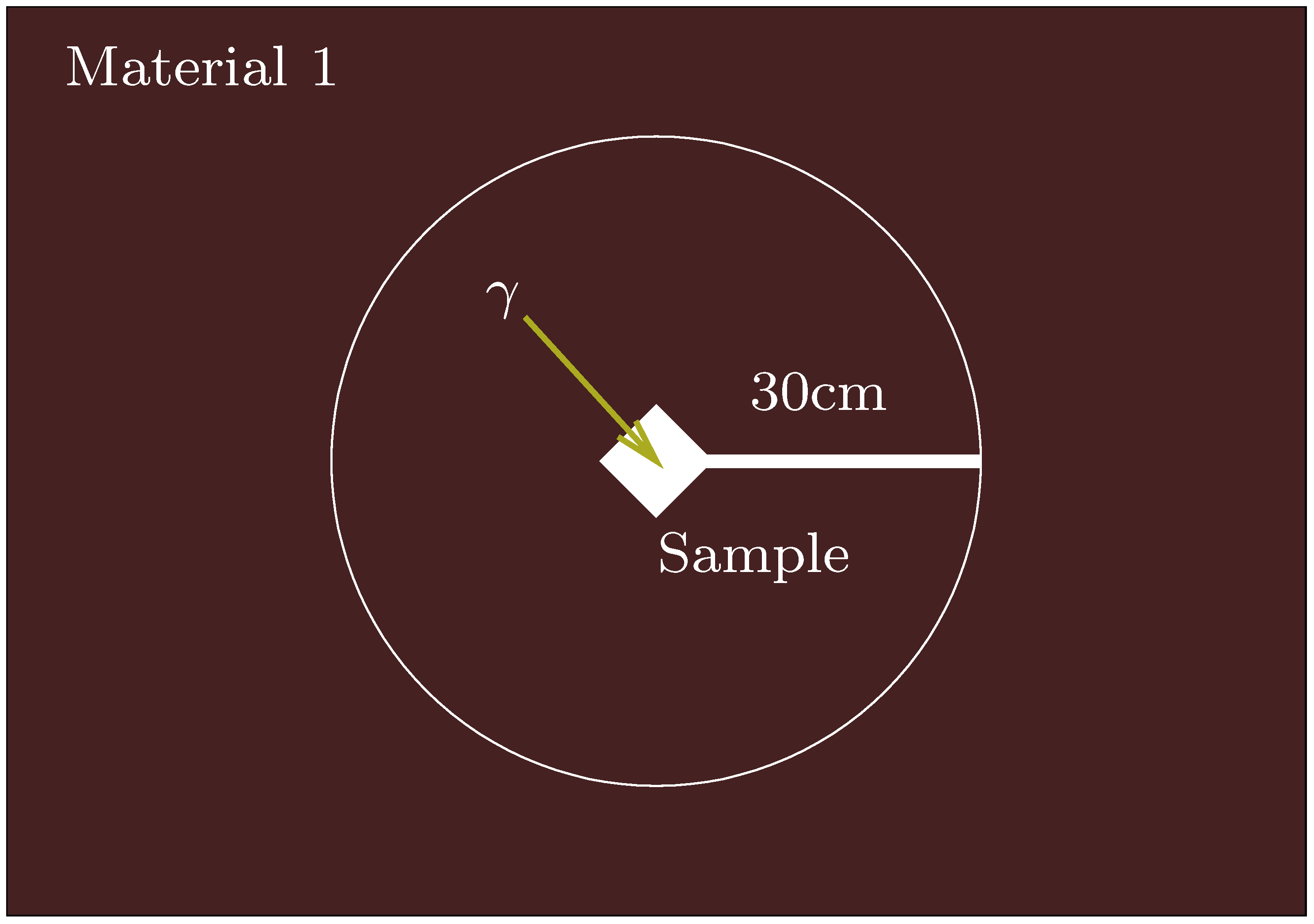
This is a good start, but what we want to know is the amount of radiation absorbed by the sample (per unit mass). Happily there is one simple case in which one is equal to the other: the case of a homogeneous material of infinite extent. In which case, by symmetry all points in the material must absorb the same radiative energy, and by the conservation of energy, this absorbed amount must be equal to the emitted amount, which we know (given the elemental breakdown). In the case where the material is not infinite, but is nonetheless considerably larger in extent than the attenuation depth of the gamma radiation (typically ∼30 cm in archaeological and geological contexts), we may treat the material as being infinite, and give the absorbed dose as being the emitted dose: this is known as the
infinite matrix assumption (Ref. [
5]: 56).
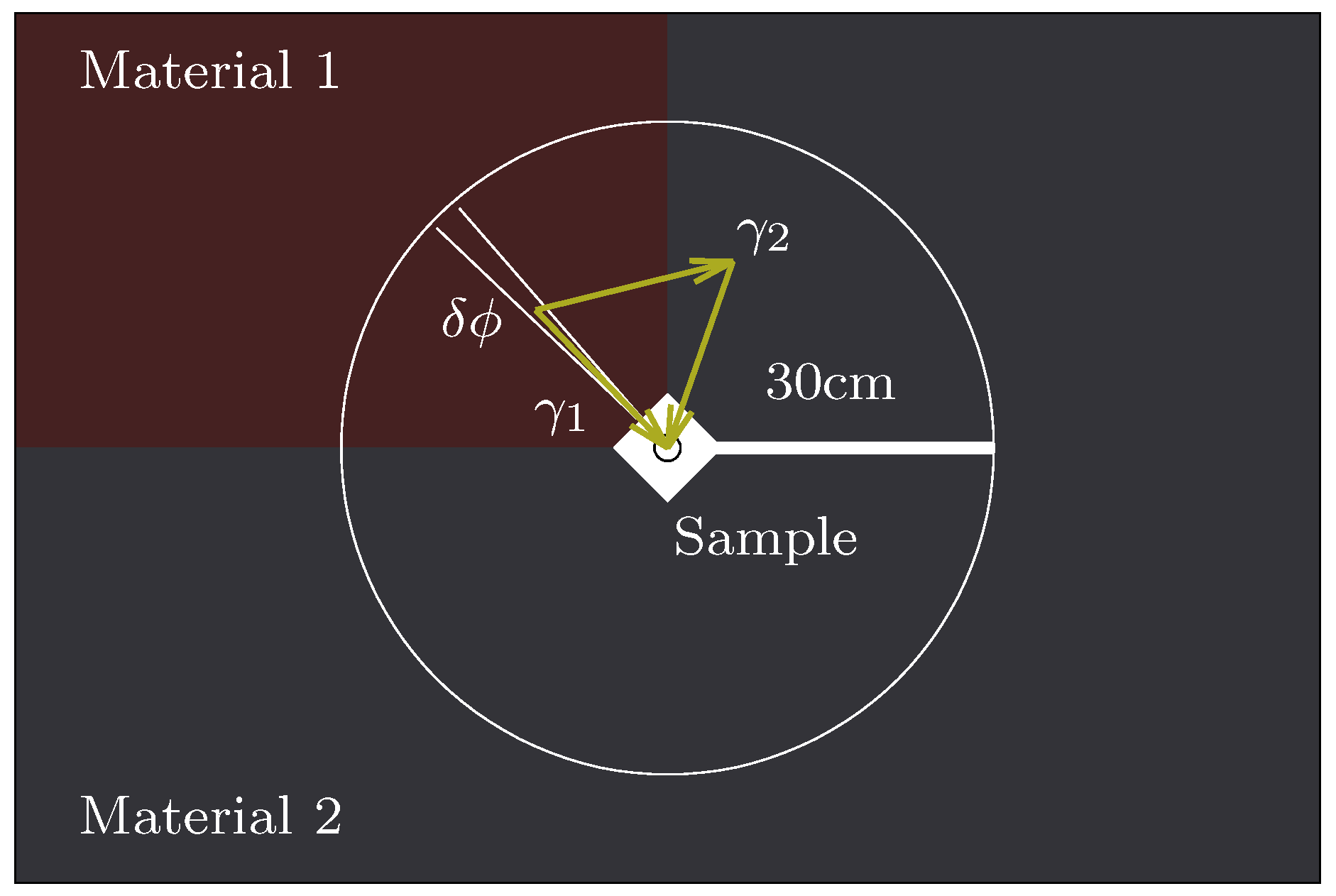
The IMA is an excellent assumption if the sample is indeed embedded in a uniform material, as shown in
Figure 1, but what if instead it is located at the boundary between two or more materials? Provided the materials can be reasonably approximated as occupying solid angles surrounding the sample, all radiation arriving at the sample only passes through one material before reaching the sample and the infinite matrix assumption still applies, weighted by the solid angles (see
Figure 2). It is possible to prove this in some circumstances and we do so in
Appendix A.
The convenient arrangement of materials in
Figure 2 is unlikely to apply in a real case. However, in the absence of any other methodology we may assume that we can still use this method, approximating the solid angles that apply to each material as the volume occupied by that material in a sphere whose radius is the gamma attenuation depth and whose centre is at the sample, divided by the total volume of the sphere. The more complex the actual arrangement of materials, the more specious this approximation, as our results in
Section 2.4 demonstrate. In the case of contexts with a simple arrangement of materials, this geometric approximation will frequently be acceptable (e.g., Reference [
6]; see extended discussion in Reference [
5]: 289). In the case of a complex archaeological context like a tomb, something more is needed.
DosiVox
The large hadron collider (LHC) at CERN causes particles to collide with such high velocity that they break up into a shower of other particles, which are seen in the detector. Because the effects of these particles in the detector are indirect it is necessary to model the origin, transport and detection of these particles and then use statistical methods to determine the most likely sequence of events (e.g., Reference [
7]).
One such model created and used at CERN is Geant-4, which simulates the creation, transport through matter and absorption of high-energy particles. Researchers at the Université Bordeaux Montaigne realised that this is exactly what was needed to model the dose rate that a luminescence sample experiences in its burial location, and thus the
DosiVox software was developed [
1].
As will be discussed further in
Section 4.1, using
DosiVox starts with making a model which includes the geospatial arrangement of all materials in the burial environment, as well as their composition. The composition of the materials includes their bulk composition, that is, the elements that make up the bulk of their mass (which affects the transport and absorption of the radiation) and the radioactive trace elements which emit the radiation (which are specified separately). We note that as well as specifying the composition and distribution of the materials, it is also possible to specify the grain-size of the sample; however, we omit this as we are only interested in the gamma radiation.
The dose absorbed by the sample location is the integral over time of the energy deposited by every gamma photon emitted from every radioisotope in the model. Since this integral is high-dimensional and expensive to calculate,
DosiVox uses Monte-Carlo methods to approximate the integral, effectively allowing a given number of gamma particles to be generated at random from within the model and measuring the dose at the sample location from each particle. Thus, the greater the number of particles, the more accurate the calculation, as discussed in
Section 4.2. For more details concerning the way
DosiVox works the reader is referred to the original paper [
1]. In this work, we wish to give a practical description of how
DosiVox was applied, in the hopes that it may be useful to others wishing to use
DosiVox in complex archaeological or geological contexts.
Other Gamma Sources
There are of course other sources of gamma radiation that might have affected the effective dose rate. Assuming that the sample was not exposed after excavation, the most notable of these is cosmic radiation. In our work here, we use the effective and well-established method of calculating the cosmic dose rate as a function of depth and global position of an archaeological/geological site that is provided by the Dose Rate and Age Calculator (DRAC) ([
8]; following Reference [
9]).
3. Discussion
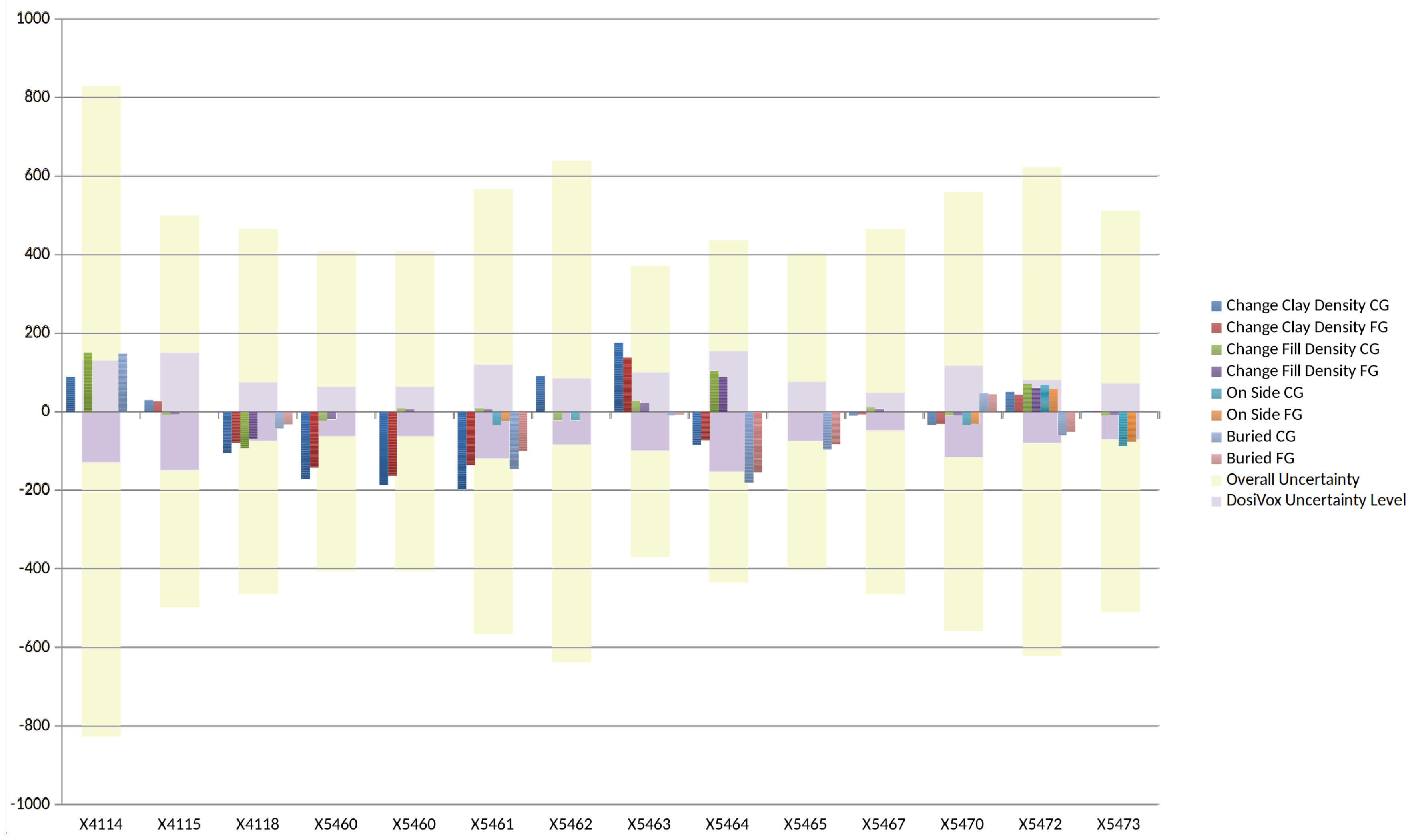
We can see from the results presented in
Table 1 and
Table 2 that the gamma dose rates obtained by using
DosiVox differ from those obtained by assuming ‘best guess’ scaled geometries. In the case of Bêt Khallaf the outcome saw
DosiVox produce a gamma dose rate far more in keeping with an assumed 4
geometry than in our ‘best guess’ scaled geometry, illustrating how
DosiVox can provide a result which is not subject to inbuilt biases and assumed geometries determined by the luminescence practitioner.
It can, of course, well be argued that the ‘best guess’ was in fact , because the roof of the tomb was of similar composition to the floor and the dry air of the tomb would only slightly attenuate the radiation. We do not dispute this; we merely observe that all of these sweeping arguments and assumptions can be replaced by a more rigorous procedure using DosiVox. One benefit of this rigorous procedure is that there are many hidden assumptions in the 4 IMA estimate that DosiVox makes explicit and testable (position of the pot, etc). More importantly, however, it is only having run DosiVox (i.e., with hindsight) that we can know that the 4 IMA assumption was acceptable. Even though it might seem a reasonable assumption about the transport of gamma radiation a priori, with DosiVox the transport and absorption of gamma radiation is modelled in a way (using Geant-4) that has been extensively tested against highly accurate particle physics experiments; thus we can be much more confident in its results and we can eliminate at least one big assumption from our chain of reasoning.
In the case of the Tomb of Djer the
DosiVox gamma dose rate was significantly different to the IMA and ‘best guess’ geometry dose rates. The complex depositional environment and the array of different elements affecting the dose rate was such that the gamma dose rate achieved using
DosiVox modelling varied significantly enough from assumed geometries that final dose rate determinations varied considerably (which in turn affects the final luminescence age calculations). (It is beyond the scope of this paper to present the final age calculations for this material. If interested, the reader is referred to References [
10,
11], noting that final ages therein obtained using
DosiVox were in good agreement with associated archaeological and historical chronologies.)
In simple geometric cases, for example, when a sample is known to have full, 4 geometry, DosiVox may be too significant an undertaking to apply to every luminescence sample and indeed will, in all likelihood, give a similar result. However, the more informative analysis and more accurate gamma dose rates achievable by DosiVox modelling in more complex burial environments, for example, that seen in the Tomb of Djer, illustrates how using the programme can improve luminescence age determination. In the case of complex sample geometries, it is therefore recommended that DosiVox modelling be incorporated into luminescence work to improve dose rate calculations and, in turn, age determinations.
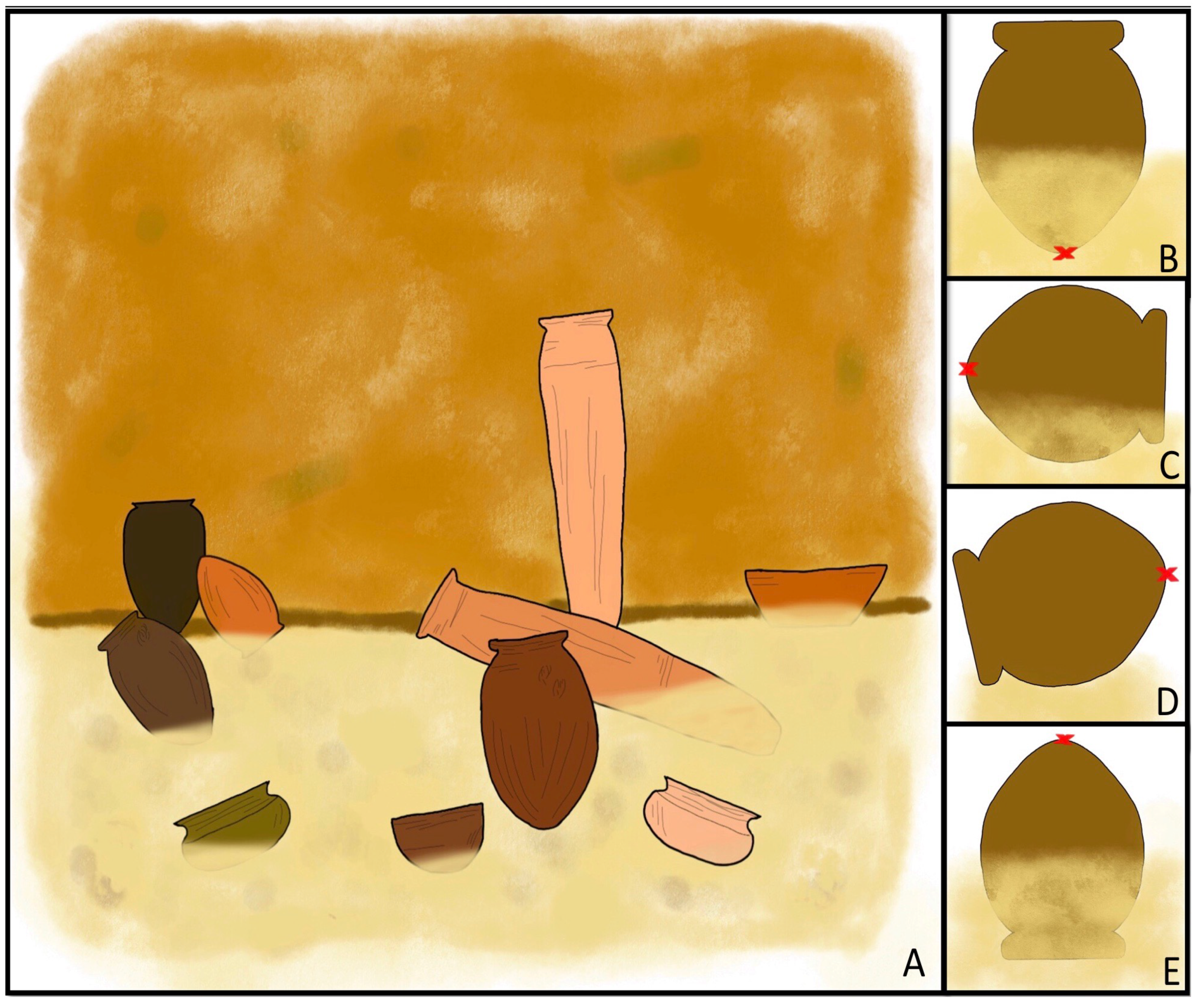
One limitation of this research is that from the tomb reports we know that the ceramics at both sites were found as caches, that is multiple vessels were found in the same deposit. However, it was impossible at either site to determine the order or precise location of the ceramics relative to one another. In an ideal situation, if this information were recorded at the time of excavation, it would be possible to improve upon the DosiVox model even further by adding in each individual ceramic into the model so that the gamma dose rate determined for each vessel would also factor in the gamma dose being emitted by the surrounding vessels. This could be easily achievable for those wanting to use DosiVox modelling of complex deposits found in current excavations or fieldwork situations.
DosiVox is a valuable new tool when dealing with samples that have complex geometry and where in situ gamma measurements are not able to be made. Using DosiVox in conjunction with current projects could yield gamma dose rates far more accurate than those achievable through a simple incorporation of the IMA. This is because, in most cases, all the elements required to construct a DosiVox model would be readily available and, as a result of the more detailed model and more limited (and explicit) assumptions, a higher degree of confidence could be placed upon such a model, thus potentially yielding more accurate gamma dose rates than the IMA alone. We recommend that DosiVox modelling is routinely carried out at locations where in situ measurements are not available.
DosiVox modelling can be used in both helping to determine the gamma dose rate at recently excavated sites, those sites excavated in the past (i.e., where the resulting material has been stored in museums) and for both geological and archaeological situations. We are of the opinion that the incorporation of DosiVox into luminescence research can be of significant value in a number of situations, and believe that more accurate gamma dose rates can be achieved using DosiVox in cases of complex sample geometry. As such, DosiVox has the ability to greatly improve the reconstruction of dating profiles at geological and archaeological sites worldwide and assist in more accurate chronologies being achieved.