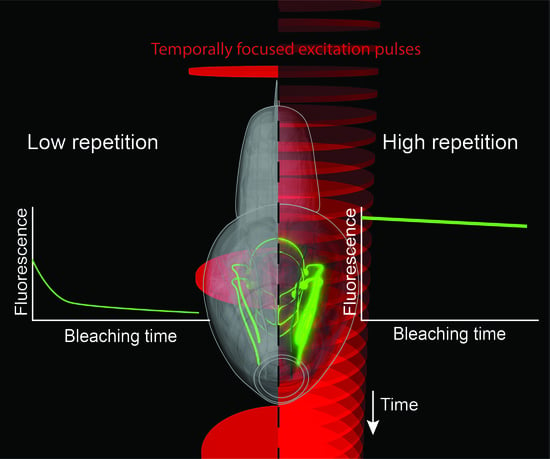
Improving Signal and Photobleaching Characteristics of Temporal Focusing Microscopy with the Increase in Pulse Repetition Rate
Abstract
1. Introduction
2. Materials and Methods
2.1. Temporal Focusing Microscopy Setup
2.2. Imaging Samples
3. Results
3.1. Signal Intensity Increases Linearly with the Repetition Rate
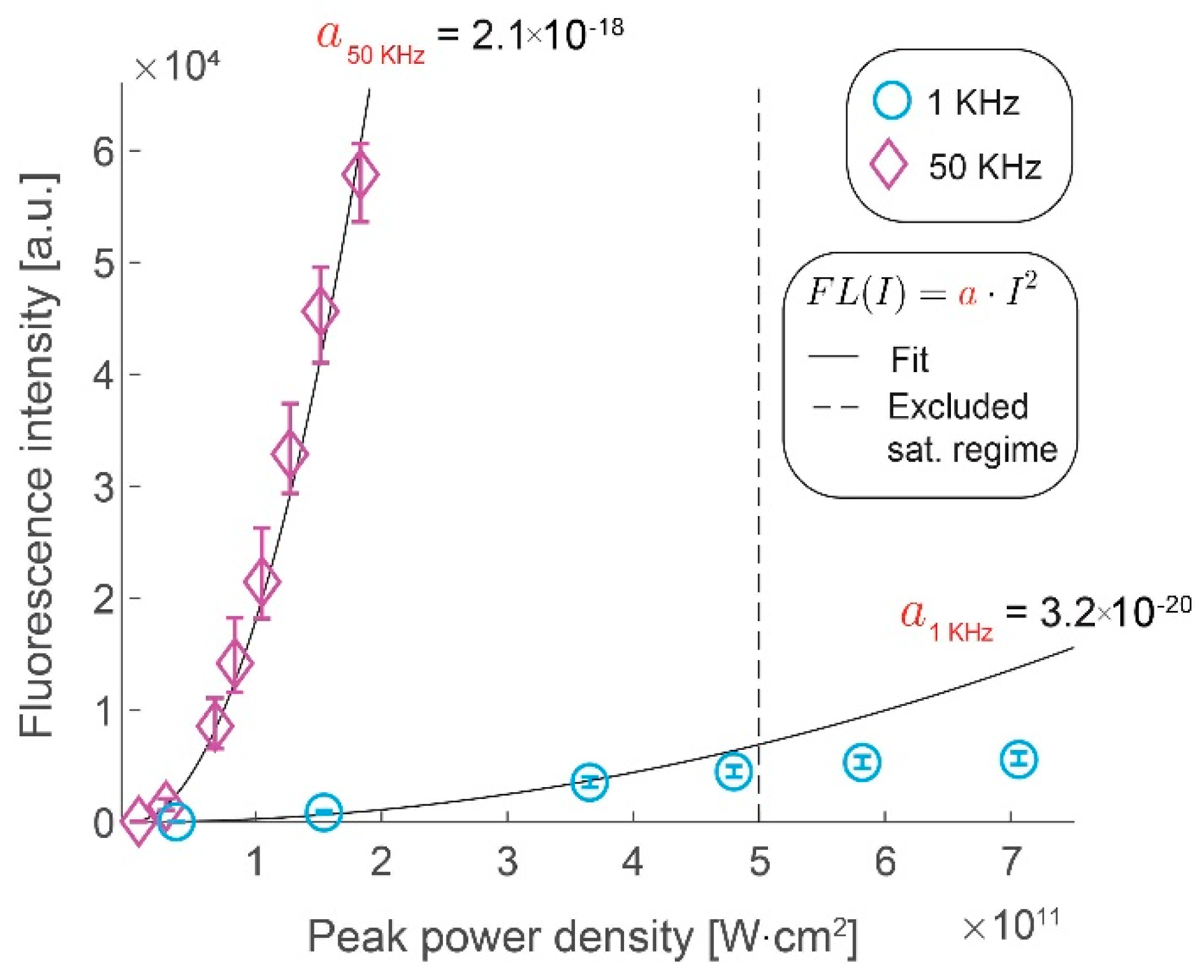
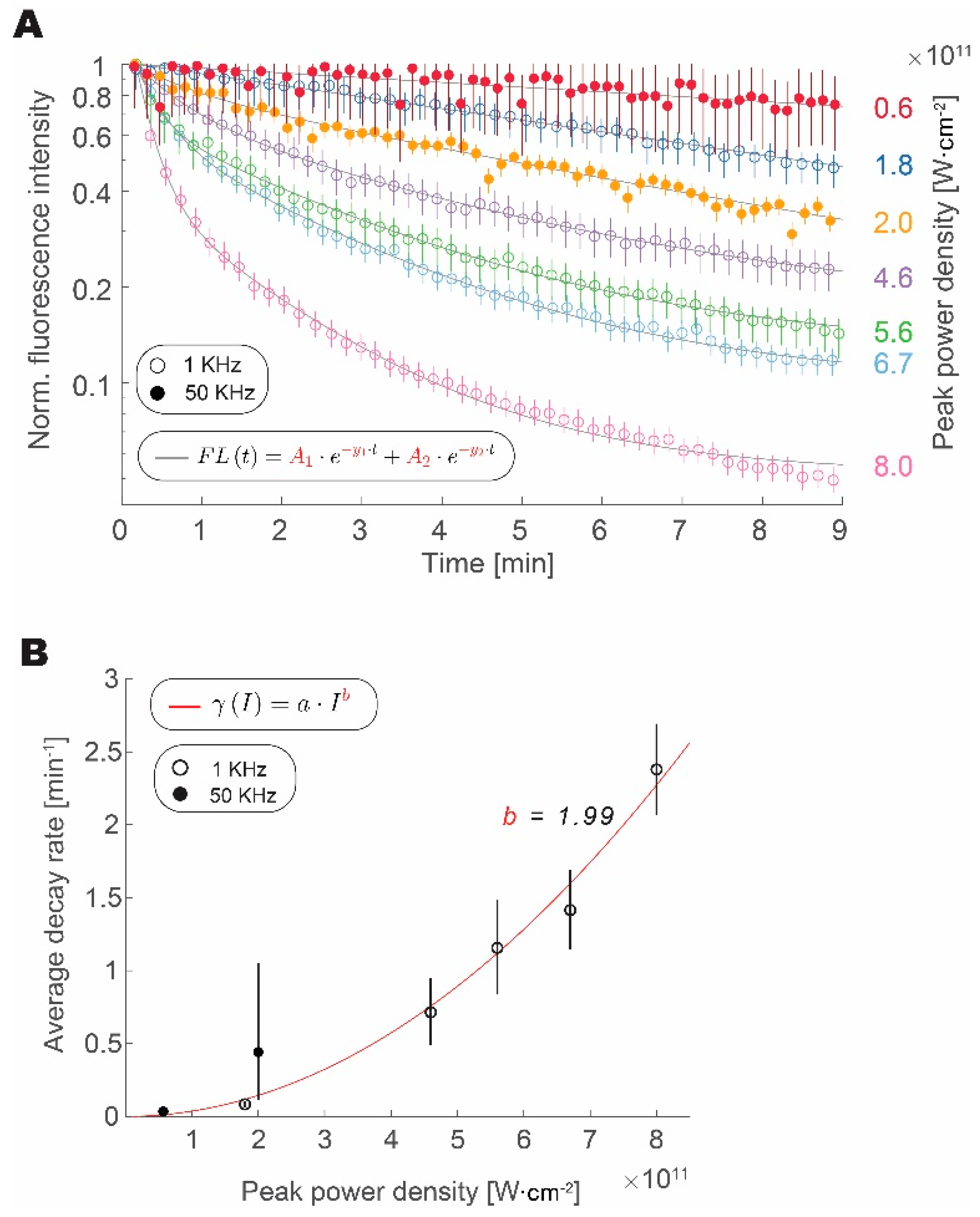
3.2. Photobleaching Rate Increases with Peak Intensity, but Not with the Repetition Rate
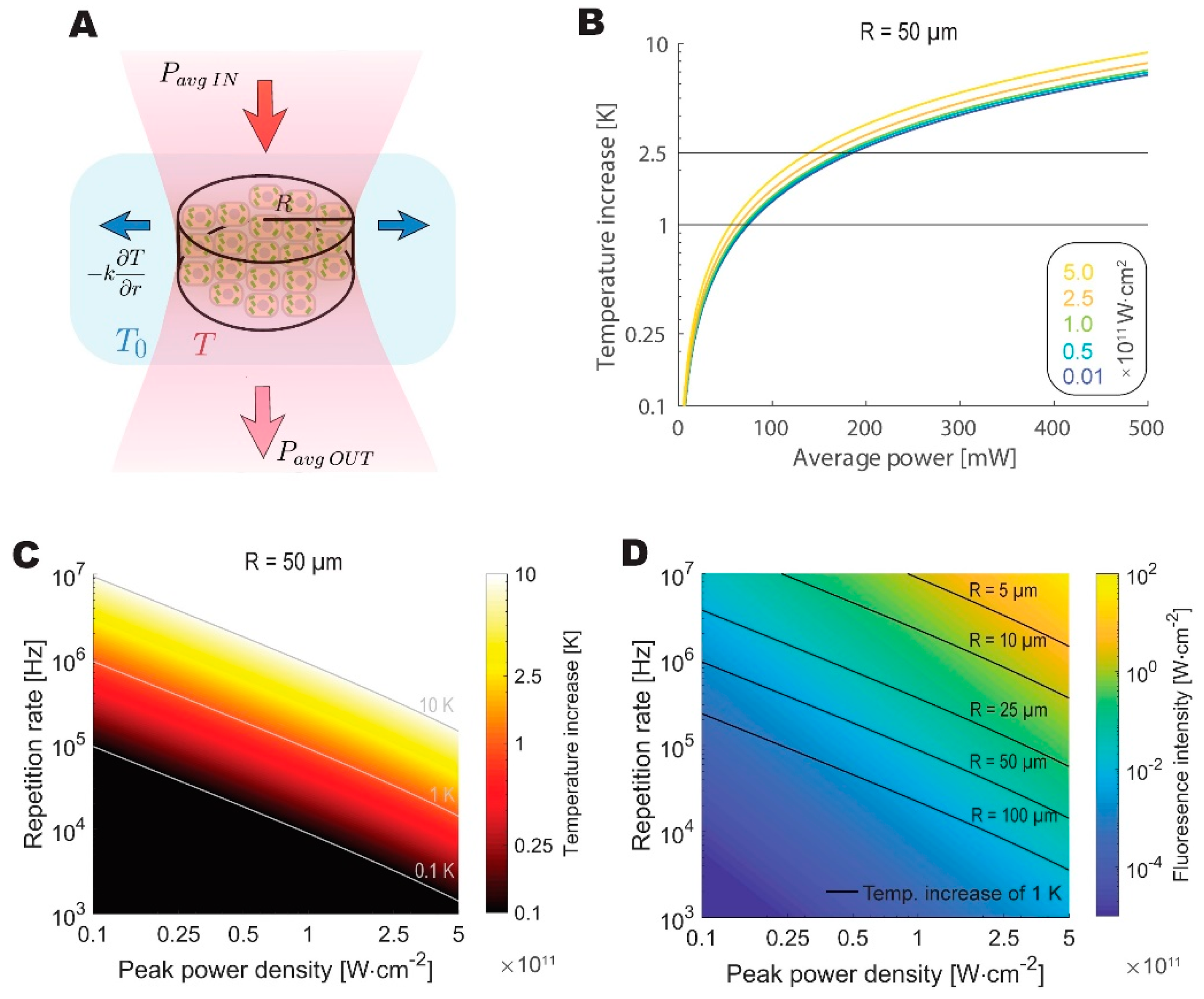
3.3. Temperature Constraints Indicate an Optimum Repetition Rate Between 0.5 and 5MHz
3.4. Live Sample Imaging at 100 kHz Yields High Signal Intensities without a Photomultiplier
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ji, N.; Freeman, J.; Smith, S.L. Technologies for imaging neural activity in large volumes. Nat. Neurosci. 2016, 19, 1154–1164. [Google Scholar] [CrossRef] [PubMed]
- Qu, J.; Liu, L.; Shao, Y.; Niu, H.; Gao, B.Z. Recent progress in multifocal multiphoton microscopy. J. Innov. Opt. Health Sci. 2012, 5, 1250018. [Google Scholar] [CrossRef] [PubMed]
- Yew, E.Y.S.; Sheppard, C.J.R.; So, P.T.C. Temporally focused wide-field two-photon microscopy: paraxial to vectorial. Opt. Express 2013, 21, 12951–12963. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Van Howe, J.; Durst, M.; Zipfel, W.; Xu, C. Simultaneous spatial and temporal focusing of femtosecond pulses. Opt. Express 2005, 13, 2153–2159. [Google Scholar] [CrossRef] [PubMed]
- Oron, D.; Silberberg, Y. Spatiotemporal coherent control using shaped, temporally focused pulses. Opt. Express 2005, 13, 9903–9908. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Wise, F.W. Recent Advances in Fiber Lasers for Nonlinear Microscopy. Nat. Photonics 2013, 7, 875. [Google Scholar] [CrossRef] [PubMed]
- Podgorski, K.; Ranganathan, G. Brain heating induced by near-infrared lasers during multiphoton microscopy. J. Neurophysiol. 2016, 116, 1012–1023. [Google Scholar] [CrossRef]
- Denk, W.; Piston, D.W.; Webb, W.W. Two-Photon Molecular Excitation in Laser-Scanning Microscopy. In Handbook of Biological Confocal Microscopy; Pawley, J.B., Ed.; Springer: Boston, MA, USA, 1995; pp. 445–458. ISBN 9781475753486. [Google Scholar]
- Durst, M.E.; Zhu, G.; Xu, C. Simultaneous Spatial and Temporal Focusing in Nonlinear Microscopy. Opt. Commun. 2008, 281, 1796–1805. [Google Scholar] [CrossRef]
- Schrödel, T.; Prevedel, R.; Aumayr, K.; Zimmer, M.; Vaziri, A. Brain-wide 3D imaging of neuronal activity in Caenorhabditis elegans with sculpted light. Nat. Methods 2013, 10, 1013–1020. [Google Scholar] [CrossRef]
- Akerboom, J.; Chen, T.W.; Wardill, T.J.; Tian, L.; Marvin, J.S.; Mutlu, S.; Calderón, N.C.; Esposti, F.; Borghuis, B.G.; Sun, X.R.; et al. Optimization of a GCaMP calcium indicator for neural activity imaging. J. Neurosci. 2012, 32, 13819–13840. [Google Scholar] [CrossRef]
- Brenner, S. The genetics of Caenorhabditis elegans. Genetics 1974, 77, 71–94. [Google Scholar]
- Collins, K.M.; Bode, A.; Fernandez, R.W.; Tanis, J.E.; Brewer, J.C.; Creamer, M.S.; Koelle, M.R. Activity of the C. elegans egg-laying behavior circuit is controlled by competing activation and feedback inhibition. Elife 2016, 5, e21126. [Google Scholar] [CrossRef]
- Stiernagle, T. Maintenance of C. elegans. WormBook 1999, 2, 51–67. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Lefort, C. A review of biomedical multiphoton microscopy and its laser sources. J. Phys. D Appl. Phys. 2017, 50, 423001. [Google Scholar] [CrossRef]
- Diaspro, A.; Chirico, G. Two-photon excitation microscopy. In Advances in Imaging and Electron Physics; Hawkes, P.W., Ed.; Elsevier: Amsterdam, The Netherlands, 2003; Volume 126, pp. 195–286. [Google Scholar]
- Diaspro, A.; Chirico, G.; Usai, C.; Ramoino, P.; Dobrucki, J. Photobleaching. In Handbook of Biological Confocal Microscopy; Pawley, J.B., Ed.; Springer: Boston, MA, USA, 2006; pp. 690–702. ISBN 9780387455242. [Google Scholar]
- Chirico, G.; Cannone, F.; Baldini, G.; Diaspro, A. Two-photon thermal bleaching of single fluorescent molecules. Biophys. J. 2003, 84, 588–598. [Google Scholar] [CrossRef]
- Kalies, S.; Kuetemeyer, K.; Heisterkamp, A. Mechanisms of high-order photobleaching and its relationship to intracellular ablation. Biomed. Opt. Express 2011, 2, 805–816. [Google Scholar] [CrossRef]
- Chen, T.S.; Zeng, S.Q.; Luo, Q.M.; Zhang, Z.H.; Zhou, W. High-order photobleaching of green fluorescent protein inside live cells in two-photon excitation microscopy. Biochem. Biophys. Res. Commun. 2002, 291, 1272–1275. [Google Scholar] [CrossRef]
- Stujenske, J.M.; Spellman, T.; Gordon, J.A. Modeling the Spatiotemporal Dynamics of Light and Heat Propagation for In Vivo Optogenetics. Cell Rep. 2015, 12, 525–534. [Google Scholar] [CrossRef]
- Picot, A.; Dominguez, S.; Liu, C.; Chen, I.-W.; Tanese, D.; Ronzitti, E.; Berto, P.; Papagiakoumou, E.; Oron, D.; Tessier, G.; et al. Temperature Rise under Two-Photon Optogenetic Brain Stimulation. Cell Rep. 2018, 24, 1243–1253. [Google Scholar] [CrossRef]
- Yang, L.; Miklavcic, S.J. Theory of light propagation incorporating scattering and absorption in turbid media. Opt. Lett. 2005, 30, 792–794. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: a review. Phys. Med. Biol. 2013, 58, 37–61. [Google Scholar] [CrossRef]
- Yaroslavsky, A.N.; Schulze, P.C.; Yaroslavsky, I.V.; Schober, R.; Ulrich, F.; Schwarzmaier, H.J. Optical properties of selected native and coagulated human brain tissues in vitro in the visible and near infrared spectral range. Phys. Med. Biol. 2002, 47, 2059–2073. [Google Scholar] [CrossRef]
- Johansson, J.D. Spectroscopic method for determination of the absorption coefficient in brain tissue. J. Biomed. Opt. 2010, 15, 057005. [Google Scholar] [CrossRef]
- Birge, R.R. Two-photon spectroscopy of protein-bound chromophores. Acc. Chem. Res. 1986, 19, 138–146. [Google Scholar] [CrossRef]
- Drobizhev, M.; Makarov, N.S.; Tillo, S.E.; Hughes, T.E.; Rebane, A. Two-photon absorption properties of fluorescent proteins. Nat. Methods 2011, 8, 393. [Google Scholar] [CrossRef]
- Ponder, E. The coefficient of thermal conductivity of blood and of various tissues. J. Gen. Physiol. 1962, 45, 545–551. [Google Scholar] [CrossRef]
- Poppendiek, H.F.; Randall, R.; Breeden, J.A.; Chambers, J.E.; Murphy, J.R. Thermal conductivity measurements and predictions for biological fluids and tissues. Cryobiology 1967, 3, 318–327. [Google Scholar] [CrossRef]
- Tian, L.; Hires, S.A.; Mao, T.; Huber, D.; Chiappe, M.E.; Chalasani, S.H.; Petreanu, L.; Akerboom, J.; McKinney, S.A.; Schreiter, E.R.; et al. Imaging neural activity in worms, flies and mice with improved GCaMP calcium indicators. Nat. Methods 2009, 6, 875–881. [Google Scholar] [CrossRef]
- Liedtke, W.; Tobin, D.M.; Bargmann, C.I.; Friedman, J.M. Mammalian TRPV4 (VR-OAC) directs behavioral responses to osmotic and mechanical stimuli in Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA 2003, 2, 14531–14536. [Google Scholar] [CrossRef]
- Oron, D.; Silberberg, Y. Temporal focusing microscopy. Cold Spring Harb. Protoc. 2015, 2015, 145–151. [Google Scholar] [CrossRef]
- Therrien, O.D.; Aubé, B.; Pagès, S.; Koninck, P.D.; Côté, D. Wide-field multiphoton imaging of cellular dynamics in thick tissue by temporal focusing and patterned illumination. Biomed. Opt. Express 2011, 2, 696–704. [Google Scholar] [CrossRef]
- Prevedel, R.; Verhoef, A.J.; Pernía-Andrade, A.J.; Weisenburger, S.; Huang, B.S.; Nöbauer, T.; Fernández, A.; Delcour, J.E.; Golshani, P.; Baltuska, A.; et al. Fast volumetric calcium imaging across multiple cortical layers using sculpted light. Nat. Methods 2016, 13, 1021. [Google Scholar] [CrossRef]

| Model Param. | Description | Values and Units | Ref. |
|---|---|---|---|
| Fa | Fraction of absorbed photons that do not result in two-photon emission | — | — |
| Na | Number of absorbed photons | — | — |
| Nτ | Total number of photons | — | — |
| N1λ | Number of photons absorbed due to one-photon absorption of the medium | — | — |
| N2λ-Nem | Number of absorbed photons that do not result in two-photon emission | — | — |
| µa | Absorption coefficient | 1 cm−1 | [25,26,27] |
| l | Propagation length (two Rayleigh lengths) | 5 µm | — |
| I | Peak power density | W·cm−2 | — |
| S | Coherence parameter | — | [28] |
| δ2λ | Two-photon cross-section at 960 nm | 31 × 10−50 cm4·s−1·molec. −1·photon−1 | [11] |
| C | Typical concentration of fluorophores | 6 × 1018 molec.·cm−3 | [29] |
| λ | Wavelength used for two-photon imaging | 960 nm | — |
| h | Planck constant | 6.62607015 × 10−34 J·s−1·photon−1 | — |
| c | Speed of light in vacuum | 299,792,458 m·s−1 | — |
| Φ | Quantum efficiency | 0.67 | [11] |
| ε | Heat source | J·m−3 | — |
| PA | Average laser power | W | — |
| V | Volume of the excitation cylinder | µm3 | — |
| qr | Heat | J | — |
| T | Temperature | K | — |
| k | Specific thermal conductivity of brain tissue | 0.5918 W·K−1·m−1 | [30,31] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisicovas, V.; Mariserla, B.M.K.; Sahoo, C.; Harding, R.T.; Man, M.K.L.; Wong, E.L.; Madéo, J.; Dani, K.M. Improving Signal and Photobleaching Characteristics of Temporal Focusing Microscopy with the Increase in Pulse Repetition Rate. Methods Protoc. 2019, 2, 65. https://doi.org/10.3390/mps2030065
Lisicovas V, Mariserla BMK, Sahoo C, Harding RT, Man MKL, Wong EL, Madéo J, Dani KM. Improving Signal and Photobleaching Characteristics of Temporal Focusing Microscopy with the Increase in Pulse Repetition Rate. Methods and Protocols. 2019; 2(3):65. https://doi.org/10.3390/mps2030065
Chicago/Turabian StyleLisicovas, Viktoras, Bala Murali Krishna Mariserla, Chakradhar Sahoo, Reuben T. Harding, Michael K. L. Man, E Laine Wong, Julien Madéo, and Keshav M. Dani. 2019. "Improving Signal and Photobleaching Characteristics of Temporal Focusing Microscopy with the Increase in Pulse Repetition Rate" Methods and Protocols 2, no. 3: 65. https://doi.org/10.3390/mps2030065
APA StyleLisicovas, V., Mariserla, B. M. K., Sahoo, C., Harding, R. T., Man, M. K. L., Wong, E. L., Madéo, J., & Dani, K. M. (2019). Improving Signal and Photobleaching Characteristics of Temporal Focusing Microscopy with the Increase in Pulse Repetition Rate. Methods and Protocols, 2(3), 65. https://doi.org/10.3390/mps2030065