Impact of Tomosynthesis Acquisition on 3D Segmentations of Breast Outline and Adipose/Dense Tissue with AI: A Simulation-Based Study
Abstract
1. Introduction
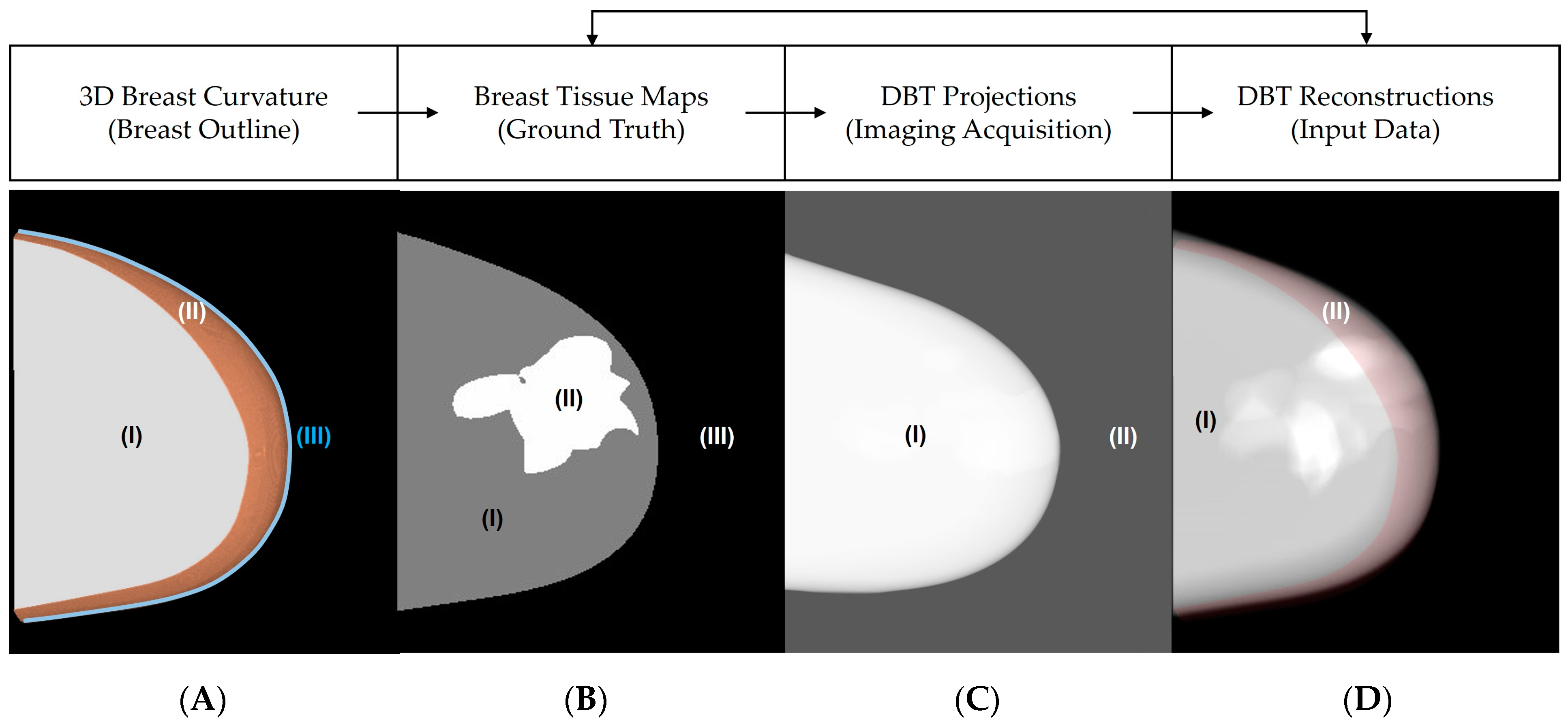
2. Materials and Methods
2.1. Breast Outline Simulation
2.2. Breast Density Simulation
2.3. Convex Hull and Tissue Segmentations
2.4. Convex Hull and Tissue Analyses
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cockmartin, L.; Marshall, N.W.; Van Ongeval, C.; Aerts, G.; Stalmans, D.; Zanca, F.; Shaheen, E.; De Keyzer, F.; Dance, D.R.; Young, K.C.; et al. Comparison of digital breast tomosynthesis and 2D digital mammography using a hybrid performance test. Phys. Med. Biol. 2015, 60, 3939–3958. [Google Scholar] [CrossRef] [PubMed]
- Zuckerman, S.P.; Conant, E.F.; Keller, B.M.; Maidment, A.D.A.; Barufaldi, B.; Weinstein, S.P.; Synnestvedt, M.; McDonald, E.S. Implementation of Synthesized Two-dimensional Mammography in a Population-based Digital Breast Tomosynthesis Screening Program. Radiology 2016, 281, 730–736. [Google Scholar] [CrossRef] [PubMed]
- Conant, E.F.; Talley, M.M.; Parghi, C.R.; Sheh, B.C.; Liang, S.-Y.; Pohlman, S.; Rane, A.; Jung, Y.; Stevens, L.A.S.; Paulus, J.K.; et al. Mammographic Screening in Routine Practice: Multisite Study of Digital Breast Tomosynthesis and Digital Mammography Screenings. Radiology 2023, 307, e221571. [Google Scholar] [CrossRef] [PubMed]
- Zuckerman, S.P.; Sprague, B.L.; Weaver, D.L.; Herschorn, S.D.; Conant, E.F. Multicenter Evaluation of Breast Cancer Screening with Digital Breast Tomosynthesis in Combination with Synthetic versus Digital Mammography. Radiology 2020, 297, 545–553. [Google Scholar] [CrossRef]
- Wahab, R.A.; Lee, S.-J.; Zhang, B.; Sobel, L.; Mahoney, M.C. A comparison of full-field digital mammograms versus 2D synthesized mammograms for detection of microcalcifications on screening. Eur. J. Radiol. 2018, 107, 14–19. [Google Scholar] [CrossRef]
- Shermis, R.B.; Wilson, K.D.; Doyle, M.T.; Martin, T.S.; Merryman, D.; Kudrolli, H.; Brenner, R.J. Supplemental Breast Cancer Screening With Molecular Breast Imaging for Women With Dense Breast Tissue. Am. J. Roentgenol. 2016, 207, 450–457. [Google Scholar] [CrossRef]
- Rauch, G.M.; Adrada, B.E. Comparison of Breast MR Imaging with Molecular Breast Imaging in Breast Cancer Screening, Diagnosis, Staging, and Treatment Response Evaluation. Magn. Reson. Imaging Clin. N. Am. 2018, 26, 273–280. [Google Scholar] [CrossRef]
- Chou, C.-P.; Lewin, J.M.; Chiang, C.-L.; Hung, B.-H.; Yang, T.-L.; Huang, J.-S.; Liao, J.-B.; Pan, H.-B. Clinical evaluation of contrast-enhanced digital mammography and contrast enhanced tomosynthesis—Comparison to contrast-enhanced breast MRI. Eur. J. Radiol. 2015, 84, 2501–2508. [Google Scholar] [CrossRef]
- Ikejimba, L.C.; Kiarashi, N.; Ghate, S.V.; Samei, E.; Lo, J.Y. Task-based strategy for optimized contrast enhanced breast imaging: Analysis of six imaging techniques for mammography and tomosynthesis. Med. Phys. 2014, 41, 061908. [Google Scholar] [CrossRef]
- Wienbeck, S.; Fischer, U.; Luftner-Nagel, S.; Lotz, J.; Uhlig, J. Contrast-enhanced cone-beam breast-CT (CBBCT): Clinical performance compared to mammography and MRI. Eur. Radiol. 2018, 28, 3731–3741. [Google Scholar] [CrossRef]
- Acciavatti, R.J.; Maidment, A.D.A. Observation of super-resolution in digital breast tomosynthesis. Med. Phys. 2012, 39, 7518–7539. [Google Scholar] [CrossRef] [PubMed]
- Acciavatti, R.J.; Barufaldi, B.; Vent, T.L.; Wileyto, E.; Maidment, A.D.A. Personalization of X-ray tube motion in digital breast tomosynthesis using virtual Defrise phantoms. In SPIE Medical Imaging 2019; SPIE Digital Library: Bellingham, WA, USA, 2019; p. 10. [Google Scholar]
- Acciavatti, R.J.; Maidment, A.D.A. Oblique reconstructions in tomosynthesis. I. Linear systems theory. Med. Phys. 2013, 40, 111911. [Google Scholar] [CrossRef] [PubMed]
- Acciavatti, R.J.; Maidment, A.D.A. Oblique reconstructions in tomosynthesis. II. Super-resolution. Med. Phys. 2013, 40, 111912. [Google Scholar] [CrossRef] [PubMed]
- Vent, T.L.; Barufaldi, B.; Acciavatti, R.J.; Krishnamoorthy, S.; Surti, S.; Maidment, A.D. Next generation tomosynthesis image acquisition optimization for dedicated PET-DBT attenuation corrections. In Proceedings of the Medical Imaging 2021, Physics of Medical Imaging, San Diego, CA, USA, 14–18 February 2021; Volume 115954, pp. 115954V1–115954V7. [Google Scholar]
- Krishnamoorthy, S.; Vent, T.; Barufaldi, B.; A Maidment, A.D.; Karp, J.S.; Surti, S. Evaluating attenuation correction strategies in a dedicated, single-gantry breast PET-tomosynthesis scanner. Phys. Med. Biol. 2020, 65, 235028. [Google Scholar] [CrossRef]
- Vent, T.L.; Barufaldi, B.; Maidment, A.D.A. Simulation and experimental validation of high-resolution test objects for evaluating a next-generation digital breast tomosynthesis prototype. Prog. Biomed. Opt. Imaging-Proc. SPIE 2019, 10948, 109480M. [Google Scholar]
- Vent, T.L.; Barufaldi, B.; Acciavatti, R.J.; Maidment, A. Simulation of high-resolution test objects using non-isocentric acquisition geometries in next-generation digital tomosynthesis. In SPIE Medical Imaging 2020; SPIE Digital Library: Bellingham, WA, USA, 2020; p. 23. [Google Scholar]
- Barufaldi, B.; Bakic, P.R.; Higginbotham, D.; Maidment, A.D.A. OpenVCT: A GPU-accelerated virtual clinical trial pipeline for mammography and digital breast tomosynthesis. In SPIE Medical Imaging 2018; SPIE Digital Library: Houston, TX, USA, 2018; p. 10573588. [Google Scholar]
- Barufaldi, B.; A Maidment, A.D.; Dustler, M.; Axelsson, R.; Tomic, H.; Zackrisson, S.; Tingberg, A.; Bakic, P.R. Virtual Clinical Trials in Medical Imaging System Evaluation and Optimisation. Radiat. Prot. Dosim. 2021, 195, 363–371. [Google Scholar] [CrossRef]
- Rodríguez-Ruiz, A.; A Agasthya, G.; Sechopoulos, I. The compressed breast during mammography and breast tomosynthesis: In vivo shape characterization and modeling. Phys. Med. Biol. 2017, 62, 6920–6937. [Google Scholar] [CrossRef]
- Rodríguez-Ruiz, A.; Feng, S.S.J.; van Zelst, J.; Vreemann, S.; Mann, J.R.; D’Orsi, C.J.; Sechopoulos, I. Improvements of an objective model of compressed breasts undergoing mammography: Generation and characterization of breast shapes. Med. Phys. 2017, 44, 2161–2172. [Google Scholar] [CrossRef]
- Teixeira, J.P.; Silva Filho, T.M.; Do Rego, T.G.; Malheiros, Y.B.; Dustler, M.; Bakic, P.R.; Vent, T.L.; Acciavatti, R.J.; Krishnamoorthy, S.; Surti, S.; et al. Novel Perlin-based phantoms using 3D models of compressed breast shapes and fractal noise. In Medical Imaging 2022: Physics of Medical Imaging; Zhao, W., Yu, L., Eds.; SPIE: Bellingham, WA, USA, 2022; p. 127. [Google Scholar]
- Acciavatti, R.J.; Rodriguez-Ruiz, A.; Vent, T.L.; Bakic, P.R.; Reiser, I.; Sechopoulos, I.; Maidment, A.D. Analysis of volume overestimation artifacts in the breast outline segmentation in tomosynthesis. In SPIE Medical Imaging; SPIE: Bellingham, WA, USA, 2018; p. 195. [Google Scholar]
- Sechopoulos, I. A review of breast tomosynthesis. Part, I. The image acquisition process. Med. Phys. 2013, 40, 014301. [Google Scholar] [CrossRef]
- Sechopoulos, I. A review of breast tomosynthesis. Part II. Image reconstruction, processing and analysis, and advanced applications. Med. Phys. 2013, 40, 014302. [Google Scholar] [CrossRef]
- Hu, Y.-H.; Zhao, B.; Zhao, W. Image artifacts in digital breast tomosynthesis: Investigation of the effects of system geometry and reconstruction parameters using a linear system approach. Med. Phys. 2008, 35, 5242–5252. [Google Scholar] [CrossRef] [PubMed]
- Vent, T.L.; Acciavatti, R.J.; Choi, C.; Barufaldi, B.; Krishnamoorthy, S.; Borges, L.; Kuo, J.; Ringer, P.; Ng, S.; Surti, S.; et al. Pre-clinical evaluation and optimization of image quality for a next generation tomosynthesis prototype. In SPIE Medical Imaging; SPIE: Bellingham, WA, USA, 2022; Volume 12031, pp. 1030–1036. [Google Scholar]
- Highnam, R.; Brady, S.M.; Yaffe, M.J.; Karssemeijer, N.; Harvey, J. Robust breast composition measurement-VolparaTM. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 342–349. [Google Scholar]
- Hartman, K.; Highnam, R.; Warren, R.; Jackson, V. Volumetric assessment of breast tissue composition from FFDM images. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; pp. 33–39. [Google Scholar]
- Gastounioti, A.; Pantalone, L.; Scott, C.G.; Cohen, E.A.; Wu, F.F.; Winham, S.J.; Jensen, M.R.; Maidment, A.D.A.; Vachon, C.M.; Conant, E.F.; et al. Fully Automated Volumetric Breast Density Estimation from Digital Breast Tomosynthesis. Radiology 2021, 301, 561–568. [Google Scholar] [CrossRef]
- Abadi, E.; Segars, W.P.; Tsui, B.M.W.; Kinahan, P.E.; Bottenus, N.; Frangi, A.F.; Maidment, A.; Lo, J.; Samei, E. Virtual clinical trials in medical imaging: A review. J. Med. Imaging 2020, 7, 042805. [Google Scholar] [CrossRef]
- Elangovan, P.; Mackenzie, A.; Dance, D.R.; Young, K.C.; Cooke, V.; Wilkinson, L.; Given-Wilson, R.M.; Wallis, M.G.; Wells, K. Design and validation of realistic breast models for use in multiple alternative forced choice virtual clinical trials. Phys. Med. Biol. 2017, 62, 2778–2794. [Google Scholar] [CrossRef]
- Vancoillie, L.; Marshall, N.W.; Cockmartin, L.; Vignero, J.; Zhang, G.; Bosmans, H. Verification of the accuracy of a hybrid breast imaging simulation framework for virtual clinical trial applications. J. Med. Imaging 2020, 7, 042804. [Google Scholar] [CrossRef]
- Badano, A.; Graff, C.G.; Badal, A.; Sharma, D.; Zeng, R.; Samuelson, F.W.; Glick, S.J.; Myers, K.J. Evaluation of Digital Breast Tomosynthesis as Replacement of Full-Field Digital Mammography Using an In Silico Imaging Trial. JAMA Netw. Open 2018, 1, e185474. [Google Scholar] [CrossRef] [PubMed]
- Pokrajac, D.D.; Maidment, A.D.A.; Bakic, P.R. Optimized generation of high resolution breast anthropomorphic software phantoms. Med. Phys. 2012, 39, 2290–2302. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Radiation Units and Measurements (ICRU) Report 44. Tissue Substitutes in Radiation Dosimetry; International Commission on Radiation Units and Measurements: Washington, DC, USA, 1989; Available online: https://scholar.google.com/scholar_lookup?t (accessed on 27 June 2023).
- Kuo, J.; Ringer, P.A.; Fallows, S.G.; Bakic, P.R.; Maidment, A.D.; Ng, S. Dynamic reconstruction and rendering of 3D tomosynthesis images. In SPIE Medical Imaging; SPIE: Orlando, FL, USA, 2011; Volume 7961, pp. 355–365. [Google Scholar]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2020, 18, 203–211. [Google Scholar] [CrossRef]
- Abraham, N.; Khan, N.M. Multimodal segmentation with MGF-Net and the focal tversky loss function. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Abraham, N.; Khan, N.M. A novel focal tversky loss function with improved attention u-net for lesion segmentation. In Proceedings of the International Symposium on Biomedical Imaging, Venice, Italy, 8–11 April 2019. [Google Scholar]
- Gomes, J.; Barbosa, Y.; Do Rego, T.; Silva, T.; Vent, T.; Maidment, A.; Barufaldi, B. Deep Learning Method for Volumetric Segmentation of Dense Tissue in Tomosynthesis Using Computer Simulations. In Proceedings of the AAPM 2021, 63nd Annual Meeting & Exhibition, AAPM, Virtual, 25–29 July 2021. [Google Scholar]
- Zhang, Y.; Chan, H.-P.; Sahiner, B.; Wei, J.; Zhou, C.; Hadjiiski, L.M. Artifact Reduction Methods for Truncated Projections in Iterative Breast Tomosynthesis Reconstruction. J. Comput. Assist. Tomogr. 2009, 33, 426–435. [Google Scholar] [CrossRef]
- Acciavatti, R.J.; Chang, A.; Woodbridge, L.; Maidment, A.D.A. Optimizing the Acquisition Geometry for Digital Breast Tomosynthesis Using the Defrise Phantom. In SPIE Medical Imaging; SPIE: Bellingham, WA, USA, 2014; p. 903315. [Google Scholar]
- Fradkin, M.; Hofmann, M.C.; Rouet, J.M.; Moore, R.H.; Kopans, D.B.; Tipton, K.; Suryanarayanan, S.; Boas, D.A.; Fang, Q. Diagnosing Breast Cancer Using Independent Diffuse Optical Tomography and X-ray Mammography Scans. In Multimodal Biomedical Imaging VIII; Azar, F.S., Intes, X., Eds.; SPIE: Paris, France, 2013; Volume 8574, pp. 58–65. [Google Scholar]
- Wu, R.C.; Maxwell, I.; Yang, F.M.I.; Jarmuske, F.M.M.B.; Boushey, F.P.M.R.P. Autologous Fat Grafting as a Novel Approach to Parastomal Soft-tissue Volume Deficiencies. Plast. Reconstr. Surg.-Glob. Open 2014, 2, e123. [Google Scholar] [CrossRef]
- Chae, M.P.; Rozen, W.M.; Spychal, R.T.; Hunter-Smith, D.J. Breast volumetric analysis for aesthetic planning in breast reconstruction: A literature review of techniques. Gland Surg. 2016, 5, 212–226. [Google Scholar] [PubMed]
- He, Y.; Liu, Y.; Dyer, B.A.; Boone, J.M.; Liu, S.; Chen, T.; Zheng, F.; Zhu, Y.; Sun, Y.; Rong, Y.; et al. 3D-printed breast phantom for multi-purpose and multi-modality imaging. Quant. Imaging Med. Surg. 2019, 9, 63–74. [Google Scholar] [CrossRef] [PubMed]
- Lagios, M.D.; Westdahl, P.R.; Rose, M.R.; Concannon, S. Pageťs disease of the nipple. Alternative management in cases without or with minimal extent of underlying breast carcinoma. Cancer 1984, 54, 545–551. [Google Scholar] [CrossRef] [PubMed]
- Dalberg, K.; Hellborg, H.; Wärnberg, F. Paget’s disease of the nipple in a population based cohort. Breast Cancer Res Treat 2008, 111, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Ji, J.; Tan, C.; Zhang, Q.; Feng, S.-Y. Erosive Adenomatosis of the Nipple Masquerading as Paget’s Disease: A Case Report. Int. J. Dermatol. Venereol. 2020, 3, 246–247. [Google Scholar] [CrossRef]

| Demographics | |
|---|---|
| Patients, count | 660 |
| Age, years, mean ± SD | 59.3 ± 10.7 |
| BMI, mean ± SD | 28.7 ± 7.7 |
| Density BI-RADS (1, 2, 3, 4), count (%) | (79 (12), 367 (56), 201 (30), 13 (2)) |
| Race (Asian, Black, White, Other), count | (25 (4), 309 (47), 320 (48), 6 (1)) |
| CBT, mm, median (1st, 3rd) IQ | 60.50 (51.50, 69.5) |
| %VBD, median (1st, 3rd) IQ | 12.75 (8.40, 20.00) |
| Acquisition Parameters | (I) Conventional | (II) T | (III) XWR |
|---|---|---|---|
| X-ray Source Direction (Translation of focal spot) | Linear Unidirectional (LR) | Linear Bidirectional (LR + PA) | Angular Unidirectional (LR) |
| Number of Acquisitions (n) | 15 | 15 | 91 |
| Radiation Exposure (mode) | AEC | AEC | 6 × AEC |
| Angular Range (°) | −7.5 to 7.5 | −7.5 to 7.5 | −45 to 45 |
| … | … | (A) Jaccard Distance (Model), Mean ± SD | (B) Improvement in Classification of Air | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| d (mm) | Slices (#) | I1 | I1&2 | II1&2 | III1&2 | I1&2/I1 | II1&2/I1 | III1&2/I1 | II1&2/I1&2 | II1&2/III1&2 |
| −37.30 | 2751 | 0.064 ± 0.037 | 0.044 ± 0.026 | 5.6 × 10−4 ± 9.7× 10−4 | 0.010 ± 0.006 | 31.95% | 99.17% | 84.27% | 98.77% | 94.70% |
| −22.40 | 2720 | 0.031 ± 0.023 | 0.027 ± 0.017 | 2.3 × 10−4 ± 5.6 × 10−4 | 0.005 ± 0.005 | 10.29% | 99.34% | 80.29% | 99.26% | 96.65% |
| −16.45 | 2725 | 0.015 ± 0.016 | 0.016 ± 0.012 | 8.3 × 10−5 ± 5.5 × 10−4 | 0.003 ± 0.002 | −11.93% | 99.54% | 78.42% | 99.60% | 97.90% |
| −11.00 | 2750 | 0.007 ± 0.009 | 0.006 ± 0.007 | 1.9 × 10−5 ± 5.8 × 10−5 | 0.001 ± 0.001 | −1.70% | 99.72% | 73.07% | 99.73% | 98.97% |
| −5.50 | 2725 | 0.003 ± 0.005 | 0.003 ± 0.004 | 1.4 × 10−5 ± 6.0 × 10−5 | 0.001 ± 0.001 | 20.86% | 99.60% | 61.80% | 99.50% | 98.97% |
| −0.05 | 2725 | 0.002 ± 0.003 | 0.001 ± 0.002 | 1.1 × 10−5 ± 5.6 × 10−5 | 6.8 × 10−4 ± 4.8 × 10−4 | 28.56% | 99.39% | 54.65% | 99.15% | 98.65% |
| 5.40 | 2750 | 0.002 ± 0.007 | 0.001 ± 0.002 | 9.4 × 10−5 ± 3.8 × 10−5 | 3.9 × 10−4 ± 4.9 × 10−4 | 16.99% | 99.28% | 71.48% | 99.13% | 97.48% |
| 10.90 | 2725 | 0.006 ± 0.019 | 0.002 ± 0.006 | 1.3 × 10−5 ± 4.3 × 10−5 | 4.3 × 10−4 ± 0.001 | 34.92% | 99.62% | 91.37% | 99.42% | 95.60% |
| 16.35 | 2737 | 0.012 ± 0.033 | 0.004 ± 0.012 | 5.6 × 10−5 ± 2.5 × 10−4 | 9.3 × 10−4 ± 0.004 | 33.06% | 99.52% | 94.05% | 99.29% | 91.97% |
| 22.30 | 2684 | 0.011 ± 0.009 | 0.007 ± 0.007 | 9.9 × 10−5 ± 3.4 × 10−4 | 4.9 × 10−4 ± 6.9 × 10−4 | 33.20% | 99.10% | 95.26% | 98.65% | 80.92% |
| Slice Average, 95% CI (low, high) | 0.015 ± 0.027 (0.014, 0.015) | 0.012 ± 0.019 (0.011, 0.012) | 1.1 × 10−4 ± 4.1 × 10−4 (1.0 × 10−4, 1.1 × 10−4) | 0.002 ± 0.004 (2.2 × 10−3, 2.3 × 10−3) | 22.21% … | 99.29% … | 83.10% … | 99.09% … | 96.82% … | |
| … | … | (A) Jaccard of Adipose Tissue (Model), Mean ± SD | (B) Jaccard of Dense Tissue (Model), Mean ± SD | ||||||
|---|---|---|---|---|---|---|---|---|---|
| d (mm) | Slices (#) | I1 | I1&2 | II1&2 | III1&2 | I1 | I1&2 | II1&2 | III1&2 |
| −37.30 | 2751 | 0.91 ± 0.06 | 0.92 ± 0.06 | 0.94 ± 0.06 | 0.98 ± 0.05 | 0.69 ± 0.22 | 0.72 ± 0.22 | 0.66 ± 0.22 | 0.90 ± 0.17 |
| −22.40 | 2720 | 0.91 ± 0.08 | 0.91 ± 0.08 | 0.93 ± 0.06 | 0.97 ± 0.03 | 0.74 ± 0.13 | 0.76 ± 0.13 | 0.72 ± 0.16 | 0.92 ± 0.06 |
| −16.45 | 2725 | 0.91 ± 0.06 | 0.92 ± 0.06 | 0.93 ± 0.05 | 0.98 ± 0.02 | 0.76 ± 0.10 | 0.78 ± 0.10 | 0.75 ± 0.10 | 0.94 ± 0.04 |
| −11.00 | 2750 | 0.92 ± 0.06 | 0.92 ± 0.05 | 0.93 ± 0.05 | 0.98 ± 0.02 | 0.76 ± 0.09 | 0.78 ± 0.08 | 0.76 ± 0.08 | 0.94 ± 0.04 |
| −5.50 | 2725 | 0.92 ± 0.05 | 0.92 ± 0.05 | 0.93 ± 0.05 | 0.98 ± 0.03 | 0.76 ± 0.08 | 0.77 ± 0.08 | 0.75 ± 0.08 | 0.93 ± 0.03 |
| −0.05 | 2725 | 0.93 ± 0.04 | 0.93 ± 0.04 | 0.93 ± 0.04 | 0.98 ± 0.04 | 0.74 ± 0.10 | 0.77 ± 0.09 | 0.74 ± 0.10 | 0.93 ± 0.04 |
| 5.40 | 2750 | 0.93 ± 0.04 | 0.94 ± 0.04 | 0.94 ± 0.04 | 0.98 ± 0.03 | 0.75 ± 0.11 | 0.77 ± 0.10 | 0.74 ± 0.10 | 0.93 ± 0.04 |
| 10.90 | 2725 | 0.93 ± 0.06 | 0.94 ± 0.05 | 0.94 ± 0.05 | 0.98 ± 0.04 | 0.76 ± 0.11 | 0.78 ± 0.10 | 0.75 ± 0.11 | 0.94 ± 0.04 |
| 16.35 | 2737 | 0.92 ± 0.08 | 0.93 ± 0.07 | 0.93 ± 0.07 | 0.98 ± 0.03 | 0.73 ± 0.15 | 0.76 ± 0.13 | 0.71 ± 0.16 | 0.94 ± 0.04 |
| 22.30 | 2684 | 0.89 ± 0.07 | 0.90 ± 0.08 | 0.93 ± 0.08 | 0.97 ± 0.07 | 0.64 ± 0.24 | 0.67 ± 0.24 | 0.64 ± 0.23 | 0.86 ± 0.25 |
| Slice Average 95% CI (low, high) | 0.92 ±0.06 (0.915, 0.917) | 0.92 ± 0.06 (0.923, 0.924) | 0.93 ± 0.06 (0.931, 0.932) | 0.98 ± 0.04 (0.977, 0.978) | 0.73 ± 0.15 (0.731, 0.735) | 0.76 ± 0.14 (0.755, 0.759) | 0.72 ± 0.15 (0.719, 0.723) | 0.92 ± 0.10 (0.921, 0.924) | |
| … | (A) Adipose Tissue Segmentation (Model), Mean ± SD | (B) Dense Tissue Segmentation (Model), Mean ± SD | ||||||
|---|---|---|---|---|---|---|---|---|
| Metric | I1 | I1&2 | II1&2 | III1&2 | I1 | I1&2 | II1&2 | III1&2 |
| Dice | 0.91 ± 0.03 | 0.92 ± 0.03 | 0.93 ± 0.03 | 0.98 ± 0.02 | 0.75 ± 0.04 | 0.78 ± 0.03 | 0.74 ± 0.04 | 0.94 ± 0.01 |
| Precision | 0.95 ± 0.04 | 0.96 ± 0.04 | 0.96 ± 0.04 | 0.99 ± 0.01 | 0.86 ± 0.06 | 0.87 ± 0.05 | 0.85 ± 0.07 | 0.97 ± 0.01 |
| Recall | 0.96 ± 0.02 | 0.96 ± 0.02 | 0.97 ± 0.02 | 0.99 ± 0.02 | 0.89 ± 0.04 | 0.89 ± 0.04 | 0.86 ± 0.05 | 0.97 ± 0.02 |
| Accuracy | 0.99 ± 0.01 | 0.99 ± 0.01 | 0.99 ± 0.01 | 0.99 ± 0.00 | 0.99 ± 0.01 | 0.99 ± 0.01 | 0.99 ± 0.01 | 0.99 ± 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barufaldi, B.; Gomes, J.; Rego, T.G.d.; Malheiros, Y.; Filho, T.M.S.; Borges, L.R.; Acciavatti, R.J.; Surti, S.; Maidment, A.D.A. Impact of Tomosynthesis Acquisition on 3D Segmentations of Breast Outline and Adipose/Dense Tissue with AI: A Simulation-Based Study. Tomography 2023, 9, 1303-1314. https://doi.org/10.3390/tomography9040103
Barufaldi B, Gomes J, Rego TGd, Malheiros Y, Filho TMS, Borges LR, Acciavatti RJ, Surti S, Maidment ADA. Impact of Tomosynthesis Acquisition on 3D Segmentations of Breast Outline and Adipose/Dense Tissue with AI: A Simulation-Based Study. Tomography. 2023; 9(4):1303-1314. https://doi.org/10.3390/tomography9040103
Chicago/Turabian StyleBarufaldi, Bruno, Jordy Gomes, Thais G. do Rego, Yuri Malheiros, Telmo M. Silva Filho, Lucas R. Borges, Raymond J. Acciavatti, Suleman Surti, and Andrew D. A. Maidment. 2023. "Impact of Tomosynthesis Acquisition on 3D Segmentations of Breast Outline and Adipose/Dense Tissue with AI: A Simulation-Based Study" Tomography 9, no. 4: 1303-1314. https://doi.org/10.3390/tomography9040103
APA StyleBarufaldi, B., Gomes, J., Rego, T. G. d., Malheiros, Y., Filho, T. M. S., Borges, L. R., Acciavatti, R. J., Surti, S., & Maidment, A. D. A. (2023). Impact of Tomosynthesis Acquisition on 3D Segmentations of Breast Outline and Adipose/Dense Tissue with AI: A Simulation-Based Study. Tomography, 9(4), 1303-1314. https://doi.org/10.3390/tomography9040103






