Dynamic Contrast-Enhanced MRI in the Abdomen of Mice with High Temporal and Spatial Resolution Using Stack-of-Stars Sampling and KWIC Reconstruction
Abstract
1. Introduction
2. Materials and Methods
2.1. Phantom Studies
2.2. Animal Model
2.3. MRI
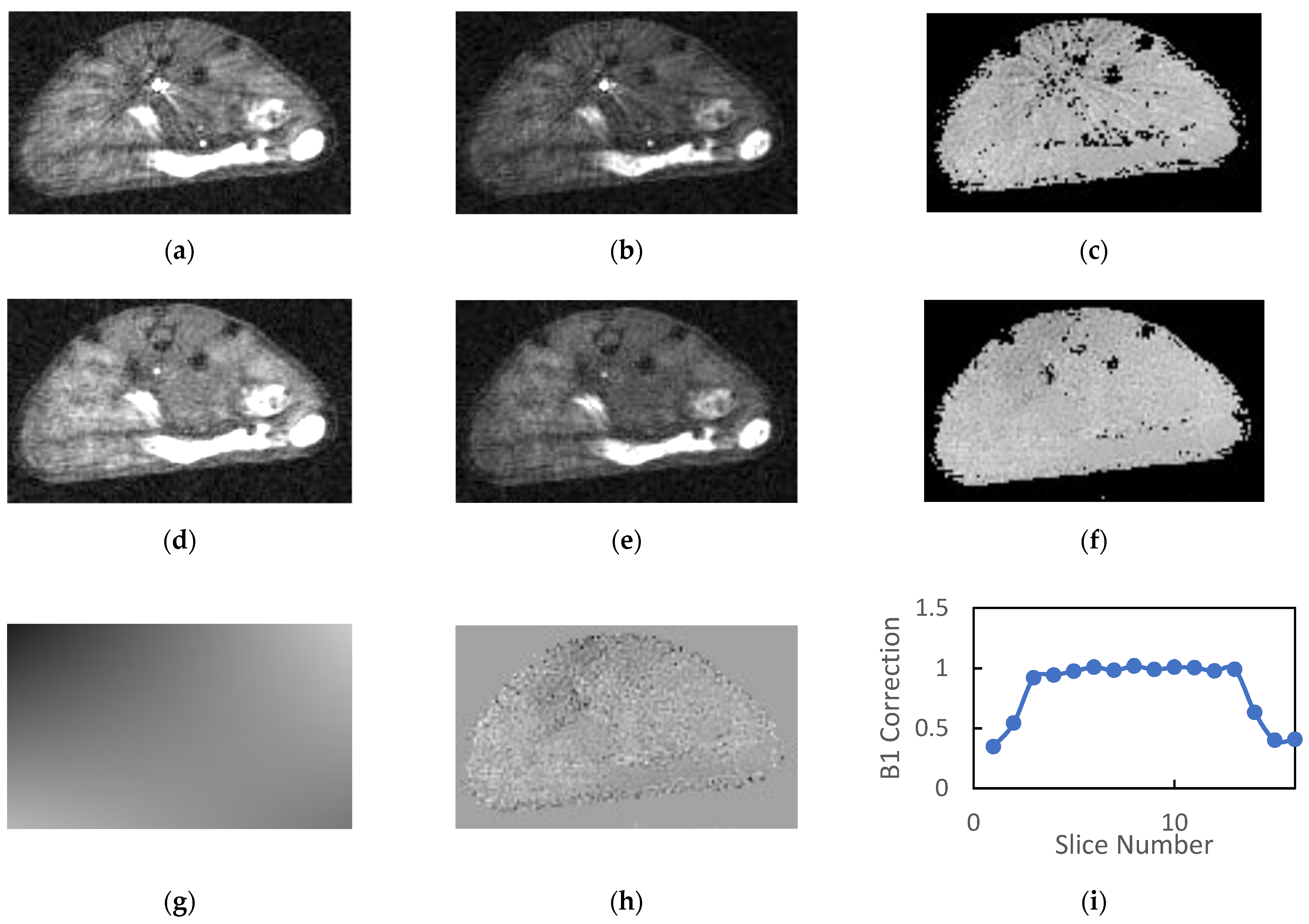
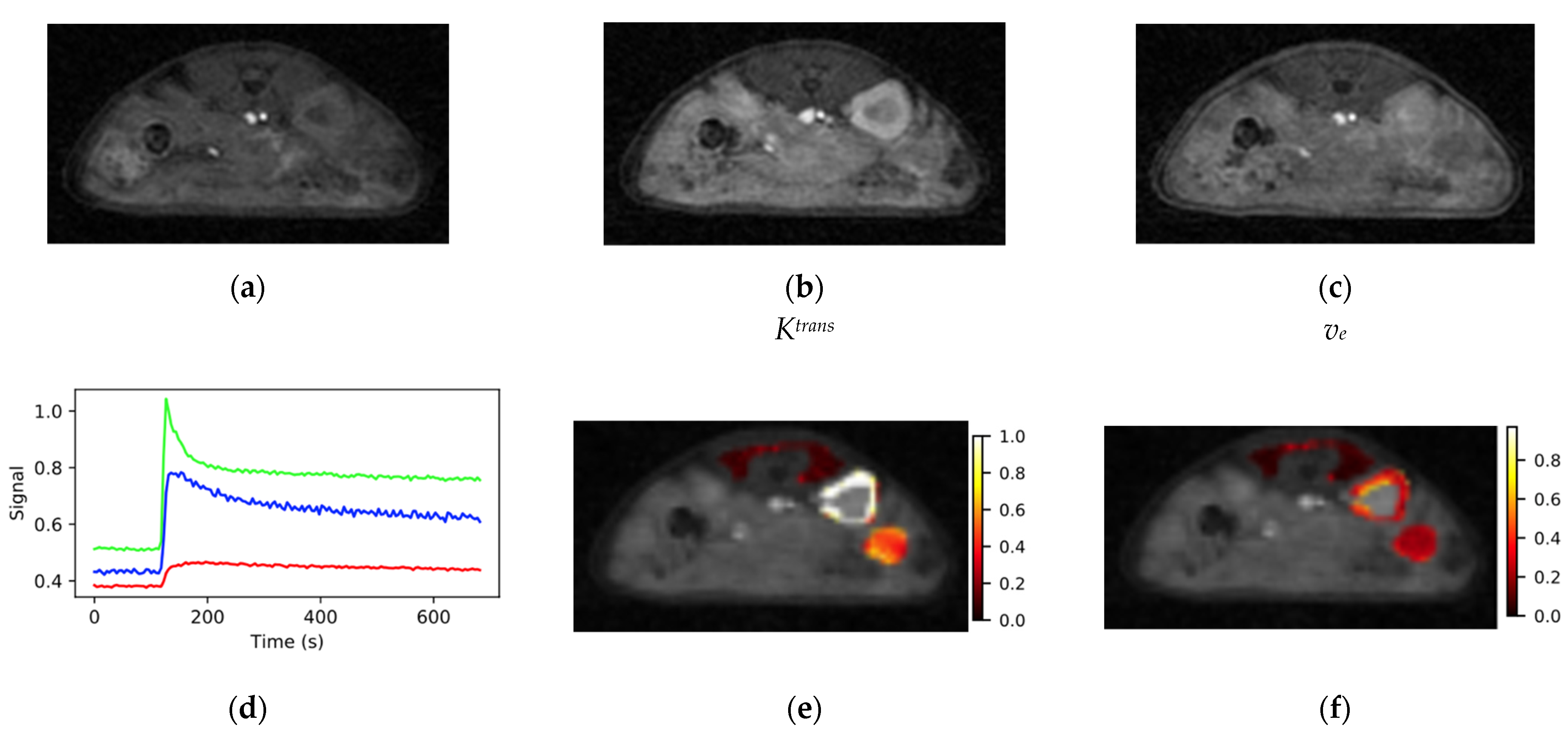
2.4. Image Reconstruction and Parameter Map Generation
3. Results
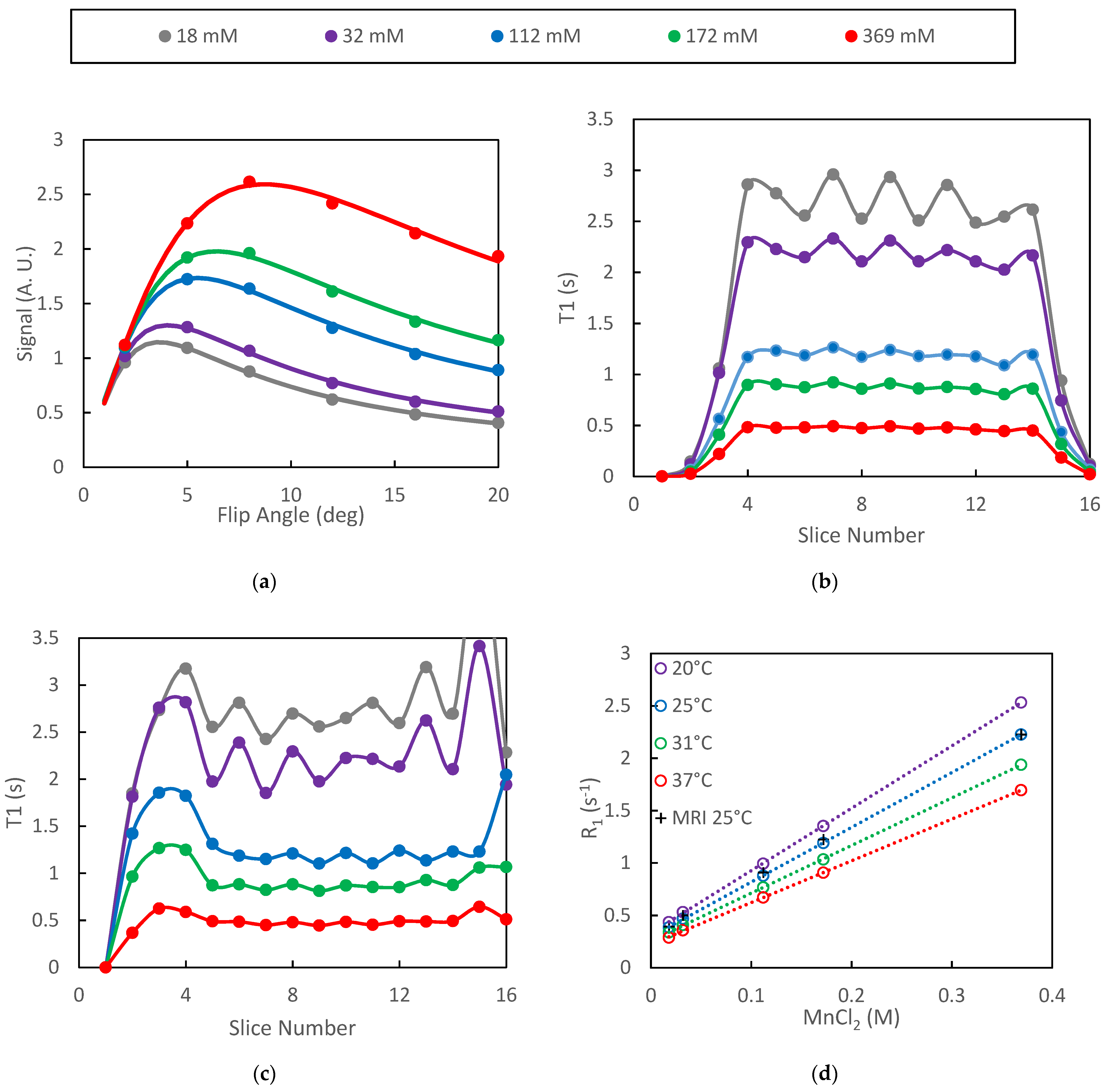
3.1. Phantom Studies
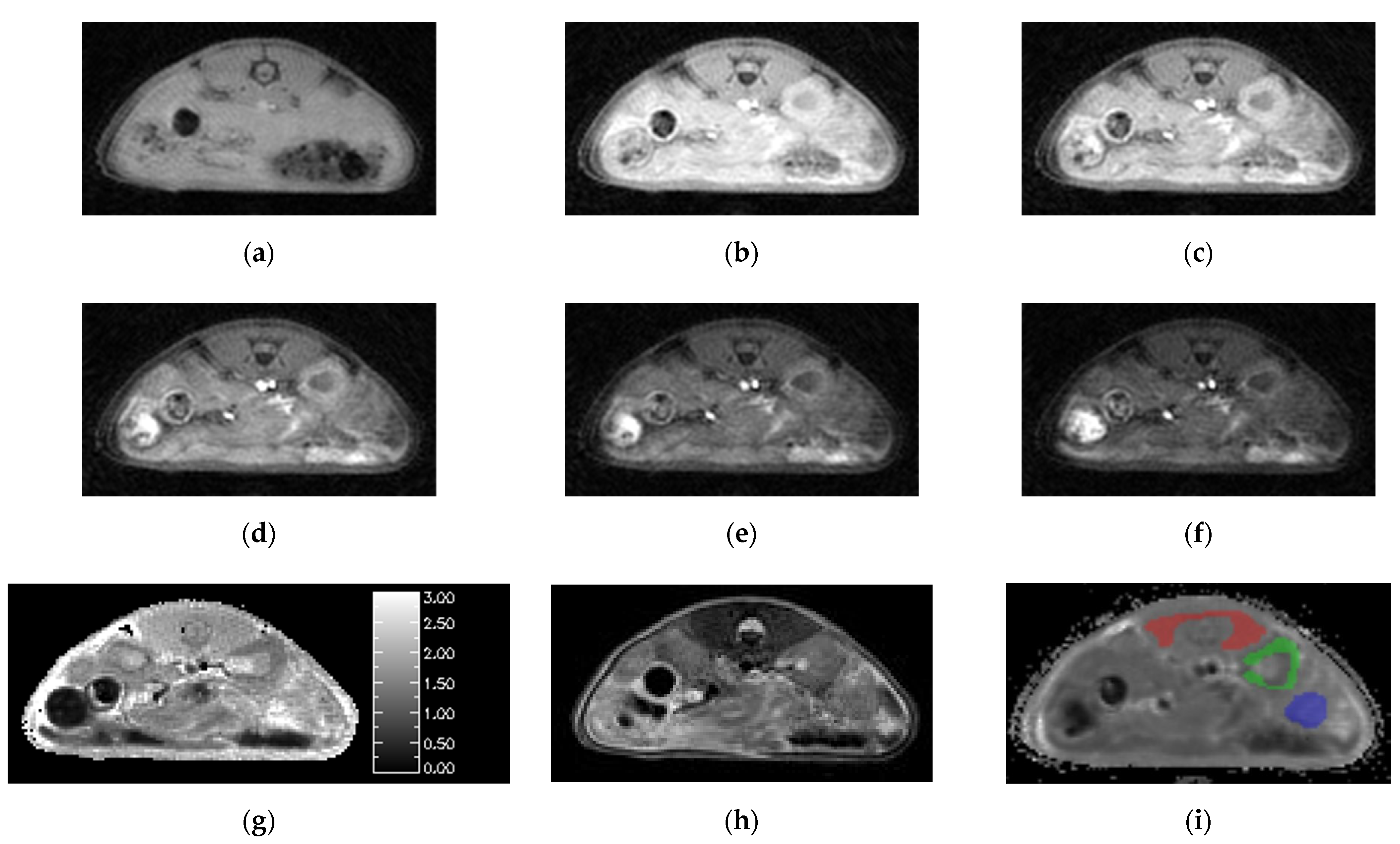
3.2. Animal Studies
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Montelius, M.; Spetz, J.; Jalnefjord, O.; Berger, E.; Nilsson, O.; Ljungberg, E. Forssell-Aronsson, Identification of Potential MR Derived Biomarkers for Tumor Tissue Response to Lu-177-Octreotate Therapy in an Animal Model of Small Intestine Neuroendocrine Tumor. Transl. Oncol. 2018, 11, 193–204. [Google Scholar] [CrossRef]
- Yamada, T.; Kashiwagi, Y.; Rokugawa, T.; Kato, H.; Konishi, H.; Hamada, T.; Nagai, R.; Masago, Y.; Itoh, M.; Suganami, T.; et al. Evaluation of hepatic function using dynamic contrast-enhanced magnetic resonance imaging in melanocortin 4 receptor-deficient mice as a model of nonalcoholic steatohepatitis. Magn. Reson. Imaging 2019, 57, 210–217. [Google Scholar] [CrossRef] [PubMed]
- Montelius, M.; Jalnefjord, O.; Spetz, J.; Nilsson, O.; Forssell-Aronsson, E.; Ljungberg, M. Multiparametric MR for non-invasive evaluation of tumour tissue histological characteristics after radionuclide therapy. Nmr Biomed. 2019, 32, 14. [Google Scholar] [CrossRef]
- O’Connor, J.P.B.; Jackson, A.; Parker, G.J.M.; Roberts, C.; Jayson, G.C. Dynamic contrast-enhanced MRI in clinical trials of antivascular therapies. Nat. Rev. Clin. Oncol. 2012, 9, 167–177. [Google Scholar] [CrossRef] [PubMed]
- Consolino, L.; Longo, D.L.; Sciortino, M.; Dastru, W.; Cabodi, S.; Giovenzana, G.B.; Aime, S. Assessing tumor vascularization as a potential biomarker of imatinib resistance in gastrointestinal stromal tumors by dynamic contrast-enhanced magnetic resonance imaging. Gastric Cancer 2017, 20, 629–639. [Google Scholar] [CrossRef] [PubMed]
- Bi, S.X.; Li, X.H.; Wei, C.S.; Xiang, H.H.; Shen, Y.X.; Yu, Y.Q. The antitumour growth and antiangiogenesis effects of xanthatin in murine glioma dynamically evaluated by dynamic contrast-enhanced magnetic resonance imaging. Phytother. Res. 2019, 33, 149–158. [Google Scholar] [CrossRef]
- Checkley, D.; Tessier, J.J.L.; Wedge, S.R.; Dukes, M.; Kendrew, J.; Curry, B.; Middleton, B.; Waterton, J.C. Dynamic contrast-enhanced MRI of vascular changes induced by the VEGF-signalling inhibitor ZD4190 in human tumour xenografts. Magn. Reson. Imaging 2003, 21, 475–482. [Google Scholar] [CrossRef]
- Piludu, F.; Marzi, S.; Pace, A.; Villani, V.; Fabi, A.; Carapella, C.M.; Terrenato, I.; Antenucci, A.; Vidiri, A. Early biomarkers from dynamic contrast-enhanced magnetic resonance imaging to predict the response to antiangiogenic therapy in high-grade gliomas. Neuroradiology 2015, 57, 1269–1280. [Google Scholar] [CrossRef]
- Sweis, R.F.; Medved, M.; Towey, S.; Karczmar, G.S.; Oto, A.; Szmulewitz, R.Z.; O’Donnell, P.H.; Fishkin, P.; Karrison, T.; Stadler, W.M. Dynamic Contrast-Enhanced Magnetic Resonance Imaging as a Pharmacodynamic Biomarker for Pazopanib in Metastatic Renal Carcinoma. Clin. Genitourin. Cancer 2017, 15, 207–212. [Google Scholar] [CrossRef][Green Version]
- Xue, W.; Du, X.S.; Wu, H.; Liu, H.; Xie, T.; Tong, H.P.; Chen, X.; Guo, Y.; Zhang, W.G. Aberrant glioblastoma neovascularization patterns and their correlation with DCE-MRI-derived parameters following temozolomide and bevacizumab treatment. Sci. Rep. 2017, 7, 10. [Google Scholar] [CrossRef]
- Fram, E.K.; Herfkens, R.J.; Johnson, G.A.; Glover, G.H.; Karis, J.P.; Shimakawa, A.; Perkins, T.G.; Pelc, N.J. Rapid Calculation of T1 Using Variable Flip Angle Gradient Refocused Imaging. Magn. Reson. Imaging 1987, 5, 201–208. [Google Scholar] [CrossRef]
- Cheng, H.L.M.; Wright, G.A. Rapid high-resolution T-1 mapping by variable flip angles: Accurate and precise measurements in the presence of radiofrequency field inhomogeneity. Magn. Reson. Med. 2006, 55, 566–574. [Google Scholar] [CrossRef] [PubMed]
- Bane, O.; Hectors, S.J.; Wagner, M.; Arlinghaus, L.L.; Aryal, M.P.; Cao, Y.; Chenevert, T.L.; Fennessy, F.; Huang, W.; Hylton, N.M.; et al. Accuracy, repeatability, and interplatform reproducibility of T-1 quantification methods used for DCE-MRI: Results from a multicenter phantom study. Magn. Reson. Med. 2018, 79, 2564–2575. [Google Scholar] [CrossRef] [PubMed]
- Yarnykh, V.L. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn. Reson. Med. 2007, 57, 192–200. [Google Scholar] [CrossRef]
- Kim, J.; Moestue, S.A.; Bathen, T.F.; Kim, E. R2* Relaxation Affects Pharmacokinetic Analysis of Dynamic Contrast-Enhanced MRI in Cancer and Underestimates Treatment Response at 7 T. Tomography 2019, 5, 308–319. [Google Scholar] [CrossRef] [PubMed]
- Pitman, K.E.; Bakke, K.M.; Kristian, A.; Malinen, E. Ultra-early changes in vascular parameters from dynamic contrast enhanced MRI of breast cancer xenografts following systemic therapy with doxorubicin and liver X receptor agonist. Cancer Imaging 2019, 19, 88. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.Y.; Cheng, Q.Q.; Huang, J.X.; Ma, M.J.; Zhang, D.; Lei, X.P.; Xiao, Z.Y.; Zhang, D.M.; Shi, C.Z.; Luo, L.P. Monitoring tumour microenvironment changes during anti-angiogenesis therapy using functional MRI. Angiogenesis 2019, 22, 457–470. [Google Scholar] [CrossRef]
- Cao, J.B.; Pickup, S.; Clendenin, C.; Blouw, B.; Choi, H.; Kang, D.; Rosen, M.; O’Dwyer, P.J.; Zhou, R. Dynamic Contrast-enhanced MRI Detects Responses to Stroma-directed Therapy in Mouse Models of Pancreatic Ductal Adenocarcinoma. Clin. Cancer Res. 2019, 25, 2314–2322. [Google Scholar] [CrossRef]
- Backhaus, P.; Buther, F.; Wachsmuth, L.; Frohwein, L.; Buchholz, R.; Karst, U.; Schafers, K.; Hermann, S.; Schafers, M.; Faber, C. Toward precise arterial input functions derived from DCE-MRI through a novel extracorporeal circulation approach in mice. Magn. Reson. Med. 2020, 84, 1404–1415. [Google Scholar] [CrossRef]
- Ge, X.; Quirk, J.D.; Engelbach, J.A.; Bretthorst, G.L.; Li, S.Q.; Shoghi, K.I.; Garbow, J.R.; Ackerman, J.J.H. Test-Retest Performance of a 1-Hour Multiparametric MR Image Acquisition Pipeline with Orthotopic Triple-Negative Breast Cancer Patient-Derived Tumor Xenografts. Tomography 2019, 5, 320–331. [Google Scholar] [CrossRef]
- Cardenas-Rodriguez, J.; Howison, C.M.; Pagel, M.D. A linear algorithm of the reference region model for DCE-MRI is robust and relaxes requirements for temporal resolution. Magn. Reson. Imaging 2013, 31, 497–507. [Google Scholar] [CrossRef] [PubMed]
- Yankeelov, T.E.; Luci, J.J.; Lepage, M.; Li, R.; Debusk, L.; Lin, P.C.; Price, R.R.; Gore, J.C. Quantitative pharmacokinetic analysis of DCE-MRI data without an arterial input function: A reference region model. Magn. Reson. Imaging 2005, 23, 519–529. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Folks, K.D.; Guo, L.L.; Stockard, C.R.; Fineberg, N.S.; Grizzle, W.E.; George, J.F.; Buchsbaum, D.J.; Morgan, D.E.; Zinn, K.R. DCE-MRI Detects Early Vascular Response in Breast Tumor Xenografts Following Anti-DR5 Therapy. Mol. Imaging Biol. 2011, 13, 94–103. [Google Scholar] [CrossRef] [PubMed]
- Jiang, K.; Tang, H.; Mishra, P.K.; Macura, S.I.; Lerman, L.O. Measurement of murine kidney functional biomarkers using DCE-MRI: A multi-slice TRICKS technique and semi-automated image processing algorithm. Magn. Reson. Imaging 2019, 63, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Subashi, E.; Moding, E.J.; Cofer, G.P.; MacFall, J.R.; Kirsch, D.G.; Qi, Y.; Johnson, G.A. A comparison of radial keyhole strategies for high spatial and temporal resolution 4D contrast-enhanced MRI in small animal tumor models. Med. Phys. 2013, 40, 10. [Google Scholar] [CrossRef]
- Gu, Y.N.; Gao, H.Y.; Kim, K.; Liu, Y.C.; Ramos-Estebanez, C.; Luo, Y.; Wang, Y.M.; Yu, X. Dynamic oxygen-17 MRI with adaptive temporal resolution using golden-means-based 3D radial sampling. Magn. Reson. Med. 2021, 85, 3112–3124. [Google Scholar] [CrossRef]
- Lin, W.; Guo, J.Y.; Rosen, M.A.; Song, H.K. Respiratory Motion-Compensated Radial Dynamic Contrast-Enhanced (DCE)-MRI of Chest and Abdominal Lesions. Magn. Reson. Med. 2008, 60, 1135–1146. [Google Scholar] [CrossRef]
- Trotier, A.J.; Castets, C.R.; Lefrancois, W.; Ribot, E.J.; Franconi, J.M.; Thiaudiere, E.; Miraux, S. USPIO-enhanced 3D-cine self-gated cardiac MRI based on a stack-of-stars golden angle short echo time sequence: Application on mice with acute myocardial infarction. J. Magn. Reson. Imaging 2016, 44, 355–365. [Google Scholar] [CrossRef]
- Hingorani, S.R.; Petricoin, E.F.; Maitra, A.; Rajapakse, V.; King, C.; Jacobetz, M.A.; Ross, S.; Conrads, T.P.; Veenstra, T.D.; Hitt, B.A.; et al. Preinvasive and invasive ductal pancreatic cancer and its early detection in the mouse. Cancer Cell 2003, 4, 437–450. [Google Scholar] [CrossRef]
- DPeters, C.; Korosec, F.R.; Grist, T.M.; Block, W.F.; Holden, J.E.; Vigen, K.K.; Mistretta, C.A. Undersampled projection reconstruction applied to MR angiography. Magn. Reson. Med. 2000, 43, 91–101. [Google Scholar] [CrossRef]
- Song, H.K.; Dougherty, L. k-space weighted image contrast (KWIC) for contrast manipulation in projection reconstruction MRI. Magn. Reson. Med. 2000, 44, 825–832. [Google Scholar] [CrossRef]
- Zur, Y.; Wood, M.L.; Neuringer, L.J. Spoiling of Transverse Magnetization in Steady-State Sequences. Magn. Reson. Med. 1991, 21, 251–263. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, S.; Schaeffter, T.; Koehler, T.; Eggers, H.; Doessel, O. An optimal radial profile order based on the golden ratio for time-resolved MRI. IEEE Trans. Med. Imaging 2007, 26, 68–76. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Jones, K.M.; Pagel, M.D.; Cárdenas-Rodríguez, J. Linearization improves the repeatability of quantitative dynamic contrast enhanced MRI. Magn. Reson. Imaging 2018, 47, 16–24. [Google Scholar] [CrossRef]
- Makihara, K.; Yamaguchi, M.; Ito, K.; Sakaguchi, K.; Hori, Y.; Semba, T.; Funahashi, Y.; Fujii, H.; Terada, Y. New Cluster Analysis Method for Quantitative Dynamic Contrast-Enhanced MRI Assessing Tumor Heterogeneity Induced by a Tumor-Microenvironmental Ameliorator (E7130) Treatment to a Breast Cancer Mouse Model. J. Magn. Reson. Imaging 2022. (Online ahead of print). [Google Scholar] [CrossRef]
- Nehrke, K. On the Steady-State Properties of Actual Flip Angle Imaging (AFI). Magn. Reson. Med. 2009, 61, 84–92. [Google Scholar] [CrossRef]
- Yarnykh, V.L. Optimal Radiofrequency and Gradient Spoiling for Improved Accuracy of T(1) and B(1) Measurements Using Fast Steady-State Techniques. Magn. Reson. Med. 2010, 63, 1610–1626. [Google Scholar] [CrossRef]
- Helms, G.; Dathe, H.; Weiskopf, N.; Dechent, P. Identification of Signal Bias in the Variable Flip Angle Method by Linear Display of the Algebraic Ernst Equation. Magn. Reson. Med. 2011, 66, 669–677. [Google Scholar] [CrossRef]
- Watanabe, T.; Frahm, J.; Michaelis, T. Reduced intracellular mobility underlies manganese relaxivity in mouse brain in vivo: MRI at 2.35 and 9.4 T. Brain Struct. Funct. 2015, 220, 1529–1538. [Google Scholar] [CrossRef]
- Kim, H.; Folks, K.D.; Guo, L.L.; Sellers, J.C.; Fineberg, N.S.; Stockard, C.R.; Grizzle, W.E.; Buchsbaum, D.J.; Morgan, D.E.; George, J.F.; et al. Early Therapy Evaluation of Combined Cetuximab and Irinotecan in Orthotopic Pancreatic Tumor Xenografts by Dynamic Contrast-Enhanced Magnetic Resonance Imaging. Mol. Imaging 2011, 10, 153–167. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Lv, P.; Zhang, H.T.; Fu, C.X.; Yao, X.Z.; Wang, C.; Zeng, M.S.; Li, Y.Y.; Wang, X.L. Dynamic contrast-enhanced (DCE) MRI assessment of microvascular characteristics in the murine orthotopic pancreatic cancer model. Magn. Reson. Imaging 2015, 33, 737–760. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Wang, C.; Yao, X.Z.; Liu, K.; Xu, Y.J.; Zhang, H.T.; Fu, C.X.; Wang, X.L.; Li, Y.Y. Application of 3.0 Tesla Magnetic Resonance Imaging for Diagnosis in the Orthotopic Nude Mouse Model of Pancreatic Cancer. Exp. Anim. 2014, 63, 403–413. [Google Scholar] [CrossRef][Green Version]
- Ritelli, R.; Ngaleu, R.N.; Bontempi, P.; Dandrea, M.; Nicolato, E.; Boschi, F.; Fiorini, S.; Calderan, L.; Scarpa, A.; Marzola, P. Pancreatic cancer growth using magnetic resonance and bioluminescence imaging. Magn. Reson. Imaging 2015, 33, 592–599. [Google Scholar] [CrossRef]
- Remus, C.C.; Sedlacik, J.; Wedegaertner, U.; Arck, P.; Hecher, K.; Adam, G.; Forkert, N.D. Application of the steepest slope model reveals different perfusion territories within the mouse placenta. Placenta 2013, 34, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Alison, M.; Quibel, T.; Balvay, D.; Autret, G.; Bourillon, C.; Chalouhi, G.E.; Deloison, B.; Salomon, L.J.; Cuenod, C.A.; Clement, O.; et al. Measurement of Placental Perfusion by Dynamic Contrast-Enhanced MRI at 4.7 T. Investig. Radiol. 2013, 48, 535–542. [Google Scholar] [CrossRef] [PubMed]
- Privratsky, J.R.; Wang, N.; Qi, Y.; Ren, J.F.; Morris, B.T.; Hunting, J.C.; Johnson, G.A.; Crowley, S.D. Dynamic contrast-enhanced MRI promotes early detection of toxin-induced acute kidney injury. Am. J. Physiol.-Ren. Physiol. 2019, 316, F351–F359. [Google Scholar] [CrossRef]
- Vautier, J.; el Tayara, N.E.; Walczak, C.; Mispelter, J.; Volk, A. Radial multigradient-echo DCE-MRI for 3D K-trans mapping with individual arterial input function measurement in mouse tumor models. Magn. Reson. Med. 2013, 70, 823–828. [Google Scholar] [CrossRef]
- Byk, K.; Jasinski, K.; Bartel, Z.; Jasztal, A.; Sitek, B.; Tomanek, B.; Chlopicki, S.; Skorka, T. MRI-based assessment of liver perfusion and hepatocyte injury in the murine model of acute hepatitis. Magn. Reson. Mater. Phys. Biol. Med. 2016, 29, 789–798. [Google Scholar] [CrossRef]
- Sakata, N.; Obenaus, A.; Chan, N.K.; Hayes, P.; Chrisler, J.; Hathout, E. Correlation between angiogenesis and islet graft function in diabetic mice: Magnetic resonance imaging assessment. J. Hepato-Biliary-Pancreat. Sci. 2010, 17, 692–700. [Google Scholar] [CrossRef]
- Song, K.D.; Choi, D.; Lee, J.H.; Im, G.H.; Yang, J.; Kim, J.H.; Lee, W.J. Evaluation of Tumor Microvascular Response to Brivanib by Dynamic Contrast-Enhanced 7-T MRI in an Orthotopic Xenograft Model of Hepatocellular Carcinoma. Am. J. Roentgenol. 2014, 202, W559–W566. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.S.; Welch, E.B.; Li, X.; Arlinghaus, L.R.; Loveless, M.E.; Koyama, T.; Gore, J.C.; Yankeelov, T.E. Quantitative effects of using compressed sensing in dynamic contrast enhanced MRI. Phys. Med. Biol. 2011, 56, 4933–4946. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Cho, H. Temporal Resolution Improvement of Calibration-Free Dynamic Contrast-Enhanced MRI With Compressed Sensing Optimized Turbo Spin Echo: The Effects of Replacing Turbo Factor with Compressed Sensing Accelerations. J. Magn. Reson. Imaging 2016, 44, 138–147. [Google Scholar] [CrossRef] [PubMed]
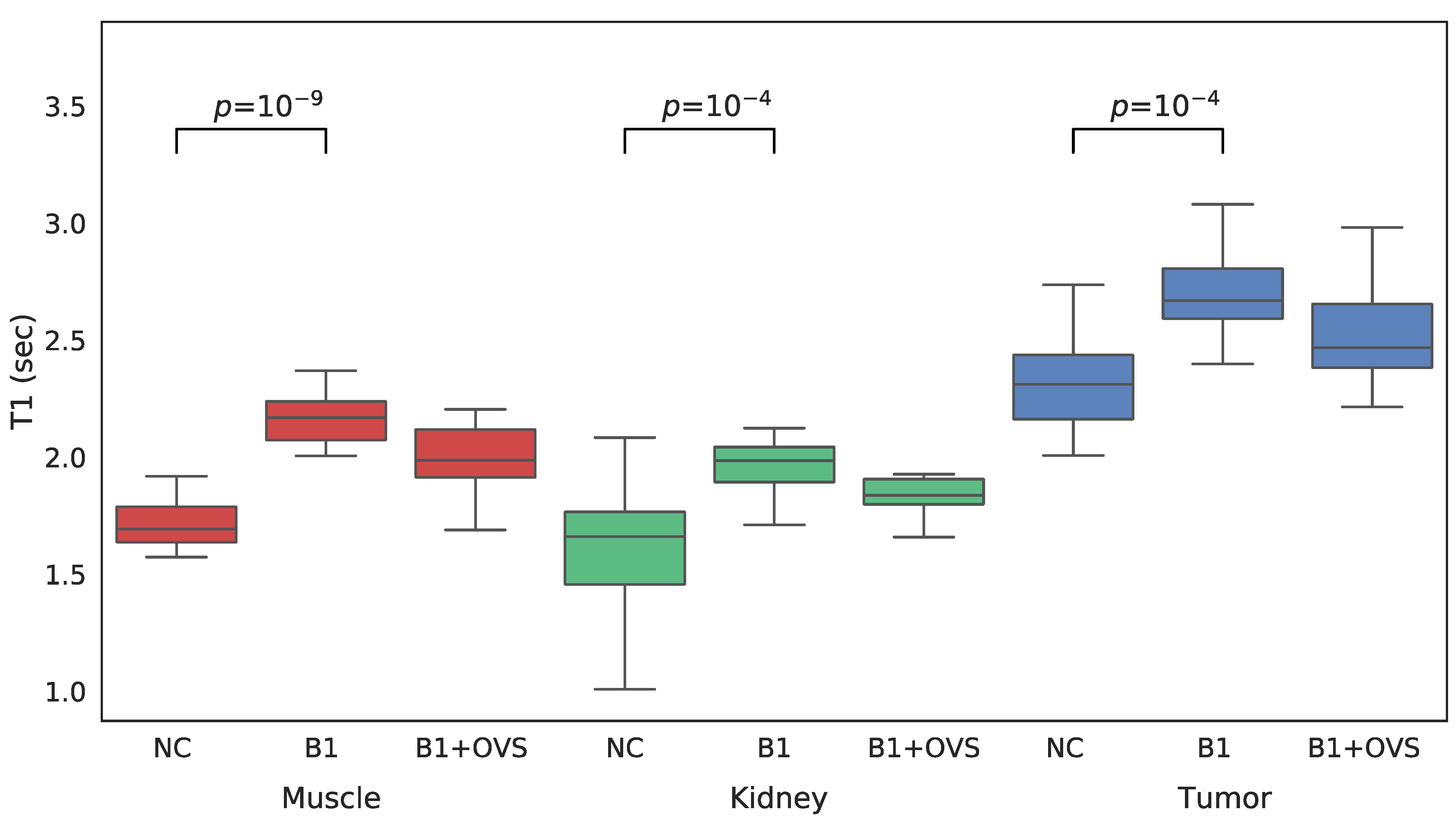
| Method | Muscle | Kidney | Tumor |
|---|---|---|---|
| No B1 Correction | 1.70 ± 0.11 | 1.60 ± 0.14 | 2.27 ± 0.19 |
| B1 Correction w/o OVS | 2.14 ± 0.08 | 1.93 ± 0.12 | 2.69 ± 0.21 |
| B1 Correction with OVS | 2.16 ± 0.07 | 1.87 ± 0.10 | 2.56 ± 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pickup, S.; Romanello, M.; Gupta, M.; Song, H.K.; Zhou, R. Dynamic Contrast-Enhanced MRI in the Abdomen of Mice with High Temporal and Spatial Resolution Using Stack-of-Stars Sampling and KWIC Reconstruction. Tomography 2022, 8, 2113-2128. https://doi.org/10.3390/tomography8050178
Pickup S, Romanello M, Gupta M, Song HK, Zhou R. Dynamic Contrast-Enhanced MRI in the Abdomen of Mice with High Temporal and Spatial Resolution Using Stack-of-Stars Sampling and KWIC Reconstruction. Tomography. 2022; 8(5):2113-2128. https://doi.org/10.3390/tomography8050178
Chicago/Turabian StylePickup, Stephen, Miguel Romanello, Mamta Gupta, Hee Kwon Song, and Rong Zhou. 2022. "Dynamic Contrast-Enhanced MRI in the Abdomen of Mice with High Temporal and Spatial Resolution Using Stack-of-Stars Sampling and KWIC Reconstruction" Tomography 8, no. 5: 2113-2128. https://doi.org/10.3390/tomography8050178
APA StylePickup, S., Romanello, M., Gupta, M., Song, H. K., & Zhou, R. (2022). Dynamic Contrast-Enhanced MRI in the Abdomen of Mice with High Temporal and Spatial Resolution Using Stack-of-Stars Sampling and KWIC Reconstruction. Tomography, 8(5), 2113-2128. https://doi.org/10.3390/tomography8050178






