Noise-Based Image Harmonization Significantly Increases Repeatability and Reproducibility of Radiomics Features in PET Images: A Phantom Study
Abstract
:1. Introduction
2. Materials and Methods
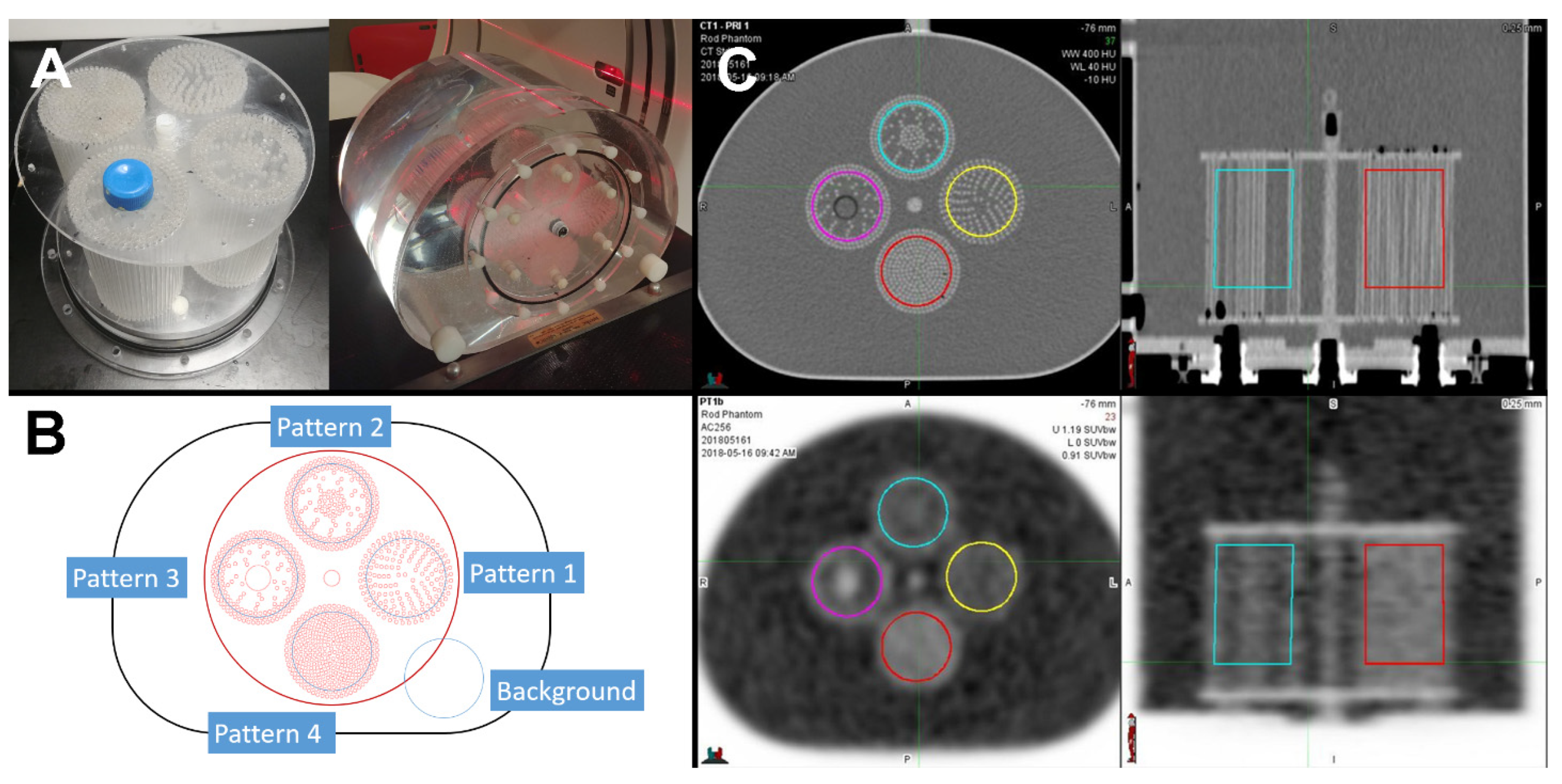
2.1. Texture Pattern Phantom
2.2. PET/CT Scans
2.3. Contouring
2.4. Standard and Harmonized Datasets (for Reproducibility)
2.5. Repeatability Dataset
2.6. Radiomics Analysis
2.7. Reproducibility and Repeatability Metrics
2.8. Pattern Sensitivity
3. Results
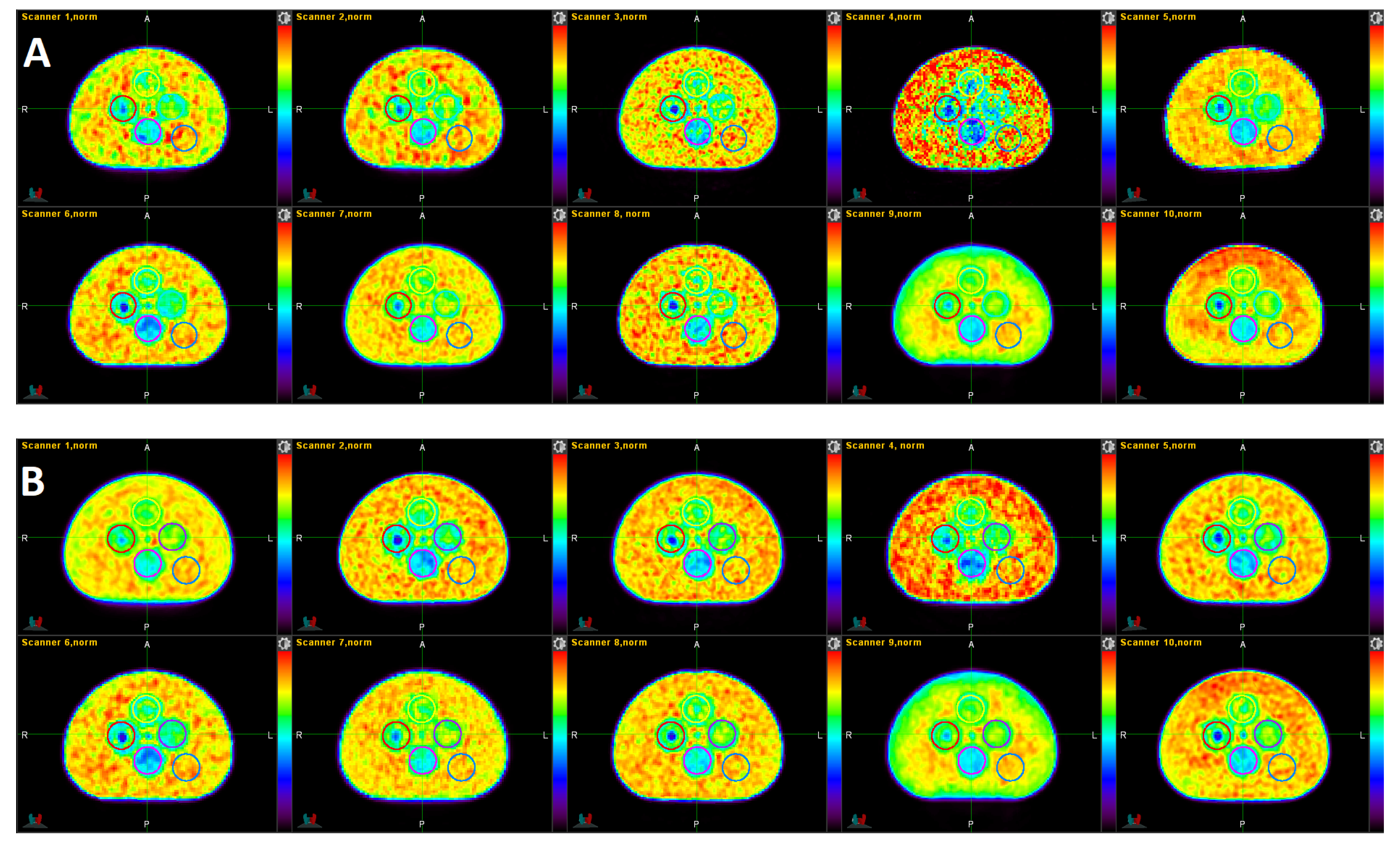
3.1. Qualitative Comparison
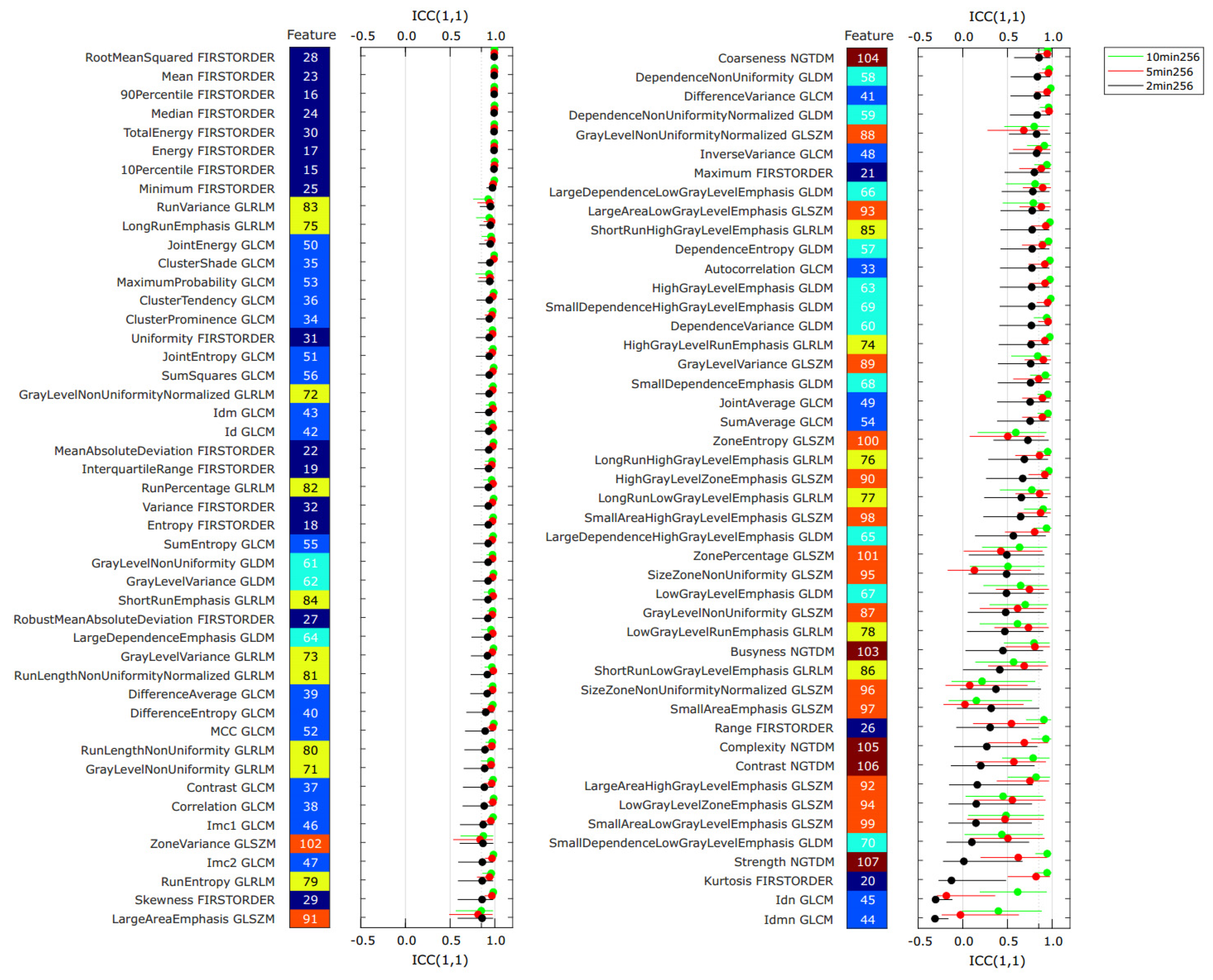
3.2. Repeatability Analysis
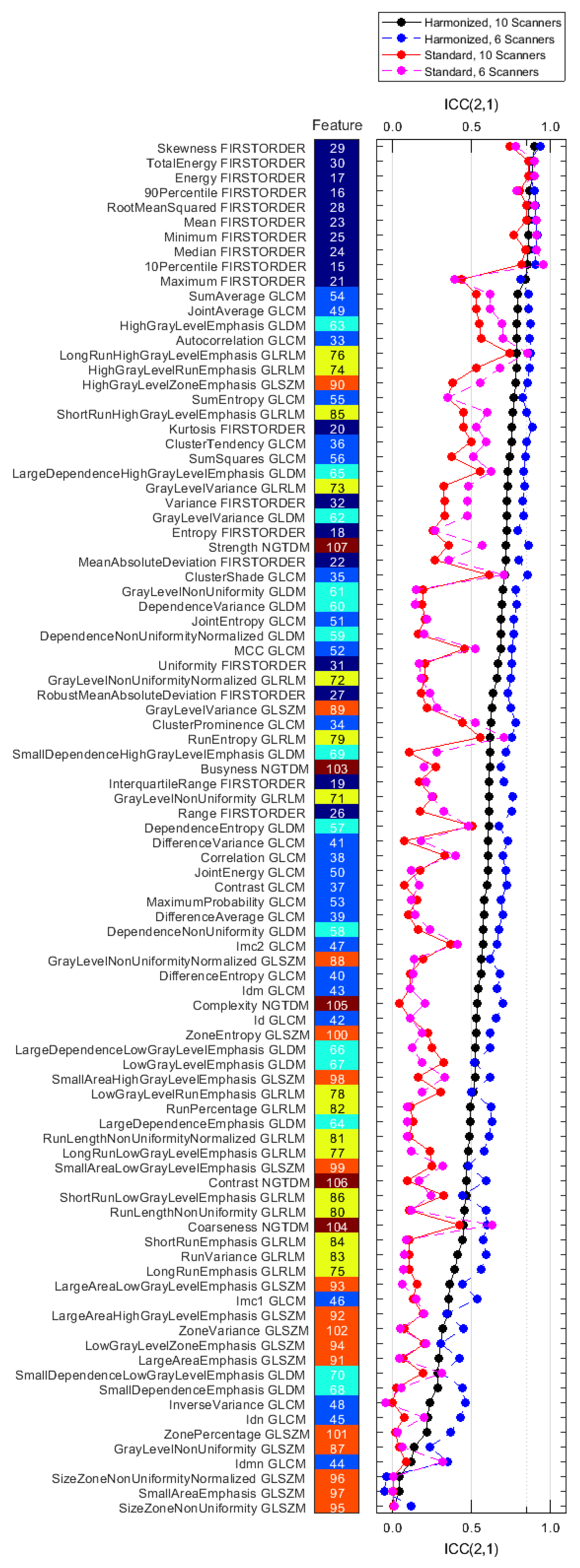
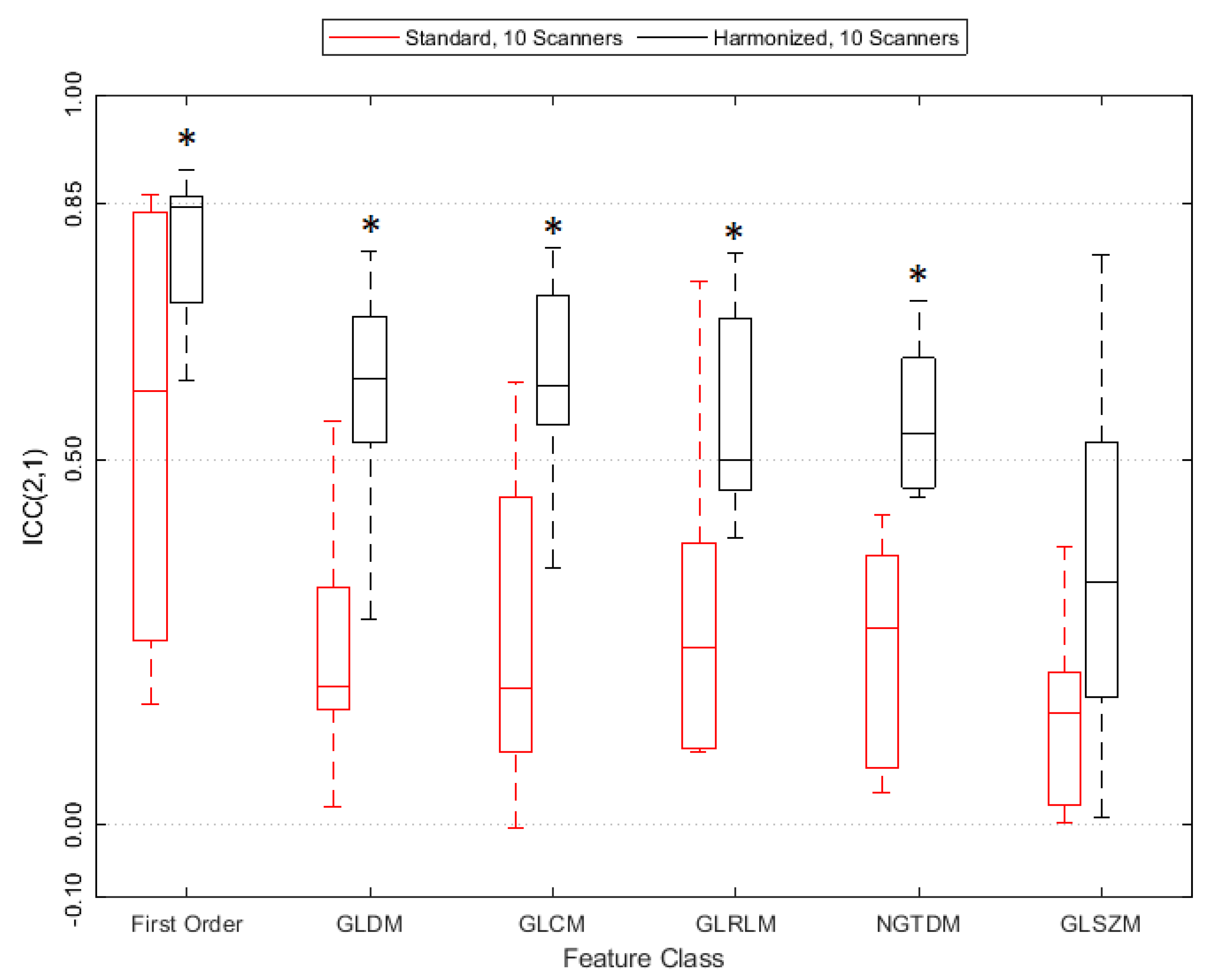
3.3. Reproducibility Analysis
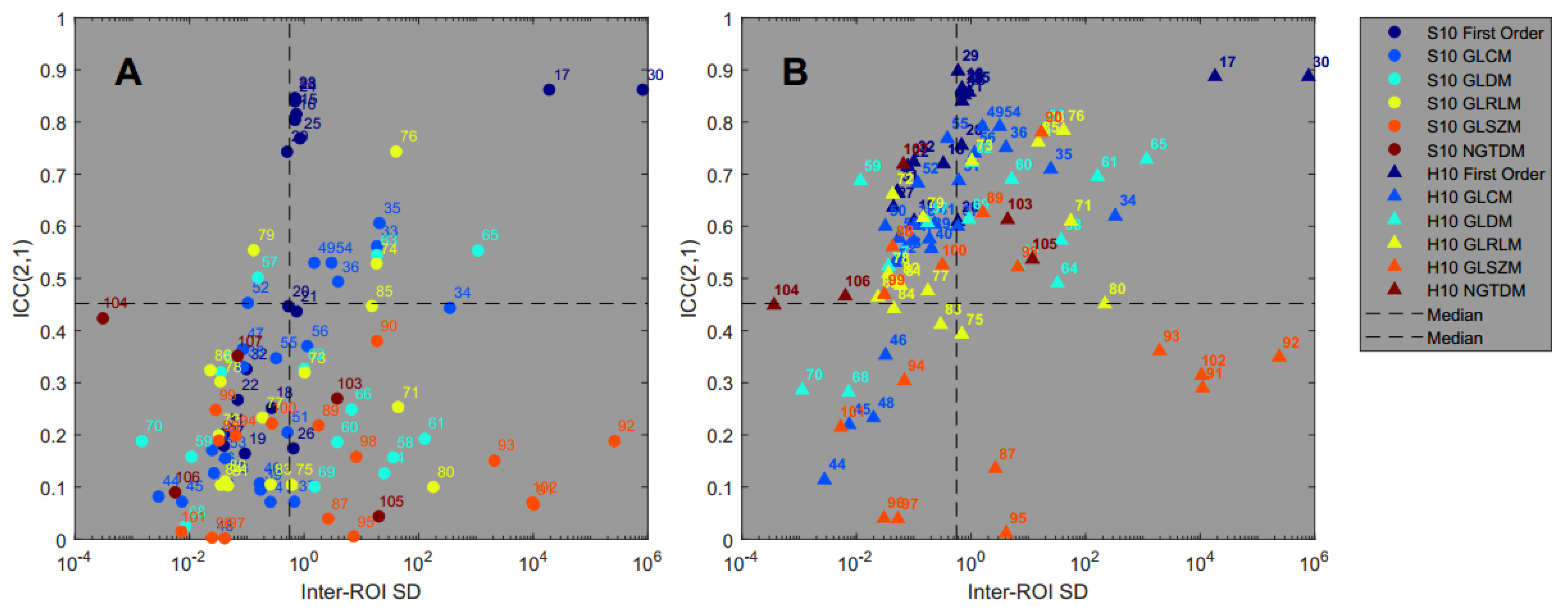
3.4. Feature Pattern Sensitivity
4. Discussion
4.1. Feature Calculation
4.2. Harmonization Method
4.3. Pattern Sensitivity
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huynh, E.; Hosny, A.; Guthier, C.; Bitterman, D.S.; Petit, S.F.; Haas-Kogan, D.A.; Kann, B.; Aerts, H.J.W.L.; Mak, R.H. Artificial intelligence in radiation oncology. Nat. Rev. Clin. Oncol. 2020, 17, 771–781. [Google Scholar] [CrossRef] [PubMed]
- Reuzé, S.; Schernberg, A.; Orlhac, F.; Sun, R.; Chargari, C.; Dercle, L.; Deutsch, E.; Buvat, I.; Robert, C. Radiomics in Nuclear Medicine Applied to Radiation Therapy: Methods, Pitfalls, and Challenges. Int. J. Radiat. Oncol. Biol. Phys. 2018, 102, 1117–1142. [Google Scholar] [CrossRef] [PubMed]
- Zwanenburg, A. Radiomics in nuclear medicine: Robustness, reproducibility, standardization, and how to avoid data analysis traps and replication crisis. Eur. J. Nucl. Med. Mol. Imaging 2019, 46, 2638–2655. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, J.W.; Frost, C. Reliability, repeatability and reproducibility: Analysis of measurement errors in continuous variables. Ultrasound Obstet. Gynecol. 2008, 31, 466–475. [Google Scholar] [CrossRef]
- Traverso, A.; Wee, L.; Dekker, A.; Gillies, R. Repeatability and Reproducibility of Radiomic Features: A Systematic Review. Int. J. Radiat. Oncol. Biol. Phys. 2018, 102, 1143–1158. [Google Scholar] [CrossRef] [Green Version]
- Forgacs, A.; Pall Jonsson, H.; Dahlbom, M.; Daver, F.; DiFranco, M.D.; Opposits, G.; Krizsan, A.K.; Garai, I.; Czernin, J.; Varga, J.; et al. A Study on the Basic Criteria for Selecting Heterogeneity Parameters of F18-FDG PET Images. PLoS ONE 2016, 11, e0164113. [Google Scholar] [CrossRef]
- Lambin, P.; Leijenaar, R.T.; Deist, T.M.; Peerlings, J.; De Jong, E.E.; Van Timmeren, J.; Sanduleanu, S.; Larue, R.T.; Even, A.J.; Jochems, A.; et al. Radiomics: The bridge between medical imaging and personalized medicine. Nat. Rev. Clin. Oncol. 2017, 14, 749–762. [Google Scholar] [CrossRef]
- Gallivanone, F.; Interlenghi, M.; D’Ambrosio, D.; Trifirò, G.; Castiglioni, I. Parameters Influencing PET Imaging Features: A Phantom Study with Irregular and Heterogeneous Synthetic Lesions. Contrast Media Mol. Imaging 2018, 2018, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Pfaehler, E.; Beukinga, R.J.; Jong, J.R.; Slart, R.H.J.A.; Slump, C.H.; Dierckx, R.A.J.O.; Boellaard, R. Repeatability of 18F-FDG PET radiomic features: A phantom study to explore sensitivity to image reconstruction settings, noise, and delineation method. Med. Phys. 2019, 46, 665–678. [Google Scholar] [CrossRef] [Green Version]
- Carles, M.; Fechter, T.; Martí-Bonmatí, L.; Baltas, D.; Mix, M. Experimental phantom evaluation to identify robust positron emission tomography (PET) radiomic features. EJNMMI Phys. 2021, 8, 46. [Google Scholar] [CrossRef]
- Kueng, R.; Driscoll, B.; Manser, P.; Fix, M.K.; Stampanoni, M.; Keller, H. Quantification of local image noise variation in PET images for standardization of noise-dependent analysis metrics. Biomed. Phys. Eng. Express 2017, 3, 025007. [Google Scholar] [CrossRef]
- Oliver, J.A.; Budzevich, M.; Hunt, D.; Moros, E.G.; Latifi, K.; Dilling, T.J.; Feygelman, V.; Zhang, G. Sensitivity of Image Features to Noise in Conventional and Respiratory-Gated PET/CT Images of Lung Cancer: Uncorrelated Noise Effects. Technol. Cancer Res. Treat. 2016, 16, 595–608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grootjans, W.; Tixier, F.; Van der Vos, C.S.; Vriens, D.; Le Rest, C.C.; Bussink, J.; Oyen, W.J.; De Geus-Oei, L.-F.; Visvikis, D.; Visser, E.P. The Impact of Optimal Respiratory Gating and Image Noise on Evaluation of Intratumor Heterogeneity on 18F-FDG PET Imaging of Lung Cancer. J. Nucl. Med. 2016, 57, 1692–1698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Da-Ano, R.; Visvikis, D.; Hatt, M. Harmonization strategies for multicenter radiomics investigations. Phys. Med. Biol. 2020, 65, 24TR02. [Google Scholar] [CrossRef] [PubMed]
- Mali, S.A.; Ibrahim, A.; Woodruff, H.C.; Andrearczyk, V.; Müller, H.; Primakov, S.; Salahuddin, Z.; Chatterjee, A.; Lambin, P. Making Radiomics More Reproducible across Scanner and Imaging Protocol Variations: A Review of Harmonization Methods. J. Pers. Med. 2021, 11, 842. [Google Scholar] [CrossRef]
- Boellaard, R.; Delgado-Bolton, R.; Oyen, W.J.; Giammarile, F.; Tatsch, K.; Eschner, W.; Verzijlbergen, F.J.; Barrington, S.F.; Pike, L.C.; Weber, W.A.; et al. FDG PET/CT: EANM procedure guidelines for tumour imaging: Version 2.0. Eur. J. Nucl. Med. Mol. Imaging 2015, 42, 328–354. [Google Scholar] [CrossRef] [PubMed]
- Quak, E.; Le Roux, P.-Y.; Hofman, M.S.; Robin, P.; Bourhis, D.; Callahan, J.; Binns, D.; Desmonts, C.; Salaun, P.-Y.; Hicks, R.J.; et al. Harmonizing FDG PET quantification while maintaining optimal lesion detection: Prospective multicentre validation in 517 oncology patients. Eur. J. Nucl. Med. Mol. Imaging 2015, 42, 2072–2082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nordstrom, R.J. The Quantitative Imaging Network in Precision Medicine. Tomography 2016, 2, 239–241. [Google Scholar] [CrossRef]
- Kirov, A.S.; Danford, C.; Schmidtlein, C.R.; Yorke, E.; Humm, J.L.; Amols, H.I. PET quantification inaccuracy of non-uniform tracer distributions for radiation therapy. In Proceedings of the 2007 IEEE Nuclear Science Symposium Conference Record, Honolulu, HI, USA, 26 October–3 November 2007; pp. 2838–2841. [Google Scholar]
- Van Griethuysen, J.J.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.; Fillion-Robin, J.-C.; Pieper, S.; Aerts, H.J. Computational Radiomics System to Decode the Radiographic Phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef] [Green Version]
- Zwanenburg, A.; Vallières, M.; Abdalah, M.A.; Aerts, H.J.; Andrearczyk, V.; Apte, A.; Ashrafinia, S.; Bakas, S.; Beukinga, R.J.; Boellaard, R.; et al. The Image Biomarker Standardization Initiative: Standardized Quantitative Radiomics for High-Throughput Image-based Phenotyping. Radiology 2020, 295, 328–338. [Google Scholar] [CrossRef] [Green Version]
- Image Biomarker Standardisation Initiative Reference Manual v 1.0. 2019. Available online: https://ibsi.readthedocs.io/ (accessed on 2 January 2022).
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Papp, L.; Rausch, I.; Grahovac, M.; Hacker, M.; Beyer, T. Optimized Feature Extraction for Radiomics Analysis of 18F-FDG PET Imaging. J. Nucl. Med. 2019, 60, 864–872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leijenaar, R.T.; Nalbantov, G.; Carvalho, S.; Van Elmpt, W.J.; Troost, E.G.; Boellaard, R.; Aerts, H.J.; Gillies, R.J.; Lambin, P. The effect of SUV discretization in quantitative FDG-PET Radiomics: The need for standardized methodology in tumor texture analysis. Sci. Rep. 2015, 5, 11075. [Google Scholar] [CrossRef] [PubMed]
- Orlhac, F.; Soussan, M.; Chouahnia, K.; Martinod, E.; Buvat, I. 18F-FDG PET-Derived Textural Indices Reflect Tissue-Specific Uptake Pattern in Non-Small Cell Lung Cancer. PLoS ONE 2015, 10, e0145063. [Google Scholar] [CrossRef]
- Escudero Sanchez, L.; Rundo, L.; Gill, A.B.; Hoare, M.; Mendes Serrao, E.; Sala, E. Robustness of radiomic features in CT images with different slice thickness, comparing liver tumour and muscle. Sci. Rep. 2021, 11, 8262. [Google Scholar] [CrossRef]
- Orlhac, F.; Boughdad, S.; Philippe, C.; Stalla-Bourdillon, H.; Nioche, C.; Champion, L.; Soussan, M.; Frouin, F.; Frouin, V.; Buvat, I. A post-reconstruction harmonization method for multicenter radiomic studies in PET. J. Nucl. Med. 2018, 59, 1321–1328. [Google Scholar] [CrossRef]
- Welch, M.L.; McIntosh, C.; Haibe-Kains, B.; Milosevic, M.F.; Wee, L.; Dekker, A.; Huang, S.H.; Purdie, T.G.; O’Sullivan, B.; Aerts, H.J.; et al. Vulnerabilities of radiomic signature development: The need for safeguards. Radiother. Oncol. 2019, 130, 2–9. [Google Scholar] [CrossRef] [Green Version]
- Orlhac, F.; Soussan, M.; Maisonobe, J.A.; Garcia, C.A.; Vanderlinden, B.; Buvat, I. Tumor Texture Analysis in 18F-FDG PET: Relationships Between Texture Parameters, Histogram Indices, Standardized Uptake Values, Metabolic Volumes, and Total Lesion Glycolysis. J. Nucl. Med. 2014, 55, 414–422. [Google Scholar] [CrossRef] [Green Version]
- Hatt, M.; Majdoub, M.; Vallières, M.; Tixier, F.; Le Rest, C.C.; Groheux, D.; Hindié, E.; Martineau, A.; Pradier, O.; Hustinx, R.; et al. 18F-FDG PET Uptake Characterization Through Texture Analysis: Investigating the Complementary Nature of Heterogeneity and Functional Tumor Volume in a Multi–Cancer Site Patient Cohort. J. Nucl. Med. 2015, 56, 38–44. [Google Scholar] [CrossRef] [Green Version]
- Reuzé, S.; Orlhac, F.; Chargari, C.; Nioche, C.; Limkin, E.; Riet, F.; Escande, A.; Haie-Meder, C.; Dercle, L.; Gouy, S.; et al. Prediction of cervical cancer recurrence using textural features extracted from 18F-FDG PET images acquired with different scanners. Oncotarget 2017, 8, 43169–43179. [Google Scholar] [CrossRef] [Green Version]
| Scanner | Manufacturer | Manufacturer Model Name | TOF Capability |
|---|---|---|---|
| 1 | GE | Discovery 600 | No |
| 2 | GE | Discovery 690 | Yes |
| 3 | GE | Discovery MI | Yes |
| 4 | GE | Discovery STE | No |
| 5 | GE | Discovery 710 | Yes |
| 6 | GE | Discovery MI DR | Yes |
| 7 | GE | Discovery 610 | No |
| 8 | Siemens | Biograph40_mCT | Yes |
| 9 | Siemens | Biograph_mMR | No |
| 10 | Siemens | Biograph64_mCT | Yes |
| ScNo | TOF | ZFilter (mm) | NIt | NSubS | FOV (cm) | M | P (mm) | S (mm) | Time (min) | CNR |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | No | 6.4 | 2 | 32 | 70 | 192 | 3.65 | 3.27 | 2.5 | 4.62 |
| 2 | No | 6.4 | 2 | 32 | 70 | 192 | 3.65 | 3.27 | 2.5 | 4.50 |
| 3 | Yes | 5 | 3 | 16 | 50 | 256 | 1.95 | 2.79 | 3 | 4.38 |
| 4 | No | 4 | 2 | 20 | 50 | 128 | 3.91 | 3.27 | 5 | 3.47 |
| 5 | Yes | 6.4 | 2 | 16 | 70 | 128 | 5.47 | 3.27 | 3 | 10.11 |
| 6 | Yes | 6.4 | 2 | 32 | 70 | 192 | 3.65 | 3.27 | 3 | 7.02 |
| 7 | No | 6.4 | 2 | 32 | 50 | 256 | 1.95 | 3.27 | 5 | 6.39 |
| 8 | Yes | 5 | 3 | 21 | 81.5 | 256 | 3.18 | 5 | 2 | 4.37 |
| 9 | No | 6 | 3 | 21 | 71.8 | 256 | 2.80 | 2.03 | 10 | 8.39 |
| 10 | Yes | 5 | 2 | 21 | 81.5 | 200 | 4.07 | 5 | 5 | 9.26 |
| CNR Mean | 6.25 | |||||||||
| CNR Standard Deviation | 2.23 | |||||||||
| Time (min) | CNR | |||||
|---|---|---|---|---|---|---|
| R1 | R2 | R3 | R4 | Mean | Std Dev | |
| 10 | 7.74 | 8.09 | 8.41 | 8.01 | 8.06 | 0.28 |
| 5 | 5.61 | 5.83 | 5.80 | 5.45 | 5.67 | 0.18 |
| 2 | 3.86 | 3.71 | 3.70 | 3.53 | 3.70 | 0.13 |
| Label | Dataset | Scanners | Number PET Images | Average CNR +/− 1 SD |
|---|---|---|---|---|
| F | Full dataset | 1–10 | 68 | 7.53 ± 2.38 |
| S10 | Standard dataset | 1–10 | 10 | 6.25 +/− 2.23 |
| H10 | Harmonized Dataset | 1–10 | 10 (*) | 7.29 +/− 0.52 |
| S6 | Subset of S10 | 1,2,3,5,8,10 | 6 | 6.21 ± 2.71 |
| H6 | Subset of H10 | 1,2,3,5,8,10 | 6 (*) | 7.38 ± 0.25 |
| ScNo | TOF | ZFilter (mm) | NIt | NSubS | FoV (cm) | M | P (mm) | S (mm) | Time (min) | CNR |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | No | 6.4 | 3 | 16 | 50 | 256 | 1.95 | 3.27 | 5 | 7.29 |
| 2 | Yes | 4.6 | 3 | 16 | 50 | 256 | 1.95 | 3.27 | 5 | 7.09 |
| 3 | Yes | 6.4 | 3 | 16 | 50 | 256 | 1.95 | 2.79 | 5 | 7.29 |
| 4 | No | 6 | 3 | 14 | 50 | 128 | 3.91 | 3.27 | 10 | 6.3 |
| 5 | Yes | 6.4 | 3 | 16 | 50 | 256 | 1.95 | 3.27 | 3 | 7.64 |
| 6 | Yes | 6.4 | 2 | 32 | 70 | 192 | 3.65 | 3.27 | 3 | 7.02 |
| 7 | No | 6.4 | 2 | 32 | 50 | 128 | 3.91 | 3.27 | 5 | 6.95 |
| 8 | Yes | 6 | 3 | 21 | 81.5 | 256 | 3.18 | 5 | 5 | 7.25 |
| 9 | No | 6 | 3 | 21 | 71.8 | 256 | 2.80 | 2.03 | 10 | 8.39 |
| 10 | Yes | 6 | 3 | 21 | 50.9 | 256 | 1.99 | 3 | 5 | 7.72 |
| CNR Mean | 7.29 | |||||||||
| CNR Standard Deviation | 0.52 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keller, H.; Shek, T.; Driscoll, B.; Xu, Y.; Nghiem, B.; Nehmeh, S.; Grkovski, M.; Schmidtlein, C.R.; Budzevich, M.; Balagurunathan, Y.; et al. Noise-Based Image Harmonization Significantly Increases Repeatability and Reproducibility of Radiomics Features in PET Images: A Phantom Study. Tomography 2022, 8, 1113-1128. https://doi.org/10.3390/tomography8020091
Keller H, Shek T, Driscoll B, Xu Y, Nghiem B, Nehmeh S, Grkovski M, Schmidtlein CR, Budzevich M, Balagurunathan Y, et al. Noise-Based Image Harmonization Significantly Increases Repeatability and Reproducibility of Radiomics Features in PET Images: A Phantom Study. Tomography. 2022; 8(2):1113-1128. https://doi.org/10.3390/tomography8020091
Chicago/Turabian StyleKeller, Harald, Tina Shek, Brandon Driscoll, Yiwen Xu, Brian Nghiem, Sadek Nehmeh, Milan Grkovski, Charles Ross Schmidtlein, Mikalai Budzevich, Yoganand Balagurunathan, and et al. 2022. "Noise-Based Image Harmonization Significantly Increases Repeatability and Reproducibility of Radiomics Features in PET Images: A Phantom Study" Tomography 8, no. 2: 1113-1128. https://doi.org/10.3390/tomography8020091
APA StyleKeller, H., Shek, T., Driscoll, B., Xu, Y., Nghiem, B., Nehmeh, S., Grkovski, M., Schmidtlein, C. R., Budzevich, M., Balagurunathan, Y., Sunderland, J. J., Beichel, R. R., Uribe, C., Lee, T.-Y., Li, F., Jaffray, D. A., & Yeung, I. (2022). Noise-Based Image Harmonization Significantly Increases Repeatability and Reproducibility of Radiomics Features in PET Images: A Phantom Study. Tomography, 8(2), 1113-1128. https://doi.org/10.3390/tomography8020091






