1. Introduction
Hawkins et al. were the first to measure bone metabolic flux (K
i) using 60-min fluorine-18 sodium fluoride ([
18F]NaF) dynamic positron emission tomography (PET) scans [
1]. The Hawkins model represents [
18F]NaF bone tracer kinetics by a two-tissue compartmental model and uses the 0–60 min bone time–activity curve (TAC) and the arterial plasma input function (AIF) to estimate the constants K
1, k
2, k
3, k
4 and F
bv. K
1 and k
2 represent the forward and backward tracer exchange rates between blood and extracellular fluid (ECF), k
3 and k
4 represent the forward and backward tracer exchange rates between ECF and bone mineral, and F
bv is the fractional blood volume within the bone volume of interest (VOI). K
1 (units: mL min
−1 mL
−1) is widely regarded as a measurement of bone blood flow [
2]. The rate constants k
2, k
3 and k
4 are in units: min
−1. K
i (units: mL min
−1 mL
−1) is the [
18F]NaF plasma clearance to bone mineral calculated using the equation:
Since K
i varies with osteoblastic activity in the bone VOI [
3] the measurement is sometimes referred to as bone metabolic flux [
4].
The 60-min scan time makes the Hawkins method uncomfortable for subjects as well as makes the investigation expensive and takes up valuable scanning time [
5]. Therefore, methods have been described for estimating K
i from a single short (4-min) static scan acquired around 60 min after tracer injection [
6]. One advantage of the static scan method is that by acquiring multiple scans at different bed positions, K
i measurements can be made at several sites (for example, at the spine and hip) with one injection of the tracer. However, because no dynamic data are acquired during the first few minutes after injection, the static scan method cannot be used to measure K
1 as well as K
i.
This study aimed to analyse 60-min dynamic scan data to examine the practicality of using fixed population average values of k2, k3, k4 and Fbv to shorten the dynamic scan and obtain Ki measurements that are still as accurate and precise as those obtained from conventionally analysed 60-min scans with variable rate constants. In particular, we discuss whether, by eliminating the statistical errors in k2, k3 and k4 when fitting the 60-min scan data to the Hawkins model, such short-scan measurements of Ki may have equal or greater statistical power for measuring response to treatment than conventionally analysed 60-min dynamic scans.
3. Results
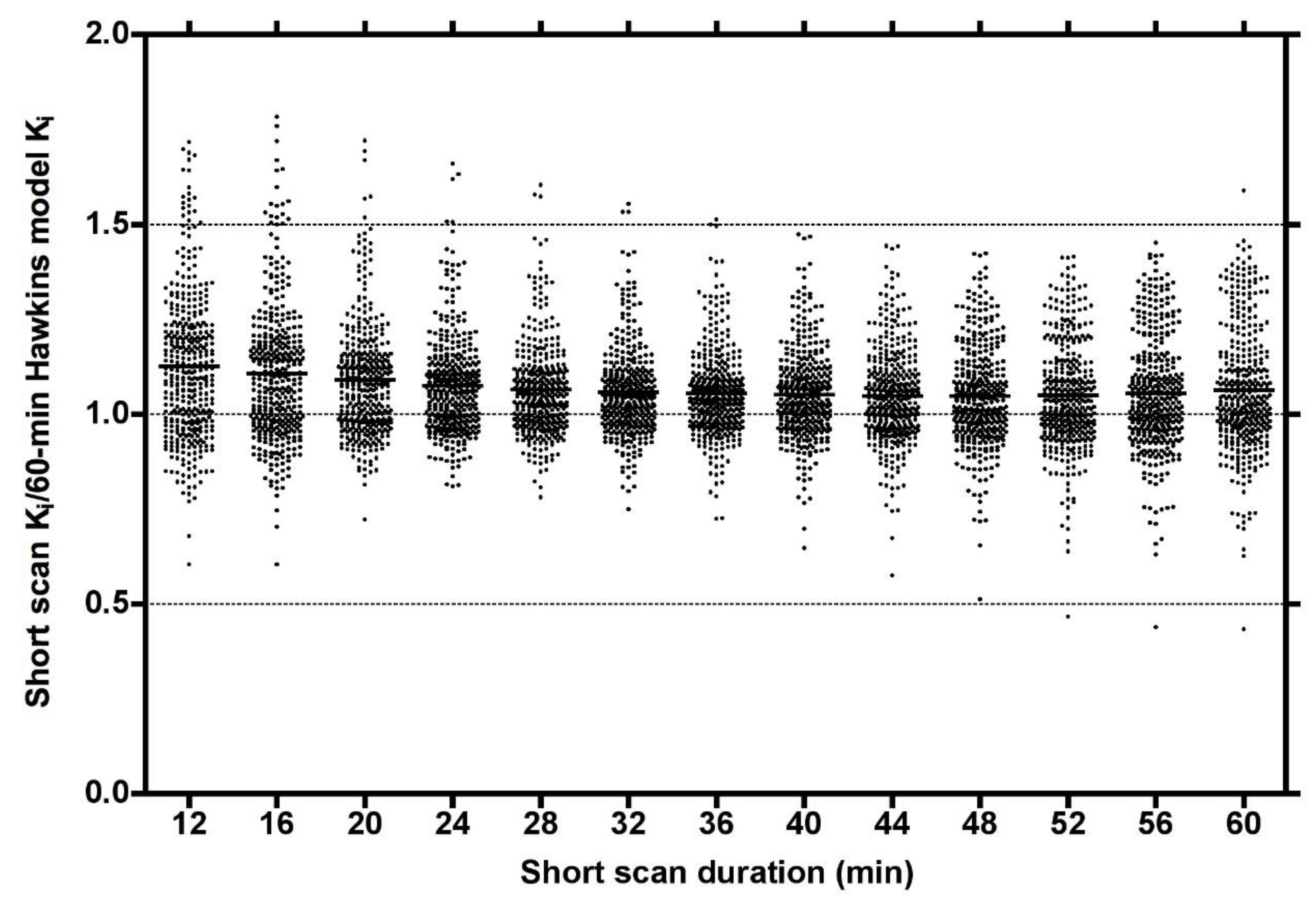
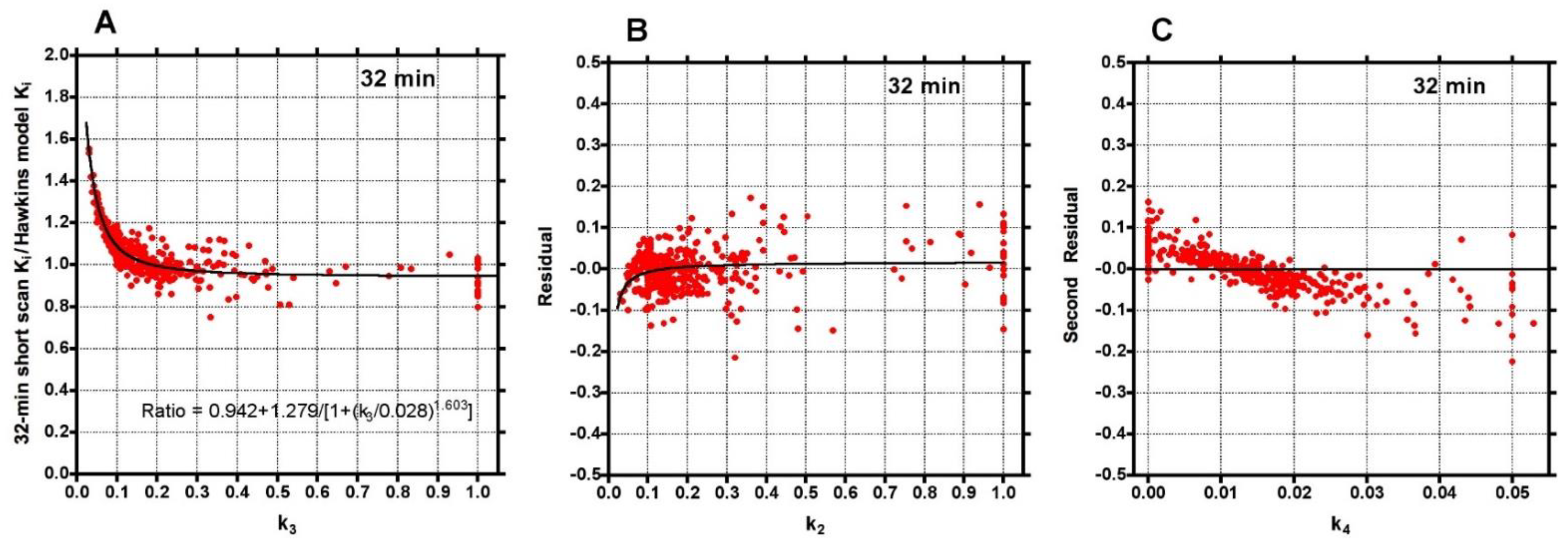
Plots of the ratio of short-scan K
i to the 60-min Hawkins model values for all scans at all VOIs for short dynamic scan times in increments from 12 to 60 min showed a range of values, which at their narrowest at around 32 min varied from 0.75 to 1.5 and had a small bias for short-scan K
i to overestimate the 60-min Hawkins model results (
Figure 2).
To investigate the factors behind the dispersion of data points in
Figure 2, the 32-min ratios were plotted against the conventionally analysed 60-min Hawkins model k
3 values (
Figure 3A). The fitted curve crossed unity at k
3 = 0.18 min
−1, equal to the fixed value of k
3 assumed for the short-scan analysis (
Table 1). For scans with conventional 60-min Hawkins model k
3 values <0.18 min
−1, ratios were systematically greater than unity, rising to 1.5 for the smallest k
3 values, while for scans with k
3 values >0.18 min
−1 the ratios tended asymptotically to 0.94. When the residuals from the curve fit in
Figure 3A were plotted against the 60-min Hawkins model k
2 values a smaller inverted trend was found (
Figure 3B). Finally, when the residuals from the k
2 curve fit in
Figure 3B were plotted against the 60-min Hawkins model k
4 values there was a trend for points with k
4 values less than the fixed k
4 value of 0.014 min
−1 to have positive residuals and points with k
4 values >0.014 min
−1 to have negative residuals (
Figure 3C). Similar results were obtained when the short-scan ratios at 12, 20, 44 and 60 min were plotted against k
3, k
2 and k
4 in the same way.
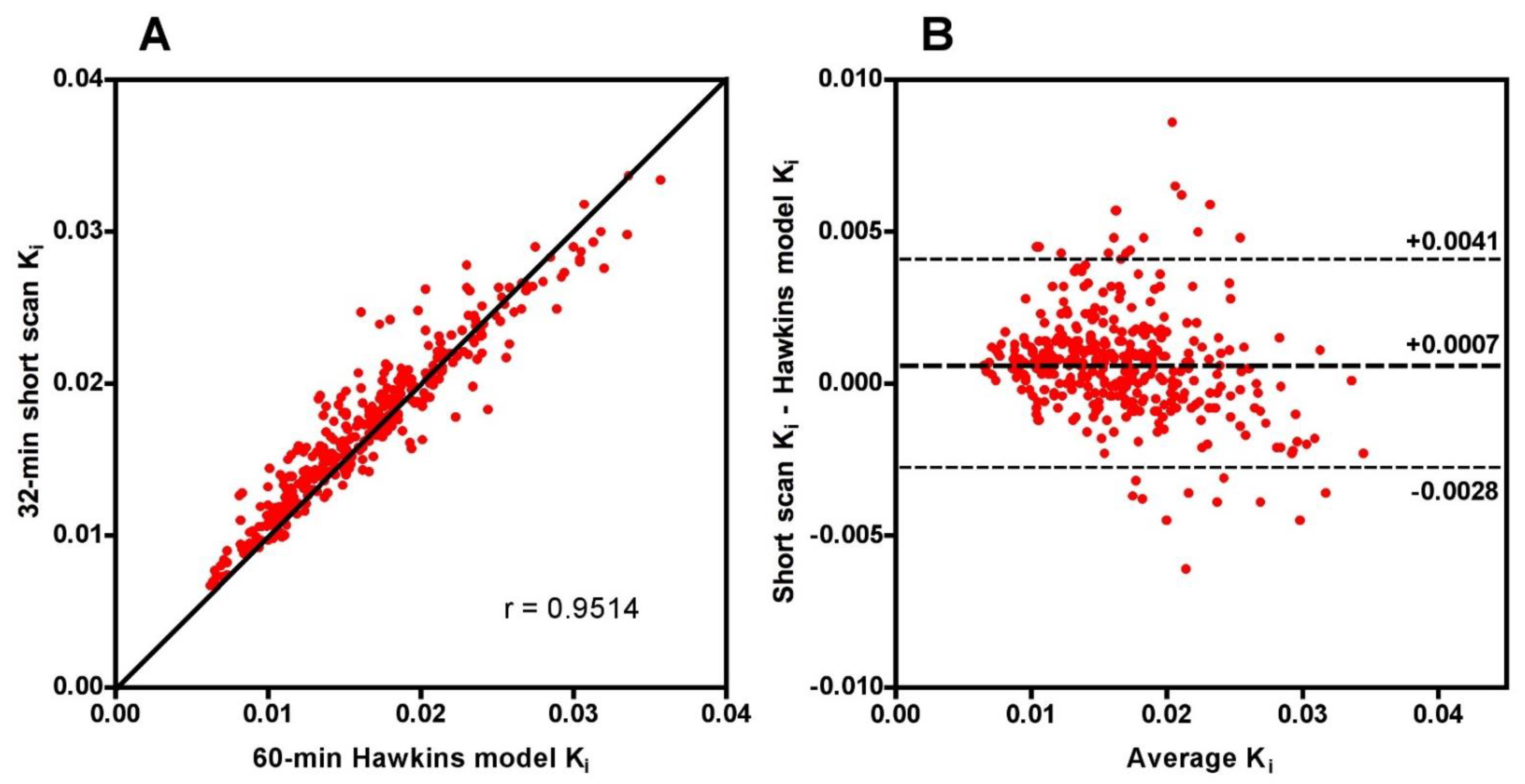
Scatter and Bland-Altman plots of short-scan K
i values against the conventional 60-min Hawkins model results showed dispersions consistent with the findings presented above with a correlation coefficient r = 0.951 and 95% LOA of −0.0028 to +0.0041 mL min
−1 mL
−1 at 32 min (
Figure A1). The question arises whether the dispersion seen in this figure means that short-scan K
i results are less accurate measures of subjects’ response to treatment than conventional 60-min dynamic scan Hawkins model measurements of K
i, or whether by fixing the values of k
2, k
3 and k
4 a source of unwanted noise in the 60-min dynamic scan measurements is eliminated and the short-scan results are the more robust measurement. To examine this point, we compared the mean percentage changes in 60-min Hawkins model K
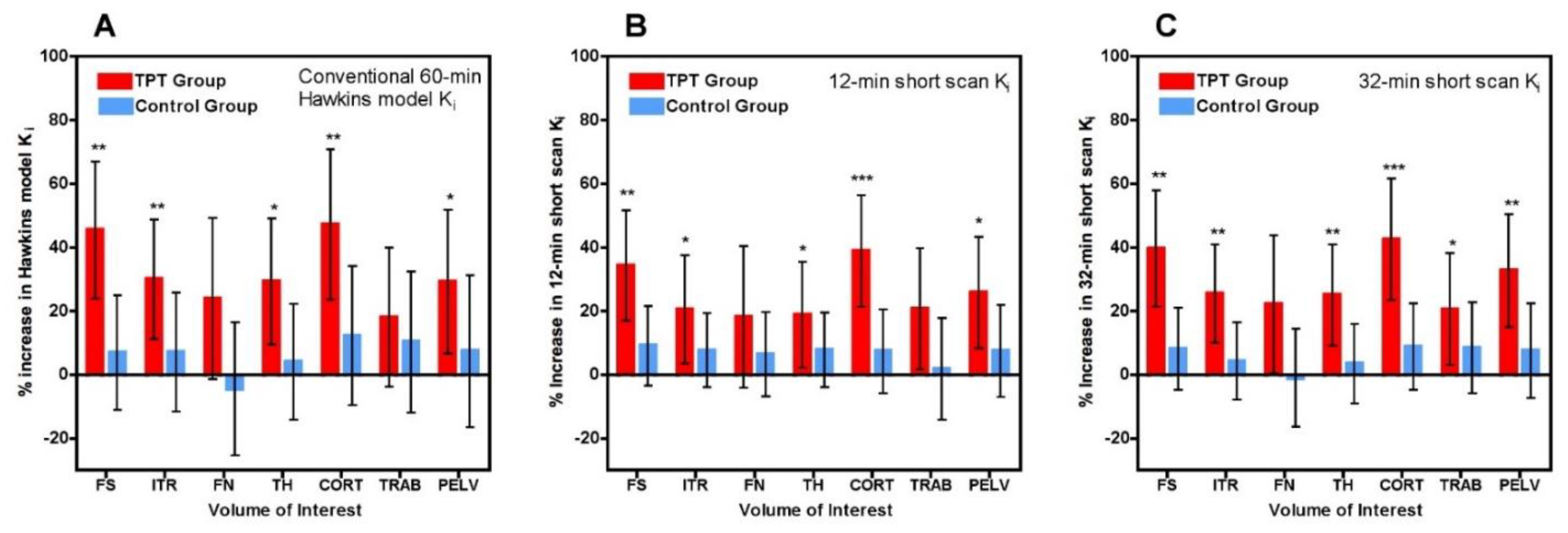
i values in the TPT and control groups in each of the seven VOIs (
Figure 4A) with the corresponding results for the 12-min (
Figure 4B) and 32-min (
Figure 4C) short-scan K
i values.
Figure 4 is annotated to show VOIs with
p < 0.05, <0.01 and <0.001 compared with baseline. Comparison of
Figure 4B,C with
Figure 4A in terms of these
p-value thresholds suggests that overall the 12-min short-scan K
i analysis performed as well as the 60-min Hawkins model analysis while the 32-min analysis performed better.
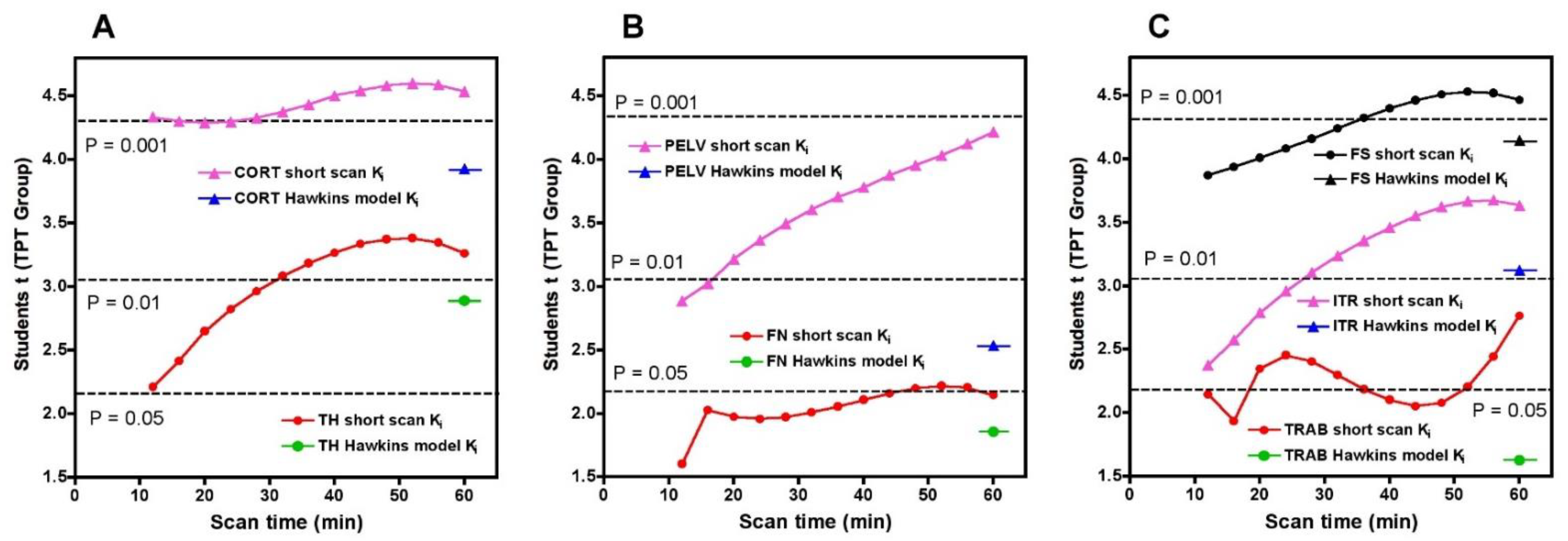
To compare the statistical significance of the short-scan and 60-min Hawkins results over the full range of short-scan times, we calculated Student’s t for the changes between baseline and 12-weeks in the TPT arm at each time point between 12 and 60 min and compared it against Student’s t for the conventionally analysed 60-min Hawkins data at each of the seven VOIs (
Figure 5). For the CORT, PELV and TRAB VOIs, short-scan K
i results had higher Student’s t values at all scan times from 12 to 60 min. For the FN VOI, short-scan K
i had higher Student’s t at all times except the 12-min scan. For the remaining three VOIs (TH, FS and ITR), short-scan K
i had higher Student’s t at all scan times from 32 to 60 min.
As shown in
Figure 5, Student’s t results for the FN and TRAB VOIs were smaller than at other sites. This is due to a recognised technical problem with hip [18F]NaF PET scans where image streaking can occur in VOIs close to high activity in the urinary bladder, distorting the bone TAC [
13]. The presence of this effect is demonstrated by the AIC data for the Hawkins model fits to the 60-min scan data (
Figure A2), with AIC results showing systematically poorer curve fits for the FN and TRAB VOIs compared with the other sites.
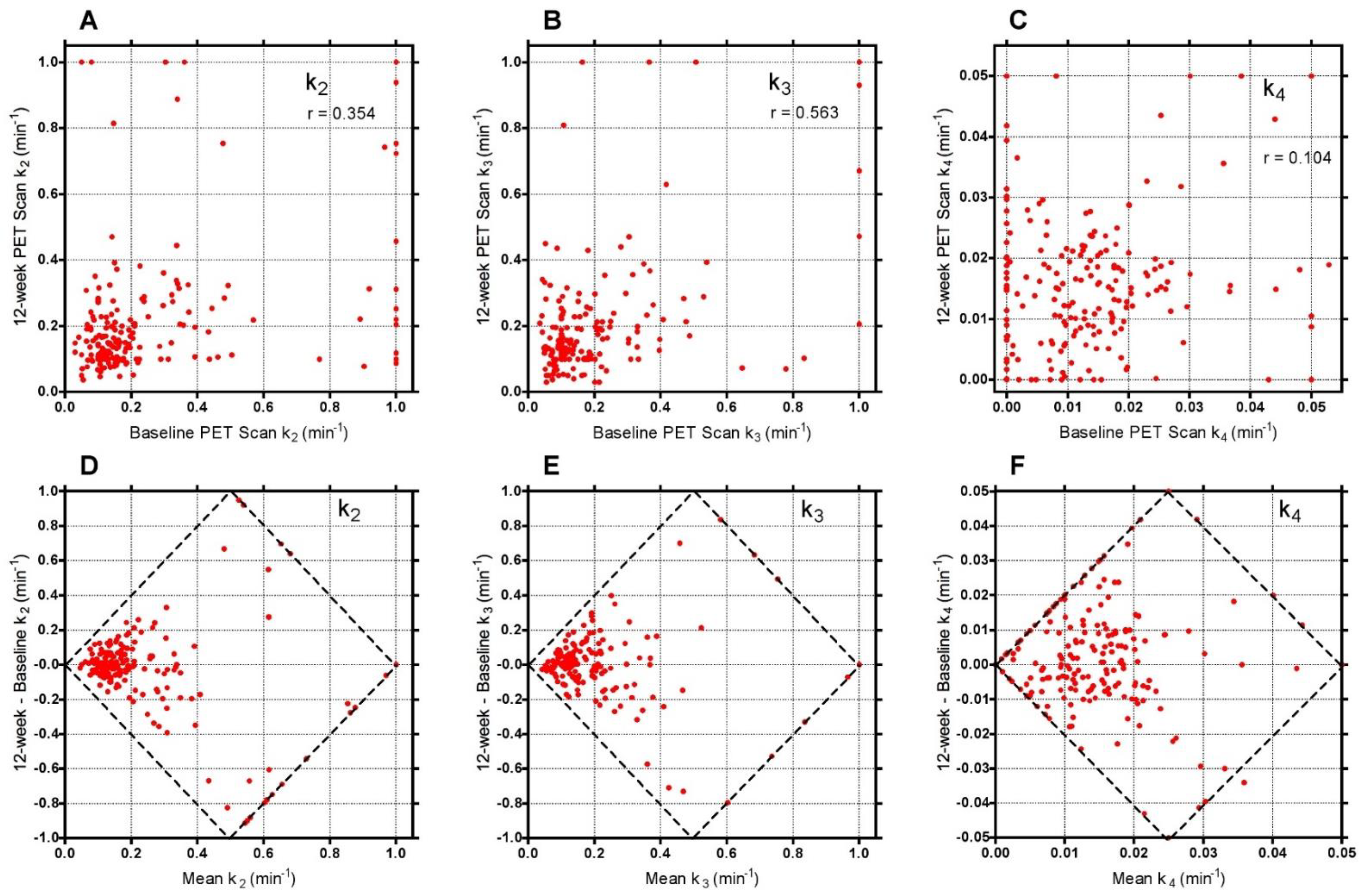
To evaluate reasons for the good statistical performance of the short-scan data compared with the findings of conventionally analysed 60-min dynamic scans in
Figure 5, scatter and Bland-Altman plots were drawn of the freely fitted Hawkins model k
2, k
3 and k
4 results measured from the 12-week 60-min scans against the equivalent baseline measurements (
Figure A3). Points in this figure with k
2 or k
3 > 0.5 min
−1 or k
4 > 0.03 min
−1 are predominantly measurements at the FN or TRAB VOIs with poor AIC. Assuming that the differences in the rate constants between baseline and follow-up scans are due to random measurement errors, we evaluated the effect of the differences in k
3 on the percentage changes in the baseline to the 12-week ratio in the 60-min Hawkins model K
i using the curve fit in
Figure 3A.
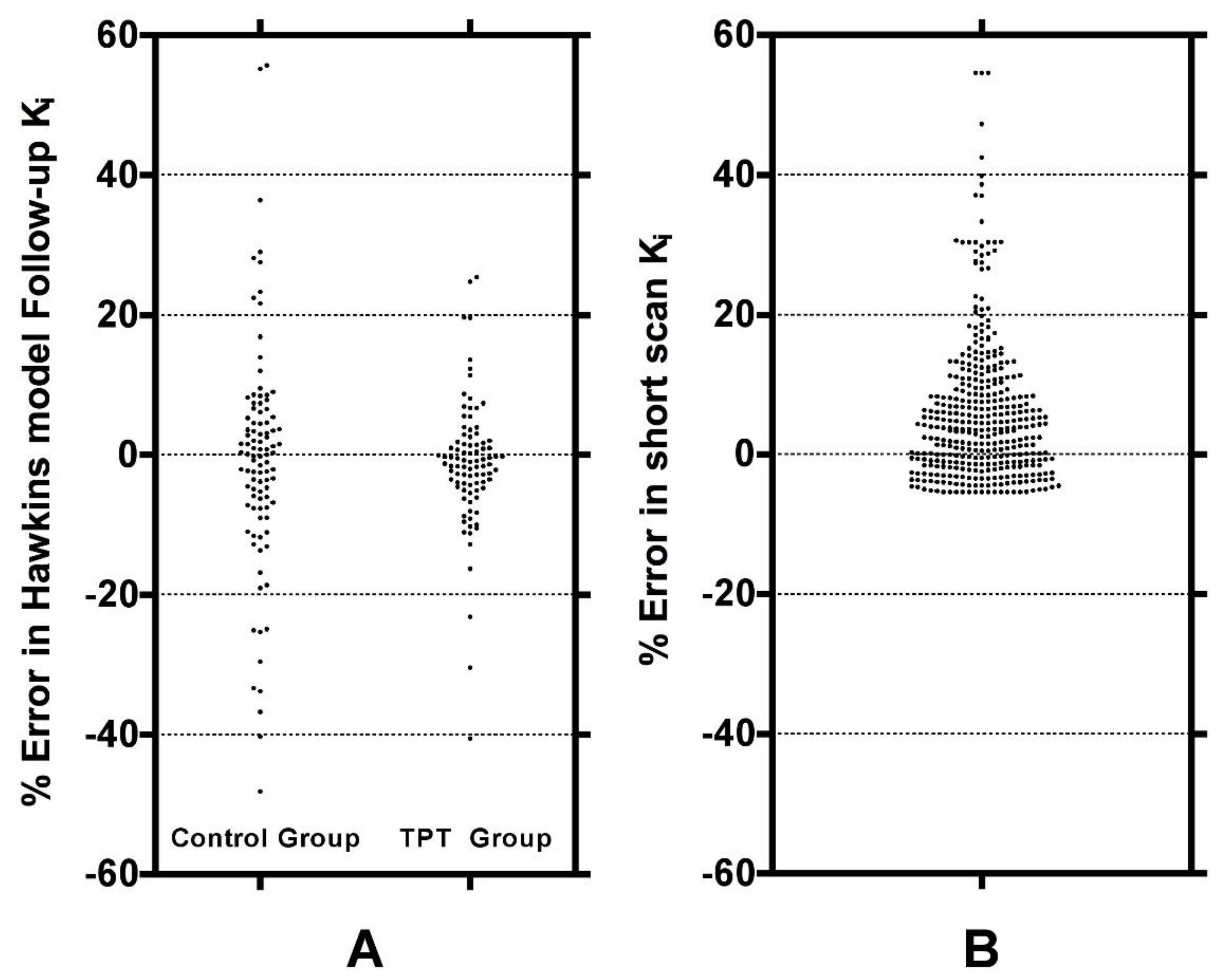
Figure 6A shows these results plotted separately for the control and TPT arms. The two distributions can be compared with the ratios of 32-min short-scan K
i to conventional 60-min Hawkins model K
i plotted in
Figure 6B.
4. Discussion
PET imaging with [
18F]NaF can play an important role during the early development of new treatments for osteoporosis by measuring changes in site specific bone formation rate [
3] as early as three months after commencement of treatment, thereby aiding pharmaceutical companies to decide whether new drugs should proceed to further trials [
7]. As the fracture site associated with the highest mortality and morbidity, the hip is an important target for these studies. However, the long acquisition time makes the conventional 60-min scan uncomfortable for clinical trial participants, is an expensive item in the research budget and competes for scanning time with routine clinical imaging services in high demand. In this study, we investigated an alternative approach using different dynamic scan times between 12 and 60 min analysed using the Hawkins model with fixed rate-constants and obtained K
i measurements with as good or better statistical power for detecting response to treatment as conventionally analysed 60-min scans with freely fitted rate constants. These results demonstrate the potential advantage of using fixed rate-constants for Hawkins model analyses.
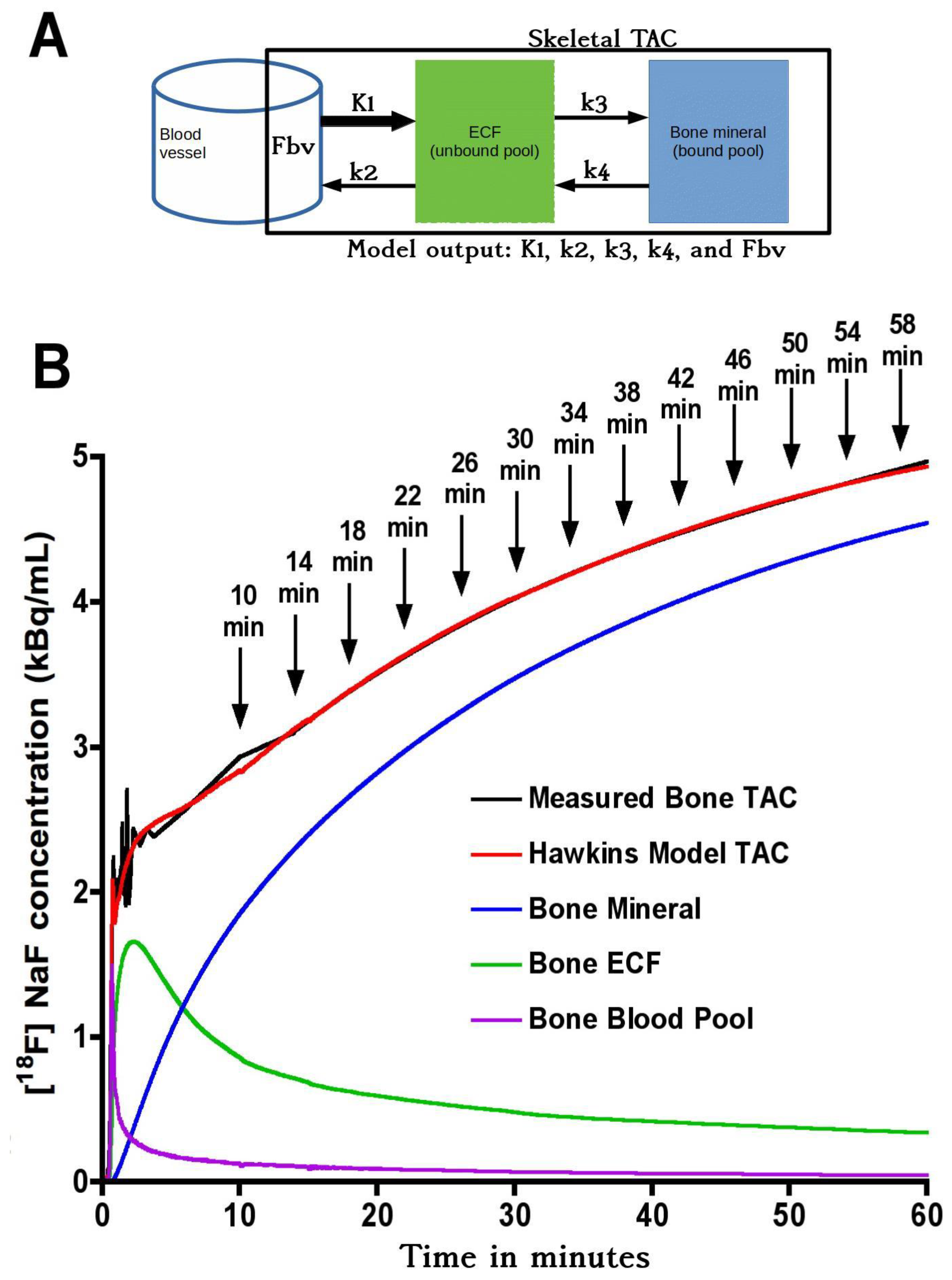
Although short-scan K
i values in
Figure 2 appear to systematically overestimate conventional 60-min Hawkins model values with a mean bias of approximately 5% at scan times around 30 min, this bias is explained by the non-linear curve fitted to the data in
Figure 3A. In this figure, the short-scan and 60-min Hawkins model K
i values become equal with no bias at the short-scan fixed k
3 value of 0.187 min
−1. The fitted curve equals 1.05 at k
3 = 0.124 min
−1, and choosing this latter as the fixed value of k
3 would remove the 5% bias noted above. The trends seen in
Figure 3 are explained by the effects of changes in the Hawkins model rate constants k
2, k
3 and k
4 on the TACs for the bone mineral compartment (the blue curve in
Figure 1B) and the bone ECF compartment (the green curve in
Figure 1B). As k
3 increases, at later time points in
Figure 1B, a greater proportion of the [
18F]NaF tracer in the bone VOI resides in the bone mineral compartment and less in the bone ECF compartment. Hence, the value of the 60-min Hawkins model K
i increases at higher k
3 values and, relative to the short-scan K
i value calculated with a fixed value of k
3, the ratio plotted on the vertical axis in
Figure 3A decreases. A detailed explanation of the trends shown in
Figure 3 is complicated by the correlations between the three rate constants obtained from the curve fits to the 60-min bone VOI TACs. Both k
2 (r = 0.557,
p < 0.001) and k
4 (r = 0.403,
p < 0.001) correlate positively with k
3. Additionally, k
3 (r = 0.227,
p < 0.001) and k
4 (r = 0.490,
p < 0.001) both correlate with K
i. Given these relationships, it seems likely that the strong trend seen in
Figure 3A already incorporates some of the dependence of K
i on k
2 and k
4 as well as k
3 and may explain the weaker trends seen in
Figure 3B,C.
A technical limitation of dynamic [
18F]NaF PET imaging of the hip is the time-varying streaking artefacts sometimes seen in VOIs in close proximity to the bladder [
13]. In the present study, this effect is seen in the systematically poorer AIC values to the Hawkins model fits for the FN and TRAB sites compared with the other five sites. This explains most of the outlier points with high k-numbers seen in
Figure 3 and some of the outliers in
Figure 2. It also explains why these VOIs performed less well at measuring the treatment effect in
Figure 4 and
Figure 5.
The difference between short-scan values of K
i calculated with fixed values of the Hawkins model rate constants and conventional 60-min dynamic scan values with freely fitted values raises the question of which method is optimal for clinical trial studies. This is a pragmatic question: the better method for clinical trials is the one with the best statistical power to discriminate changes in K
i values due to therapies that modify bone metabolism. The optimum method can be identified as the one that gives
p-values with higher statistical significance or allows research studies to achieve the same
p-value with fewer participants.
Figure 4 demonstrates that short-scan results with scan times around 30 min gave similar % changes in K
i values as conventionally analysed 60-min scans but with smaller
p-values at four of the seven sites.
Figure 5 shows that as assessed by a Student’s t analysis, all seven sites performed better at 60-min if analysed using fixed values of the Hawkins model rate constants rather than freely fitted values. At three sites a 12-min short-scan performed better than the conventional 60-min analysis. The above findings suggest that the poor repeatability of the Hawkins model rate constants apparent in
Figure A3 is a contributory factor to imprecision in the resulting K
i values and that any errors entailed in the short-scan method using fixed rate-constants may be preferable to the random measurement errors in the freely fitted 60-min Hawkins rate constants.
Figure 6 demonstrates that scan-to-scan changes in 60-min Hawkins model K
i results explained by the relationship with k
3 shown in
Figure 3A are comparable to the differences between the short-scan K
i values calculated with fixed k-numbers and the conventional Hawkins model analysis with freely fitted k-numbers.
Previous authors have examined the advantages of short dynamic PET scans. Torizuka et al. [
14] proposed a short dynamic [
18F]FDG PET scan and found a good correlation between the K
i values obtained from 30-min and 60-min scans in patients with lung cancer. However, their study did not examine the effect of the shorter scan time on the statistical analysis of longitudinal studies. Strauss et al. [
15] compared the use of a 10-min dynamic [
18F]FDG PET scan combined with a static scan at 60 min for predicting individual k-values (K
1, k
2, k
3, k
4, F
bv, K
i) in tumours compared with a full 60-min dynamic scan. Again, although good correlations were reported, the study did not address the issue of longitudinal studies and required a static scan at a later time point, which defeats the benefits of a short early scan. Subsequently, Disselhorst et al. [
16] drew attention to the fact that delineation of tumour VOIs may differ significantly depending on time after injection and that this might be an issue for short-scan protocols. This was not a problem in the present study as the VOIs were delineated on CT images and then transferred to the PET dynamic image frames. Peters et al. [
17] evaluated a 30-min dynamic [
18F]NaF PET protocol for assessing bone metabolic activity after spinal fusion surgery by comparing VOIs at the control and operated sites. However, they did not compare their K
i results from 30 min scan against the standard 60 min scan due to the infeasibility of long scan times in patients with back pain.
Limitations of this study include the fact that we only studied the short-scan method for measurements in VOIs at the hip, which required previously calculated population average values of parameters from the full 60-min dynamic scan as listed in
Table 1. The lumbar spine is also an important site for [
18F]NaF PET imaging and has the advantage that bone tracer uptake at this site is typically three times greater than at the hip [
18], and hence the 60-min Hawkins model rate constants might be more reproducible. Additionally, in the present study, we were unable to compare measurements of the Hawkins model parameter K
1 between short-scan and conventional 60-min scans. Unlike measurements of bone metabolic flux using 60-min dynamic scans, for which the terminal exponential accounts for 80% of the area under the plasma curve [
9], bone blood flow measurements are best performed using individual measurements of the arterial input function over the peak of the bolus injection. Limitations of the short dynamic scan method described here include the fact that additional static scans are required if bone metabolic flux is measured at additional bed positions using the static scan method [
6]. However, the overall PET scanning time would still be shorter compared with performing a 60-min dynamic scan.