Simultaneous Multislice Brain MRI T1 Mapping with Improved Low-Rank Modeling
Abstract
:1. Introduction
2. Materials and Methods
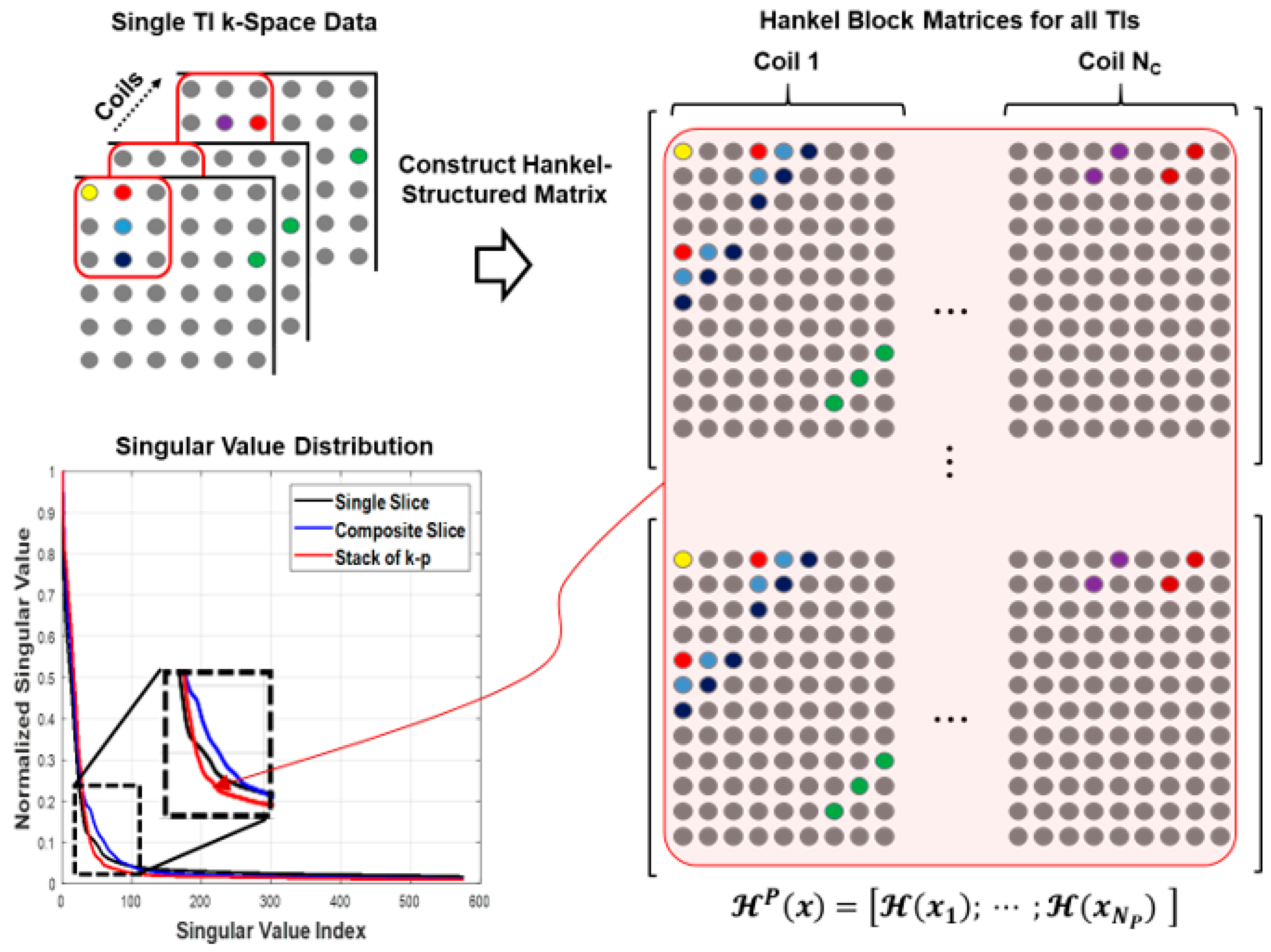
2.1. Introduction to SMS-HSL
2.2. Extension to Parameter Dimension
- (1)
- concatenating the individual parameter Hankel structured matrices;
- (2)
- applying SVD to block Hankel matrix;
- (3)
- taking the right singular vectors corresponding to the low singular values.
2.3. Optimization Algorithm
2.4. Experimental Setup
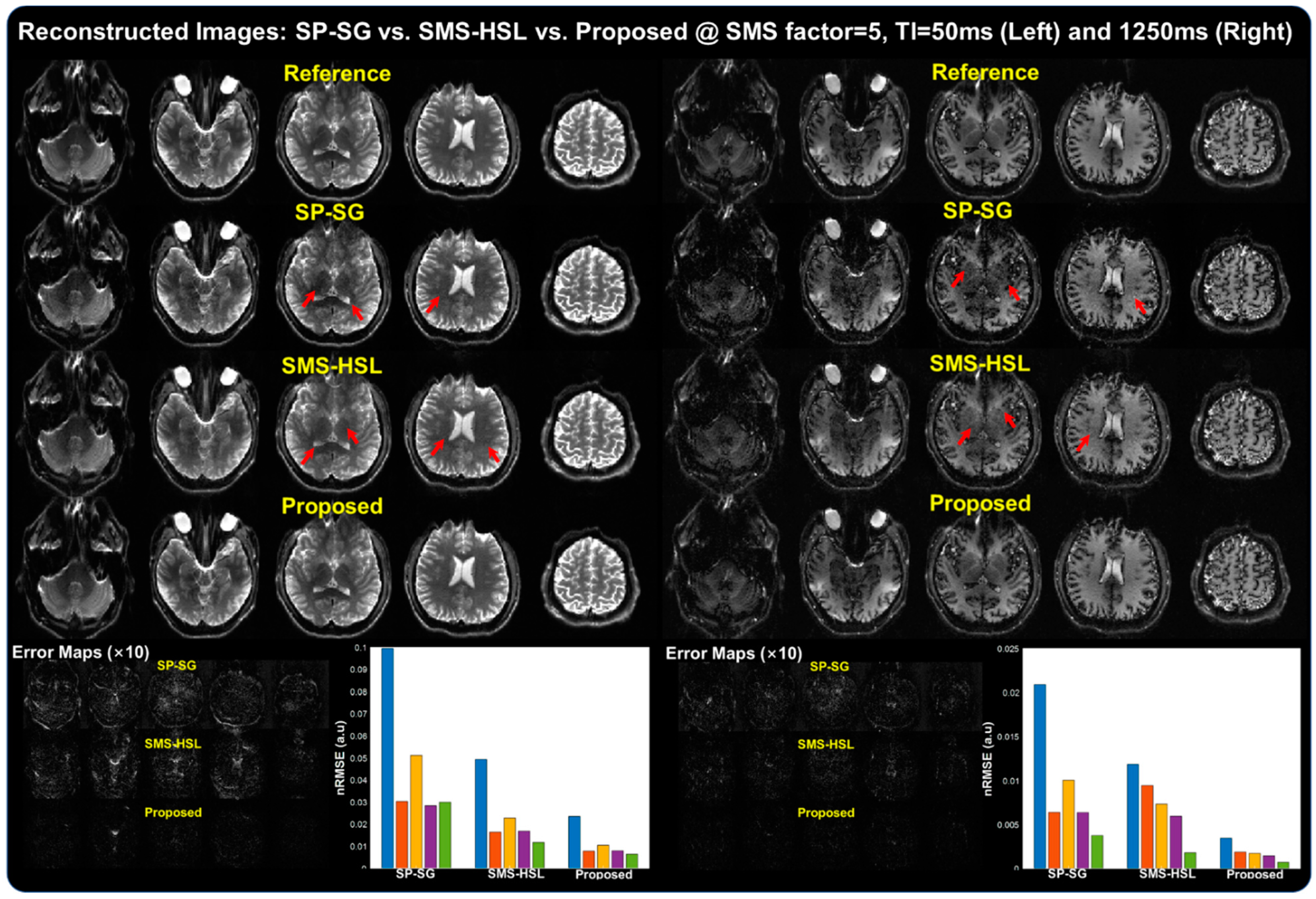
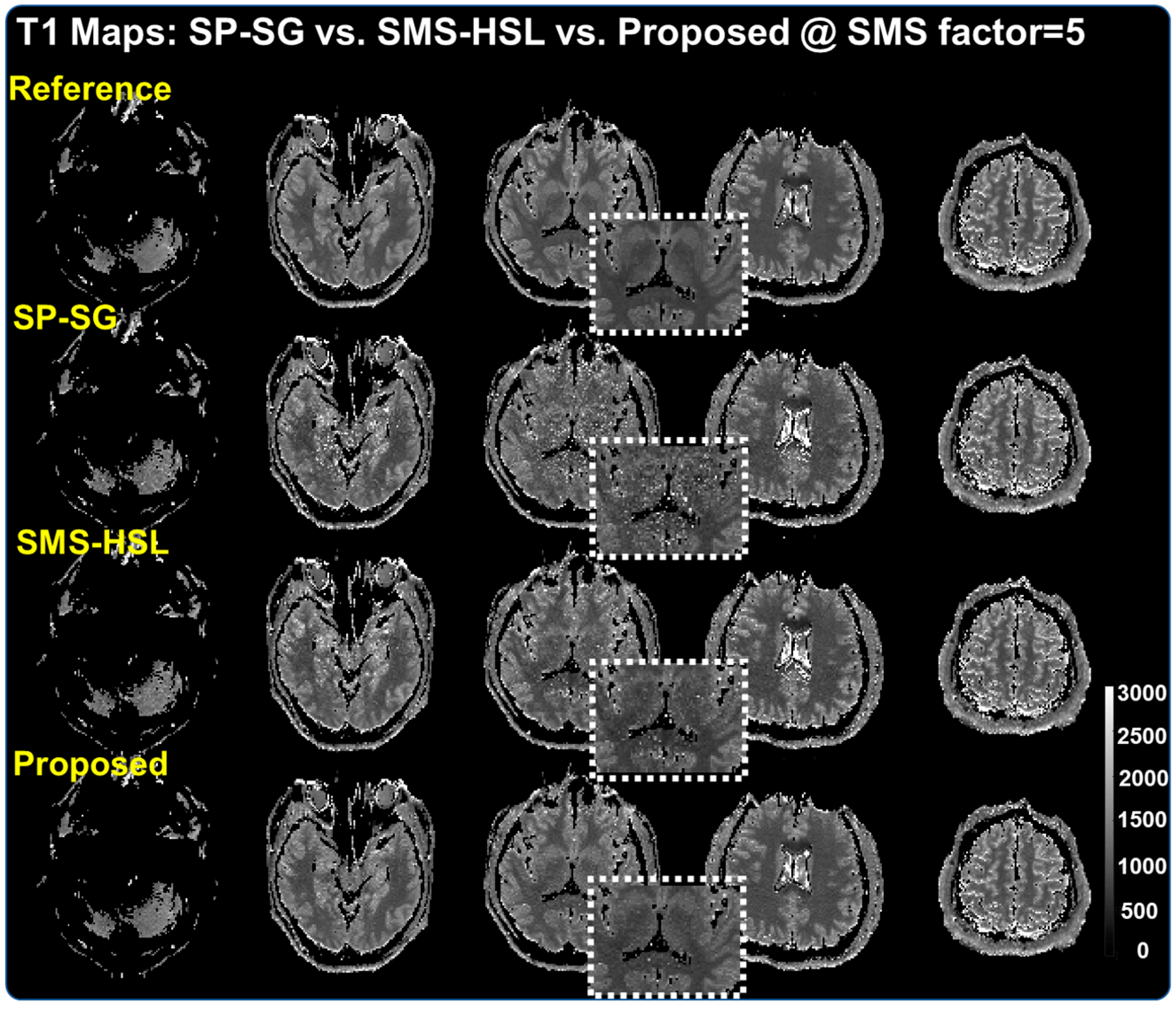
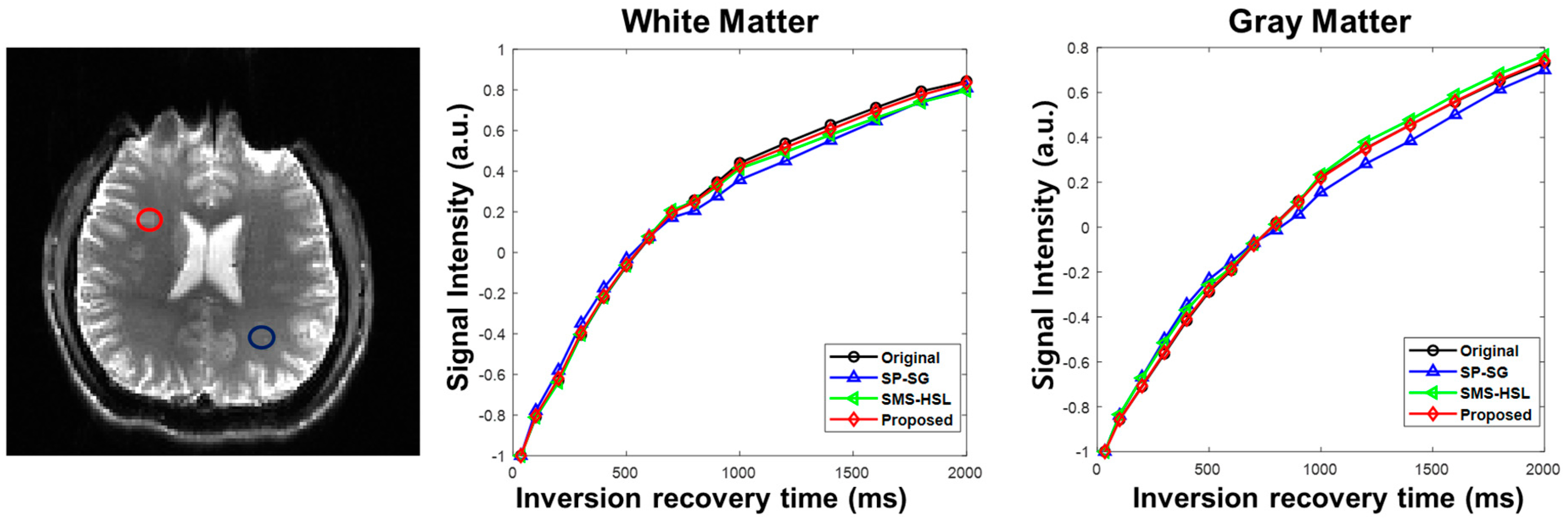
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Warntjes, J.B.; Leinhard, O.D.; West, J.; Lundberg, P. Rapid magnetic resonance quantification on the brain: Optimization for clinical usage. Magn. Reson. Med. 2008, 60, 320–329. [Google Scholar] [CrossRef]
- Alexander, A.; Hurley, S.; Samsonov, A.; Adluru, N.; Hosseinbor, A.; Mossahebi, P. Characterization of cerebral white matter properties using quantitative magnetic resonance imaging stains. Brain Connect. 2011, 1, 423–446. [Google Scholar] [CrossRef]
- Cheng, H.; Stikov, N.; Ghugre, N.; Wright, G. Practical medical applications of quantitative MR relaxometry. J. Magn. Reson. Imaging 2012, 36, 805–824. [Google Scholar] [CrossRef] [PubMed]
- Komiyama, M.; Yagura, H.; Baba, M.; Yasui, T.; Hakuba, A.; Nishimura, S. MR imaging: Possibility of tissue characterization of brain tumors using T1 and T2 values. Am. J. Neuroradiol. 1987, 8, 65–70. [Google Scholar] [PubMed]
- Larkman, D.; Hajnal, J.; Herlihy, A.; Coutts, G.; Young, I.; Ehnholm, G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J. Magn. Reson. Imaging 2001, 13, 313–317. [Google Scholar] [CrossRef]
- Moeller, S.; Yacoub, E.; Olman, C.; Auerbach, E.; Strupp, J.; Harel, N.; Uğurbil, K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn. Reson. Med. 2010, 63, 1144–1153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feinberg, D.; Moeller, S.; Smith, S.; Auerbach, E.; Ramanna, S.; Gunther, M.; Glasser, M.; Miller, K.; Ugurbil, K.; Yacoub, E. Multiplexed echo planar imaging for sub-second whole brain fMRI and fast diffusion imaging. PLoS ONE 2010, 5, e15710. [Google Scholar] [CrossRef] [Green Version]
- Pruessmann, K.; Weiger, M.; Scheidegger, M.; Boesiger, P. SENSE: Sensitivity encoding for fast MRI, Magn. Reson. Med. 1999, 42, 952–962. [Google Scholar] [CrossRef]
- Griswold, M.; Jakob, P.; Heidemann, R.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar] [CrossRef] [Green Version]
- Zhu, K.; Kerr, A.; Pauly, J. Autocalibrating CAIPIRINHA: Reformulating CAIPIRINHA as a 3D problem. In Proceedings of the 20rd Annual Meeting of ISMRM, Melbourne, Australia, 5–11 May 2012. [Google Scholar]
- Zahneisen, B.; Poser, B.A.; Ernst, T.; Stenger, V.A. Three-dimensional Fourier encoding of simultaneously excited slices: Generalized acquisition and reconstruction framework. Magn. Reson. Med. 2014, 71, 2071–2081. [Google Scholar] [CrossRef] [Green Version]
- Setsompop, K.; Gagoski, B.; Polimeni, J.; Witzel, T.; Wedeen, V.; Wald, L. Blippedcontrolled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med. 2012, 67, 1210–1224. [Google Scholar] [CrossRef] [Green Version]
- Breuer, F.; Blaimer, M.; Heidemann, R.; Mueller, M.; Griswold, M.; Jakob, P. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn. Reson. Med. 2005, 53, 684–691. [Google Scholar] [CrossRef]
- Cauley, S.; Polimeni, J.; Bhat, H.; Wald, L.; Setsompop, K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn. Reson. Med. 2014, 72, 93–102. [Google Scholar] [CrossRef] [Green Version]
- HashemizadehKolowri, S.K.; Chen, R.R.; Adluru, G.; Ying, L.; DiBella, E.V. Coil-combined split slice-GRAPPA for simultaneous multi-slice diffusion MRI. Magn. Reson. Imaging 2020, 66, 9–21. [Google Scholar] [CrossRef] [PubMed]
- HashemizadehKolowri, S.K.; Chen, R.R.; Adluru, G.; Dean, D.C.; Wilde, E.A.; Alexander, A.L.; DiBella, E.V. Simultaneous multi-slice image reconstruction using regularized image domain split slice-GRAPPA for diffusion MRI. Med. Image Anal. 2021, 70, 102000. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Park, J. SMS-HSL: Simultaneous multislice aliasing separation exploiting Hankel subspace learning. Magn. Reson. Med. 2017, 78, 1392–1404. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Jin, K.; Kim, Y.; Park, S.H.; Ye, J. Acceleration of MR parameter mapping using annihilating filter-based low rank Hankel matrix (ALOHA). Magn. Reson. Med. 2016, 76, 1848–1864. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Yin, W.; Zhang, Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Math. Program. Comput. 2012, 4, 333–361. [Google Scholar] [CrossRef]
- Shen, Y.; Wen, Z.; Zhang, Y. Augmented Lagrangian alternating direction method for matrix separation based on low-rank factorization. Optim. Methods Softw. 2014, 29, 239–263. [Google Scholar] [CrossRef] [Green Version]
- Lingala, S.G.; Jacob, M. Blind compressive sensing dynamic MRI. IEEE Trans. Med. Imaging 2013, 32, 1132–1145. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.; Vijayakumar, S.; Li, Y.; Hertel, S.; Duensing, G.R. A software channel compression technique for faster reconstruction with many channels. Magn. Reson. Imaging 2008, 26, 133–141. [Google Scholar] [CrossRef]
- Buehrer, M.; Pruessmann, K.P.; Boesiger, P.; Kozerke, S. Array compression for MRI with large coil arrays. Magn. Reson. Med. 2007, 57, 1131–1139. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Park, S. Simultaneous Multislice Brain MRI T1 Mapping with Improved Low-Rank Modeling. Tomography 2021, 7, 545-554. https://doi.org/10.3390/tomography7040047
Kim S, Park S. Simultaneous Multislice Brain MRI T1 Mapping with Improved Low-Rank Modeling. Tomography. 2021; 7(4):545-554. https://doi.org/10.3390/tomography7040047
Chicago/Turabian StyleKim, Sugil, and Suhyung Park. 2021. "Simultaneous Multislice Brain MRI T1 Mapping with Improved Low-Rank Modeling" Tomography 7, no. 4: 545-554. https://doi.org/10.3390/tomography7040047
APA StyleKim, S., & Park, S. (2021). Simultaneous Multislice Brain MRI T1 Mapping with Improved Low-Rank Modeling. Tomography, 7(4), 545-554. https://doi.org/10.3390/tomography7040047




