Assessment of Influencing Factors and Robustness of Computable Image Texture Features in Digital Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Volume Simulation
2.2. Volume Reconstruction
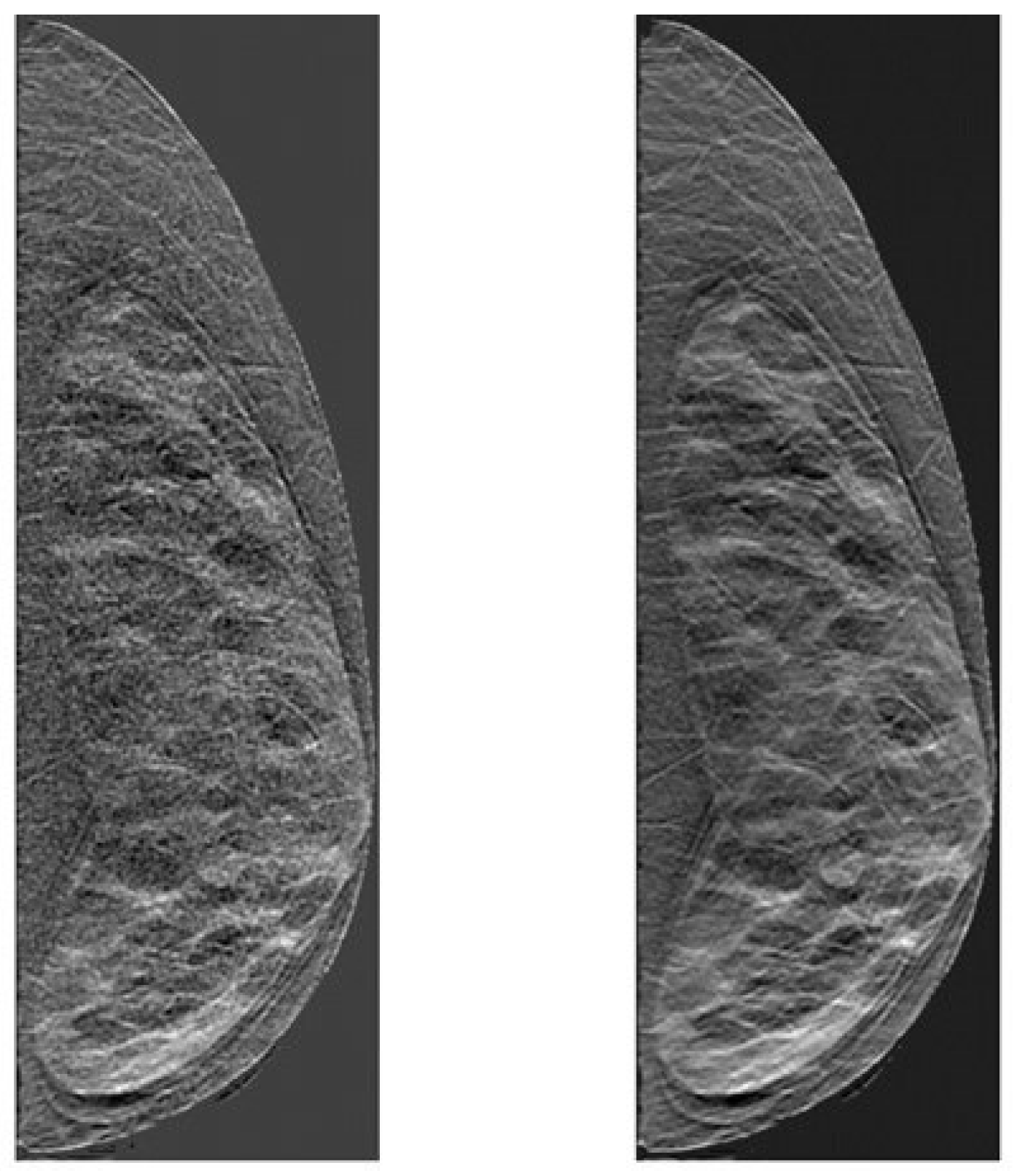
2.3. Clinical Data
2.4. Texture Calculations
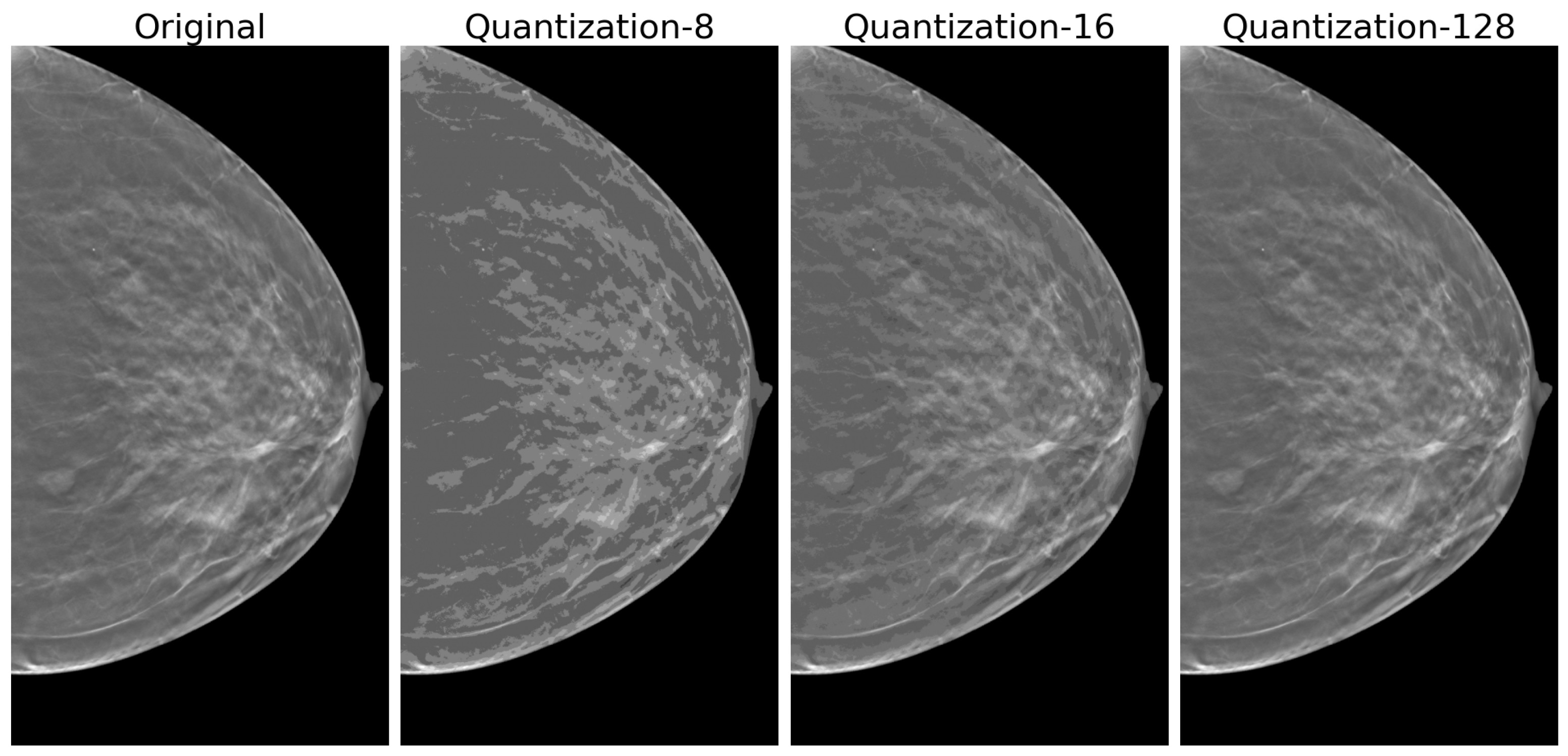
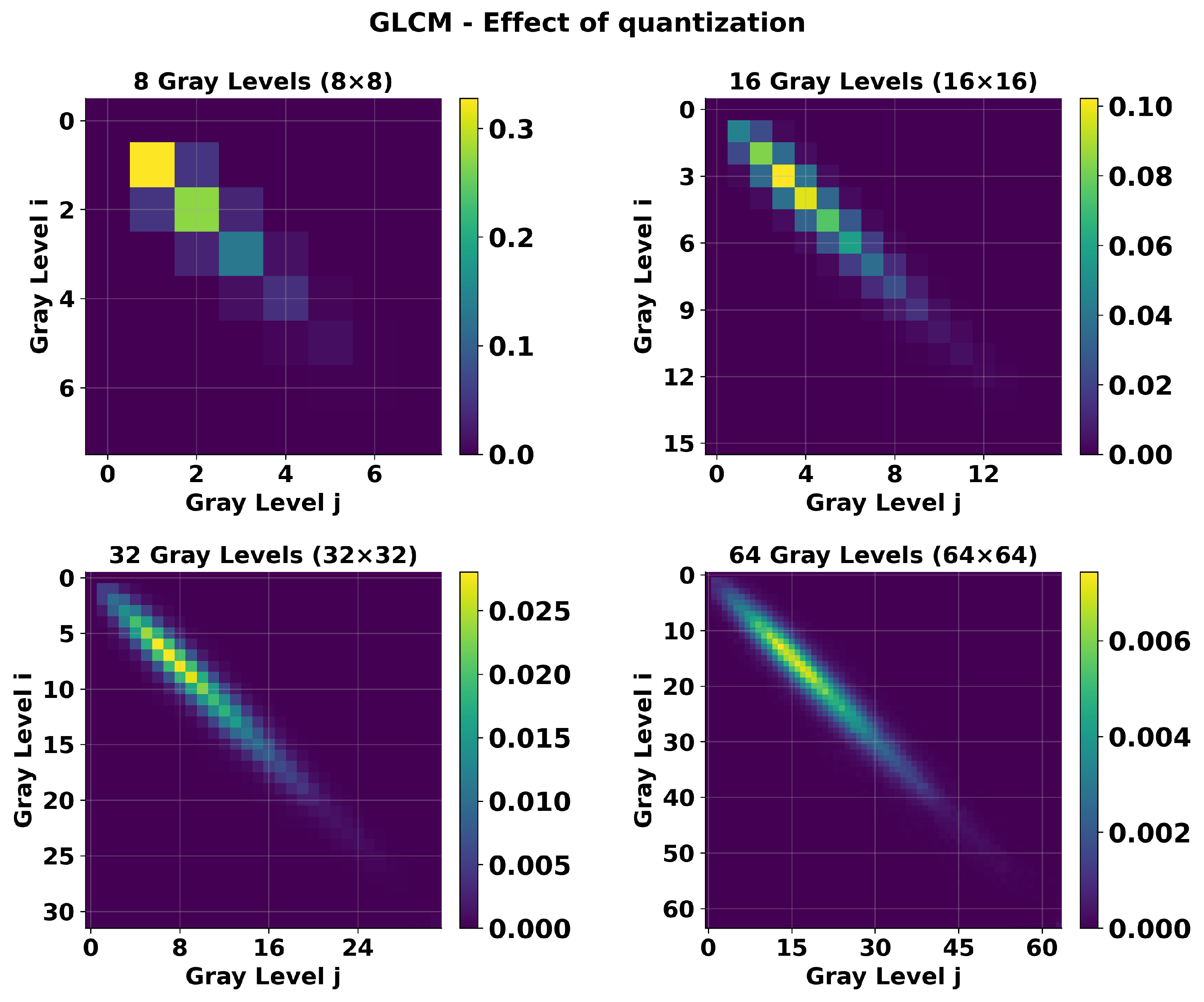
2.4.1. Quantization
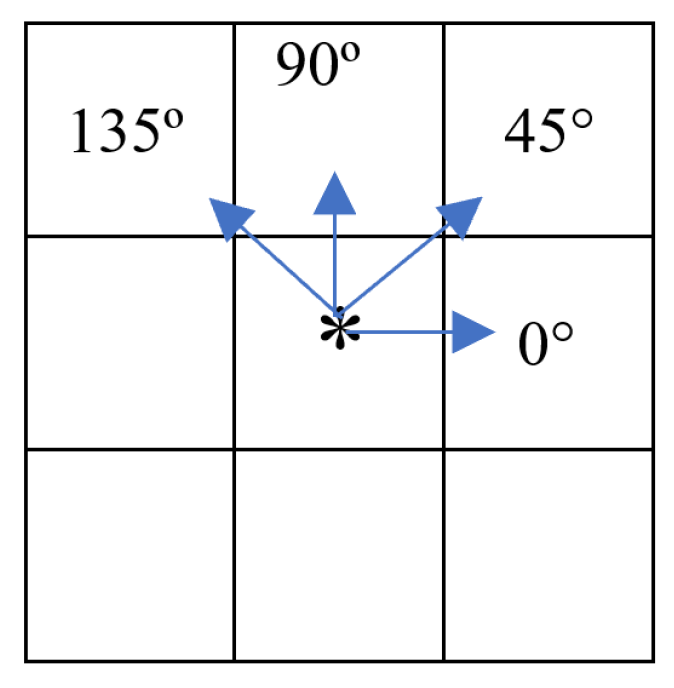
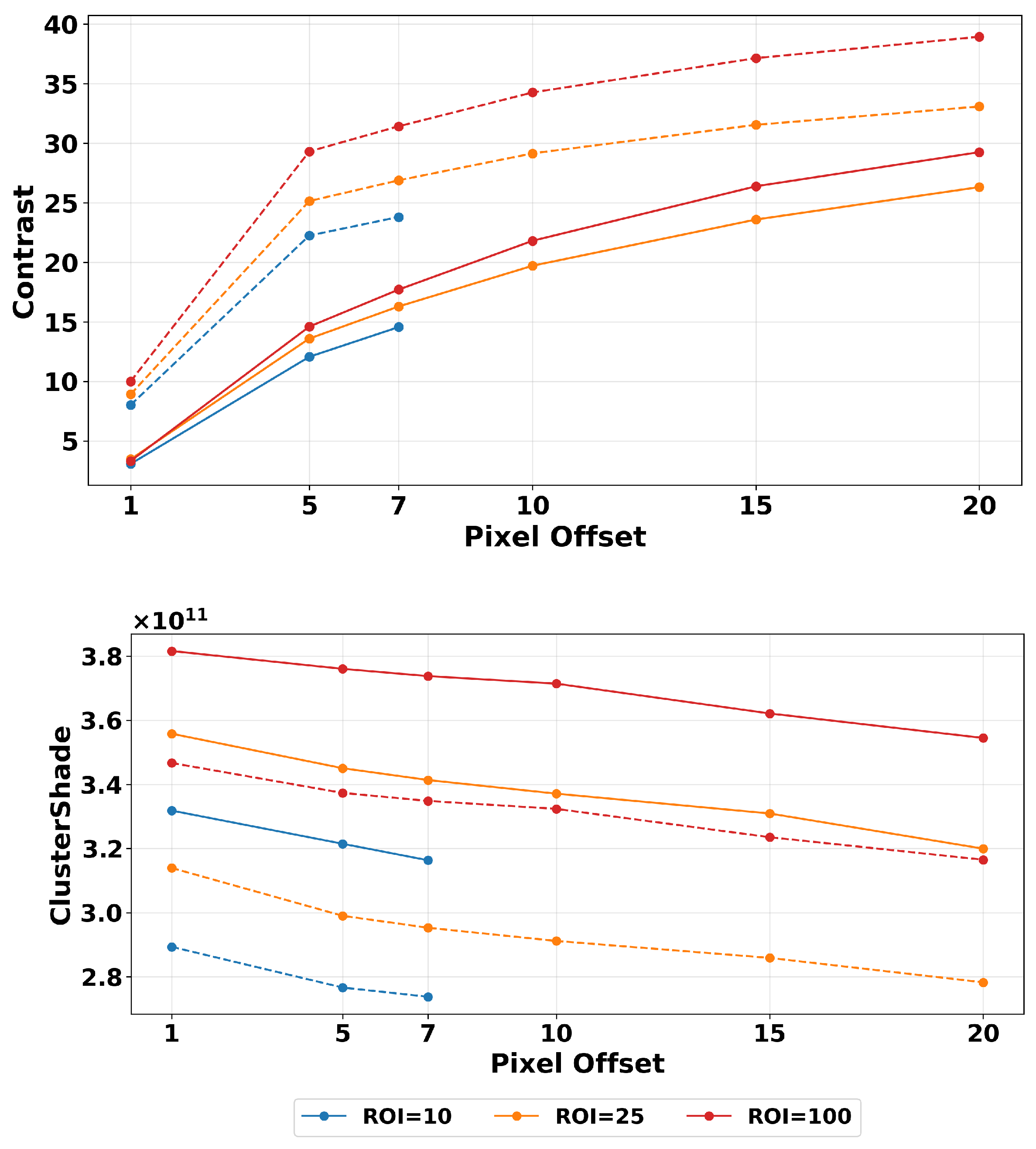
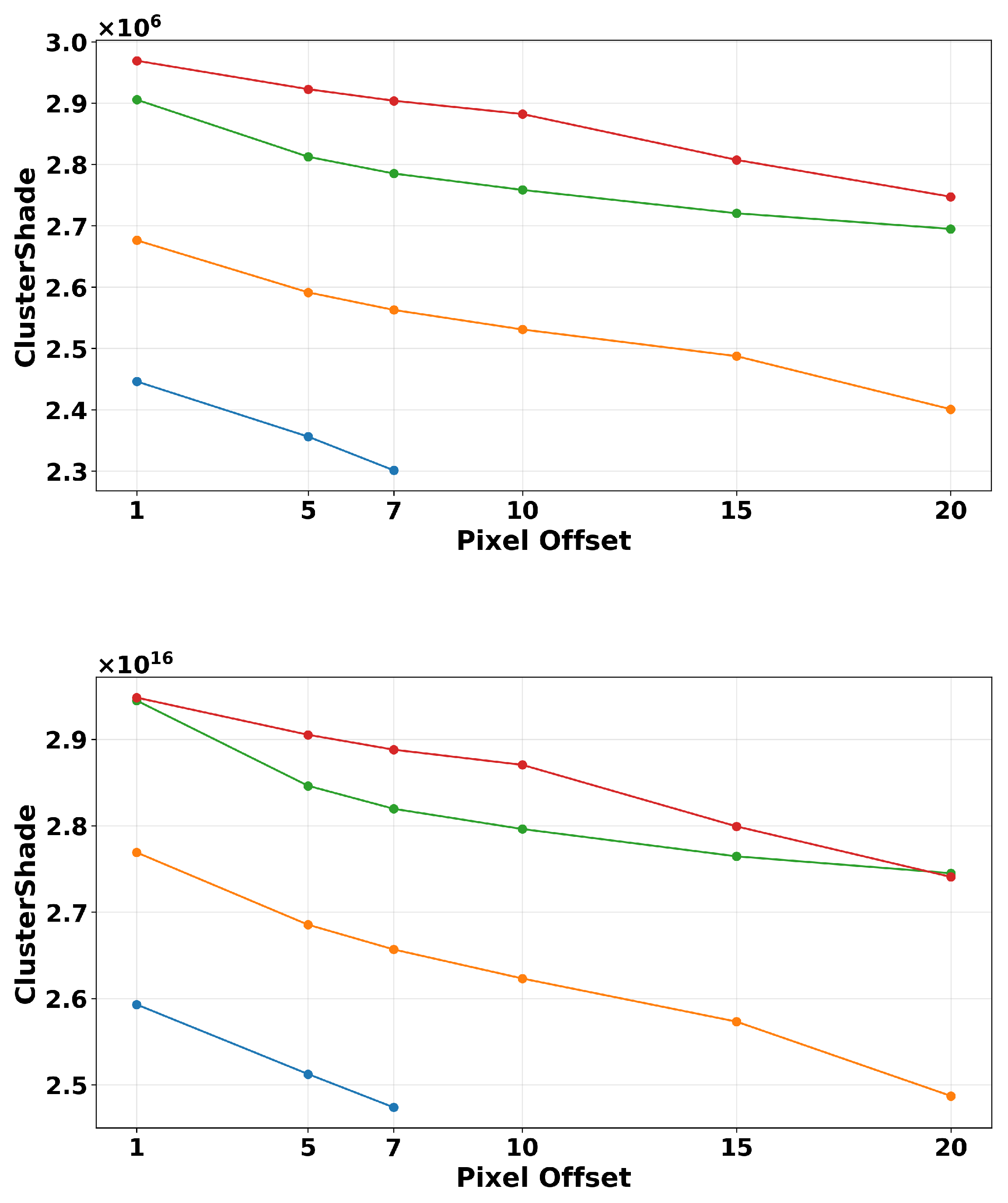
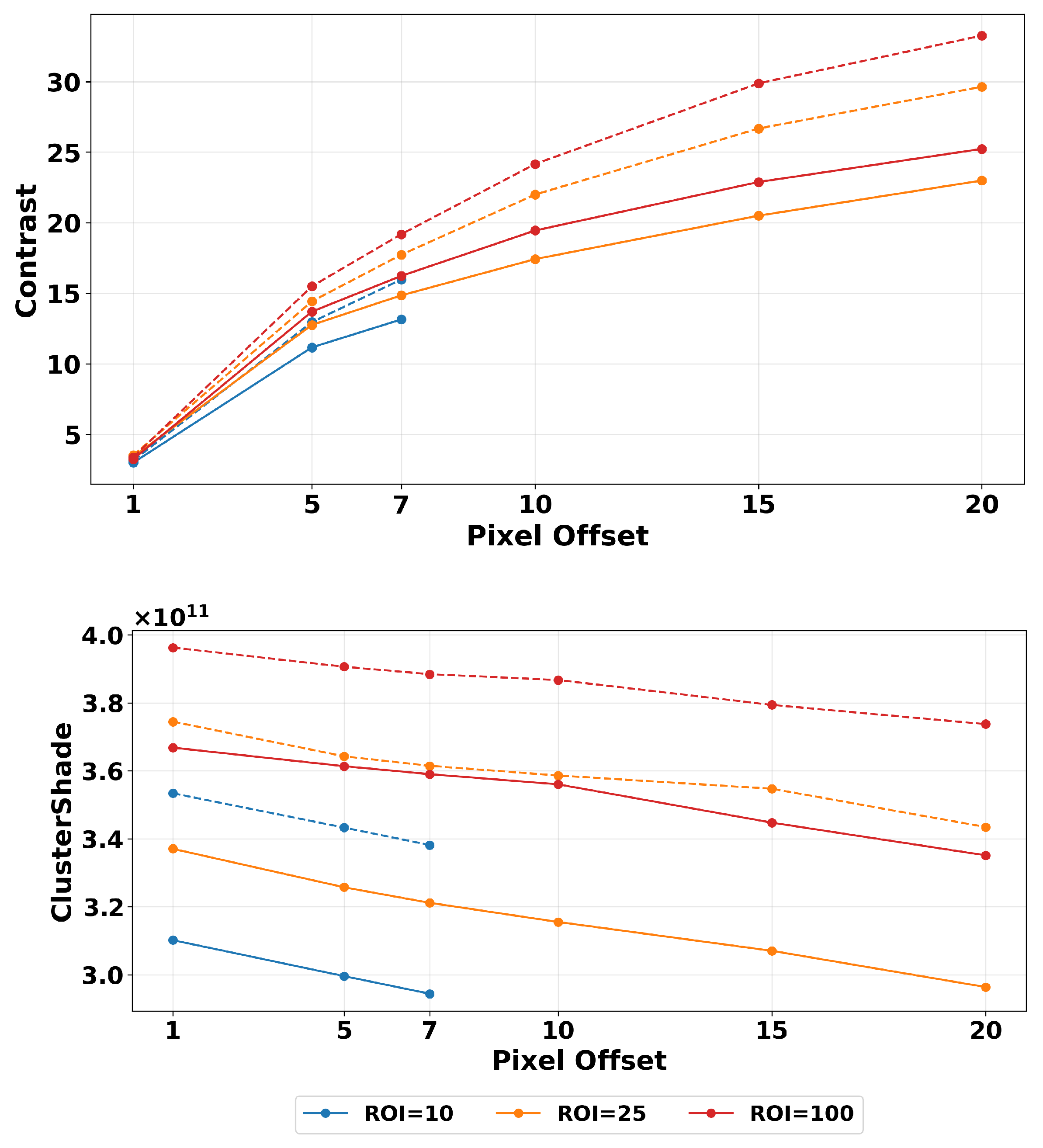
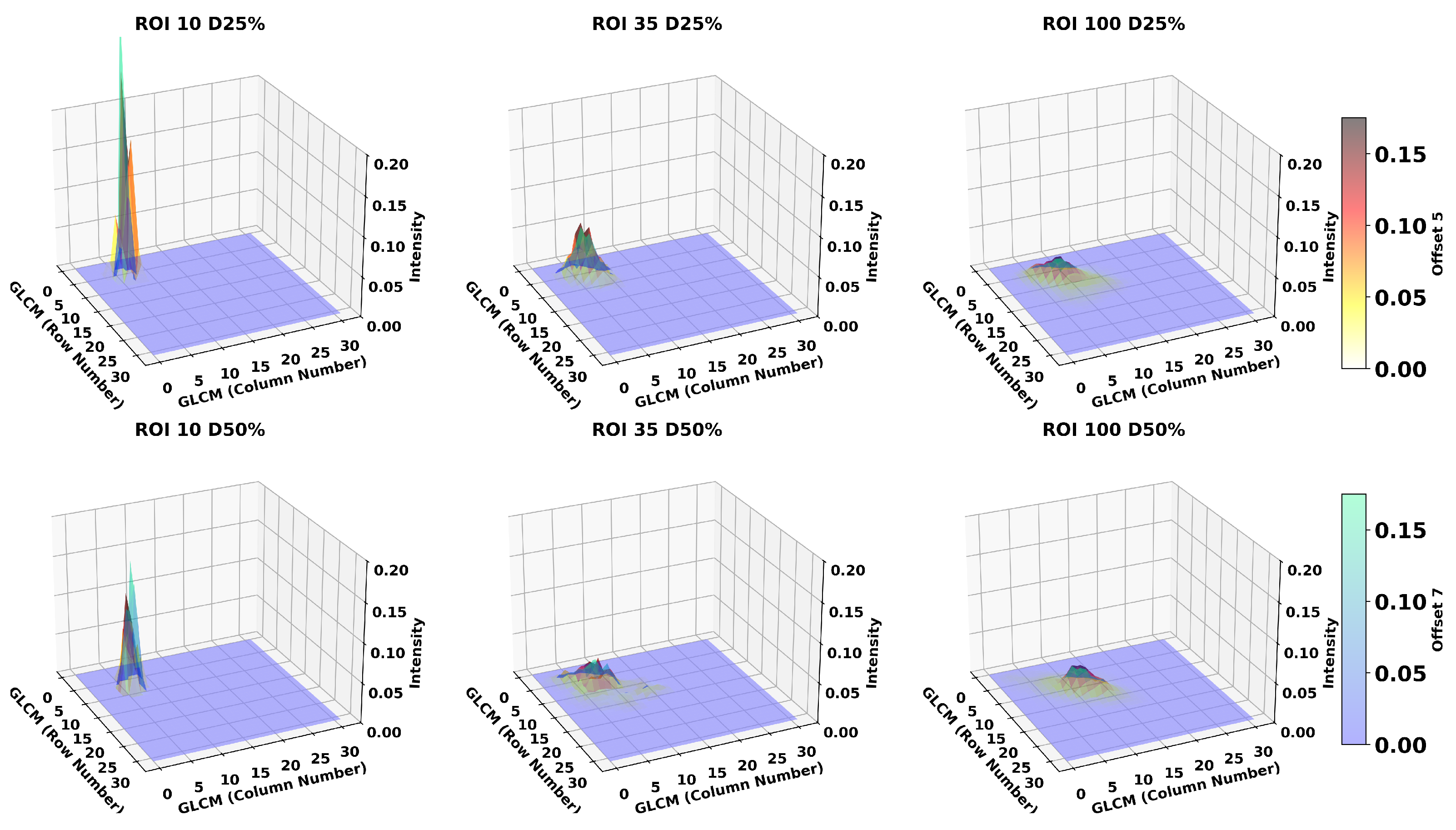
2.4.2. ROI Segmentation, GLCM Angle, and Offset Selection
2.4.3. GLCM Calculation
2.4.4. Textures Calculations
- represents the probability of the pair of pixels in the image.
- denotes the angle at which the GLCM is calculated.
- d represents the pixel distance between the pixels .
- represents the mean, and corresponds to the standard deviation.
3. Results
3.1. Filtering
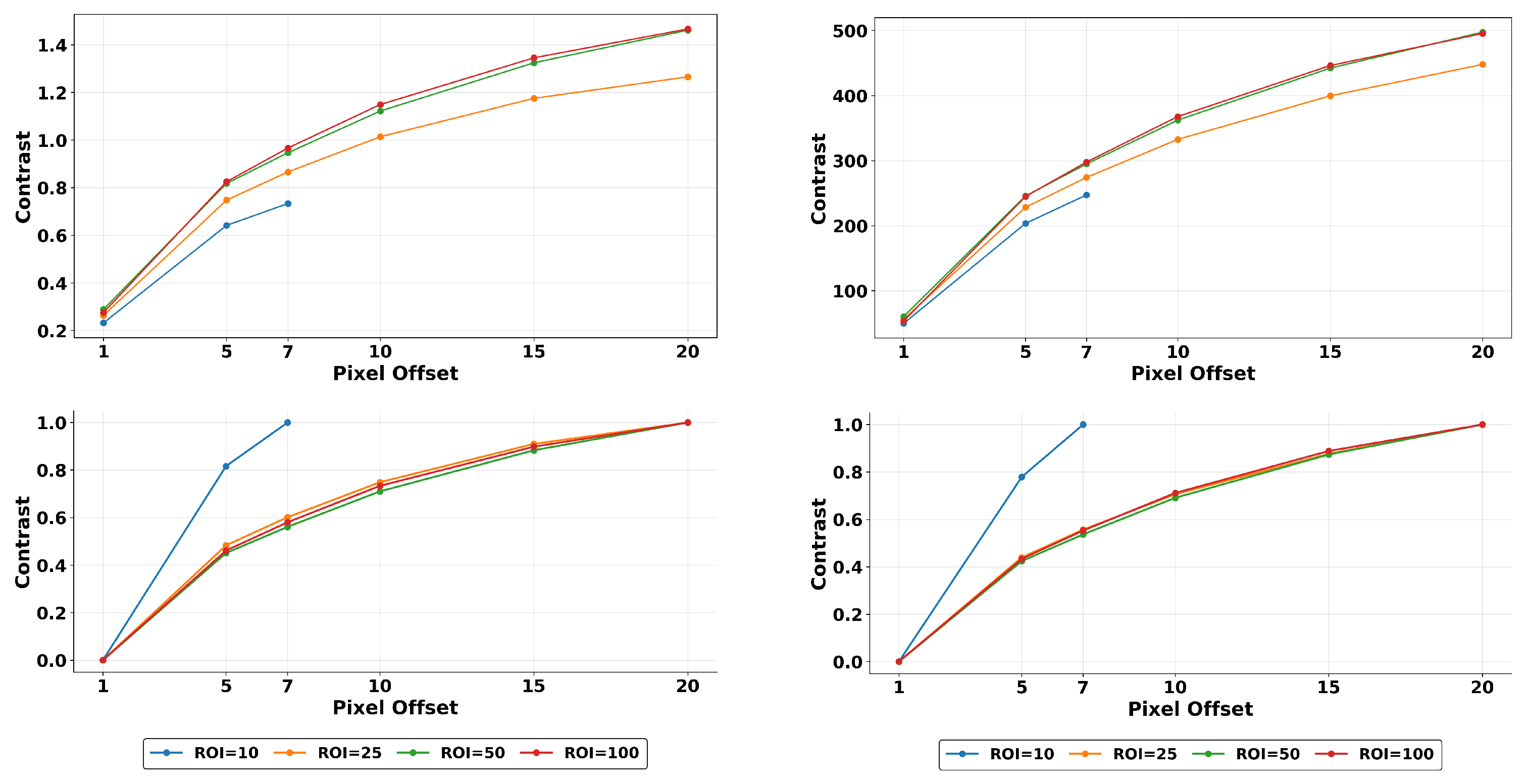
3.2. Quantization Effects
3.3. Breast Density
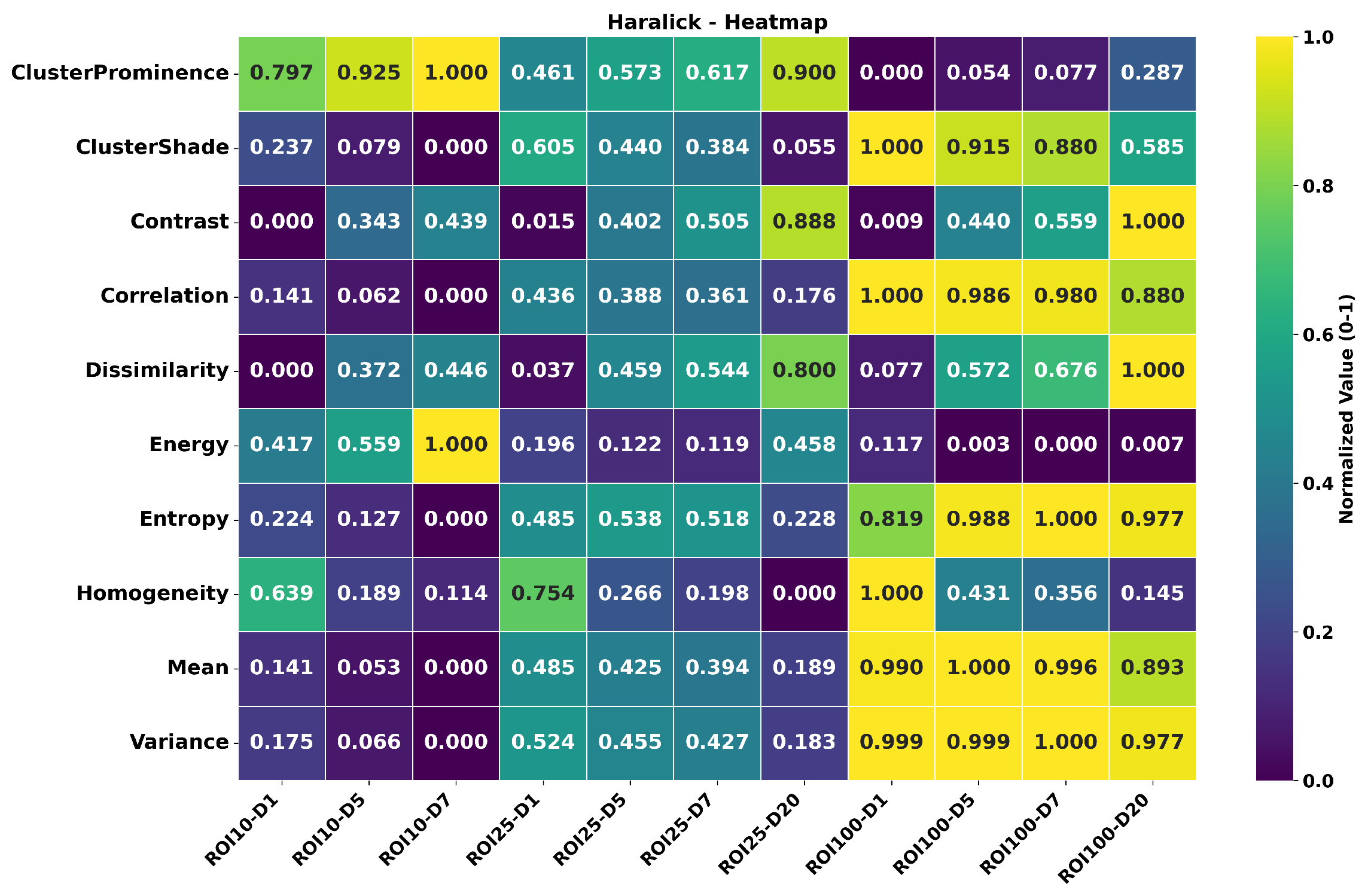
3.4. MANOVA
- Parameter optimization cannot be performed independently for each factor.
- Texture analysis protocols should specify all three parameters.
- Cross-study comparisons require identical parameter configurations.
- Feature robustness varies significantly with the specific parameters combination used.
3.5. Multi-Resolution Normalization
3.6. Simulated and Clinical Data
4. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DBT | Digital Breast Tomosynthesis |
| GLCM | Gray Level Co-occurrence Matrix |
| ROI | Region of Interest |
| VOI | Volume of Interest |
References
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Julesz, B. Textons, the elements of texture perception, and their interactions. Nature 1981, 290, 91–97. [Google Scholar] [CrossRef]
- Amadasun, M.; King, R. Textural features corresponding to textural properties. IEEE Trans. Syst. Man Cybern. 1989, 19, 1264–1274. [Google Scholar] [CrossRef]
- Galloway, M.M. Texture analysis using grey level run lengths. Nasa Sti/Recon Tech. Rep. 1974, 75, 18555. [Google Scholar]
- Anys, H.; He, D.C. Evaluation of textural and multipolarization radar features for crop classification. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1170–1181. [Google Scholar] [CrossRef]
- Pearlstine, L.; Portier, K.M.; Smith, S.E. Textural discrimination of an invasive plant, Schinus terebinthifolius, from low altitude aerial digital imagery. Photogramm. Eng. Remote Sens. 2005, 71, 289–298. [Google Scholar] [CrossRef]
- Hall-Beyer, M. Practical guidelines for choosing GLCM textures to use in landscape classification tasks over a range of moderate spatial scales. Int. J. Remote Sens. 2017, 38, 1312–1338. [Google Scholar] [CrossRef]
- Szantoi, Z.; Escobedo, F.; Abd-Elrahman, A.; Smith, S.; Pearlstine, L. Analyzing fine-scale wetland composition using high resolution imagery and texture features. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 204–212. [Google Scholar] [CrossRef]
- Rampun, A.; Strange, H.; Zwiggelaar, R. Texture segmentation using different orientations of GLCM features. In Proceedings of the 6th International Conference on Computer Vision/Computer Graphics Collaboration Techniques and Applications, Berlin, Germany, 6–7 June 2013; pp. 1–8. [Google Scholar]
- Gotlieb, C.C.; Kreyszig, H.E. Texture descriptors based on co-occurrence matrices. Comput. Vision Graph. Image Process. 1990, 51, 70–86. [Google Scholar] [CrossRef]
- Poli, G.; Llapa, E.; Cecatto, J.; Saito, J.H.; Peters, J.F.; Ramanna, S.; Nicoletti, M. Solar flare detection system based on tolerance near sets in a GPU–CUDA framework. Knowl.-Based Syst. 2014, 70, 345–360. [Google Scholar] [CrossRef]
- Ntwaetsile, K.; Geach, J.E. Rapid sorting of radio galaxy morphology using Haralick features. Mon. Not. R. Astron. Soc. 2021, 502, 3417–3425. [Google Scholar] [CrossRef]
- Hussain, A.; Khunteta, A. Semantic segmentation of brain tumor from MRI images and SVM classification using GLCM features. In Proceedings of the 2020 Second International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 15–17 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 38–43. [Google Scholar]
- Tesař, L.; Shimizu, A.; Smutek, D.; Kobatake, H.; Nawano, S. Medical image analysis of 3D CT images based on extension of Haralick texture features. Comput. Med. Imaging Graph. 2008, 32, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Maurya, R.; Singh, S.K.; Maurya, A.K.; Kumar, A. GLCM and Multi Class Support vector machine based automated skin cancer classification. In Proceedings of the 2014 International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 5–7 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 444–447. [Google Scholar]
- Zulpe, N.; Pawar, V. GLCM textural features for brain tumor classification. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 354. [Google Scholar]
- Abbas, Z.; Rehman, M.u.; Najam, S.; Rizvi, S.D. An efficient gray-level co-occurrence matrix (GLCM) based approach towards classification of skin lesion. In Proceedings of the 2019 Amity International Conference on Artificial Intelligence (AICAI), Dubai, United Arab Emirates, 4–6 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 317–320. [Google Scholar]
- Tan, J.; Gao, Y.; Liang, Z.; Cao, W.; Pomeroy, M.J.; Huo, Y.; Li, L.; Barish, M.A.; Abbasi, A.F.; Pickhardt, P.J. 3D-GLCM CNN: A 3-dimensional gray-level Co-occurrence matrix-based CNN model for polyp classification via CT colonography. IEEE Trans. Med. Imaging 2019, 39, 2013–2024. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; Tian, Q.; Li, B.; Wu, Y.; Yang, Z.; Liang, Z.; Liu, Y.; Cui, G.; Lu, H. Radiomics assessment of bladder cancer grade using texture features from diffusion-weighted imaging. J. Magn. Reson. Imaging 2017, 46, 1281–1288. [Google Scholar] [CrossRef]
- Aerts, H.J.; Velazquez, E.R.; Leijenaar, R.T.; Parmar, C.; Grossmann, P.; Carvalho, S.; Bussink, J.; Monshouwer, R.; Haibe-Kains, B.; Rietveld, D.; et al. Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nat. Commun. 2014, 5, 4006. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Tan, Y.; Tsai, W.Y.; Qi, J.; Xie, C.; Lu, L.; Schwartz, L.H. Reproducibility of radiomics for deciphering tumor phenotype with imaging. Sci. Rep. 2016, 6, 23428. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Wei, X.; Zhang, Z.; Yang, R.; Zhu, Y.; Jiang, X. Differentiation of true-progression from pseudoprogression in glioblastoma treated with radiation therapy and concomitant temozolomide by GLCM texture analysis of conventional MRI. Clin. Imaging 2015, 39, 775–780. [Google Scholar] [CrossRef]
- Huang, S.y.; Franc, B.L.; Harnish, R.J.; Liu, G.; Mitra, D.; Copeland, T.P.; Arasu, V.A.; Kornak, J.; Jones, E.F.; Behr, S.C.; et al. Exploration of PET and MRI radiomic features for decoding breast cancer phenotypes and prognosis. NPJ Breast Cancer 2018, 4, 24. [Google Scholar] [CrossRef]
- Hotta, M.; Minamimoto, R.; Gohda, Y.; Miwa, K.; Otani, K.; Kiyomatsu, T.; Yano, H. Prognostic value of 18F-FDG PET/CT with texture analysis in patients with rectal cancer treated by surgery. Ann. Nucl. Med. 2021, 35, 843–852. [Google Scholar] [CrossRef] [PubMed]
- Heidari, M.; Mirniaharikandehei, S.; Khuzani, A.Z.; Qian, W.; Qiu, Y.; Zheng, B. Assessment of a quantitative mammographic imaging marker for breast cancer risk prediction. In Proceedings of the Medical Imaging 2019: Image Perception, Observer Performance, and Technology Assessment, San Diego, CA, USA, 20–21 February 2019; SPIE: Bellingham, WA, USA, 2019; Volume 10952, pp. 221–227. [Google Scholar]
- Althubiti, S.A.; Paul, S.; Mohanty, R.; Mohanty, S.N.; Alenezi, F.; Polat, K. Ensemble learning framework with GLCM texture extraction for early detection of lung cancer on CT images. Comput. Math. Methods Med. 2022, 2022, 2733965. [Google Scholar] [CrossRef]
- Mao, N.; Yin, P.; Wang, Q.; Liu, M.; Dong, J.; Zhang, X.; Xie, H.; Hong, N. Added value of radiomics on mammography for breast cancer diagnosis: A feasibility study. J. Am. Coll. Radiol. 2019, 16, 485–491. [Google Scholar] [CrossRef]
- Chaddad, A.; Zinn, P.O.; Colen, R.R. Radiomics texture feature extraction for characterizing GBM phenotypes using GLCM. In Proceedings of the 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), Brooklyn, NY, USA, 16–19 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 84–87. [Google Scholar]
- Cho, H.h.; Park, H. Classification of low-grade and high-grade glioma using multi-modal image radiomics features. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Republic of Korea, 11–15 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3081–3084. [Google Scholar]
- Robins, M.; Solomon, J.; Hoye, J.; Abadi, E.; Marin, D.; Samei, E. Systematic analysis of bias and variability of texture measurements in computed tomography. J. Med. Imaging 2019, 6, 033503. [Google Scholar]
- Keller, B.M.; Oustimov, A.; Wang, Y.; Chen, J.; Acciavatti, R.J.; Zheng, Y.; Ray, S.; Gee, J.C.; Maidment, A.D.; Kontos, D. Parenchymal texture analysis in digital mammography: Robust texture feature identification and equivalence across devices. J. Med. Imaging 2015, 2, 024501. [Google Scholar] [CrossRef]
- Ponti, M.; Nazaré, T.S.; Thumé, G.S. Image quantization as a dimensionality reduction procedure in color and texture feature extraction. Neurocomputing 2016, 173, 385–396. [Google Scholar] [CrossRef]
- Löfstedt, T.; Brynolfsson, P.; Asklund, T.; Nyholm, T.; Garpebring, A. Gray-level invariant Haralick texture features. PLoS ONE 2019, 14, e0212110. [Google Scholar] [CrossRef]
- Tamal, M. A phantom study to investigate robustness and reproducibility of grey level co-occurrence matrix (GLCM)-based radiomics features for PET. Appl. Sci. 2021, 11, 535. [Google Scholar] [CrossRef]
- Leijenaar, R.T.; Nalbantov, G.; Carvalho, S.; Van Elmpt, W.J.; Troost, E.G.; Boellaard, R.; Aerts, H.J.; Gillies, R.J.; Lambin, P. The effect of SUV discretization in quantitative FDG-PET Radiomics: The need for standardized methodology in tumor texture analysis. Sci. Rep. 2015, 5, 11075. [Google Scholar] [CrossRef]
- Mottola, M.; Ursprung, S.; Rundo, L.; Sanchez, L.E.; Klatte, T.; Mendichovszky, I.; Stewart, G.D.; Sala, E.; Bevilacqua, A. Reproducibility of CT-based radiomic features against image resampling and perturbations for tumour and healthy kidney in renal cancer patients. Sci. Rep. 2021, 11, 11542. [Google Scholar] [CrossRef] [PubMed]
- Galavis, P.E.; Hollensen, C.; Jallow, N.; Paliwal, B.; Jeraj, R. Variability of textural features in FDG PET images due to different acquisition modes and reconstruction parameters. Acta Oncol. 2010, 49, 1012–1016. [Google Scholar] [CrossRef]
- Mahmood, U.; Apte, A.P.; Deasy, J.O.; Schmidtlein, C.R.; Shukla-Dave, A. Investigating the robustness neighborhood gray tone difference matrix and gray level co-occurrence matrix radiomic features on clinical computed tomography systems using anthropomorphic phantoms: Evidence from a multivendor study. J. Comput. Assist. Tomogr. 2017, 41, 995–1001. [Google Scholar] [CrossRef] [PubMed]
- Varghese, B.A.; Hwang, D.; Cen, S.Y.; Lei, X.; Levy, J.; Desai, B.; Goodenough, D.J.; Duddalwar, V.A. Identification of robust and reproducible CT-texture metrics using a customized 3D-printed texture phantom. J. Appl. Clin. Med. Phys. 2021, 22, 98–107. [Google Scholar] [CrossRef] [PubMed]
- Foy, J.J.; Robinson, K.R.; Li, H.; Giger, M.L.; Al-Hallaq, H.; Armato, S.G., III. Variation in algorithm implementation across radiomics software. J. Med. Imaging 2018, 5, 044505. [Google Scholar] [CrossRef] [PubMed]
- Nisbett, W.H.; Kavuri, A.; Das, M. On the correlation between second order texture features and human observer detection performance in digital images. Sci. Rep. 2020, 10, 13510. [Google Scholar] [CrossRef]
- Nisbett, W.H.; Kavuri, A.; Fredette, N.R.; Das, M. On the impact of local image texture parameters on search and localization in digital breast imaging. In Proceedings of the Medical Imaging 2017: Image Perception, Observer Performance, and Technology Assessment, Orlando, FL, USA, 11–16 February 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10136, pp. 31–36. [Google Scholar]
- Nisbett, W.H.; Kavuri, A.; Das, M. Investigating the contributions of anatomical variations and quantum noise to image texture in digital breast tomosynthesis. In Proceedings of the Medical Imaging 2018: Physics of Medical Imaging, Houston, TX, USA, 12–15 February 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10573, pp. 123–128. [Google Scholar]
- Kavuri, A.; Das, M. Relative contributions of anatomical and quantum noise in signal detection and perception of tomographic digital breast images. IEEE Trans. Med. Imaging 2020, 39, 3321–3330. [Google Scholar] [CrossRef]
- Das, M.; Lin, H.; Andrade, D.; Gifford, H.C. Combining image texture and morphological features in low-resource perception models for signal detection tasks. In Proceedings of the Medical Imaging 2025: Image Perception, Observer Performance, and Technology Assessment, San Diego, CA, USA, 16–20 February 2025; SPIE: Bellingham, WA, USA, 2025; Volume 13409, p. 134090E. [Google Scholar]
- Del Corso, G.; Germanese, D.; Caudai, C.; Anastasi, G.; Belli, P.; Formica, A.; Nicolucci, A.; Palma, S.; Pascali, M.A.; Pieroni, S.; et al. Adaptive Machine Learning Approach for Importance Evaluation of Multimodal Breast Cancer Radiomic Features. J. Imaging Inform. Med. 2024, 37, 1642–1651. [Google Scholar] [CrossRef]
- Murtas, F.; Landoni, V.; Ordòñez, P.; Greco, L.; Ferranti, F.R.; Russo, A.; Perracchio, L.; Vidiri, A. Clinical-radiomic models based on digital breast tomosynthesis images: A preliminary investigation of a predictive tool for cancer diagnosis. Front. Oncol. 2023, 13, 1152158. [Google Scholar] [CrossRef]
- Favati, B.; Borgheresi, R.; Giannelli, M.; Marini, C.; Vani, V.; Marfisi, D.; Linsalata, S.; Moretti, M.; Mazzotta, D.; Neri, E. Radiomic applications on digital breast Tomosynthesis of BI-RADS category 4 calcifications sent for vacuum-assisted breast biopsy. Diagnostics 2022, 12, 771. [Google Scholar] [CrossRef]
- Tagliafico, A.S.; Valdora, F.; Mariscotti, G.; Durando, M.; Nori, J.; La Forgia, D.; Rosenberg, I.; Caumo, F.; Gandolfo, N.; Houssami, N.; et al. An exploratory radiomics analysis on digital breast tomosynthesis in women with mammographically negative dense breasts. Breast 2018, 40, 92–96. [Google Scholar] [CrossRef]
- Bevilacqua, V.; Brunetti, A.; Guerriero, A.; Trotta, G.F.; Telegrafo, M.; Moschetta, M. A performance comparison between shallow and deeper neural networks supervised classification of tomosynthesis breast lesions images. Cogn. Syst. Res. 2019, 53, 3–19. [Google Scholar] [CrossRef]
- Kontos, D.; Ikejimba, L.C.; Bakic, P.R.; Troxel, A.B.; Conant, E.F.; Maidment, A.D. Analysis of parenchymal texture with digital breast tomosynthesis: Comparison with digital mammography and implications for cancer risk assessment. Radiology 2011, 261, 80–91. [Google Scholar] [CrossRef][Green Version]
- Kontos, D.; Bakic, P.R.; Carton, A.K.; Troxel, A.B.; Conant, E.F.; Maidment, A.D. Parenchymal texture analysis in digital breast tomosynthesis for breast cancer risk estimation: A preliminary study. Acad. Radiol. 2009, 16, 283–298. [Google Scholar] [CrossRef][Green Version]
- Wang, D.; Liu, M.; Zhuang, Z.; Wu, S.; Zhou, P.; Chen, X.; Zhu, H.; Liu, H.; Zhang, L. Radiomics analysis on digital breast tomosynthesis: Preoperative evaluation of lymphovascular invasion status in invasive breast cancer. Acad. Radiol. 2022, 29, 1773–1782. [Google Scholar] [CrossRef]
- Tagliafico, A.S.; Bignotti, B.; Rossi, F.; Matos, J.; Calabrese, M.; Valdora, F.; Houssami, N. Breast cancer Ki-67 expression prediction by digital breast tomosynthesis radiomics features. Eur. Radiol. Exp. 2019, 3, 1–6. [Google Scholar] [CrossRef]
- Jiang, T.; Jiang, W.; Chang, S.; Wang, H.; Niu, S.; Yue, Z.; Yang, H.; Wang, X.; Zhao, N.; Fang, S.; et al. Intratumoral analysis of digital breast tomosynthesis for predicting the Ki-67 level in breast cancer: A multi-center radiomics study. Med. Phys. 2022, 49, 219–230. [Google Scholar] [CrossRef]
- Liu, J.; Yan, C.; Liu, C.; Wang, Y.; Chen, Q.; Chen, Y.; Guo, J.; Chen, S. Predicting Ki-67 expression levels in breast cancer using radiomics-based approaches on digital breast tomosynthesis and ultrasound. Front. Oncol. 2024, 14, 1403522. [Google Scholar] [CrossRef] [PubMed]
- Vedula, A.A.; Glick, S.J.; Gong, X. Computer simulation of CT mammography using a flat-panel imager. In Medical Imaging 2003: Physics of Medical Imaging; SPIE: Bellingham, WA, USA, 2003; Volume 5030, pp. 349–360. [Google Scholar]
- Jiang, Z.; Das, M.; Gifford, H.C. Analyzing visual-search observers using eye-tracking data for digital breast tomosynthesis images. JOSA A 2017, 34, 838–845. [Google Scholar] [CrossRef] [PubMed]
- Lau, B.A.; Das, M.; Gifford, H.C. Towards visual-search model observers for mass detection in breast tomosynthesis. In Proceedings of the Medical Imaging 2013: Physics of Medical Imaging, Lake Buena Vista, FL, USA, 11–14 February 2013; SPIE: Bellingham, WA, USA, 2013; Volume 8668, pp. 242–250. [Google Scholar]
- Das, M.; Gifford, H.C. Comparison of model-observer and human-observer performance for breast tomosynthesis: Effect of reconstruction and acquisition parameters. In Proceedings of the Medical Imaging 2011: Physics of Medical Imaging, Lake Buena Vista, FL, USA, 13–17 February 2011; SPIE: Bellingham, WA, USA, 2011; Volume 7961, pp. 375–383. [Google Scholar]
- Gifford, H.; Karbaschi, Z.; Banerjee, K.; Das, M. Visual-search models for location-known detection tasks. In Proceedings of the Medical Imaging 2017: Image Perception, Observer Performance, and Technology Assessment, Orlando, FL, USA, 11–16 February 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10136, pp. 282–287. [Google Scholar]
- Bakic, P.R.; Zhang, C.; Maidment, A.D. Development and characterization of an anthropomorphic breast software phantom based upon region-growing algorithm. Med. Phys. 2011, 38, 3165–3176. [Google Scholar] [CrossRef]
- Hendrick, R.E.; Pisano, E.D.; Averbukh, A.; Moran, C.; Berns, E.A.; Yaffe, M.J.; Herman, B.; Acharyya, S.; Gatsonis, C. Comparison of acquisition parameters and breast dose in digital mammography and screen-film mammography in the American College of Radiology Imaging Network digital mammographic imaging screening trial. Am. J. Roentgenol. 2010, 194, 362–369. [Google Scholar] [CrossRef] [PubMed]
- Kavuri, A.; Das, M. Examining the influence of digital phantom models in virtual imaging trials for tomographic breast imaging. J. Med. Imaging 2025, 12, 015501. [Google Scholar] [CrossRef] [PubMed]
- Vieira, M.A.; Bakic, P.R.; Maidment, A.D. Effect of denoising on the quality of reconstructed images in digital breast tomosynthesis. In Proceedings of the Medical Imaging 2013: Physics of Medical Imaging, Lake Buena Vista, FL, USA, 11–14 February 2013; SPIE: Bellingham, WA, USA, 2013; Volume 8668, pp. 56–69. [Google Scholar]
- Buda, M.; Saha, A.; Walsh, R.; Ghate, S.; Li, N.; Święcicki, A.; Lo, J.Y.; Mazurowski, M.A. Breast Cancer Screening—Digital Breast Tomosynthesis (BCS-DBT) (Version 5) [Dataset]; The Cancer Imaging Archive: Palo Alto, CA, USA, 2020. [Google Scholar] [CrossRef]
- Buda, M.; Saha, A.; Walsh, R.; Ghate, S.; Li, N.; Święcicki, A.; Lo, J.Y.; Mazurowski, M.A. A data set and deep learning algorithm for the detection of masses and architectural distortions in digital breast tomosynthesis images. JAMA Netw. Open 2021, 4, e2119100. [Google Scholar] [CrossRef] [PubMed]


| Texture Feature | Formula |
|---|---|
| Order Features | |
| Energy | |
| Entropy | |
| Contrast/Structure Features | |
| Homogeneity | |
| Contrast | |
| GLCM Descriptive Statistics Features | |
| GLCM— Mean | |
| GLCM—Variance | |
| GLCM—Correlation | |
| Cluster Features | |
| Cluster—Tendency | |
| Cluster—Shade | |
| Cluster—Prominence | |
| Without Wiener Filter | With Wiener Filter | ||||
|---|---|---|---|---|---|
| Texture—ROI Size | Avg. Change | Avg. Percentage Change | Avg. Change | Avg. Percentage Change | |
| Contrast | 10 | 1.56 | 7.01% | 2.50 | 20.72% |
| 25 | 1.99 | 7.11% | 3.18 | 18.02% | |
| 100 | 2.41 | 7.38% | 3.66 | 19.08% | |
| Cluster Shade | 10 | −1.04% | −1.60% | ||
| 25 | −1.78% | −1.87% | |||
| 100 | −1.58% | −1.46% | |||
| Quantization—8 | Quantization—128 | ||||
|---|---|---|---|---|---|
| Texture—ROI Size | Min | Max | Min | Max | |
| Contrast | 10 | 0.18 | 1.09 | 31.52 | 407.48 |
| 25 | 0.20 | 2.09 | 36.43 | 815.71 | |
| 50 | 0.20 | 2.32 | 38.47 | 868.53 | |
| 100 | 0.20 | 2.26 | 35.07 | 836.42 | |
| Cluster Shade | 10 | ||||
| 25 | |||||
| 50 | |||||
| 100 | |||||
| Density 25% | Density 50% | ||||
|---|---|---|---|---|---|
| Texture—ROI Size | Avg. Change | Avg. Percentage Change | Avg. Change | Avg. Percentage Change | |
| Contrast | 10 | 1.981 | 17.75% | 3.018 | 23.29% |
| 25 | 2.095 | 16.42% | 3.300 | 22.88% | |
| 100 | 2.528 | 18.46% | 3.691 | 23.82% | |
|
Cluster Shade | 10 | −1.73% | −1.49% | ||
| 25 | −1.40% | −0.77% | |||
| 100 | −0.65% | −0.56% | |||
| Feature | ROI | Distance | Quantization | |
|---|---|---|---|---|
| F-Value | F-Value | F-Value | ||
| Energy | 0.906 | 2685.14 * | 71.45 * | 48,474.57 * |
| Entropy | 0.921 | 22,500.12 * | 266.16 * | 38,692.21 * |
| Homogeneity | 0.971 | 4135.10 * | 12,421.33 * | 154,412.77 * |
| Contrast | 0.759 | 27.37 * | 1227.18 * | 14,536.80 * |
| Mean | 0.962 | 2126.72 * | 44.69 * | 134,999.03 * |
| Correlation | 0.987 | 3763.39 * | 82.09 * | 397,647.75 * |
| Feature | 2-Way | 3-Way | ROI × D | ROI × Qt | D × Qt | 3-Way |
|---|---|---|---|---|---|---|
| Energy | 0.948 | 0.950 | * | * | * | * |
| Entropy | 0.991 | 0.993 | * | * | * | * |
| Homogeneity | 0.988 | 0.988 | * | * | * | * |
| Contrast | 0.917 | 0.917 | * | * | * | * |
| Mean | 0.972 | 0.972 | * | * | NS | * |
| Correlation | 0.998 | 0.998 | * | * | * | * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrade, D.; Gifford, H.C.; Das, M. Assessment of Influencing Factors and Robustness of Computable Image Texture Features in Digital Images. Tomography 2025, 11, 87. https://doi.org/10.3390/tomography11080087
Andrade D, Gifford HC, Das M. Assessment of Influencing Factors and Robustness of Computable Image Texture Features in Digital Images. Tomography. 2025; 11(8):87. https://doi.org/10.3390/tomography11080087
Chicago/Turabian StyleAndrade, Diego, Howard C. Gifford, and Mini Das. 2025. "Assessment of Influencing Factors and Robustness of Computable Image Texture Features in Digital Images" Tomography 11, no. 8: 87. https://doi.org/10.3390/tomography11080087
APA StyleAndrade, D., Gifford, H. C., & Das, M. (2025). Assessment of Influencing Factors and Robustness of Computable Image Texture Features in Digital Images. Tomography, 11(8), 87. https://doi.org/10.3390/tomography11080087





