Influence of Magnetic Field Strength on Intravoxel Incoherent Motion Parameters in Diffusion MRI of the Calf
Abstract
1. Introduction
2. Materials and Methods
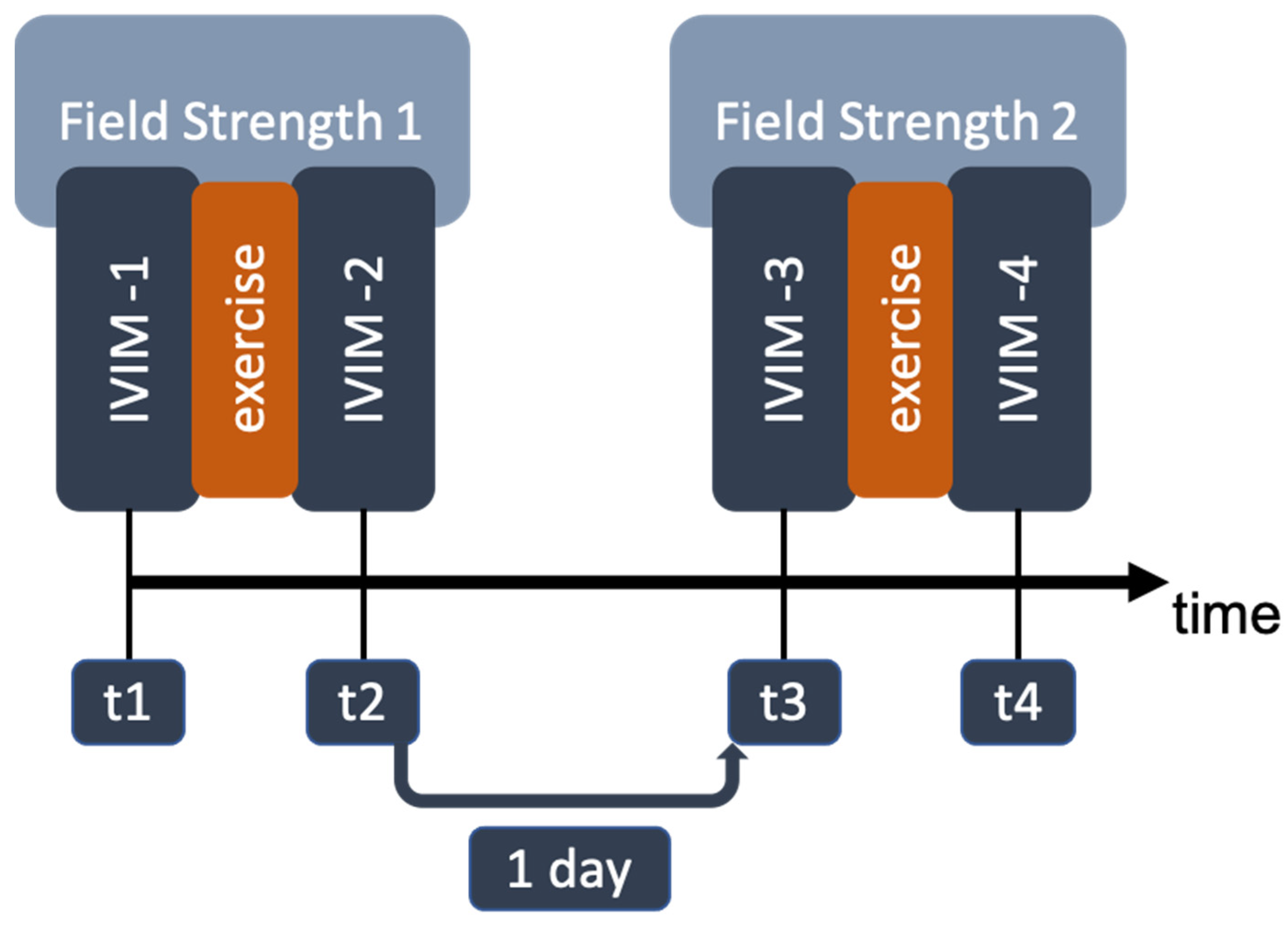
2.1. Data Acquisition
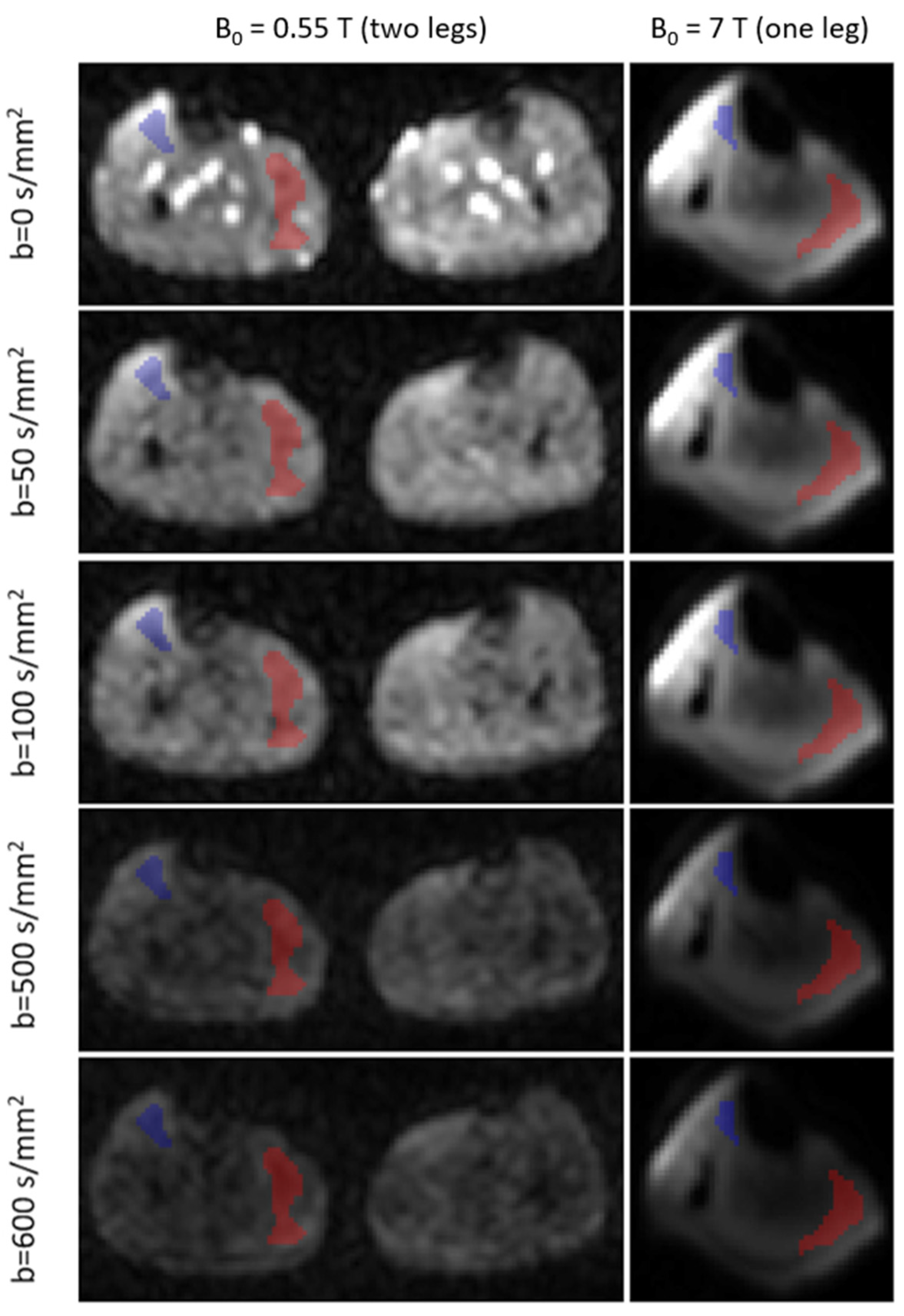
2.2. MR Image Analysis
2.3. Statistics
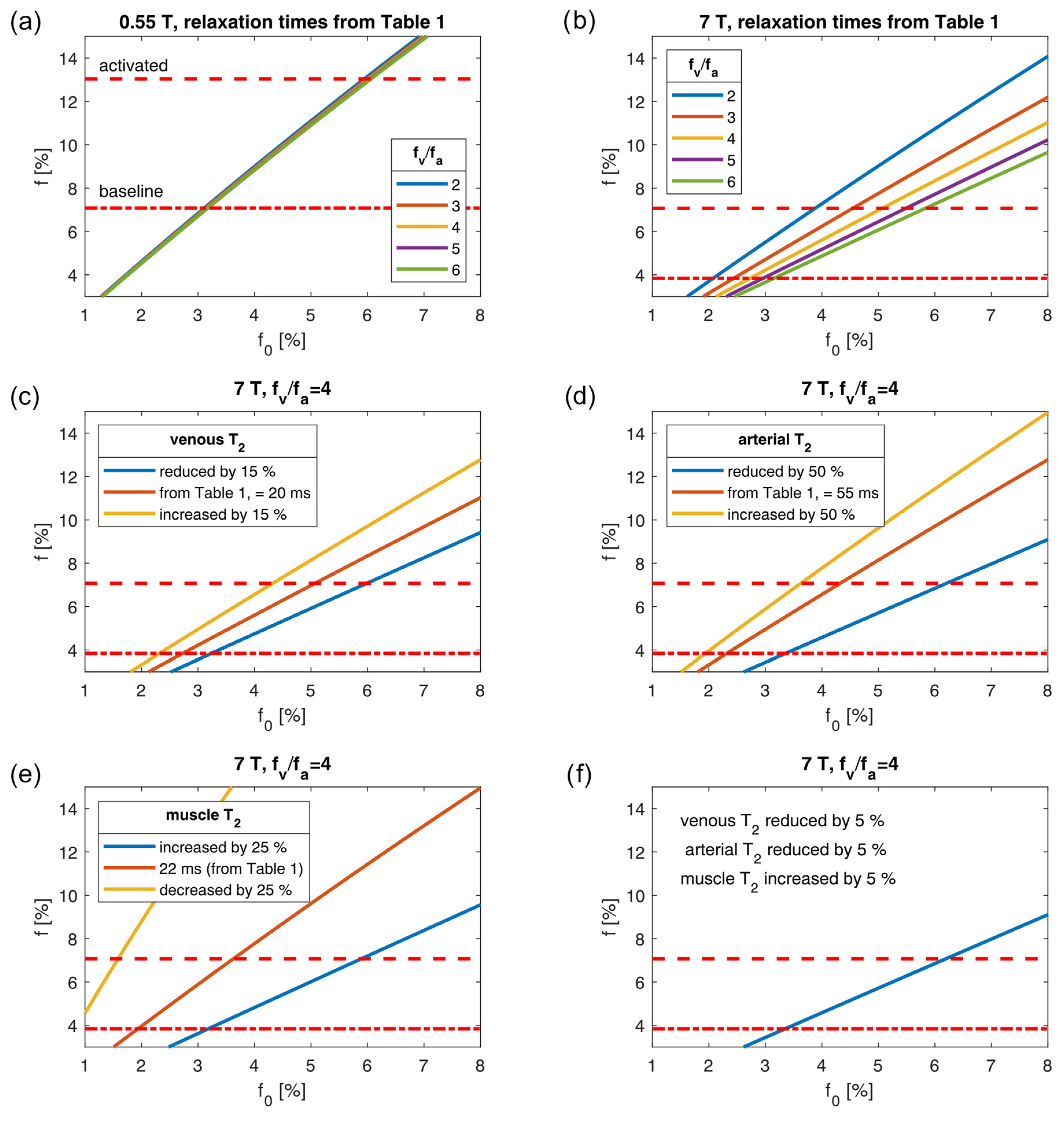
2.4. Plausibility Assessment
| 0.55 T | 1.5 T | 3 T | 4.7 T | 7 T | |
|---|---|---|---|---|---|
| Venous blood | 1434 ms (Y = 72 %, 23 °C) [35] | 1584 ms (Y = 69 %) [36] | 1370 ms (Y = 60 %) [37] | 2090 ms (Y = 66 %) [34] | |
| Arterial blood | 1122 ms [18] | 1441–1898 ms [18] 1435 ms (Y = 97 %, 23 °C) [35] | 1664 ms (Y = 92 %) [36] | 1700 ms (Y = 100 %) [37] | 2290 ms (Y = 95.6–99 %) [34] |
| Muscle | 1008 ms [13] | 1391 ms [15] 1412 ms [13] | 1864 ms [15] | ||
| Myocardium | 701 ms [18] | 950–1030 ms [18] |
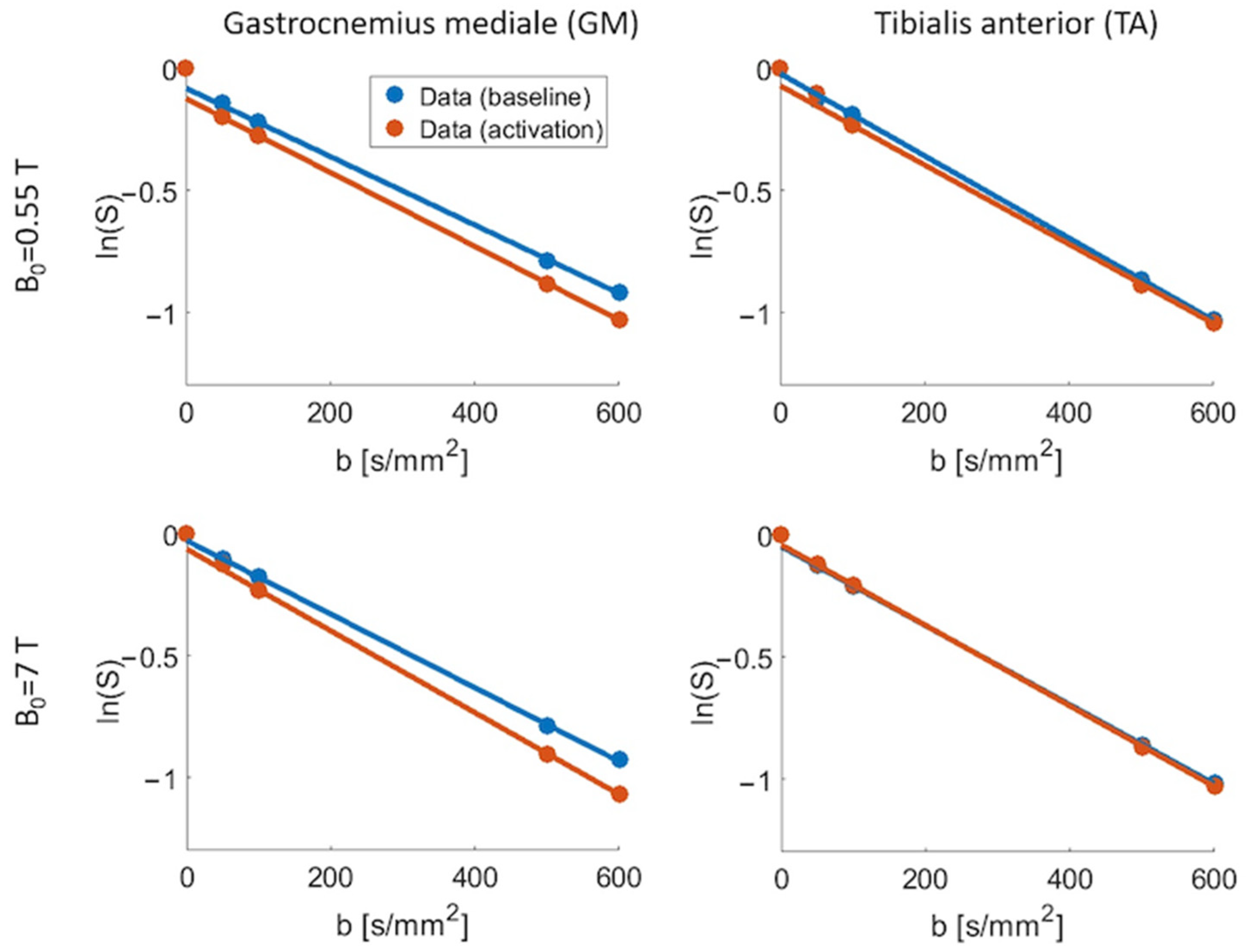
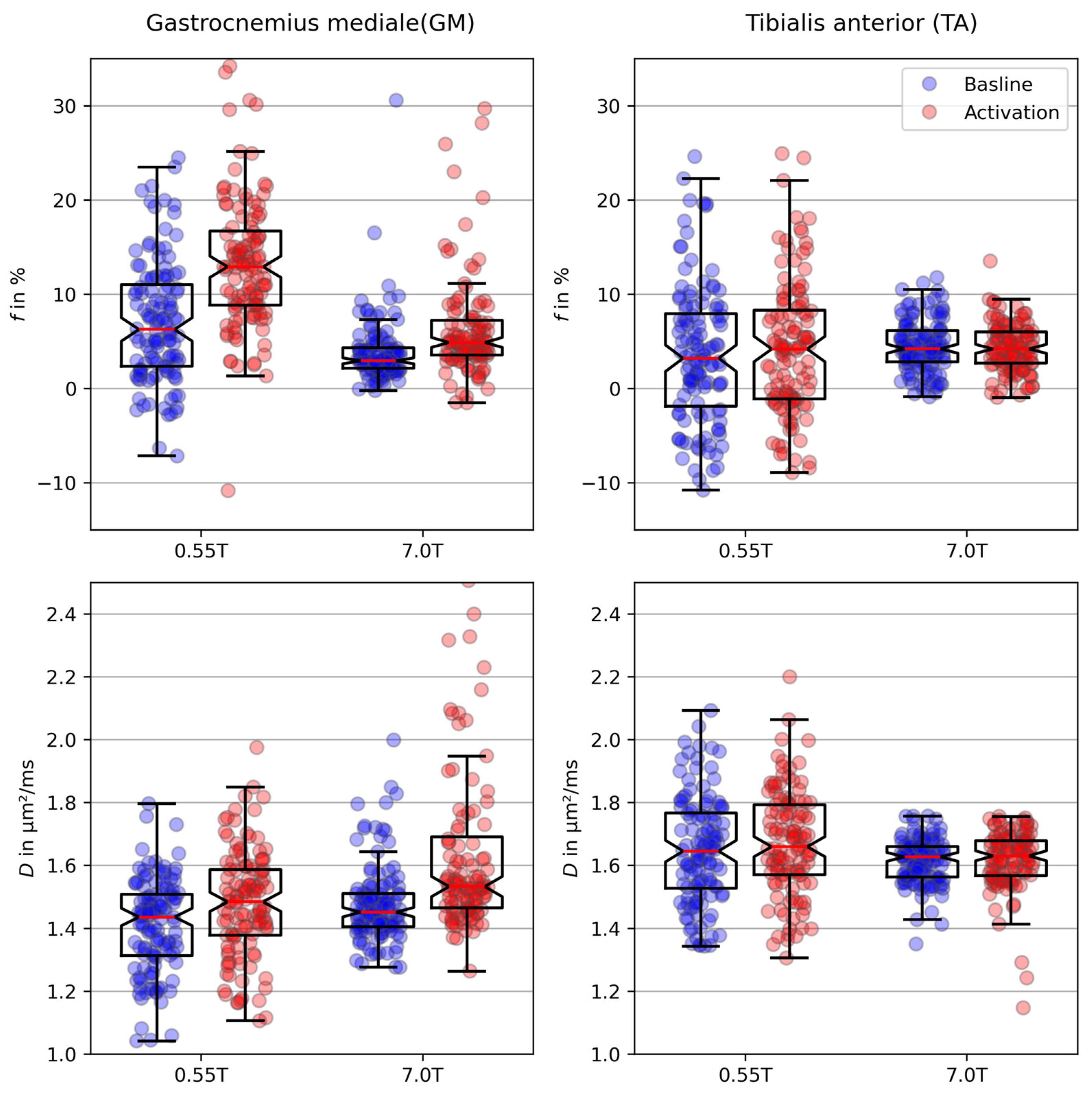
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Le Bihan, D.; Breton, E.; Lallemand, D.; Aubin, M.L.; Vignaud, J.; Laval-Jeantet, M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988, 168, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S. NMR survey of reflected Brownian motion. Rev. Mod. Phys. 2007, 79, 1077–1137. [Google Scholar] [CrossRef]
- Laun, F.B.; Wetscherek, A. Chapter 5: Separating Flow from Diffusion Using Velocity-compensated Diffusion Encoding. In Advanced Diffusion Encoding Methods in MRI; The Royal Society of Chemistry: London, UK, 2020; pp. 123–153. [Google Scholar]
- Englund, E.K.; Reiter, D.A.; Shahidi, B.; Sigmund, E.E. Intravoxel Incoherent Motion Magnetic Resonance Imaging in Skeletal Muscle: Review and Future Directions. J. Magn. Reson. Imaging 2022, 55, 988–1012. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Olsen, N.J.; Price, R.R.; Winston, J.A.; Park, J.H. Diffusion-weighted imaging of inflammatory myopathies: Polymyositis and dermatomyositis. J. Magn. Reson. Imaging 2008, 27, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Ngamsom, S.; Nakamura, S.; Sakamoto, J.; Kotaki, S.; Tetsumura, A.; Kurabayashi, T. The intravoxel incoherent motion MRI of lateral pterygoid muscle: A quantitative analysis in patients with temporomandibular joint disorders. Dentomaxillofac. Radiol. 2017, 46, 20160424. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, E.E.; Baete, S.H.; Luo, T.; Patel, K.; Wang, D.; Rossi, I.; Duarte, A.; Bruno, M.; Mossa, D.; Femia, A.; et al. MRI assessment of the thigh musculature in dermatomyositis and healthy subjects using diffusion tensor imaging, intravoxel incoherent motion and dynamic DTI. Eur. Radiol. 2018, 28, 5304–5315. [Google Scholar] [CrossRef] [PubMed]
- Suo, S.; Zhang, L.; Tang, H.; Ni, Q.; Li, S.; Mao, H.; Liu, X.; He, S.; Qu, J.; Lu, Q.; et al. Evaluation of skeletal muscle microvascular perfusion of lower extremities by cardiovascular magnetic resonance arterial spin labeling, blood oxygenation level-dependent, and intravoxel incoherent motion techniques. J. Cardiovasc. Magn. Reson. 2018, 20, 18. [Google Scholar] [CrossRef]
- Ran, J.; Yin, C.; Liu, C.; Li, Y.; Hou, B.; Morelli, J.N.; Dai, B.; Li, X. The Diagnostic Value of MR IVIM and T2 Mapping in Differentiating Autoimmune Myositis From Muscular Dystrophy. Acad. Radiol. 2021, 28, e182–e188. [Google Scholar] [CrossRef] [PubMed]
- Federau, C.; Kroismayr, D.; Dyer, L.; Farshad, M.; Pfirrmann, C. Demonstration of asymmetric muscle perfusion of the back after exercise in patients with adolescent idiopathic scoliosis using intravoxel incoherent motion (IVIM) MRI. NMR Biomed. 2020, 33, e4194. [Google Scholar] [CrossRef]
- Lemke, A.; Laun, F.B.; Simon, D.; Stieltjes, B.; Schad, L.R. An in vivo verification of the intravoxel incoherent motion effect in diffusion-weighted imaging of the abdomen. Magn. Reson. Med. 2010, 64, 1580–1585. [Google Scholar] [CrossRef]
- Jerome, N.P.; d’Arcy, J.A.; Feiweier, T.; Koh, D.M.; Leach, M.O.; Collins, D.J.; Orton, M.R. Extended T2-IVIM model for correction of TE dependence of pseudo-diffusion volume fraction in clinical diffusion-weighted magnetic resonance imaging. Phys. Med. Biol. 2016, 61, N667–N680. [Google Scholar] [CrossRef]
- Stanisz, G.J.; Odrobina, E.E.; Pun, J.; Escaravage, M.; Graham, S.J.; Bronskill, M.J.; Henkelman, R.M. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn. Reson. Med. 2005, 54, 507–512. [Google Scholar] [CrossRef]
- Silvennoinen, M.J.; Clingman, C.S.; Golay, X.; Kauppinen, R.A.; van Zijl, P.C. Comparison of the dependence of blood R2 and R2* on oxygen saturation at 1.5 and 4.7 Tesla. Magn. Reson. Med. 2003, 49, 47–60. [Google Scholar] [CrossRef]
- Marschar, A.M.; Breithaupt, M.; Berger, M.C.; Nagel, A.M. T1 and T2 relaxation times of the human calf at 7 Tesla. In Proceedings of the 23rd Annual Meeting of the ISMRM, Milan, Italy, 10–16 May 2014; p. 1842. [Google Scholar]
- Riexinger, A.J.; Martin, J.; Rauh, S.; Wetscherek, A.; Pistel, M.; Kuder, T.A.; Nagel, A.M.; Uder, M.; Hensel, B.; Muller, L.; et al. On the Field Strength Dependence of Bi- and Triexponential Intravoxel Incoherent Motion (IVIM) Parameters in the Liver. J. Magn. Reson. Imaging 2019, 50, 1883–1892. [Google Scholar] [CrossRef]
- Barbieri, S.; Donati, O.F.; Froehlich, J.M.; Thoeny, H.C. Comparison of Intravoxel Incoherent Motion Parameters across MR Imagers and Field Strengths: Evaluation in Upper Abdominal Organs. Radiology 2016, 279, 784–794. [Google Scholar] [CrossRef]
- Campbell-Washburn, A.E.; Ramasawmy, R.; Restivo, M.C.; Bhattacharya, I.; Basar, B.; Herzka, D.A.; Hansen, M.S.; Rogers, T.; Bandettini, W.P.; McGuirt, D.R.; et al. Opportunities in Interventional and Diagnostic Imaging by Using High-Performance Low-Field-Strength MRI. Radiology 2019, 293, 384–393. [Google Scholar] [CrossRef]
- Heiss, R.; Nagel, A.M.; Laun, F.B.; Uder, M.; Bickelhaupt, S. Low-Field Magnetic Resonance Imaging: A New Generation of Breakthrough Technology in Clinical Imaging. Investig. Radiol. 2021, 56, 726–733. [Google Scholar] [CrossRef]
- Ladd, M.E.; Bachert, P.; Meyerspeer, M.; Moser, E.; Nagel, A.M.; Norris, D.G.; Schmitter, S.; Speck, O.; Straub, S.; Zaiss, M. Pros and cons of ultra-high-field MRI/MRS for human application. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 109, 1–50. [Google Scholar] [CrossRef]
- Adelnia, F.; Shardell, M.; Bergeron, C.M.; Fishbein, K.W.; Spencer, R.G.; Ferrucci, L.; Reiter, D.A. Diffusion-weighted MRI with intravoxel incoherent motion modeling for assessment of muscle perfusion in the thigh during post-exercise hyperemia in younger and older adults. NMR Biomed. 2019, 32, e4072. [Google Scholar] [CrossRef]
- Fritzsche, K.H.; Neher, P.F.; Reicht, I.; van Bruggen, T.; Goch, C.; Reisert, M.; Nolden, M.; Zelzer, S.; Meinzer, H.P.; Stieltjes, B. MITK diffusion imaging. Methods Inf. Med. 2012, 51, 441–448. [Google Scholar] [CrossRef]
- Patel, J.; Sigmund, E.E.; Rusinek, H.; Oei, M.; Babb, J.S.; Taouli, B. Diagnosis of cirrhosis with intravoxel incoherent motion diffusion MRI and dynamic contrast-enhanced MRI alone and in combination: Preliminary experience. J. Magn. Reson. Imaging 2010, 31, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, E.E.; Vivier, P.H.; Sui, D.; Lamparello, N.A.; Tantillo, K.; Mikheev, A.; Rusinek, H.; Babb, J.S.; Storey, P.; Lee, V.S.; et al. Intravoxel incoherent motion and diffusion-tensor imaging in renal tissue under hydration and furosemide flow challenges. Radiology 2012, 263, 758–769. [Google Scholar] [CrossRef] [PubMed]
- Klauß, M.; Mayer, P.; Bergmann, F.; Maier-Hein, K.; Hase, J.; Hackert, T.; Kauczor, H.U.; Grenacher, L.; Stieltjes, B. Correlation of Histological Vessel Characteristics and Diffusion-Weighted Imaging Intravoxel Incoherent Motion-Derived Parameters in Pancreatic Ductal Adenocarcinomas and Pancreatic Neuroendocrine Tumors. Investig. Radiol. 2015, 50, 792–797. [Google Scholar] [CrossRef]
- Wu, C.H.; Ho, M.C.; Jeng, Y.M.; Liang, P.C.; Hu, R.H.; Lai, H.S.; Shih, T.T. Assessing hepatic fibrosis: Comparing the intravoxel incoherent motion in MRI with acoustic radiation force impulse imaging in US. Eur. Radiol. 2015, 25, 3552–3559. [Google Scholar] [CrossRef] [PubMed]
- Chung, S.R.; Lee, S.S.; Kim, N.; Yu, E.S.; Kim, E.; Kuhn, B.; Kim, I.S. Intravoxel incoherent motion MRI for liver fibrosis assessment: A pilot study. Acta Radiol. 2015, 56, 1428–1436. [Google Scholar] [CrossRef] [PubMed]
- Park, H.J.; Sung, Y.S.; Lee, S.S.; Lee, Y.; Cheong, H.; Kim, Y.J.; Lee, M.G. Intravoxel incoherent motion diffusion-weighted MRI of the abdomen: The effect of fitting algorithms on the accuracy and reliability of the parameters. J. Magn. Reson. Imaging 2017, 45, 1637–1647. [Google Scholar] [CrossRef] [PubMed]
- Führes, T.; Riexinger, A.J.; Loh, M.; Martin, J.; Wetscherek, A.; Kuder, T.A.; Uder, M.; Hensel, B.; Laun, F.B. Echo time dependence of biexponential and triexponential intravoxel incoherent motion parameters in the liver. Magn. Reson. Med. 2022, 87, 859–871. [Google Scholar] [CrossRef]
- Gudbjartsson, H.; Patz, S. The Rician Distribution of Noisy Mri Data. Magnet. Reson. Med. 1995, 34, 910–914. [Google Scholar] [CrossRef]
- Gardeback, M.; Settergren, G.; Brodin, L.A. Hepatic blood flow and right ventricular function during cardiac surgery assessed by transesophageal echocardiography. J. Cardiothor. Vasc. An. 1996, 10, 318–322. [Google Scholar] [CrossRef]
- Zhao, J.M.; Clingman, C.S.; Narvainen, M.J.; Kauppinen, R.A.; van Zijl, P.C. Oxygenation and hematocrit dependence of transverse relaxation rates of blood at 3T. Magn. Reson. Med. 2007, 58, 592–597. [Google Scholar] [CrossRef]
- Lin, A.L.; Qin, Q.; Zhao, X.; Duong, T.Q. Blood longitudinal (T1) and transverse (T2) relaxation time constants at 11.7 Tesla. Magn. Reson. Mater. Phys. 2012, 25, 245–249. [Google Scholar] [CrossRef] [PubMed]
- Rane, S.D.; Gore, J.C. Measurement of T1 of human arterial and venous blood at 7T. Magn. Reson. Imaging 2013, 31, 477–479. [Google Scholar] [CrossRef] [PubMed]
- Barth, M.; Moser, E. Proton NMR relaxation times of human blood samples at 1.5 T and implications for functional MRI. Cell Mol. Biol. 1997, 43, 783–791. [Google Scholar] [PubMed]
- Lu, H.Z.; Clingman, C.; Golay, X.; van Zijl, P.C.M. Determining the longitudinal relaxation time (T-1) of blood at 3.0 tesla. Magnet. Reson. Med. 2004, 52, 679–682. [Google Scholar] [CrossRef] [PubMed]
- Silvennoinen, M.J.; Kettunen, M.I.; Kauppinen, R.A. Effects of hematocrit and oxygen saturation level on blood spin-lattice relaxation. Magn. Reson. Med. 2003, 49, 568–571. [Google Scholar] [CrossRef] [PubMed]
- Slator, P.J.; Palombo, M.; Miller, K.L.; Westin, C.F.; Laun, F.; Kim, D.; Haldar, J.P.; Benjamini, D.; Lemberskiy, G.; de Almeida Martins, J.P.; et al. Combined diffusion-relaxometry microstructure imaging: Current status and future prospects. Magn. Reson. Med. 2021, 86, 2987–3011. [Google Scholar] [CrossRef] [PubMed]
- Topgaard, D. Multidimensional diffusion MRI. J. Magn. Reson. 2017, 275, 98–113. [Google Scholar] [CrossRef]
- de Bazelaire, C.M.; Duhamel, G.D.; Rofsky, N.M.; Alsop, D.C. MR imaging relaxation times of abdominal and pelvic tissues measured in vivo at 3.0 T: Preliminary results. Radiology 2004, 230, 652–659. [Google Scholar] [CrossRef] [PubMed]
- Egnell, L.; Jerome, N.P.; Andreassen, M.M.S.; Bathen, T.F.; Goa, P.E. Effects of echo time on IVIM quantifications of locally advanced breast cancer in clinical diffusion-weighted MRI at 3 T. NMR Biomed. 2022, 35, e4654. [Google Scholar] [CrossRef]
- Wu, X.P.; Auerbach, E.J.; Vu, A.T.; Moeller, S.; Lenglet, C.; Schmitter, S.; Van de Moortele, P.F.; Yacoub, E.; Ugurbil, K. High-resolution whole-brain diffusion MRI at 7T using radiofrequency parallel transmission. Magn. Reson. Med. 2018, 80, 1857–1870. [Google Scholar] [CrossRef]
- Frost, R.; Jezzard, P.; Douaud, G.; Clare, S.; Porter, D.A.; Miller, K.L. Scan time reduction for readout-segmented EPI using simultaneous multislice acceleration: Diffusion-weighted imaging at 3 and 7 Tesla. Magn. Reson. Med. 2015, 74, 136–149. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.K.; Gore, J.C.; Anderson, A.W. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn. Reson. Med. 2013, 69, 793–802. [Google Scholar] [CrossRef]
- Riexinger, A.; Laun, F.B.; Hoger, S.A.; Wiesmueller, M.; Uder, M.; Hensel, B.; Forst, R.; Hotfiel, T.; Heiss, R. Effect of compression garments on muscle perfusion in delayed-onset muscle soreness: A quantitative analysis using intravoxel incoherent motion MR perfusion imaging. NMR Biomed. 2021, 34, e4487. [Google Scholar] [CrossRef] [PubMed]
- Filli, L.; Boss, A.; Wurnig, M.C.; Kenkel, D.; Andreisek, G.; Guggenberger, R. Dynamic intravoxel incoherent motion imaging of skeletal muscle at rest and after exercise. NMR Biomed. 2015, 28, 240–246. [Google Scholar] [CrossRef]
- Mastropietro, A.; Porcelli, S.; Cadioli, M.; Rasica, L.; Scalco, E.; Gerevini, S.; Marzorati, M.; Rizzo, G. Triggered intravoxel incoherent motion MRI for the assessment of calf muscle perfusion during isometric intermittent exercise. NMR Biomed. 2018, 31, e3922. [Google Scholar] [CrossRef]
- Mills, R. Self-Diffusion in Normal and Heavy-Water in Range 1–45 Degrees. J. Phys. Chem-Us 1973, 77, 685–688. [Google Scholar] [CrossRef]
- Wagner, F.; Laun, F.B.; Kuder, T.A.; Mlynarska, A.; Maier, F.; Faust, J.; Demberg, K.; Lindemann, L.; Rivkin, B.; Nagel, A.M.; et al. Temperature and concentration calibration of aqueous polyvinylpyrrolidone (PVP) solutions for isotropic diffusion MRI phantoms. PLoS ONE 2017, 12, e0179276. [Google Scholar] [CrossRef]
- Fieremans, E.; Lemberskiy, G.; Veraart, J.; Sigmund, E.E.; Gyftopoulos, S.; Novikov, D.S. In vivo measurement of membrane permeability and myofiber size in human muscle using time-dependent diffusion tensor imaging and the random permeable barrier model. NMR Biomed. 2017, 30, e3612. [Google Scholar] [CrossRef]
- Martin, J.; Reymbaut, A.; Schmidt, M.; Doerfler, A.; Uder, M.; Laun, F.B.; Topgaard, D. Nonparametric D-R(1)-R(2) distribution MRI of the living human brain. Neuroimage 2021, 245, 118753. [Google Scholar] [CrossRef] [PubMed]
- van Baalen, S.; Leemans, A.; Dik, P.; Lilien, M.R.; Ten Haken, B.; Froeling, M. Intravoxel incoherent motion modeling in the kidneys: Comparison of mono-, bi-, and triexponential fit. J. Magn. Reson. Imaging 2017, 46, 228–239. [Google Scholar] [CrossRef]
- van der Bel, R.; Gurney-Champion, O.J.; Froeling, M.; Stroes, E.S.G.; Nederveen, A.J.; Krediet, C.T.P. A tri-exponential model for intravoxel incoherent motion analysis of the human kidney: In silico and during pharmacological renal perfusion modulation. Eur. J. Radiol. 2017, 91, 168–174. [Google Scholar] [CrossRef]
- Wurnig, M.C.; Germann, M.; Boss, A. Is there evidence for more than two diffusion components in abdominal organs?—A magnetic resonance imaging study in healthy volunteers. NMR Biomed. 2018, 31, e3852. [Google Scholar] [CrossRef]
- Wurnig, M.C.; Donati, O.F.; Ulbrich, E.; Filli, L.; Kenkel, D.; Thoeny, H.C.; Boss, A. Systematic analysis of the intravoxel incoherent motion threshold separating perfusion and diffusion effects: Proposal of a standardized algorithm. Magn. Reson. Med. 2015, 74, 1414–1422. [Google Scholar] [CrossRef] [PubMed]
- Wurnig, M.C.; Kenkel, D.; Filli, L.; Boss, A. A Standardized Parameter-Free Algorithm for Combined Intravoxel Incoherent Motion and Diffusion Kurtosis Analysis of Diffusion Imaging Data. Investig. Radiol. 2016, 51, 203–210. [Google Scholar] [CrossRef]
- Hanspach, J.; Nagel, A.M.; Hensel, B.; Uder, M.; Koros, L.; Laun, F.B. Sample size estimation: Current practice and considerations for original investigations in MRI technical development studies. Magn. Reson. Med. 2021, 85, 2109–2116. [Google Scholar] [CrossRef] [PubMed]
- Gold, G.E.; Han, E.; Stainsby, J.; Wright, G.; Brittain, J.; Beaulieu, C. Musculoskeletal MRI at 3.0 T: Relaxation times and image contrast. AJR Am. J. Roentgenol. 2004, 183, 343–351. [Google Scholar] [CrossRef]
- Funck, C.; Laun, F.B.; Wetscherek, A. Characterization of the diffusion coefficient of blood. Magn. Reson. Med. 2018, 79, 2752–2758. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, D.; Guo, W.; Liu, Z.; Zhao, X. Utility of mono-exponential, bi-exponential, and stretched exponential signal models of intravoxel incoherent motion (IVIM) to predict prognosis and survival risk in laryngeal and hypopharyngeal squamous cell carcinoma (LHSCC) patients after chemoradiotherapy. Jpn. J. Radiol. 2023, 41, 712–722. [Google Scholar] [CrossRef]
- Suo, S.T.; Lin, N.; Wang, H.; Zhang, L.B.; Wang, R.; Zhang, S.; Hua, J.; Xu, J.R. Intravoxel incoherent motion diffusion-weighted MR imaging of breast cancer at 3.0 tesla: Comparison of different curve-fitting methods. J. Magn. Reson. Imaging 2015, 42, 362–370. [Google Scholar] [CrossRef]
- Ioannidis, G.S.; Marias, K.; Galanakis, N.; Perisinakis, K.; Hatzidakis, A.; Tsetis, D.; Karantanas, A.; Maris, T.G. A correlative study between diffusion and perfusion MR imaging parameters on peripheral arterial disease data. Magn. Reson. Imaging 2019, 55, 26–35. [Google Scholar] [CrossRef]
- Di Pietro, G.; Palombo, M.; Capuani, S. Internal Magnetic Field Gradients in Heterogeneous Porous Systems: Comparison Between Spin-Echo and Diffusion Decay Internal Field (DDIF) Method. Appl. Magn. Reson. 2014, 45, 771–784. [Google Scholar] [CrossRef]
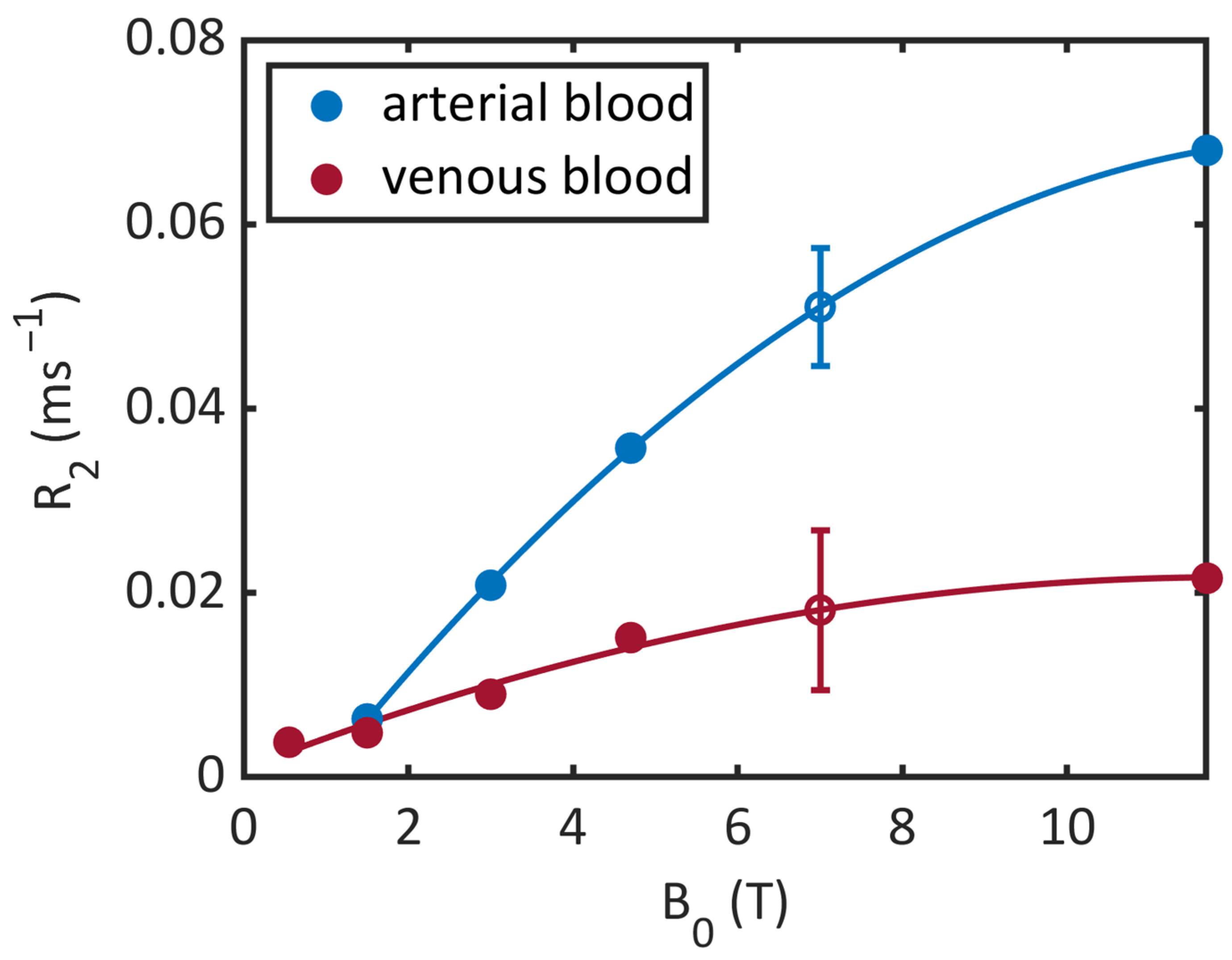
| 0.55 T | 1.5 T | 3 T | 4.7 T | 7 T | |
|---|---|---|---|---|---|
| Venous blood | 148 ms (Y = 72 %) [14] | 48 ms (Y = 72 %) [32] | 28 ms (Y = 72 %) [14] | 20 ms | |
| Arterial blood | 263 ms [12] | 207 ms (Y = 98 %) [14] 254–290 ms [18] | 111 ms (Y = 98 %) [32] | 66 ms (Y = 98 %) [14] | 55 ms |
| Muscle | 44 ms [13] 35.3 ms [33] | 31.7 ms [33] 27 ms [9] | 22 ms [15] | ||
| Myocardium | 58 ms [18] | 40–58 ms [18] |
| B0 (T) | GMBaseline | GMActivation | TABaseline | TAActivation | |
|---|---|---|---|---|---|
| (%) | 0.55 | 7.08 (±6.41) | 13.40 (±7.34) | 3.62 (±7.33) | 4.06 (±7.45) |
| 7 | 3.84 (±3.50) | 7.07 (±8.08) | 4.53 (±2.73) | 4.28 (±2.50) | |
| (µm2/ms) | 0.55 | 1.41 (±0.15) | 1.47 (±0.18) | 1.65 (±0.17) | 1.67 (±0.17) |
| 7 | 1.47 (±0.13) | 1.67 (±0.37) | 1.61 (±0.07) | 1.61 (±0.09) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bäuchle, T.A.; Stuprich, C.M.; Loh, M.; Nagel, A.M.; Uder, M.; Laun, F.B. Influence of Magnetic Field Strength on Intravoxel Incoherent Motion Parameters in Diffusion MRI of the Calf. Tomography 2024, 10, 773-788. https://doi.org/10.3390/tomography10050059
Bäuchle TA, Stuprich CM, Loh M, Nagel AM, Uder M, Laun FB. Influence of Magnetic Field Strength on Intravoxel Incoherent Motion Parameters in Diffusion MRI of the Calf. Tomography. 2024; 10(5):773-788. https://doi.org/10.3390/tomography10050059
Chicago/Turabian StyleBäuchle, Tamara Alice, Christoph Martin Stuprich, Martin Loh, Armin Michael Nagel, Michael Uder, and Frederik Bernd Laun. 2024. "Influence of Magnetic Field Strength on Intravoxel Incoherent Motion Parameters in Diffusion MRI of the Calf" Tomography 10, no. 5: 773-788. https://doi.org/10.3390/tomography10050059
APA StyleBäuchle, T. A., Stuprich, C. M., Loh, M., Nagel, A. M., Uder, M., & Laun, F. B. (2024). Influence of Magnetic Field Strength on Intravoxel Incoherent Motion Parameters in Diffusion MRI of the Calf. Tomography, 10(5), 773-788. https://doi.org/10.3390/tomography10050059