Impact of Deep Learning Denoising Algorithm on Diffusion Tensor Imaging of the Growth Plate on Different Spatial Resolutions
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. MRI
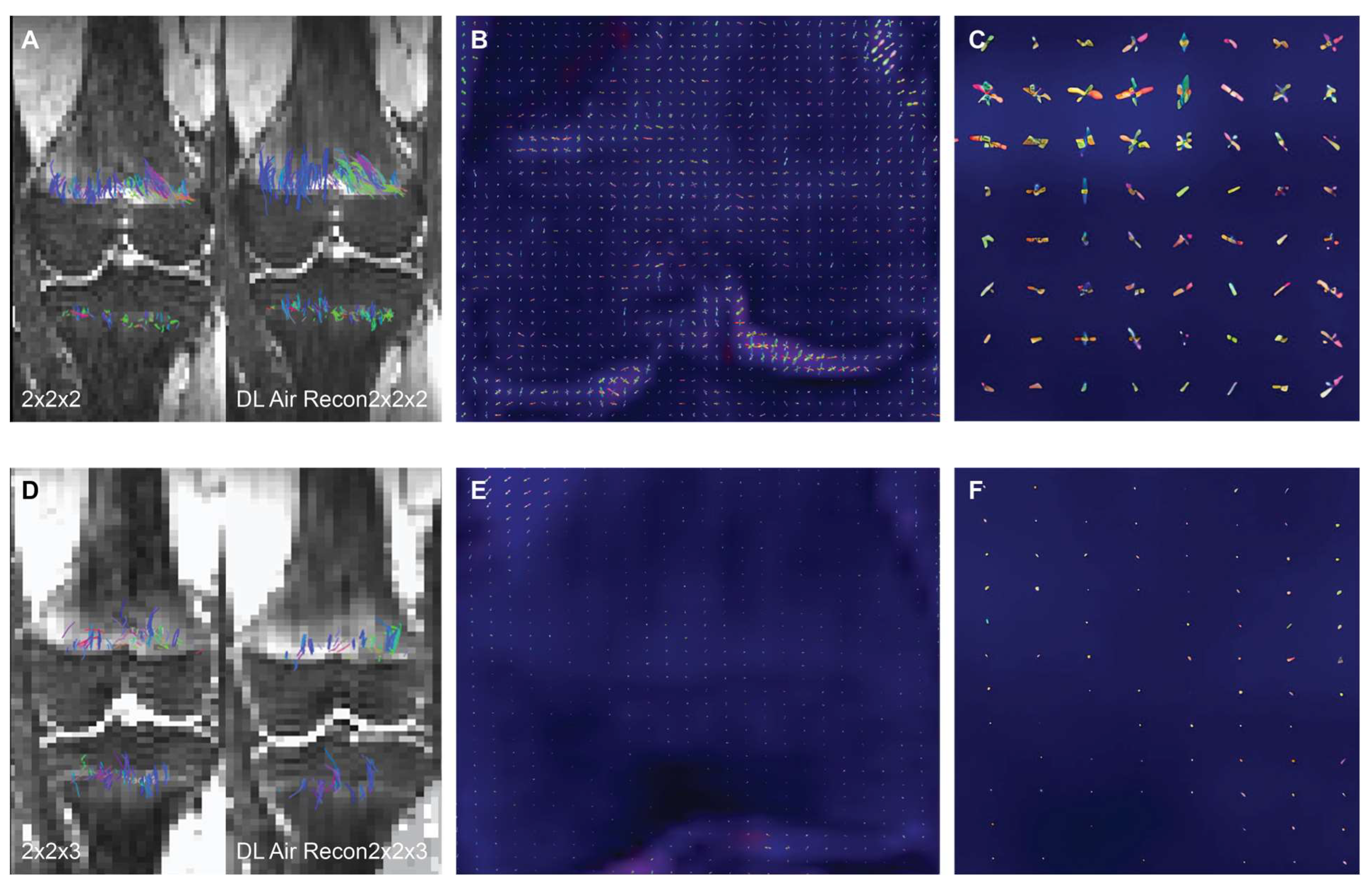
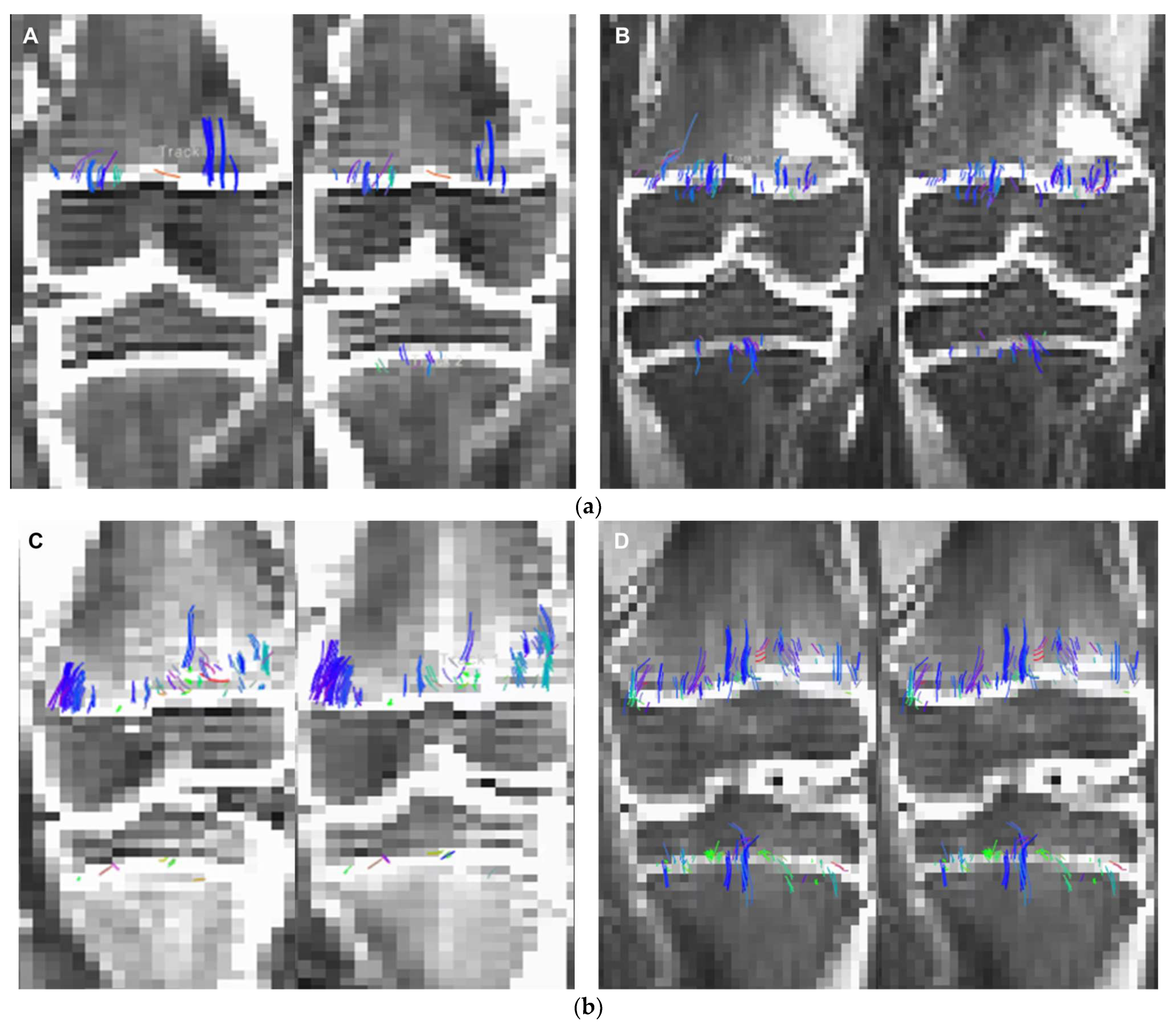
2.3. Intra-Voxel Tensor Visualization at Different Spatial Resolutions
2.4. AIRTM Recon DL Algorithm (GE Healthcare, Waukesha, WI)
2.5. Segmentation
2.6. Signal-to-Noise Ratio Measurements
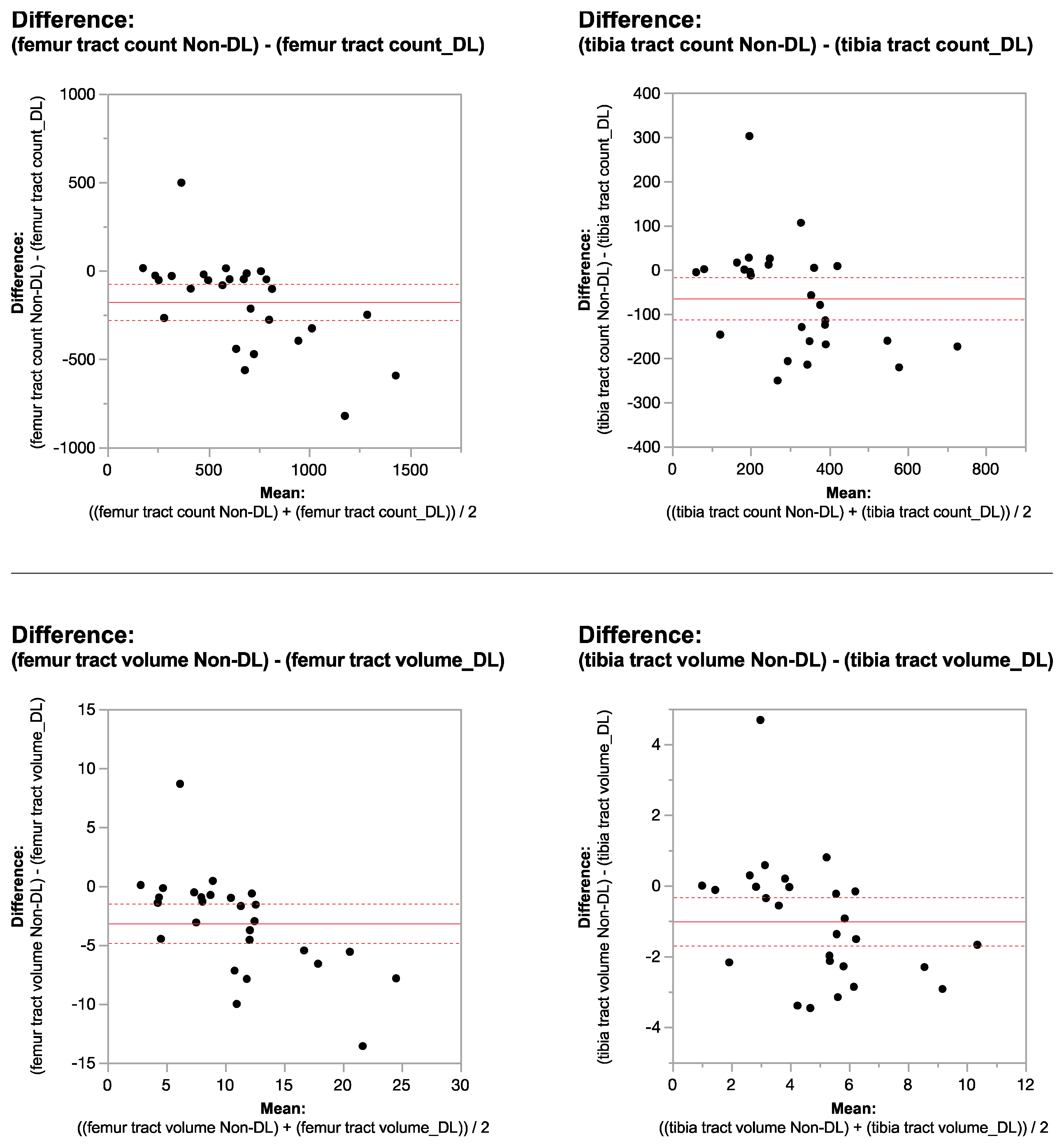
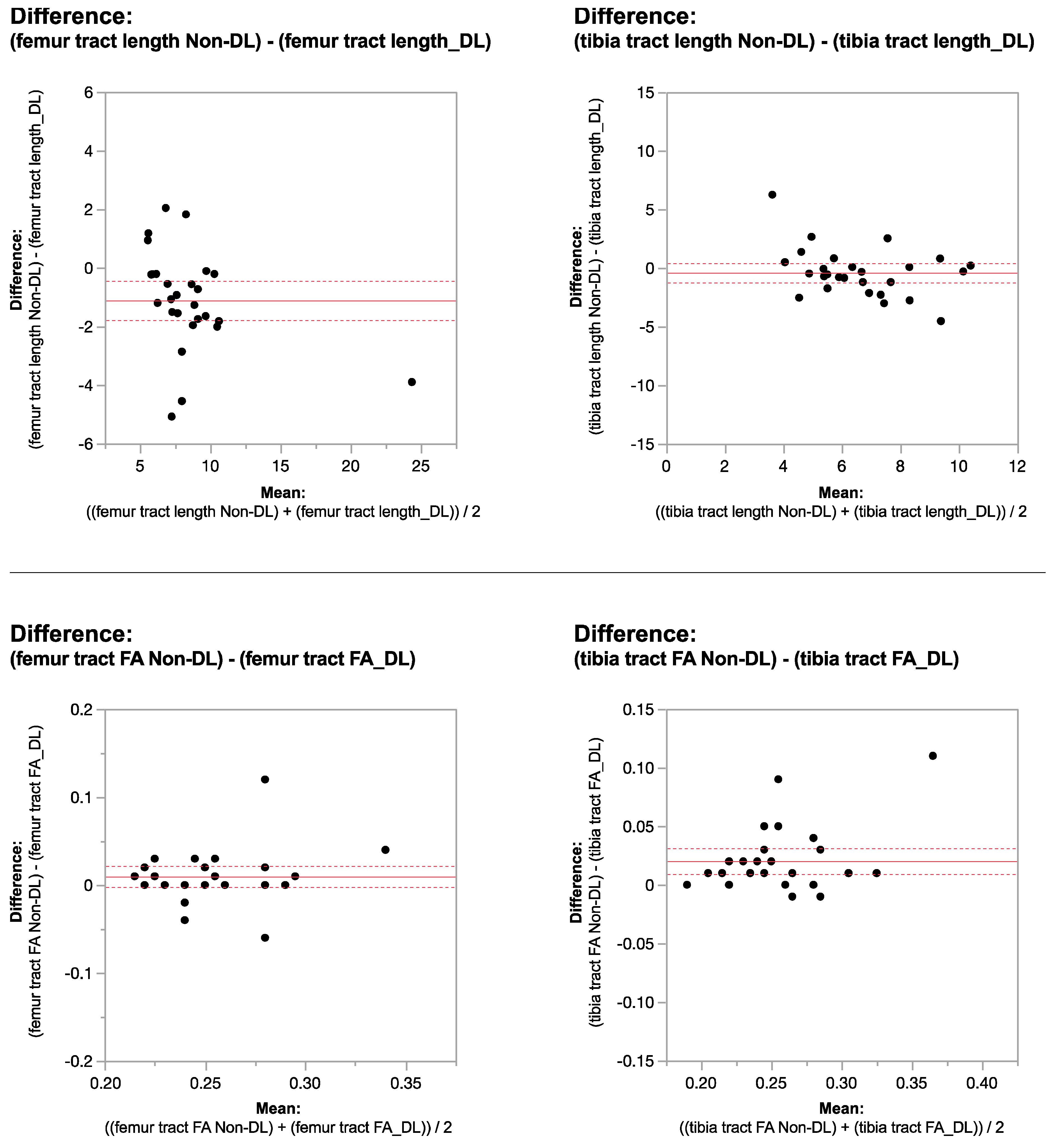
2.7. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soares, J.M.; Marques, P.; Alves, V.; Sousa, N. A Hitchhiker’s Guide to Diffusion Tensor Imaging. Front. Neurosci. 2013, 7, 31. [Google Scholar] [CrossRef] [PubMed]
- Ranzenberger, L.R.; Das, M.; Snyder, T. Diffusion Tensor Imaging. In StatPearls 2023, November 12; StatPearls Publishing: Treasure Island, FL, USA, 2024. [Google Scholar]
- Chen, Q.; Abrigo, J.; Deng, M.; Shi, L.; Wang, Y.X.; Chu, W.C.W. Alzheimer’s Disease Neuroimaging Initiative. Diffusion Changes in Hippocampal Cingulum in Early Biologically Defined Alzheimer’s Disease. J. Alzheimer’s Dis. 2023, 91, 1007–1017. [Google Scholar] [CrossRef] [PubMed]
- Alexander, A.L.; Lee, J.E.; Lazar, M.; Field, A.S. Diffusion Tensor Imaging of the Brain. Neurotherapeutics 2007, 4, 316–329. [Google Scholar] [CrossRef] [PubMed]
- Vedantam, A.; Jirjis, M.B.; Schmit, B.D.; Wang, M.C.; Ulmer, J.L.; Kurpad, S.N. Diffusion Tensor Imaging of the Spinal Cord: Insights from Animal and Human Studies. Neurosurgery 2014, 74, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Jambawalikar, S.; Baum, J.; Button, T.; Li, H.; Geronimo, V.; Gould, E.S. Diffusion Tensor Imaging of Peripheral Nerves. Skelet. Radiol. 2010, 39, 1073–1079. [Google Scholar] [CrossRef] [PubMed]
- Jaimes, C.; Berman, J.I.; Delgado, J.; Ho-Fung, V.; Jaramillo, D. Diffusion-Tensor Imaging of the Growing Ends of Long Bones: Pilot Demonstration of Columnar Structure in the Physes and Metaphyses of the Knee. Radiology 2014, 273, 491–501. [Google Scholar] [CrossRef] [PubMed]
- Kvist, O.; Damberg, P.; Dou, Z.; Berglund, J.S.; Flodmark, C.E.; Nilsson, O.; Diaz, S. Magnetic Resonance and Diffusion Tensor Imaging of the Adolescent Rabbit Growth Plate of the Knee. Magn. Reson. Med. 2023, 89, 331–342. [Google Scholar] [CrossRef] [PubMed]
- Bedoya, M.A.; Delgado, J.; Berman, J.I.; Chauvin, N.A.; Zurakowski, D.; Ramirez-Grueso, R.; Ntoulia, A.; Jaramillo, D. Diffusion-Tensor Imaging of the Physes: A Possible Biomarker for Skeletal Growth-Experience with 151 Children. Radiology 2017, 284, 210–218. [Google Scholar] [CrossRef]
- Delgado, J.; Jaramillo, D.; Chauvin, N.A.; Chauvin, N.A.; Zurakowski, D.; Ramirez-Grueso, R.; Ntoulia, A.; Jaramillo, D. Evaluating Growth Failure with Diffusion Tensor Imaging in Pediatric Survivors of High-Risk Neuroblastoma Treated with High-Dose cis-Retinoic Acid. Pediatr. Radiol. 2019, 49, 1056–1065. [Google Scholar] [CrossRef]
- Duong, P.; Mostoufi-Moab, S.; Raya, J.G.; Jaimes, C.; Delgado, J.; Jaramillo, D. Imaging Biomarkers of the Physis: Cartilage Volume on MRI vs. Tract Volume and Length on Diffusion Tensor Imaging. J. Magn. Reson. Imaging 2020, 52, 544–551. [Google Scholar] [CrossRef]
- Barrera, C.A.; Bedoya, M.A.; Delgado, J.; Berman, J.I.; Chauvin, N.A.; Edgar, J.C. Correlation between Diffusion Tensor Imaging Parameters of the Distal Femoral Physis and Adjacent Metaphysis, and Subsequent Adolescent Growth. Pediatr. Radiol. 2019, 49, 1192–1200. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo, D.; Duong, P.; Nguyen, J.C.; Mostoufi-Moab, S.; Nguyen, M.K.; Moreau, A.; Barrera, C.A.; Hong, S.; Raya, J.G. Diffusion Tensor Imaging of the Knee to Predict Childhood Growth. Radiology 2022, 303, 655–663. [Google Scholar] [CrossRef] [PubMed]
- Tian, Q.; Li, Z.; Fan, Q.; Polimeni, J.R.; Bilgic, B.; Salat, D.H.; Huang, S.Y. SDnDTI: Self-supervised Deep Learning-based Denoising for Diffusion Tensor MRI. Neuroimage 2022, 253, 119033. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Fei, L.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.W. Deep Learning on Image Denoising: An Overview. Neural Netw. 2020, 131, 251–275. [Google Scholar] [CrossRef] [PubMed]
- Tian, Q.; Bilgic, B.; Fan, Q.; Liao, C.; Ngamsombat, C.; Hu, Y.; Witzel, T.; Setsompop, K.; Polimeni, J.R.; Huang, S.Y. DeepDTI: High-fidelity Six-direction Diffusion Tensor Imaging using Deep Learning. Neuroimage 2020, 219, 117017. [Google Scholar] [CrossRef] [PubMed]
- Vidyadharan, S.; Prabhakar Rao, B.V.V.S.N.; Perumal, Y.; Chandrasekharan, K.; Rajagopalan, V. Deep Learning Classifies Low- and High-Grade Glioma Patients with High Accuracy, Sensitivity, and Specificity Based on Their Brain White Matter Networks Derived from Diffusion Tensor Imaging. Diagnostics 2022, 12, 3216. [Google Scholar] [CrossRef] [PubMed]
- Sneag, D.B.; Zochowski, K.C.; Tan, E.T.; Queler, S.C.; Burge, A.; Endo, Y.; Lin, B.; Fung, M.; Shin, J. Denoising of Diffusion MRI Improves Peripheral Nerve Conspicuity and Reproducibility. J. Magn. Reson. Imaging 2020, 51, 1128–1137. [Google Scholar] [CrossRef] [PubMed]
- Charles, J.P.; Grant, B.; D’Août, K.; Bates, K.T. Subject-specific Muscle Properties from Diffusion Tensor Imaging Significantly Improve the Accuracy of Musculoskeletal Models. J. Anat. 2020, 237, 941–959. [Google Scholar] [CrossRef] [PubMed]
- Malis, V.; Sinha, U.; Csapo, R.; Narici, M.; Smitaman, E.; Sinha, S. Diffusion Tensor Imaging and Diffusion Modeling: Application to Monitoring Changes in the Medial Gastrocnemius in Disuse Atrophy Induced by Unilateral Limb Suspension. J. Magn. Reson. Imaging 2019, 49, 1655–1664. [Google Scholar] [CrossRef]
- Mazzoli, V.; Moulin, K.; Kogan, F.; Hargreaves, B.A.; Gold, G.E. Diffusion Tensor Imaging of Skeletal Muscle Contraction Using Oscillating Gradient Spin Echo. Front. Neurol. 2021, 12, 608549. [Google Scholar] [CrossRef]
- Zhao, Q.; Ridout, R.P.; Shen, J.; Wang, N. Effects of Angular Resolution and b Value on Diffusion Tensor Imaging in Knee Joint. Cartilage 2021, 13 (Suppl. S2), 295S–303S. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Mirando, A.J.; Cofer, G.; Qi, Y.; Hilton, M.J.; Johnson, G.A. Characterization complex collagen fiber architecture in knee joint using high-resolution diffusion imaging. Magn. Reson. Med. 2020, 84, 908–919. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Mirando, A.J.; Cofer, G.; Qi, Y.; Hilton, M.J.; Johnson, G.A. Diffusion tractography of the rat knee at microscopic resolution. Magn. Reson. Med. 2019, 81, 3775–3786. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, P.; Chung, S.W.; Berman, J.I.; Hess, C.P.; Henry, R.G. Diffusion Tensor MR Imaging and Fiber Tractography: Technical Considerations. AJNR Am. J. Neuroradiol. 2008, 29, 843–852. [Google Scholar] [CrossRef] [PubMed]
- Tournier, J.D.; Smith, R.; Raffelt, D.; Tabbara, R.; Dhollander, T.; Pietsch, M.; Christiaens, D.; Jeurissen, B.; Yeh, C.-H.; Connelly, A. MRtrix3: A Fast, Flexible and Open Software Framework for Medical Image Processing and Visualisation. Neuroimage 2019, 202, 116137. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, L.J.; Westin, C.F. An Introduction to Diffusion Tensor Image Analysis. Neurosurg. Clin. N. Am. 2011, 22, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Dhollander, T.; Raffelt, D.; Connelly, A. Unsupervised 3-tissue Response Function Estimation from Single-shell or Multi-shell Diffusion MR Data without a Co-registered T1 Image. In Proceedings of the ISMRM Workshop on Breaking the Barriers of Diffusion MRI, Lisbon, Portugal, 11–16 September 2016. [Google Scholar]
- Tournier, J.D.; Calamante, F.; Connelly, A. Robust Determination of the Fibre Orientation Distribution in Diffusion MRI: Non-negativity Constrained Super-resolved Spherical Deconvolution. Neuroimage 2007, 35, 1459–1472. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.J.; Yamamura, J.; Keller, S. Signal-to-noise Ratio Assessment of Muscle Diffusion Tensor Imaging using Single Image Set and Validation by the Difference Image Method. Br. J. Radiol. 2019, 92, 20190133. [Google Scholar] [CrossRef] [PubMed]
- Mulder, M.J.; Keuken, M.C.; Bazin, P.L.; Alkemade, A.; Forstmann, B.U. Size and shape matter: The impact of voxel geometry on the identification of small nuclei. PLoS ONE 2019, 14, e0215382. [Google Scholar] [CrossRef]
- Kaplan, P.E. Fractional Anisotropy. In Encyclopedia of Clinical Neuropsychology; Kreutzer, J.S., DeLuca, J., Caplan, B., Eds.; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Gattu, R.; Latif, Z.; Kou, Z.; Haacke, E.M.; Benson, R.R. Effect of Voxel Size on DTI Fractional Anisotropy. Proc. Intl. Soc. Mag. Reson. Med. 2009, 17, 3578. Available online: https://archive.ismrm.org/2009/3579.html (accessed on 21 June 2023).
- St-Jean, S.; Coupé, P.; Descoteaux, M. Non Local Spatial and Angular Matching: Enabling higher spatial resolution diffusion MRI datasets through adaptive denoising. Med. Image Anal. 2016, 32, 115–130. [Google Scholar] [CrossRef] [PubMed]
- Seo, Y.; Rollins, N.K.; Wang, Z.J. Reduction of Bias in the Evaluation of Fractional Anisotropy and Mean Diffusivity in Magnetic Resonance Diffusion Tensor Imaging Using Region-of-Interest Methodology. Sci. Rep. 2019, 9, 13095. [Google Scholar] [CrossRef] [PubMed]
- Sagawa, H.; Fushimi, Y.; Nakajima, S.; Fujimoto, K.; Miyake, K.K.; Numamoto, H.; Koizumi, K.; Nambu, M.; Kataoka, H.; Nakamoto, Y.; et al. Deep Learning-based Noise Reduction for Fast Volume Diffusion Tensor Imaging: Assessing the Noise Reduction Effect and Reliability of Diffusion Metrics. Magn. Reson. Med. Sci. 2021, 20, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Froeling, M.; Nederveen, A.J.; Nicolay, K.; Strijkers, G.J. DTI of Human Skeletal Muscle: The Effects of Diffusion Encoding Parameters, Signal-to-noise Ratio and T2 on Tensor Indices and Fiber Tracts. NMR Biomed. 2013, 26, 1339–1352. [Google Scholar] [CrossRef] [PubMed]


| DTI METRIC | AIr Recon DL | AIr Recon DL | p-Value |
|---|---|---|---|
| Isovolumetric 2 mm3 | 2 mm × 2 mm × 3 mm | ||
| femur tract count | 753.03 ± 409.17 | 410.37 ± 308.29 | <0.0001 * |
| femur tract volume | 12.47 ± 7.05 | 9.52 ± 7.17 | <0.0006 * |
| femur tract length | 8.83 ± 2.48 | 9.07 ± 3.93 | 0.9 |
| femur FA | 0.29 ± 0.04 | 0.25 ± 0.02 | <0.0001 * |
| tibia tract count | 341.62 ± 187.3 | 137.44 ± 177.31 | <0.0001 * |
| tibia tract volume | 5.34 ± 2.7 | 4.50 ± 8.36 | 0.0005 * |
| tibia tract length | 5.36 ± 0.84 | 6.81 ± 2.42 | 0.002 * |
| tibia FA | 0.34 ± 0.05 | 0.24 ± 0.03 | <0.0001 * |
| DTI METRIC | Raw Data | Raw Data | p-Value |
|---|---|---|---|
| Isovolumetric 2 mm3 | 2 mm × 2 mm × 3 mm | ||
| femur tract count | 576.85 ± 257.21 | 388.62 ± 274.57 | <0.0001 * |
| femur tract volume | 9.3 ± 4.45 | 9.03 ± 6.4 | 0.13 |
| femur tract length | 6.11 ± 1.39 | 7.96 ± 3.25 | 0.001 * |
| femur FA | 0.31 ± 0.04 | 0.26 ± 0.03 | 0.0001 * |
| tibia tract count | 277.22 ± 133.89 | 123.44 ± 112.03 | 0.0001 * |
| tibia tract volume | 4.33 ± 1.99 | 2.74 ± 2.2 | 0.0001 * |
| tibia tract length | 4.26 ± 0.62 | 6.43 ± 1.75 | 0.0001 * |
| tibia FA | 0.36 ± 0.06 | 0.26 ± 0.04 | 0.0001 * |
| DTI METRIC | Raw Data | AIr Recon DL | p-Value |
|---|---|---|---|
| Isovolumetric 2 mm3 | Isovolumetric 2 mm3 | ||
| femur tract count | 576.85 | 753.03 | <0.0001 * |
| femur tract volume | 9.3 | 12.47 | <0.0001 * |
| femur tract length | 6.11 | 8.83 | <0.0001 * |
| femur FA | 0.31 | 0.29 | <0.0001 * |
| tibia tract count | 277.22 | 341.62 | 0.013 * |
| tibia tract volume | 4.33 | 5.34 | 0.001 * |
| tibia tract length | 4.26 | 5.36 | <0.0001 * |
| tibia FA | 0.36 | 0.34 | 0.005 * |
| DTI METRIC | Raw Data | AIr Recon DL | p-Value |
|---|---|---|---|
| 2 mm × 2 mm × 3 mm | 2 mm × 2 mm × 3 mm | ||
| femur tract count | 388.62 | 410.37 | 0.1 |
| femur tract volume | 9.03 | 9.52 | 0.14 |
| femur tract length | 7.96 | 9.07 | 0.001 * |
| femur FA | 0.26 | 0.25 | 0.017 * |
| tibia tract count | 123.44 | 137.44 | 0.14 |
| tibia tract volume | 2.74 | 4.5 | 0.29 |
| tibia tract length | 6.43 | 6.81 | 0.16 |
| tibia FA | 0.26 | 0.24 | <0.0001 * |
| Voxel Size Comparison of ROI SNRs for b0 and b600 DTI with and without DL | |||
|---|---|---|---|
| 2 mm3 | DL | Non-DL | p-value |
| femur_b0 | 44.2 | 31.7 | <0.0001 * |
| femur_b600 | 18.9 | 13.7 | <0.0001 * |
| tibia_b0 | 36.4 | 25.8 | <0.0001 * |
| tibia_b600 | 16.6 | 11.9 | <0.0001 * |
| 2 mm × 2 mm × 3 mm | DL | Non-DL | p-value |
| femur_b0 | 67.1 | 49.0 | <0.0001 * |
| femur_b600 | 29.6 | 20.9 | <0.0001 * |
| tibia_b0 | 54.1 | 39.3 | <0.0001 * |
| tibia_b600 | 25.4 | 17.9 | <0.0001 * |
| SNR Increase (Mean Difference SNR/Non-DL SNR) | 2 mm3 | 2 mm × 2 mm × 3 mm |
|---|---|---|
| femur_b0 | 0.39 | 0.37 |
| tibia_b0 | 0.41 | 0.38 |
| femur_b600 | 0.39 | 0.42 |
| tibia_b600 | 0.4 | 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, L.; Hsu, H.-Y.; Nelson, R.R., Jr.; Sullivan, B.; Shin, J.; Fung, M.; Lebel, M.R.; Jambawalikar, S.; Jaramillo, D. Impact of Deep Learning Denoising Algorithm on Diffusion Tensor Imaging of the Growth Plate on Different Spatial Resolutions. Tomography 2024, 10, 504-519. https://doi.org/10.3390/tomography10040039
Santos L, Hsu H-Y, Nelson RR Jr., Sullivan B, Shin J, Fung M, Lebel MR, Jambawalikar S, Jaramillo D. Impact of Deep Learning Denoising Algorithm on Diffusion Tensor Imaging of the Growth Plate on Different Spatial Resolutions. Tomography. 2024; 10(4):504-519. https://doi.org/10.3390/tomography10040039
Chicago/Turabian StyleSantos, Laura, Hao-Yun Hsu, Ronald R. Nelson, Jr., Brendan Sullivan, Jaemin Shin, Maggie Fung, Marc R. Lebel, Sachin Jambawalikar, and Diego Jaramillo. 2024. "Impact of Deep Learning Denoising Algorithm on Diffusion Tensor Imaging of the Growth Plate on Different Spatial Resolutions" Tomography 10, no. 4: 504-519. https://doi.org/10.3390/tomography10040039
APA StyleSantos, L., Hsu, H.-Y., Nelson, R. R., Jr., Sullivan, B., Shin, J., Fung, M., Lebel, M. R., Jambawalikar, S., & Jaramillo, D. (2024). Impact of Deep Learning Denoising Algorithm on Diffusion Tensor Imaging of the Growth Plate on Different Spatial Resolutions. Tomography, 10(4), 504-519. https://doi.org/10.3390/tomography10040039








