Explainable Ensemble Learning and Multilayer Perceptron Modeling for Compressive Strength Prediction of Ultra-High-Performance Concrete
Abstract
1. Introduction
2. Materials and Methods
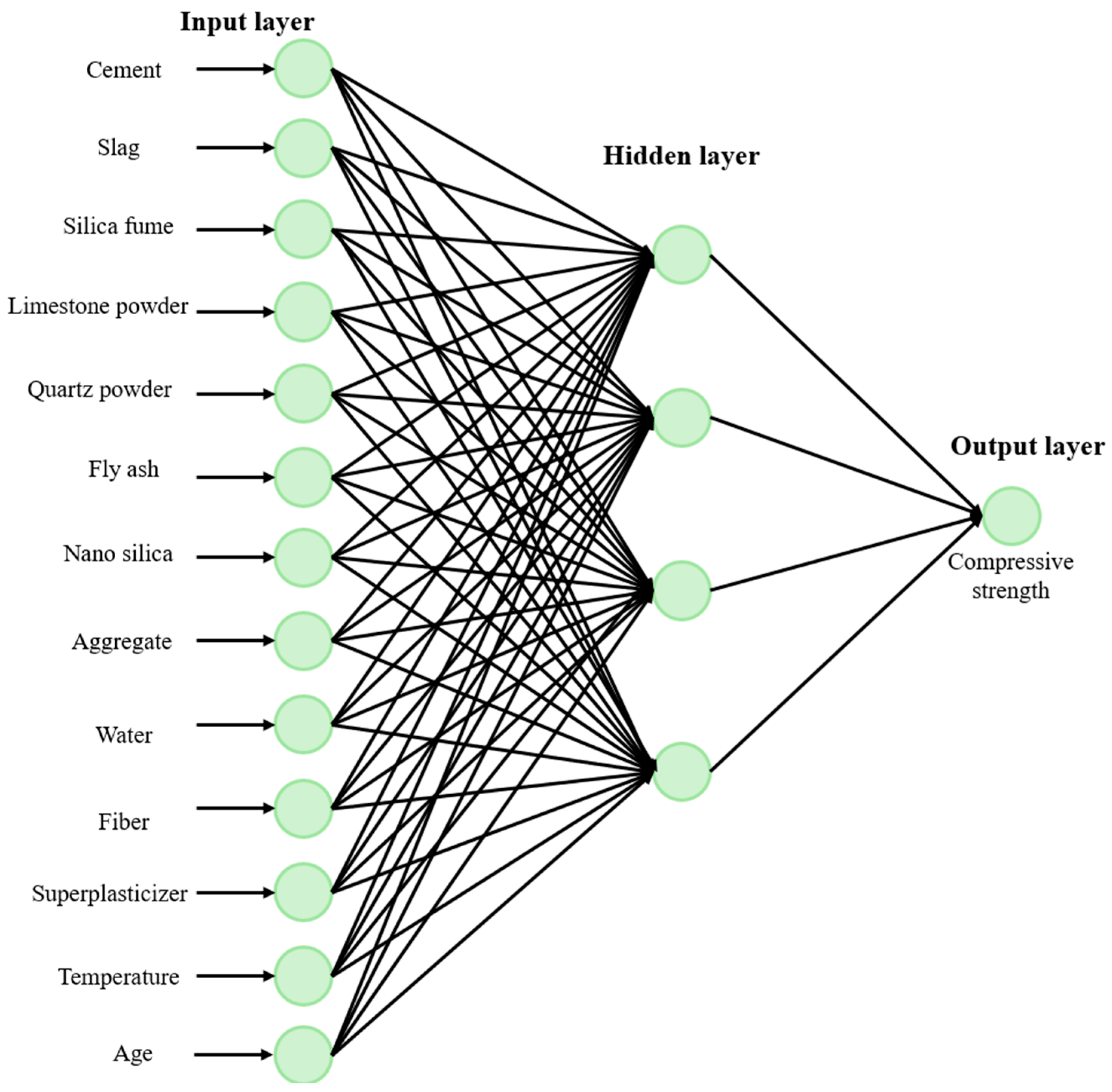
2.1. Multilayer Perceptron (MLP)
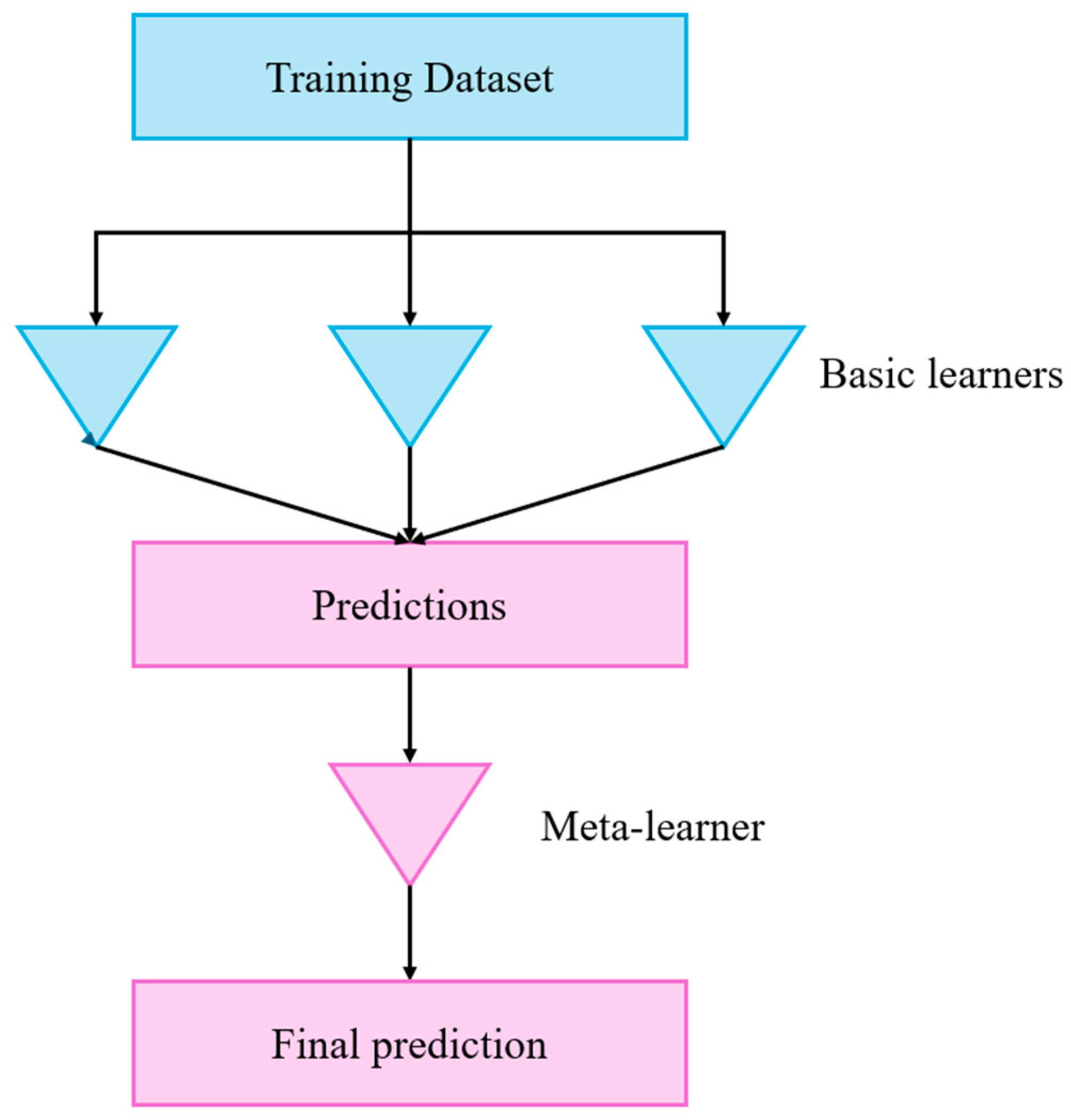
2.2. Stacking
2.3. Extreme Gradient Boosting (XGBoost)
2.4. Category Boosting (CatBoost)
2.5. Light Gradient Boosting Machine (LightGBM)
2.6. Extra Trees
2.7. Dataset Description
2.8. Performance Evaluation
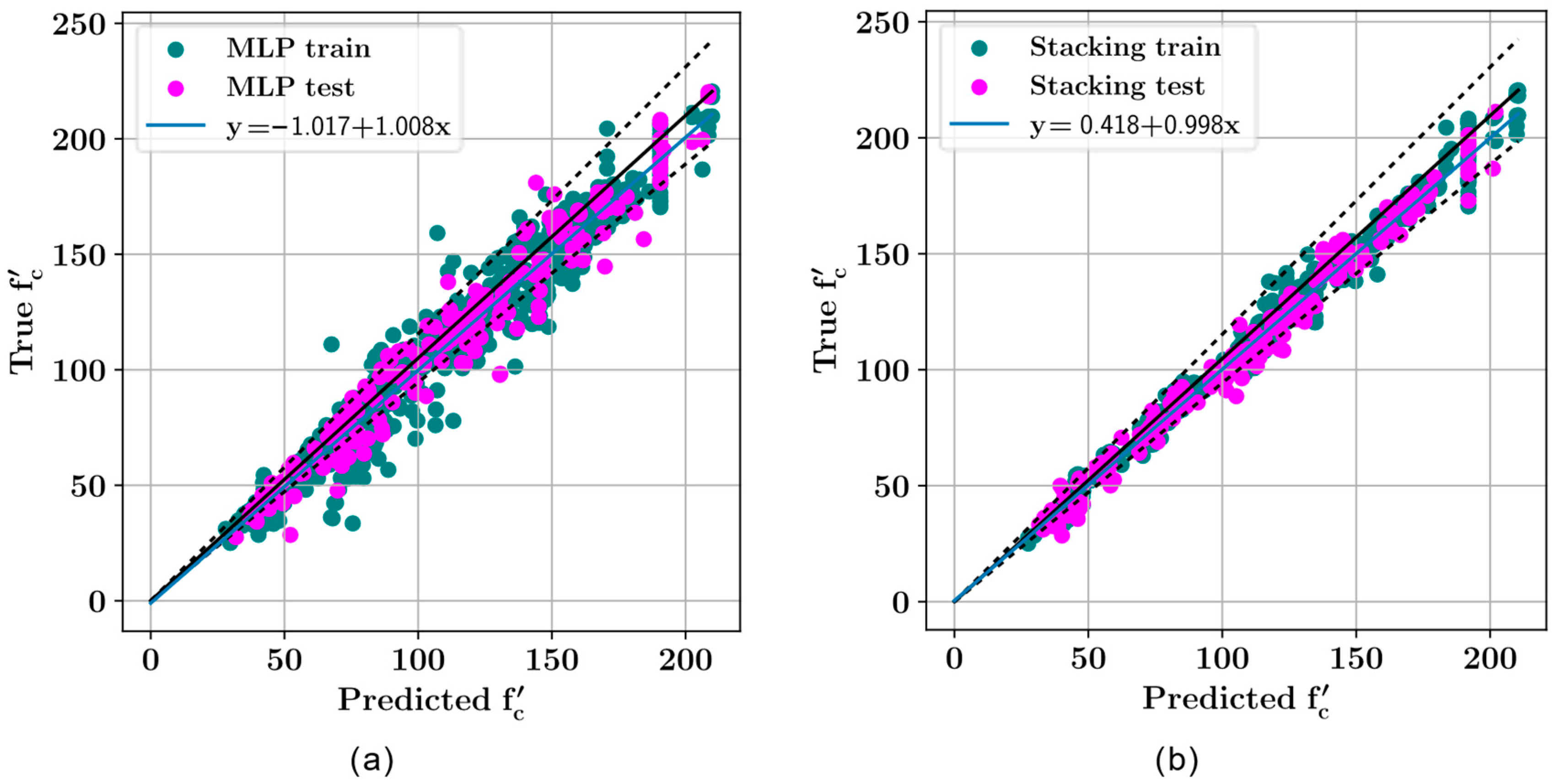
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Aluminium Association. Aluminium in Cars. In 2006: Sustainability of the European Aluminium Industry; European Aluminium Association: Brussels, Switzerland, 2006. [Google Scholar]
- Barr, A.E.; Lohmann Siegel, K.; Danoff, J.V.; McGarvey, C.L., III; Tomasko, A.; Sable, I.; Stanhope, S.J. Biomechanical comparison of the energy-storing capabilities of SACH and Carbon Copy II prosthetic feet during the stance phase of gait in a person with below-knee amputation. Phys. Ther. 1992, 72, 344–354. [Google Scholar] [CrossRef] [PubMed]
- Richard, P.; Cheyrezy, M. Composition of reactive powder concretes. Cem. Concr. Res. 1995, 25, 1501–1511. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C.; Wu, Z. Hardening, microstructure, and shrinkage development of UHPC: A review. J. Asian Concr. Fed. 2019, 5, 1–19. [Google Scholar] [CrossRef]
- Nilsson, L. Development of UHPC Concrete Using Mostly Locally Available Raw Materials. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2018. [Google Scholar]
- Holbrook, G. Hämtat från ASCE Pittsburgh Section. Available online: https://www.asce-pgh.org/ (accessed on 25 January 2018).
- Nematollahi, B.; Saifulnaz, M.R.; Jaafar, S.; Voo, Y.L. A review on ultra high performance ‘ductile’ concrete (UHPdC) technology. Int. J. Civ. Struct. Eng. 2012, 2, 1003–1018. [Google Scholar] [CrossRef]
- Matte, V.; Richet, C.; Moranville, M.; Torrenti, J.M. Characterization of reactive powder concrete as a candidate for the storage of nuclear wastes. In Symposium on High-Performance and Reactive Powder Concretes; Kassel University Press: Kassel, Germany, 1998; pp. 75–88. [Google Scholar]
- Kocataşkın, F. Composition of High Strength Concrete, 2nd ed.; Bet. Congress, High Strength Concrete; Kardeşler Printing House: Istanbul, Turkey, 1991; pp. 211–226, (TMMOB Chamber of Civil Engineers). [Google Scholar]
- Huiskes, R.; van Rietbergen, B. Biomechanics of bone. Basic Orthop. Biomech. Mechano-Biol. 2005, 3, 123–179. [Google Scholar]
- Turner, C.H.; Burr, D.B. Basic biomechanical measurements of bone: A tutorial. Bone 1993, 14, 595–608. [Google Scholar] [CrossRef]
- Rincón-Kohli, L.; Zysset, P.K. Multi-axial mechanical properties of human trabecular bone. Biomech. Model. Mechanobiol. 2009, 8, 195–208. [Google Scholar] [CrossRef]
- Yuvaraj, P.; Murthy, A.R.; Iyer, N.R.; Samui, P.; Sekar, S.K. Prediction of fracture characteristics of high strength and ultra high strength concrete beams based on relevance vector machine. Int. J. Damage Mech. 2014, 23, 979–1004. [Google Scholar] [CrossRef]
- Marani, A.; Jamali, A.; Nehdi, M.L. Predicting ultra-high-performance concrete compressive strength using tabular generative adversarial networks. Materials 2020, 13, 4757. [Google Scholar] [CrossRef]
- Solhmirzaei, R.; Salehi, H.; Kodur, V.; Naser, M.Z. Machine learning framework for predicting failure mode and shear capacity of ultra high performance concrete beams. Eng. Struct. 2020, 224, 111221. [Google Scholar] [CrossRef]
- Jiang, C.S.; Liang, G.Q. Modeling shear strength of medium-to ultra-high-strength concrete beams with stirrups using SVR and genetic algorithm. Soft Comput. 2021, 25, 10661–10675. [Google Scholar] [CrossRef]
- Kumar, A.; Arora, H.C.; Kapoor, N.R.; Mohammed, M.A.; Kumar, K.; Majumdar, A.; Thinnukool, O. Compressive Strength Prediction of Lightweight Concrete: Machine Learning Models. Sustainability 2022, 14, 2404. [Google Scholar] [CrossRef]
- Shen, Z.; Deifalla, A.F.; Kamiński, P.; Dyczko, A. Compressive strength evaluation of ultra-high-strength concrete by machine learning. Materials 2022, 15, 3523. [Google Scholar] [CrossRef] [PubMed]
- Liu, B. Estimating the ultra-high-performance concrete compressive strength with a machine learning model via meta-heuristic algorithms. Multiscale Multidiscip. Model. Exp. Des. 2023, 7, 1807–1818. [Google Scholar] [CrossRef]
- Hiew, S.Y.; Teoh, K.B.; Raman, S.N.; Kong, D.; Hafezolghorani, M. Prediction of ultimate conditions and stress–strain behaviour of steel-confined ultra-high-performance concrete using sequential deep feed-forward neural network modelling strategy. Eng. Struct. 2023, 277, 115447. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, X.; Luo, Y.; Jia, Y.; Wang, C.; Fang, Z.; Zhuang, X.; Zhou, S. Prediction of early compressive strength of ultrahigh-performance concrete using machine learning methods. Int. J. Comput. Methods 2023, 20, 2141023. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Nguyen, T.A.; Ly, H.B. Ensemble XGBoost schemes for improved compressive strength prediction of UHPC. Structures 2023, 57, 105062. [Google Scholar] [CrossRef]
- Gong, N.; Zhang, N. Predict the compressive strength of ultra high-performance concrete by a hybrid method of machine learning. J. Eng. Appl. Sci. 2023, 70, 107. [Google Scholar] [CrossRef]
- Ye, M.; Li, L.; Yoo, D.Y.; Li, H.; Zhou, C.; Shao, X. Prediction of shear strength in UHPC beams using machine learning-based models and SHAP interpretation. Constr. Build. Mater. 2023, 408, 133752. [Google Scholar] [CrossRef]
- Zhang, Y.; An, S.; Liu, H. Employing the optimization algorithms with machine learning framework to estimate the compressive strength of ultra-high-performance concrete (UHPC). Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 97–108. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Abellán-García, J.; Lee, S.; Vo, T.P. From machine learning to semi-empirical formulas for estimating compressive strength of Ultra-High Performance Concrete. Expert Syst. Appl. 2024, 237, 121456. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Ren, C.; Wang, L.; Ning, X. Predicting the Compressive Strength of Ultra-High-Performance Concrete Based on Machine Learning Optimized by Meta-Heuristic Algorithm. Buildings 2024, 14, 1209. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Alam, M.S. Performance-based seismic design of Ultra-High-Performance Concrete (UHPC) bridge columns with design example–Powered by explainable machine learning model. Eng. Struct. 2024, 314, 118346. [Google Scholar] [CrossRef]
- Zhu, P.; Cao, W.; Zhang, L.; Zhou, Y.; Wu, Y.; Ma, Z.J. Interpretable Machine Learning Models for Prediction of UHPC Creep Behavior. Buildings 2024, 14, 2080. [Google Scholar] [CrossRef]
- Das, P.; Kashem, A. Hybrid machine learning approach to prediction of the compressive and flexural strengths of UHPC and parametric analysis with shapley additive explanations. Case Stud. Constr. Mater. 2024, 20, e02723. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media Inc.: Sebastopol, CA, USA, 2022. [Google Scholar]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends® Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef]
- Car, Z.; Baressi Šegota, S.; Anđelić, N.; Lorencin, I.; Mrzljak, V. Modeling the spread of COVID-19 infection using a multilayer perceptron. Comput. Math. Methods Med. 2020, 1, 5714714. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S. An efficient hybrid multilayer perceptron neural network with grasshopper optimization. Soft Comput. 2019, 23, 7941–7958. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J.; Data, M. Practical machine learning tools and techniques. In Data Mining; Elsevier: Amsterdam, The Netherlands, 2005; Volume 2, pp. 403–413. [Google Scholar]
- Kumar, A.; Mayank, J. Ensemble Learning for AI Developers; BApress: Berkeley, CA, USA, 2020. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Jabeur, S.B.; Mefteh-Wali, S.; Viviani, J.L. Forecasting gold price with the XGBoost algorithm and SHAP interaction values. Ann. Oper. Res. 2024, 334, 679–699. [Google Scholar] [CrossRef]
- Zhou, F.; Pan, H.; Gao, Z.; Huang, X.; Qian, G.; Zhu, Y.; Xiao, F. Fire prediction based on catboost algorithm. Math. Probl. Eng. 2021, 2021, 1929137. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 3147–3155. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Abul, K.; Rezaul, K.; Chandra, M.S.; Pobithra, D. Ultra-High-Performance Concrete (UHPC), version 1; Mendeley Data. 2023. [Google Scholar] [CrossRef]
- Ünal, A. From Waste to Product Iron-Steel’s Slag. Master’s Thesis, Marmara University, İstanbul, Turkey, 2017. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]









| Mechanical Properties | UHPC |
|---|---|
| Compressive strength (MPa) | 200–800 |
| Elasticity modulus (GPa) | 60–75 |
| Flexural strength (MPa) | 50–140 |
| Fracture energy (J/m2) | 1200–40,000 |
| Variable | Description |
|---|---|
| Cement | A binding material |
| Slag | A by-product of the smelting of metals or ores containing metals, which is a complex of oxides and silicates lighter than the metal and deposited on the surface due to density difference [45]. |
| Silica fume | Micro-sized material that can be used in concrete as mineral admixture and pozzolanic admixture. |
| Limestone powder | A fine powder obtained by pulverizing clay and other materials by heat treatment in a furnace at high temperatures. |
| Quartz powder | A micronized powder made of natural quartz. |
| Fly ash | An artificial pozzolan used as a mineral admixture in concrete. |
| Nano silica | Material consisting of high purity amorphous silica powder. |
| Aggregate | Materials such as sand, gravel, and crushed stone used in concrete production. |
| Water | The higher the water/cement ratio, the lower the concrete strength. |
| Fiber | Improves the properties of concrete. |
| Superplasticizer | Reduces the water/cement ratio of high-performance concrete to provide very high compressive strength. |
| Temperature | Temperature affects the properties of concrete. |
| Age | Time until the concrete reaches sufficient strength. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydın, Y.; Cakiroglu, C.; Bekdaş, G.; Geem, Z.W. Explainable Ensemble Learning and Multilayer Perceptron Modeling for Compressive Strength Prediction of Ultra-High-Performance Concrete. Biomimetics 2024, 9, 544. https://doi.org/10.3390/biomimetics9090544
Aydın Y, Cakiroglu C, Bekdaş G, Geem ZW. Explainable Ensemble Learning and Multilayer Perceptron Modeling for Compressive Strength Prediction of Ultra-High-Performance Concrete. Biomimetics. 2024; 9(9):544. https://doi.org/10.3390/biomimetics9090544
Chicago/Turabian StyleAydın, Yaren, Celal Cakiroglu, Gebrail Bekdaş, and Zong Woo Geem. 2024. "Explainable Ensemble Learning and Multilayer Perceptron Modeling for Compressive Strength Prediction of Ultra-High-Performance Concrete" Biomimetics 9, no. 9: 544. https://doi.org/10.3390/biomimetics9090544
APA StyleAydın, Y., Cakiroglu, C., Bekdaş, G., & Geem, Z. W. (2024). Explainable Ensemble Learning and Multilayer Perceptron Modeling for Compressive Strength Prediction of Ultra-High-Performance Concrete. Biomimetics, 9(9), 544. https://doi.org/10.3390/biomimetics9090544









