Simulation and Controller Design for a Fish Robot with Control Fins
Abstract
1. Introduction
2. Equation of Motion and Dynamics of Fins
2.1. Equation of Motion
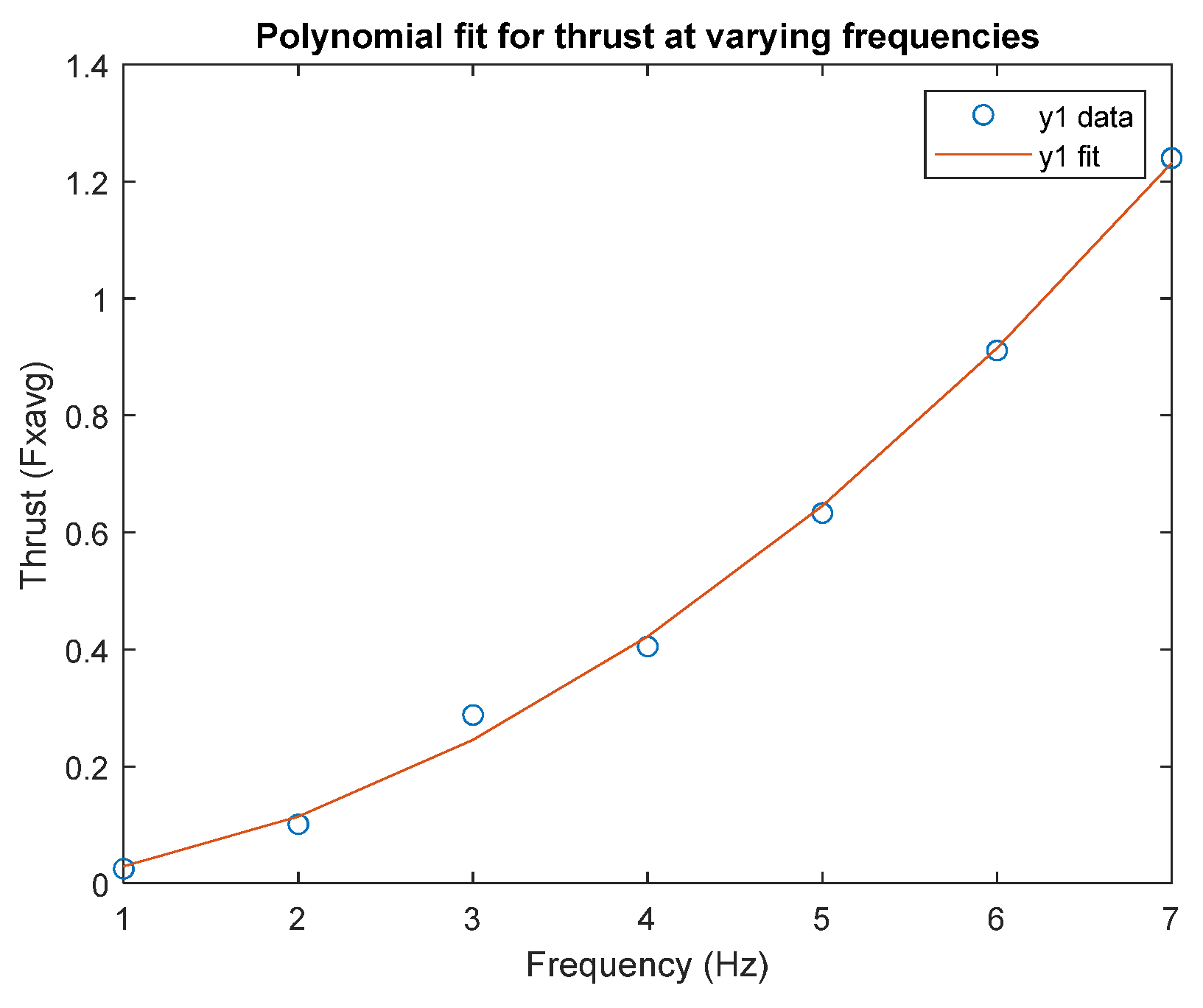
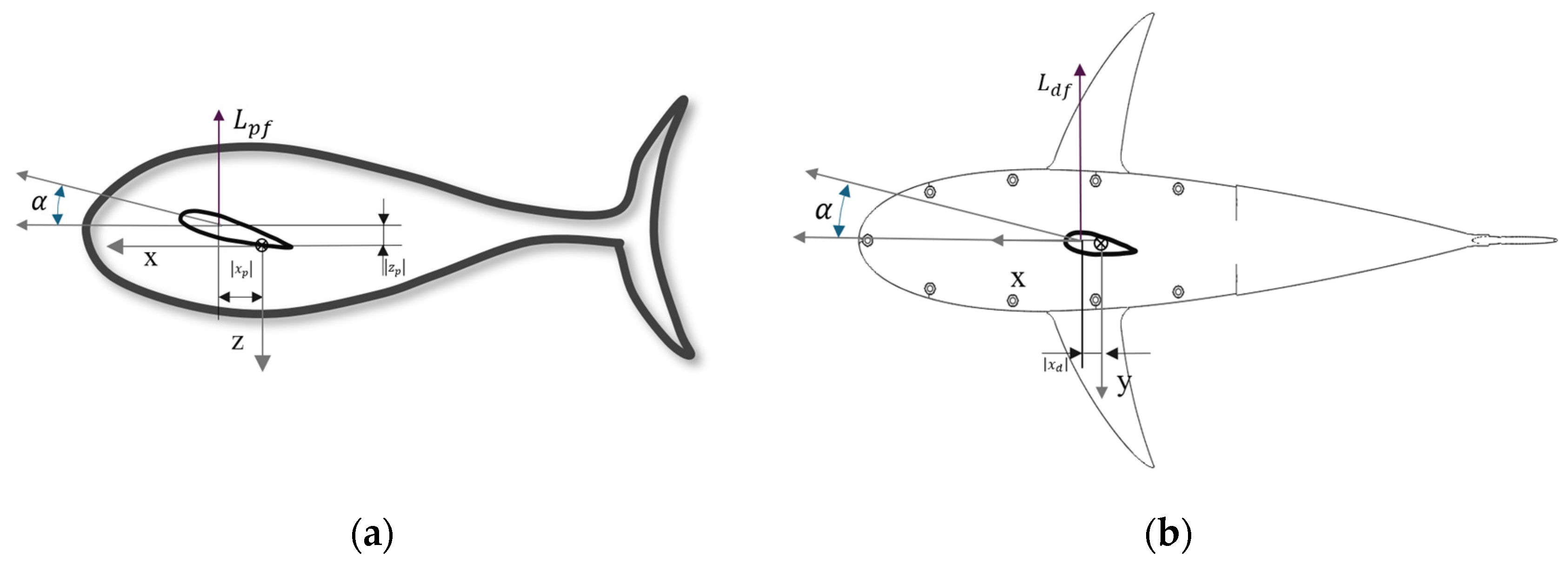
2.2. Forces and Moments Due to Control Fins
3. Simulation and Controller Design Results
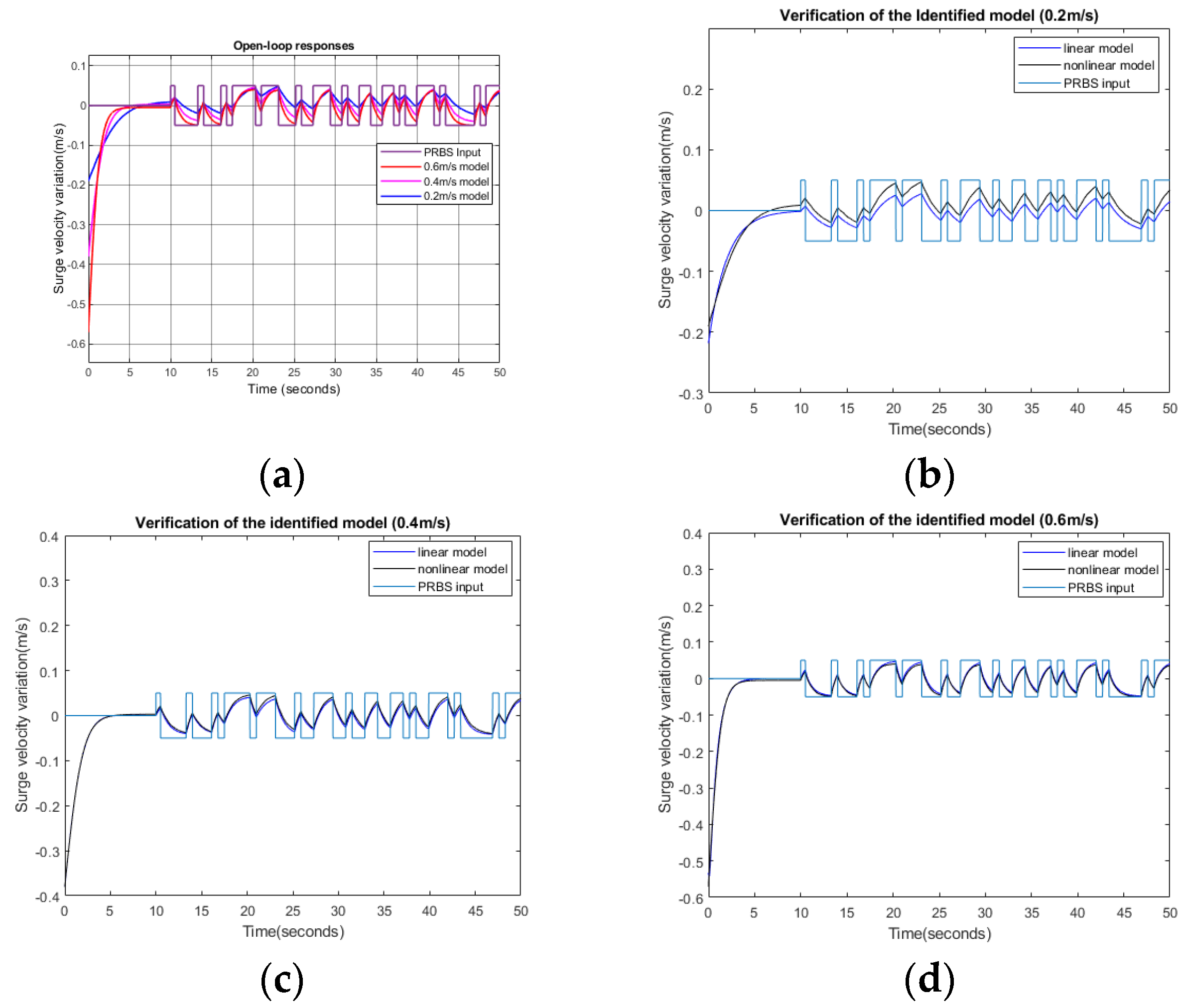
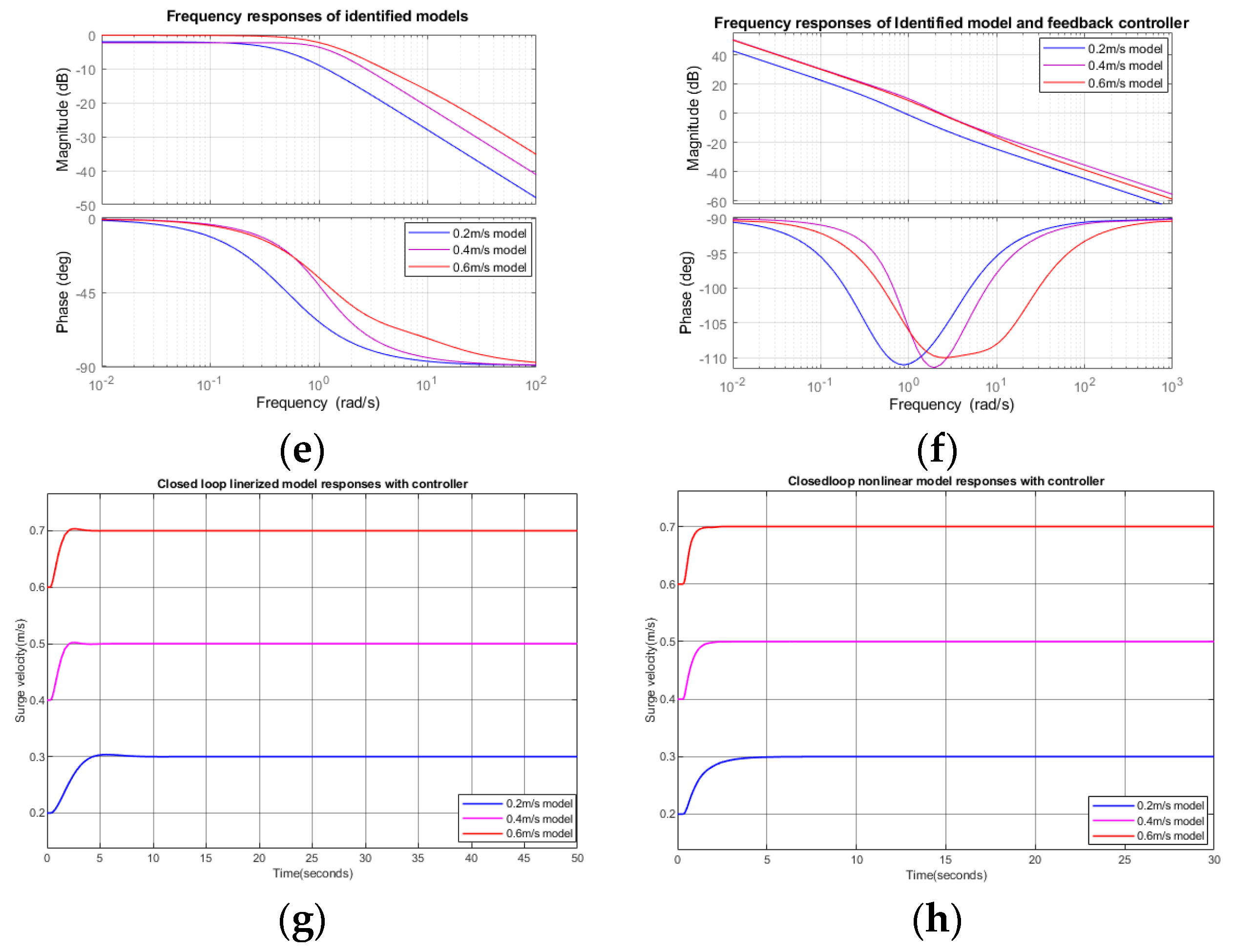
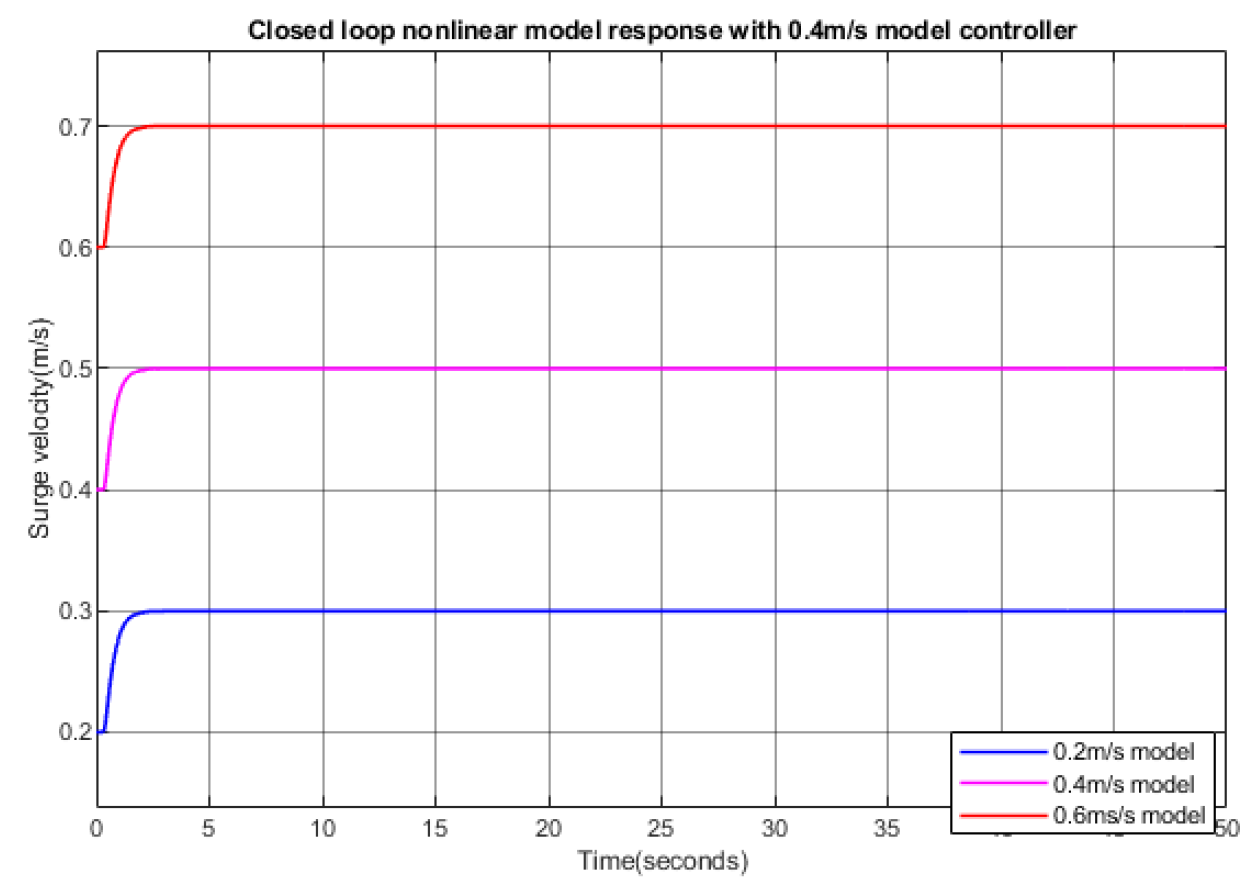
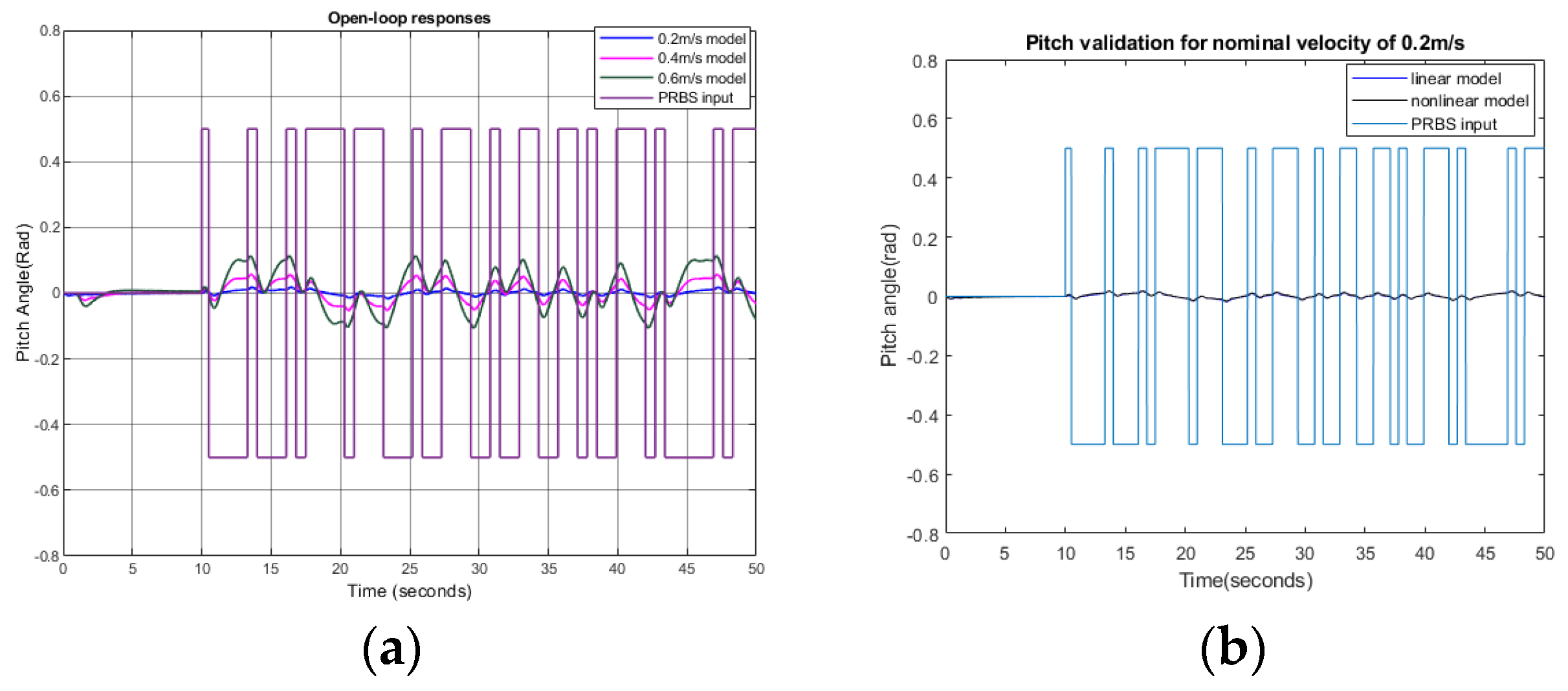
3.1. Surge Response and Velocity Controller Design
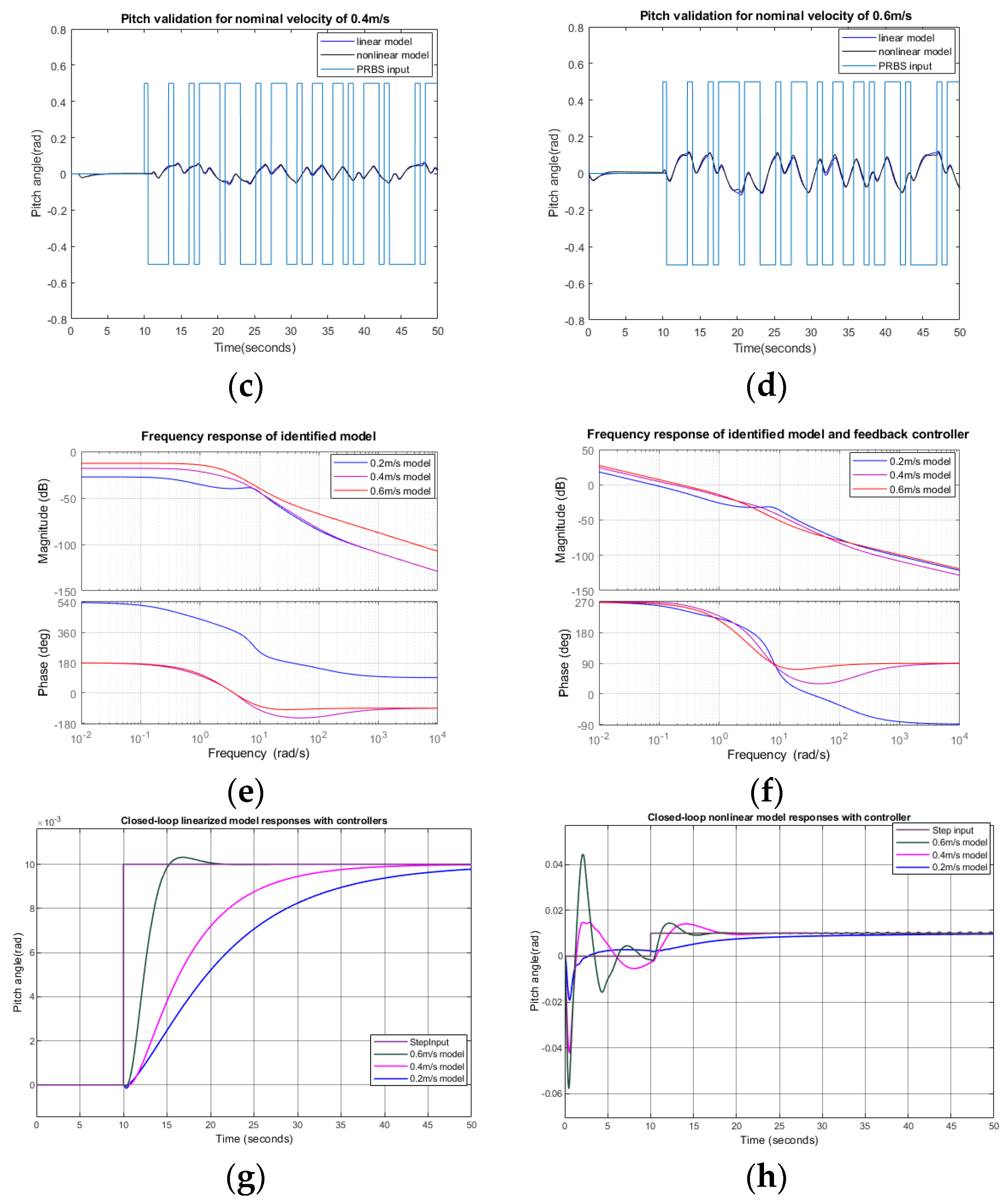
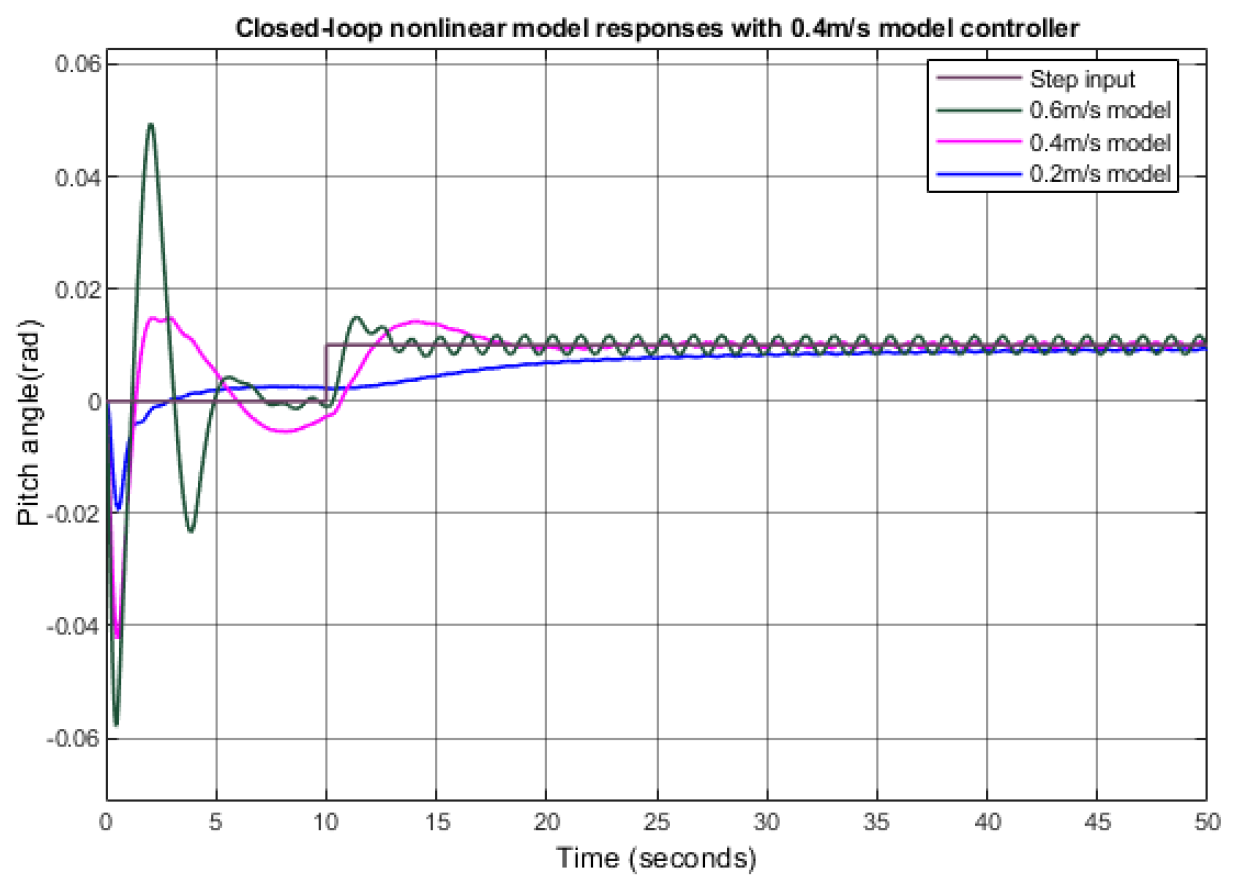
3.2. Pitch Response and Pitch Controller Design
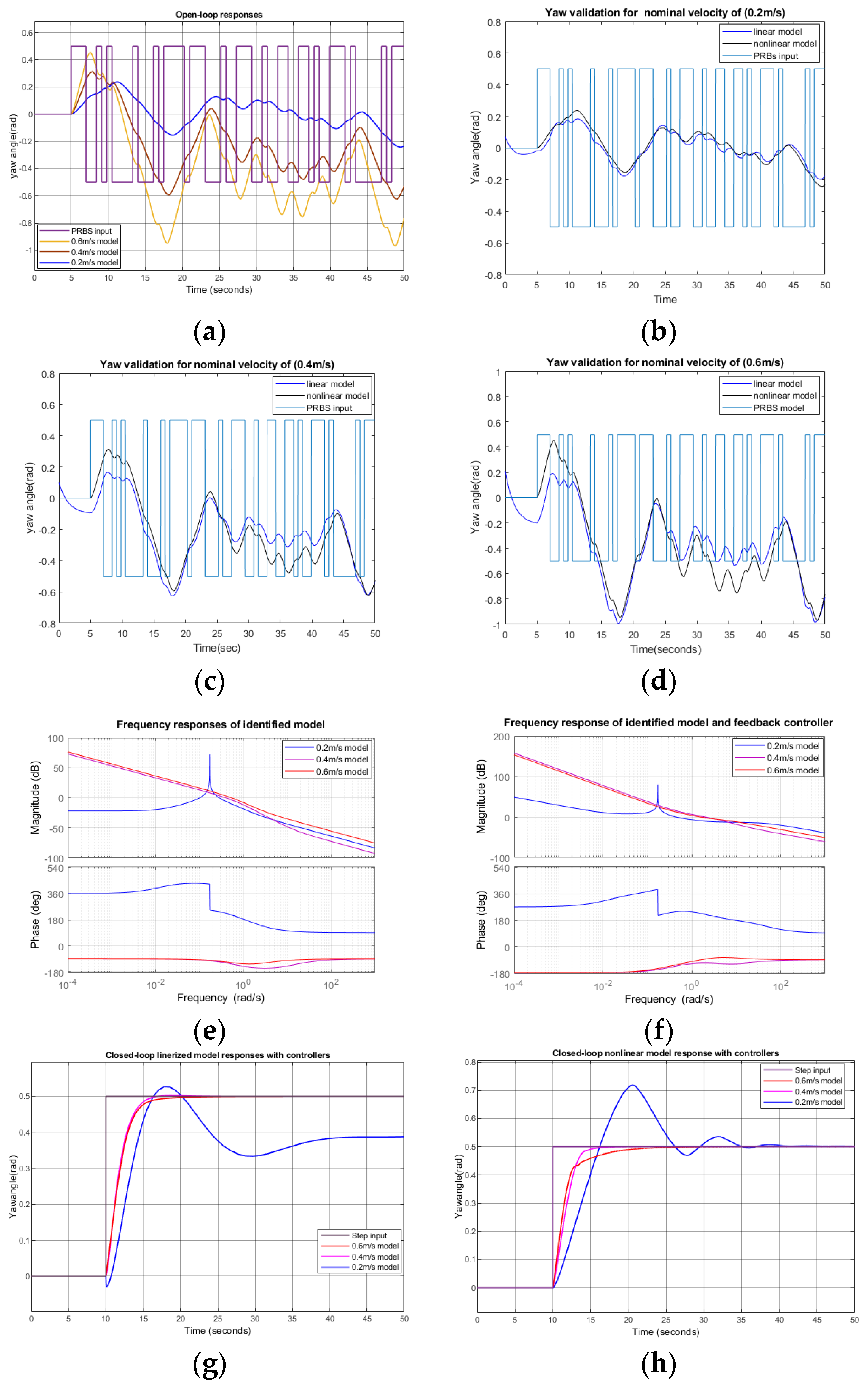
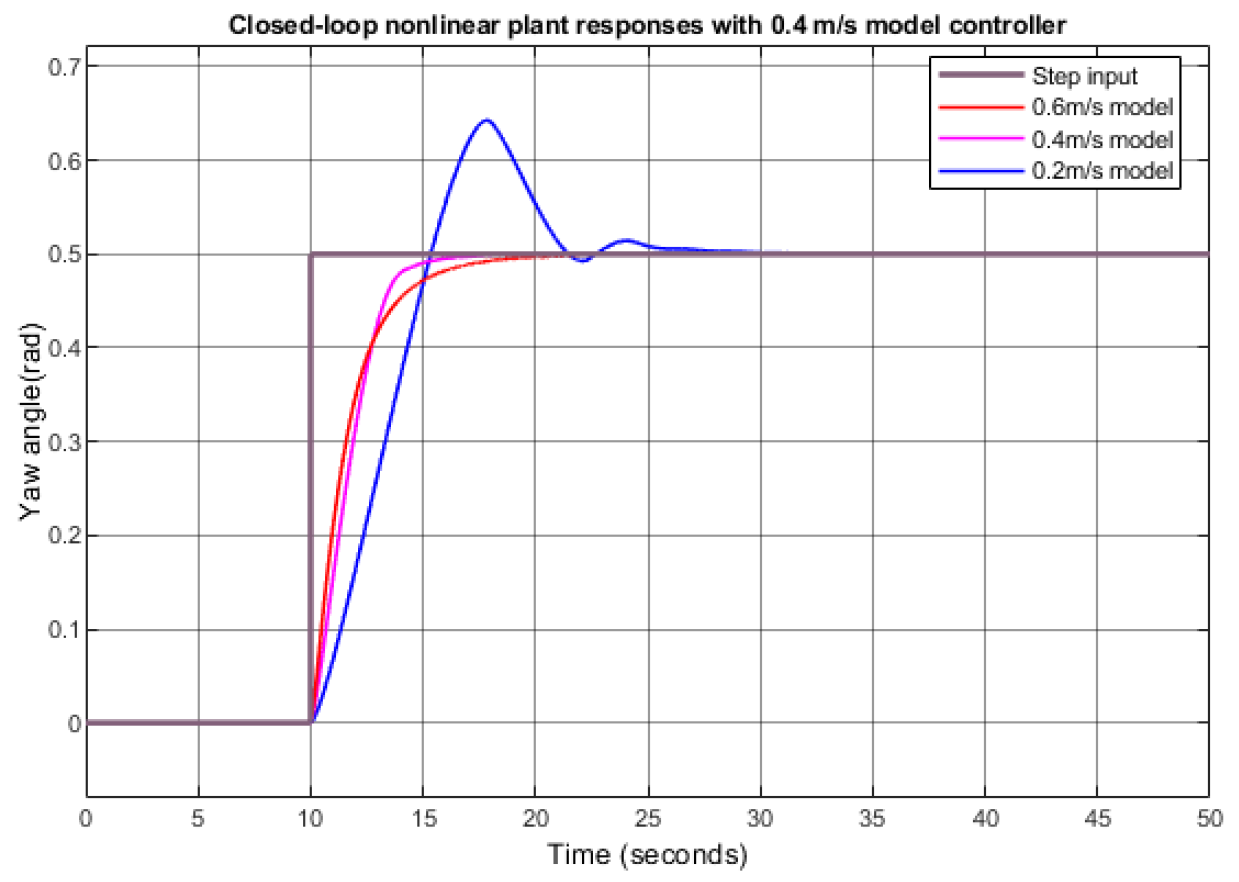
3.3. Yaw Response and Yaw Controller Design
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Cai, W.; Lu, J.; Ding, X.; Yang, J. Design, Modeling, Control, and Experiments for Multiple AUVs Formation. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2776–2787. [Google Scholar] [CrossRef]
- Wang, R.; Wang, S.; Wang, Y.u.; Cheng, L.; Tan, M. Development and Motion Control of Biomimetic Underwater Robots: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 833–844. [Google Scholar] [CrossRef]
- Humphreys, D.E. Development of the Equations of Motion and Transfer Functions for Underwater Vehicles; Naval Coastal Systems Laboratory, NCSL: Panama City, FL, USA, 1976. [Google Scholar]
- Nahon, M. A simplified dynamics model for Autonomous Underwater Vehicles. In Proceedings of the Symposium on Autonomous Underwater Vehicle Technology, Monterey, CA, USA, 2–6 June 1996; pp. 373–379. [Google Scholar] [CrossRef]
- Tang, S.C. Modelling and Simulation of the Autonomous Underwater Vehicle, Autolycus. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/80002/42806612-MIT.pdf (accessed on 14 February 2023).
- Anderson, J.M.; Chhabra, N.K. Maneuvering and stability performance of a robotic tuna. Integr. Comp. Biol. 2002, 42, 118–126. [Google Scholar] [CrossRef]
- Van den Berg, S.C.; Scharff, R.B.N.; Rusák, Z.; Wu, J. OpenFish: Biomimetic design of a soft robotic fish for high-speed locomotion. HardwareX 2022, 12, e00320. [Google Scholar] [CrossRef]
- Van den Berg, S.C.; Scharff, R.B.N.; Rusák, Z.; Wu, J. Biomimetic design of a soft robotic fish for high-speed locomotion. In Biomimetic and Biohybrid Systems; Springer: Cham, Switzerland, 2021; pp. 366–377. [Google Scholar] [CrossRef]
- White, C.H.; Lauder, G.V.; Bart-Smith, H. Tunabot Flex: A tuna-inspired robot with body flexibility improves high-performance swimming. Bioinspiration Biomim. 2021, 16, 026019. [Google Scholar] [CrossRef] [PubMed]
- Masoomi, S.F.; Gutschmidt, S.; Chen, X.; Sellier, M. The Kinematics and Dynamics of Undulatory Motion of a Tuna-Mimetic Robot. Int. J. Adv. Robot. Syst. 2015, 12, 83. [Google Scholar] [CrossRef]
- Hu, Q.; Hedgepeth, D.R.; Xu, L.; Tan, X. A framework for modeling steady turning of robotic fish. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2669–2674. [Google Scholar] [CrossRef]
- Nguyen, K.; Park, H.C. Feasibility study on mimicking the tail-beating supported gliding flight of Flying Fish. Ocean Eng. 2023, 287, 115745. [Google Scholar] [CrossRef]
- Nguyen, K.; Han, G.H.; Park, H.C. Preliminary design of a fish-like fast-swimming robot by scaling of the KUFish. In Proceedings of the International Conference on Intelligent Unmanned Systems, Adelaide, Australia, 5–7 July 2023. [Google Scholar]
- Clapham, R.J.; Hu, H. ISplash-i: High performance swimming motion of a carangiform robotic fish with full-body coordination. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar] [CrossRef]
- Clapham, R.J.; Hu, H. ISplash-II: Realizing fast carangiform swimming to outperform a real fish. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, Z.; Du, R. Robot fish with two-DOF pectoral fins and a wire-driven caudal fin. Adv. Robot. 2017, 32, 25–36. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, Z.; Du, R. The design and prototyping of a wire-driven robot fish with pectoral fins. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013. [Google Scholar] [CrossRef]
- Castano, M.L.; Tan, X. Rapid maneuvering control of pectoral fin-actuated robotic fish. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Delft, The Netherlands, 12–16 July 2021. [Google Scholar] [CrossRef]
- Koca, O.G.; Bal, C.; Korkmaz, D.; Bingol, M.C.; Ay, M.; Akpolat, Z.H.; Yetkin, S. Three-Dimensional Modeling of a Robotic Fish Based on Real Carp Locomotion. Appl. Sci. 2018, 8, 180. [Google Scholar] [CrossRef]
- Suebsaiprom, P.; Lin, C.L. Maneuverability modeling and trajectory tracking for Fish Robot. Control Eng. Pract. 2015, 45, 22–36. [Google Scholar] [CrossRef]
- Zeng, X.; Xia, M.; Luo, Z.; Shang, J.; Xu, Y.; Yin, Q. Design and Control of an Underwater Robot Based on Hybrid Propulsion of Quadrotor and Bionic Undulating Fin. J. Mar. Sci. Eng. 2022, 10, 1327. [Google Scholar] [CrossRef]
- Kim, M.; Joe, H.; Kim, J.; Yu, S.C. Integral sliding mode controller for precise maneuvering of autonomous underwater vehicle in the presence of unknown environmental disturbances. Int. J. Control 2015, 88, 2055–2065. [Google Scholar] [CrossRef]
- Aruna, M.V.; Ananthakrishnan, P. Trajectory tracking of biomimetic autonomous underwater vehicle using different control strategies. Int. J. Dyn. Control 2023, 11, 2924–2939. [Google Scholar] [CrossRef]
- Xiang, X.; Chen, D.; Yu, C.; Ma, L. Coordinated 3D path following for autonomous underwater vehicles via classic PID Controller. IFAC Proc. Vol. 2013, 46, 327–332. [Google Scholar] [CrossRef]
- Yang, E.; Gu, D. Nonlinear formation-keeping and mooring control of multiple autonomous underwater vehicles. IEEE/ASME Trans. Mechatron. 2007, 12, 164–178. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Trajectory tracking control of AUVs via adaptive fast nonsingular integral terminal sliding mode control. IEEE Trans. Ind. Inform. 2020, 16, 1248–1258. [Google Scholar] [CrossRef]
- Oktafianto, K.; Herlambang, T.; Mardlijah; Nurhadi, H. Design of Autonomous Underwater vehicle motion control using sliding mode control method. In Proceedings of the International Conference on Advanced Mechatronics, Intelligent Manufacture, and Industrial Automation (ICAMIMIA), Surabaya, Indonesia, 15–17 October 2015. [Google Scholar]
- The MathWorks, Inc. Optimization Toolbox Version: 9.4 (R2022b). Available online: https://www.mathworks.com (accessed on 1 January 2023).
- Ljung, L. System Identification Toolbox for Use with MATLAB. 2011. Available online: https://www.mathworks.com/products/sysid.html (accessed on 14 February 2024).
- Sen, D.T.; Vinh, T.C. Determination of Added Mass and Inertia Moment of Marine Ships Moving in 6 Degrees of Freedom. Int. J. Transp. Eng. Technol. 2016, 2, 8–14. [Google Scholar] [CrossRef]
- Carbone, G.; Martinat, G.; Farcy, D.; Harion, J.L. Added Masses of generic shape bodies interacting with external walls. Aerosp. Sci. Technol. 2019, 90, 70–84. [Google Scholar] [CrossRef]
- Yu, J.; Su, Z.; Wu, Z.; Tan, M. Development of a Fast-Swimming Dolphin Robot Capable of Leaping. IEEE/ASME Trans. Mechatron. 2016, 21, 2307–2316. [Google Scholar] [CrossRef]
- Chan, W.L.; Kang, T.S. Simultaneous Determination of Drag Coefficient and Added Mass. IEEE J. Ocean. Eng. 2011, 36, 422–430. [Google Scholar] [CrossRef]
- Romano, D.; Wahi, A.; Miraglia, M.; Stefanini, C. Development of a Novel Underactuated Robotic Fish with Magnetic Transmission System. Machines 2022, 10, 755. [Google Scholar] [CrossRef]
- Lighthill, M.J. Note on the swimming of slender fish. J. Fluid Mech. 1960, 9, 305–317. [Google Scholar] [CrossRef]
- Morgansen, K.A.; Triplett, B.I.; Klein, D.J. Geometric Methods for Modeling and Control of Free-Swimming Fin-Actuated Underwater Vehicles. IEEE Trans. Robot. 2007, 23, 1184–1199. [Google Scholar] [CrossRef]
- Nguyen, K.; Pham, T.H.; Park, H.C. Numerical investigation of hydrodynamics for a fish-like robot under undulatory forward swimming. In Proceedings of the International Session-Korea Society of Mechanical Engineers (KSME), Jeju, Republic of Korea, 9–12 November 2022. [Google Scholar]
- Farid, G.; Benjamin, C. Kuo. Automatic Control Systems, 9th ed.; Wiley Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ullah, S.; Mehmood, A.; Khan, Q.; Rehman, S.; Iqbal, J. Robust Integral Sliding Mode Control Design for Stability Enhancement of Under-actuated Quadcopter. Int. J. Control. Autom. Syst. 2020, 18, 1671–1678. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Mehmood, A.; Kirmani, S.A.M.; Mechali, O. Neuro-adaptive fast integral terminal sliding mode control design with variable gain robust exact differentiator for under-actuated quadcopter UAV. ISA Trans. 2022, 120, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Shen, D.; Xu, J.X. Motion Control of Robotic Fish Under Dynamic Environmental Conditions Using Adaptive Control Approach. IEEE J. Ocean. Eng. 2018, 43, 381–390. [Google Scholar] [CrossRef]
- Shen, F.; Cao, Z.; Zhou, C.; Xu, D.; Gu, N. Depth Control for Robotic Dolphin Based on Fuzzy PID Control. Int. J. Offshore Polar Eng. 2013, 23, 166–171. [Google Scholar]
- Kim, S.H. Electric Motor Control; Elsevier: Amsterdam, The Netherlands, 2017; pp. 39–93. [Google Scholar]
- Nam, S.L.; Aurecianus, S.; Phan, H.V.; Kang, T.S.; Park, H.C. Experimental study on the phase delay of low-cost IMU, low pass, and Kalman filter and its effect on the phase margin of angle estimation. In Proceedings of the 10th International Micro Air Vehicle Competition and Conference, Melbourne, Australia, 22–23 November 2018; pp. 81–85. [Google Scholar]
- Aurecianus, S.; Phan, H.V.; Kang, T.S.; Park, H.C. Longitudinal mode model-based controller design for tailless flapping wing robot with loop shaping compensator. Bioinspiration Biomim. 2020, 15, 056004. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Length | |||
| Weight | |||
| Buoyancy | |||
| Moment of inertia in x-axis | |||
| Moment of inertia in y-axis | |||
| Moment of inertia in z-axis | |||
| Position of CB | (0,0,0) | ||
| Position of CG | ) |
| Added Mass | Nonlinear Damping Coefficients |
|---|---|
| = −2.77 | |
| = −2.77 | |
| kg m | 0 |
| kg m |
| Nominal Caudal Frequency (Hz) | Nominal Surge Velocity Condition | Linearly Obtained Transfer Function |
|---|---|---|
| 2.00 | Condition 1 (0.2 m/s) | |
| 4.00 | Condition 2 (0.4 m/s) | |
| 6.00 | Condition 3 (0.6 m/s) |
| Model | P | I | D | N | b | c |
|---|---|---|---|---|---|---|
| Condition 1 | ||||||
| Condition 2 | ||||||
| Condition 3 |
| Model | Gain Margin (Decibels) | Phase Margin (Degrees) |
|---|---|---|
| Condition 1 | Infinity | 69 at 0.90 rad/s |
| Condition 2 | Infinity | 69 at 2.32 rad/s |
| Condition 3 | Infinity | 70 at 2.19 rad/s |
| Nominal Surge Condition | Linearly Obtained Transfer Function |
|---|---|
| Condition 1 | |
| Condition 2 | |
| Condition 3 |
| Model | P | I | D | N | b | c |
|---|---|---|---|---|---|---|
| Condition 1 | ||||||
| Condition 2 | ||||||
| Condition 3 |
| Model | Gain Margin (Decibels) | Phase Margin (Degrees) |
|---|---|---|
| Condition 1 | 32.1 at 3.53 rad/s | 81 at 0.07 rad/s |
| Condition 2 | 26.3 at 2.88 rad/s | 85 at 0.17 rad/s |
| Condition 3 | 22.2 at 1.88 rad/s | 76 at 0.23 rad/s |
| Nominal Surge Condition | Linearly Obtained Transfer Function |
|---|---|
| Condition 1 | |
| Condition 2 | |
| Condition 3 |
| Model | P | I | D | N | b | c |
|---|---|---|---|---|---|---|
| Condition 1 | ||||||
| Condition 2 | ||||||
| Condition 3 |
| Model | Gain Margin (Decibels) | Phase Margin (Degrees) |
|---|---|---|
| Condition 1 | 13.0 at 9.15 rad/s | 57 at 0.43 rad/s |
| Condition 2 | Infinity | 69 at 2.00 rad/s |
| Condition 3 | Infinity | 85 at 1.52 rad/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gumpina, S.; Lee, S.; Kim, J.-H.; Park, H.C.; Kang, T. Simulation and Controller Design for a Fish Robot with Control Fins. Biomimetics 2024, 9, 317. https://doi.org/10.3390/biomimetics9060317
Gumpina S, Lee S, Kim J-H, Park HC, Kang T. Simulation and Controller Design for a Fish Robot with Control Fins. Biomimetics. 2024; 9(6):317. https://doi.org/10.3390/biomimetics9060317
Chicago/Turabian StyleGumpina, Sandhyarani, Seungyeon Lee, Jeong-Hwan Kim, Hoon Cheol Park, and Taesam Kang. 2024. "Simulation and Controller Design for a Fish Robot with Control Fins" Biomimetics 9, no. 6: 317. https://doi.org/10.3390/biomimetics9060317
APA StyleGumpina, S., Lee, S., Kim, J.-H., Park, H. C., & Kang, T. (2024). Simulation and Controller Design for a Fish Robot with Control Fins. Biomimetics, 9(6), 317. https://doi.org/10.3390/biomimetics9060317








