Acinonyx jubatus-Inspired Quadruped Robotics: Integrating Neural Oscillators for Enhanced Locomotion Control
Abstract
1. Introduction
2. Materials and Methods
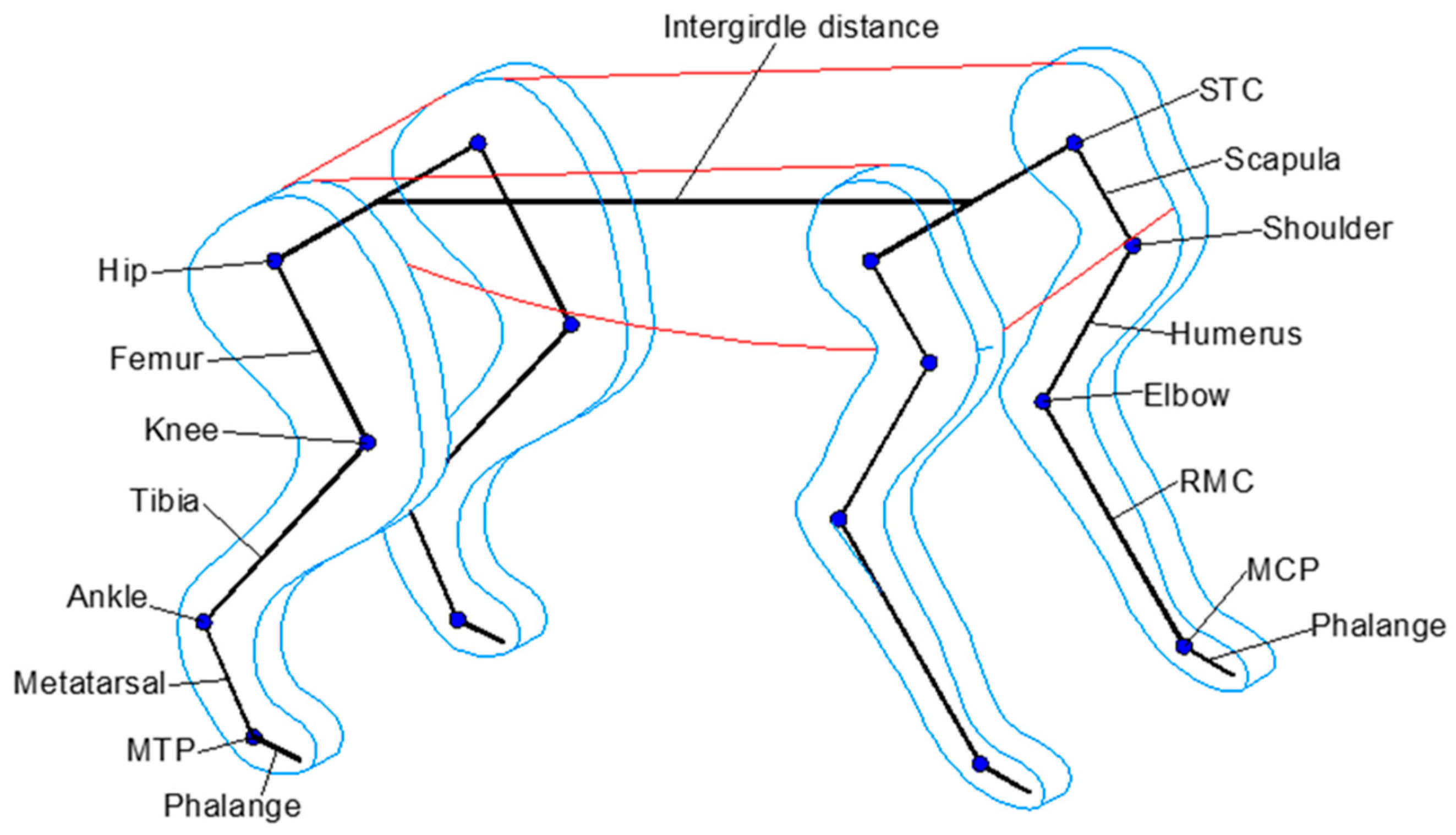
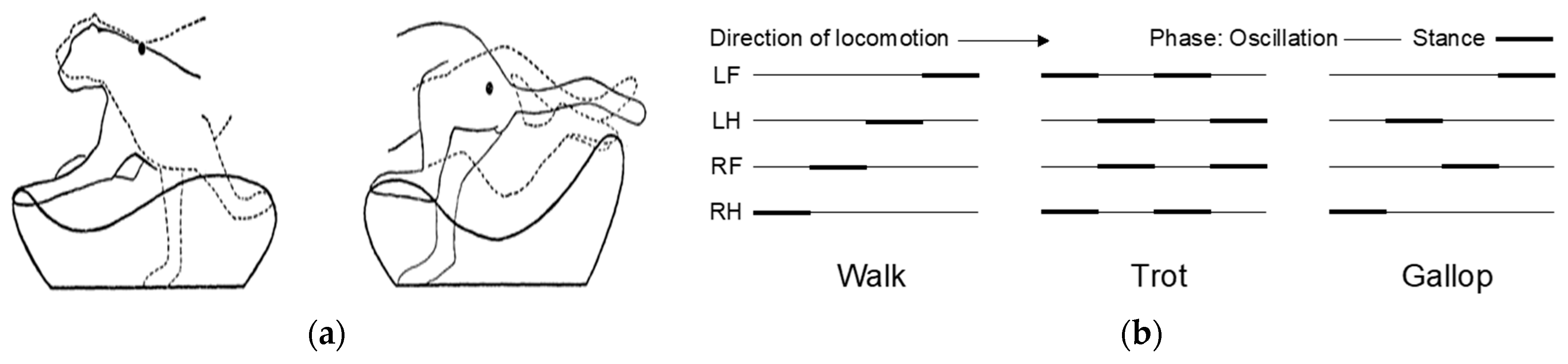
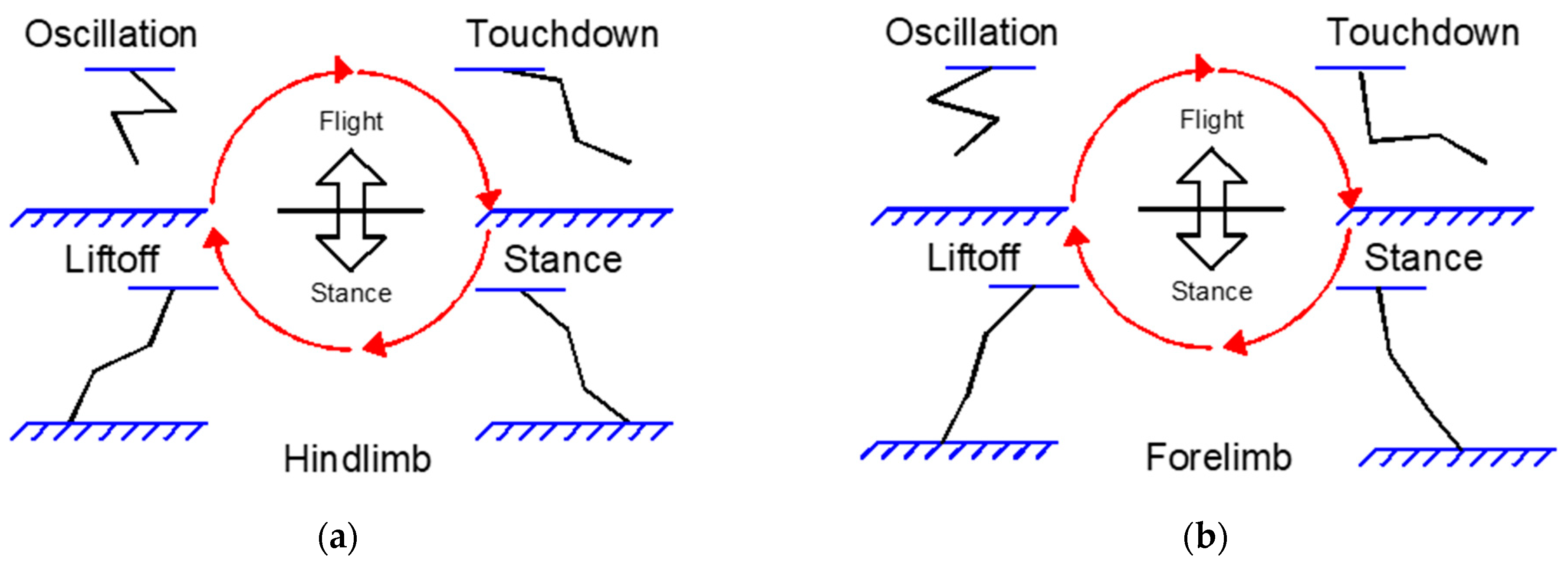
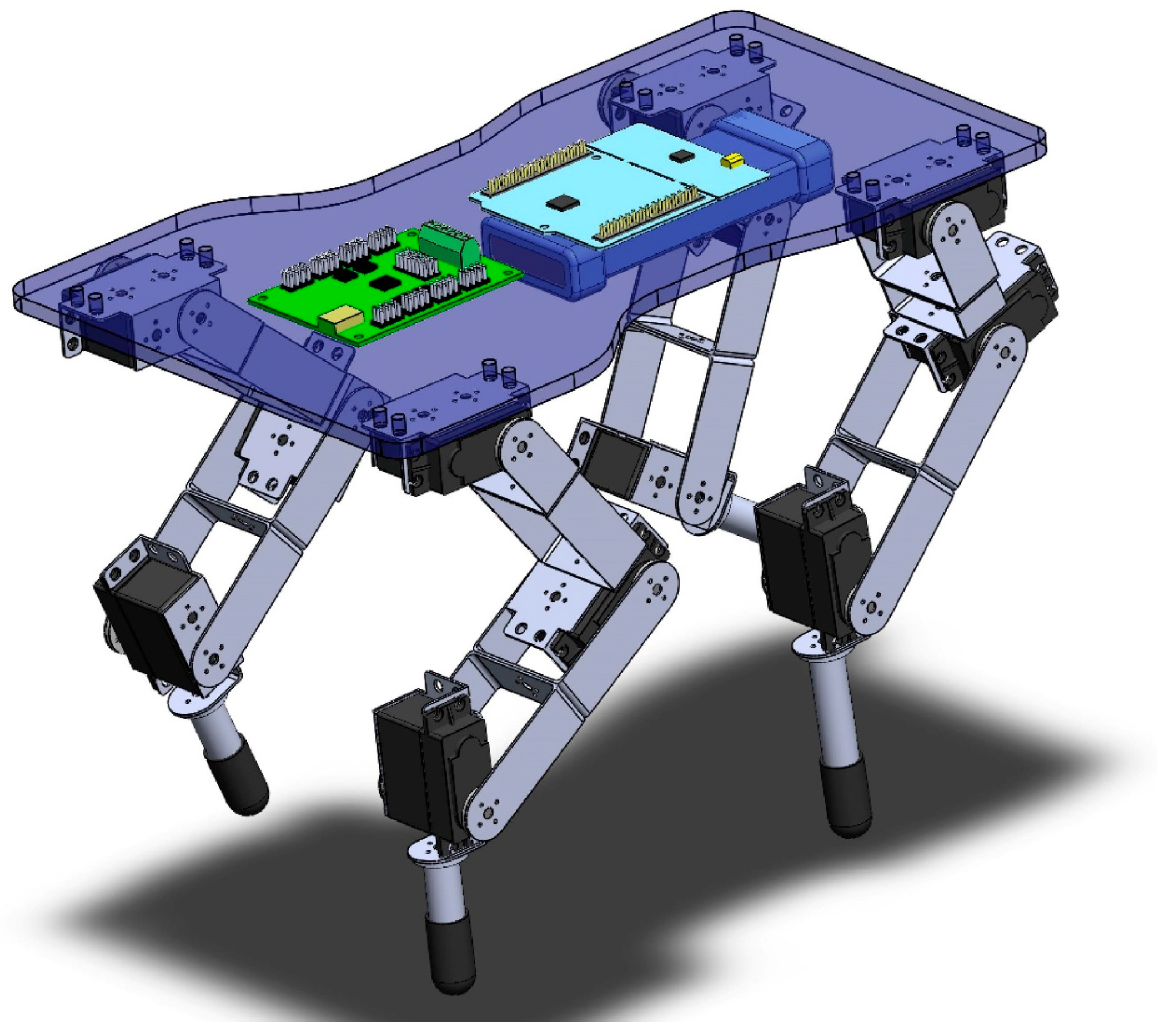
2.1. Biological Inspiration: Acinonyx jubatus Locomotive Framework
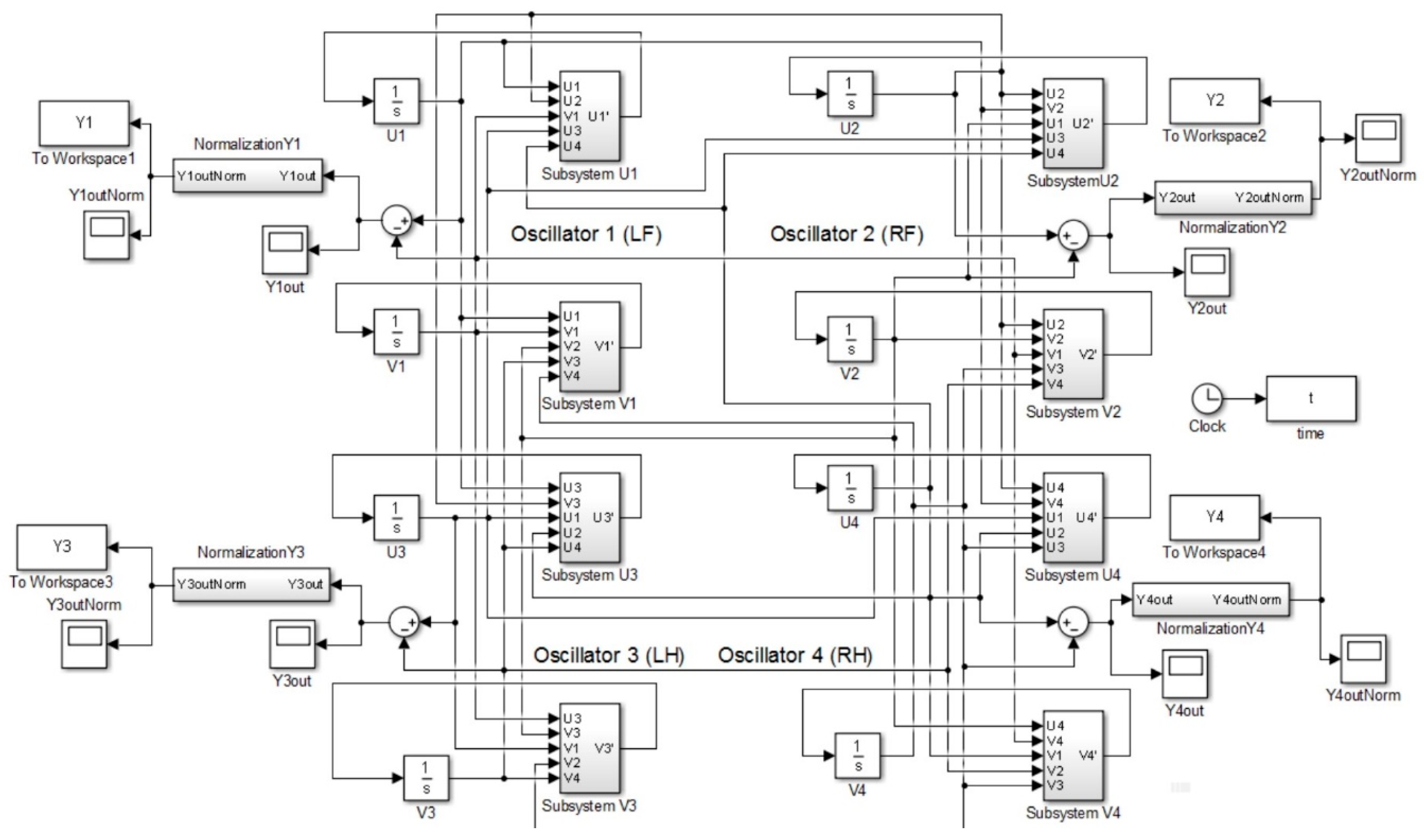
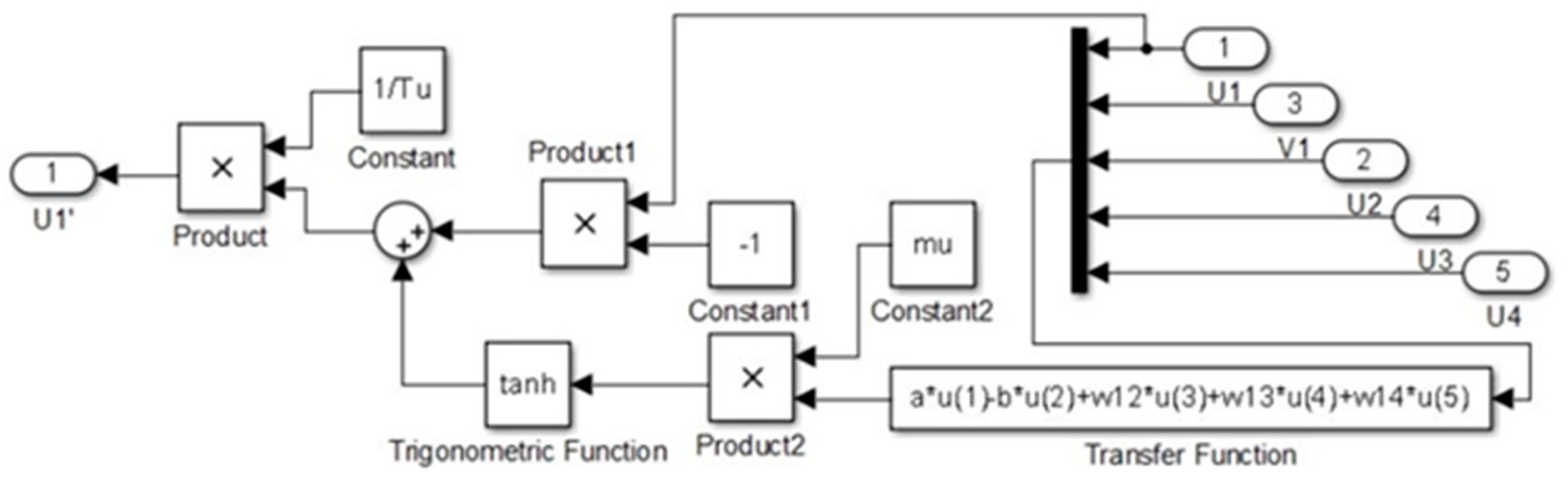
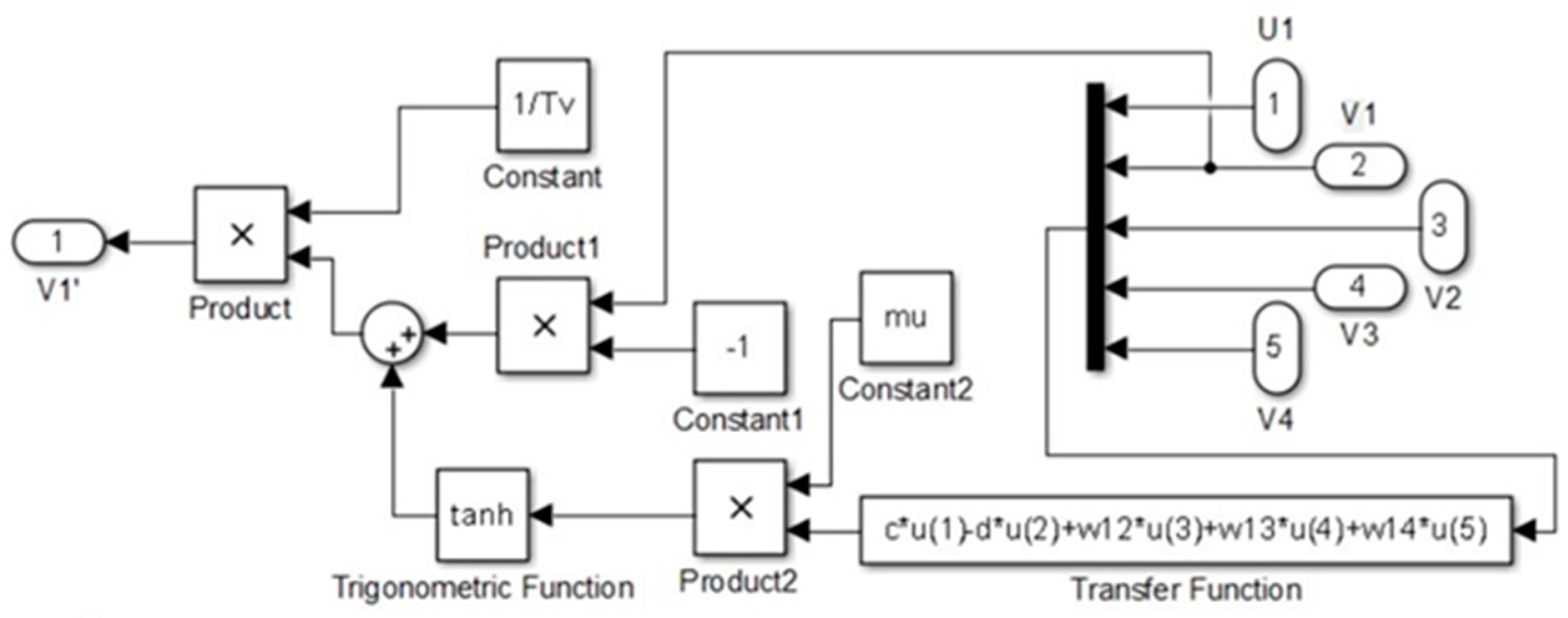
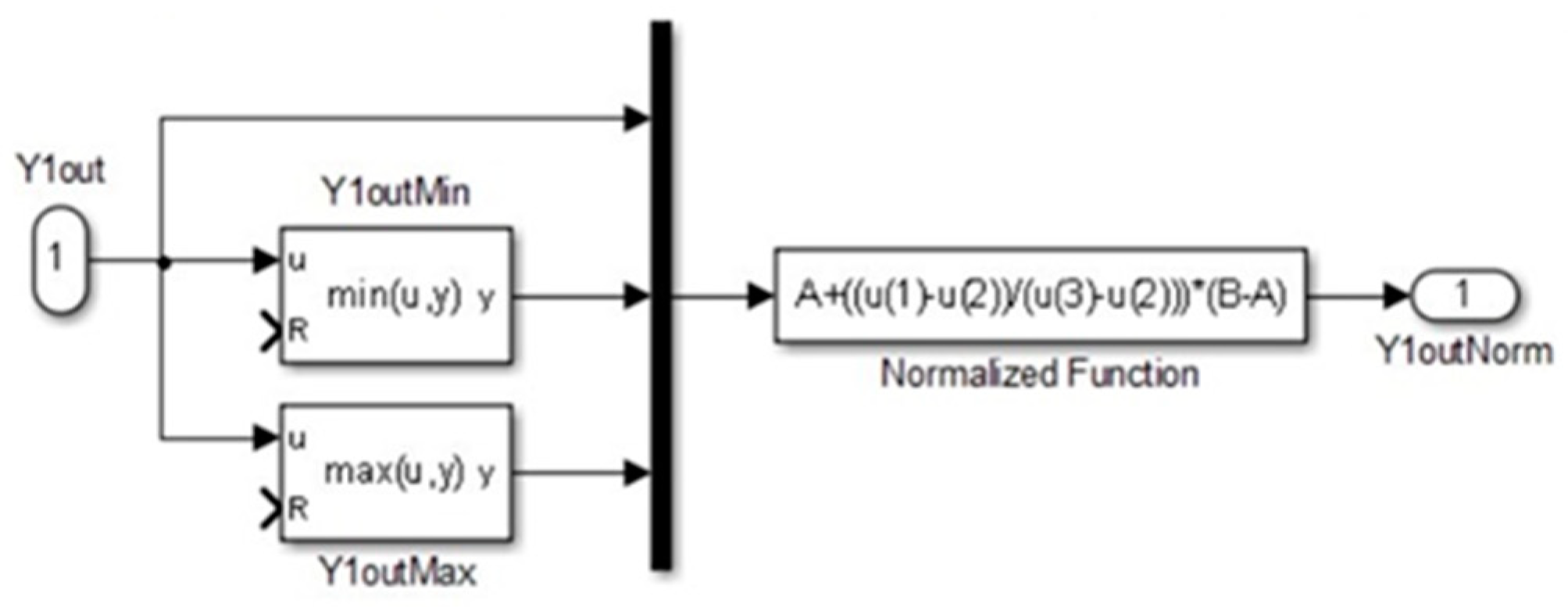
2.2. Mechanism Modeling for Autonomous Locomotion Control Based on Wilson–Cowan Neural Oscillators
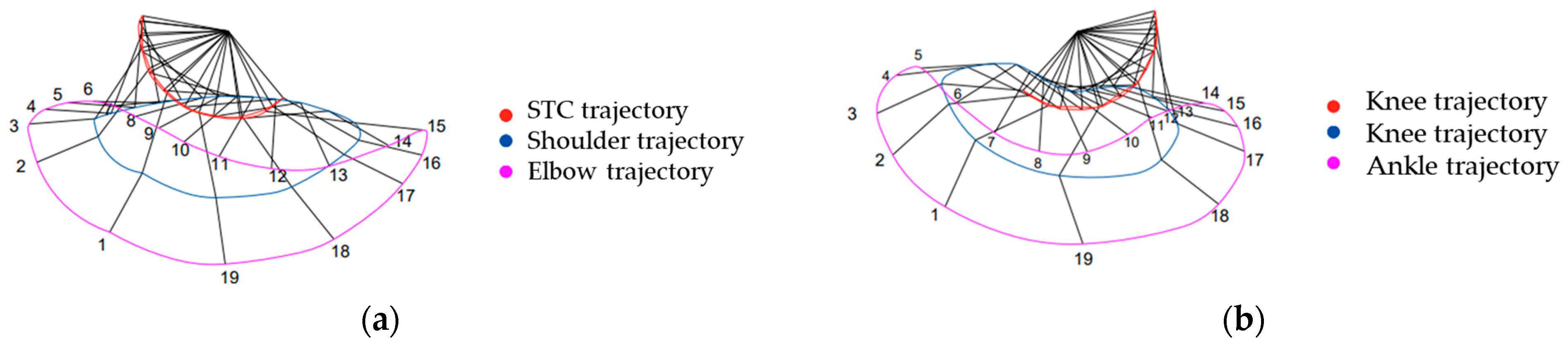
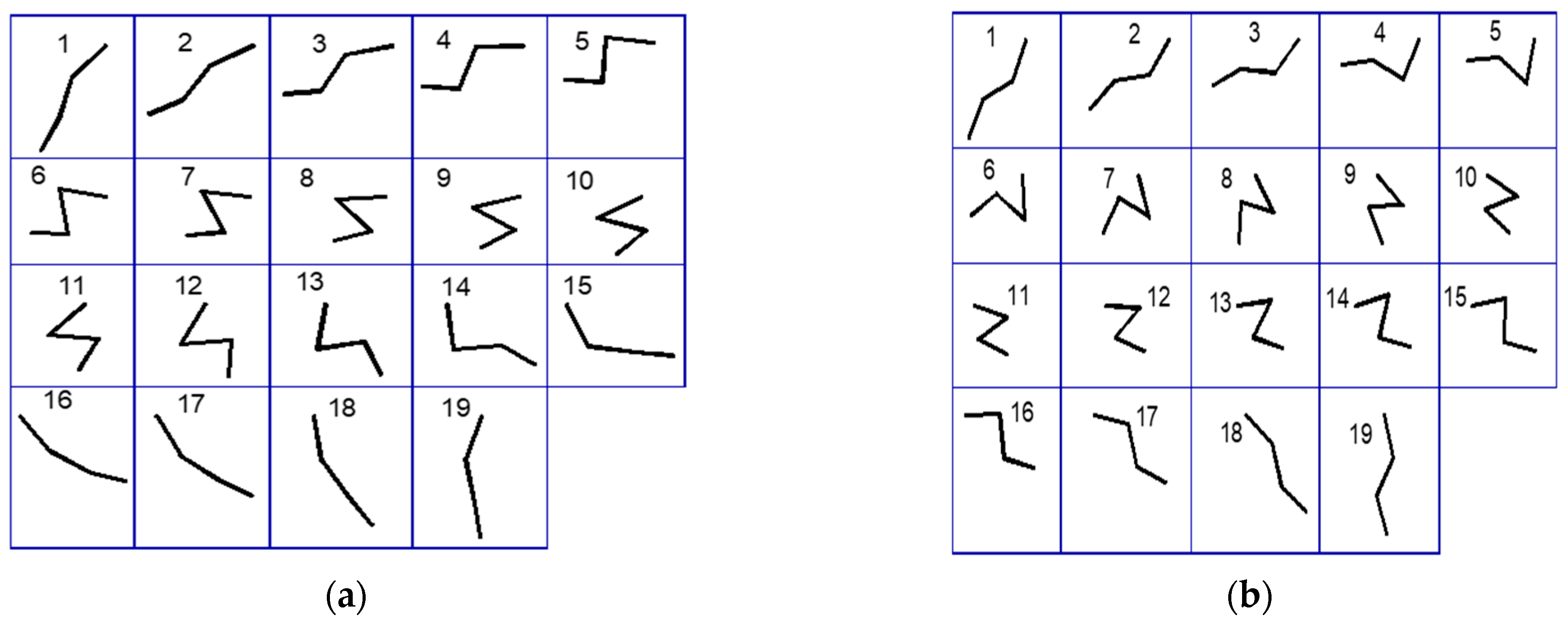
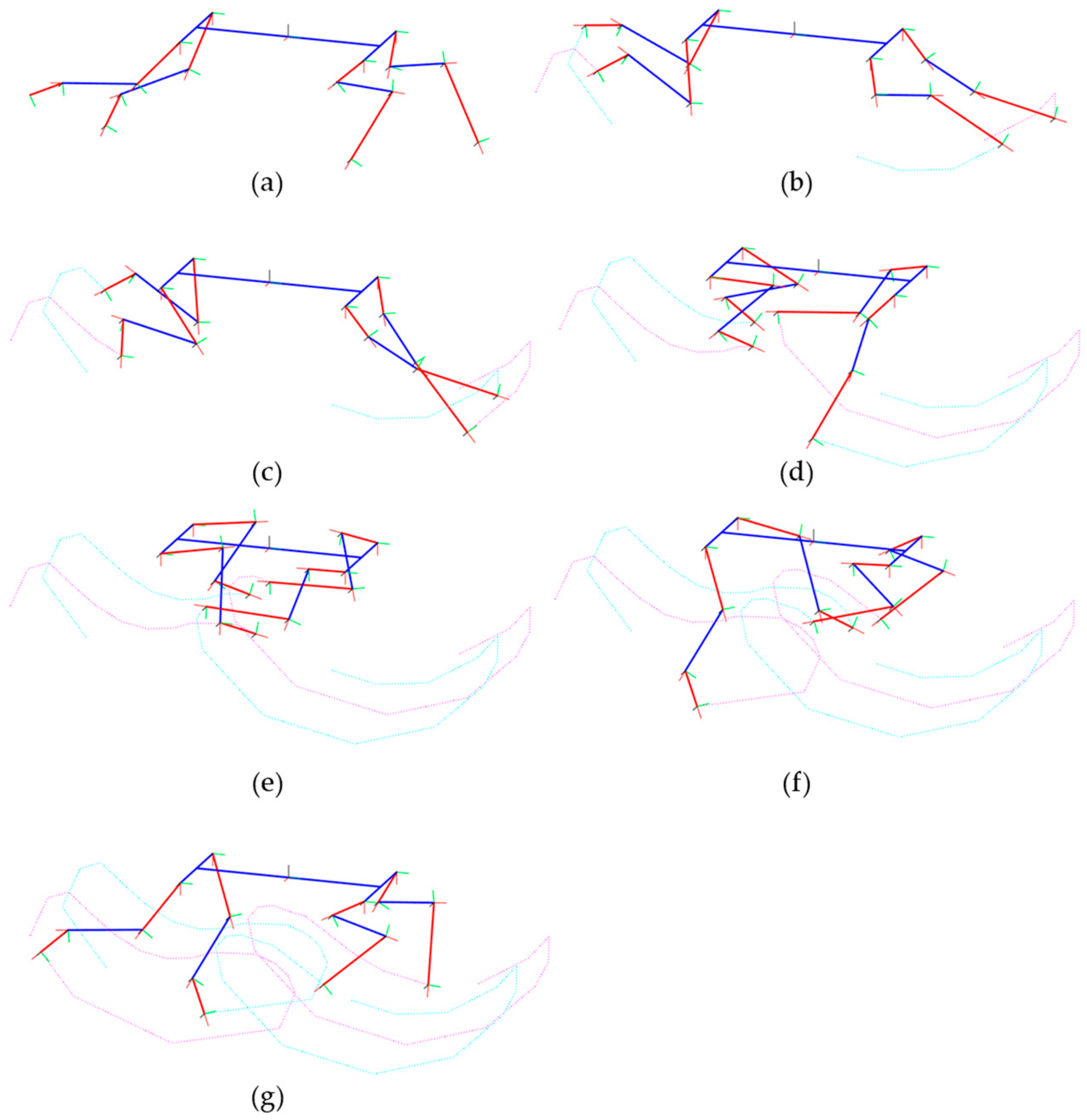
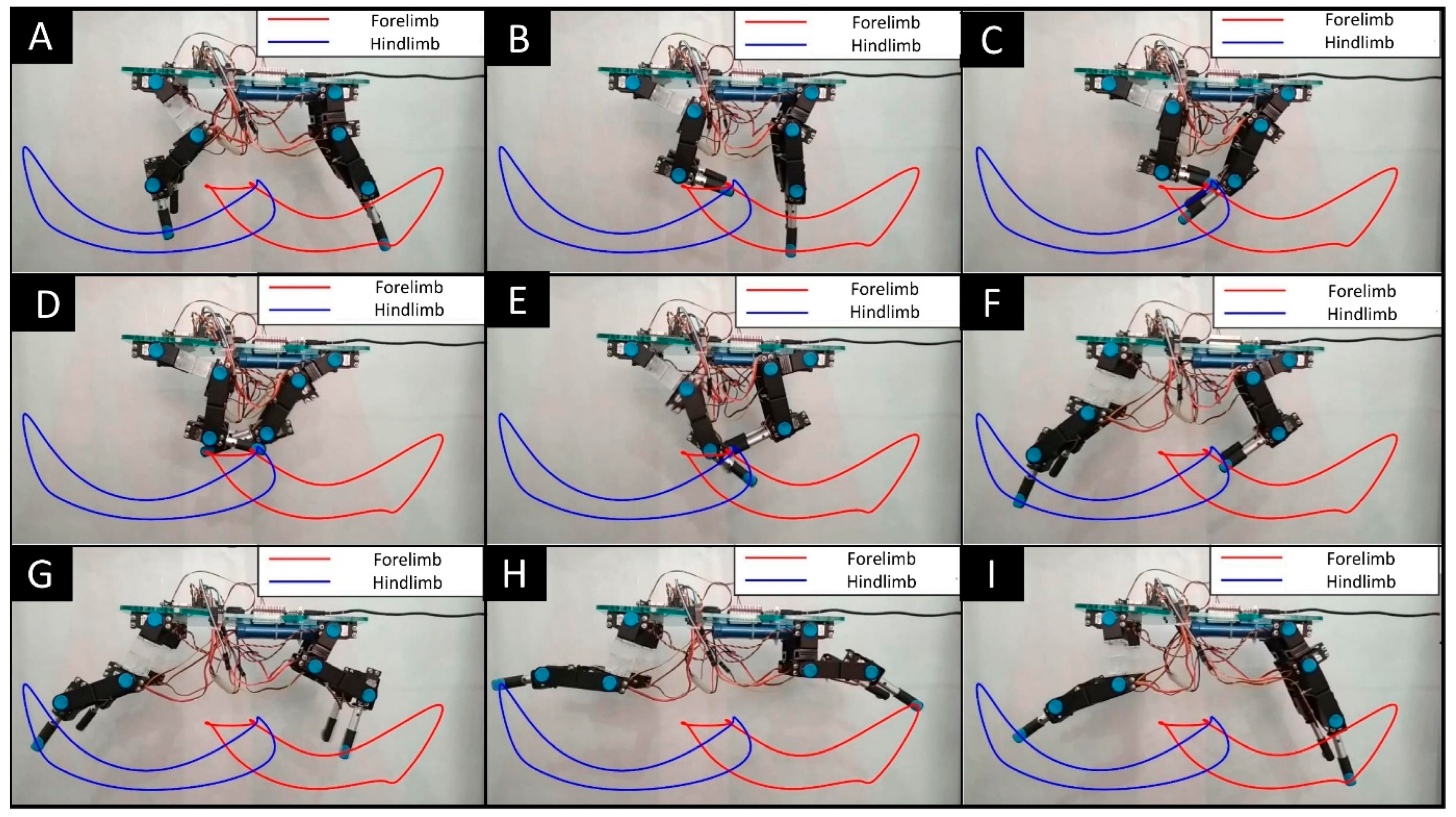
2.3. Kinematic Analysis of Quadruped Locomotion
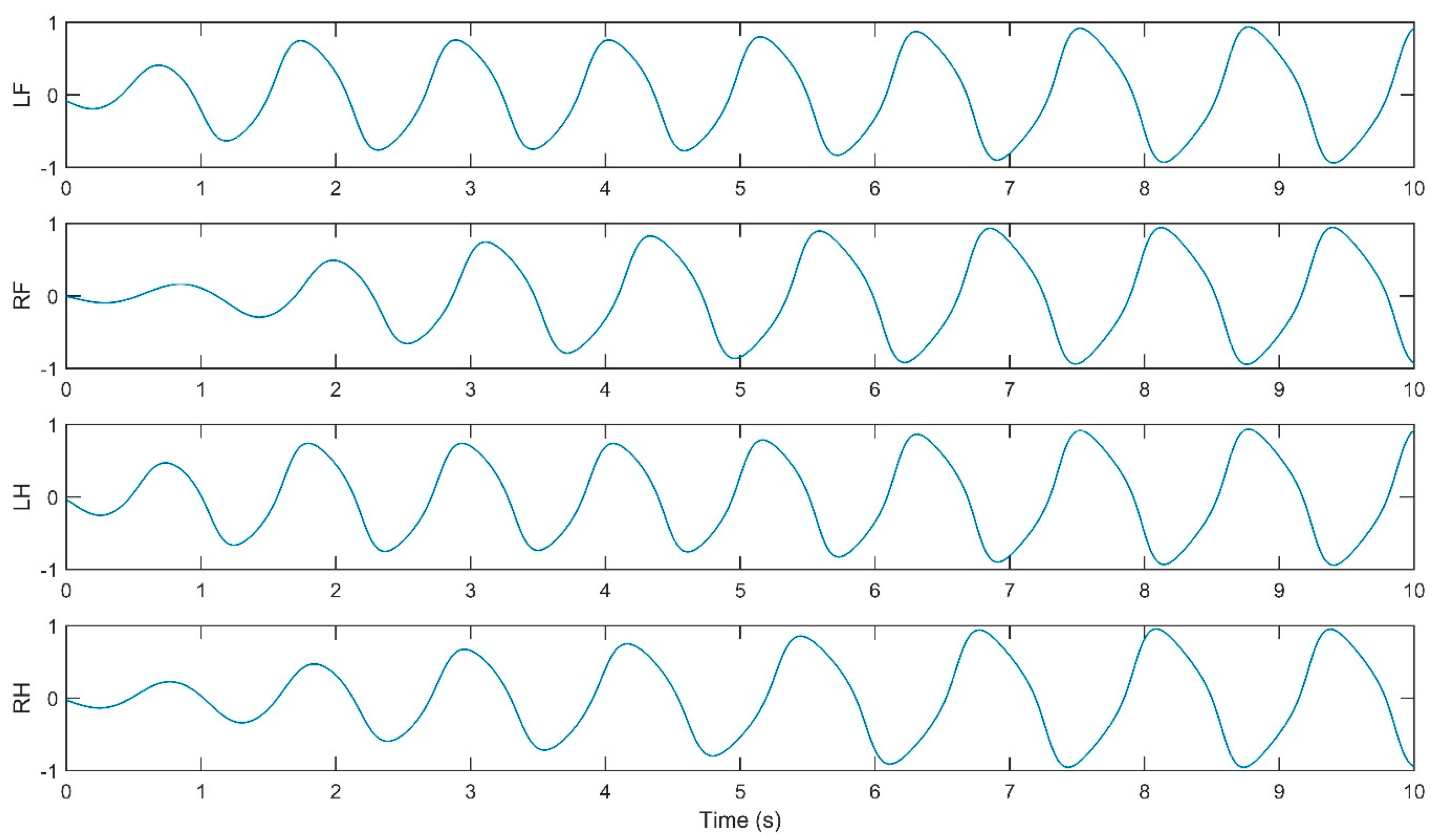
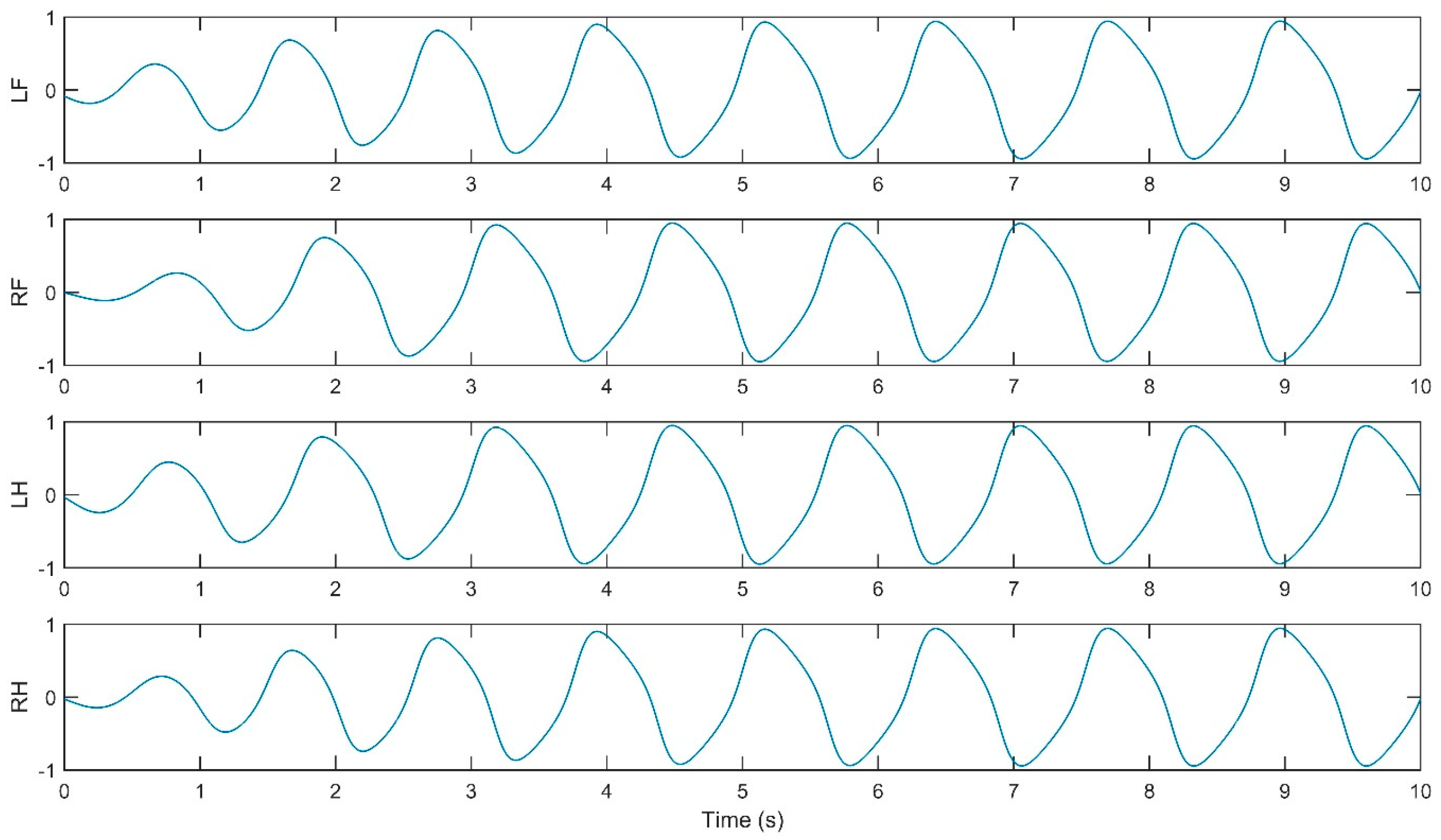
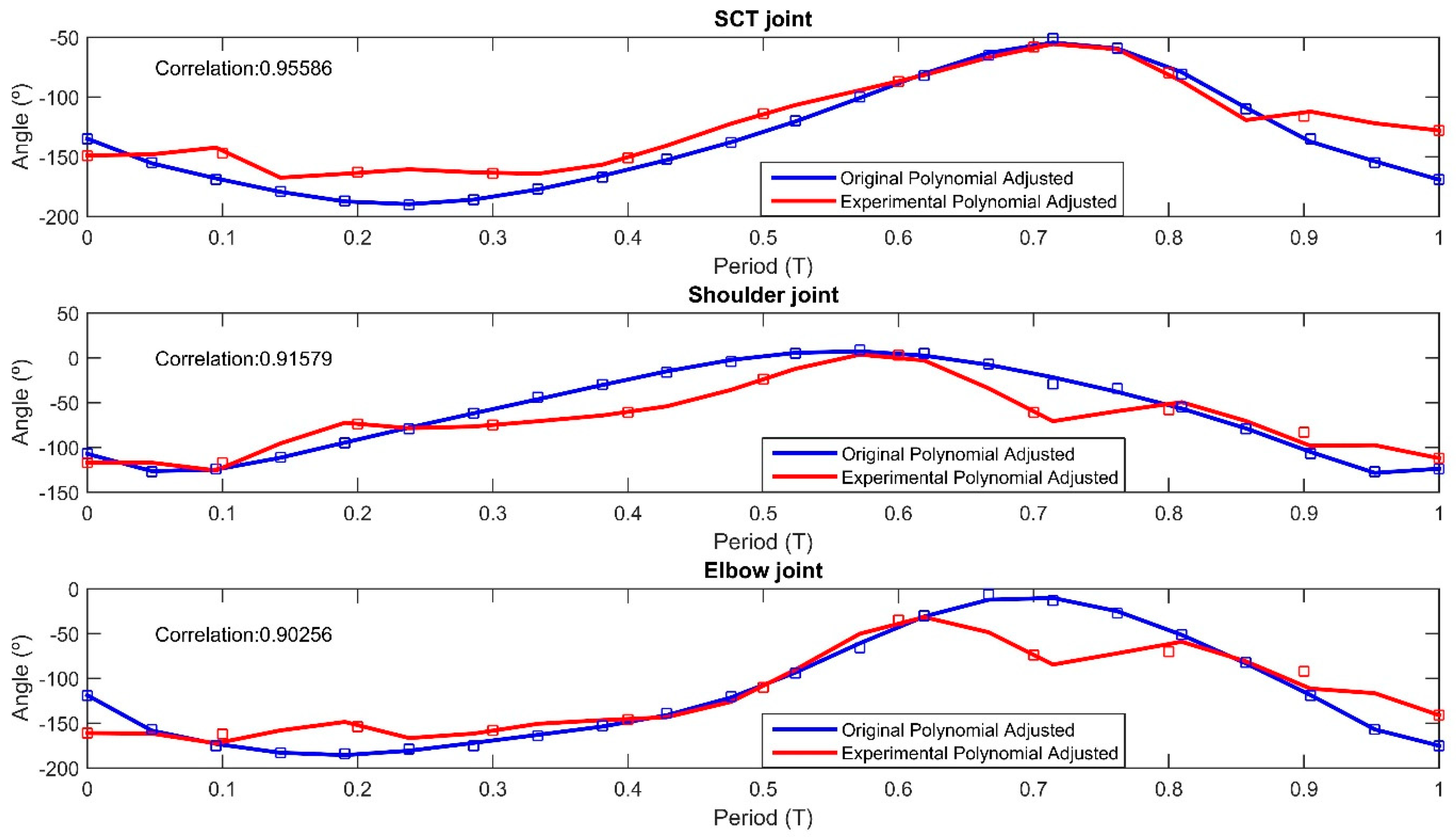
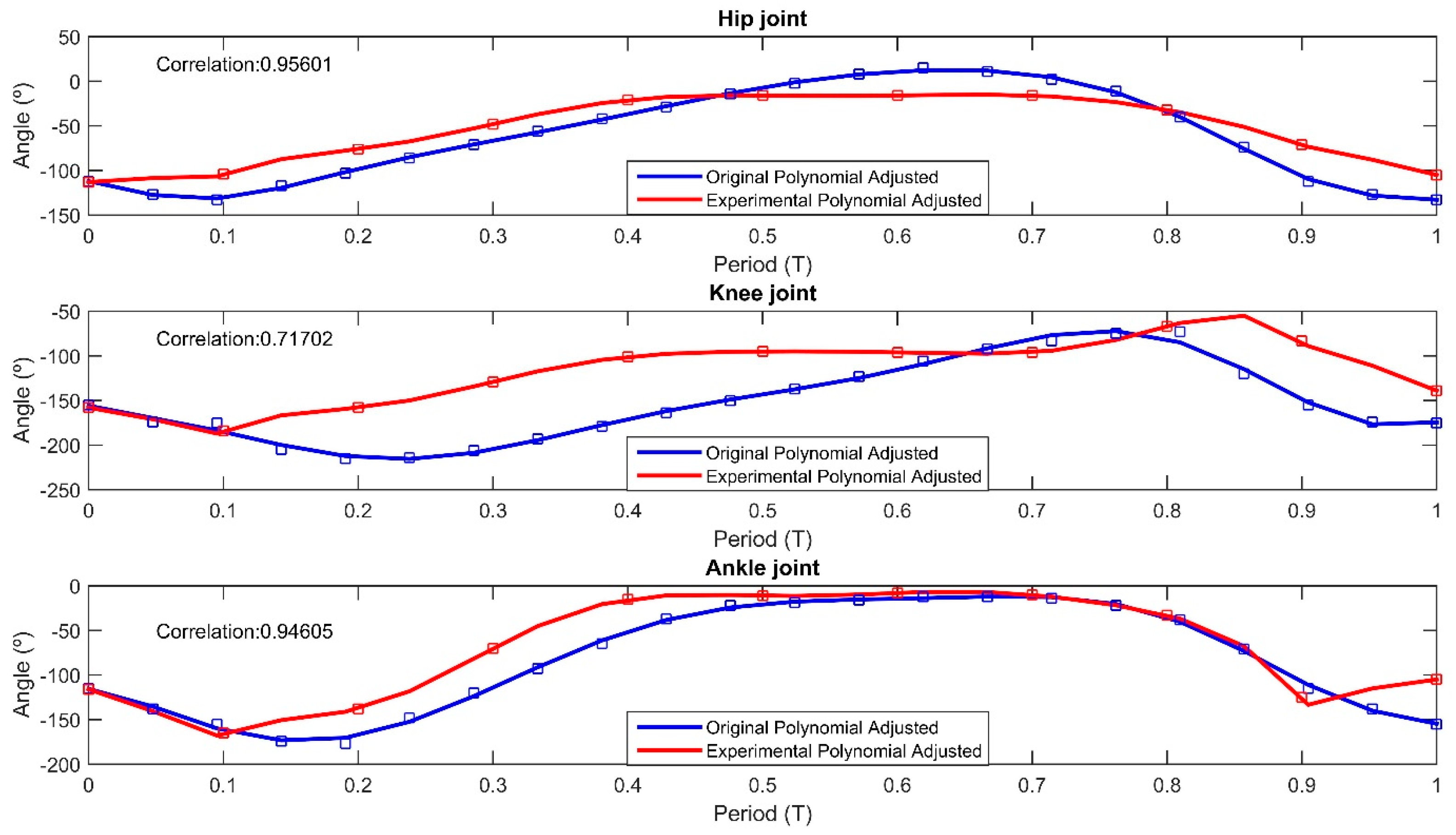
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koechling, J.; Raibert, M. How Fast Can a Legged Robot Run. In Symposium in Robotics; American Society of Mechanical Engineers, Dynamic Systems and Control Division (DSC): IL, USA, 1988; Volume 11. [Google Scholar]
- Li, M.; Wang, X.; Guo, W.; Wang, P.; Sun, L. System Design of a Cheetah Robot toward Ultra-High Speed. Int. J. Adv. Robot. Syst. 2014, 11, 73. [Google Scholar] [CrossRef]
- Wang, X.; Li, M.; Wang, P.; Guo, W.; Sun, L. Bio-Inspired Controller for a Robot Cheetah with a Neural Mechanism Controlling Leg Muscles. J. Bionic Eng. 2012, 9, 282–293. [Google Scholar] [CrossRef]
- Carius, J.; Ranftl, R.; Koltun, V.; Hutter, M. Trajectory Optimization for Legged Robots with Slipping Motions. IEEE Robot. Autom. Lett. 2019, 4, 3013–3020. [Google Scholar] [CrossRef]
- Guo, K.; Li, S.; Huang, D. Real-Time Quadruped Robot Control System Based on Xenomai. In Proceedings of the 2015 Chinese Automation Congress, CAC 2015, Wuhan, China, 27–29 November 2015; pp. 342–347. [Google Scholar] [CrossRef]
- Palmer, L.R.; Orin, D.E. Intelligent Control of High-Speed Turning in a Quadruped. J. Intell. Robot. Syst. Theory Appl. 2010, 58, 47–68. [Google Scholar] [CrossRef]
- Lewis, M.A.; Bunting, M.R.; Salemi, B.; Hoffmann, H. Toward Ultra High Speed Locomotors: Design and Test of a Cheetah Robot Hind Limb. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Whoa: Boston Dynamics Announces New WildCat Quadruped Robot—IEEE Spectrum. Available online: https://spectrum.ieee.org/whoa-boston-dynamics-announces-new-wildcat-quadruped (accessed on 18 February 2024).
- Cheetah-Cub—BioRob—EPFL. Available online: https://www.epfl.ch/labs/biorob/research/quadruped/quadruped-past/cheetah-cub-2/ (accessed on 18 February 2024).
- Heim, S.W.; Ajallooeian, M.; Eckert, P.; Vespignani, M.; Ijspeert, A.J. On Designing an Active Tail for Legged Robots: Simplifying Control via Decoupling of Control Objectives. Ind. Robot 2016, 43, 338–346. [Google Scholar] [CrossRef]
- Chen, H.; Hong, Z.; Yang, S.; Wensing, P.M.; Zhang, W. Quadruped Capturability and Push Recovery via a Switched-Systems Characterization of Dynamic Balance. IEEE Trans. Robot. 2023, 39, 2111–2130. [Google Scholar] [CrossRef]
- Yu, J.; Tan, M.; Chen, J.; Zhang, J. A Survey on CPG-Inspired Control Models and System Implementation. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 441–456. [Google Scholar] [CrossRef] [PubMed]
- Shan, J.; Nagashima, F.; Laborator, F. Neural Locomotion Controller Design and Implementation for Humanoid Robot HOAP-1. In Proceedings of the 20th Annual Conference of the Robotics Society of Japan, Osaka, Japan, 12–14 October 2002. [Google Scholar]
- Kimura, H.; Fukuoka, Y.; Cohen, A.H. Adaptive Dynamic Walking of a Quadruped Robot on Natural Ground Based on Biological Concepts. Int. J. Robot. Res. 2007, 26, 475–490. [Google Scholar] [CrossRef]
- Spröwitz, A.; Pouya, S.; Bonardi, S.; Van Den Kieboom, J.; Möckel, R.; Billard, A.; Dillenbourg, P.; Ijspeert, A. Roombots: Reconfigurable Robots for Adaptive Furniture. IEEE Comput. Intell. Mag. 2010, 5, 20–32. [Google Scholar] [CrossRef]
- Liu, C.; Chen, Q.; Wang, D. CPG-Inspired Workspace Trajectory Generation and Adaptive Locomotion Control for Quadruped Robots. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2011, 41, 867–880. [Google Scholar] [CrossRef]
- Wang, T.; Guo, W.; Li, M.; Zha, F.; Sun, L. CPG Control for Biped Hopping Robot in Unpredictable Environment. J. Bionic Eng. 2012, 9, 29–38. [Google Scholar] [CrossRef]
- Hudson, P.E.; Corr, S.A.; Payne-Davis, R.C.; Clancy, S.N.; Lane, E.; Wilson, A.M. Functional Anatomy of the Cheetah (Acinonyx jubatus) Forelimb. J. Anat. 2011, 218, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.E.; Corr, S.A.; Wilson, A.M. High Speed Galloping in the Cheetah (Acinonyx jubatus) and the Racing Greyhound (Canis Familiaris): Spatio-Temporal and Kinetic Characteristics. J. Exp. Biol. 2012, 215, 2425–2434. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Li, Y.; Rong, X. Gait Generation and Transitions of Quadruped Robot Based on Wilson-Cowan Weakly Neural Networks. In Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics, ROBIO 2010, Tianjin, China, 14–18 December 2010; pp. 19–24. [Google Scholar] [CrossRef]
- Pinto, C.M.A.; Santos, A.P. Modelling Gait Transition in Two-Legged Animals. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4625–4631. [Google Scholar] [CrossRef]
- Bertram, J.E.A.; Gutmann, A. Motions of the Running Horse and Cheetah Revisited: Fundamental Mechanics of the Transverse and Rotary Gallop. J. R. Soc. Interface 2009, 6, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Hildebrand, M. Motions of the Running Cheetah and Horse. J. Mammal. 1959, 40, 481. [Google Scholar] [CrossRef]
- Hildebrand, M. Further Studies on Locomotion of the Cheetah. J. Mammal. 1961, 42, 84–91. [Google Scholar] [CrossRef]
- Nakada, K.; Asai, T.; Amemiya, Y. Biologically-Inspired Locomotion Controller for a Quadruped Walking Robot: Analog IC Implementation of a CPG-Based Controller. J. Robot. Mechatron. 2004, 16, 397. [Google Scholar] [CrossRef]
- Hildebrand, M.; Hurley, J.P. Energy of the Oscillating Legs of a Fast-moving Cheetah, Pronghorn, Jackrabbit, and Elephant. J. Morphol. 1985, 184, 23–31. [Google Scholar] [CrossRef]
- Herr, H.M.; McMahon, T.A. Galloping Horse Model. Int. J. Robot. Res. 2001, 20, 26–37. [Google Scholar] [CrossRef]
- De Wit, B.; De Clercq, D.; Aerts, P. Biomechanical Analysis of the Stance Phase during Barefoot and Shod Running. J. Biomech. 2000, 33, 269–278. [Google Scholar] [CrossRef] [PubMed]
- Seyfarth, A.; Geyer, H.; Herr, H. Swing-Leg Retraction: A Simple Control Model for Stable Running. J. Exp. Biol. 2003, 206, 2547–2555. [Google Scholar] [CrossRef] [PubMed]
- Baruzzi, V.; Lodi, M.; Storace, M. Optimization Strategies to Obtain Smooth Gait Transitions through Biologically Plausible Central Pattern Generators. Phys. Rev. E 2024, 109, 014404. [Google Scholar] [CrossRef] [PubMed]
- Hoppensteadt, F.C.; Izhikevich, E.M. Weakly Connected Neural Networks; Springer: New York, NY, USA, 1997; Volume 126. [Google Scholar]
- Wilson, H.R.; Cowan, J.D. Excitatory and Inhibitory Interactions in Localized Populations of Model Neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Cao, J.; Huang, Y. Fabrication and Testing of the Rescue Quadruped Robot for Post-Disaster Search and Rescue Operations. In Proceedings of the 2023 IEEE 3rd International Conference on Electronic Technology, Communication and Information, ICETCI 2023, Changchun, China, 26–28 May 2023. [Google Scholar]
- Ulloa, C.C.; del Cerro, J.; Barrientos, A. Mixed-Reality for Quadruped-Robotic Guidance in SAR Tasks. J. Comput. Des. Eng. 2023, 10, 1479–1489. [Google Scholar] [CrossRef]
- He, J.; Shao, J.; Sun, G.; Shao, X. Survey of Quadruped Robots Coping Strategies in Complex Situations. Electronics 2019, 8, 1414. [Google Scholar] [CrossRef]
- Fan, Y.; Pei, Z.; Wang, C.; Li, M.; Tang, Z.; Liu, Q. A Review of Quadruped Robots: Structure, Control, and Autonomous Motion. Adv. Intell. Syst. 2024; Early View. [Google Scholar]
- Siregar, B.; Bagustiawan, H.; Sitompul, O.S. Environmental Mapping Automation by Quadruped Robot Using Lidar Technology. In Proceedings of the ICEEIE 2023—International Conference on Electrical, Electronics and Information Engineering, Virtual, 28–29 September 2023. [Google Scholar]
- Skrba, L.; Reveret, L.; Hétroy, F.; Cani, M.P.; O’Sullivan, C. Animating Quadrupeds: Methods and Applications. Comput. Graph. Forum 2009, 28, 1541–1560. [Google Scholar] [CrossRef]






| Year | Authors | Key Features | Speed | Weight | Degrees of Freedom |
|---|---|---|---|---|---|
| 2004 | Palmer and Marhefka [6]. | Mammal-like limb configuration, three degrees of freedom. | 25 km/h | 75 kg | 3 |
| 2011 | Lewis M. A. et al. [7]. | Back member employing biarticular muscle concept, light leg generating 90 N of force. | Not specified | Leg: 1.7 kg | Not specified |
| 2012 | Boston Dynamics [8]. | Methanol combustion engine, hydraulic drive system, 14 degrees of freedom. | 29 km/h | 154 kg | 14 |
| 2013 | BioRob [9]. | Lightweight, 8 degrees of freedom. | 1.42 m/s | 1 kg | 8 |
| 2016 | Steve W. Heim et al. [10]. | Active tail for legged robots to simplify control via decoupling objectives. | Not specified | Not specified | Not specified |
| 2023 | Hua Chen et al. [11]. | Capturability and push recovery via switched systems for dynamic balance. | Not specified | Not specified | Not specified |
| Year | Authors | Locomotion | Methodology |
|---|---|---|---|
| 2002 | J. Shan and F. Nagashima [13]. | Humanoid Biped | CPG circuit modeled by recurrent neural networks. |
| 2007 | H. Kimura, Y. Fukuoka, and A. H. Cohen [14]. | Quadruped | Artificial neural system model consisting of a CPG and reflexes, reflex mechanisms, and spring mechanisms. |
| 2010 | A. Spröwitz et al. [15]. | Reconfigurable | CPG as a distributed motion controller connected with certain optimization algorithms. |
| 2011 | C. Liu, Q. Chen, and D. Wang [16]. | Quadruped | CPG-based 3D workspace trajectory generator and a motion engine. |
| 2012 | T. Wang et al. [17]. | Biped Hopping | Two-level CPG control mechanism coupled with feedback information. |
| Variables | Unit | Values | |
|---|---|---|---|
| Intergirdle distance | mm | 760 ± 10 | |
| Mass | kg | 48 ± 6 | |
| Forelimb length (without scapula) | mm | 670 ± 10 | |
| Hindlimb length | mm | 820 ± 10 | |
| Scapula length | mm | 160 ± 10 | |
| Forelimb segment without scapula (% forelimb length) | Humerus | % | 34.0 ± 1.3 |
| Radius | % | 38.8 ± 1.2 | |
| Metacarpal | % | 15.0 ± 0.7 | |
| Phalanges | % | 12.2 ± 0.3 | |
| Femur | % | 31.7 ± 0.7 | |
| Hindlimb segment (% hindlimb length) | Tibia | % | 38.0 ± 0.9 |
| Metatarsal | % | 19.2 ± 0.5 | |
| Phalanges | % | 11.1 ± 0.5 | |
| Variables | Size [mm] | |
|---|---|---|
| Intergirdle distance (Forelimb–Hindlimb) | 255 | |
| Intergirdle distance (Left–Right) | 120 | |
| Forelimb length (without scapula) | 225 | |
| Hindlimb length | 27.5 | |
| Scapula length | 55 | |
| Forelimb segment without scapula | Humerus | 75 |
| Radius–Metacarpal | 120 | |
| Hindlimb segment | Femur | 90 |
| Tibia | 105 | |
| Metatarsal | 55 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Flores, E.A.; Hernández-Rodríguez, Y.M.; Munguía-Fuentes, R.; Bayareh-Mancilla, R.; Cigarroa-Mayorga, O.E. Acinonyx jubatus-Inspired Quadruped Robotics: Integrating Neural Oscillators for Enhanced Locomotion Control. Biomimetics 2024, 9, 318. https://doi.org/10.3390/biomimetics9060318
Hernández-Flores EA, Hernández-Rodríguez YM, Munguía-Fuentes R, Bayareh-Mancilla R, Cigarroa-Mayorga OE. Acinonyx jubatus-Inspired Quadruped Robotics: Integrating Neural Oscillators for Enhanced Locomotion Control. Biomimetics. 2024; 9(6):318. https://doi.org/10.3390/biomimetics9060318
Chicago/Turabian StyleHernández-Flores, Eric Alberto, Yazmín Mariela Hernández-Rodríguez, Rosario Munguía-Fuentes, Rafael Bayareh-Mancilla, and Oscar Eduardo Cigarroa-Mayorga. 2024. "Acinonyx jubatus-Inspired Quadruped Robotics: Integrating Neural Oscillators for Enhanced Locomotion Control" Biomimetics 9, no. 6: 318. https://doi.org/10.3390/biomimetics9060318
APA StyleHernández-Flores, E. A., Hernández-Rodríguez, Y. M., Munguía-Fuentes, R., Bayareh-Mancilla, R., & Cigarroa-Mayorga, O. E. (2024). Acinonyx jubatus-Inspired Quadruped Robotics: Integrating Neural Oscillators for Enhanced Locomotion Control. Biomimetics, 9(6), 318. https://doi.org/10.3390/biomimetics9060318







