Design, Characterization, and Preliminary Assessment of a Two-Degree-of-Freedom Powered Ankle–Foot Prosthesis
Abstract
1. Introduction
2. Materials and Methods
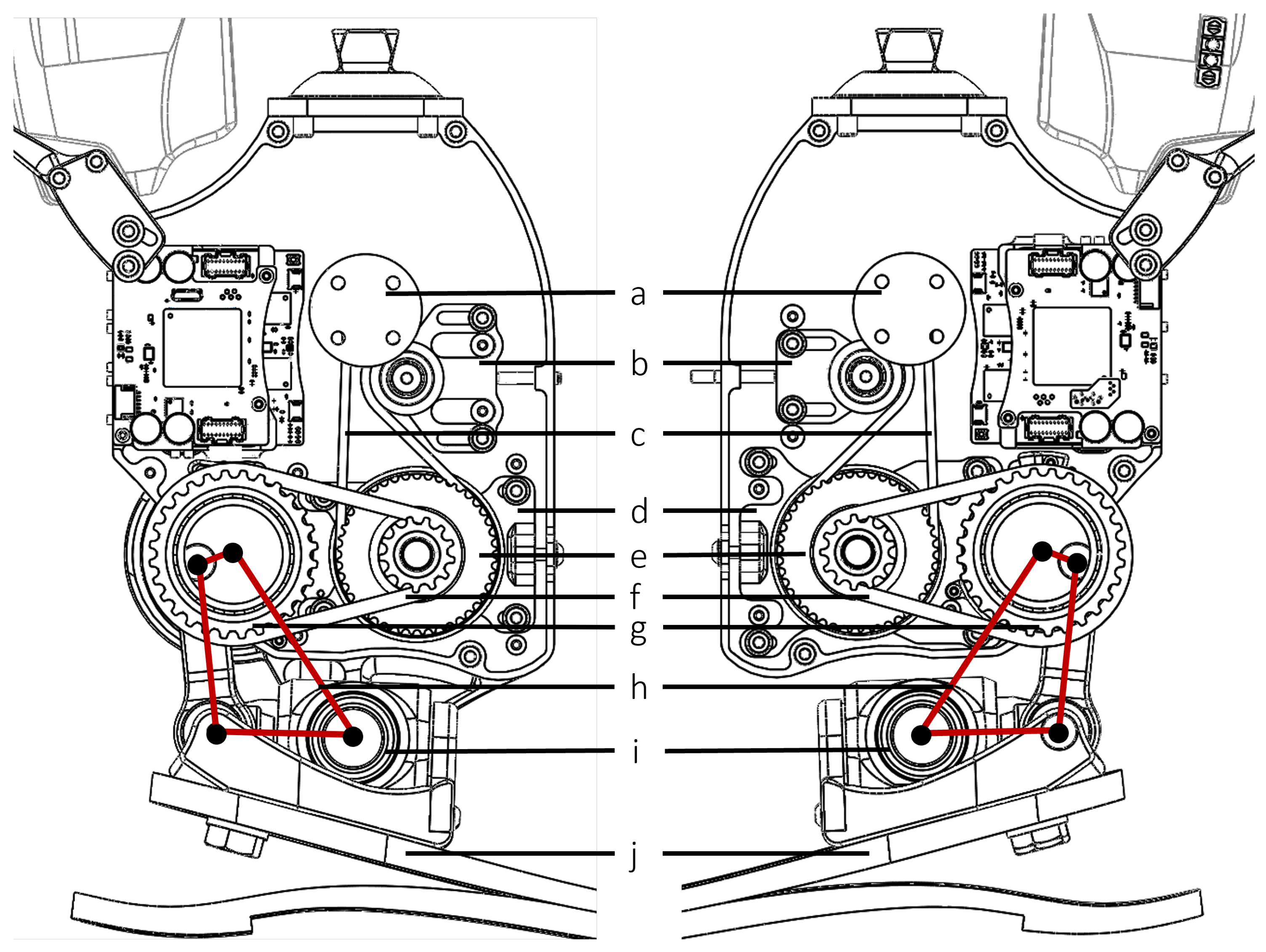
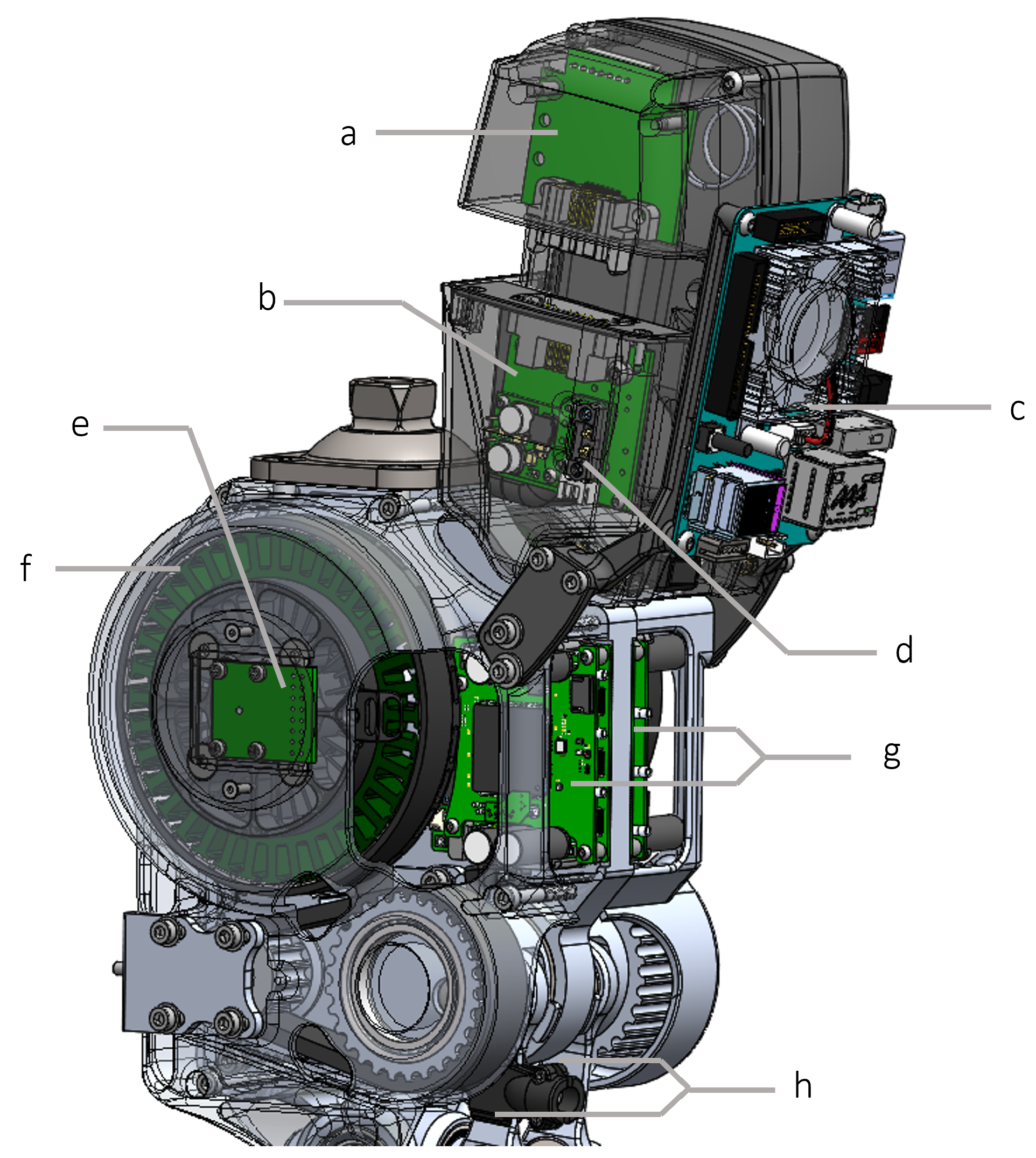
2.1. Mechanical Design
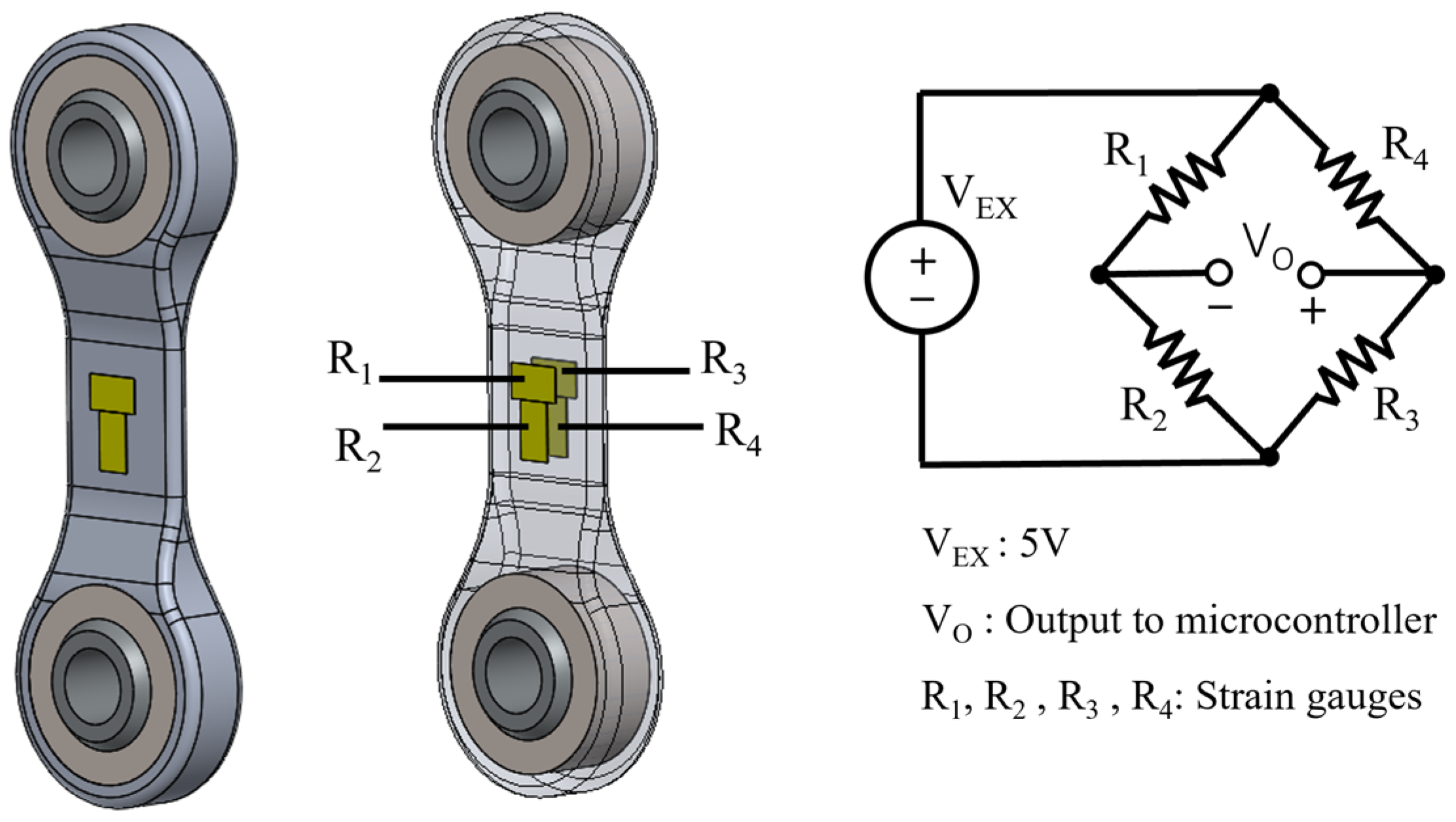
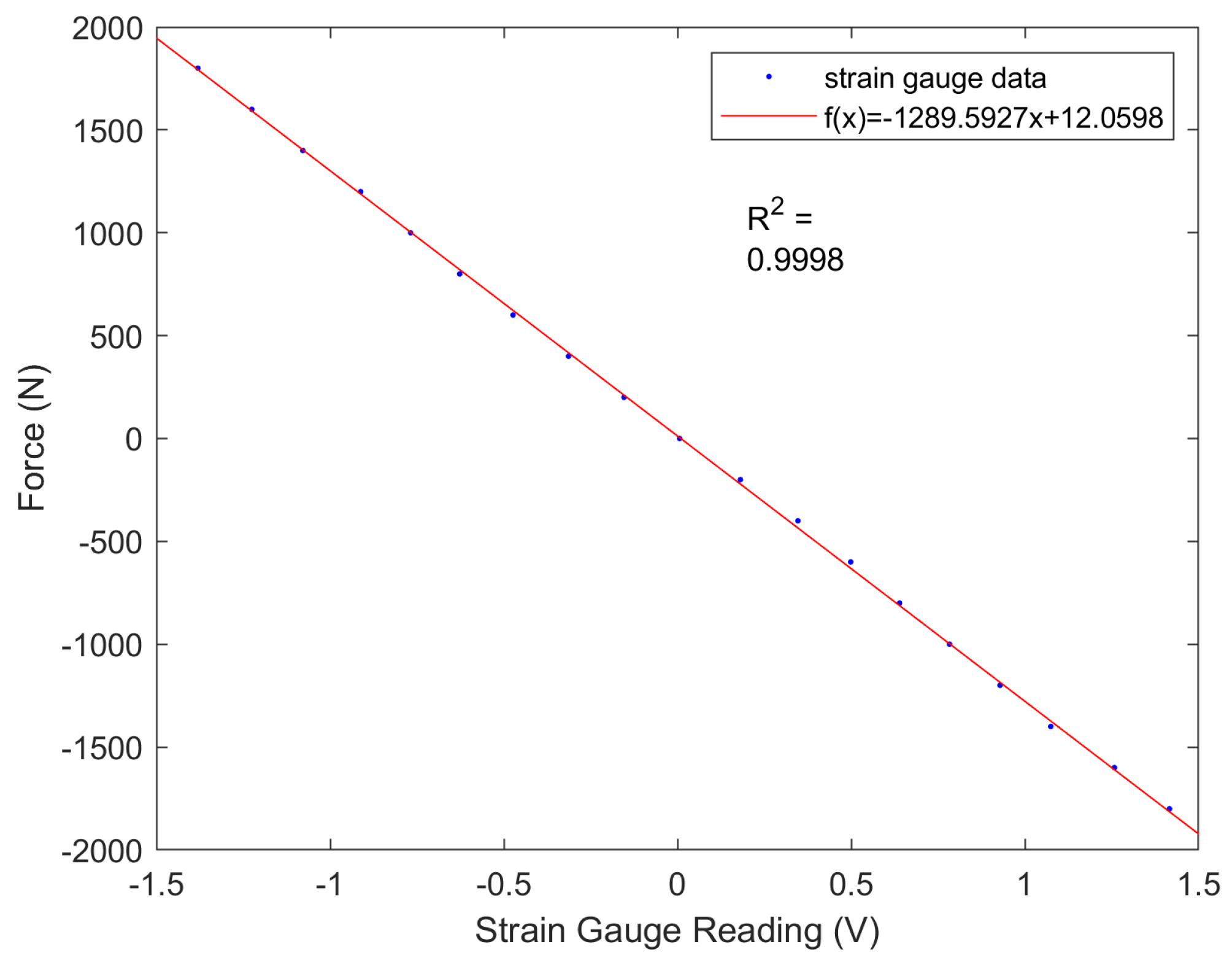
2.2. Force and Torque Sensing
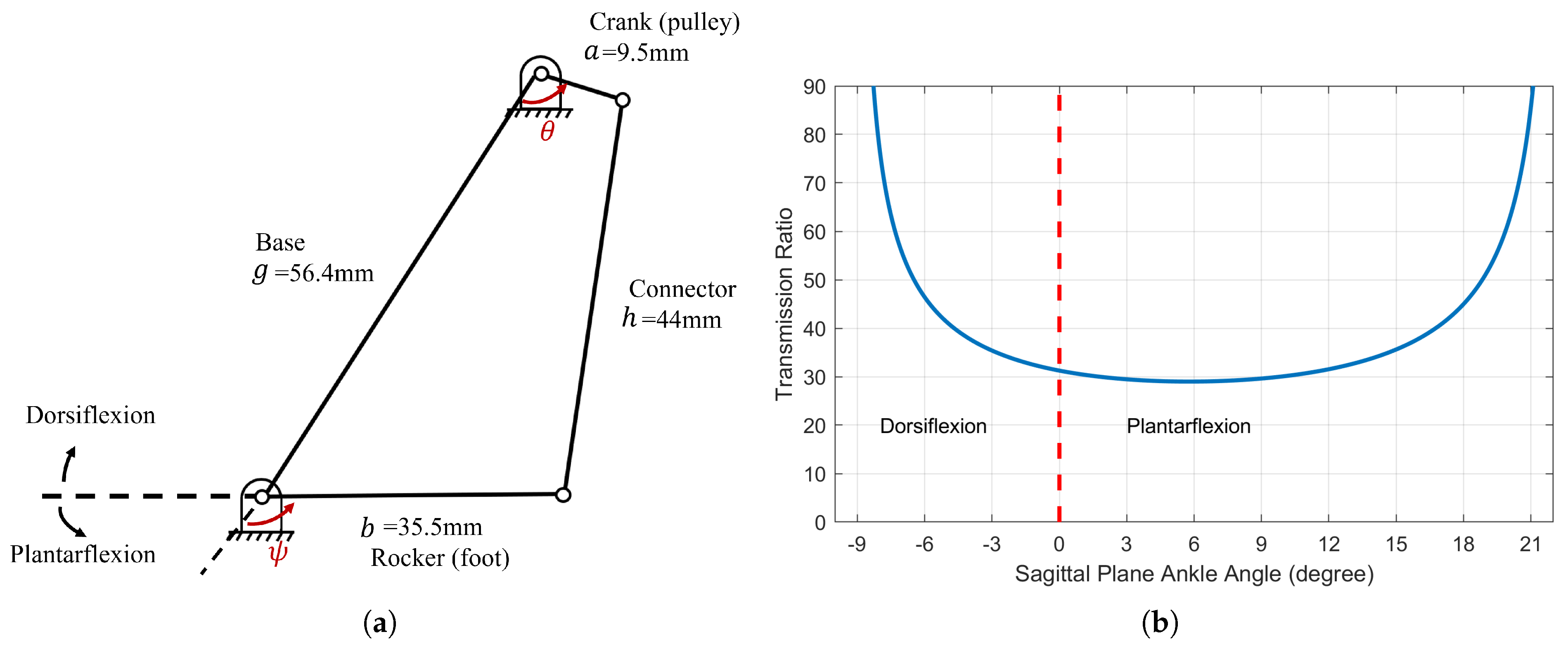
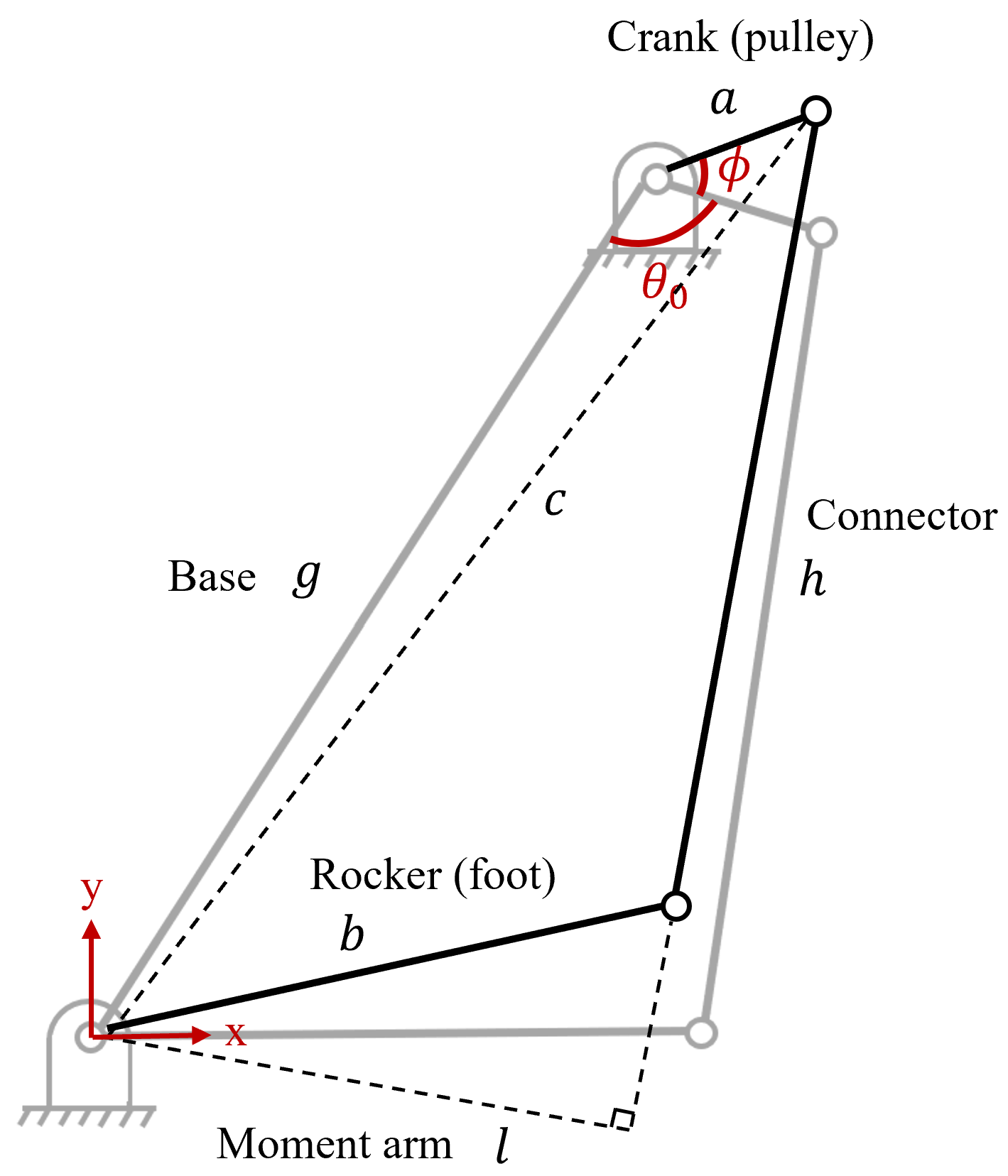
2.3. Kinematics Model
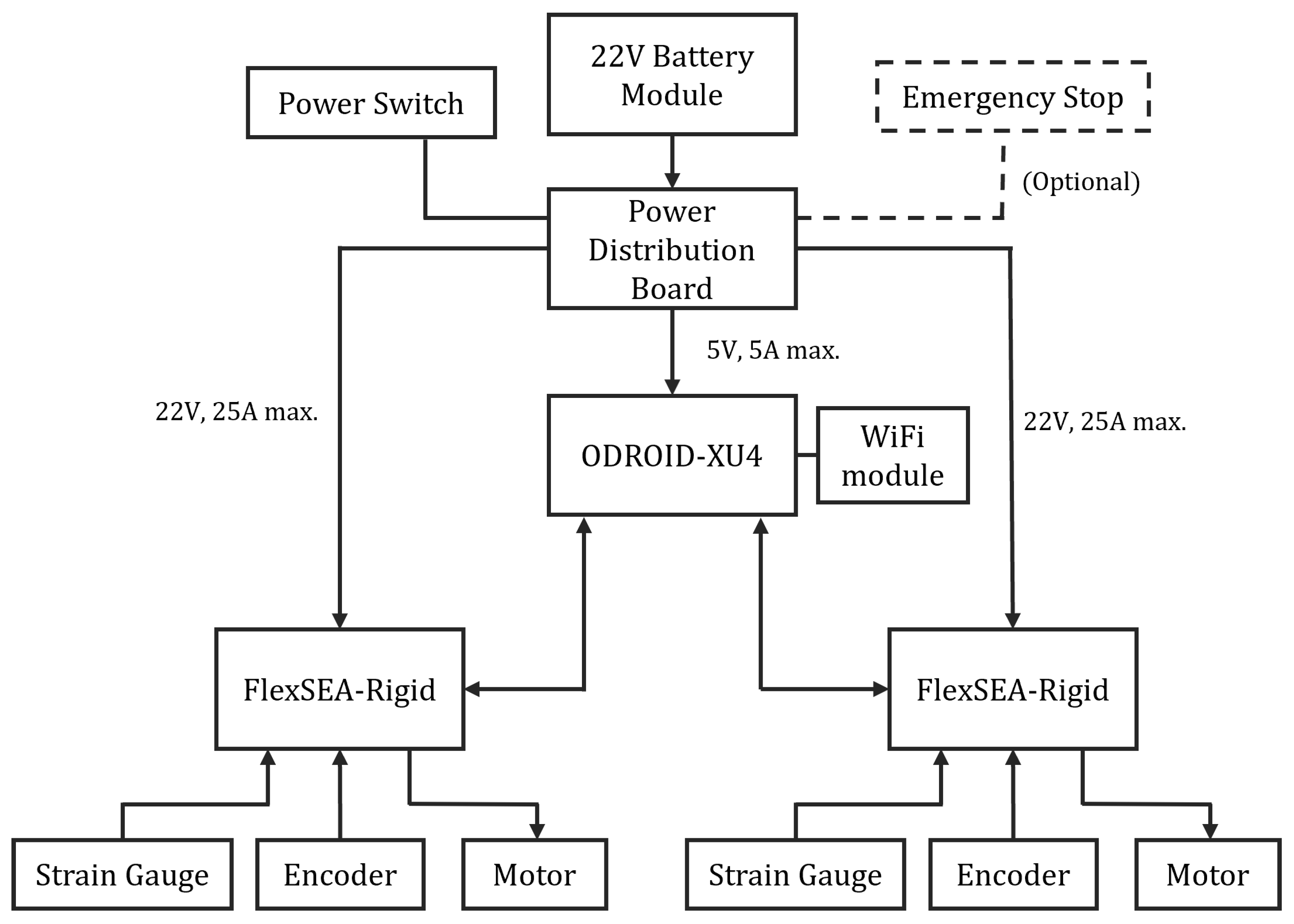
2.4. Electronics and Embedded System
2.5. Control System Design and Evaluation
3. Results
3.1. Integration of Dual Two-Stage Belt Drives and Four-Bar Linkage in Compact Design
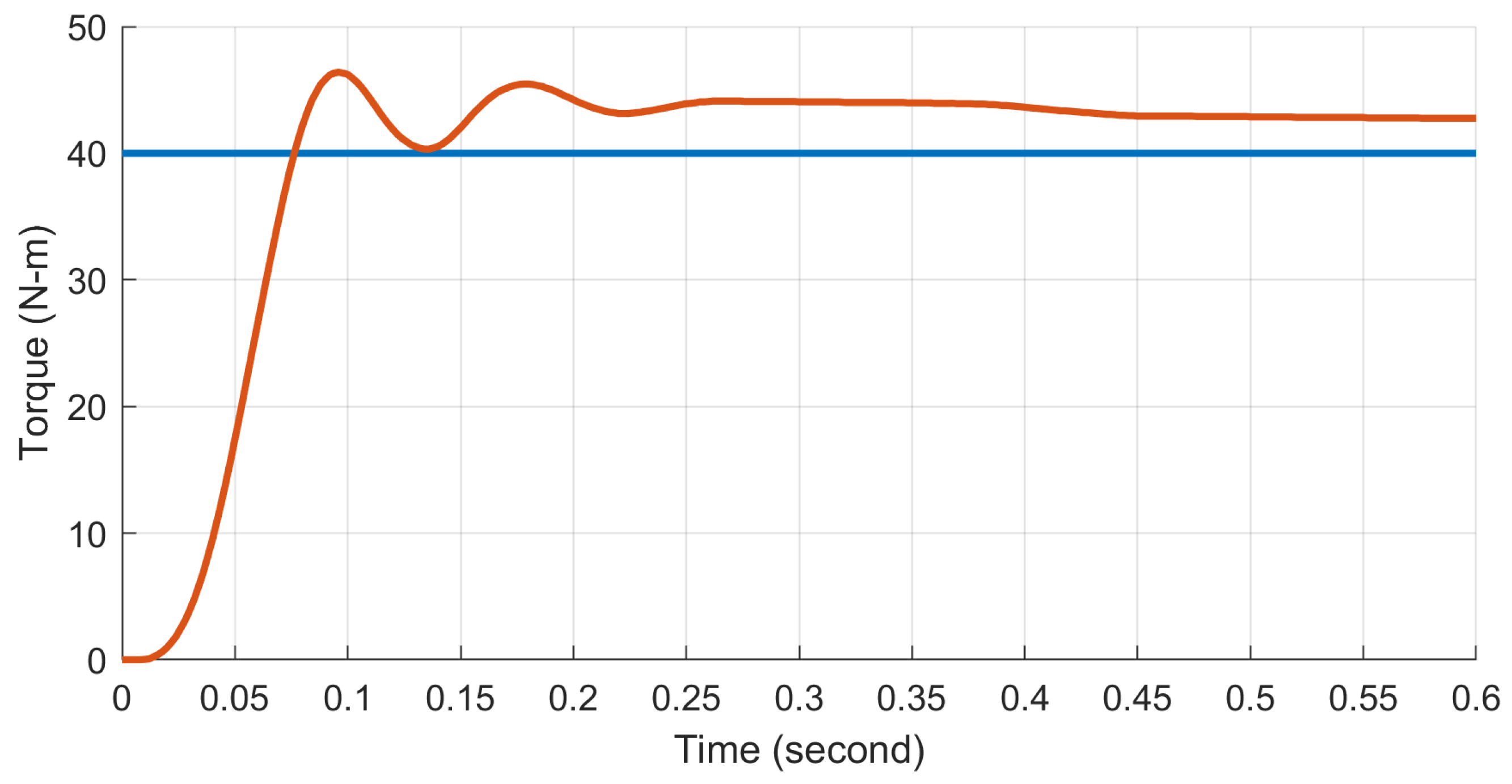
3.2. Dynamic Responses of the System
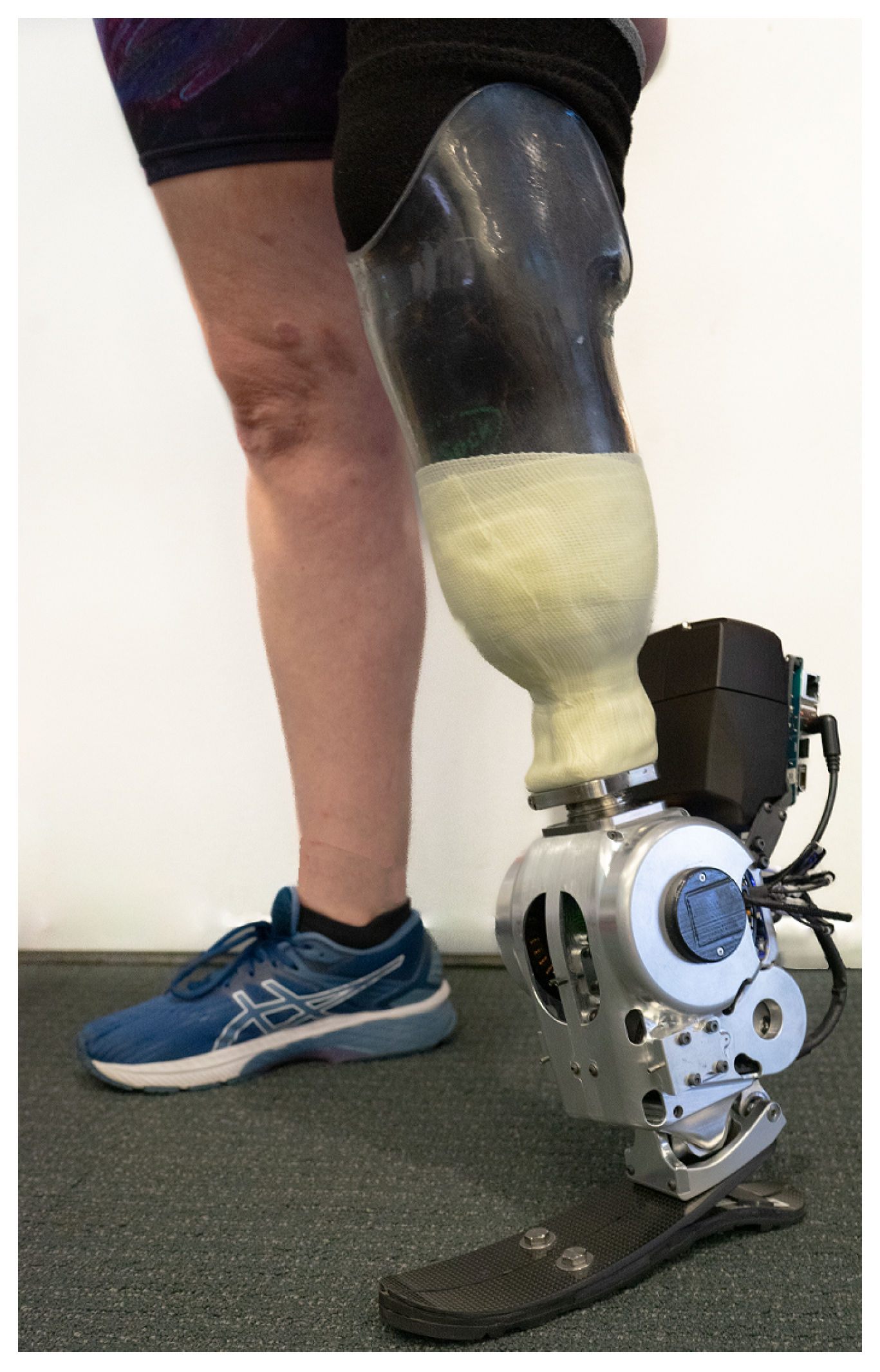
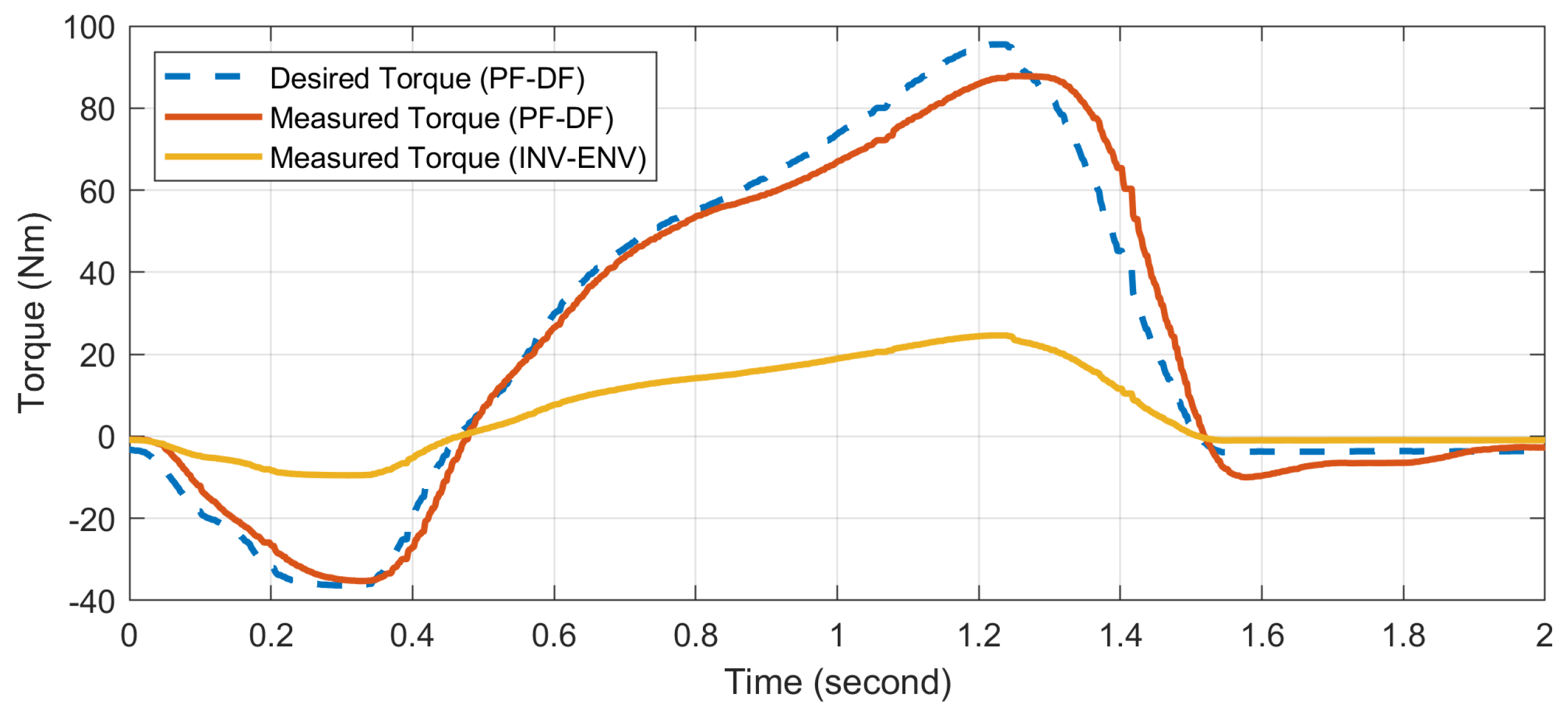
3.3. Prosthesis Performance Evaluation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Herr, H.M.; Grabowski, A.M. Bionic Ankle-Foot Prosthesis Normalizes Walking Gait for Persons with Leg Amputation. Proc. R. Soc. 2012, 279, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Au, S.K.-W. Powered Ankle-Foot Prosthesis for the Improvement of Amputee Walking Economy. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Montgomery, J.R.; Grabowski, A.M. Use of a powered ankle-foot prosthesis reduces the metabolic cost of uphill walking and improves leg work symmetry in people with transtibial amputations. J. R. Soc. Interface 2018, 15, 20180442. [Google Scholar] [CrossRef] [PubMed]
- Ottobock. Empower Ankle. Available online: https://www.ottobockus.com/prosthetics/lower-limb-prosthetics/solution-overview/empower-ankle/ (accessed on 1 October 2023).
- Össur. PROPRIO FOOT®. Available online: https://www.ossur.com/prosthetic-solutions/products/dynamic-solutions/proprio-foot (accessed on 1 October 2023).
- Winter, D.A. Human Balance and Posture Control during Standing and Walking. Gait Posture 1995, 3, 193–214. [Google Scholar] [CrossRef]
- Matsusaka, N. Control of the Medial-Lateral Balance in Walking. Acta Orthop. Scand. 1986, 57, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Clites, T.R.; Carty, M.J.; Ullauri, J.B.; Carney, M.E.; Mooney, L.M.; Duval, J.F.; Srinivasan, S.S.; Herr, H.M. Proprioception from a Neurally Controlled Lower-Extremity Prosthesis. Sci. Transl. Med. 2018, 10, eaap8373. [Google Scholar] [CrossRef] [PubMed]
- Bellman, R.D.; Holgate, M.A.; Sugar, T.G. SPARKy 3: Design of an Active Robotic Ankle Prosthesis with Two Actuated Degrees of Freedom using Regenerative Kinetics. In Proceedings of the 2008 2nd IEEE RAS EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008. [Google Scholar] [CrossRef]
- Ficanha, E.M.; Ribeiro, G.A.; Dallali, H.; Rastgaar, M. Design and Preliminary Evaluation of a Two DOFs Cable-Driven Ankle-Foot Prosthesis with Active Dorsiflexion-Plantarflexion and Inversion-Eversion. Front. Bioeng. Biotechnol. 2016, 4, 36. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Chen, T.; Chen, T.; Collins, S.H. An Ankle–Foot Prosthesis Emulator with Control of Plantarflexion and Inversion–Eversion Torque. IEEE Trans. Robot. 2018, 34, 1183–1194. [Google Scholar] [CrossRef]
- Kim, M.; Collins, S.H. Step-to-Step Ankle Inversion/Eversion Torque Modulation Can Reduce Effort Associated with Balance. Front. Neurorobot. 2017, 11, 62. [Google Scholar] [CrossRef] [PubMed]
- Jang, W.-S.; Kim, D.Y.; Choi, Y.S.; Kim, Y.J. Self-Contained 2-DOF Ankle-Foot Prosthesis with Low-Inertia Extremity for Agile Walking on Uneven Terrain. IEEE Robot. Autom. Lett. 2021, 6, 8134–8141. [Google Scholar] [CrossRef]
- Hill, D.A. A 3D Neuromuscular Model of the Human Ankle-Foot Complex Based on Multi-Joint Biplanar Fluoroscopy Gait Analysis. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2018. [Google Scholar]
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating Musculoskeletal Dynamics and Neuromuscular Control to Study Human and Animal Movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef] [PubMed]
- Bovi, G.; Rabuffetti, M.; Mazzoleni, P.; Ferrarin, M. A Multiple-Task Gait Analysis Approach: Kinematic, Kinetic and EMG Reference Data for Healthy Young and Adult Subjects. Gait Posture 2011, 33, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Uicker, J.J., Jr.; Pennock, G.R.; Shigley, J.E. Theory of Machines and Mechanisms; Oxford University Press: Oxford, UK, 2017; Chapter 3. [Google Scholar]
- Raspberry Pi. Available online: https://www.raspberrypi.com/ (accessed on 2 October 2023).
- Duval, J.-F.; Herr, H.M. FlexSEA: Flexible, Scalable Electronics Architecture for Wearable Robotic Applications. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016. [Google Scholar] [CrossRef]
- Hogan, N. Impedance control: An approach to manipulation: Part 1—Theory, Part 2—Implementation, and Part 3—Applications. ASME J. Dyn. Syst. Meas. Control 1985, 107, 1–24. [Google Scholar] [CrossRef]
- Sup, F.; Bohara, A.; Goldfarb, M. Design and Control of a Powered Transfemoral Prosthesis. Int. J. Robot. Res. 2008, 27, 263–273. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Weight without Battery (kg) | 2.42 |
| Battery Weight (kg) | 0.33 |
| Height a (mm) | 210.8 |
| Width (mm) | 126.6 |
| Max. Allowable Inversion (deg) | 13.5 |
| Max. Allowable Eversion (deg) | 13.5 |
| Max. Allowable Dorsiflexion (deg) | 9 |
| Max. Allowable Plantarflexion (deg) | 21 |
| Transmission Ratio | 32 ± 28 |
| Peak PF-DF * Torque (N·m) | 110 |
| Peak INV-EV * Torque (N·m) | 44 |
| Battery Voltage (V) | 22.2 |
| Peak Current (A) | 50 |
| Motor Torque Constant (N·m/A) | 0.088 |
| Actuator Torque Bandwidth (Hz) | 9.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, T.-H.; Song, H.; Shu, T.; Qiao, J.; Yeon, S.H.; Carney, M.; Mooney, L.; Duval, J.-F.; Herr, H. Design, Characterization, and Preliminary Assessment of a Two-Degree-of-Freedom Powered Ankle–Foot Prosthesis. Biomimetics 2024, 9, 76. https://doi.org/10.3390/biomimetics9020076
Hsieh T-H, Song H, Shu T, Qiao J, Yeon SH, Carney M, Mooney L, Duval J-F, Herr H. Design, Characterization, and Preliminary Assessment of a Two-Degree-of-Freedom Powered Ankle–Foot Prosthesis. Biomimetics. 2024; 9(2):76. https://doi.org/10.3390/biomimetics9020076
Chicago/Turabian StyleHsieh, Tsung-Han, Hyungeun Song, Tony Shu, Junqing Qiao, Seong Ho Yeon, Matthew Carney, Luke Mooney, Jean-François Duval, and Hugh Herr. 2024. "Design, Characterization, and Preliminary Assessment of a Two-Degree-of-Freedom Powered Ankle–Foot Prosthesis" Biomimetics 9, no. 2: 76. https://doi.org/10.3390/biomimetics9020076
APA StyleHsieh, T.-H., Song, H., Shu, T., Qiao, J., Yeon, S. H., Carney, M., Mooney, L., Duval, J.-F., & Herr, H. (2024). Design, Characterization, and Preliminary Assessment of a Two-Degree-of-Freedom Powered Ankle–Foot Prosthesis. Biomimetics, 9(2), 76. https://doi.org/10.3390/biomimetics9020076







