FTDZOA: An Efficient and Robust FS Method with Multi-Strategy Assistance
Abstract
1. Introduction
- The fractional order search strategy is introduced to improve the exploitation of ZOA in solving FS problems.
- The introduction of the triple mean point guidance strategy effectively improves the exploration capability of ZOA and also ensures the exploitation of the algorithm.
- Introducing a differential strategy to enhance the global exploration capability of ZOA.
- A FS method based on FTDZOA is proposed by combining the above strategies.
- The FTDZOA-based FS method is used for 23 FS problems and achieves efficient performance.
2. Zebra Optimization Algorithm
2.1. Initialization Phase
2.2. Foraging Phase
2.3. Defense Phase
2.4. Implementation of ZOA
3. Mathematical Modeling of FTDZOA
3.1. Fractional Order Search Strategy
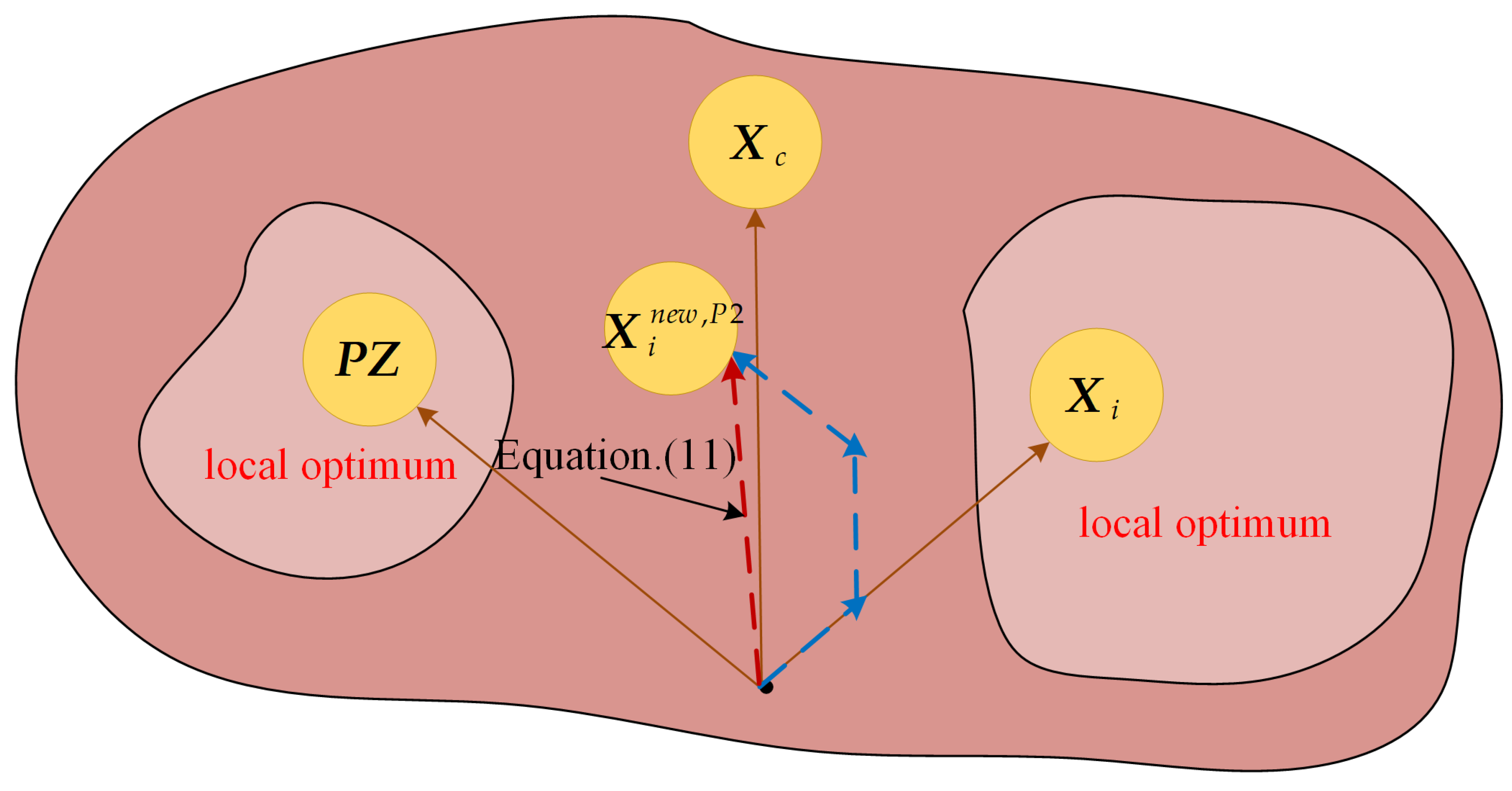
3.2. Triple Mean Point Guidance Strategy
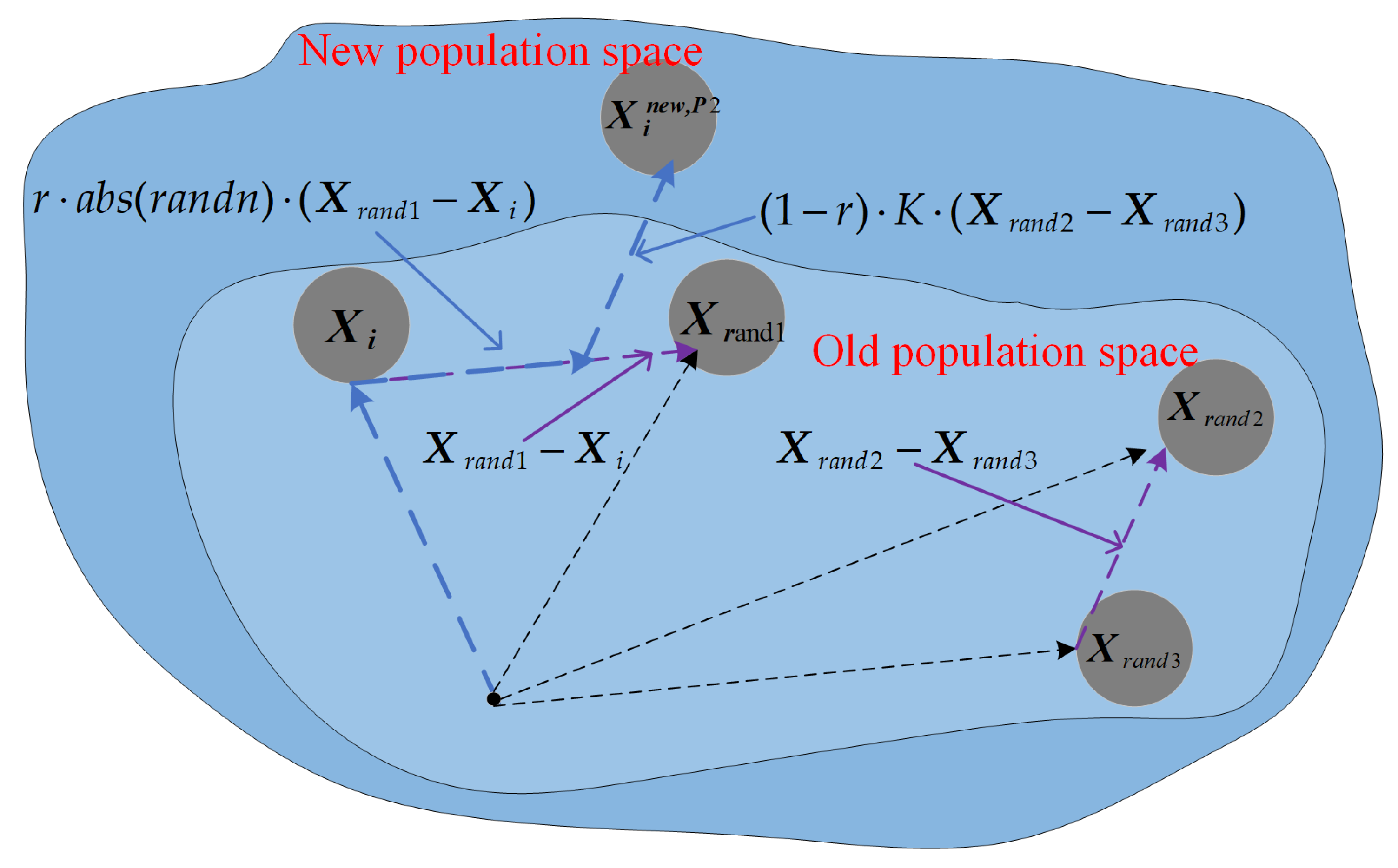
3.3. Differential Strategy
3.4. Implementation of FTDZOA
4. Results and Discussion
4.1. FS Optimization Model
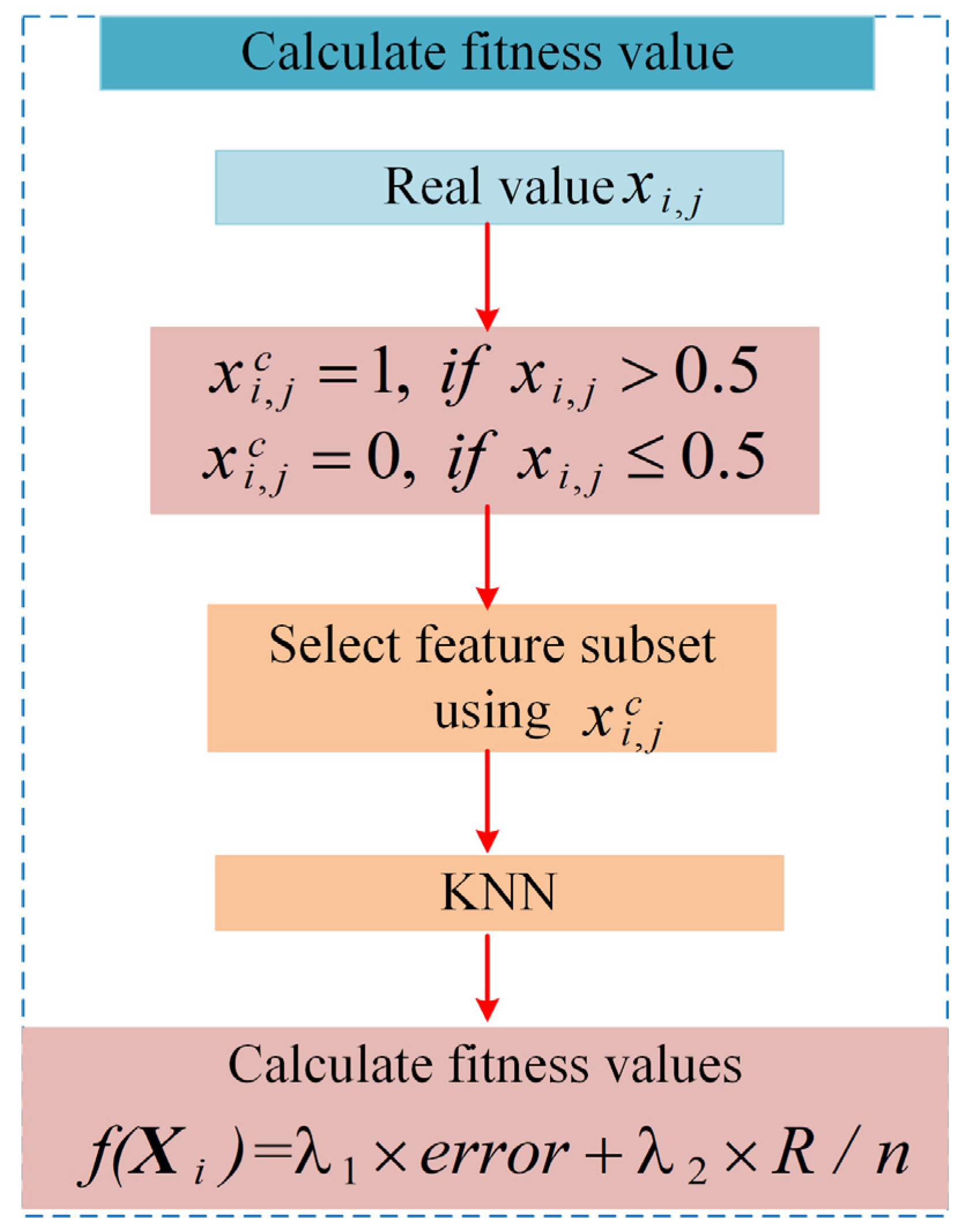
- Step 1: real-valued individual is converted to a discrete-valued individual , expressed as the following Equation (14):
- Step 2: Selection of feature subsets in the original dataset by discrete-valued individual , where means that the feature is selected and vice versa means that the feature is not selected.
- Step 3: The selected subset of features is used to calculate the classification accuracy using KNN. In this paper, K takes the value of 5.
- Step 4: Calculate the fitness value using Equation (13).
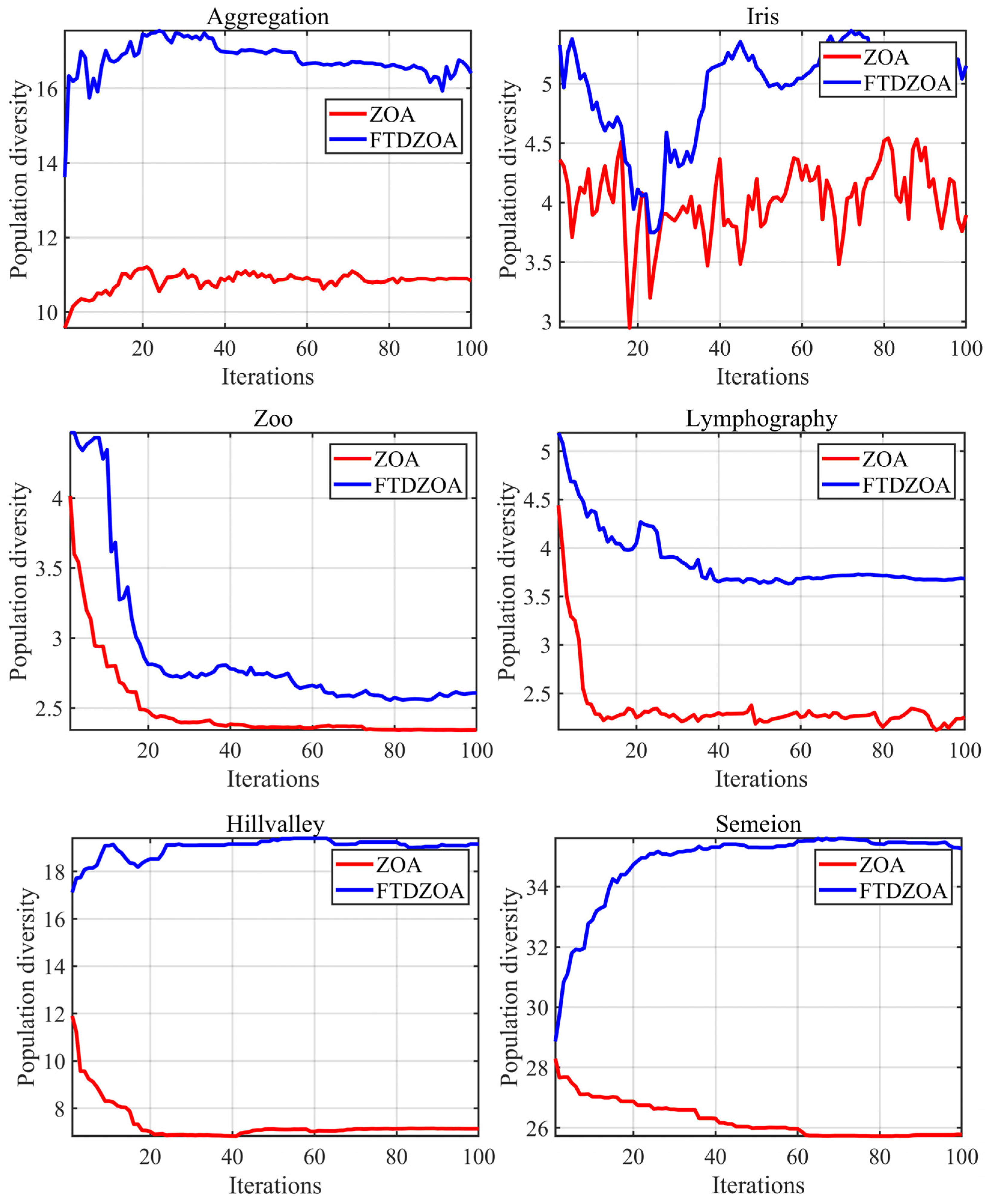
4.2. Population Diversity Analysis
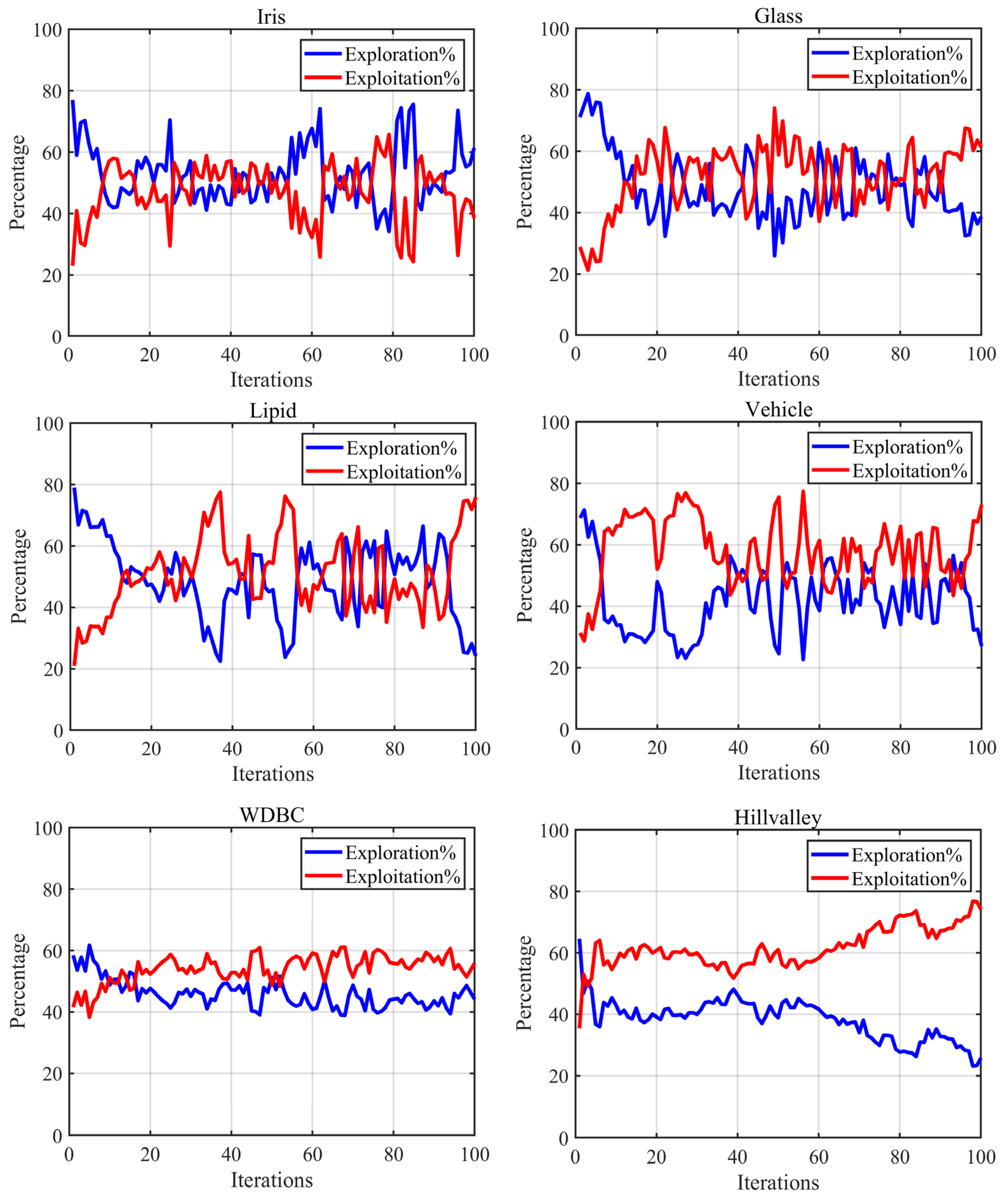
4.3. Exploration-Exploitation Balance Analysis
4.4. Strategies Effectiveness Testing
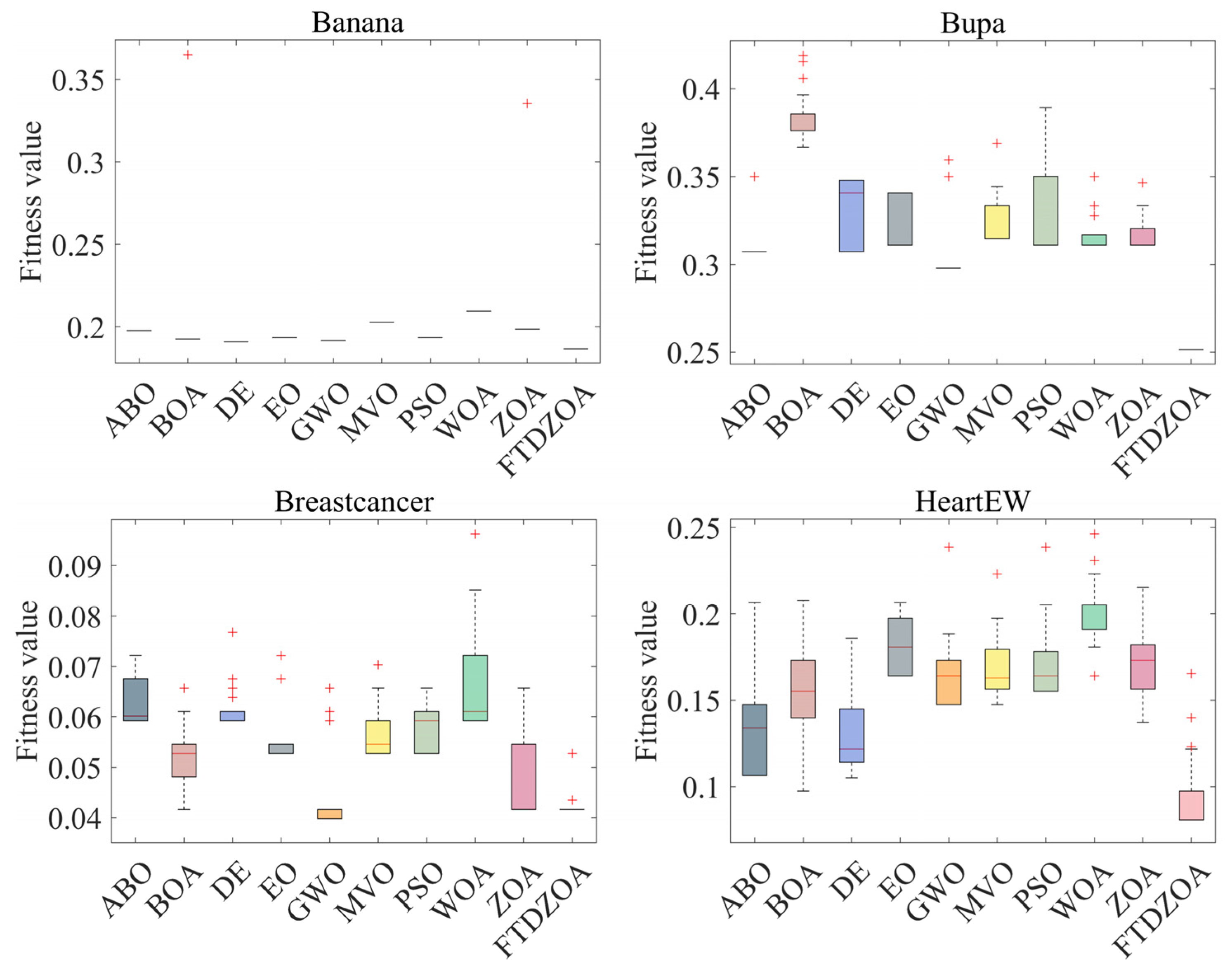
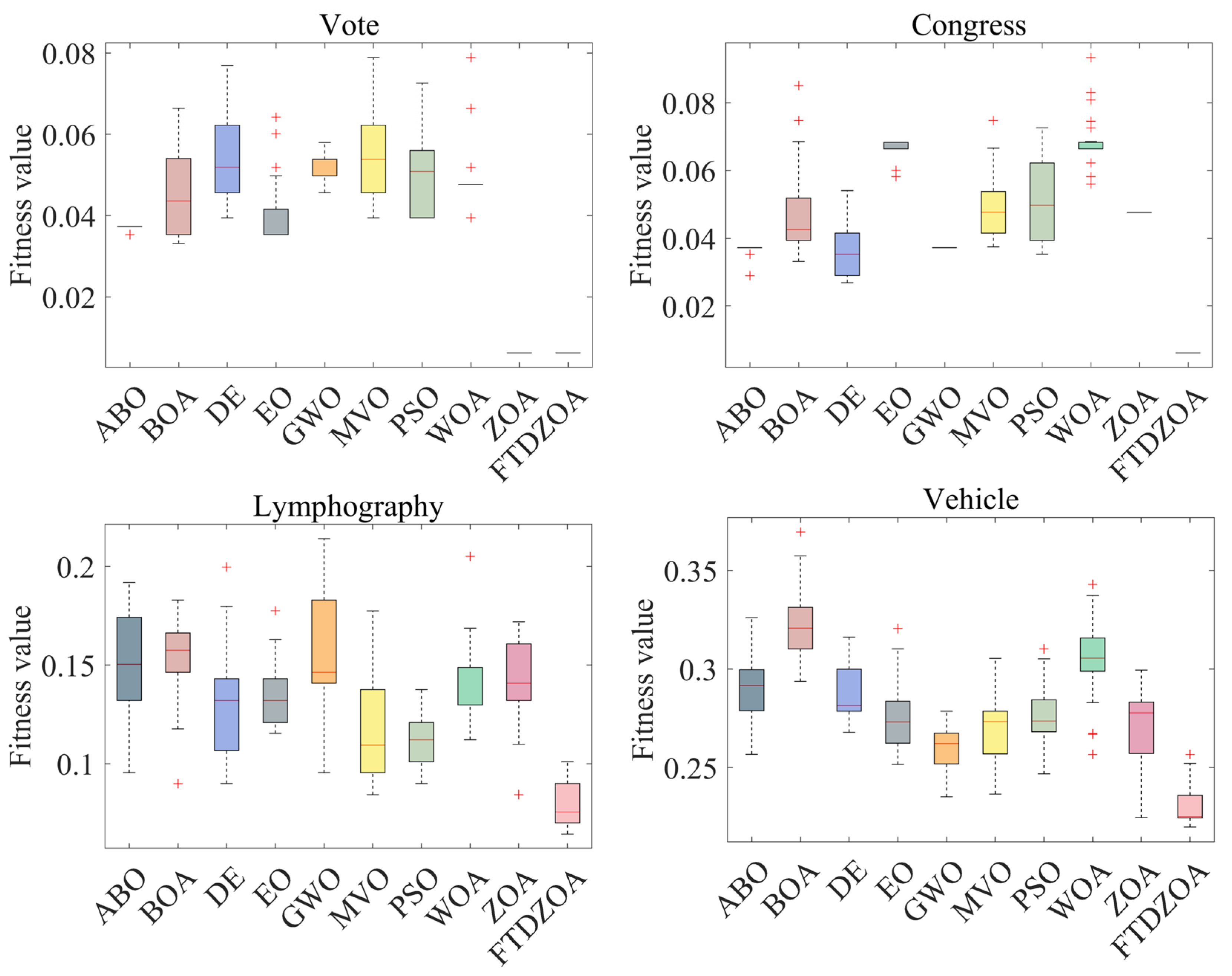
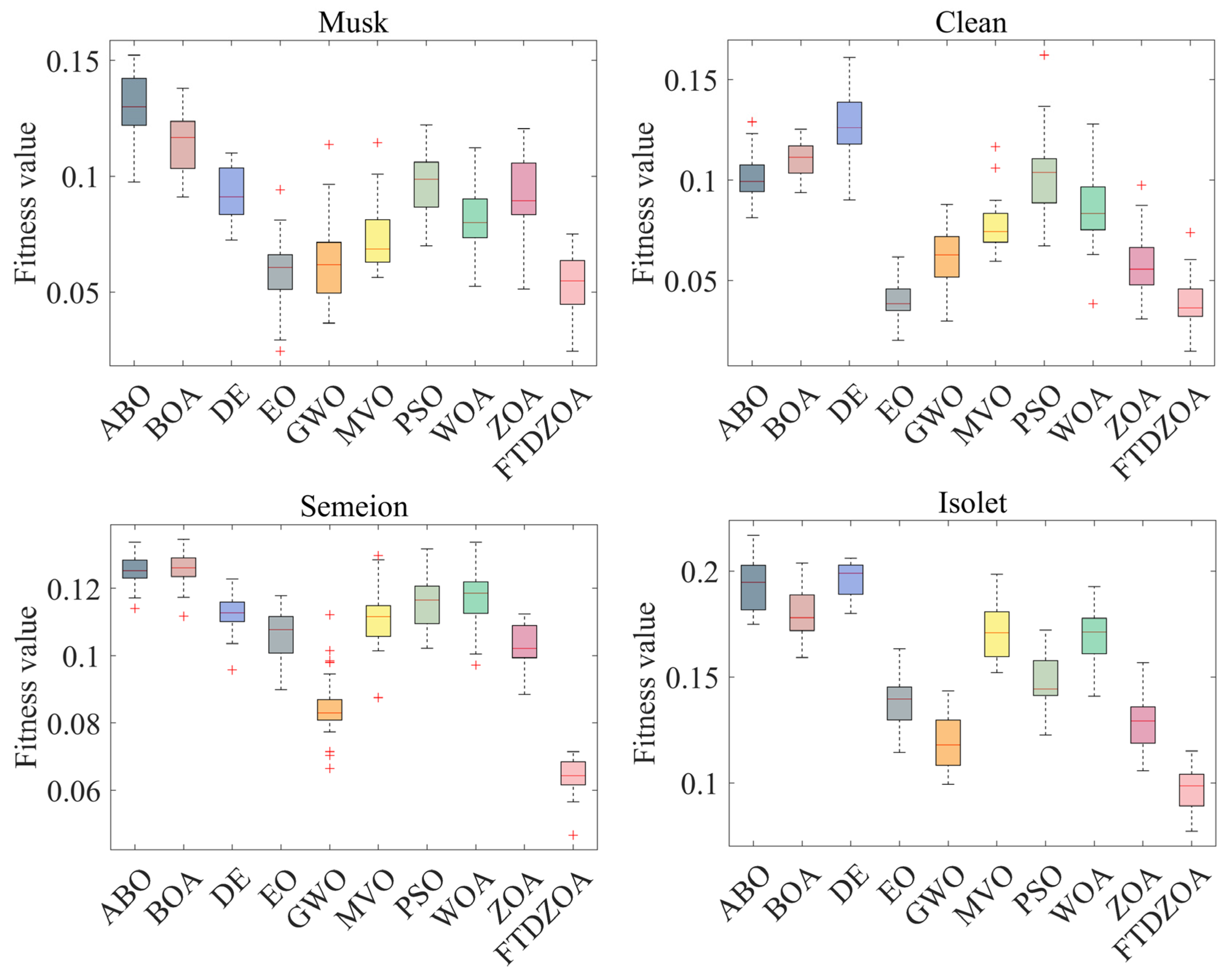
4.5. Fitness Value Analysis
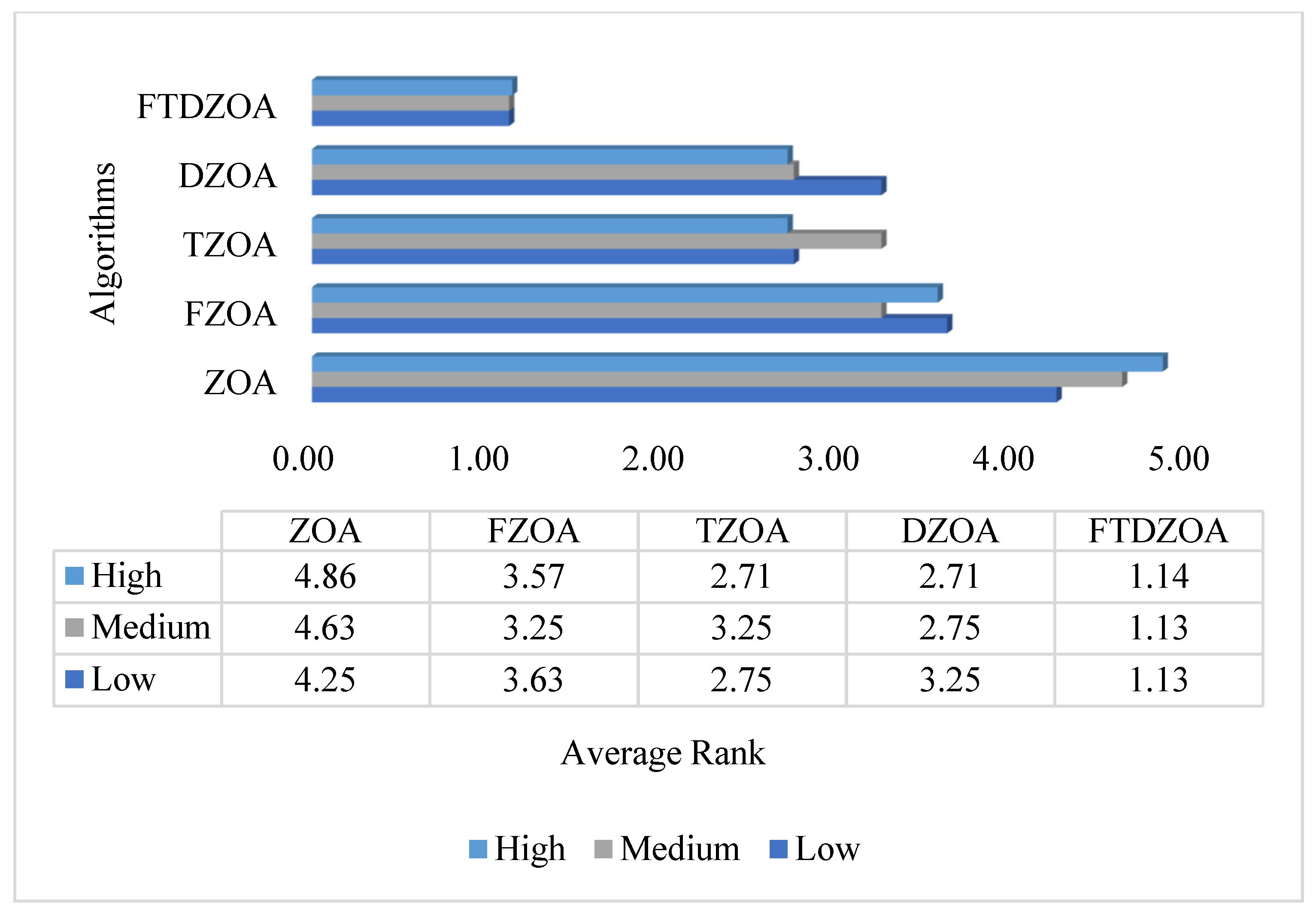
4.6. Nonparametric Analysis
4.7. Convergence Analysis
4.8. Feature Subset and Accuracy Analysis
4.9. Runtime Analysis
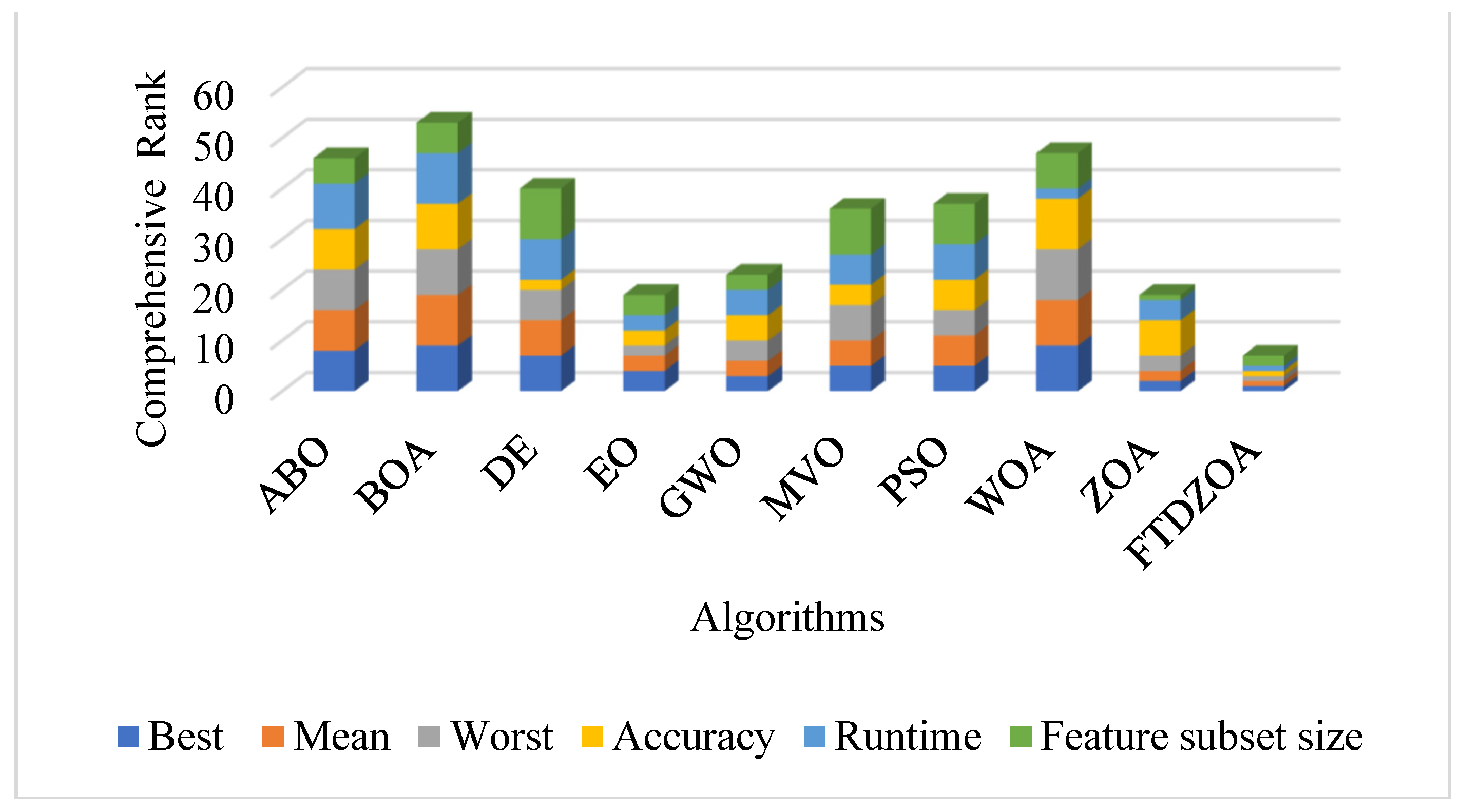
4.10. Synthesized Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Albukhanajer, W.A.; Briffa, J.A.; Jin, Y. Evolutionary multiobjective image feature extraction in the presence of noise. IEEE Trans. Cybern. 2014, 45, 1757–1768. [Google Scholar] [CrossRef]
- Sun, T.; Lv, J.; Zhao, X.; Li, W.; Zhang, Z.; Nie, L. In vivo liver function reserve assessments in alcoholic liver disease by scalable photoacoustic imaging. Photoacoustics 2023, 34, 100569. [Google Scholar] [CrossRef]
- Huang, H.H.; Shu, J.; Liang, Y. MUMA: A multi-omics meta-learning algorithm for data interpretation and classification. IEEE J. Biomed. Health Inform. 2024, 28, 2428–2436. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Song, J.; Zhou, Q.; Rasol, J.; Ma, L. Planet craters detection based on unsupervised domain adaptation. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7140–7152. [Google Scholar] [CrossRef]
- Zhang, C.; Ge, H.; Zhang, S.; Liu, D.; Jiang, Z.; Lan, C.; Hu, R. Hematoma evacuation via image-guided para-corticospinal tract approach in patients with spontaneous intracerebral hemorrhage. Neurol. Ther. 2021, 10, 1001–1013. [Google Scholar] [CrossRef]
- Huang, H.; Wu, N.; Liang, Y.; Peng, X.; Shu, J. SLNL: A novel method for gene selection and phenotype classification. Int. J. Intell. Syst. 2022, 37, 6283–6304. [Google Scholar] [CrossRef]
- Zawbaa, H.M.; Emary, E.; Grosan, C.; Snasel, V. Large-dimensionality small-instance set feature selection: A hybrid bio-inspired heuristic approach. Swarm Evol. Comput. 2018, 42, 29–42. [Google Scholar] [CrossRef]
- Manbari, Z.; AkhlaghianTab, F.; Salavati, C. Hybrid fast unsupervised feature selection for high-dimensional data. Expert Syst. Appl. 2019, 124, 97–118. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. Evol. Comput. 2015, 20, 606–626. [Google Scholar] [CrossRef]
- Tubishat, M.; Ja’afar, S.; Alswaitti, M.; Mirjalili, S.; Idris, N.; Ismail, M.A.; Omar, M.S. Dynamic salp swarm algorithm for feature selection. Expert Syst. Appl. 2021, 164, 113873. [Google Scholar] [CrossRef]
- Kamath, U.; De Jong, K.; Shehu, A. Effective automated feature construction and selection for classification of biological sequences. PLoS ONE 2014, 9, e99982. [Google Scholar] [CrossRef]
- Crone, S.F.; Kourentzes, N. Feature selection for time series prediction–A combined filter and wrapper approach for neural networks. Neurocomputing 2010, 73, 1923–1936. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Xiong, T.; Chiong, R. Hybrid filter–wrapper feature selection for short-term load forecasting. Eng. Appl. Artif. Intell. 2015, 40, 17–27. [Google Scholar] [CrossRef]
- Wang, A.; An, N.; Chen, G.; Li, L.; Alterovitz, G. Accelerating wrapper-based feature selection with K-nearest-neighbor. Knowl.-Based Syst. 2015, 83, 81–91. [Google Scholar] [CrossRef]
- Jiménez-Cordero, A.; Morales, J.M.; Pineda, S. A novel embedded min-max approach for feature selection in nonlinear support vector machine classification. Eur. J. Oper. Res. 2021, 293, 24–35. [Google Scholar] [CrossRef]
- Nemnes, G.A.; Filipoiu, N.; Sipica, V. Feature selection procedures for combined density functional theory—Artificial neural network schemes. Phys. Scr. 2021, 96, 065807. [Google Scholar] [CrossRef]
- Xie, R.; Li, S.; Wu, F. An Improved Northern Goshawk Optimization Algorithm for Feature Selection. J. Bionic Eng. 2024, 21, 2034–2072. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Beyer, H.G.; Schwefel, H.P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Kaveh, A.; Dadras, A. A novel meta-heuristic optimization algorithm: Thermal exchange optimization. Adv. Eng. Softw. 2017, 110, 69–84. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, C.; Wang, X.; Han, T.; Li, Y. Nuclear reaction optimization: A novel and powerful physics-based algorithm for global optimization. IEEE Access 2019, 7, 66084–66109. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Shabani, A.; Asgarian, B.; Salido, M.; Gharebaghi, S.A. Search and rescue optimization algorithm: A new optimization method for solving constrained engineering optimization problems. Expert Syst. Appl. 2020, 161, 113698. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. Cybern. 2014, 45, 191–204. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Wang, Y.; Ran, S.; Wang, G.G. Role-oriented binary grey wolf optimizer using foraging-following and Lévy flight for feature selection. Appl. Math. Model. 2024, 126, 310–326. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Khedr, A.M.; Al Aghbari, Z.; Afyouni, I.; Kamel, I.; Ahmed, N. An adaptive hybrid mutated differential evolution feature selection method for low and high-dimensional medical datasets. Knowl.-Based Syst. 2024, 283, 111218. [Google Scholar] [CrossRef]
- Gao, J.; Wang, Z.; Jin, T.; Cheng, J.; Lei, Z.; Gao, S. Information gain ratio-based subfeature grouping empowers particle swarm optimization for feature selection. Knowl.-Based Syst. 2024, 286, 111380. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Alzoubi, H.; Sheta, A. Feature selection based nature inspired capuchin search algorithm for solving classification problems. Expert Syst. Appl. 2024, 235, 121128. [Google Scholar] [CrossRef]
- Askr, H.; Abdel-Salam, M.; Hassanien, A.E. Copula entropy-based golden jackal optimization algorithm for high-dimensional feature selection problems. Expert Syst. Appl. 2024, 238, 121582. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; Askr, H.; Hassanien, A.E. Adaptive chaotic dynamic learning-based gazelle optimization algorithm for feature selection problems. Expert Syst. Appl. 2024, 256, 124882. [Google Scholar] [CrossRef]
- Singh, L.K.; Khanna, M.; Garg, H.; Singh, R. Emperor penguin optimization algorithm-and bacterial foraging optimization algorithm-based novel feature selection approach for glaucoma classification from fundus images. Soft Comput. 2024, 28, 2431–2467. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Bui, N.D.H.; Duong, T.L. An Improved Zebra Optimization Algorithm for Solving Transmission Expansion Planning Problem with Penetration of Renewable Energy Sources. Int. J. Intell. Eng. Syst. 2024, 17, 202–211. [Google Scholar]
- Qi, Z.; Peng, S.; Wu, P.; Tseng, M.L. Renewable Energy Distributed Energy System Optimal Configuration and Performance Analysis: Improved Zebra Optimization Algorithm. Sustainability 2024, 16, 5016. [Google Scholar] [CrossRef]
- Amin, R.; El-Taweel, G.; Ali, A.F.; Tahoun, M. Hybrid Chaotic Zebra Optimization Algorithm and Long Short-Term Memory for Cyber Threats Detection. IEEE Access 2024, 12, 93235–93260. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, W.; Rahmani, A. Fractional-order artificial bee colony algorithm with application in robot path planning. Eur. J. Oper. Res. 2023, 306, 47–64. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Spider wasp optimizer: A novel meta-heuristic optimization algorithm. Artif. Intell. Rev. 2023, 56, 11675–11738. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proc. IEEE Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Rocca, P.; Oliveri, G.; Massa, A. Differential evolution as applied to electromagnetics. IEEE Antennas Propag. Mag. 2011, 53, 38–49. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Qi, X.; Zhu, Y.; Zhang, H. A new meta-heuristic butterfly-inspired algorithm. J. Comput. Sci. 2017, 23, 226–239. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]





| Algorithms | Accuracy | Time | Error | Feature |
|---|---|---|---|---|
| BFLGWO | Yes | No | Yes | Yes |
| A-HMDE | Yes | No | Yes | No |
| ISPSO | No | No | Yes | Yes |
| LCBCSA | No | Yes | No | Yes |
| BEGJO | Yes | No | Yes | No |
| ACD-GOA | No | Yes | No | No |
| EPO-BFO | No | Yes | No | Yes |
| Category | Name | Features Size | Classification Size | Dataset Size |
|---|---|---|---|---|
| Aggregation | 2 | 7 | 788 | |
| Banana | 2 | 2 | 5300 | |
| Iris | 4 | 3 | 150 | |
| Low | Bupa | 6 | 2 | 345 |
| Glass | 9 | 7 | 214 | |
| Breastcancer | 9 | 2 | 699 | |
| Lipid | 10 | 2 | 583 | |
| HeartEW | 13 | 2 | 270 | |
| Zoo | 16 | 7 | 101 | |
| Vote | 16 | 2 | 435 | |
| Congress | 16 | 2 | 435 | |
| Medium | Lymphography | 18 | 4 | 148 |
| Vehicle | 18 | 4 | 846 | |
| WDBC | 30 | 2 | 569 | |
| BreastEW | 30 | 2 | 569 | |
| SonarEW | 60 | 2 | 208 | |
| Libras | 90 | 15 | 360 | |
| Hillvalley | 100 | 2 | 606 | |
| MUSK | 166 | 2 | 476 | |
| High | Clean | 167 | 2 | 476 |
| Semeion | 256 | 10 | 1593 | |
| Meadelon | 500 | 2 | 2600 | |
| Isolet | 617 | 26 | 1559 |
| Algorithms | Proposed Time | Parameters Settings |
|---|---|---|
| Particle Swarm Optimization (PSO) [43] | 1995 | |
| Differential Evolution (DE) [44] | 1997 | |
| Grey Wolf Optimizer (GWO) [45] | 2014 | |
| Multi-Verse Optimizer (MVO) [46] | 2016 | |
| Whale Optimization Algorithm (WOA) [47] | 2016 | |
| Artificial Butterfly Optimization (ABO) [48] | 2017 | |
| Butterfly Optimization Algorithm (BOA) [49] | 2019 | |
| Equilibrium Optimizer (EO) [50] | 2020 | |
| ZOA | 2022 | No parameters |
| FTDZOA | NA | No parameters |
| Category | Datasets | Metric | ABO | BOA | DE | EO | GWO | MVO | PSO | WOA | ZOA | FTDZOA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aggregation | Best | 0.100 | 0.106 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | |
| Mean | 0.100 | 0.115 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | ||
| Worst | 0.100 | 0.377 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | 0.100 | ||
| Rank | 1/1/1 | 0/10/10 | 1/1/1 | 1/1/1 | 1/1/1 | 1/1/1 | 1/1/1 | 1/1/1 | 1/1/1 | 1/1/1 | ||
| Banana | Best | 0.198 | 0.193 | 0.191 | 0.193 | 0.192 | 0.203 | 0.193 | 0.210 | 0.198 | 0.187 | |
| Mean | 0.198 | 0.198 | 0.191 | 0.193 | 0.192 | 0.203 | 0.193 | 0.210 | 0.208 | 0.187 | ||
| Worst | 0.198 | 0.365 | 0.191 | 0.193 | 0.192 | 0.203 | 0.193 | 0.210 | 0.335 | 0.187 | ||
| Rank | 7/6/6 | 4/7/10 | 2/2/2 | 5/4/4 | 3/3/3 | 9/8/7 | 5/4/4 | 10/10/8 | 8/9/9 | 1/1/1 | ||
| Iris | Best | 0.025 | 0.025 | 0.080 | 0.025 | 0.025 | 0.050 | 0.055 | 0.080 | 0.025 | 0.025 | |
| Mean | 0.025 | 0.025 | 0.080 | 0.025 | 0.026 | 0.051 | 0.059 | 0.082 | 0.025 | 0.025 | ||
| Worst | 0.025 | 0.025 | 0.080 | 0.025 | 0.050 | 0.080 | 0.080 | 0.110 | 0.025 | 0.025 | ||
| Low | Rank | 1/1/1 | 1/1/1 | 9/9/7 | 1/1/1 | 1/6/6 | 7/7/7 | 8/8/7 | 9/10/10 | 1/1/1 | 1/1/1 | |
| Bupa | Best | 0.307 | 0.367 | 0.307 | 0.311 | 0.298 | 0.314 | 0.311 | 0.311 | 0.311 | 0.251 | |
| Mean | 0.310 | 0.382 | 0.334 | 0.322 | 0.305 | 0.323 | 0.324 | 0.318 | 0.318 | 0.251 | ||
| Worst | 0.350 | 0.419 | 0.348 | 0.341 | 0.359 | 0.369 | 0.389 | 0.350 | 0.346 | 0.251 | ||
| Rank | 3/3/5 | 0/10/10 | 3/9/4 | 5/6/2 | 2/2/7 | 9/7/8 | 5/8/9 | 5/4/5 | 5/5/3 | 1/1/1 | ||
| Glass | Best | 0.344 | 0.248 | 0.279 | 0.279 | 0.312 | 0.226 | 0.269 | 0.217 | 0.280 | 0.183 | |
| Mean | 0.352 | 0.293 | 0.299 | 0.284 | 0.314 | 0.243 | 0.279 | 0.237 | 0.297 | 0.196 | ||
| Worst | 0.376 | 0.322 | 0.355 | 0.290 | 0.323 | 0.302 | 0.302 | 0.271 | 0.344 | 0.248 | ||
| Rank | 0/10/10 | 4/6/6 | 6/8/9 | 6/5/3 | 9/9/7 | 3/3/5 | 5/4/4 | 2/2/2 | 8/7/8 | 1/1/1 | ||
| Breastcancer | Best | 0.059 | 0.042 | 0.059 | 0.053 | 0.040 | 0.053 | 0.053 | 0.059 | 0.042 | 0.042 | |
| Mean | 0.063 | 0.052 | 0.061 | 0.054 | 0.043 | 0.057 | 0.058 | 0.066 | 0.048 | 0.043 | ||
| Worst | 0.072 | 0.066 | 0.077 | 0.072 | 0.066 | 0.070 | 0.066 | 0.096 | 0.066 | 0.053 | ||
| Rank | 8/9/7 | 2/4/2 | 8/8/9 | 5/5/7 | 1/2/2 | 5/6/6 | 5/7/2 | 8/10/10 | 2/3/2 | 2/1/1 | ||
| Lipid | Best | 0.258 | 0.227 | 0.219 | 0.263 | 0.239 | 0.232 | 0.232 | 0.227 | 0.258 | 0.216 | |
| Mean | 0.262 | 0.243 | 0.257 | 0.264 | 0.247 | 0.238 | 0.245 | 0.253 | 0.260 | 0.233 | ||
| Worst | 0.266 | 0.266 | 0.304 | 0.266 | 0.274 | 0.266 | 0.266 | 0.297 | 0.266 | 0.266 | ||
| Rank | 8/9/1 | 3/3/1 | 2/7/10 | 10/10/1 | 7/5/8 | 5/2/1 | 5/4/1 | 3/6/9 | 8/8/1 | 1/1/1 | ||
| HeartEW | Best | 0.106 | 0.097 | 0.105 | 0.164 | 0.147 | 0.147 | 0.155 | 0.164 | 0.137 | 0.081 | |
| Mean | 0.136 | 0.156 | 0.130 | 0.182 | 0.164 | 0.168 | 0.169 | 0.198 | 0.171 | 0.094 | ||
| Worst | 0.206 | 0.208 | 0.186 | 0.206 | 0.238 | 0.223 | 0.238 | 0.246 | 0.215 | 0.165 | ||
| Rank | 4/3/3 | 2/4/5 | 3/2/2 | 9/9/3 | 6/5/8 | 6/6/7 | 8/7/8 | 9/10/10 | 5/8/6 | 1/1/1 | ||
| Zoo | Best | 0.038 | 0.038 | 0.044 | 0.044 | 0.044 | 0.031 | 0.044 | 0.031 | 0.031 | 0.025 | |
| Mean | 0.103 | 0.086 | 0.056 | 0.066 | 0.100 | 0.039 | 0.081 | 0.096 | 0.045 | 0.038 | ||
| Worst | 0.154 | 0.121 | 0.089 | 0.115 | 0.154 | 0.050 | 0.140 | 0.134 | 0.089 | 0.076 | ||
| Rank | 5/10/9 | 5/7/6 | 7/4/3 | 7/5/5 | 7/9/9 | 2/2/1 | 7/6/8 | 2/8/7 | 2/3/3 | 1/1/2 | ||
| Vote | Best | 0.035 | 0.033 | 0.039 | 0.035 | 0.046 | 0.039 | 0.039 | 0.039 | 0.006 | 0.006 | |
| Mean | 0.037 | 0.046 | 0.054 | 0.042 | 0.051 | 0.055 | 0.051 | 0.049 | 0.006 | 0.006 | ||
| Worst | 0.037 | 0.066 | 0.077 | 0.064 | 0.058 | 0.079 | 0.073 | 0.079 | 0.006 | 0.006 | ||
| Rank | 4/3/3 | 3/5/6 | 6/9/8 | 4/4/5 | 10/8/4 | 6/10/9 | 6/7/7 | 6/6/9 | 1/1/1 | 1/1/1 | ||
| Congress | Best | 0.029 | 0.033 | 0.027 | 0.058 | 0.037 | 0.038 | 0.035 | 0.056 | 0.048 | 0.006 | |
| Mean | 0.036 | 0.048 | 0.036 | 0.066 | 0.037 | 0.049 | 0.051 | 0.069 | 0.048 | 0.006 | ||
| Worst | 0.037 | 0.085 | 0.054 | 0.068 | 0.037 | 0.075 | 0.073 | 0.093 | 0.048 | 0.006 | ||
| Rank | 3/3/2 | 4/6/9 | 2/2/5 | 10/9/6 | 6/4/2 | 7/7/8 | 5/8/7 | 9/10/10 | 8/5/4 | 1/1/1 | ||
| Medium | Lymphography | Best | 0.095 | 0.090 | 0.090 | 0.115 | 0.095 | 0.084 | 0.090 | 0.112 | 0.084 | 0.064 |
| Mean | 0.148 | 0.154 | 0.129 | 0.133 | 0.154 | 0.118 | 0.112 | 0.140 | 0.140 | 0.078 | ||
| Worst | 0.192 | 0.183 | 0.200 | 0.177 | 0.214 | 0.177 | 0.138 | 0.205 | 0.172 | 0.101 | ||
| Rank | 7/8/7 | 4/10/6 | 4/4/8 | 10/5/4 | 7/9/10 | 2/3/4 | 4/2/2 | 9/6/9 | 2/7/3 | 1/1/1 | ||
| Vehicle | Best | 0.257 | 0.294 | 0.268 | 0.252 | 0.235 | 0.237 | 0.247 | 0.257 | 0.225 | 0.220 | |
| Mean | 0.291 | 0.321 | 0.287 | 0.275 | 0.261 | 0.269 | 0.278 | 0.306 | 0.270 | 0.231 | ||
| Worst | 0.326 | 0.370 | 0.316 | 0.320 | 0.279 | 0.305 | 0.310 | 0.343 | 0.299 | 0.257 | ||
| Rank | 7/8/8 | 10/10/10 | 9/7/6 | 6/5/7 | 3/2/2 | 4/3/4 | 5/6/5 | 7/9/9 | 2/4/3 | 1/1/1 | ||
| WDBC | Best | 0.034 | 0.041 | 0.041 | 0.045 | 0.026 | 0.056 | 0.041 | 0.042 | 0.039 | 0.026 | |
| Mean | 0.054 | 0.064 | 0.050 | 0.049 | 0.052 | 0.072 | 0.056 | 0.063 | 0.046 | 0.033 | ||
| Worst | 0.076 | 0.086 | 0.064 | 0.070 | 0.066 | 0.090 | 0.090 | 0.085 | 0.062 | 0.039 | ||
| Rank | 3/6/6 | 5/9/8 | 5/4/3 | 9/3/5 | 1/5/4 | 10/10/9 | 5/7/9 | 8/8/7 | 4/2/2 | 1/1/1 | ||
| BreastEW | Best | 0.035 | 0.059 | 0.040 | 0.031 | 0.036 | 0.027 | 0.027 | 0.063 | 0.031 | 0.013 | |
| Mean | 0.045 | 0.069 | 0.056 | 0.042 | 0.048 | 0.047 | 0.041 | 0.081 | 0.051 | 0.030 | ||
| Worst | 0.059 | 0.080 | 0.068 | 0.054 | 0.065 | 0.066 | 0.059 | 0.098 | 0.068 | 0.041 | ||
| Rank | 6/4/3 | 9/9/9 | 8/8/8 | 4/3/2 | 7/6/5 | 2/5/6 | 2/2/3 | 0/10/10 | 4/7/7 | 1/1/1 | ||
| SonarEW | Best | 0.108 | 0.069 | 0.069 | 0.013 | 0.037 | 0.054 | 0.030 | 0.066 | 0.032 | 0.013 | |
| Mean | 0.139 | 0.117 | 0.090 | 0.033 | 0.075 | 0.093 | 0.048 | 0.119 | 0.071 | 0.029 | ||
| Worst | 0.174 | 0.170 | 0.102 | 0.057 | 0.106 | 0.133 | 0.084 | 0.182 | 0.098 | 0.049 | ||
| Rank | 10/10/9 | 9/8/8 | 8/6/5 | 1/2/2 | 5/5/6 | 6/7/7 | 3/3/3 | 7/9/10 | 4/4/4 | 1/1/1 | ||
| Libras | Best | 0.116 | 0.176 | 0.142 | 0.130 | 0.131 | 0.148 | 0.172 | 0.162 | 0.100 | 0.069 | |
| Mean | 0.175 | 0.201 | 0.154 | 0.165 | 0.150 | 0.188 | 0.199 | 0.214 | 0.141 | 0.106 | ||
| Worst | 0.205 | 0.231 | 0.164 | 0.185 | 0.168 | 0.217 | 0.225 | 0.284 | 0.176 | 0.133 | ||
| Rank | 3/6/6 | 10/9/9 | 6/4/2 | 4/5/5 | 5/3/3 | 7/7/7 | 9/8/8 | 8/10/10 | 2/2/4 | 1/1/1 | ||
| Hillvalley | Best | 0.350 | 0.334 | 0.348 | 0.286 | 0.265 | 0.375 | 0.315 | 0.300 | 0.272 | 0.256 | |
| Mean | 0.371 | 0.361 | 0.371 | 0.299 | 0.300 | 0.408 | 0.346 | 0.333 | 0.296 | 0.281 | ||
| Worst | 0.394 | 0.381 | 0.385 | 0.321 | 0.319 | 0.437 | 0.369 | 0.365 | 0.323 | 0.306 | ||
| Rank | 9/8/9 | 7/7/7 | 8/9/8 | 4/3/3 | 2/4/2 | 0/10/10 | 6/6/6 | 5/5/5 | 3/2/4 | 1/1/1 | ||
| Musk | Best | 0.097 | 0.091 | 0.072 | 0.025 | 0.037 | 0.056 | 0.070 | 0.053 | 0.051 | 0.025 | |
| Mean | 0.131 | 0.114 | 0.093 | 0.058 | 0.063 | 0.074 | 0.096 | 0.081 | 0.092 | 0.054 | ||
| Worst | 0.152 | 0.138 | 0.110 | 0.094 | 0.114 | 0.115 | 0.122 | 0.112 | 0.120 | 0.075 | ||
| Rank | 0/10/10 | 9/9/9 | 8/7/3 | 1/2/2 | 3/3/5 | 6/4/6 | 7/8/8 | 5/5/4 | 4/6/7 | 1/1/1 | ||
| High | Clean | Best | 0.081 | 0.094 | 0.090 | 0.020 | 0.030 | 0.060 | 0.067 | 0.038 | 0.031 | 0.015 |
| Mean | 0.101 | 0.111 | 0.129 | 0.042 | 0.062 | 0.077 | 0.102 | 0.085 | 0.058 | 0.039 | ||
| Worst | 0.129 | 0.125 | 0.161 | 0.062 | 0.088 | 0.117 | 0.162 | 0.128 | 0.098 | 0.074 | ||
| Rank | 8/7/7 | 10/9/6 | 9/10/9 | 2/2/1 | 3/4/3 | 6/5/5 | 7/8/10 | 5/6/7 | 4/3/4 | 1/1/2 | ||
| Semeion | Best | 0.114 | 0.112 | 0.096 | 0.090 | 0.066 | 0.088 | 0.102 | 0.097 | 0.088 | 0.047 | |
| Mean | 0.126 | 0.126 | 0.112 | 0.107 | 0.085 | 0.111 | 0.116 | 0.118 | 0.103 | 0.064 | ||
| Worst | 0.134 | 0.135 | 0.123 | 0.118 | 0.112 | 0.130 | 0.132 | 0.134 | 0.112 | 0.071 | ||
| Rank | 10/9/8 | 9/10/10 | 6/6/5 | 5/4/4 | 2/2/2 | 3/5/6 | 8/7/7 | 7/8/8 | 4/3/3 | 1/1/1 | ||
| Meadelon | Best | 0.176 | 0.230 | 0.217 | 0.111 | 0.114 | 0.183 | 0.196 | 0.190 | 0.113 | 0.100 | |
| Mean | 0.260 | 0.261 | 0.237 | 0.162 | 0.140 | 0.214 | 0.225 | 0.236 | 0.156 | 0.133 | ||
| Worst | 0.313 | 0.304 | 0.269 | 0.227 | 0.193 | 0.262 | 0.247 | 0.271 | 0.248 | 0.181 | ||
| Rank | 5/9/10 | 10/10/9 | 9/8/7 | 2/4/3 | 4/2/2 | 6/5/6 | 8/6/4 | 7/7/8 | 3/3/5 | 1/1/1 | ||
| Isolet | Best | 0.175 | 0.159 | 0.180 | 0.114 | 0.099 | 0.152 | 0.123 | 0.141 | 0.106 | 0.077 | |
| Mean | 0.193 | 0.179 | 0.197 | 0.139 | 0.119 | 0.172 | 0.147 | 0.169 | 0.128 | 0.097 | ||
| Worst | 0.217 | 0.204 | 0.206 | 0.163 | 0.143 | 0.198 | 0.172 | 0.193 | 0.157 | 0.115 | ||
| Rank | 9/9/10 | 8/8/8 | 10/10/9 | 4/4/4 | 2/2/2 | 7/7/7 | 5/5/5 | 6/6/6 | 3/3/3 | 1/1/1 | ||
| Mean Rank | Best | 6.130 | 6.435 | 6.043 | 5.000 | 4.217 | 5.609 | 5.609 | 6.435 | 3.826 | 1.043 | |
| Mean | 6.609 | 7.435 | 6.261 | 4.391 | 4.391 | 5.652 | 5.739 | 7.217 | 4.217 | 1.000 | ||
| Worst | 6.174 | 7.174 | 5.783 | 3.478 | 4.478 | 5.957 | 5.565 | 7.565 | 3.826 | 1.087 | ||
| Final Rank | Best | 8 | 9 | 7 | 4 | 3 | 5 | 5 | 9 | 2 | 1 | |
| Mean | 8 | 10 | 7 | 3 | 3 | 5 | 6 | 9 | 2 | 1 | ||
| Worst | 8 | 9 | 6 | 2 | 4 | 7 | 5 | 10 | 3 | 1 |
| Category | Datasets | ABO | BOA | DE | EO | GWO | MVO | PSO | WOA | ZOA | FTDZOA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Aggregation | 5.95 | 5.98 | 5.88 | 6.08 | 5.98 | 5.92 | 6.13 | 6.10 | 5.97 | 1.00 | |
| Banana | 6.97 | 4.20 | 2.00 | 5.47 | 3.00 | 8.90 | 5.47 | 9.90 | 8.10 | 1.00 | |
| Iris | 3.60 | 3.55 | 9.28 | 3.65 | 3.52 | 6.97 | 8.03 | 9.47 | 3.52 | 3.42 | |
| Low | Bupa | 3.40 | 9.97 | 6.90 | 5.90 | 2.93 | 6.75 | 6.03 | 5.77 | 6.35 | 1.00 |
| Glass | 9.97 | 6.62 | 6.37 | 5.58 | 8.42 | 2.77 | 4.98 | 2.43 | 6.77 | 1.10 | |
| Breastcancer | 8.28 | 4.70 | 7.78 | 4.85 | 1.98 | 6.03 | 6.48 | 8.70 | 3.90 | 2.28 | |
| Lipid | 7.97 | 4.13 | 5.87 | 8.32 | 5.02 | 3.48 | 4.23 | 6.00 | 7.20 | 2.78 | |
| HeartEW | 3.63 | 5.22 | 2.90 | 8.10 | 5.80 | 5.95 | 6.20 | 9.37 | 6.50 | 1.33 | |
| Zoo | 8.05 | 7.00 | 4.58 | 5.35 | 7.72 | 2.53 | 6.87 | 7.65 | 3.00 | 2.25 | |
| Vote | 3.72 | 6.13 | 7.93 | 4.93 | 7.70 | 7.82 | 7.23 | 6.53 | 1.52 | 1.48 | |
| Congress | 3.37 | 5.88 | 3.38 | 8.97 | 3.70 | 6.67 | 6.37 | 9.22 | 6.45 | 1.00 | |
| Medium | Lymphography | 7.32 | 7.83 | 5.33 | 5.80 | 7.53 | 4.23 | 3.52 | 6.10 | 6.32 | 1.02 |
| Vehicle | 7.08 | 9.58 | 6.63 | 5.02 | 2.95 | 4.28 | 5.35 | 8.25 | 4.68 | 1.17 | |
| WDBC | 5.37 | 7.77 | 5.15 | 4.17 | 5.63 | 9.03 | 5.88 | 7.28 | 3.60 | 1.12 | |
| BreastEW | 4.58 | 8.88 | 7.28 | 3.72 | 5.07 | 4.80 | 3.60 | 9.88 | 5.62 | 1.57 | |
| SonarEW | 9.43 | 8.22 | 6.17 | 2.07 | 5.03 | 6.60 | 2.98 | 8.30 | 4.62 | 1.58 | |
| Libras | 6.03 | 8.33 | 3.77 | 5.07 | 3.52 | 7.40 | 8.37 | 8.93 | 2.55 | 1.03 | |
| Hillvalley | 7.97 | 7.30 | 8.28 | 2.93 | 3.12 | 9.97 | 6.08 | 5.33 | 2.57 | 1.45 | |
| High | Musk | 9.70 | 8.65 | 6.63 | 2.53 | 2.90 | 4.17 | 6.87 | 5.02 | 6.50 | 2.03 |
| Clean | 7.35 | 8.67 | 9.60 | 2.02 | 3.75 | 5.18 | 7.47 | 5.93 | 3.33 | 1.70 | |
| Semeion | 9.07 | 9.13 | 5.77 | 4.70 | 2.10 | 5.55 | 6.62 | 7.47 | 3.57 | 1.03 | |
| Madelon | 8.77 | 9.10 | 7.50 | 3.20 | 2.37 | 5.47 | 6.47 | 7.27 | 2.93 | 1.93 | |
| Isolet | 9.10 | 7.73 | 9.37 | 3.93 | 2.57 | 6.83 | 4.53 | 6.63 | 3.27 | 1.03 | |
| Mean Rank | 6.81 | 7.16 | 6.28 | 4.88 | 4.45 | 5.97 | 5.90 | 7.28 | 4.73 | 1.54 | |
| Final Rank | 8 | 9 | 7 | 4 | 2 | 6 | 5 | 10 | 3 | 1 |
| Category | Datasets | ABO | BOA | DE | EO | GWO | MVO | PSO | WOA | ZOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Aggregation | 4.16 × 10−14/− | 4.16 × 10−14/− | 6.14 × 10−14/− | 6.14 × 10−14/− | 4.16 × 10−14/− | 4.16 × 10−14/− | 6.14 × 10−14/− | 6.14 × 10−14/− | 4.16 × 10−14/− | |
| Banana | 1.69 × 10−14/− | 2.71 × 10−14/− | 1.69 × 10−14/− | 1.69 × 10−14/− | 1.69 × 10−14/− | 1.69 × 10−14/− | 1.69 × 10−14/− | 1.69 × 10−14/− | 4.16 × 10−14/− | |
| Iris | 3.34 × 10−1/= | 3.34 × 10−1/= | 1.69 × 10−14/− | 3.34 × 10−1/= | 3.34 × 10−1/= | 4.16 × 10−14/− | 1.18 × 10−13/− | 1.19 × 10−13/− | 3.34 × 10−1/= | |
| Low | Bupa | 4.16 × 10−14/− | 9.27 × 10−13/− | 7.56 × 10−13/− | 3.80 × 10−13/− | 8.70 × 10−14/− | 4.98 × 10−13/− | 3.00 × 10−13/− | 6.49 × 10−13/− | 6.89 × 10−13/− |
| Glass | 7.21 × 10−12/− | 1.01 × 10−11/− | 7.71 × 10−12/− | 6.81 × 10−12/− | 6.42 × 10−12/− | 2.57 × 10−9/− | 7.27 × 10−12/− | 9.75 × 10−9/− | 8.14 × 10−12/− | |
| Breastcancer | 4.92 × 10−12/− | 1.50 × 10−7/− | 3.35 × 10−12/− | 1.76 × 10−11/− | 1.16 × 10−4/− | 1.42 × 10−11/− | 1.68 × 10−11/− | 6.31 × 10−12/− | 7.35 × 10−2/= | |
| Lipid | 1.13 × 10−10/− | 8.62 × 10−3/− | 1.04 × 10−3/− | 1.23 × 10−10/− | 8.49 × 10−4/− | 5.65 × 10−2/= | 3.49 × 10−3/− | 1.39 × 10−5/− | 1.27 × 10−10/− | |
| HeartEW | 4.42 × 10−8/− | 4.14 × 10−10/− | 2.99 × 10−7/− | 2.60 × 10−11/− | 8.80 × 10−11/− | 7.66 × 10−11/− | 6.74 × 10−11/− | 1.14 × 10−11/− | 5.22 × 10−11/− | |
| Zoo | 1.78 × 10−9/− | 1.35 × 10−9/− | 1.53 × 10−7/− | 1.13 × 10−8/− | 1.86 × 10−10/− | 1.08 × 10−1/= | 1.11 × 10−9/− | 1.23 × 10−9/− | 2.26 × 10−2/− | |
| Vote | 1.97 × 10−13/− | 1.13 × 10−12/− | 1.15 × 10−12/− | 6.52 × 10−13/− | 7.82 × 10−13/− | 1.18 × 10−12/− | 1.08 × 10−12/− | 1.59 × 10−13/− | 3.34 × 10−1/= | |
| Congress | 1.58 × 10−13/− | 1.06 × 10−12/− | 1.03 × 10−12/− | 3.77 × 10−13/− | 1.69 × 10−14/− | 1.16 × 10−12/− | 1.17 × 10−12/− | 8.79 × 10−13/− | 1.69 × 10−14/− | |
| Medium | Lymphography | 4.99 × 10−11/− | 5.00 × 10−11/− | 2.41 × 10−10/− | 2.62 × 10−11/− | 3.12 × 10−11/− | 3.42 × 10−9/− | 1.41 × 10−10/− | 2.34 × 10−11/− | 1.58 × 10−10/− |
| Vehicle | 2.79 × 10−11/− | 2.65 × 10−11/− | 2.62 × 10−11/− | 3.78 × 10−11/− | 1.30 × 10−9/− | 5.20 × 10−10/− | 8.80 × 10−11/− | 2.81 × 10−11/− | 1.91 × 10−9/− | |
| WDBC | 5.00 × 10−10/− | 1.92 × 10−11/− | 1.69 × 10−11/− | 1.03 × 10−11/− | 2.72 × 10−10/− | 1.89 × 10−11/− | 1.87 × 10−11/− | 1.90 × 10−11/− | 2.74 × 10−9/− | |
| BreastEW | 1.06 × 10−9/− | 2.90 × 10−11/− | 3.89 × 10−11/− | 1.78 × 10−8/− | 8.80 × 10−11/− | 2.98 × 10−8/− | 9.41 × 10−6/− | 2.92 × 10−11/− | 4.39 × 10−10/− | |
| SonarEW | 2.91 × 10−11/− | 2.92 × 10−11/− | 2.77 × 10−11/− | 9.98 × 10−2/= | 2.06 × 10−10/− | 2.91 × 10−11/− | 2.90 × 10−5/− | 2.93 × 10−11/− | 2.38 × 10−10/− | |
| Libras | 6.96 × 10−11/− | 2.98 × 10−11/− | 2.92 × 10−11/− | 4.02 × 10−11/− | 3.29 × 10−11/− | 2.97 × 10−11/− | 2.97 × 10−11/− | 2.98 × 10−11/− | 2.20 × 10−9/− | |
| Hillvalley | 2.90 × 10−11/− | 3.01 × 10−11/− | 3.00 × 10−11/− | 6.74 × 10−8/− | 1.35 × 10−7/− | 3.00 × 10−11/− | 3.01 × 10−11/− | 3.29 × 10−11/− | 6.75 × 10−5/− | |
| High | Musk | 3.01 × 10−11/− | 3.01 × 10−11/− | 4.06 × 10−11/− | 2.74 × 10−1/= | 7.24 × 10−2/= | 9.18 × 10−6/− | 7.37 × 10−11/− | 1.05 × 10−8/− | 6.70 × 10−10/− |
| Clean | 3.00 × 10−11/− | 3.01 × 10−11/− | 3.01 × 10−11/− | 2.67 × 10−1/= | 3.37 × 10−7/− | 1.32 × 10−10/− | 4.06 × 10−11/− | 6.11 × 10−10/− | 3.32 × 10−6/− | |
| Semeion | 3.01 × 10−11/− | 3.01 × 10−11/− | 3.02 × 10−11/− | 3.01 × 10−11/− | 9.42 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | |
| Meadelon | 3.34 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 4.71 × 10−4/− | 1.76 × 10−1/= | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.03 × 10−3/− | |
| Isolet | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.02 × 10−11/− | 3.34 × 10−11/− | 1.56 × 10−8/− | 3.02 × 10−11/− | 3.01 × 10−11/− | 3.02 × 10−11/− | 1.46 × 10−10/− | |
| +/−/= | 0/22/1 | 0/22/1 | 0/23/0 | 0/19/4 | 0/20/3 | 0/21/2 | 0/23/0 | 0/23/0 | 0/20/3 |
| Datasets | ABO | BOA | DE | EO | GWO | MVO | PSO | WOA | ZOA | FTDZOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Aggregation | 100.00 | 96.38 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 1 | 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Banana | 89.15 | 88.89 | 89.91 | 89.62 | 89.81 | 88.58 | 89.62 | 87.83 | 87.67 | 90.38 |
| 6 | 7 | 2 | 4 | 3 | 8 | 4 | 9 | 10 | 1 | |
| Iris | 100.00 | 100.00 | 96.67 | 100.00 | 100.00 | 99.78 | 96.67 | 96.11 | 100.00 | 100.00 |
| 1 | 1 | 8 | 1 | 1 | 7 | 8 | 10 | 1 | 1 | |
| Bupa | 69.37 | 63.14 | 70.43 | 70.48 | 71.59 | 70.58 | 69.57 | 69.13 | 69.37 | 73.91 |
| 8 | 10 | 5 | 4 | 2 | 3 | 6 | 9 | 7 | 1 | |
| Glass | 63.10 | 71.90 | 70.16 | 72.46 | 70.00 | 76.90 | 73.57 | 80.00 | 71.67 | 82.06 |
| 10 | 6 | 8 | 5 | 9 | 3 | 4 | 2 | 7 | 1 | |
| Breastcancer | 96.35 | 96.79 | 96.86 | 97.29 | 98.47 | 97.22 | 97.10 | 95.85 | 97.29 | 97.60 |
| 9 | 8 | 7 | 3 | 1 | 5 | 6 | 10 | 3 | 2 | |
| Lipid | 71.95 | 74.68 | 74.14 | 73.36 | 75.26 | 76.64 | 75.95 | 73.13 | 72.47 | 76.67 |
| 10 | 5 | 6 | 7 | 4 | 2 | 3 | 8 | 9 | 1 | |
| HeartEW | 88.58 | 85.86 | 90.06 | 82.59 | 85.19 | 85.31 | 85.62 | 80.12 | 83.58 | 93.02 |
| 3 | 4 | 2 | 9 | 7 | 6 | 5 | 10 | 8 | 1 | |
| Zoo | 92.17 | 95.33 | 98.50 | 96.83 | 92.67 | 100.00 | 96.00 | 94.83 | 99.33 | 99.67 |
| 10 | 7 | 4 | 5 | 9 | 1 | 6 | 8 | 3 | 2 | |
| Vote | 97.09 | 97.70 | 96.93 | 98.08 | 96.17 | 96.82 | 96.67 | 95.71 | 100.00 | 100.00 |
| 5 | 4 | 6 | 3 | 9 | 7 | 8 | 10 | 1 | 1 | |
| Congress | 97.01 | 97.43 | 98.81 | 93.95 | 96.55 | 97.43 | 97.24 | 94.33 | 95.40 | 100.00 |
| 6 | 3 | 2 | 10 | 7 | 4 | 5 | 9 | 8 | 1 | |
| Lymphography | 87.36 | 86.32 | 90.11 | 88.74 | 85.52 | 90.92 | 92.07 | 87.24 | 86.78 | 95.40 |
| 6 | 9 | 4 | 5 | 10 | 3 | 2 | 7 | 8 | 1 | |
| Vehicle | 71.44 | 67.97 | 72.90 | 73.12 | 74.42 | 74.75 | 73.63 | 69.70 | 73.61 | 77.44 |
| 8 | 10 | 7 | 6 | 3 | 2 | 4 | 9 | 5 | 1 | |
| WDBC | 95.87 | 95.46 | 97.35 | 95.55 | 95.37 | 94.72 | 96.28 | 94.48 | 95.87 | 97.17 |
| 4 | 7 | 1 | 6 | 8 | 9 | 3 | 10 | 5 | 2 | |
| BreastEW | 98.14 | 96.28 | 98.85 | 97.94 | 97.26 | 98.91 | 98.82 | 94.37 | 96.43 | 98.64 |
| 5 | 9 | 2 | 6 | 7 | 1 | 3 | 10 | 8 | 4 | |
| SonarEW | 87.48 | 89.67 | 95.85 | 98.37 | 93.58 | 94.23 | 98.37 | 89.92 | 93.98 | 98.70 |
| 10 | 9 | 4 | 2 | 7 | 5 | 2 | 8 | 6 | 1 | |
| Libras | 83.33 | 80.00 | 88.89 | 83.70 | 85.60 | 84.03 | 82.18 | 78.43 | 86.16 | 90.79 |
| 7 | 9 | 2 | 6 | 4 | 5 | 8 | 10 | 3 | 1 | |
| Hillvalley | 60.17 | 61.35 | 65.70 | 68.68 | 67.47 | 59.45 | 66.23 | 63.58 | 67.99 | 71.46 |
| 9 | 8 | 6 | 2 | 4 | 10 | 5 | 7 | 3 | 1 | |
| Musk | 89.37 | 90.84 | 96.74 | 95.96 | 95.89 | 96.60 | 94.21 | 95.30 | 91.58 | 96.70 |
| 10 | 9 | 1 | 4 | 5 | 3 | 7 | 6 | 8 | 2 | |
| Clean | 92.00 | 90.88 | 92.84 | 98.07 | 95.96 | 96.39 | 93.37 | 94.88 | 95.93 | 97.93 |
| 9 | 10 | 8 | 1 | 4 | 3 | 7 | 6 | 5 | 2 | |
| Semeion | 91.25 | 90.25 | 94.79 | 93.38 | 94.15 | 93.11 | 92.47 | 91.99 | 93.87 | 96.72 |
| 9 | 10 | 2 | 5 | 3 | 6 | 7 | 8 | 4 | 1 | |
| Madelon | 75.67 | 74.07 | 81.18 | 84.08 | 86.80 | 81.72 | 80.38 | 77.75 | 83.90 | 87.11 |
| 9 | 10 | 6 | 3 | 2 | 5 | 7 | 8 | 4 | 1 | |
| Isolet | 82.08 | 82.68 | 85.36 | 87.32 | 89.57 | 86.29 | 88.95 | 84.48 | 88.40 | 91.21 |
| 10 | 9 | 7 | 5 | 2 | 6 | 3 | 8 | 4 | 1 | |
| Mean Rank | 7.17 | 7.57 | 4.39 | 4.48 | 4.87 | 4.57 | 4.96 | 7.96 | 5.26 | 1.35 |
| Final Rank | 8 | 9 | 2 | 3 | 5 | 4 | 6 | 10 | 7 | 1 |
| Datasets | ABO | BOA | DE | EO | GWO | MVO | PSO | WOA | ZOA | FTDZOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Aggregation | 2.00 | 1.97 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | |
| Banana | 2.00 | 1.97 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 1.93 | 2.00 |
| 3 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 3 | |
| Iris | 1.00 | 1.00 | 2.00 | 1.00 | 1.03 | 1.97 | 1.17 | 1.87 | 1.00 | 1.00 |
| 1 | 1 | 10 | 1 | 6 | 9 | 7 | 8 | 1 | 1 | |
| Bupa | 2.07 | 3.03 | 4.07 | 3.37 | 2.97 | 3.47 | 3.00 | 2.43 | 2.57 | 1.00 |
| 2 | 7 | 10 | 8 | 5 | 9 | 6 | 3 | 4 | 1 | |
| Glass | 1.80 | 3.60 | 2.70 | 3.27 | 3.93 | 3.20 | 3.67 | 5.10 | 3.77 | 3.13 |
| 1 | 6 | 2 | 5 | 9 | 4 | 7 | 10 | 8 | 3 | |
| Breastcancer | 2.70 | 2.07 | 2.97 | 2.70 | 2.60 | 2.87 | 2.90 | 2.60 | 2.10 | 1.90 |
| 6 | 2 | 10 | 6 | 4 | 8 | 9 | 4 | 3 | 1 | |
| Lipid | 1.00 | 1.50 | 2.47 | 2.40 | 2.47 | 2.80 | 2.83 | 1.17 | 1.20 | 2.33 |
| 1 | 4 | 7 | 6 | 7 | 9 | 10 | 2 | 3 | 5 | |
| HeartEW | 4.33 | 3.80 | 5.23 | 3.30 | 4.00 | 4.63 | 5.20 | 2.47 | 2.97 | 4.00 |
| 7 | 4 | 10 | 3 | 5 | 8 | 9 | 1 | 2 | 5 | |
| Zoo | 5.17 | 7.00 | 6.73 | 6.07 | 5.50 | 6.30 | 7.17 | 7.97 | 6.20 | 5.67 |
| 1 | 8 | 7 | 4 | 2 | 6 | 9 | 10 | 5 | 3 | |
| Vote | 1.70 | 4.00 | 4.27 | 3.97 | 2.67 | 4.27 | 3.30 | 1.60 | 1.00 | 1.00 |
| 4 | 8 | 9 | 7 | 5 | 9 | 6 | 3 | 1 | 1 | |
| Congress | 1.53 | 3.93 | 4.10 | 1.87 | 1.00 | 4.17 | 4.17 | 2.87 | 1.00 | 1.00 |
| 4 | 7 | 8 | 5 | 1 | 9 | 9 | 6 | 1 | 1 | |
| Lymphography | 6.23 | 5.63 | 7.23 | 5.70 | 4.30 | 6.50 | 7.33 | 4.50 | 3.83 | 6.63 |
| 6 | 4 | 9 | 5 | 2 | 7 | 10 | 3 | 1 | 8 | |
| Vehicle | 6.20 | 5.93 | 7.80 | 5.97 | 5.50 | 7.50 | 7.27 | 5.93 | 5.80 | 5.00 |
| 7 | 4 | 10 | 6 | 2 | 9 | 8 | 4 | 3 | 1 | |
| WDBC | 4.93 | 7.00 | 7.87 | 2.67 | 3.07 | 7.23 | 6.90 | 3.87 | 2.60 | 2.17 |
| 6 | 8 | 10 | 3 | 4 | 9 | 7 | 5 | 2 | 1 | |
| BreastEW | 8.57 | 10.77 | 13.80 | 7.03 | 7.00 | 11.10 | 9.17 | 9.17 | 5.73 | 5.20 |
| 5 | 8 | 10 | 4 | 3 | 9 | 6 | 6 | 2 | 1 | |
| SonarEW | 15.67 | 14.50 | 31.60 | 11.23 | 10.20 | 24.53 | 20.23 | 17.17 | 10.13 | 10.27 |
| 6 | 5 | 10 | 4 | 2 | 9 | 8 | 7 | 1 | 3 | |
| Libras | 22.37 | 19.03 | 48.70 | 16.50 | 18.80 | 39.60 | 35.17 | 18.17 | 14.67 | 20.63 |
| 7 | 5 | 10 | 2 | 4 | 9 | 8 | 3 | 1 | 6 | |
| Hillvalley | 12.13 | 13.10 | 62.67 | 17.03 | 7.50 | 42.83 | 41.67 | 5.63 | 7.93 | 24.30 |
| 4 | 5 | 10 | 6 | 2 | 9 | 8 | 1 | 3 | 7 | |
| Musk | 57.83 | 51.87 | 105.13 | 36.57 | 42.87 | 72.20 | 73.27 | 64.03 | 26.50 | 40.03 |
| 6 | 5 | 10 | 2 | 4 | 8 | 9 | 7 | 1 | 3 | |
| Clean | 48.53 | 47.83 | 107.03 | 41.13 | 42.67 | 74.00 | 70.43 | 64.73 | 36.07 | 34.57 |
| 6 | 5 | 10 | 3 | 4 | 9 | 8 | 7 | 2 | 1 | |
| Semeion | 119.83 | 98.20 | 167.70 | 121.57 | 83.37 | 125.67 | 122.93 | 118.23 | 122.07 | 87.93 |
| 5 | 3 | 10 | 6 | 1 | 9 | 8 | 4 | 7 | 2 | |
| Madelon | 205.67 | 140.60 | 337.17 | 92.03 | 108.23 | 245.93 | 243.73 | 178.10 | 55.10 | 86.20 |
| 7 | 5 | 10 | 3 | 4 | 9 | 8 | 6 | 1 | 2 | |
| Isolet | 198.00 | 145.40 | 401.17 | 152.93 | 154.87 | 297.43 | 295.90 | 181.63 | 146.83 | 112.37 |
| 7 | 2 | 10 | 4 | 5 | 9 | 8 | 6 | 3 | 1 | |
| Mean Rank | 4.52 | 4.74 | 8.565217 | 4.26 | 3.74 | 7.87 | 7.52 | 4.83 | 2.52 | 2.70 |
| Final Rank | 5 | 6 | 10 | 4 | 3 | 9 | 8 | 7 | 1 | 2 |
| Datasets | ABO | BOA | DE | EO | GWO | MVO | PSO | WOA | ZOA | FTDZOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Aggregation | 5.60 | 6.11 | 3.51 | 2.70 | 3.39 | 3.46 | 3.44 | 3.25 | 2.03 | 2.59 |
| 9 | 10 | 8 | 3 | 5 | 7 | 6 | 4 | 1 | 2 | |
| Banana | 10.22 | 11.17 | 6.56 | 4.81 | 6.10 | 6.42 | 6.30 | 6.10 | 3.31 | 4.54 |
| 9 | 10 | 8 | 3 | 5 | 7 | 6 | 4 | 1 | 2 | |
| Iris | 4.34 | 5.01 | 3.16 | 2.91 | 3.09 | 3.11 | 2.96 | 2.90 | 2.51 | 1.95 |
| 9 | 10 | 8 | 4 | 6 | 7 | 5 | 3 | 2 | 1 | |
| Bupa | 5.27 | 5.69 | 3.28 | 3.22 | 3.23 | 3.27 | 3.26 | 2.97 | 2.84 | 2.19 |
| 9 | 10 | 8 | 4 | 5 | 7 | 6 | 3 | 2 | 1 | |
| Glass | 5.39 | 5.27 | 3.20 | 3.17 | 3.18 | 3.19 | 3.19 | 3.01 | 2.99 | 2.13 |
| 10 | 9 | 8 | 4 | 5 | 6 | 7 | 3 | 2 | 1 | |
| Breastcancer | 5.13 | 5.69 | 3.49 | 3.41 | 3.44 | 3.47 | 3.48 | 3.20 | 3.43 | 2.27 |
| 9 | 10 | 8 | 3 | 5 | 6 | 7 | 2 | 4 | 1 | |
| Lipid | 4.62 | 5.79 | 3.42 | 3.30 | 3.31 | 3.37 | 3.43 | 2.73 | 3.25 | 2.05 |
| 9 | 10 | 7 | 4 | 5 | 6 | 8 | 2 | 3 | 1 | |
| HeartEW | 5.16 | 5.78 | 3.26 | 3.21 | 3.24 | 3.26 | 3.26 | 2.80 | 3.22 | 2.14 |
| 9 | 10 | 8 | 3 | 5 | 7 | 6 | 2 | 4 | 1 | |
| Zoo | 5.88 | 5.77 | 3.13 | 3.13 | 3.14 | 3.17 | 3.15 | 2.93 | 3.10 | 2.15 |
| 10 | 9 | 5 | 4 | 6 | 8 | 7 | 2 | 3 | 1 | |
| Vote | 4.37 | 5.89 | 3.34 | 3.22 | 3.28 | 3.34 | 3.33 | 2.74 | 3.31 | 2.11 |
| 9 | 10 | 7 | 3 | 4 | 8 | 6 | 2 | 5 | 1 | |
| Congress | 4.36 | 5.07 | 3.32 | 3.25 | 3.27 | 3.34 | 3.34 | 2.85 | 3.30 | 2.06 |
| 9 | 10 | 6 | 3 | 4 | 7 | 8 | 2 | 5 | 1 | |
| Lymphography | 5.14 | 5.60 | 3.17 | 3.18 | 3.18 | 3.19 | 3.20 | 2.78 | 3.15 | 2.12 |
| 9 | 10 | 4 | 5 | 6 | 7 | 8 | 2 | 3 | 1 | |
| Vehicle | 6.43 | 6.69 | 3.61 | 3.61 | 3.61 | 3.66 | 3.67 | 3.34 | 3.52 | 2.48 |
| 9 | 10 | 5 | 4 | 6 | 7 | 8 | 2 | 3 | 1 | |
| WDBC | 5.12 | 5.65 | 3.34 | 3.39 | 3.42 | 3.41 | 3.44 | 2.98 | 3.33 | 2.13 |
| 9 | 10 | 4 | 5 | 7 | 6 | 8 | 2 | 3 | 1 | |
| BreastEW | 6.04 | 6.24 | 3.16 | 3.49 | 3.49 | 3.29 | 3.40 | 3.14 | 3.36 | 2.23 |
| 9 | 10 | 3 | 7 | 8 | 4 | 6 | 2 | 5 | 1 | |
| SonarEW | 5.90 | 5.85 | 3.05 | 3.04 | 3.06 | 3.05 | 3.07 | 2.89 | 3.04 | 2.07 |
| 10 | 9 | 6 | 4 | 7 | 5 | 8 | 2 | 3 | 1 | |
| Libras | 6.29 | 6.13 | 3.29 | 3.13 | 3.14 | 3.25 | 3.29 | 3.03 | 3.18 | 2.20 |
| 10 | 9 | 8 | 3 | 4 | 6 | 7 | 2 | 5 | 1 | |
| Hillvalley | 5.93 | 6.23 | 3.68 | 3.23 | 3.29 | 3.49 | 3.55 | 3.03 | 3.35 | 2.20 |
| 9 | 10 | 8 | 3 | 4 | 6 | 7 | 2 | 5 | 1 | |
| Musk | 6.43 | 6.33 | 3.78 | 3.29 | 3.34 | 3.58 | 3.66 | 3.27 | 3.39 | 2.40 |
| 10 | 9 | 8 | 3 | 4 | 6 | 7 | 2 | 5 | 1 | |
| Clean | 6.57 | 6.29 | 3.80 | 3.33 | 3.35 | 3.56 | 3.67 | 3.27 | 3.40 | 2.41 |
| 10 | 9 | 8 | 3 | 4 | 6 | 7 | 2 | 5 | 1 | |
| Semeion | 17.28 | 18.53 | 14.15 | 8.32 | 8.13 | 11.12 | 11.22 | 10.19 | 8.45 | 7.10 |
| 9 | 10 | 8 | 3 | 2 | 6 | 7 | 5 | 4 | 1 | |
| Madelon | 23.76 | 34.92 | 58.25 | 19.77 | 22.83 | 42.06 | 42.16 | 30.88 | 27.94 | 24.78 |
| 3 | 7 | 10 | 1 | 2 | 8 | 9 | 6 | 5 | 4 | |
| Isolet | 20.18 | 23.14 | 29.85 | 11.30 | 14.57 | 22.64 | 23.07 | 14.79 | 16.48 | 13.36 |
| 6 | 9 | 10 | 1 | 3 | 7 | 8 | 4 | 5 | 2 | |
| Mean Rank | 8.87 | 9.57 | 7.09 | 3.48 | 4.87 | 6.52 | 7.04 | 2.70 | 3.61 | 1.26 |
| Final Rank | 9 | 10 | 8 | 3 | 5 | 6 | 7 | 2 | 4 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Ye, S.; Xu, L.; Xie, R. FTDZOA: An Efficient and Robust FS Method with Multi-Strategy Assistance. Biomimetics 2024, 9, 632. https://doi.org/10.3390/biomimetics9100632
Chen F, Ye S, Xu L, Xie R. FTDZOA: An Efficient and Robust FS Method with Multi-Strategy Assistance. Biomimetics. 2024; 9(10):632. https://doi.org/10.3390/biomimetics9100632
Chicago/Turabian StyleChen, Fuqiang, Shitong Ye, Lijuan Xu, and Rongxiang Xie. 2024. "FTDZOA: An Efficient and Robust FS Method with Multi-Strategy Assistance" Biomimetics 9, no. 10: 632. https://doi.org/10.3390/biomimetics9100632
APA StyleChen, F., Ye, S., Xu, L., & Xie, R. (2024). FTDZOA: An Efficient and Robust FS Method with Multi-Strategy Assistance. Biomimetics, 9(10), 632. https://doi.org/10.3390/biomimetics9100632








