Peak Identification in Evolutionary Multimodal Optimization: Model, Algorithms, and Metrics
Abstract
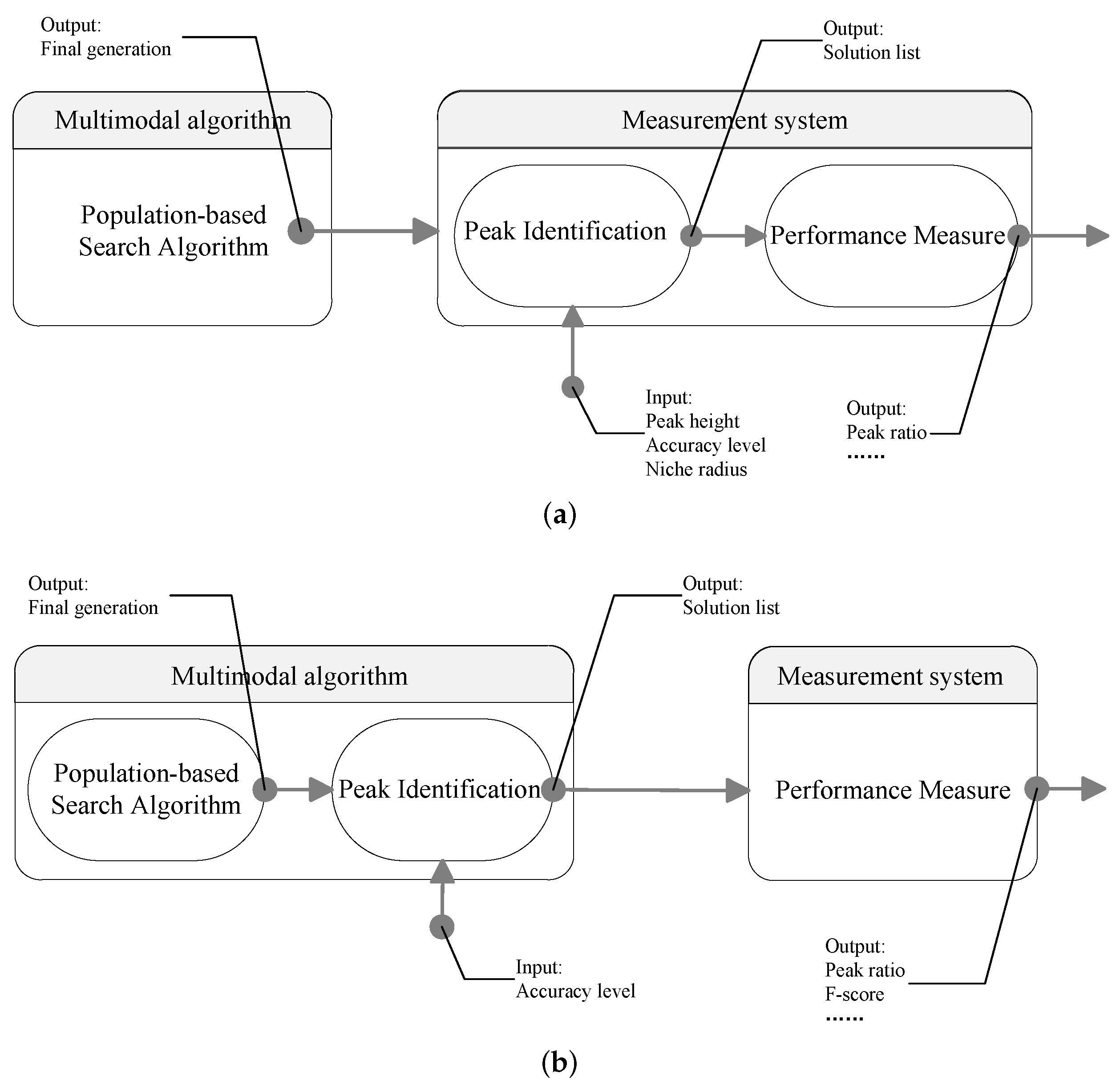
1. Introduction
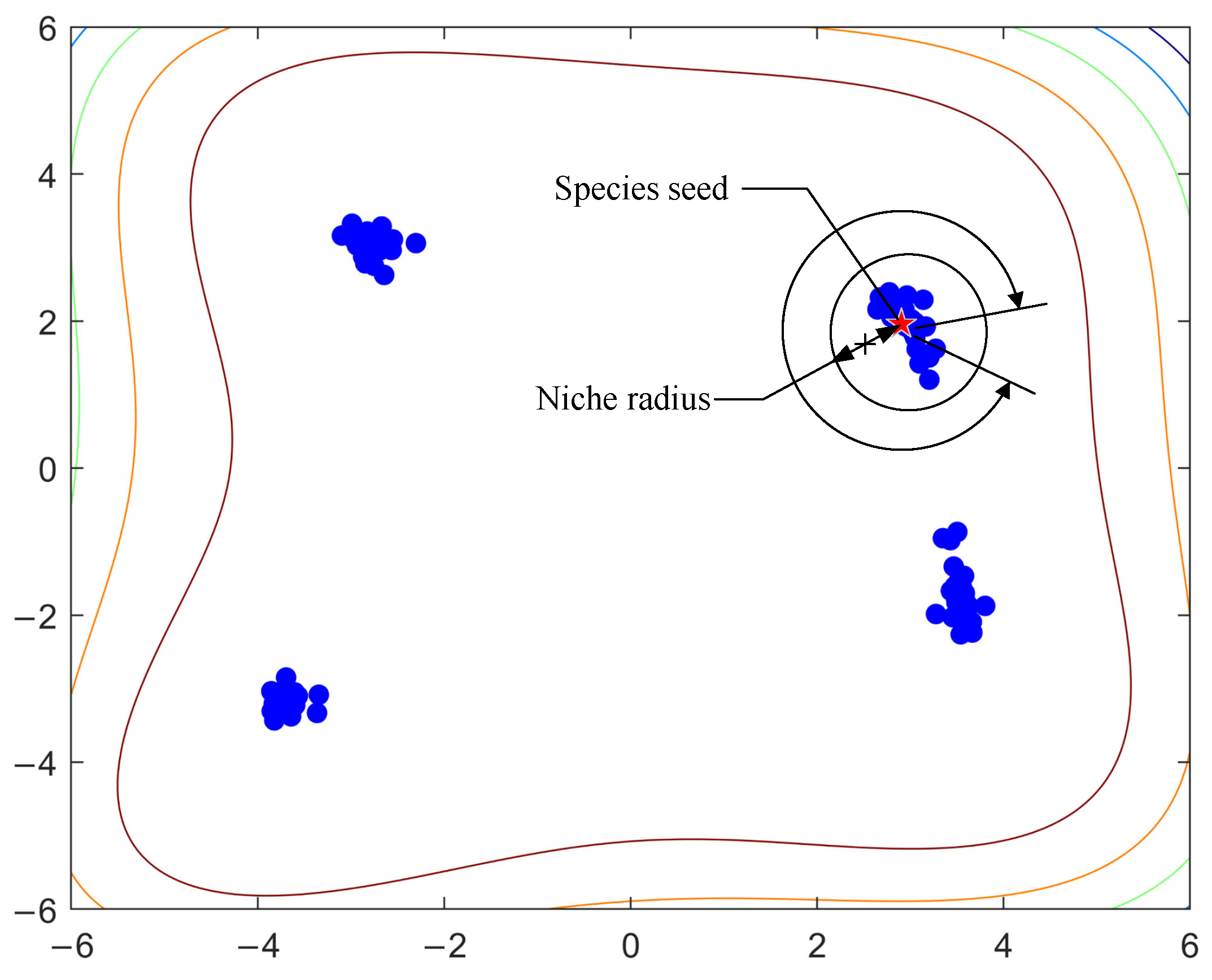
2. Niche Radius-Based Peak Identification
2.1. PL Algorithm
| Algorithm 1 PL |
| Input: –individuals sorted in descending order; r–niche radius; –accuracy level; –the fitness of global optima; Output:
|
- 1.
- The difference between the optimal fitness value and the fitness of the individual is less than the specified accuracy level ;
- 2.
- The individual belongs to a different niche from those in S:where denotes the Euclidean distance between s and X.
2.2. Complexity Analysis of PL Algorithm
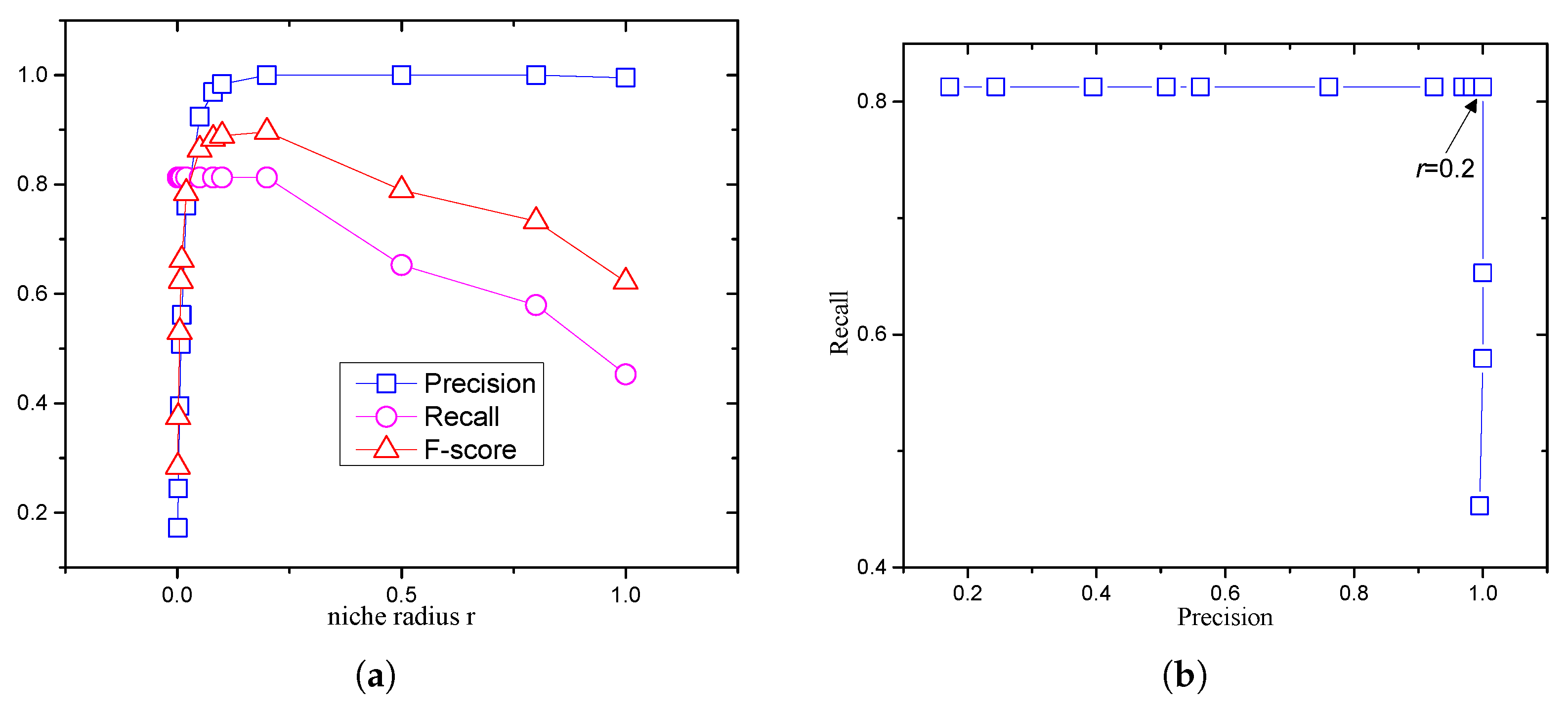
2.3. Difficulty of Setting the Niche Radius
3. The Proposed Topology-Based Peak Identification Algorithm
- 1.
- HVPI: a hill–valley-based peak identification algorithm.
- 2.
- HVPIC: a hill–valley-based peak identification algorithm coupling with clustering.
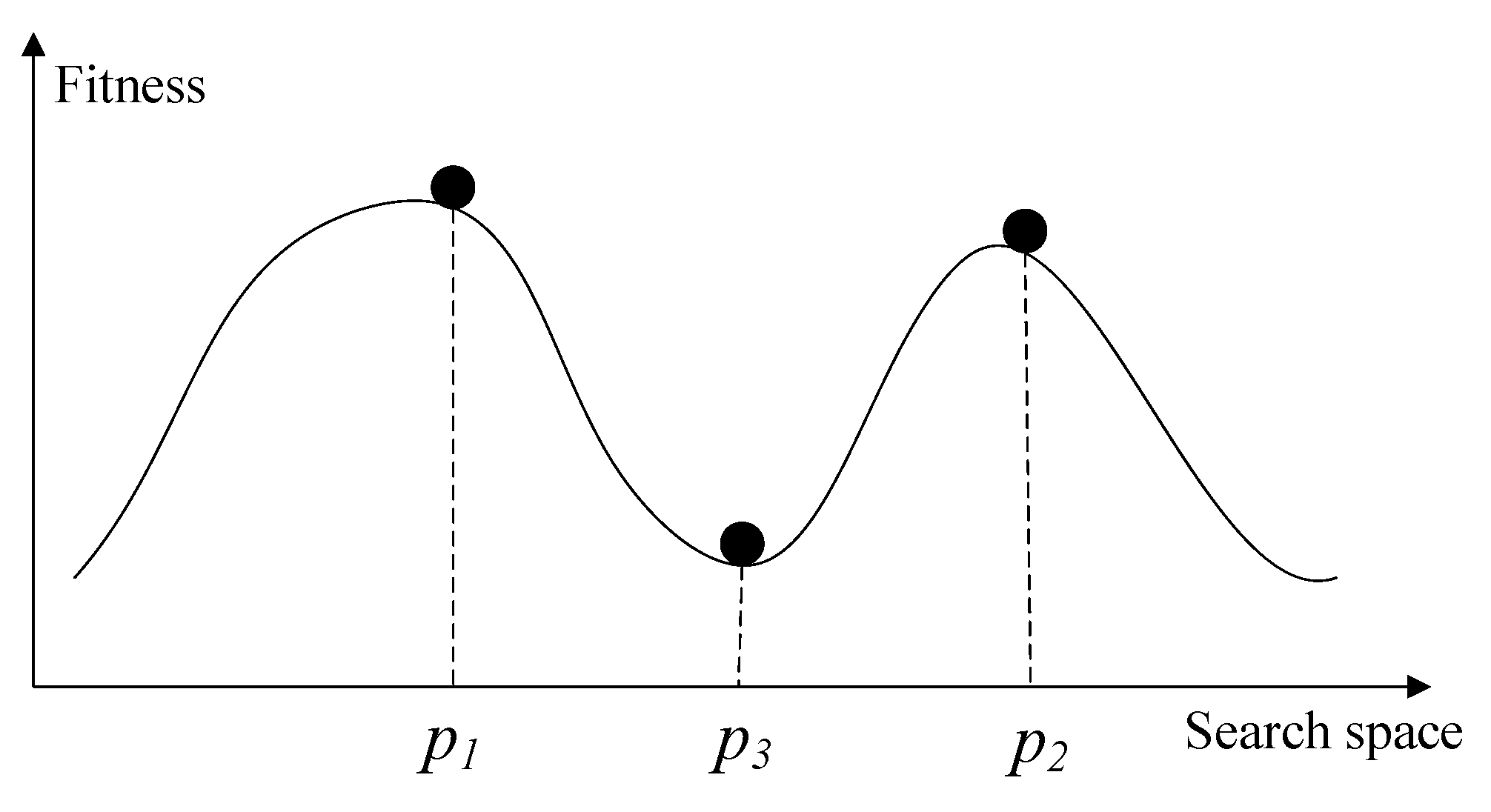
3.1. Hill–Valley-Based Peak Identification (HVPI)
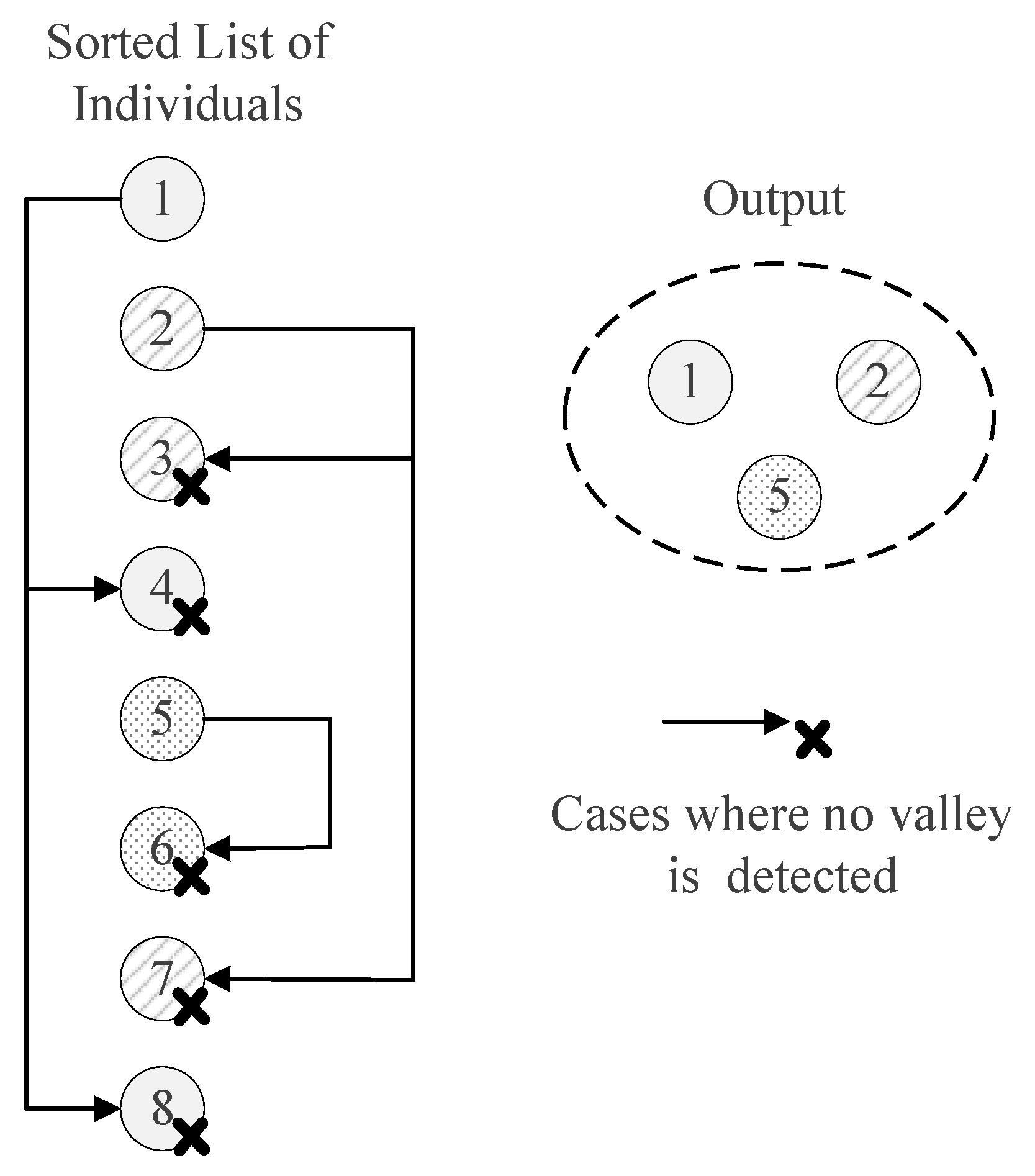
3.1.1. The HVPI Algorithm
| Algorithm 2 hill–valley |
| Input: –two individuals; Output:
|
| Algorithm 3 HVPI |
| Input: –individuals sorted in decreasing fitness values; –accuracy level; –the fitness of global optima; Output:
|
3.1.2. Discussion
3.2. Hill–Valley-Based Peak Identification Using Clustering (HVPIC)
3.2.1. Rationale
3.2.2. K-Means and Bisecting K-Means
| Algorithm 4 bisecting K-means |
| Input: – a set of points to be clustered; K–number of clusters; Output:
|
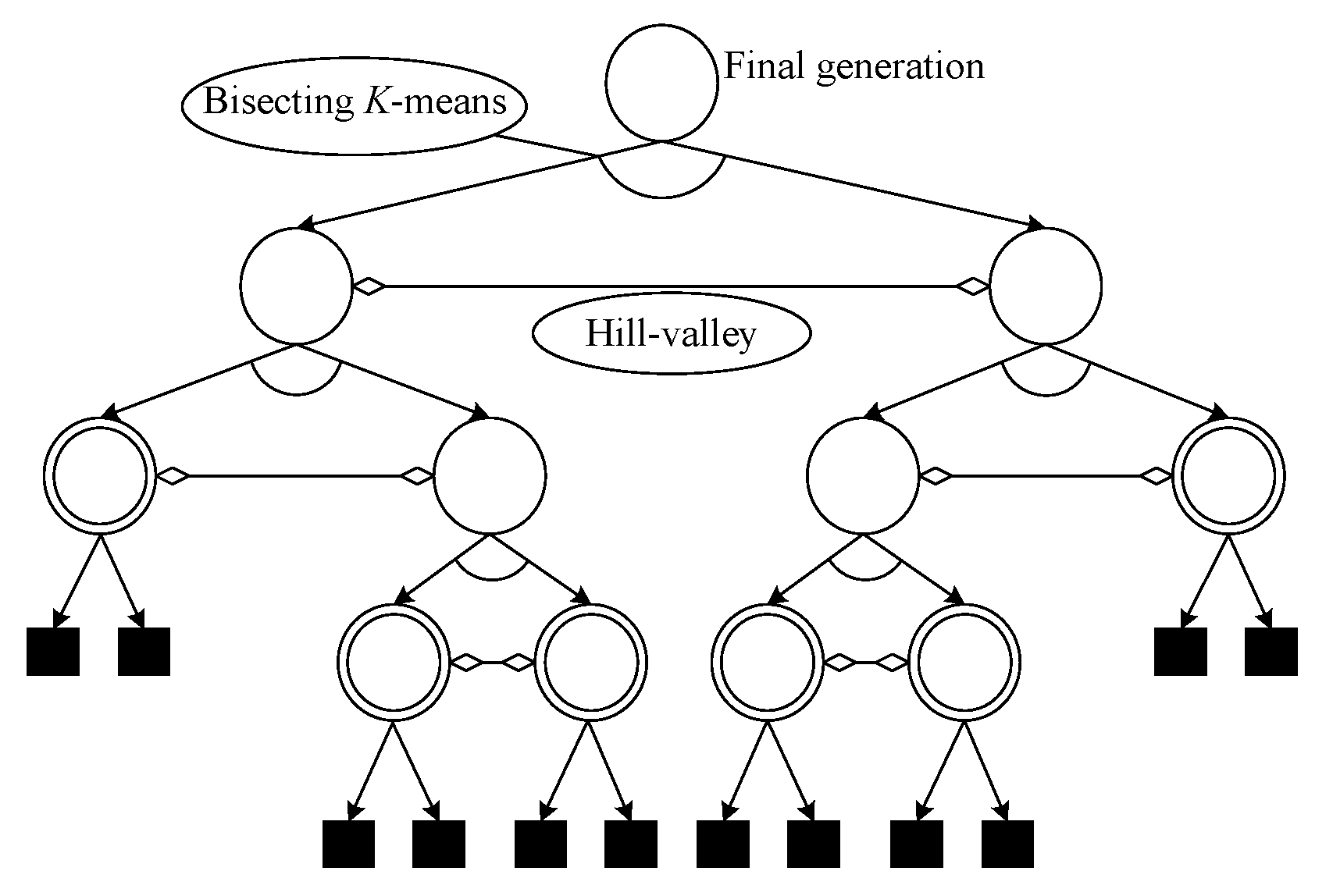
3.2.3. The HVPIC Algorithm
| Algorithm 5 HVPIC |
| Input: –the final generation of an EA; –accuracy level; Output:
|
- 1.
- The selection of the cluster to be bisected is simplified. In bisecting K-means, the cluster is chosen using specific rules (choose the largest cluster or the one with the largest SSE). In the HVPIC algorithm, the cluster at the head of the list is chosen.
- 2.
- The rule that determines whether new clusters should be added to the cluster list is redesigned. In bisecting K-means, two new clusters are added to the cluster list. In HVPIC, only clusters consisting of individuals from different niches are added to the cluster list.
- 3.
- The termination criterion of HVPIC also differs from bisecting K-means. Bisecting K-means terminates when there are K clusters in the cluster list. In comparison, HVPIC terminates when the cluster list is empty. The number of executions of the do-while block depends on the distribution of the population and the landscape of the problem at hand. This eliminates the need for specifying the number of clusters (species).
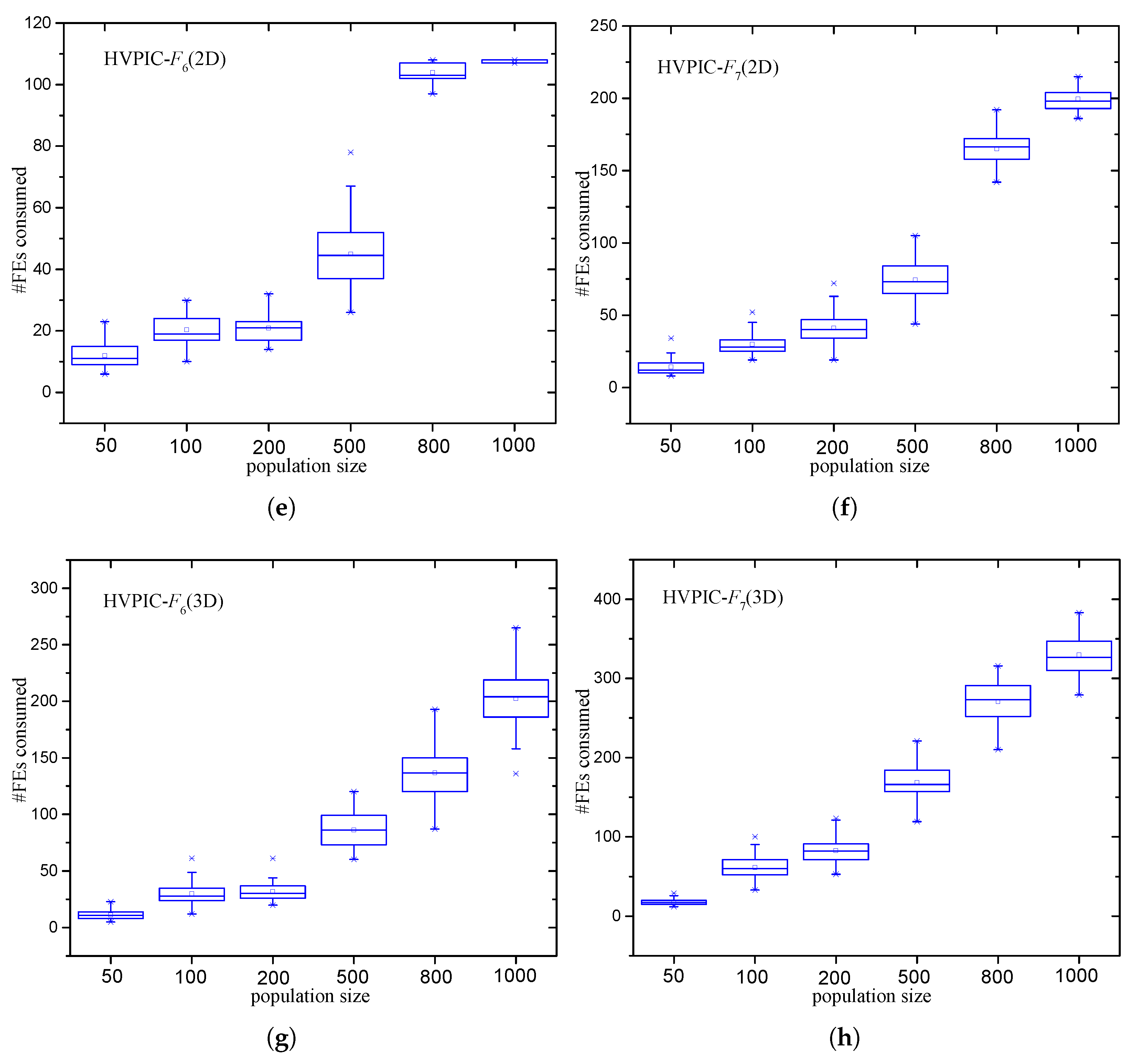
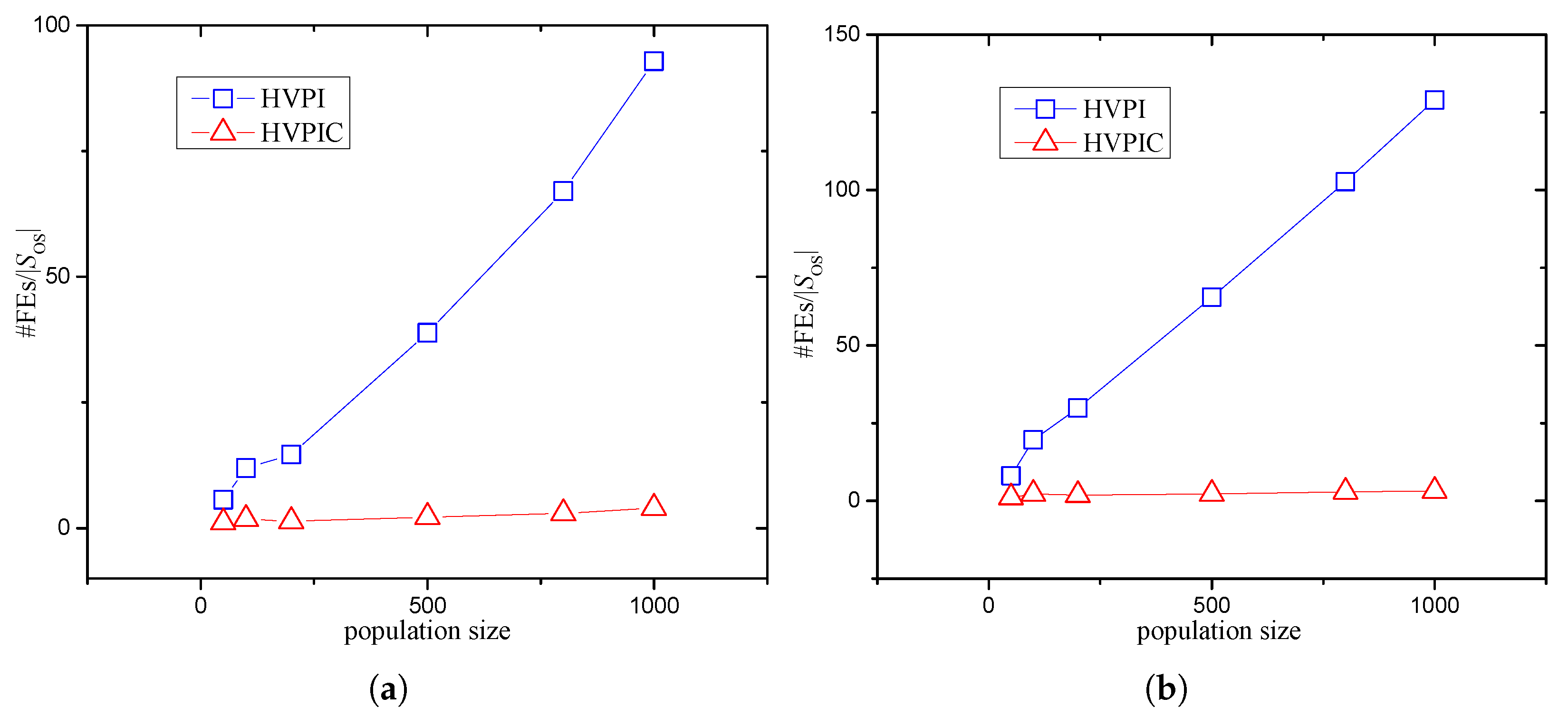
3.2.4. Analysis of the Number of FEs Required by HVPIC
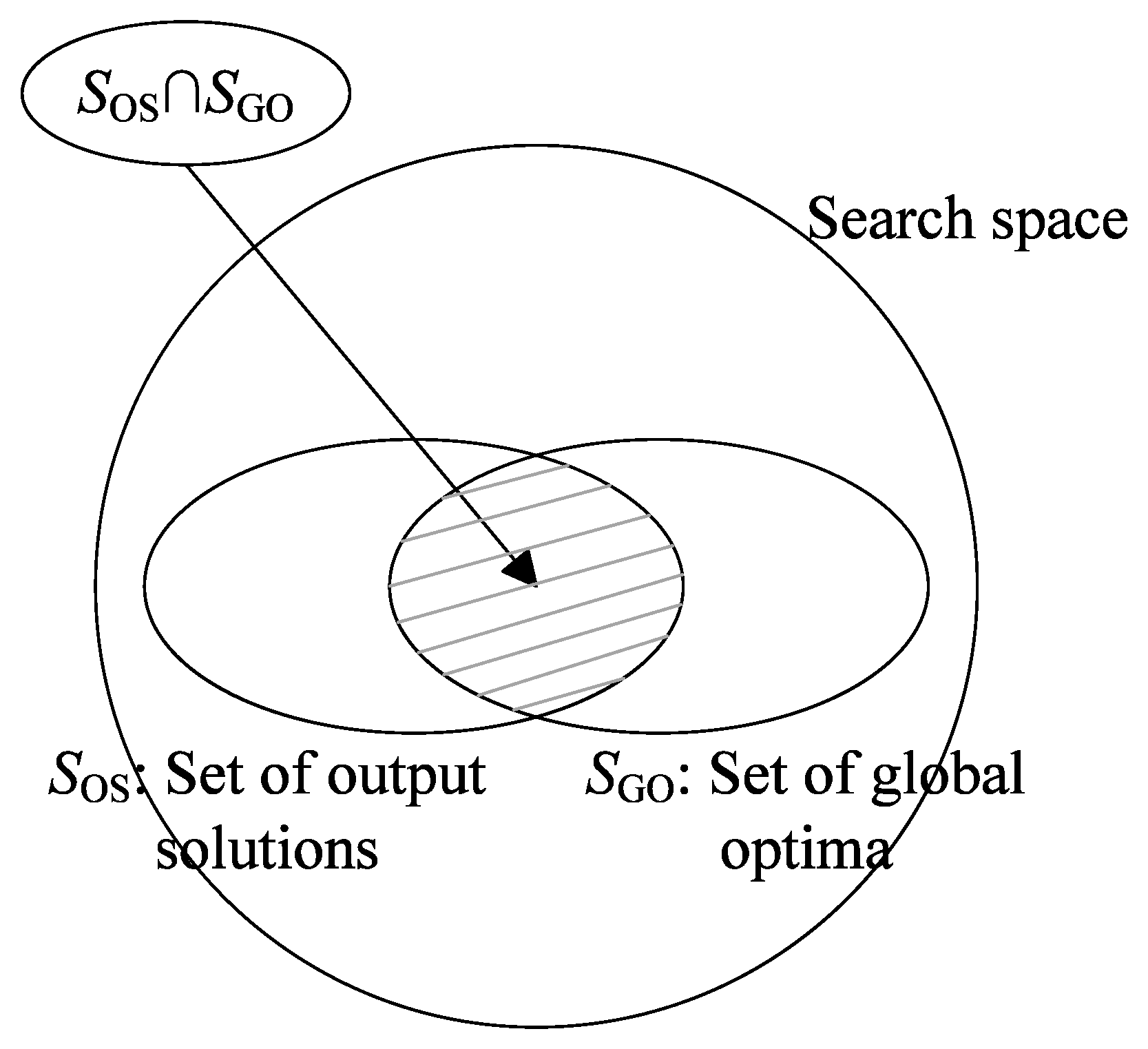
4. Performance Measure
5. Experiments
5.1. Experimental Setup
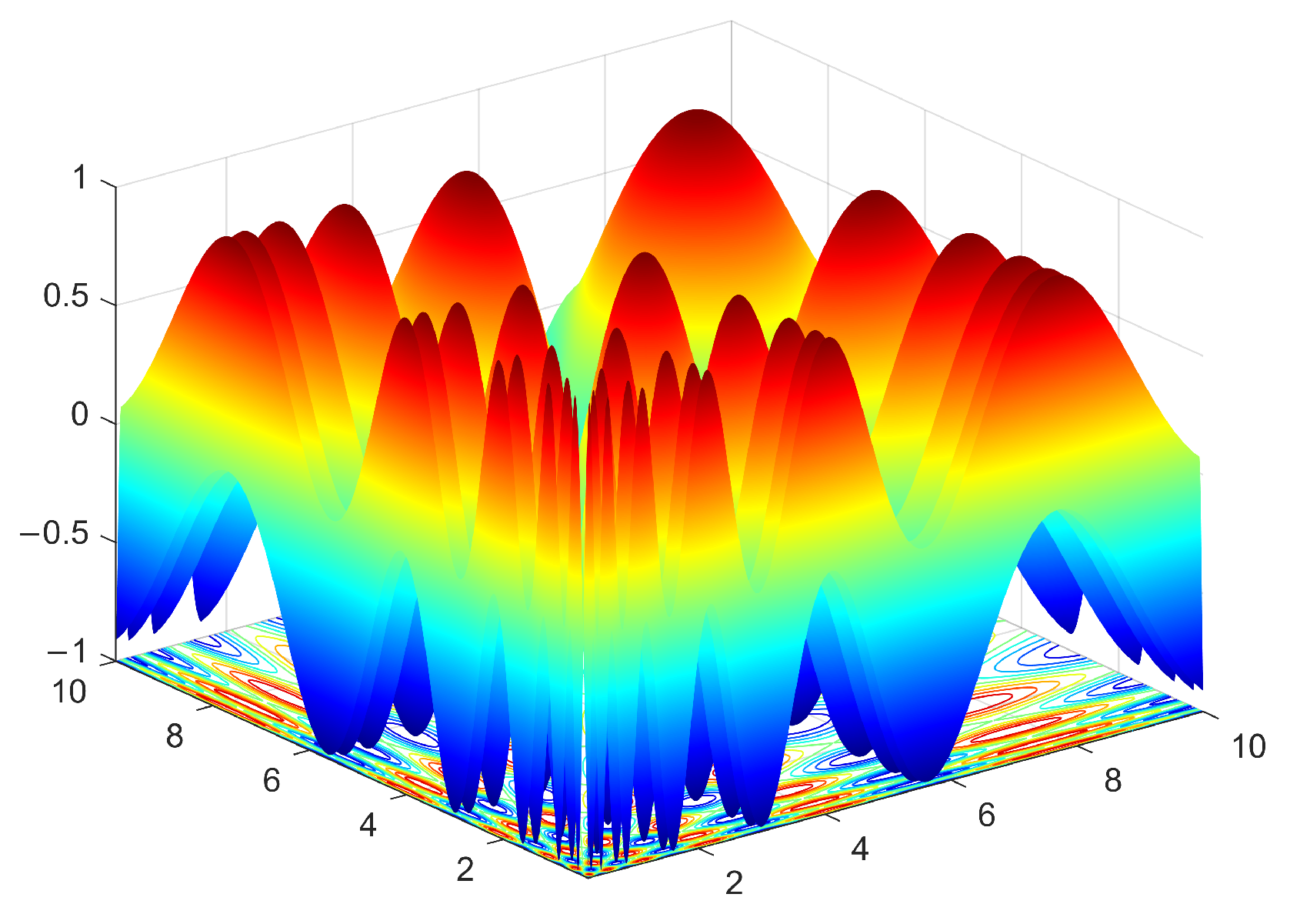
5.1.1. Benchmark Functions
5.1.2. Population-Based Search Algorithms and Parameter Settings
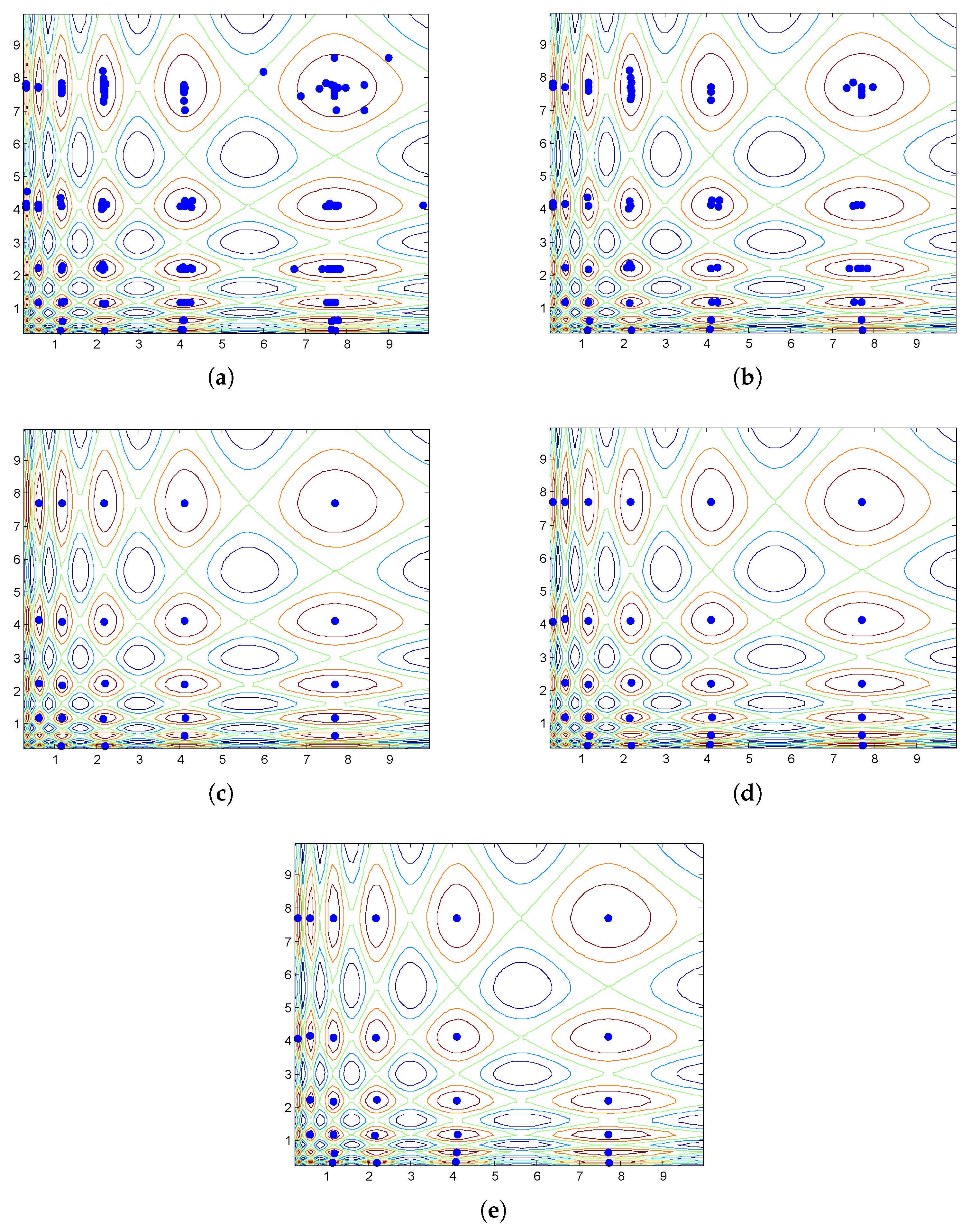
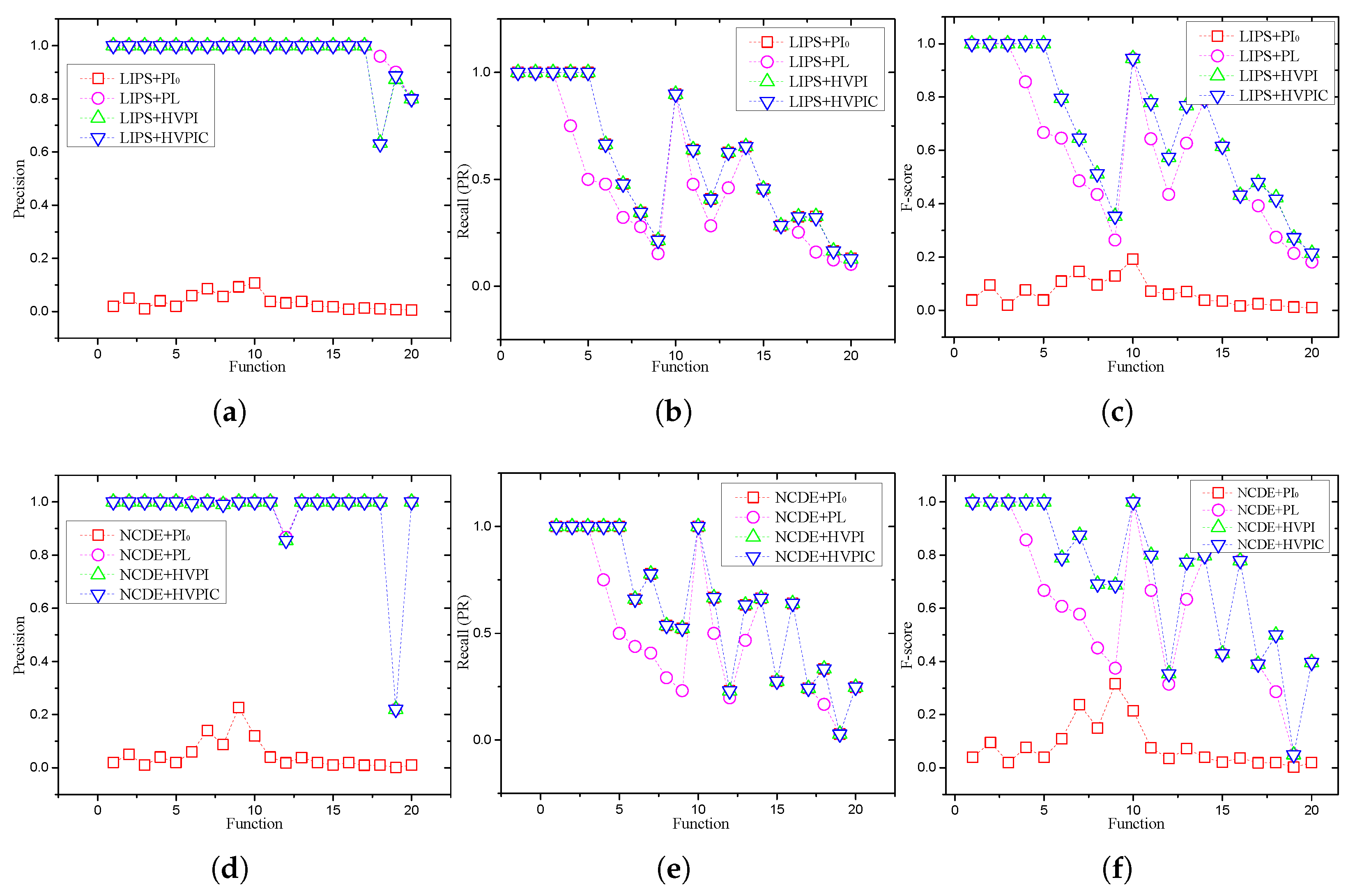
5.2. Overall Performance
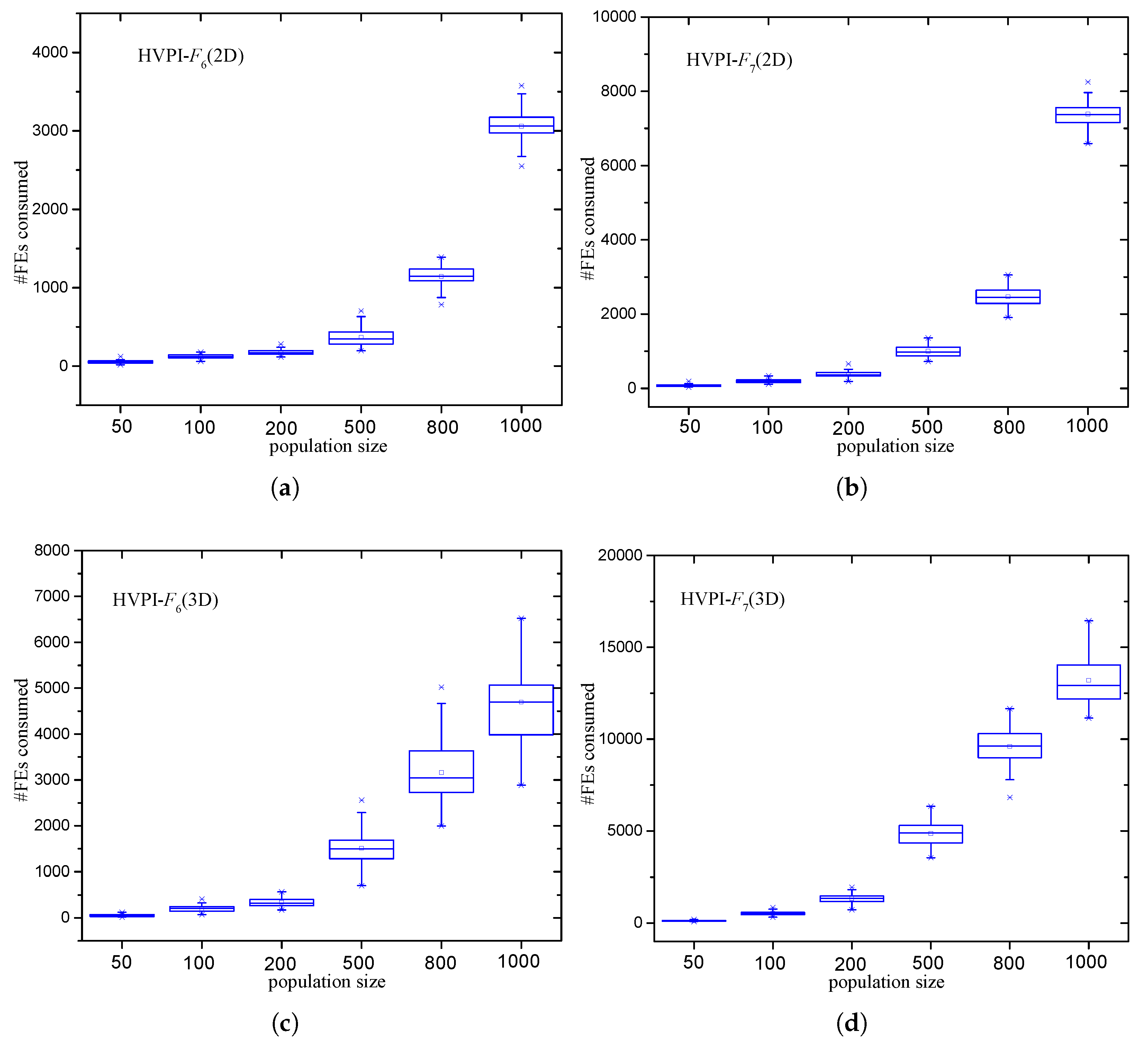
5.3. Effect of Population Size
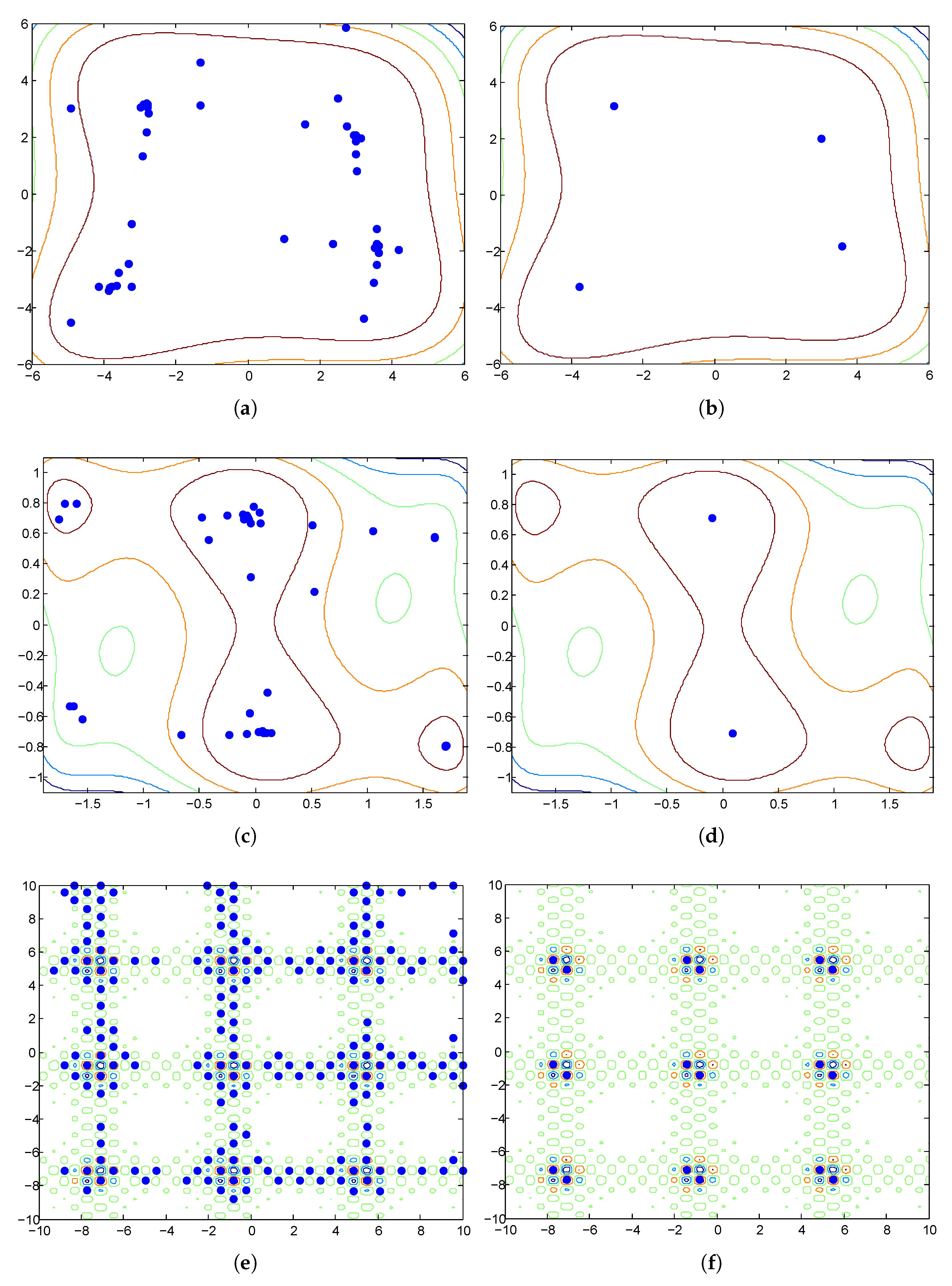
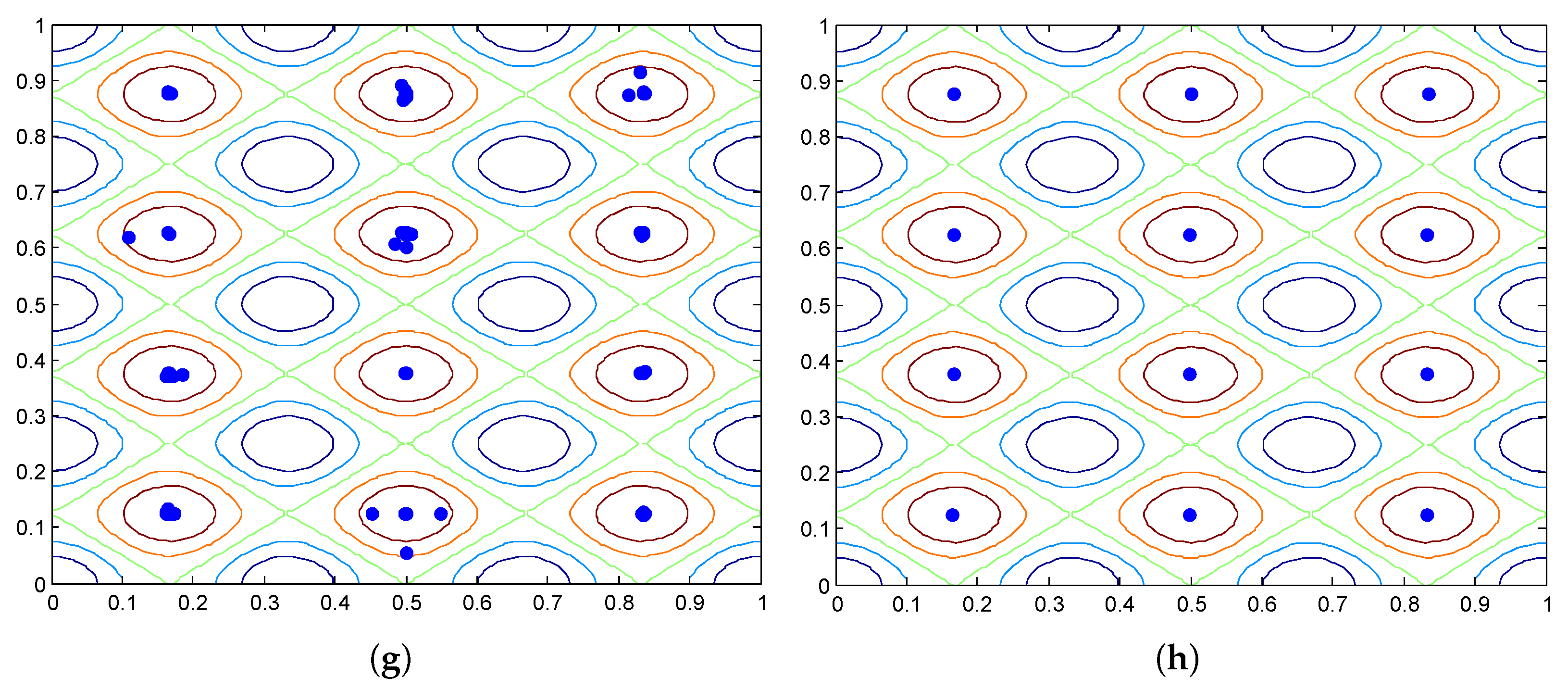
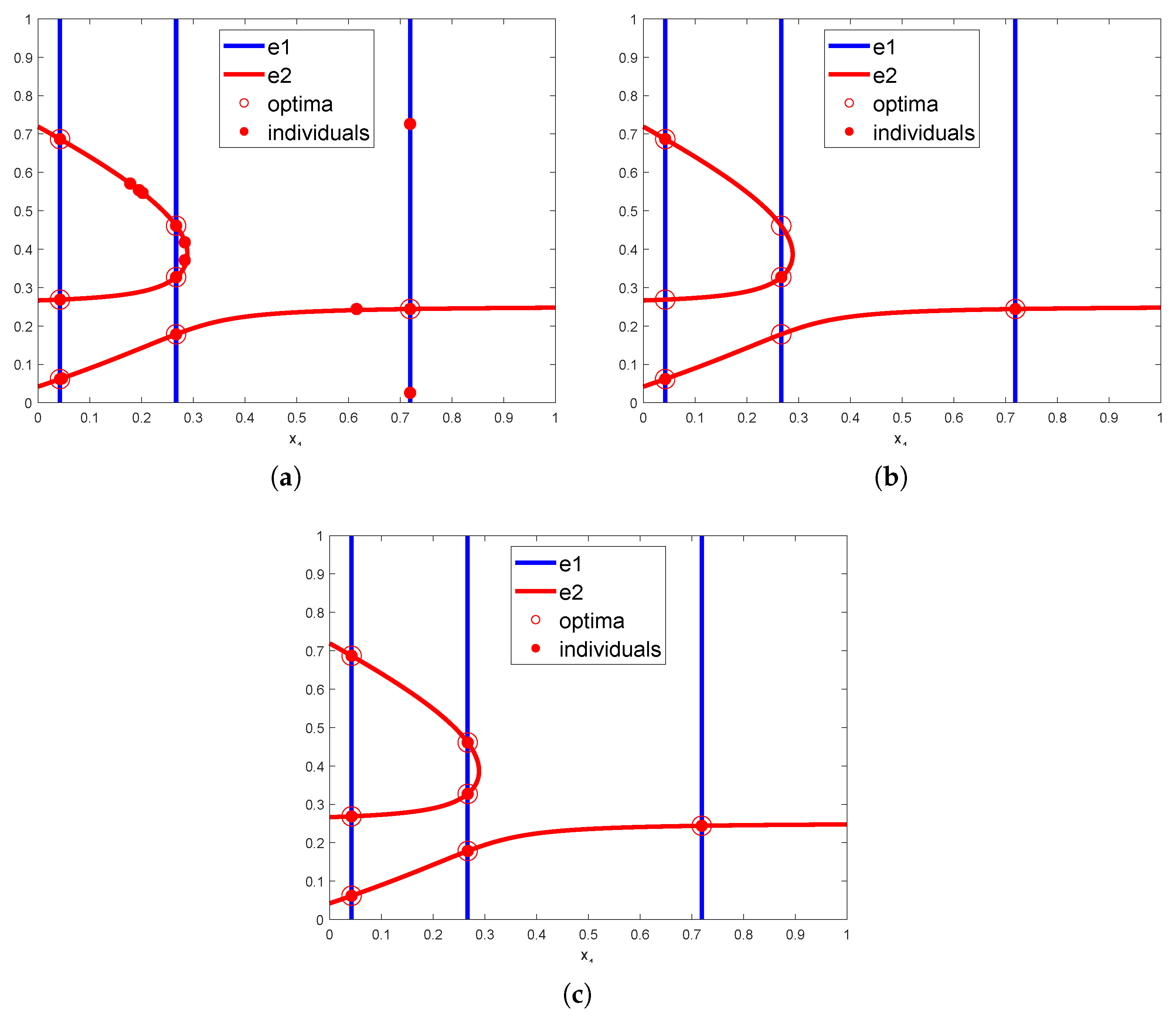
5.4. Effect of Convergence Degree
5.5. Effect of Accuracy Level
5.6. Application to Engineering Problems
- Multiple Steady States Problem: Evaluating multiple steady states in reaction networks is crucial in various chemical engineering applications, particularly in the analysis and design of chemical reactors. Steady states refer to conditions where the reaction rates and physical properties remain constant over time. Multiple steady states can exist in complex reaction networks, meaning there are several sets of conditions that satisfy the system’s governing equations.
- Molecular Conformation Problem: In molecular biology and drug design, determining the three-dimensional structure of a molecule is critical, particularly when identifying the minimum energy state or low-energy states. These low-energy conformations are likely the natural shapes of the molecule, significantly influencing its chemical reactivity, physical properties, and biological activity.
- Robot Kinematics Problem: A fundamental problem in robotics, kinematics studies the relationship between a robot’s joint configuration and the resulting motion of its end-effector. Understanding kinematics is crucial in determining the position, orientation, and velocity of robot components, without considering the forces driving the motion.
5.7. Embedding HVPI and HVPIC into Group-Based Optimization Algorithms
6. Conclusions
- 1.
- We proposed a practical two-phase multimodal optimization model. The first phase is the population-based search algorithm that has been extensively studied in the literature. The second phase is the peak identification (PI) procedure. The new model containing PI eliminates the users’ burden of dealing with redundant solutions.
- 2.
- New PI algorithms that alleviate the need for problem-specific knowledge were developed. Specifically, a PI algorithm previously used in the evaluation system was integrated with the hill–valley approach, to avoid having to preset the niche radius. Furthermore, to reduce the number of FEs required by the hill–valley approach, we combined HVPI with bisecting K-means in the HVPIC algorithm. Theoretical analysis showed that the number of FEs consumed by the HVPIC algorithm was proportional to the number of identified optima.
- 3.
- To evaluate the performance of multimodal algorithms, the F-measure, which considers both precision and recall values, was introduced. Compared to the PR and SR measures that are widely used in the literature, the F-measure is more comprehensive, since it is capable of evaluating the redundancy rate of the outputs of multimodal algorithms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Liao, B.; Li, J.; Li, S. A Survey on Biomimetic and Intelligent Algorithms with Applications. Biomimetics 2024, 9, 453. [Google Scholar] [CrossRef] [PubMed]
- Kong, S.; Wu, F.; Liu, H.; Zhang, W.; Sun, J.; Wang, J.; Yu, J. Bio-Inspired Optimization Algorithm Associated with Reinforcement Learning for Multi-Objective Operating Planning in Radioactive Environment. Biomimetics 2024, 9, 438. [Google Scholar] [CrossRef] [PubMed]
- Varna, F.T.; Husbands, P. Two New Bio-Inspired Particle Swarm Optimisation Algorithms for Single-Objective Continuous Variable Problems Based on Eavesdropping and Altruistic Animal Behaviours. Biomimetics 2024, 9, 538. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.J.; Jian, J.R.; Zhan, Z.H.; Li, Y.; Kwong, S.; Zhang, J. Gene Targeting Differential Evolution: A Simple and Efficient Method for Large-Scale Optimization. IEEE Trans. Evol. Comput. 2023, 27, 964–979. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, R.; Guo, J.; Li, B.; Song, K.; Tan, X.; Liu, G.; Bian, J.; Yang, Y. Connecting large language models with evolutionary algorithms yields powerful prompt optimizers. arXiv 2023, arXiv:2309.08532. [Google Scholar]
- Song, Y.; Zhao, G.; Zhang, B.; Chen, H.; Deng, W.; Deng, W. An enhanced distributed differential evolution algorithm for portfolio optimization problems. Eng. Appl. Artif. Intell. 2023, 121, 106004. [Google Scholar] [CrossRef]
- Zhou, X.; Cai, X.; Zhang, H.; Zhang, Z.; Jin, T.; Chen, H.; Deng, W. Multi-strategy competitive-cooperative co-evolutionary algorithm and its application. Inf. Sci. 2023, 635, 328–344. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhan, Z.H.; Yu, W.J.; Lin, Y.; Zhang, J.; Gu, T.L.; Zhang, J. Dynamic group learning distributed particle swarm optimization for large-scale optimization and its application in cloud workflow scheduling. IEEE Trans. Cybern. 2019, 50, 2715–2729. [Google Scholar] [CrossRef]
- Li, J.; Dong, R.; Wu, X.; Huang, W.; Lin, P. A Self-Learning Hyper-Heuristic Algorithm Based on a Genetic Algorithm: A Case Study on Prefabricated Modular Cabin Unit Logistics Scheduling in a Cruise Ship Manufacturer. Biomimetics 2024, 9, 516. [Google Scholar] [CrossRef]
- Felix-Saul, J.C.; García-Valdez, M.; Merelo Guervós, J.J.; Castillo, O. Extending Genetic Algorithms with Biological Life-Cycle Dynamics. Biomimetics 2024, 9, 476. [Google Scholar] [CrossRef]
- Mahfoud, S.W. Niching Methods for Genetic Algorithms. Ph.D. Thesis, Department of Computer Science, University of Illinois Urbana-Champaign, Urbana, IL, USA, 1995. [Google Scholar]
- Preuss, M.; Epitropakis, M.; Li, X.; Fieldsend, J.E. Multimodal optimization: Formulation, heuristics, and a decade of advances. In Metaheuristics for Finding Multiple Solutions; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–26. [Google Scholar]
- Jong, K.D. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Thomsen, R. Multimodal optimization using crowding-based differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; pp. 1382–1389. [Google Scholar]
- Goldberg, D.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization. In Proceedings of the International Conference Genetic Algorithms and Their Application, Cambridge, MA, USA, 28–31 July 1987; pp. 41–49. [Google Scholar]
- Harik, G.R. Finding multimodal solutions using restricted tournament selection. In Proceedings of the 6th International Conference on Genetic Algorithms, Pittsburgh, PA, USA, 15–19 July 1995; pp. 24–31. [Google Scholar]
- Li, J.P.; Balazs, M.E.; Parks, G.T.; Clarkson, P.J. A species conserving genetic algorithm for multimodal function optimization. Evol. Comput. 2002, 10, 207–234. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Sun, S.; Cheng, S.; Shi, Y. An adaptive niching method based on multi-strategy fusion for multimodal optimization. Memetic Comput. 2021, 13, 341–357. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhan, Z.H.; Li, Y.; Kwong, S.; Jeon, S.W.; Zhang, J. Fitness and distance based local search with adaptive differential evolution for multimodal optimization problems. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 684–699. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Liu, J. Minimum spanning tree niching-based differential evolution with knowledge-driven update strategy for multimodal optimization problems. Appl. Soft Comput. 2023, 145, 110589. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhan, Z.H.; Lin, Y.; Yu, W.J.; Wang, H.; Kwong, S.; Zhang, J. Automatic niching differential evolution with contour prediction approach for multimodal optimization problems. IEEE Trans. Evol. Comput. 2019, 24, 114–128. [Google Scholar] [CrossRef]
- Zhou, T.; Hu, Z.; Su, Q.; Xiong, W. A clustering differential evolution algorithm with neighborhood-based dual mutation operator for multimodal multiobjective optimization. Expert Syst. Appl. 2023, 216, 119438. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhan, Z.H.; Lin, Y.; Yu, W.J.; Yuan, H.Q.; Gu, T.L.; Kwong, S.; Zhang, J. Dual-strategy differential evolution with affinity propagation clustering for multimodal optimization problems. IEEE Trans. Evol. Comput. 2017, 22, 894–908. [Google Scholar] [CrossRef]
- Liao, Z.; Mi, X.; Pang, Q.; Sun, Y. History archive assisted niching differential evolution with variable neighborhood for multimodal optimization. Swarm Evol. Comput. 2023, 76, 101206. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Yang, Q.; Wang, Y.; Liu, D.; Jeon, S.W.; Zhang, J. Proximity ranking-based multimodal differential evolution. Swarm Evol. Comput. 2023, 78, 101277. [Google Scholar] [CrossRef]
- Wang, R.; Hao, K.; Huang, B.; Zhu, X. Adaptive niching particle swarm optimization with local search for multimodal optimization. Appl. Soft Comput. 2023, 133, 109923. [Google Scholar] [CrossRef]
- Sheng, W.; Wang, X.; Wang, Z.; Li, Q.; Chen, Y. Adaptive memetic differential evolution with niching competition and supporting archive strategies for multimodal optimization. Inf. Sci. 2021, 573, 316–331. [Google Scholar] [CrossRef]
- Parrott, D.; Li, X. Locating and tracking multiple dynamic optima by a particle swarm model using speciation. IEEE Trans. Evol. Comput. 2006, 10, 440–458. [Google Scholar] [CrossRef]
- Li, X.; Engelbrecht, A.; Epitropakis, M.G. Benchmark Functions for CEC 2013 Special Session and Competition on Niching Methods for Multimodal Function Optimization; Tech. Rep; Evolutionary Computation and Machine Learning Group, RMIT University: Melbourne, Australia, 2013. [Google Scholar]
- Ursem, R. Multinational evolutionary algorithms. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; pp. 1633–1640. [Google Scholar]
- Shaw, W.; Burgin, R.; Howell, P. Performance Standards and Evaluations in IR Test Collections: Cluster-Based Retrieval Models. Inf. Process. Manag. 1997, 33, 1–14. [Google Scholar] [CrossRef]
- Mayr, E. Systematics and the Origin of Species, from the Viewpoint of a Zoologist; Harvard University Press: Boston, MA, USA, 1999. [Google Scholar]
- Deb, K.; Goldberg, D.E. An investigation of niche and species formation in genetic function optimization. In Proceedings of the 3rd International Conference on Genetic Algorithms, Fairfax, VA, USA, 2–9 June 1989; pp. 42–50. [Google Scholar]
- Li, X. Niching without niching parameters: Particle swarm optimization using a ring topology. IEEE Trans. Evol. Comput. 2010, 14, 150–169. [Google Scholar] [CrossRef]
- Stoean, C.; Preuss, M.; Stoean, R.; Dumitrescu, D. Multimodal optimization by means of a topological species conservation algorithm. IEEE Trans. Evol. Comput. 2010, 14, 842–864. [Google Scholar] [CrossRef]
- Yao, J.; Kharma, N.; Grogono, P. Bi-objective multipopulation genetic algorithm for multimodal function optimization. IEEE Trans. Evol. Comput. 2010, 14, 80–102. [Google Scholar]
- Jelasty, M.; Dombi, J. GAS, a concept on modeling species in genetic algorithms. Artif. Intell. 1998, 99, 1–19. [Google Scholar] [CrossRef]
- Qu, B.Y.; Suganthan, P.N.; Liang, J.J. Differential evolution with neighborhood mutation for multimodal optimization. IEEE Trans. Evol. Comput. 2012, 16, 601–614. [Google Scholar] [CrossRef]
- Li, Y.; Huang, L.; Gao, W.; Wei, Z.; Huang, T.; Xu, J.; Gong, M. History information-based hill-valley technique for multimodal optimization problems. Inf. Sci. 2023, 631, 15–30. [Google Scholar] [CrossRef]
- Maree, S.C.; Thierens, D.; Alderliesten, T.; Bosman, P.A. Two-phase real-valued multimodal optimization with the hill-valley evolutionary algorithm. In Metaheuristics for Finding Multiple Solutions; Springer: Berlin/Heidelberg, Germany, 2021; pp. 165–189. [Google Scholar]
- Navarro, R.; Kim, C.H. Niching multimodal landscapes faster yet effectively: Vmo and hillvallea benefit together. Mathematics 2020, 8, 665. [Google Scholar] [CrossRef]
- Liu, Q.; Du, S.; Van Wyk, B.J.; Sun, Y. Niching particle swarm optimization based on Euclidean distance and hierarchical clustering for multimodal optimization. Nonlinear Dyn. 2020, 99, 2459–2477. [Google Scholar] [CrossRef]
- Liu, Q.; Du, S.; van Wyk, B.J.; Sun, Y. Double-layer-clustering differential evolution multimodal optimization by speciation and self-adaptive strategies. Inf. Sci. 2021, 545, 465–486. [Google Scholar] [CrossRef]
- Tan, P.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Addison-Wesley: Reading, MA, USA, 2005. [Google Scholar]
- Steinbach, M.; Karypis, G.; Kumar, V. A comparison of document clustering techniques. In Proceedings of the Workshop Text Mining, 6th ACM SIGKDD, Boston, MA, USA, 20–23 August 2000; pp. 20–23. [Google Scholar]
- Zou, Z.; Chen, K.; Shi, Z.; Guo, Y.; Ye, J. Object detection in 20 years: A survey. Proc. IEEE 2023, 111, 257–276. [Google Scholar] [CrossRef]
- Qu, B.Y.; Suganthan, P.N.; Das, S. A distance-based locally informed particle swarm model for multimodal optimization. IEEE Trans. Evol. Comput. 2013, 17, 387–402. [Google Scholar] [CrossRef]
- Floudas, C.A. Recent advances in global optimization for process synthesis, design and control: Enclosure of all solutions. Comput. Chem. Eng. 1999, 23, S963–S973. [Google Scholar] [CrossRef]
- Emiris, I.Z.; Mourrain, B. Computer algebra methods for studying and computing molecular conformations. Algorithmica 1999, 25, 372–402. [Google Scholar] [CrossRef]
- Grosan, C.; Abraham, A. A new approach for solving nonlinear equations systems. IEEE Trans. Syst. Man Cybern.-Part A Syst. Humans 2008, 38, 698–714. [Google Scholar] [CrossRef]


| No. | Function | Name | ||
|---|---|---|---|---|
| 1 | (1D) | Five-Uneven-Peak Trap | 200 | 2 |
| 2 | (1D) | Equal Maxima | 1 | 5 |
| 3 | (1D) | Uneven Decreasing Maxima | 1 | 1 |
| 4 | (2D) | Himmelblau | 200 | 4 |
| 5 | (2D) | Six-hump Camel Back | 1.03163 | 2 |
| 6 | (2D) | Shubert | 186.7309 | 18 |
| 7 | (2D) | Vincent | 1 | 36 |
| 8 | (3D) | Shubert | 2709.0935 | 81 |
| 9 | (3D) | Vincent | 1 | 216 |
| 10 | (2D) | Modified Rastrigin | −2 | 12 |
| 11 | (2D) | Composition Function 1 | 0 | 6 |
| 12 | (2D) | Composition Function 2 | 0 | 8 |
| 13 | (2D) | Composition Function 3 | 0 | 6 |
| 14 | (3D) | Composition Function 3 | 0 | 6 |
| 15 | (3D) | Composition Function 4 | 0 | 8 |
| 16 | (5D) | Composition Function 3 | 0 | 6 |
| 17 | (5D) | Composition Function 4 | 0 | 8 |
| 18 | (10D) | Composition Function 3 | 0 | 6 |
| 19 | (10D) | Composition Function 4 | 0 | 8 |
| 20 | (20D) | Composition Function 4 | 0 | 8 |
| Function | Popsize | MaxFEs |
|---|---|---|
| to (1D or 2D) | 100 | 1.00 × 104 |
| to (2D) | 200 | 2.00 × 104 |
| to (2D) | 100 | 5.00 × 104 |
| to (3D) | 500 | 5.00 × 104 |
| to (3D or higher) | 200 | 1.00 × 105 |
| Function | NCDE+HVPI | NCDE+HVPIC | LIPS+HVPI | LIPS+HVPIC |
|---|---|---|---|---|
| (1D) | 1.00 | 1.00 | 1.00 | 1.00 |
| (1D) | 475.12 | 29.94 | 220.00 | 30.18 |
| (1D) | 52.10 | 4.90 | 42.90 | 5.00 |
| (2D) | 266.70 | 23.00 | 590.44 | 23.00 |
| (2D) | 210.90 | 11.00 | 378.00 | 11.00 |
| (2D) | 74.20 | 11.36 | 104.50 | 17.88 |
| (2D) | 1827.04 | 120.92 | 1800.94 | 94.42 |
| (3D) | 1008.60 | 43.22 | 440.52 | 31.94 |
| (3D) | 13,443.90 | 379.76 | 9368.30 | 254.48 |
| (2D) | 323.52 | 47.44 | 65.56 | 10.48 |
| (2D) | 73.14 | 14.70 | 7.32 | 3.54 |
| (2D) | 8.14 | 2.96 | 4.90 | 2.66 |
| (2D) | 76.12 | 22.48 | 5.28 | 2.76 |
| (3D) | 206.00 | 15.20 | 5.76 | 2.92 |
| (3D) | 98.32 | 11.70 | 6.20 | 2.84 |
| (5D) | 326.34 | 21.74 | 2.08 | 1.30 |
| (5D) | 173.48 | 10.64 | 4.24 | 2.20 |
| (10D) | 170.84 | 10.90 | 10.30 | 5.74 |
| (10D) | 5.80 | 1.70 | 19.62 | 5.58 |
| (20D) | 289.34 | 10.88 | 88.20 | 7.46 |
| Function | HVPI | HVPIC | ||||
|---|---|---|---|---|---|---|
| Precision | Recall | F | Precision | Recall | F | |
| (1D) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (2D) | 0.99 | 0.66 | 0.79 | 0.99 | 0.66 | 0.79 |
| (2D) | 1.00 | 0.78 | 0.87 | 1.00 | 0.78 | 0.87 |
| (3D) | 0.99 | 0.54 | 0.69 | 0.99 | 0.54 | 0.69 |
| (3D) | 1.00 | 0.52 | 0.69 | 1.00 | 0.52 | 0.69 |
| (2D) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| (2D) | 1.00 | 0.67 | 0.80 | 1.00 | 0.67 | 0.80 |
| (2D) | 0.86 | 0.23 | 0.35 | 0.86 | 0.23 | 0.35 |
| (2D) | 1.00 | 0.63 | 0.77 | 1.00 | 0.63 | 0.77 |
| (3D) | 1.00 | 0.66 | 0.80 | 1.00 | 0.66 | 0.80 |
| (3D) | 1.00 | 0.28 | 0.43 | 1.00 | 0.28 | 0.43 |
| (5D) | 1.00 | 0.64 | 0.78 | 1.00 | 0.64 | 0.78 |
| (5D) | 1.00 | 0.24 | 0.39 | 1.00 | 0.24 | 0.39 |
| (10D) | 1.00 | 0.33 | 0.50 | 1.00 | 0.33 | 0.50 |
| (10D) | 0.22 | 0.03 | 0.05 | 0.22 | 0.03 | 0.05 |
| (20D) | 1.00 | 0.25 | 0.40 | 1.00 | 0.25 | 0.40 |
| Function | PI | HVPI | HVPIC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 0.88 | 1.00 | 0.02 | 1.00 | 0.91 | 0.99 | 0.02 | 1.00 | 0.91 | 0.99 | 0.02 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (3D) | 1.00 | 0.93 | 0.99 | 0.02 | 1.00 | 0.93 | 0.99 | 0.02 | 1.00 | 0.93 | 0.99 | 0.02 |
| (3D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 0.00 | 0.87 | 0.31 | 1.00 | 0.00 | 0.86 | 0.31 | 1.00 | 0.00 | 0.86 | 0.31 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (3D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (3D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (5D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (5D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (10D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (10D) | 1.00 | 0.00 | 0.22 | 0.41 | 1.00 | 0.00 | 0.22 | 0.41 | 1.00 | 0.00 | 0.22 | 0.41 |
| (20D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| Function | PI | HVPI | HVPIC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 0.75 | 0.75 | 0.75 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 0.50 | 0.50 | 0.50 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 0.50 | 0.28 | 0.44 | 0.05 | 0.89 | 0.44 | 0.66 | 0.10 | 0.89 | 0.44 | 0.66 | 0.10 |
| (2D) | 0.47 | 0.33 | 0.41 | 0.03 | 0.86 | 0.69 | 0.78 | 0.04 | 0.86 | 0.69 | 0.78 | 0.04 |
| (3D) | 0.32 | 0.20 | 0.29 | 0.03 | 0.75 | 0.28 | 0.54 | 0.10 | 0.75 | 0.28 | 0.54 | 0.10 |
| (3D) | 0.26 | 0.20 | 0.23 | 0.01 | 0.61 | 0.46 | 0.52 | 0.03 | 0.61 | 0.46 | 0.52 | 0.03 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 0.50 | 0.50 | 0.50 | 0.00 | 0.67 | 0.67 | 0.67 | 0.00 | 0.67 | 0.67 | 0.67 | 0.00 |
| (2D) | 0.38 | 0.00 | 0.20 | 0.11 | 0.50 | 0.00 | 0.23 | 0.12 | 0.50 | 0.00 | 0.23 | 0.12 |
| (2D) | 0.50 | 0.33 | 0.47 | 0.07 | 0.67 | 0.50 | 0.63 | 0.07 | 0.67 | 0.50 | 0.63 | 0.07 |
| (3D) | 0.67 | 0.50 | 0.66 | 0.02 | 0.67 | 0.50 | 0.66 | 0.02 | 0.67 | 0.50 | 0.66 | 0.02 |
| (3D) | 0.38 | 0.25 | 0.28 | 0.05 | 0.38 | 0.25 | 0.28 | 0.05 | 0.38 | 0.25 | 0.28 | 0.05 |
| (5D) | 0.67 | 0.50 | 0.64 | 0.06 | 0.67 | 0.50 | 0.64 | 0.06 | 0.67 | 0.50 | 0.64 | 0.06 |
| (5D) | 0.25 | 0.13 | 0.24 | 0.03 | 0.25 | 0.13 | 0.24 | 0.03 | 0.25 | 0.13 | 0.24 | 0.03 |
| (10D) | 0.17 | 0.17 | 0.17 | 0.00 | 0.33 | 0.33 | 0.33 | 0.00 | 0.33 | 0.33 | 0.33 | 0.00 |
| (10D) | 0.13 | 0.00 | 0.03 | 0.05 | 0.13 | 0.00 | 0.03 | 0.05 | 0.13 | 0.00 | 0.03 | 0.05 |
| (20D) | 0.25 | 0.13 | 0.25 | 0.02 | 0.25 | 0.13 | 0.25 | 0.02 | 0.25 | 0.13 | 0.25 | 0.02 |
| Function | PI | HVPI | HVPIC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (3D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (3D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (3D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (3D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (5D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (5D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (10D) | 1.00 | 0.00 | 0.96 | 0.20 | 1.00 | 0.00 | 0.63 | 0.18 | 1.00 | 0.00 | 0.63 | 0.17 |
| (10D) | 1.00 | 0.00 | 0.90 | 0.30 | 1.00 | 0.00 | 0.87 | 0.30 | 1.00 | 0.00 | 0.89 | 0.30 |
| (20D) | 1.00 | 0.00 | 0.80 | 0.40 | 1.00 | 0.00 | 0.80 | 0.40 | 1.00 | 0.00 | 0.80 | 0.40 |
| Function | PI | HVPI | HVPIC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | Best | Worst | Avg. | Std. | |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (1D) | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 0.75 | 0.75 | 0.75 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 0.50 | 0.50 | 0.50 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 |
| (2D) | 0.50 | 0.39 | 0.48 | 0.03 | 0.89 | 0.44 | 0.66 | 0.09 | 0.89 | 0.44 | 0.66 | 0.09 |
| (2D) | 0.39 | 0.25 | 0.32 | 0.03 | 0.58 | 0.39 | 0.48 | 0.05 | 0.58 | 0.39 | 0.48 | 0.05 |
| (3D) | 0.33 | 0.22 | 0.28 | 0.02 | 0.43 | 0.27 | 0.35 | 0.03 | 0.43 | 0.27 | 0.35 | 0.03 |
| (3D) | 0.18 | 0.13 | 0.15 | 0.01 | 0.27 | 0.18 | 0.21 | 0.02 | 0.27 | 0.18 | 0.21 | 0.02 |
| (2D) | 1.00 | 0.75 | 0.90 | 0.07 | 1.00 | 0.75 | 0.90 | 0.07 | 1.00 | 0.75 | 0.90 | 0.07 |
| (2D) | 0.50 | 0.33 | 0.48 | 0.06 | 0.67 | 0.50 | 0.64 | 0.06 | 0.67 | 0.50 | 0.64 | 0.06 |
| (2D) | 0.50 | 0.13 | 0.28 | 0.08 | 0.63 | 0.25 | 0.41 | 0.09 | 0.63 | 0.25 | 0.41 | 0.09 |
| (2D) | 0.50 | 0.33 | 0.46 | 0.07 | 0.67 | 0.50 | 0.63 | 0.07 | 0.67 | 0.50 | 0.63 | 0.07 |
| (3D) | 0.67 | 0.50 | 0.65 | 0.05 | 0.67 | 0.50 | 0.65 | 0.05 | 0.67 | 0.50 | 0.65 | 0.05 |
| (3D) | 0.63 | 0.13 | 0.46 | 0.12 | 0.63 | 0.13 | 0.46 | 0.12 | 0.63 | 0.13 | 0.46 | 0.12 |
| (5D) | 0.50 | 0.17 | 0.28 | 0.10 | 0.50 | 0.17 | 0.28 | 0.10 | 0.50 | 0.17 | 0.28 | 0.10 |
| (5D) | 0.50 | 0.13 | 0.25 | 0.10 | 0.50 | 0.13 | 0.33 | 0.11 | 0.50 | 0.13 | 0.33 | 0.11 |
| (10D) | 0.17 | 0.00 | 0.16 | 0.03 | 0.50 | 0.00 | 0.33 | 0.15 | 0.50 | 0.00 | 0.32 | 0.14 |
| (10D) | 0.25 | 0.00 | 0.12 | 0.05 | 0.25 | 0.00 | 0.17 | 0.08 | 0.25 | 0.00 | 0.17 | 0.08 |
| (20D) | 0.25 | 0.00 | 0.10 | 0.05 | 0.50 | 0.00 | 0.13 | 0.10 | 0.50 | 0.00 | 0.13 | 0.10 |
| MaxFEs | 10,000 | 25,000 | 50,000 | 100,000 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Alg. | Avg. | Std. | Avg. | Std. | Avg. | Std. | Avg. | Std. | |
| PI0 | 11.36 | 2.36 | 40.20 | 3.05 | 58.98 | 3.98 | 67.66 | 3.35 | |
| Precision | 0.02 | 0.00 | 0.08 | 0.01 | 0.12 | 0.01 | 0.14 | 0.01 | |
| Recall | 0.05 | 0.01 | 0.19 | 0.01 | 0.27 | 0.02 | 0.31 | 0.02 | |
| F | 0.01 | 0.01 | 0.01 | 0.01 | |||||
| PL | 11.92 | 2.35 | 30.90 | 2.20 | 39.00 | 2.56 | 42.80 | 2.74 | |
| 10.90 | 2.08 | 30.90 | 2.20 | 39.00 | 2.56 | 42.80 | 2.74 | ||
| Precision | 0.92 | 0.10 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | |
| Recall | 0.05 | 0.01 | 0.14 | 0.01 | 0.18 | 0.01 | 0.20 | 0.01 | |
| F | 0.10 | 0.02 | 0.02 | 0.02 | 0.02 | ||||
| HVPI | 12.58 | 2.68 | 40.22 | 3.07 | 58.98 | 3.98 | 67.66 | 3.35 | |
| 11.36 | 2.36 | 40.20 | 3.05 | 58.98 | 3.98 | 67.66 | 3.35 | ||
| Precision | 0.91 | 0.11 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | |
| Recall | 0.05 | 0.01 | 0.19 | 0.01 | 0.27 | 0.02 | 0.31 | 0.02 | |
| F | 0.10 | 0.02 | 0.31 | 0.02 | 0.43 | 0.02 | 0.48 | 0.02 | |
| #FEs | 174.18 | 56.28 | 3761.56 | 405.11 | 9210.18 | 578.32 | 11,439.86 | 572.74 | |
| HVPIC | 12.58 | 2.68 | 40.22 | 3.07 | 59.00 | 3.99 | 67.66 | 3.35 | |
| 11.36 | 2.36 | 40.20 | 3.05 | 58.98 | 3.98 | 67.66 | 3.35 | ||
| Precision | 0.91 | 0.11 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | |
| Recall | 0.05 | 0.01 | 0.19 | 0.01 | 0.27 | 0.02 | 0.31 | 0.02 | |
| F | 0.10 | 0.02 | 0.31 | 0.02 | 0.43 | 0.02 | 0.48 | 0.02 | |
| #FEs | 35.14 | 8.87 | 188.16 | 15.66 | 300.70 | 17.26 | 355.16 | 15.32 | |
| Accuracy Level | 0.1 | 0.01 | 0.001 | 0.0001 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Alg. | Avg. | Std. | Avg. | Std. | Avg. | Std. | Avg. | Std. | |
| PI0 | 78.18 | 5.19 | 58.98 | 3.98 | 42.14 | 2.59 | 31.00 | 2.88 | |
| Precision | 0.16 | 0.01 | 0.12 | 0.01 | 0.08 | 0.01 | 0.06 | 0.01 | |
| Recall | 0.36 | 0.02 | 0.27 | 0.02 | 0.20 | 0.01 | 0.14 | 0.01 | |
| F | 0.01 | 0.01 | 0.01 | 0.01 | |||||
| PL | 44.42 | 2.32 | 39.00 | 2.56 | 32.52 | 2.26 | 25.80 | 2.37 | |
| 44.38 | 2.36 | 39.00 | 2.56 | 32.52 | 2.26 | 25.80 | 2.37 | ||
| Precision | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | |
| Recall | 0.21 | 0.01 | 0.18 | 0.01 | 0.15 | 0.01 | 0.12 | 0.01 | |
| F | 0.02 | 0.02 | 0.02 | 0.02 | |||||
| HVPI | 78.18 | 5.19 | 58.98 | 3.98 | 42.14 | 2.59 | 31.00 | 2.88 | |
| 78.18 | 5.19 | 58.98 | 3.98 | 42.14 | 2.59 | 31.00 | 2.88 | ||
| Precision | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | |
| Recall | 0.36 | 0.02 | 0.27 | 0.02 | 0.20 | 0.01 | 0.14 | 0.01 | |
| F | 0.53 | 0.03 | 0.43 | 0.02 | 0.33 | 0.02 | 0.25 | 0.02 | |
| #FEs | 12,145.56 | 668.27 | 9210.18 | 578.32 | 6158.72 | 593.62 | 3227.04 | 428.20 | |
| HVPIC | 78.18 | 5.28 | 58.98 | 3.98 | 42.14 | 2.59 | 31.00 | 2.88 | |
| 77.86 | 5.20 | 58.98 | 3.98 | 42.14 | 2.59 | 31.00 | 2.88 | ||
| Precision | 1.00 | 0.01 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | |
| Recall | 0.36 | 0.02 | 0.27 | 0.02 | 0.20 | 0.01 | 0.14 | 0.01 | |
| F | 0.53 | 0.03 | 0.43 | 0.02 | 0.33 | 0.02 | 0.25 | 0.02 | |
| #FEs | 366.48 | 23.60 | 300.78 | 17.27 | 229.84 | 15.88 | 165.10 | 16.09 | |
| Problem | PL | HVPI | HVPIC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Precision | Recall | F | Precision | Recall | F | Precision | Recall | F | |
| P1 | 1.00 | 0.53 | 0.69 | 1.00 | 0.94 | 0.97 | 1.00 | 0.94 | 0.97 |
| P2 | 1.00 | 0.06 | 0.12 | 1.00 | 0.41 | 0.58 | 1.00 | 0.41 | 0.58 |
| P3 | 1.00 | 0.30 | 0.46 | 1.00 | 0.53 | 0.69 | 1.00 | 0.53 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.-H.; Wang, Z.-J. Peak Identification in Evolutionary Multimodal Optimization: Model, Algorithms, and Metrics. Biomimetics 2024, 9, 643. https://doi.org/10.3390/biomimetics9100643
Zhang Y-H, Wang Z-J. Peak Identification in Evolutionary Multimodal Optimization: Model, Algorithms, and Metrics. Biomimetics. 2024; 9(10):643. https://doi.org/10.3390/biomimetics9100643
Chicago/Turabian StyleZhang, Yu-Hui, and Zi-Jia Wang. 2024. "Peak Identification in Evolutionary Multimodal Optimization: Model, Algorithms, and Metrics" Biomimetics 9, no. 10: 643. https://doi.org/10.3390/biomimetics9100643
APA StyleZhang, Y.-H., & Wang, Z.-J. (2024). Peak Identification in Evolutionary Multimodal Optimization: Model, Algorithms, and Metrics. Biomimetics, 9(10), 643. https://doi.org/10.3390/biomimetics9100643








