Running Gait and Control of Quadruped Robot Based on SLIP Model
Abstract
1. Introduction
2. Dynamic Analysis of Quadruped Robot High-Speed Running Gaits
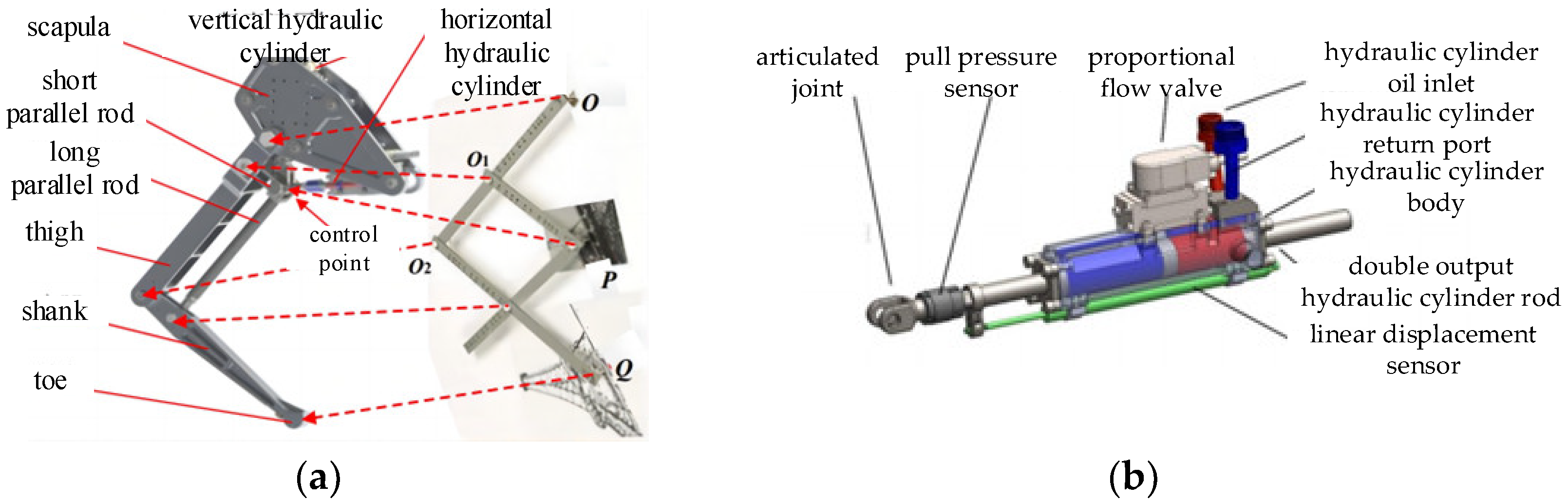
2.1. Leg Mechanical Structure and Actuators
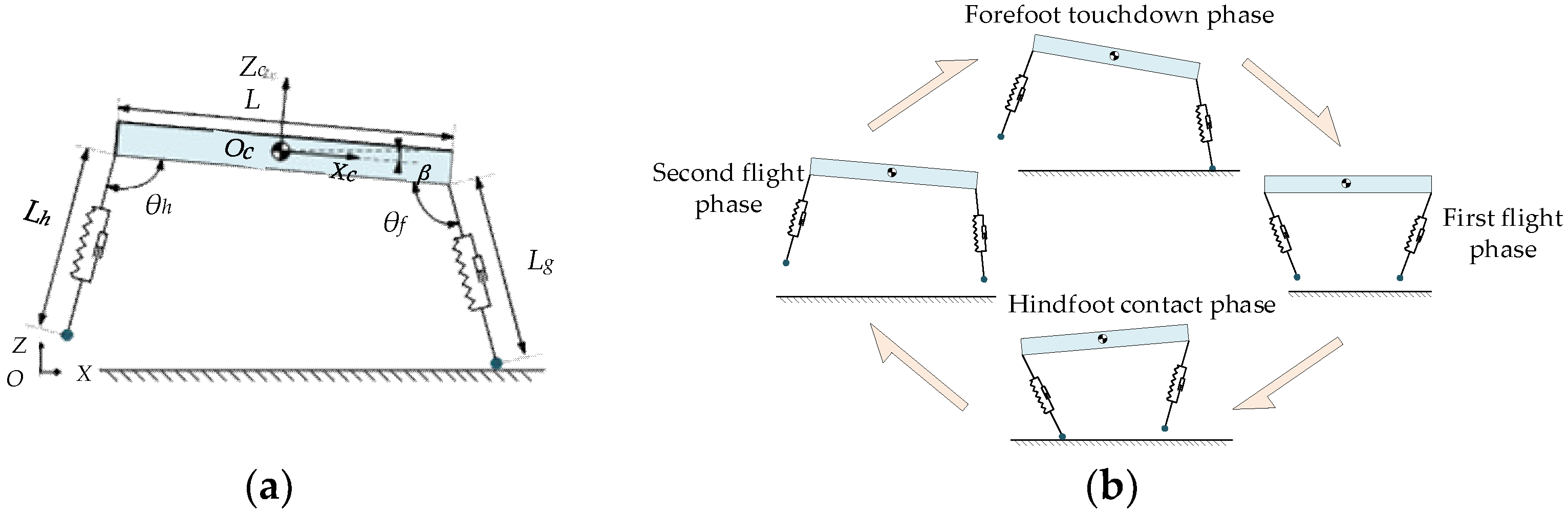
2.2. Dynamic Analysis of the Double Flying Phase Bound Gait
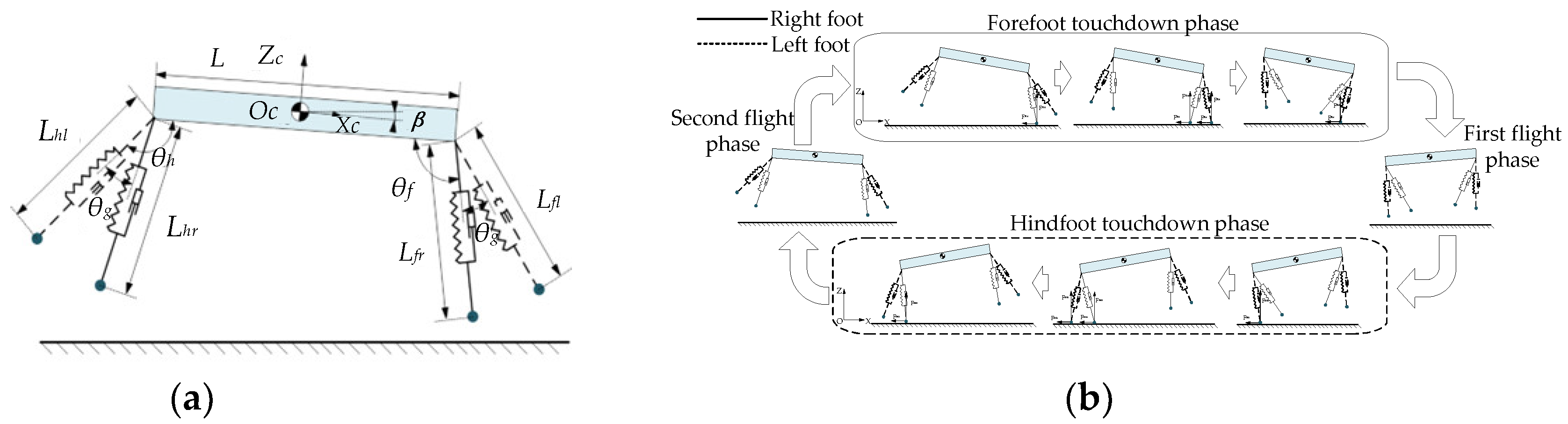
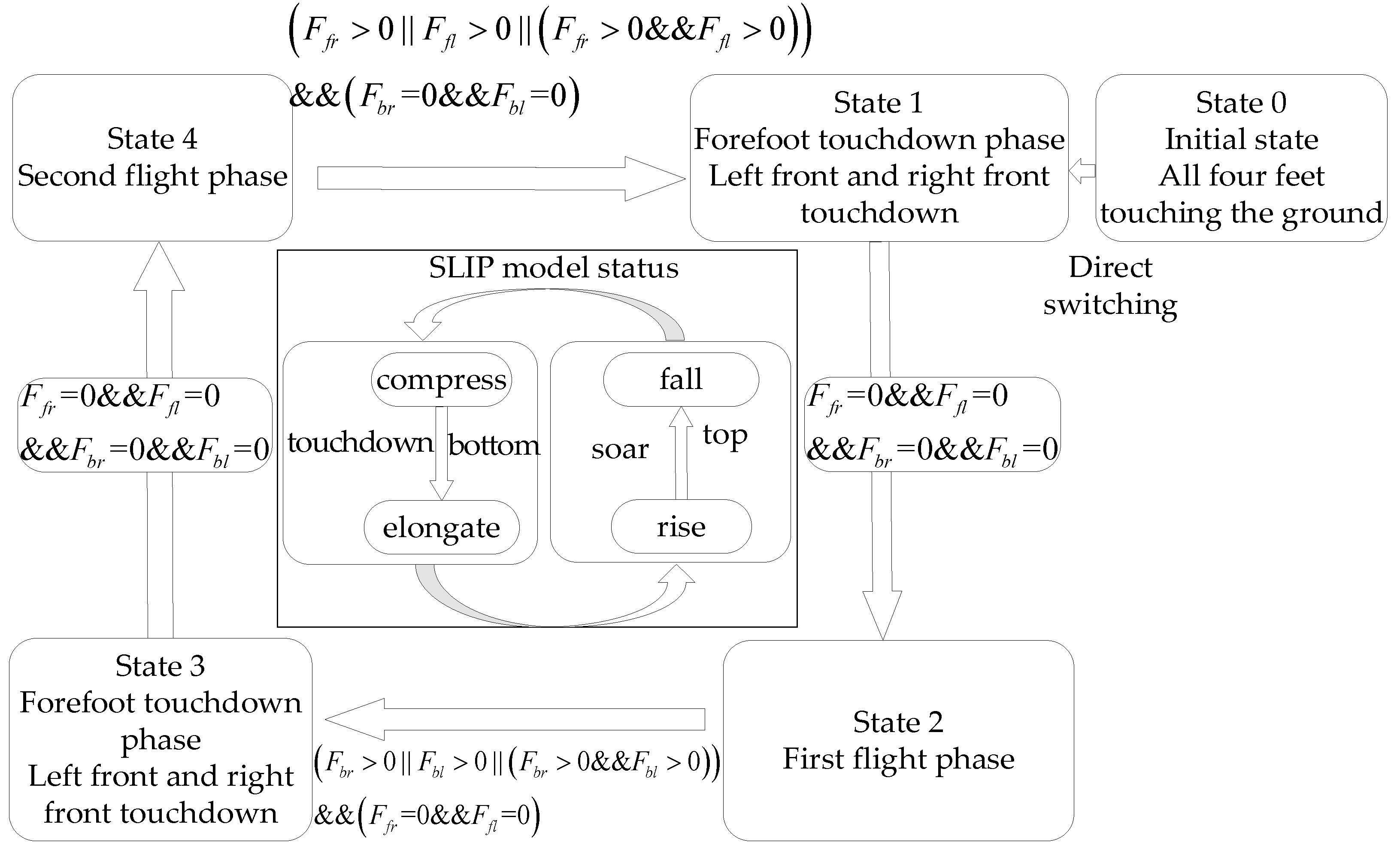
2.3. Dynamic Analysis of Rotatory Gallop Gait
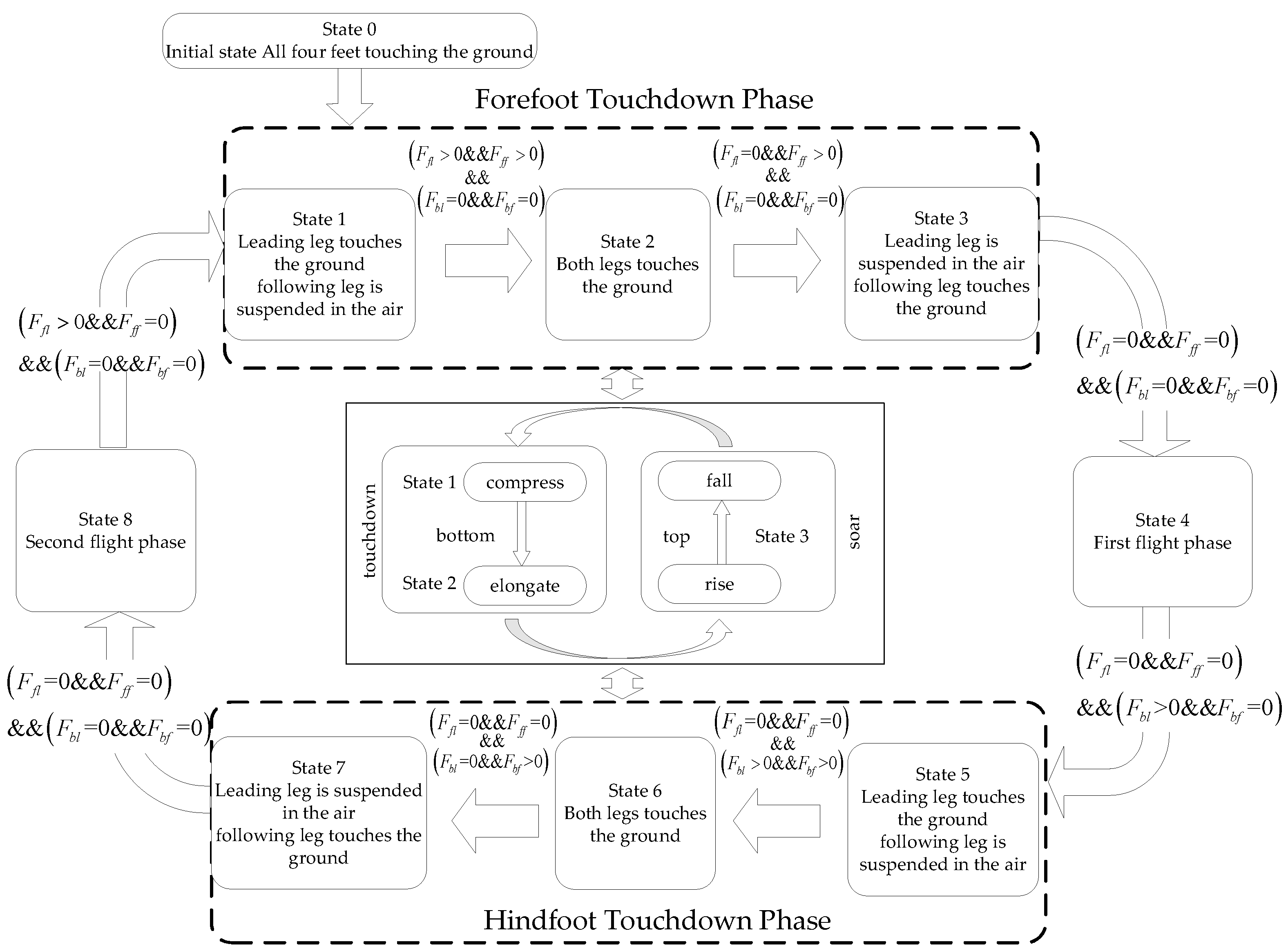
3. High-Speed Running Gait Control Strategy Design
3.1. Double Flying Phase Bound Gait Control Strategy Design
3.1.1. Control Strategy Based on the SLIP Model
3.1.2. Double Flying Phase Bound Gait Control Strategy Based on the SLIP Model
3.2. Optimization of Rotatory Gallop Gait Model and Control Strategy Design
3.2.1. D-SLIP Model Control Strategy
3.2.2. Control of Rotatory Gallop Gait Based on the D-SLIP Model
4. Simulation Verification
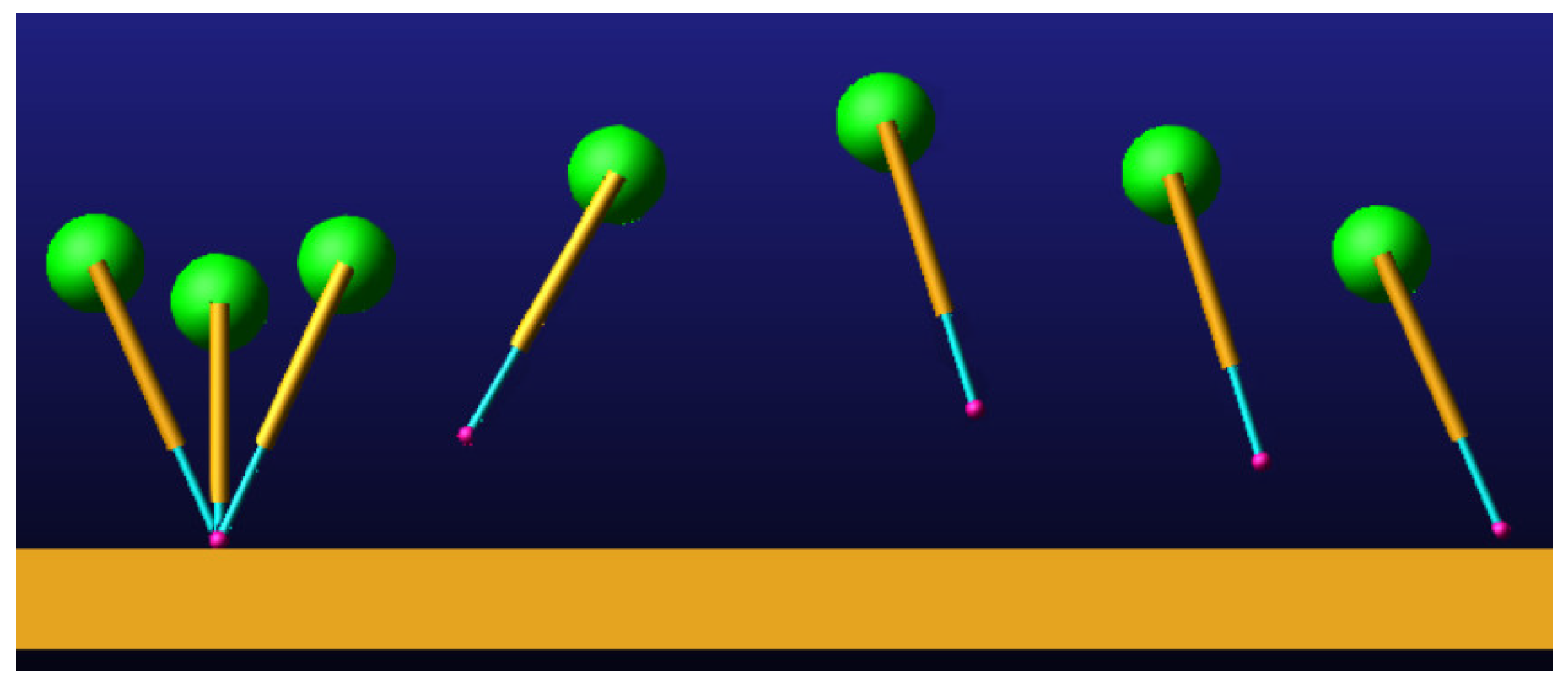
4.1. Simulation of SLIP Model and D-SLIP Model
4.2. Simulation of Double Flying Phase Bound Gait
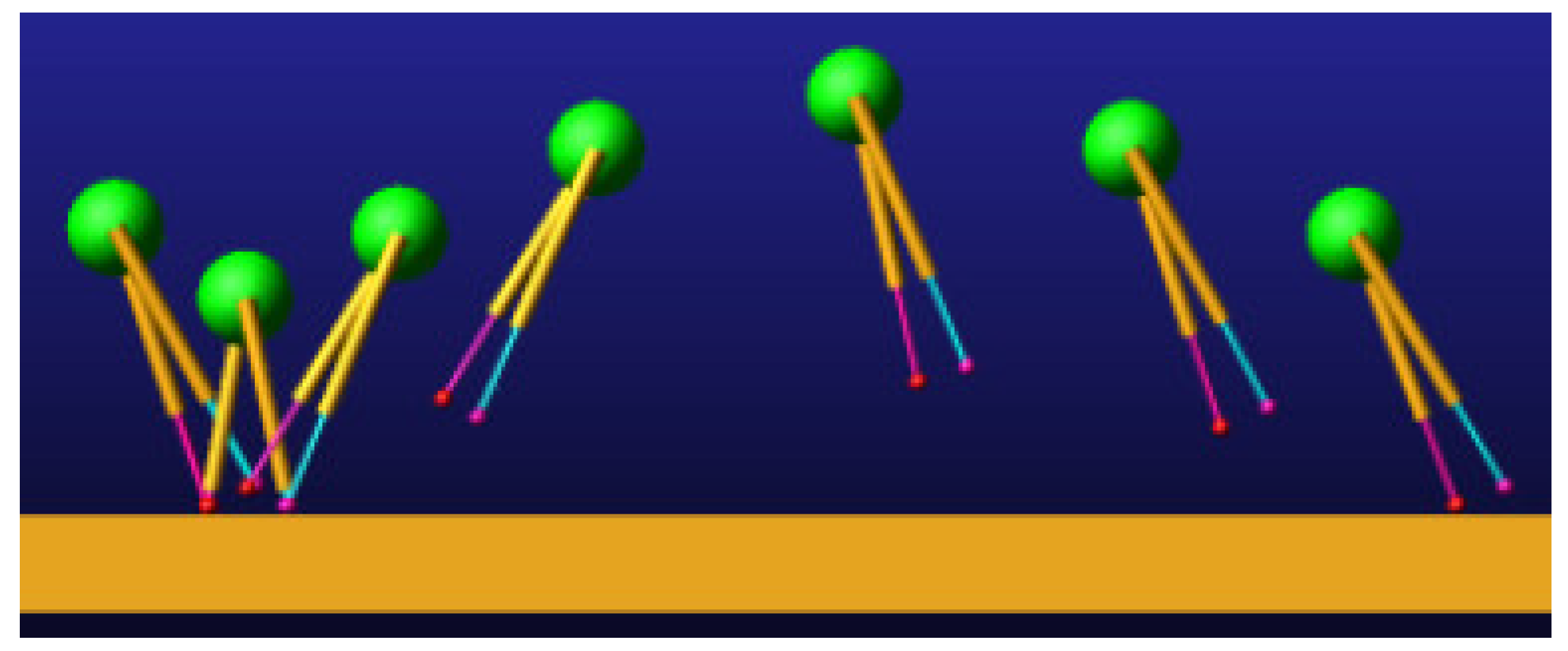
4.3. Rotatory Gallop Gait Simulation
5. Experimental Verification
5.1. Design of Robot Leg Control Method
5.2. High-Speed Running Robot Prototype Introduction
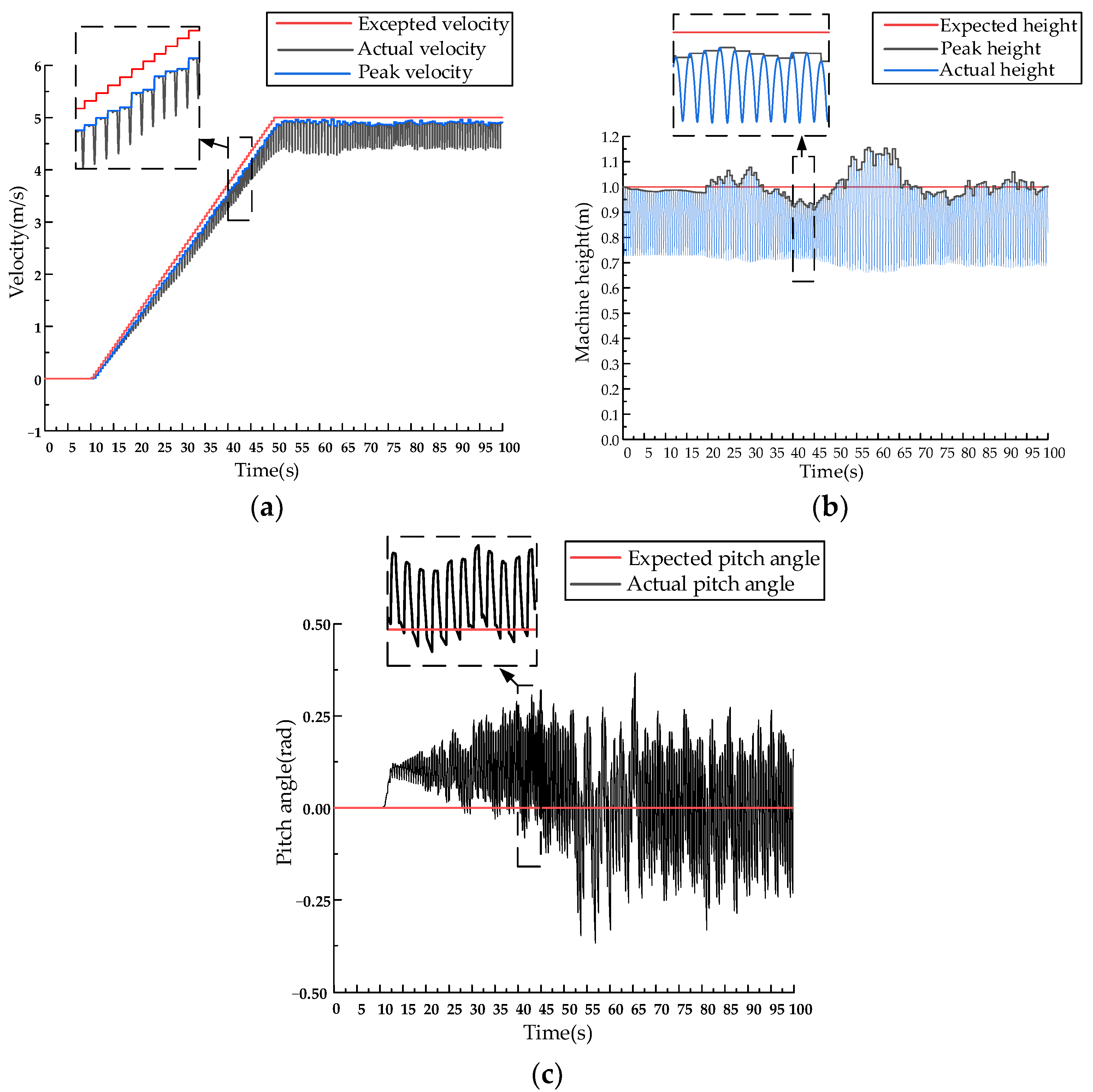
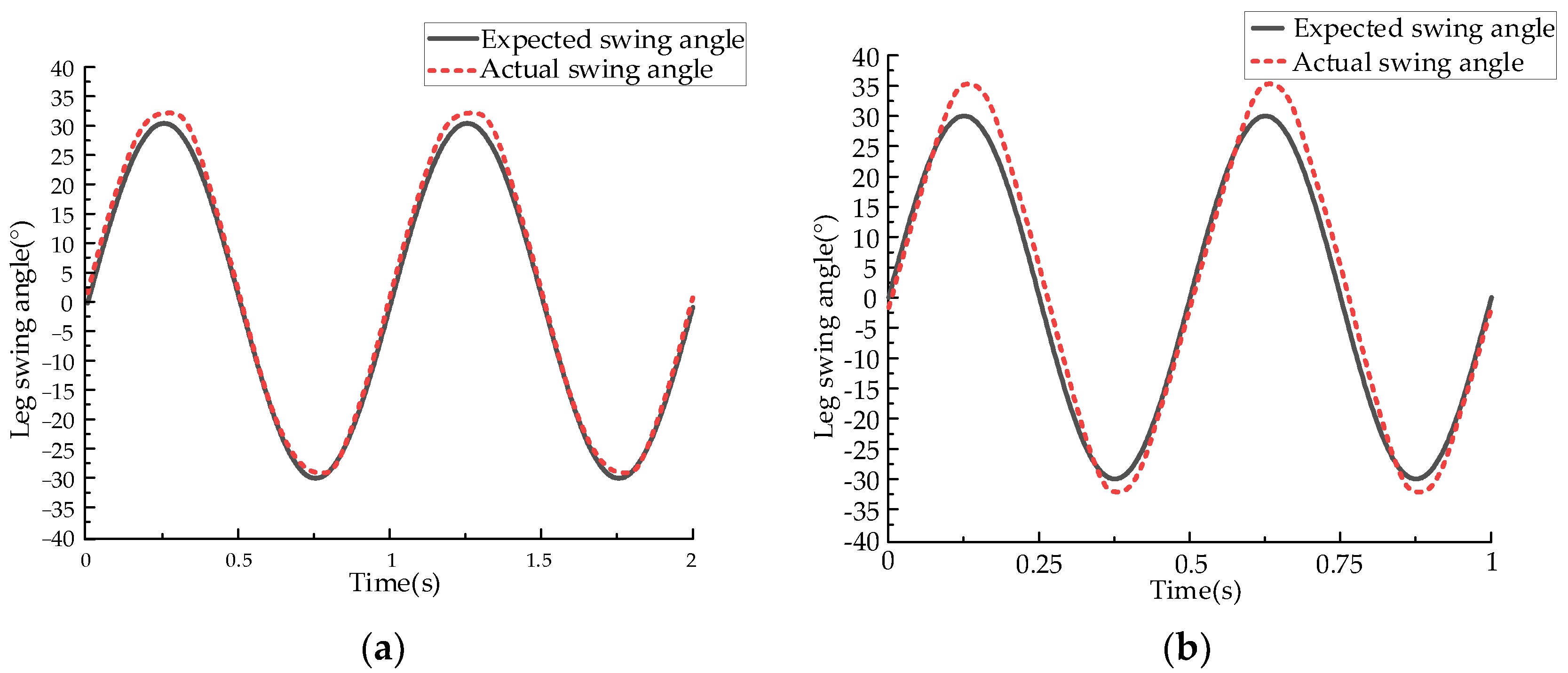
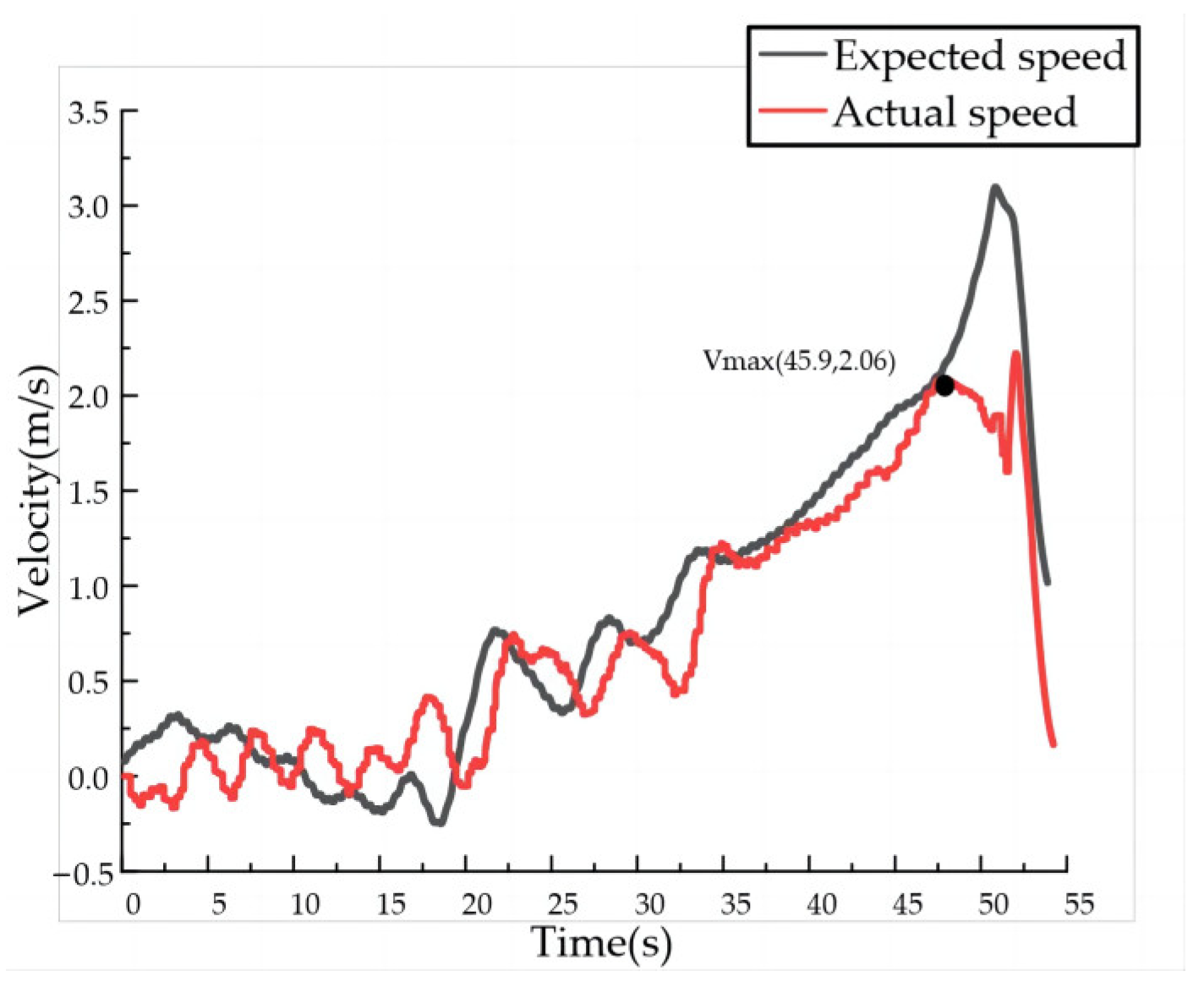
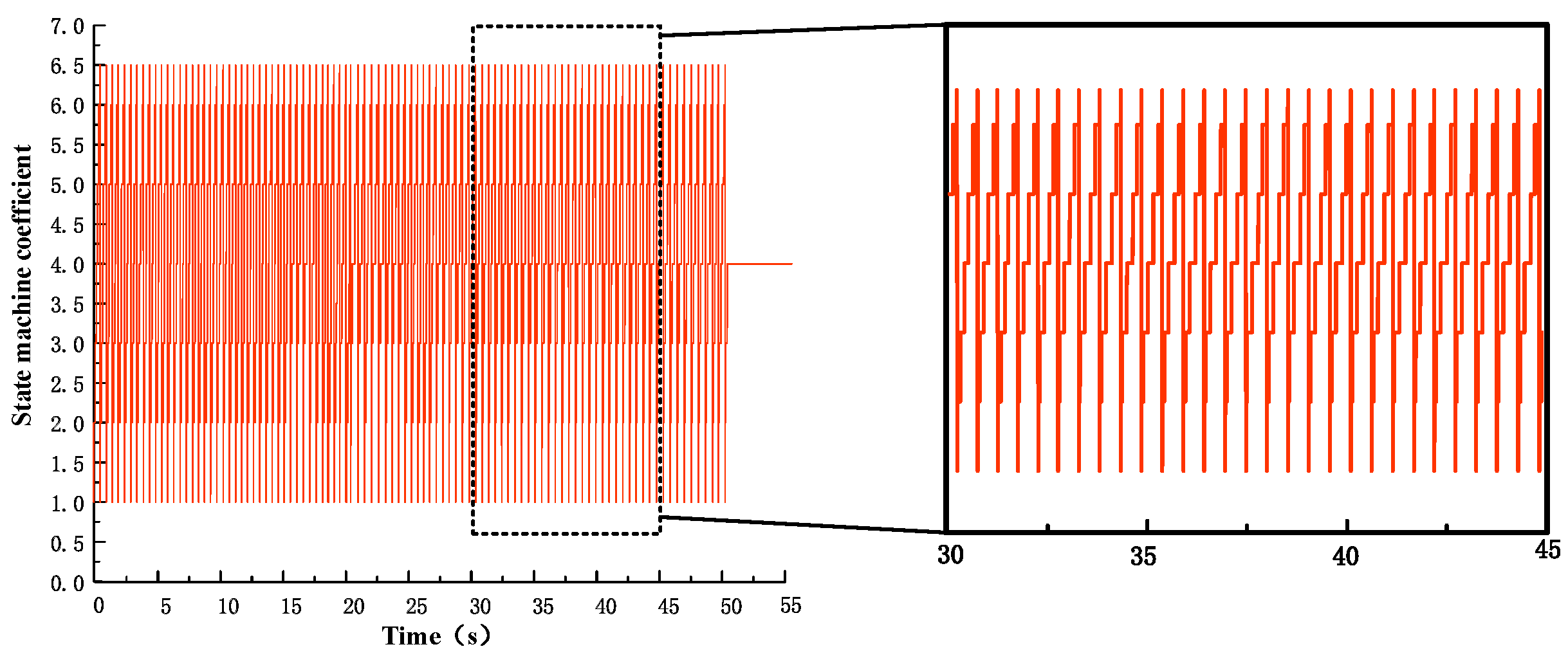
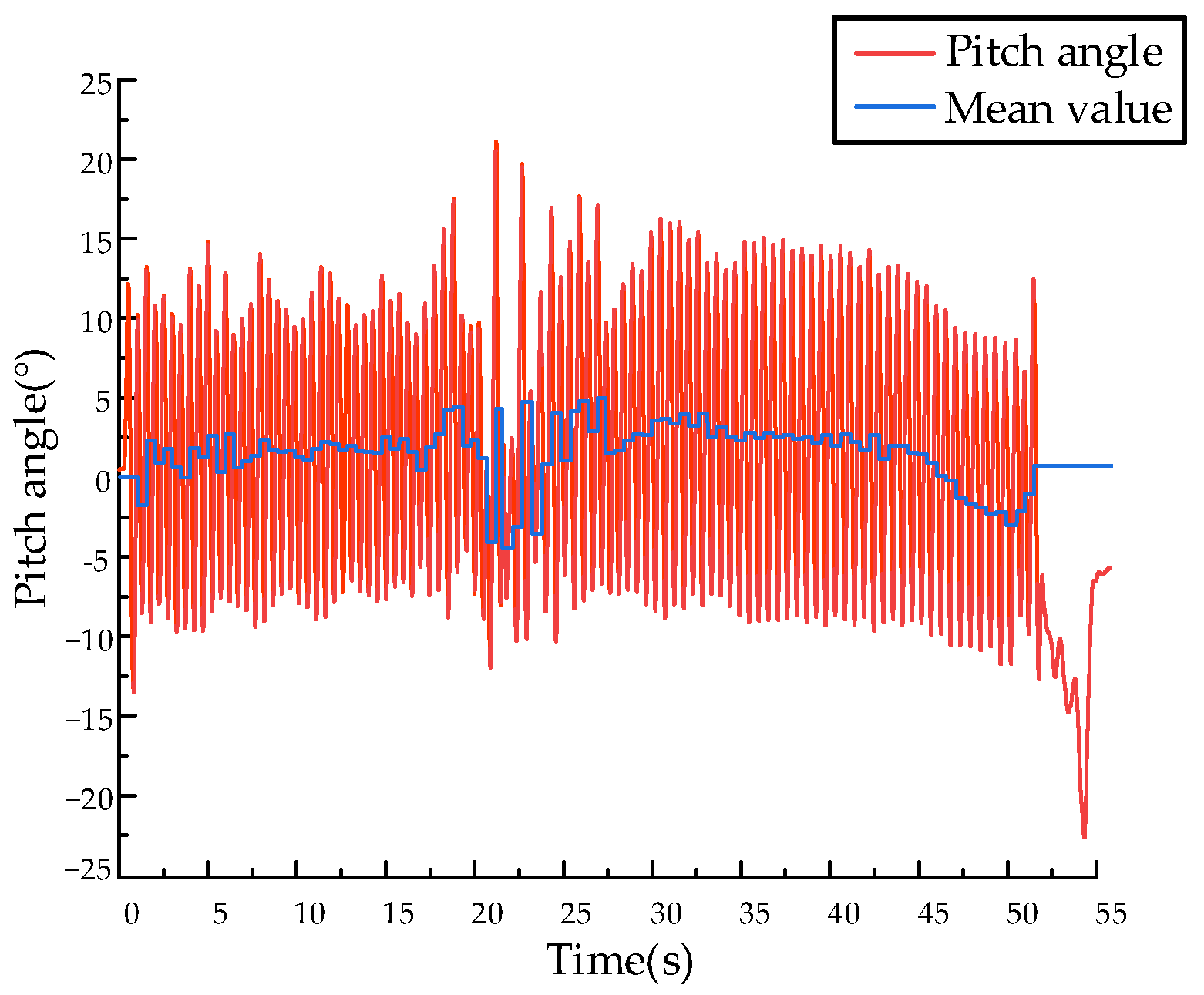
5.3. High-Speed Robot Running Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sonker, R.; Dutta, A. Adding Terrain Height to Improve Model Learning for Path Tracking on Uneven Terrain by a Four Wheel Robot. IEEE Robot. Autom. Lett. 2021, 6, 239–246. [Google Scholar]
- Chen, Z.H.; Wang, S.K.; Wang, J.Z.; Xu, K.; Lei, T.; Zhang, H.; Wang, X.W.; Liu, D.H.; Si, J.G. Control strategy of stable walking for a hexapod wheel-legged robot. Isa Trans. 2021, 108, 367–380. [Google Scholar] [CrossRef] [PubMed]
- Grigore, L.S.; Oncioiu, I.; Priescu, I.; Joita, D. Development and Evaluation of the Traction Characteristics of a Crawler EOD Robot. Appl. Sci. 2021, 11, 3757. [Google Scholar] [CrossRef]
- Fukui, R.; Yamada, Y.; Mitsudome, K.; Sano, K.; Warisawa, S. HanGrawler: Large-Payload and High-Speed Ceiling Mobile Robot Using Crawler. IEEE Trans. Robot. 2020, 36, 1053–1066. [Google Scholar] [CrossRef]
- Ba, K.X.; Song, Y.H.; Yu, B.; Wang, C.Y.; Li, H.S.; Zhang, J.X.; Ma, G.L. Kinematics correction algorithm for the LHDS of a legged robot with semi-cylindrical foot end based on V-DOF. Mech. Syst. Signal Pr. 2022, 167. [Google Scholar] [CrossRef]
- Chen, G.R.; Wei, N.Z.; Li, J.; Lu, H.F. Design and simulation analysis of a bionic ostrich robot. Biomech. Model. Mechanobiol. 2022, 21, 1781–1801. [Google Scholar] [CrossRef]
- Reher, J.; Ames, A.D. Dynamic Walking: Toward Agile and Efficient Bipedal Robots. Annu. Rev. Control. Robot. Auton. Syst. 2021, 4, 535–572. [Google Scholar] [CrossRef]
- Wang, P. Research on Quadruped Robot Steadily Walking Planning and Controlling Technology. Doctorate Dissertation, Harbin Institute of Technology, Harbin, China, 2007. [Google Scholar]
- Ba, K.X.; Song, Y.H.; Shi, Y.P.; Wang, C.Y.; Ma, G.L.; Wang, Y.; Yu, B.; Yuan, L.P. A novel one-dimensional force sensor calibration method to improve the contact force solution accuracy for legged robot. Mech. Mach. Theory 2022, 169. [Google Scholar] [CrossRef]
- Ning, M.; Yang, J.; Zhang, Z.; Li, J.; Wang, Z.; Wei, L.; Feng, P. Method of Changing Running Direction of Cheetah-Inspired Quadruped Robot. Sensors 2022, 22, 9601. [Google Scholar] [CrossRef]
- Wang, A.S.-P.; Chen, W.W.-L.; Lin, P.-C. Control of a 2-D Bounding Passive Quadruped Model with Poincare Map Ap-proximation and Model Predictive Control. In Proceedings of the International Conference on Advanced Robotics and In-telligent Systems, ARIS, Taipei, Taiwan, 31 August–2 September 2016. [Google Scholar]
- Bledt, G.; Powell, M.J.; Katz, B.; Di Carlo, J.; Wensing, P.M.; Kim, S.; Kosecka, J. MIT Cheetah 3: Design and Control of a Robust, Dynamic Quadruped Robot. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2245–2252. [Google Scholar]
- Kurtz, V.; Li, H.; Wensing, P.M.; Lin, H. Mini Cheetah, the Falling Cat: A Case Study in Machine Learning and Trajectory Optimization for Robot Acrobatics. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA, Philadelphia, PA, USA, 23–27 May 2022; pp. 4635–4641. [Google Scholar]
- Kim, D.; Carlo, J.D.; Katz, B.; Bledt, G.; Kim, S. Highly dynamic quadruped locomotion via whole-body impulse control and model predictive control. arXiv 2019, arXiv:1909.06586. [Google Scholar]
- Park, H.-W.; Park, S.; Kim, S. Variable-speed Quadrupedal Bounding Using Impulse Planning: Untethered High-speed 3D Running of MIT Cheetah 2. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA, Seattle, WA, USA, 25–30 May 2015; pp. 5163–5170. [Google Scholar]
- Guo, W.; Cai, C.; Li, M.; Zha, F.; Wang, P.; Wang, K. A Parallel Actuated Pantograph Leg for High-speed Locomotion. J. Bionic Eng. 2017, 14, 202–217. [Google Scholar] [CrossRef]
- Chen, T.; Sun, X.; Xu, Z.; Li, Y.; Rong, X.; Zhou, L. A Trot and Flying Trot Control Method for Quadruped Robot Based on Optimal Foot Force Distribution. J. Bionic Eng. 2019, 16, 621–632. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, W.; Xie, A.; Zhang, Y.; Wu, J.; Zhu, Q. Hybrid Bipedal Locomotion Based on Reinforcement Learning and Heu-ristics. Micromachines 2022, 13, 1688. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Yang, J.; Jia, Y.; Li, Q.; Wang, C. Spring-Loaded Inverted Pendulum Hopping via Hybrid Averaging and Control Lyapunov Function. J. Bionic Eng. 2023, 20, 291–307. [Google Scholar] [CrossRef]
- Ding, C.; Zhou, L.; Li, Y.; Rong, X. A Novel Dynamic Locomotion Control Method for Quadruped Robots Running on Rough Terrains. IEEE Access 2020, 8, 150435–150446. [Google Scholar] [CrossRef]
- Doan Nhat, T.; Hayashi, T.; Yamakita, M. High speed running of flat foot Biped robot with Inerter using SLIP model. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM, Busan, Republic of Korea, 7–11 July 2015; pp. 110–115. [Google Scholar]
- Tseng, K.-Y.; Lin, P.-C. A model-based strategy for quadruped running with differentiated fore- and hind-leg morphologies. Bioinspiration Biomim. 2022, 17, 026008. [Google Scholar] [CrossRef]
- Yu, H.; Gao, H.; Fan, Z.; Deng, Z.; Zhang, L. Dual-SLIP Model Based Galloping Gait Control for Quadruped Robot: A Task-Space Formulation. In Proceedings of the American Control Conference, ACC, Seattle, WA, USA, 24–26 May 2017; pp. 191–197. [Google Scholar]
- Wensing, P.M.; Orin, D.E. High-Speed Humanoid Running Through Control with a 3D-SLIP Model. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS, Tokyo, Japan, 3–7 November 2013; pp. 5134–5140. [Google Scholar]
- Wu, J.; Guo, L.; Yan, S.; Li, Y.; Yao, Y.-A. Design and performance analysis of a novel closed-chain elastic-bionic leg with one actuated degree of freedom. Mech. Mach. Theory 2021, 165, 104432. [Google Scholar] [CrossRef]
- Karagoz, O.K.; Secer, G.; Ankarali, M.M.; Saranli, U. Analysis and control of a running spring-mass model with a trunk based on virtual pendulum concept. Bioinspiration Biomim. 2022, 17, 046009. [Google Scholar] [CrossRef]
- Han, B.; Yi, H.; Xu, Z.; Yang, X.; Luo, X. 3D-SLIP model based dynamic stability strategy for legged robots with impact dis-turbance rejection. Sci. Rep. 2022, 12, 5892. [Google Scholar] [CrossRef]
- Dini, N.; Majd, V.J. An MPC-based two-dimensional push recovery of a quadruped robot in trotting gait using its reduced virtual model. Mech. Mach. Theory 2020, 146, 103737. [Google Scholar] [CrossRef]
- Ba, K.X.; Yu, B.; Gao, Z.J.; Zhu, Q.X.; Ma, G.L.; Kong, X.D. An improved force-based impedance control method for the HDU of legged robots. Isa Trans. 2019, 84, 187–205. [Google Scholar] [CrossRef] [PubMed]
- Ba, K.-X.; Song, Y.-H.; Yu, B.; He, X.-L.; Huang, Z.-P.; Li, C.-H.; Yuan, L.-P.; Kong, X.-D. Dynamics compensation of impedance based motion control for LHDS of legged robot. Robot. Auton. Syst. 2021, 139, 103704. [Google Scholar] [CrossRef]


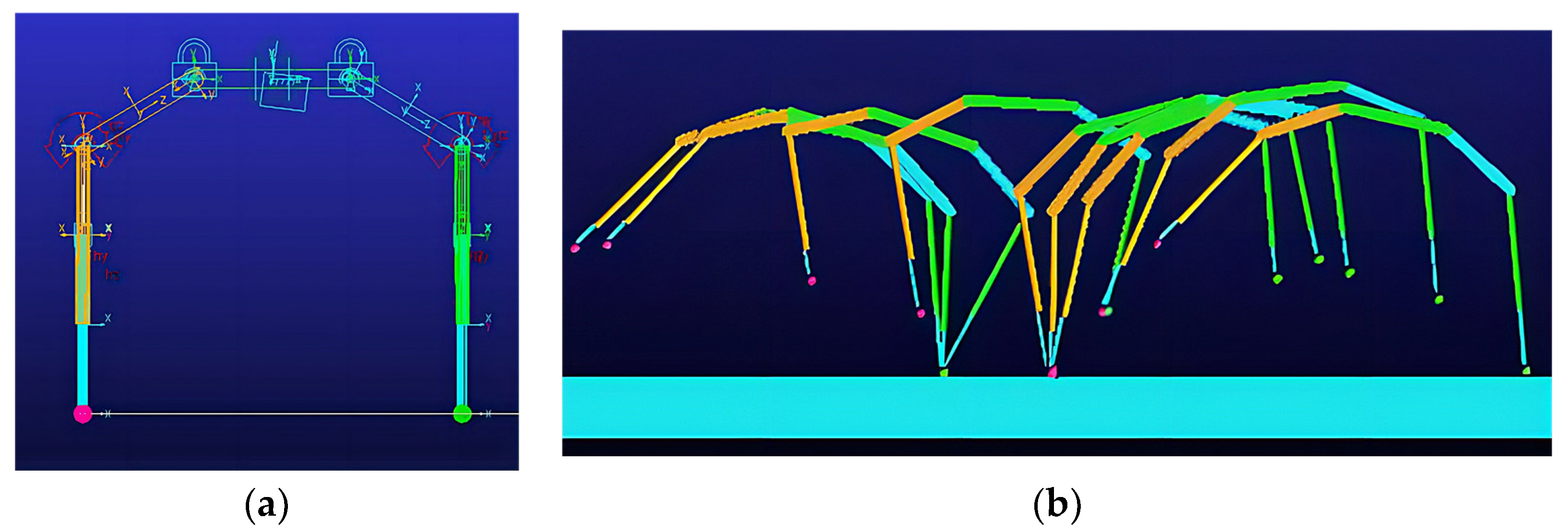
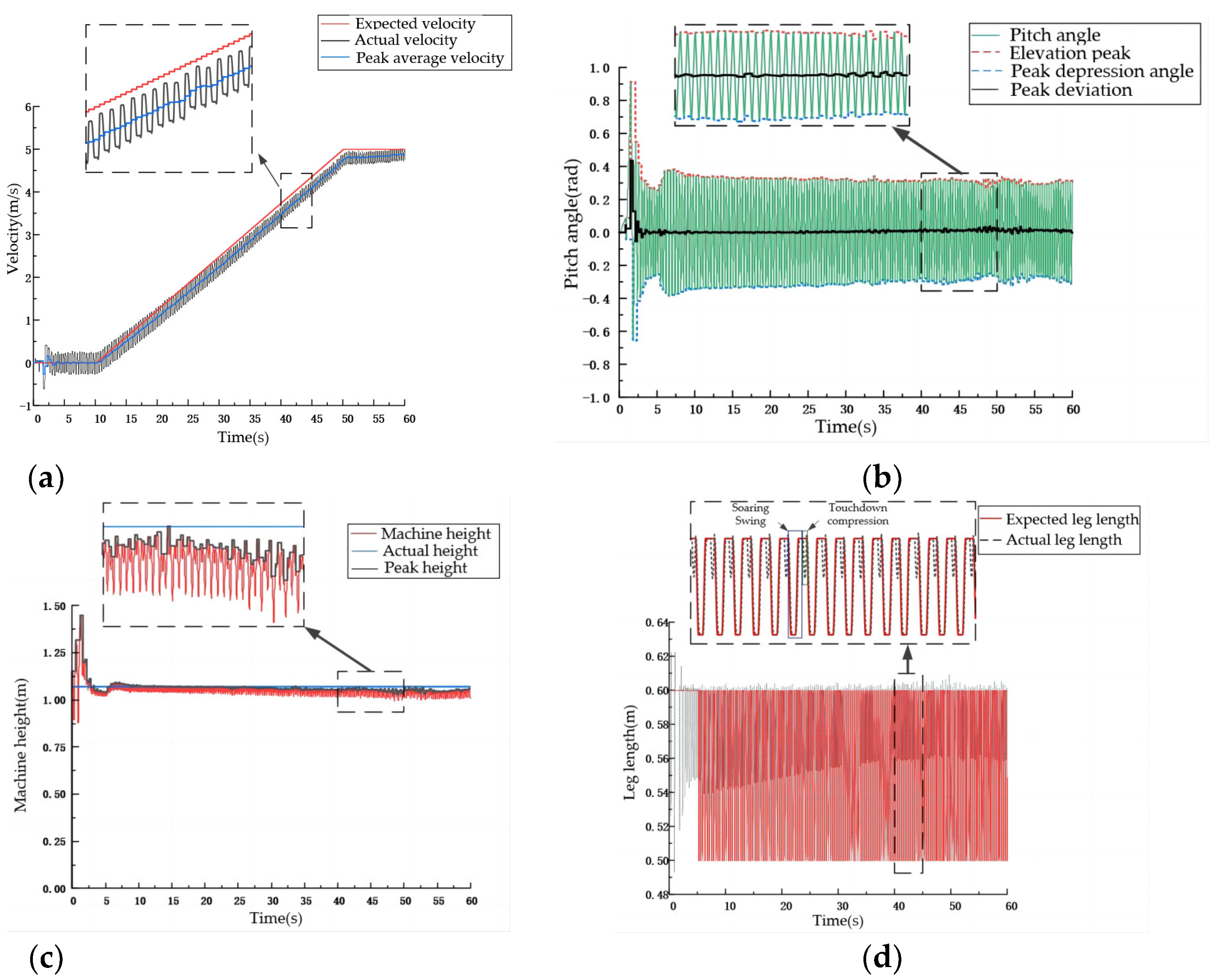

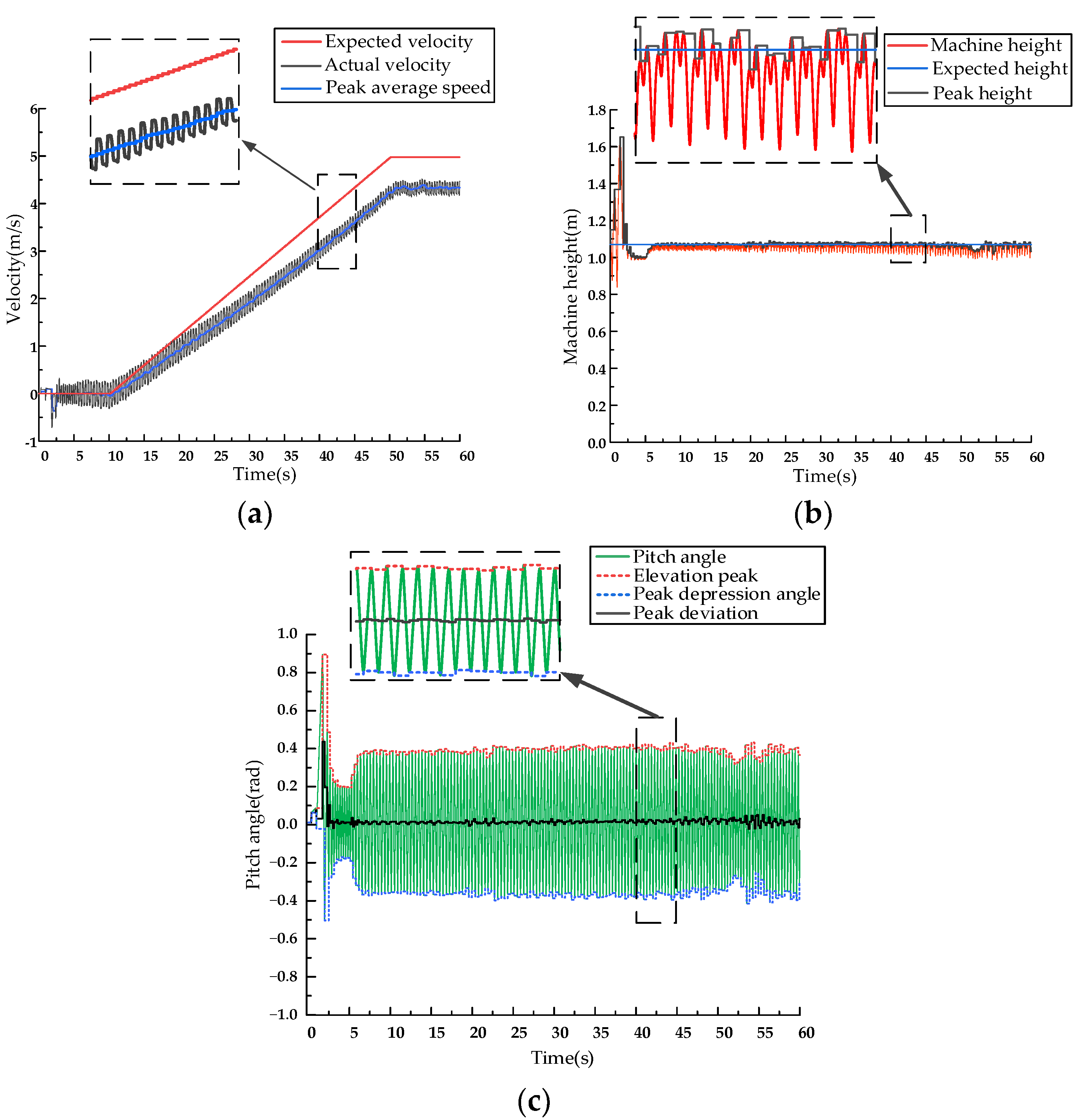



| Parameter | Value | Unit |
|---|---|---|
| Mass of the body | 50 | kg |
| Rotational damper | 0.3 | N·m·s/rad |
| Upper leg mass | 0.3 | kg |
| Lower leg mass | 0.2 | kg |
| Translational damper | 15 | N·s/m |
| Foot contact force stiffness | 1000 | MN/m |
| Static friction coefficient | 1 | \ |
| Dynamic friction coefficient | 0.8 | \ |
| Velocity control PID parameters | 1.1, 0, 0.2 | \ |
| Fuselage altitude control PID parameters | 10, 60, 0 | \ |
| Pitch angle control PID parameters | 50, 40, 0 | \ |
| Leg stiffness | 15 | N/mm |
| Leg original length | 0.6 | m |
| Height setpoint thrust | 140 | N |
| Parameter | Value | Unit |
|---|---|---|
| Mass of the body | 50 | kg |
| Damper for left and right hip joint rotation | 0.15 | N·m·s/rad |
| Mass of the upper part of the left and right leg | 0.15 | kg |
| Mass of the lower part of the left and right leg | 0.1 | kg |
| Damper for left and right leg movement | 15 | N·s/m |
| Foot contact force stiffness | 1000 | MN/m |
| Static friction coefficient | 1 | \ |
| Dynamic friction coefficient | 0.8 | \ |
| Lead, follow leg angle | π/18 | rad |
| Velocity control PID parameters | 1.5, 0.05, 0 | \ |
| Fuselage altitude control PID parameters | 60, 120, 0 | \ |
| Pitch angle control PID parameters | 70, 200, 5 | \ |
| Leg stiffness | 15 | N/mm |
| Leg original length | 0.6 | m |
| Height setpoint thrust | 300 | N |
| Parameter | Value | Unit |
|---|---|---|
| Mass of the body | 75 | kg |
| Damper for front and hind hip joint rotation | 0.6 | N·m·s/rad |
| Mass of the upper part of the front and hind leg | 0.6 | kg |
| Mass of the lower part of the front and hind leg | 0.4 | kg |
| Damper for front and hind leg movement | 30 | N·s/m |
| Foot contact force stiffness | 1000 | MN/m |
| Static friction coefficient | 1 | \ |
| Dynamic friction coefficient | 0.8 | \ |
| Velocity control PID parameters | 4, 0.3, 0 | \ |
| Fuselage altitude control PID parameters | 0.35, 0.8, 0 | \ |
| Pitch angle control PID parameters | 0.2, 1.5, 0 | \ |
| Leg stiffness | 15 | N/mm |
| Leg original length | 0.6 | m |
| Height setpoint thrust | 500 | N |
| Parameter | Value | Unit |
|---|---|---|
| Mass of the body | 75 | kg |
| Damper for front and hind hip joint rotation | 0.3 | N·m·s/rad |
| Upper leg mass | 0.3 | kg |
| Lower leg mass | 0.2 | kg |
| Translational damper | 15 | N·s/m |
| Foot contact force stiffness | 1000 | MN/m |
| Static friction coefficient | 1 | \ |
| Dynamic friction coefficient | 0.8 | \ |
| Lead, follow leg angle | Pi/18 | rad |
| Velocity control PID parameters | 2.5, 0.01, 0.2 | \ |
| Fuselage altitude control PID parameters | 2, 4, 0 | \ |
| Pitch angle control PID parameters | 0.5, 1.5, 0 | \ |
| Leg stiffness | 10 | N/mm |
| Leg original length | 0.6 | m |
| Height setpoint thrust | 500 | N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Li, X.; Wang, X.; Meng, F.; Guan, X.; Jiang, Z.; Yuan, L.; Ba, K.; Ma, G.; Yu, B. Running Gait and Control of Quadruped Robot Based on SLIP Model. Biomimetics 2024, 9, 24. https://doi.org/10.3390/biomimetics9010024
He X, Li X, Wang X, Meng F, Guan X, Jiang Z, Yuan L, Ba K, Ma G, Yu B. Running Gait and Control of Quadruped Robot Based on SLIP Model. Biomimetics. 2024; 9(1):24. https://doi.org/10.3390/biomimetics9010024
Chicago/Turabian StyleHe, Xiaolong, Xinjie Li, Xiangji Wang, Fantuo Meng, Xikang Guan, Zhenyu Jiang, Lipeng Yuan, Kaixian Ba, Guoliang Ma, and Bin Yu. 2024. "Running Gait and Control of Quadruped Robot Based on SLIP Model" Biomimetics 9, no. 1: 24. https://doi.org/10.3390/biomimetics9010024
APA StyleHe, X., Li, X., Wang, X., Meng, F., Guan, X., Jiang, Z., Yuan, L., Ba, K., Ma, G., & Yu, B. (2024). Running Gait and Control of Quadruped Robot Based on SLIP Model. Biomimetics, 9(1), 24. https://doi.org/10.3390/biomimetics9010024




