Biomimetic Random Pulse Computation or Why Do Humans Play Basketball Better than Robots?
Abstract
:1. Introduction
2. Random Pulse Computation Paradigm
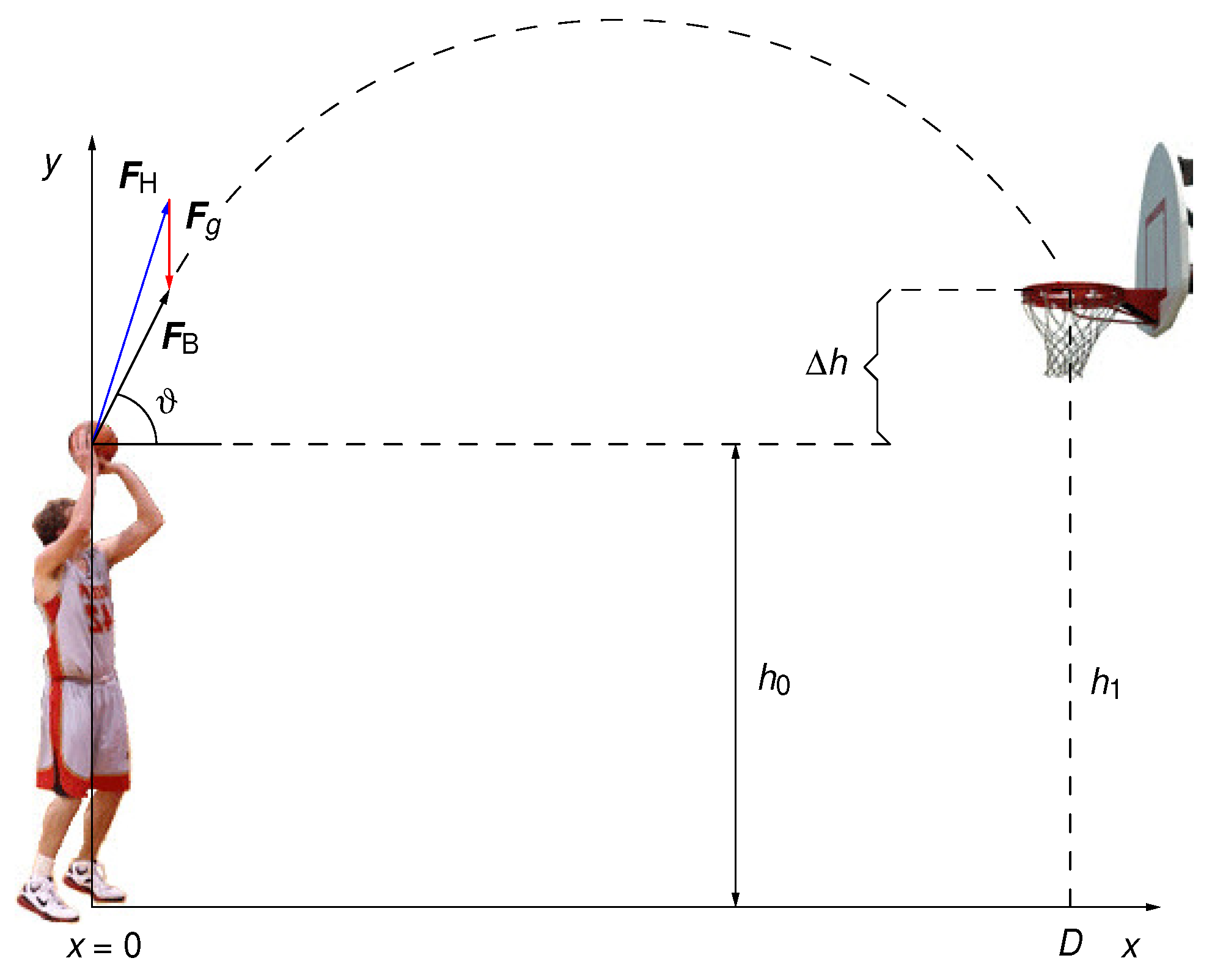
3. Physical Model
4. Methods
5. Results
6. Discussion and Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Madhavan, T.; Thomas, P.S. Fujitsu (A). Vikalpa 1993, 18, 41–56. [Google Scholar] [CrossRef]
- Weik, M.H. The ENIAC Story. Ordnance, 1961. Volume 45, no. 244; pp. 571–575. Available online: http://www.jstor.org/stable/45363261 (accessed on 11 November 2023).
- Saundade, M.; Kurle, P. Speech Recognition Using Digital Signal Processing. Int. J. Electron. Commun. Soft Comput. Sci. Eng. 2013, 2, 31–34. [Google Scholar]
- Alaghi, A.; Qian, W.; Hayes, J.P. The Promise and Challenge of Stochastic Computing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 1515–1531. [Google Scholar] [CrossRef]
- Li, P.; Lilja, D.J.; Qian, W.; Bazargan, K.; Riedel, M. The synthesis of complex arithmetic computation on stochastic bit streams using sequential logic. In Proceedings of the International Conference on Computer-Aided Design—ICCAD’12, San Jose, CA, USA, 5–8 November 2012. [Google Scholar] [CrossRef]
- Joe, H.; Kim, Y. Novel Stochastic Computing for Energy-Efficient Image Processors. Electronics 2019, 8, 720. [Google Scholar] [CrossRef]
- Alaghi, A.; Chan, W.T.J.; Hayes, J.P.; Kahng, A.B.; Li, J. Optimizing Stochastic Circuits for Accuracy-Energy Tradeoffs. In Proceedings of the 2015 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Austin, TX, USA, 2–6 November 2015; pp. 178–185. [Google Scholar] [CrossRef]
- Qian, W.; Li, X.; Riedel, M.D.; Bazargan, K.; Lilja, D.J. An Architecture for Fault-Tolerant Computation with Stochastic Logic. IEEE Trans. Comput. 2011, 60, 93–105. [Google Scholar] [CrossRef]
- Lee, V.T.; Alaghi, A.; Hayes, J.P.; Sathe, V.; Ceze, L. Energy-efficient hybrid stochastic-binary neural networks for near-sensor computing. In Proceedings of the Design, Automation and Test in Europe Conference and Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017. [Google Scholar] [CrossRef]
- Schober, P.; Estiri, S.N.; Aygun, S.; Jalilvand, A.H.; Najafi, M.H.; TaheriNejad, N. Stochastic Computing Design and Implementation of a Sound Source Localization System. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 295–311. [Google Scholar] [CrossRef]
- von Neumann, J. Probabilistic logics and the synthesis of reliable organisms from unreliable components. In The Neumann Compendium; Bródy, F., Tibor, V., Eds.; World Scientific: Singapore, 1995; pp. 567–616. ISBN 978-981-02-2201-7. [Google Scholar]
- von Neumann, J. Probabilistic logics and synthesis of reliable organisms from unreliable components. Autom. Stud. 1956, 34, 3–98. [Google Scholar]
- Ribeiro, S.T. Random-Pulse Machines. IEEE Trans. Electron. Comput. 1967, 16, 261–276. [Google Scholar] [CrossRef]
- Gaines, B.R. Stochastic Computing Systems. In Advances in Information Systems Science; Springer: New York, NY, USA, 1969; pp. 37–172. [Google Scholar] [CrossRef]
- Lawlor, R.C. Computer Utilizing Random Pulse Trains. U.S. Patent, 3,612,845, 1971. Priority Date 5 July 1968, Granted Date 12 October 1971. Available online: https://patentimages.storage.googleapis.com/4e/75/af/bb84c38d96742a/US3612845.pdf (accessed on 11 November 2023).
- Texas Instruments. High-Speed CMOS Logic Presettable Synchronous 4-Bit Up/Down Counters. Datasheet. Available online: https://www.ti.com/lit/ds/symlink/cd54hct193.pdf (accessed on 11 November 2023).
- Pouget, A.; Beck, J.; Ma, W.; Latham, P. Probabilistic brains: Knowns and unknowns. Nat. Neurosci. 2013, 16, 1170–1178. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Ríos, C.; Pernice, W.H.P.; Wright, C.D.; Bhaskaran, H. On-chip photonic synapse. Sci. Adv. 2017, 3, e1700160. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, G.M.; Brayton, R.K. Logic operations are properties of computer-simulated interactions between excitable dendritic spines. Neuroscience 1987, 21, 151–165. [Google Scholar] [CrossRef] [PubMed]
- Stipčević, M.; Batelić, M. Entropy consideration in improved circuits for a biologically-inspired random pulse computer. Sci. Rep. 2022, 12, 115. [Google Scholar] [CrossRef] [PubMed]
- Silverberg, L.; Tran, C.; Adams, T. Optimal Targets for the Bank Shot in Men’s Basketball. J. Quant. Anal. Sport. 2011, 7, 3. [Google Scholar] [CrossRef]
- Tran, C.M.; Silverberg, L.M. Optimal release conditions for the free throw in men’s basketball. J. Sport. Sci. 2008, 26, 1147–1155. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, M.; McKenzie, R.A.; Irani, R.A.; Ahmadi, M. Robot-mounted sensing and local calibration for high-accuracy manufacturing. Robot. Comput.-Integr. Manuf. 2022, 79, 102429. [Google Scholar] [CrossRef]
- Oberman, S.F.; Flynn, M.J. An Analysis of Division Algorithms and Implementations. Technical Report CSL-TR-95-675, July 1995. Available online: http://i.stanford.edu/pub/cstr/reports/csl/tr/95/675/CSL-TR-95-675.pdf (accessed on 11 November 2023).
- Wikipedia—“Division Algorithm”. Available online: https://en.wikipedia.org/wiki/Division_algorithm (accessed on 11 November 2023).
- Fischer, H. A History of the Central Limit Theorem: From Classical to Modern Probability Theory; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stipčević, M. Biomimetic Random Pulse Computation or Why Do Humans Play Basketball Better than Robots? Biomimetics 2023, 8, 594. https://doi.org/10.3390/biomimetics8080594
Stipčević M. Biomimetic Random Pulse Computation or Why Do Humans Play Basketball Better than Robots? Biomimetics. 2023; 8(8):594. https://doi.org/10.3390/biomimetics8080594
Chicago/Turabian StyleStipčević, Mario. 2023. "Biomimetic Random Pulse Computation or Why Do Humans Play Basketball Better than Robots?" Biomimetics 8, no. 8: 594. https://doi.org/10.3390/biomimetics8080594
APA StyleStipčević, M. (2023). Biomimetic Random Pulse Computation or Why Do Humans Play Basketball Better than Robots? Biomimetics, 8(8), 594. https://doi.org/10.3390/biomimetics8080594








