Some Mechanical Constraints to the Biomimicry with Peripheral Nerves
Abstract
:1. Introduction
2. Methods
3. Results
3.1. Error Evaluation for Different Polynomial Stress Functions
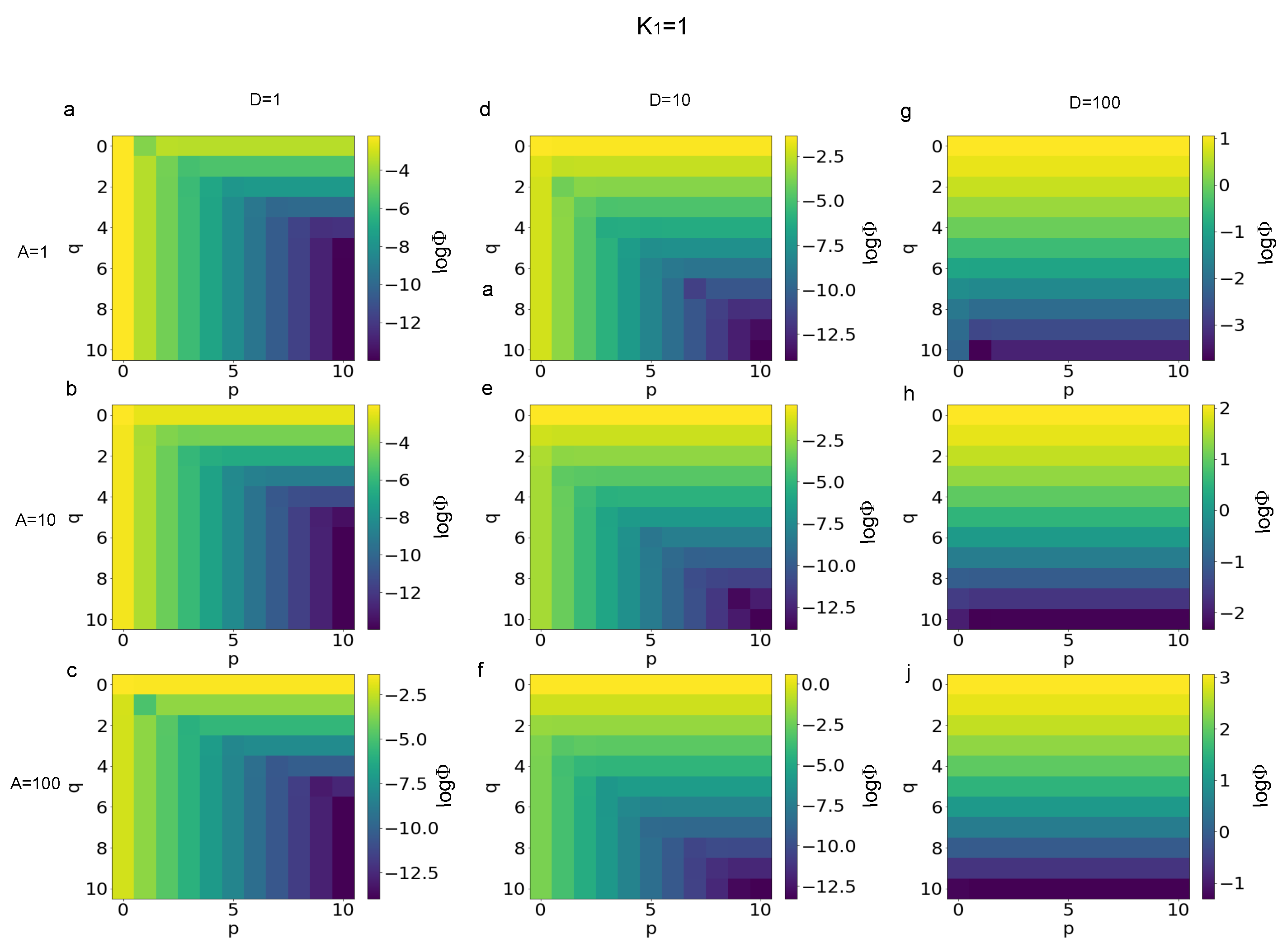
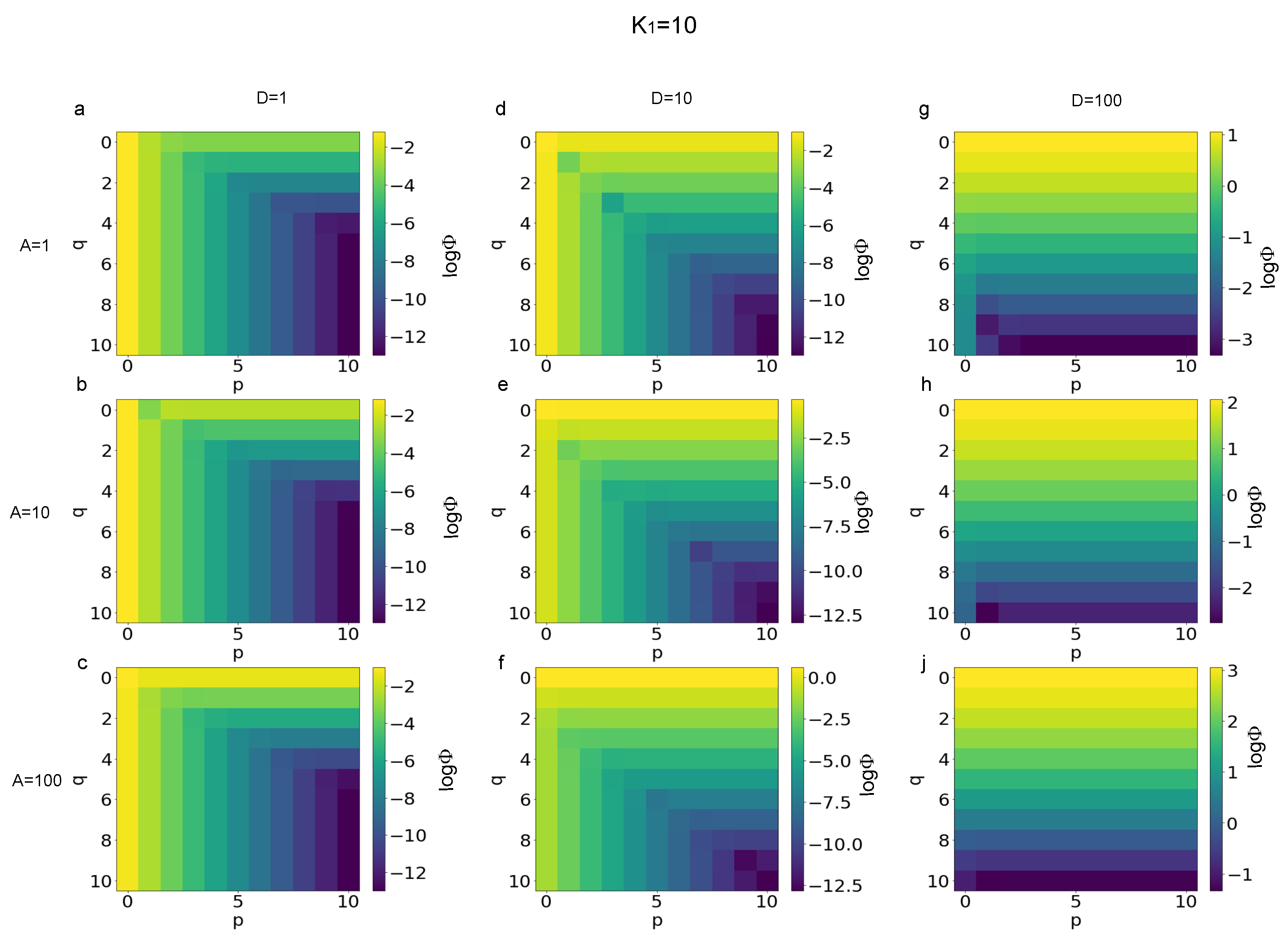
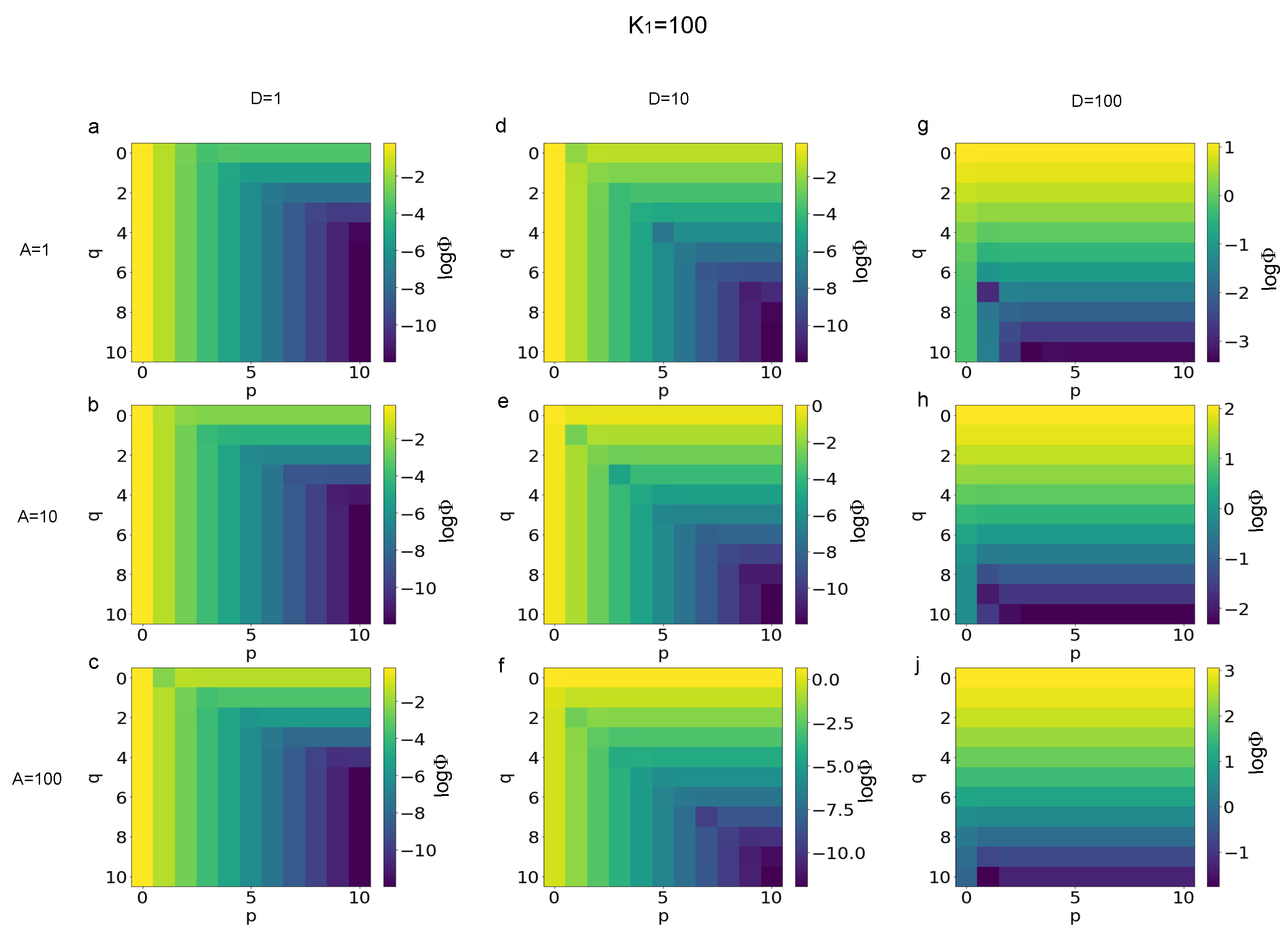
3.2. Sensitivity of Different Polynomial Stress Functions to Parameters
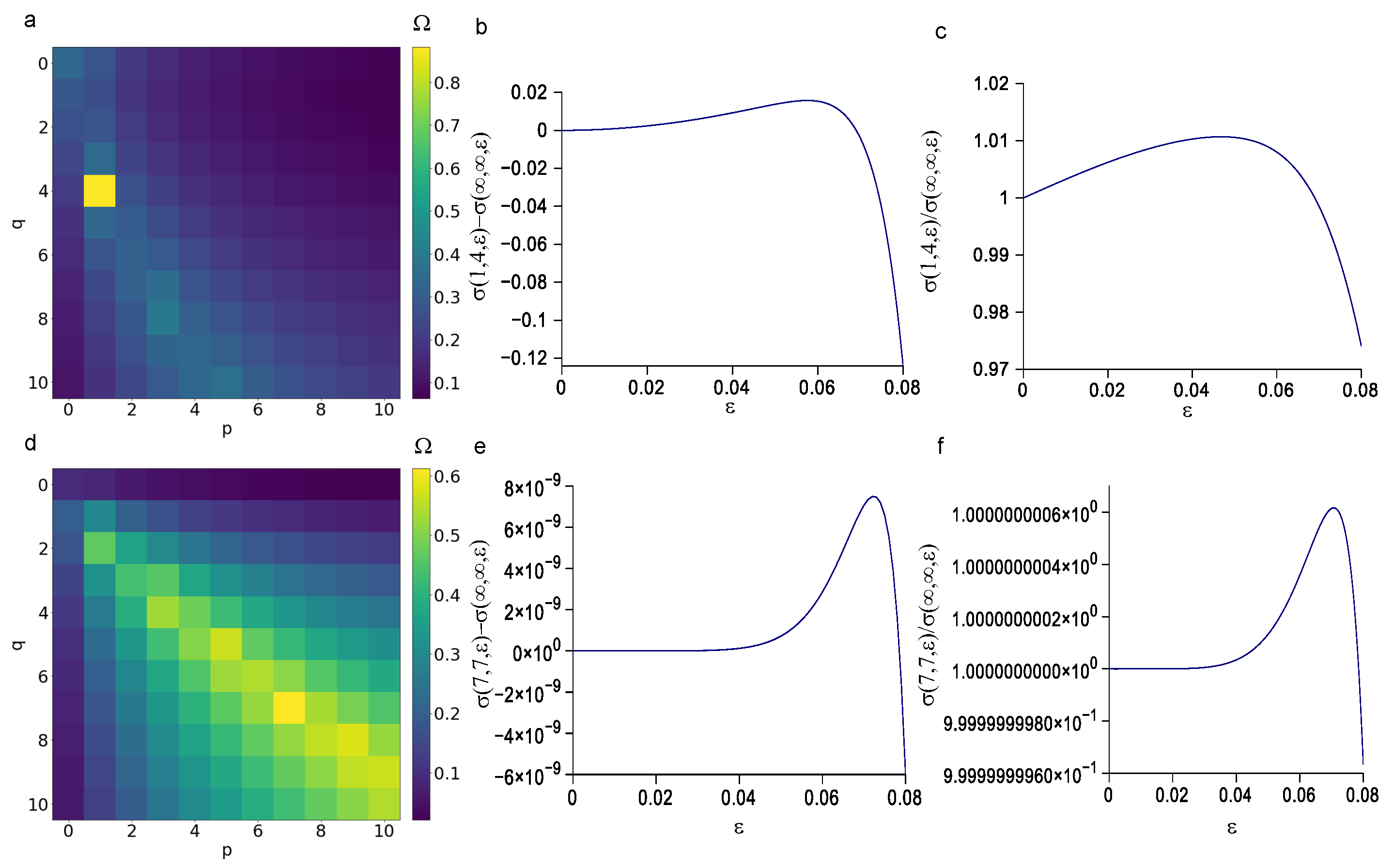
3.3. Minimization of the p and q Values
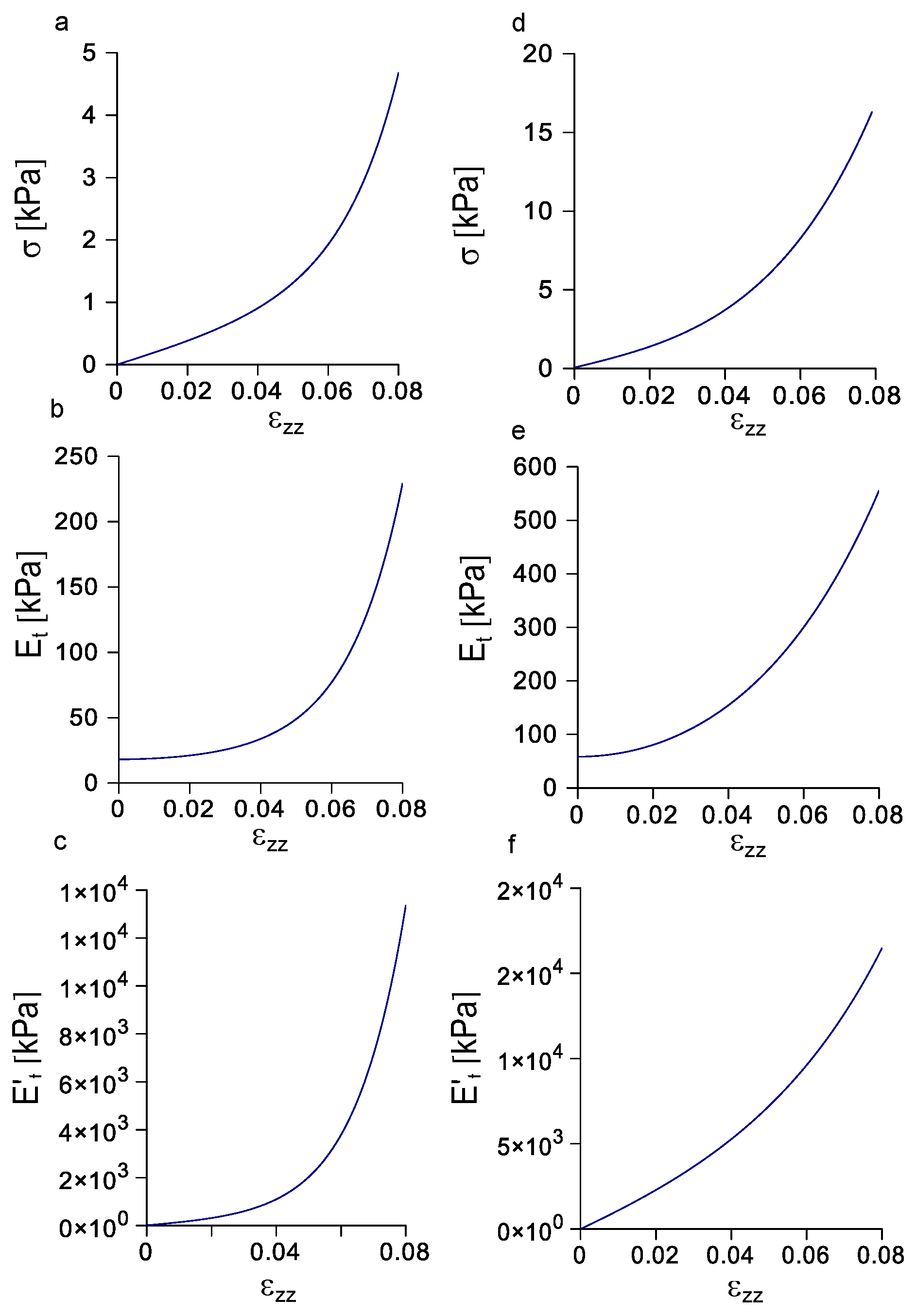
3.4. Evolution of Stress, Tangent Modulus, and Rate of Change of the Tangent Modulus with Strain
3.5. Analysis of the Correlation among Longitudinal Stress, Tangent Modulus, and Rate of Change of the Tangent Modulus with Strain
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Vincent, J.F. Chapter 17—Biomimetic Materials. In Materials Experience; Karana, E., Pedgley, O., Rognoli, V., Eds.; Butterworth-Heinemann: Boston, MA, USA, 2014; pp. 235–246. [Google Scholar] [CrossRef]
- Koffler, J.; Zhu, W.; Qu, X.; Platoshyn, O.; Dulin, J.N.; Brock, J.; Graham, L.; Lu, P.; Sakamoto, J.; Marsala, M.; et al. Biomimetic 3D-printed scaffolds for spinal cord injury repair. Nat. Med. 2019, 25, 263–269. [Google Scholar] [CrossRef]
- Ul Haq, A.; Montaina, L.; Pescosolido, F.; Carotenuto, F.; Trovalusci, F.; De Matteis, F.; Tamburri, E.; Di Nardo, P. Electrically conductive scaffolds mimicking the hierarchical structure of cardiac myofibers. Sci. Rep. 2023, 13, 2863. [Google Scholar] [CrossRef]
- Huang, L.; Chen, L.; Chen, H.; Wang, M.; Jin, L.; Zhou, S.; Gao, L.; Li, R.; Li, Q.; Wang, H.; et al. Biomimetic Scaffolds for Tendon Tissue Regeneration. Biomimetics 2023, 8, 246. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Alonso, S.; Lafuente-Merchan, M.; Ciriza, J.; del Burgo, L.S.; Pedraz, J.L. Tendon tissue engineering: Cells, growth factors, scaffolds and production techniques. J. Control. Release 2021, 333, 448–486. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Kim, G.E.; Attia Abdou, M.; Kim, S.; Kim, D.; Park, S.; Kim, Y.K.; Gwon, Y.; Jeong, S.E.; Kim, M.S.; et al. Tendon-Inspired Nanotopographic Scaffold for Tissue Regeneration in Rotator Cuff Injuries. ACS Omega 2020, 5, 13913–13925. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Ning, L.J.; Wu, F.P.; Hu, R.N.; Li, X.; He, S.K.; Zhang, Y.J.; Luo, J.J.; Luo, J.C.; Qin, T.W. Biomechanically and biochemically functional scaffold for recruitment of endogenous stem cells to promote tendon regeneration. NPJ Regen. Med. 2022, 7, 26. [Google Scholar] [CrossRef]
- Ng, J.; Spiller, K.; Bernhard, J.; Vunjak-Novakovic, G. Biomimetic Approaches for Bone Tissue Engineering. Tissue Eng. Part B Rev. 2017, 23, 480–493. [Google Scholar] [CrossRef]
- Qu, H.; Fu, H.; Han, Z.; Sun, Y. Biomaterials for bone tissue engineering scaffolds: A review. RSC Adv. 2019, 9, 26252–26262. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Z.; Guan, J.; Mao, Y.; Zhou, P. Hydrogel: A potential therapeutic material for bone tissue engineering. AIP Adv. 2021, 11, 010701. [Google Scholar] [CrossRef]
- Lei, Z.; Wu, P. A supramolecular biomimetic skin combining a wide spectrum of mechanical properties and multiple sensory capabilities. Nat. Commun. 2018, 9, 1134. [Google Scholar] [CrossRef]
- Malheiro, A.; Morgan, F.; Baker, M.; Moroni, L.; Wieringa, P. A three-dimensional biomimetic peripheral nerve model for drug testing and disease modelling. Biomaterials 2020, 257, 120230. [Google Scholar] [CrossRef] [PubMed]
- Malheiro, A.; Seijas-Gamardo, A.; Harichandan, A.; Mota, C.; Wieringa, P.; Moroni, L. Development of an In Vitro Biomimetic Peripheral Neurovascular Platform. ACS Appl. Mater. Interfaces 2022, 14, 31567–31585. [Google Scholar] [CrossRef] [PubMed]
- Guedan-Duran, A.; Jemni-Damer, N.; Orueta-Zenarruzabeitia, I.; Guinea, G.V.; Perez-Rigueiro, J.; Gonzalez-Nieto, D.; Panetsos, F. Biomimetic Approaches for Separated Regeneration of Sensory and Motor Fibers in Amputee People: Necessary Conditions for Functional Integration of Sensory Motor Prostheses with the Peripheral Nerves. Front. Bioeng. Biotechnol. 2020, 8, 584823. [Google Scholar] [CrossRef] [PubMed]
- Ingber, D.E. Mechanical control of tissue growth: Function follows form. Proc. Natl. Acad. Sci. USA 2005, 102, 11571–11572. [Google Scholar] [CrossRef] [PubMed]
- Millesi, H.; Zoch, G.; Reihsner, R. Mechanical properties of peripheral nerves. Clin. Orthop. Relat. Res. 1995, 314, 76–83. [Google Scholar] [CrossRef]
- Bianchi, F.; Hofmann, F.; Smith, A.J.; Ye, H.; Thompson, M.S. Probing multi-scale mechanics of peripheral nerve collagen and myelin by X-ray diffraction. J. Mech. Behav. Biomed. Mater. 2018, 87, 205–212. [Google Scholar] [CrossRef]
- Sergi, P.N.; Jensen, W.; Yoshida, K. Interactions among biotic and abiotic factors affect the reliability of tungsten microneedles puncturing in vitro and in vivo peripheral nerves: A hybrid computational approach. Mater. Sci. Eng. C 2016, 59, 1089–1099. [Google Scholar] [CrossRef]
- Giannessi, E.; Stornelli, M.R.; Coli, A.; Sergi, P.N. A Quantitative Investigation on the Peripheral Nerve Response within the Small Strain Range. Appl. Sci. 2019, 9, 1115. [Google Scholar] [CrossRef]
- Main, E.K.; Goetz, J.E.; Rudert, M.J.; Goreham-Voss, C.M.; Brown, T.D. Apparent transverse compressive material properties of the digital flexor tendons and the median nerve in the carpal tunnel. J. Biomech. 2011, 44, 863–868. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, S.; Tan, J.S.; Myer, C.; Njus, N.M.; Xia, Z. In vitro and in vivo mechanical properties of human ulnar and median nerves. J. Biomed. Mater. Res. A 2013, 101, 2718–2725. [Google Scholar] [CrossRef]
- Giannessi, E.; Stornelli, M.R.; Sergi, P.N. A unified approach to model peripheral nerves across different animal species. PeerJ 2017, 5, e4005. [Google Scholar] [CrossRef] [PubMed]
- Giannessi, E.; Stornelli, M.R.; Sergi, P.N. Fast in silico assessment of physical stress for peripheral nerves. Med. Biol. Eng. Comput. 2018, 56, 1541–1551. [Google Scholar] [CrossRef] [PubMed]
- Giannessi, E.; Stornelli, M.R.; Sergi, P.N. Strain stiffening of peripheral nerves subjected to longitudinal extensions in vitro. Med. Eng. Phys. 2020, 76, 47–55. [Google Scholar] [CrossRef]
- Layton, B.E.; Sastry, A.M. A Mechanical Model for Collagen Fibril Load Sharing in Peripheral Nerve of Diabetic and Nondiabetic Rats. J. Biomech. Eng. 2005, 126, 803–814. [Google Scholar] [CrossRef]
- Layton, B.E.; Sastry, A.M. Equal and local-load-sharing micromechanical models for collagens: Quantitative comparisons in response of non-diabetic and diabetic rat tissue. Acta Biomater. 2006, 2, 595–607. [Google Scholar] [CrossRef] [PubMed]
- Sergi, P.N. Deterministic and Explicit: A Quantitative Characterization of the Matrix and Collagen Influence on the Stiffening of Peripheral Nerves Under Stretch. Appl. Sci. 2020, 10, 6372. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics, Mechanical Properties of Living Tissues; Springer: New York, NY, USA, 1993. [Google Scholar]
- Holzapfel, G.A.; Ogden, R. (Eds.) Biomechanical Modelling at the Molecular, Cellular and Tissue Level; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tassler, P.; Dellon, A.; Canoun, C. Identification of elastic fibres in the peripheral nerve. J. Hand Surg. Br. Eur. Vol. 1994, 19, 48–54. [Google Scholar] [CrossRef]
- Zilic, L.; Garner, P.E.; Yu, T.; Roman, S.; Haycock, J.W.; Wilshaw, S.P. An anatomical study of porcine peripheral nerve and its potential use in nerve tissue engineering. J. Anat. 2015, 227, 302–314. [Google Scholar] [CrossRef]
- Mason, S.; Phillips, J.B. An ultrastructural and biochemical analysis of collagen in rat peripheral nerves: The relationship between fibril diameter and mechanical properties. J. Peripher. Nerv. Syst. 2011, 16, 261–269. [Google Scholar] [CrossRef]
- Sunderland, S. The intraneural topography of the radial, median and ulnar nerves. Brain 1945, 68, 243–299. [Google Scholar] [CrossRef]
- Thomas, P. The connective tissue of peripheral nerve: An electron microscope study. J. Anat. 1963, 97, 35–44. [Google Scholar] [PubMed]
- Gamble, H.J.; Eames, R.A. An electron microscope study of the connective tissues of human peripheral nerves. J. Anat. 1964, 98, 655–663. [Google Scholar] [PubMed]
- Topp, K.S.; Boyd, B.S. Structure and biomechanics of peripheral nerves: Nerve responses to physical stresses and implications for physical therapist practice. Phys. Ther. 2006, 86, 92–109. [Google Scholar] [CrossRef] [PubMed]
- Zochodne, D.W. Neurobiology of Peripheral Nerve Regeneration; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Topp, K.S.; Boyd, B.S. Peripheral Nerve: From the Microscopic Functional Unit of the Axon to the Biomechanically Loaded Macroscopic Structure. J. Hand Ther. 2012, 25, 142–152. [Google Scholar] [CrossRef]
- Seddon, H.J. Three types of nerve injury. Brain 1943, 66, 237–288. [Google Scholar] [CrossRef]
- Sunderland, S. Rate of regeneration in human peripheral nerves: Analysis of the interval between injury and onset of recovery. Arch. Neurol. Psychiatry 1947, 58, 251–295. [Google Scholar] [CrossRef]
- Sergi, P.N.; Jensen, W.; Micera, S.; Yoshida, K. In vivo interactions between tungsten microneedles and peripheral nerves. Med. Eng. Phys. 2012, 34, 747–755. [Google Scholar] [CrossRef]
- Sergi, P.N.; Jensen, W.; Yoshida, K. Geometric Characterization of Local Changes in Tungsten Microneedle Tips after In-Vivo Insertion into Peripheral Nerves. Appl. Sci. 2022, 12, 8938. [Google Scholar] [CrossRef]
- Green, R.A.; Lovell, N.H.; Wallace, G.G.; Poole-Warren, L.A. Conducting polymers for neural interfaces: Challenges in developing an effective long-term implant. Biomaterials 2008, 29, 3393–3399. [Google Scholar] [CrossRef]
- Grill, W.M.; Norman, S.E.; Bellamkonda, R.V. Implanted Neural Interfaces: Biochallenges and Engineered Solutions. Annu. Rev. Biomed. Eng. 2009, 11, 1–24. [Google Scholar] [CrossRef]
- Lacour, S.P.; Courtine, G.; Guck, J. Materials and technologies for soft implantable neuroprostheses. Nat. Rev. Mater. 2016, 1, 16063. [Google Scholar] [CrossRef]
- Ciofani, G.; Sergi, P.N.; Carpaneto, J.; Micera, S. A hybrid approach for the control of axonal outgrowth: Preliminary simulation results. Med Biol. Eng. Comput. 2011, 49, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Sergi, P.N.; Cavalcanti-Adam, E.A. Biomaterials and computation: A strategic alliance to investigate emergent responses of neural cells. Biomater. Sci. 2017, 5, 648–657. [Google Scholar] [CrossRef]
- Sergi, P.N.; Morana Roccasalvo, I.; Tonazzini, I.; Cecchini, M.; Micera, S. Cell Guidance on Nanogratings: A Computational Model of the Interplay between PC12 Growth Cones and Nanostructures. PLoS ONE 2013, 8, e70304. [Google Scholar] [CrossRef]
- Sergi, P.N.; Marino, A.; Ciofani, G. Deterministic control of mean alignment and elongation of neuron-like cells by grating geometry: A computational approach. Integr. Biol. 2015, 7, 1242–1252. [Google Scholar] [CrossRef]
- Roccasalvo, I.M.; Micera, S.; Sergi, P.N. A hybrid computational model to predict chemotactic guidance of growth cones. Sci. Rep. 2015, 5, 11340. [Google Scholar] [CrossRef] [PubMed]
- Sergi, P.N.; Valle, J.d.; Oliva, N.d.l.; Micera, S.; Navarro, X. A data-driven polynomial approach to reproduce the scar tissue outgrowth around neural implants. J. Mater. Sci. Mater. Med. 2020, 31, 59. [Google Scholar] [CrossRef]
- Sergi, P.N.; De la Oliva, N.; del Valle, J.; Navarro, X.; Micera, S. Physically Consistent Scar Tissue Dynamics from Scattered Set of Data: A Novel Computational Approach to Avoid the Onset of the Runge Phenomenon. Appl. Sci. 2021, 11, 8568. [Google Scholar] [CrossRef]
- Anderson, J.M.; Rodriguez, A.; Chang, D.T. Foreign body reaction to biomaterials. Semin. Immunol. 2008, 20, 86–100. [Google Scholar] [CrossRef]
- Nachemson, A.K.; Lundborg, G.; Myrhage, R.; Rank, F. Nerve regeneration and pharmacological suppression of the scar reaction at the suture site. An experimental study on the effect of estrogen-progesterone, methylprednisolone-acetate and cis-hydroxyproline in rat sciatic nerve. Scand. J. Plast. Reconstr. Surg. 1985, 19, 255–260. [Google Scholar] [CrossRef]
- Tringides, C.M.; Vachicouras, N.; de Lazaro, I.; Wang, H.; Trouillet, A.; Seo, B.R.; Elosegui-Artola, A.; Fallegger, F.; Shin, Y.; Casiraghi, C.; et al. Viscoelastic surface electrode arrays to interface with viscoelastic tissues. Nat. Nanotechnol. 2021, 16, 1019–1029. [Google Scholar] [CrossRef] [PubMed]

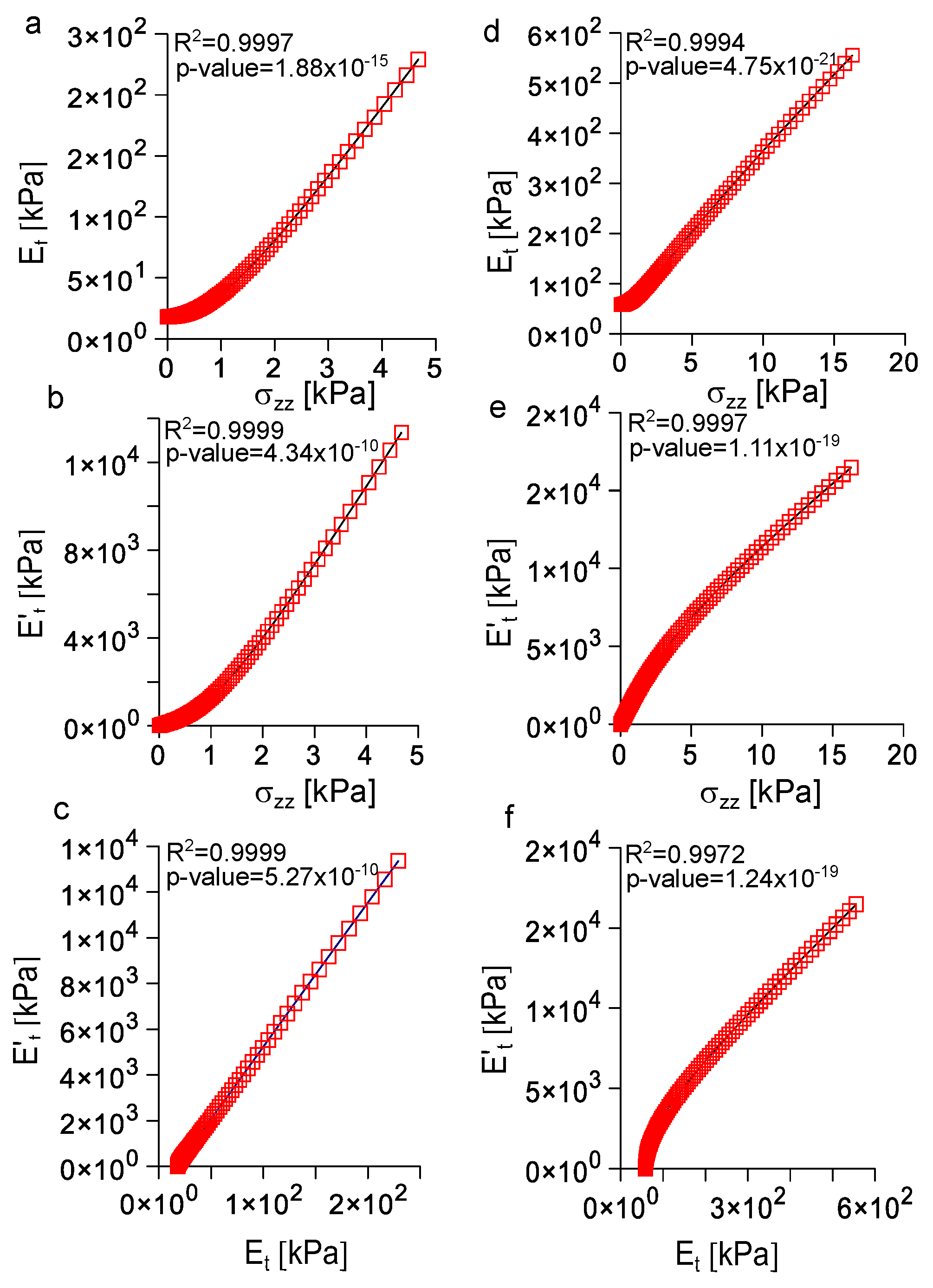
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sergi, P.N. Some Mechanical Constraints to the Biomimicry with Peripheral Nerves. Biomimetics 2023, 8, 544. https://doi.org/10.3390/biomimetics8070544
Sergi PN. Some Mechanical Constraints to the Biomimicry with Peripheral Nerves. Biomimetics. 2023; 8(7):544. https://doi.org/10.3390/biomimetics8070544
Chicago/Turabian StyleSergi, Pier Nicola. 2023. "Some Mechanical Constraints to the Biomimicry with Peripheral Nerves" Biomimetics 8, no. 7: 544. https://doi.org/10.3390/biomimetics8070544
APA StyleSergi, P. N. (2023). Some Mechanical Constraints to the Biomimicry with Peripheral Nerves. Biomimetics, 8(7), 544. https://doi.org/10.3390/biomimetics8070544





