Performance Optimization for Bionic Robotic Dolphin with Active Variable Stiffness Control
Abstract
1. Introduction
2. Overview of the Robotic Dolphin with Torque Mode-Based Variable Stiffness Mechanism
2.1. Overview of the Robotic Dolphin
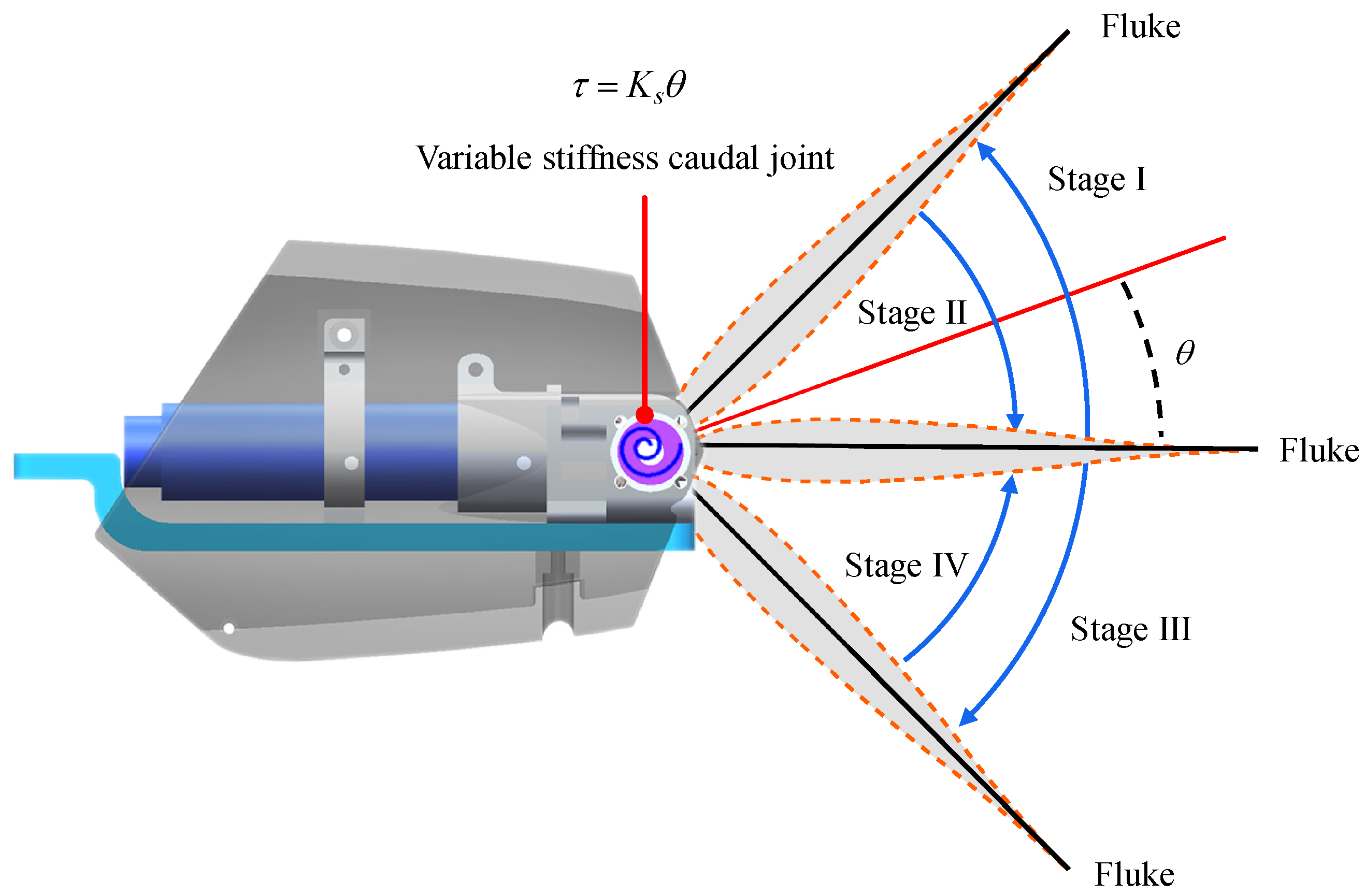
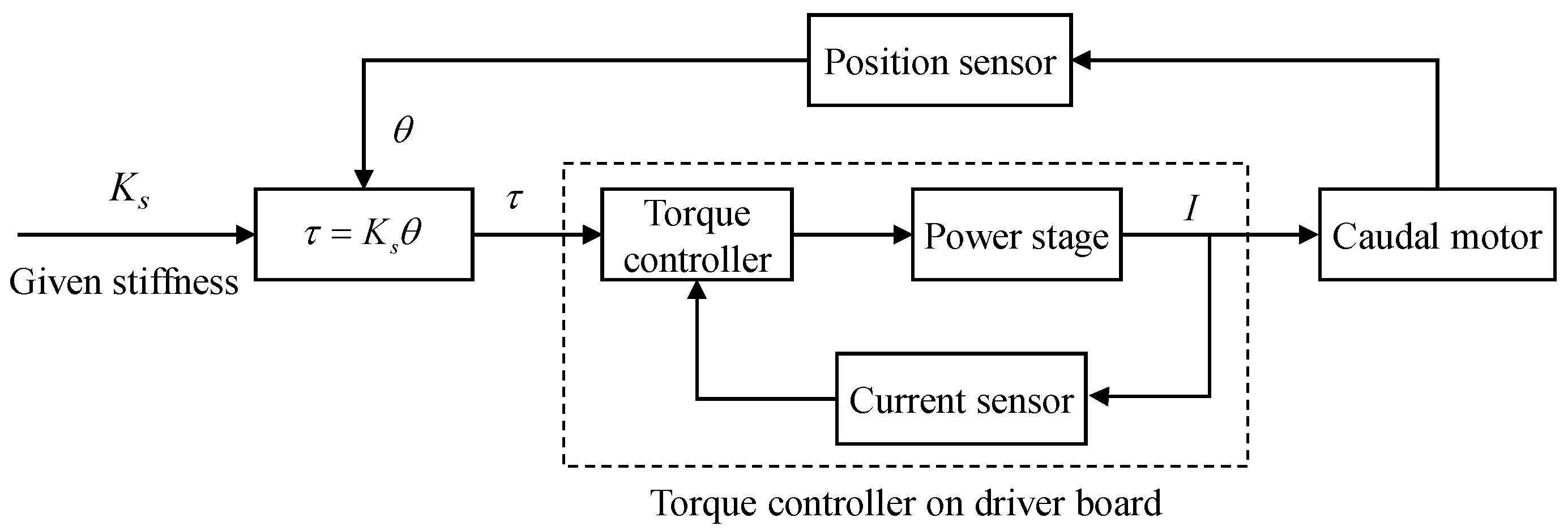
2.2. Torque Control-Based Variable Stiffness Mechanism
3. Dynamic Modeling of Robotic Dolphin
3.1. Kinematic Analysis
3.2. Lagrangian Dynamic Modeling
3.3. Hydrodynamic Analysis
4. Experiments and Stiffness Optimization
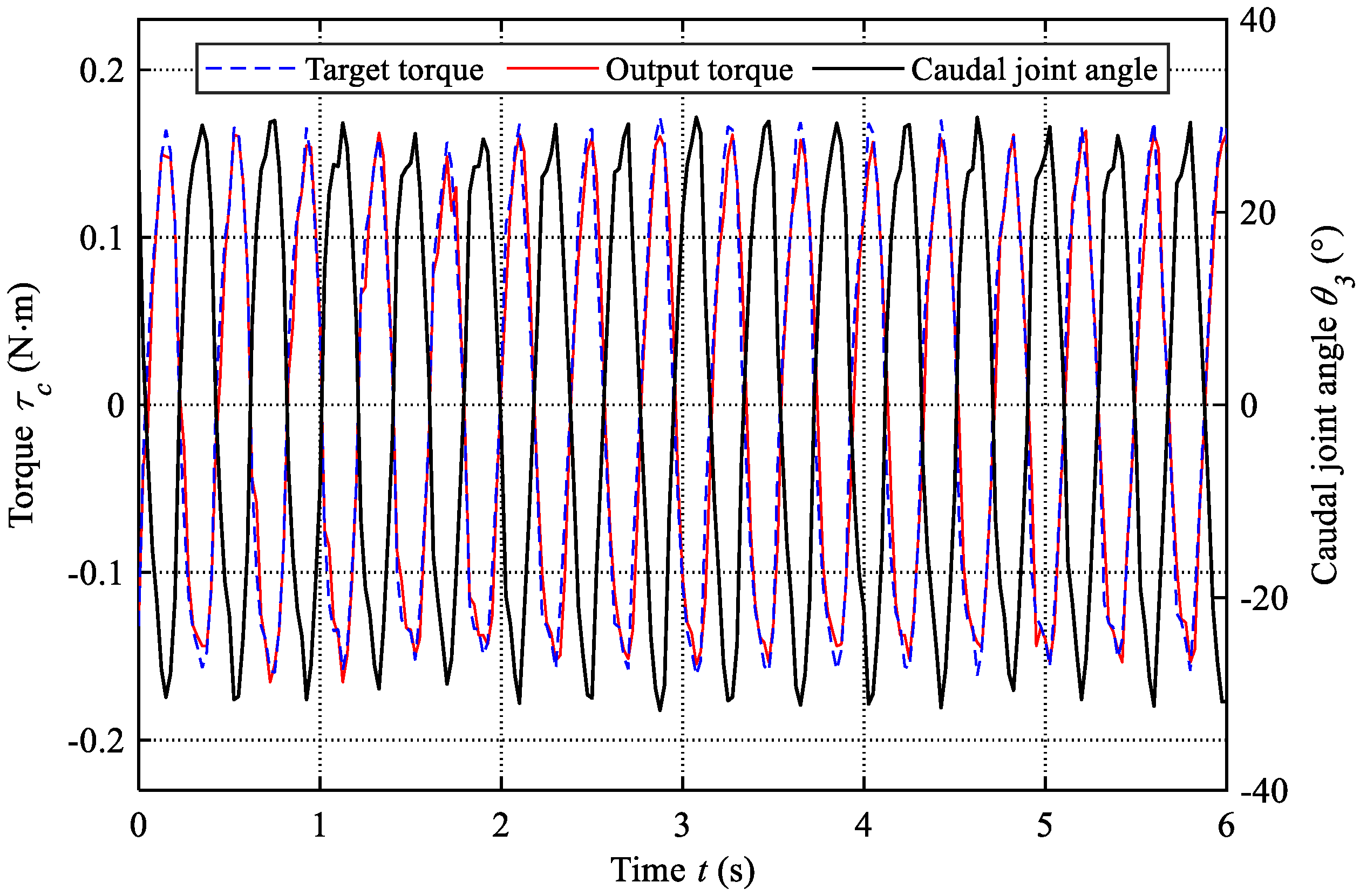
4.1. Parameters Identification
4.2. Experiments Testing
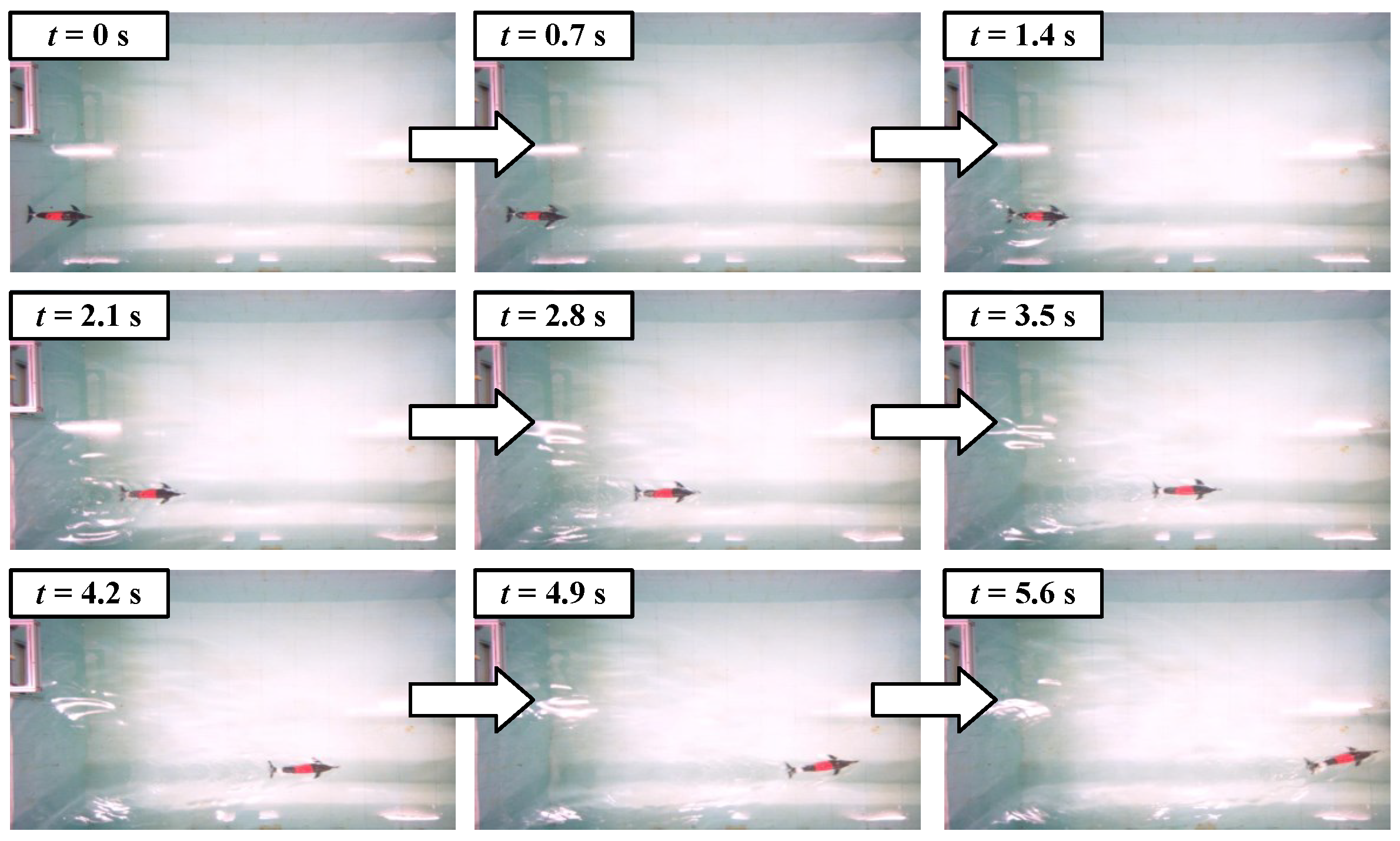
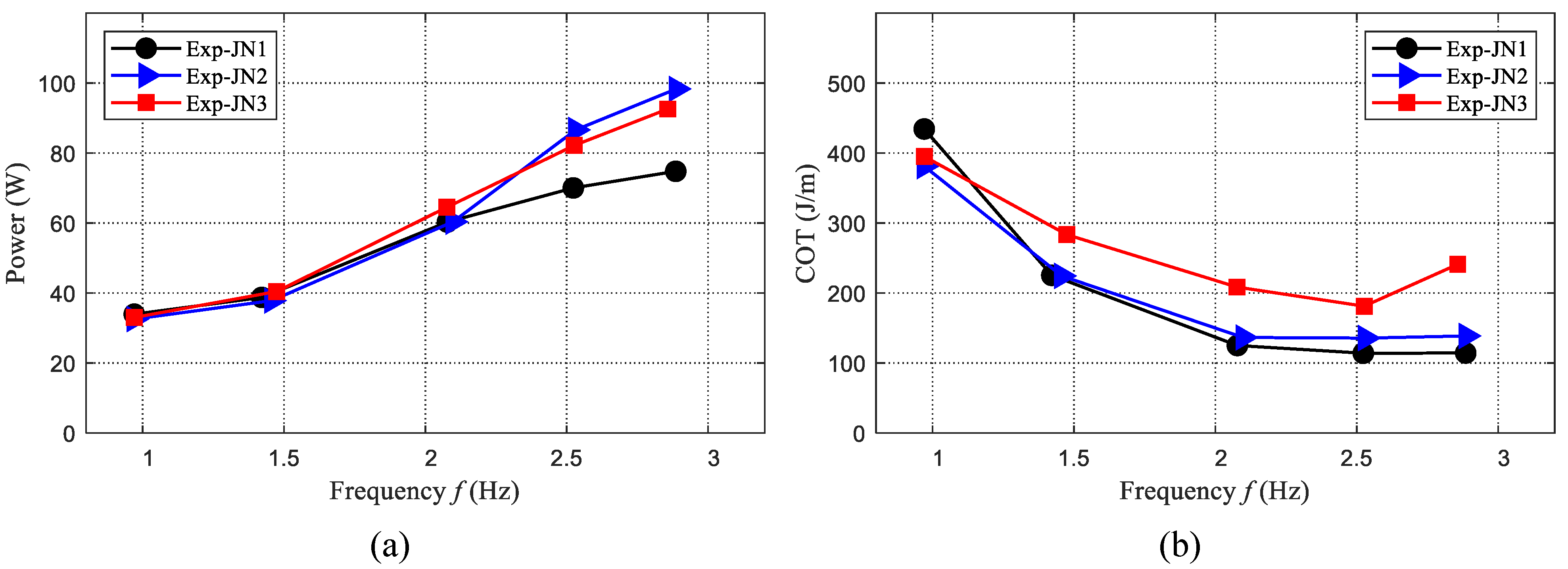
4.2.1. Speed Testing
4.2.2. Power Testing
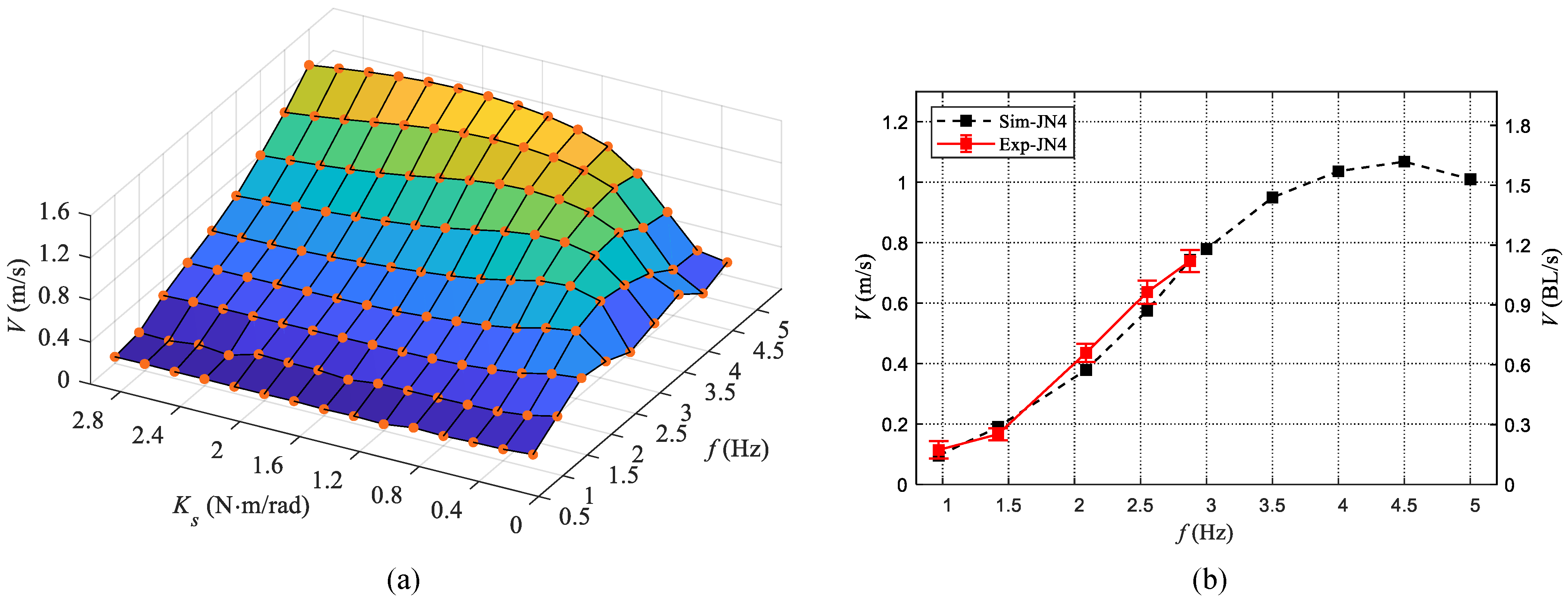
4.3. Performance Optimization
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fish, F.E. Advantages of natural propulsive systems. Mar. Technol. Soc. J. 2013, 47, 37–44. [Google Scholar] [CrossRef]
- Raj, A.; Thakur, A. Fish-inspired robots: Design, sensing, actuation, and autonomy—A review of research. Bioinspir. Biomim. 2016, 11, 031001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, Z.; Wang, J.; Tan, M. Design and analysis of a bionic gliding robotic dolphin. Biomimetics 2023, 8, 151. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Wang, T.; Chen, D.; Meng, Y. Quantifying the leaping motion using a self-propelled bionic robotic dolphin platform. Biomimetics 2023, 8, 21. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Liu, Z.; Ju, J. Line-of-sight based three-dimensional path following control for an underactuated robotic dolphin. Sci. China Inf. Sci. 2021, 64, 112210. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, J.; Yu, J.; Fang, H. Development of a novel robotic dolphin and its application to water quality monitoring. IEEE/ASME Trans. Mechatron. 2017, 22, 2130–2140. [Google Scholar] [CrossRef]
- Tan, X. Autonomous robotic fish as mobile sensor platforms: Challenges and potential solutions. Mar. Technol. Soc. J. 2011, 45, 31–40. [Google Scholar] [CrossRef]
- Katzschmann, R.K.; DelPreto, J.; MacCurdy, R.; Rus, D. Exploration of underwater life with an acoustically controlled soft robotic fish. Sci. Robot. 2018, 3, eaar3449. [Google Scholar] [CrossRef]
- Li, G.; Chen, X.; Zhou, F.; Liang, Y.; Xiao, Y.; Cao, X.; Zhang, Z.; Zhang, M.; Wu, B.; Yin, S.; et al. Self-powered soft robot in the Mariana Trench. Nature 2021, 591, 66–71. [Google Scholar] [CrossRef]
- Yu, J.; Wu, Z.; Wang, M.; Tan, M. CPG network optimization for a biomimetic robotic fish via PSO. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1962–1968. [Google Scholar] [CrossRef]
- Hong, Z.; Wang, Q.; Zhong, Y. Parameters optimization of body wave control method for multi-joint robotic fish based on deep reinforcement learning. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Jinghong, China, 5–9 December 2022; pp. 604–609. [Google Scholar]
- Shao, H.; Dong, B.; Zheng, C.; Li, T.; Zuo, Q.; Xu, Y.; Fang, H.; He, K.; Xie, F. Thrust improvement of a biomimetic robotic fish by using a deformable caudal fin. Biomimetics 2022, 7, 113. [Google Scholar] [CrossRef]
- Zou, Q.; Zhou, C.; Lu, B.; Liao, X.; Zhang, Z. Tail-stiffness optimization for a flexible robotic fish. Bioinspir. Biomim. 2022, 17, 066003. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Zhou, C.; Zou, Q.; Wang, J.; Lu, B. Dynamic modeling and performance analysis for a wire-driven elastic robotic fish. IEEE Robot. Autom. Lett. 2022, 7, 11174–11181. [Google Scholar] [CrossRef]
- Zhu, J.; White, C.H.; Wainwright, D.K.; Di Santo, V.; Lauder, G.V.; Bart-Smith, H. Tuna robotics: A high-frequency experimental platform exploring the performance space of swimming fishes. Sci. Robot. 2019, 4, eaax4615. [Google Scholar] [CrossRef]
- White, C.H.; Lauder, G.V.; Bart-Smith, H. Tunabot Flex: A tuna-inspired robot with body flexibility improves high-performance swimming. Bioinspir. Biomim. 2021, 16, 026019. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Wu, Z.; Dong, H.; Tan, M.; Yu, J. Exploration of swimming performance for a biomimetic multi-joint robotic fish with a compliant passive joint. Bioinspir. Biomim. 2020, 16, 026007. [Google Scholar] [CrossRef]
- Chen, D.; Wu, Z.; Meng, Y.; Tan, M.; Yu, J. Development of a high-speed swimming robot with the capability of fish-like leaping. IEEE/ASME Trans. Mechatron. 2022, 27, 3579–3589. [Google Scholar] [CrossRef]
- Chen, D.; Wu, Z.; Zhang, P.; Tan, M.; Yu, J. Performance improvement of a high-speed swimming robot for fish-like leaping. IEEE Robot. Autom. Lett. 2022, 7, 1936–1943. [Google Scholar] [CrossRef]
- Chen, B.; Jiang, H. Body stiffness variation of a tensegrity robotic fish using antagonistic stiffness in a kinematically singular configuration. IEEE Trans. Robot. 2021, 37, 1712–1727. [Google Scholar] [CrossRef]
- Quinn, D.; Lauder, G.V. Tunable stiffness in fish robotics: Mechanisms and advantages. Bioinspir. Biomim. 2021, 17, 011002. [Google Scholar] [CrossRef]
- Park, Y.J.; Huh, T.M.; Park, D.; Cho, K.J. Design of a variable-stiffness flapping mechanism for maximizing the thrust of a bio-inspired underwater robot. Bioinspir. Biomim. 2014, 9, 036002. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Park, D.; Cho, K. Design and manufacturing a robotic dolphin to increase dynamic performance. In Proceedings of the 10th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Republic of Korea, 30 October–2 November 2013; pp. 76–77. [Google Scholar]
- Zhu, C.; Deng, L.; Wang, X.; Yin, Z.; Zhou, C. Design and modeling of elastic variable stiffness robotic fish tail. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Guilin, China, 7–10 August 2022; pp. 1251–1256. [Google Scholar]
- Jusufi, A.; Vogt, D.M.; Wood, R.J.; Lauder, G.V. Undulatory swimming performance and body stiffness modulation in a soft robotic fish-inspired physical model. Soft Robot. 2017, 4, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Q.; Zhu, J.; Fish, F.E.; Kerr, S.J.; Downs, A.M.; Bart-Smith, H.; Quinn, D.B. Tunable stiffness enables fast and efficient swimming in fish-like robots. Sci. Robot. 2021, 6, eabe4088. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Jiang, H.; Wang, S.; Yu, J. A soft robotic fish with variable-stiffness decoupled mechanisms. J. Bionic Eng. 2018, 15, 599–609. [Google Scholar] [CrossRef]
- Qiu, C.; Wu, Z.; Wang, J.; Tan, M.; Yu, J. Locomotion optimization of a tendon-driven robotic fish with variable passive tail fin. IEEE Trans. Ind. Electron. 2023, 70, 4983–4992. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Lueth, T.C. Optimization of stress distribution in tendon-driven continuum robots using fish-tail-inspired method. IEEE Robot. Autom. Lett. 2022, 7, 3380–3387. [Google Scholar] [CrossRef]
- Wang, T.; Yu, J.; Chen, D.; Meng, Y. A torque control strategy for a robotic dolphin platform based on angle of attack feedback. Biomimetics 2023, 8, 291. [Google Scholar] [CrossRef] [PubMed]
- Kopman, V.; Laut, J.; Acquaviva, F.; Rizzo, A.; Porfiri, M. Dynamic modeling of a robotic fish propelled by a compliant tail. IEEE J. Ocean. Eng. 2015, 40, 209–221. [Google Scholar] [CrossRef]
- El-Hawary, F. The Ocean Engineering Handbook, 1st ed.; CRC Press LLC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Morgansen, K.A.; Triplett, B.I.; Klein, D.J. Geometric methods for modeling and control of free-swimming fin-actuated underwater vehicles. IEEE Trans. Robot. 2007, 23, 1184–1199. [Google Scholar] [CrossRef]
- Yu, J.; Yuan, J.; Wu, Z.; Tan, M. Data-driven dynamic modeling for a swimming robotic fish. IEEE Trans. Ind. Electron. 2016, 63, 5632–5640. [Google Scholar] [CrossRef]
- Yuan, J.; Yu, J.; Wu, Z.; Tan, M. Precise planar motion measurement of a swimming multi-joint robotic fish. Sci. China Inf. Sci. 2016, 59, 92208. [Google Scholar] [CrossRef][Green Version]
- Lu, B.; Zhou, C.; Wang, J.; Fu, Y.; Cheng, L.; Tan, M. Development and stiffness optimization for a flexible-tail robotic fish. IEEE Robot. Autom. Lett. 2022, 7, 834–841. [Google Scholar] [CrossRef]






| Items | Characteristics |
|---|---|
| Total mass | 3.91 kg |
| Length × Width × Height | 0.66 m × 0.11 m × 0.12 m |
| Power supply | 24 V rechargeable batteries |
| Communication unit | Wireless (RF200, 433 MHz) |
| Sensor | AHRS, MS5803 01BA |
| Controller | STM32F407VGT6, 168 MHz |
| Motor | DC motor × 2, servo motor × 3 |
| Items | Unit | ||||
|---|---|---|---|---|---|
| kg | 0.287 | 2.830 | 0.662 | 0.134 | |
| m | 0.134 | 0.285 | 0.148 | 0.093 | |
| kgm () | 3.207 | 79.738 | 3.742 | 0.23 | |
| m | – | – | – | 0.034 | |
| m () | – | – | – | 9.396 |
| Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | 0.27 | 0.18 | 0.26 | 0.039 | 0.034 | 0.015 | 2.55 | 4.0 | 5.8 |
| Prototype | Frequency (Hz) | Swimming Speed (m/s) | Swimming Speed (BL/s) | Swimming Mode |
|---|---|---|---|---|
| Robotic fish [25] | 0.55 | 0.13 | 0.76 | tethered |
| Robotic fish [26] | 6.0 | 0.70 | 2.0 | tethered |
| Robotic fish [27] | 2.4 | 0.17 | 0.54 | untethered |
| Robotic fish [28] | 2.2 | 0.47 | 1.04 | untethered |
| Our robotic dolphin | 2.88 | 0.74 | 1.12 | untethered |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Xiong, Y.; Wang, B.; Tong, R.; Meng, Y.; Yu, J. Performance Optimization for Bionic Robotic Dolphin with Active Variable Stiffness Control. Biomimetics 2023, 8, 545. https://doi.org/10.3390/biomimetics8070545
Chen D, Xiong Y, Wang B, Tong R, Meng Y, Yu J. Performance Optimization for Bionic Robotic Dolphin with Active Variable Stiffness Control. Biomimetics. 2023; 8(7):545. https://doi.org/10.3390/biomimetics8070545
Chicago/Turabian StyleChen, Di, Yan Xiong, Bo Wang, Ru Tong, Yan Meng, and Junzhi Yu. 2023. "Performance Optimization for Bionic Robotic Dolphin with Active Variable Stiffness Control" Biomimetics 8, no. 7: 545. https://doi.org/10.3390/biomimetics8070545
APA StyleChen, D., Xiong, Y., Wang, B., Tong, R., Meng, Y., & Yu, J. (2023). Performance Optimization for Bionic Robotic Dolphin with Active Variable Stiffness Control. Biomimetics, 8(7), 545. https://doi.org/10.3390/biomimetics8070545







