Abstract
To solve the problems of low convergence accuracy, slow speed, and common falls into local optima of the Chicken Swarm Optimization Algorithm (CSO), a performance enhancement strategy of the CSO algorithm (PECSO) is proposed with the aim of overcoming its deficiencies. Firstly, the hierarchy is established by the free grouping mechanism, which enhances the diversity of individuals in the hierarchy and expands the exploration range of the search space. Secondly, the number of niches is divided, with the hen as the center. By introducing synchronous updating and spiral learning strategies among the individuals in the niche, the balance between exploration and exploitation can be maintained more effectively. Finally, the performance of the PECSO algorithm is verified by the CEC2017 benchmark function. Experiments show that, compared with other algorithms, the proposed algorithm has the advantages of fast convergence, high precision and strong stability. Meanwhile, in order to investigate the potential of the PECSO algorithm in dealing with practical problems, three engineering optimization cases and the inverse kinematic solution of the robot are considered. The simulation results indicate that the PECSO algorithm can obtain a good solution to engineering optimization problems and has a better competitive effect on solving the inverse kinematics of robots.
1. Introduction
Swarm intelligence algorithms have been widely recognized since they were proposed in the 1990s [1]. They have a simple structure, good scalability, wide adaptability and strong robustness. Based on different biological habits and social behaviors, scholars have proposed numerous swarm intelligence algorithms, such as particle swarm optimization algorithm (PSO) [2], genetic algorithm (GA) [3], bat algorithm (BA) [4], social spider optimizer [5], CSO algorithm [6], moth–flame optimization algorithm (MFO) [7], whale optimization algorithm (WOA) [8], marine predators algorithm [9], battle royale optimization algorithm (BRO) [10], groundwater flow algorithm [11], egret swarm optimization algorithm [12], coati optimization algorithm [13], wild geese migration optimization algorithm [14], drawer algorithm [15], snake optimizer [16], fire hawk optimizer [17], etc. The algorithms are studied in terms of parameter set, convergence, topology and application. Among them, the CSO algorithm is a bionic swarm intelligent optimization technology proposed by Meng et al., named after the foraging behavior of chickens. Its main idea is to construct a random search method by simulating the behavior of roosters, hens and chicks in a chicken flock. On this basis, the optimization problem is solved through three chicken position update equations in the hierarchy. The principle of this algorithm is simple and easy to implement.
The algorithm has the advantages of simple principles, easy implementation and simple parameter setting. It has been widely used in the fields of trajectory optimization, economic dispatching, power system, image processing, wind speed prediction [18], and so on. For example, Mu et al. [19] used the CSO algorithm to optimize a robot trajectory for polishing a metal surface. The target of the optimization is to minimize the running time under kinematic constraints such as velocity and acceleration. Li et al. [20] applied a CSO algorithm to hypersonic vehicle trajectory optimization. Yu et al. [21] proposed a hybrid localization scheme for mine monitoring using a CSO algorithm and wheel graph, which minimized the inter-cluster complexity and improved the localization accuracy. Lin et al. [22] designed a CSO algorithm (GCSO) based on a high-efficiency graphics processing unit, which increased the population diversity and accelerated the convergence speed through parallel operations.
With the continuous expansion of application fields and the increase in problem complexity [23], the CSO algorithm has shown some deficiencies in solving these complex, high-dimensional problems, including low convergence accuracy and poor global exploration ability [24]. To solve these problems, many scholars have improved it, and now there are many variants of the CSO algorithm. In terms of initializing the population, the diversity of the population is enhanced by introducing a variety of strategies, such as chaos theory, mutation mechanisms, elimination–dispersion operations and deduplication factors [25,26], which are more conducive to finding the optimal solution to the problem. However, most means of improvement have been designed for individual update methods. Meng and Li [27] proposed to improve the CSO algorithm by using quantum theory to modify the update method of chicks. The algorithm was applied to the parameter optimization of the improved Dempster–Shafer structural probability fuzzy logic system, achieving good results for wind speed forecasting. Wang et al. [28] introduced an exploration–exploitation balance strategy in the CSO algorithm; 102 benchmark functions and two practical problems verified its excellent performance. Liang et al. [29] innovated an ICSO algorithm by using Lévy flight and nonlinear weight reduction to verify its outstanding performance in robot path planning. The other type is hybrid meta-heuristic algorithms, the combination of CSO with other algorithms. Wang et al. [30] provided an effective method to solve the multi-objective optimization problem based on an optimized CSO algorithm. The improved scheme includes dual external archives, a boundary learning strategy and fast, non-dominated sorting, and its superior performance has been verified by 14 benchmark functions. Li et al. [31] introduced the information-sharing strategy, spiral motion strategy and chaotic perturbation mechanisms into the CSO algorithm, which improved the identity of the photovoltaic model’s parameters. In addition, the combination of multiple algorithms is also a hot research topic. Deore et al. [32] integrated a chimp–CSO algorithm into the training of the network intrusion detection process. Torabi and Safi-Esfahani [33] combined the improved raven roosts optimization algorithm with the CSO algorithm to solve the task scheduling problem. Pushpa et al. [34] integrated a fractional artificial bee–CSO algorithm for virtual machine placement in the cloud. These hybrid algorithms have proved to have superior computational performance.
In summary, the CSO algorithm outperforms many naturally inspired algorithms for most benchmark functions and when solving practical problems. However, the “no free lunch theorem” shows that it is of great significance to further research the improvement of the CSO algorithm [35]. Therefore, an improved CSO algorithm with a performance-enhanced strategy is proposed, named the PECSO algorithm. It introduces the free grouping mechanism, synchronous updates and spiral learning strategy. The position updating method of the roosters, hens and chicks is redesigned.
The main contributions of this paper are summarized as follows:
- A hierarchy using a free grouping mechanism is proposed, which not only bolsters the diversity of individuals within this hierarchy but also enhances the overall search capability of the population;
- Synchronous updating and spiral learning strategies are implemented that fortify the algorithm’s ability to sidestep local optima. This approach also fosters a more efficient balance between exploitation and exploration;
- PECSO algorithm exhibits superior global search capability, faster convergence speed and higher accuracy, as confirmed by the CEC2017 benchmark function;
- The exceptional performance of the PECSO algorithm is further substantiated by its successful application to two practical problems.
The rest of this paper is organized as follows: Section 2 explains the foundational principles of the CSO algorithm. Section 3 introduces our proposed PECSO algorithm and elaborates on its various facets. In Section 4, we conduct benchmark function experiments using the PECSO algorithm. Section 5 demonstrates the resolution of two practical problems employing the PECSO algorithm. Finally, in Section 6, we provide a comprehensive summary of the paper, discuss the study’s limitations, and suggest directions for future research.
2. Chicken Swarm Optimization Algorithm
The classical CSO algorithm regards the solution of the problem as a source of food for chickens, and the fitness value in the algorithm represents the quality of the food. According to the fitness value, individuals in the chicken flock are sorted, and the flock is divided into several subgroups. Each subgroup divides the individuals into three levels: roosters, hens and chicks, and the proportions of roosters, hens and chicks are Nr, Nh and Nc, respectively.
In the algorithm, represents the position of the i-th chicken in the t-th iteration of the j-dimensional search space. The individuals with the lowest fitness value are selected as the roosters. The roosters walk randomly in the search space, and their position is updated, as shown in Equation (1).
where is a Gaussian distribution random number. The calculation of is shown in Equation (2).
Individuals with better fitness are selected as hens, which move following the rooster. The hen’s position is updated as shown in Equation (3).
where r1 is the individual rooster followed by the i-th hen. The r2 is a randomly selected rooster or hen (r2 ≠ r1). Calculate the weights and . and are fitness values corresponding to r1 and r2, respectively.
Except for the roosters and hens, other individuals are defined as chicks. The chicks follow their mother’s movement, and the chick’s position is updated, as shown in Equation (4).
where FL [0, 2], is the position of the i-th mother chick.
3. Improved CSO Algorithm
Many variants of the CSO algorithm have been proposed. However, slow convergence speed and falling into local optimization are still the main shortcomings of the CSO algorithm in solving practical optimization problems. Therefore, to improve the convergence accuracy and speed of the CSO algorithm, a better balance between exploitation and exploration has been achieved. In this paper, we propose the PECSO algorithm, which is based on a free grouping mechanism, synchronous update and spiral learning strategies. We present the PECSO algorithm in detail, give the mathematical model and pseudocode of the PECSO algorithm, and perform a time complexity analysis.
3.1. New Population Distribution
The hierarchy structure of the CSO algorithm is established by the fitness value, which is simple but suffers from the disadvantage of the low diversity of individuals in the hierarchy. Therefore, we introduced a free grouping mechanism to redesign the swarm hierarchy, which improves the diversity of individuals in different hierarchies of the algorithm. Firstly, the method freely divides the randomly initialized population into 0.5Nr groups. Within each group, roosters (nr), hens (nh) and chicks (nc) are selected based on the size of the fitness value. Secondly, multiple niches are established within the group, with the hens as the center and L as the radius, as shown in Equation (5). Finally, the hen summons her chicks within the niche, as shown in Equation (6). The population distribution state is formed as shown in Figure 1.
where / is the upper/lower boundary of the D-dimensional solution space. is the radius factor of the niche.
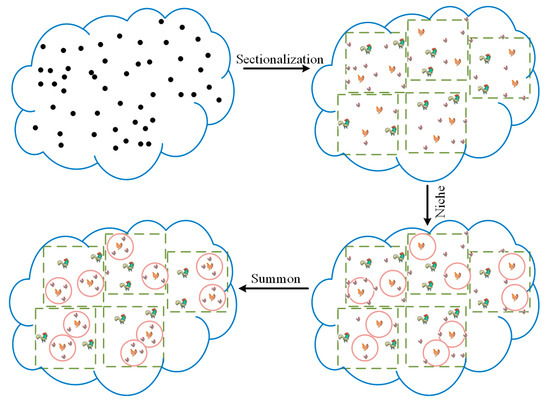
Figure 1.
Hierarchy distribution strategy based on the free grouping mechanism.
3.2. Individual Updating Methods
This subsection introduces several updating methods that we propose, including a best-guided search for roosters, a bi-objective search for hens and a simultaneous and spiral search for chicks.
3.2.1. Best-Guided Search for Roosters
Roosters are the leaders carrying the excellent message, and their selection and updating is important. Therefore, this paper proposes the best-guided search method for roosters. Specifically, we discarded the practice of selecting a single rooster in the traditional CSO algorithm and instead selected multiple individuals with better fitness values within the group as roosters. Meanwhile, the exploration is carried out with the goal of the global optimal individual (). The improved roosters can effectively utilize the historical experience of the population and have a stronger exploitation ability to overcome the problem of low convergence accuracy of the CSO algorithm. The updating step of the roosters is shown in Equation (7).
The updated position of the roosters is shown in Equation (8).
3.2.2. Bi-Objective Search for Hens
Hens are the middle level of the CSO population and should have both exploration and exploitation capabilities and coordinate the roles of both. On the one hand, they can inherit the excellent information of the rooster. On the other hand, they repel other hens and protect the chicks from being disturbed while performing their exploratory functions. On this basis, this paper reconsiders the search goal of hens and proposes a bi-objective search strategy. Specifically, (1) combining the current optimal solution position with the position of the optimal rooster r1 in the group realizes the full utilization of the optimal information and improves the exploitation ability of the hen. (2) Combining the position of rooster r2 within the group (r1 ≠ r2) with the hen positions within other niches. It enhances diversity and enables large-scale exploration. The updating step () of the hens is shown in Equation (9).
The updated position of the hens is shown in Equation (10).
where p [0, 1]. , , , are random numbers between 0 and 1. is a rooster indexed by a hen, is a randomly selected rooster (r2 ≠ r1), and is a competing hen (k ≠ h). and are the position of the i-th rooster and hen at the t-th iteration, respectively. (0, 1) is the moving step factor of the niche.
3.2.3. Simultaneous and Spiral Search for Chicks
The chicks are followers of the hen and develop excellent exploration abilities by observing and learning the exploration behavior of the hen. Based on this, we propose synchronous updating and spiral learning strategies for chicks. Synchronized updating means that all chicks follow the same direction and step size as the hen for updating movement within a niche. This method can ensure the consistency of the hen and the chicks in the niche, which enhances the local exploration ability and jointly explores the potential solution space. The process of synchronous update is shown in Figure 2. Spiral learning means that individual chicks can move towards the hen (central point) in the niche, and the step size is gradually reduced during the movement, thus searching for the optimum more accurately. Specifically, the distance between the current individual chick and the hen is calculated, and the spiral radius is determined according to certain rules. Afterwards, the chick’s position is updated through the spiral radius and angle increments, and the movement trajectory is shown in Figure 3. Compared with the traditional linear updating method, the spiral update can expand the updating dimension of the chick’s position, make it more diverse and enhance the exploration ability of the algorithm. Through the synergy of synchronous updating and spiral learning, we can obtain the spiral updating step of the chicks, as shown in Equation (11).
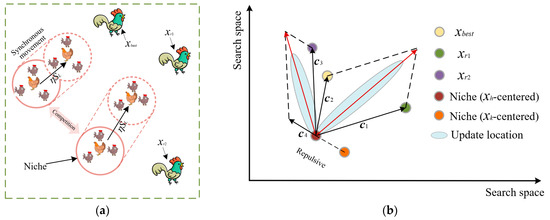
Figure 2.
Synchronous update process of individuals in the niche. (a) Synchronous update trajectory. (b) Synchronous update of the navigation map.
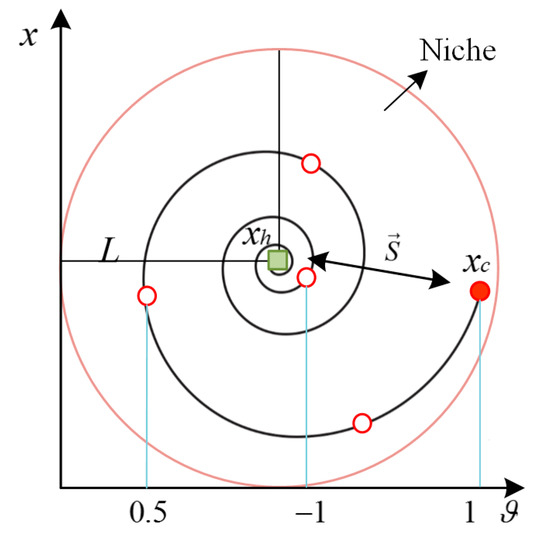
Figure 3.
Chick’s spiral update position.
The updated position of the chicks is shown in Equation (12).
where , = 1 is the logarithmic helix coefficient, and , (0, 1) is a random number.
3.3. The Implementation and Computational Complexity of PECSO Algorithm
3.3.1. The Implementation of PECSO Algorithm
The PECSO algorithm is used to optimize the diversity and update methods of individuals in different levels of the CSO algorithm. The specific pseudocode is given in Algorithm 1, and Figure 4 shows the flowchart of the PECSO algorithm.
| Algorithm 1: Pseudocode of PECSO algorithm |
| Initialize a population of N chickens and define the related parameters; While t < Gmax If (t % G == 0) Free grouping of populations and selection of roosters and hens within each group based on fitness values; Many niches are established with the hens as the center and L as the radius, according to Equations (5) and (6); Chicks are summoned by hens within the niche to recreate the hierarchy mechanism and to mark them. End if For i = 1: Nr Update the position of the roosters by Equation (8); End for For i = 1: Nh Synchronous update step of the niche is calculated by Equation (9); Update the position of the hens by Equation (10); End for For i = 1: Nc Spiral learning of chicks by Equation (11); Update the position of the chicks by Equation (12); End for Evaluate the new solution, and update them if they are superior to the previous ones; End while |
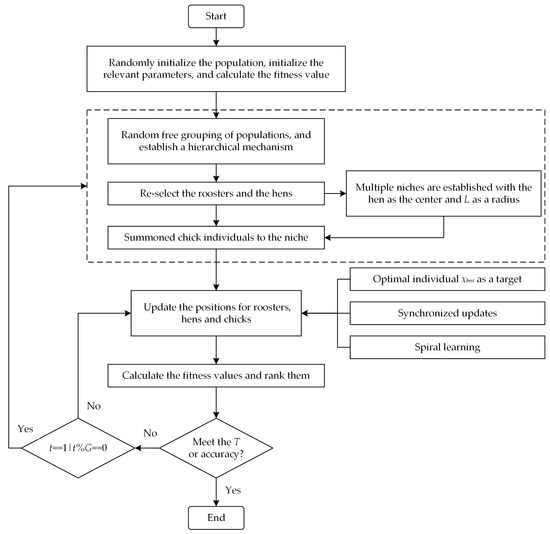
Figure 4.
Flowchart of the PECSO algorithm.
3.3.2. The Computational Complexity of PECSO Algorithm
The computational complexity refers to the amount of computational work required during the algorithm’s execution. It mainly depends on the number of problems executed repeatedly. The computational complexity of the PECSO algorithm is described by BigO notation. According to Algorithm 1, the population size, maximum number of iterations and dimension are represented by N, T and D, respectively.
The computational complexity of the CSO algorithm mainly includes population initialization , population update and regime update . Therefore, is shown in Equation (13).
The computational complexity of the PECSO algorithm mainly includes the population initialization , the position update of individuals within the population , and the establishment of hierarchy based on the free grouping strategies (messing up the order, free grouping, summoning chicks). Therefore, is shown in Equation (14).
It can be seen from Equations (13) and (14) that the computational complexity of the PECSO and CSO algorithms is of the same order of magnitude. However, the PECSO algorithm adds two steps in updating the hierarchical relationship every G time, including the disruption of the population order and the summoning of the chicks by the hens. Therefore, the computational complexity of the PECSO algorithm is slightly higher than the CSO algorithm.
4. Simulation Experiment and Result Analysis
In this section, first, we perform the experimental settings, including the selection of parameters and benchmark functions. Secondly, the qualitative analysis of the PECSO algorithm is carried out in terms of four indexes (2D search history, 1D trajectory, average fitness values and convergence curves). Finally, the computational performance of the PECSO algorithm is quantitatively analyzed and compared with the other seven algorithms, in which three measurement criteria, including mean, standard deviation (std) and time, are considered; the unit of time is seconds (s).
4.1. Experimental Settings
Parameters: the common parameters of all algorithms are set to the same, where N = 100, T = 500, D = 10, 30, 50. All common parameters of the CSO algorithm include , , , . Other main parameters of the algorithm are shown in Table 1. In addition, the experiment of each benchmark function is repeated 50 times to reduce the influence of random factors.

Table 1.
The main parameters of the 8 algorithms.
Benchmark Function: this paper selects the CEC2017 benchmark function for experiments (excluding F2) [36]. The unimodal functions (F1, F3) have only one extreme point in the search space, and it is difficult to converge to the global optimum. Therefore, the unimodal function is used to test the search accuracy. The multimodal functions (F4–F10) have multiple local extreme points, which can be used to test the global search performance. The hybrid functions (F11–F20) and composition functions (F21–F30) are a combination of unimodal and multimodal functions. More complex functions can further test the algorithm’s ability to balance exploration and exploitation.
4.2. Qualitative Analysis
The qualitative results of the PECSO algorithm are given in Figure 5, including the visualization of the benchmark function, the search history of the PECSO algorithm on the 2D benchmark test problem, the first-dimensional trajectory, the average fitness and the convergence curve. The discussion is as follows.
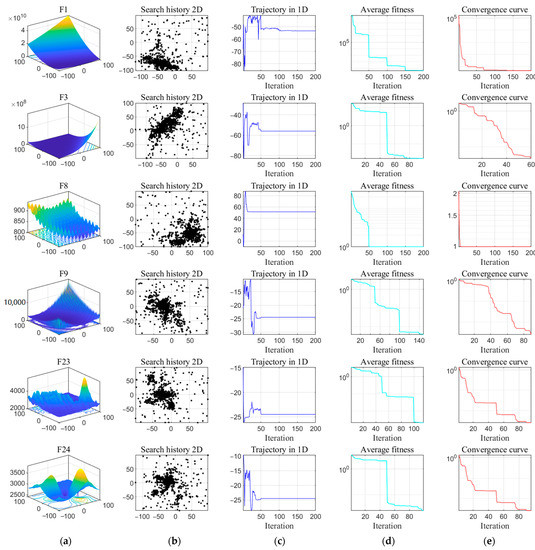
Figure 5.
Qualitative results of PECSO algorithm: (a) visual diagram; (b) search history; (c) trajectory; (d) average fitness; (e) convergence curve.
The second column of search history shows the location history information of each individual in the search space. It can be seen that the individuals are sparsely distributed in the search space, mostly clustered around the global optimal solution. This indicates that individuals reasonably cover a large area of the search space, and the PECSO algorithm has the exploration and exploitation abilities. However, the search history cannot show the exploratory order of individuals during the iterative process. Therefore, the third column gives the first-dimensional trajectory curves of representative individuals in each iteration. It shows the mutation of the individual during the initial iteration, which is gradually weakened throughout the iterations. According to references [37,38], this behavior ensures that the PECSO algorithm eventually converges to one point of the search space. The average fitness values and convergence curves are given in the fourth and fifth columns; it is known that the PECSO algorithm gradually approaches the optimal solution in the iterative process. Multiple convergence stages indicate that the PECSO algorithm can jump out of the local optimal value and search again, which shows that the PECSO algorithm has good local optimal avoidance ability and strong convergence ability. In brief, the PECSO algorithm effectively maintains a balance between exploitation and exploration, exhibiting advantages such as rapid convergence speed and robust global optimization capability.
4.3. Quantitative Analysis
This section compares the PECSO algorithm with the other seven algorithms, including PSO, CSO, MFO, WOA, and BRO, as well as the ICSO algorithm (ICSO1) proposed by Liang [29] and the improved CSO algorithm (ICSO2) proposed by Li [39], through the fitness value evaluation. The results are shown in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, and we can draw the following conclusions.

Table 2.
Results and comparison of all algorithms on unimodal and multimodal functions (D = 10).

Table 3.
Results and comparison of all algorithms on hybrid and composition functions (D = 10).

Table 4.
Results and comparison of all algorithms on unimodal and multimodal functions (D = 30).

Table 5.
Results and comparison of all algorithms on hybrid and composition functions (D = 30).

Table 6.
Results and comparison of all algorithms on unimodal and multimodal functions (D = 50).

Table 7.
Results and comparison of all algorithms on hybrid and composition functions (D = 50).
- From the unimodal and multimodal functions, we can find that the PECSO algorithm achieves the minimum mean and standard deviation. From the hybrid and composition functions, the PECSO algorithm obtained the best value of 80%. This shows that the PECSO algorithm has high convergence accuracy and strong global exploration ability, and its computing performance is more competitive;
- The experimental results show that the solving ability of unimodal and multimodal functions is not affected by dimensional changes, while hybrid and composite functions get more excellent computational results in higher dimensions. This indicates that the PECSO algorithm can balance the exploitation and exploration well and has a strong ability to jump out of the local optimum. The possible reason is that the free grouping mechanism improves the establishment of the hierarchy and increases the diversity of roosters in the population. Meanwhile, synchronous updating of individuals in niche and spiral learning of chicks can effectively improve the exploitation breadth and exploration depth of the PECSO algorithm;
- The running time of the PECSO algorithm is slightly higher than that of the CSO algorithm, but they have the same order of magnitude. It shows that the PECSO algorithm effectively improves computational performance;
- We rank the test results of all algorithms on the benchmark function, and the average value is the indicator. Figure 6 finds that the convergence results of the PECSO algorithm are outstanding in different test dimensions.
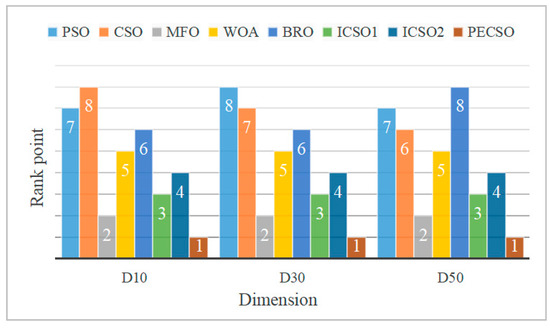 Figure 6. Average ranking of 8 algorithms in different dimensions.
Figure 6. Average ranking of 8 algorithms in different dimensions.
The box plots of the eight algorithms for some benchmark functions (D = 30, independent experiments 50 times) are given in Figure 7. The solid line in the middle of each box represents the median fitness value, and the shorter the box and whiskers, the more concentrated the convergence results. It can be seen that the PECSO algorithm has strong stability.
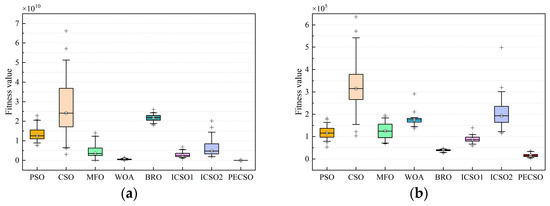
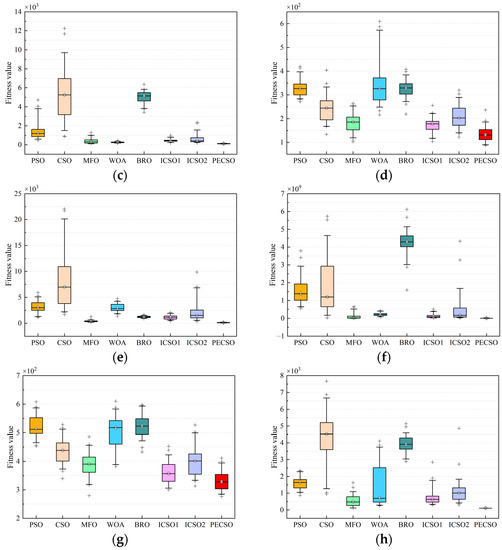
Figure 7.
Box plots of 8 algorithms on some benchmark functions, the functions are selected as (a) F1; (b) F3; (c) F4; (d) F5; (e) F11; (f) F12; (g) F21; (h) F22.
Figure 8 shows the convergence curves on some benchmark functions in the case of D = 30. Figure 8a–d shows the convergence curves of the PECSO algorithm on some unimodal and multimodal functions, which achieve the best convergence accuracy and speed. The convergence curves of the PECSO algorithm on some hybrid and composite functions are given in Figure 8f–h. In fact, there are 20 functions of this type, and the PECSO algorithm has achieved the best convergence effect on 17 benchmark functions, ranking second on three functions (F20, F23, F26). This further demonstrates the excellent convergence capability of the PECSO algorithm.
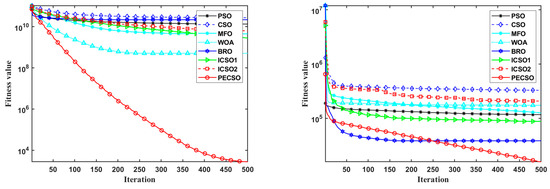
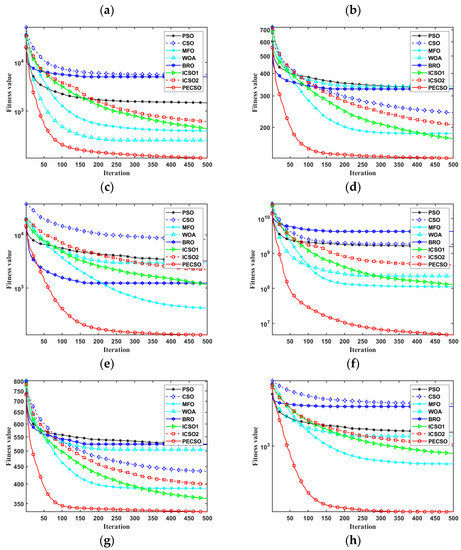
Figure 8.
Average convergence results of 8 algorithms on benchmark functions, the functions are selected as (a) F1; (b) F3; (c) F4; (d) F5; (e) F11; (f) F12; (g) F21; (h) F22.
5. Case Analysis of Practical Application Problems
In this section, we further investigate the performance of the PECSO algorithm by solving three classical engineering optimization problems and robot inverse kinematics. Moreover, compared with other algorithms reported in the literature.
5.1. Engineering Optimization Problems
This section selects three classical engineering application problems to test the computational potential of the PECSO algorithm in dealing with practical problems. This mainly includes the three-bar truss design [40], pressure vessel design [41] and tension/compression spring design [42]; the constraint design can be regarded as the optimal solution of the function F31, F32 and F33. For details, refer to Table 8. Their structures are shown in Figure 9.

Table 8.
The basic information of the engineering optimization problem.
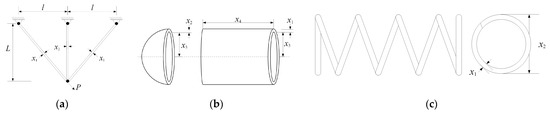
Figure 9.
The schematic of three engineering optimization problems: (a) three-bar truss; (b) pressure vessel; (c) tension/compression spring.
Table 9 shows the statistical results of the three engineering optimization problems. The PECSO algorithm performs better than the CSO algorithm on three engineering optimization problems, and the results are compared with those of the FCSO algorithm in reference [43]. The results obtained by the PECSO algorithm are within the scope of practical applications and meet the constraint requirements. Meanwhile, the PECSO algorithm shows excellent applicability and stability in engineering optimization problems.

Table 9.
Statistical results of three engineering optimization problems.
5.2. Solve Inverse Kinematics of PUMA 560 Robot
In this section, the PECSO algorithm is used to solve the inverse kinematics of the PUMA 560 robot, which includes the kinematics modeling, the establishment of the objective function and the simulation experiment.
5.2.1. Kinematic Modeling and Objective Function Establishment
The kinematic modeling of the robots involves establishing a coordinate system on each link of the kinematic chain, refer to Figure 10. The posture of the robot end effector is described in cartesian space by a homogeneous transformation. The kinematic equation is shown in Equation (15).
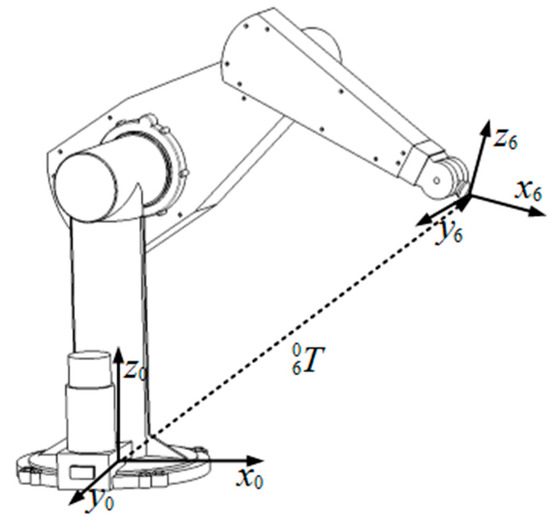
Figure 10.
Kinematic chains solid shape of PUMA 560 robot joints.
The coordinate transformation relationship between adjacent links in the robot kinematic chain is obtained by the Denavit–Hartenberg (D-H) parameter method [10], as shown in Equation (16).
The positive kinematics equation of the PUMA 560 robot can be obtained by the combination of Equations (15) and (16), as shown in Equation (17) [44].
where, and represent rotational elements of the pose matrix, and represents the elements of the position vector.
The objective function of the solution is the Euclidean distance between the desired and actual end positions, as shown in Equation (18).
where represents the desired position, and represents the actual position.
Each joint variable needs to meet a different boundary constraint range, which is restricted by the mechanical principle of the robot, as shown in Equation (19).
where / represents the upper/lower limits of the i-th joint variable, respectively. The specific values are shown in Table 10.

Table 10.
D-H parameters of PUMA 560 robot.
5.2.2. Simulation Experiment and Analysis
The simulation experiment for solving inverse kinematics is carried out by the PECSO and CSO algorithms. The test point is a randomly selected end position within the range of movement of the PUMA 560 robot. The relevant parameter settings are the same as in Section 4.1, and the experimental results are shown in Table 11; among them, the results of the BRO algorithm are taken from reference [10]. The results show that the PECSO algorithm has higher solution accuracy than the CSO and BRO algorithms, which also indicates that the PECSO algorithm is feasible for solving the robot kinematic inverse. Moreover, with the increase in the N and the T, the computational performance of all algorithms is gradually enhanced. We find that the change of the T has a greater impact on the calculation results.

Table 11.
Comparison results for inverse kinematics of PUMA 560 robot.
6. Conclusions
This paper proposes a CSO algorithm with a performance-enhanced strategy. The algorithm utilizes a free grouping mechanism to establish a hierarchy and select the roosters and hens. Establishing a niche centered around hens and gathering chicks. Roosters are updated with the goal of global optimum, and hens and chicks are updated synchronously in the niche. To increase exploration capability, chicks also perform spiral learning. They improve the singularity of rooster selection and the simplicity of individual position updating and effectively enhance the overall performance of the CSO algorithm. In the simulation, 29 benchmark functions are utilized to verify that the PECSO algorithm has outstanding performance in comparison with the other seven algorithms. In addition, three engineering optimization problems and PMUA 560 robot inverse kinematics solutions are solved based on the PECSO algorithm. It shows that the PECSO algorithm has excellent universality in complex practical problems and has certain practicability and development prospects in solving optimization problems.
The high-performance PECSO algorithm is of great significance for solving complex problems, improving search efficiency, enhancing robustness and adapting to dynamic environments. However, there are still some limitations. From the qualitative analysis, it can be found that the running time of the PECSO algorithm is slightly higher than that of the CSO algorithm. When dealing with large-scale data and complex problems, it may lead to an increase in computational complexity, and the running time of the PECSO algorithm will also increase, which may result in a large distance from the CSO algorithm in terms of running time. Next, to obtain better results, we can focus our main research direction on reducing the computational complexity of the algorithms.
Author Contributions
Conceptualization, Y.Z.; methodology, Y.Z.; software, Y.Z.; validation, Y.Z.; data curation, Y.Z.; resources, Y.Z.; writing—original draft preparation, Y.Z., L.W. and J.Z.; writing—review and editing, Y.Z., L.W. and J.Z.; supervision, J.Z.; project administration, L.W.; funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Social Science Fund of China under Grant No. 22BTJ057.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included within the article and are also available from the corresponding authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, N.; Shaikh, A.A.; Mahato, S.K.; Bhunia, A.K. Applications of new hybrid algorithm based on advanced cuckoo search and adaptive Gaussian quantum behaved particle swarm optimization in solving ordinary differential equations. Expert Syst. Appl. 2021, 172, 114646. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer: Cham, Switzerland, 2019; Volume 780, pp. 43–55. [Google Scholar]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). In Studies in Computational Intelligence; González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284, pp. 65–74. [Google Scholar]
- Cuevas, E.; Cienfuegos, M.; Zaldívar, D.; Pérez-Cisneros, M. A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Syst. Appl. 2013, 40, 6374–6384. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A new bio-inspired algorithm: Chicken swarm optimization. In Proceedings of the International Conference in Swarm Intelligence, Hefei, China, 17–20 October 2014; pp. 86–94. [Google Scholar]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine predators algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Rahkar Farshi, T. Battle royale optimization algorithm. Neural Comput. Appl. 2021, 33, 1139–1157. [Google Scholar] [CrossRef]
- Guha, R.; Ghosh, S.; Ghosh, K.K.; Cuevas, E.; Perez-Cisneros, M.; Sarkar, R. Groundwater flow algorithm: A novel hydro-geology based optimization algorithm. IEEE Access 2022, 10, 132193–132211. [Google Scholar] [CrossRef]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Song, L.; Zhang, Y.; Gu, L.; Zhao, X. Wild Geese Migration Optimization Algorithm: A New Meta-Heuristic Algorithm for Solving Inverse Kinematics of Robot. Comput. Intel. Neurosc. 2022, 2022, 5191758. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Leiva, V. Drawer Algorithm: A New Metaheuristic Approach for Solving Optimization Problems in Engineering. Biomimetics 2023, 8, 239. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Azizi, M.; Talatahari, S.; Gandomi, A.H. Fire Hawk Optimizer: A novel metaheuristic algorithm. Artif. Intell. Rev. 2023, 56, 287–363. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, F.; Liu, H.; Ding, J.; Gao, C. Interruptible load scheduling model based on an improved chicken swarm optimization algorithm. CSEE J. Power Energy 2020, 7, 232–240. [Google Scholar]
- Mu, Y.; Zhang, L.; Chen, X.; Gao, X. Optimal trajectory planning for robotic manipulators using chicken swarm optimization. In Proceedings of the 2016 8th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 27–28 August 2016; Volume 2, pp. 369–373. [Google Scholar]
- Li, Y.; Wu, Y.; Qu, X. Chicken swarm–based method for ascent trajectory optimization of hypersonic vehicles. J. Aerosp. Eng. 2017, 30, 04017043. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, L.; Li, X. A novel hybrid localization scheme for deep mine based on wheel graph and chicken swarm optimization. Comput. Netw. 2019, 154, 73–78. [Google Scholar] [CrossRef]
- Lin, M.; Zhong, Y.; Chen, R. Graphic process units-based chicken swarm optimization algorithm for function optimization problems. Concurr. Comput. Pract. Exp. 2021, 33, e5953. [Google Scholar] [CrossRef]
- Li, M.; Bi, X.; Wang, L.; Han, X.; Wang, L.; Zhou, W. Text Similarity Measurement Method and Application of Online Medical Community Based on Density Peak Clustering. J. Organ. End User Comput. 2022, 34, 1–25. [Google Scholar] [CrossRef]
- Zouache, D.; Arby, Y.O.; Nouioua, F.; Abdelaziz, F.B. Multi-objective chicken swarm optimization: A novel algorithm for solving multi-objective optimization problems. Comput. Ind. Eng. 2019, 129, 377–391. [Google Scholar] [CrossRef]
- Ahmed, K.; Hassanien, A.E.; Bhattacharyya, S. A novel chaotic chicken swarm optimization algorithm for feature selection. In Proceedings of the 2017 Third International Conference on Research in Computational Intelligence and Communication Networks, Kolkata, India, 3–5 November 2017; pp. 259–264. [Google Scholar]
- Deb, S.; Gao, X.Z.; Tammi, K.; Kalita, K.; Mahanta, P. Recent studies on chicken swarm optimization algorithm: A review (2014–2018). Artif. Intell. Rev. 2020, 53, 1737–1765. [Google Scholar] [CrossRef]
- Meng, X.B.; Li, H.X. Dempster-Shafer based probabilistic fuzzy logic system for wind speed prediction. In Proceedings of the 2017 International Conference on Fuzzy Theory and Its Applications, Pingtung, Taiwan, 12–15 November 2017; pp. 1–5. [Google Scholar]
- Wang, Y.; Sui, C.; Liu, C.; Sun, J.; Wang, Y. Chicken swarm optimization with an enhanced exploration–exploitation tradeoff and its application. Soft Comput. 2023, 27, 8013–8028. [Google Scholar] [CrossRef]
- Liang, X.; Kou, D.; Wen, L. An improved chicken swarm optimization algorithm and its application in robot path planning. IEEE Access 2020, 8, 49543–49550. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Guo, Y.; Han, M.; Wan, B.; Liang, S. A multi-objective chicken swarm optimization algorithm based on dual external archive with various elites. Appl. Soft Comput. 2023, 133, 109920. [Google Scholar] [CrossRef]
- Li, M.; Li, C.; Huang, Z.; Huang, J.; Wang, G.; Liu, P.X. Spiral-based chaotic chicken swarm optimization algorithm for parameters identification of photovoltaic models. Soft Comput. 2021, 25, 12875–12898. [Google Scholar] [CrossRef]
- Deore, B.; Bhosale, S. Hybrid Optimization Enabled Robust CNN-LSTM Technique for Network Intrusion Detection. IEEE Access 2022, 10, 65611–65622. [Google Scholar] [CrossRef]
- Torabi, S.; Safi-Esfahani, F. A dynamic task scheduling framework based on chicken swarm and improved raven roosting optimization methods in cloud computing. J. Supercomput. 2018, 74, 2581–2626. [Google Scholar] [CrossRef]
- Pushpa, R.; Siddappa, M. Fractional Artificial Bee Chicken Swarm Optimization technique for QoS aware virtual machine placement in cloud. Concurr. Comput. Pract. Exp. 2023, 35, e7532. [Google Scholar] [CrossRef]
- Adam, S.P.; Alexandropoulos, S.A.N.; Pardalos, P.M.; Vrahatis, M.N. No free lunch theorem: A review. In Approximation and Optimization: Algorithms, Complexity and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 57–82. [Google Scholar]
- Chhabra, A.; Hussien, A.G.; Hashim, F.A. Improved bald eagle search algorithm for global optimization and feature selection. Alex. Eng. J. 2023, 68, 141–180. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inform. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Osuna-Enciso, V.; Cuevas, E.; Castañeda, B.M. A diversity metric for population-based metaheuristic algorithms. Inform. Sci. 2022, 586, 192–208. [Google Scholar] [CrossRef]
- Li, Y.C.; Wang, S.W.; Han, M.X. Truss structure optimization based on improved chicken swarm optimization algorithm. Adv. Civ. Eng. 2019, 2019, 6902428. [Google Scholar] [CrossRef]
- Xu, X.; Hu, Z.; Su, Q.; Li, Y.; Dai, J. Multivariable grey prediction evolution algorithm: A new metaheuristic. Appl. Soft Comput. 2020, 89, 106086. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovský, P. Serval Optimization Algorithm: A New Bio-Inspired Approach for Solving Optimization Problems. Biomimetics 2022, 7, 204. [Google Scholar] [CrossRef] [PubMed]
- Trojovský, P.; Dehghani, M. Subtraction-Average-Based Optimizer: A New Swarm-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 149. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, C.; Wan, B. An Adaptive Fuzzy Chicken Swarm Optimization Algorithm. Math. Probl. Eng. 2021, 2021, 8896794. [Google Scholar] [CrossRef]
- Lopez-Franco, C.; Hernandez-Barragan, J.; Alanis, A.Y.; Arana-Daniel, N. A soft computing approach for inverse kinematics of robot manipulators. Eng. Appl. Artif. Intell. 2018, 74, 104–120. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).