Application of an Enhanced Whale Optimization Algorithm on Coverage Optimization of Sensor
Abstract
1. Introduction
1.1. Wireless Sensor Network Coverage Model
1.2. Overview of Whale Optimization Algorithm (WOA)
1.3. The Lévy Flight Method
1.4. Genetic Algorithm
2. Proposed WOA-LFGA
2.1. Initialization Based on Chaotic Map
2.2. Enhanced Exploitation Phase
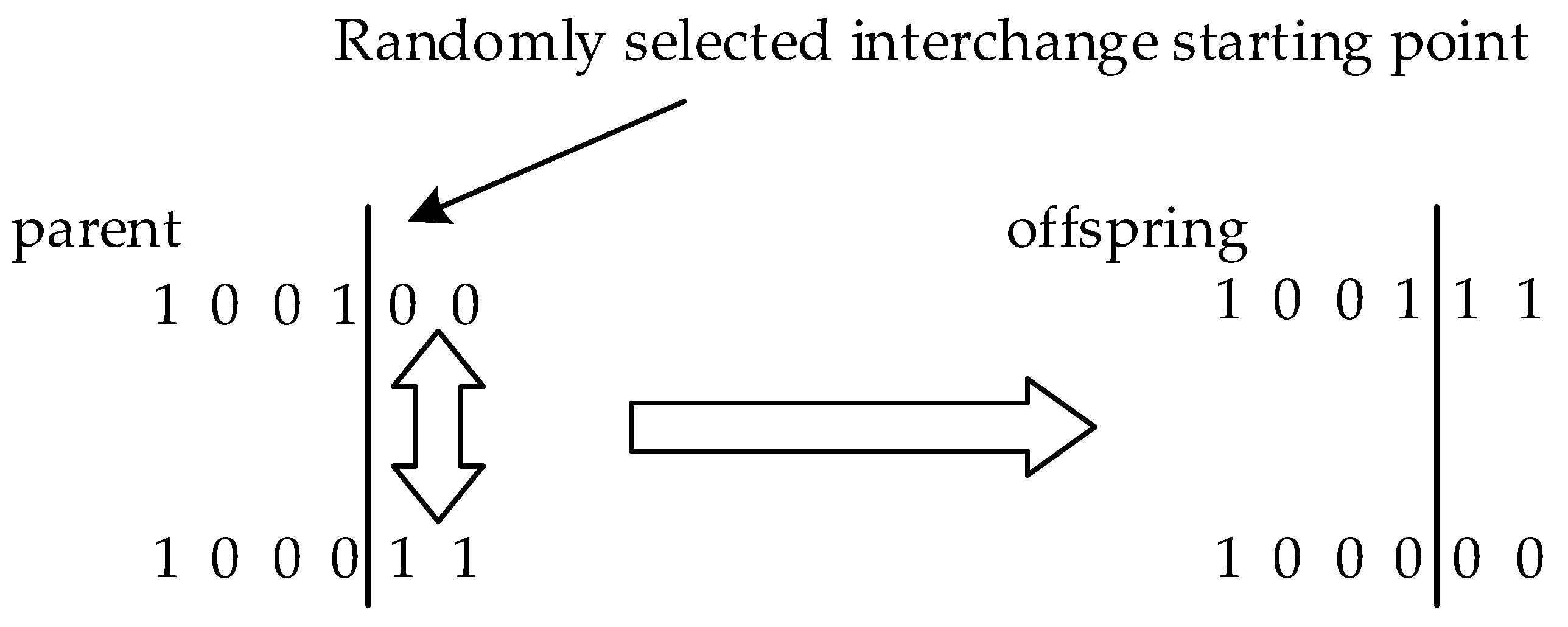
2.3. An Improved Method Based on Genetic Algorithm
2.4. Boundary Processing Strategy
| Algorithm 1: WOA-LFGA |
| Input: Fitness function Output: Available optimal solution (i) Initialization process Step1: Initialize parameter and variable values used in the algorithm. Step2: Initialize the whales population X = Xi (i = 1, 2,…, N) using chaotic mapping by Equation (19). Step3: Calculate the fitness for X and select the best individual and assign it to X*. Step4: Set the iteration counter to t = 0. (ii) Iterative process Step5: While t < maxiter, Do. Step6: Update the position for Xi by Equation (7) (if p < 0.5 and |A| < 1) or Equation (14) (if p < 0.5 and |A| ≥ 1) or Equation (12) (if p ≥ 0.5). Step7: Select the best 10% and the worst 20% of individuals and use crossover and mutation strategies to update individuals for the worst 20% based on the best 10% of individuals. Step8: Return the search agents that go beyond the boundaries of the search space using Equation (22). Step9: Calculate the fitness for X and update X* if there is a better solution. Step10: Iterate the counter t = t + 1. End. (iii) Results obtained Step11: Output the best agent X*. The end. |
3. Results and Discussion
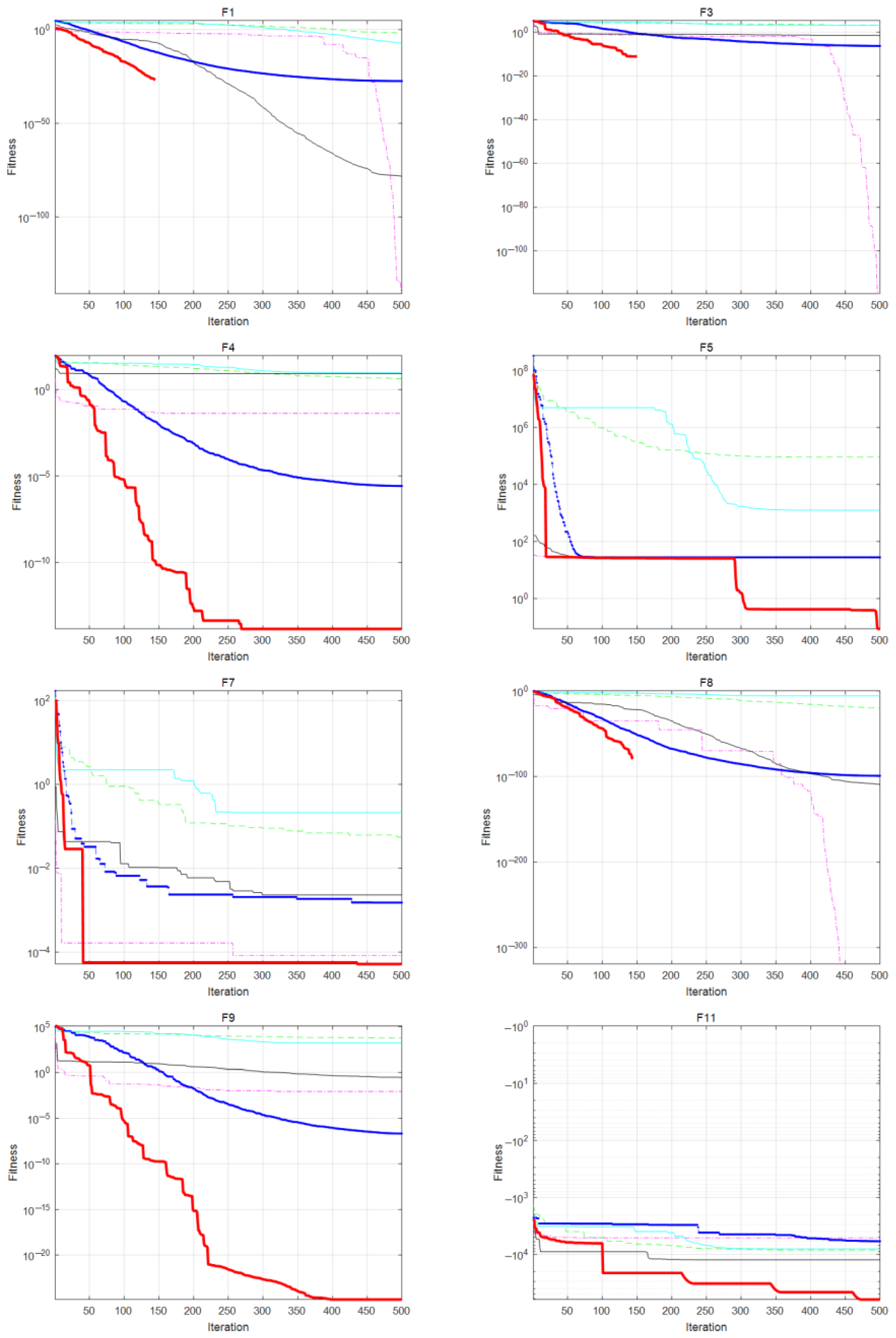
3.1. WOA-LFGA for Function Optimization
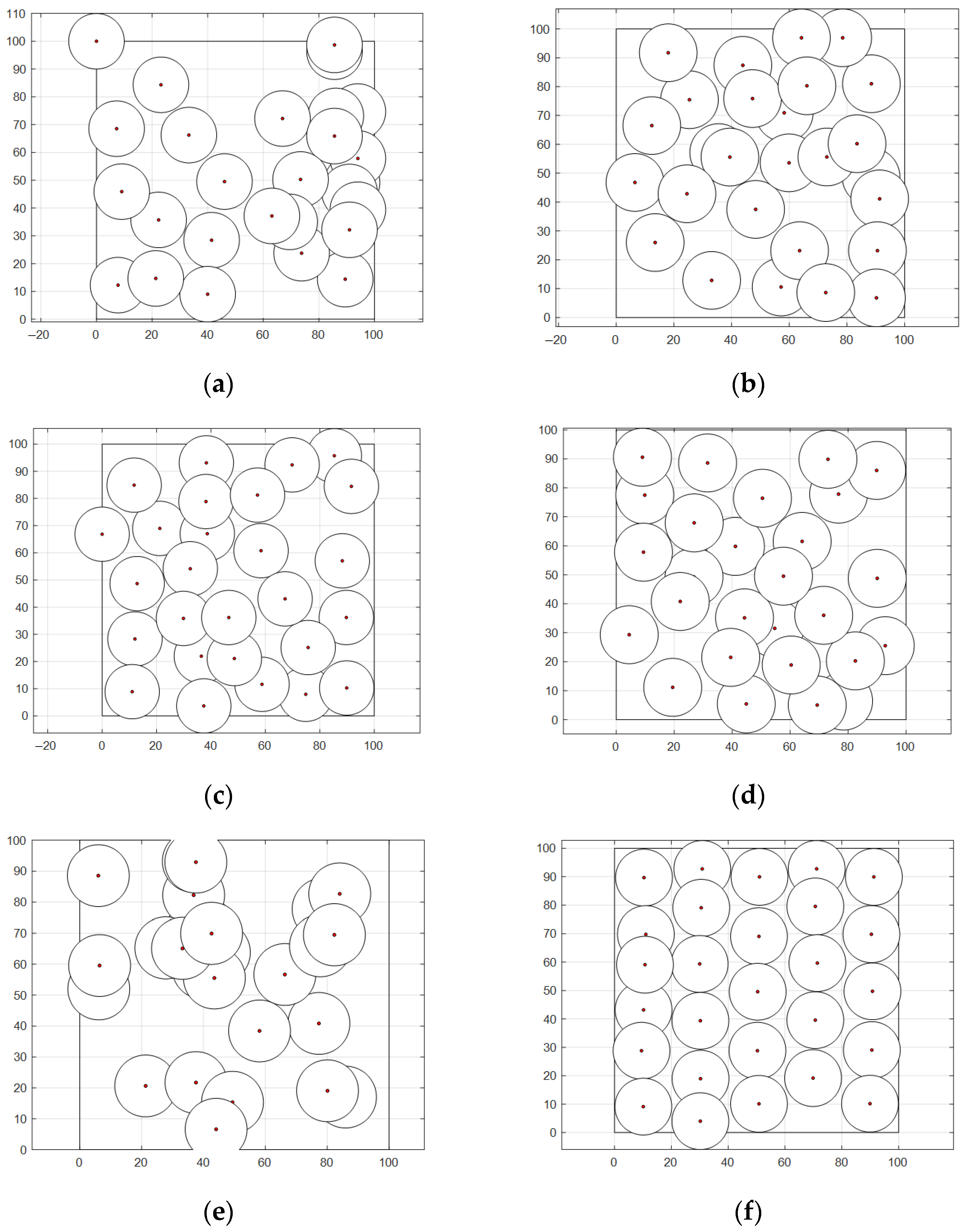
3.2. WOA-LFGA for WSN Coverage Optimization Problem
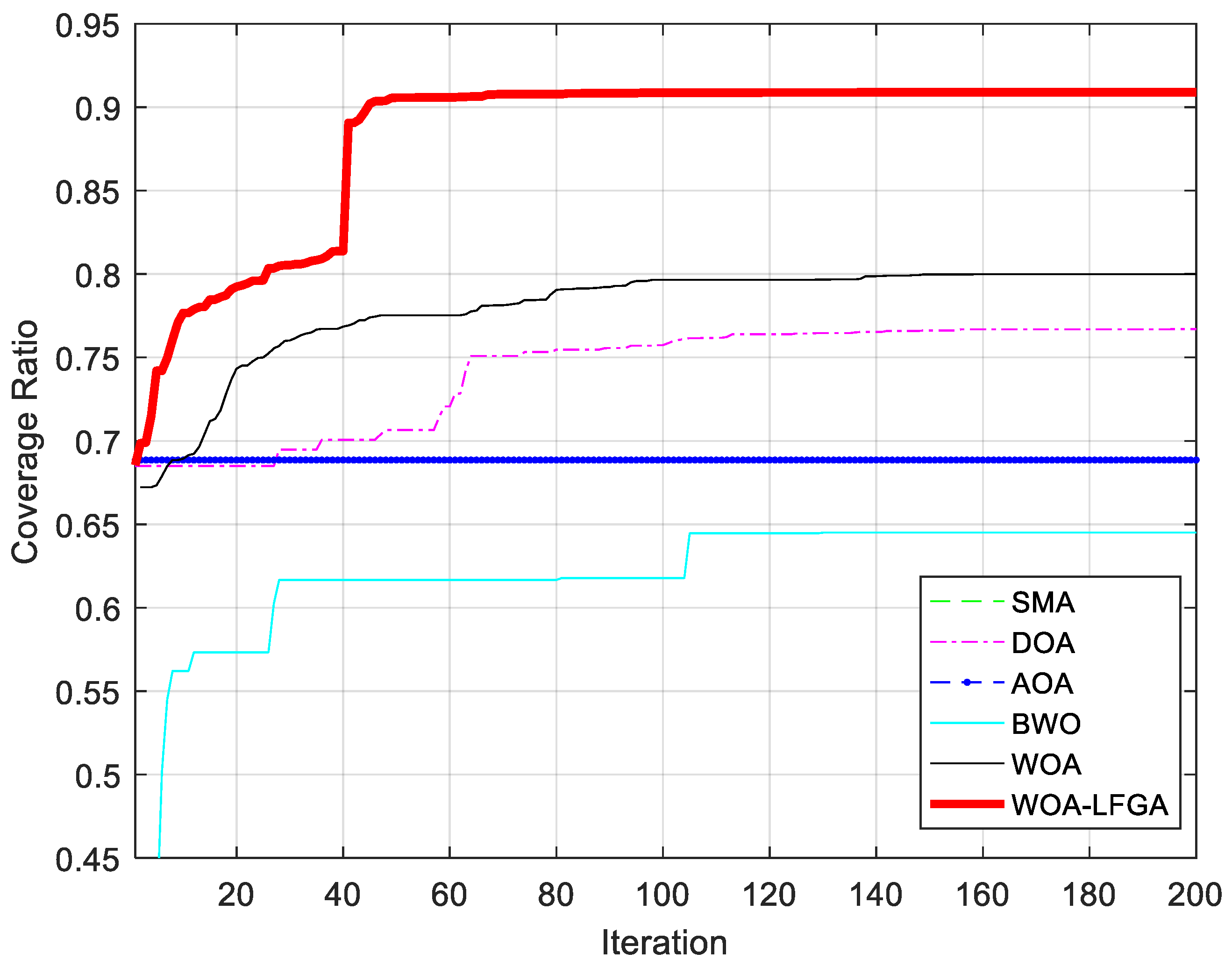
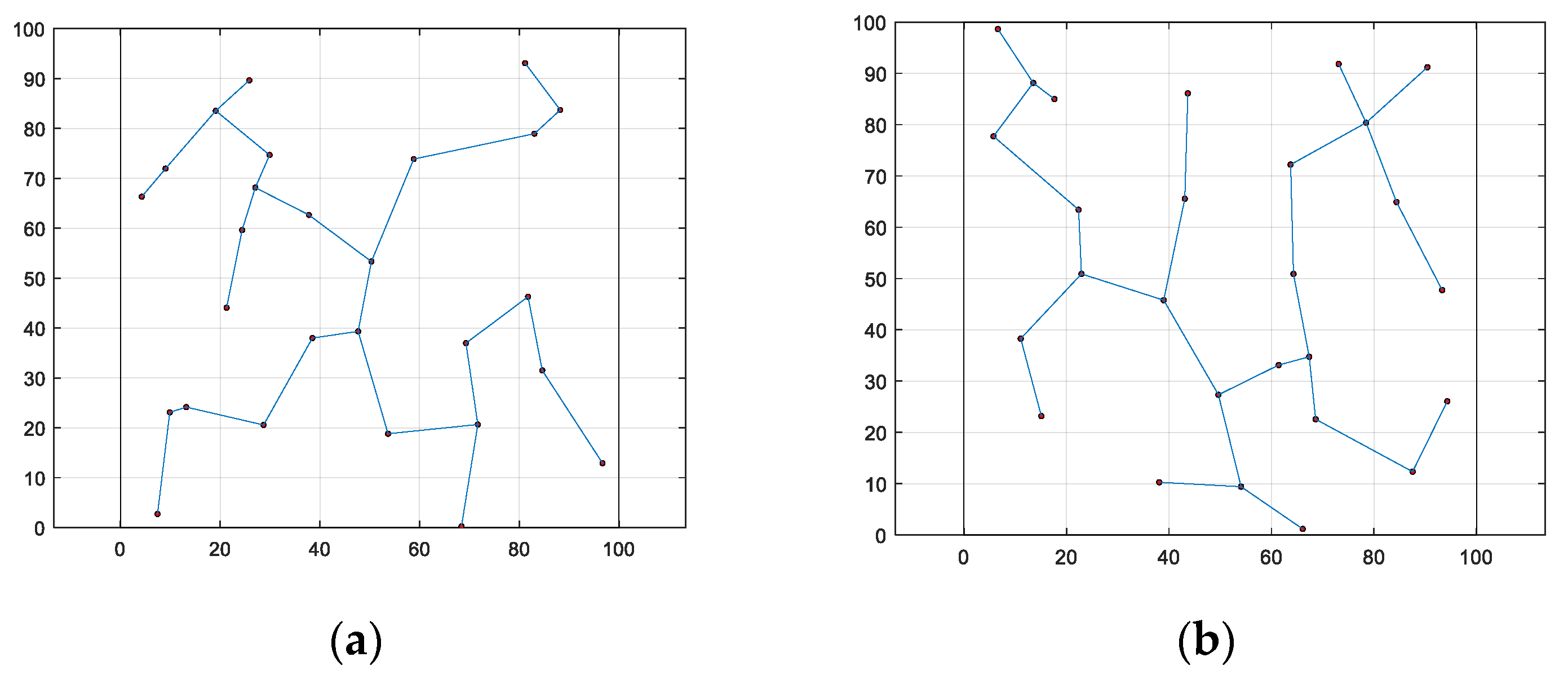
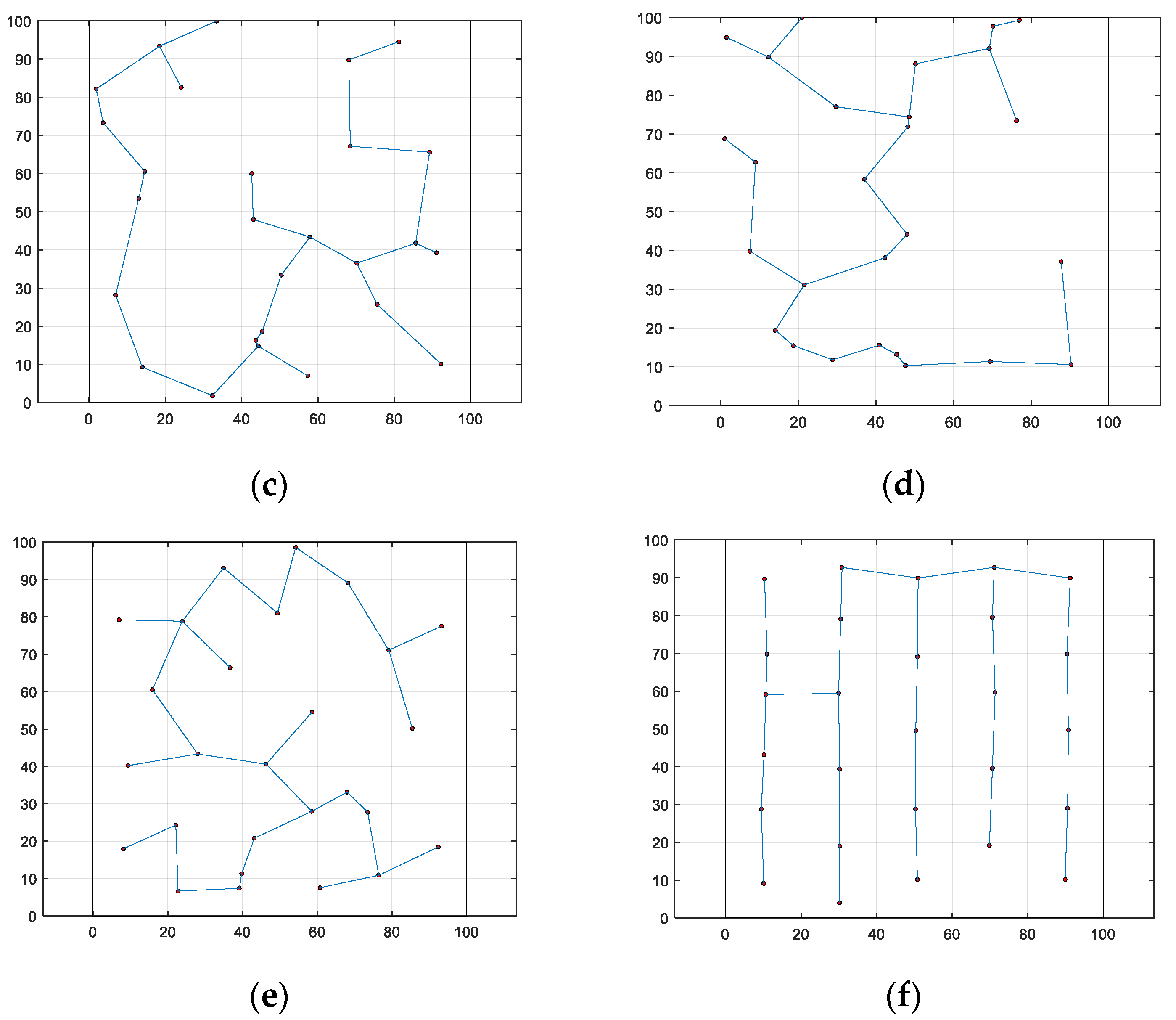
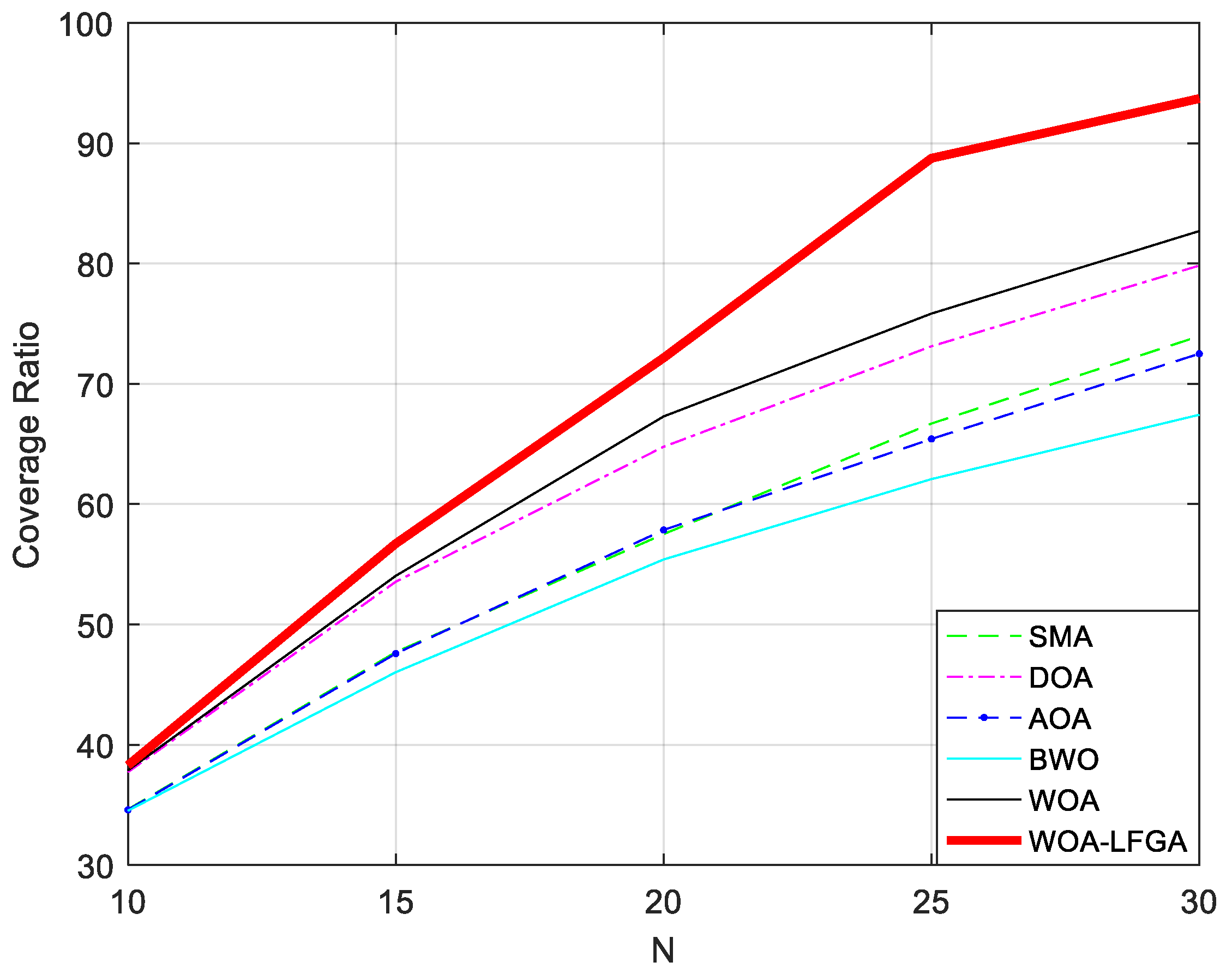
3.2.1. Comparison of WOA-LFGA with Other Basic Algorithms
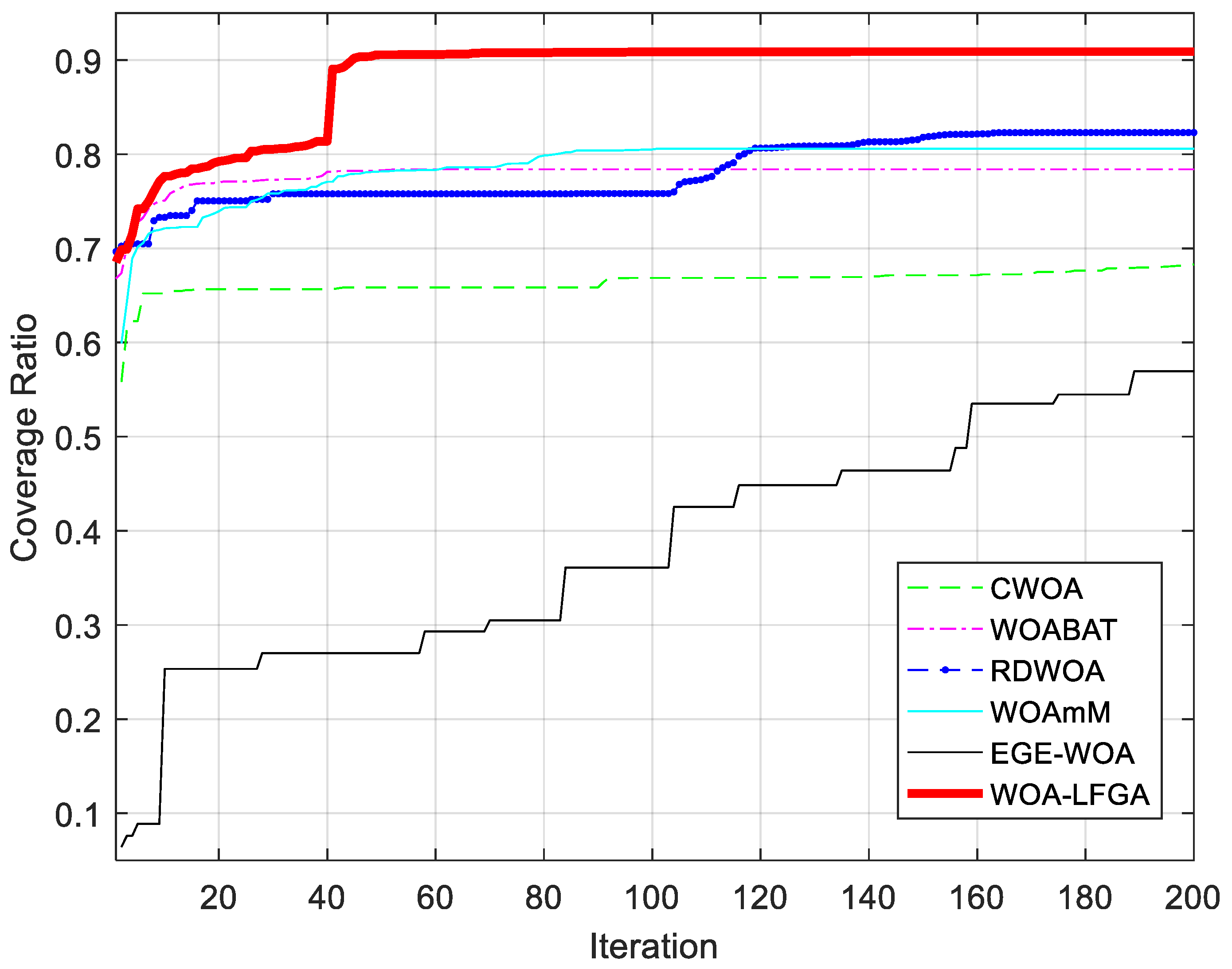
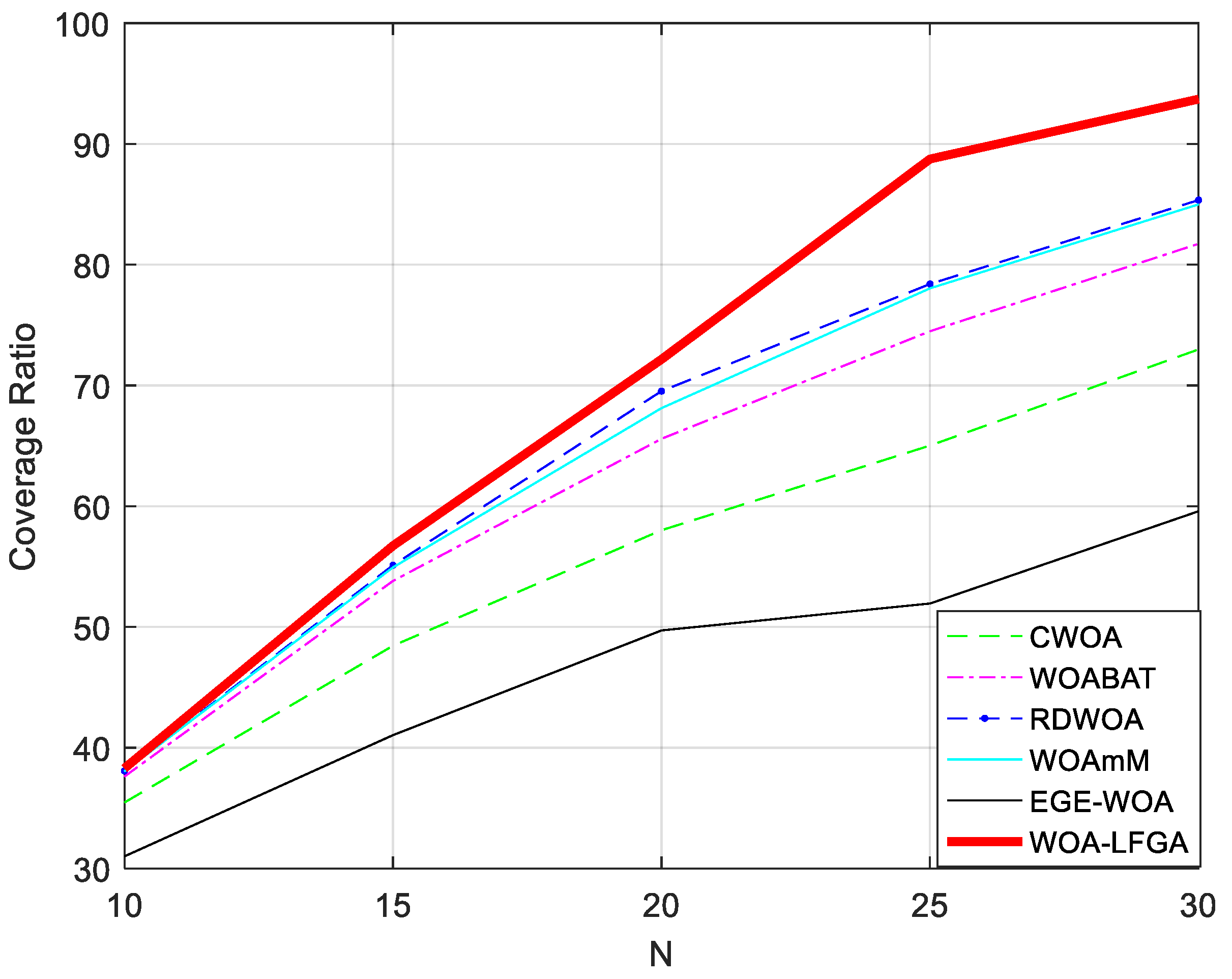
3.2.2. Comparison of WOA-LFGA with Different Modified WOA
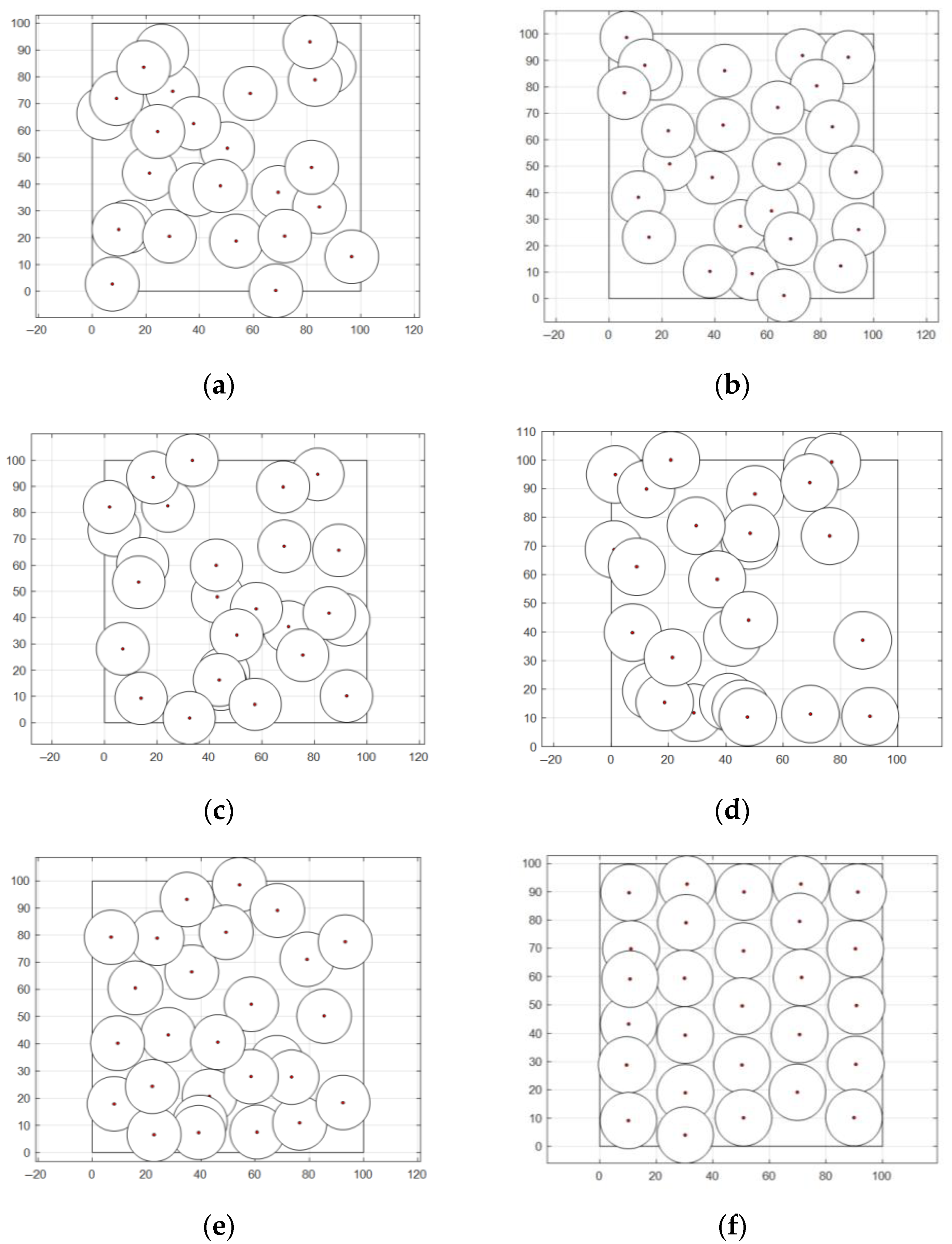
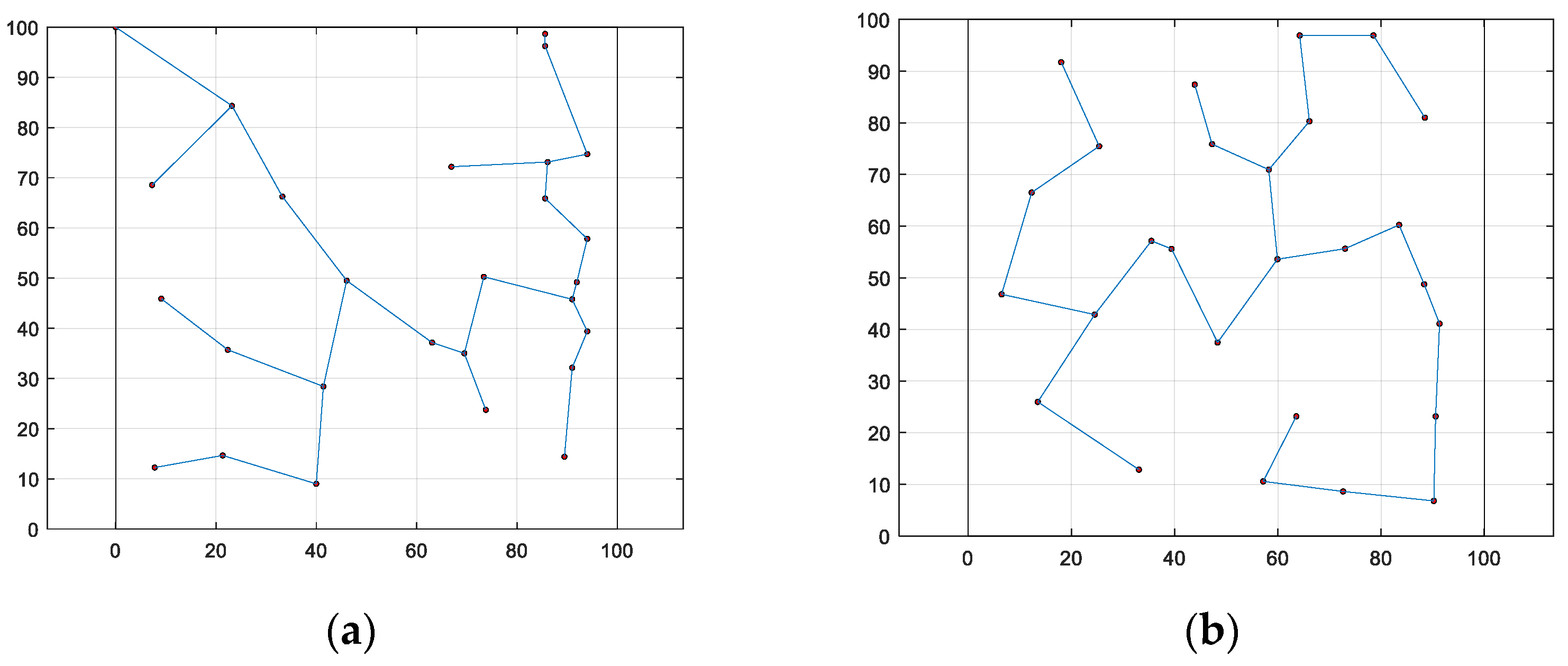
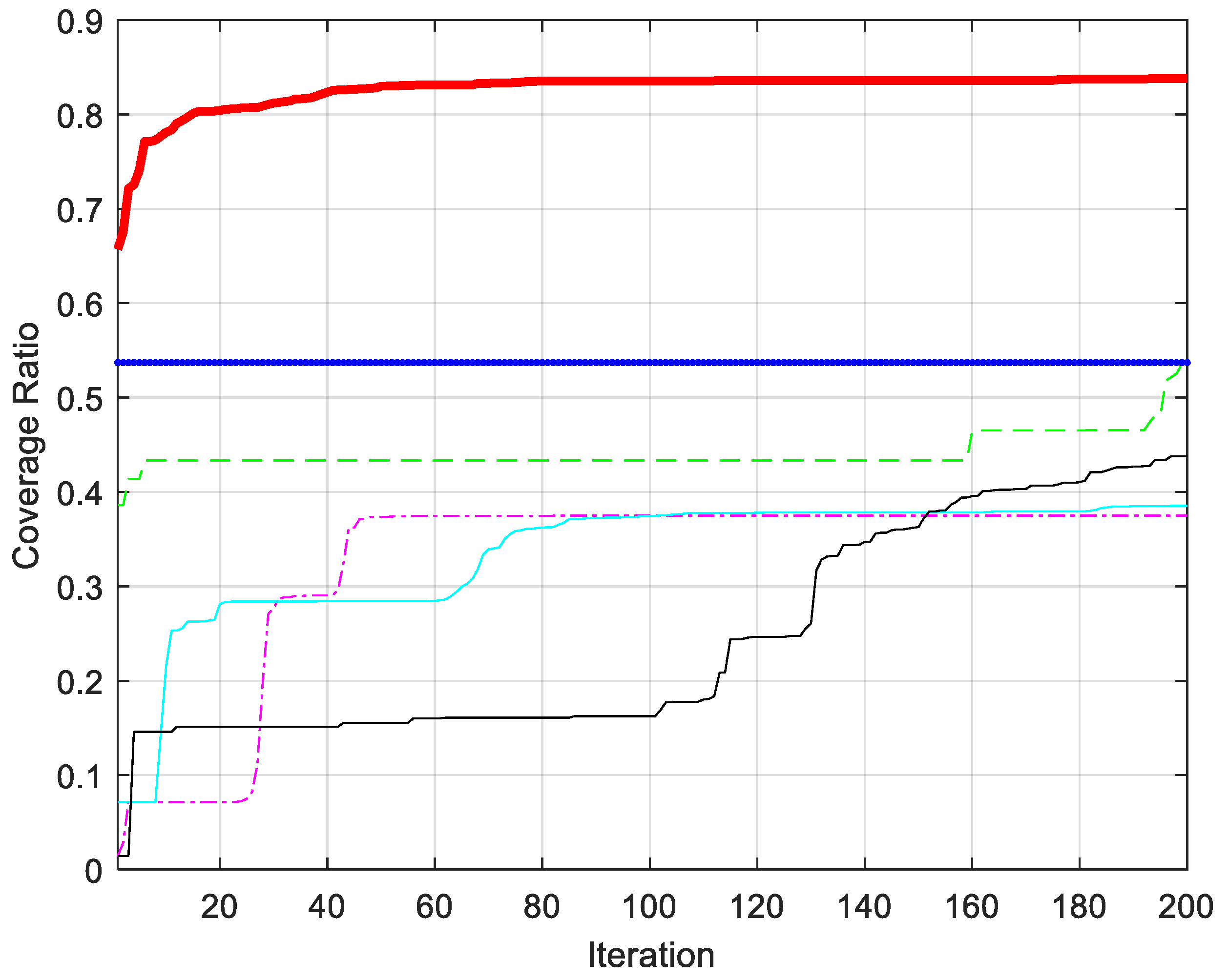
3.3. WOA-LFGA for WSN Coverage Practical Application
3.3.1. Comparison of WOA-LFGA with Other Basic Algorithms
3.3.2. Comparison of WOA-LFGA with Different Modified WOA
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Mukherjee, M.; Adhikary, I.; Mondal, S.; Mondal, A.K.; Pundir, M.; Chowdary, V. Vision of IoT: Applications, Challenges, and Opportunities with Dehradun Perspective. In Proceeding of International Conference on Intelligent Communication, Control and Devices; Advances in Intelligent Systems and Computing; Springer: Singapore, 2017. [Google Scholar]
- Da Xu, L.; He, W.; Li, S. Internet of Things in Industries: A Survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar]
- Zhao, X.; Askari, H.; Chen, J. Nanogenerators for smart cities in the era of 5G and Internet of Things. Joule 2021, 5, 1391–1431. [Google Scholar] [CrossRef]
- Majid, M.; Habib, S.; Javed, A.R.; Rizwan, M.; Srivastava, G.; Gadekallu, T.R.; Lin, J.C.W. Applications of Wireless Sensor Networks and Internet of Things Frameworks in the Industry Revolution 4.0: A Systematic Literature Review. Sensors 2022, 22, 2087. [Google Scholar] [CrossRef] [PubMed]
- Rashid, B.; Rehmani, M.H. Applications of wireless sensor networks for urban areas: A survey. J. Netw. Comput. Appl. 2016, 60, 192–219. [Google Scholar] [CrossRef]
- Li, M.; Li, Z.; Vasilakos, A.V. A Survey on Topology Control in Wireless Sensor Networks: Taxonomy, Comparative Study, and Open Issues. Proc. IEEE 2013, 101, 2538–2557. [Google Scholar] [CrossRef]
- Yoon, Y.; Kim, Y.H. Maximizing the coverage of sensor deployments using a memetic algorithm and fast coverage estimation. IEEE Trans. Cybern. 2021, 52, 6531–6542. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Du, H.T. K-Sweep coverage with mobile sensor nodes in wireless sensor networks. IEEE Internet Things J. 2021, 8, 13888–13899. [Google Scholar] [CrossRef]
- Wang, W.; Huang, H.; He, F.; Xiao, F.; Sha, C. An enhanced virtual force algorithm for diverse k-coverage deployment of 3d underwater wireless sensor networks. Sensors 2019, 19, 3496. [Google Scholar] [CrossRef] [PubMed]
- Paulswamy, S.L.; Roobert, A.A.; Hariharan, K. A novel coverage improved deployment strategy for wireless sensor network. Wirel. Pers. Commun. 2021, 124, 868–891. [Google Scholar] [CrossRef]
- Priyadarshi, R.; Gupta, B. 2-D coverage optimization in obstacle-based FOI in WSN using modified PSO. J. Supercomput. 2022, 79, 4847–4869. [Google Scholar] [CrossRef]
- Zhu, W.; Huang, C.L.; Yeh, W.C.; Jiang, Y.; Tan, S.Y. A Novel Bi-Tuning SSO Algorithm for Optimizing the Budget-Limited Sensing Coverage Problem in Wireless Sensor Networks. Appl. Sci. 2021, 11, 10197. [Google Scholar] [CrossRef]
- Nematzadeh, S.; Torkamanian-Afshar, M.; Seyyedabbasi, A.; Kiani, F. Maximizing coverage and maintaining connectivity in WSN and decentralized IoT: An efficient metaheuristic-based method for environment-aware node deployment. Neural Comput. Appl. 2022, 35, 611–641. [Google Scholar] [CrossRef]
- Dao, T.K.; Chu, S.C.; Nguyen, T.T.; Nguyen, T.D.; Nguyen, V.T. An Optimal WSN Node Coverage Based on Enhanced Archimedes Optimization Algorithm. Entropy 2022, 24, 1018. [Google Scholar] [CrossRef] [PubMed]
- ZainEldin, H.; Badawy, M.; Elhosseini, M.; Arafat, H.; Abraham, A. An improved dynamic deployment technique based-on genetic algorithm (IDDT-GA) for maximizing coverage in wireless sensor networks. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 4177–4194. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A.D. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.S. Improved Whale Optimization Algorithm Based On Nonlinear Adaptive Weight and Golden Sine Operator. IEEE Access 2020, 8, 77013–77048. [Google Scholar] [CrossRef]
- Liu, J.; Shi, J.; Hao, F.; Dai, M. A novel enhanced global exploration whale optimization algorithm based on Lévy flights and judgment mechanism for global continuous optimization problems. Eng. Comput. 2022, 39, 2433–2461. [Google Scholar] [CrossRef]
- Kaur, G.; Arora, S. Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284. [Google Scholar] [CrossRef]
- Bozorgi, S.M.; Yazdani, S. IWOA: An improved whale optimization algorithm for optimization problems. J. Comput. Des. Eng. 2019, 6, 243–259. [Google Scholar]
- Luo, J.; Shi, B.Y. A hybrid whale optimization algorithm based on modified differential evolution for global optimization problems. Appl. Intell. 2019, 49, 1982–2000. [Google Scholar] [CrossRef]
- Mafarja, M.; Jaber, I.; Ahmed, S.; Thaher, T. Whale Optimisation Algorithm for high-dimensional small-instance feature selection. Int. J. Parallel Emergent Distrib. Syst. 2019, 32, 80–96. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Q.; Chen, H.; Heidari, A.A.; Cai, Z.; Li, J.; Abdelrahim, E.M.; Mansour, R.F. Whale Optimization with Random Contraction and Rosenbrock Method for COVID-19 disease prediction. Biomed. Signal Process. Control 2023, 83, 104638. [Google Scholar] [CrossRef] [PubMed]
- Shivahare, B.D.; Gupta, S.K. Efficient covid-19 ct scan image segmentation by automatic clustering algorithm. J. Healthc. Eng. 2022, 2022, 9009406. [Google Scholar] [CrossRef] [PubMed]
- Tong, W. A hybrid algorithm framework with learning and complementary fusion features for whale optimization algorithm. Sci. Program. 2020, 2020, 5684939. [Google Scholar] [CrossRef]
- Prabhakar, D.; Satyanarayana, M. Side lobe pattern synthesis using hybrid sswoa algorithm for conformal antenna array. Eng. Sci. Technol. Int. J. 2019, 22, 1169–1174. [Google Scholar] [CrossRef]
- Mohammed, H.; Rashid, T. A novel hybrid GWO with WOA for global numerical optimization and solving pressure vessel design. Neural Comput. Appl. 2020, 32, 14701–14718. [Google Scholar] [CrossRef]
- Mantegna, R.N. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic processes. Phys. Rev. E 1994, 49, 4677–4683. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Peraza-Vázquez, H.; Peña-Delgado, A.F.; Echavarría-Castillo, G.; Morales-Cepeda, A.B.; Velasco-Álvarez, J.; Ruiz-Perez, F. A Bio-Inspired Method for Engineering Design Optimization Inspired by Dingoes Hunting Strategies. Math. Probl. Eng. 2021, 2021, 9107547. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl. Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Prim, R. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Mohammed, H.M.; Umar, S.U.; Rashid, T.A. A Systematic and Meta-Analysis Survey of Whale Optimization Algorithm. Comput. Intell. Neurosci. 2019, 2019, 8718571. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, H.M.; Umar, S.U.; Rashid, T.A. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Syst. Appl. 2020, 154, 113018. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Sharma, S.; Mirjalili, S.; Chakraborty, R. A novel enhanced whale optimization algorithm for global optimization. Comput. Ind. Eng. 2021, 153, 107086. [Google Scholar] [CrossRef]





| Function | D | Range | fmin |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 | |
| 30 | [−1, 1] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−5, 10] | 0 |
| Function | D | Range | fmin |
|---|---|---|---|
| 30 | [−500, 500] | −418.98 × D | |
| 30 | [−10, 10] | 0 | |
| 30 | [−5, 5] | −39.166 × D | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−10, 10] | −1 | |
| 30 | [−50, 50] | 0 | |
| 30 | [−50, 50] | 0 | |
| 2 | [−65, 65] | 1 | |
| 4 | [−5, 5] | 0.00030 | |
| 2 | [−5, 5] | −10.316 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | −3 | |
| 3 | [1, 3] | −3.86 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10.1532 | |
| 4 | [0, 10] | −10.4028 | |
| 4 | [0, 10] | −10.5363 |
| Function | D | Range | fmin |
|---|---|---|---|
| F30(CF1): f1, f2, f3,…, f10 = Sphere Function [σ1, σ2, σ3,…, σ10] = [1, 1, 1,…, 1] [λ1, λ2, λ3,…, λ10] = [5/100, 5/100, 5/100,…, 5/100] | 10 | [−5, 5] | 0 |
| F31(CF2): f1, f2, f3,…, f10 = Griewank’s Function [σ1, σ2, σ3,…, σ10] = [1, 1, 1,…, 1] [λ1, λ2, λ3,…, λ10] = [5/100, 5/100, 5/100,…, 5/100] | 10 | [−5, 5] | 0 |
| F32(CF3): f1, f2, f3,…, f10 = Griewank’s Function [σ1, σ2, σ3,…, σ10] = [1, 1, 1,…, 1] [λ1, λ2, λ3,…, λ10] = [1, 1, 1,…, 1] | 10 | [−5, 5] | 0 |
| F33(CF4): f1, f2 = Ackley’s Function, f3, f4 = Rastrigin’s Function, f5, f6 = Weierstrass Function, f7, f8 = Griewank’s Function, f9, f10 = Sphere’s Function [σ1, σ2, σ3,…, σ10] = [1, 1, 1,…, 1] [λ1, λ2, λ3,…, λ10] = [5/32, 5/32, 1, 1, 5/0.5, 5/0.5, 5/100, 5/100, 5/100, 5/100] | 10 | [−5, 5] | 0 |
| F34(CF5): f1, f2 = Rastrigin’s Function, f3, f4 = Weierstrass Function, f5, f6 = Griewank’s Function, f7, f8 = Ackley’s Function, f9, f10 = Sphere’s Function [σ1, σ2, σ3,…, σ10] = [1, 1, 1,…, 1] [λ1, λ2, λ3,…, λ10] = [1/5, 1/5, 5/0.5, 5/0.5, 5/100, 5/100, 5/32, 5/32, 5/100, 5/100] | 10 | [−5, 5] | 0 |
| F35(CF6): f1, f2 = Rastrigin’s Function, f3, f4 = Weierstrass Function, f5, f6 = Griewank’s Function, f7, f8 = Ackley’s Function, f9, f10 = Sphere’s Function [σ1, σ2, σ3,…, σ10] = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1] [λ1, λ2, λ3,…, λ10] = [0.1 × 1/5, 0.2 × 1/5, 0.3 × 5/0.5, 0.4 × 5/0.5, 0.5 × 5/100, 0.6 × 5/100, 0.7 × 5/32, 0.8 × 5/32, 0.9 × 5/100, 1 × 5/100] | 10 | [−5, 5] | 0 |
| PSO | AOA | GWO | SSA | WOA | WOA-LFGA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ave | std | ave | std | ave | std | ave | std | ave | std | ave | std | |
| F1 | 0.01145 | 0.016214 | 1.82 × 10−20 | 9.99 × 10−20 | 2.71 × 10−27 | 7.04 × 10−27 | 1.42 × 10−07 | 1.62 × 10−07 | 2.31 × 10−71 | 1.14 × 10−70 | 0 | 0 |
| F2 | 2.020543 | 4.065539 | 0 | 0 | 1.08 × 10−16 | 8.93 × 10−17 | 2.285371 | 1.666859 | 1.07 × 10−50 | 4.58 × 10−50 | 0 | 0 |
| F3 | 2444.118 | 1926.835 | 0.003659 | 0.007401 | 9.85 × 10−06 | 1.90 × 10−05 | 1382.524 | 777.8525 | 71.50822 | 172.5122 | 0 | 0 |
| F4 | 7.036386 | 1.311499 | 0.025943 | 0.019751 | 8.16 × 10−07 | 8.64 × 10−07 | 11.60046 | 3.603777 | 1.293207 | 1.217586 | 1.65 × 10−10 | 7.94 × 10−10 |
| F5 | 237.9364 | 552.168 | 28.43077 | 0.241825 | 27.0996 | 0.744425 | 358.5001 | 543.5524 | 27.72318 | 0.381725 | 20.77285 | 10.26487 |
| F6 | 0.008698 | 0.014406 | 3.18966 | 0.252549 | 0.767048 | 0.393704 | 2.80 × 10−07 | 5.94 E−07 | 0.263031 | 0.199383 | 0.070958 | 0.122792 |
| F7 | 0.049637 | 0.017275 | 6.93 × 10−05 | 6.73 E−05 | 0.001663 | 0.0008 | 0.190837 | 0.075292 | 0.003031 | 0.002759 | 0.001748 | 0.003825 |
| F8 | 1.62 × 10−18 | 7.45 × 10−18 | 0 | 0 | 1.60 × 10−94 | 8.74 × 10−94 | 1.60 × 10−06 | 1.04 × 10−06 | 8.07 × 10−101 | 4.42 × 10−100 | 0 | 0 |
| F9 | 3715.167 | 3804.074 | 0.006306 | 0.015188 | 1.00 × 10−05 | 1.44 × 10−05 | 1543.173 | 827.1876 | 139.0415 | 349.0566 | 3.84 × 10−26 | 1.99 × 10−25 |
| F10 | 135.1749 | 86.41104 | 278.754 | 50.12035 | 3.35 × 10−07 | 7.80 × 10−07 | 43.32593 | 15.77741 | 25.84223 | 104.563 | 6.12 × 10−17 | 3.35 × 10−16 |
| F11 | −8588.58 | 743.6667 | −5347.08 | 428.9775 | −5856.44 | 736.0021 | −7429.88 | 767.0725 | −10327.8 | 1815.032 | −62304.4 | 2.22 × 10−11 |
| F12 | 1.85834 | 0.705254 | 0 | 0 | 2.08691 | 2.001494 | 1 | 1.48 × 10−09 | 0.129003 | 0.407659 | 0 | 0 |
| F13 | −1010.53 | 32.04003 | −488.895 | 65.78818 | −906.163 | 66.86702 | −999.69 | 41.44037 | −1173.67 | 3.427174 | −1174.98 | 0.005266 |
| F14 | 54.17668 | 12.63687 | 0 | 0 | 1.948371 | 3.150168 | 47.85746 | 15.99706 | 1.89 × 10−15 | 1.04 × 10−14 | 0 | 0 |
| F15 | 0.768649 | 0.668676 | 8.88 × 10−16 | 0 | 1.03 × 10−13 | 1.69 × 10−14 | 2.481978 | 0.913383 | 4.20 × 10−15 | 2.46 × 10−15 | 8.88 × 10−16 | 0 |
| F16 | 0.035694 | 0.042562 | 0.182622 | 0.131219 | 0.004629 | 0.008419 | 0.015976 | 0.00876 | 0.01046 | 0.039824 | 0 | 0 |
| F17 | 7.94 × 10−15 | 4.29 × 10−14 | 7.38 × 10−08 | 6.46 × 10−08 | 1.19 × 10−15 | 3.31 × 10−16 | 2.39 × 10−16 | 1.31 × 10−15 | −1 | 4.61 × 10−17 | −1 | 0 |
| F18 | 0.170733 | 0.276331 | 0.521644 | 0.051792 | 0.054542 | 0.02857 | 6.834328 | 2.62791 | 0.01398 | 0.016893 | 0.006835 | 0.019706 |
| F19 | 0.156988 | 0.196888 | 2.840098 | 0.098464 | 0.628701 | 0.19635 | 13.60701 | 14.96327 | 0.278207 | 0.185077 | 0.208052 | 0.199385 |
| F20 | 0.998004 | 5.83 × 10−17 | 8.2796 | 4.850009 | 3.676116 | 3.874222 | 1.295293 | 0.827786 | 2.865604 | 2.997616 | 1.687328 | 1.873362 |
| F21 | 0.002626 | 0.006021 | 0.012879 | 0.022459 | 0.004451 | 0.008095 | 0.001558 | 0.003563 | 0.000612 | 0.000297 | 0.000362 | 0.000218 |
| F22 | −1.03163 | 6.45 × 10−16 | −1.03163 | 1.30 × 10−07 | −1.03163 | 2.57 × 10−08 | −1.03163 | 2.67 × 10−14 | −1.03163 | 9.35 × 10−10 | −1.03163 | 4.91 × 10−16 |
| F23 | 0.397887 | 0 | 0.40893 | 0.008738 | 0.397889 | 2.69 × 10−06 | 0.397887 | 3.68 × 10−14 | 0.397891 | 8.11 × 10−06 | 0.397887 | 6.37 × 10−15 |
| F24 | 3 | 1.24 × 10−15 | 6.60127 | 9.334635 | 3.00005 | 6.62 × 10−05 | 3 | 2.13 × 10−13 | 3.900112 | 4.929503 | 3 | 1.63 × 10−06 |
| F25 | −3.86278 | 2.65 × 10−15 | −3.85196 | 0.004077 | −3.8615 | 0.00228 | −3.86278 | 1.89 × 10−11 | −3.85717 | 0.009316 | −3.86278 | 2.14 × 10−15 |
| F26 | −3.26514 | 0.07867 | −3.06929 | 0.075255 | −3.25627 | 0.085463 | −3.21838 | 0.05356 | −3.25865 | 0.122607 | −3.28633 | 0.055417 |
| F27 | −6.01714 | 3.525257 | −3.58449 | 1.100864 | −8.51535 | 2.579639 | −8.65039 | 2.831563 | −6.57441 | 2.361348 | −10.1532 | 3.51 × 10−14 |
| F28 | −8.44332 | 3.329769 | −4.01415 | 1.838357 | −10.4014 | 0.000913 | −8.44212 | 3.093598 | −7.38245 | 2.669453 | −10.4029 | 2.28 × 10−13 |
| F29 | −7.2628 | 3.864573 | −3.45313 | 1.352861 | −9.81322 | 2.238027 | −8.03092 | 3.636316 | −7.68458 | 2.925501 | −10.5364 | 1.29 × 10−12 |
| PSO | AOA | GWO | SSA | WOA | WOA-LFGA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ave | std | ave | std | ave | std | ave | std | ave | std | ave | std | |
| F30 | 188.4598 | 104.2843 | 429.9201 | 122.6024 | 165.2451 | 120.3013 | 143.3333 | 138.1736 | 147.113 | 109.1869 | 81.9337 | 109.8375 |
| F31 | 210.1492 | 147.6265 | 603.8082 | 141.238 | 217.9645 | 110.3465 | 193.744 | 119.9475 | 212.4452 | 102.3541 | 167.121 | 119.973 |
| F32 | 254.4012 | 118.5757 | 739.0197 | 169.9494 | 218.669 | 100.6576 | 329.7179 | 239.0358 | 494.4398 | 203.5997 | 438.3484 | 132.1945 |
| F33 | 497.786 | 191.054 | 853.3283 | 70.53408 | 709.6582 | 188.0356 | 630.5518 | 272.5582 | 633.3295 | 174.6679 | 576.9929 | 128.6628 |
| F34 | 249.408 | 231.7561 | 493.5288 | 182.9644 | 187.0822 | 137.7849 | 182.7982 | 202.8263 | 206.8386 | 159.906 | 165.38 | 111.3664 |
| F35 | 826.5022 | 155.8774 | 877.2691 | 66.94098 | 837.5018 | 152.0384 | 762.027 | 185.1875 | 824.9949 | 159.4651 | 814.3615 | 167.8058 |
| PSO | AOA | GWO | SSA | WOA | WOA-LFGA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | ave | std | ave | std | ave | std | ave | std | ave | std | ave | std | |
| F1 | 50 | 10.86347 | 14.44537 | 0.000863 | 0.001639 | 6.16 × 10−20 | 4.36 × 10−20 | 0.85548 | 1.003725 | 1.66 × 10−73 | 7.15 × 10−73 | 0 | 0 |
| 100 | 2316.109 | 3668.931 | 0.021699 | 0.008517 | 1.75 × 10−12 | 1.2 × 10−12 | 1471.517 | 385.5454 | 3.39 × 10−72 | 1.51 × 10−71 | 0 | 0 | |
| 500 | 235236.4 | 25977.07 | 0.6333 | 0.037321 | 0.001453 | 0.000521 | 96418.89 | 5452.527 | 1.71 × 10−73 | 5.04 × 10−73 | 0 | 0 | |
| F2 | 50 | 10.53083 | 11.77191 | 2.3 × 10−147 | 1 × 10−146 | 2.51 × 10−12 | 1.32 × 10−12 | 8.895375 | 2.801584 | 2.35 × 10−49 | 1.05 × 10−48 | 0 | 0 |
| 100 | 65.36263 | 22.83761 | 2.42 × 10−53 | 1.08 × 10−52 | 4.11 × 10−08 | 1.52 × 10−08 | 48.25606 | 7.948359 | 8.59 × 10−50 | 1.89 × 10−49 | 0 | 0 | |
| 500 | 1390.407 | 110.3861 | 0.001232 | 0.001668 | 0.010938 | 0.00145 | 541.6126 | 19.43979 | 3.87 × 10−49 | 1.68 × 10−48 | 0 | 0 | |
| F3 | 50 | 16884.77 | 4607.752 | 0.103386 | 0.097921 | 0.333669 | 0.597959 | 9735.95 | 5803.166 | 565.1298 | 762.9405 | 3.86 × 10−19 | 1.73 × 10−18 |
| 100 | 101956.4 | 11759.16 | 1.127456 | 1.75346 | 636.1386 | 928.2477 | 64451 | 32153.11 | 4706.516 | 7708.618 | 3.07 × 10−17 | 1.37 × 10−16 | |
| 500 | 2764988 | 318150.2 | 33.67954 | 16.67636 | 334085.1 | 95550.54 | 1275053 | 728370.7 | 88474.96 | 146520.3 | 2.52 × 10−12 | 1.13 × 10−11 | |
| F4 | 50 | 17.96243 | 1.707676 | 0.046721 | 0.015961 | 0.000272 | 0.000202 | 20.63042 | 4.258961 | 2.152591 | 2.361506 | 2.43 × 10−10 | 1.07 × 10−09 |
| 100 | 40.44695 | 3.397269 | 0.092903 | 0.010875 | 0.587254 | 0.433484 | 27.99427 | 2.744113 | 3.388053 | 2.958831 | 1.38 × 10−10 | 4.27 × 10−10 | |
| 500 | 76.60742 | 3.587335 | 0.180715 | 0.013151 | 65.33815 | 5.519397 | 40.29455 | 2.292022 | 3.380097 | 2.410942 | 9.41 × 10−09 | 3.08 × 10−08 | |
| F5 | 50 | 5662.017 | 19968.47 | 48.77104 | 0.157029 | 47.43632 | 0.947389 | 3276.49 | 5682.868 | 48.04747 | 0.403162 | 34.7513 | 20.54994 |
| 100 | 203892.7 | 68214.38 | 98.87163 | 0.115737 | 97.96276 | 0.542074 | 156566.4 | 75343.73 | 98.13826 | 0.19119 | 49.03683 | 48.75961 | |
| 500 | 4.59 × 10+08 | 1.37 × 10+08 | 499.0966 | 0.064668 | 498.083 | 0.237754 | 37597520 | 3829547 | 495.8758 | 0.415621 | 161.4206 | 225.6898 | |
| F6 | 50 | 8.762354 | 7.964543 | 7.148222 | 0.382553 | 2.763138 | 0.603988 | 0.594813 | 0.590689 | 0.838658 | 0.362111 | 0.528771 | 0.43255 |
| 100 | 2473.402 | 3667.765 | 18.2289 | 0.63456 | 10.5705 | 1.229664 | 1426.96 | 511.486 | 2.277557 | 0.810151 | 2.215489 | 1.824284 | |
| 500 | 229660.1 | 31072.21 | 116.0074 | 1.081187 | 92.01562 | 1.958327 | 93586.05 | 6284.008 | 19.57877 | 7.912018 | 19.30641 | 21.22633 | |
| F7 | 50 | 0.596402 | 1.806843 | 7.14 × 10−05 | 5.37 × 10−05 | 0.003166 | 0.001527 | 0.564758 | 0.128404 | 0.003614 | 0.004185 | 0.002136 | 0.003517 |
| 100 | 6.536545 | 8.826638 | 6.06 × 10−05 | 5.39 × 10−05 | 0.006948 | 0.004253 | 2.843964 | 0.659053 | 0.003686 | 0.003096 | 0.001628 | 0.004275 | |
| 500 | 3707.805 | 687.6992 | 8.02 × 10−05 | 8.17 × 10−05 | 0.049075 | 0.012875 | 276.4369 | 53.53303 | 0.003276 | 0.004661 | 0.000924 | 0.000913 | |
| F8 | 50 | 1.44 × 10−14 | 3.85 × 10−14 | 0 | 0 | 1.86 × 10−88 | 6.35 × 10−88 | 2.19 × 10−06 | 1.69 × 10−06 | 1.2 × 10−107 | 5.5 × 10−107 | 0 | 0 |
| 100 | 2.64 × 10−11 | 8.42 × 10−11 | 0 | 0 | 2.15 × 10−35 | 9.61 × 10−35 | 2.29 × 10−06 | 1.67 × 10−06 | 9.8 × 10−104 | 2.8 × 10−103 | 0 | 0 | |
| 500 | 1.88 × 10−05 | 4.2 × 10−05 | 0 | 0 | 0.000271 | 0.001131 | 5.71 × 10−06 | 7.21 × 10−06 | 1.3 × 10−110 | 5.7 × 10−110 | 0 | 0 | |
| F9 | 50 | 18886.55 | 5430.519 | 0.05631 | 0.049453 | 0.367136 | 0.657843 | 10379.31 | 5073.609 | 711.4174 | 1668.814 | 1.98 × 10−14 | 8.84 × 10−14 |
| 100 | 106450 | 15037.64 | 1.059031 | 0.969092 | 641.6541 | 619.2241 | 43718.87 | 25770.16 | 5269.864 | 7375.078 | 1.21 × 10−20 | 5.02 × 10−20 | |
| 500 | 2696744 | 385835 | 38.4927 | 28.86932 | 328280.4 | 66473.19 | 1217109 | 526500.8 | 1625552 | 6833751 | 3.41 × 10−18 | 1.36 × 10−17 | |
| F10 | 50 | 624.1645 | 207.4525 | 798.6709 | 98.33566 | 0.073548 | 0.07947 | 391.2071 | 89.38285 | 46.64148 | 192.6738 | 0.004231 | 0.018922 |
| 100 | 2536.807 | 451.22 | 2051.827 | 173.7202 | 122.6674 | 52.30159 | 1956.498 | 227.5388 | 227.8372 | 676.5795 | 4.18 × 10−05 | 0.000187 | |
| 500 | 24484.75 | 1175.066 | 8.84 ×10+14 | 3.54 ×10+15 | 3854.575 | 356.6187 | 10441.52 | 642.2583 | 559.5588 | 1632.451 | 500.7807 | 1714.189 | |
| F11 | 50 | −12786.3 | 798.5763 | −6730.6 | 555.5429 | −9006.98 | 796.4451 | −11829.8 | 1409.544 | −17237.6 | 3259.934 | −103841 | 2.99 × 10−11 |
| 100 | −21997.3 | 1611.842 | −9932.03 | 556.0954 | −16523.7 | 1163.17 | −22109.6 | 1951.76 | −33053 | 6993.32 | −207681 | 5.97 × 10−11 | |
| 500 | −65272.3 | 2572.758 | −22147.4 | 1418.863 | −53823.4 | 13825.98 | −60450.6 | 5024.125 | −183344 | 28730.99 | 1038407 | 1.19 × 10−10 | |
| F12 | 50 | 3.512278 | 1.823459 | 0 | 0 | 1.997852 | 0.767904 | 1.00591 | 0.009882 | 0 | 0 | 0 | 0 |
| 100 | 8.708894 | 3.634477 | 0 | 0 | 2.969532 | 0.649941 | 3.56948 | 0.820859 | 0.052619 | 0.235318 | 0 | 0 | |
| 500 | 116.9072 | 9.152489 | 6.35 × 10−06 | 1.81 × 10−06 | 28.20371 | 59.83419 | 107.274 | 4.117031 | 5.55 × 10 −18 | 2.48 × 10 −17 | 0 | 0 | |
| F13 | 50 | −1681.47 | 45.5754 | −675.226 | 76.99906 | −1352.15 | 90.40042 | −1648.11 | 38.54963 | −1956.64 | 1.398103 | −1958.07 | 0.215703 |
| 100 | −3303.19 | 63.15214 | −1084.03 | 124.9054 | −2299.99 | 157.4946 | −3023.55 | 71.17438 | −3910.89 | 5.958551 | −3915.88 | 0.840303 | |
| 500 | −12380.6 | 261.834 | −3680.81 | 261.3991 | −7753.78 | 531.8809 | −10816.8 | 224.6012 | −19540.2 | 34.90968 | −19567.5 | 37.75219 | |
| F14 | 50 | 119.9365 | 28.58934 | 0 | 0 | 4.178933 | 4.74967 | 88.4886 | 30.73374 | 0 | 0 | 0 | 0 |
| 100 | 382.7355 | 54.84386 | 0 | 0 | 10.74289 | 7.341498 | 230.9327 | 35.07983 | 0 | 0 | 0 | 0 | |
| 500 | 4449.093 | 186.3669 | 5.97 × 10−06 | 5.37 × 10−06 | 70.76179 | 18.02281 | 3151.214 | 160.9733 | 4.55 × 10−14 | 2.03 × 10−13 | 0 | 0 | |
| F15 | 50 | 2.715587 | 0.484115 | 8.88 × 10−16 | 0 | 4.53 × 10−11 | 3.17 × 10−11 | 4.635025 | 1.206284 | 4.26 × 10−15 | 2.44 × 10−15 | 8.88 × 10−16 | 0 |
| 100 | 6.525648 | 2.065837 | 0.000484 | 0.000793 | 1.22 × 10−07 | 4.02 × 10−08 | 10.2093 | 1.047667 | 4.26 × 10−15 | 2.7 × 10−15 | 8.88 × 10−16 | 0 | |
| 500 | 18.05284 | 0.448287 | 0.007914 | 0.000662 | 0.001876 | 0.000293 | 14.24981 | 0.224026 | 3.55 × 10−15 | 2.27 × 10−15 | 8.88 × 10−16 | 0 | |
| F16 | 50 | 1.059217 | 0.145573 | 1.062206 | 0.144497 | 0.003473 | 0.007606 | 0.508193 | 0.177961 | 0.008673 | 0.038785 | 0 | 0 |
| 100 | 35.28278 | 50.71112 | 585.2056 | 187.6203 | 0.003466 | 0.008471 | 12.83264 | 2.844918 | 5.55 × 10 −18 | 2.48 × 10 −17 | 0 | 0 | |
| 500 | 2133.145 | 209.9714 | 10516.47 | 2772.351 | 0.004728 | 0.020304 | 867.917 | 65.88722 | 0 | 0 | 0 | 0 | |
| F17 | 50 | 1.53 × 10−21 | 1.16 × 10−21 | 2.82 × 10−12 | 3.22 × 10−12 | 2.6 × 10−22 | 6.62 × 10−22 | 1.47 × 10−21 | 8.59 × 10−22 | −1 | 6.24 × 10−17 | −1 | 0 |
| 100 | 6.52 × 10−41 | 1.2 × 10−40 | 2.17 × 10−23 | 2.7 × 10−23 | 8.56 × 10−41 | 1.9 × 10−40 | 3.66 × 10−41 | 4.07 × 10−41 | −0.85 | 0.366348 | −1 | 0 | |
| 500 | 4.8 × 10−177 | 0 | 1.3 × 10−111 | 4.4 × 10−111 | 1.1 × 10−173 | 0 | 1.4 × 10−182 | 0 | −0.7 | 0.470162 | −1 | 0 | |
| F18 | 50 | 3.386843 | 1.228704 | 0.734116 | 0.044766 | 0.106871 | 0.047385 | 11.49135 | 2.713314 | 0.012943 | 0.007324 | 0.012762 | 0.020302 |
| 100 | 2936.118 | 6291.82 | 0.901293 | 0.025436 | 0.276781 | 0.060778 | 31.0403 | 10.6664 | 0.020269 | 0.011114 | 0.016797 | 0.022049 | |
| 500 | 4.79 × 10+08 | 2.04 × 10+08 | 1.082153 | 0.010931 | 0.766924 | 0.058279 | 1530375 | 926662 | 0.024601 | 0.011647 | 0.044441 | 0.070781 | |
| F19 | 50 | 42.53796 | 20.41387 | 4.875282 | 0.080773 | 2.085256 | 0.373575 | 76.36419 | 12.04896 | 0.413098 | 0.227486 | 0.314442 | 0.409962 |
| 100 | 73149.61 | 62122.54 | 9.968205 | 0.057886 | 6.84329 | 0.459763 | 9531.26 | 15735.96 | 1.139066 | 0.584451 | 1.134865 | 1.559223 | |
| 500 | 1.5 × 10+09 | 2.72 × 10+08 | 50.221 | 0.039006 | 50.05496 | 1.3932 | 34036361 | 9213893 | 7.216821 | 3.138501 | 4.851414 | 6.68935 | |
| Parameter | Value |
|---|---|
| Region size | 100 m × 100 m |
| Sensing range | 11 m |
| Sensor nodes number N | 27 |
| Individual number | 50 |
| Iterations | 200 |
| Test times | 30 |
| Method | ave | std | C |
|---|---|---|---|
| SMA | 68.9237% | 0.0173 | 0.6715 |
| DOA | 76.2457% | 0.0183 | 0.7429 |
| AOA | 68.3437% | 0.0137 | 0.6659 |
| BWO | 64.1613% | 0.0205 | 0.6251 |
| WOA | 79.6813% | 0.0231 | 0.7763 |
| WOA-LFGA | 90.9703% | 0.0019 | 0.8863 |
| N = 10 | N = 15 | N = 20 | N = 25 | N = 30 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | ave | std | ave | std | ave | std | ave | std | ave | std |
| SMA | 34.63% | 0.00877 | 47.70% | 0.01028 | 57.51% | 0.01102 | 66.70% | 0.01215 | 73.96% | 0.02138 |
| DOA | 37.73% | 0.00657 | 53.55% | 0.01176 | 64.77% | 0.01743 | 73.12% | 0.02305 | 79.83% | 0.01749 |
| AOA | 34.59% | 0.00685 | 47.58% | 0.01183 | 57.85% | 0.0186 | 65.42% | 0.01425 | 72.50% | 0.01506 |
| BWO | 34.52% | 0.00919 | 46.03% | 0.01634 | 55.40% | 0.02252 | 62.08% | 0.02008 | 67.43% | 0.02664 |
| WOA | 37.87% | 0.00264 | 54.04% | 0.01373 | 67.29% | 0.01785 | 75.84% | 0.02531 | 82.70% | 0.02263 |
| WOA-LFGA | 38.29% | 0.00042 | 56.72% | 0.00381 | 72.16% | 0.00747 | 88.75% | 0.00105 | 93.71% | 0.00272 |
| Method | ave | std | C |
|---|---|---|---|
| CWOA | 68.3363% | 0.0263 | 0.6658 |
| WOABAT | 78.0493% | 0.0217 | 0.7604 |
| RDWOA | 81.9797% | 0.0171 | 0.7987 |
| WOAmM | 81.2440% | 0.0250 | 0.7916 |
| EGE-WOA | 56.2650% | 0.0489 | 0.5482 |
| WOA-LFGA | 90.9703% | 0.0019 | 0.8863 |
| N = 10 | N = 15 | N = 20 | N = 25 | N = 30 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | ave | std | ave | std | ave | std | Ave | std | ave | std |
| CWOA | 35.46% | 0.0116 | 48.44% | 0.0223 | 58.01% | 0.0253 | 65.02% | 0.0186 | 72.98% | 0.0251 |
| WOABAT | 37.61% | 0.0040 | 53.81% | 0.0103 | 65.58% | 0.0160 | 74.49% | 0.0234 | 81.73% | 0.0210 |
| RDWOA | 38.08% | 0.0021 | 55.11% | 0.0076 | 69.53% | 0.0078 | 78.40% | 0.0157 | 85.35% | 0.0236 |
| WOAmM | 38.04% | 0.0020 | 54.93% | 0.0108 | 68.12% | 0.0120 | 78.04% | 0.0200 | 84.99% | 0.0214 |
| EGE-WOA | 31.00% | 0.0221 | 41.04% | 0.0443 | 49.71% | 0.0391 | 51.94% | 0.0535 | 59.58% | 0.0627 |
| WOA-LFGA | 38.29% | 0.0004 | 56.72% | 0.0038 | 72.16% | 0.0074 | 88.75% | 0.0010 | 93.71% | 0.0027 |
| Parameter | Value |
|---|---|
| Region size | 440,400 m2 |
| Sensing range | 100 m |
| Sensor nodes number N | 13 |
| Individual number | 50 |
| Iterations | 200 |
| Test times | 30 |
| Method | ave | std | C |
|---|---|---|---|
| SMA | 11.4011% | 0.0159 | 0.1229 |
| DOA | 53.0607% | 0.0530 | 0.5722 |
| AOA | 52.3511% | 0.0306 | 0.5645 |
| BWO | 52.2743% | 0.0579 | 0.5637 |
| WOA | 37.2967% | 0.0935 | 0.4022 |
| WOA-LFGA | 83.7718% | 0.0035 | 0.9033 |
| Method | ave | std | C |
|---|---|---|---|
| CWOA | 53.4095% | 0.0666 | 0.5759 |
| WOABAT | 37.4971% | 0.0527 | 0.4043 |
| RDWOA | 51.3324% | 0.0508 | 0.5535 |
| WOAmM | 38.7471% | 0.0452 | 0.4178 |
| EGE-WOA | 43.9632% | 0.0366 | 0.4741 |
| WOA-LFGA | 83.7718% | 0.0035 | 0.9033 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhang, B.; Zhang, Y. Application of an Enhanced Whale Optimization Algorithm on Coverage Optimization of Sensor. Biomimetics 2023, 8, 354. https://doi.org/10.3390/biomimetics8040354
Xu Y, Zhang B, Zhang Y. Application of an Enhanced Whale Optimization Algorithm on Coverage Optimization of Sensor. Biomimetics. 2023; 8(4):354. https://doi.org/10.3390/biomimetics8040354
Chicago/Turabian StyleXu, Yong, Baicheng Zhang, and Yi Zhang. 2023. "Application of an Enhanced Whale Optimization Algorithm on Coverage Optimization of Sensor" Biomimetics 8, no. 4: 354. https://doi.org/10.3390/biomimetics8040354
APA StyleXu, Y., Zhang, B., & Zhang, Y. (2023). Application of an Enhanced Whale Optimization Algorithm on Coverage Optimization of Sensor. Biomimetics, 8(4), 354. https://doi.org/10.3390/biomimetics8040354






