A Bio-Inspired Decision-Making Method of UAV Swarm for Attack-Defense Confrontation via Multi-Agent Reinforcement Learning
Abstract
1. Introduction
- This paper proposes a bio-inspired decision-making method for UAV swarms for attack-defense confrontation via MARL. Traditional MARL methods suffer from an exponential increase in training time as the swarm size increases. To overcome this problem, the main idea of our method is to make the strategy trained for a small-sized UAV group applicable to a large-scale UAV swarm. Inspired by the phenomenon that predators hunt for prey in small groups, we propose the grouping mechanism, which divides the swarm into two types of groups. Through the grouping mechanism, interference between groups is avoided, so the strategy trained for small groups can be applied to a large-scale swarm, and the scalability of the UAV swarm is increased;
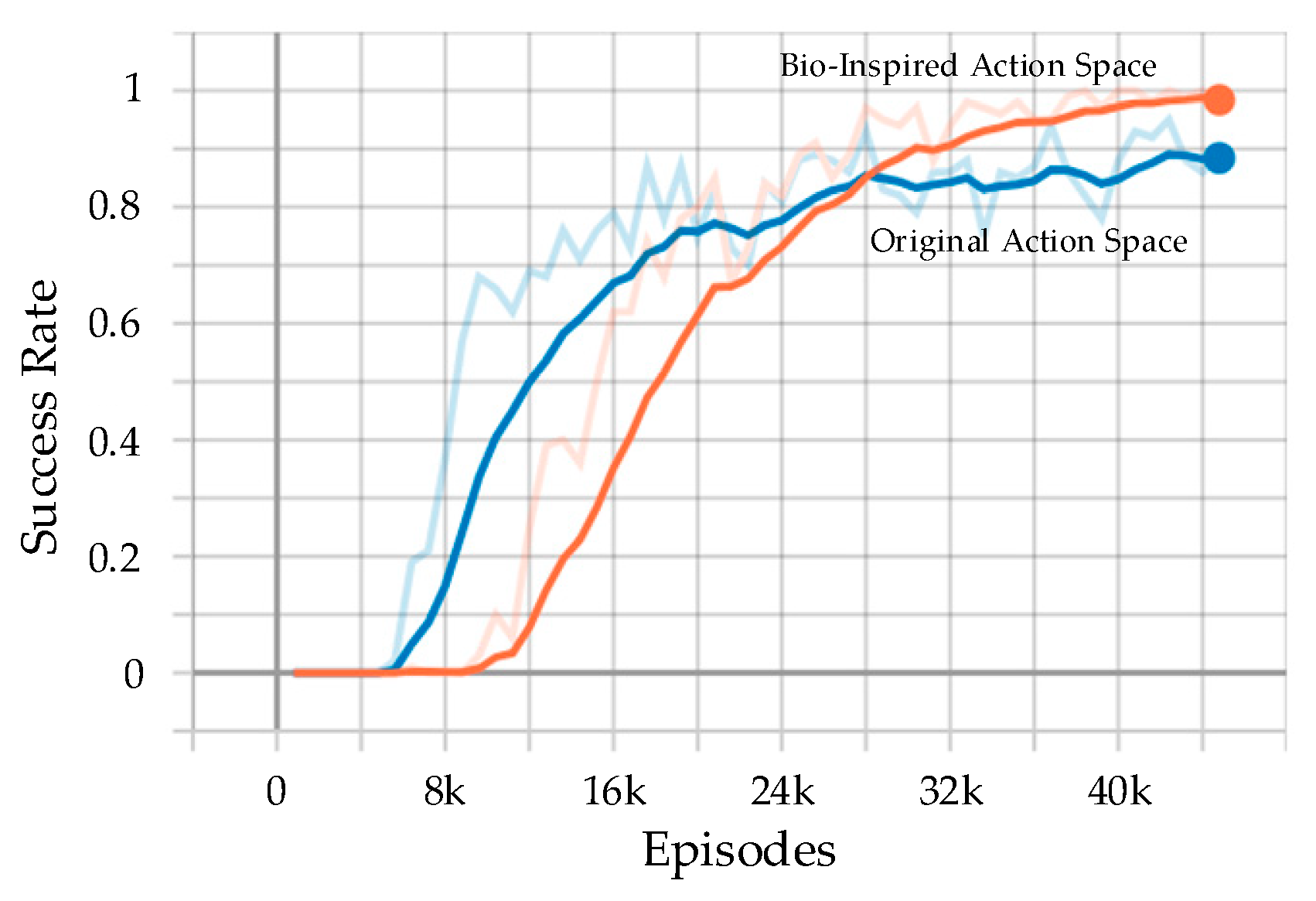
- To prevent the problem that the strategy is stuck in a local optimum during training, a bio-inspired action space is designed. Inspired by group hunting behavior in nature, we abstracted six types of actions that have a clear interactive effect. Compared with standard action space, the bio-inspired action space improves the success rate of the confrontation. Furthermore, as it is hard for the strategy to converge under a sparse reward, we design four types of dense rewards evaluating the status of the mission to accelerate the convergence of the strategy. The results show that an effective strategy can be obtained after adding dense rewards;
- The numerical experiments are conducted to evaluate our method. The results show that our method can obtain effective strategies and take advantage of the UAV swarm. The success rate of the confrontation is increased, and the UAV swarm can intercept the enemy, which is faster than itself, through cooperation.
2. Preliminaries
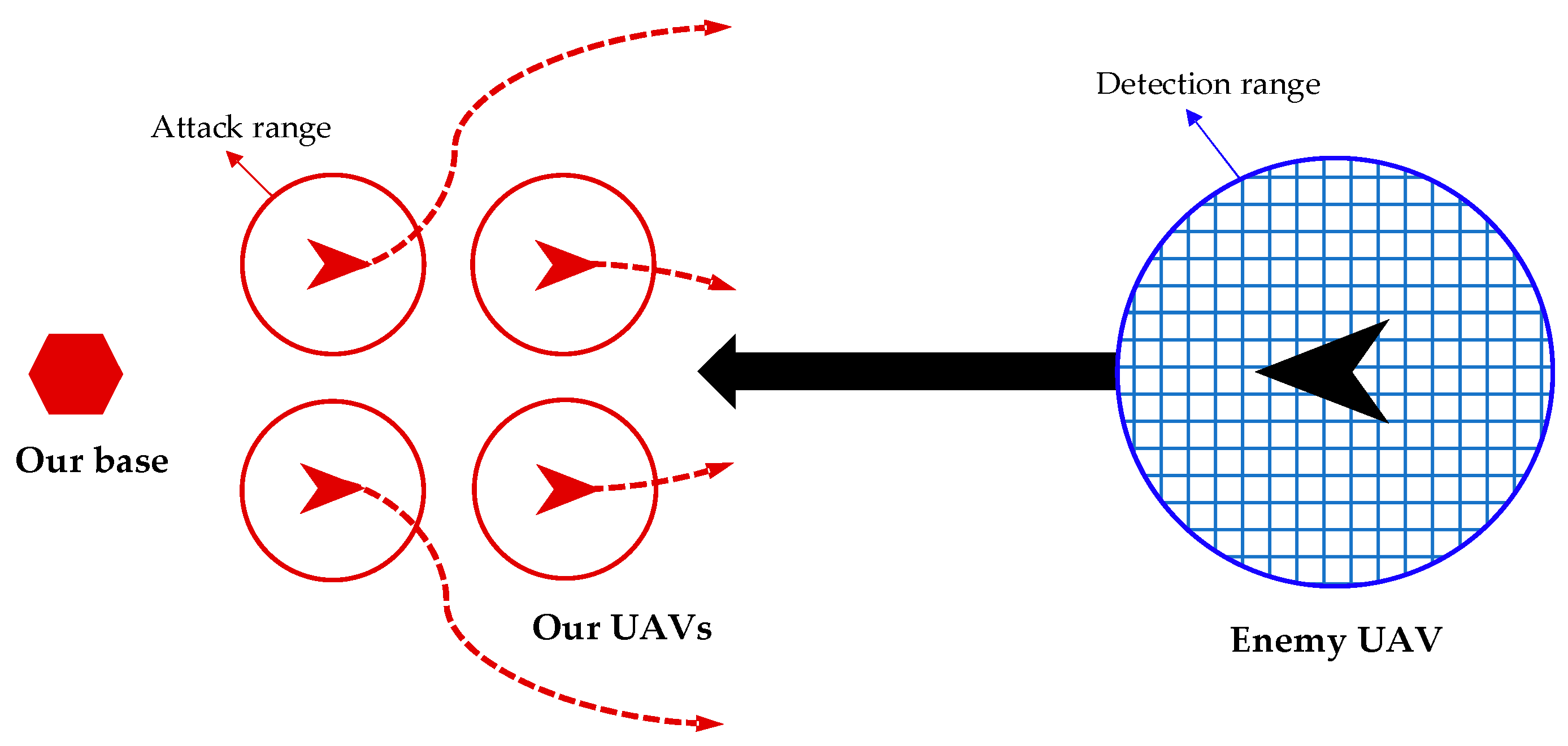
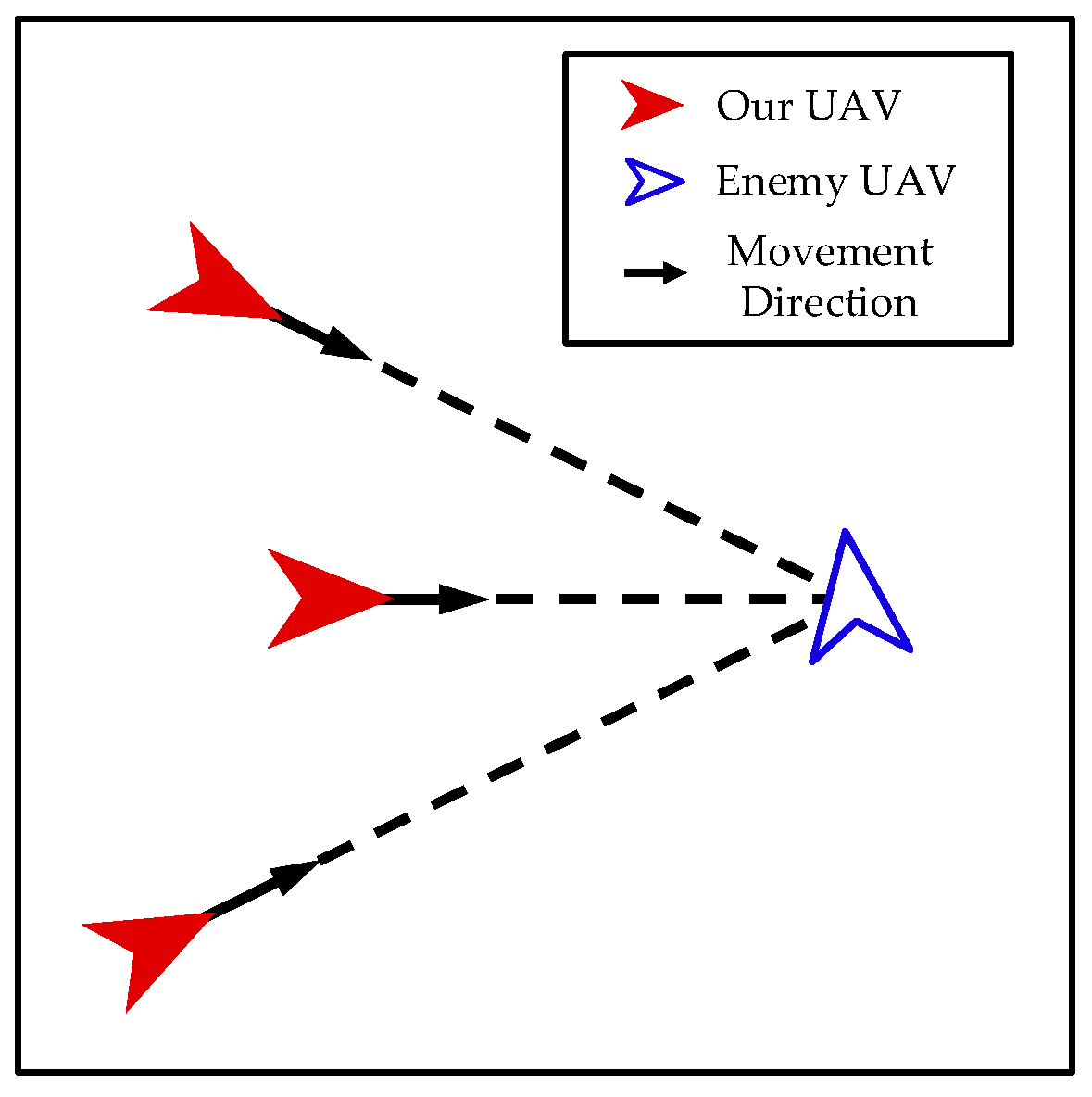
2.1. Attack-Defense Confrontation Problem
2.2. Dynamics Model of the UAV
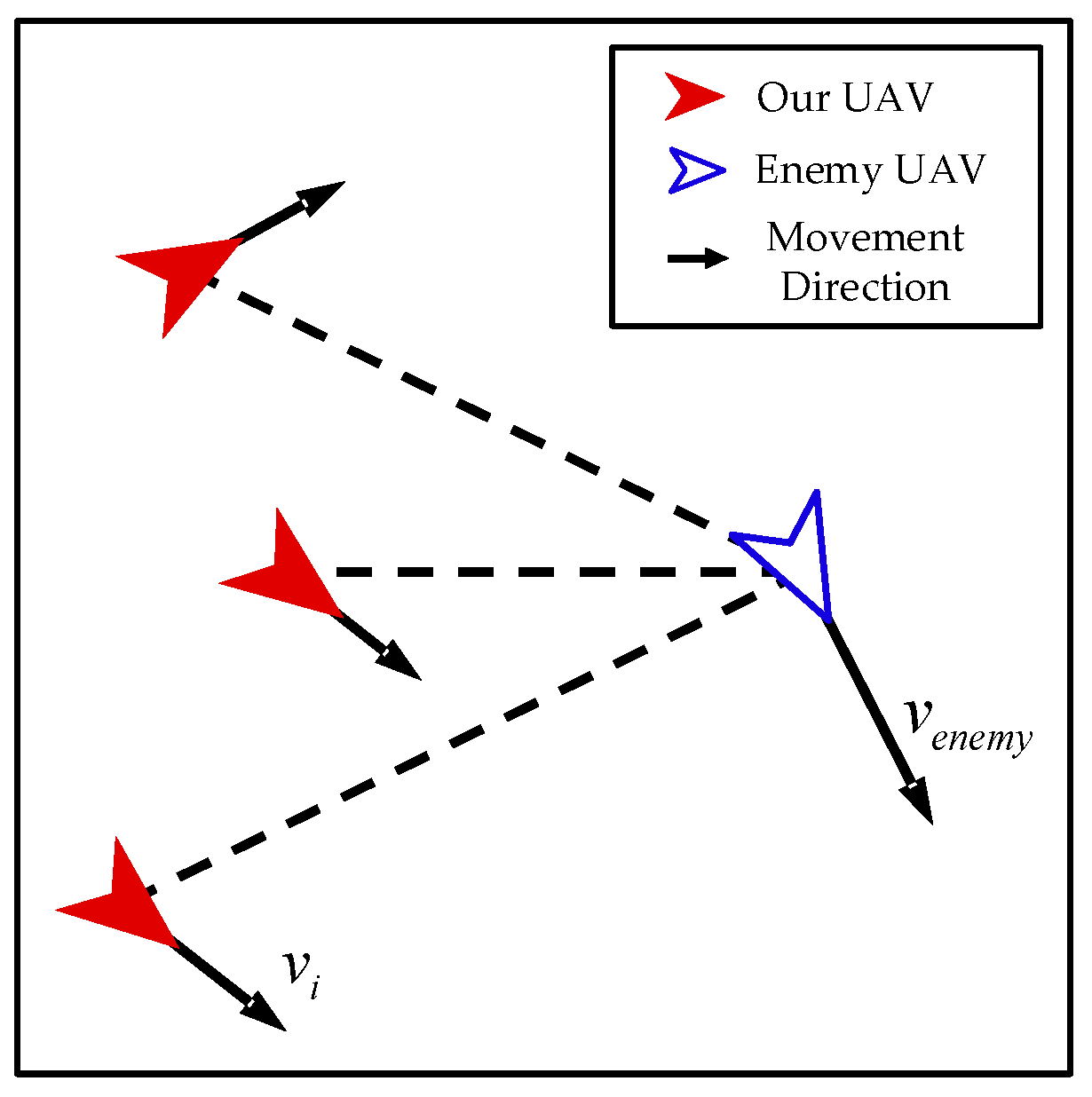
2.3. Movement Strategy of Enemy UAV
2.4. Multi-Agent Reinforcement Learning
3. Methods
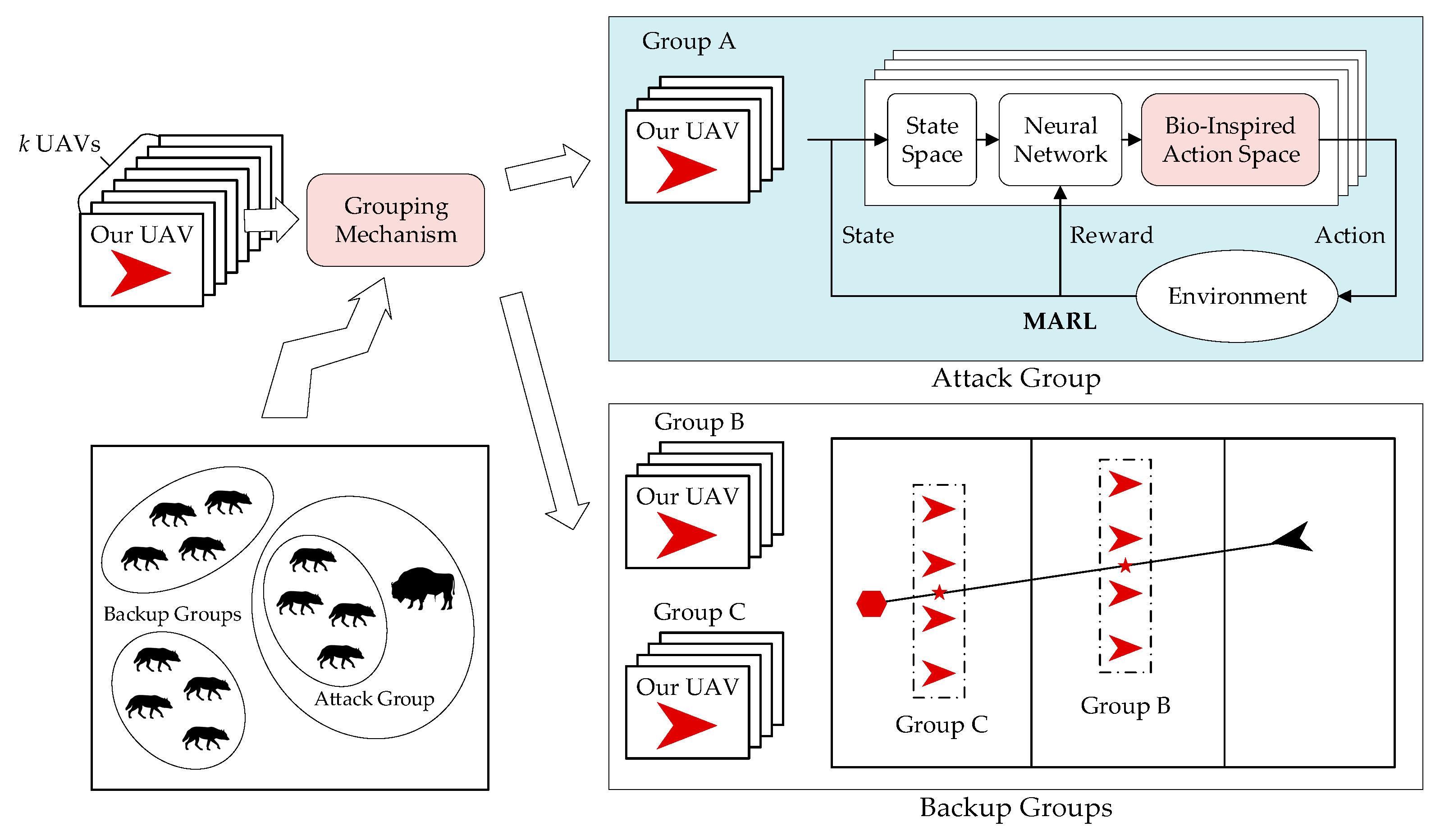
3.1. Framework
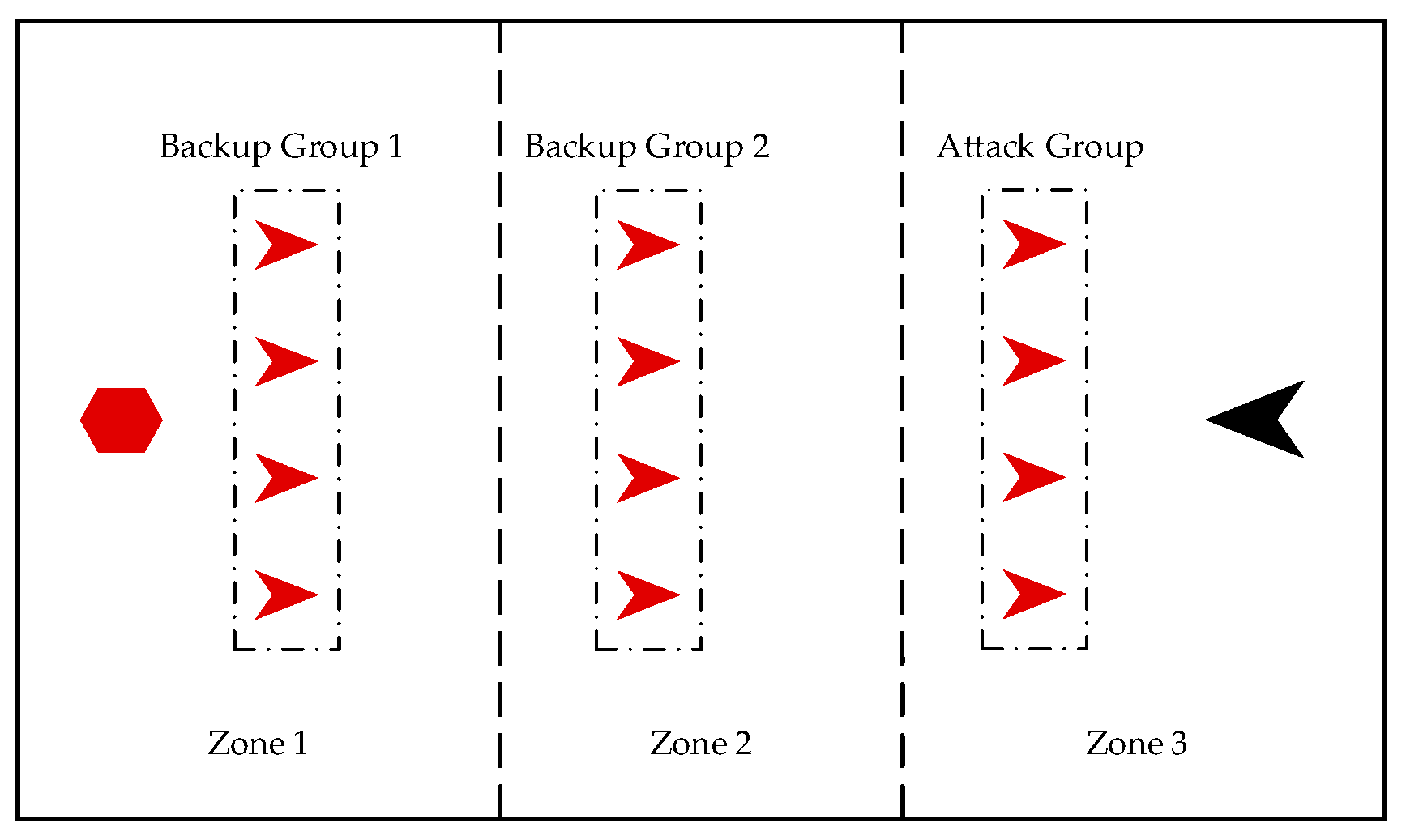
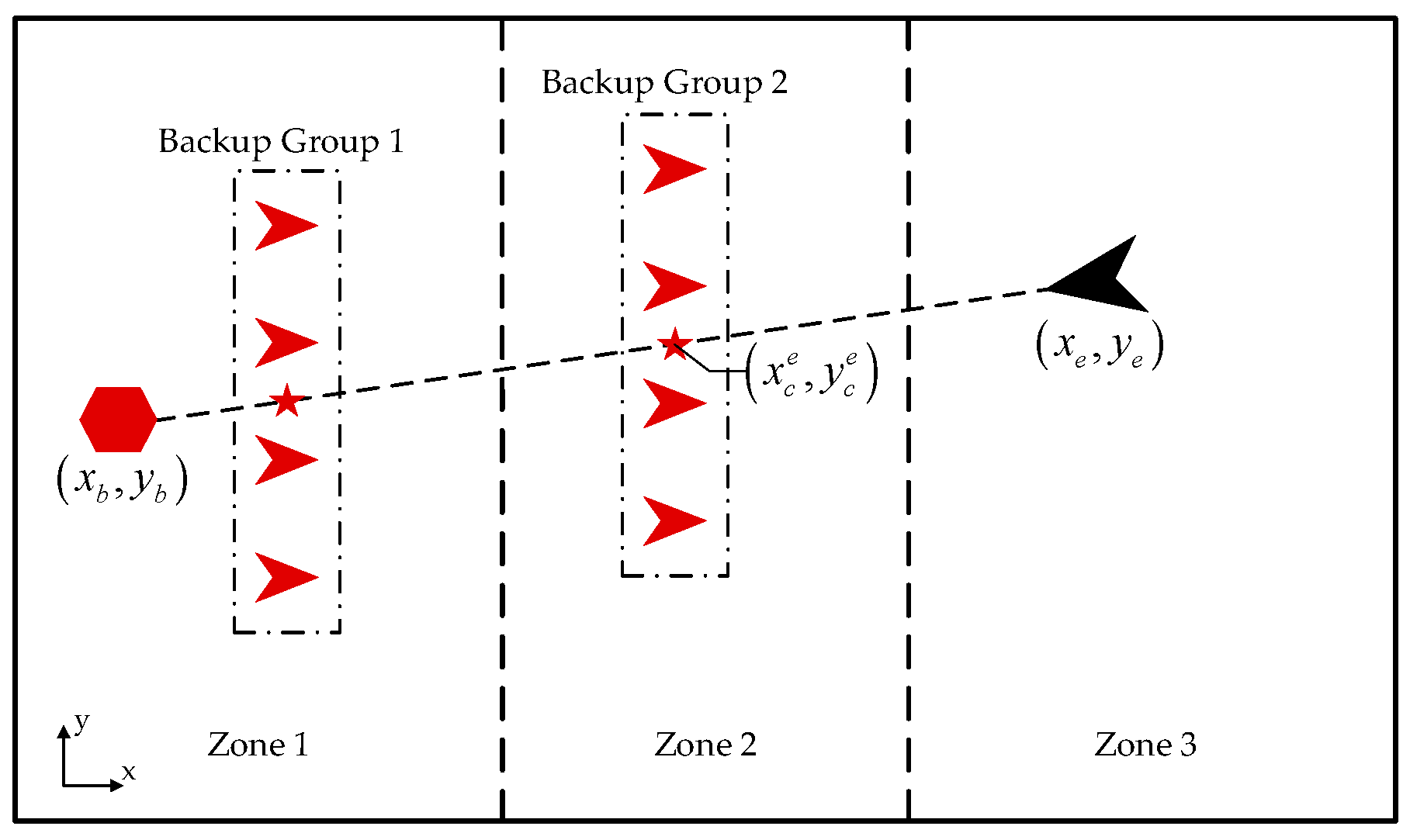
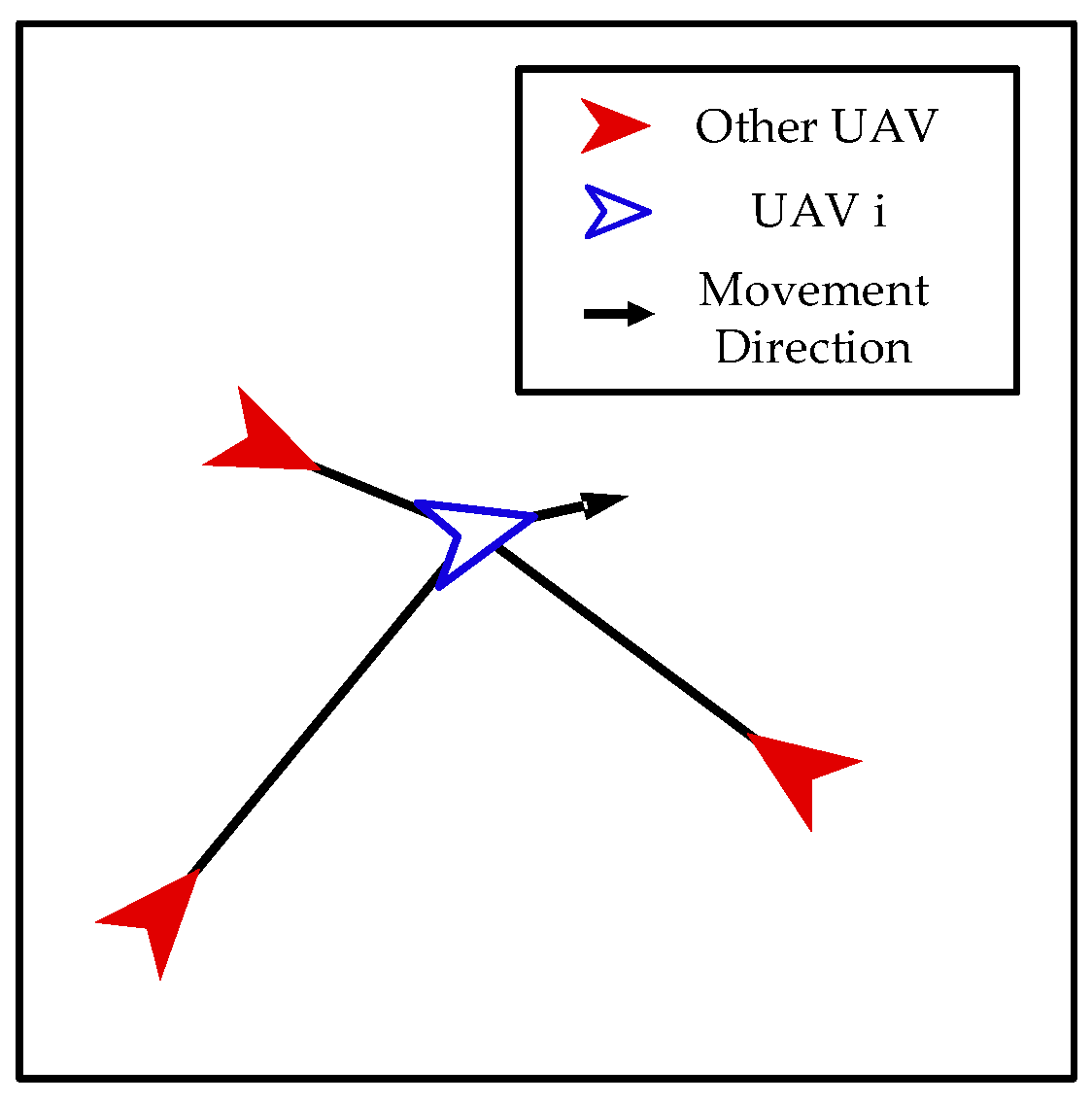
3.2. Grouping Mechanism
3.3. Design of MARL
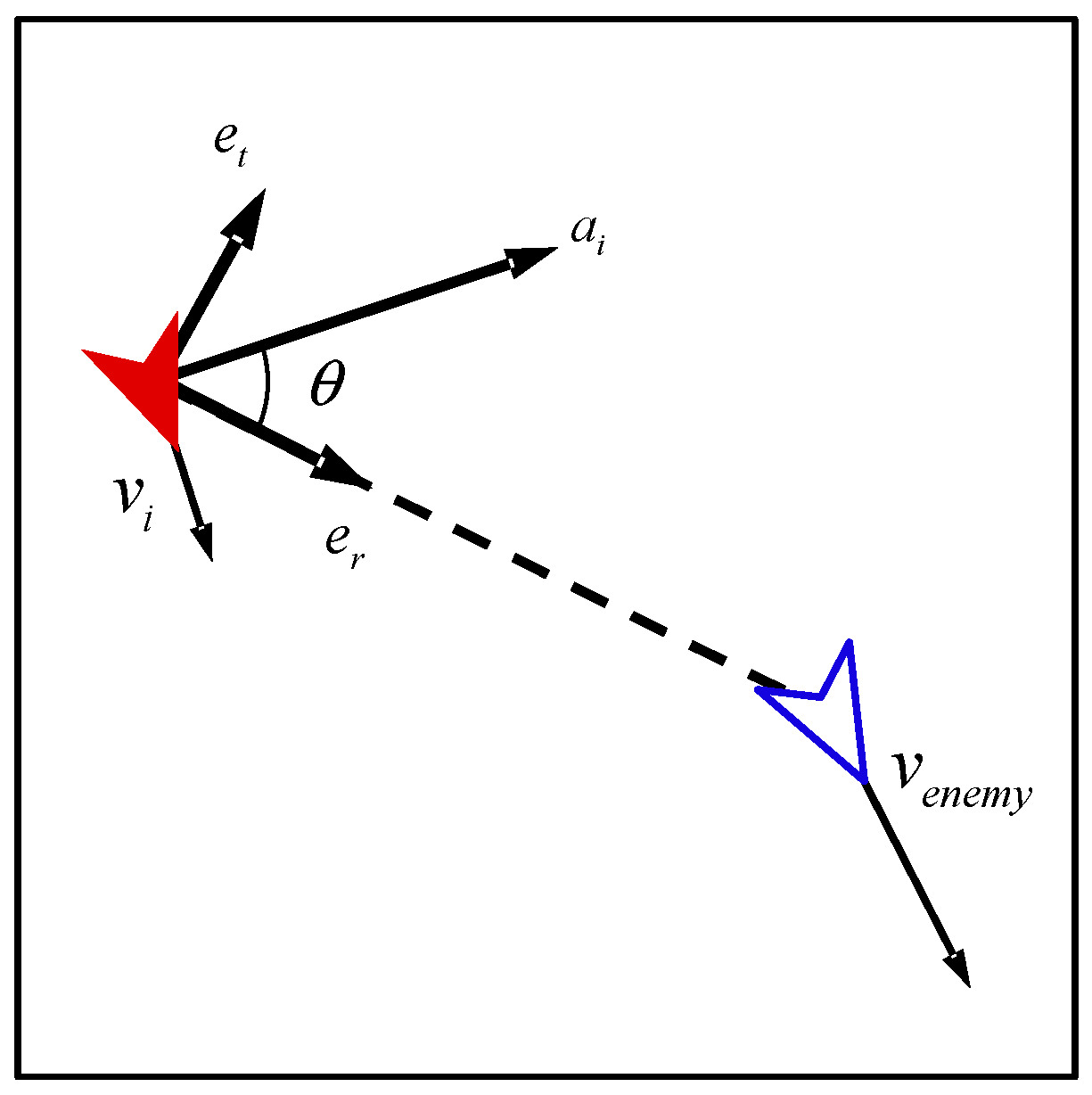
3.3.1. Bio-Inspired Action Space
- (1)
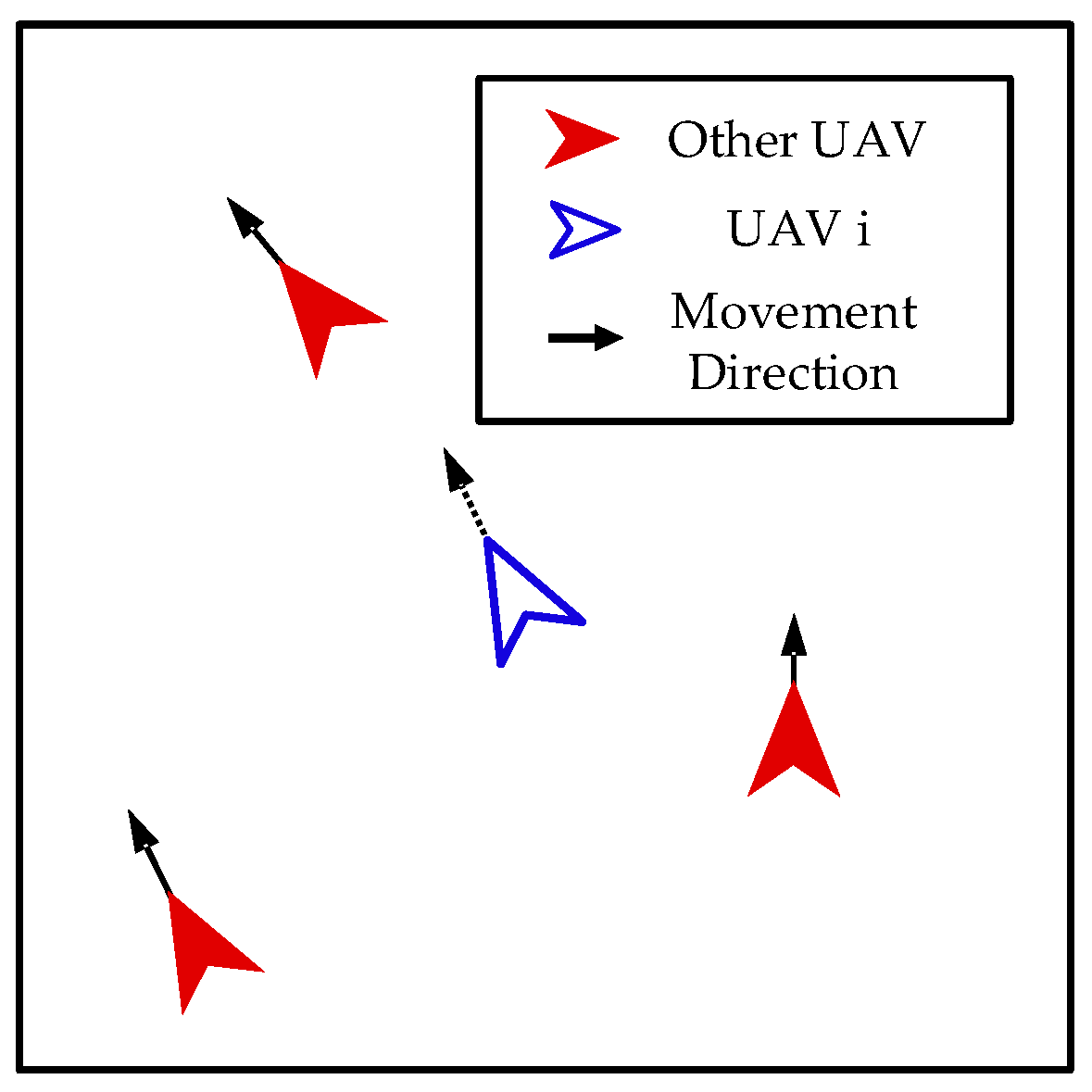
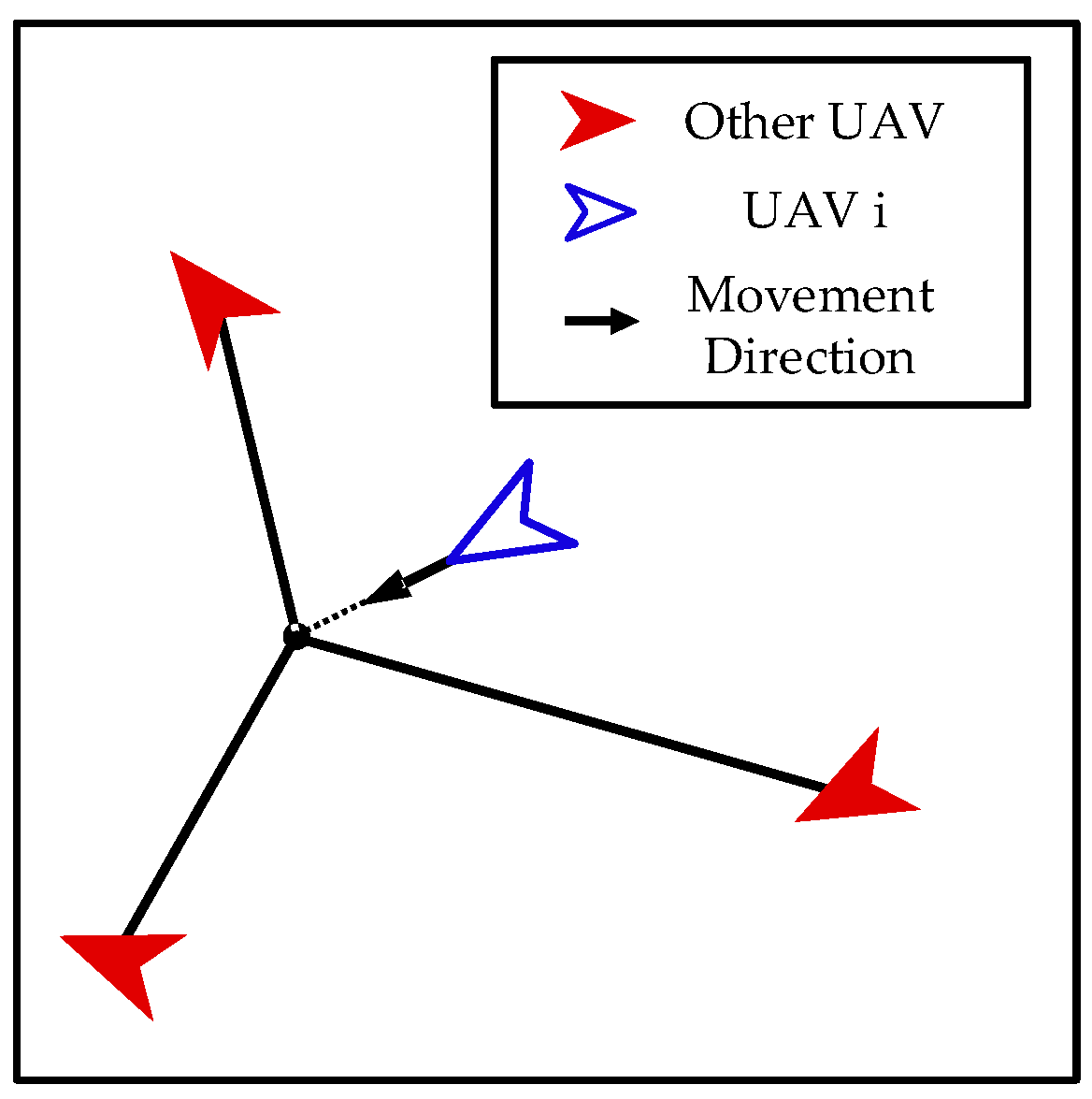
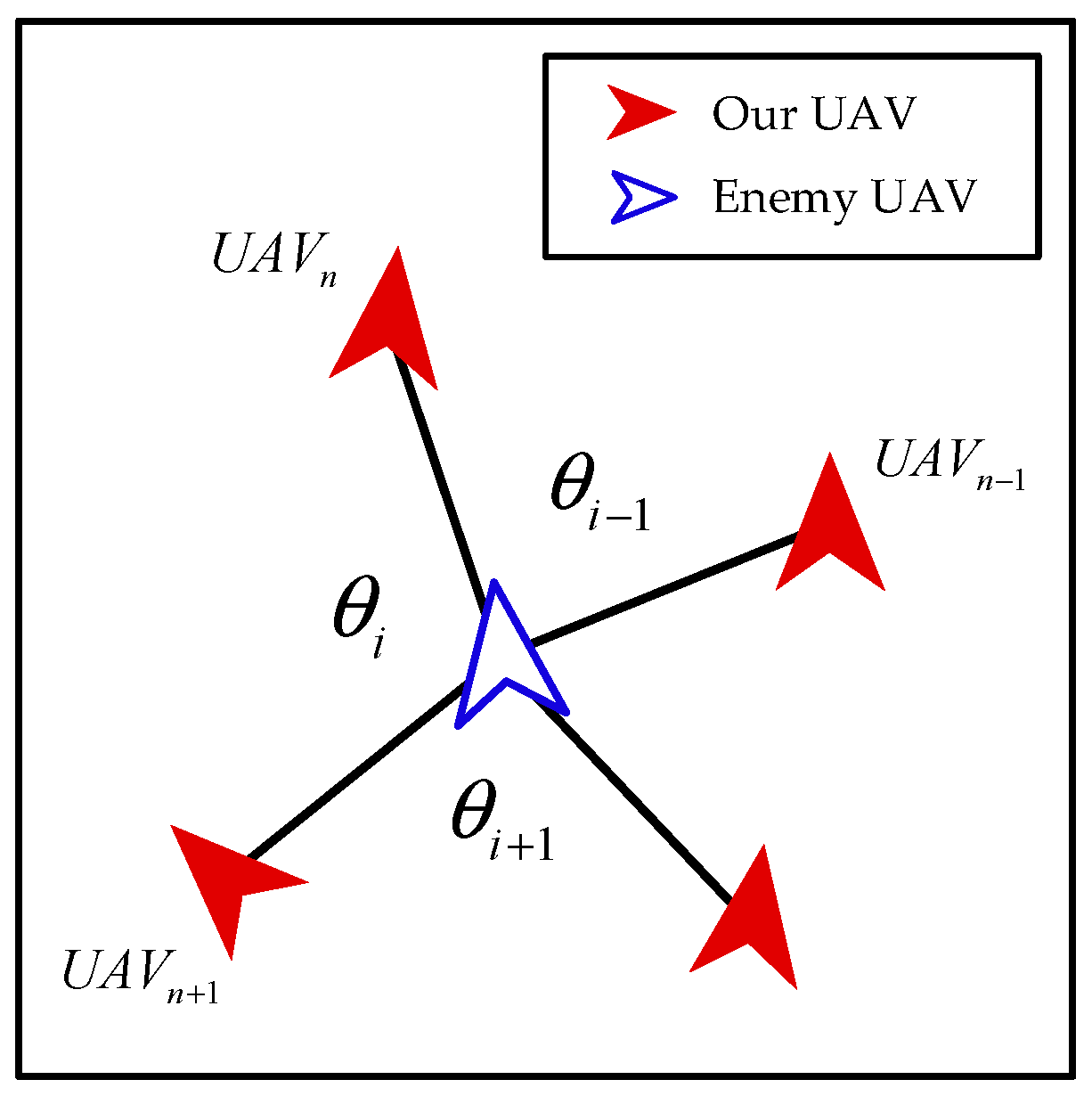
- Interaction between Enemy UAVs and Our UAVs
- (2)
- Interaction among Our UAVs
- (3)
- Action Space
3.3.2. State Space
3.3.3. Reward Function
4. Numerical Experiments
4.1. Experiment Setup
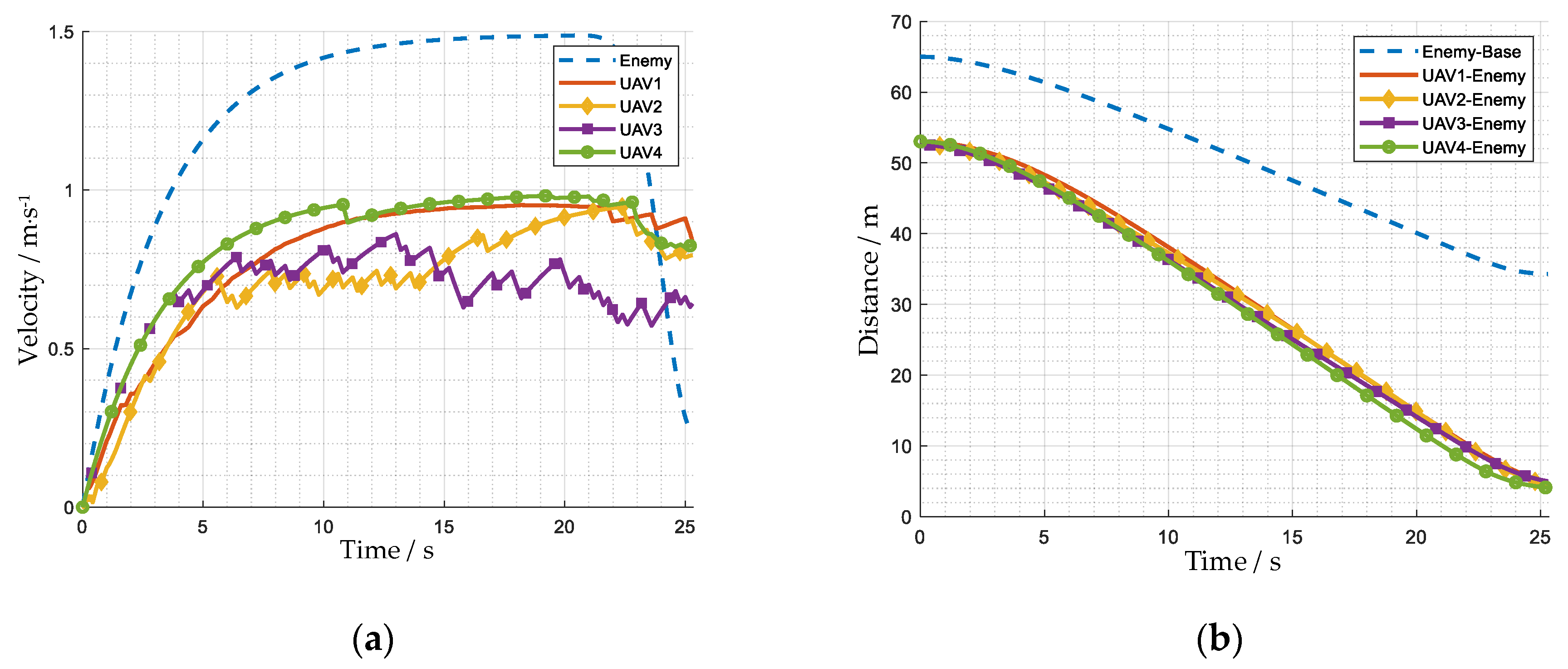
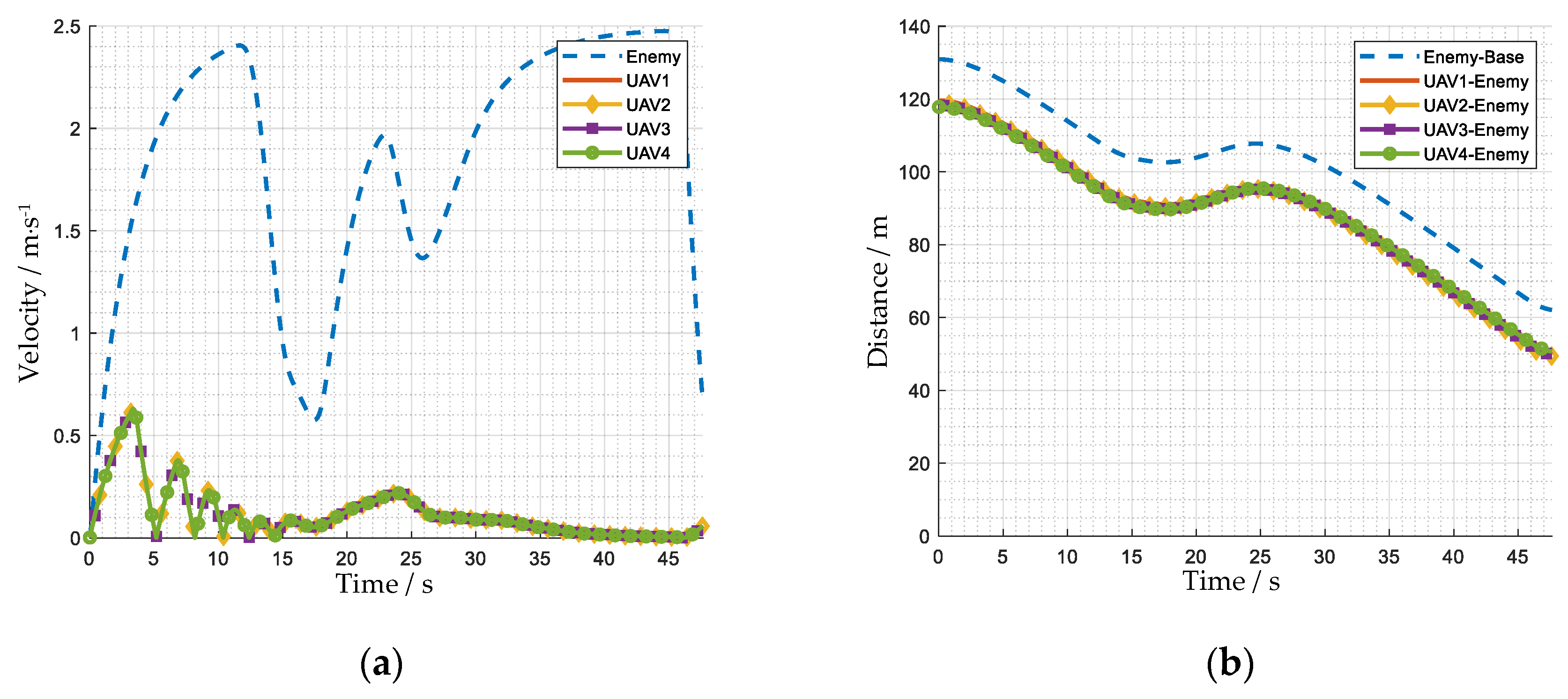
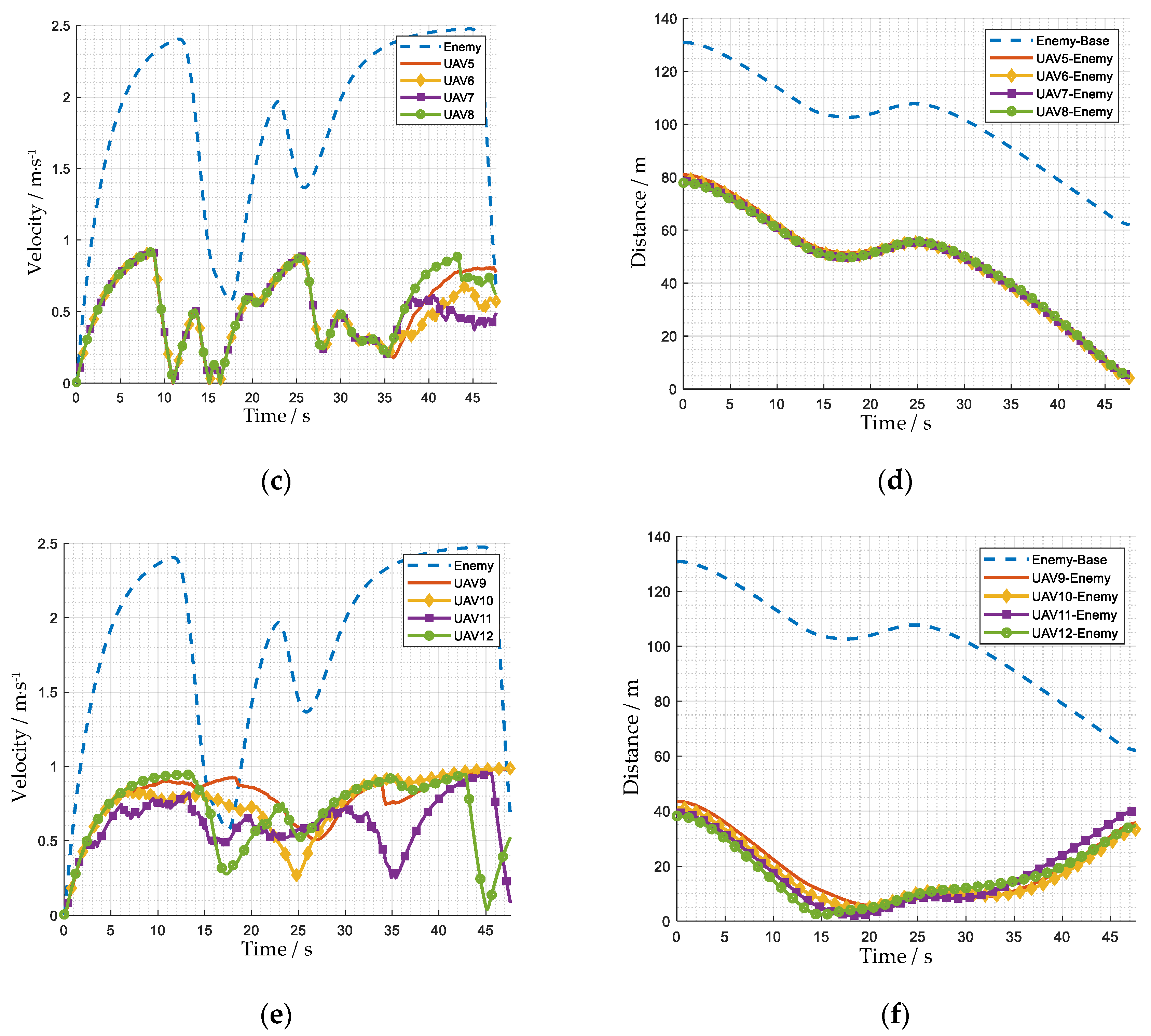
4.2. Performance Analysis
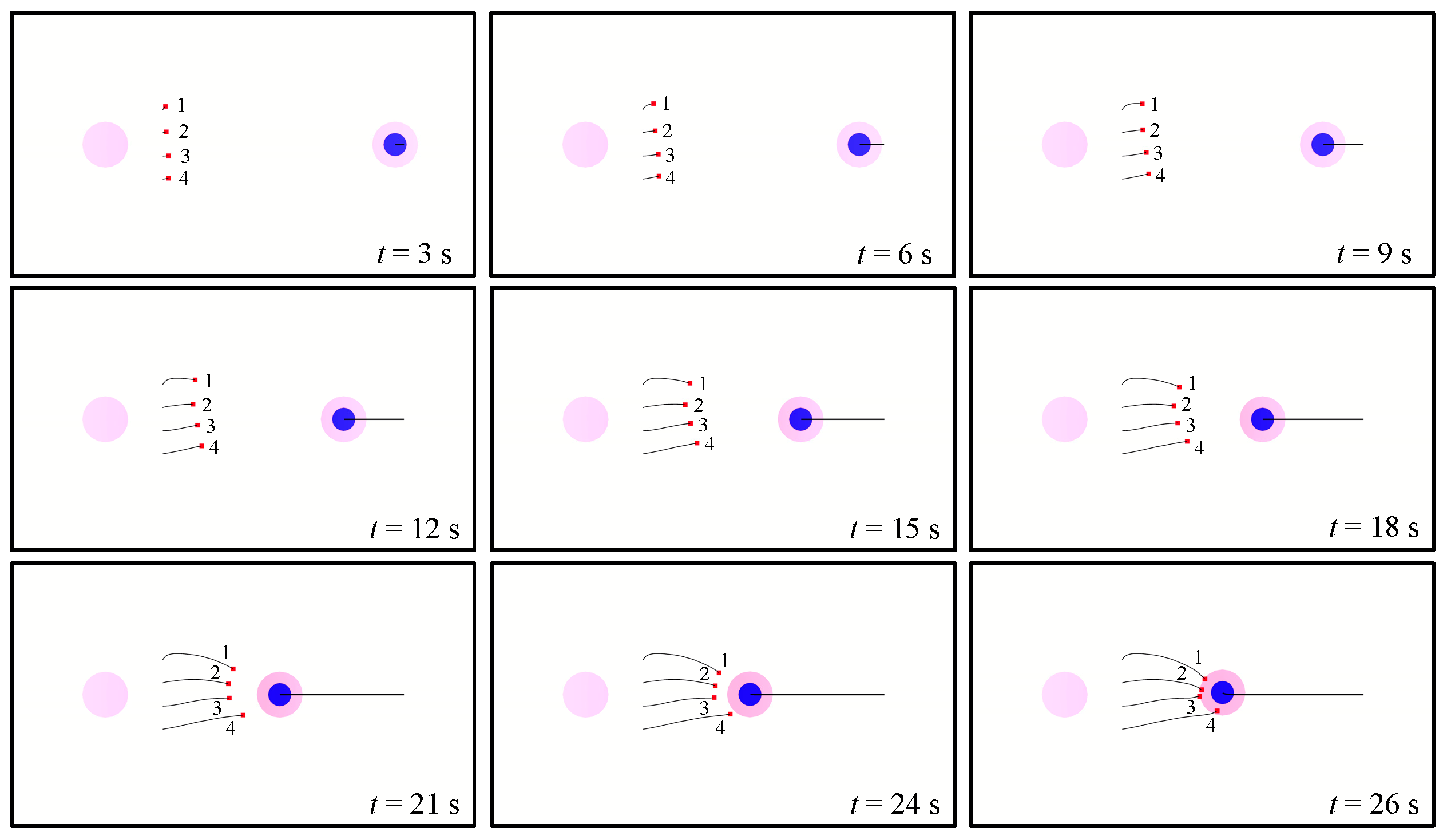
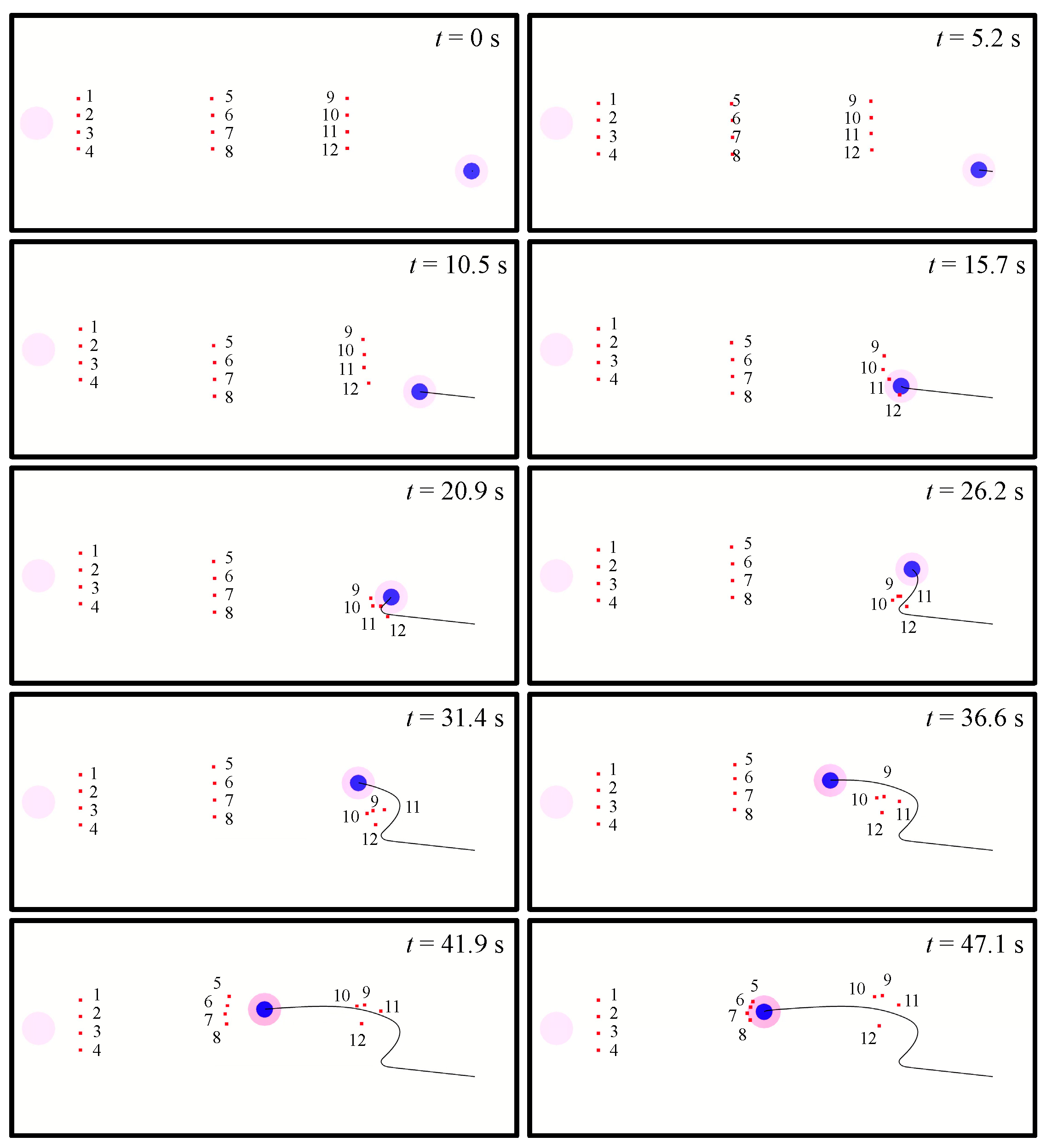
4.3. Demonstration of Attack-Defense Confrontation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Muchiri, N.; Kimathi, S. A Review of Applications and Potential Applications of UAV. In Proceedings of the 2016 Annual Conference on Sustainable Research and Innovation, Milan, Italy, 4 May 2016. [Google Scholar]
- Fan, B.; Li, Y.; Zhang, R.; Fu, Q. Review on the Technological Development and Application of UAV Systems. Chin. J. Electron. 2020, 29, 199–207. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Hu, C. Path Planning with Time Windows for Multiple UAVs Based on Gray Wolf Algorithm. Biomimetics 2022, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X. Analysis of Military Application of UAV Swarm Technology. In Proceedings of the 2020 3rd International Conference on Unmanned Systems, Harbin, China, 27 November 2020; pp. 1200–1204. [Google Scholar]
- Peng, Q.; Wu, H.; Xue, R. Review of Dynamic Task Allocation Methods for UAV Swarms Oriented to Ground Targets. Complex Syst. Model. Simul. 2021, 1, 163–175. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, X.; Miao, Y. Starling-Behavior-Inspired Flocking Control of Fixed-Wing Unmanned Aerial Vehicle Swarm in Complex Environments with Dynamic Obstacles. Biomimetics 2022, 7, 214. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Ma, H. Research on UAV Swarm Cooperative Reconnaissance and Combat Technology. In Proceedings of the 2020 3rd International Conference on Unmanned Systems, Harbin, China, 27 November 2020; pp. 996–999. [Google Scholar]
- Wang, Y.; Bai, P.; Liang, X.; Wang, W.; Zhang, J.; Fu, Q. Reconnaissance Mission Conducted by UAV Swarms Based on Distributed PSO Path Planning Algorithms. IEEE Access 2019, 7, 105086–105099. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, A.; Bi, W.; Tang, Y. Multi-UAV Mission Allocation under Constraint. Appl. Sci. 2019, 9, 2184. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.; Gao, X.; Xie, T. UAV Swarm Confrontation Using Hierarchical Multiagent Reinforcement Learning. Int. J. Aerosp. Eng. 2021, 2021, 3360116. [Google Scholar] [CrossRef]
- Xiang, L.; Xie, T. Research on UAV Swarm Confrontation Task Based on MADDPG Algorithm. In Proceedings of the 2020 5th International Conference on Mechanical, Control and Computer Engineering, Harbin, China, 25 December 2022; pp. 1513–1518. [Google Scholar]
- Xuan, S.; Ke, L. UAV Swarm Attack-Defense Confrontation Based on Multi-Agent Reinforcement Learning. In Advances in Guidance, Navigation and Control, Proceedings of the 2020 International Conference on Guidance, Navigation and Control, Tianji, China, 23–25 October 2020; Yan, L., Duan, H., Yu, X., Eds.; Springer: Singapore; pp. 5599–5608.
- Wang, Z.; Liu, F.; Guo, J.; Hong, C.; Chen, M.; Wang, E.; Zhao, Y. UAV Swarm Confrontation Based on Multi-Agent Deep Reinforcement Learning. In Proceedings of the 2022 41st Chinese Control Conference, Hefei, China, 25 July 2022; pp. 4996–5001. [Google Scholar]
- Wang, B.; Li, S.; Gao, X.; Xie, T. Weighted Mean Field Reinforcement Learning for Large-Scale UAV Swarm Confrontation. Appl. Intell. 2022, 53, 5274–5289. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Y.; Xu, X.; Dai, H. Multiagent Reinforcement Learning for Swarm Confrontation Environments. In Intelligent Robotics and Applications, Proceedings of the 12th International Conference on Intelligent Robotics and Applications, Shenyang, China, 8–11 August 2019; Yu, H., Liu, J., Liu, L., Ju, Z., Liu, Y., Zhou, D., Eds.; Springer: Cham, Switzerland; pp. 533–543.
- Zhan, G.; Zhang, X.; Li, Z.; Xu, L.; Zhou, D.; Yang, Z. Multiple-UAV Reinforcement Learning Algorithm Based on Improved PPO in Ray Framework. Drones 2022, 6, 166. [Google Scholar] [CrossRef]
- Lowe, R.; WU, Y.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017; Volume 30. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of PPO in Cooperative, Multi-Agent Games. arXiv 2021, arXiv:2103.01955. [Google Scholar]
- MacNulty, D.R.; Smith, D.W.; Mech, L.D.; Vucetich, J.A.; Packer, C. Nonlinear Effects of Group Size on the Success of Wolves Hunting Elk. Behav. Ecol. 2012, 23, 75–82. [Google Scholar] [CrossRef]
- MacNulty, D.R.; Mech, L.D.; Smith, D.W. A Proposed Ethogram of Large-Carnivore Predatory Behavior, Exemplified by the Wolf. J. Mammal. 2007, 88, 595–605. [Google Scholar] [CrossRef]





| Parameter | Specification | Value |
|---|---|---|
| Linear drag coefficient of the UAV | 0.3 s−1 | |
| Maximum acceleration of our UAVs | 0.3 m·s−2 | |
| Maximum speed of our UAVs | 1.0 m·s−1 | |
| Attack range of our UAVs | 5.0 m | |
| Maximum acceleration of the enemy UAV | 0.45 m·s−2 | |
| Maximum speed of the enemy UAV | 1.5 m·s−1 | |
| Detection range of the enemy UAV | 5.0 m | |
| Maximum time of the mission | 500 s |
| Parameter | Value |
|---|---|
| Learning rate | 0.00005 |
| Batch size | 1024 |
| Buffer size | 10,240 |
| Discount factor | 0.99 |
| Hidden units | 512 |
| Fully connected layers | 2 |
| Method | Final Success Rate |
|---|---|
| Original Action Space | 89% |
| Bio-Inspired Action Space | 97% |
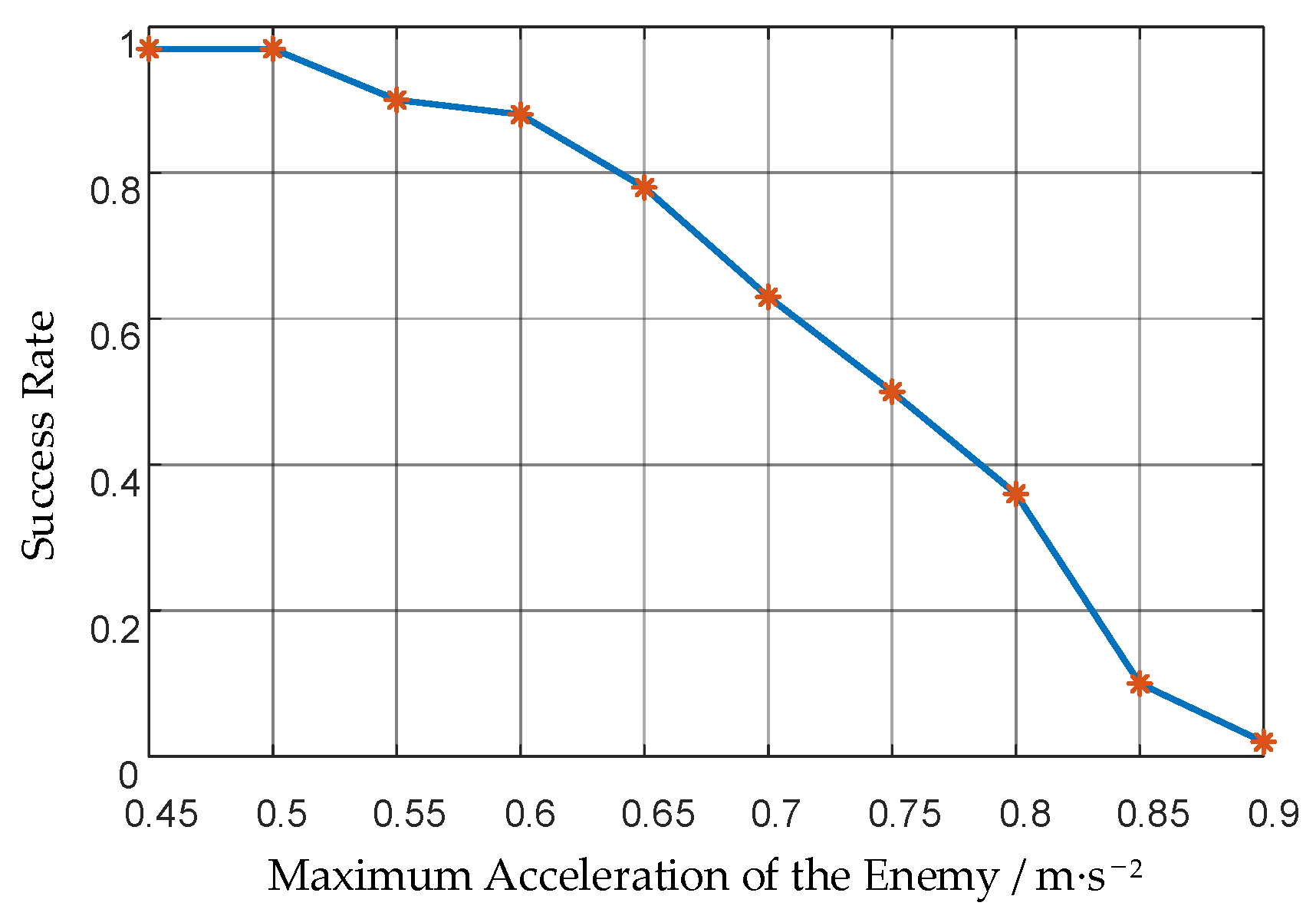
| Maximum Acceleration of the Enemy/m·s−2 | Maximum Acceleration of Our UAVs/m·s−2 | Acceleration Ratio | Success Rate |
|---|---|---|---|
| 0.45 | 0.3 | 1.5 | 97% |
| 0.5 | 1.67 | 97% | |
| 0.55 | 1.83 | 90% | |
| 0.6 | 2 | 88% | |
| 0.65 | 2.17 | 78% | |
| 0.7 | 2.33 | 63% | |
| 0.75 | 2.5 | 50% | |
| 0.8 | 2.67 | 36% | |
| 0.85 | 2.83 | 10% | |
| 0.9 | 3 | 2% |
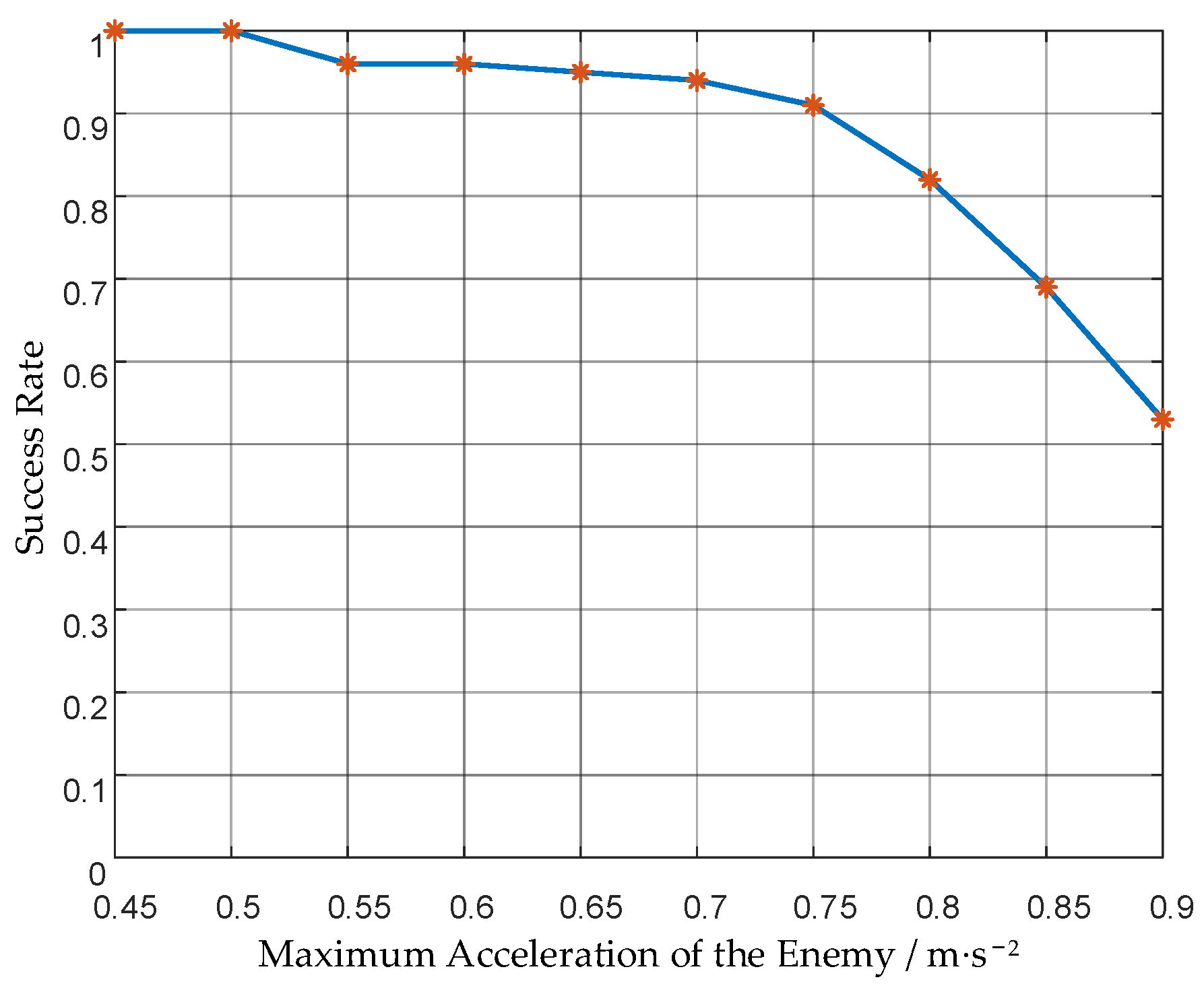
| Maximum Acceleration of the Enemy/m·s−2 | Maximum Acceleration of Our UAVs/m·s−2 | Acceleration Ratio | Success Rate |
|---|---|---|---|
| 0.45 | 0.3 | 1.5 | 100% |
| 0.5 | 1.67 | 100% | |
| 0.55 | 1.83 | 96% | |
| 0.6 | 2 | 96% | |
| 0.65 | 2.17 | 95% | |
| 0.7 | 2.33 | 94% | |
| 0.75 | 2.5 | 91% | |
| 0.8 | 2.67 | 82% | |
| 0.85 | 2.83 | 69% | |
| 0.9 | 3 | 53% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, P.; Wei, J.; Wu, K.; Di, B.; Wang, Y. A Bio-Inspired Decision-Making Method of UAV Swarm for Attack-Defense Confrontation via Multi-Agent Reinforcement Learning. Biomimetics 2023, 8, 222. https://doi.org/10.3390/biomimetics8020222
Chi P, Wei J, Wu K, Di B, Wang Y. A Bio-Inspired Decision-Making Method of UAV Swarm for Attack-Defense Confrontation via Multi-Agent Reinforcement Learning. Biomimetics. 2023; 8(2):222. https://doi.org/10.3390/biomimetics8020222
Chicago/Turabian StyleChi, Pei, Jiahong Wei, Kun Wu, Bin Di, and Yingxun Wang. 2023. "A Bio-Inspired Decision-Making Method of UAV Swarm for Attack-Defense Confrontation via Multi-Agent Reinforcement Learning" Biomimetics 8, no. 2: 222. https://doi.org/10.3390/biomimetics8020222
APA StyleChi, P., Wei, J., Wu, K., Di, B., & Wang, Y. (2023). A Bio-Inspired Decision-Making Method of UAV Swarm for Attack-Defense Confrontation via Multi-Agent Reinforcement Learning. Biomimetics, 8(2), 222. https://doi.org/10.3390/biomimetics8020222





