Variation in the Elastic Modulus and Increased Energy Dissipation Induced by Cyclic Straining of Argiope bruennichi Major Ampullate Gland Silk
Abstract
1. Introduction
2. Materials and Methods
3. Results
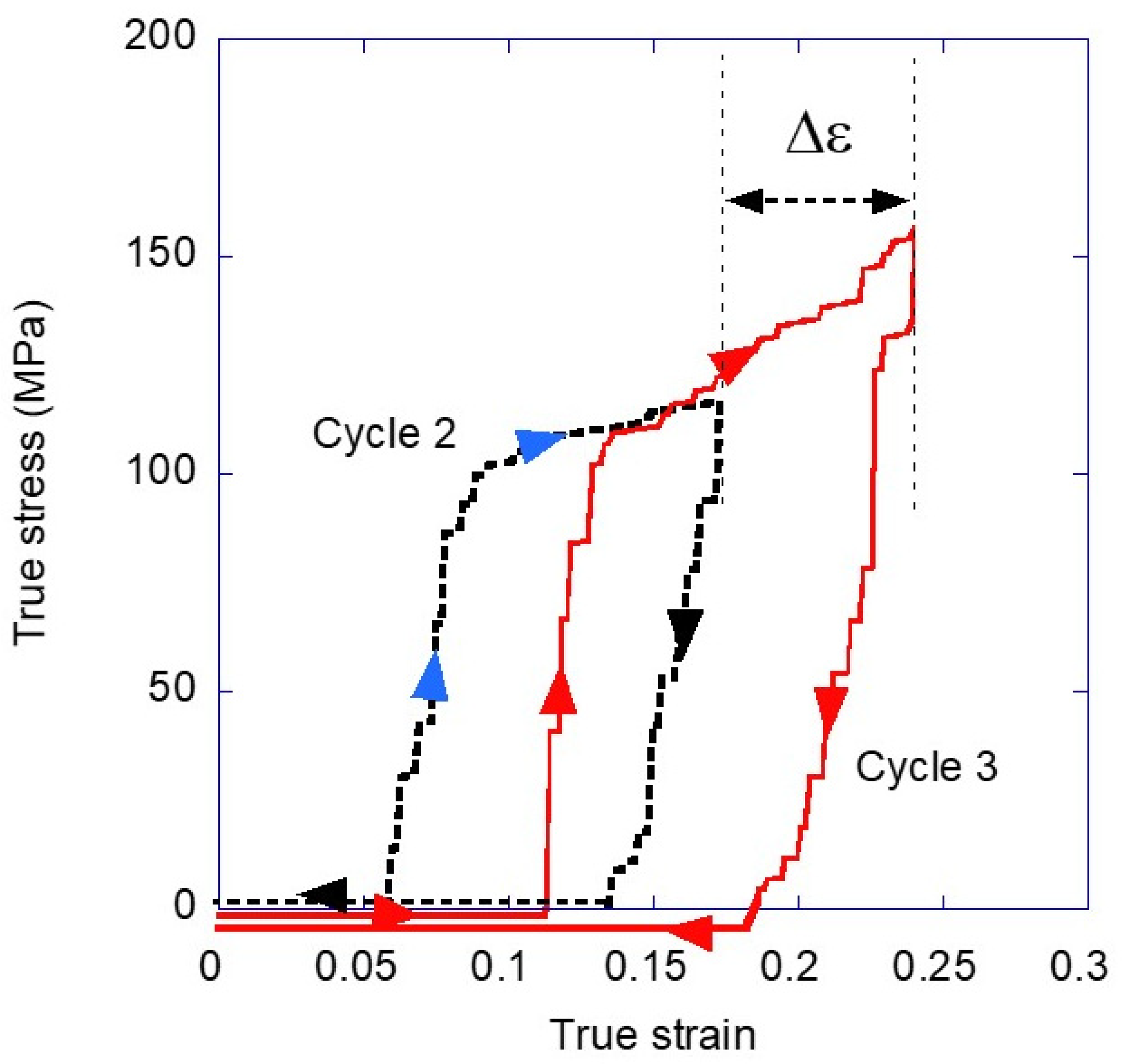
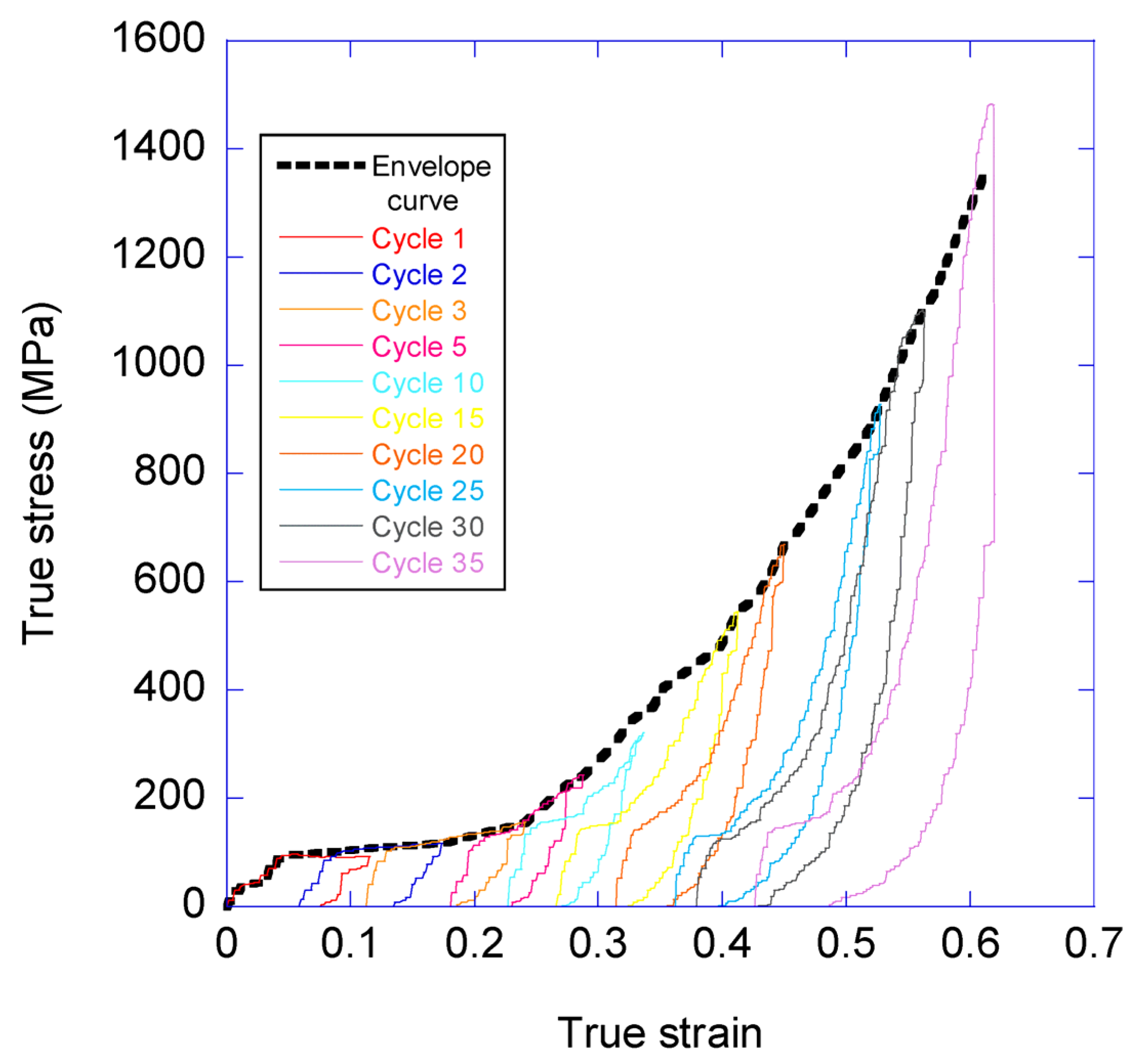
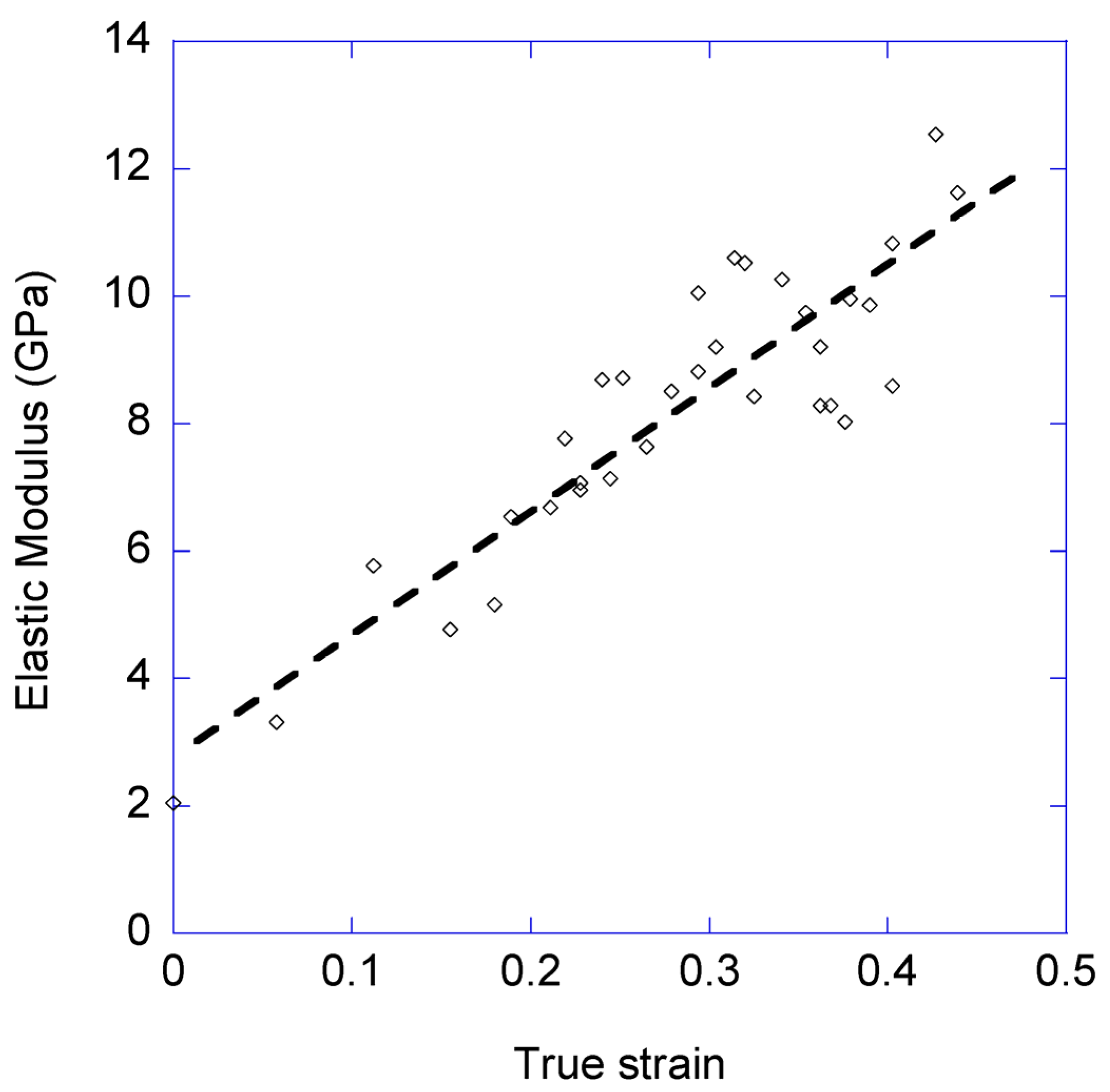
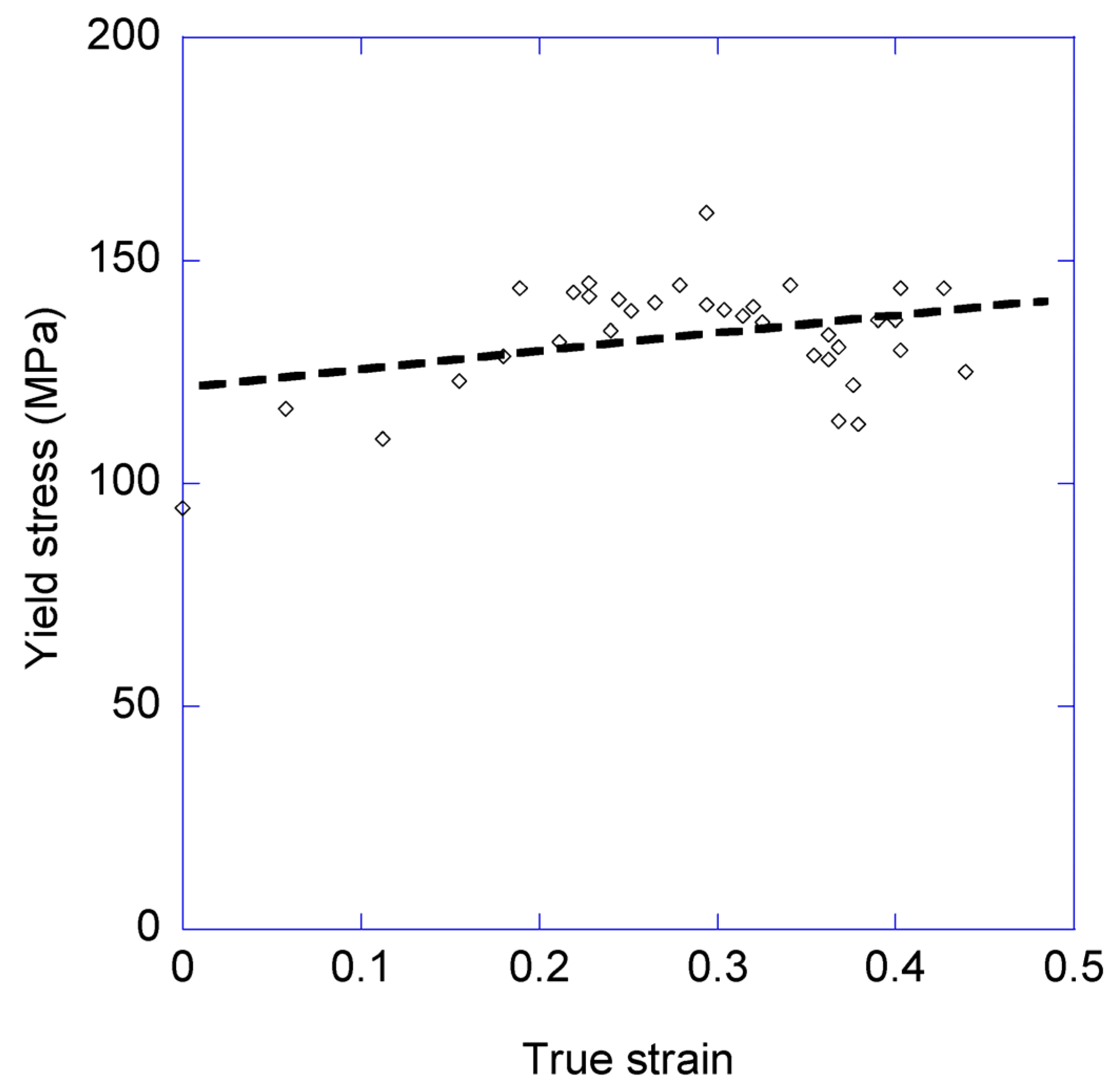
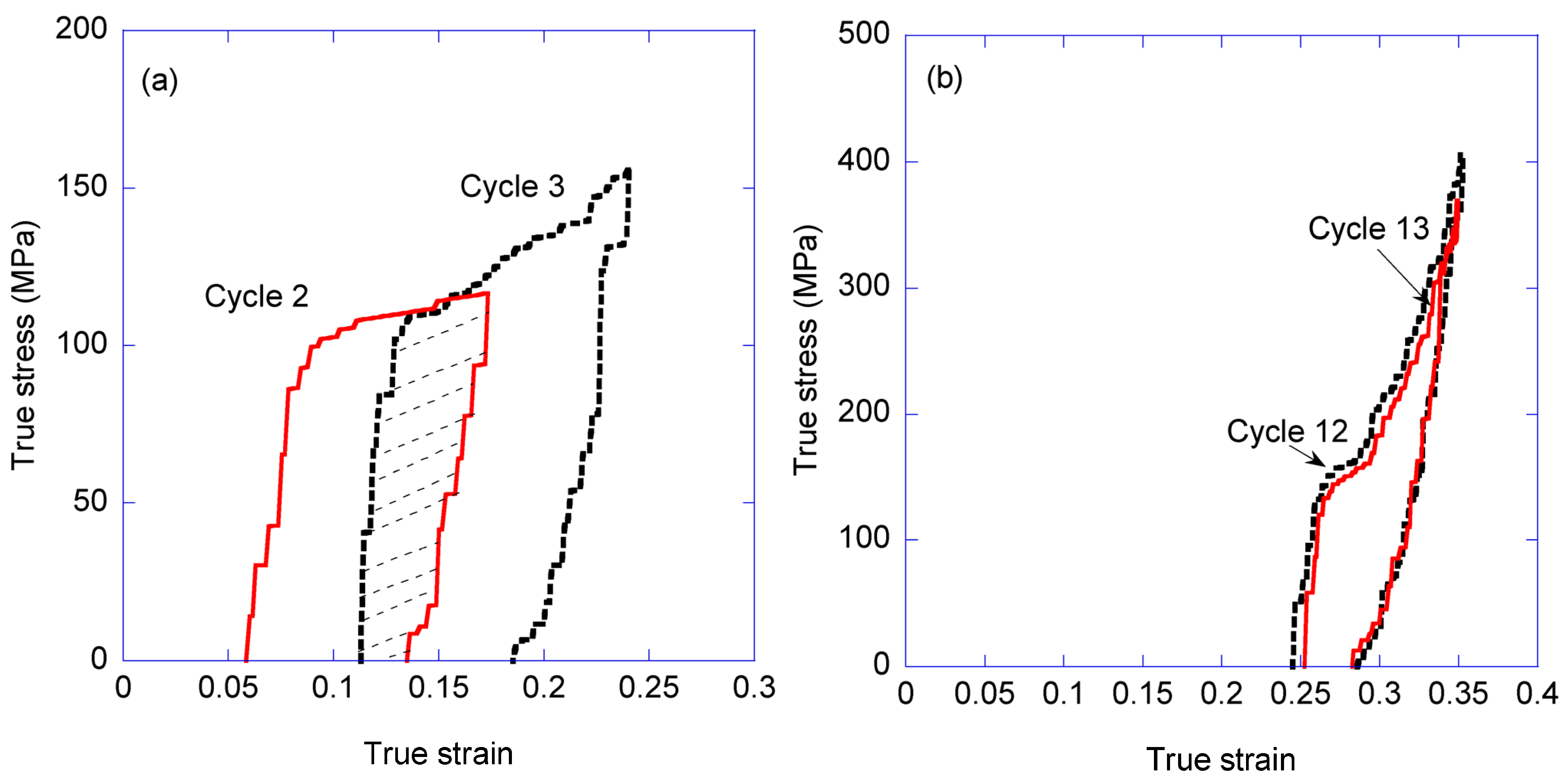
3.1. Variation of the Elastic Modulus and Yield Stress with the Loading-Unloading Cycles
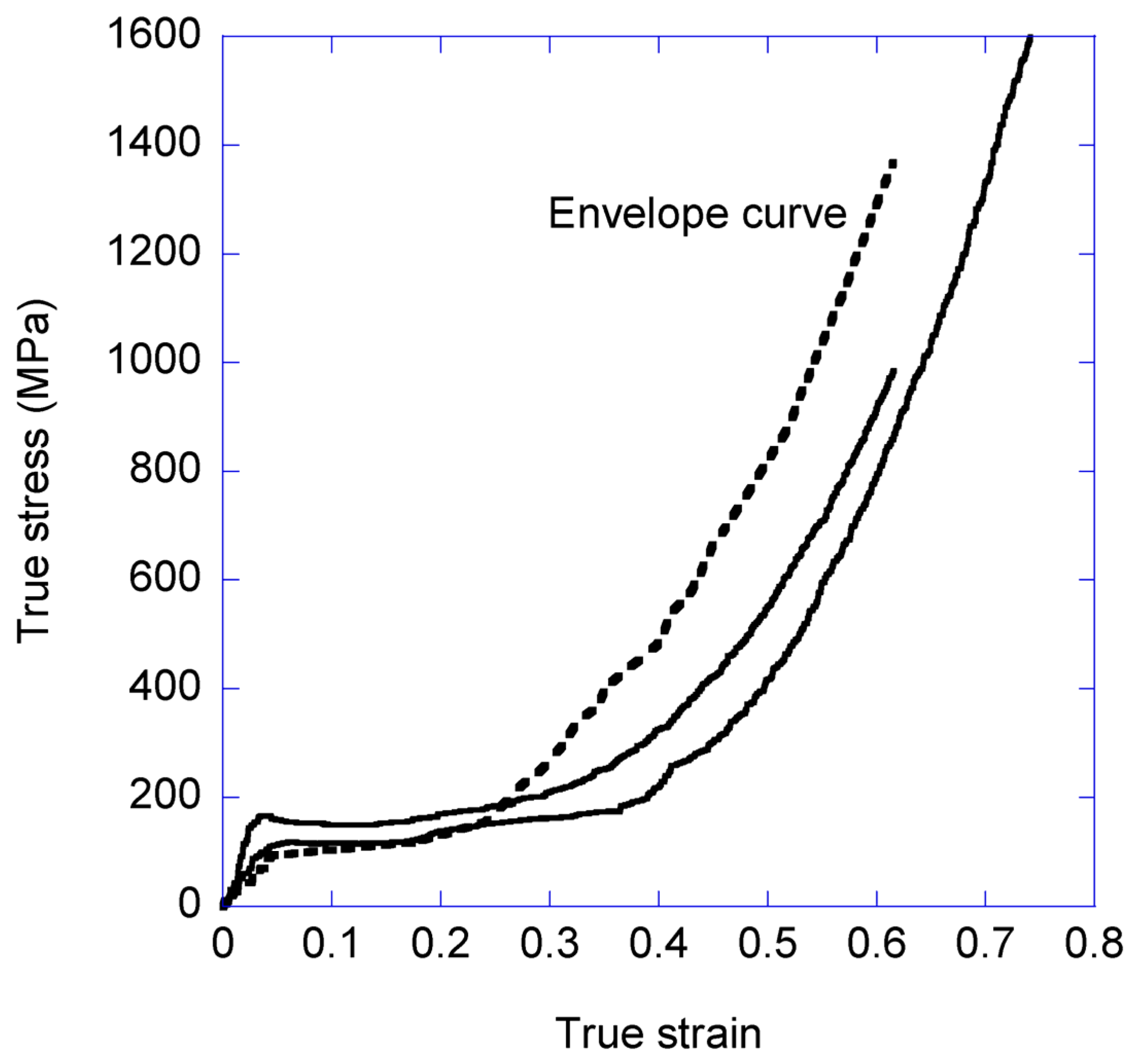
3.2. Energy Absorption and Dissipation with the Loading-Unloading Cycles
4. Discussion
5. Conclusions
- (1)
- The true stress-true strain curve beyond a given value of true strain is independent from the previous loading history of the sample.
- (2)
- The elastic modulus measured in the loading steps increases monotonously with increasing values of true strain reached in the cycles.
- (3)
- In contrast, a marginal variation is found in the values of the yield stress measured in the different cycles.
- (4)
- The ability of spider silk to absorb and dissipate energy is increased if the material is tested following a series of loading-unloading cycles in comparison with the values found in a conventional tensile test. Previous studies show, however, that this irreversible effect can be reverted if the fiber is immersed in water and allowed to supercontract.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lazaris, A.; Arcidiacono, S.; Huang, Y.; Zhou, J.F.; Duguay, F.; Chretien, N.; Welsh, E.A.; Soares, J.W.; Karatzas, C.N. Spider silk fibers spun from soluble recombinant silk produced in mammalian cells. Science 2002, 295, 472–476. [Google Scholar] [CrossRef] [PubMed]
- Andersson, M.; Jia, Q.; Abella, A.; Lee, X.; Landreh, M.; Purhonen, P.; Hebert, H.; Tenje, M.; Robinson, C.V.; Meng, Q.; et al. Biomimetic spinning of artificial spider silk from a chimeric minispidroin. Nat. Chem. Biol. 2017, 13, 262–264. [Google Scholar] [CrossRef] [PubMed]
- Rammensee, S.; Slotta, U.; Scheibel, T.; Bausch, A.R. Assembly mechanism of recombinant spider silk proteins. Proc. Natl. Acad. Sci. USA 2008, 105, 6590–6595. [Google Scholar] [CrossRef] [PubMed]
- Anton, A.M.; Heidebrecht, A.; Mahmood, N.; Beiner, M.; Scheibel, T.; Kremer, F. Foundation of the Outstanding Toughness in Biomimetic and Natural Spider Silk. Biomacromolecules 2017, 18, 3954–3962. [Google Scholar] [CrossRef]
- Blackledge, T.A.; Hayashi, C.Y. Silken toolkits: Biomechanics of silk fibers spun by the orb web spider Argiope argentata (Fabricius 1775). J. Exp. Biol. 2006, 209, 2452–2461. [Google Scholar] [CrossRef]
- Agnarsson, I.; Kuntner, M.; Blackledge, T.A. Bioprospecting Finds the Toughest Biological Material: Extraordinary Silk from a Giant Riverine Orb Spider. PLoS ONE 2010, 5, e11234. [Google Scholar] [CrossRef]
- Meinel, L.; Fajardo, R.; Hofmann, S.; Langer, R.; Chen, J.; Snyder, B.; Vunjak-Novakovic, G.; Kaplan, D. Silk implants for the healing of critical size bone defects. Bone 2005, 37, 688–698. [Google Scholar] [CrossRef]
- Vepari, C.; Kaplan, D. Silk as a biomaterial. Prog. Polym. Sci. 2007, 32, 991–1007. [Google Scholar] [CrossRef]
- Meinel, L.; Hofmann, S.; Betz, O.; Fajardo, R.; Merkle, H.P.; Langer, R.; Evans, C.H.; Vunjak-Novakovic, G.; Kaplan, D.L. Osteogenesis by human mesenchymal stem cells cultured on silk biomaterials: Comparison of adenovirus mediated gene transfer and protein delivery of BMP-2. Biomaterials 2006, 27, 4993–5002. [Google Scholar] [CrossRef]
- Slotta, U.K.; Rammensee, S.; Gorb, S.; Scheibel, T. An engineered spider silk protein forms microspheres. Angew. Chem. Int. Ed. 2008, 47, 4592–4594. [Google Scholar] [CrossRef]
- Aoyanagi, Y.; Okumura, K. Simple Model for the Mechanics of Spider Webs. Phys. Rev. Lett. 2010, 104, 038102. [Google Scholar] [CrossRef] [PubMed]
- Cranford, S.W.; Tarakanova, A.; Pugno, N.M.; Buehler, M.J. Nonlinear material behaviour of spider silk yields robust webs. Nature 2012, 482, 72–76. [Google Scholar] [CrossRef]
- Kiakojouri, F.; De Biagi, V.; Abbracciavento, L. Design for robustness: Bio-inspired perspectives in Structural Engineering. Biomimetics 2023, 8, 95. [Google Scholar] [CrossRef] [PubMed]
- Elices, M.; Perez-Rigueiro, J.; Plaza, G.; Guinea, G.V. Recovery in spider silk fibers. J. Appl. Polym. Sci. 2004, 92, 3537–3541. [Google Scholar] [CrossRef]
- Work, R.W. Dimensions, Birefringences, and Force-Elongation Behavior of Major and Minor Ampullate Silk Fibers from Orb-Web-Spinning Spiders—Effects of Wetting on these Properties. Text Res. J. 1977, 47, 650–662. [Google Scholar] [CrossRef]
- Work, R.W.; Morosoff, N. A Physicochemical Study of the Supercontraction of Spider Major Ampullate Silk Fibers. Text Res. J. 1982, 52, 349–356. [Google Scholar] [CrossRef]
- Boutry, C.; Blackledge, T.A. Evolution of supercontraction in spider silk: Structure-function relationship from tarantulas to orb-weavers. J. Exp. Biol. 2010, 213, 3505–3514. [Google Scholar] [CrossRef]
- Blackledge, T.A.; Boutry, C.; Wong, S.; Baji, A.; Dhinojwala, A.; Sahni, V.; Agnarsson, I. How super is supercontraction? Persistent versus cyclic responses to humidity in spider dragline silk. J. Exp. Biol. 2009, 212, 1980–1988. [Google Scholar] [CrossRef]
- Blackledge, T.A.; Pérez-Rigueiro, J.; Plaza, G.R.; Perea, B.; Navarro, A.; Guinea, G.V.; Elices, M. Sequential origin in the high performance properties of orb spider dragline silk. Sci. Rep. 2012, 2, 782. [Google Scholar] [CrossRef]
- Work, R.W.; Emerson, P.D. An Apparatus and Technique for the Forcible Silking of Spiders. J. Arachnol. 1982, 10, 1–10. [Google Scholar]
- Perez-Rigueiro, J.; Viney, C.; Llorca, J.; Elices, M. Silkworm silk as an engineering material. J. Appl. Polym. Sci. 1998, 70, 2439–2447. [Google Scholar] [CrossRef]
- Perez-Riguero, J.; Elices, M.; Llorca, J.; Viney, C. Tensile properties of Argiope trifasciata drag line silk obtained from the spider’s web. J. Appl. Polym. Sci. 2001, 82, 2245–2251. [Google Scholar] [CrossRef]
- Perez-Rigueiro, J.; Elices, M.; Guinea, G.V. Controlled supercontraction tailors the tensile behaviour of spider silk. Polymer 2003, 44, 3733–3736. [Google Scholar] [CrossRef]
- Guinea, G.V.; Perez-Rigueiro, J.; Plaza, G.R.; Elices, M. Volume constancy during stretching of spider silk. Biomacromolecules 2006, 7, 2173–2177. [Google Scholar] [CrossRef]
- Perez-Rigueiro, J.; Elices, M.; Plaza, G.; Real, J.I.; Guinea, G.V. The effect of spinning forces on spider silk properties. J. Exp. Biol. 2005, 208, 2633–2639. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, G.V.; Plaza, G.R.; Real, J.I.; Perez-Rigueiro, J. Example of microprocessing in a natural polymeric fiber: Role of reeling stress in spider silk. J. Mater Res. 2006, 21, 1931–1938. [Google Scholar] [CrossRef]
- Garrote, J.; Ruiz, V.; Troncoso, O.P.; Torres, F.G.; Arnedo, M.; Elices, M.; Guinea, G.V.; Perez-Rigueiro, J. Application of the Spider Silk Standardization Initiative ((SI)-I-3) methodology to the characterization of major ampullate gland silk fibers spun by spiders from Pantanos de Villa wetlands (Lima, Peru). J. Mech. Behav. Biomed. Mater. 2020, 111, 104023. [Google Scholar] [CrossRef]
- Madurga, R.; Plaza, G.R.; Blackledge, T.A.; Guinea, G.V.; Elices, M.; Perez-Rigueiro, J. Material properties of evolutionary diverse spider silks described by variation in a single structural parameter. Sci. Rep. 2016, 6, 18991. [Google Scholar] [CrossRef]
- ASTM D5045-99; Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials. American Society for Testing and Materials: West Conshohocken, PA, USA, 1983; E-399.
- Heim, M.; Keerl, D.; Scheibel, T. Spider silk: From soluble protein to extraordinary fiber. Angew. Chem. Int. Ed. Engl. 2009, 48, 3584–3596. [Google Scholar] [CrossRef]
- Perez-Rigueiro, J.; Elices, M.; Plaza, G.R.; Guinea, G. Basic Principles in the Design of Spider Silk Fibers. Molecules 2021, 26, 1794. [Google Scholar] [CrossRef]
- Nova, A.; Keten, S.; Pugno, N.M.; Redaelli, A.; Buehler, M.J. Molecular and Nanostructural Mechanisms of Deformation, Strength and Toughness of Spider Silk Fibrils. Nano Lett. 2010, 10, 2626–2634. [Google Scholar] [CrossRef] [PubMed]
- Keten, S.; Buehler, M.J. Nanostructure and molecular mechanics of spider dragline silk protein assemblies. J. R. Soc. Interface 2010, 7, 1709–1721. [Google Scholar] [CrossRef] [PubMed]
- Keten, S.; Xu, Z.P.; Ihle, B.; Buehler, M.J. Nanoconfinement controls stiffness, strength and mechanical toughness of beta-sheet crystals in silk. Nat. Mater. 2010, 9, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Belen Perea, G.; Solanas, C.; Plaza, G.R.; Guinea, G.V.; Jorge, I.; Vazquez, J.; Perez Mateos, J.M.; Mari-Buye, N.; Elices, M.; Perez-Rigueiro, J. Unexpected behavior of irradiated spider silk links conformational freedom to mechanical performance. Soft Matter 2015, 11, 4868–4878. [Google Scholar] [CrossRef]
- Pacios, L.F.; Arguelles, J.; Hayashi, C.Y.; Guinea, G.V.; Elices, M.; Perez-Rigueiro, J. Differences in the Elastomeric Behavior of Polyglycine-Rich Regions of Spidroin 1 and 2 Proteins. Polymers 2022, 14, 5263. [Google Scholar] [CrossRef]
- Gosline, J.M.; Guerette, P.A.; Ortlepp, C.S.; Savage, K.N. The mechanical design of spider silks: From fibroin sequence to mechanical function. J. Exp. Biol. 1999, 202, 3295–3303. [Google Scholar] [CrossRef]
- Madsen, B.; Shao, Z.Z.; Vollrath, F. Variability in the mechanical properties of spider silks on three levels: Interspecific, intraspecific and intraindividual. Int. J. Biol. Macromol. 1999, 24, 301–306. [Google Scholar] [CrossRef]
- Liu, Y.; Shao, Z.Z.; Vollrath, F. Elasticity of spider silks. Biomacromolecules 2008, 9, 1782–1786. [Google Scholar] [CrossRef]
- Riekel, C.; Branden, C.; Craig, C.; Ferrero, C.; Heidelbach, F.; Muller, M. Aspects of X-ray diffraction on single spider fibers. Int. J. Biol. Macromol. 1999, 24, 179–186. [Google Scholar] [CrossRef]
- Madurga, R.; Blackledge, T.A.; Perea, B.; Plaza, G.R.; Riekel, C.; Burghammer, M.; Elices, M.; Guinea, G.; Perez-Rigueiro, J. Persistence and variation in microstructural design during the evolution of spider silk. Sci. Rep. 2015, 5, 14820. [Google Scholar] [CrossRef]
- Asakura, T.; Tasei, Y.; Aoki, A.; Nishimura, A. Mixture of Rectangular and Staggered Packing Arrangements of Polyalanine Region in Spider Dragline Silk in Dry and Hydrated States As Revealed by C-13 NMR and X-ray Diffraction. Macromolecules 2018, 51, 1058–1068. [Google Scholar] [CrossRef]
- Termonia, Y. Molecular Modeling of Spider Silk Elasticity. Macromolecules 1994, 27, 7378–7381. [Google Scholar] [CrossRef]
- Termonia, Y. Molecular modelling of the stress/strainbehaviour of spider dragline. In Amsterdam; Elices, M., Ed.; Pergamon Press: Oxford, UK, 2000; pp. 335–349. [Google Scholar]
- Riekel, C.; Muller, M.; Vollrath, F. In situ X-ray diffraction during forced silking of spider silk. Macromolecules 1999, 32, 4464–4466. [Google Scholar] [CrossRef]
- Savage, K.N.; Guerette, P.A.; Gosline, J.M. Supercontraction stress in spider webs. Biomacromolecules 2004, 5, 675–679. [Google Scholar] [CrossRef] [PubMed]
- Gosline, J.M.; Denny, M.W.; Demont, M.E. Spider Silk as Rubber. Nature 1984, 309, 551–552. [Google Scholar] [CrossRef]
- Rousseau, M.E.; Lefevre, T.; Beaulieu, L.; Asakura, T.; Pezolet, M. Study of protein conformation and orientation in silkworm and spider silk fibers using Raman microspectroscopy. Biomacromolecules 2004, 5, 2247–2257. [Google Scholar] [CrossRef]
- Rousseau, M.; Lefevre, T.; Pezolet, M. Conformation and Orientation of Proteins in Various Types of Silk Fibers Produced by Nephila clavipes Spiders. Biomacromolecules 2009, 10, 2945–2953. [Google Scholar] [CrossRef]
- Gatesy, J.; Hayashi, C.; Motriuk, D.; Woods, J.; Lewis, R. Extreme diversity, conservation, and convergence of spider silk fibroin sequences. Science 2001, 291, 2603–2605. [Google Scholar] [CrossRef]
- Babb, P.L.; Lahens, N.F.; Correa-Garhwal, S.M.; Nicholson, D.N.; Kim, E.J.; Hogenesch, J.B.; Kuntner, M.; Higgins, L.; Hayashi, C.Y.; Agnarsson, I.; et al. The Nephila clavipes genome highlights the diversity of spider silk genes and their complex expression. Nat. Genet. 2017, 49, 895–903. [Google Scholar] [CrossRef]
- Asakura, T.; Suzuki, Y.; Nakazawa, Y.; Yazawa, K.; Holland, G.P.; Yarger, J.L. Silk structure studied with nuclear magnetic resonance. Prog. Nucl. Magn. Reason. Spectrosc. 2013, 69, 23–68. [Google Scholar] [CrossRef]
- Jenkins, J.E.; Creager, M.S.; Butler, E.B.; Lewis, R.V.; Yarger, J.L.; Holland, G.P. Solid-state NMR evidence for elastin-like beta-turn structure in spider dragline silk. Chem. Commun. 2010, 46, 6714–6716. [Google Scholar] [CrossRef] [PubMed]
- Plaza, G.R.; Pérez-Rigueiro, J.; Riekel, C.; Perea, G.B.; Agulló-Rueda, F.; Burghammer, M.; Guinea, G.V.; Elices, M. Relationship between microstructure and mechanical properties in spider silk fibers: Two regimes in the microstructural changes. Soft Matter 2012, 8, 6015–6026. [Google Scholar] [CrossRef]
- Perea, G.B.; Riekel, C.; Guinea, G.V.; Madurga, R.; Daza, R.; Burghammer, M.; Hayashi, C.; Elices, M.; Plaza, G.R.; Perez-Rigueiro, J. Identification and dynamics of polyglycine II nanocrystals in Argiope trifasciata flagelliform silk. Sci. Rep. 2013, 3, 3061. [Google Scholar] [CrossRef]
- Work, R. Viscoelastic behaviour and wet supercontraction of major ampullate silk fibres of certain orb-web-building spiders (Araneae). J. Exp. Biol. 1985, 118, 379–404. [Google Scholar] [CrossRef]
- Brooks, A.E.; Brothers, T.J.; Creager, M.S.; Lewis, R.V. A novel methodology to explore the viscoelasticity of spider major ampullate silk. J. Appl. Biomater. Biomech. 2007, 5, 158–165. [Google Scholar]
- Sahni, V.; Blackledge, T.A.; Dhinojwala, A. Viscoelastic solids explain spider web stickiness. Nat. Commun. 2010, 1, 19. [Google Scholar] [CrossRef]
- Emile, O.; Le Floch, A.; Vollrath, F. Shape memory in spider draglines. Biopolymers 2006, 440, 621. [Google Scholar] [CrossRef]
- Ashley, S. Alchemy of a supermetal—Serendipity delivers a process that may cut the cost of a high-tech material. Sci. Am. 2003, 289, 38–40. [Google Scholar] [CrossRef]
- Strobl, G. The Physics of Polymers; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Kartsovnik, V.I.; Volchenkov, D. Elastic Entropic Forces in Polymer Deformation. Entropy 2022, 24, 1260. [Google Scholar] [CrossRef]
- Cetinkaya, M.; Xiao, S.; Graeter, F. Effects of crystalline subunit size on silk fiber mechanics. Soft Matter 2011, 7, 8142–8148. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, J.; Peng, B.; Hu, B.; Chen, X.; Shao, Z. Understanding the Mechanical Properties and Structure Transition of Antheraea pernyi Silk Fiber Induced by Its Contraction. Biomacromolecules 2018, 19, 1999–2006. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shao, Z.Z.; Vollrath, F. Extended wet-spinning can modify spider silk properties. Chem. Commun. 2005, 19, 2489–2491. [Google Scholar] [CrossRef] [PubMed]
- Guinea, G.V.; Elices, M.; Plaza, G.R.; Perea, G.B.; Daza, R.; Riekel, C.; Agullo-Rueda, F.; Hayashi, C.; Zhao, Y.; Perez-Rigueiro, J. Minor Ampullate Silks from Nephila and Argiope Spiders: Tensile Properties and Microstructural Characterization. Biomacromolecules 2012, 13, 2087–2098. [Google Scholar] [CrossRef] [PubMed]
- Martel, A.; Burghammer, M.; Davies, R.J.; Riekel, C. Thermal Behavior of Bombyx mori silk: Evolution of crystalline parameters, molecular structure, and mechanical properties. Biomacromolecules 2007, 8, 3548–3556. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Wu, L.; Hu, M.; Tang, S.; Qiu, Z.; Lv, T.; Elices, M.; Guinea, G.V.; Pérez-Rigueiro, J. Variation in the Elastic Modulus and Increased Energy Dissipation Induced by Cyclic Straining of Argiope bruennichi Major Ampullate Gland Silk. Biomimetics 2023, 8, 164. https://doi.org/10.3390/biomimetics8020164
Jiang P, Wu L, Hu M, Tang S, Qiu Z, Lv T, Elices M, Guinea GV, Pérez-Rigueiro J. Variation in the Elastic Modulus and Increased Energy Dissipation Induced by Cyclic Straining of Argiope bruennichi Major Ampullate Gland Silk. Biomimetics. 2023; 8(2):164. https://doi.org/10.3390/biomimetics8020164
Chicago/Turabian StyleJiang, Ping, Lihua Wu, Menglei Hu, Sisi Tang, Zhimin Qiu, Taiyong Lv, Manuel Elices, Gustavo V. Guinea, and José Pérez-Rigueiro. 2023. "Variation in the Elastic Modulus and Increased Energy Dissipation Induced by Cyclic Straining of Argiope bruennichi Major Ampullate Gland Silk" Biomimetics 8, no. 2: 164. https://doi.org/10.3390/biomimetics8020164
APA StyleJiang, P., Wu, L., Hu, M., Tang, S., Qiu, Z., Lv, T., Elices, M., Guinea, G. V., & Pérez-Rigueiro, J. (2023). Variation in the Elastic Modulus and Increased Energy Dissipation Induced by Cyclic Straining of Argiope bruennichi Major Ampullate Gland Silk. Biomimetics, 8(2), 164. https://doi.org/10.3390/biomimetics8020164






