Comparative Analysis of the Self-Propelled Locomotion of a Pitching Airfoil near the Flat and Wavy Ground
Abstract
1. Introduction
2. Problem Description and Methodology
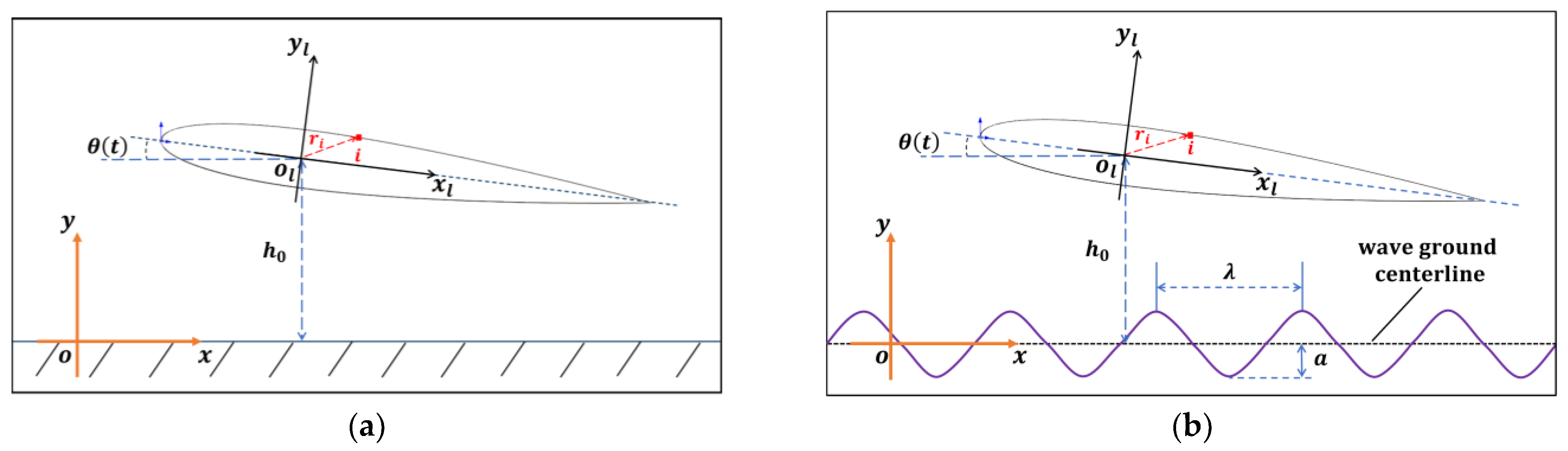
2.1. Problem Description
- The translational velocity in inertial frame is defined as:
- 2.
- The linear velocity generated by the airfoil rotating around the COM in the local rotating frame is defined as:
2.2. Numerical Method
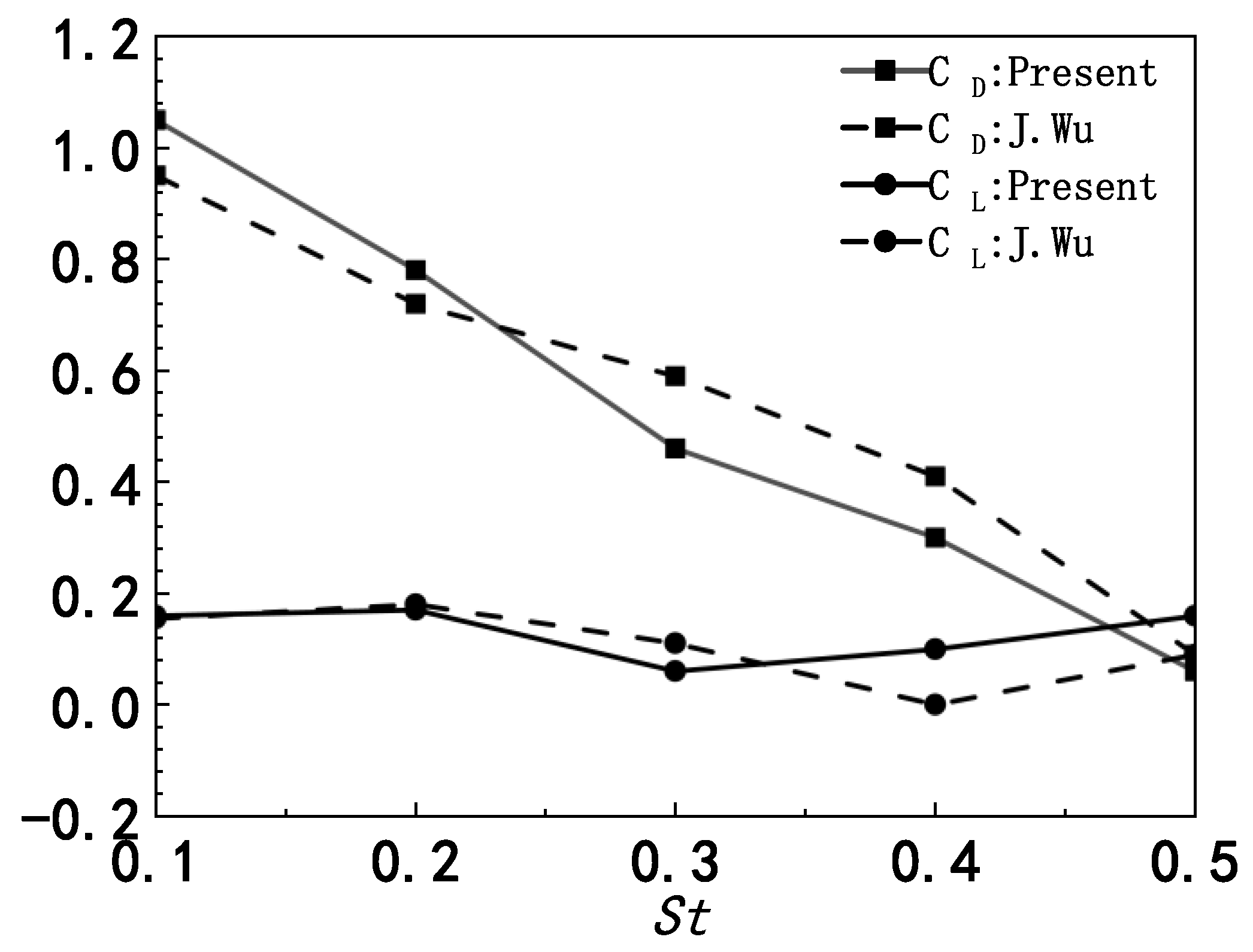
2.3. Numerical Validation
2.3.1. Immersed Boundary Method Validation
2.3.2. Mesh and Time Step Sensitivity Test
3. Results
3.1. Unsteady Motion above the Flat Ground
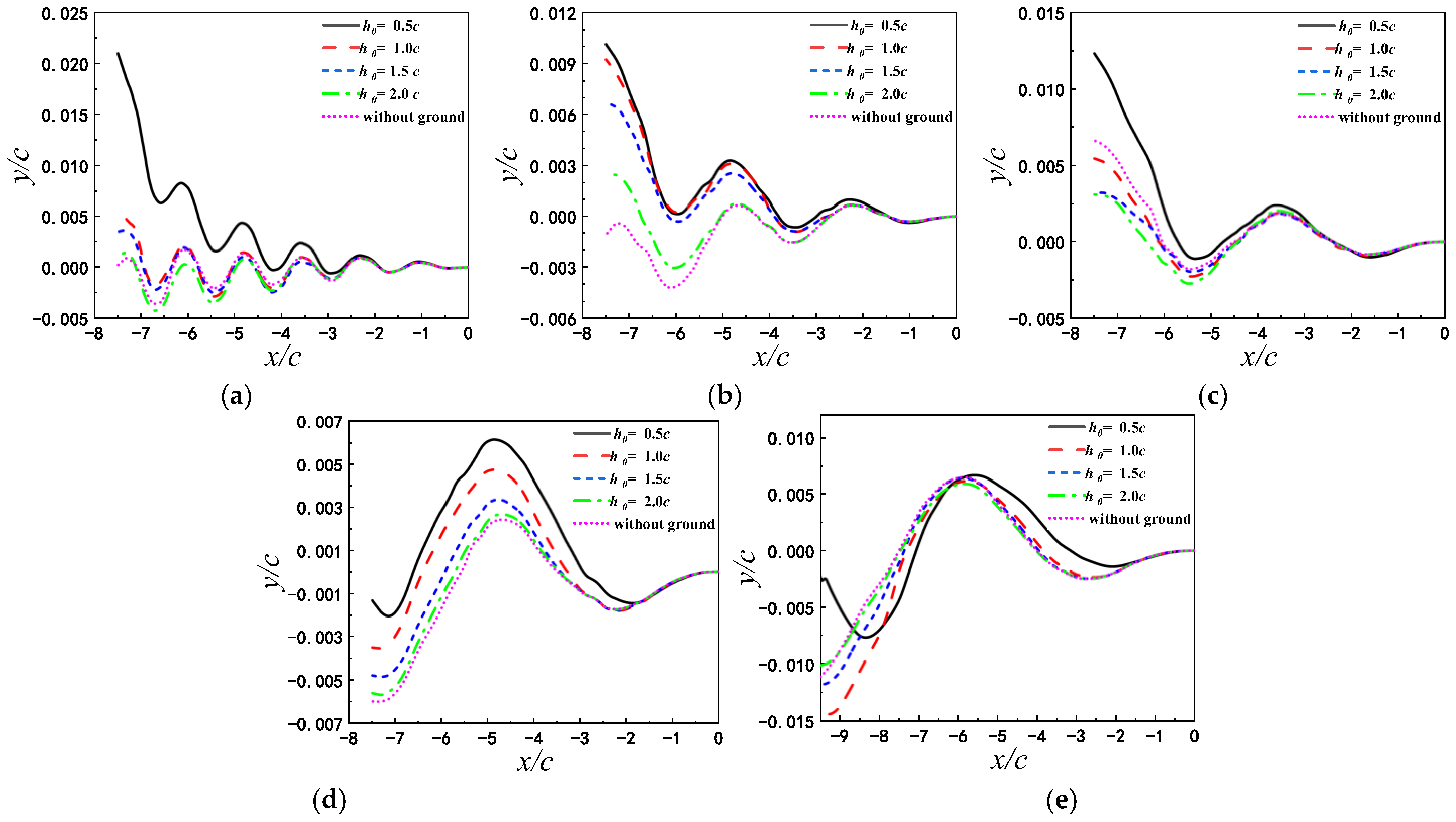
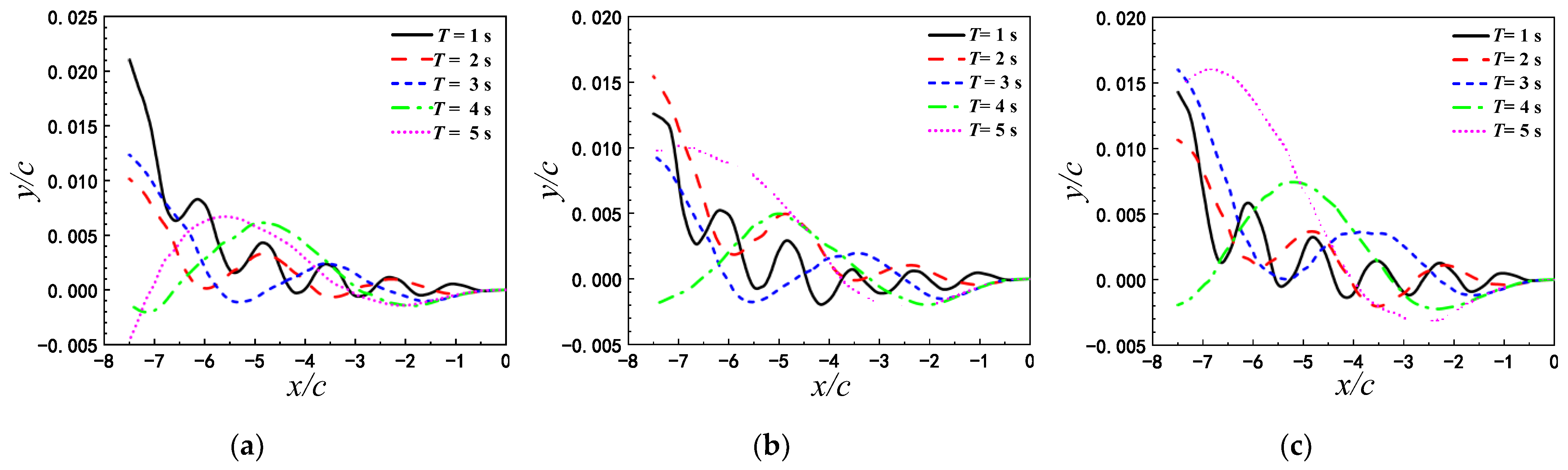
3.1.1. Trajectory
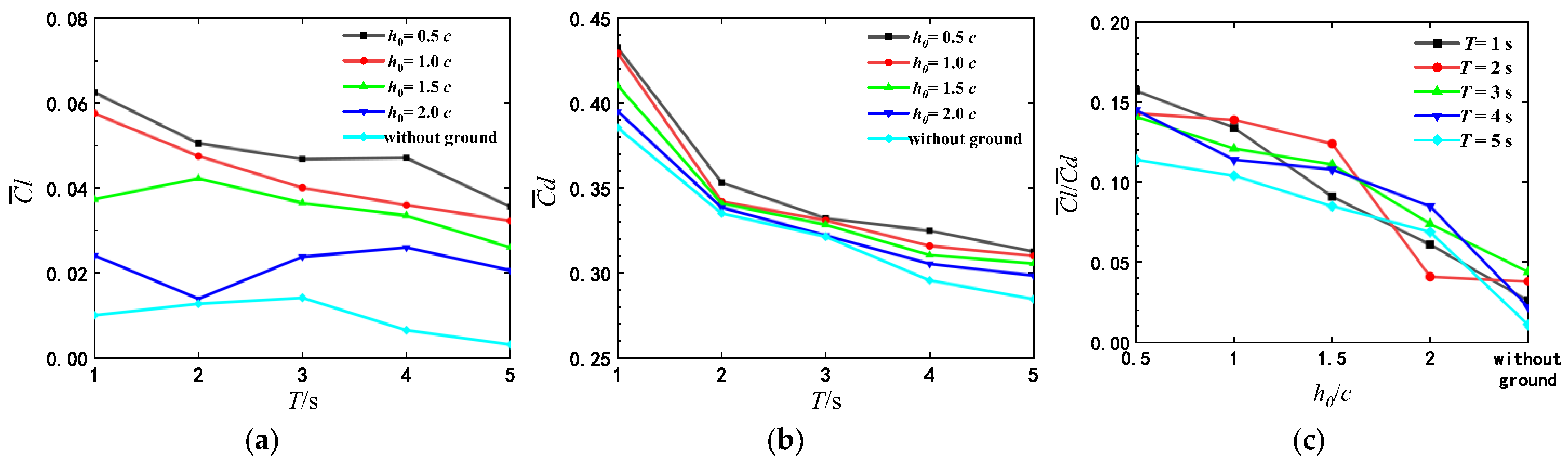
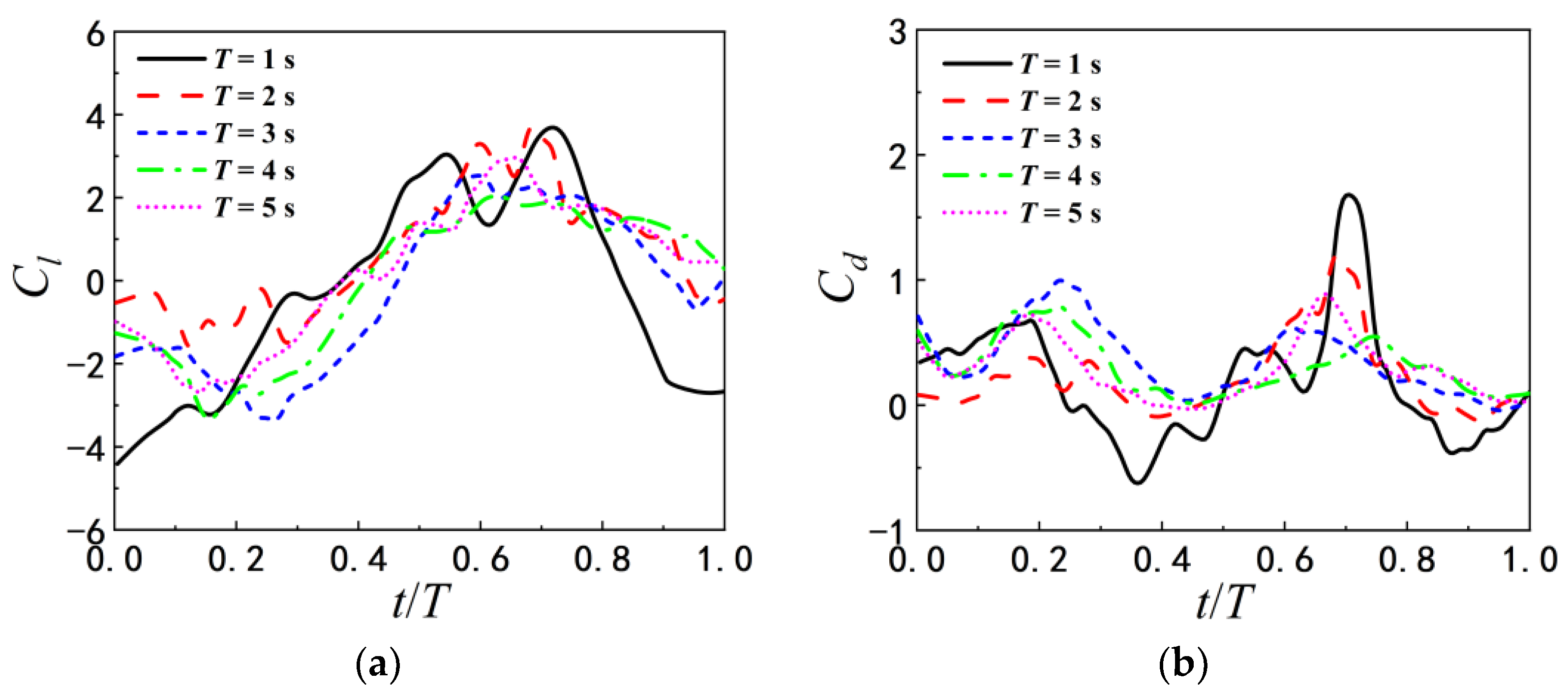
3.1.2. Hydrodynamics
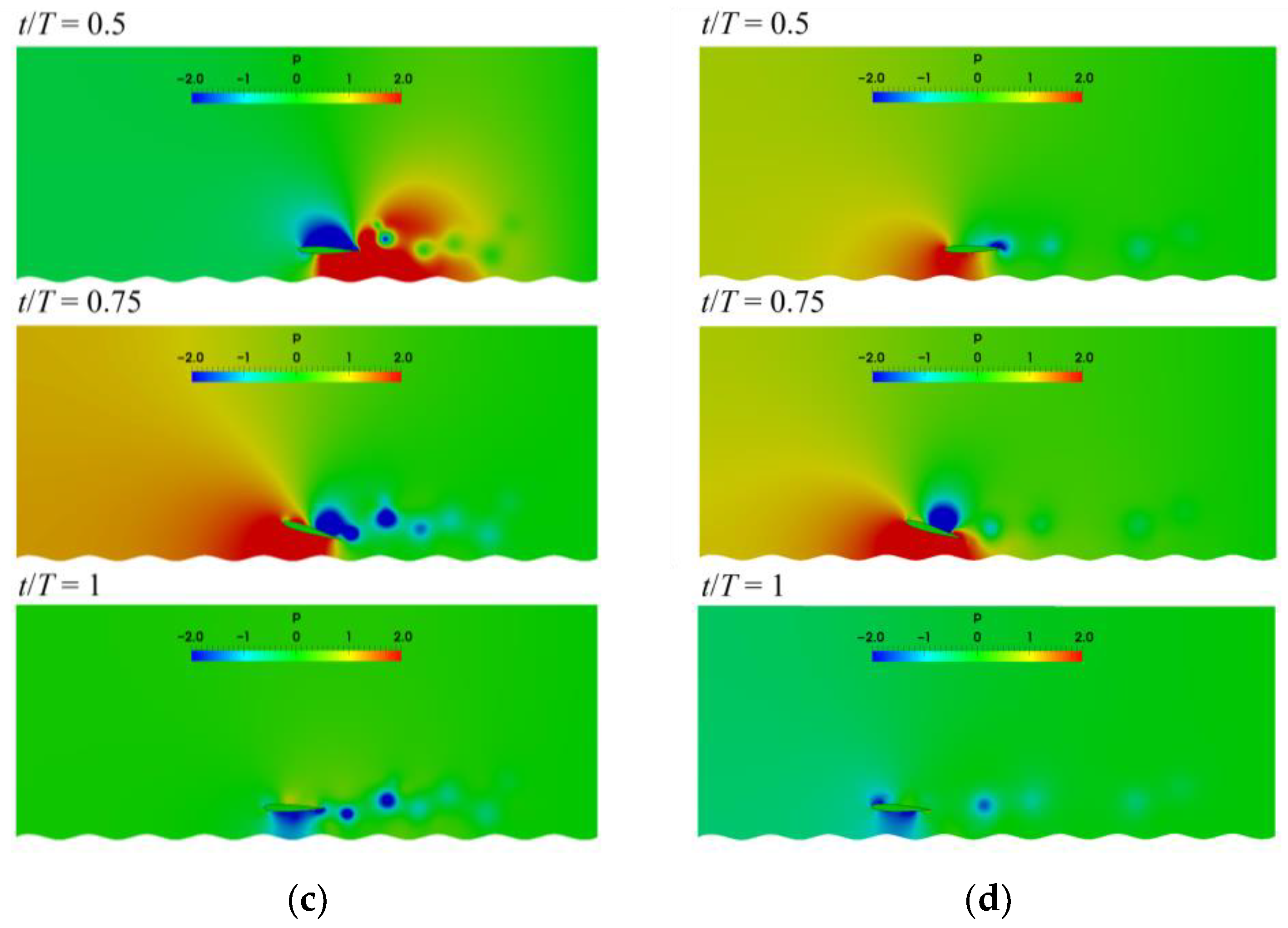
3.2. Unsteady Motion above the Wavy Ground
3.2.1. Trajectory
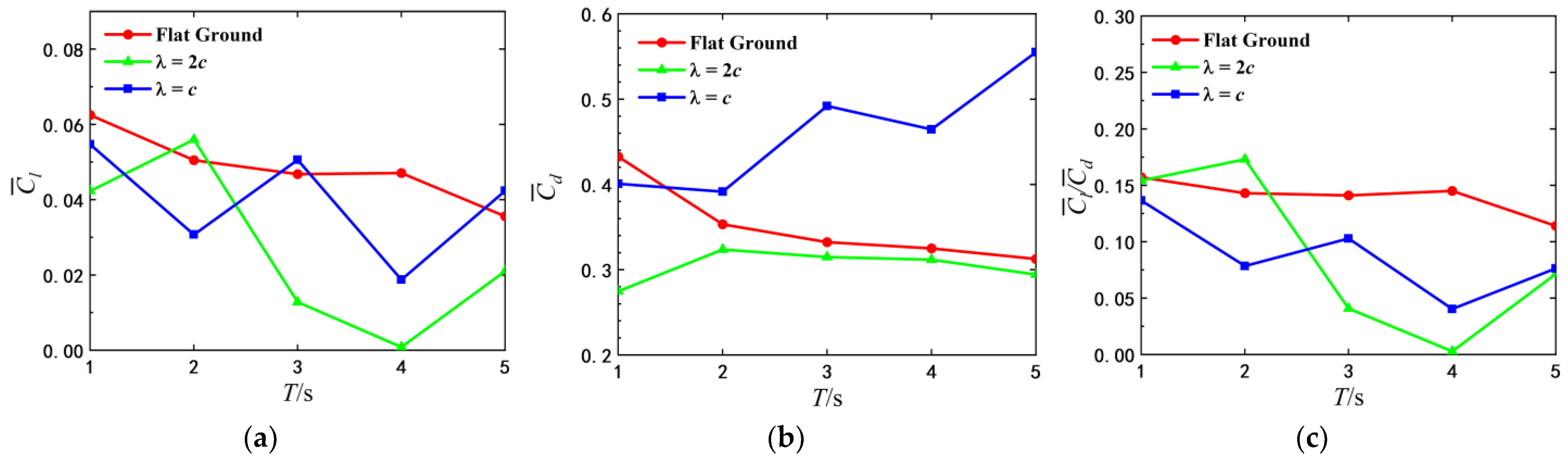
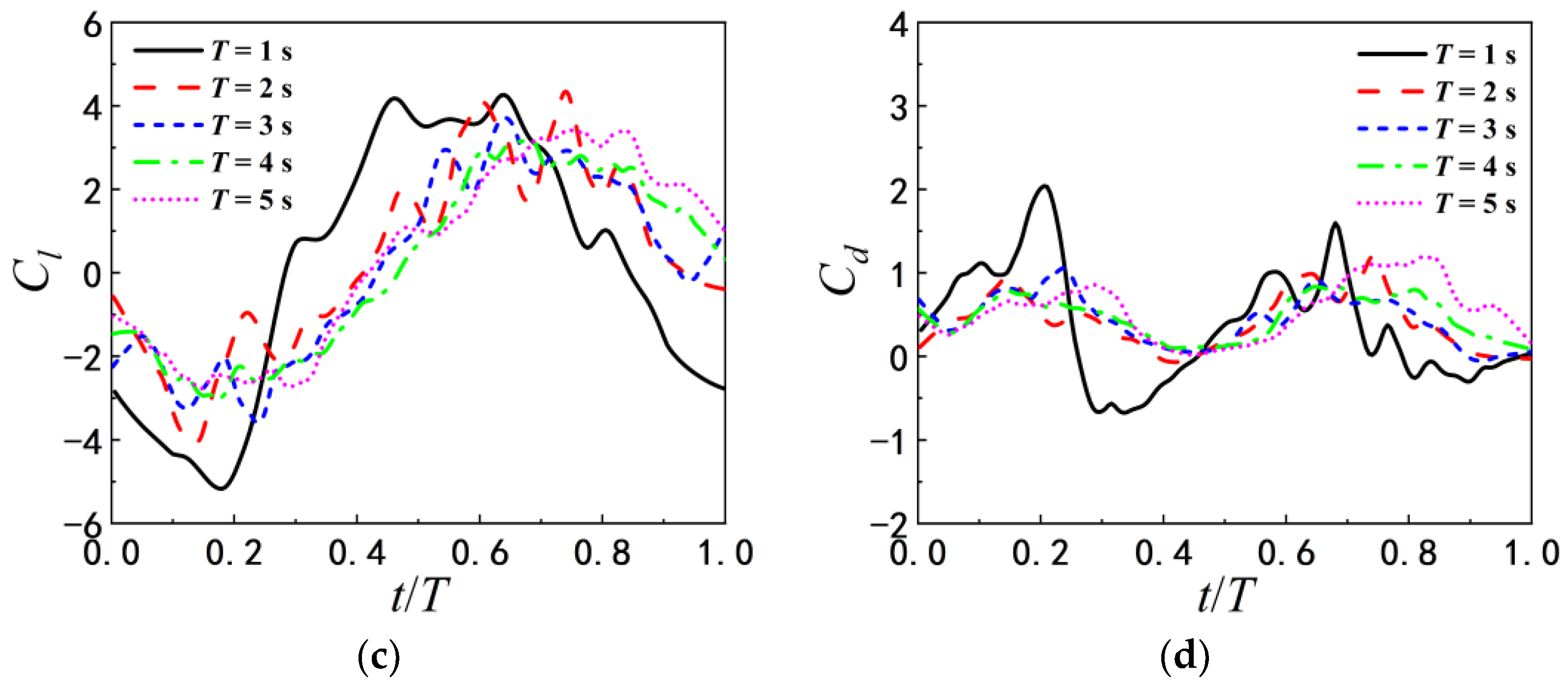
3.2.2. Hydrodynamics
3.3. Mechanism of Ground Effect on the Self-Propelled Airfoil
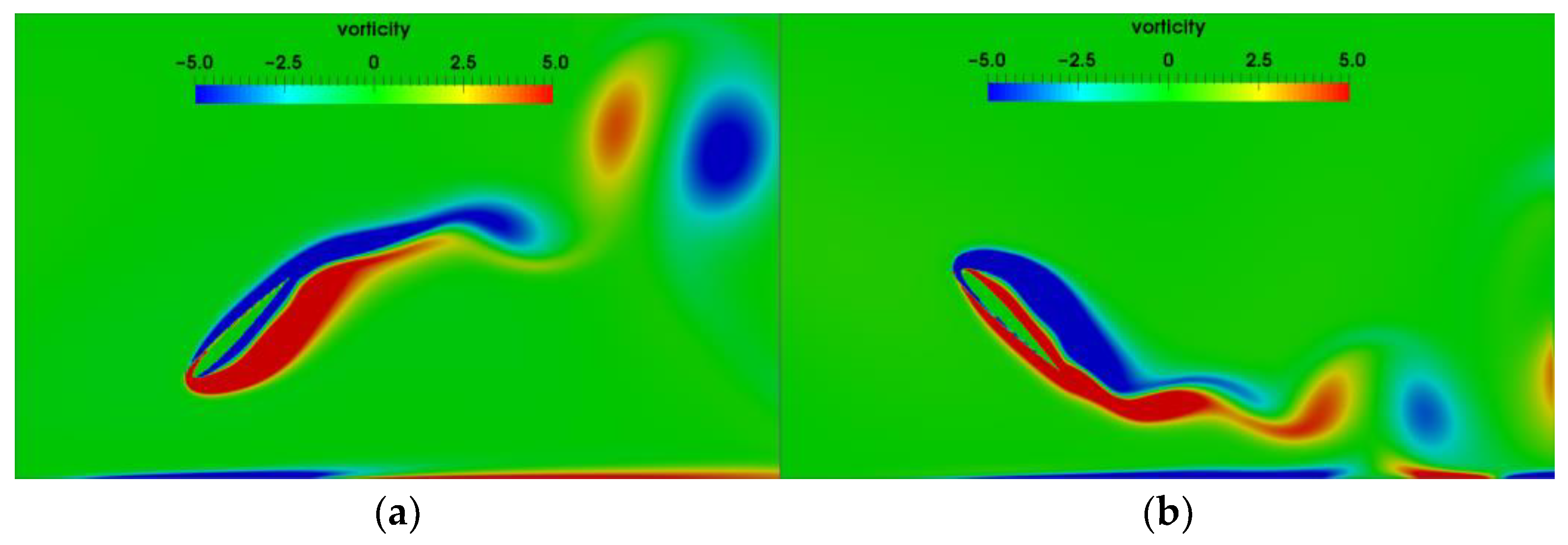
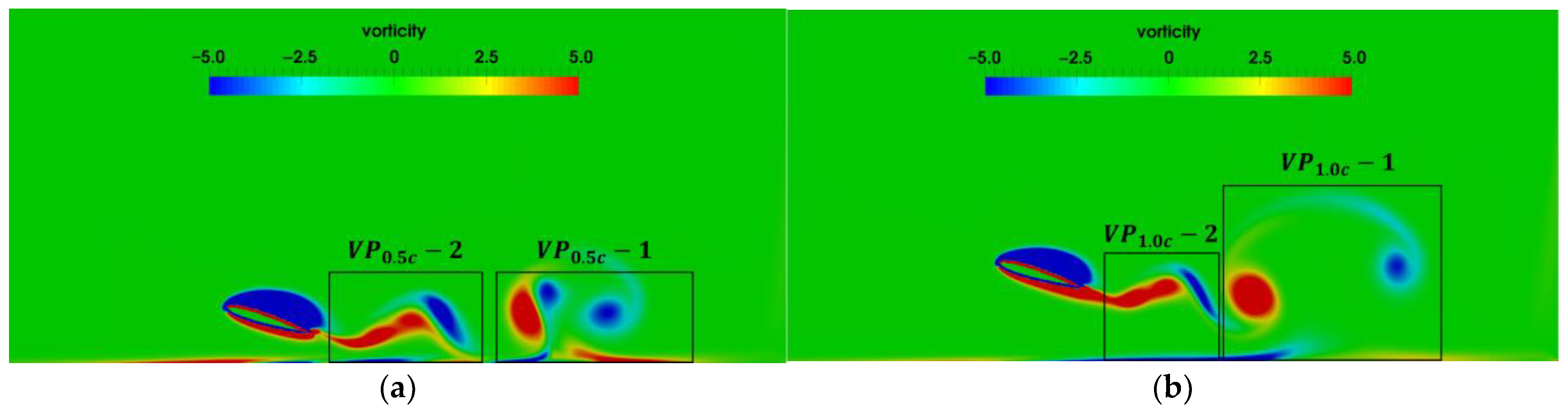
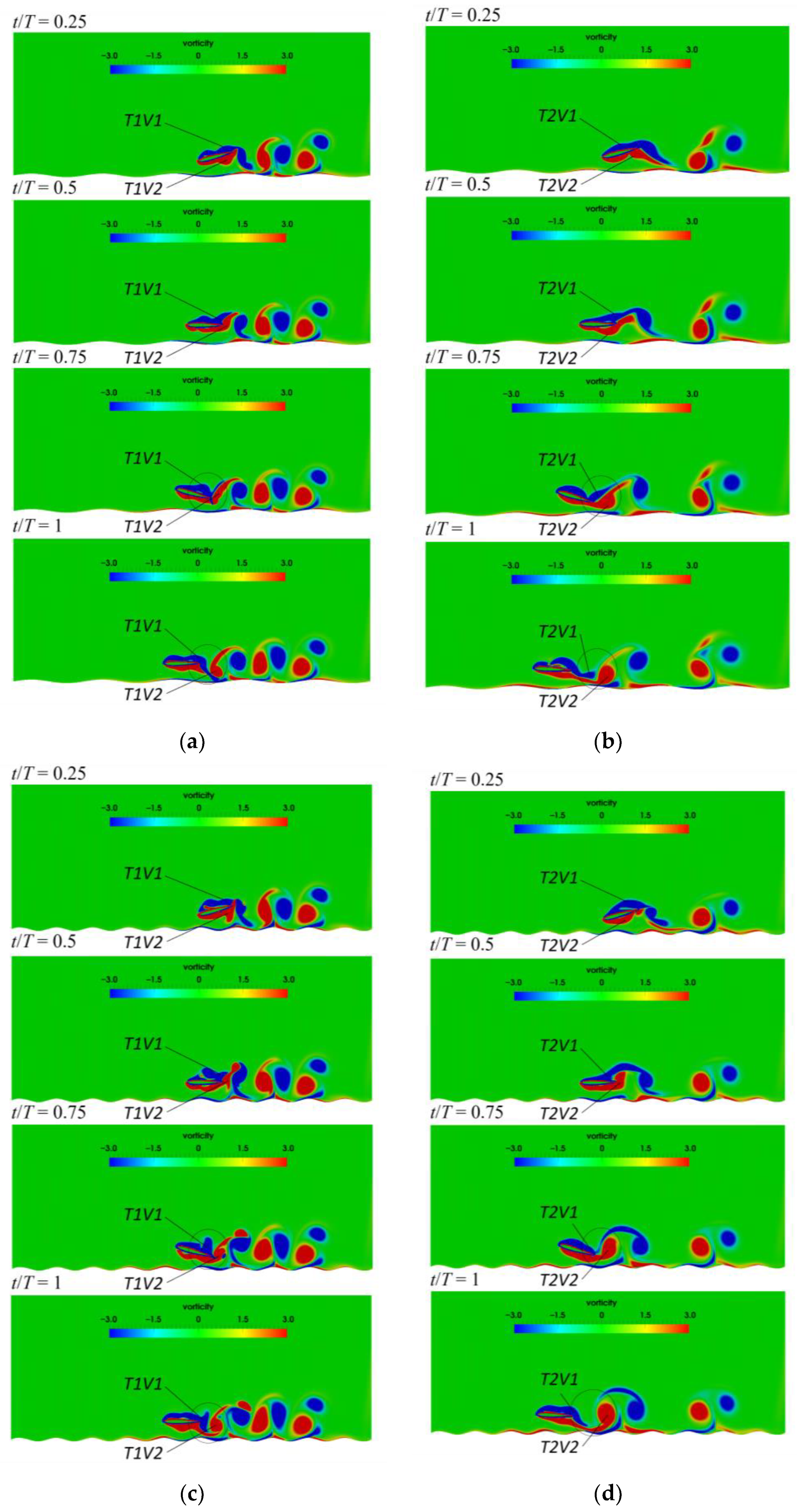
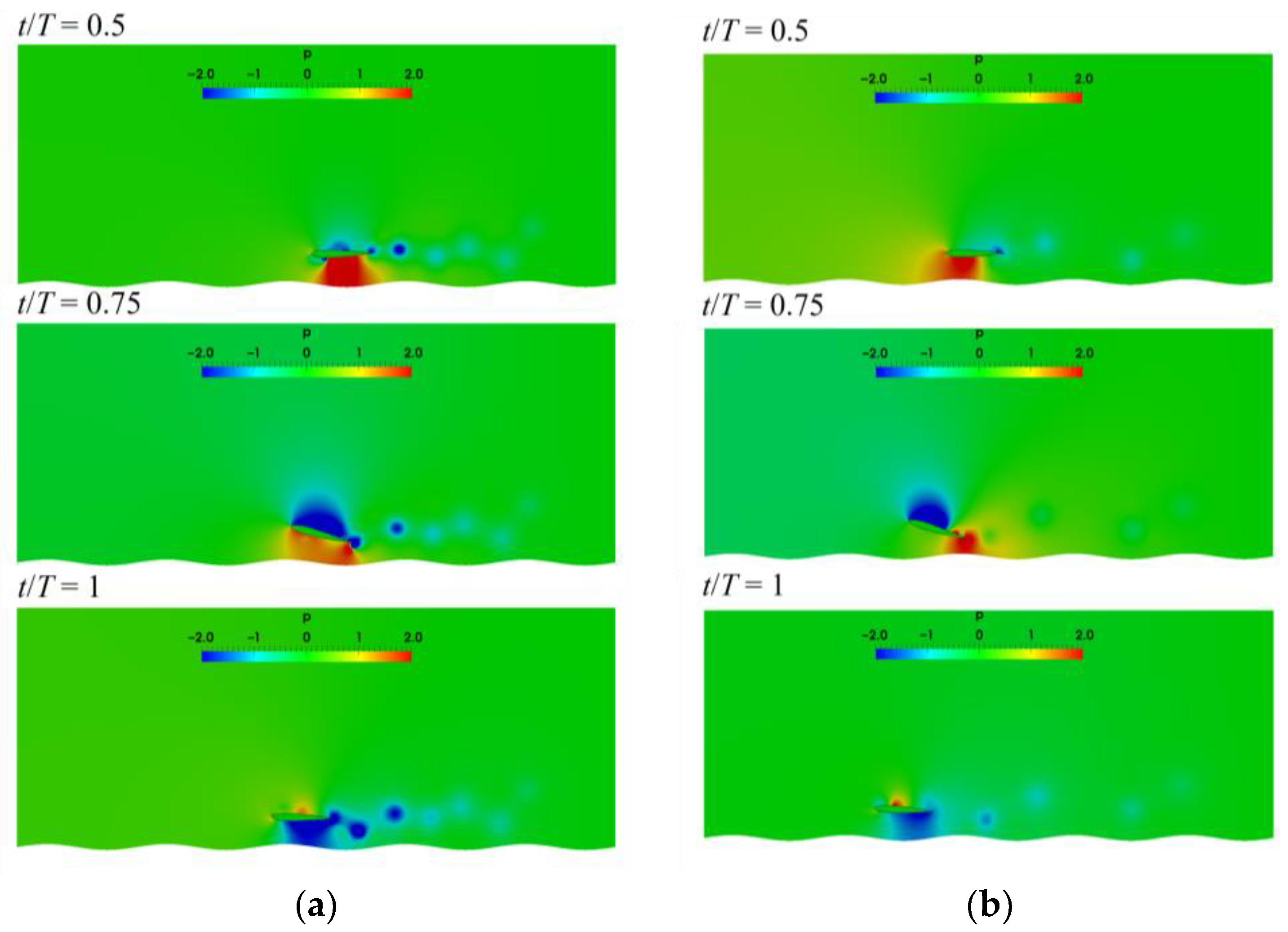
3.3.1. Vortex Structure and Its Effect Near the Flat Ground
3.3.2. Evolution of the Wake Vortices and Its Effect Near the Wavy Ground
4. Conclusions
- When the airfoil pitching with a smaller period is in close proximity to the flat ground, the airfoil can obtain a larger lift and lift-to-drag ratio due to the ground effect. Thus, the mean vertical displacement of the pitching airfoil increases with decreasing . With the increase of pitching period, the influence of the ground proximity on the lift and drag coefficients gradually weakens. That’s because that the wake vortices near the trailing edge of the airfoil pitching with a larger period become slenderer, and moreover, the transverse vortex spacing is larger. By comparing the lift-to-drag ratios for different T and , it is found that there are the corresponding optimal pitching periods for the pitching airfoil at different initial heights.
- Regardless of the flat or wavy ground, the pitching airfoil can obtain the larger lift and higher vertical displacement at and . However, compared with the flat ground, the airfoils pitching with other appropriate periods also achieve the higher vertical displacement in wavy ground effect. At the same initial height, the optimal pitching periods for different ground conditions are not identical. The occurrence times and the amplitudes of the peak and valley of lift and drag coefficients mainly depend on the pitching period T. But the structure of the vortex cores is correspondingly adjusted by the wave length of ground and the strength of the vortex cores increase slightly with decreasing the ground wavelength. This leads to the changes of the amplitudes and the occurrence times of the peak and valley of lift and drag force.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, H.; Choi, H. Aerodynamic characteristics of flying fish in gliding flight. J. Exp. Biol. 2010, 213, 3269–3279. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Zhang, L.X.; Liu, Z.Y. Numerical prediction of aerodynamic performance for a flying fish during gliding flight. Bioinspir. Biomim. 2019, 14, 046009. [Google Scholar] [CrossRef] [PubMed]
- Blevins, E.; Lauder, G.V. Swimming near the substrate: A simple robotic model of stingray locomotion. Bioinspir. Biomim. 2013, 8, 016005. [Google Scholar] [CrossRef] [PubMed]
- Qu, Q.L.; Jia, X.; Wang, W.; Liu, P.Q.; Agarwal, R.K. Numerical study of the aerodynamics of a NACA 4412 airfoil in dynamic ground effect. Aerosp. Sci. Technol. 2014, 38, 56–63. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, N. Ground Effect on Flapping Wing. Procedia Eng. 2013, 67, 295–302. [Google Scholar] [CrossRef]
- Chawla, M.D.; Edwards, L.C.; Franke, M.E. Wind-tunnel investigation of wing-in-ground effects. J. Aircr. 1990, 27, 289–293. [Google Scholar] [CrossRef]
- Ahmed, M.R.; Takasaki, T.; Kohama, Y. Aerodynamics of a NACA4412 Airfoil in Ground Effect. AIAA J. 2007, 45, 37–47. [Google Scholar] [CrossRef]
- Zerihan, J.; Zhang, X. Aerodynamics of a single element wing in ground effect. J. Aircr. 2000, 37, 1058–1064. [Google Scholar] [CrossRef]
- Quinn, D.B.; Moored, K.W.; Dewey, P.A.; Smits, A.J. Unsteady propulsion near a solid boundary. J. Fluid Mech. 2014, 742, 152–170. [Google Scholar] [CrossRef]
- Mivehchi, A.; Dahl, J.; Licht, S. Heaving and pitching oscillating foil propulsion in ground effect. J. Fluids Struct. 2016, 63, 174–187. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S.C.; Shu, C.; Zhao, N.; Yan, W.W. Ground effect on the power extraction performance of a flapping wing biomimetic energy generator. J. Fluids Struct. 2015, 54, 247–262. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, J.; Zhang, W. Impact of the ground effect on the energy extraction properties of a flapping wing. Ocean Eng. 2020, 209, 107376. [Google Scholar] [CrossRef]
- Wang, L.; Tian, F.B. Numerical simulation of flow over a parallel cantilevered flag in the vicinity of a rigid wall. Phys. Rev. E 2019, 99, 053111. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; He, G.; Zhang, X. Self-propelled swimming of a flexible plunging foil near a solid wall. Bioinspir. Biomim. 2016, 11, 046005. [Google Scholar] [CrossRef] [PubMed]
- Park, S.G.; Kim, B.; Sung, H.J. Hydrodynamics of a self-propelled flexible fin near the ground. Phys. Fluids 2017, 29, 051902. [Google Scholar] [CrossRef]
- Tang, C.; Huang, H.B.; Gao, P.; Lu, X.Y. Self-propulsion of a flapping flexible plate near the ground. Phys. Rev. E 2016, 94, 033113. [Google Scholar] [CrossRef]
- Ogunka, U.E.; Daghooghi, M.; Akbarzadeh, A.M.; Borazjani, I. The Ground Effect in Anguilliform Swimming. Biomimetics 2020, 5, 9. [Google Scholar] [CrossRef]
- Tremblay-Dionne, V.; Lee, T. Experimental Study on Effect of Wavelength and Amplitude of Wavy Ground on a NACA 0012Airfoil. J. Aerospace Eng. 2019, 32, 04019064. [Google Scholar] [CrossRef]
- Tremblay-Dionne, V.; Lee, T. Effect of Trailing-Edge Flap Deflection on a Symmetric Airfoil over a Wavy Ground. J. Fluids Eng. 2019, 141, 064501. [Google Scholar] [CrossRef]
- Gao, B.; Qu, Q.L.; Agrwal, R.K. Aerodynamics of a Transonic Airfoil above Wavy Ground. In Proceedings of the 56th AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Hu, H.; Ma, D. Airfoil Aerodynamics in Proximity to Wavy Ground for a Wide Range of Angles of Attack. Appl. Sci. 2020, 10, 6773. [Google Scholar] [CrossRef]
- Xin, Z.Q.; Wu, C.J. Vorticity dynamics and control of the turning locomotion of 3D bionic fish. Proc. Inst. Mech. Eng. Part C. 2018, 232, 2524–2535. [Google Scholar] [CrossRef]
- Borazjani, I.; Sotiropoulos, F. On the role of form and kinematics on the hydrodynamics of self-propelled body/caudal fin swimming. J. Exp. Biol. 2010, 213, 89–107. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.J.; Wang, L. Where is the rudder of a fish?: The mechanism of swimming and control of self-propelled fish school. Acta Mech. Sin. 2010, 26, 45–65. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Jasak, H.; Tuković, Ž. ImmersedBoundary. Available online: http://www.tfd.chalmers.se/hani/kurser/OS_CFD_2015/HrvojeJasak/ImmersedBoundary.pdf (accessed on 10 September 2022).
- Jasak, H.; Rigler, D.; Tuković, Ž. Design and implementation of immersed boundary method with discrete forcing approach for boundary conditions. In Proceedings of the 6th European Congress on Computational Fluid Dynamics, Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Feng, H.; Wang, Z.M.; Todd, P.A.; Lee, H.P. Simulations of self-propelled anguilliform swimming using the immersed boundary method in OpenFOAM. Eng. Appl. Comp. Fluid 2019, 13, 438–452. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C.; Zhao, N.; Yan, W.W. Fluid Dynamics of Flapping Insect Wing in Ground Effect. J. Bionic. Eng. 2014, 11, 52–60. [Google Scholar] [CrossRef]
- Lee, T.; Tremblay-Dionne, V. Experimental Investigation of the Aerodynamics and Flowfield of a NACA 0015 Airfoil Over a Wavy Ground. J. Fluids Eng. 2018, 140, 071202. [Google Scholar] [CrossRef]






| Number of Grids | ||||
|---|---|---|---|---|
| 50,000 | 0.02 | 0.01 | 0.2923 | 0.6925 |
| 150,000 | 0.01 | 0.005 | 0.2224 | 0.3580 |
| 250,000 | 0.005 | 0.005 | 0.2287 | 0.3473 |
| 250,000 | 0.005 | 0.0025 | 0.2275 | 0.3466 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Z.; Cai, Z.; Ren, Y.; Liu, H. Comparative Analysis of the Self-Propelled Locomotion of a Pitching Airfoil near the Flat and Wavy Ground. Biomimetics 2022, 7, 239. https://doi.org/10.3390/biomimetics7040239
Xin Z, Cai Z, Ren Y, Liu H. Comparative Analysis of the Self-Propelled Locomotion of a Pitching Airfoil near the Flat and Wavy Ground. Biomimetics. 2022; 7(4):239. https://doi.org/10.3390/biomimetics7040239
Chicago/Turabian StyleXin, Zhiqiang, Zhiming Cai, Yiming Ren, and Huachen Liu. 2022. "Comparative Analysis of the Self-Propelled Locomotion of a Pitching Airfoil near the Flat and Wavy Ground" Biomimetics 7, no. 4: 239. https://doi.org/10.3390/biomimetics7040239
APA StyleXin, Z., Cai, Z., Ren, Y., & Liu, H. (2022). Comparative Analysis of the Self-Propelled Locomotion of a Pitching Airfoil near the Flat and Wavy Ground. Biomimetics, 7(4), 239. https://doi.org/10.3390/biomimetics7040239





