The Design and Testing of a PEA Powered Ankle Prosthesis Driven by EHA
Abstract
1. Introduction
2. Design Concept
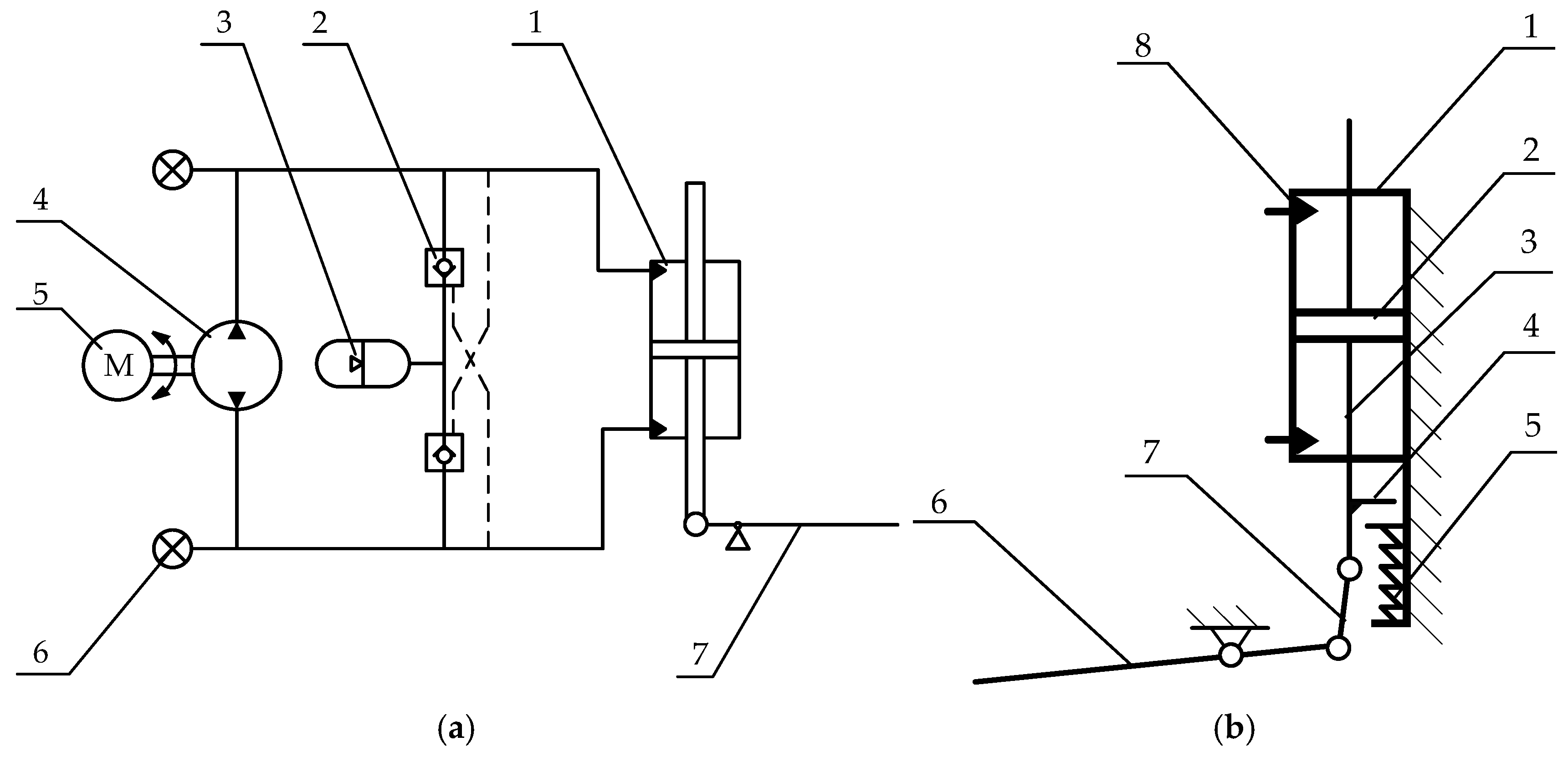
2.1. Principal Design of the Mechanism and Hydraulic System
2.2. Motor Selection
2.3. Transmission Ratio
2.4. Spring
2.4.1. Driver System Modeling
2.4.2. Limits and the Indicator of the Optimization
2.4.3. The Optimization Results
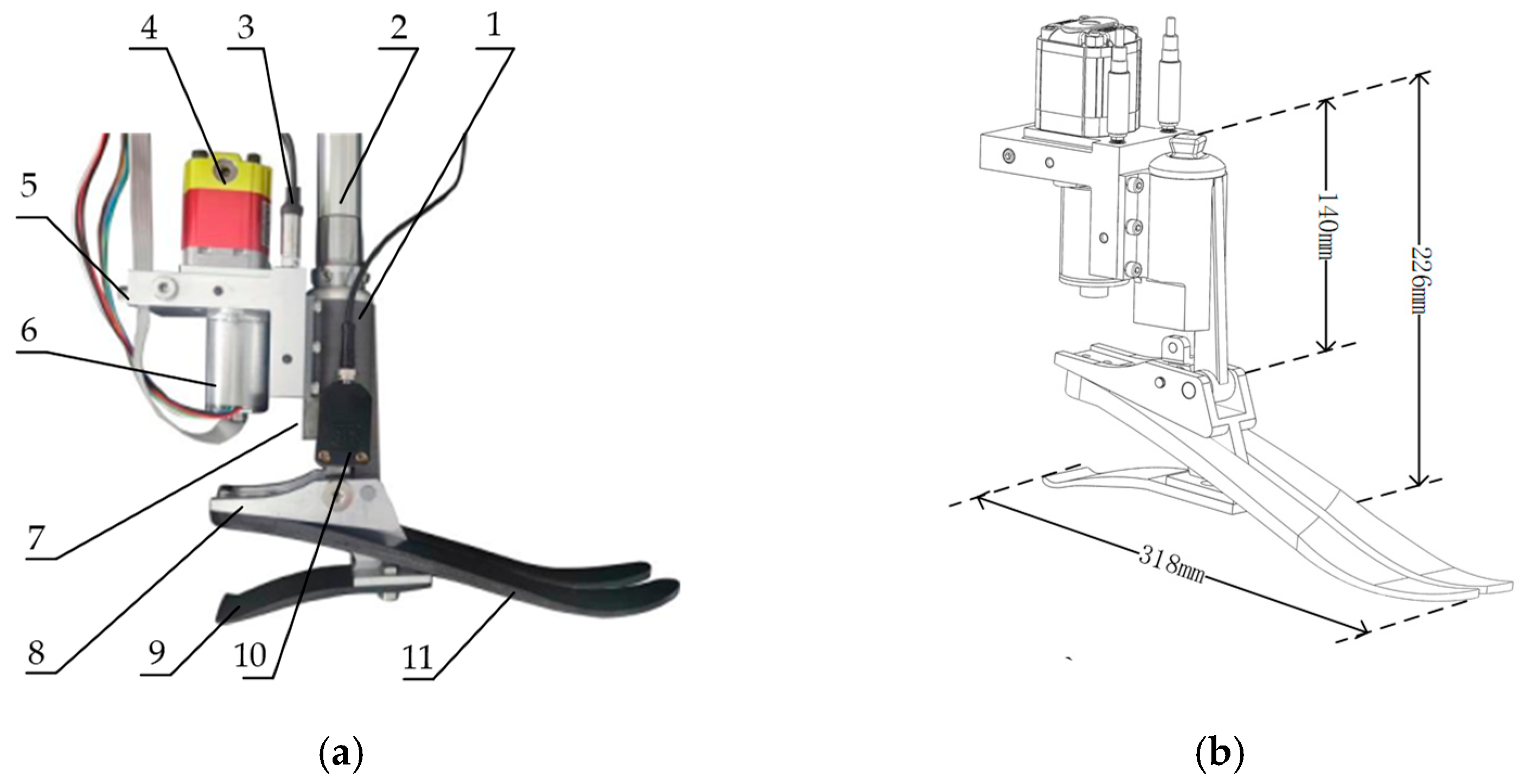
3. Specific Implementation
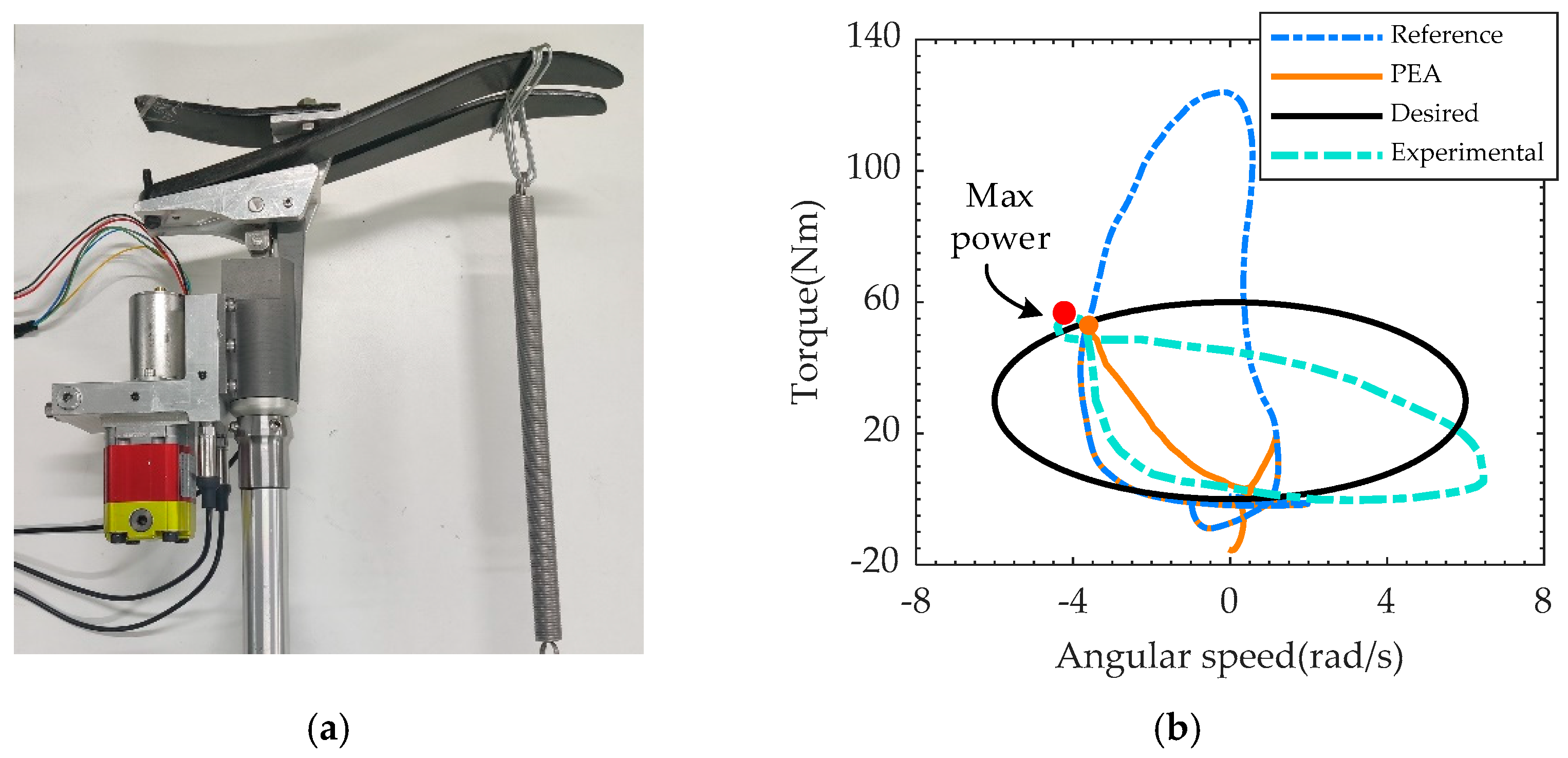
3.1. The Overall Design
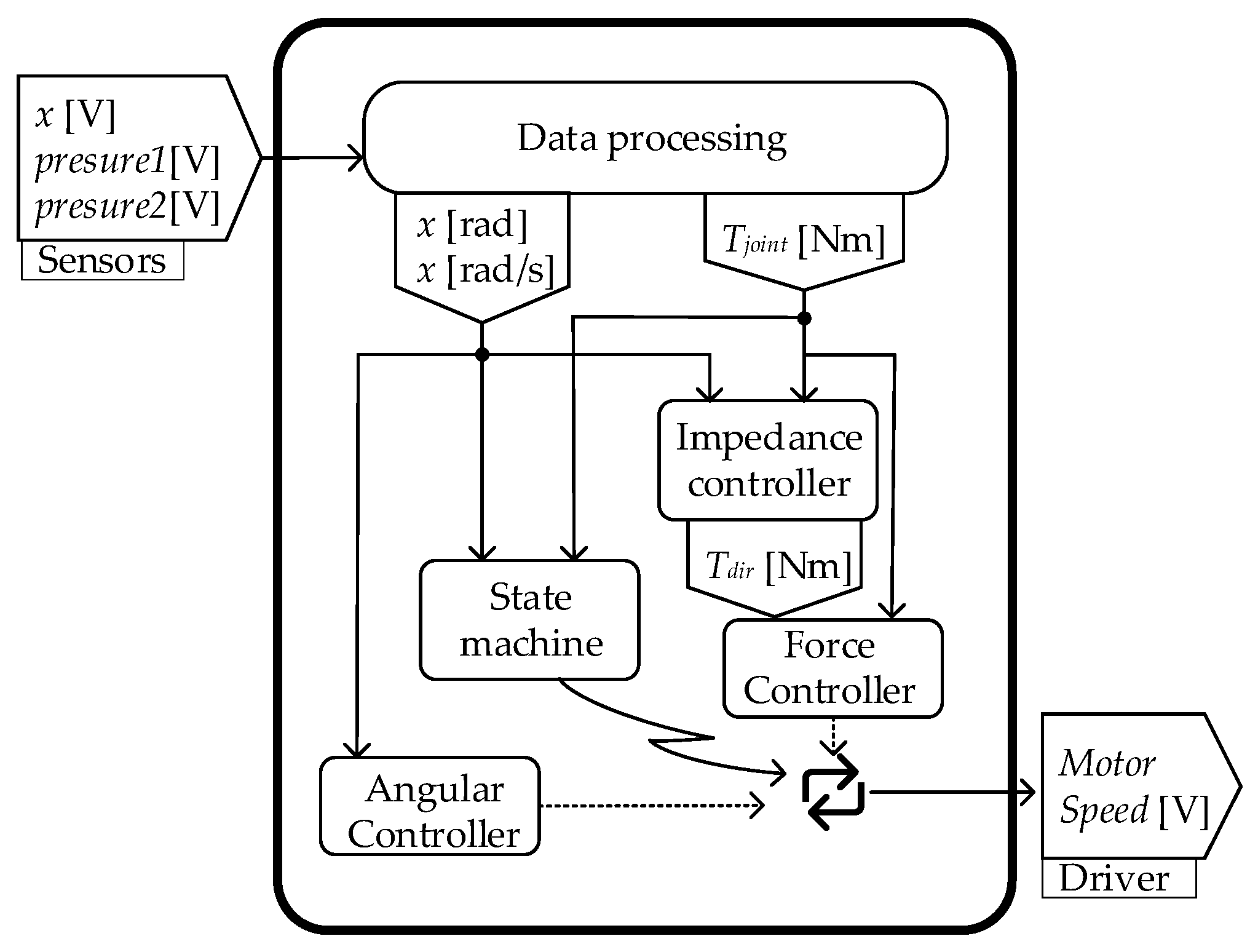
3.2. Control System
4. Experiments
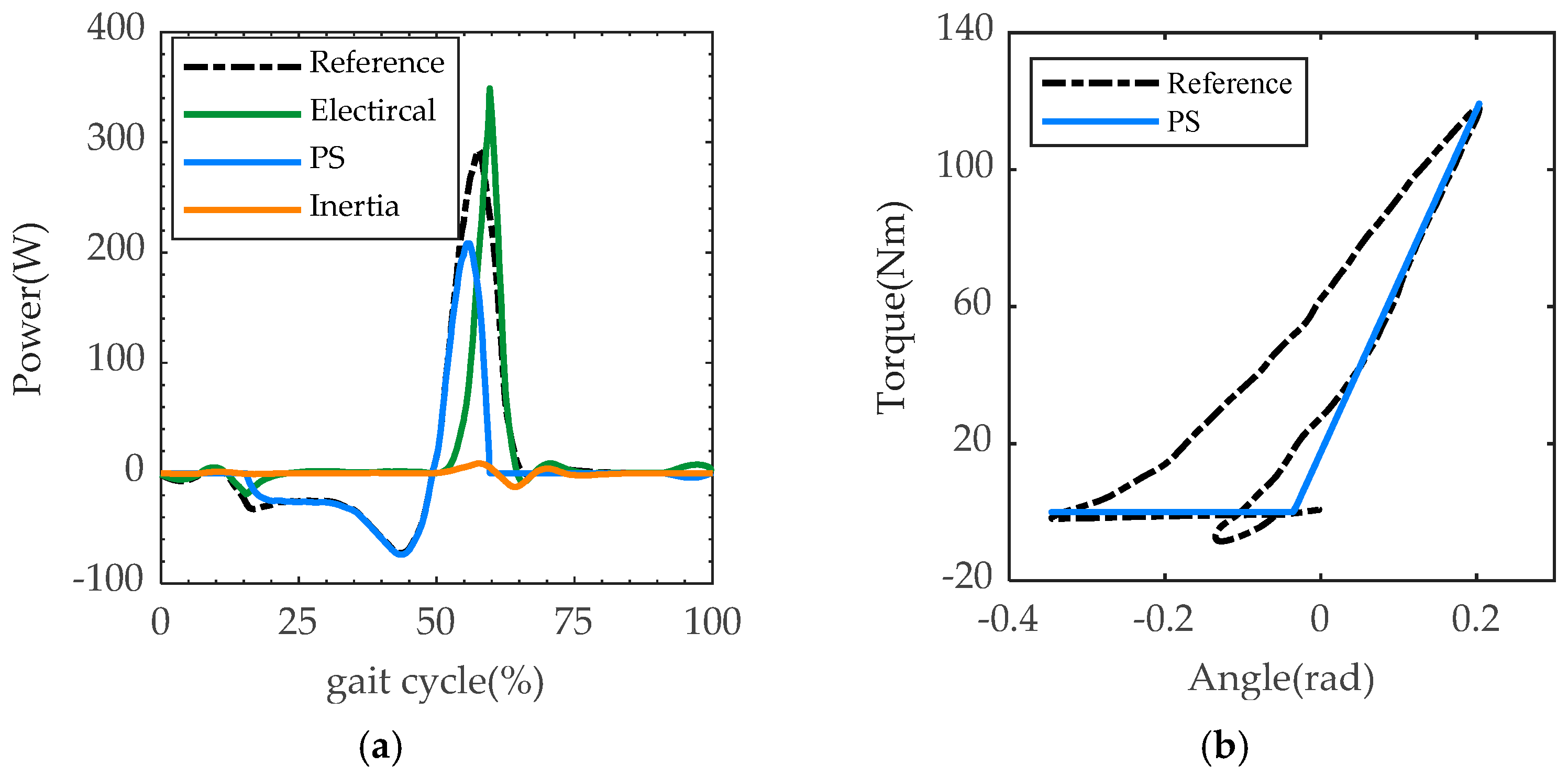
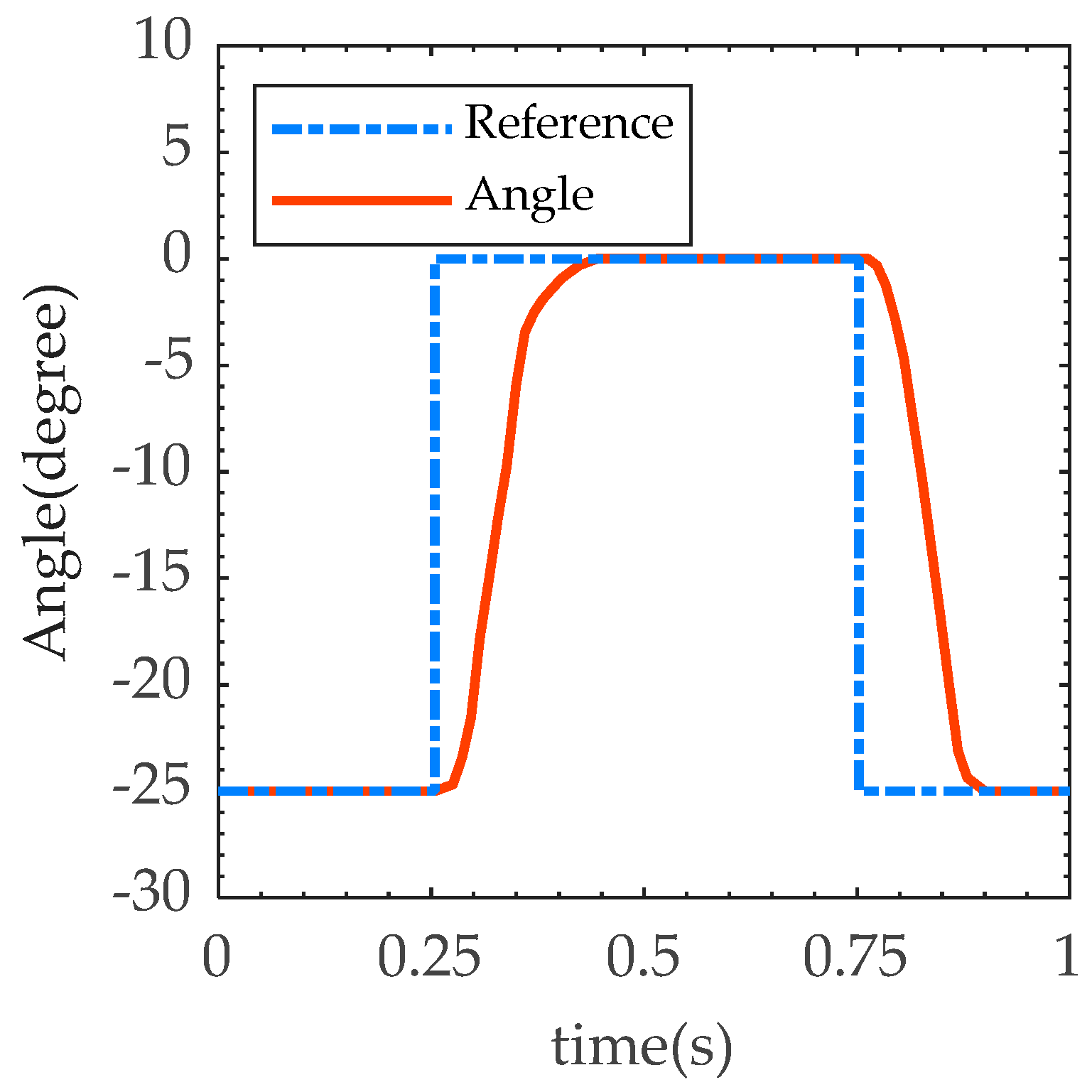
4.1. Fast Response Test
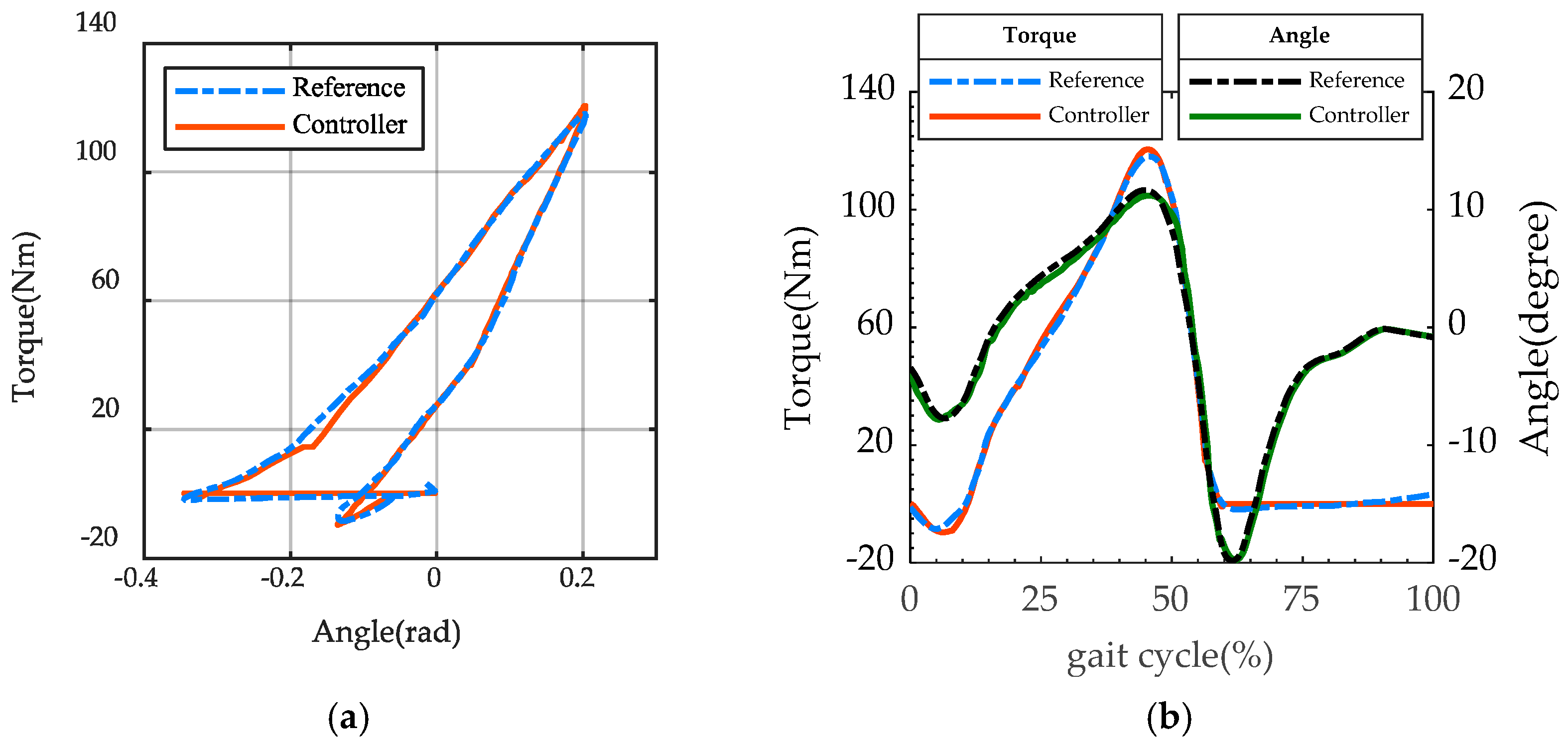
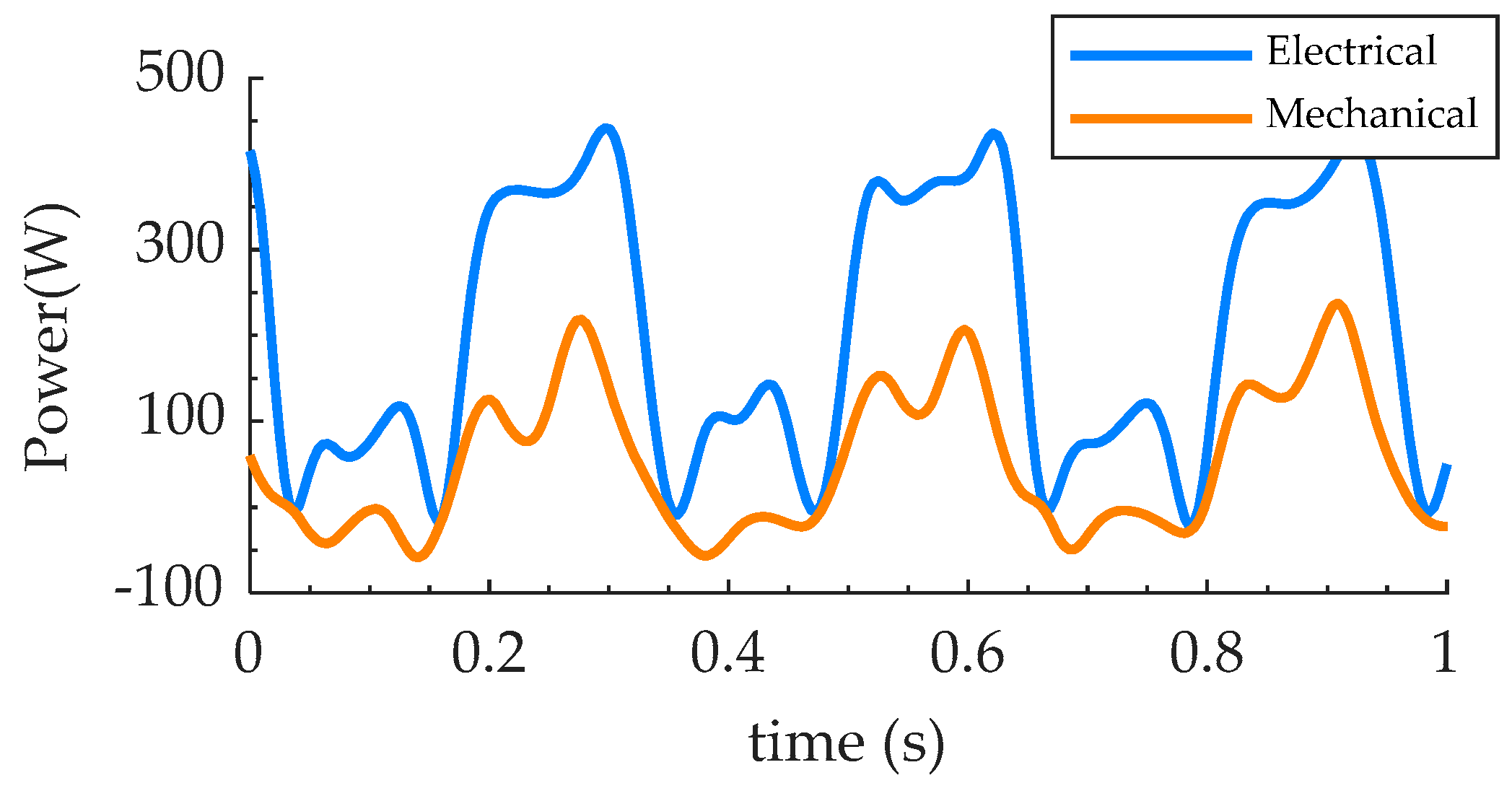
4.2. Loading Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Össur. Life without Limitations. Available online: https://www.ossur.com/region-selector (accessed on 30 September 2022).
- Waters, R.L.; Mulroy, S. The Energy Expenditure of Normal and Pathologic Gait. Gait Posture 1999, 9, 207–231. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Biomechanics and Motor Control of Human Gait: Normal, Elderly and Pathological, 2nd ed.; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1991. [Google Scholar]
- Palmer, M.L. Sagittal Plane Characterization of Normal Human Ankle Function across a Range of Walking Gait Speeds; Massachusetts Institute of Technology: Cambridge, MA, USA, 2002; p. 74. [Google Scholar]
- Au, S.K.; Herr, H.; Weber, J.; Martinez-Villalpando, E.C. Powered Ankle-Foot Prosthesis for the Improvement of Amputee Ambulation. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 3020–3026. [Google Scholar]
- Au, S.K.; Weber, J.; Herr, H. Powered Ankle—Foot Prosthesis Improves Walking Metabolic Economy. IEEE Trans. Robot. 2009, 25, 51–66. [Google Scholar] [CrossRef]
- Pratt, G.A.; Williamson, M.M. Series Elastic Actuators. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; Volume 1, pp. 399–406. [Google Scholar]
- Paluska, D.; Herr, H. Series Elasticity and Actuator Power Output. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 1830–1833. [Google Scholar]
- Hitt, J.; Sugar, T.; Holgate, M.; Bellman, R.; Hollander, K. Robotic Transtibial Prosthesis with Biomechanical Energy Regeneration. Ind. Robot Int. J. 2009, 36, 441–447. [Google Scholar] [CrossRef]
- Hitt, J.K.; Sugar, T.G.; Holgate, M.; Bellman, R. An Active Foot-Ankle Prosthesis with Biomechanical Energy Regeneration. J. Med. Devices 2010, 4, 011003. [Google Scholar] [CrossRef]
- Bellman, R.D.; Holgate, M.A.; Sugar, T.G. SPARKy 3: Design of an Active Robotic Ankle Prosthesis with Two Actuated Degrees of Freedom Using Regenerative Kinetics. In Proceedings of the 2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; pp. 511–516. [Google Scholar]
- Grimmer, M.; Holgate, M.; Holgate, R.; Boehler, A.; Ward, J.; Hollander, K.; Sugar, T.; Seyfarth, A. A Powered Prosthetic Ankle Joint for Walking and Running. Biomed. Eng. OnLine 2016, 15, 141. [Google Scholar] [CrossRef] [PubMed]
- Carney, M.; Herr, H. Energetic Consequences of Series and Parallel Springs in Lower-Extremity Powered Prostheses; engrXiv: Menomonie, WI, USA, 2019. [Google Scholar]
- Cherelle, P.; Mathijssen, G.; Wang, Q.; Vanderborght, B.; Lefeber, D. Advances in Propulsive Bionic Feet and Their Actuation Principles. Adv. Mech. Eng. 2014, 6, 984046. [Google Scholar] [CrossRef]
- Verstraten, T.; Geeroms, J.; Mathijssen, G.; Convens, B.; Vanderborght, B.; Lefeber, D. Optimizing the Power and Energy Consumption of Powered Prosthetic Ankles with Series and Parallel Elasticity. Mech. Mach. Theory 2017, 116, 419–432. [Google Scholar] [CrossRef]
- Sup, F.; Varol, H.A.; Mitchell, J.; Withrow, T.J.; Goldfarb, M. Preliminary Evaluations of a Self-Contained Anthropomorphic Transfemoral Prosthesis. IEEE ASME Trans. Mechatron. 2009, 14, 667–676. [Google Scholar] [CrossRef] [PubMed]
- Van den Bossche, D. The a 380 Flight control electrohydrostatic actuators, achievements and lessons learnt. In Proceedings of the 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- Electrohydrostatic. Available online: https://www.moog.com/products/actuators-servoactuators/actuation-technologies/electrohydrostatic.html (accessed on 30 September 2022).
- Kaminaga, H.; Yamamoto, T.; Ono, J.; Nakamura, Y. Backdrivable Miniature Hydrostatic Transmission for Actuation of Anthropomorphic Robot Hands. In Proceedings of the 2007 7th IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, PA, USA, 29 November–1 December 2007; pp. 36–41. [Google Scholar]
- Kaminaga, H.; Ono, J.; Nakashima, Y.; Nakamura, Y. Development of Backdrivable Hydraulic Joint Mechanism for Knee Joint of Humanoid Robots. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1577–1582. [Google Scholar]
- Yu, T.; Plummer, A.R.; Iravani, P.; Bhatti, J.; Zahedi, S.; Moser, D. The Design, Control, and Testing of an Integrated Electrohydrostatic Powered Ankle Prosthesis. IEEE ASME Trans. Mechatron. 2019, 24, 1011–1022. [Google Scholar] [CrossRef]
- Fang, J.; Wang, X.; Li, R.; Wang, S.; Wang, W. Active Ankle Prosthesis Powered by Electrohydrostatic Actuation Technology: Design and Implementation. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2018), Guiyang, China, 19–22 June 2018; pp. 1170–1175. [Google Scholar]
- Tessari, F.; Galluzzi, R.; Tonoli, A.; Amati, N.; Laffranchi, M.; De Michieli, L. Analysis, Development and Evaluation of Electro-Hydrostatic Technology for Lower Limb Prostheses Applications. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2019–24 January 2020; pp. 3377–3382. [Google Scholar]
- Huang, Q.; Li, B.; Jia, F.; Wang, P. A Novel Design of Electro-Hydraulic Driven Active Powered Ankle-Foot Prosthesis. In Intelligent Robotics and Applications; Liu, X.-J., Nie, Z., Yu, J., Xie, F., Song, R., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2021; Volume 13013, pp. 622–630. ISBN 978-3-030-89094-0.27. [Google Scholar]
- Zhao, G.; Grimmer, M.; Seyfarth, A. The Mechanisms and Mechanical Energy of Human Gait Initiation from the Lower-Limb Joint Level Perspective. Sci. Rep. 2021, 11, 22473. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Huang, Q.; Tong, Z. Simulation and Analysis of a Full-Active Electro-Hydrostatic Powered Ankle Prosthesis. In Proceedings of the 2019 19th International Conference on Advanced Robotics (ICAR), Belo Horizonte, Brazil, 2–6 December 2019; pp. 81–86. [Google Scholar]
- Askew, G.N.; McFarlane, L.A.; Minetti, A.E.; Buckley, J.G. Energy Cost of Ambulation in Trans-Tibial Amputees Using a Dynamic-Response Foot with Hydraulic versus Rigid ‘Ankle’: Insights from Body Centre of Mass Dynamics. J. NeuroEng. Rehabil. 2019, 16, 39. [Google Scholar] [CrossRef] [PubMed]
- Eslamy, M.; Grimmer, M.; Rinderknecht, S.; Seyfarth, A. Does It Pay to Have a Damper in a Powered Ankle Prosthesis? A Power-Energy Perspective. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; pp. 1–8. [Google Scholar]

| ROM | Max Speed | Max Torque | SW Period |
|---|---|---|---|
| 40° (−20°~20°) | 4 rad/s | 1.6 Nm/Kg | 0.4 s |
| Parameters | Value |
|---|---|
| Torque constant | 0.091 Nm/A |
| Speed constant | 105 rpm/V |
| Terminal resistance | 1.01 Ω |
| Terminal inductance | 0.995 mH |
| Motor inertia | 44 gcm2 |
| Friction coefficient | 5.21 × 106 Nms/rad |
| Maximum permissive speed | 8000 rpm |
| Maximum continuous current | 2.39 A |
| 48 V | 15 A | 7 gcm2 | 70% |
| 500 Nm/rad | −2° | 348.6 W | 208.3 W | 524.7 W | 18.3 J | 29.1 J | 64.2 J |
| Main Component | Features | |
|---|---|---|
| Maxon ECi-40 (P/N 488607) Brushless DC Motor | Nominal Voltage | 48 V |
| Rated Power | 100 W | |
| Nominal Speed | 5000 rpm | |
| Escon 50/5 Servo Controller | Nominal Voltage | 10–50 V |
| Maximum Output Current | 48 A | |
| VIVOIL Reversible Gear Pump | Displacement | 0.92 cc/rev |
| Integrated Ankle Joint Cylinder | Working Area Movement Range | 6.5 cm2 35° |
| Carbon fiber Sole | Poisson’s ratio | 0.31 |
| Elastic modulus | 2.1 × 105 MPa | |
| 200 Nm/rad | 0.3 rad | 20 rad/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Li, B.; Xu, H. The Design and Testing of a PEA Powered Ankle Prosthesis Driven by EHA. Biomimetics 2022, 7, 234. https://doi.org/10.3390/biomimetics7040234
Huang Q, Li B, Xu H. The Design and Testing of a PEA Powered Ankle Prosthesis Driven by EHA. Biomimetics. 2022; 7(4):234. https://doi.org/10.3390/biomimetics7040234
Chicago/Turabian StyleHuang, Qitao, Bowen Li, and Hongguang Xu. 2022. "The Design and Testing of a PEA Powered Ankle Prosthesis Driven by EHA" Biomimetics 7, no. 4: 234. https://doi.org/10.3390/biomimetics7040234
APA StyleHuang, Q., Li, B., & Xu, H. (2022). The Design and Testing of a PEA Powered Ankle Prosthesis Driven by EHA. Biomimetics, 7(4), 234. https://doi.org/10.3390/biomimetics7040234







