A Non-Flat Terrain Biped Gait Planner Based on DIRCON
Abstract
1. Introduction
2. Related Work
2.1. Constrained Hybrid System Dynamics
2.2. Trajectory Optimization and Constrained Direct Collocation
3. Approaches
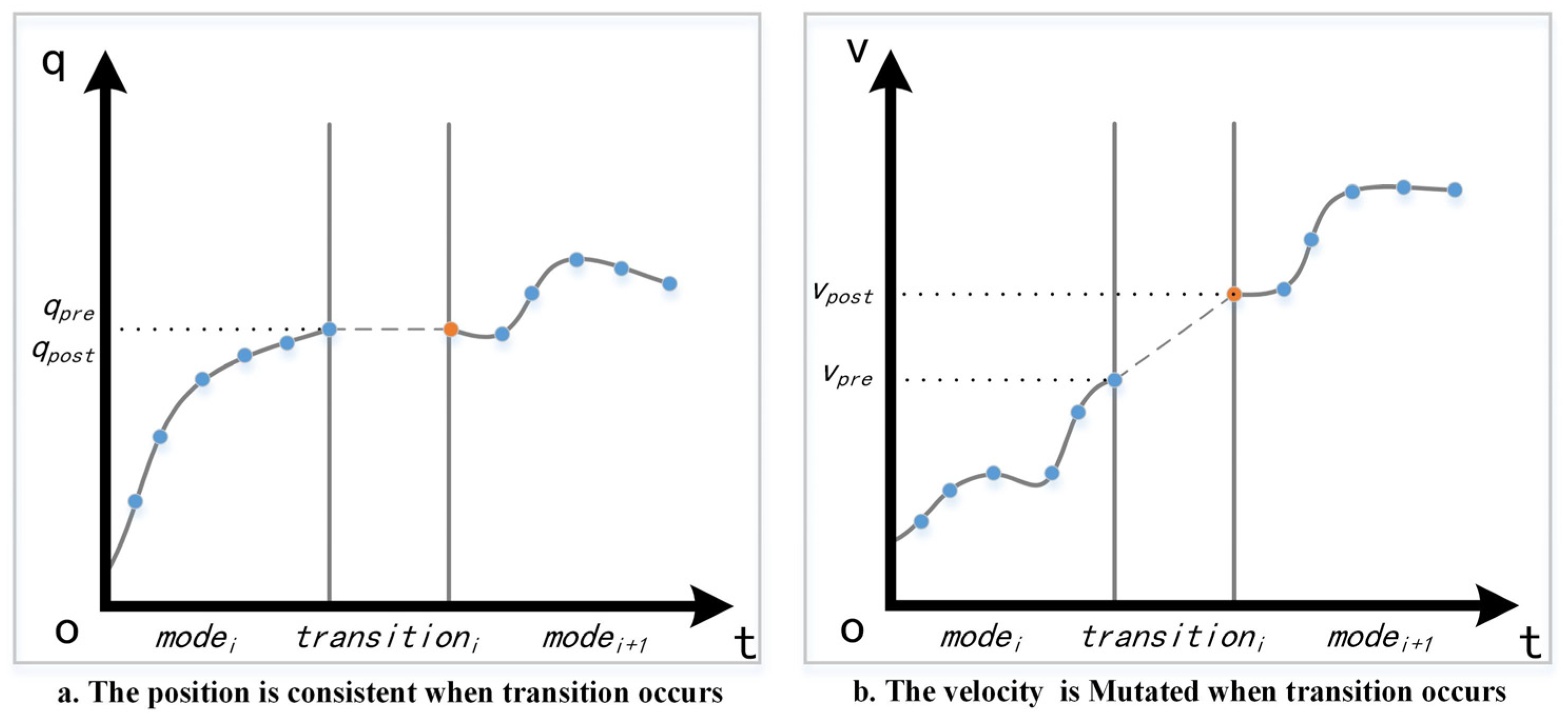
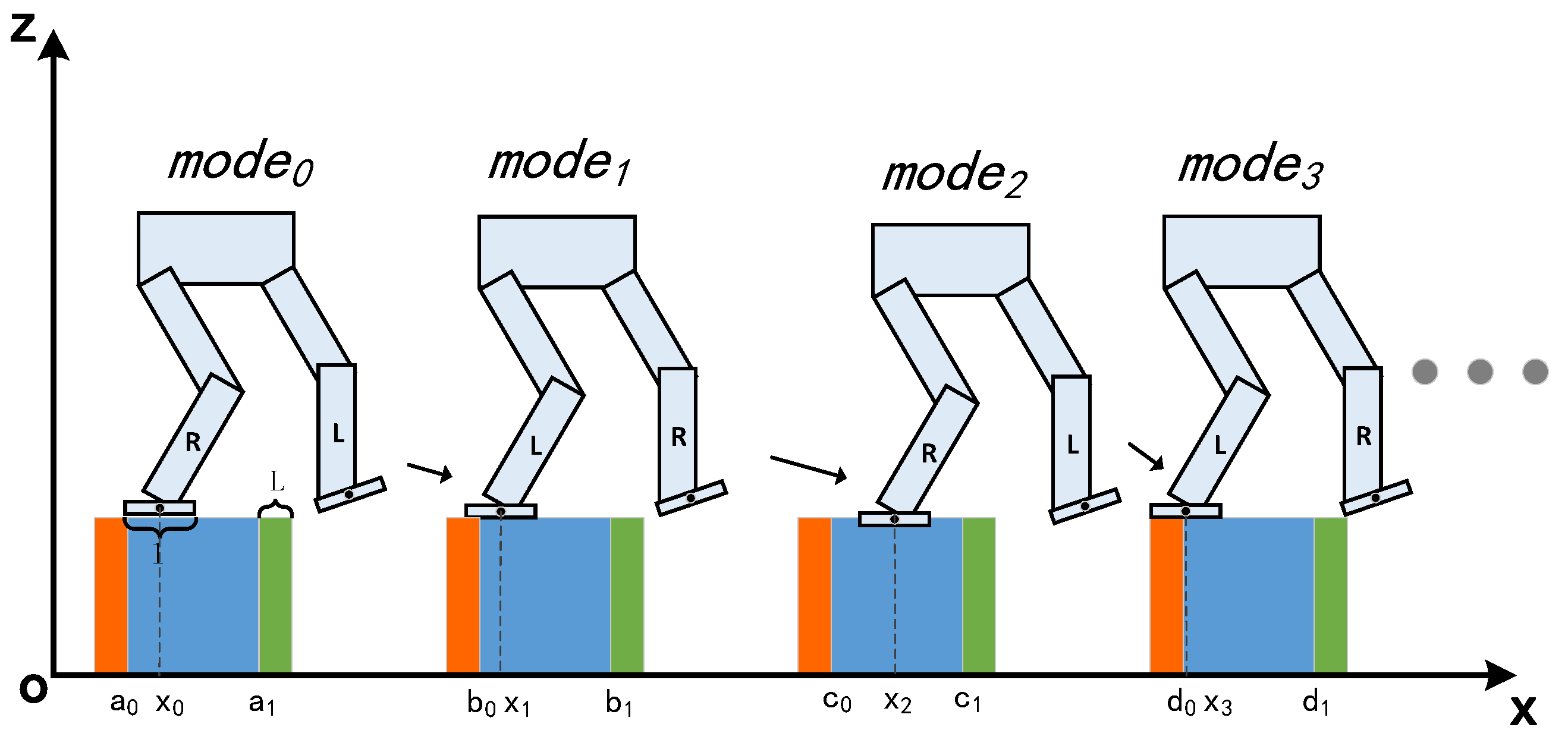
3.1. Virtual Knots and Multi-Modal Gait Planning
3.2. Slacked Complementary Constraint of Terrain Information
3.2.1. Constraints of Support Location Selection
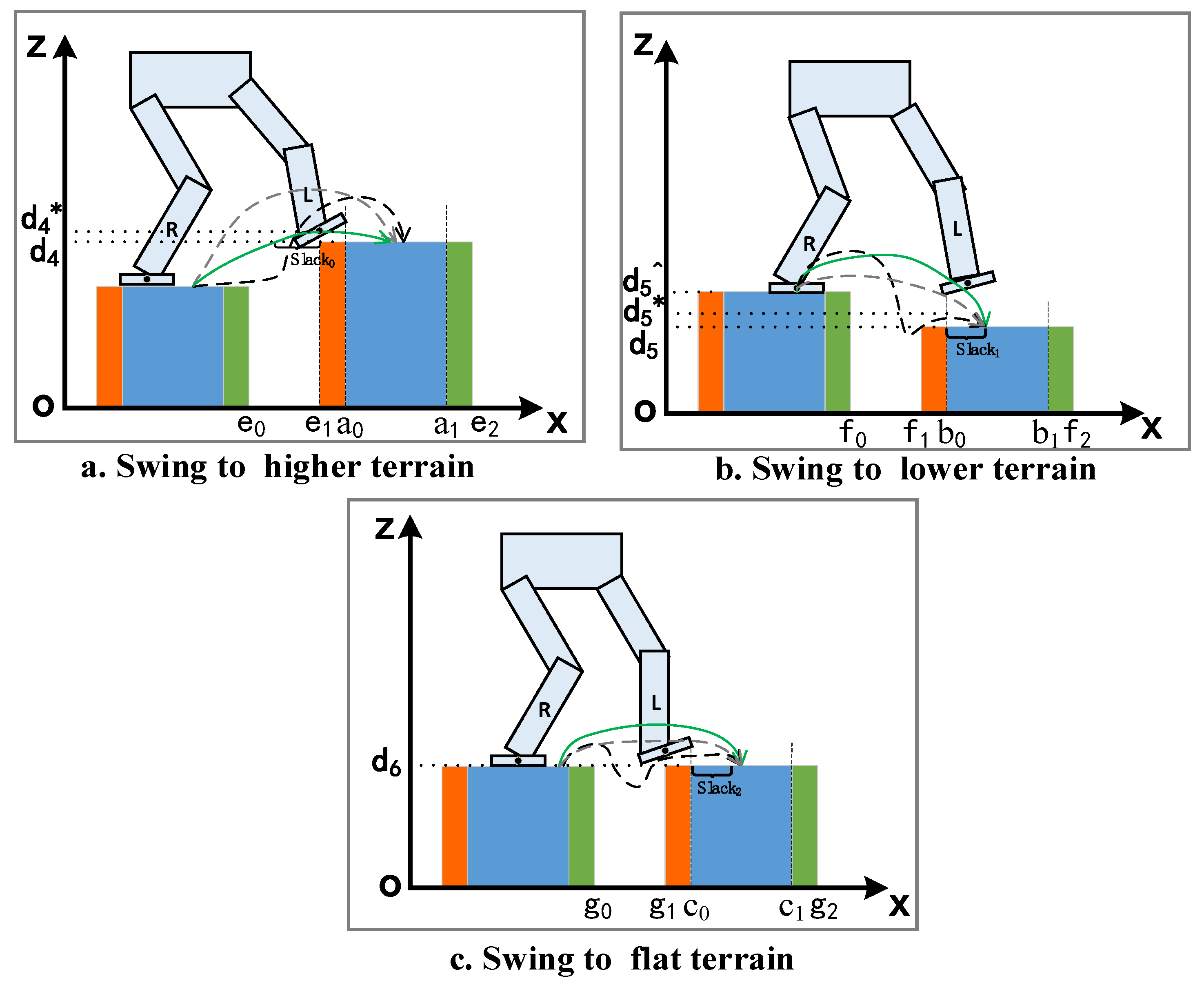
3.2.2. Slacked Complementary Constraint of Obstacle Avoidance of the Swing Foot
- Swing to higher terrain
- b.
- Swing to lower and flat terrain
3.3. Hybrid DIRCON with Slacked Complementary Constraints
4. Experiments
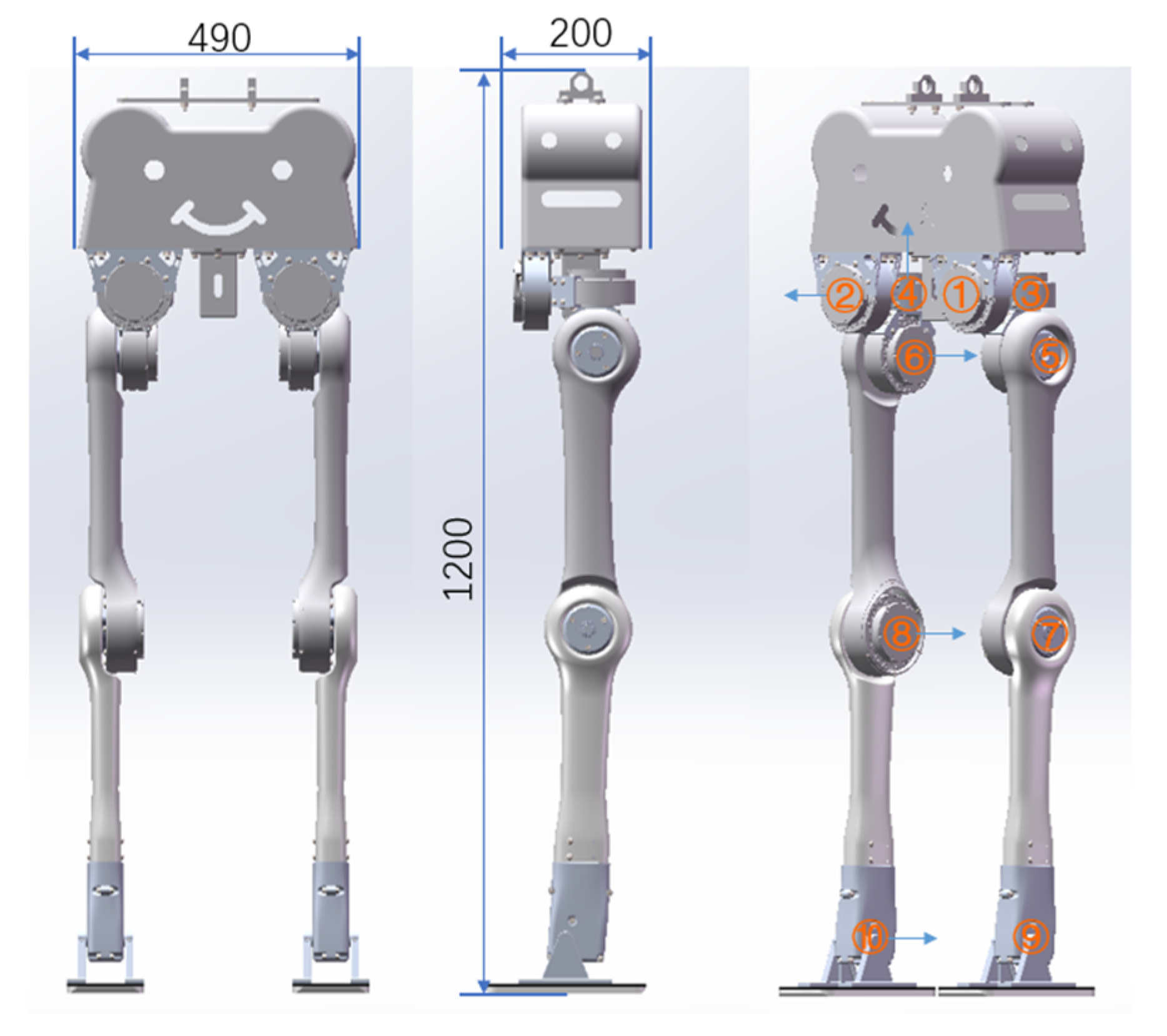
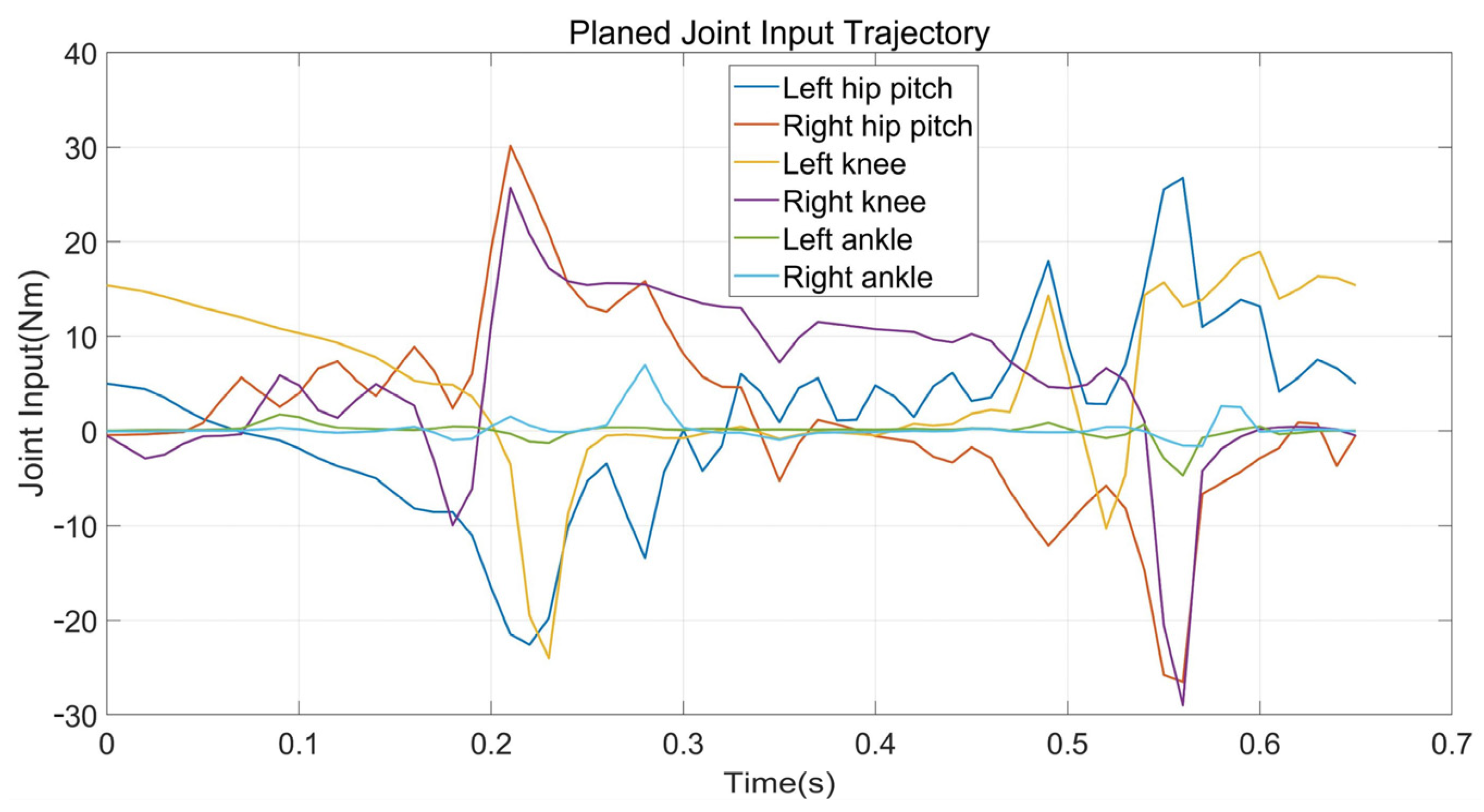
4.1. Robot Model and Details of Implementation
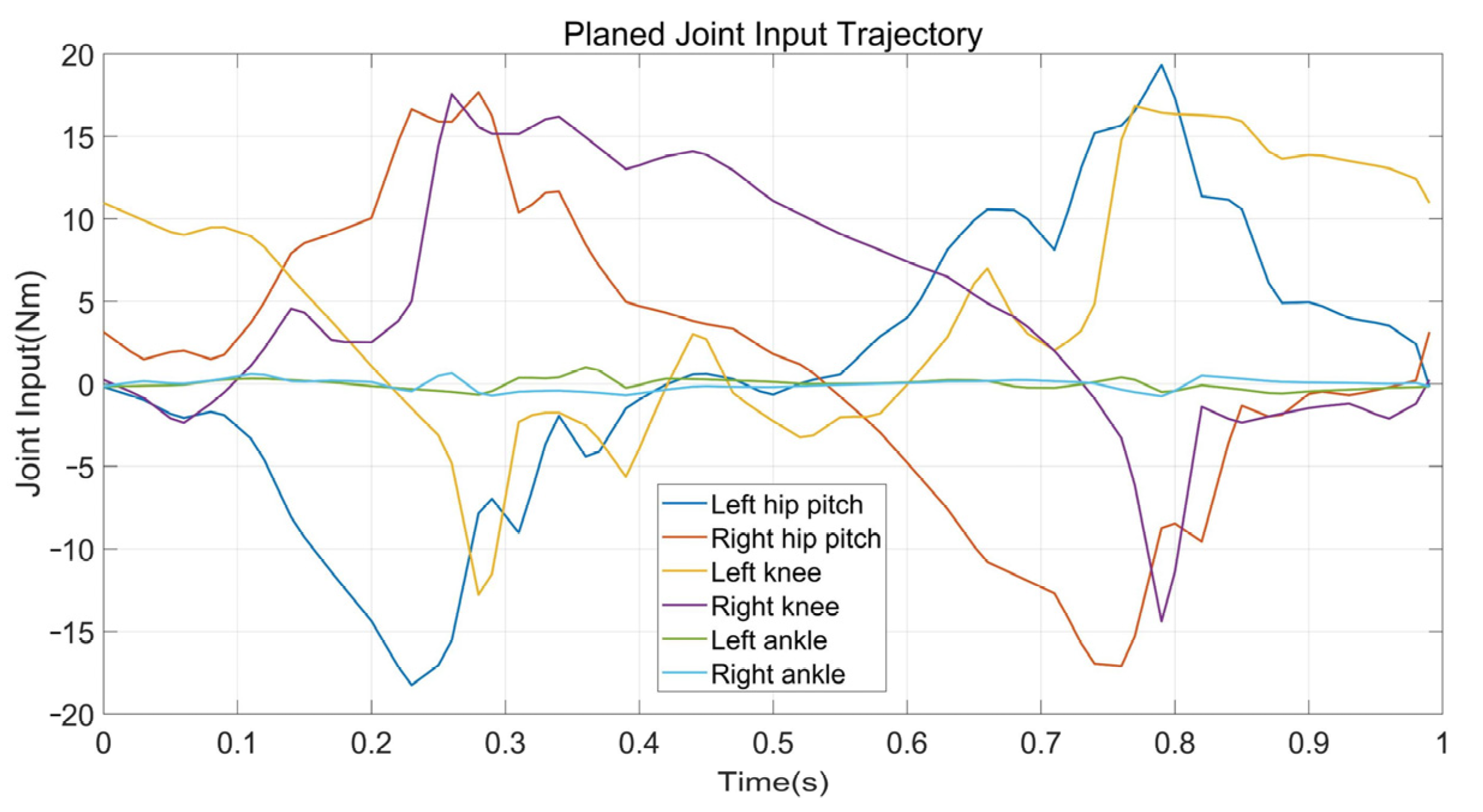
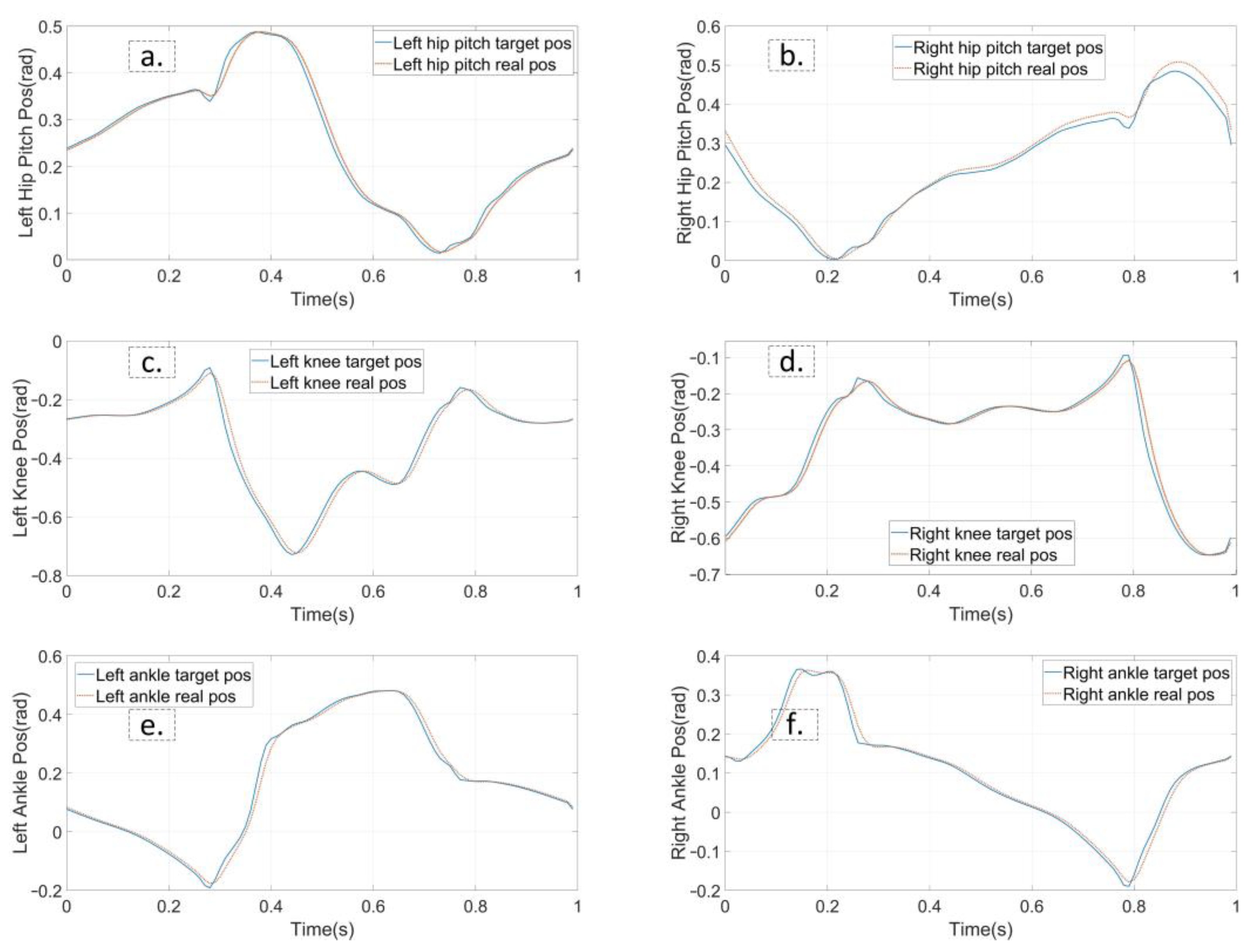
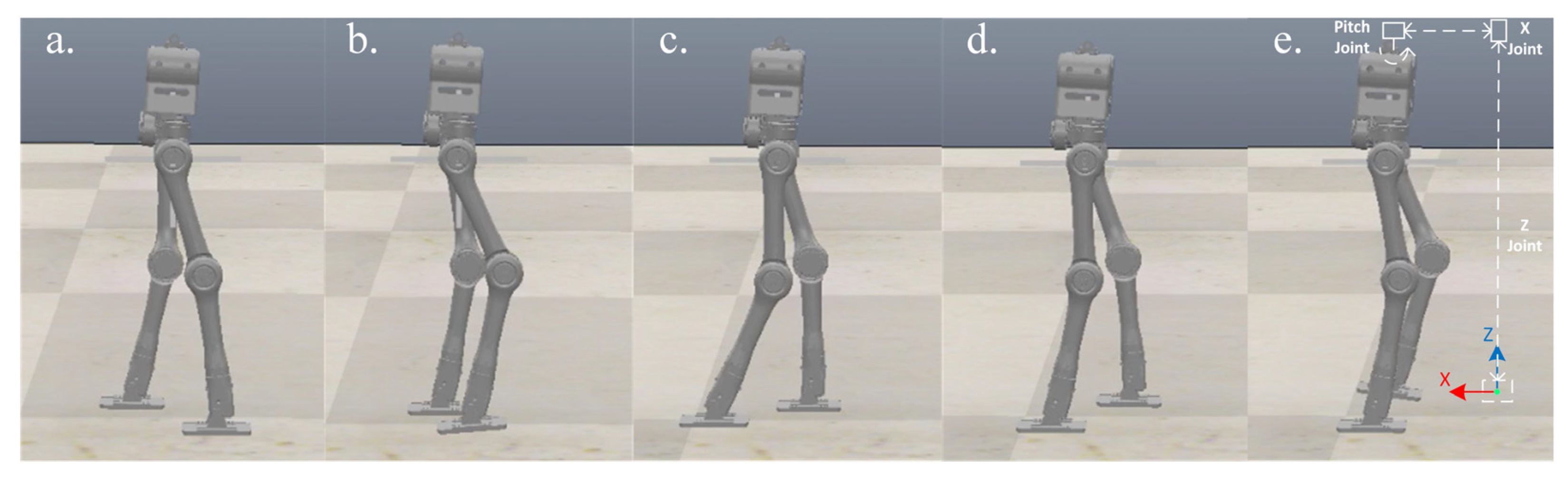
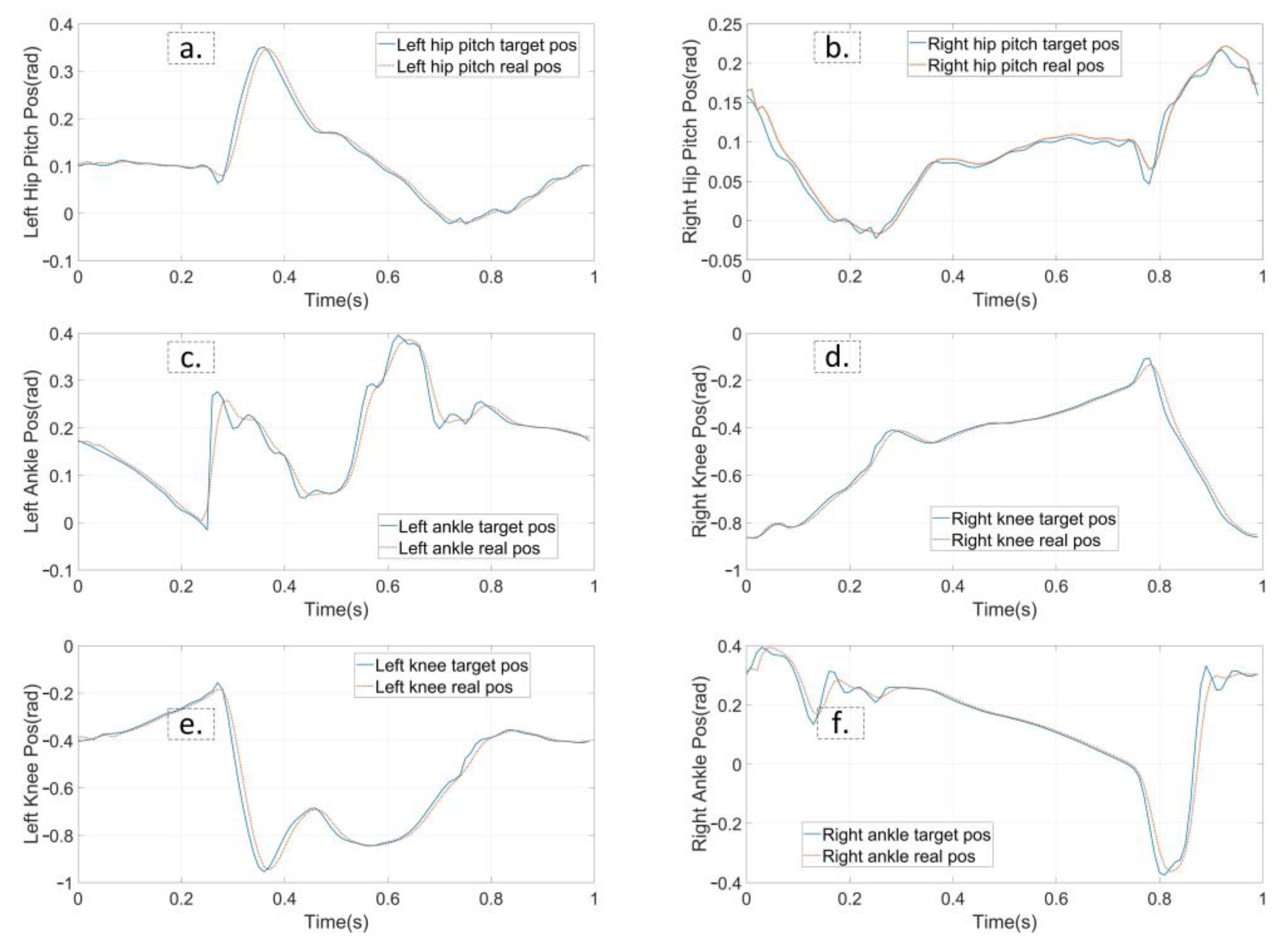
4.2. Flat Terrain Walking
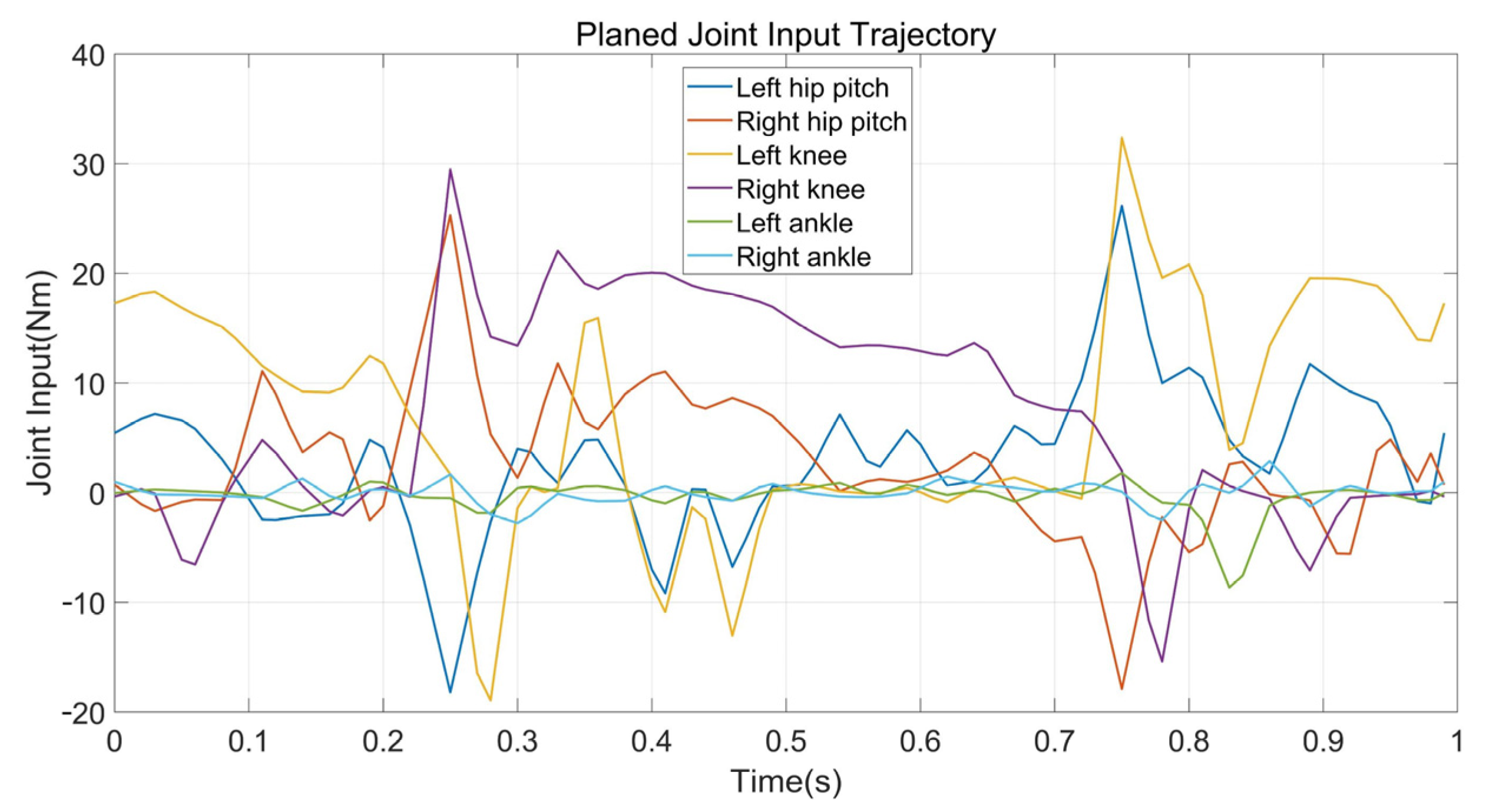
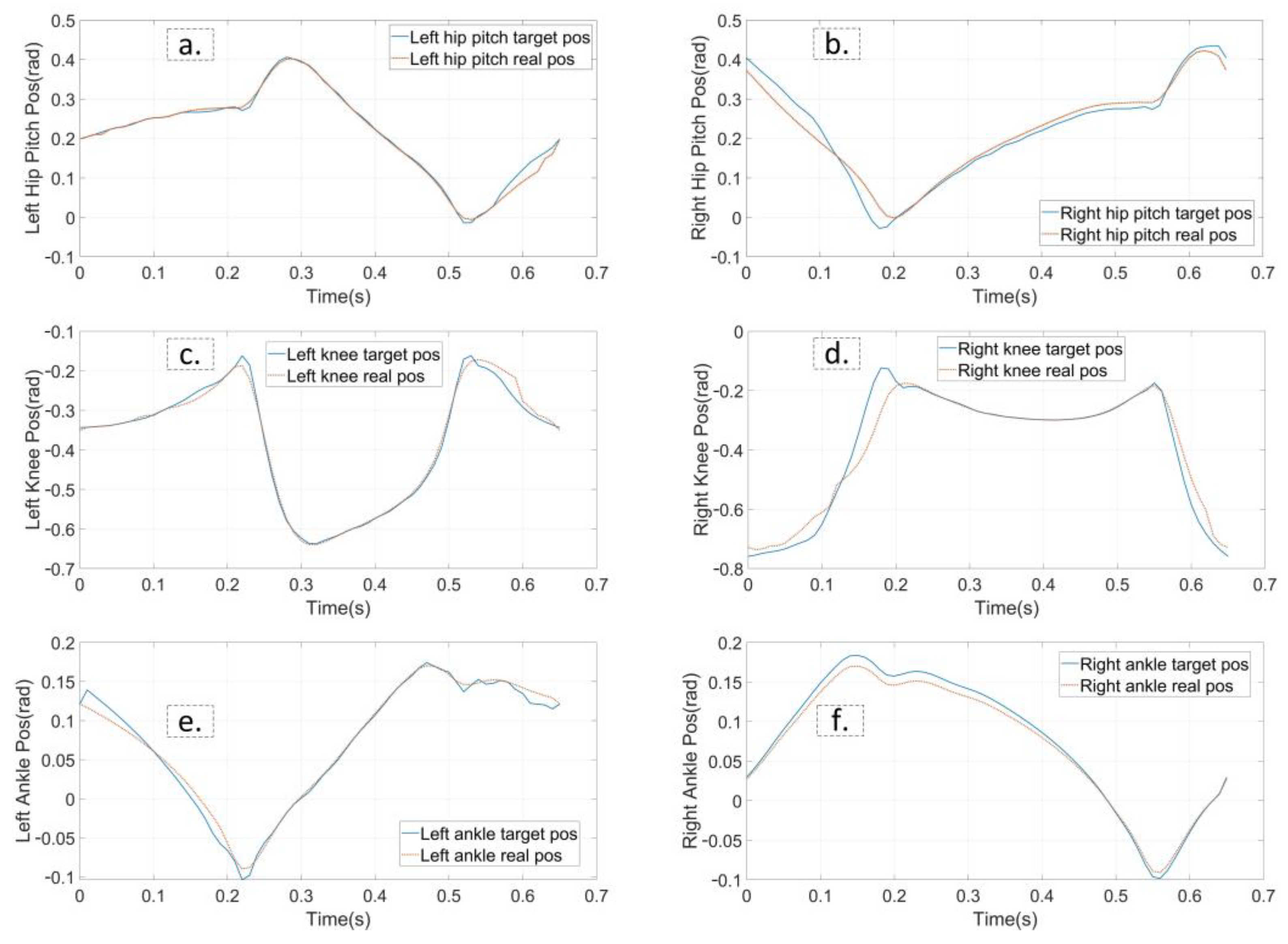
4.3. Stepping Upstairs
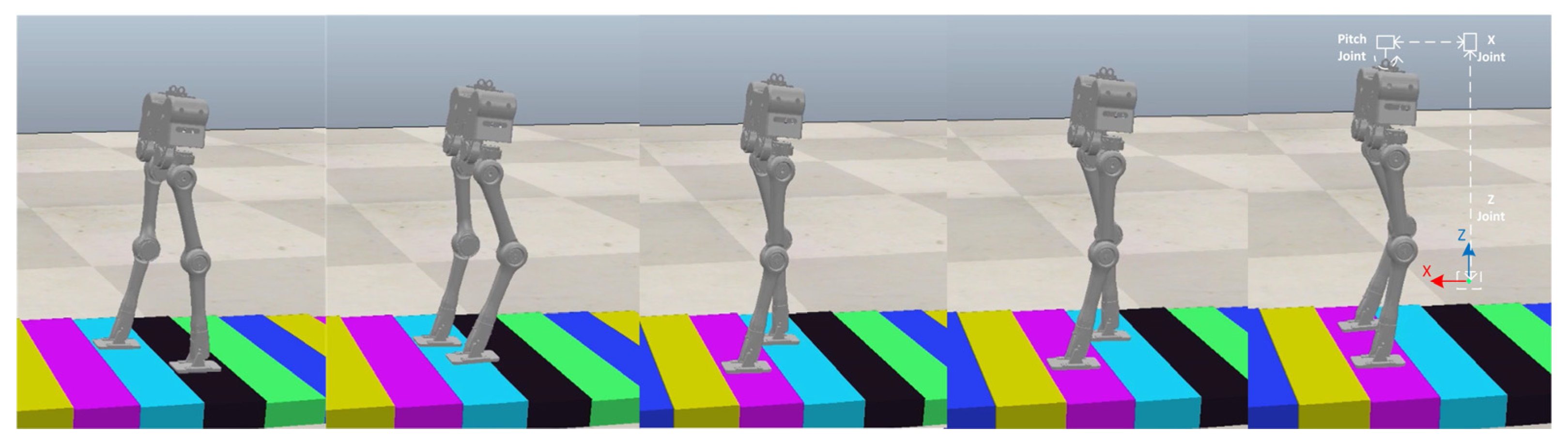
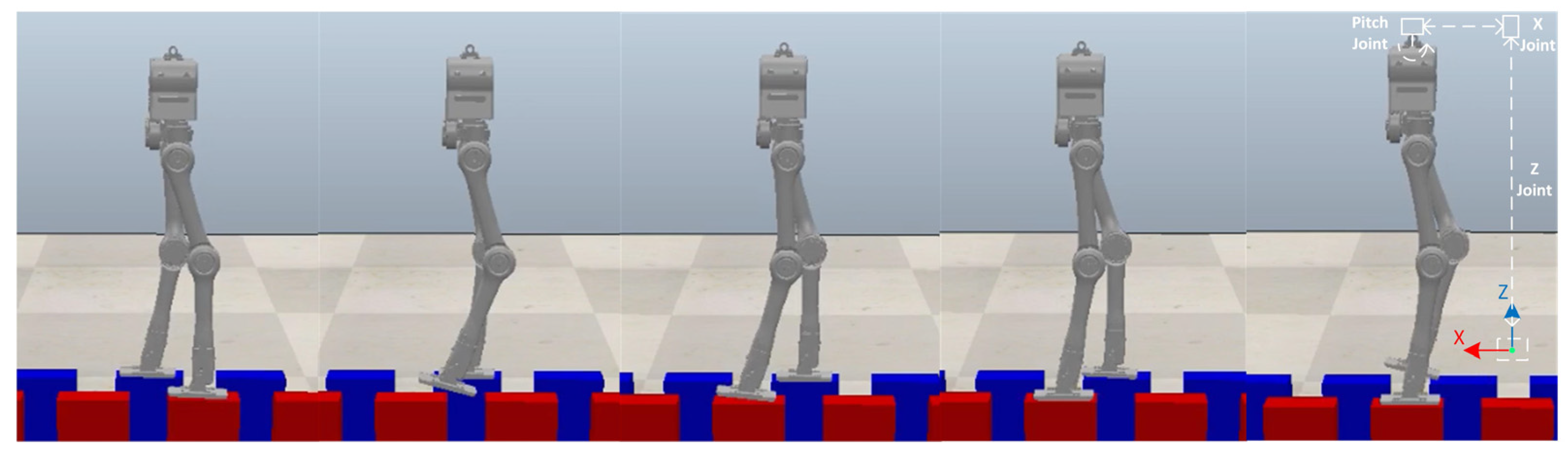
4.4. Quincuncial Piles Walking
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hereid, A.; Hubicki, C.M.; Cousineau, E.A.; Ames, A.D. Dynamic Humanoid Locomotion: A Scalable Formulation for HZD Gait Optimization. IEEE Trans. Robot. 2018, 34, 370–387. [Google Scholar] [CrossRef]
- Ma, W.-L.; Hamed, K.A.; Ames, A.D. First Steps Towards Full Model Based Motion Planning and Control of Quadrupeds: A Hybrid Zero Dynamics Approach. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 5498–5503. [Google Scholar] [CrossRef]
- Hereid, A.; Cousineau, E.A.; Hubicki, C.M.; Ames, A.D. 3D dynamic walking with underactuated humanoid robots: A direct collocation framework for optimizing hybrid zero dynamics. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1447–1454. [Google Scholar] [CrossRef]
- Gil, C.R.; Calvo, H.; Sossa, H. Learning an efficient gait cycle of a biped robot based on reinforcement learning and artificial neural networks. Appl. Sci. 2019, 9, 502. [Google Scholar] [CrossRef]
- Xie, Z.; Clary, P.; Dao, J.; Morais, P.; Hurst, J.; van de Panne, M. Iterative reinforcement learning based design of dynamic locomotion skills for cassie. arXiv 2019, arXiv:1903.09537. [Google Scholar]
- Castillo, G.A.; Weng, B.; Zhang, W.; Hereid, A. Robust Feedback Motion Policy Design Using Reinforcement Learning on a 3D Digit Bipedal Robot. arXiv 2021, arXiv:2103.15309. [Google Scholar]
- Li, Z.; Cheng, X.; Bin Peng, X.; Abbeel, P.; Levine, S.; Berseth, G.; Sreenath, K. Reinforcement Learning for Robust Parameterized Locomotion Control of Bipedal Robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 2811–2817. [Google Scholar] [CrossRef]
- Posa, M.; Kuindersma, S.; Tedrake, R. Optimization and stabilization of trajectories for constrained dynamical systems. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1366–1373. [Google Scholar]
- Winkler, A.W.; Bellicoso, C.D.; Hutter, M.; Buchli, J. Gait and trajectory optimization for legged systems through phase-based end-effector parameterization. IEEE Robot. Autom. Lett. 2018, 3, 1560–1567. [Google Scholar] [CrossRef]
- Posa, M.; Cantu, C.; Tedrake, R. A direct method for trajectory optimization of rigid bodies through contact. Int. J. Robot. Res. 2014, 33, 69–81. [Google Scholar] [CrossRef]
- Khan, A.T.; Li, S.; Zhou, X. Trajectory optimization of 5-link biped robot using beetle antennae search. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3276–3280. [Google Scholar] [CrossRef]
- Hong, Y.D. Real-time footstep planning including capture point trajectory optimization for stable biped navigation. Trans. Inst. Meas. Control 2021, 43, 2058–2068. [Google Scholar] [CrossRef]
- Hereid, A.; Harib, O.; Hartley, R.; Gong, Y.; Grizzle, J.W. Rapid trajectory optimization using C-frost with illustration on a cassie-series dynamic walking biped. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4722–4729. [Google Scholar]
- Dafarra, S.; Bertrand, S.; Griffin, R.J.; Metta, G.; Pucci, D.; Pratt, J. Non-Linear Trajectory Optimization for Large Step-Ups: Application to the Humanoid Robot Atlas. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 3884–3891. [Google Scholar]
- Apgar, T.; Clary, P.; Green, K.; Fern, A.; Hurst, J.W. Fast Online Trajectory Optimization for the Bipedal Robot Cassie. In Proceedings of the Robotics: Science and Systems 2018, Pittsburgh, PA, USA, 29–30 June 2018; Volume 101, p. 14. [Google Scholar]
- Kim, I.S.; Han, Y.J.; Hong, Y.D. Stability control for dynamic walking of bipedal robot with real-time capture point trajectory optimization. J. Intell. Robot. Syst. 2019, 96, 345–361. [Google Scholar] [CrossRef]
- Li, L.; Xie, Z.; Luo, X.; Li, J. Trajectory Planning of Flexible Walking for Biped Robots Using Linear Inverted Pendulum Model and Linear Pendulum Model. Sensors 2021, 21, 1082. [Google Scholar] [CrossRef] [PubMed]
- Kumar, J.; Dutta, A. Using bilateral symmetry of the biped robot mechanism for efficient and faster optimal gait learning on uneven terrain. Int. J. Intell. Robot. Appl. 2021, 5, 429–464. [Google Scholar] [CrossRef]
- Pardo, D.; Neunert, M.; Winkler, A.W.; Grandia, R.; Buchli, J. Hybrid direct collocation and control in the constraint-consistent subspace for dynamic legged robot locomotion. In Proceedings of the Robotics: Science and Systems 2017, Cambridge, MA, USA, 12–16 July 2017; Volume 10. [Google Scholar]
- Kelly, M. An introduction to trajectory optimization: How to do your own direct collocation. SIAM Rev. 2017, 59, 849–904. [Google Scholar] [CrossRef]
- Shi, X.; Gao, J.; Lu, Y.; Tian, D.; Liu, Y. Biped Walking Based on Stiffness Optimization and Hierarchical Quadratic Programming. Sensors 2021, 21, 1696. [Google Scholar] [CrossRef] [PubMed]
- Hereid, A.; Hubicki, C.M.; Cousineau, E.A.; Hurst, J.W.; Ames, A.D. Hybrid zero dynamics based multiple shooting optimization with applications to robotic walking. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Wittmann, R.; Hildebrandt, A.-C.; Wahrmann, D.; Rixen, D.; Buschmann, T. Real-time nonlinear model predictive footstep optimization for biped robots. In Proceedings of the 2015 IEEE-RAS 15th International Conference on Humanoid Robots (Humanoids), Seoul, Korea, 3–5 November 2015. [Google Scholar]
- Haddadin, S.; De Luca, A.; Albu-Schäffer, A. Robot collisions: A survey on detection, isolation, and identification. IEEE Trans. Robot. 2017, 33, 1292–1312. [Google Scholar] [CrossRef]
- Main Page of CoppeliaSim. Available online: https://www.coppeliarobotics.com/ (accessed on 21 July 2021).
- Main Page of Drake. Available online: https://drake.mit.edu/ (accessed on 18 August 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Zang, X.; Zhang, Y.; Gao, L.; Zhu, Y.; Zhao, J. A Non-Flat Terrain Biped Gait Planner Based on DIRCON. Biomimetics 2022, 7, 203. https://doi.org/10.3390/biomimetics7040203
Chen B, Zang X, Zhang Y, Gao L, Zhu Y, Zhao J. A Non-Flat Terrain Biped Gait Planner Based on DIRCON. Biomimetics. 2022; 7(4):203. https://doi.org/10.3390/biomimetics7040203
Chicago/Turabian StyleChen, Boyang, Xizhe Zang, Yue Zhang, Liang Gao, Yanhe Zhu, and Jie Zhao. 2022. "A Non-Flat Terrain Biped Gait Planner Based on DIRCON" Biomimetics 7, no. 4: 203. https://doi.org/10.3390/biomimetics7040203
APA StyleChen, B., Zang, X., Zhang, Y., Gao, L., Zhu, Y., & Zhao, J. (2022). A Non-Flat Terrain Biped Gait Planner Based on DIRCON. Biomimetics, 7(4), 203. https://doi.org/10.3390/biomimetics7040203





