Virtual Quartz Crystal Microbalance: Bioinspired Resonant Frequency Tracking
Abstract
1. Introduction
2. Materials and Methods
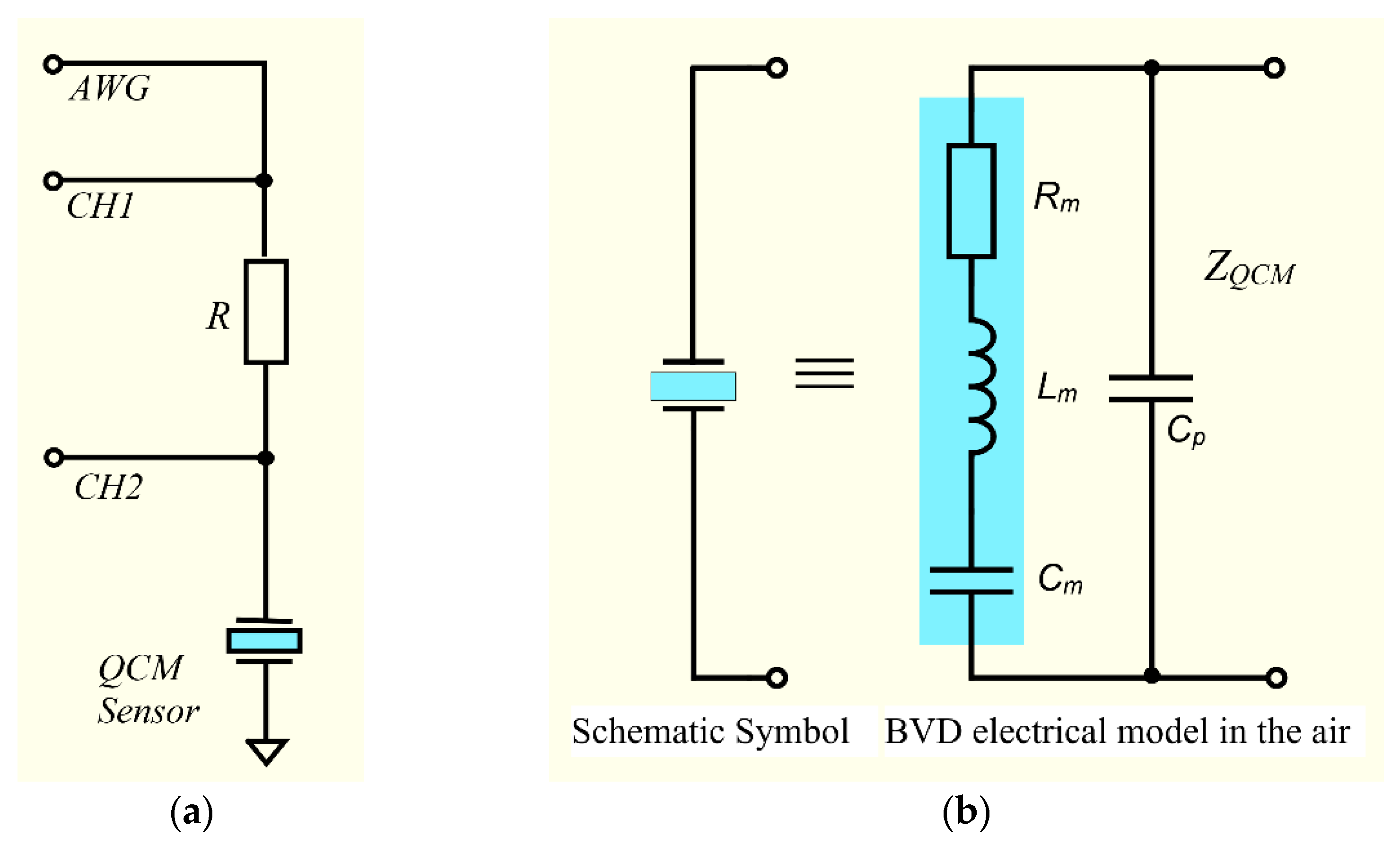
2.1. Virtual Impedance Analyzer and BVD Model of the QCM Sensor
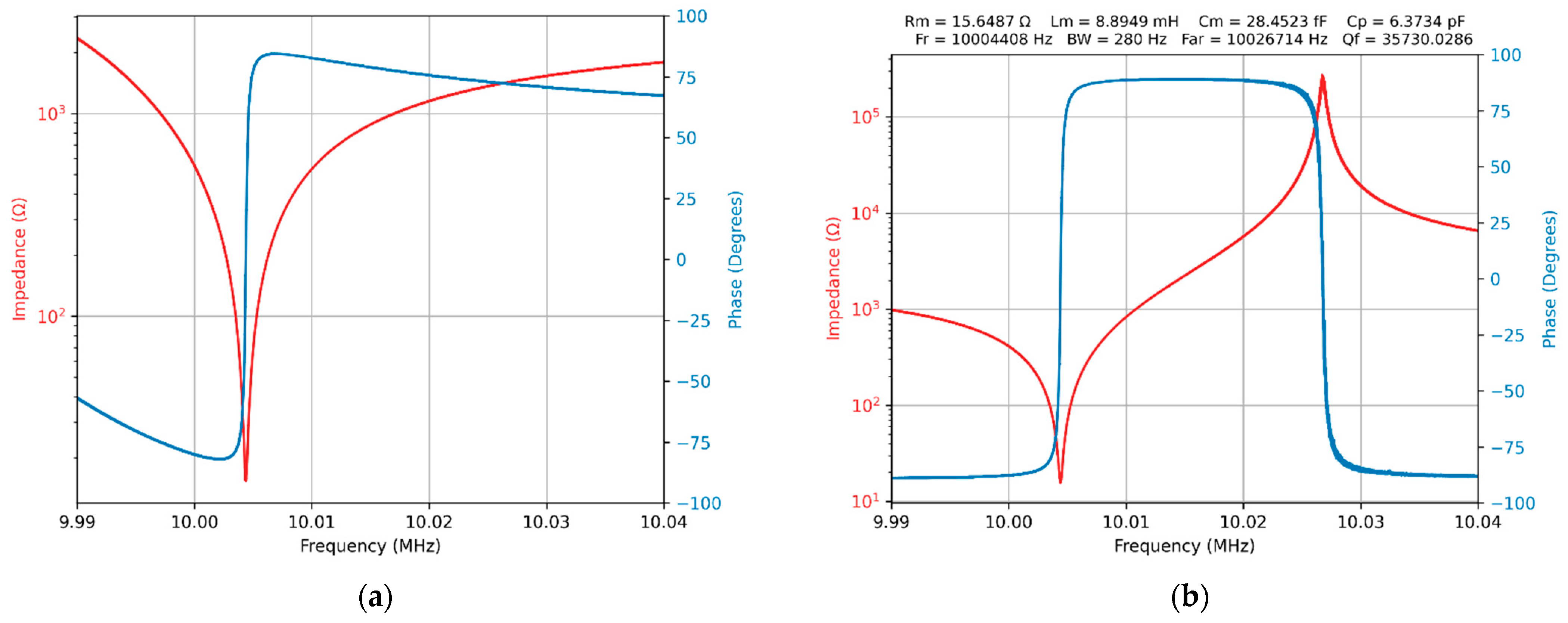
2.2. Impedance Spectroscopy of the QCM Sensor
2.3. Compensation of the Virtual Impedance Analyzer
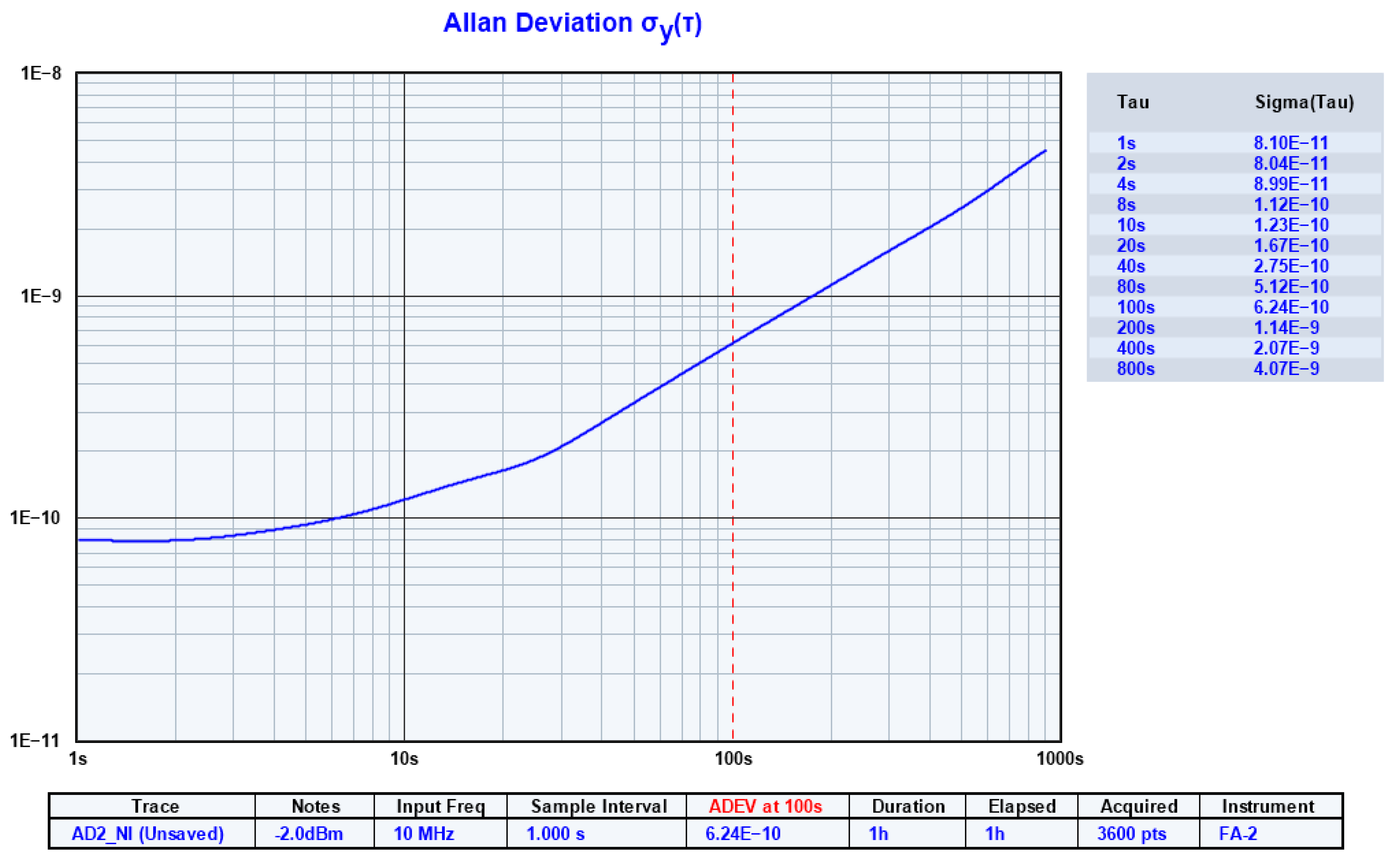
2.4. Allan Deviation Analysis
3. Results
3.1. Series Resonance Frequency Tracking Range
3.2. Scanning Step Effect
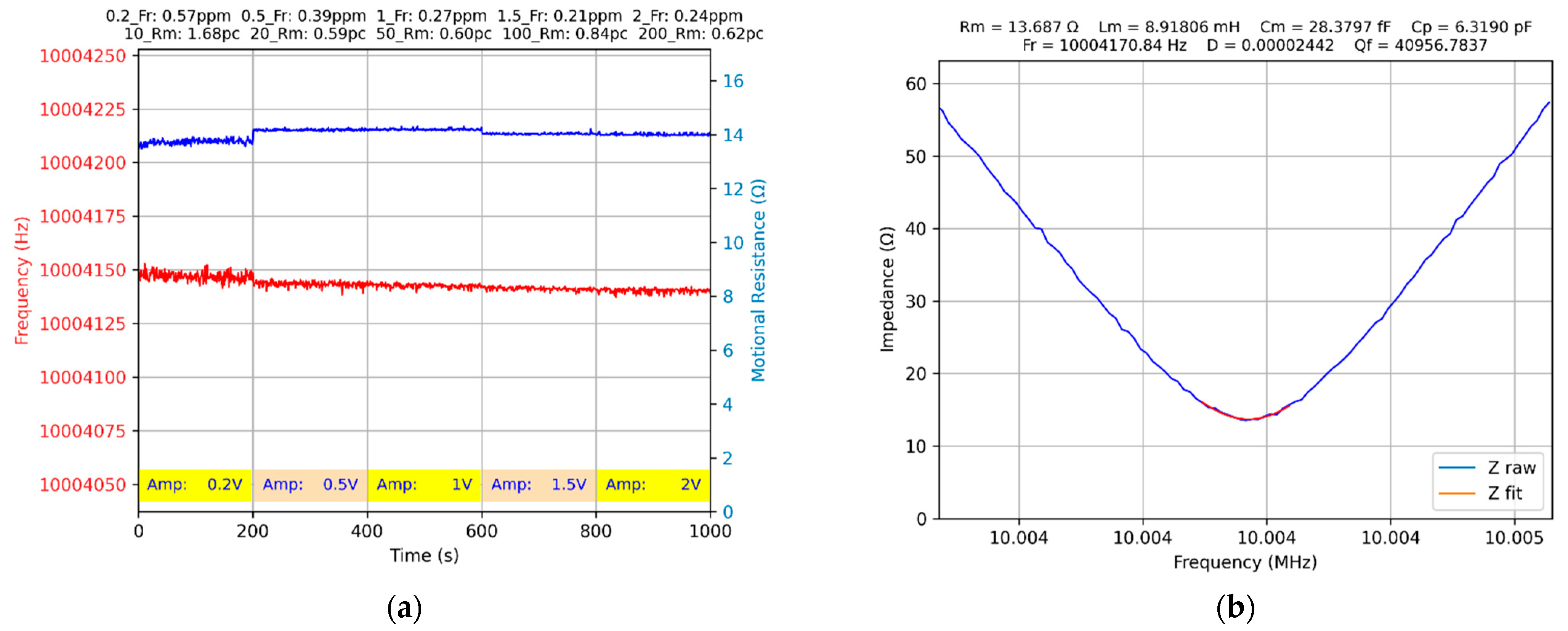
3.3. Drive Level Dependence
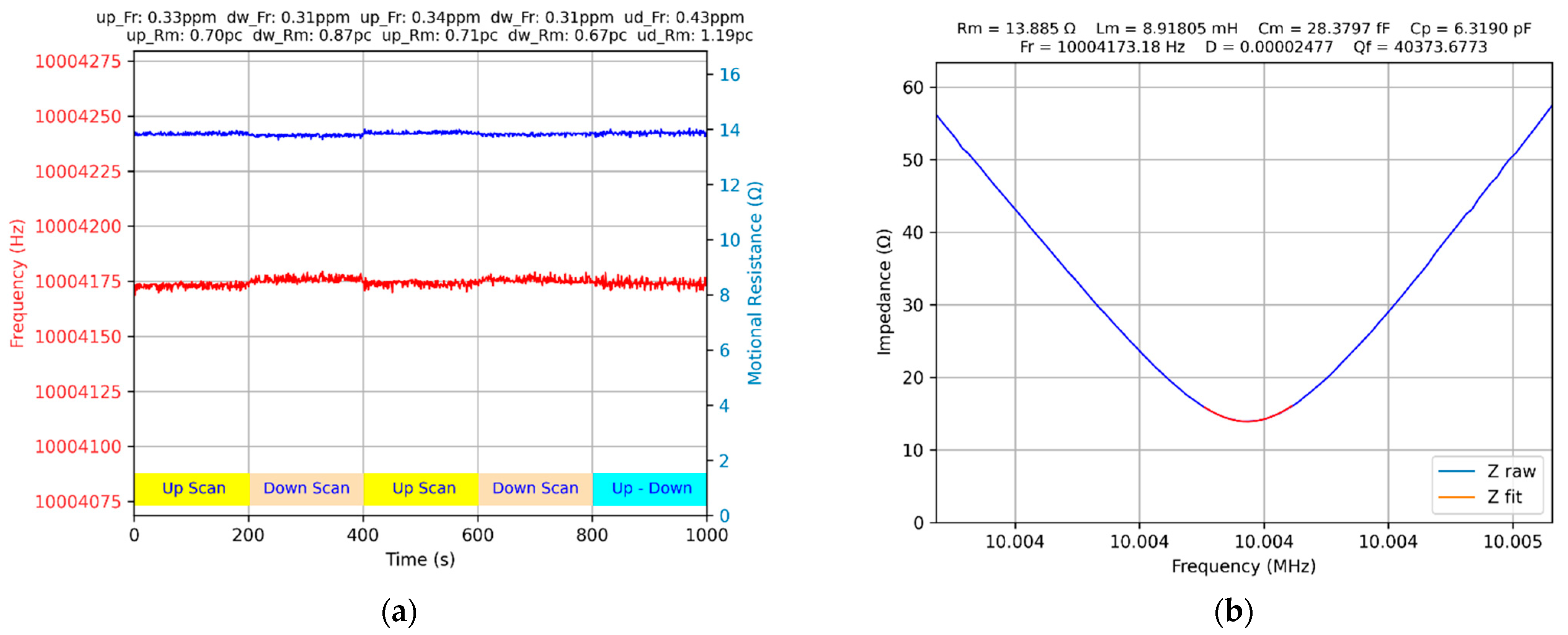
3.4. Scanning Direction Effect
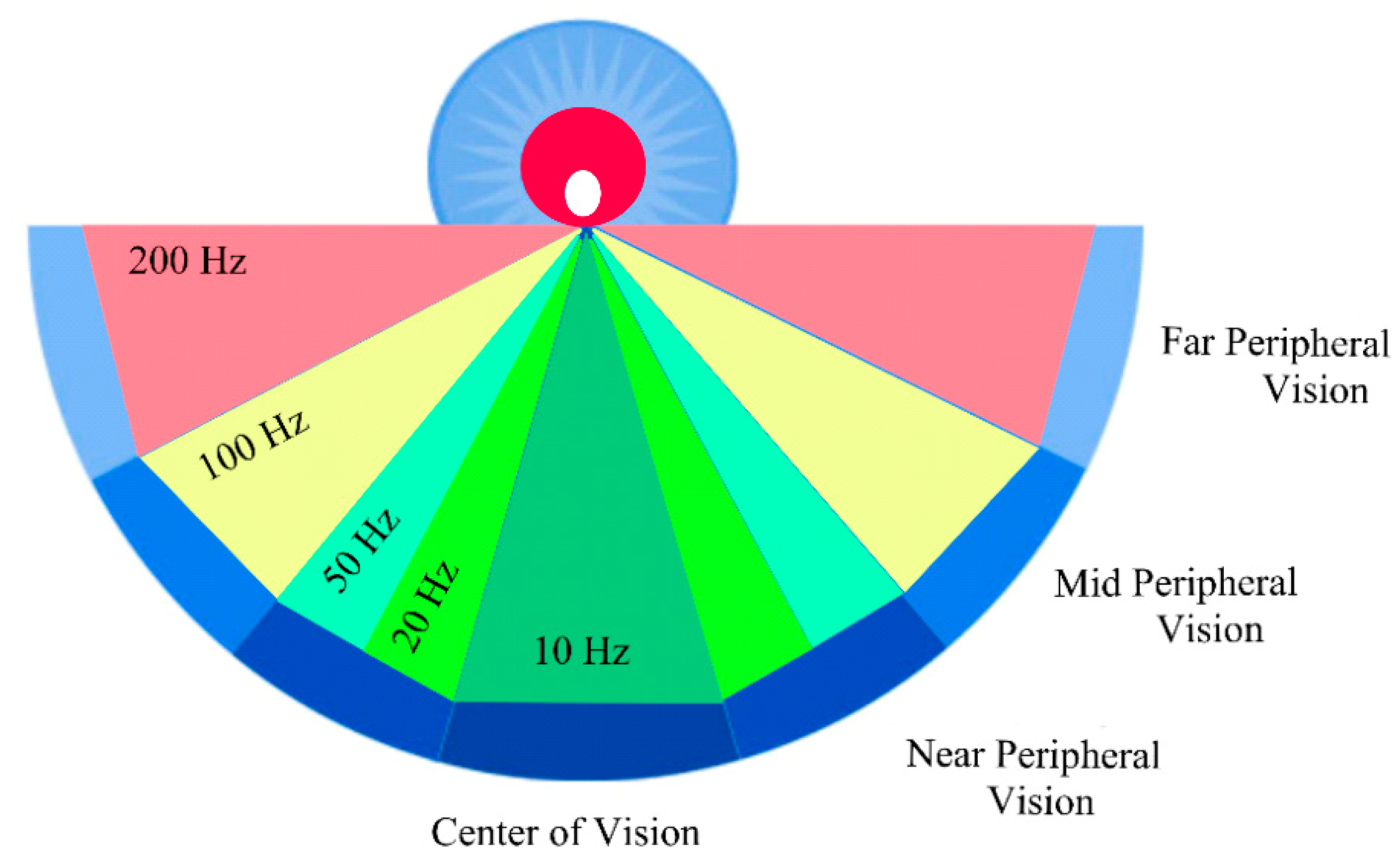
3.5. Bioinspired Series Resonant Frequency Tracking
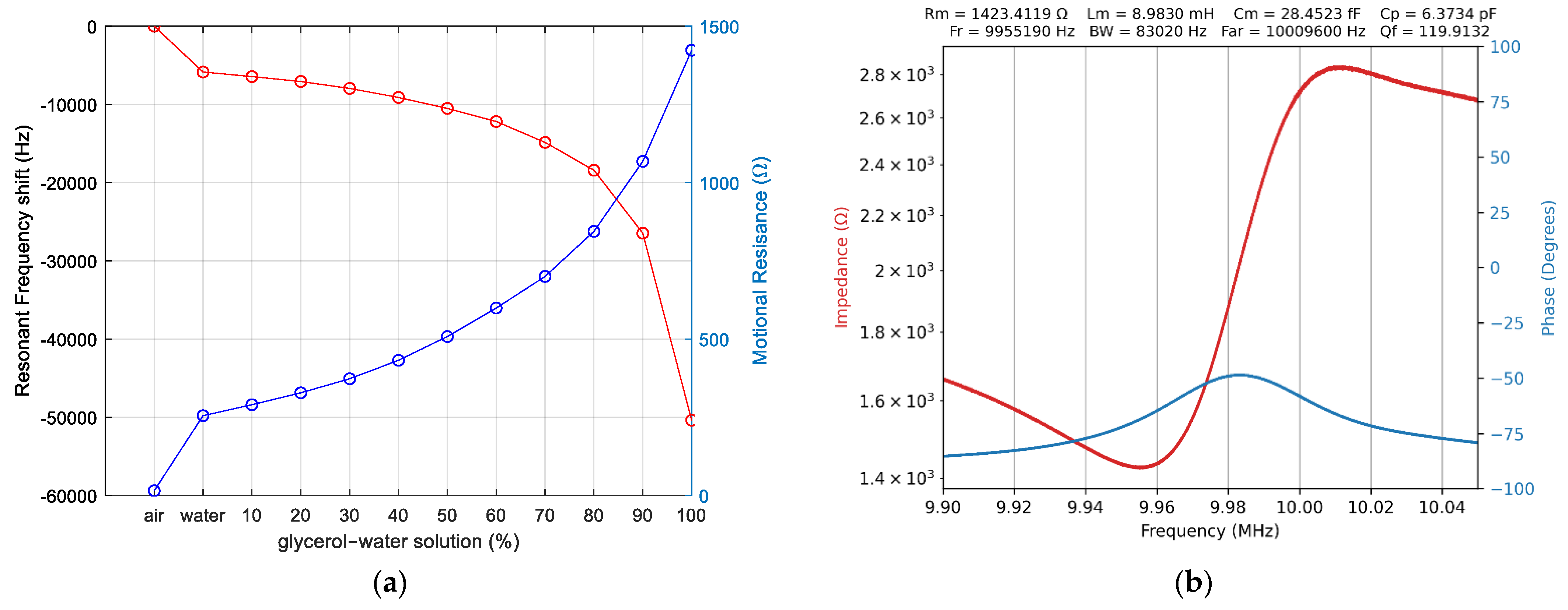
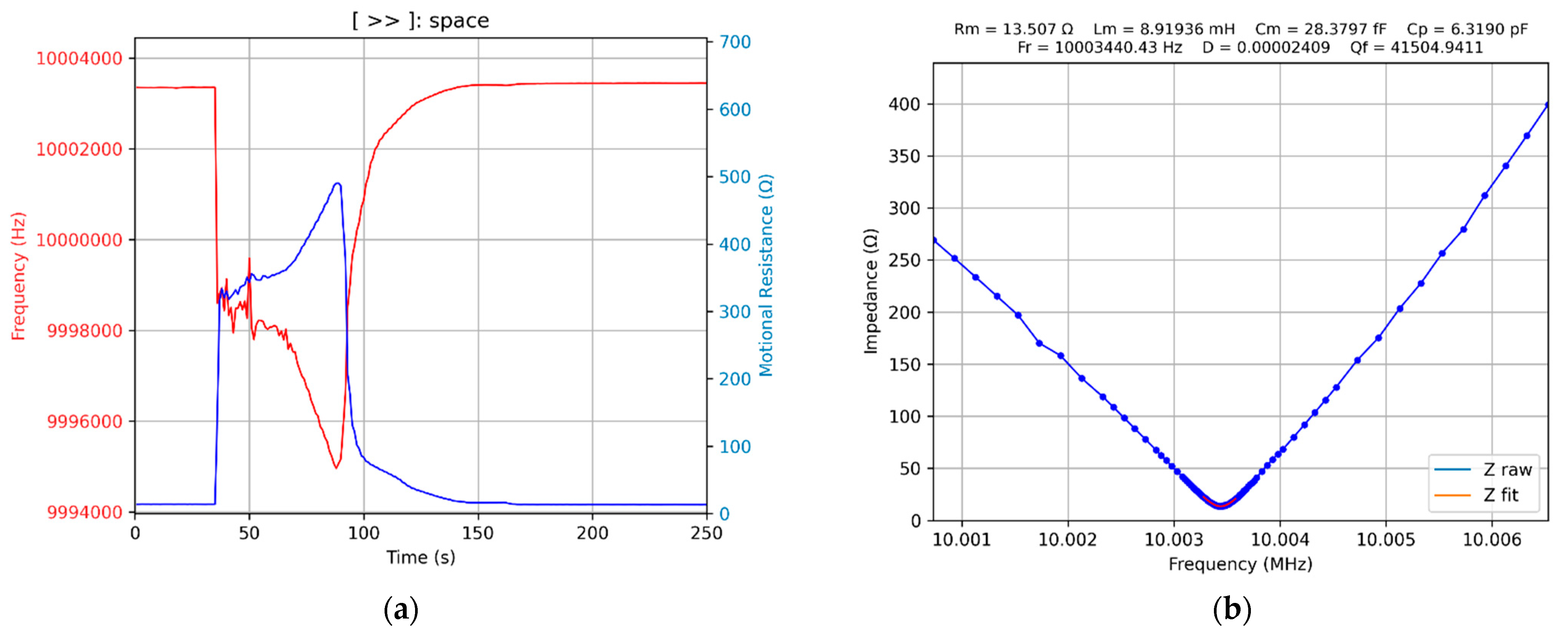
3.6. Evaporation of an Isopropyl Alcohol Drop
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Henschel, J. Tool Use by Spiders: Stone Selection and Placement by Corolla Spiders Ariadna (Segestriidae) of the Namib Desert. Ethology 2010, 101, 187–199. [Google Scholar] [CrossRef]
- Karan, S.K.; Maiti, S.; Kwon, O.; Paria, S.; Maitra, A.; Si, S.K.; Kim, Y.; Kim, J.K.; Khatua, B.B. Nature driven spider silk as high energy conversion efficient bio-piezoelectric nanogenerator. Nano Energy 2018, 49, 655–666. [Google Scholar] [CrossRef]
- Wen, D.L.; Sun, D.H.; Huang, P.; Huang, W.; Su, M.; Wang, Y.; Han, M.D.; Kim, B.; Brugger, B.; Zhang, H.X.; et al. Recent progress in silk fibroin-based flexible electronics. Microsyst. Nanoeng. 2021, 7, 35. [Google Scholar] [CrossRef] [PubMed]
- Curie, J.; Curie, P. Development, via compression, of electric polarization in hemihedral crystals with inclined faces. Bull. Soc. Minerol. Fr. 1880, 91, 90–93. Available online: https://www.persee.fr/doc/bulmi_0150-9640_1880_num_3_4_1564 (accessed on 12 May 2022).
- Shaul, K. Who knew piezoelectricity? Rutherford and Langevin on submarine detection and the invention of sonar. Notes Rec. R. Soc. 2012, 66, 141–157. [Google Scholar] [CrossRef]
- Odom, A.L.; Rink, W.J. Natural accumulation of Schottky-Frenkel defects: Implications for a quartz geochronometer. Geology 1989, 17, 55–58. [Google Scholar] [CrossRef]
- Bottom, V.E. A History of the quartz crystal industry in the USA. In Proceedings of the 35th Annual Frequency Control Symposium, Abilene, TX, USA, 27–29 May 1981; pp. 3–12. [Google Scholar] [CrossRef]
- Marrison, W.A. The Evolution of the Quartz Crystal Clock. Bell Syst. Technol. J. 1948, 27, 510–588. [Google Scholar] [CrossRef]
- Kinsman, R.G. A History of crystal filters. In Proceedings of the 1998 IEEE International Frequency Control Symposium (Cat. No. 98CH36165), Pasadena, CA, USA, 27 May 1998; pp. 563–570. [Google Scholar] [CrossRef]
- Matko, V. Next Generation AT-Cut Quartz Crystal Sensing Devices. Sensors 2011, 11, 4474–4482. [Google Scholar] [CrossRef] [PubMed]
- Filler, R.L. The acceleration sensitivity of quartz crystal oscillators: A review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 297–305. [Google Scholar] [CrossRef] [PubMed]
- Patel, M.S.; Yong, Y.-K.; Tanaka, M. Drive level dependency in quartz resonators. Int. J. Solids Struct. 2009, 46, 1856–1871. [Google Scholar] [CrossRef]
- Sauerbrey, G. Use of quartz crystals for weighing thin layers and for microweighing. Z. Physik. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Nomura, T.; Hattori, O. Determination of micromolar concentrations of cyanide in solution with a piezoelectric detector. Anal. Chim. Acta 1980, 115, 323–326. [Google Scholar] [CrossRef]
- Kanazawa, K.K.; Gordon, J.G., II. The oscillation frequency of a quartz resonator in contact with a liquid. Anal. Chim. Acta 1985, 175, 99–105. [Google Scholar] [CrossRef]
- Nakamoto, T.; Kobayashi, T. Development of circuit for measuring both Q variation and resonant frequency shift of quartz crystal microbalance. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1994, 41, 806–811. [Google Scholar] [CrossRef] [PubMed]
- Matko, V.; Jezernik, K. New Quartz Oscillator Switching Method for Nano-Henry Range Inductance Measurements. Sensors 2012, 12, 3105–3117. [Google Scholar] [CrossRef] [PubMed]
- Alassi, A.; Benammar, M.; Brett, D. Quartz Crystal Microbalance Electronic Interfacing Systems: A Review. Sensors 2017, 17, 2799. [Google Scholar] [CrossRef]
- Rodahl, M.; Hook, F.; Krozer, A.; Brzezinski, P.; Kasemo, B. Quartz-crystal microbalance setup for frequency and Q-factor measurements in gaseous and liquid environments. Rev. Sci. Instrum. 1995, 66, 3924–3930. [Google Scholar] [CrossRef]
- Rodahl, M.; Kasemo, B. A simple setup to simultaneously measure the resonant frequency and the absolute dissipation factor of a quartz crystal microbalance. Rev. Sci. Instrum. 1996, 67, 3238–3241. [Google Scholar] [CrossRef]
- Johannsmann, D. Studies of viscoelasticity with the QCM. In Piezoelectric Sensors; Springer: Berlin/Heidelberg, Germany, 2007; pp. 49–109. [Google Scholar]
- Burda, I. A Study on Regenerative Quartz Crystal Microbalance. Chemosensors 2022, 10, 262. [Google Scholar] [CrossRef]
- Stéphane, M. Chapter 3—Discrete revolution. In A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Cambridge, MA, USA, 2009; pp. 59–88. [Google Scholar] [CrossRef]
- Song, C.; Ma, Z.; Li, C.; Zhang, H.; Zhu, Z.; Wang, J. Application of Heat-Enhancement for Improving the Sensitivity of Quartz Crystal Microbalance. Biosensors 2022, 12, 643. [Google Scholar] [CrossRef]
- Joyce, M.J.; Todaro, P.; Penfold, R.; Port, S.N.; May, J.A.W.; Barnes, C.; Peyton, A.J. Evaporation of Sessile Drops: Application of the Quartz Crystal Microbalance. Langmuir 2000, 16, 4024–4033. [Google Scholar] [CrossRef]
- Torres, R.; García, J.V.; Arnau, A.; Perrot, H.; To Thi Kim, L.; Gabrielli, C. Improved frequency/voltage converters for fast quartz crystal microbalance applications. Rev. Sci. Instrum. 2008, 79, 045113. [Google Scholar] [CrossRef] [PubMed]
- Burda, I.; Tunyagi, A. Quartz crystal microbalance based on passive frequency to voltage converter. Rev. Sci. Instrum. 2012, 83, 025107. [Google Scholar] [CrossRef] [PubMed]
- Butterworth, S. On a Null Method of Testing Vibration Galvanometers. Proc. Phys. Soc. Lond. 1913, 26, 264. [Google Scholar] [CrossRef][Green Version]
- Van Dyke, K.S. The Piezo-Electric Resonator and Its Equivalent Network. Proc. Inst. Radio Eng. 1928, 16, 742–764. [Google Scholar] [CrossRef]
- Schröder, J.; Borngräber, R.; Lucklum, R.; Hauptmann, P. Network analysis based interface electronics for quartz crystal microbalance. Rev. Sci. Instrum. 2001, 72, 2750–2755. [Google Scholar] [CrossRef]
- Burda, I. Quartz Crystal Microbalance with Impedance Analysis Based on Virtual Instruments: Experimental Study. Sensors 2022, 22, 1506. [Google Scholar] [CrossRef]
- Mills, C.A.; Chai, K.T.C.; Milgrew, M.J.; Glidle, A.; Cooper, J.M.; Cumming, D.R.S. A Multiplexed Impedance Analyzer for Characterizing Polymer-Coated QCM Sensor Arrays. IEEE Sens. J. 2006, 6, 996–1002. [Google Scholar] [CrossRef]
- Sun, H.-T.; Faccio, M.; Cantalini, C.; Pelino, M. Impedence analysis and circuit simulation of quartz resonator in water at different temperatures. Sens. Actuators B Chem. 1996, 32, 169–173. [Google Scholar] [CrossRef]
- Burda, I. Advanced Impedance Spectroscopy for QCM Sensor in Liquid Medium. Sensors 2022, 22, 2337. [Google Scholar] [CrossRef]
- Horton, W.H.; Hague, G.E. Amplitude-frequency effects in VHF quartz resonators. In Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005. [Google Scholar] [CrossRef]
- Fernandez, R.; Calero, M.; Garcia-Narbon, J.V.; Reiviakine, I.; Arnau, A.; Jimenez, Y. A Fast Method for Monitoring the Shifts in Resonance Frequency and Dissipation of the QCM Sensors of a Monolithic Array in Biosensing Applications. IEEE Sens. J. 2021, 21, 6643–6651. [Google Scholar] [CrossRef]
- Del Valle, M. Bioinspired Sensor Systems. Sensors 2011, 11, 10180–10186. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.J.; Granstaff, V.E.; Frye, G.C. Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading. Anal. Chem. 1991, 63, 2272–2281. [Google Scholar] [CrossRef]
- Schmutz, P.; Landolt, D. Electrochemical quartz crystal microbalance study of the transient response of passive Fe-25Cr alloy. Electrochim. Acta 1999, 45, 899–911. [Google Scholar] [CrossRef]
- Analod Discovery 2 Reference Manual. Available online: https://digilent.com/reference/test-and-measurement/analog-discovery-2/reference-manual (accessed on 24 May 2022).
- Ojarand, J.; Min, M.; Koel, A. Multichannel Electrical Impedance Spectroscopy Analyzer with Microfluidic Sensors. Sensors 2019, 19, 1891. [Google Scholar] [CrossRef] [PubMed]
- Kasper, M.; Traxler, L.; Salopek, J.; Grabmayr, H.; Ebner, A.; Kienberger, F. Broadband 120 MHz Impedance Quartz Crystal Microbalance (QCM) with Calibrated Resistance and Quantitative Dissipation for Biosensing Measurements at Higher Harmonic Frequencies. Biosensors 2016, 6, 23. [Google Scholar] [CrossRef]
- Xu, Z.; Yao, J.; Wang, Z.; Liu, Y.; Wang, H.; Chen, B.; Wu, H. Development of a portable electrical impedance tomography system for biomedical applications. IEEE Sens. J. 2018, 18, 8117–8124. [Google Scholar] [CrossRef]
- Allan, D.W. Statistics of atomic frequency standards. Proc. IEEE 1966, 54, 221–230. [Google Scholar] [CrossRef]
- TimeLab. Available online: https://www.miles.io/timelab/beta.htm (accessed on 24 May 2022).
- Geelhood, S.J.; Frank, C.W.; Kanazawa, K. Transient Quartz Crystal Microbalance Behaviors Compared. J. Electrochem. Soc. 2002, 149, H33. [Google Scholar] [CrossRef]
- Brendel, R.; Addouche, M.; Salzenstein, P.; Rubiola, E.; Shmaliy, Y.S. Drive level dependence in quartz crystal resonators at low drive levels: A review. In Proceedings of the 18th European Frequency and Time Forum (EFTF 2004), Guilford, UK, 5–7 April 2004. [Google Scholar] [CrossRef]
- Liao, F.; Zhou, Z.; Kim, B.J.; Chen, J.; Wang, J.; Wan, T.; Zhou, Y.; Hoang, A.T.; Wang, C.; Kang, J.; et al. Bioinspired in-sensor visual adaptation for accurate perception. Nat. Electron. 2022, 5, 84–91. [Google Scholar] [CrossRef]
- Iwasaki, M.; Inomata, H. Relation between superficial capillaries and foveal structures in the human retina. Invest. Ophthalmol. Vis. Sci. 1986, 27, 1698–1705. Available online: https://pubmed.ncbi.nlm.nih.gov/3793399/ (accessed on 10 May 2022). [PubMed]




| Scanning Step (Hz) | ppm | % (pc) |
|---|---|---|
| 200 | 1.57 | 21.87 |
| 100 | 0.99 | 13.14 |
| 50 | 0.60 | 5.40 |
| 20 | 0.27 | 1.47 |
| 10 | 0.26 | 0.74 |
| Drive Level (V) | ppm | % (pc) |
|---|---|---|
| 0.2 | 0.57 | 1.68 |
| 0.5 | 0.39 | 0.59 |
| 1.0 | 0.27 | 0.60 |
| 1.5 | 0.21 | 0.84 |
| 2.0 | 0.24 | 0.62 |
| Scanning Step (Hz) | Steps | Range 1 (Hz) |
|---|---|---|
| 200 | 2 × 10 | 4000 |
| 100 | 2 × 5 | 1000 |
| 50 | 2 × 5 | 500 |
| 20 | 2 × 5 | 200 |
| 10 | 50 | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burda, I. Virtual Quartz Crystal Microbalance: Bioinspired Resonant Frequency Tracking. Biomimetics 2022, 7, 156. https://doi.org/10.3390/biomimetics7040156
Burda I. Virtual Quartz Crystal Microbalance: Bioinspired Resonant Frequency Tracking. Biomimetics. 2022; 7(4):156. https://doi.org/10.3390/biomimetics7040156
Chicago/Turabian StyleBurda, Ioan. 2022. "Virtual Quartz Crystal Microbalance: Bioinspired Resonant Frequency Tracking" Biomimetics 7, no. 4: 156. https://doi.org/10.3390/biomimetics7040156
APA StyleBurda, I. (2022). Virtual Quartz Crystal Microbalance: Bioinspired Resonant Frequency Tracking. Biomimetics, 7(4), 156. https://doi.org/10.3390/biomimetics7040156








