Development of a Material Design Space for 4D-Printed Bio-Inspired Hygroscopically Actuated Bilayer Structures with Unequal Effective Layer Widths
Abstract
:1. Introduction
2. Materials and Methods
2.1. Development of Mechanical Models
2.2. Measurements of Established System’s Parameters
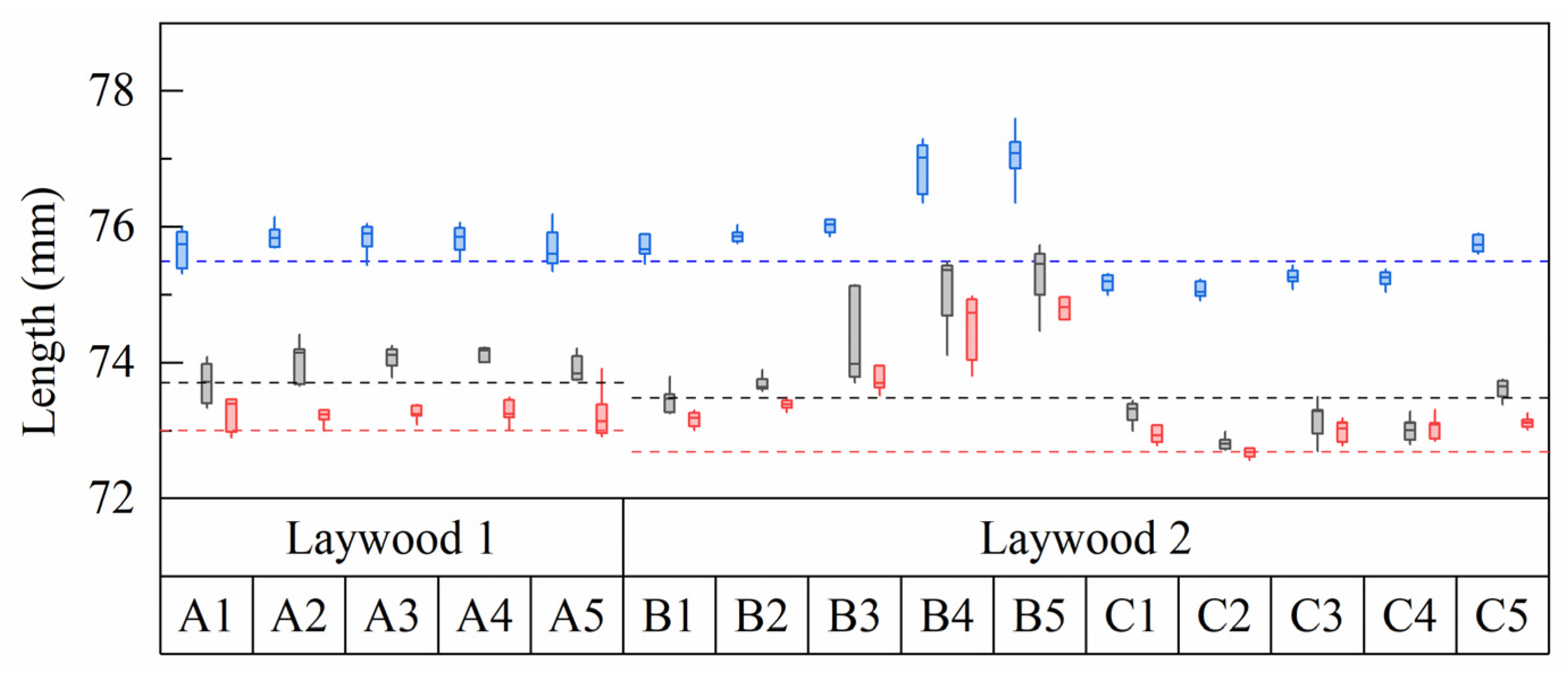
2.2.1. Sample Production
2.2.2. Measurements of Young’s Modulus and Swelling Strains
2.2.3. Bilayer Deflection and Curvature Measurements
3. Results
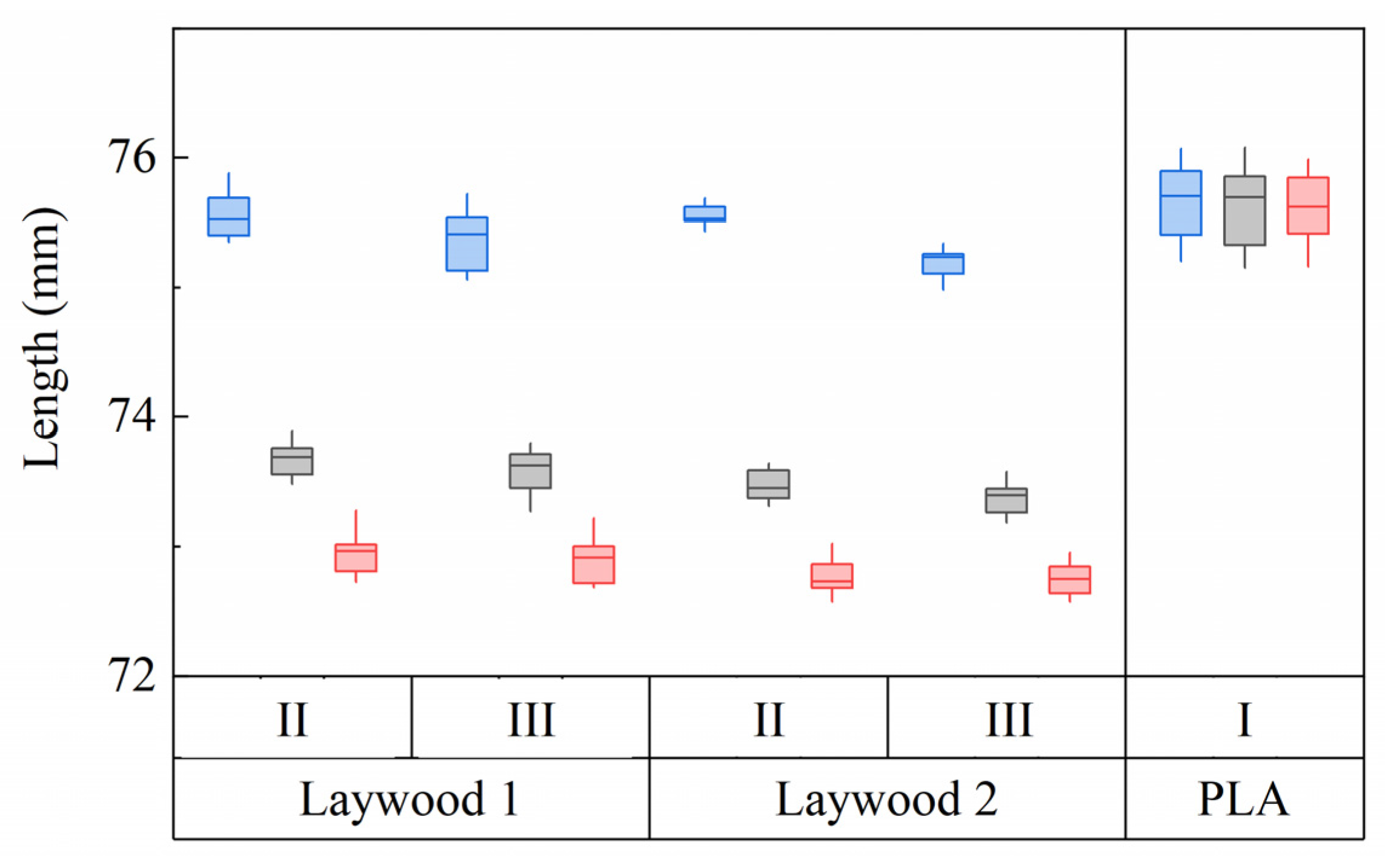
3.1. Material Parameters of the Established Bilayer System
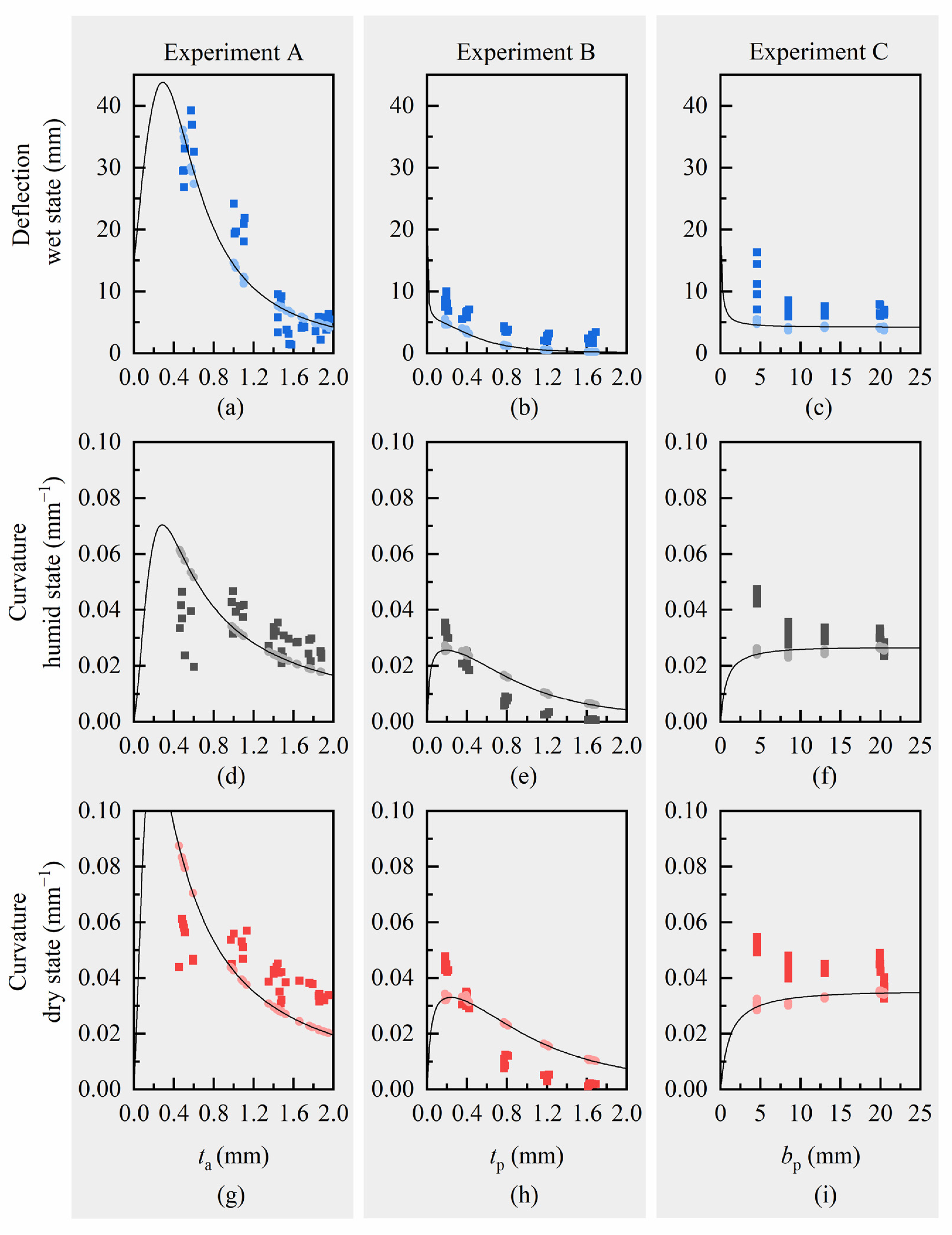
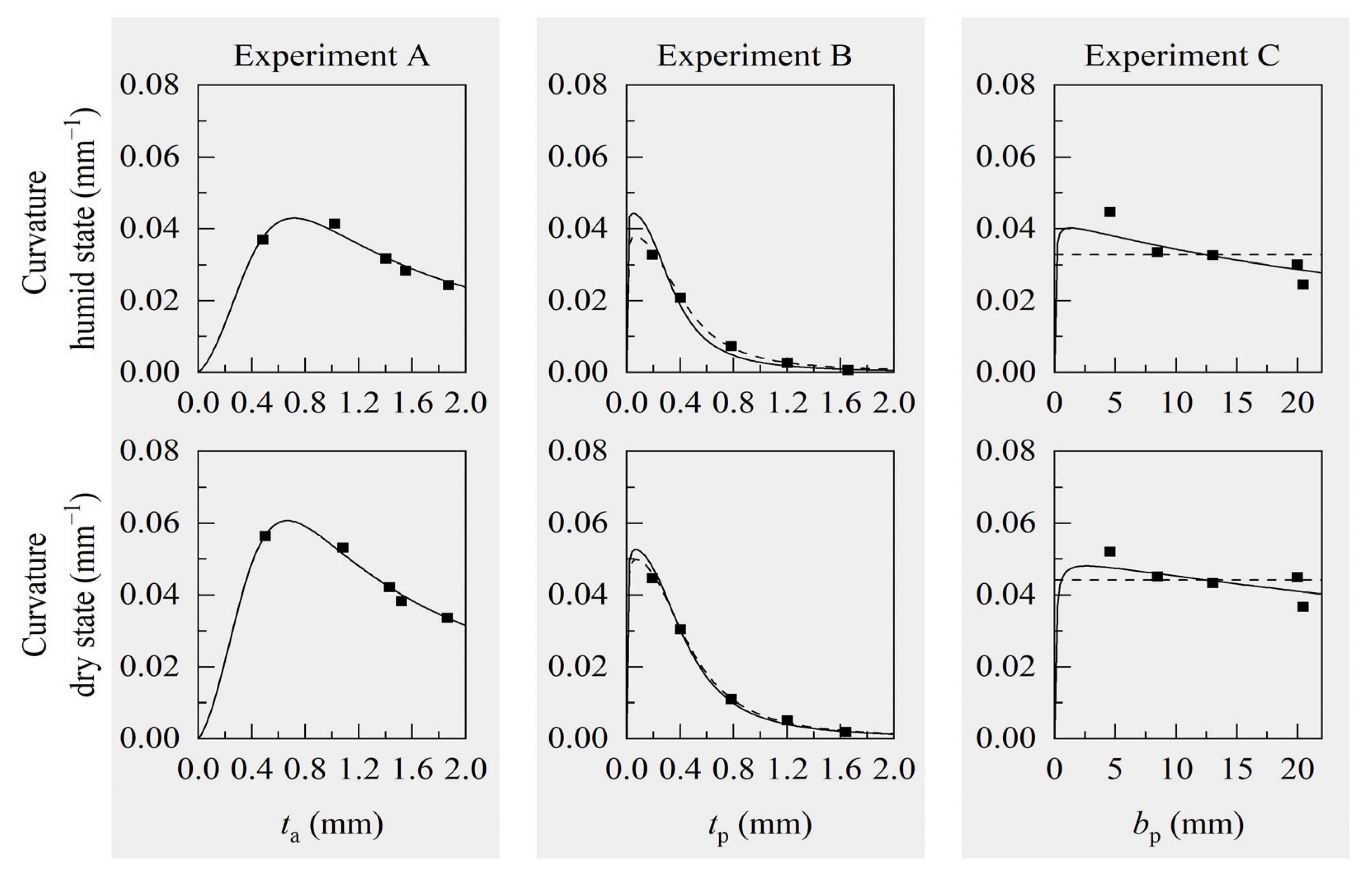
3.2. Comparison of Measured Bilayer Deflections and Curvatures with Computed Values
4. Discussion
4.1. Evaluation of Computed Deflections and Curvatures
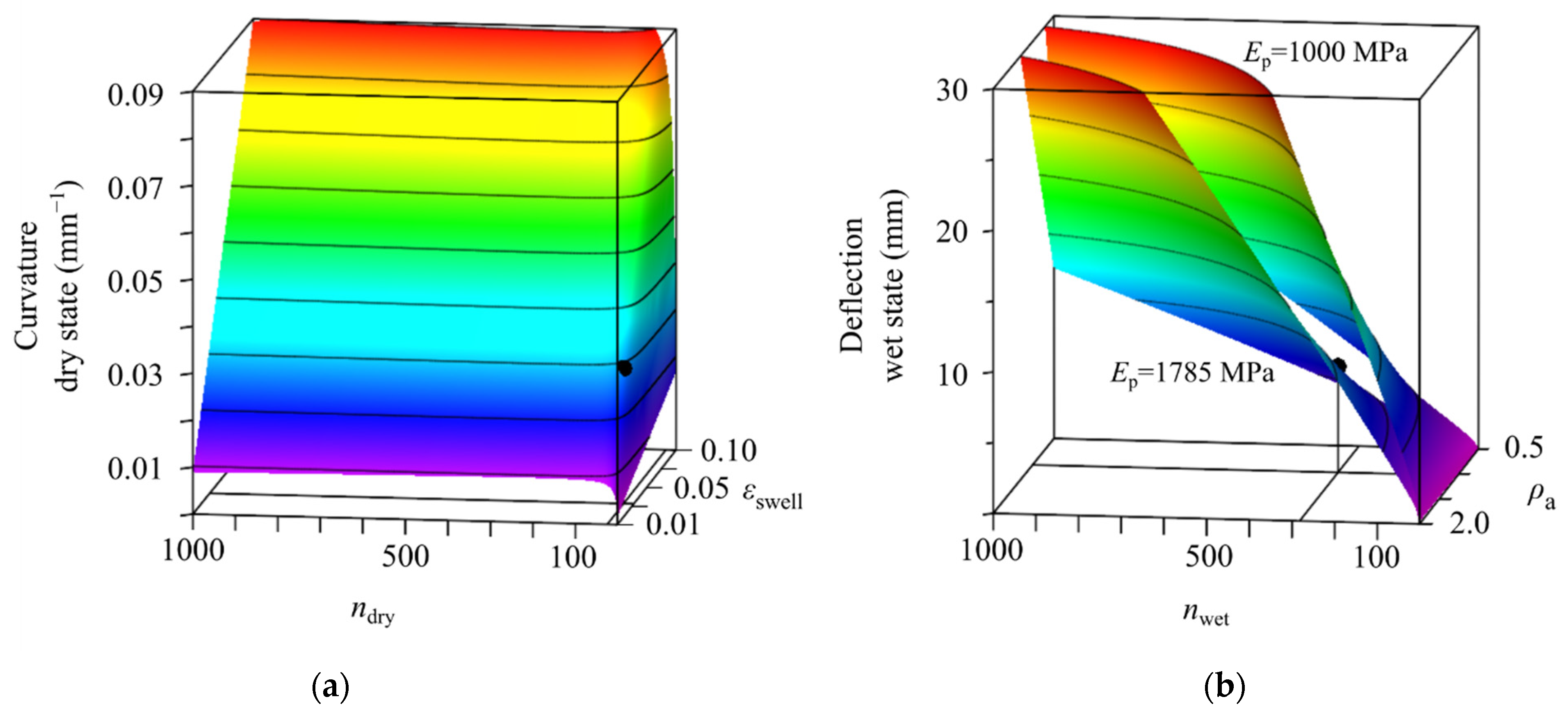
4.2. Development of a Design Space
4.3. Usage and Limitations of Material Design Space for Material Selection or Development
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Active Layer Laywood Meta 5 | Passive Layer PLA | |
|---|---|---|
| Layer height | 0.2 mm | 0.2 mm |
| E-value | 0.040 | 0.033 |
| Nozzle temperature | 210 °C | 210 °C |
| Bed temperature | 55 °C | 55 °C |
| Printing speed (feed rate) | 1200 mm/min | 1200 mm/min |
Appendix C
| Experiment | ta mm | tp mm | ba mm | bp mm | L mm | ρa mg/mm3 | ρp mg/mm3 | Ea MPa | Ep MPa | |
|---|---|---|---|---|---|---|---|---|---|---|
| wet state | A | free | 0.15 | 20.61 | 8.45 | 72.94 | 1.03 | 1.43 | 6.3 | 1785.4 |
| B | 1.45 | free | 20.69 | 9.10 | 73.11 | 1.02 | 1.03 | 9.7 | 1785.4 | |
| C | 1.46 | 0.22 | 20.69 | free | 72.64 | 1.02 | 0.99 | 9.7 | 1785.4 | |
| Experiment | ta in mm | tp in mm | ba in mm | bp in mm | Ea in MPa | Ep in MPa | εswell | |
|---|---|---|---|---|---|---|---|---|
| humid state | A | free | 0.15 | 20.42 | 8.45 | 37.6 | 2188.7 | 0.026 |
| B | 1.38 | free | 20.43 | 9.10 | 61.9 | 2188.7 | 0.028 | |
| C | 1.37 | 0.22 | 20.48 | free | 61.9 | 2188.7 | 0.028 | |
| dry state | A | free | 0.15 | 20.30 | 8.45 | 99.0 | 2467.9 | 0.035 |
| B | 1.36 | free | 20.36 | 9.10 | 110.4 | 2467.9 | 0.037 | |
| C | 1.37 | 0.22 | 20.37 | free | 110.4 | 2467.9 | 0.037 | |
Appendix D

References
- Oriani, A.; Scatena, V.L. The movement of involucral bracts of Syngonanthus elegans (Eriocaulaceae-Poales): Anatomical and ecological aspects. Flora-Morphol. Distrib. Funct. Ecol. Plants 2009, 204, 518–527. [Google Scholar] [CrossRef]
- Evangelista, D.; Hotton, S.; Dumais, J. The mechanics of explosive dispersal and self-burial in the seeds of the filaree, Erodium cicutarium (Geraniaceae). J. Exp. Biol. 2011, 214, 521–529. [Google Scholar] [CrossRef] [Green Version]
- Abraham, Y.; Elbaum, R. Hygroscopic movements in Geraniaceae: The structural variations that are responsible for coiling or bending. New Phytol. 2013, 199, 584–594. [Google Scholar] [CrossRef]
- Elbaum, R.; Zaltzman, L.; Burgert, I.; Fratzl, P. The role of wheat awns in the seed dispersal unit. Science 2007, 316, 884–886. [Google Scholar] [CrossRef]
- Dawson, C.; Vincent, J.F.V.; Rocca, A.-M. How pine cones open. Nature 1997, 390, 668. [Google Scholar] [CrossRef]
- Poppinga, S.; Nestle, N.; Šandor, A.; Reible, B.; Masselter, T.; Bruchmann, B.; Speck, T. Hygroscopic motions of fossil conifer cones. Sci. Rep. 2017, 7, 40302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elbaum, R.; Gorb, S.; Fratzl, P. Structures in the cell wall that enable hygroscopic movement of wheat awns. J. Struct. Biol. 2008, 164, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Fratzl, P.; Elbaum, R.; Burgert, I. Cellulose fibrils direct plant organ movements. Faraday Discuss. 2008, 139, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Fratzl, P.; Barth, F.G. Biomaterial systems for mechanosensing and actuation. Nature 2009, 462, 442–448. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, S.; Liu, H.; Xing, M.; Ding, B.; Li, B. Pinecone-Inspired Nanoarchitectured Smart Microcages Enable Nano/Microparticle Drug Delivery. Adv. Funct. Mater. 2020, 30, 2002434. [Google Scholar] [CrossRef]
- Reichert, S.; Menges, A.; Correa, D. Meteorosensitive architecture: Biomimetic building skins based on materially embedded and hygroscopically enabled responsiveness. Comput. Aided Des. 2015, 60, 50–69. [Google Scholar] [CrossRef]
- Rüggeberg, M.; Burgert, I. Bio-inspired wooden actuators for large scale applications. PLoS ONE 2015, 10, e0120718. [Google Scholar] [CrossRef] [PubMed]
- Vailati, C.; Hass, P.; Burgert, I.; Rüggeberg, M. Upscaling of wood bilayers: Design principles for controlling shape change and increasing moisture change rate. Mater. Struct. 2017, 50, 250. [Google Scholar] [CrossRef]
- Erb, R.M.; Sander, J.S.; Grisch, R.; Studart, A.R. Self-shaping composites with programmable bioinspired microstructures. Nat. Commun. 2013, 4, 1712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arslan, H.; Nojoomi, A.; Jeon, J.; Yum, K. 3D Printing of Anisotropic Hydrogels with Bioinspired Motion. Adv. Sci. 2019, 6, 1800703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Le Duigou, A.; Keryvin, V.; Beaugrand, J.; Pernes, M.; Scarpa, F.; Castro, M. Humidity responsive actuation of bioinspired hygromorph biocomposites (HBC) for adaptive structures. Compos. Part A Appl. Sci. Manuf. 2019, 116, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Le Duigou, A.; Castro, M. Moisture-induced self-shaping flax-reinforced polypropylene biocomposite actuator. Ind. Crop. Prod. 2015, 71, 1–6. [Google Scholar] [CrossRef]
- Tahouni, Y.; Krüger, F.; Poppinga, S.; Wood, D.; Pfaff, M.; Rühe, J.; Speck, T.; Menges, A. Programming sequential motion steps in 4D-printed hygromorphs by architected mesostructure and differential hygro-responsiveness. Bioinspir. Biomim. 2021. [Google Scholar] [CrossRef]
- Correa, D.; Poppinga, S.; Mylo, M.D.; Westermeier, A.S.; Bruchmann, B.; Menges, A.; Speck, T. 4D pine scale: Biomimetic 4D printed autonomous scale and flap structures capable of multi-phase movement. Philos. Trans. R. Soc. A 2020, 378, 20190445. [Google Scholar] [CrossRef]
- Tahouni, Y.; Cheng, T.; Wood, D.; Sachse, R.; Thierer, R.; Bischoff, M.; Menges, A. Self-shaping Curved Folding: A 4D-printing method for fabrication of self-folding curved crease structures. In Symposium on Computational Fabrication; Symposium on Computational Fabrication, Virtual Event USA, 05 11 2020 06 11 2020; Association for Computing Machinery: New York, NY, USA, 2020; Article 5; pp. 1–11. ISBN 9781450381703. [Google Scholar]
- Reyssat, E.; Mahadevan, L. Hygromorphs: From pine cones to biomimetic bilayers. J. R. Soc. Interface 2009, 6, 951–957. [Google Scholar] [CrossRef] [Green Version]
- Langhansl, M.; Dörrstein, J.; Hornberger, P.; Zollfrank, C. Fabrication of 3D-printed hygromorphs based on different cellulosic fillers. Funct. Compos. Mater. 2021, 2. [Google Scholar] [CrossRef]
- Timoshenko, S. Analysis of bi-metal thermostats. Josa 1925, 11, 233–255. [Google Scholar] [CrossRef]
- Wayne, R. ImageJ.; National Institues of Health: Stapleton, NY, USA, 2012. [Google Scholar]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dave, M. Calculating Properties of a Triangle’s Circumcircle. Available online: https://bitbucket.org/davemason/threepointcircumcircle/src/master/ (accessed on 12 July 2021).


| Young’s Modulus in MPa | |||
|---|---|---|---|
| Wet | Humid | Dry | |
| Laywood, batch 1 | 6.3 (0.8) | 37.6 (11.4) | 99.0 (12.8) |
| Laywood, batch 2 | 9.7 (0.5) | 61.9 (10.5) | 110 (36.9) |
| PLA | 1785 (558) | 2189 (303) | 2467 (569) |
| Modified Model (Equation (1)) | Original Model (Timoshenko) | ||||
|---|---|---|---|---|---|
| Experiment | n | εswell | n | εswell | |
| Humid state | A | 691.2 | 0.034 | 286.0 | 0.034 |
| B,C | 610.4 | 0.043 | 149.2 | 0.037 | |
| Dry state | A | 561.9 | 0.045 | 233.9 | 0.045 |
| B,C | 299.7 | 0.051 | 111.6 | 0.048 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krüger, F.; Thierer, R.; Tahouni, Y.; Sachse, R.; Wood, D.; Menges, A.; Bischoff, M.; Rühe, J. Development of a Material Design Space for 4D-Printed Bio-Inspired Hygroscopically Actuated Bilayer Structures with Unequal Effective Layer Widths. Biomimetics 2021, 6, 58. https://doi.org/10.3390/biomimetics6040058
Krüger F, Thierer R, Tahouni Y, Sachse R, Wood D, Menges A, Bischoff M, Rühe J. Development of a Material Design Space for 4D-Printed Bio-Inspired Hygroscopically Actuated Bilayer Structures with Unequal Effective Layer Widths. Biomimetics. 2021; 6(4):58. https://doi.org/10.3390/biomimetics6040058
Chicago/Turabian StyleKrüger, Friederike, Rebecca Thierer, Yasaman Tahouni, Renate Sachse, Dylan Wood, Achim Menges, Manfred Bischoff, and Jürgen Rühe. 2021. "Development of a Material Design Space for 4D-Printed Bio-Inspired Hygroscopically Actuated Bilayer Structures with Unequal Effective Layer Widths" Biomimetics 6, no. 4: 58. https://doi.org/10.3390/biomimetics6040058
APA StyleKrüger, F., Thierer, R., Tahouni, Y., Sachse, R., Wood, D., Menges, A., Bischoff, M., & Rühe, J. (2021). Development of a Material Design Space for 4D-Printed Bio-Inspired Hygroscopically Actuated Bilayer Structures with Unequal Effective Layer Widths. Biomimetics, 6(4), 58. https://doi.org/10.3390/biomimetics6040058






