Obstacle Avoidance Path Planning for Worm-like Robot Using Bézier Curve
Abstract
:1. Introduction
2. Materials and Methods
2.1. Worm-Like Robot Structure and Kinematics
2.2. Bézier Curves
2.3. Path Generation with Obstacle Avoidance
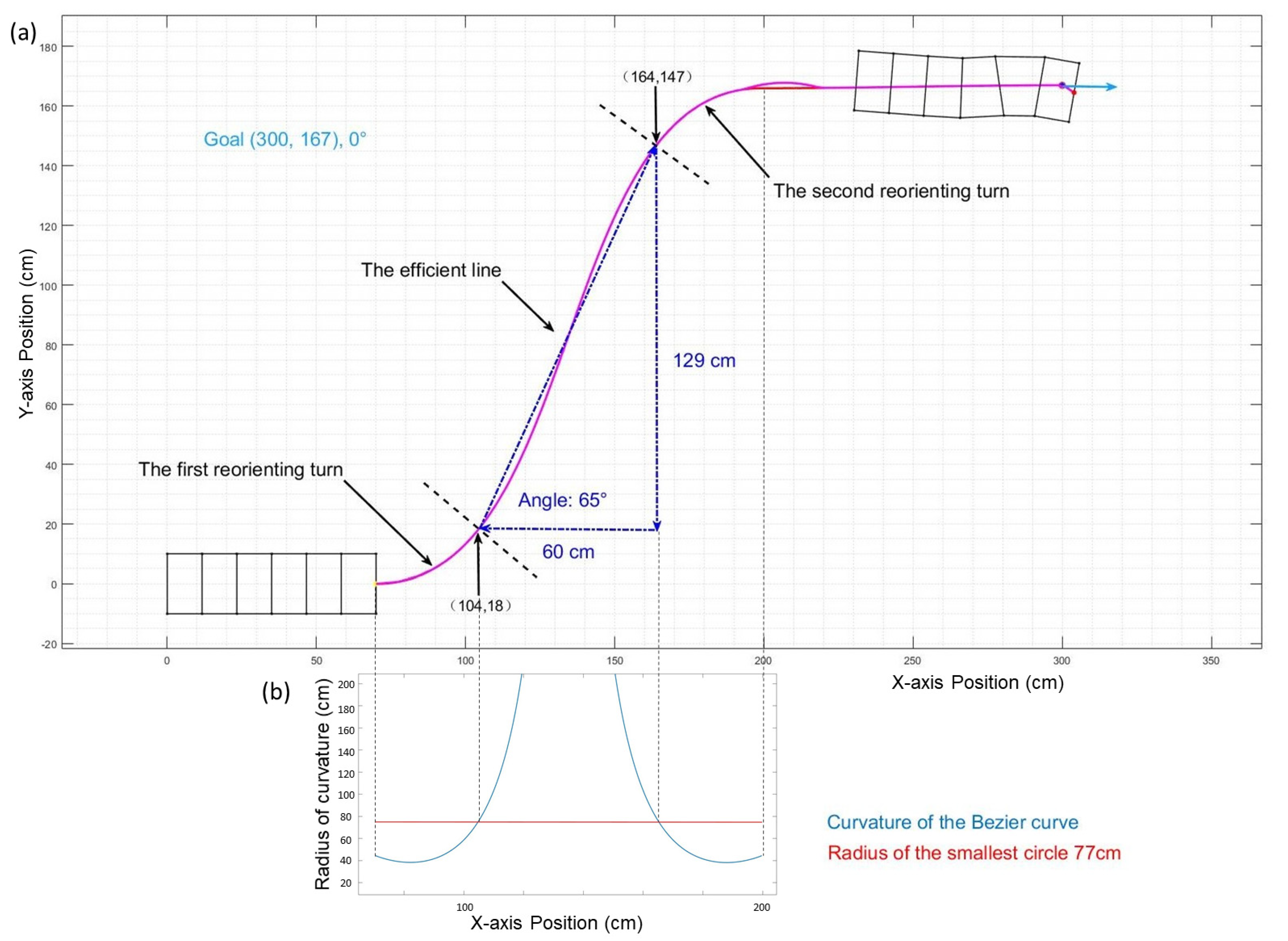
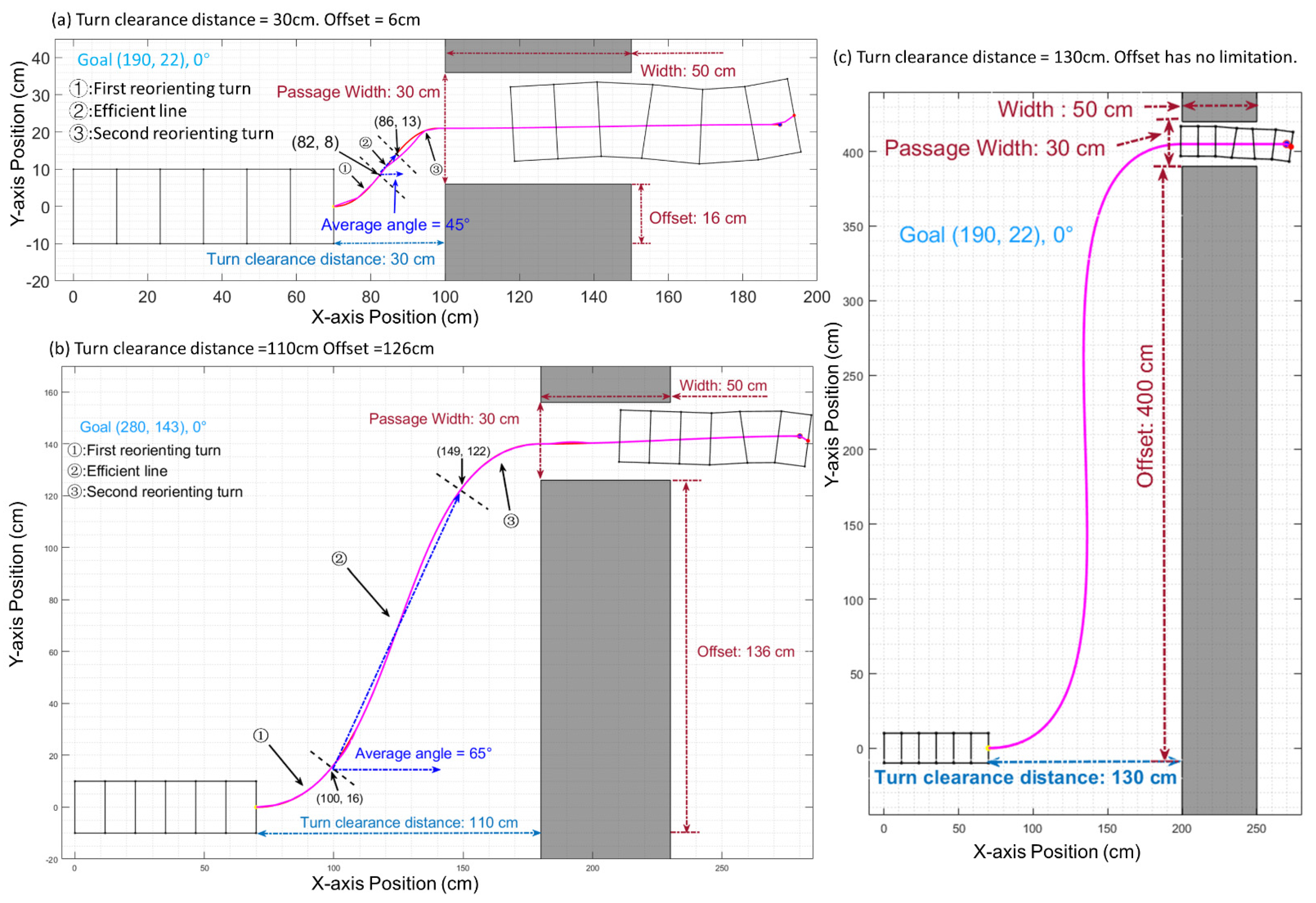
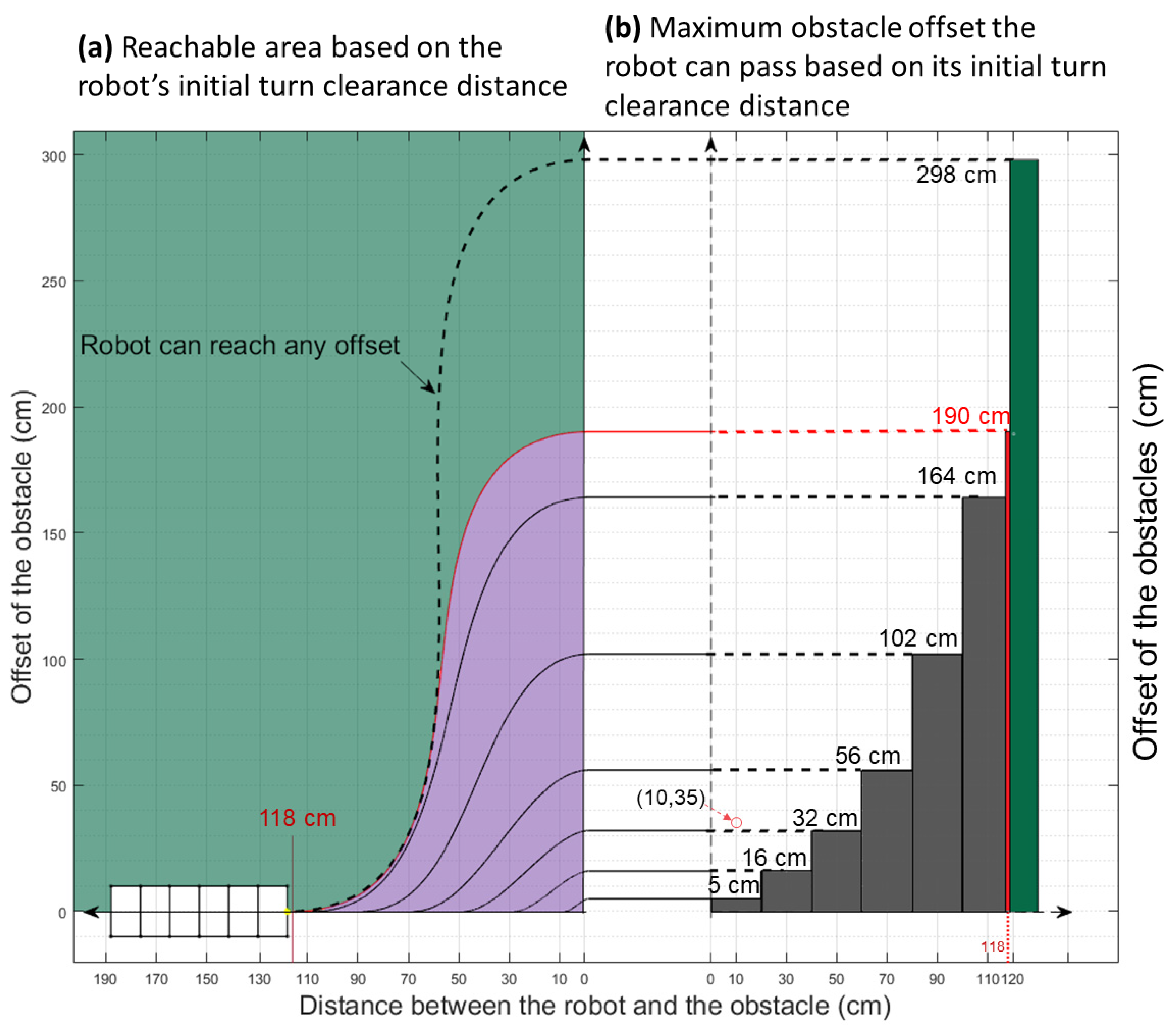
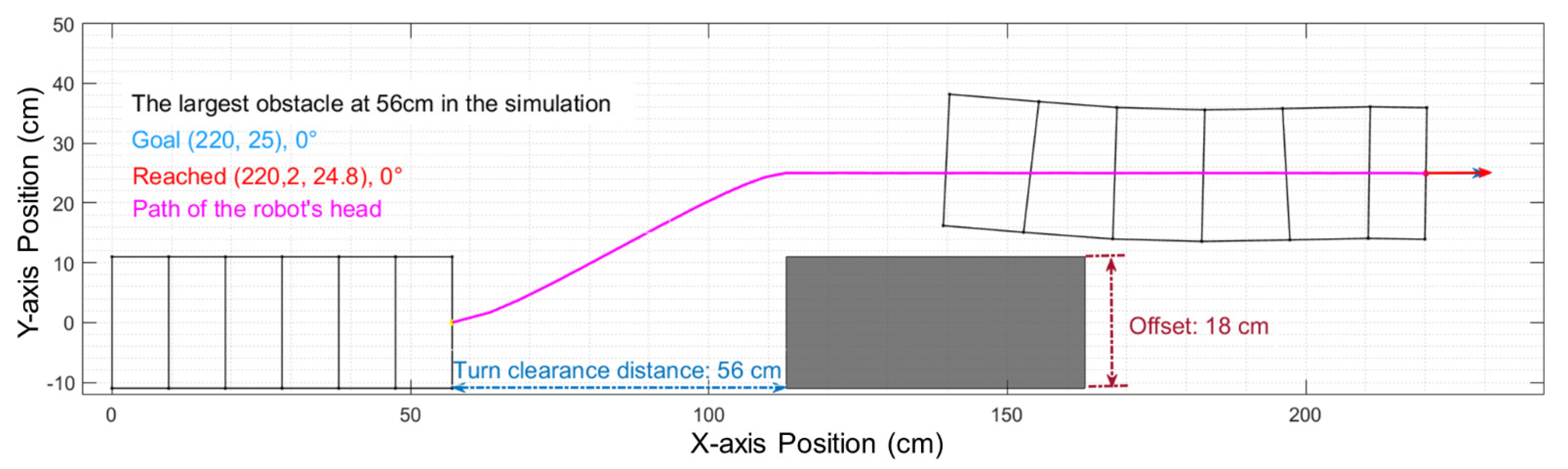
2.4. Analysis of Limiting Factors: Radius, Offset, and Clearance
3. Results
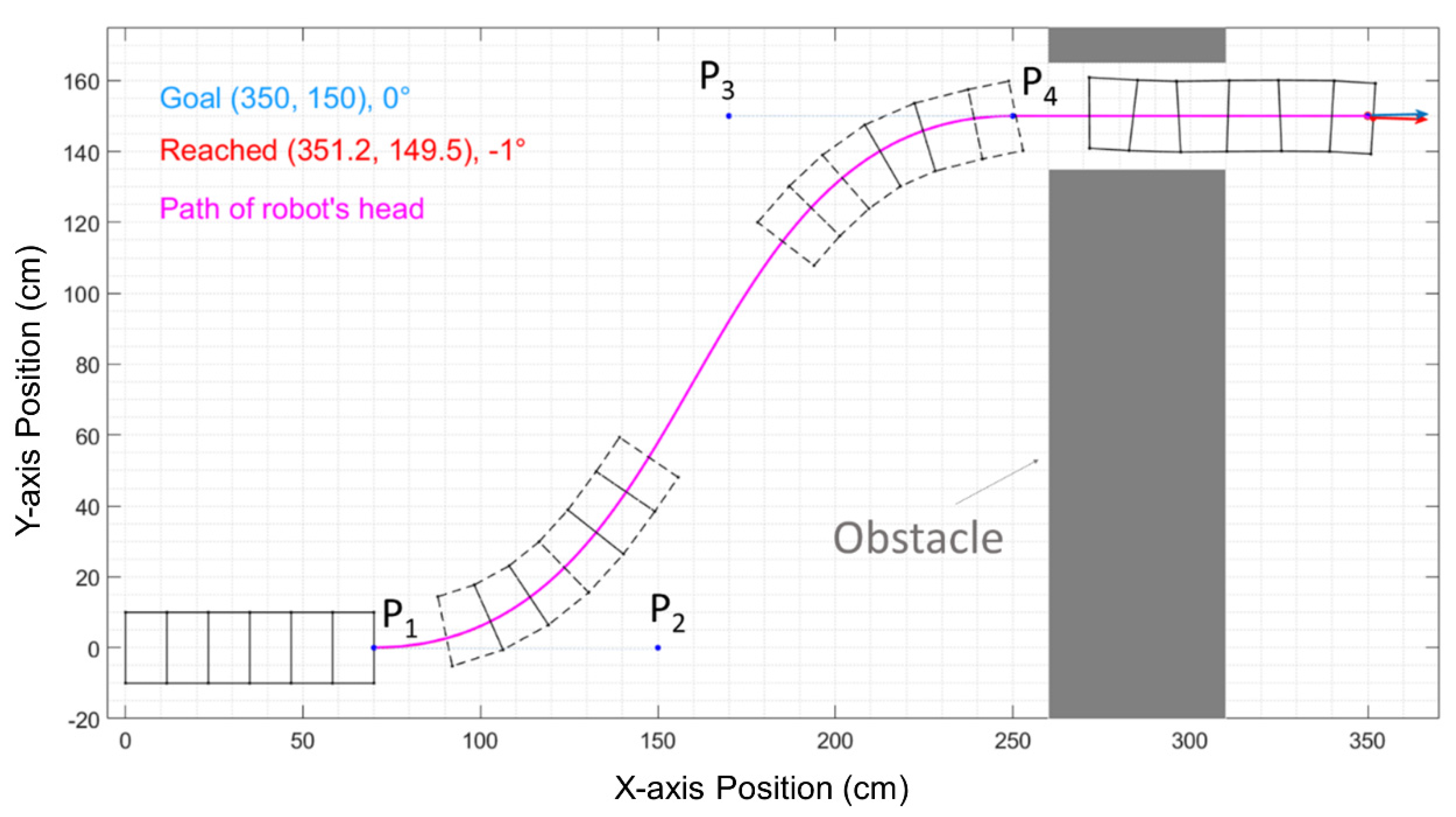
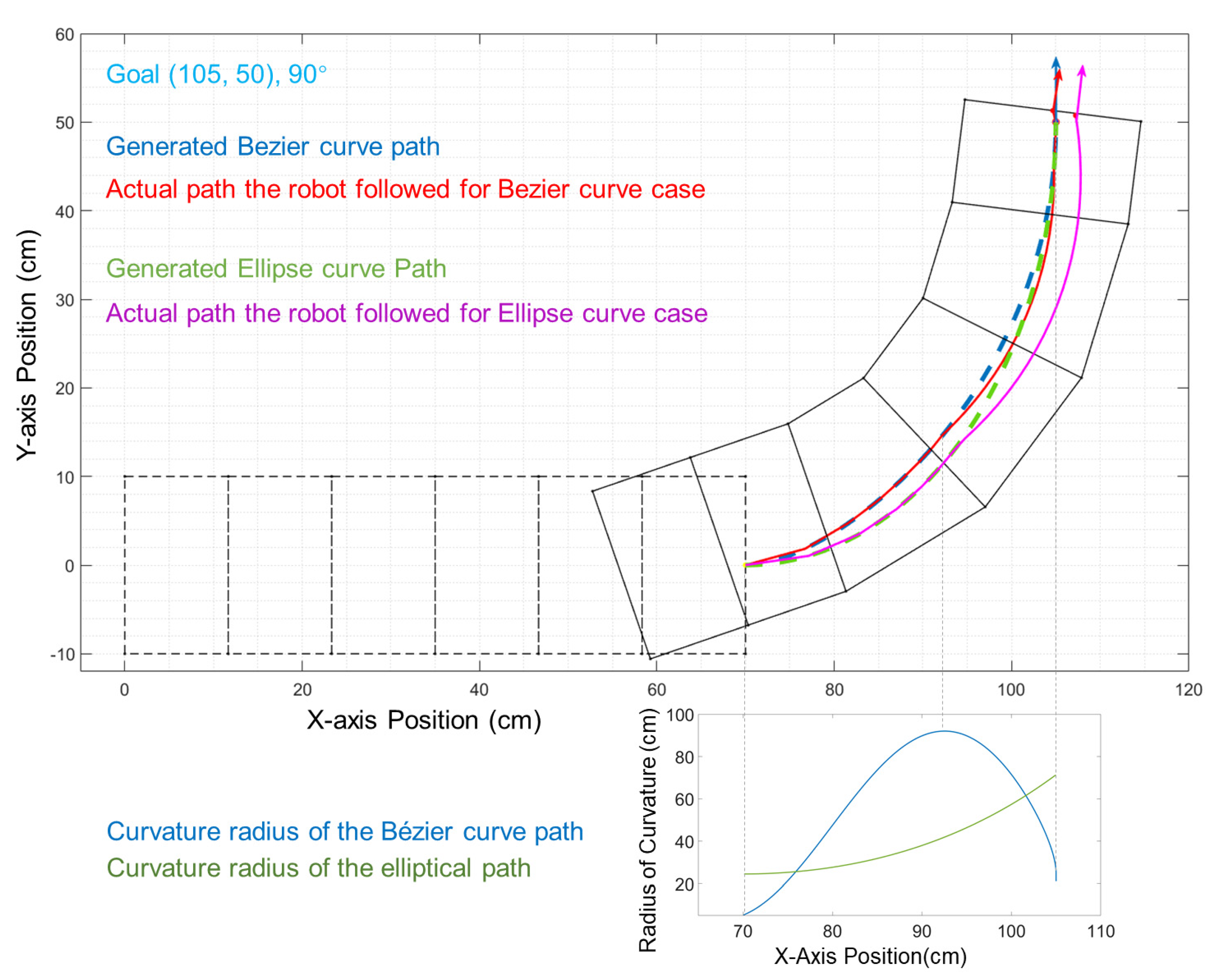
3.1. Path Improvements by Bézier Curves Application
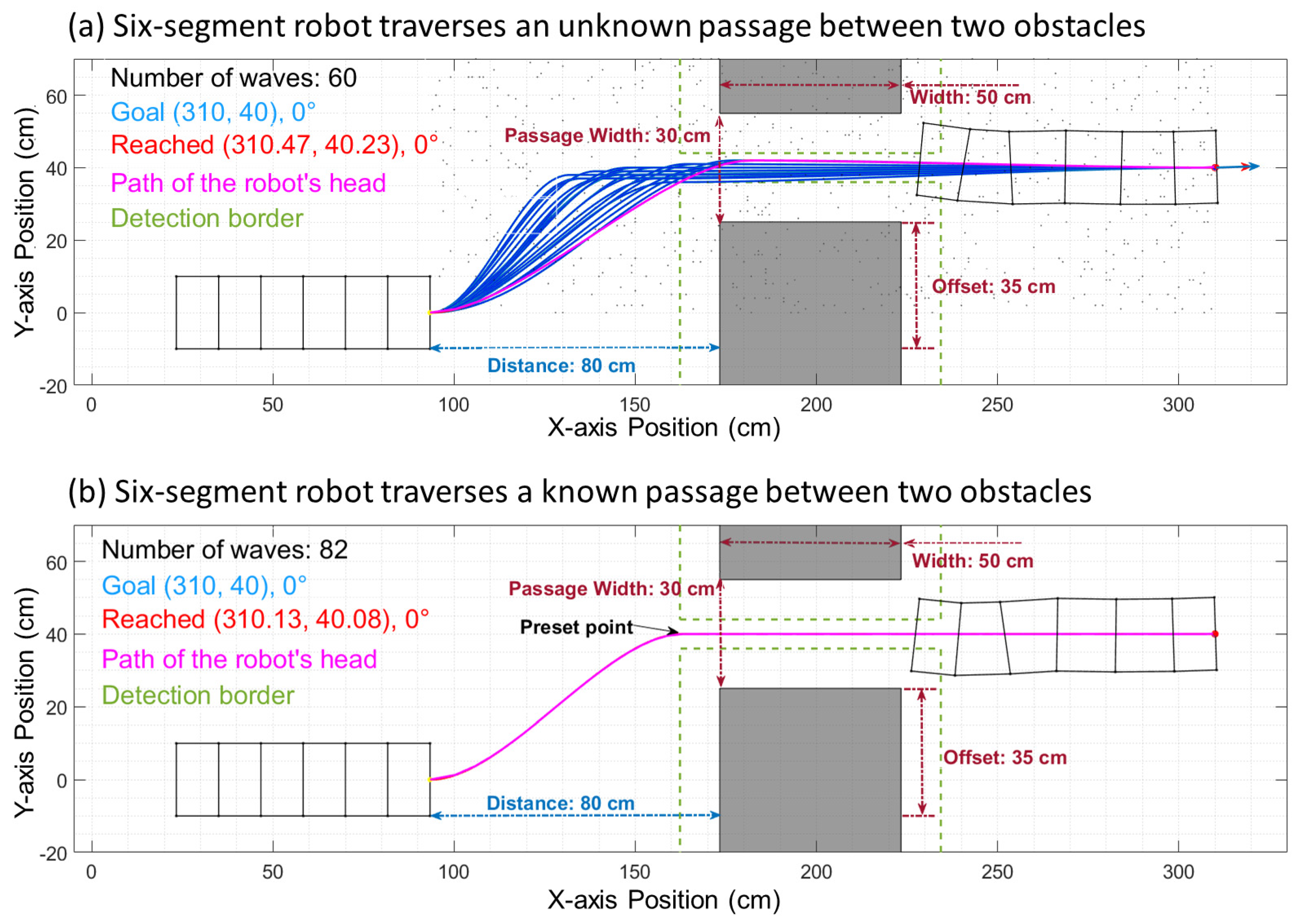
3.2. Offset Clearance Limitations for Six-Segment Robot
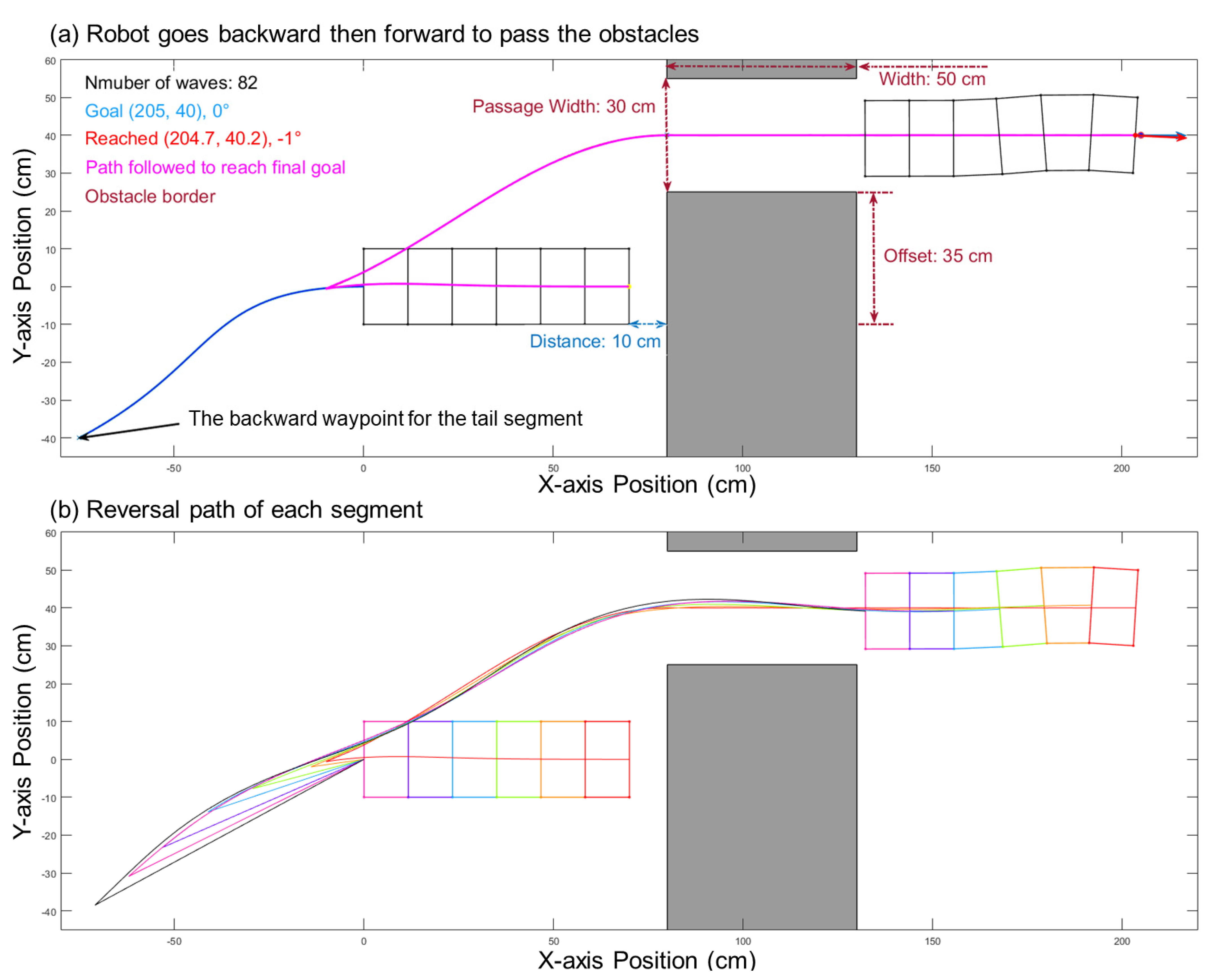
3.3. Backward Movement
3.4. The Influence on Turning by the Total Number of Segments
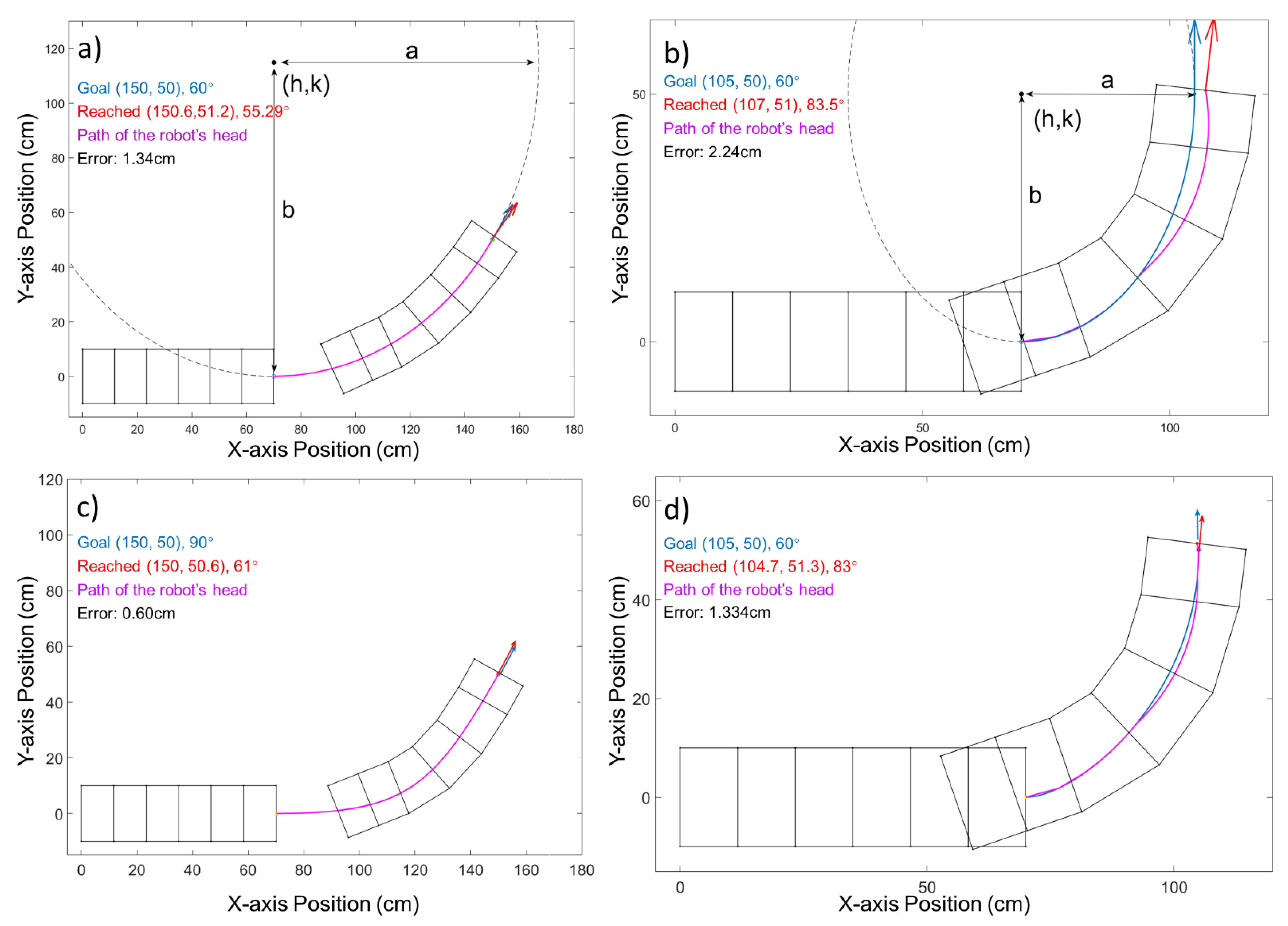
3.5. Empirical Comparison with Physical Robot
3.5.1. Differences between the Simulation and the Physical Robot
3.5.2. Offset Clearance Limitations of the Physical Robot
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Input: Acquire the initial and desired configuration of the robot, the position of the obstacles, and the maximum number of samples, Nmax. |
Output: Bézier curve Path.
|
| Input: Get the initial and desired configuration of the robot and the position of the obstacles. |
Output: Bézier curve Path.
|
Appendix B
| Input: Initial and desired configuration of the robot; the distance of the obstacles; the initial offset of the obstacle, ; the maximum number of iterations, Nmax. |
Output: Bézier curve Path and the offset of the largest obstacle.
|
References
- Zhang, B.; Fan, Y.; Yang, P.; Cao, T.; Liao, H. Worm-Like Soft Robot for Complicated Tubular Environments. Soft Robot. 2019, 6, 399–413. [Google Scholar] [CrossRef] [PubMed]
- Reina, G.; Ojeda, L.; Milella, A.; Borenstein, J. Wheel slippage and sinkage detection for planetary rovers. IEEE/ASME Trans. Mechatronics 2006, 11, 185–195. [Google Scholar] [CrossRef] [Green Version]
- Kandhari, A.; Wang, Y.; Chiel, H.; Daltorio, K.A. Turning in Worm-Like Robots: The Geometry of Slip Elimination Suggests Nonperiodic Waves. Soft Robot. 2019, 6, 560–577. [Google Scholar] [CrossRef] [PubMed]
- Raja, P.; Pugazhenthi, S. Optimal path planning of mobile robots: A review. Int. J. Phys. Sci. 2012, 7, 1314–1320. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Wang, Y.; Pandit, P.; Kandhari, A.; Liu, Z.; Daltorio, K.A. Rapidly Exploring Random Tree Algorithm-Based Path Planning for Worm-Like Robot. Biomimetics 2020, 5, 26. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Cao, Z.; Zhou, M. An Efficient RRT-Based Framework for Planning Short and Smooth Wheeled Robot Motion Under Kinodynamic Constraints. IEEE Trans. Ind. Electron. 2021, 68, 3292–3302. [Google Scholar] [CrossRef]
- Kang, J.-G.; Lim, D.-W.; Choi, Y.-S.; Jang, W.-J.; Jung, J.-W. Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors 2021, 21, 333. [Google Scholar] [CrossRef] [PubMed]
- Hassani, V.; Lande, S.V. Path Planning for Marine Vehicles using Bézier Curves. IFAC-PapersOnLine 2018, 51, 305–310. [Google Scholar] [CrossRef]
- Choi, J.-W.; Curry, R.; Elkaim, G. Path Planning Based on Bézier Curve for Autonomous Ground Vehicles. In Proceedings of the Advances in Electrical and Electronics Engineering—IAENG Special Edition of the World Congress on Engineering and Computer Science 2008, San Francisco, CA, USA, 22–24 October 2008; pp. 158–166. [Google Scholar]
- Jollyb, K.G.; Sreerama Kumar, R.; Vijayakumara, R. A Bézier curve based path planning in a multi-agent robot soccer system without violating the acceleration limits. Robot. Auton. Syst. 2009, 57, 23–33. [Google Scholar] [CrossRef]
- Baydas, S.; Karakas, B. Defining a curve as a Bezier curve. J. Taibah Univ. Sci. 2019, 13, 522–528. [Google Scholar] [CrossRef]
- JGreer, J.D.; Blumenschein, L.H.; Okamura, A.M.; Hawkes, E.W. Obstacle-Aided Navigation of a Soft Growing Robot. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]
- Dutta, A.K.; Debnath, S.K.; Das, S.K. Path-Planning of Snake-Like Robot in Presence of Static Obstacles Using Critical-SnakeBug Algorithm. In Advances in Computer, Communication and Control; Springer: Singapore, 2019; pp. 449–458. [Google Scholar]
- Zarrouk, D.; Sharf, I.; Shoham, M. Analysis of earthworm-like robotic locomotion on compliant surfaces. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 1574–1579. [Google Scholar] [CrossRef]
- Kandhari, A.; Daltorio, K.A. A kinematic model to constrain slip in soft body peristaltic locomotion. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 309–314. [Google Scholar] [CrossRef]
- Kandhari, A. Control and Analysis of Soft Body Locomotion on a Robotic Platform. Electronic Ph.D. Dissertation, 2020. Available online: https://etd.ohiolink.edu/ (accessed on 7 September 2021).
- Horchler, A.D.; Kandhari, A.; Daltorio, K.A.; Moses, K.C.; Ryan, J.C.; Stultz, K.A.; Kanu, E.N.; Andersen, K.B.; Kershaw, J.A.; Bachmann, R.J.; et al. Peristaltic Locomotion of a Modular Mesh-Based Worm Robot: Precision, Compliance, and Friction. Soft Robot. 2015, 2, 135–145. [Google Scholar] [CrossRef]
- Chowdhury, A.; Ansari, S.; Bhaumik, S. Earthworm like modular robot using active surface gripping mechanism for peristaltic locomotion. In Proceedings of the Advances in Robotics (AIR ‘17), New Delhi, India, 28 June–2 July 2017; Association for Computing Machinery: New York, NY, USA, 2017. Article 54. pp. 1–6. [Google Scholar] [CrossRef]
- Gough, E.; Conn, A.T.; Rossiter, J. Planning for a Tight Squeeze: Navigation of Morphing Soft Robots in Congested Environments. IEEE Robot. Autom. Lett. 2021, 6, 4752–4757. [Google Scholar] [CrossRef]
- Kandhari, A.; Wang, Y.; Chiel, H.J.; Quinn, R.D.; Daltorio, K.A. An Analysis of Peristaltic Locomotion for Maximizing Velocity or Minimizing Cost of Transport of Earthworm-Like Robots. Soft Robot. 2021, 8, 485–505. [Google Scholar] [CrossRef]
- Trivedi, D.; Rahn, C.D.; Kier, W.M.; Walker, I.D. Soft Robotics: Biological Inspiration, State of the Art, and Future Research. Appl. Bionics Biomech. 2008, 5, 99–117. [Google Scholar] [CrossRef]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft Robotics: Review of Fluid-Driven Intrinsically Soft Devices; Manufacturing, Sensing, Control, and Applications in Human-Robot Interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Ariff, M.; Zamzuri, H.; Nordin, M.; Yahya, W.; Mazlan, S.A.; Rahman, M. Optimal Control Strategy for Low Speed and High Speed Four-Wheel-Active Steering Vehicle. J. Mech. Eng. Sci. 2015, 8, 1516–1528. [Google Scholar] [CrossRef]
- Kandhari, A.; Huang, Y.; Daltorio, K.; Chiel, H.; Quinn, R. Body stiffness in orthogonal directions oppositely affects worm-like robot turning and straight-line locomotion. Bioinspir. Biomim. 2018, 13, 026003. [Google Scholar] [CrossRef] [PubMed]
- Horchler, A.D.; Kandhari, A.; Daltorio, K.A.; Moses, K.C.; Andersen, K.B.; Bunnelle, H.; Kershaw, J.; Tavel, W.H.; Bachmann, R.J.; Chiel, H.J.; et al. Worm-like robotic locomotion with a compliant modular mesh. In Living Machines 2015; LNCS; Wilson, S.P., Verschure, P.F., Mura, A., Prescott, T.J., Eds.; Springer: Heidelberg, Berlin, 2015; Volume 9222, pp. 26–37. [Google Scholar]
- Hernandez, B.; Giraldo, E. A Review of Path Planning and Control for Autonomous Robots. In Proceedings of the 2018 IEEE 2nd Colombian Conference on Robotics and Automation (CCRA), Barranquilla, Colombia, 1–3 November 2018. [Google Scholar]
- Coad, M.M.; Blumenschein, L.H.; Cutler, S.; Zepeda, J.A.R.; Naclerio, N.D.; El-Hussieny, H.; Mehmood, U.; Ryu, J.-H.; Hawkes, E.W.; Okamura, A.M. Vine Robots: Design, Teleoperation, and Deployment for Navigation and Exploration. IEEE Robot. Autom. Mag. 2019, 27, 120–132. [Google Scholar] [CrossRef] [Green Version]
- Kandhari, A.; Stover, M.C.; Jayachandran, P.R.; Rollins, A.; Chiel, H.J.; Quinn, R.D.; Daltorio, K.A. Distributed Sensing for Soft Worm Robot Reduces Slip for Locomotion in Confined Environments. Biomim. Biohybrid Syst. 2018, 10928, 236–248. [Google Scholar] [CrossRef]
- An, D.; Wang, H. VPH: A new laser radar based obstacle avoidance method for intelligent mobile robots. In Proceedings of the Fifth World Congress on Intelligent Control and Automation, Hangzhou, China, 15–19 June 2004. [Google Scholar]
- Mattamala, M.; Ramezani, M.; Camurri, M.; Fallon, M. Learning Camera Performance Models for Active Multi-Camera Visual Teach and Repeat. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Transeth, A.A.; Leine, R.I.; Glocker, C.; Pettersen, K.Y.; Liljebäck, P. Snake Robot Obstacle-Aided Locomotion: Modeling, Simulations, and Experiments. IEEE Trans. Robot. 2008, 24, 88–104. [Google Scholar] [CrossRef] [Green Version]


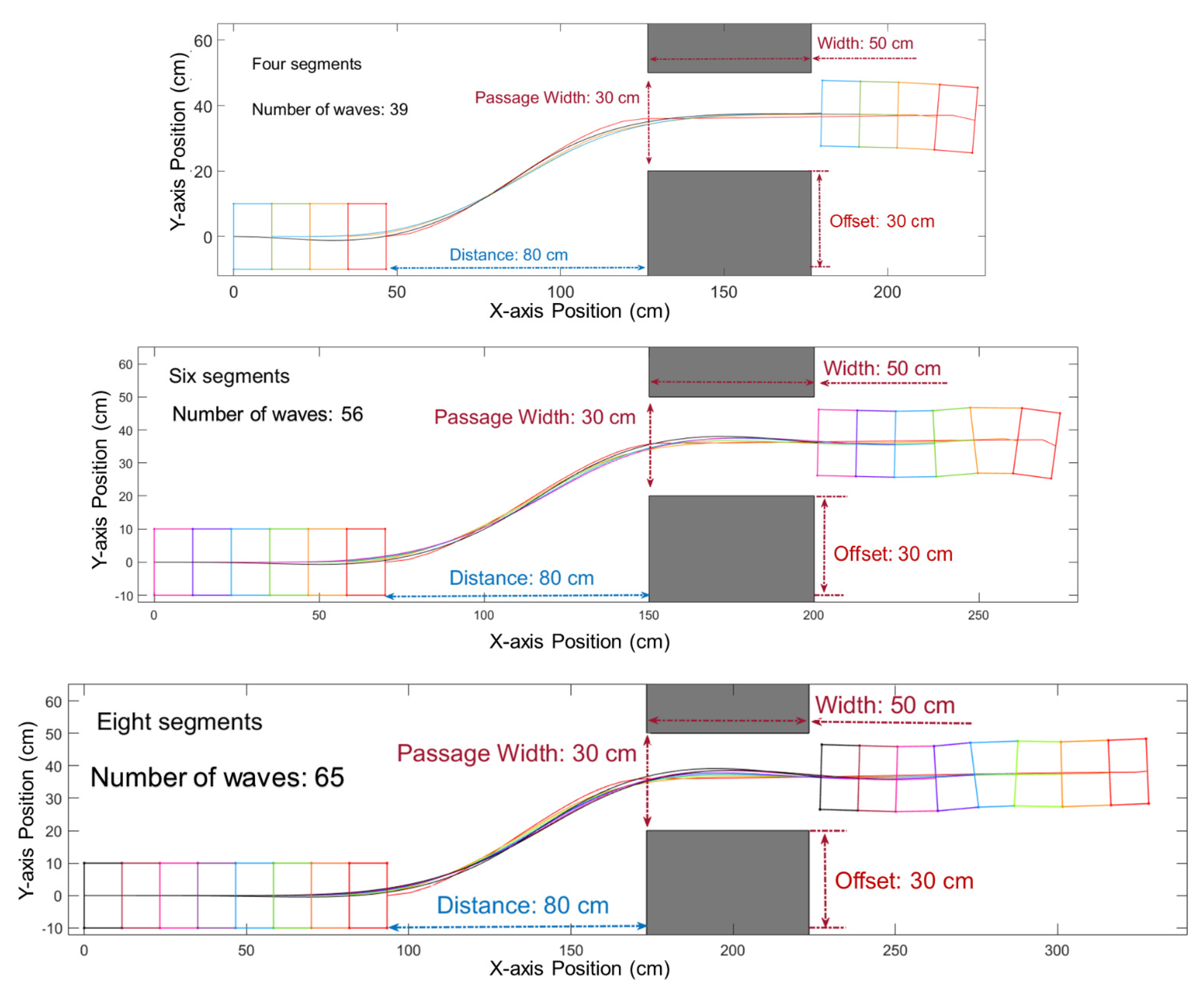
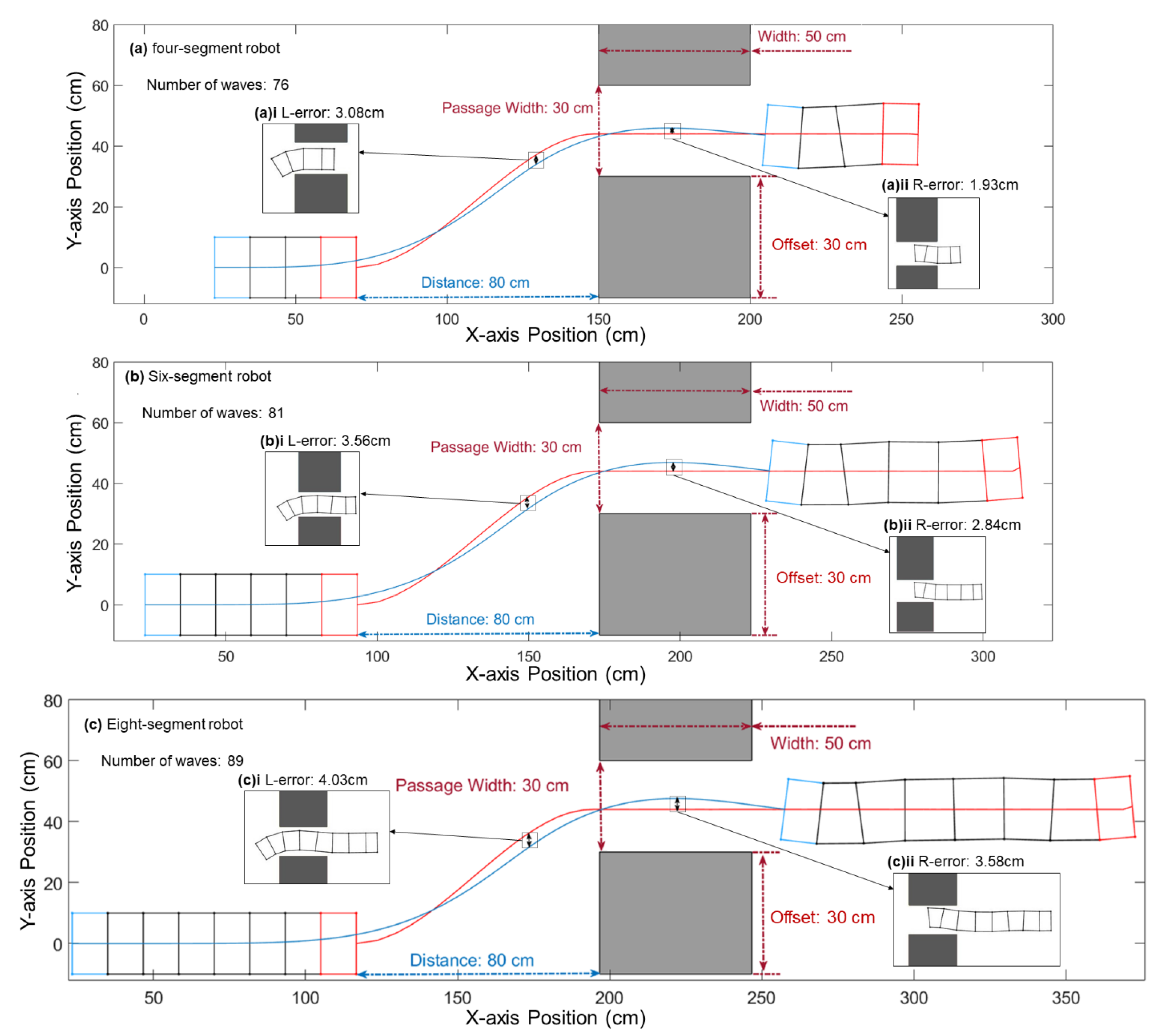


| Path Error | 4 Segments | 6 Segments | 8 Segments |
|---|---|---|---|
| L-Error | 15.40% | 17.80 | 20.20% |
| R-Error | 9.60% | 14.20% | 17.90% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, Z.; Kandhari, A.; Daltorio, K.A. Obstacle Avoidance Path Planning for Worm-like Robot Using Bézier Curve. Biomimetics 2021, 6, 57. https://doi.org/10.3390/biomimetics6040057
Wang Y, Liu Z, Kandhari A, Daltorio KA. Obstacle Avoidance Path Planning for Worm-like Robot Using Bézier Curve. Biomimetics. 2021; 6(4):57. https://doi.org/10.3390/biomimetics6040057
Chicago/Turabian StyleWang, Yifan, Zehao Liu, Akhil Kandhari, and Kathryn A. Daltorio. 2021. "Obstacle Avoidance Path Planning for Worm-like Robot Using Bézier Curve" Biomimetics 6, no. 4: 57. https://doi.org/10.3390/biomimetics6040057
APA StyleWang, Y., Liu, Z., Kandhari, A., & Daltorio, K. A. (2021). Obstacle Avoidance Path Planning for Worm-like Robot Using Bézier Curve. Biomimetics, 6(4), 57. https://doi.org/10.3390/biomimetics6040057






