Deformation Behavior of Elastomer-Glass Fiber-Reinforced Plastics in Dependence of Pneumatic Actuation
Abstract
:1. Introduction
1.1. Previous Work
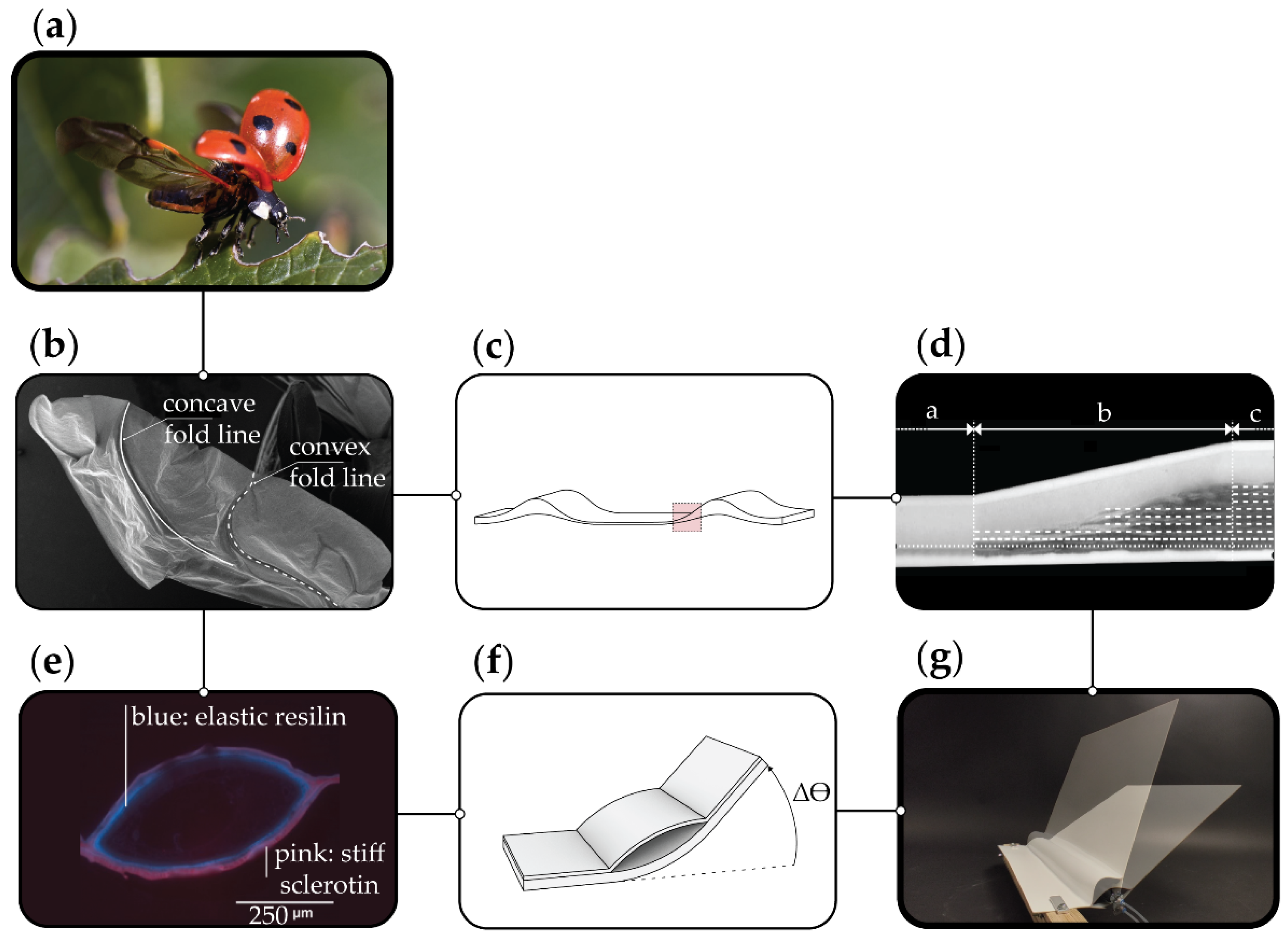
1.2. Biomimetic Background
2. Materials and Methods
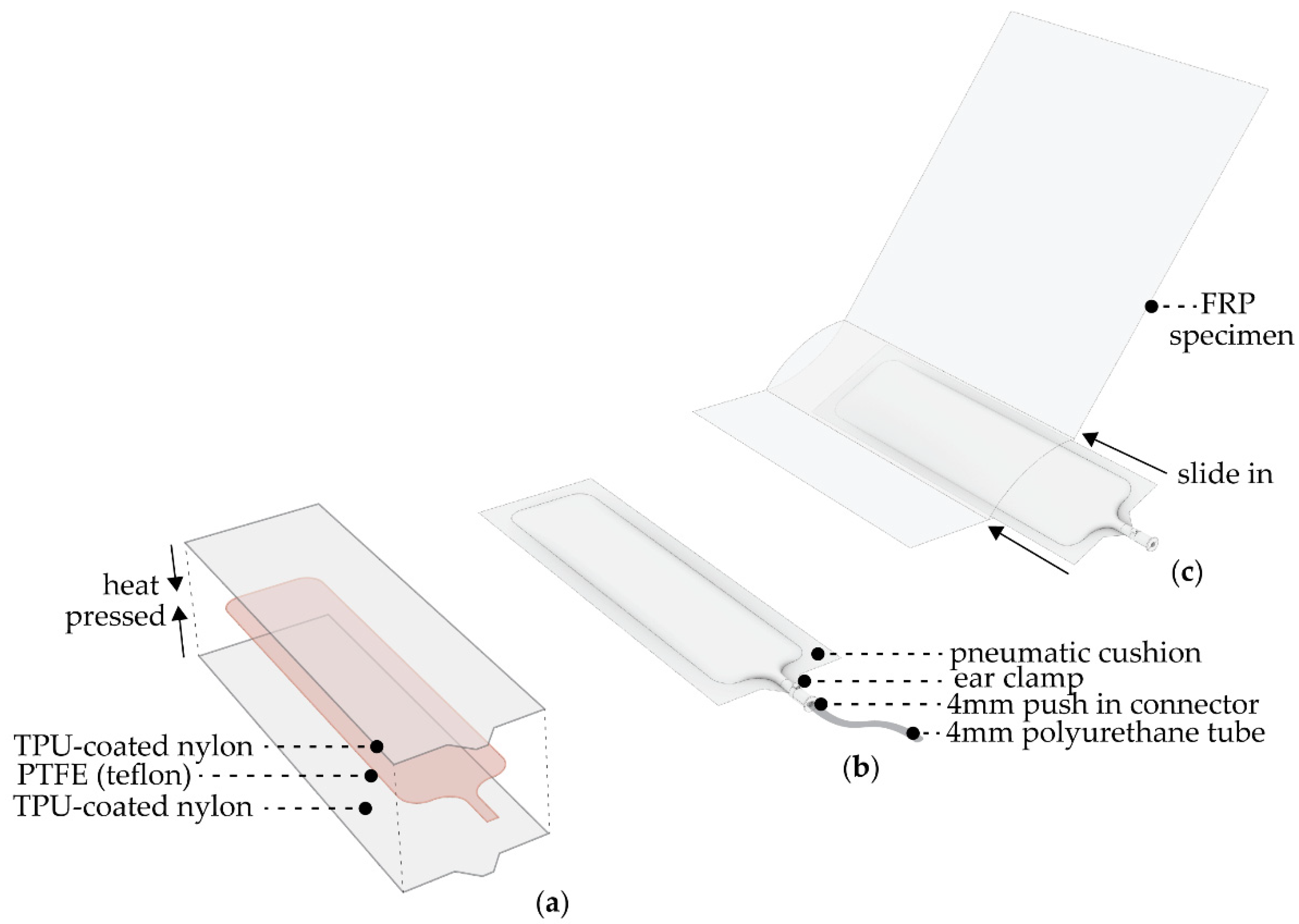
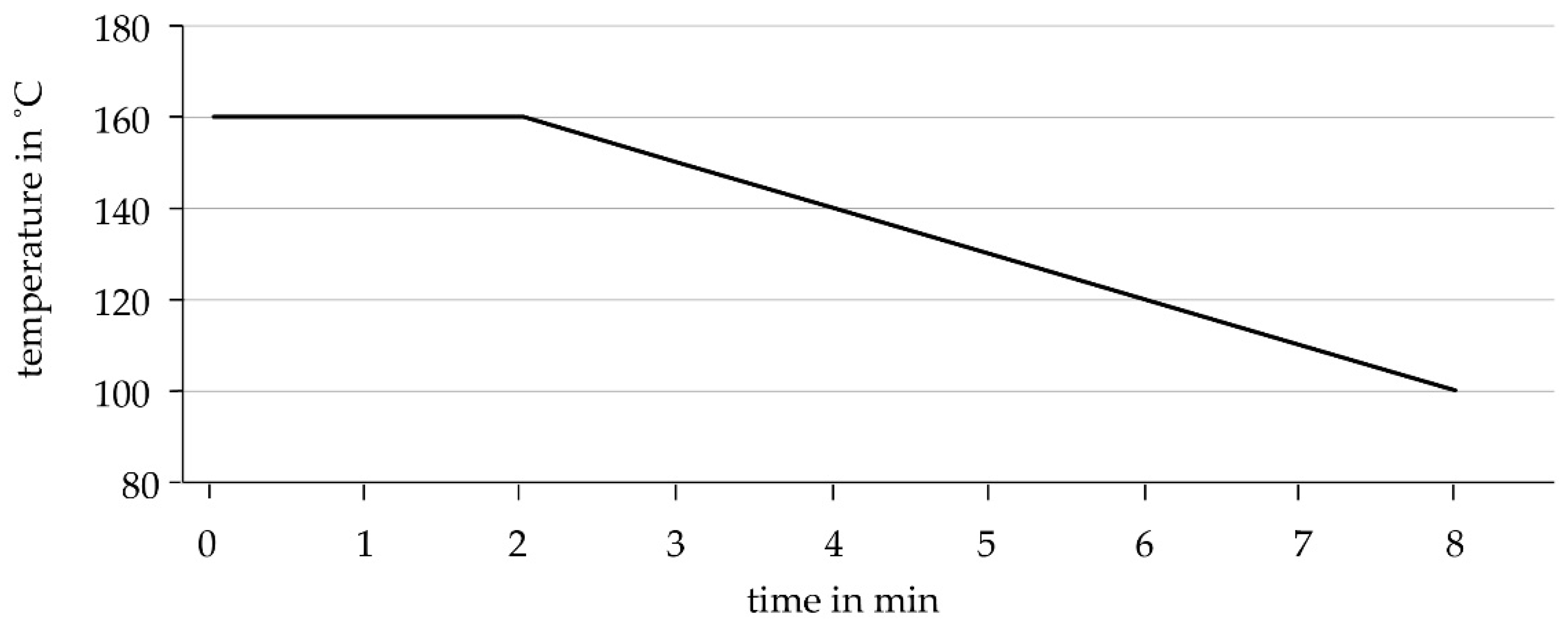
2.1. Elastomer-Glass Fiber-Reinforced Plastic (E-GFRP) Hybrid Laminate
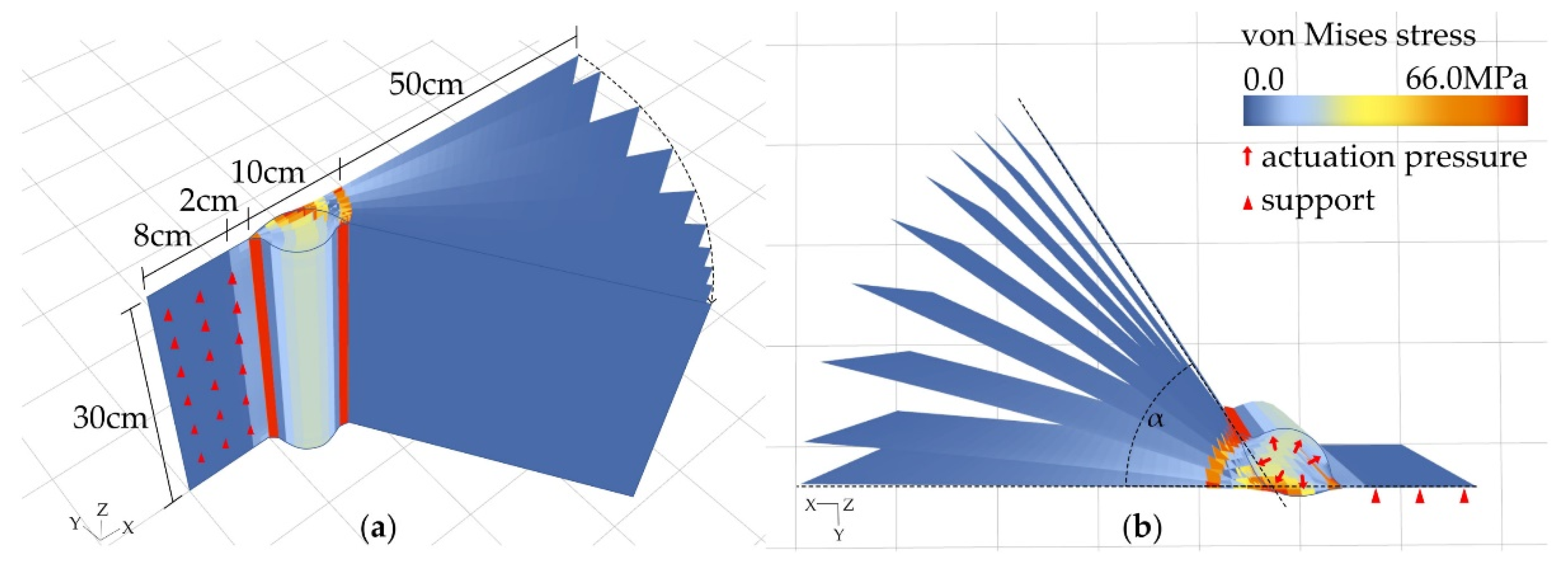
2.2. Simulation of E-GFRP Hybrid Laminates
2.3. Pneumatic Actuators
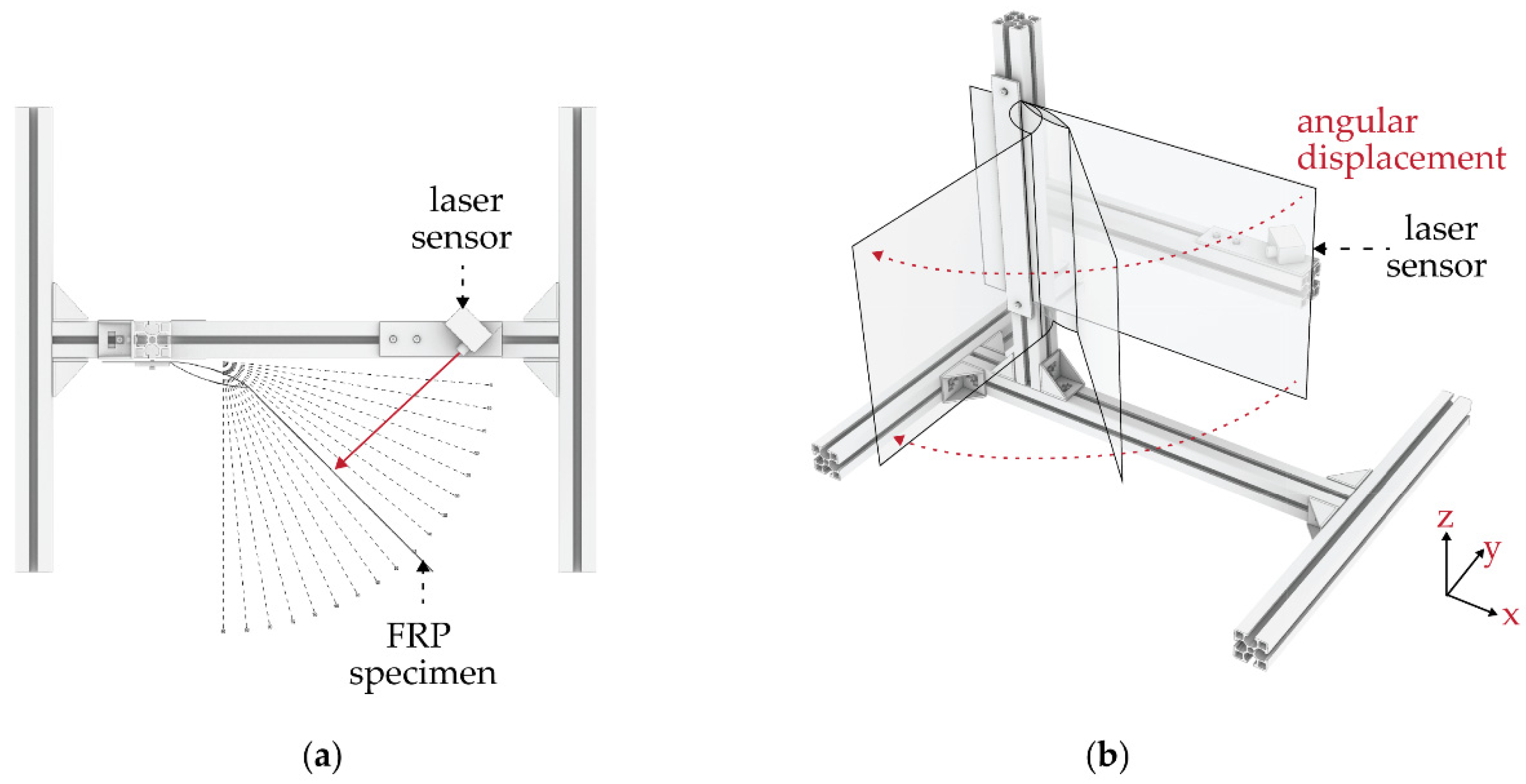
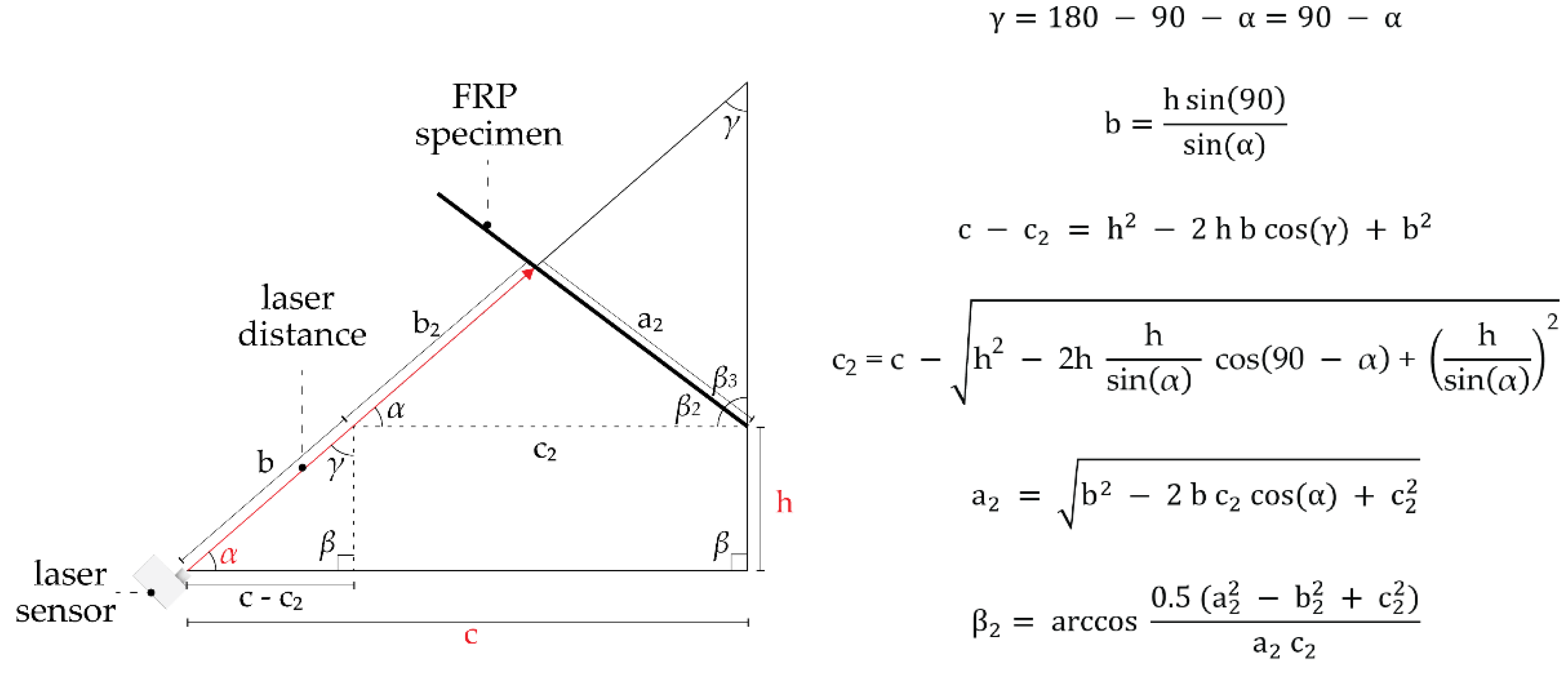
2.4. Actuation and Bending Test Set-Up
3. Results
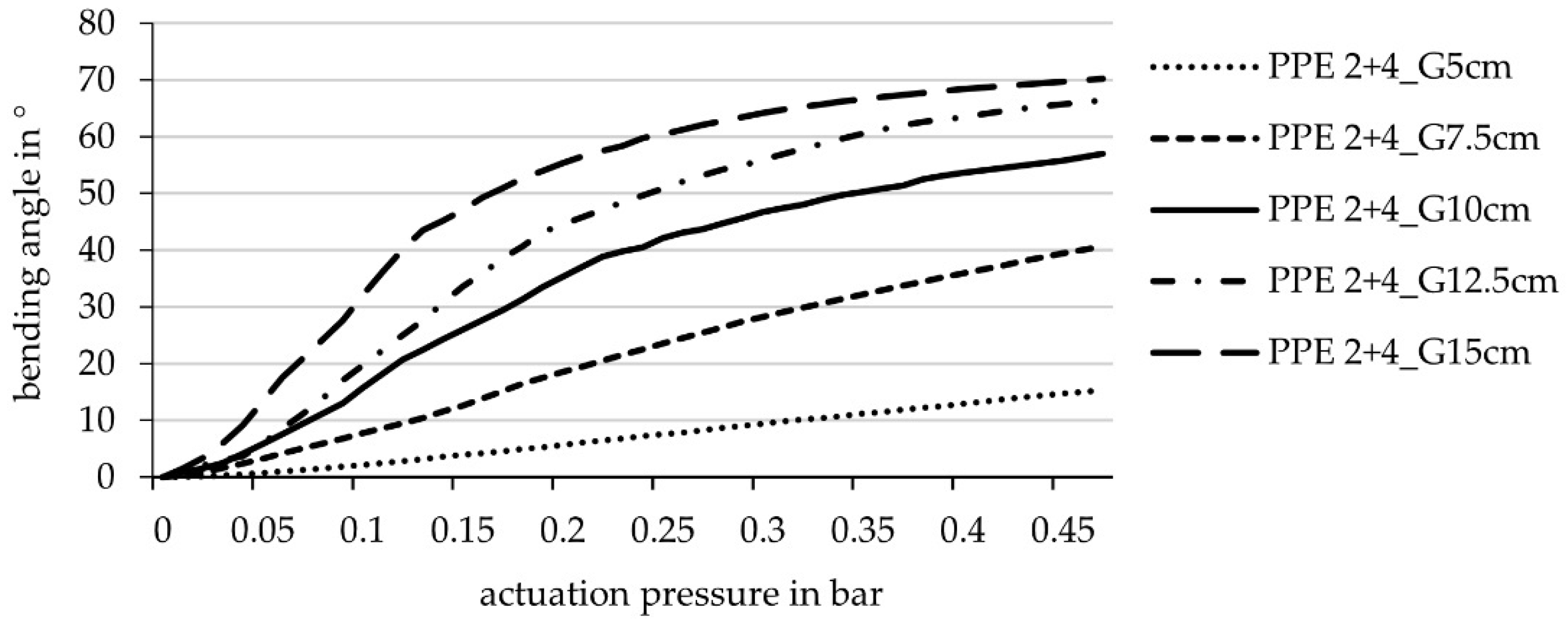
3.1. Simulative Investigation of the Geometrical Parameters of an Actuated Hinge
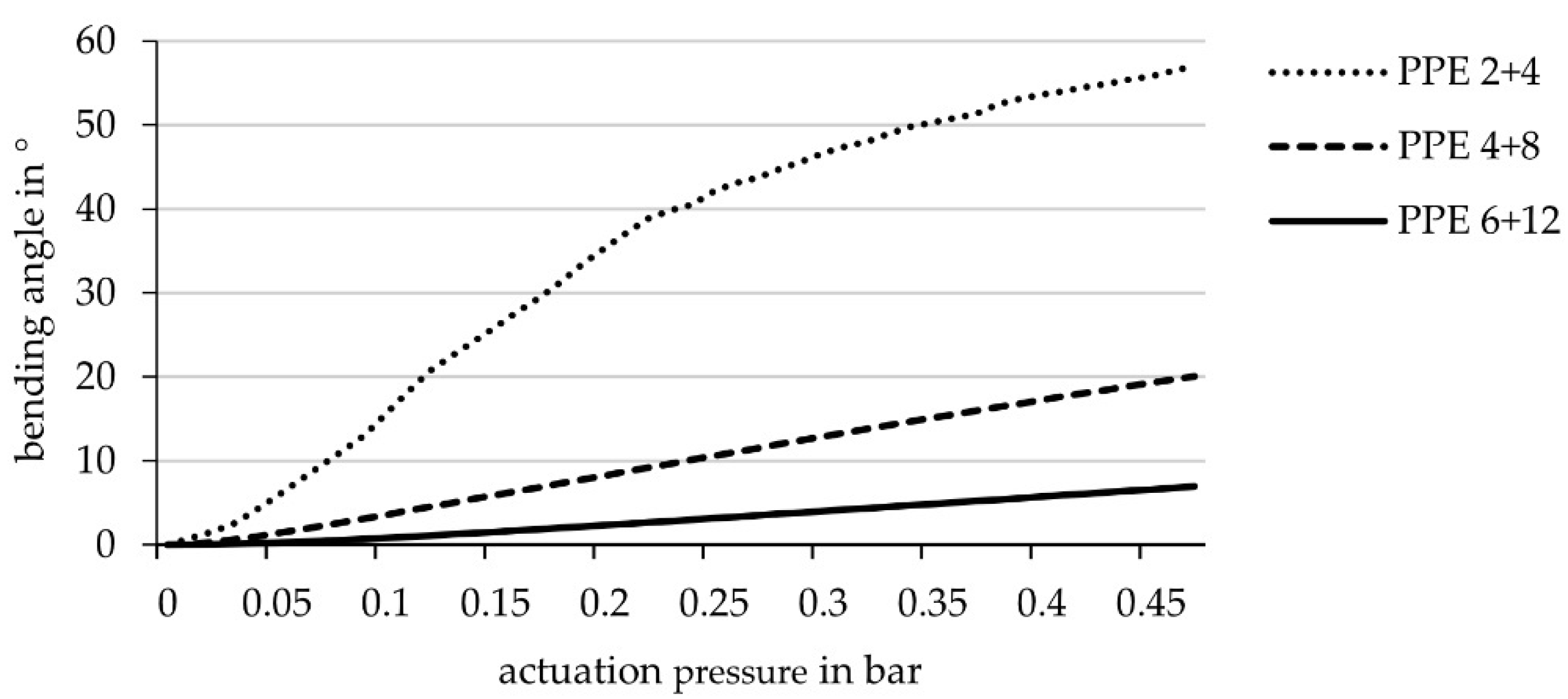
3.2. Mechanical Investigation of the Geometrical Parameters of an Actuated Hinge
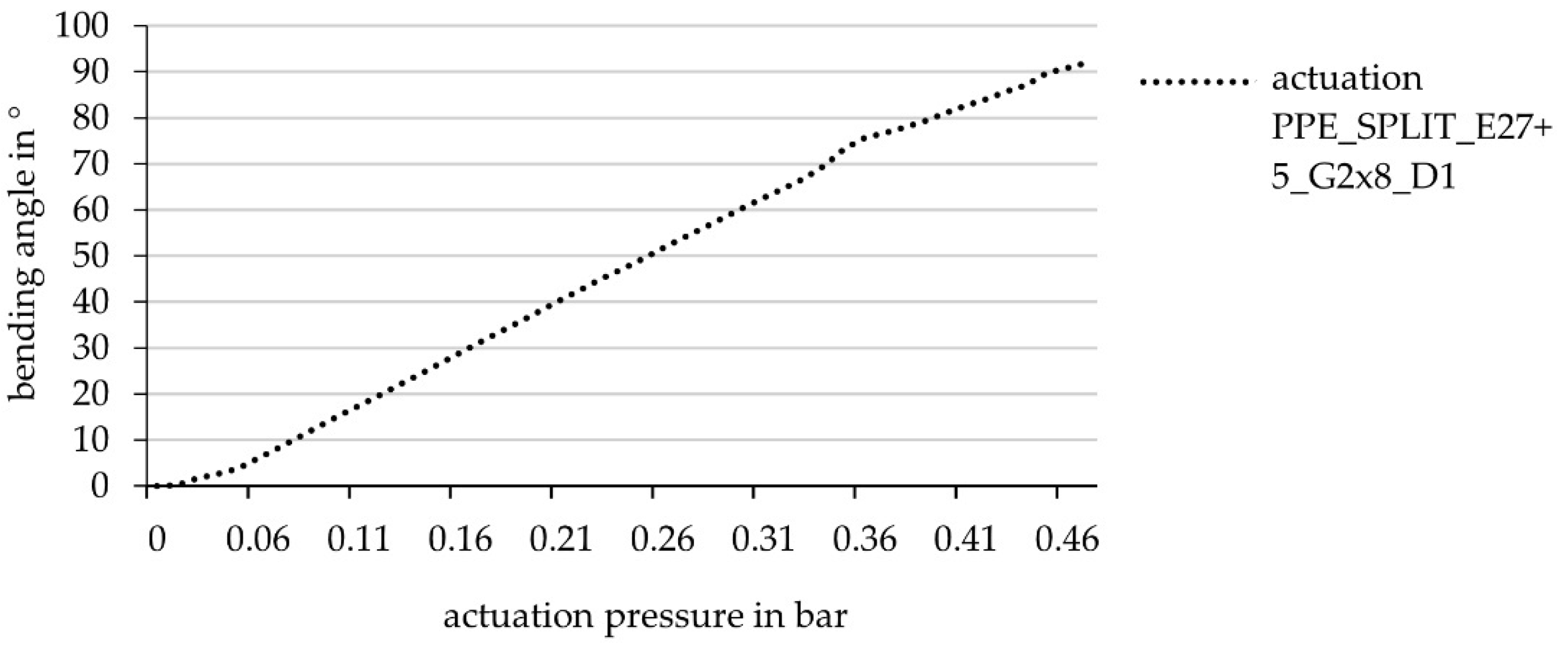
3.3. Component Actuated with Multiple Cushions
3.3.1. Regression Model from Simulative Investigation
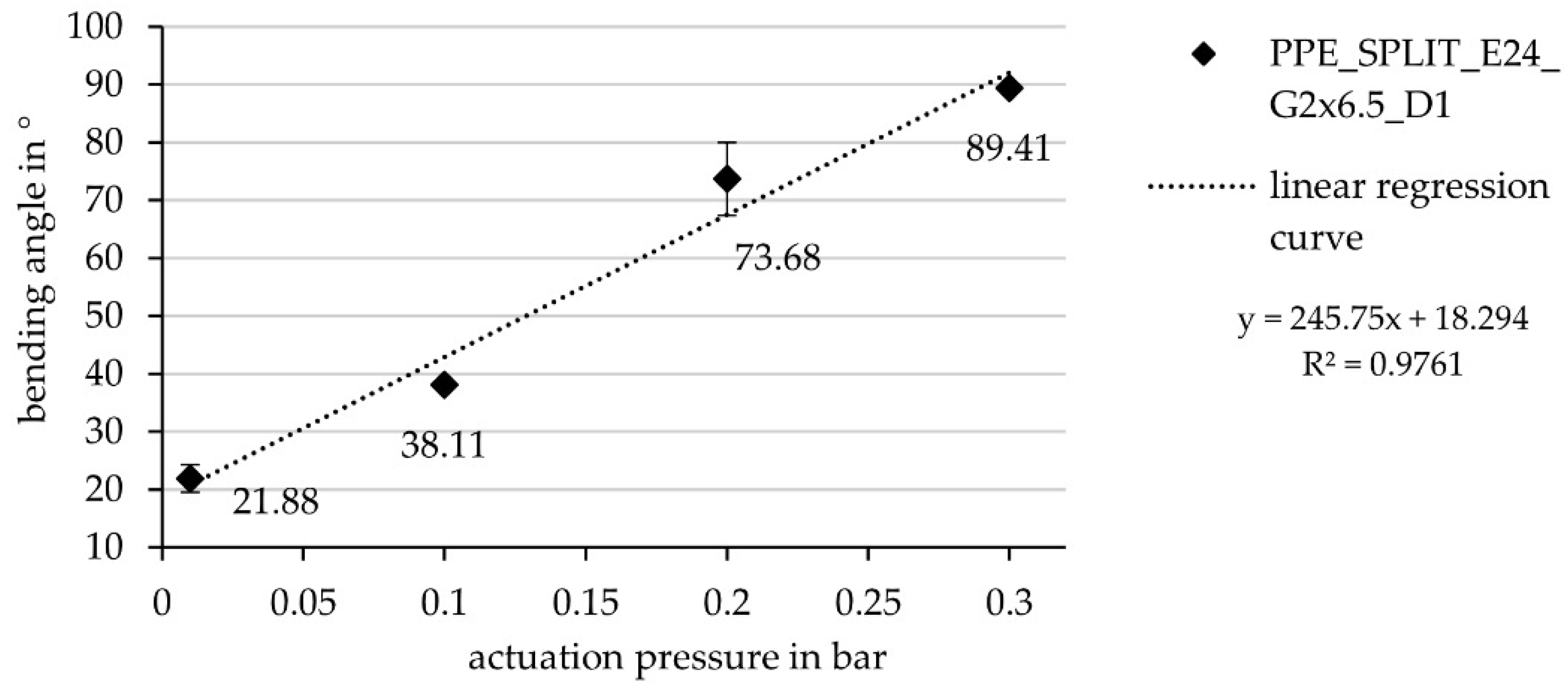
3.3.2. Validation of Simulative Investigation via Physical Tests
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Energy Performance of Buildings Directive: Energy Performance of Buildings Standards. Available online: https://ec.europa.eu/energy/topics/energy-efficiency/energy-efficient-buildings/energy-performance-buildings-directive_en#energy-performance-of-buildings-standards (accessed on 26 April 2021).
- Loonen, R.C.; Favoino, F.; Hensen, J.L.; Overend, M. Review of current status, requirements and opportunities for building performance simulation of adaptive facades. J. Build. Perform. Simul. 2017, 10, 205–223. [Google Scholar] [CrossRef] [Green Version]
- Barozzi, M.; Lienhard, J.; Zanelli, A.; Monticelli, C. The Sustainability of Adaptive Envelopes: Developments of Kinetic Architecture. Procedia Eng. 2016, 155, 275–284. [Google Scholar] [CrossRef] [Green Version]
- Sandak, A.; Sandak, J.; Brzezicki, M.; Kutnar, A. Bio-Based Building Skin; Springer: Singapore, 2019; ISBN 978-981-13-3746-8. [Google Scholar]
- Lienhard, J.; Schleicher, S.; Poppinga, S.; Masselter, T.; Milwich, M.; Speck, T.; Knippers, J. Flectofin: A hingeless flapping mechanism inspired by nature. Bioinspir. Biomim. 2011, 6, 45001. [Google Scholar] [CrossRef] [PubMed]
- Körner, A.; Born, L.; Mader, A.; Sachse, R.; Saffarian, S.; Westermeier, A.S.; Poppinga, S.; Bischoff, M.; Gresser, G.T.; Milwich, M.; et al. Flectofold—a biomimetic compliant shading device for complex free form facades. Smart Mater. Struct. 2018, 27, 17001. [Google Scholar] [CrossRef]
- Schieber, G.; Born, L.; Bergmann, P.; Körner, A.; Mader, A.; Saffarian, S.; Betz, O.; Milwich, M.; Gresser, G.T.; Knippers, J. Hindwings of insects as concept generator for hingeless foldable shading systems. Bioinspir. Biomim. 2017, 13, 16012. [Google Scholar] [CrossRef] [PubMed]
- Mader, A.; Born, L.; Körner, A.; Schieber, G.; Masset, P.-A.; Milwich, M.; Gresser, G.T.; Knippers, J. Bio-inspired integrated pneumatic actuation for compliant fiber-reinforced plastics. Compos. Struct. 2020, 233, 111558. [Google Scholar] [CrossRef]
- Körner, A.; Born, L.; Bucklin, O.; Suzuki, S.; Vasey, L.; Gresser, G.T.; Menges, A.; Knippers, J. Integrative design and fabrication methodology for bio-inspired folding mechanisms for architectural applications. Comput. Aided Des. 2021, 133, 102988. [Google Scholar] [CrossRef]
- Coleoptera Coccinellidae. Available online: https://www.pexels.com/de-de/foto/roter-und-schwarzer-kafer-36485/ (accessed on 30 April 2021).
- Hindwing Coleoptera Coccinellidae. Available online: https://www.itke.uni-stuttgart.de/de/forschung/icd-itke-forschungspavillons/itech-forschungsdemonstrator-2018-19 (accessed on 30 April 2021).
- Born, L. Grundlagen für die Auslegung und Gestaltung eines Hybridmaterials für Außen Liegende, Adaptive Fassadenbauteile aus Faserverbundkunststoff. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 23 September 2020. [Google Scholar]
- Born, L.; Körner, A.; Mader, A.; Schieber, G.; Milwich, M.; Knippers, J.; Gresser, G.T. Adaptive FRP Structures For Exterior Applications. Adv. Mater. Lett. 2019, 10, 913–918. [Google Scholar] [CrossRef]
- Born, L.; Körner, A.; Schieber, G.; Westermeier, A.S.; Poppinga, S.; Sachse, R.; Bergmann, P.; Betz, O.; Bischoff, M.; Speck, T.; et al. Fiber-Reinforced Plastics with Locally Adapted Stiffness for Bio-Inspired Hingeless, Deployable Architectural Systems. Key Eng. Mater. 2017, 742, 689–696. [Google Scholar] [CrossRef]
- Gerlach, J. Systementwicklung einer Steuerung und Regelung für Pneumatisch Aktuierte Verschattungselemente. Master’s Thesis, University of Stuttgart, Stuttgart, Germany, 27 October 2020. [Google Scholar]
- Mouritz, A.P. Review of z-pinned composite laminates. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2383–2397. [Google Scholar] [CrossRef]
- Pingkarawat, K.; Mouritz, A.P. Improving the mode I delamination fatigue resistance of composites using z-pins. Compos. Sci. Technol. 2014, 92, 70–76. [Google Scholar] [CrossRef]




| ID 1 | Material | Supplier | Trade Name | Fiber Orientation in ° | Tensile Strength in MPa | Young’s Modulus in MPa | Poisson’s Ratio- |
|---|---|---|---|---|---|---|---|
| ET222 | GFRP 2 | Toray Group Composite Materials (Italy) s.r.l. | ET222 | 0/90 | 546.50 | 16,628.61 | 0.20 |
| HHZ99 | Elastomer | Kraiburg GmbH & Co. KG | Kraibon HHZ9578/99 | - | 1.89 | 15.98 | 0.30 |
| TPU | TPU 3 | Gerlinger Industries GmbH | 4980 | - | 7.16 | 126.43 | 0.35 |
| ID 1 | Hinge Width in cm | Continuous Layers ET222 (±45)° | Width HHZ99 in cm | Layers ET222 (0/90)° (Replacing HHZ99) 3 | |
|---|---|---|---|---|---|
| Laminate (A) 2 | Laminate (B) 2 | ||||
| PPE_2 + 4 | 10 | 2 | 4 | continuous | - |
| PPE_4 + 8 | 10 | 4 | 8 | continuous | - |
| PPE_6 + 12 | 10 | 6 | 12 | continuous | - |
| PPE_2 + 4_G5 | 5 | 2 | 4 | continuous | - |
| PPE_2 + 4_G7.5 | 7.5 | 2 | 4 | continuous | - |
| PPE_2 + 4_G10 | 10 | 2 | 4 | continuous | - |
| PPE_2 + 4_G12.5 | 12.5 | 2 | 4 | continuous | - |
| PPE_2 + 4_G15 | 15 | 2 | 4 | continuous | - |
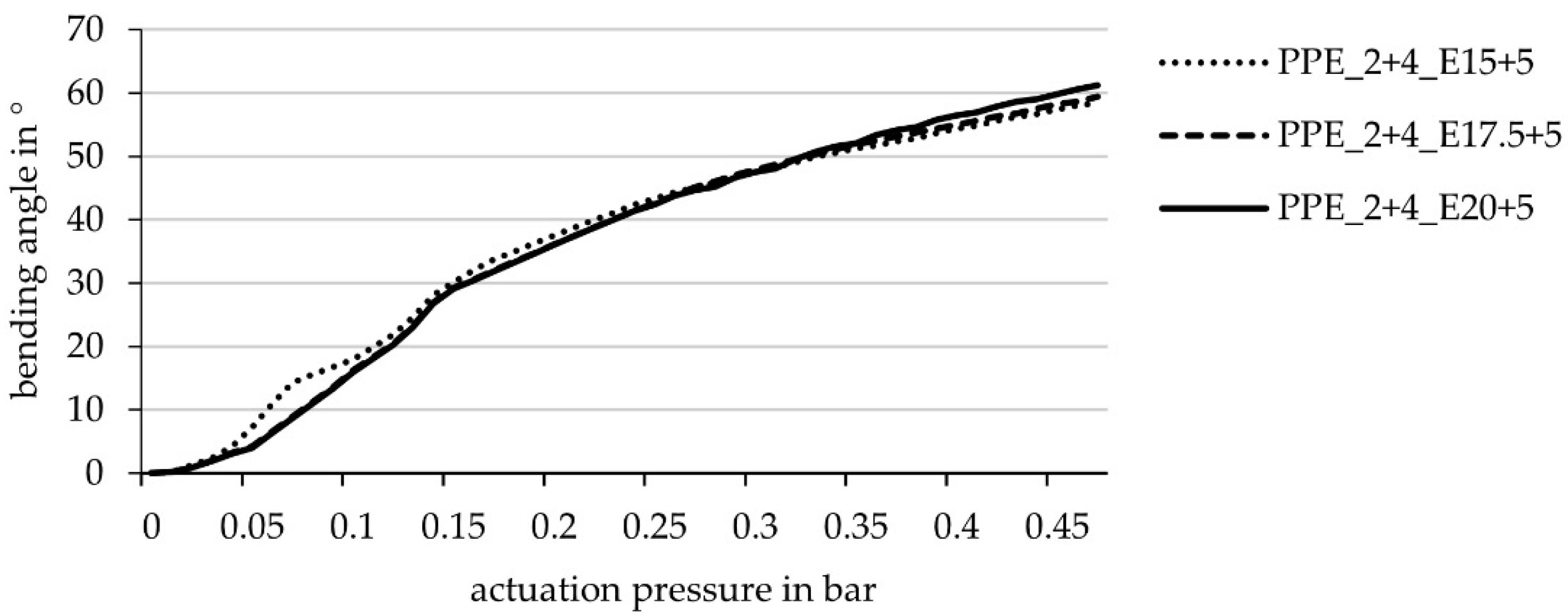
| PPE_2 + 4_E15 + 5 | 10 | 2 | 4 | 15 (+5) | 4 layers ET222 |
| PPE_2 + 4_E17.5 + 5 | 10 | 2 | 4 | 17.5 (+5) | 4 layers ET222 |
| PPE_2 + 4_E20 + 5 | 10 | 2 | 4 | 20 (+5) | 4 layers ET222 |
| Simulations | Prediction Based on Diagram | ||||
|---|---|---|---|---|---|
| Hinge Width in cm | Angle in ° | Hinge Width in cm | Angle in ° | Angle in ° | Hinge Width in cm |
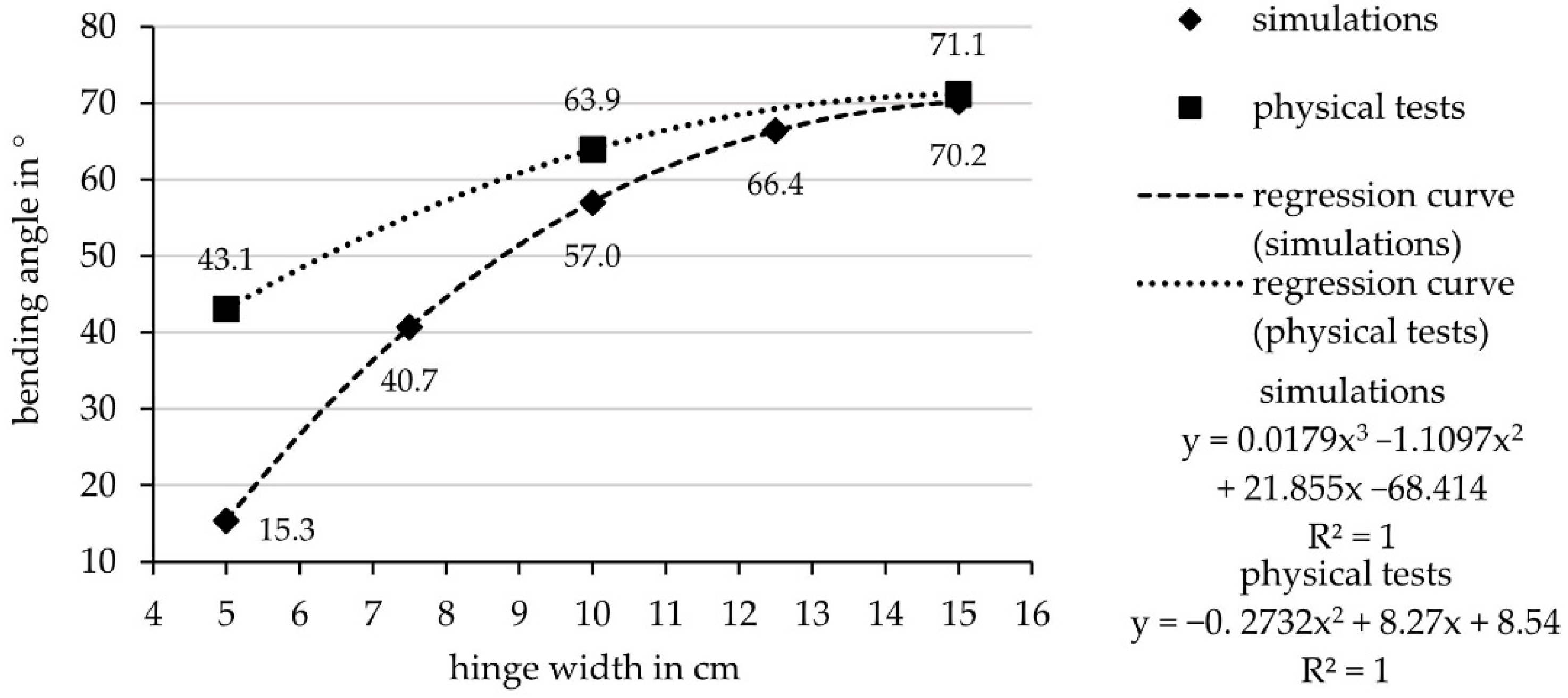
| 5 | 15.3 | 6 | 26.3 | 35 | 6.92 |
| 7.5 | 40.7 | 7 | 35.7 | 40 | 7.50 |
| 10 | 57.0 | 8 | 44.0 | 45 | 8.14 |
| 12.5 | 66.4 | 9 | 51.1 | 50 | 8.84 |
| 15 | 70.2 | 10 | 57.1 | 55 | 9.63 |
| Physical Tests | Prediction Based on Diagram | ||||
|---|---|---|---|---|---|
| Hinge Width in cm | Angle in ° | Hinge Width in cm | Angle in ° | Angle in ° | Hinge Width in cm |
| 5 | 43.1 | 4 | 37.2 | 35 | 3.64 |
| 10 | 63.9 | 4.5 | 40.2 | 40 | 4.46 |
| 15 | 71.1 | 5 | 43.1 | 45 | 5.36 |
| 6 | 58.3 | 50 | 6.34 | ||
| 6.5 | 50.7 | 55 | 7.45 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mühlich, M.; González, E.A.; Born, L.; Körner, A.; Schwill, L.; Gresser, G.T.; Knippers, J. Deformation Behavior of Elastomer-Glass Fiber-Reinforced Plastics in Dependence of Pneumatic Actuation. Biomimetics 2021, 6, 43. https://doi.org/10.3390/biomimetics6030043
Mühlich M, González EA, Born L, Körner A, Schwill L, Gresser GT, Knippers J. Deformation Behavior of Elastomer-Glass Fiber-Reinforced Plastics in Dependence of Pneumatic Actuation. Biomimetics. 2021; 6(3):43. https://doi.org/10.3390/biomimetics6030043
Chicago/Turabian StyleMühlich, Mona, Edith A. González, Larissa Born, Axel Körner, Lena Schwill, Götz T. Gresser, and Jan Knippers. 2021. "Deformation Behavior of Elastomer-Glass Fiber-Reinforced Plastics in Dependence of Pneumatic Actuation" Biomimetics 6, no. 3: 43. https://doi.org/10.3390/biomimetics6030043
APA StyleMühlich, M., González, E. A., Born, L., Körner, A., Schwill, L., Gresser, G. T., & Knippers, J. (2021). Deformation Behavior of Elastomer-Glass Fiber-Reinforced Plastics in Dependence of Pneumatic Actuation. Biomimetics, 6(3), 43. https://doi.org/10.3390/biomimetics6030043






