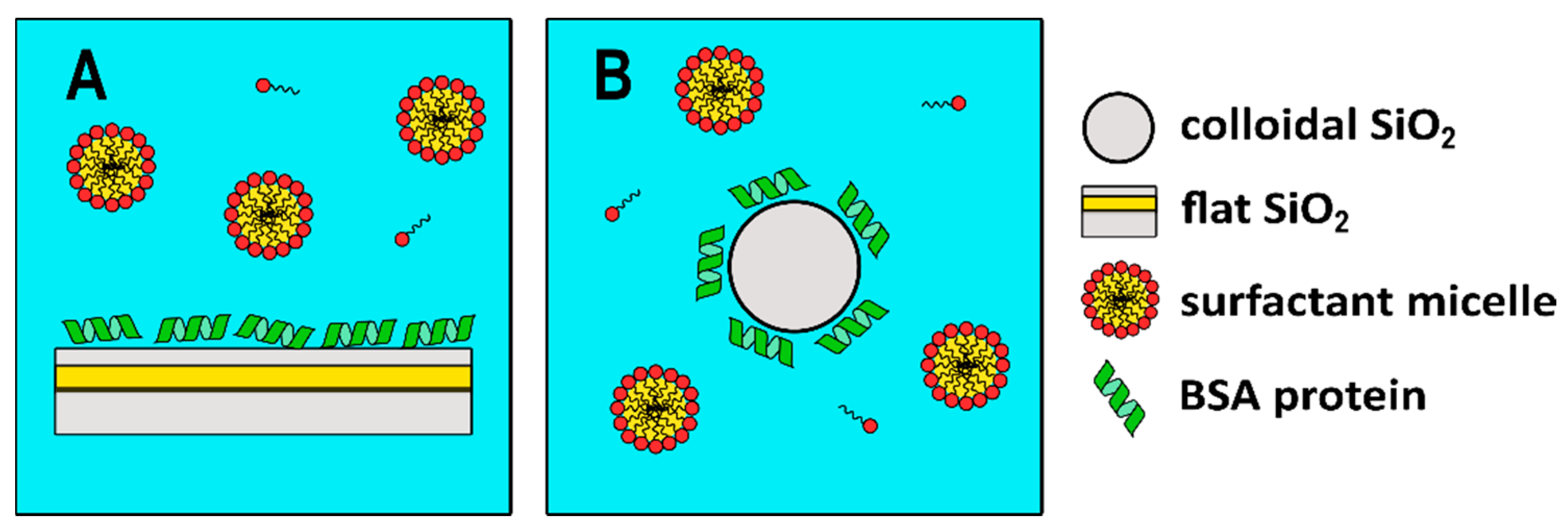
The experimental strategy used in this investigation is as follows: from SPR experiments it is possible to obtain information on the deposition of the analytes on a flat SiO2 surface. Then, DLS and EDL can be used to obtain the same information on a nano-sized SiO2 surface. The comparison of both sets of experiments allows us to compare the use of flat versus nanosized surfaces from the interaction of BSA and further interaction between BSA and a non-ionic C10PEG surfactant.
3.1. Interaction of BSA on a Silica Surface
A first analysis of the interaction between BSA and SiO
2 is necessary to understand how to obtain a monolayer with a good surface coverage of the protein on the sensor chip’s surface. Moreover, understanding the deposition of BSA on the SiO
2 surface is crucial to further investigate its interaction with surfactants. Therefore, we injected increasing concentrations of the protein to extract information about the affinity and needed concentration to create a good coverage on the chip. The experiment shown in
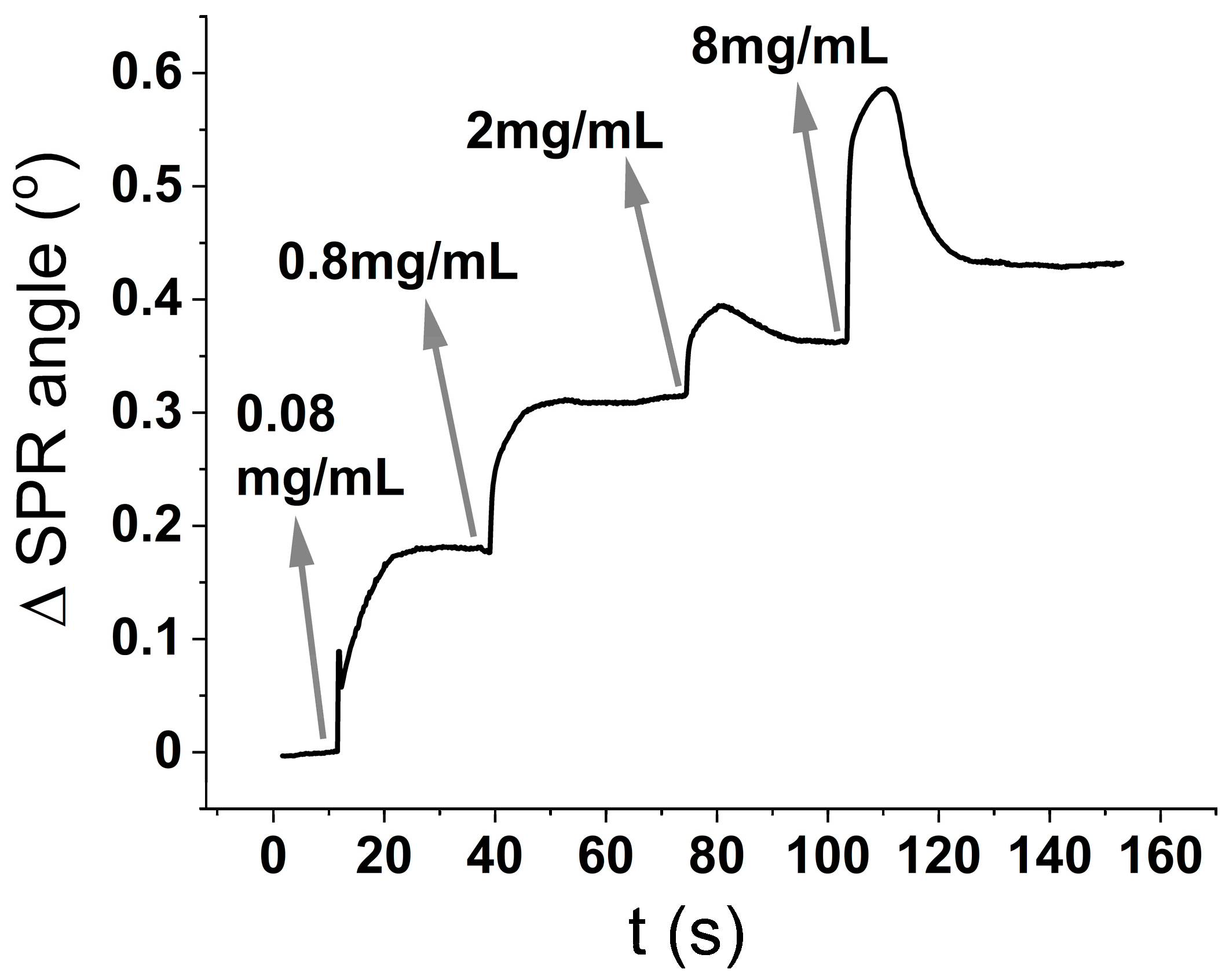
Figure 1 is performed by sequential injections (also called kinetic titration) of the analyte (BSA) in increasing concentrations. After the first injection is finished, and only the buffer is being flushed, the SPR intensity signal reaches a stable plateau, meaning that the analyte is not being desorbed from the surface. Then, the second analyte concentration is injected, and so on. The change in the minimum angle with time can be related to either, an increase in the thickness of the deposited layer, or an increase in surface coverage.
The surface coverage (ng/cm
2) is usually calculated using the De Feiter equation(Equation (1)) [
18], which predicts the surface coverage to be the optical thickness (
D0 in Equation (2)) divided by the refractive index increment with concentration (
dn/dC Equation (3)):
where
d is the thickness of the deposited layer on the sensor, which was calculated by fitting the SPR curves at the plateau after each injection step using Winspall 3.02 and using 1.52 as the refractive index of BSA. The refractive index increment in Equation (1) can be calculated from a single wavelength measurement by knowing the shift in the total internal reflection (TIR) angle (
) caused by the change in the refractive index of the ligand bulk solution at a certain concentration
Cx.
where
G is a sensitivity factor for the change in the TIR angle with the change in the bulk solution refractive index.
G is a constant for each measurement wavelength (86.3° for 670 nm, 87.5° for 785 nm). Since the calculated optical thickness increase (
) after each injection step (
nm) is significantly smaller than the size of a BSA molecule (
nm), the increase in the minimum angle after injections of BSA is solely related to an increase in the surface coverage and not to a formation of multiple layers. This result agrees with previous literature on the field, since the formation of negatively-charged BSA (−10 mV) monolayers onto negative silica surfaces (−50 mV) has been proven in the presence of PBS buffer and room temperature [
12,
14,
15]. In the present case, the surface coverage increases upon exposure to increasing concentrations of BSA, and the surface coverage values can be plotted against analyte concentration obtaining the corresponding adsorption isotherm of
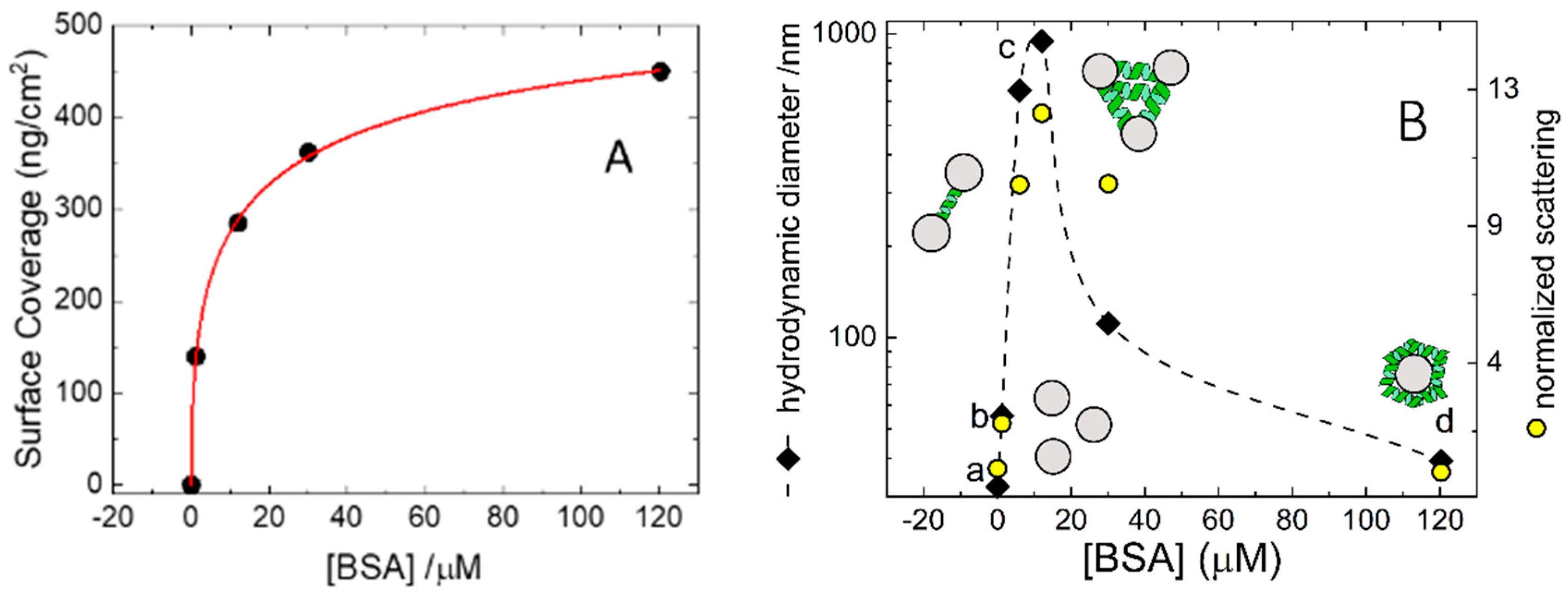
Figure 2A. The adsorption isotherm relates the fraction
θ of surface sites occupied by the adsorbed molecules to the concentration of adsorbate A at equilibrium, [A]
e. If the surface density of adsorption sites is
Q, the surface coverage Γ (in units of mass/area) of an adsorbate of mass
ma is:
At the lowest level of complexity, the adsorption takes place as monolayer binding at sites are equivalent without any lateral interaction between the adsorbed molecules according to the Langmuir’s adsorption isotherm [
19]:
A real solid surface is, of course, generally characterized by different adsorption energies and therefore different Langmuir’s constants. For such an inhomogeneous system the overall adsorption isotherm is obtained integrating Equation (5) over all the
KL values. It has been shown [
20], that for a suitable distribution of adsorption energy, the result is what is called Sips [
20] or the Langmuir–Freundlich equation [
21]:
where
K is an average
KL. In addition, for Equation (6), the constraint that the adsorbent can make only a monolayer as can be observed holds. The above equation is formally equivalent to the Hill’s model for the cooperative binding of a ligand to a receptor with
n binding sites [
22] but in the case of adsorption onto a surface the heterogeneity index
n ≤ 1.
Accordingly, the surface coverage of
Figure 2A was fitted to Equations (4) and (6).
An analogous set of experiments was performed in solution by means of DLS using colloidal silica particles (Ludox) at a concentration of 5 mg/mL. DLS measures time-dependent fluctuations in the light scattering intensity, arising from particles undergoing Brownian motion in solution. At this concentration Ludox scatters almost ten times more than the highest BSA tested concentration and therefore DLS essentially probes the diffusional properties of the Ludox particles. The average sizes collected at all BSA concentrations are shown in
Figure 2B, where the data can be easily compared with the adsorption isotherm measured on a macroscopic glass slide.
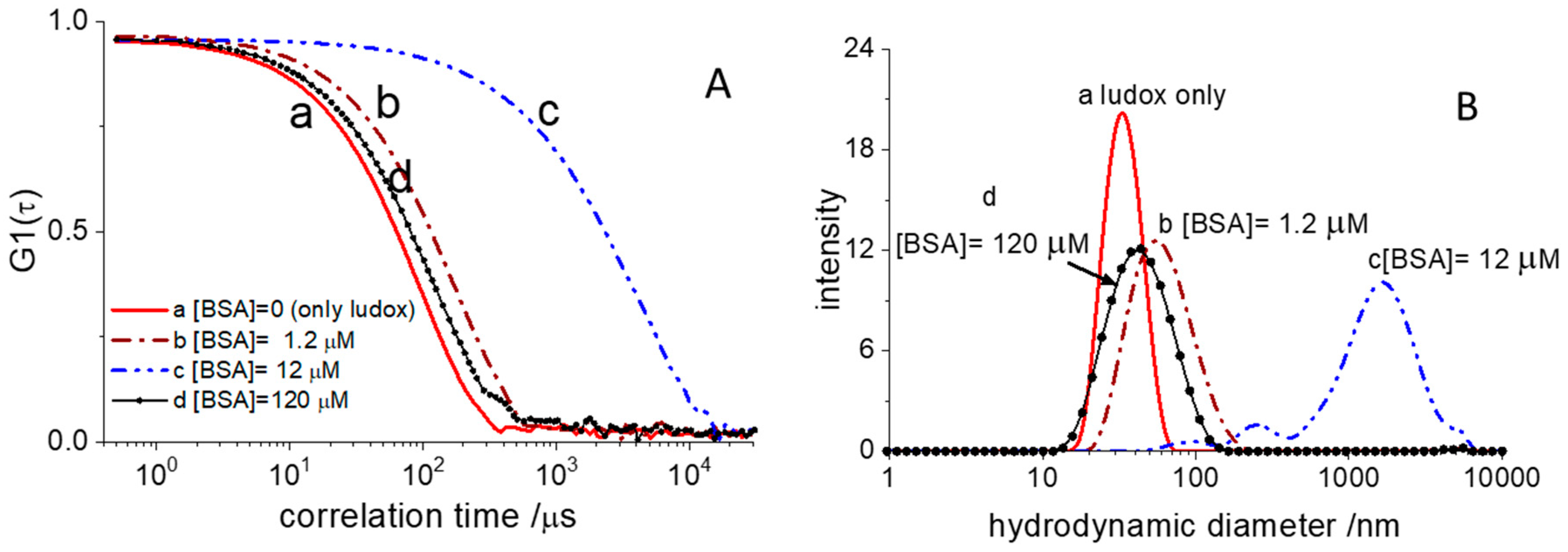
Figure 3A shows representative autocorrelation functions (ACF) of the scattered light collected in these experiments.
The ACF of pristine Ludox (sample A) decays to zero at shorter correlation time than those measured in the presence of BSA. This behavior is an indication of BSA adsorption on the surface of the silica particles, thus increasing their hydrodynamic size. The most straightforward way to grasp such an evolution of dimensions is in terms of the size intensity distribution. This is the fraction of light scattered by particles of different hydrodynamic diameters and can be retrieved from the ACF, according to well-assessed numerical methods. The corresponding intensity distribution functions are shown in
Figure 3B. The pristine Ludox particles are characterized by a narrow size distribution centered around 30 nm. Upon loading the sample with 1.2 µM BSA, the distribution moves towards larger sizes and becomes broader. For the sake of readability in
Figure 3, we have shown only DLS experiments collected at four BSA concentrations. Initial addition of BSA triggers a dramatic increase in the hydrodynamic size that reaches micrometric values for BSA concentrations of 12 µM (
Figure 3B) at which we expect half-saturation of the glass surface. At this concentration, the size distribution is extremely broad and multimodal. Overall, the DLS data collected at BSA = 12 µM suggests the presence of a large cluster population made by aggregated silica beads. Further BSA addition, however, leads to a decrease in cluster size that, at BSA = 120 µM, is only slightly larger than the original particles.
A further indication of the presence of bead aggregates at intermediate concentrations comes from the intensity of the scattered light. The normalized scattering intensity can be calculated as the ratio between scattered intensity and the one collected for pristine non-aggregates Ludox. Assuming that most of the scattered light is due to the silica particles, whose concentration is constant throughout the experiment, and neglecting intraparticle interference, we can suppose the intensity of the scattered light is proportional to the aggregate’s molecular weight. Therefore, the normalized scattering intensity gives an estimate of the number of particles in the aggregates. These values are plotted in
Figure 2B (right abscissa) and are parallel to the trend observed for the hydrodynamic size. At 120 µM BSA the normalized scattering is larger than 10 meaning that the micron-sized aggregates are made by more than 10 Ludox particles. The high affinity of BSA for macroscopic silica surface (
Figure 2A) when exerted in solution of colloidal glass, accounts for the bell-shaped dependence of the aggregation with the BSA concentration observed in the experiments of
Figure 2B.
When BSA concentration is low, the available protein is not enough to saturate the silica surface and there are many free binding sites on the silica nanoparticles. At BSA concentrations close to K
−1, there are roughly the same amount of free and occupied binding sites. These are the conditions for a dramatic growth of three-dimensional clusters (akin to a gel formation). Experimentally, such a condition is fulfilled at a BSA concentration of 12 µM where, indeed, stable µm-sized aggregates form. The absence of macroscopic sedimentation suggests that, because of steric hindrance, a protein can bind only two nanoparticles and once the proteins have all been engaged there is no further aggregation. Increasing the BSA concentration, the system moves along the adsorption isotherm towards the surface saturation and the probability that an already bound BSA molecule will encounter another nanoparticle with an empty binding site decreases. When there is enough BSA to saturate the silica surface, the size of the aggregates decreases until only single silica nanoparticle coated by BSA is present (see
Figure 2B for a pictorial representation)
It is interesting to note how we find a monodisperse size distribution in the presence of BSA 120 µM with a mean size matching that of a Ludox sphere (30 nm) covered with a monolayer of protein (7 nm × 2 = 14 nm, 30 nm + 14 nm = 44 nm). Further confirmation comes from the electrophoretic mobilities, that are −2.43 ± 0.04 µm⋅cm/sV for pristine Ludox and −0.84 ± 0.11 µm⋅cm/sV for Ludox in the presence of BSA 120 µM. Assuming the particles are spheres, one can calculate the corresponding ζ-potential according to the Smoluchowski approximation to obtain −31.0 ± 0.5 for pristine Ludox and −11 ± 1 mV Ludox in the presence of BSA 120 µM. The latter value coincides with the ζ-potential measured for BSA in the same buffer and, therefore, strongly supports the scenario that under these conditions the system is formed by glass beads coated by BSA and thus represents the colloidal counterpart of the macroscopic silica surface covered by 450 ng/cm2 of BSA.
3.2. Surfactant Interactions with BSA-Coated Silica
The surfactant subject of this study is a decanol ethoxylated with an average number of eight ethoxy groups on the hydrophilic moiety (hereafter denoted as C
10PEG) that is widely used in detergent formulations. With respect to the interactions of other conventional surfactants relevant for industry, C
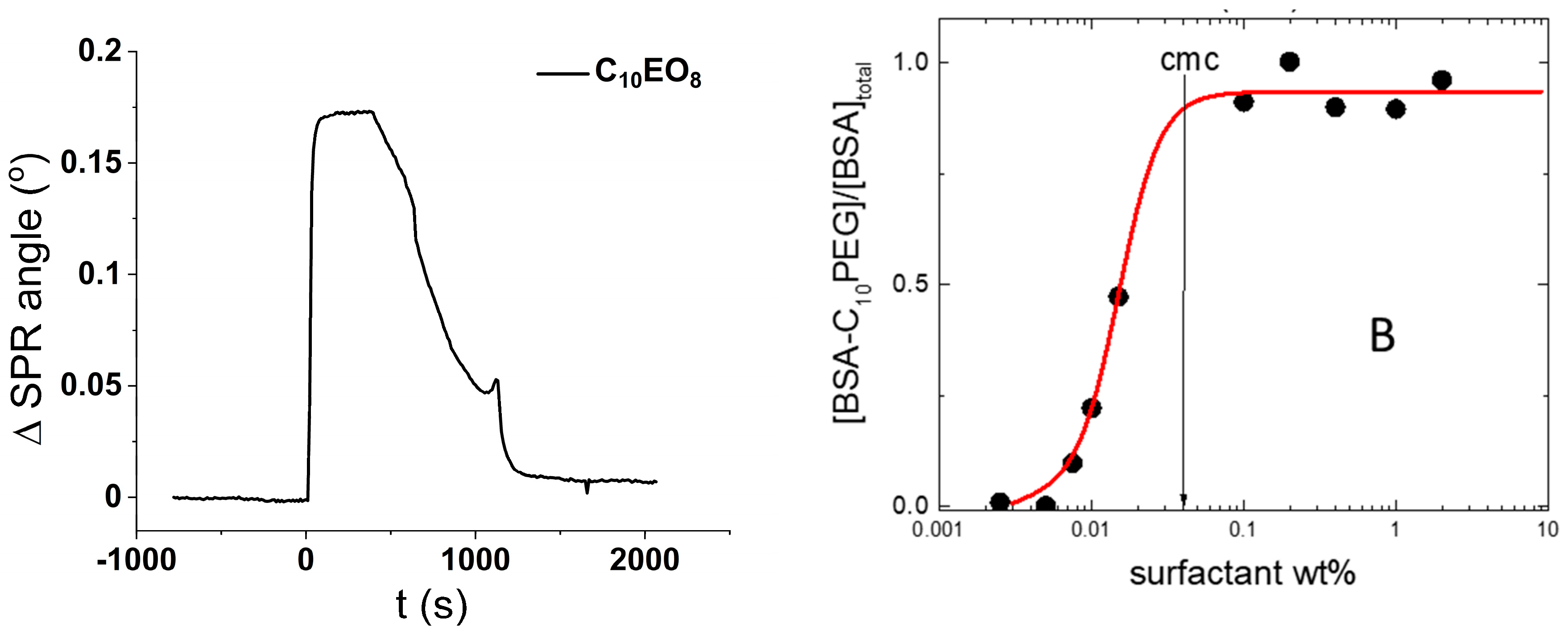
10PEG has a negligible affinity for the glass surface as demonstrated in
Figure 4A, which shows the SPR response to the exposure of a silica surface to a C
10PEG solution (1 wt%). The initial jump after the injection of the surfactant solution is a mere transient, due to the high refractive index of the solution, and rinsing with water returns the very same SPR signal of the pristine silica. This means that the surfactant does not adsorb on the silica surface.
On the other hand, the interaction of C
10PEG with BSA in solution is very mild and limited to the binding of few surfactant molecules to the protein without reaching denaturation [
17]. A representative binding isotherm is shown in
Figure 4B where the fraction of protein bound to surfactant is plotted against the surfactant concentration (the details of these fluorescence experiments are reported elsewhere [
17]). It is clear from
Figure 4B that the binding involves monomeric surfactants. Indeed, it starts well below the critical micelle concentration (CMC) and saturates just above the CMC.
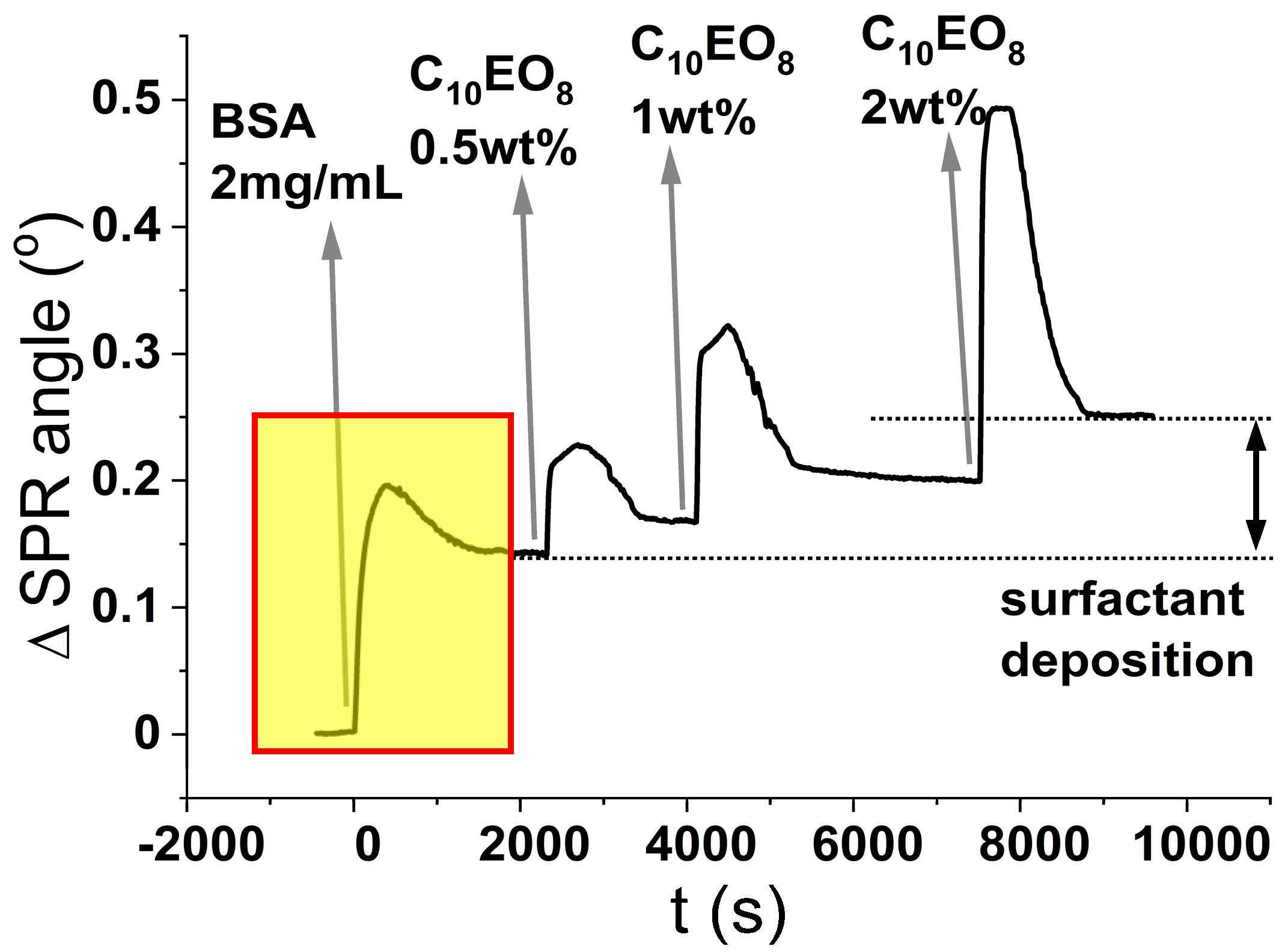
In light of these premises, the results of the experiments shown in
Figure 5 are unexpected. As seen from the isotherm presented in
Figure 2A, the surface coverage of SiO
2 by BSA reaches a plateau after injection of 30 μM BSA (= 2 mg/mL). We, therefore, used this concentration to pre-treat a new sensor surface onto which, we further injected increasing concentrations of surfactant. In this set of experiments, performed on the macroscopic planar surface of a SPR sensor, the silica surface was first exposed at a 30 µM BSA solution, a condition that leads to the formation of a stable protein layer as demonstrated by the stable plateau (0.15°) in the SPR response after rinsing (this takes place in the boxed region of the sensogram in
Figure 5). After this, we flushed solutions of surfactant at increasing concentrations (0.5, 1, and 2 wt%) over the BSA-coated glass surface. Flushing with C
10PEG results in a sequential increase of the SPR signal of sequential plateaus, which denotes an interaction at the sensor’s surface between surfactant and protein.
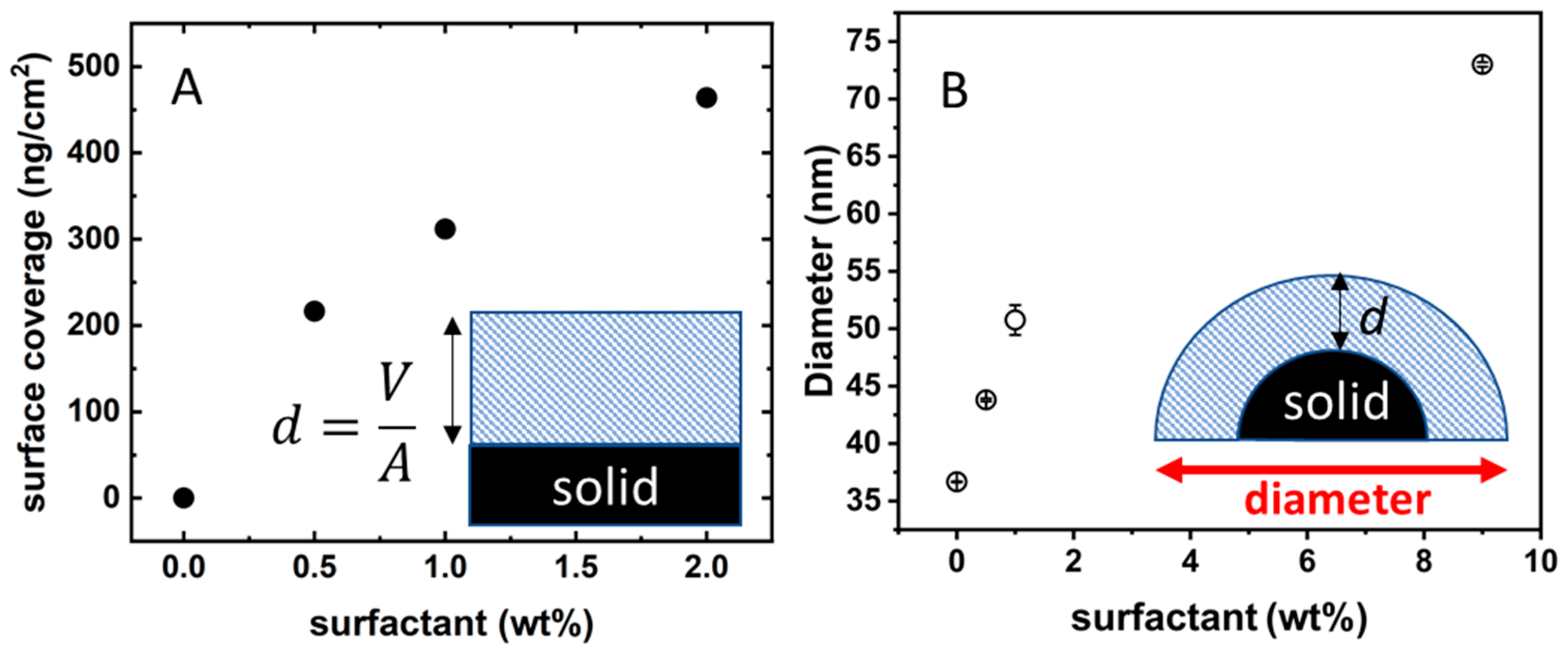
It is possible to transform the SPR degree-signal into surface coverage as described in the previous section. The isotherm in
Figure 6A shows the surface coverage (expressed as ng of dry surfactant per cm
2) as a function of surfactant concentration. There are two very peculiar features in
Figure 6A. First, when the BSA-coated silica surface is in contact with a 2 wt% C
10PEG solution, the adsorption seems to be far from the saturation in marked contrast with the situation found for bare silica where there is no surfactant adsorption (
Figure 4A). The second point is related to the values of surface coverage. The highest measured datum is 460 ng/cm
2; taking as average molecular weight of 511 g/mol (of pure octaethylene glycol monododecyl ether) this corresponds to an average area per surfactant molecule of 18 Å. This is definitely too low for an area occupied by a surfactant with a bulky poly-ethoxylated moiety [
23]. A possible explanation of both these features is that the surfactant is arranged in the form of multilayers.
To check such a hypothesis, we moved to analogous experiments performed on colloidal silica where we could easily follow the change in size upon addition of surfactant. The Ludox beads were first exposed to BSA 120 µM in order to have well-dispersed nanoparticles fully coated by proteins (diameter 39 ± 5 nm). The BSA-coated Ludox solution was then loaded with increasing amounts of C
10PEG. The presence of surfactant induces a continuous increase in the hydrodynamic size of the particles, as shown in
Figure 6B.
The increase in size is not as huge as expected in the case of particle–particle coagulation (see for example,
Figure 2B) but it is however large. The lowest C
10PEG addition is able to increase the hydrodynamic diameter by 7 nm which is the size of a C
10PEG micelle. Loading with 9 wt% surfactant almost doubles the hydrodynamic size of the particles (remember BSA-coated Ludox has a size around 39 ± 5 nm and the increase at 9 wt% is of 36 nm). An increase of 36 nm in the hydrodynamic diameter indicates the adsorption of a layer of 16 nm, much larger than what one expects for the formation of a surfactant monolayer (~3.5 nm). Therefore, also the experiments performed on colloidal glass coated with BSA points towards the multilayer adsorption of C
10PEG over the protein coating.
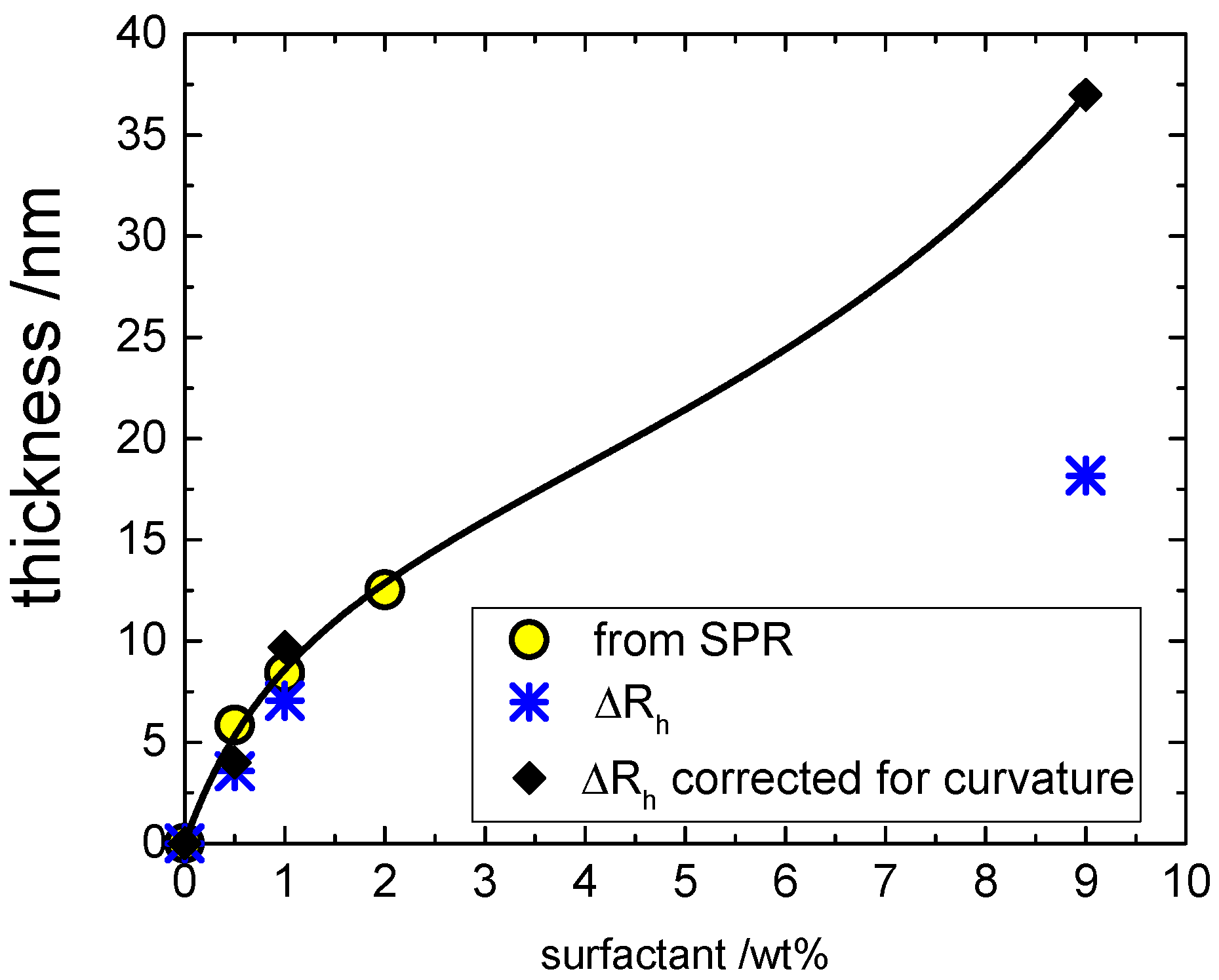
Of course, a quantitative comparison between the results obtained by SPR on flat surfaces and DLS on colloidal surfaces is very interesting. To have a fair comparison, we must take into account that DLS measures a hydrodynamic thickness that refers to a curved surface and that includes bound water. On the other hand, the surface coverage evaluated by SPR refers to a planar surface and is expressed in terms of dry mass of surfactant.
Here we propose to compare the results from these two experimental approaches in terms of effective thickness of a planar surface by correcting the SPR results for the bound water and the DLS data for the curvature as detailed in the following.
(1) SPR. Several papers point towards an average value of six water molecules associated to each EO group of non-ionic surfactants [
24,
25,
26]. Having an average number of eight ethoxy group per surfactant molecule gives 48 hydration water molecules per polar head. Thus, one mol of C
10PEG (511 cm
3 assuming a density close to one) is associated to 864 cm
3 of water giving an effective molar volume of 1375 cm
3/mol. The surface coverage allows to evaluate the volume (water + surfactant) of the film deposited above the BSA-coated silica. For a planar surface, the volume-to-area ratio (V/A) equals the thickness of the film (assumed to be incompressible and homogeneous) as sketched in the inset of
Figure 6A. The corresponding values of thickness of the hydrated film are shown in
Figure 7 as yellow circles. Of course, such a calculation assumes the EO hydration in the micelles is not very different from the one found on the surfactant film. The validity of such an assumption was tested comparing the film thickness with the observed changes in the hydrodynamic size of glass beads (point 2 below).
(2) DLS.
Figure 7 also depicts the hydrodynamic thickness (Δ
rh asterisks) obtained by the DLS as the difference between the hydrodynamic radius in the presence of surfactant (
rh) and the hydrodynamic radius of the original BSA-coated silica nanoparticle (
r°
h); in formula: Δ
rh =
rh –
r°
h. The two sets of data are in reasonable agreement, demonstrating that the correction of SPR data for hydration is consistent. However, the Δ
rh values are systematically lower than the corresponding film thickness coming from SPR. This is because the thickness of a curved layer underestimates the corresponding volume. For example, the volume of a spherical coating
V = (4π/3)[(
R +
d)
3 –
R3] is larger than the product area × thickness = 4πR
2d. For a film characterized by a mean and Gaussian curvature (
Hc and
Kc, respectively), it can be demonstrated that the relation between V/A and the thickness
d is [
27,
28]:
where
Hc and
Kc are evaluated at the surface A. For a sphere of radius
R the following equalities hold:
Hc =
R−1 and
Kc =
R−2 and we refer to the surface of the BSA-coated silica bead with a radius
R ~ 20 nm so that it is possible to evaluate the corresponding thickness of a planar surface inserting the hydrodynamic thickness in the above equation obtaining
The corresponding values of thickness for planar surface are shown in
Figure 7 as black diamonds. It is clear that not only are they are in good agreement with the SPR results within the shared range of concentrations by the two approaches, but the DLS results obtained at high concentration clearly do not have any saturation. Instead, the overall isotherm has the classical shape of a type II adsorption isotherm [
29] and accordingly it is accounted for by a Brunauer–Emmett–Teller (BET) isotherm [
30]:
where the surface coverage is now expressed as volume of adsorbed hydrated surfactant per unit area (
d =
V/
A nm
3/nm
2 in
Figure 7),
KL is the affinity constant for the first monolayer (equivalent to the Langmuir’s constant), q
1 is the corresponding saturation coverage, and
Kml is the affinity constant of the multilayers. The best-fit parameters are listed in the caption of
Figure 7.
The data obtained by means of SPR and DLS indicate a strong affinity of the non-ionic surfactant for the BSA-coated surfaces that becomes an effective adsorption at concentrations well above the CMC. This contrasts with the experiments performed in solution (in the absence of any glass surface) where an interaction between surfactant and proteins takes place only at low concentration (below the CMC) as shown in
Figure 4B. A weak point of the fluorescence experiments of
Figure 4B is that they probe the protein (i.e., the saturation indicates that from the protein point of view the conformational changes induced by the surfactant binding have levelled off). In principle, it could be possible that the surfactant continues to adsorb on the protein. To check such a possibility, we have studied the surfactant/BSA interactions by means of diffusion-NMR (dNMR) [
30]. This is a technique that allows the measurement of the surfactant self-diffusion coefficient (for a recent review on the applications of this technique to binding process see [
31]). The rationale of the experiment is straightforward: by dNMR one measures the self-diffusion coefficient of the surfactant alone and in the presence of BSA without any interference from the protein (they have different NMR peaks). If a non-negligible fraction of the surfactant is bound to the slow-diffusing protein the observed diffusion coefficient will be reduced with respect to that of a micellar solution without BSA. For example, the binding of a cationic surfactant to BSA results in a 30% decrease in the surfactant diffusion and further elaboration of this evidence allows the quantification of the amount of bound surfactant [
17].
In the case of a solution of C10PEG 2 wt% we measured a diffusion coefficient of (1.00 ± 0.05) × 10−10 m2/s. Loading this solution with BSA up to 4 mg/mL (60 µM) does not change the value of the diffusion coefficient within the experimental error. Such evidence is fully understandable if the surfactant saturates the protein below the CMC so that the maximum fraction of bound C10PEG is 0.02% of the total.
The markedly different affinity of C
10PEG for BSA in solution and adsorbed on a solid surface is unexpected. We found two different studies in literature that are in line with our evidence. Fully atomistic molecular dynamics simulation indicates that, upon adsorption on silica, BSA does not unfold but, however, undergoes a change in orientation that exposed towards the water more hydrophobic regions (while the more hydrophilic ones interact with silica) [
15]. In another study, the changes induced by the adsorption are so large that it was possible to evaluate experimentally differences in the Hansen solubility parameters of BSA when it is in aqueous solution and in the form of an adsorbed layer [
32].