Optimal Flow Sensing for Schooling Swimmers
Abstract
1. Introduction
2. Materials and Methods
2.1. Flow Simulations
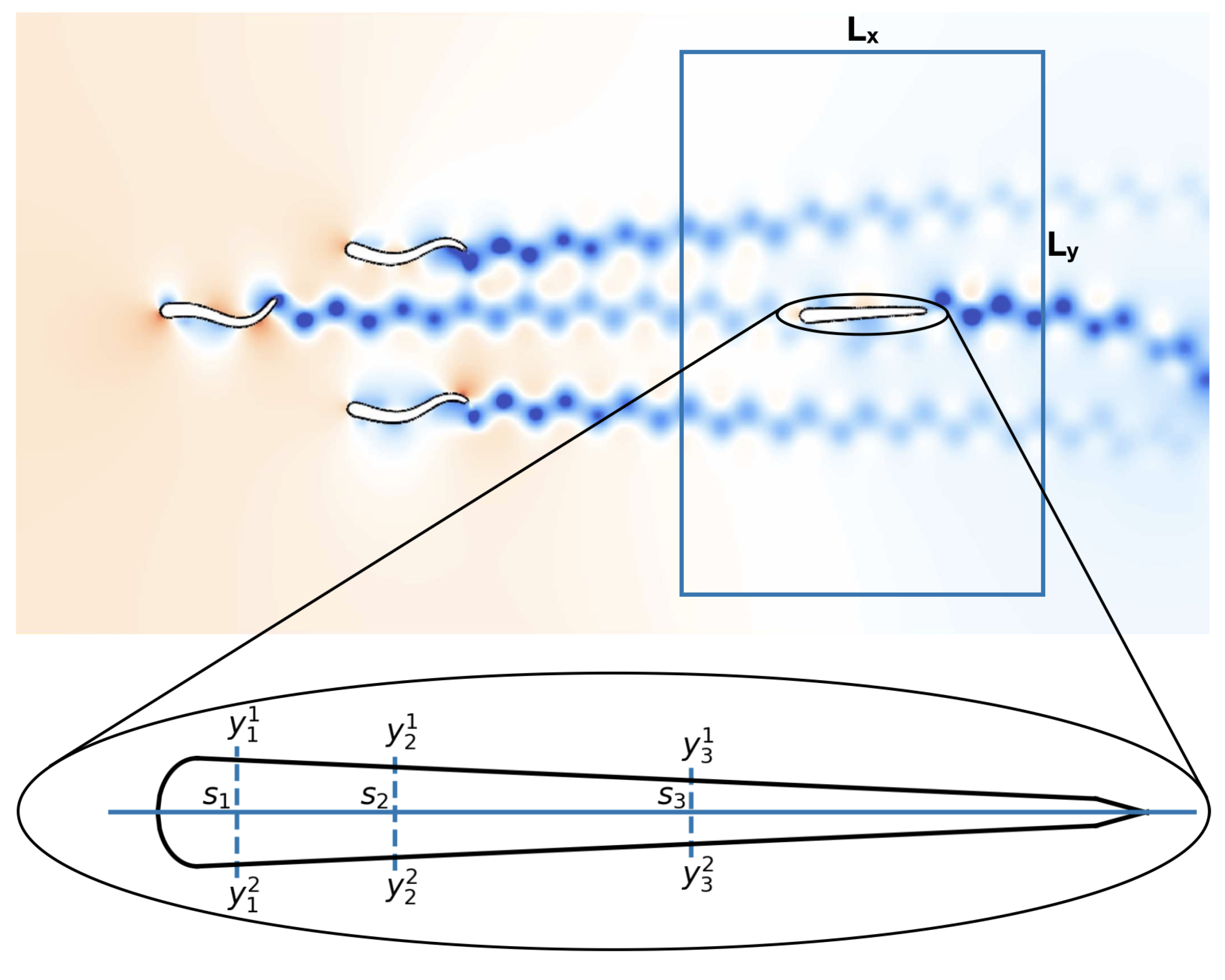
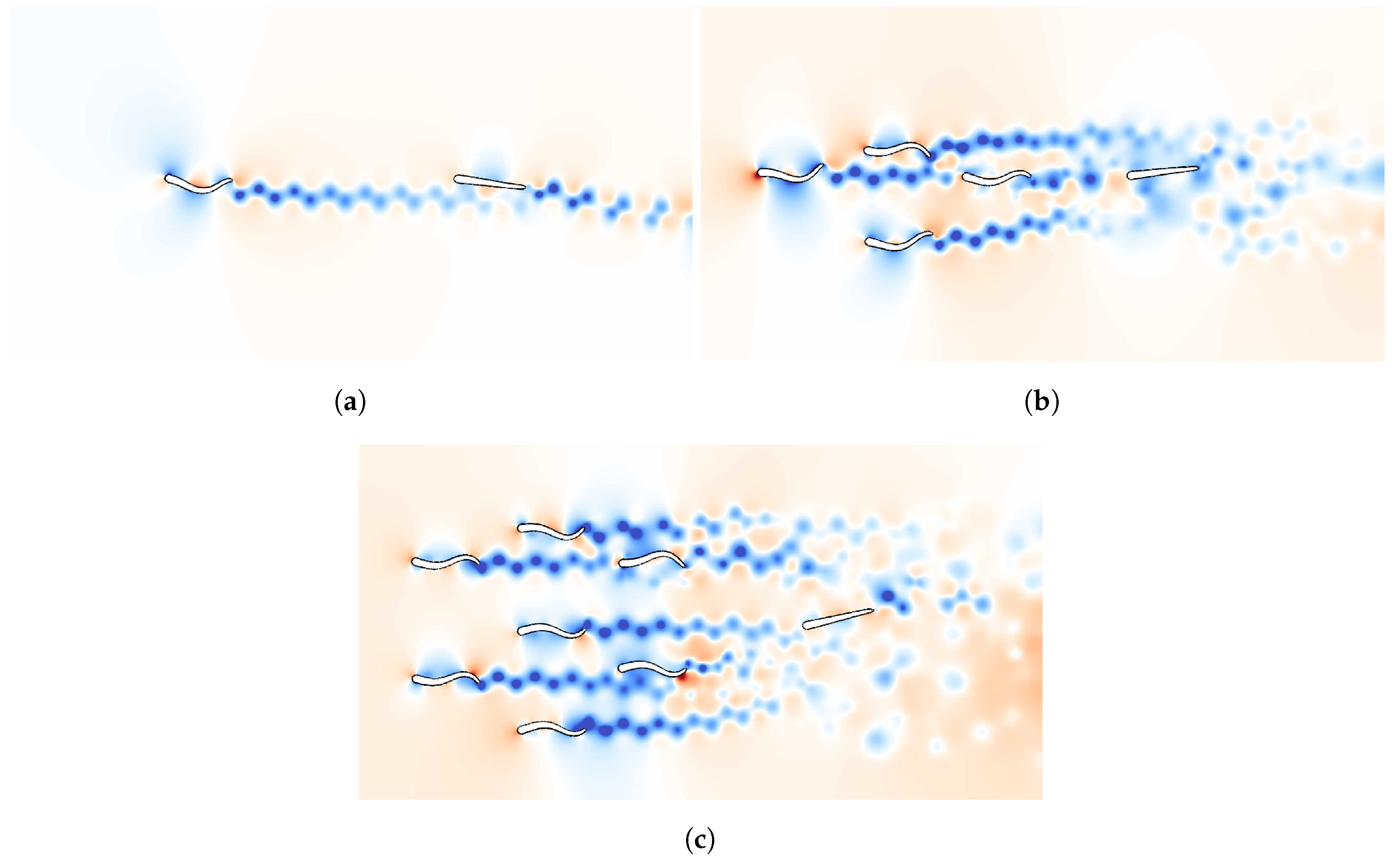
2.1.1. Schooling Formation
2.1.2. Flow Sensors
2.2. Optimal Sensor Placement Based on Information Gain
2.2.1. Bayesian Estimation of Swimmers
2.2.2. Estimated Expected Utility for Continuous Random Variables: School Location
2.2.3. Estimated Expected Utility for Discrete Random Variables: School Size
2.2.4. Optimization of the Expected Utility Function
3. Results
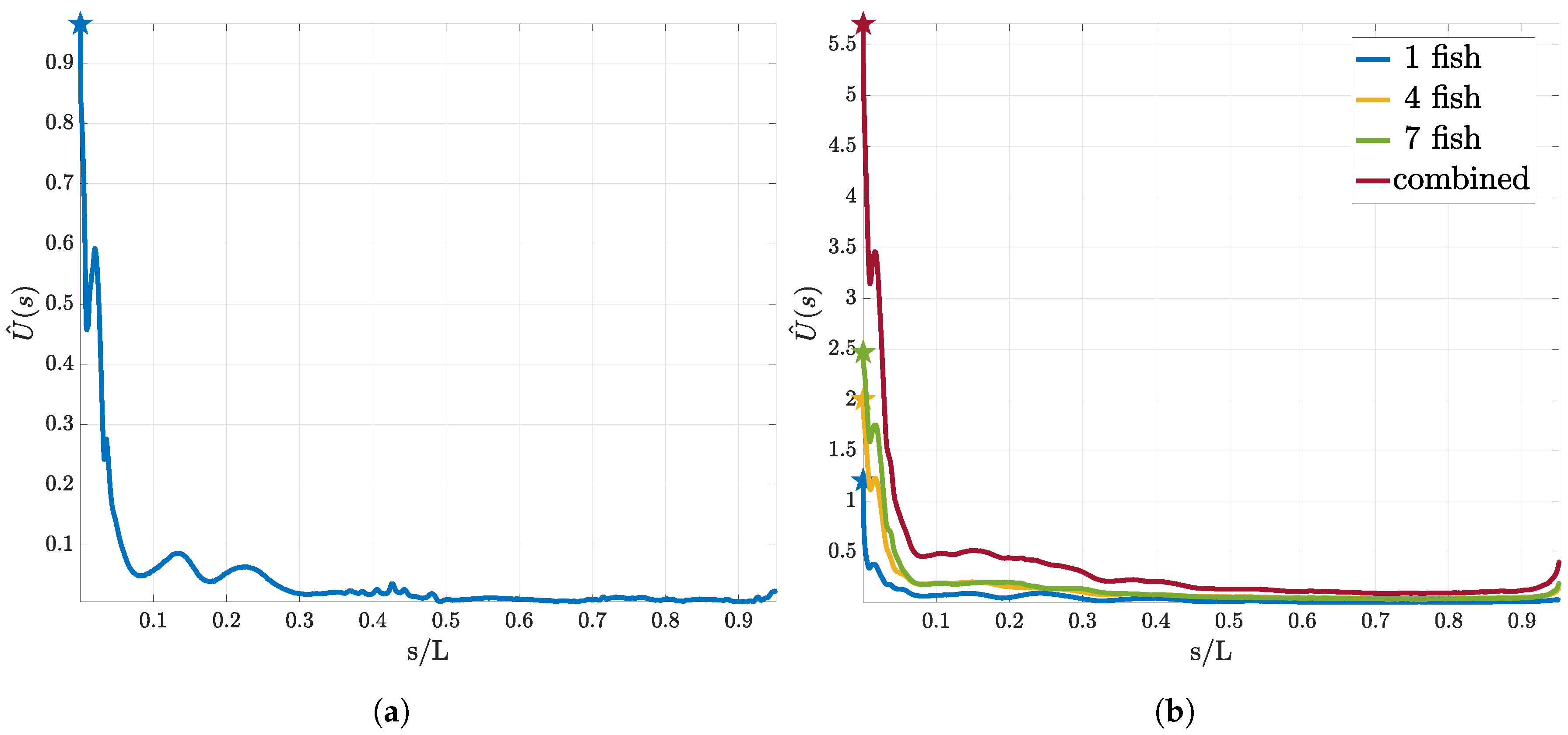
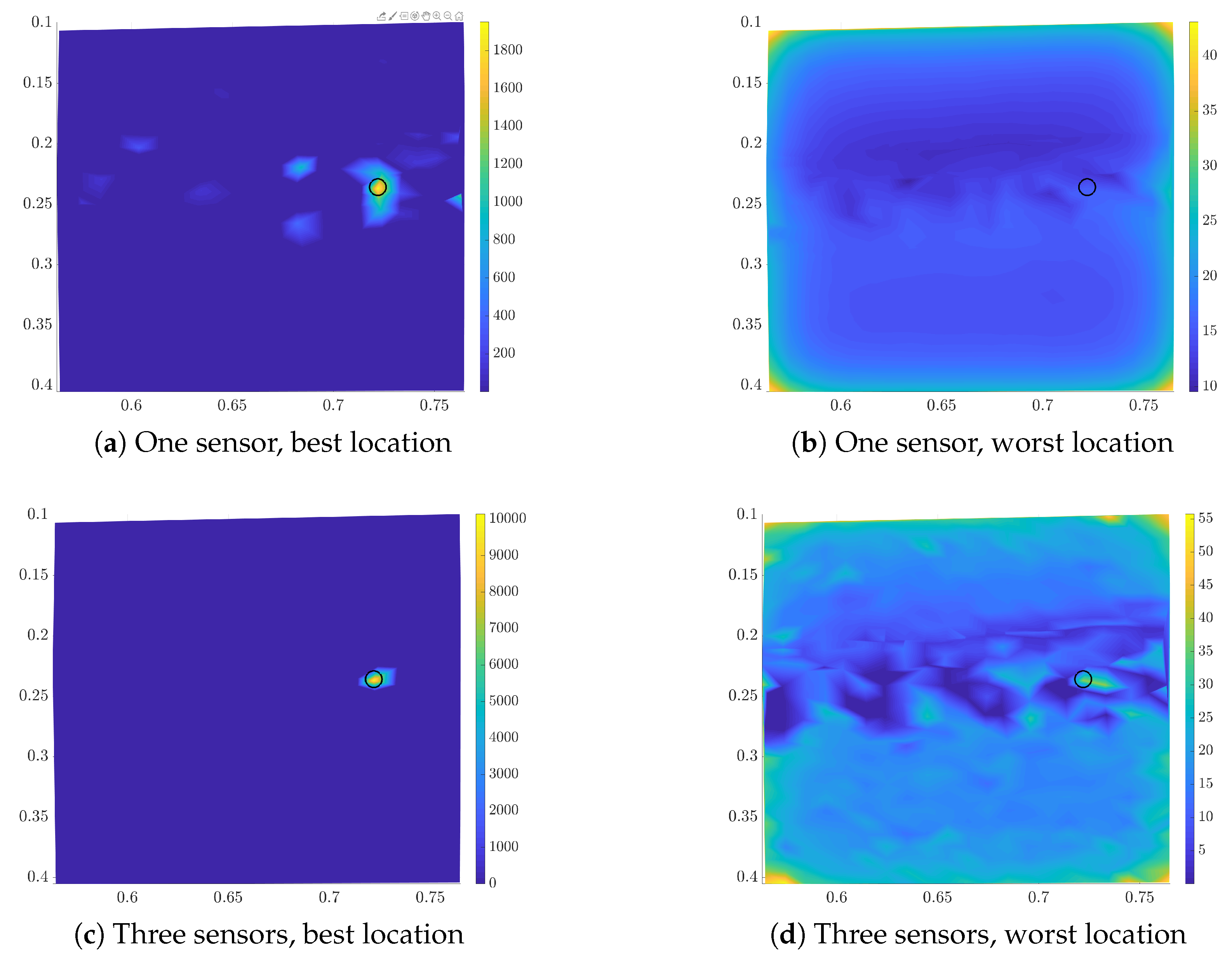
3.1. Utility Function for the First Sensor
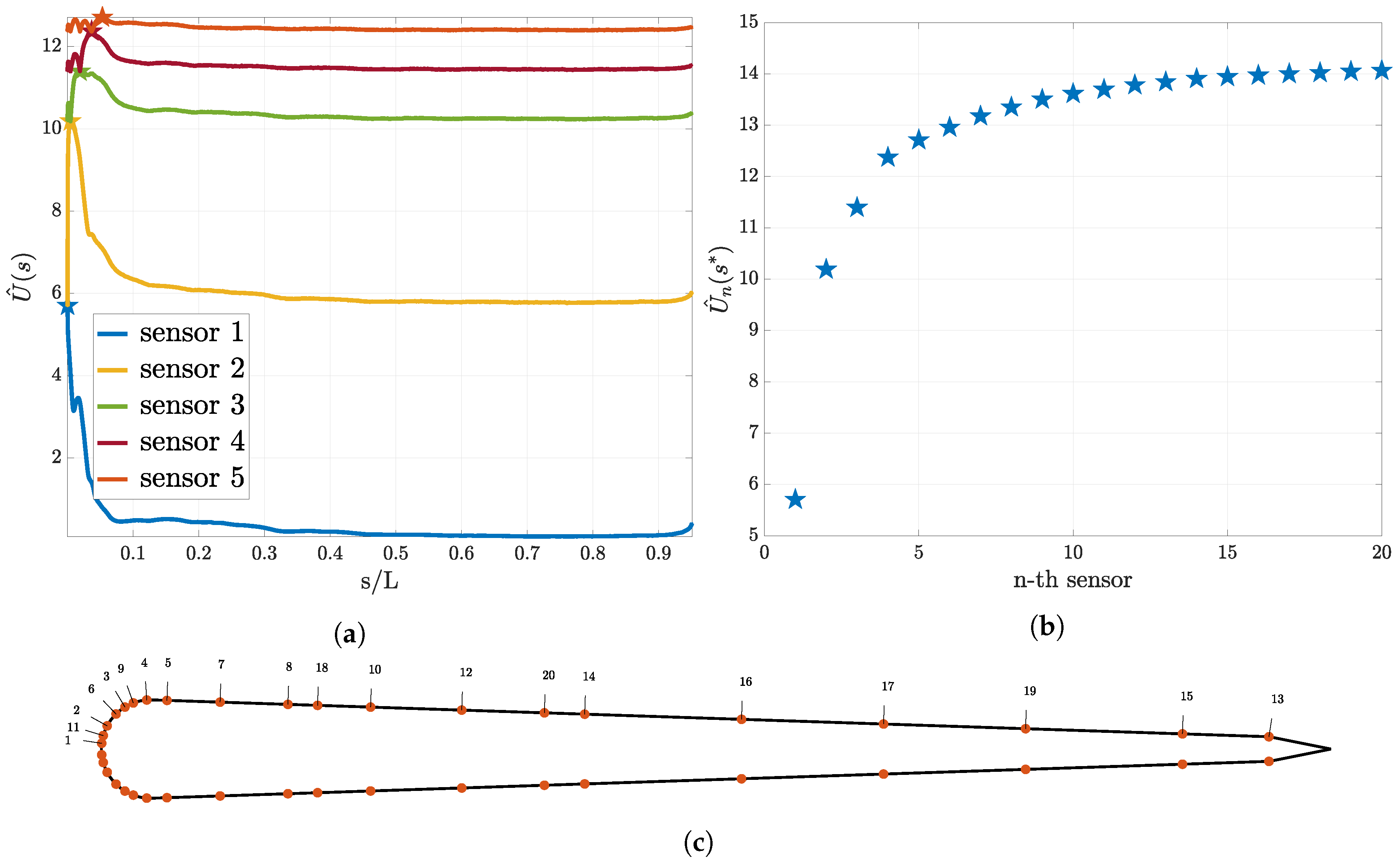
3.2. Sequential Sensor Placement
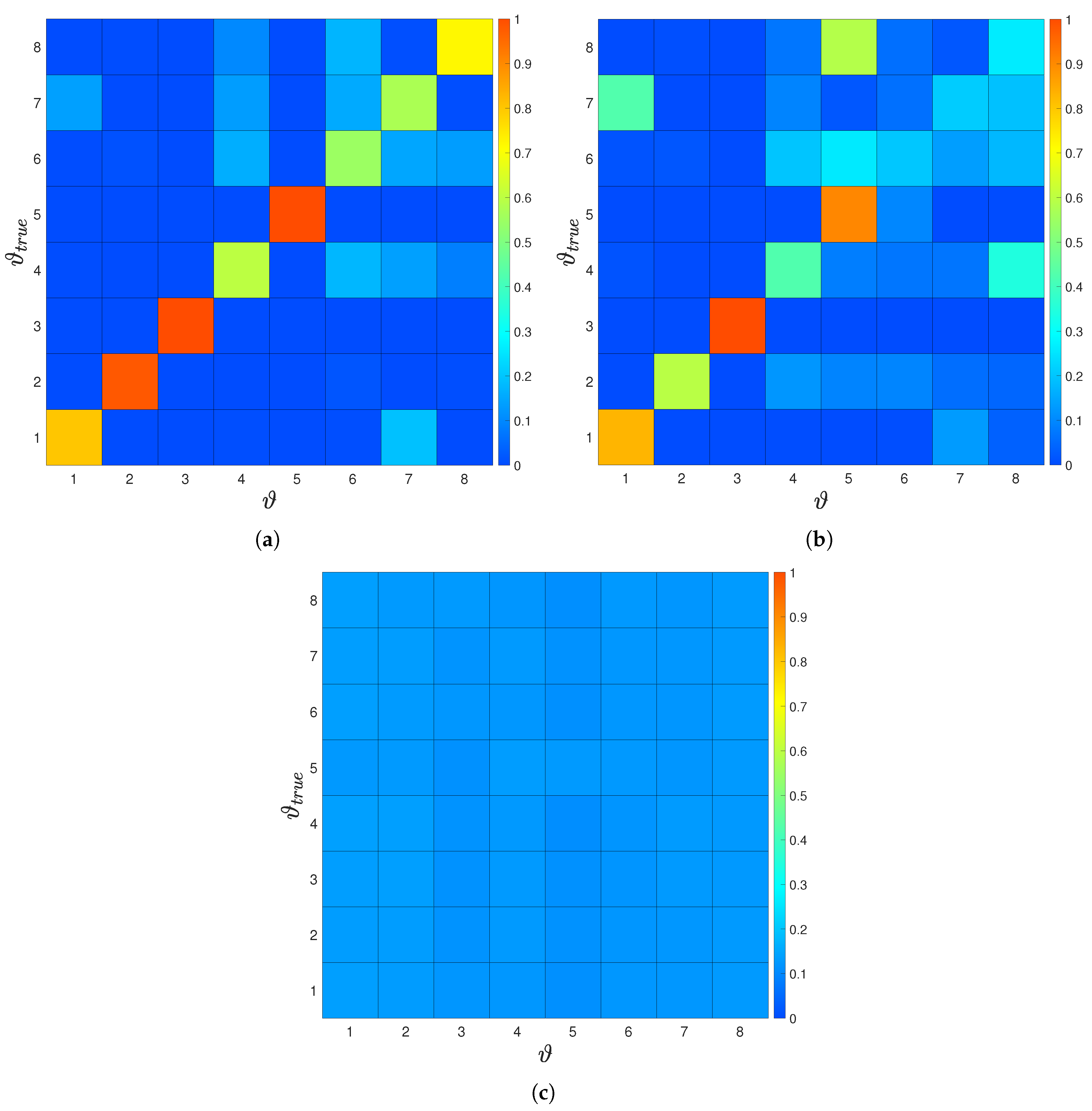
3.3. Inference of the Environment
3.4. Shear Stress Sensors
4. Discussion
Author Contributions
Funding
Conflicts of Interest
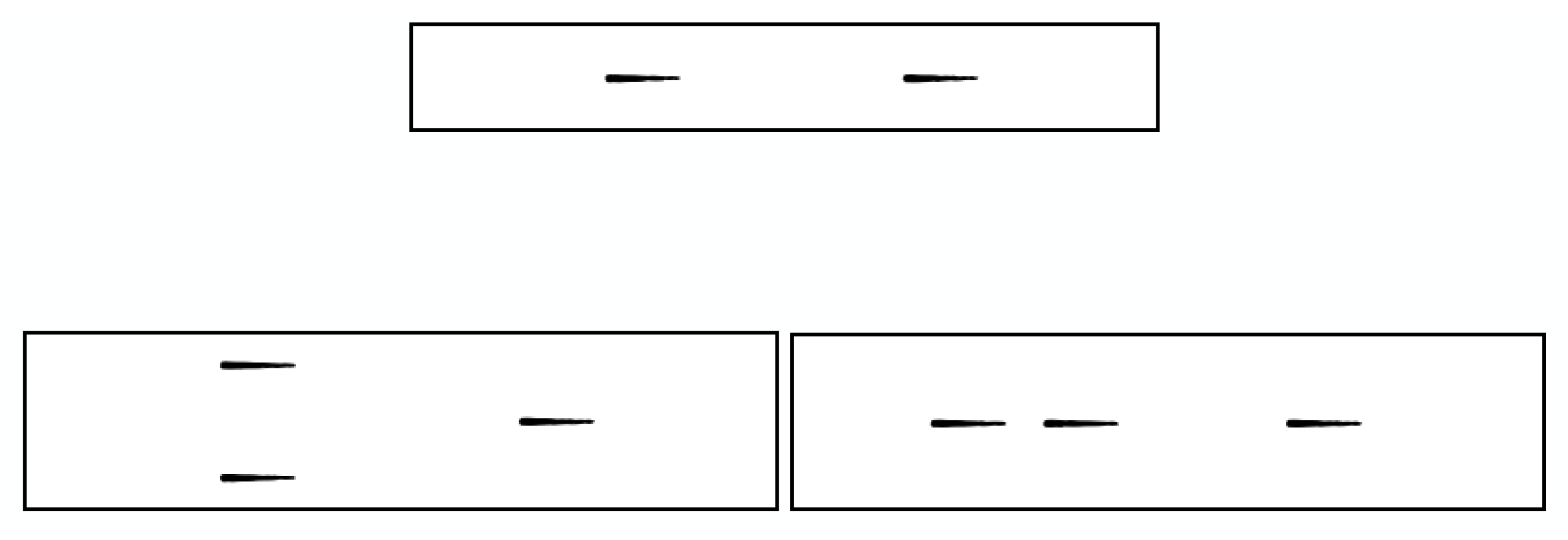
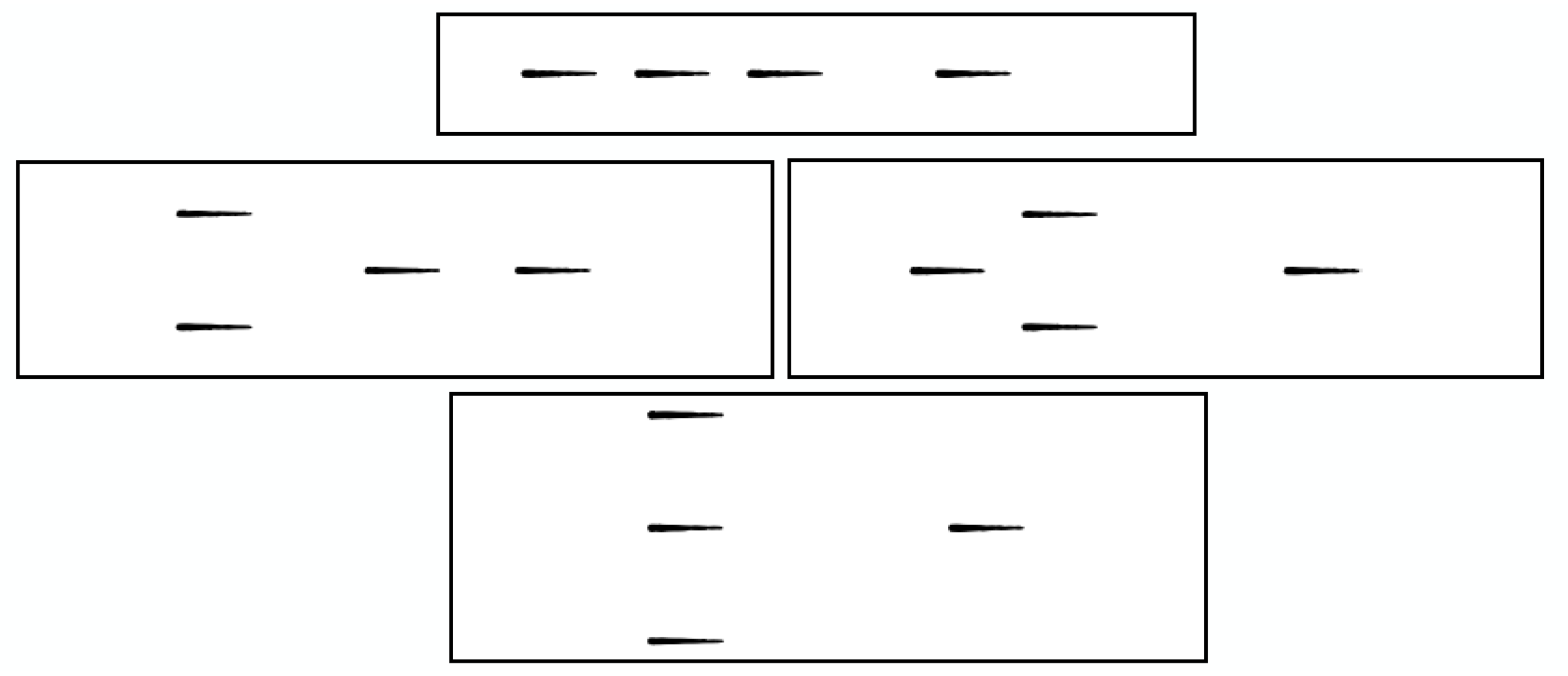
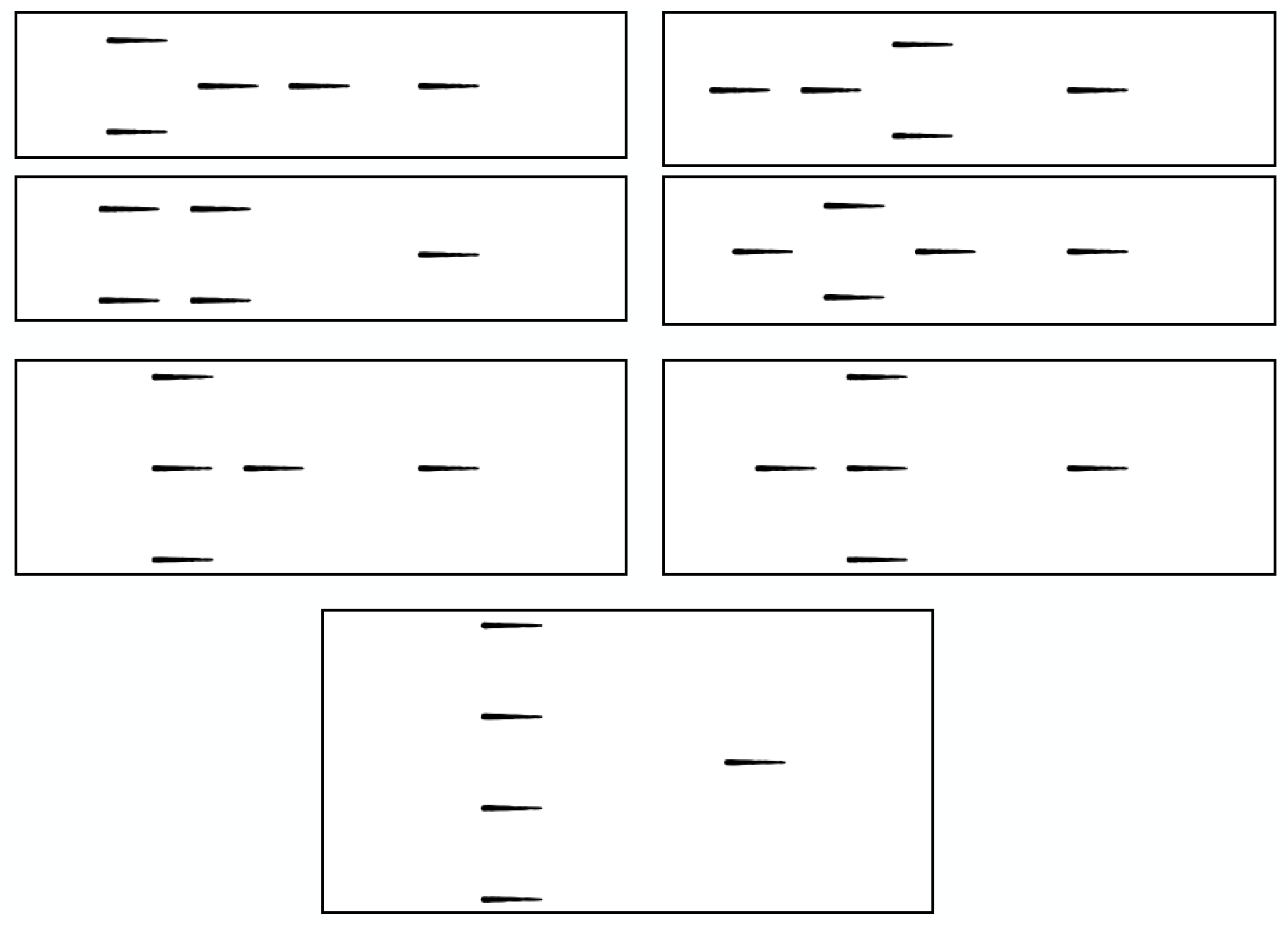
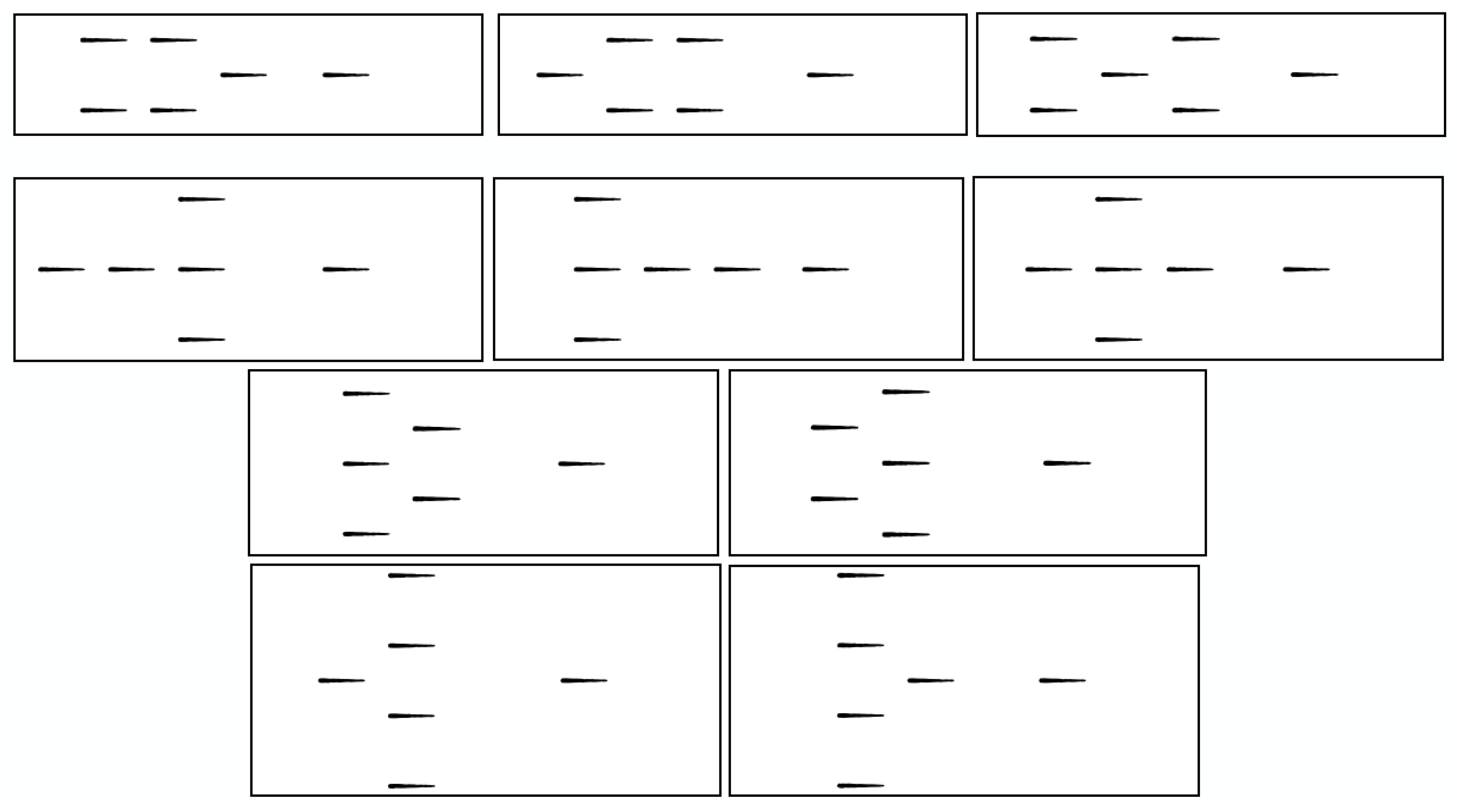
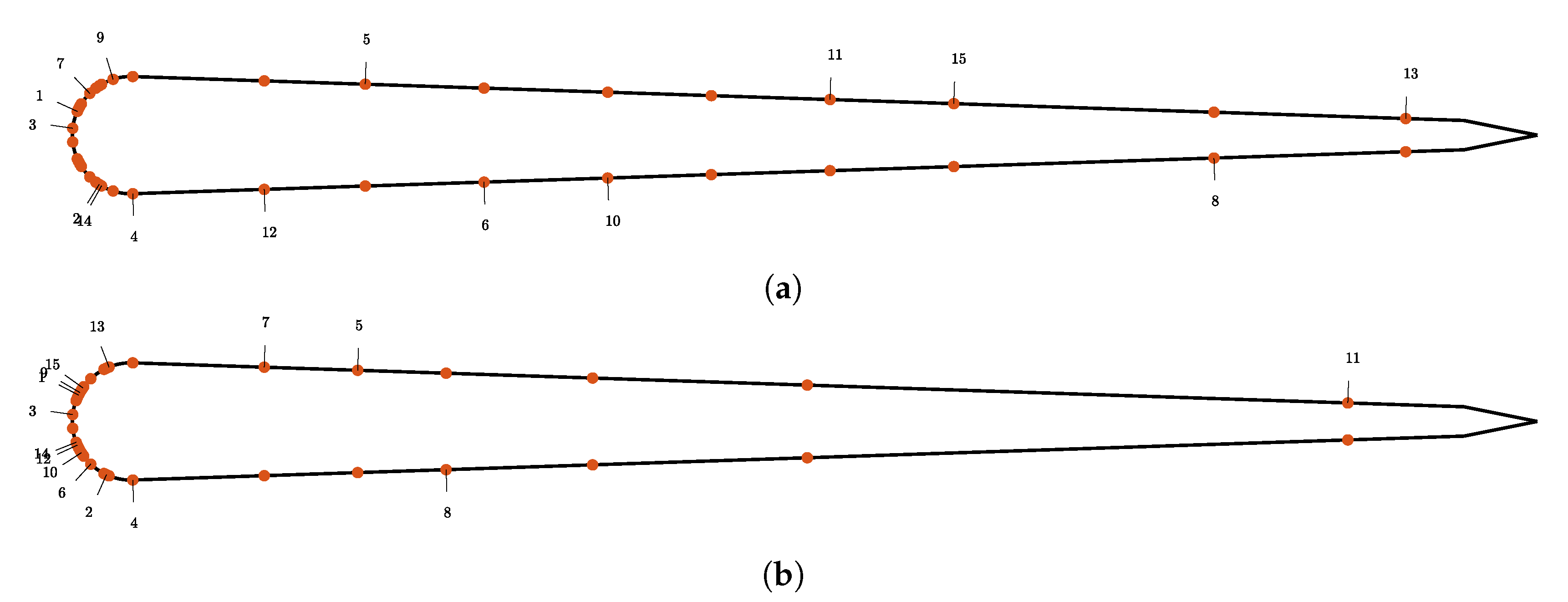
Appendix A. Configurations

Appendix B. The Posterior Is Not Symmetric
References
- Morrow, J.E. Schooling Behavior in Fishes. Q. Rev. Biol. 1948, 23, 27–38. [Google Scholar] [CrossRef] [PubMed]
- Partridge, B.L.; Pitcher, T. The sensory basis of fish schools: Relative roles of lateral line and vision. J. Comp. Physiol. 1980, 135, 315–325. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Weymouth, G.D.; Miao, J. Biomimetic Survival Hydrodynamics and Flow Sensing. Annu. Rev. Fluid Mech. 2016, 48, 1–24. [Google Scholar] [CrossRef]
- Ward, A.J.W.; Sumpter, D.J.T.; Couzin, I.D.; Hart, P.J.B.; Krause, J. Quorum decision-making facilitates information transfer in fish shoals. Proc. Natl. Acad. Sci. USA 2008, 105, 6948–6953. [Google Scholar] [CrossRef]
- Puckett, J.G.; Pokhrel, A.R.; Giannini, J.A. Collective gradient sensing in fish schools. Sci. Rep. 2018, 8, 7587. [Google Scholar] [CrossRef]
- Dykgraaf, S. Untersuchungen über die Funktion der Seitenorgane an Fischen. Zeitschrift für Vergleichende Physiologie 1933, 20, 162–214. [Google Scholar] [CrossRef]
- Dykgraaf, S. The functioning and significance of the lateral-line organs. Biol. Rev. Camb. Philos. Soc. 1963, 38, 51–105. [Google Scholar] [CrossRef]
- Bleckmann, H.; Przybilla, A.; Klein, A.; Schmitz, A.; Kunze, S.; Brücker, C. Station Holding of Trout: Behavior, Physiology and Hydrodynamics. In Nature-Inspired Fluid Mechanics: Results of the DFG Priority Programme 1207 ”Nature-Inspired Fluid Mechanics” 2006–2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 161–177. [Google Scholar] [CrossRef]
- Sutterlin, A.; Waddy, S. Possible Role of the Posterior Lateral Line in Obstacle Entrainment by Brook Trout (Salvelinus fontinalis). J. Fish. Res. Board Can. 2011, 32, 2441–2446. [Google Scholar] [CrossRef]
- Akanyeti, O.; Venturelli, R.; Visentin, F.; Chambers, L.; Megill, W.M.; Fiorini, P. What information do Kármán streets offer to flow sensing? Bioinspir. Biomim. 2011, 6, 036001. [Google Scholar] [CrossRef]
- Chambers, L.D.; Akanyeti, O.; Venturelli, R.; Ježov, J.; Brown, J.; Kruusmaa, M.; Fiorini, P.; Megill, W.M. A fish perspective: Detecting flow features while moving using an artificial lateral line in steady and unsteady flow. J. R. Soc. Interface 2014, 11. [Google Scholar] [CrossRef]
- von Campenhausen, C.; Riess, I.; Weissert, R. Detection of stationary objects by the blind Cave FishAnoptichthys jordani (Characidae). J. Comp. Physiol. 1981, 143, 369–374. [Google Scholar] [CrossRef]
- Hassan, E.S. Hydrodynamic Imaging of the Surroundings by the Lateral Line of the Blind Cave Fish Anoptichthys jordani. In The Mechanosensory Lateral Line; Coombs, S., Görner, P., Münz, H., Eds.; Springer: New York, NY, USA, 1989; pp. 217–227. [Google Scholar]
- Windsor, S.P.; Norris, S.E.; Cameron, S.M.; Mallinson, G.D.; Montgomery, J.C. The flow fields involved in hydrodynamic imaging by blind Mexican cave fish (Astyanax fasciatus). Part I: Open water and heading towards a wall. J. Exp. Biol. 2010, 213, 3819–3831. [Google Scholar] [CrossRef] [PubMed]
- Windsor, S.P.; Norris, S.E.; Cameron, S.M.; Mallinson, G.D.; Montgomery, J.C. The flow fields involved in hydrodynamic imaging by blind Mexican cave fish (Astyanax fasciatus). Part II: Gliding parallel to a wall. J. Exp. Biol. 2010, 213, 3832–3842. [Google Scholar] [CrossRef] [PubMed]
- Hoekstra, D.; Janssen, J. Non-visual feeding behavior of the mottled sculpin, Cottus bairdi, in Lake Michigan. Environ. Biol. Fishes 1985, 12, 111–117. [Google Scholar] [CrossRef]
- Pitcher, T.; Partridge, B.; Wardle, C. A blind fish can school. Science 1976, 194, 963–965. [Google Scholar] [CrossRef]
- Satou, M.; Takeuchi, H.A.; Nishii, J.; Tanabe, M.; Kitamura, S.; Okumoto, N.; Iwata, M. Behavioral and electrophysiological evidences that the lateral line is involved in the inter-sexual vibrational communication of the himé salmon (landlocked red salmon, Oncorhynchus nerka). J. Comp. Physiol. A 1994, 174, 539–549. [Google Scholar] [CrossRef]
- Huijbers, C.M.; Nagelkerken, I.; Lössbroek, P.A.C.; Schulten, I.E.; Siegenthaler, A.; Holderied, M.W.; Simpson, S.D. A test of the senses: Fish select novel habitats by responding to multiple cues. Ecology 2012, 93, 46–55. [Google Scholar] [CrossRef]
- Montgomery, J.C.; Baker, C.F.; Carton, A.G. The lateral line can mediate rheotaxis in fish. Nature 1997, 389, 960–963. [Google Scholar] [CrossRef]
- Coombs, S.; Janssen, J.; Webb, J.F. Diversity of lateral line systems: Evolutionary and functional considerations. In Sensory Biology of Aquatic Animals; Springer: Berlin/Heidelberg, Germany, 1988; pp. 553–593. [Google Scholar]
- Coombs, S.; Görner, P.; Münz, H. A Brief Overview of the Mechanosensory Lateral Line System and the Contributions to This Volume. In The Mechanosensory Lateral Line; Coombs, S., Görner, P., Münz, H., Eds.; Springer: New York, NY, USA, 1989; pp. 3–5. [Google Scholar]
- Denton, E.J.; Gray, J.A.B. Some Observations on the Forces Acting on Neuromasts in Fish Lateral Line Canals. In The Mechanosensory Lateral Line; Coombs, S., Görner, P., Münz, H., Eds.; Springer: New York, NY, USA, 1989; pp. 229–246. [Google Scholar]
- Coombs, S.; Braun, C.B. Information Processing by the Lateral Line System. In Sensory Processing in Aquatic Environments; Springer: New York, NY, USA, 2003; pp. 122–138. [Google Scholar] [CrossRef]
- Coombs, S.; Netten, S.V. The Hydrodynamics and Structural Mechanics of the Lateral Line System. In Fish Physiology; Elsevier: Amsterdam, The Netherlands, 2005; Volume 23, pp. 103–139. [Google Scholar] [CrossRef]
- Bleckmann, H. Peripheral and central processing of lateral line information. J. Comp. Physiol. A 2008, 194, 145–158. [Google Scholar] [CrossRef]
- Jiang, Y.; Ma, Z.; Zhang, D. Flow field perception based on the fish lateral line system. Bioinspir. Biomim. 2019, 14, 041001. [Google Scholar] [CrossRef]
- Engelmann, J.; Hanke, W.; Mogdans, J.; Bleckmann, H. Hydrodynamic stimuli and the fish lateral line. Nature 2000, 408, 1476–4687. [Google Scholar] [CrossRef] [PubMed]
- Kottapalli, A.G.P.; Asadnia, M.; Miao, J.M.; Barbastathis, G.; Triantafyllou, M.S. A flexible liquid crystal polymer MEMS pressure sensor array for fish-like underwater sensing. Smart Mater. Struct. 2012, 21, 115030. [Google Scholar] [CrossRef]
- Tao, J.; Yu, X. Hair flow sensors: From bio-inspiration to bio-mimicking—A review. Smart Mater. Struct. 2012, 21, 113001. [Google Scholar] [CrossRef]
- Asadnia, M.; Kottapalli, A.G.P.; Miao, J.; Warkiani, M.E.; Triantafyllou, M.S. Artificial fish skin of self-powered micro-electromechanical systems hair cells for sensing hydrodynamic flow phenomena. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Kottapalli, A.G.P.; Bora, M.; Sengupta, D.; Miao, J.; Triantafyllou, M.S. Hydrogel-CNT Biomimetic Cilia for Flow Sensing. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Wolf, B.J.; Morton, J.A.S.; MacPherson, W.N.; van Netten, S.M. Bio-inspired all-optical artificial neuromast for 2D flow sensing. Bioinspir. Biomim. 2018, 13, 026013. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, J.; Engel, J.; Pandya, S.; Chen, N.; Tucker, C.; Coombs, S.; Jones, D.L.; Liu, C. Distant touch hydrodynamic imaging with an artificial lateral line. Proc. Natl. Acad. Sci. USA 2006, 103, 18891–18895. [Google Scholar] [CrossRef]
- Yang, Y.; Nguyen, N.; Chen, N.; Lockwood, M.; Tucker, C.; Hu, H.; Bleckmann, H.; Liu, C.; Jones, D.L. Artificial lateral line with biomimetic neuromasts to emulate fish sensing. Bioinspir. Biomim. 2010, 5, 016001. [Google Scholar] [CrossRef]
- Strokina, N.; Kämäräinen, J.; Tuhtan, J.A.; Fuentes-Pérez, J.F.; Kruusmaa, M. Joint Estimation of Bulk Flow Velocity and Angle Using a Lateral Line Probe. IEEE Trans. Instrum. Meas. 2016, 65, 601–613. [Google Scholar] [CrossRef]
- Xu, Y.; Mohseni, K. A Pressure Sensory System Inspired by the Fish Lateral Line: Hydrodynamic Force Estimation and Wall Detection. IEEE J. Ocean. Eng. 2017, 42, 532–543. [Google Scholar] [CrossRef]
- Sengupta, D.; Chen, S.H.; Kottapalli, A.G.P. Nature-Inspired Self-Powered Sensors and Energy Harvesters. In Self-Powered and Soft Polymer MEMS/NEMS Devices; Springer: Cham, Swizerland, 2019; pp. 61–81. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, X.; Shen, Z.; Xie, T.; Miao, J. A New Self-Powered Sensor Using the Radial Field Piezoelectric Diaphragm in d33 Mode for Detecting Underwater Disturbances. Sensors 2019, 19, 962. [Google Scholar] [CrossRef]
- Kruusmaa, M.; Fiorini, P.; Megill, W.; de Vittorio, M.; Akanyeti, O.; Visentin, F.; Chambers, L.; El Daou, H.; Fiazza, M.; Ježov, J.; et al. FILOSE for Svenning: A Flow Sensing Bioinspired Robot. IEEE Robot. Autom. Mag. 2014, 21, 51–62. [Google Scholar] [CrossRef]
- DeVries, L.; Lagor, F.D.; Lei, H.; Tan, X.; Paley, D.A. Distributed flow estimation and closed-loop control of an underwater vehicle with a multi-modal artificial lateral line. Bioinspir. Biomim. 2015, 10, 025002. [Google Scholar] [CrossRef] [PubMed]
- Ježov, J.; Akanyeti, O.; Chambers, L.D.; Kruusmaa, M. Sensing oscillations in unsteady flow for better robotic swimming efficiency. In Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Seoul, Korea, 14–17 October 2012; pp. 91–96. [Google Scholar] [CrossRef]
- Yen, W.; Sierra, D.M.; Guo, J. Controlling a Robotic Fish to Swim Along a Wall Using Hydrodynamic Pressure Feedback. IEEE J. Ocean. Eng. 2018, 43, 369–380. [Google Scholar] [CrossRef]
- Krieg, M.; Nelson, K.; Mohseni, K. Distributed sensing for fluid disturbance compensation and motion control of intelligent robots. Nat. Mach. Intell. 2019, 1, 216–224. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, M.; Zheng, J.; Tian, R.; Xiong, M.; Xie, G. Artificial lateral line based longitudinal separation sensing for two swimming robotic fish with leader-follower formation. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019; pp. 2539–2544. [Google Scholar] [CrossRef]
- Ćurčić-Blake, B.; van Netten, S.M. Source location encoding in the fish lateral line canal. J. Exp. Biol. 2006, 209, 1548–1559. [Google Scholar] [CrossRef]
- Ristroph, L.; Liao, J.C.; Zhang, J. Lateral Line Layout Correlates with the Differential Hydrodynamic Pressure on Swimming Fish. Phys. Rev. Lett. 2015, 114, 018102. [Google Scholar] [CrossRef]
- Zhang, F.; Lagor, F.; Yeo, D.; Washington, P.; Paley, D. Distributed Flow Sensing Using Bayesian Estimation for a Flexible Fish Robot. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015. [Google Scholar] [CrossRef]
- Ahrari, A.; Lei, H.; Sharif, M.A.; Deb, K.; Tan, X. Design optimization of artificial lateral line system under uncertain conditions. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 1807–1814. [Google Scholar] [CrossRef]
- Ahrari, A.; Lei, H.; Sharif, M.A.; Deb, K.; Tan, X. Reliable underwater dipole source characterization in 3D space by an optimally designed artificial lateral line system. Bioinspir. Biomim. 2017, 12, 036010. [Google Scholar] [CrossRef]
- Boulogne, L.H.; Wolf, B.J.; Wiering, M.A.; van Netten, S.M. Performance of neural networks for localizing moving objects with an artificial lateral line. Bioinspir. Biomim. 2017, 12, 056009. [Google Scholar] [CrossRef]
- Colvert, B.; Alsalman, M.; Kanso, E. Classifying vortex wakes using neural networks. Bioinspir. Biomim. 2018, 13, 025003. [Google Scholar] [CrossRef]
- Wolf, B.J.; Pirih, P.; Kruusmaa, M.; Van Netten, S.M. Shape Classification Using Hydrodynamic Detection via a Sparse Large-Scale 2D-Sensitive Artificial Lateral Line. IEEE Access 2020, 8, 11393–11404. [Google Scholar] [CrossRef]
- Wolf, B.; van de Wolfshaar, J.; van Netten, S. Three-dimensional multi-source localization of underwater objects using convolutional neural networks for artificial lateral lines. J. R. Soc. Interface 2020, 17, 20190616. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Lv, Z.; Zeng, H.; Bessaih, H.; Sun, B. Sensor placement optimization in the artificial lateral line using optimal weight analysis combining feature distance and variance evaluation. ISA Trans. 2019, 86, 110–121. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Papadimitriou, C.; Lüthen, N.; Arampatzis, G.; Koumoutsakos, P. Optimal sensor placement for artificial swimmers. J. Fluid Mech. 2020, 884, A24. [Google Scholar] [CrossRef]
- Kern, S.; Koumoutsakos, P. Simulations of optimized anguilliform swimming. J. Exp. Biol. 2006, 209, 4841–4857. [Google Scholar] [CrossRef]
- Gazzola, M.; Chatelain, P.; van Rees, W.M.; Koumoutsakos, P. Simulations of single and multiple swimmers with non-divergence free deforming geometries. J. Comput. Phys. 2011, 230, 7093–7114. [Google Scholar] [CrossRef]
- Kern, S.; Chatelain, P.; Koumoutsakos, P. Modeling, Simulation and Optimization of Anguilliform Swimmers. In Bio-Mechanisms of Swimming and Flying: Fluid Dynamics, Biomimetic Robots, and Sports Science; Springer: Berlin/Heidelberg, Germany, 2008; p. 167. [Google Scholar]
- Carling, J.; Williams, T.L.; Bowtell, G. Self-propelled anguilliform swimming: Simultaneous solution of the two-dimensional Navier–Stokes equations and Newton’s laws of motion. J. Exp. Biol. 1998, 201, 3143–3166. [Google Scholar]
- Angot, P.; Bruneau, C.H.; Fabrie, P. A penalization method to take into account obstacles in incompressible viscous flows. Numer. Math. 1999, 81, 497–520. [Google Scholar] [CrossRef]
- Coquerelle, M.; Cottet, G.H. A vortex level set method for the two-way coupling of an incompressible fluid with colliding rigid bodies. J. Comput. Phys. 2008, 227, 9121–9137. [Google Scholar] [CrossRef]
- Towers, J.D. Finite difference methods for approximating Heaviside functions. J. Comput. Phys. 2009, 228, 3478–3489. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical Solution of the Navier–Stokes Equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Novati, G.; Verma, S.; Alexeev, D.; Rossinelli, D.; van Rees, W.M.; Koumoutsakos, P. Synchronised Swimming of Two Fish. arXiv 2016, arXiv:1610.04248. [Google Scholar]
- Kroese, A.B.; Schellart, N.A. Velocity- and acceleration-sensitive units in the trunk lateral line of the trout. J. Neurophysiol. 1992, 68, 2212–2221. [Google Scholar] [CrossRef] [PubMed]
- Bleckmann, H.; Zelick, R. Lateral line system of fish. Integr. Zool. 2009, 4, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberl, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020. [Google Scholar] [CrossRef] [PubMed]
- Dierckx, P. An algorithm for smoothing, differentiation and integration of experimental data using spline functions. J. Comput. Appl. Math. 1975, 1, 165–184. [Google Scholar] [CrossRef]
- Huan, X.; Marzouk, Y.M. Simulation-based optimal Bayesian experimental design for nonlinear systems. J. Comput. Phys. 2013, 232, 288–317. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Lombaert, G. The effect of prediction error correlation on optimal sensor placement in structural dynamics. Mech. Syst. Signal Process. 2012, 28, 105–127. [Google Scholar] [CrossRef]
- Simoen, E.; Papadimitriou, C.; Lombaert, G. On prediction error correlation in Bayesian model updating. J. Sound Vib. 2013, 332, 4136–4152. [Google Scholar] [CrossRef]
- Ryan, K.J. Estimating Expected Information Gains for Experimental Designs With Application to the Random Fatigue-Limit Model. J. Comput. Graph. Stat. 2003, 12, 585–603. [Google Scholar] [CrossRef]
- Papadimitriou, D.I.; Papadimitriou, C. Optimal sensor placement for the estimation of turbulence model parameters in CFD. Int. J. Uncertain. Quant. 2015, 5, 545–568. [Google Scholar] [CrossRef]
- Papadimitriou, C. Optimal sensor placement methodology for parametric identification of structural systems. J. Sound Vib. 2004, 278, 923–947. [Google Scholar] [CrossRef]

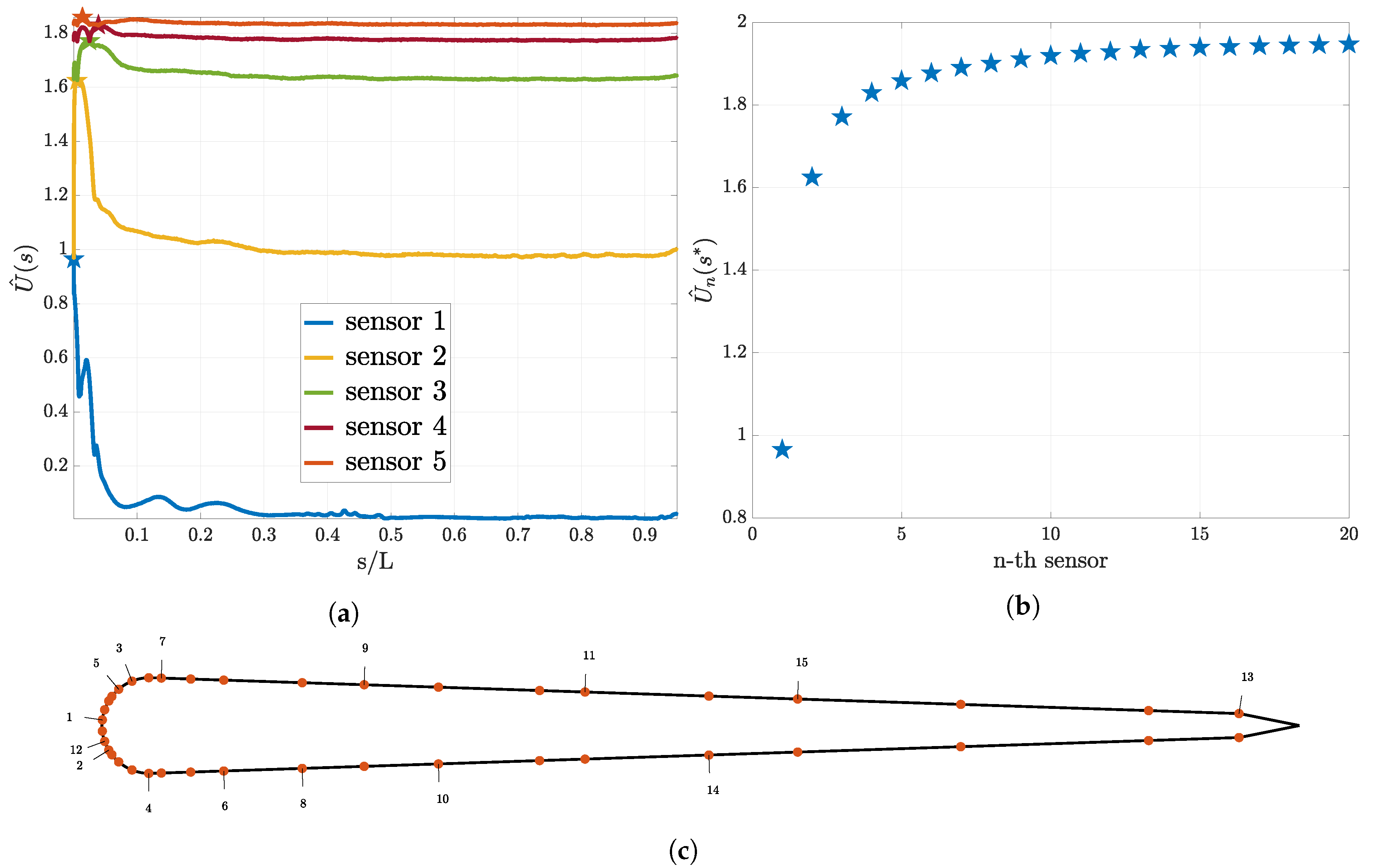
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, P.; Arampatzis, G.; Novati, G.; Verma, S.; Papadimitriou, C.; Koumoutsakos, P. Optimal Flow Sensing for Schooling Swimmers. Biomimetics 2020, 5, 10. https://doi.org/10.3390/biomimetics5010010
Weber P, Arampatzis G, Novati G, Verma S, Papadimitriou C, Koumoutsakos P. Optimal Flow Sensing for Schooling Swimmers. Biomimetics. 2020; 5(1):10. https://doi.org/10.3390/biomimetics5010010
Chicago/Turabian StyleWeber, Pascal, Georgios Arampatzis, Guido Novati, Siddhartha Verma, Costas Papadimitriou, and Petros Koumoutsakos. 2020. "Optimal Flow Sensing for Schooling Swimmers" Biomimetics 5, no. 1: 10. https://doi.org/10.3390/biomimetics5010010
APA StyleWeber, P., Arampatzis, G., Novati, G., Verma, S., Papadimitriou, C., & Koumoutsakos, P. (2020). Optimal Flow Sensing for Schooling Swimmers. Biomimetics, 5(1), 10. https://doi.org/10.3390/biomimetics5010010





