Biomechanical Modeling of Prosthetic Mesh and Human Tissue Surrogate Interaction
Abstract
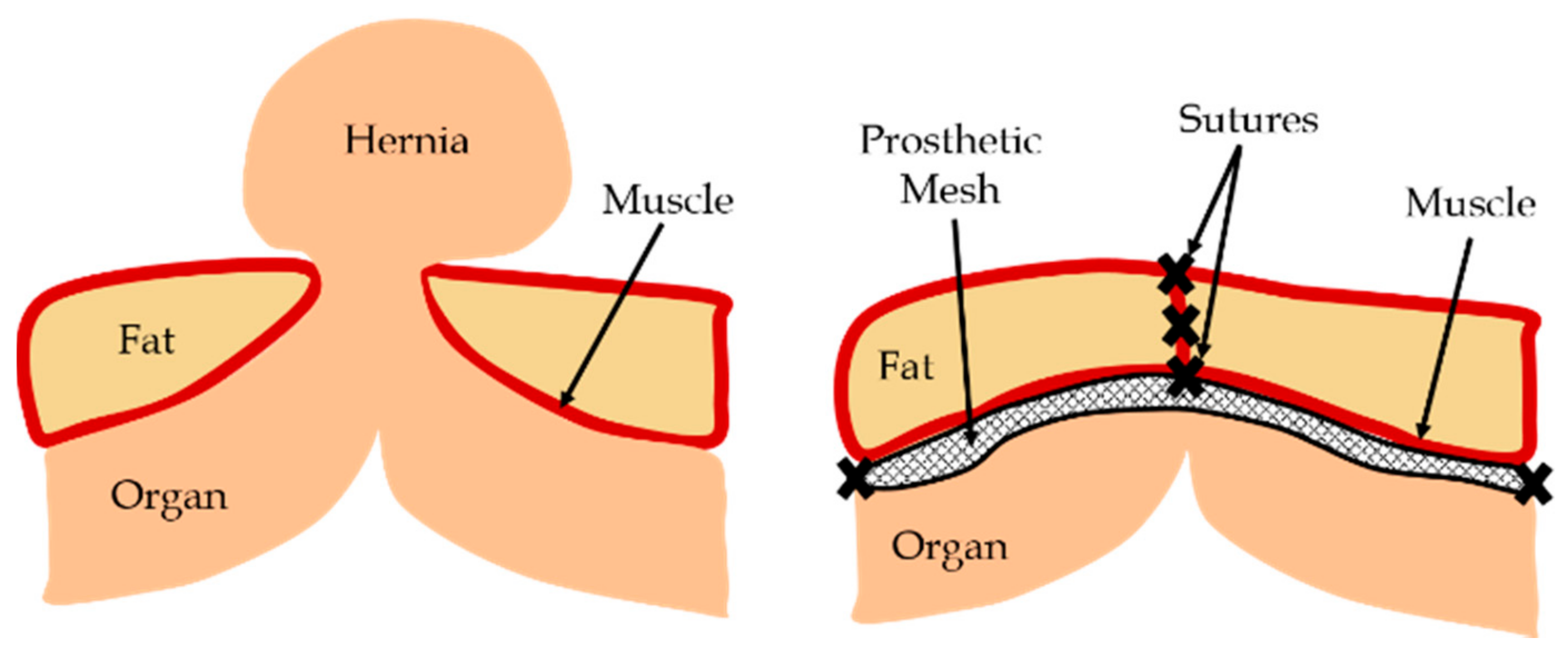
:1. Introduction
2. Materials and Methods
2.1. Tissue Phantom Fabrication
2.2. Experimental Testing
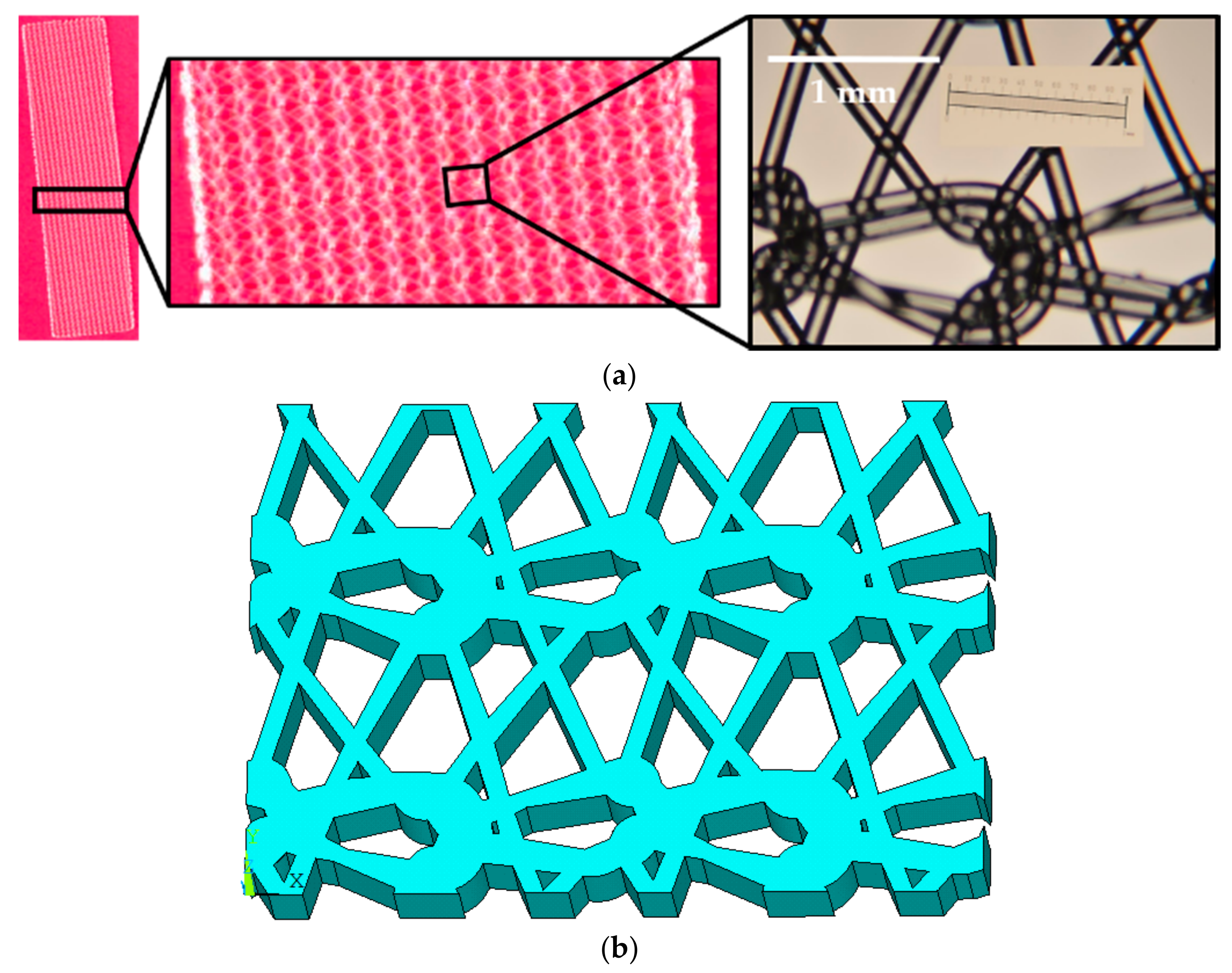
2.3. Finite Element Modeling of Mesh, Tissue, and Sutures
2.4. Material Modeling
2.5. Data Analysis
3. Results and Discussion
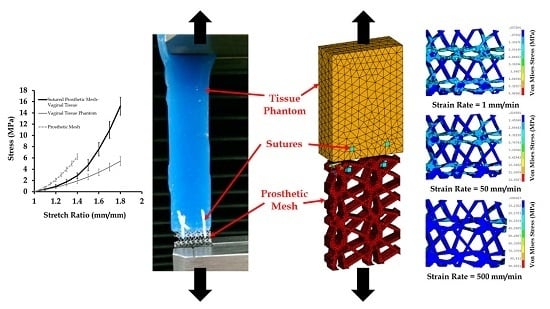
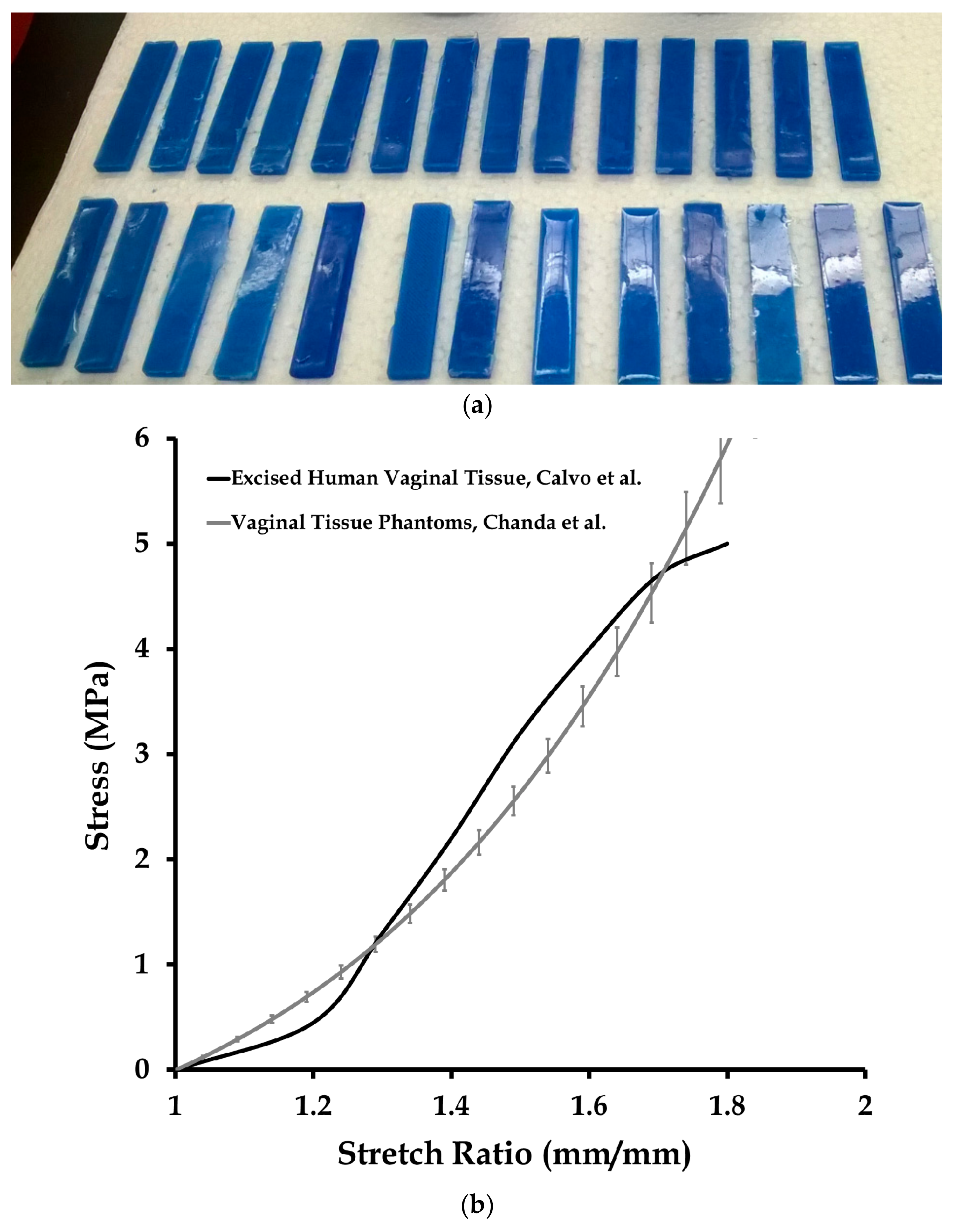
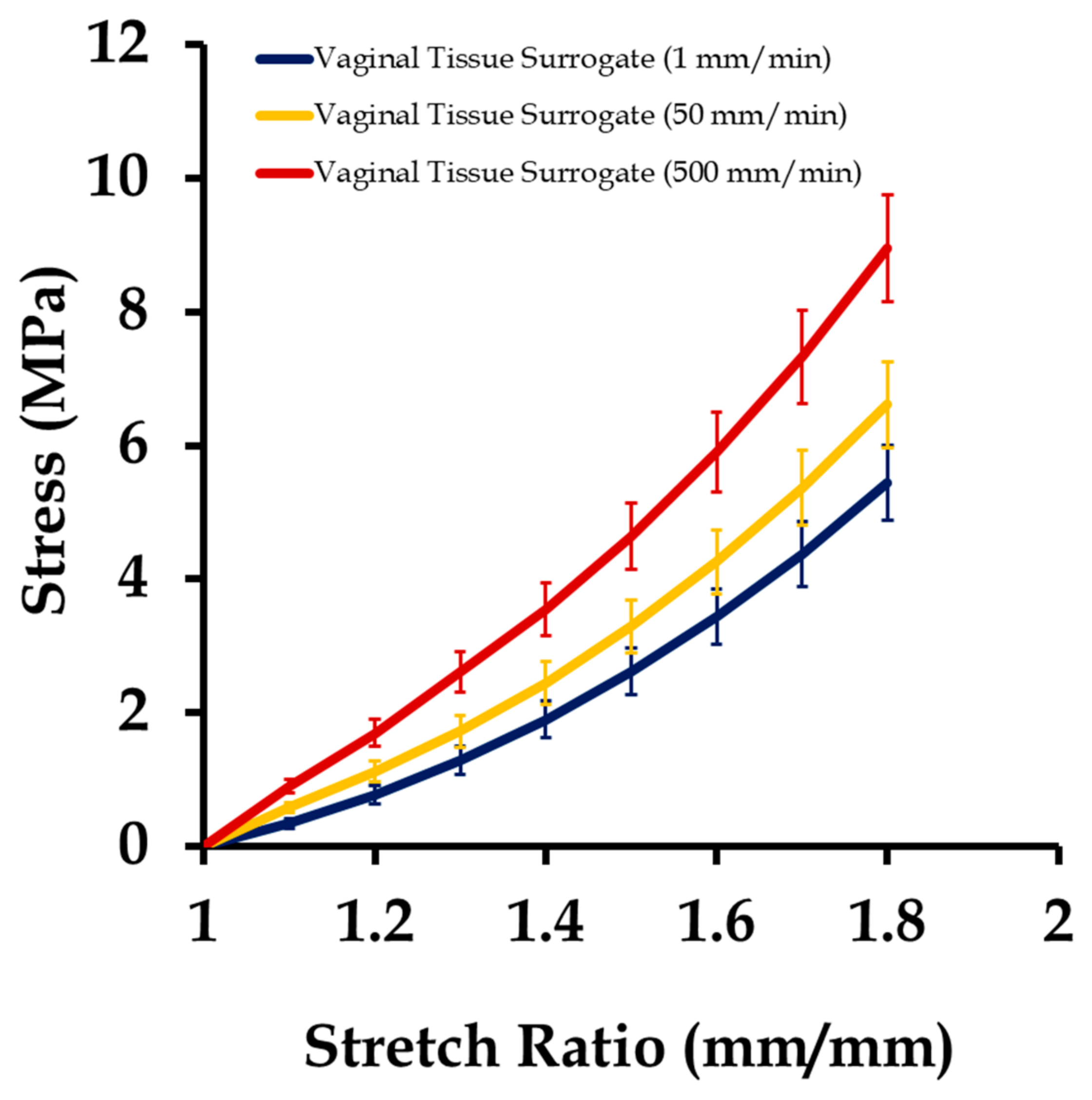
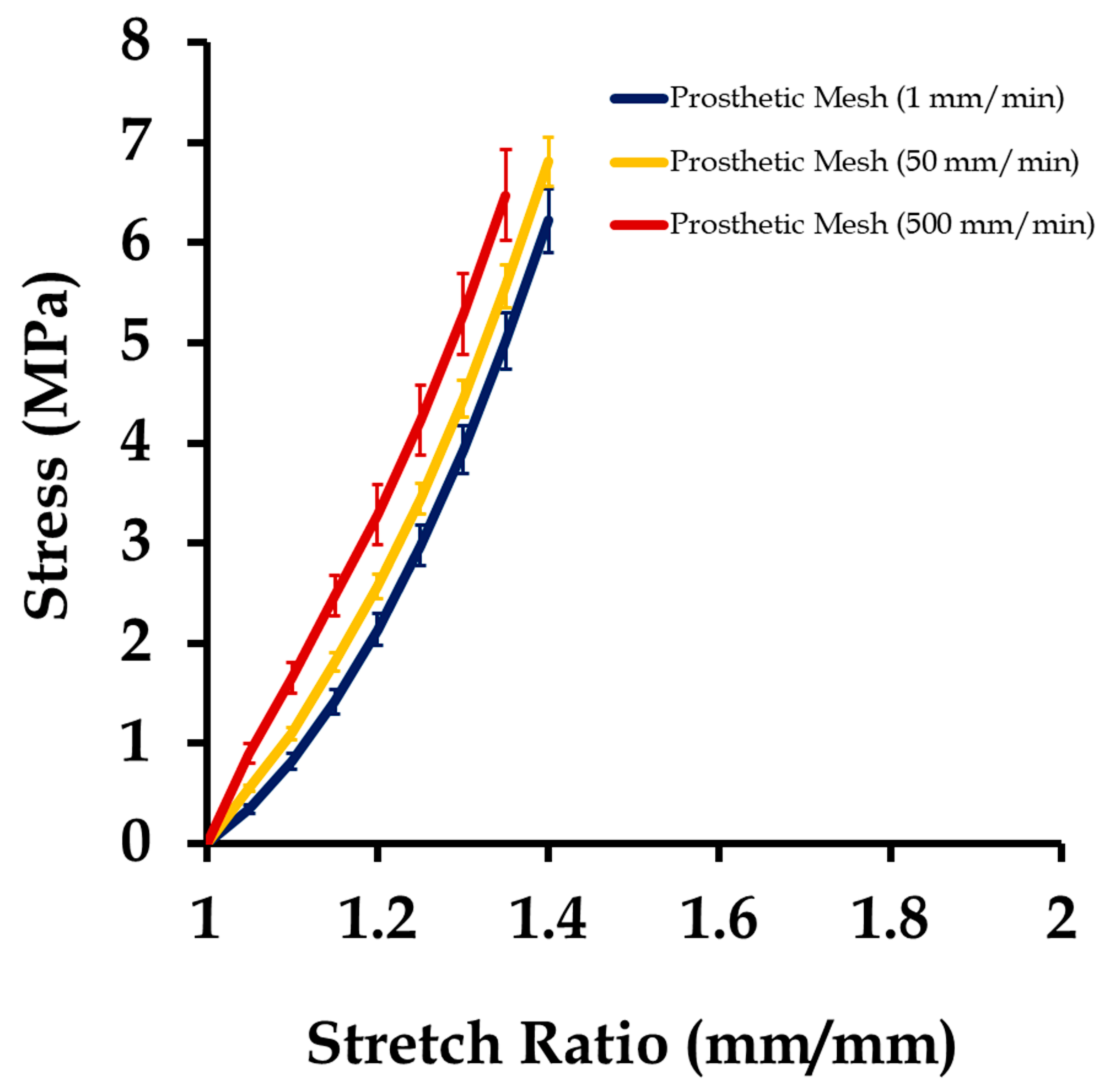
3.1. Mechanical Testing and Characterization of Vaginal Tissue Phantoms and Prosthetic Mesh
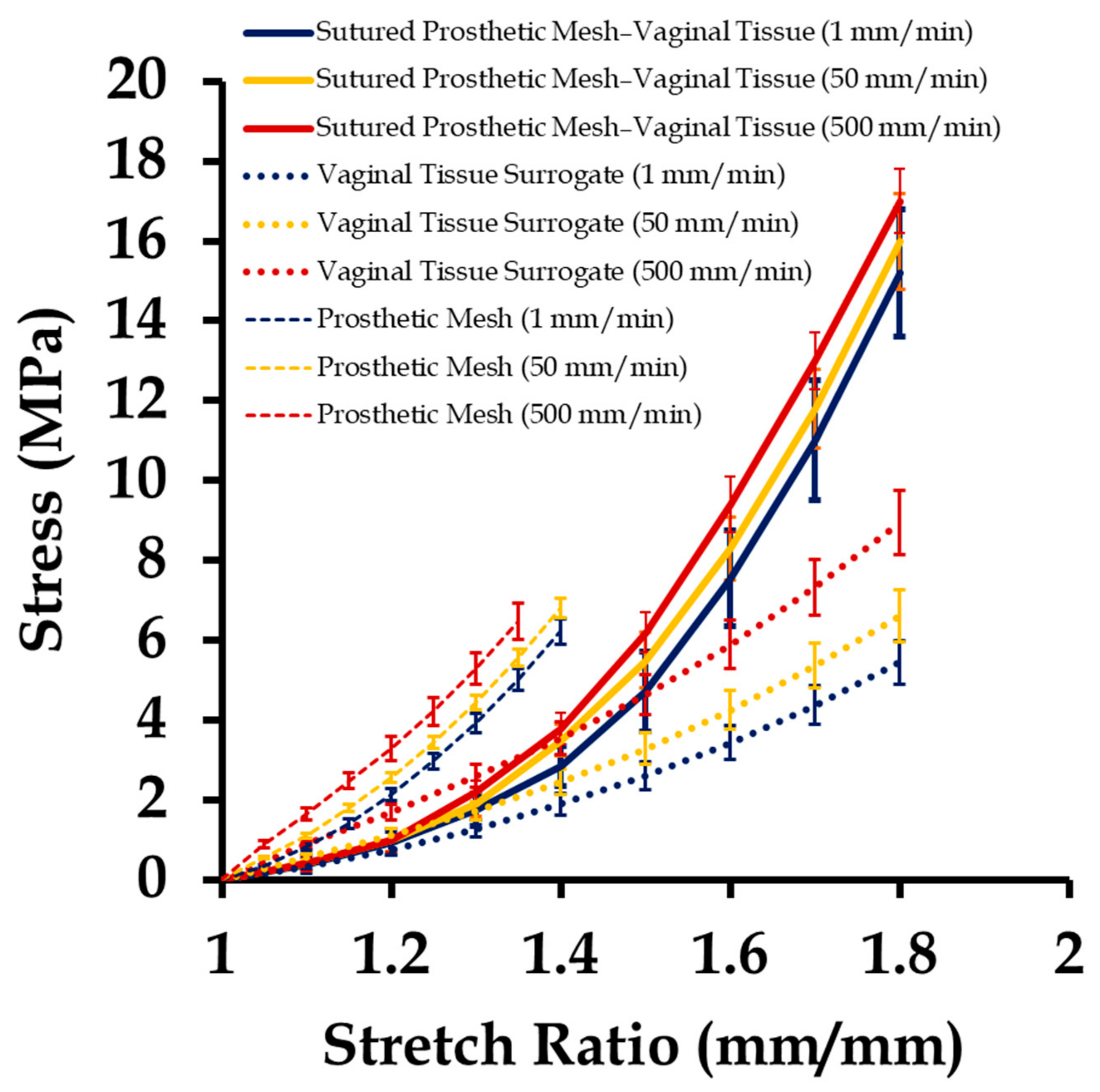
3.2. Mechanical Testing of Sutured Prosthetic Mesh–Vaginal Tissue Phantoms
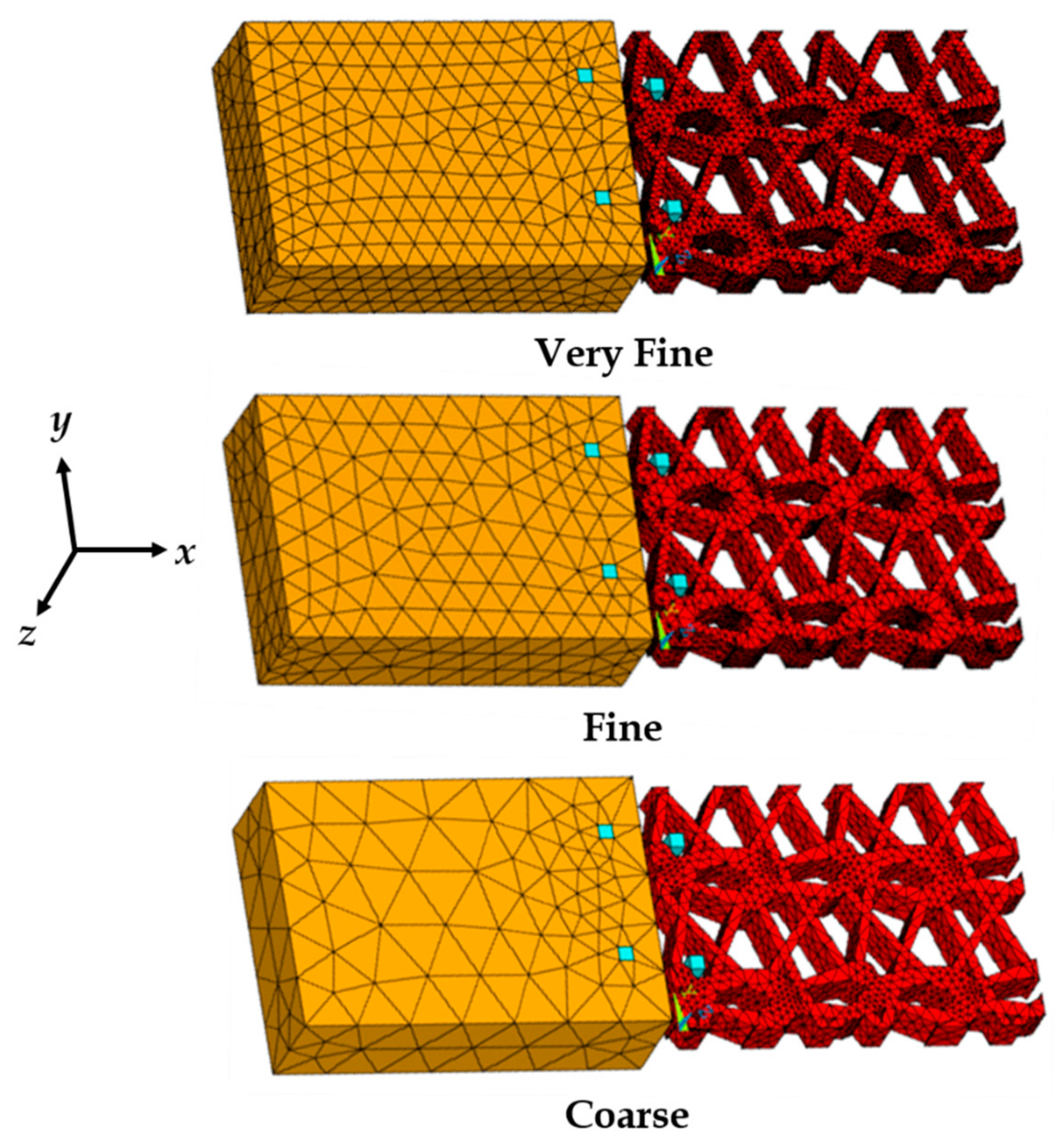
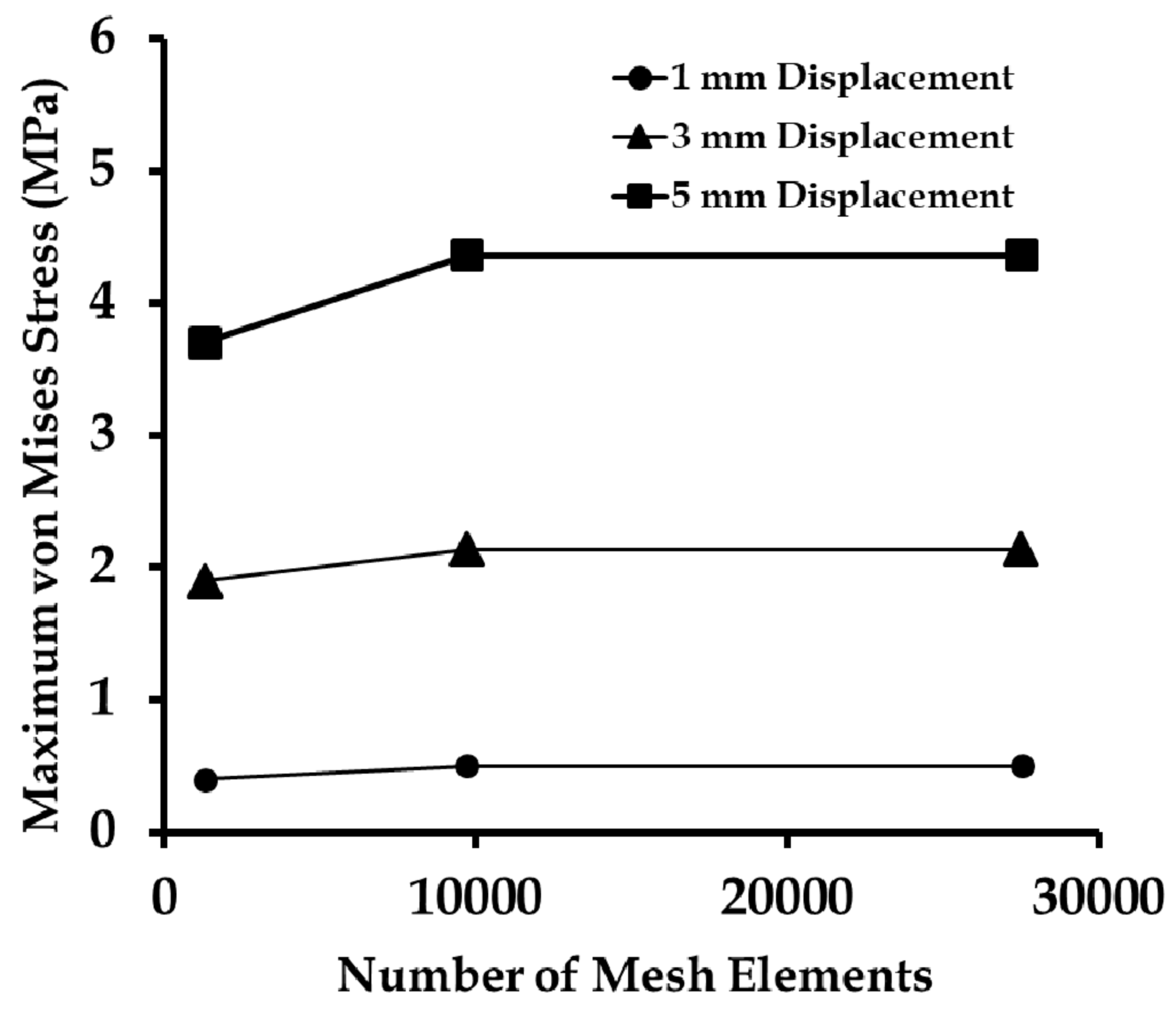
3.3. Finite Element Mesh Convergence Results
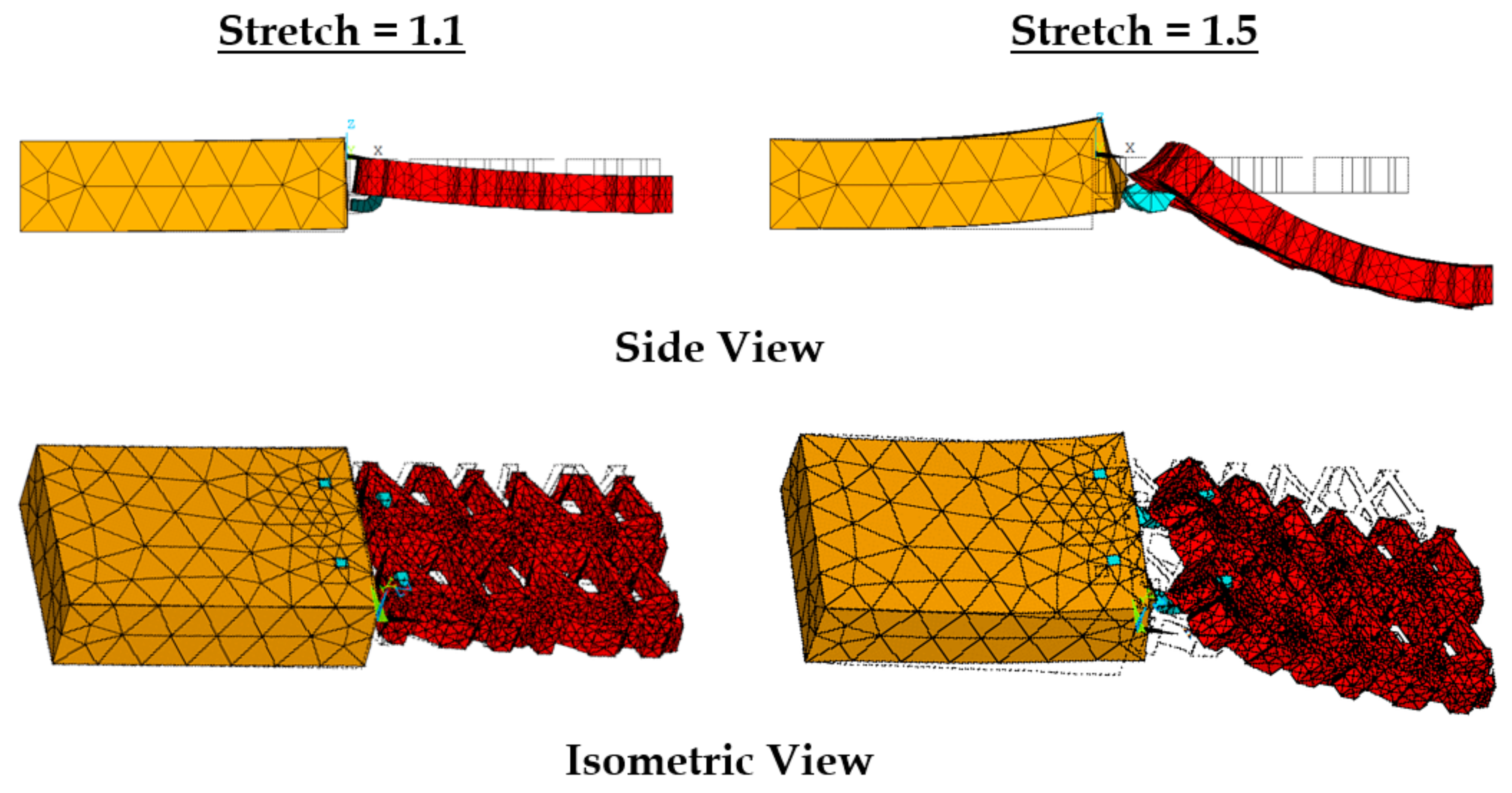
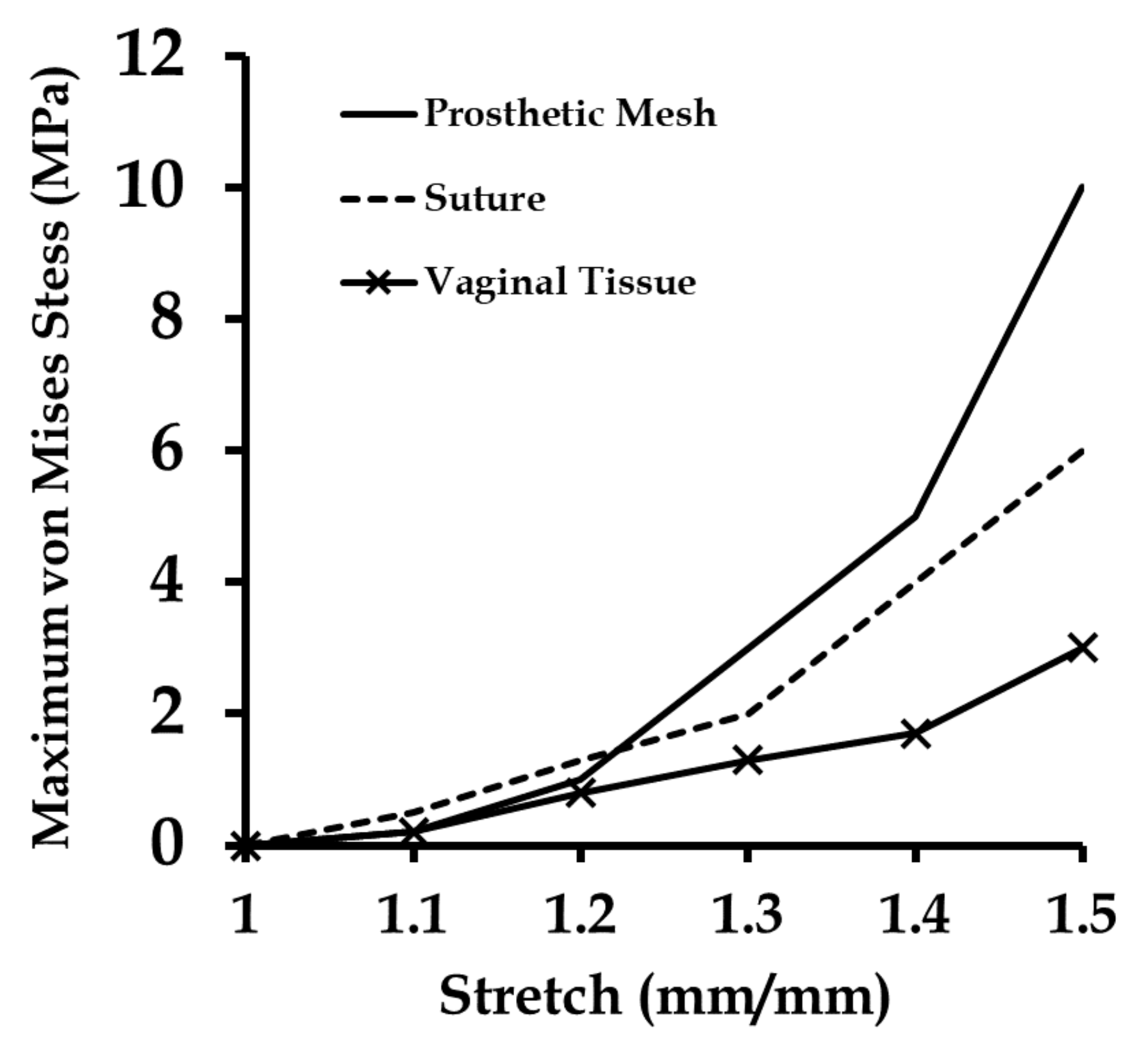
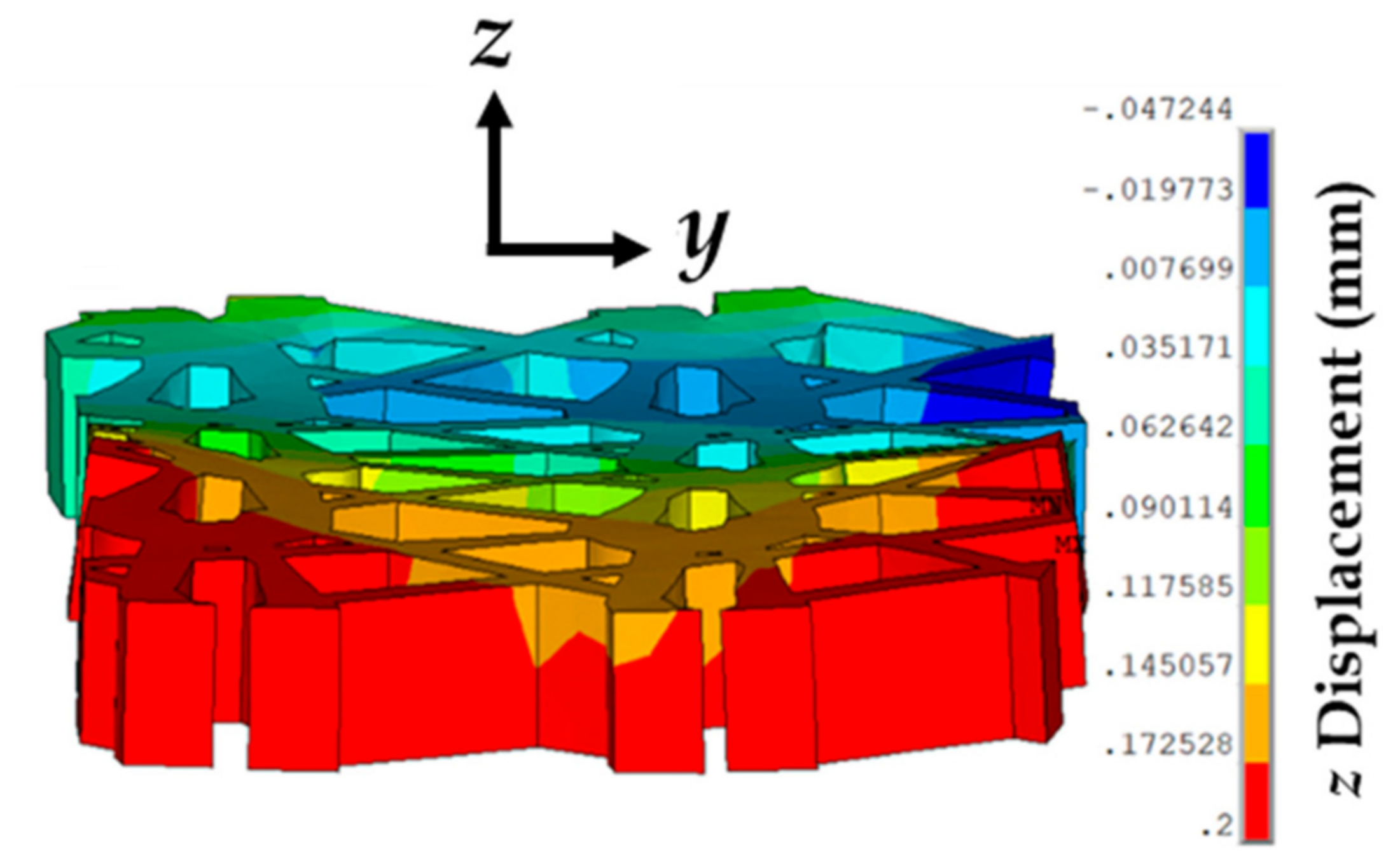
3.4. Effect of Varying Strains on the Sutured Prosthetic Mesh–Vaginal Tissue Phantom Finite Element Model
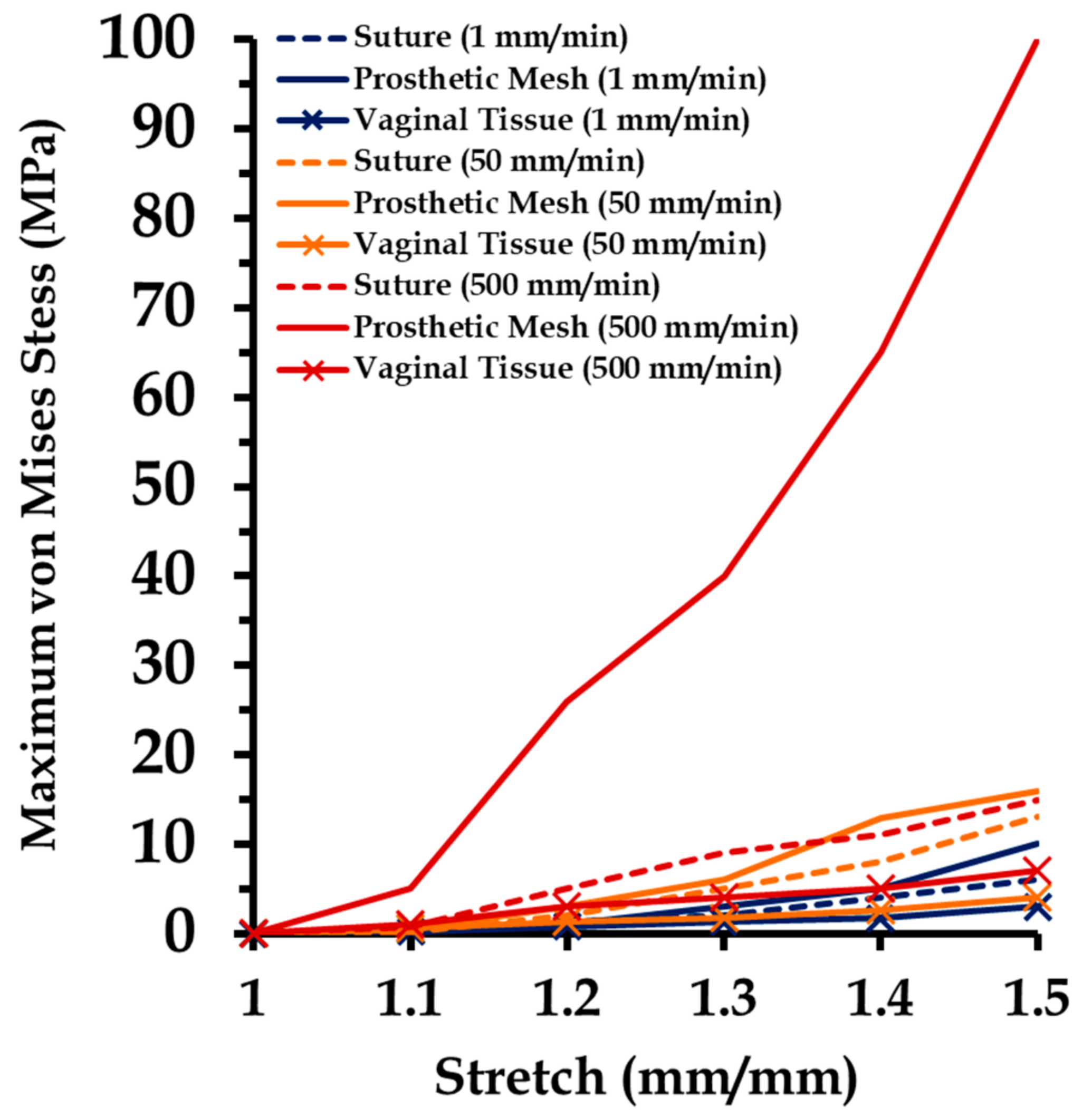
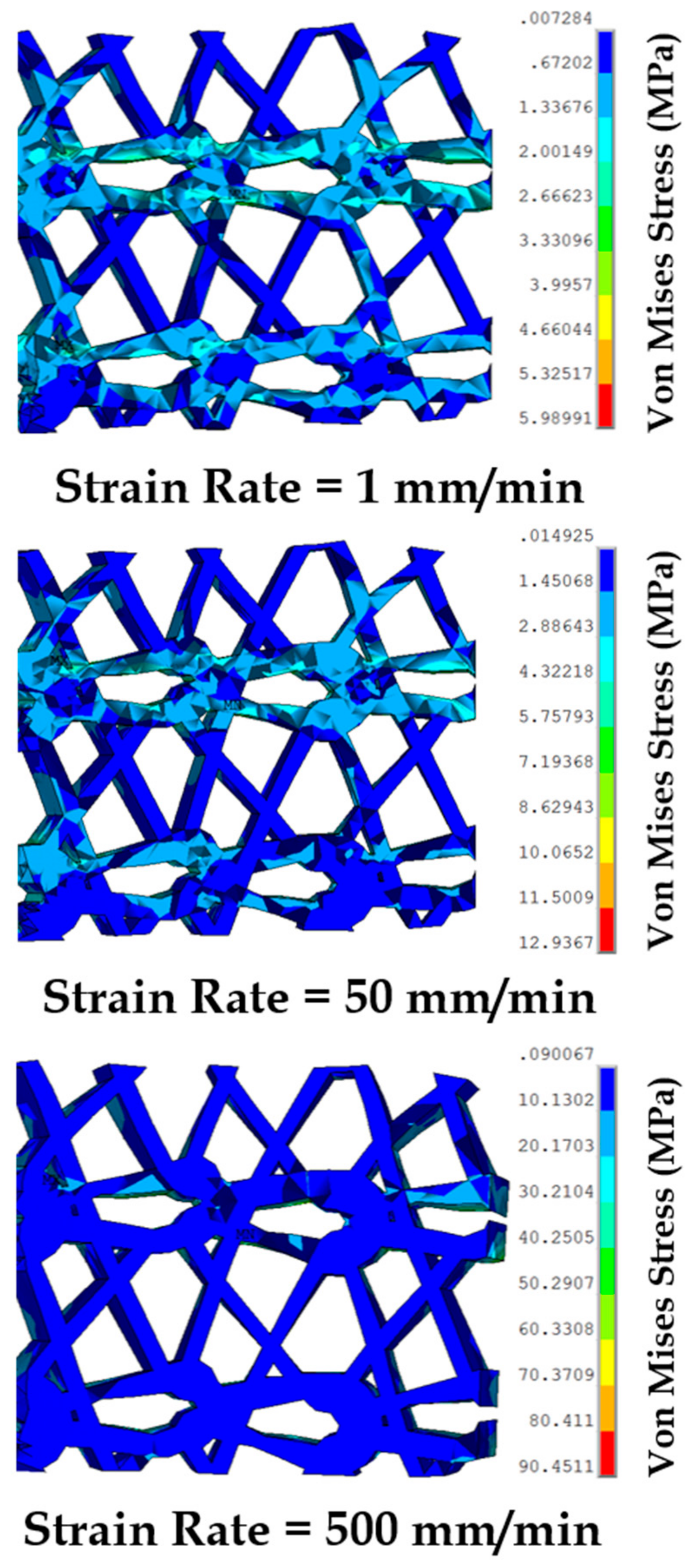
3.5. Effect of Varying Strain Rates on Sutured Prosthetic Mesh–Vaginal Tissue Phantom Finit Element Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gilbert, A.I. An anatomic and functional classification for the diagnosis and treatment of inguinal hernia. Am. J. Surg. 1989, 157, 331–333. [Google Scholar] [CrossRef]
- Milligan, L. Types of hernia. In Handbook of Clinical Anaesthesia 3E; Churchill Livingstone: London, UK, 2011; p. 443. [Google Scholar]
- Chanda, A.; Unnikrishnan, V.; Roy, S.; Richter, H.E. Computational modeling of the female pelvic support structures and organs to understand the mechanism of pelvic organ prolapse: A review. Appl. Mech. Rev. 2015, 67, 040801. [Google Scholar] [CrossRef]
- Baessler, K.; Hewson, A.D.; Tunn, R.; Schuessler, B.; Maher, C.F. Severe mesh complications following intravaginal slingplasty. Obstet. Gynecol. 2005, 106, 713–716. [Google Scholar] [CrossRef] [PubMed]
- Gerullis, H. Autologous Plasma Coating—A New Approach for Improvement of the Biocompatibility of Mesh Implants. Ph.D. Thesis, University of Szeged, Szeged, Hungary, 2014. [Google Scholar]
- Bazi, T.; Ammouri, A.; Hamade, R. Effect of the Stretch Rate During Uniaxial Testing on the Mechanical Properties of Prolene®. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 559–563. [Google Scholar]
- Röhrnbauer, B. Mechanical Characterization and Modeling of Prosthetic Meshes. Ph.D. Thesis, Eidgenössische Technische Hochschule ETH Zürich, Zürich, Switzerland, 2013. [Google Scholar]
- Bazi, T.; Ammouri, A.H.; Hamade, R.F. On the relevance of uniaxial tensile testing of urogynecological prostheses: The effect of displacement rate. Int. Urogynecol. J. 2013, 24, 161–167. [Google Scholar] [CrossRef] [PubMed]
- Abramowitch, S.D.; Feola, A.; Jallah, Z.; Moalli, P.A. Tissue mechanics, animal models, and pelvic organ prolapse: A review. Eur. J. Obstet. Gynecol. Reprod. Biol. 2009, 144, S146–S158. [Google Scholar] [CrossRef] [PubMed]
- Feola, A.; Abramowitch, S.; Jallah, Z.; Stein, S.; Barone, W.; Palcsey, S.; Moalli, P. Deterioration in biomechanical properties of the vagina following implantation of a high-stiffness prolapse mesh. BJOG Int. J. Obstet. Gynaecol. 2013, 120, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Siniscalchi, R.; Palma, P.; Riccetto, C.; Maciel, L.; Ens, G.; Del Fabbro, I. Biomechanical effects of the inclusion of holes to facilitate the integration in monofilament polypropylene meshes: An experimental study. Actas Urol. Esp. 2011, 35, 599–604. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Upchurch, W. Review of recent advances in vaginal mesh tissue interaction. Res. Dev. Mater. Sci. 2018, 5, RDMS.000601. [Google Scholar] [CrossRef]
- Chanda, A. Biofidelic Soft Composites—Experimental and Computational Modeling. Ph.D. Thesis, University of Alabama Libraries, Tuscaloosa, AL, USA, 2017. [Google Scholar]
- Chanda, A.; Flynn, Z.; Unnikrishnan, V. Biomechanical characterization of normal and prolapsed vaginal tissue surrogates. J. Mech. Med. Biol. 2018, 18, 1750100. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Flynn, Z. Biofidelic Human Skin Simulant. U.S. Patent Application No. 62/189,504, 7 July 2015. [Google Scholar]
- Chanda, A.; Unnikrishnan, V.; Flynn, Z.; Lackey, K. Experimental study on tissue phantoms to understand the effect of injury and suturing on human skin mechanical properties. Proc. Inst. Mech. Eng Part H J. Eng. Med. 2017, 231, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A. Biomechanical modeling of human skin tissue surrogates. Biomimetics 2018, 3, 18. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Lackey, K. Biofidelic Conductive Synthetic Skin Composites. In Proceedings of the 32nd Annual American Society for Composites Technical Conference, West Lafayette, IN, USA, 22–25 October 2017. [Google Scholar]
- Chanda, A.; Callaway, C. Tissue anisotropy modeling using soft composite materials. Appl. Bionics Biomech. 2018, 2018, 4838157. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Curry, K. Patient-specific biofidelic human coronary artery surrogates. J. Mech. Med. Biol. 2018, 18, 1890049. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V. Customized Insoles for Diabetic and Pressure Ulcers. U.S. Patent US20180008000A1, 11 January 2018. [Google Scholar]
- Calvo, B.; Pena, E.; Martins, P.; Mascarenhas, T.; Doblare, M.; Natal Jorge, R.; Ferreira, A. On modelling damage process in vaginal tissue. J. Biomech. 2009, 42, 642–651. [Google Scholar] [CrossRef] [PubMed]
- Nienhuijs, S.; Van Oort, I.; Keemers-Gels, M.; Strobbe, L.; Rosman, C. Randomized trial comparing the Prolene® Hernia System, mesh plug repair and Lichtenstein method for open inguinal hernia repair. Br. J. Surg. 2005, 92, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Milani, R.; Salvatore, S.; Soligo, M.; Pifarotti, P.; Meschia, M.; Cortese, M. Functional and anatomical outcome of anterior and posterior vaginal prolapse repair with prolene mesh. BJOG Int. J. Obstet. Gynaecol. 2005, 112, 107–111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morch, A.; Pouseele, B.; Doucède, G.; Witz, J.-F.; Lesaffre, F.; Lecomte-Grosbras, P.; Brieu, M.; Cosson, M.; Rubod, C. Experimental study of the mechanical behavior of an explanted mesh: The influence of healing. J. Mech. Behav. Biomed. Mater. 2017, 65, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V. A realistic 3D computational model of the closure of skin wound with interrupted sutures. J. Mech. Med. Biol. 2017, 17, 1750025. [Google Scholar] [CrossRef]
- Stack, A.M.; Wiley, J.F. Closure of Skin Wounds with Sutures. 2011. Available online: https://www.uptodate.com/contents/closure-of-minor-skin-wounds-with-sutures (accessed on 13 September 2018).
- Chanda, A.; Ghoneim, H. Pumping potential of a two-layer left-ventricle-like flexible-matrix-composite structure. Compos. Struct. 2015, 122, 570–575. [Google Scholar] [CrossRef]
- Ghoneim, H.; Chanda, A. Pumping Potential of a Left-Ventricle-Like Flexiblematrix-Composite Structure. In Proceedings of the 19th International Conference on Composite Materials (ICCM19), Montreal, QC, Canada, 28 July–2 August 2013; pp. 7457–7462. [Google Scholar]
- Chanda, A.; Ruchti, T.; Unnikrishnan, V. Computational modeling of wound suture: A review. IEEE Rev. Biomed. Eng. 2018, 11, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Graeter, R.; Unnikrishnan, V. Effect of blasts on subject-specific computational models of skin and bone sections at various locations on the human body. AIMS Mater. Sci. 2015, 2, 425–447. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V. Human tissue simulants for study of traumatic brain injury (TBI). In Proceedings of the 31st Annual American Society for Composites Technical Conference, Williamsburg, VA, USA, 19–22 September 2016. [Google Scholar]
- Chanda, A.; Callaway, C.; Clifton, C.; Unnikrishnan, V. Biofidelic Human Brain Tissue Surrogates; Taylor & Francis: Abingdon, UK, 2016. [Google Scholar]
- Chanda, A.; Callaway, C. Computational modeling of blast induced whole-body injury: A review. J. Med. Eng. Technol. 2018, 42, 88–104. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V.; Flynn, Z. Biofidelic Skin Simulant. U.S. Patent US20170011657A1, 12 January 2017. [Google Scholar]
- Chanda, A.; Meyer, I.; Richter, H.E.; Lockhart, M.E.; Moraes, F.R.D.; Unnikrishnan, V. Vaginal changes due to varying degrees of rectocele prolapse: A computational study. J. Biomech. Eng. 2017, 139, 101001. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V.; Richter, H.E.; Lockhart, M.E. Computational modeling of anterior and posterior pelvic organ prolapse (POP). In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 1–17 November 2016; p. V009T012A085. [Google Scholar]
- Chanda, A.; Graeter, R. Human skin-like composite materials for blast induced injury mitigation. J. Compos. Sci. 2018, 2, 44. [Google Scholar] [CrossRef]
- Martins, P.; Natal Jorge, R.; Ferreira, A. A Comparative study of several material models for prediction of hyperelastic properties: Application to silicone-rubber and soft tissues. Strain 2006, 42, 135–147. [Google Scholar] [CrossRef]
- Chanda, A.; Unnikrishnan, V.; Richter, H.E.; Lockhart, M.E. A biofidelic computational model of the female pelvic system to understand effect of bladder fill and progressive vaginal tissue stiffening due to prolapse on anterior vaginal wall. Int. J. Numer. Methods Biomed. Eng. 2016, 32. [Google Scholar] [CrossRef] [PubMed]
- Chanda, A.; Unnikrishnan, V. Effect of bladder and rectal loads on the vaginal canal and levator ani in varying pelvic floor conditions. Mech. Adv. Mater. Struct. 2017, 25, 1214–1223. [Google Scholar] [CrossRef]
- Greenwald, D.; Shumway, S.; Albear, P.; Gottlieb, L. Mechanical comparison of 10 suture materials before and after in vivo incubation. J. Surg. Res. 1994, 56, 372–377. [Google Scholar] [CrossRef] [PubMed]
- Annaidh, A.N.; Bruyère, K.; Destrade, M.; Gilchrist, M.D.; Otténio, M. Characterization of the anisotropic mechanical properties of excised human skin. J. Mech. Behav. Biomed. Mater. 2012, 5, 139–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chanda, A.; Flynn, Z.; Unnikrishnan, V. Biofidelic Vaginal Tissue Surrogate. U.S. Provisional Patent 62/263,942, 18 November 2015. [Google Scholar]
- Shergold, O.A.; Fleck, N.A.; Radford, D. The uniaxial stress versus strain response of pig skin and silicone rubber at low and high strain rates. Int. J. Impact Eng. 2006, 32, 1384–1402. [Google Scholar] [CrossRef]

| Veronda–Westmann’s Hyperelastic Model | Linear Elastic Model | ||||
|---|---|---|---|---|---|
| Material | Strain Rate (mm/min) | E (MPa) | Poisson’s Ratio | ||
| Vaginal Tissue Surrogate | 1 | 5.6 | 0.18 | - | - |
| 50 | 6.1 | 0.21 | - | - | |
| 500 | 7.4 | 0.25 | - | - | |
| Prosthetic Mesh | 1 | 10.1 | 0.30 | - | - |
| 50 | 10.5 | 0.31 | - | - | |
| 500 | 11.1 | 0.37 | - | - | |
| Suture | - | - | - | 130 | 0.23 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanda, A.; Ruchti, T.; Upchurch, W. Biomechanical Modeling of Prosthetic Mesh and Human Tissue Surrogate Interaction. Biomimetics 2018, 3, 27. https://doi.org/10.3390/biomimetics3030027
Chanda A, Ruchti T, Upchurch W. Biomechanical Modeling of Prosthetic Mesh and Human Tissue Surrogate Interaction. Biomimetics. 2018; 3(3):27. https://doi.org/10.3390/biomimetics3030027
Chicago/Turabian StyleChanda, Arnab, Tysum Ruchti, and Weston Upchurch. 2018. "Biomechanical Modeling of Prosthetic Mesh and Human Tissue Surrogate Interaction" Biomimetics 3, no. 3: 27. https://doi.org/10.3390/biomimetics3030027
APA StyleChanda, A., Ruchti, T., & Upchurch, W. (2018). Biomechanical Modeling of Prosthetic Mesh and Human Tissue Surrogate Interaction. Biomimetics, 3(3), 27. https://doi.org/10.3390/biomimetics3030027