A Planning Framework Based on Semantic Segmentation and Flipper Motions for Articulated Tracked Robot in Obstacle-Crossing Terrain
Abstract
1. Introduction
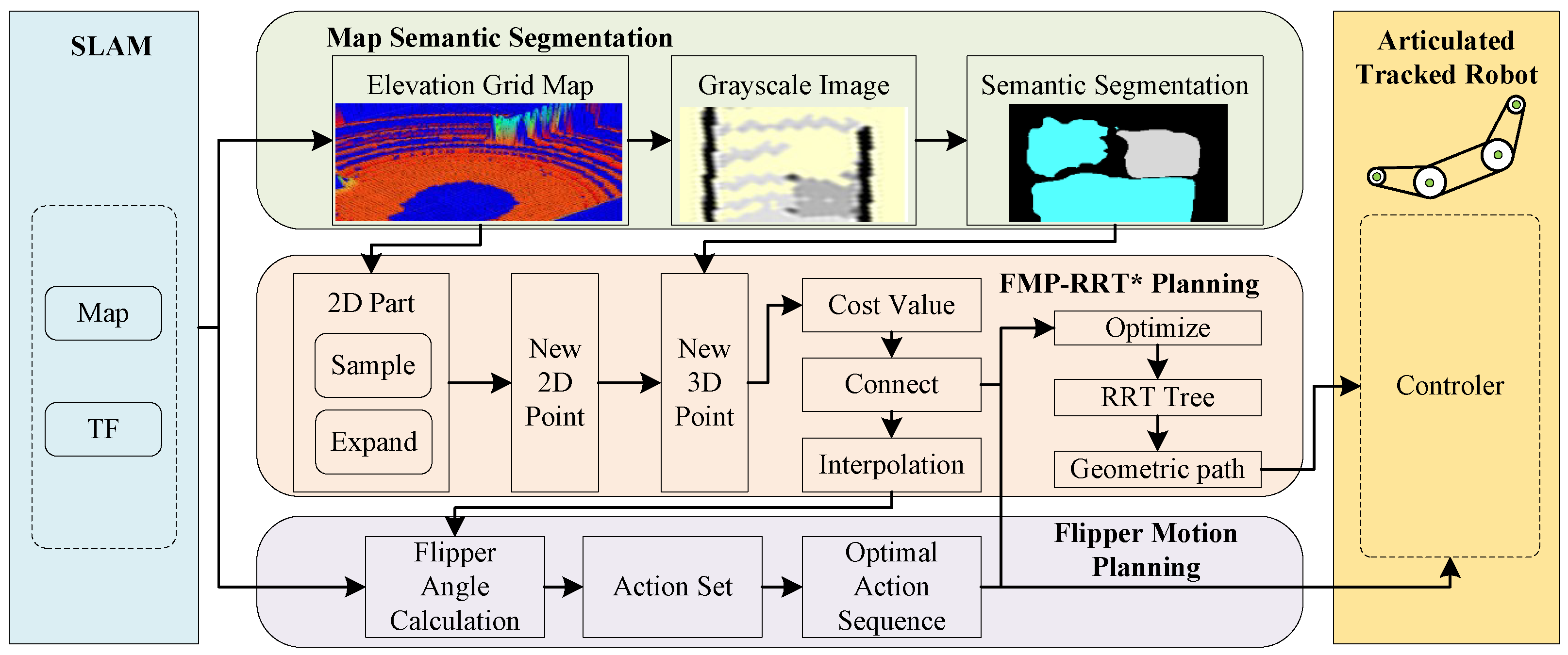
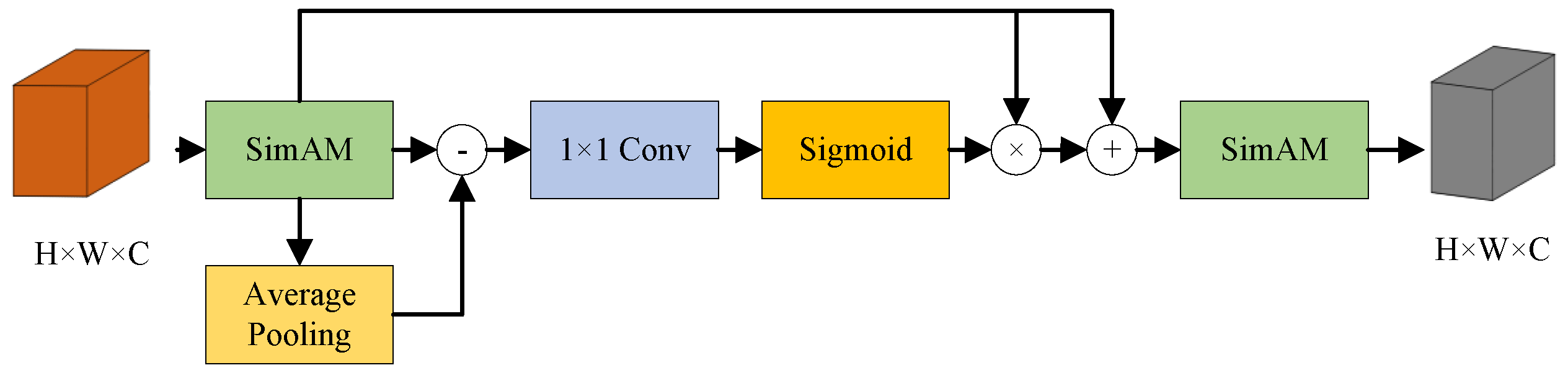
2. Map Semantic Segmentation
3. Calculation of Flipper Posture
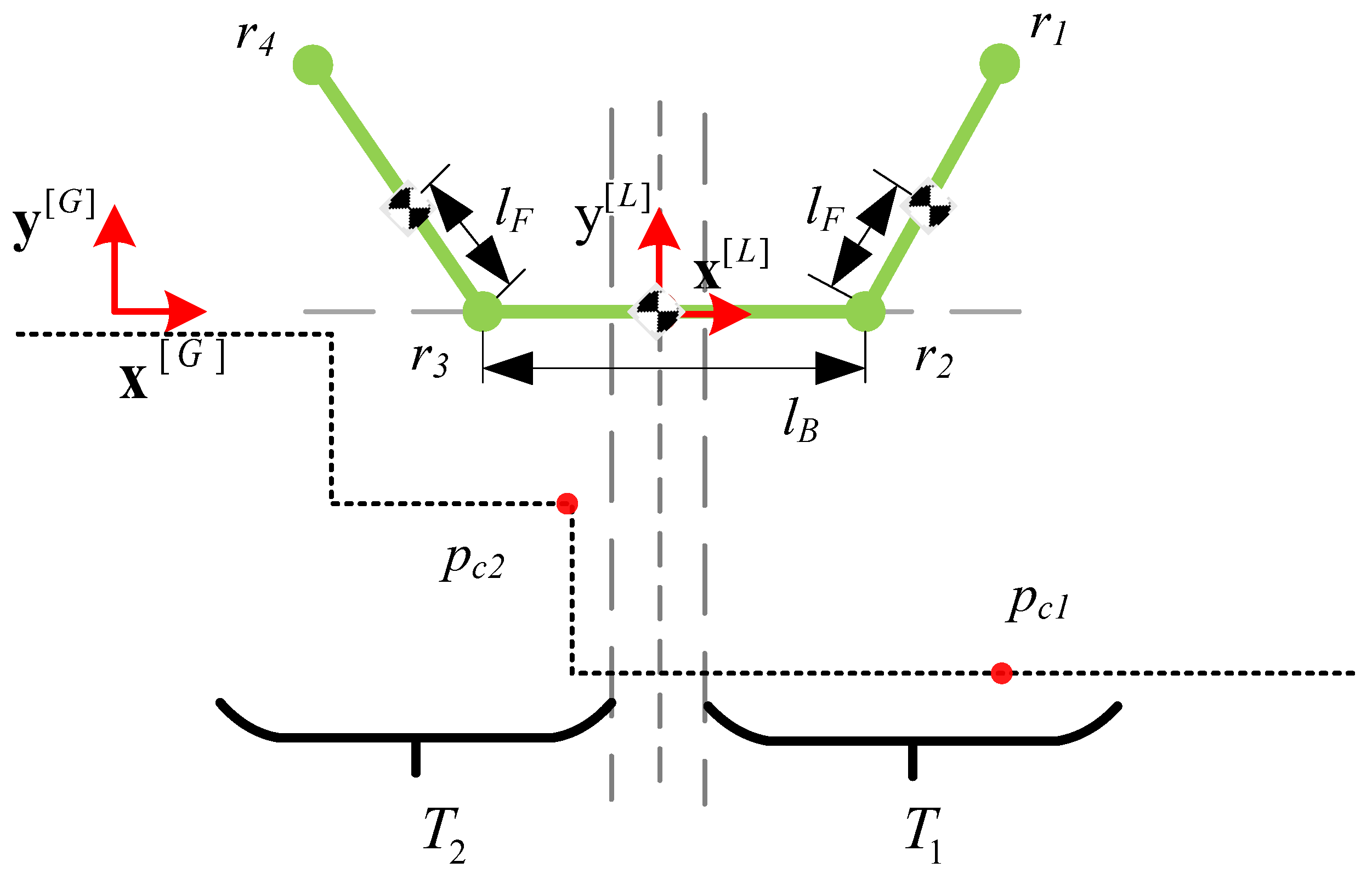
3.1. Simplified Modeling of the Robot
3.2. Model Calculation
- T: The set of points in the terrain.
- : The x-axis coordinate of the chassis center in
- : The angle of the robot’s front flipper, the counterclockwise is positive.
- : The angle of the robot’s rear flipper, the clockwise is positive.
- : Coordinate on the y-axis of the center of the chassis in .
- : The pitch angle of the robot in , positive when counterclockwise.
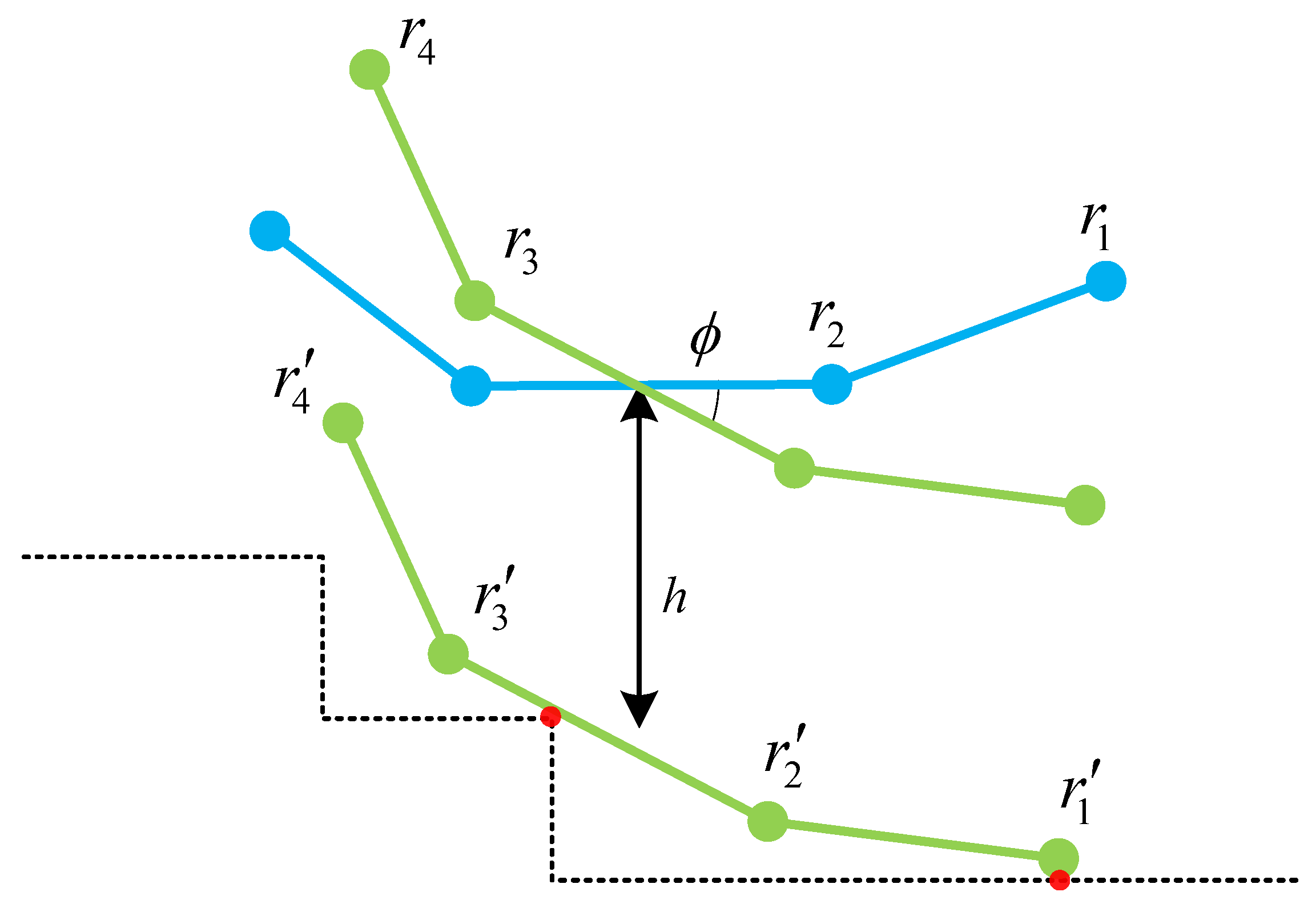
- Condition 1: The existence of more than one point of contact with the terrain on each side of the front and back of the robot’s center of mass is an essential condition for stability;
- Condition 2: The pose of the robot, determined by the contact points, must ensure that every point of the robot lies above all points of the terrain within its reachable range—a fundamental physical constraint that prevents collisions with the ground.
- is on the front flipper, and is on the rear flipper;
- is on the front flipper and is on the chassis;
- is on the chassis, and is on the rear flipper;
- is on the chassis, and is on the chassis.
4. Flipper Motion Planning RRT* Algorithm
- denotes a spatial point.
- denotes the state of the robot, including the height of the center of mass of the body z, the angle of inclination of the body , the angle of front flipper , and the angle of rear flipper .
- indicates a planar point projected onto the plane from space.
- denotes the location of the robot center on the terrain.
- H denotes a path consisting of a series of states.
- SampleEllipsoid(): sampling is conducted in the elliptical area from the starting point to the ending point.
- RandomSample(): global random sampling.
- FindNearest(T, ): find the nearest point in the tree T to .
- Steer(, ): move a fixed distance from to to obtain new points.
- FindNeighbors(V, ): look for the set of neighboring points of in the set of nodes V.
- FindParent(, ): look for the parent node of in .
- Rewire(T, , ): reconnect the tree T to optimize the path, specifically, in the neighborhood nodes near , checking whether is used as the parent node can reduce the path cost f(, ) of these neighborhood nodes. If possible, reconnect its parent node as .
- InGoalRegion(): determine whether is near the finish line.
- Pos(): given 2D raster point coordinates , returns the corresponding node N.
- Posture Calculation (, , b, c): given the initial angles and of the robot’s front and rear flippers and the resolution b and c of the angle prediction, solve for and under different arm angle conditions to form the set of possible robot states , , , ….
- Configuration Planning (, ): Given two nodes, calculate the best at the node, including the best angles of the front and rear flipper , , the best body height and the best body angle of pitch .
| Algorithm 1 FMP-RRT* (, , k) |
|
- Step 1: Specify the robot’s starting node and the desired target node . At this point, the robot state set at the desired target node has already been calculated by the preceding ’PostureCalculation function’ (line 13 of the pseudocode algorithm).
- Step 2: Identify the optimal state within the target node’s robot state set that minimizes the cost function gall. This state becomes the new node’s .
- Step 3: Upon encountering the next desired target node, calculate the cumulative cost of all previous transition states. Update the optimal state for all nodes, along with the optimal front/rear flippers angles , , chassis height and chassis pitch angle .
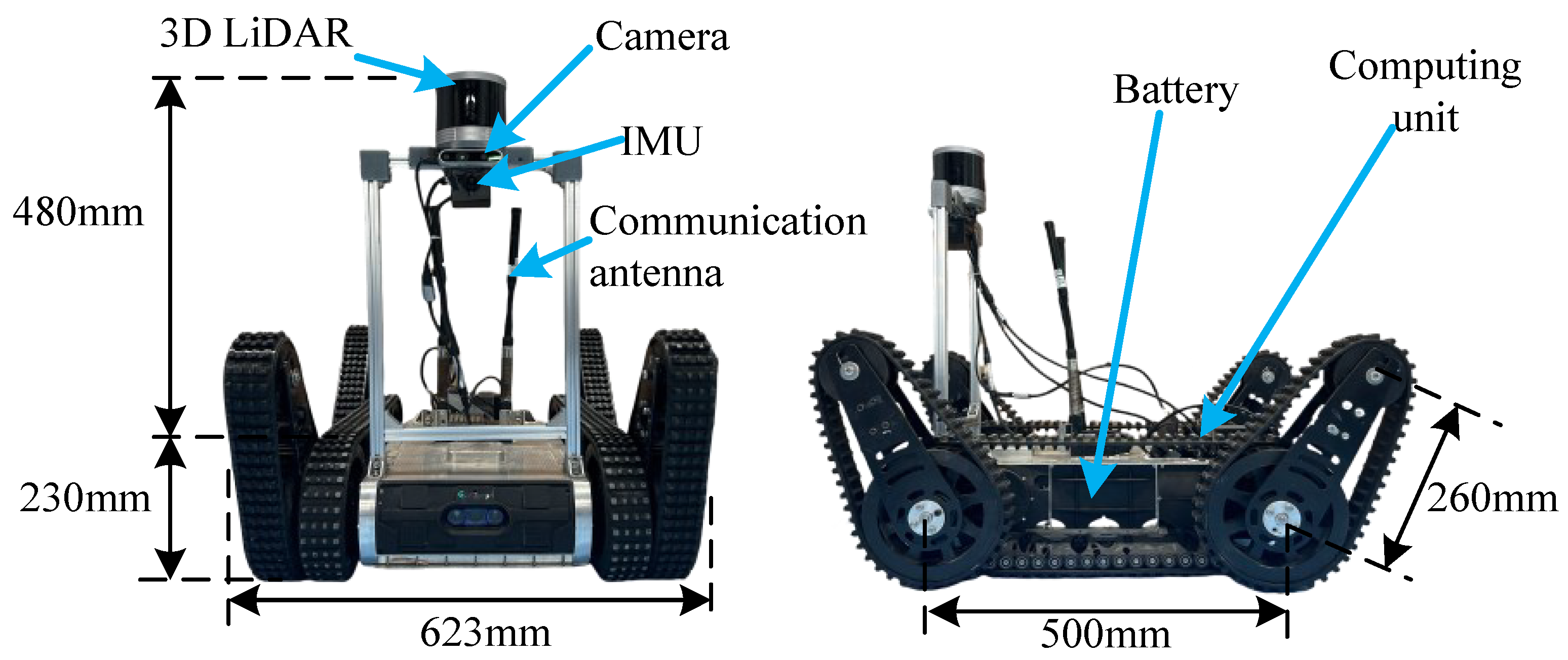
5. Experiments and Results
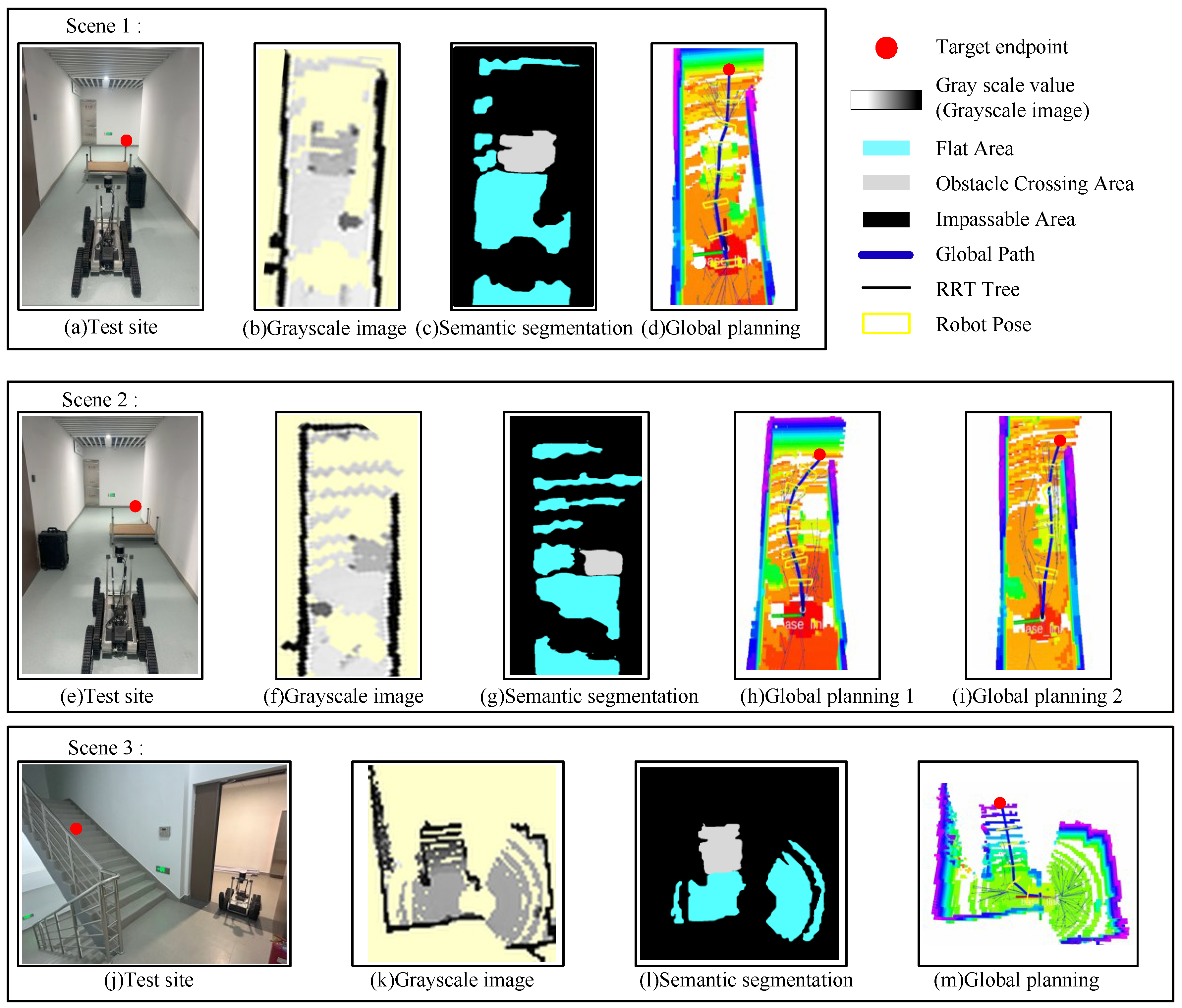
5.1. Map Semantic Segmentation
5.2. Validation of Planning Algorithms
5.3. Movement Quality Analysis
- Time: total movement time.
- Max : the maximum absolute pitch angle, the larger it is, the more likely the robot will fall.
- Rot.Ang: the cumulative absolute pitch angle of the front and rear flippers.
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ATRs | Articulated Tracked Robot |
| RRT | Rapidly-exploring Random Tree |
| FMP-RRT* | Flipper Motion Planning-Rapidly Exploring Random Tree |
| BAM | Boundary Aware Module |
References
- Li, F.; Hou, S.; Bu, C.; Qu, B. Rescue robots for the urban earthquake environment. Disaster Med. Public Health Prep. 2022, 17, e98. [Google Scholar] [CrossRef] [PubMed]
- Niroui, F.; Zhang, K.; Kashino, Z.; Nejat, G. Deep reinforcement learning robot for search and rescue applications: Exploration in unknown cluttered environments. IEEE Robot. Autom. Lett. 2019, 4, 610–617. [Google Scholar] [CrossRef]
- Putz, S.; Simon, J.S.; Hertzberg, J. Move base flex: A highly flexible navigation framework for mobile robots. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3416–3421. [Google Scholar]
- Bansal, S.; Tolani, V.; Gupta, S.; Malik, J.; Tomlin, C. Combining optimal control and learning for visual navigation in novel environments. In Proceedings of the Conference on Robot Learning, London, UK, 18–20 November 2020; Volume 100, pp. 420–429. [Google Scholar]
- Kalogeiton, V.S.; Ioannidis, K.; Sirakoulis, G.C.; Kosmatopoulos, E.B. Real-time active SLAM and obstacle avoidance for an autonomous robot based on stereo vision. Cybern. Syst. 2019, 50, 239–260. [Google Scholar] [CrossRef]
- Yuan, W.; Li, Z.; Su, C. Multisensor-based navigation and control of a mobile service robot. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 2624–2634. [Google Scholar] [CrossRef]
- Xiao, A.; Luan, H.; Zhao, Z.; Hong, Y.; Zhao, J.; Chen, W.; Wang, J.; Meng, M.Q. Robotic autonomous trolley collection with progressive perception and nonlinear model predictive control. In Proceedings of the 2022 IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 4480–4486. [Google Scholar]
- Wermelinger, M.; Fankhauser, P.; Diethelm, R.; Krusi, P.; Siegwart, R.; Hutter, M. Navigation planning for legged robots in challenging terrain. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 1184–1189. [Google Scholar]
- Chavez-Garcia, R.O.; Guzzi, J.; Gambardella, L.M.; Giusti, A. Image Classification for Ground Traversability Estimation in Robotics; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; pp. 325–336. [Google Scholar]
- Krüsi, P.; Furgale, P.; Bosse, M.; Siegwart, R. Driving on point clouds: Motion planning, trajectory optimization, and terrain assessment in generic nonplanar environments. J. Field Robot. 2016, 34, 940–984. [Google Scholar] [CrossRef]
- Oleynikova, H.; Taylor, Z.; Fehr, M.; Siegwart, R.; Nieto, J. Voxblox: Incremental 3D Euclidean signed distance fields for on-board MAV planning. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1366–1373. [Google Scholar]
- Mccormac, J.; Handa, A.; Davison, A.; Leutenegger, S. SemanticFusion: Dense 3D semantic mapping with convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4628–4635. [Google Scholar]
- Tateno, K.; Tombari, F.; Laina, I.; Navab, N. CNN-SLAM: Real-time dense monocular SLAM with learned depth prediction. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6565–6574. [Google Scholar]
- Wellhausen, L.; Dosovitskiy, A.; Ranftl, R.; Walas, K.; Cadena, C.; Hutter, M. Where should I walk? Predicting terrain properties from images via self-supervised learning. IEEE Robot. Autom. Lett. 2019, 4, 1509–1516. [Google Scholar] [CrossRef]
- Colas, F.; Mahesh, S.; Pomerleau, F.; Liu, N.M.; Siegwart, R. 3D path planning and execution for search and rescue ground robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 722–727. [Google Scholar]
- Yuan, Y.; Wang, L.; Schwertfeger, S. Configuration-space flipper planning for rescue robots. In Proceedings of the 2019 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Chemnitz, Germany, 28–31 October 2019; pp. 37–42. [Google Scholar]
- Yuan, Y.; Xu, Q.; Schwertfeger, S. Configuration-space flipper planning on 3D terrain. In Proceedings of the 2020 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 12–15 October 2020; pp. 318–325. [Google Scholar]
- Ohno, K.; Morimura, S.; Tadokoro, S.; Koyanagi, E.; Yoshida, T. Semi-autonomous control system of rescue crawler robot having flippers for getting over unknown-steps. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29–31 October 2007; pp. 3392–3397. [Google Scholar]
- Xu, Z.; Chen, Y.; Jian, Z.; Tan, J.; Wang, X.; Liang, B.L. Hybrid trajectory optimization for autonomous terrain traversal of articulated tracked robots. IEEE Robot. Autom. Lett. 2023, 9, 755–762. [Google Scholar] [CrossRef]
- Sokolov, M.; Afanasyev, I.; Klimchik, A.; Mavridis, N. HyperNEAT-based flipper control for a crawler robot motion in 3D simulation environment. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 16–19 December 2017; pp. 2652–2656. [Google Scholar]
- Pecka, M.; Salansky, V.; Zimmermann, K.; Svoboda, T. Autonomous flipper control with safety constraints. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 2889–2894. [Google Scholar]
- Mitriakov, A.; Papadakis, P.; Kerdreux, J.; Garlatti, S. Reinforcement learning based, staircase negotiation learning: Simulation and transfer to reality for articulated tracked robots. IEEE Robot. Autom. Mag. 2021, 28, 10–20. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder—Decoder with Atrous Separable Convolution for Semantic Image Segmentation; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; pp. 762–778. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNet V3. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Zhang, Z.; Bao, L.; Xiang, S.; Xie, G.; Gao, R. B2CNet: A progressive change boundary-to-center refinement network for multitemporal remote sensing images change detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 11322–11338. [Google Scholar] [CrossRef]
- Deng, W.; Huang, K.; Chen, X.; Zhou, Z.; Shi, C.; Guo, R.; Zhang, H. Semantic RGB-D SLAM for rescue robot navigation. IEEE Access 2020, 8, 221320–221329. [Google Scholar] [CrossRef]
- Chen, B.; Huang, K.; Pan, H.; Ren, H.; Chen, X.; Xiao, J.; Wu, W.; Lu, H. Geometry-based flipper motion planning for articulated tracked robots traversing rough terrain in real-time. J. Field Robot. 2023, 40, 2010–2029. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Chen, K.; Nemiroff, R.; Lopez, B.T. Direct LiDAR-inertial odometry: Lightweight LIO with continuous-time motion correction. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023. [Google Scholar]



| Algorithm | Backbone | MIOU/% | MPA/% | FPS (Frame/s) |
|---|---|---|---|---|
| PSPNet | Resnet50 | 82.37 | 92.35 | 16.67 |
| Mobilenet v2 | 83.51 | 91.88 | 65.89 | |
| UNet | Resnet50 | 79.22 | 91.43 | 10.38 |
| Vgg | 81.23 | 91.68 | 6.35 | |
| DeepLab V3+ | Xception | 78.98 | 91.26 | 10.10 |
| Mobilenet V2 | 84.87 | 92.24 | 25.13 | |
| Mobilenet V3-Large | 91.31 | 93.77 | 29.57 | |
| Mobilenet V3-Small | 88.22 | 93.45 | 57.33 | |
| MB-DeepLab V3+ | 92.44 | 93.98 | 56.45 | |
| Scenario | Method | Time (s) | Max (∘) | Rot. Ang (∘) |
|---|---|---|---|---|
| 1 | Manual operation | 40.48 | 37.28 | 478.36 |
| Autonomous movement | 30.23 | 30.56 | 386.56 | |
| 2-crossing | Manual operation | 42.42 | 37.62 | 435.98 |
| Autonomous movement | 31.44 | 30.88 | 390.23 | |
| 2-avoiding | Manual operation | 28.32 | 0.00 | 0.00 |
| Autonomous movement | 25.14 | 0.00 | 0.00 | |
| 3 | Manual operation | 30.23 | 31.23 | 268.21 |
| Autonomous movement | 26.56 | 29.32 | 196.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Liu, J.; Fu, Y.; Sun, J. A Planning Framework Based on Semantic Segmentation and Flipper Motions for Articulated Tracked Robot in Obstacle-Crossing Terrain. Biomimetics 2025, 10, 627. https://doi.org/10.3390/biomimetics10090627
Zhang P, Liu J, Fu Y, Sun J. A Planning Framework Based on Semantic Segmentation and Flipper Motions for Articulated Tracked Robot in Obstacle-Crossing Terrain. Biomimetics. 2025; 10(9):627. https://doi.org/10.3390/biomimetics10090627
Chicago/Turabian StyleZhang, Pu, Junhang Liu, Yongling Fu, and Jian Sun. 2025. "A Planning Framework Based on Semantic Segmentation and Flipper Motions for Articulated Tracked Robot in Obstacle-Crossing Terrain" Biomimetics 10, no. 9: 627. https://doi.org/10.3390/biomimetics10090627
APA StyleZhang, P., Liu, J., Fu, Y., & Sun, J. (2025). A Planning Framework Based on Semantic Segmentation and Flipper Motions for Articulated Tracked Robot in Obstacle-Crossing Terrain. Biomimetics, 10(9), 627. https://doi.org/10.3390/biomimetics10090627







